Automated Surgical Approach Planning for Complex Skull Base Targets: Development and Validation of a Cost Function and Semantic At-las

Abstract

Successful multidisciplinary treatment of skull base pathology requires precise preoperative planning. Current surgical approach (pathway) selection for these complex procedures depends on an individual surgeon’s experiences and background training. Because of anatomical variation in both normal tissue and pathology (eg, tumor), a successful surgical pathway used on one patient is not necessarily the best approach on another patient. The question is how to define and obtain optimized patient-specific surgical approach pathways? In this article, we demonstrate that the surgeon’s knowledge and decision making in preoperative planning can be modeled by a multiobjective cost function in a retrospective analysis of actual complex skull base cases. Two different approaches— weighted-sum approach and Pareto optimality—were used with a defined cost function to derive optimized surgical pathways based on preoperative computed tomography (CT) scans and manually designated pathology. With the first method, surgeon’s preferences were input as a set of weights for each objective before the search. In the second approach, the surgeon’s preferences were used to select a surgical pathway from the computed Pareto optimal set. Using preoperative CT and magnetic resonance imaging, the patient-specific surgical pathways derived by these methods were similar (85% agreement) to the actual approaches performed on patients. In one case where the actual surgical approach was different, revision surgery was required and was performed utilizing the computationally derived approach pathway.

Introduction

Skull base pathology is challenging to treat because of the anatomical location adjacent to critical structures. There are greater than 50 well-recognized open and endoscopic surgical approaches, and it is not clear which approach may be best for a specific patient with a unique tumor.¹ Each surgical approach is associated with risks to critical structures, but they are not all equal in the degree of risk imposed on a given structure (eg, optic nerve) and provide different accesses that may be better in certain situations based on the size and specific location of the pathology. The risks of skull base surgeries include stroke; intracranial hemorrhage; cranial nerve injury, including blindness; and Cerebrospinal Fluid (CSF) leak, which can occur with a frequency higher than 17%.^2,3

In the past few decades, technological advances in optics, materials, and surgical navigation permit more endoscopic surgical approaches to reach locations in the skull base, thus dramatically reducing morbidity compared with open craniotomies that require a large skin incision and retraction of the brain. Although these operations provide benefits to patients through faster recovery, shorter hospital stays, better cosmesis, and improved quality of life after surgery, the required skills to perform the procedure are highly complex because of the density of critical neuromuscular structures and the narrow anatomical confines in this region.^4–7 Furthermore, as the number of endoscopic surgical options has increased, the challenge of which surgical approach to choose is even greater. A method to systematically analyze and select patient-specific optimal surgical approach(es) is needed to improve patient care, reduce complications, and improve morbidity.⁸

A cost function and optimization algorithm to plan complex skull base surgeries is proposed. The objective is not only to better understand surgical pathway selection, but also to improve and track clinical outcomes with objective data, and aid in surgical education and the design of new surgical approaches.

Skull base preoperative planning consists of identifying the lesions and selecting an appropriate surgical pathway for treatment. The surgical pathway is a 3D volume that provides a conduit through which surgical instruments are inserted and the surgical task (eg, lesion removal or bone reconstruction) is performed at the target site. Selection of a surgical pathway is critical and correlates directly with the outcome of the surgery.⁹ Through the selected surgical approach, the surgeon must gain sufficient access to the target site to perform the surgical task (ie, complete tumor removal or incisional biopsy). The selected surgical approach travels through (or adjacent to) structures that are removed or temporarily retracted. It is important to select pathways that are least disruptive and, therefore, reduce impact on morbidity. Some structures are acceptable to remove or retract (eg, paranasal sinuses), whereas other structures such as the optic nerve or carotid artery will cause permanent and serious complications if they are injured. Pathway selection is driven by many variables, including patient anatomy, the location and type of the lesion, and the indication for surgery.¹⁰

Surgical approach selection decisions are often made at a multidisciplinary tumor board conference. In these meetings, clinical history and preoperative images of the patient are typically reviewed in 2D slices (standard axial, coronal, and sagittal planes). The surgeon is rarely able to view the segmented pathology in 3D with virtual endoscopy. Instead, the surgeon relies on years of experience to interpret the 2D radiographic images. This process is challenging and time-consuming and may be error prone for new surgeons. Furthermore, the lack of standardization in selecting the surgical pathways makes the process a difficult task.

Often, the selected surgical pathway is influenced by surgical training, experience, and background of the surgeon. Typically, the chosen pathway is only one of a subset of all available surgical approaches (or combination of approaches). As a result, there are potentially advantageous approaches that are not considered and/or offered to the patient. There is a need to introduce objective metrics into the process of surgical approach selection.

The contribution of this study is to define a cost function to compare and rank surgical pathways to treat skull base lesions and to determine if the computationally derived surgical approach pathways correlate with those chosen by a panel of expert surgeons.

Methods and Materials

Approval was obtained from University of Washington Institutional Review Board. A relative value for voxels on preoperative imaging was defined in focus group sessions with 3 surgeons. For this initial work, values were assigned for bone in sinuses, bone adjacent to orbit, bone along anterior cranial fossa, air, orbit, globe, extraocular muscles, optic nerve, internal carotid artery, nasal bones, nasal septum (cartilage and bone), and soft tissue not contained in already segmented structures. In computing cost functions for a surgical approach, the relative cost of the pathway was defined by the number of voxels it traverses and the voxel value.

Patient-Specific Treatment

One of the inputs to the decision making of the surgical approach is the patient’s preoperative images. The selected surgical pathway is specific to the patient based on the unique anatomy and location of the pathology. In this study, all necessary structures—both bone and soft tissue, as mentioned above—were segmented using patients’ preoperative computed tomography (CT) and magnetic resonance imaging (MRI) scans with semiautomatic or automatic methods.^11–13

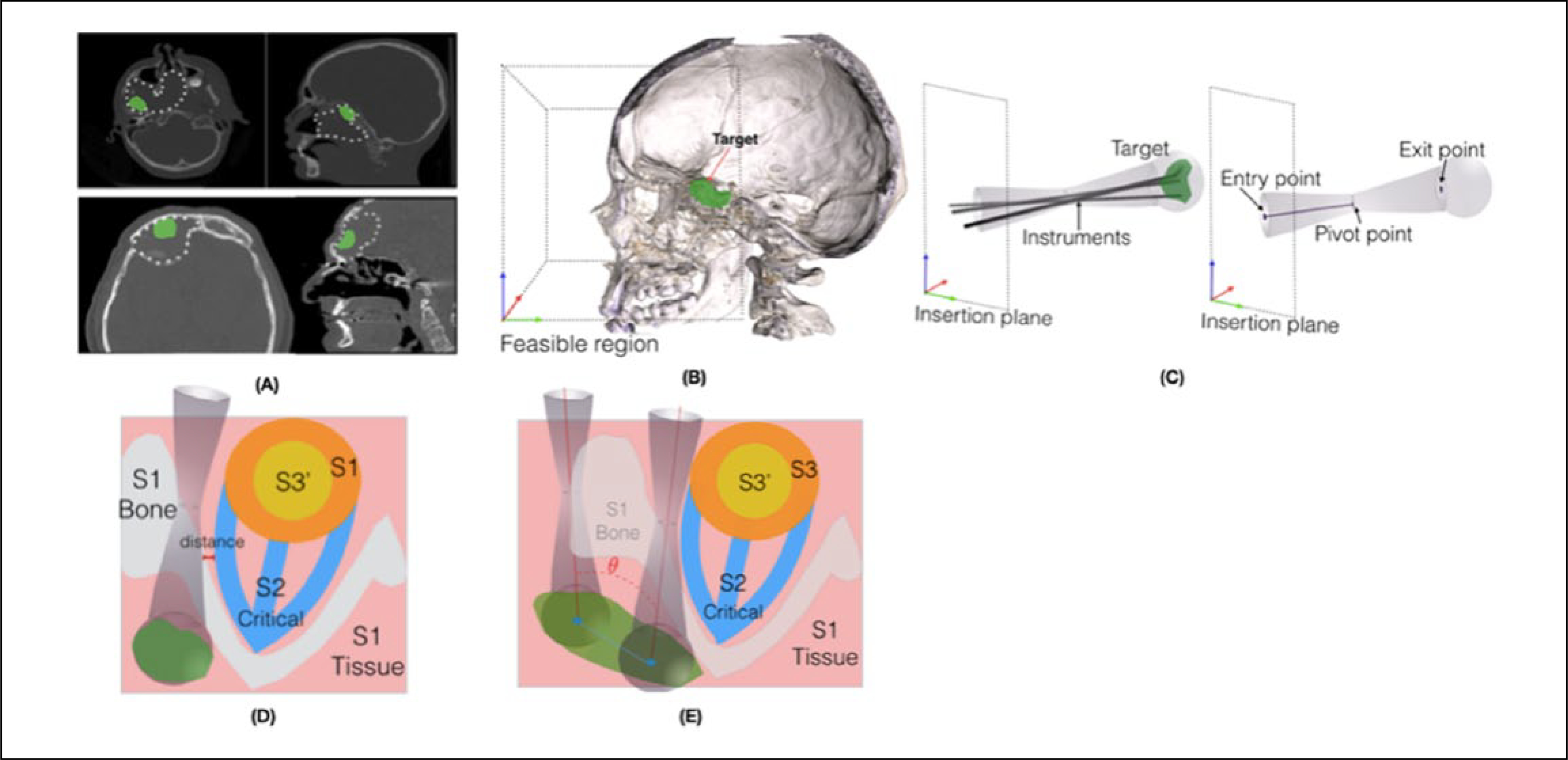
Three surgeons evaluated the CT and MRI scans, which each contained skull base pathology. They agreed on subvolume (or subvolumes) of the tumor that represented the challenging region(s) to access surgically. Therefore, a case could have multiple targets, and an independent plan was made for each subregion of interest (Figure 1A).

Figure 1.

A. Surgical target visualization for an example case: the target used in optimization is the subregion of the pathology that is surgically challenging to access. B. Insertion plane and volume boundary conditions in which a surgical approach can be selected. C. The surgical pathway model, biconical shape with 6 parameters. D. Schematic of the cost function for a single pathway. E. Schematic of the cost function for optimizing 2 simultaneous pathways.

Surgical Pathway Model

Surgical pathways are often named after the entrance region that begins the surgical pathway (eg, transnasal, transmaxillary). An insertion zone was defined as a plane parallel to the coronal plane and covered the entire facial region to consider all possible pathway candidates. The feasible region was a cuboid that contained the insertion plane and a parallel plane distal to the target to contain the target completely (Figure 1B).

Surgical pathways were defined as cylindrical or biconical shapes with diameters of 10 mm at either end and 8 mm at the pivot location where 1 or 2 instruments can travel inside the pathway based on current instrument size for endoscopic skull base surgery.¹⁴ The distance from the entry to pivot location of the pathway was a variable and could be outside or inside of the skull. This created a segment of a cone or a biconical shape, enabling the algorithm to produce a variety of pathway shapes. A spherical volume was added to the end of the pathway to represent the workspace of instruments, including those with angled tips. In total, a surgical pathway was characterized by 6 parameters: entry point on the insertion plane (2D position), end point on the target (3D position), and the distance of the entry point to the pivot point (Figure 1C).

Cost Function and Optimization Method

The surgical decision making for complex skull base surgeries can be formulated as a multiobjective cost function. The structures inside the feasible region were categorized into 3 groups (Figures 1D and 1E).

1. Bone and soft tissue not included in critical structures listed below: removal of these structures may be necessary, often to gain access to the target; however, patients recover from such a removal. Structures inside this region may have different morbidity values. The morbidity cost assignments were made based on clinical judgment of skull base surgeons and the consequences of removing such a region.

2. Critical structures (eg, optic nerve, orbit, extraocular muscles, carotid artery): Removal of these structures will cause a serious complication for the patient. To ensure the patient’s safety, the minimum distance of the surgical pathway (2 mm) from these structures was defined as a hard constraint.

3. Deformable tissues (eg, eye globes, septum): because of the elasticity property of these structures, a surgical pathway may intersect with these structures to a degree. During the surgery these structures can be retracted to allow instrument movement. To model the deformability of these organs, these structures were divided into critical and noncritical tissue. This division is based on the amount of deformability of the organ and the size of the pathway. The critical segment of these structures was defined as a hard constraint. When the noncritical constraint is violated, the surgical pathway could overlap the structure even by deforming it during the surgery.

There are different approaches to multiobjective optimization, such as the following: (1) combining the individual objective functions into a single composite function, (2) providing the decision makers with a set of promising solutions based on the objectives, or (3) keeping one objective and defining the remainder of the objectives as constraints.¹⁵ In this work, we used the first 2 approaches with methods such as weighted sum and finding the Pareto optimal set.^16,17

The key difference between these methods can be found in how and when the surgeons’ (as the decision makers’) preferences are brought into the process. For the weighted-sum method, the surgeon’s preferences are the weights of each objective. However, in the second method, the surgeons are provided with a set of surgical pathways rather than 1 optimized approach, and therefore, the final pathway is selected based on the surgeon’s preferences.

Weighted-Sum Preoperative Planning

The weighted-sum method was used to obtain single or 2 jointly optimized surgical pathways (Equation 1). The weights were assigned by the surgeons based on their preference and patient health history; the sum of weights = 1. For instance, bone removal (nasal bone 0.2 and all other bony structures 0.2), tissue removal (0.2), target removal (0.2), distance to critical structure (0.1), and globe retraction (0.1). Lower weights were assigned to distance to critical structures and globe retraction because of the hard constraints for both these objectives.

$$\begin{gathered} \mathrm{Min}f(X)=\sum _{a=1}^{N_a}{w}_a\left(P\cap S_a\right)-w_b(P\cap T+O\cap T) \\ -w_c\sum _{i=1}^{n_2}\left({\mathrm{Dist}}_{\min }\left(S_{2_i},P\right)\right), \end{gathered}$$ (1)

such that

$$P\cap S_{3^{\prime }}=\varnothing ,$$

$${\mathrm{dist}}_{\min }\left(P,S_{2_i}\right)>d_m\forall j\in \left\{1,\dots ,n_2\right\},$$

where P is the pathway, W_a,b,c the weight associated with each objective, S_a the a-th object in a specific category, T the target, O the spherical volume of the operation region, $S_{3^{\prime }}$ the critical segment of deformable structures, d_m the minimum safe distance of path to critical structures, N_a the number of different category of structures, and n_i the number of regions in each category.

In the case of 2 simultaneous surgical pathways, the cost function had the same objectives as for the single pathway; however, 2 more objectives were added: (1) To avoid collision of the surgeon’s hands at the entry points of the pathways, the angle between the pathways should be considered and maintained at 20° or more⁹; (2) to ensure complete removal of lesions, each pathway should cover nonoverlapping regions of the target, and therefore, the distance between 2 exit points of the pathways must be maximized while the hard constraints are satisfied.

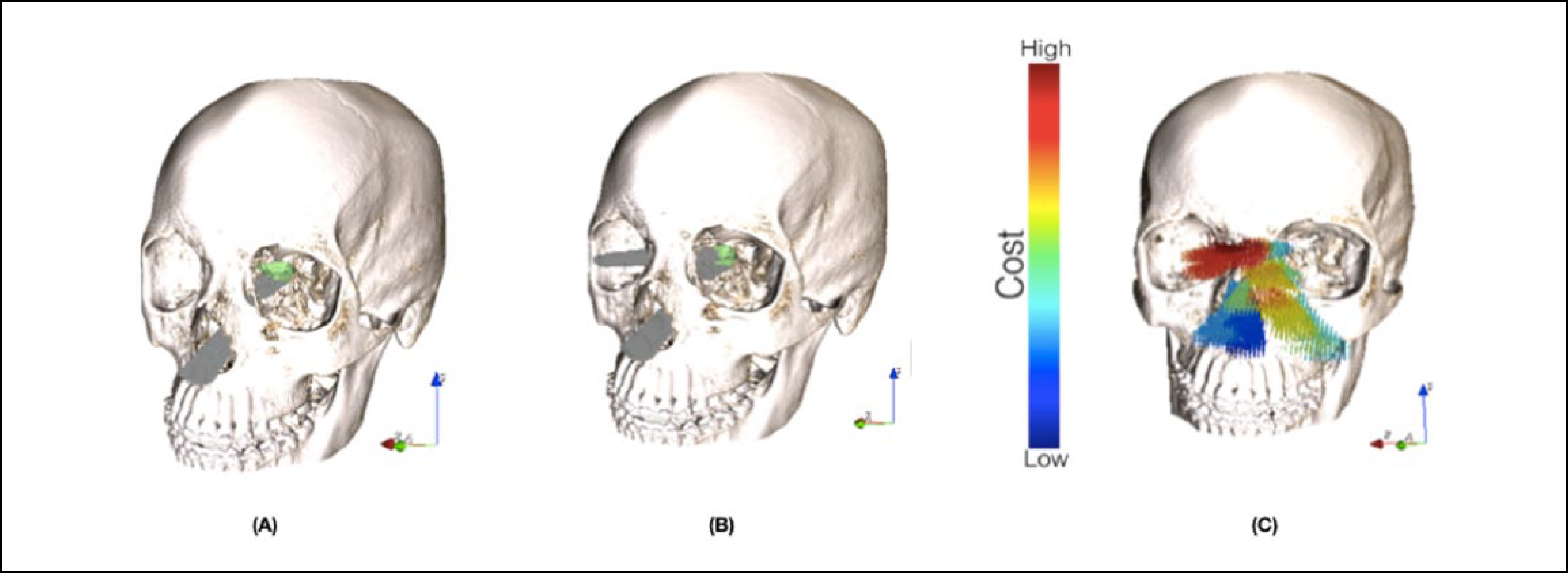
Because different objective functions can have different units and magnitudes, normalization was required. Each objective function is normalized by the differences of optimal function values in the estimated Utopia and Nadir points.¹⁸ The described cost function is nonconvex and discrete; therefore, numerical analysis using simulated annealing was performed to obtain the optimized surgical pathways (Figures 2A and 2B).¹⁹

Figure 2.

A. Optimized surgical pathway using weighted-sum–based cost function for an example case. B. Two simultaneously optimized surgical pathways using weighted-sum–based cost function for an example case. C. Pareto-optimal set solution sorted based on a single objective, the amount of bone removal for an example case (blue corresponds to low cost and red corresponds to high cost).

Pareto-optimal Preoperative Planning

In multiobjective optimization (Equation 2), a vector X* is in the Pareto-optimal set if all other vectors X in the feasible space have a higher value for at least one of the objective functions or have the same value for all the objective functions. A Pareto optimal solution cannot be improved with respect to any objective without reducing at least 1 other objective. Often, in multiobjective optimization, determining the entire Pareto optimal set is not feasible and, therefore, the solution is approximated by the “best-known Pareto set” that represents the true Pareto optimal set as much as possible.^20,21 In this work, Genetic algorithm (NSGA-II) was used to approximate the Pareto optimal set (Figure 2C).²²

$$\text{Min}{f}_n(X)=n=1,2,3,$$ (2)

$f_1=P\cap S_{Bone}$ is the amount of bone removal,

$f_2=P\cap S_{\text{Tissue}}$ is the amount of tissue removal, and

f₃ = −dist_min (P,S_Critical ) is the distance to critical structures, such that

$$P\cap S3\prime =\varnothing ,$$

$${\mathrm{dist}}_{\min }\left(P,S_{2_i}\right)>d_m\forall j\in \left\{1,\dots ,n_2\right\}.$$

Results

Cost Function Validation

Using deidentified preoperative CT scans of 3 cases, 15 different pathways were generated (5 for each patient) based on the defined cost function. The pathways (5 for each patient) were selected to sample the range of cost values from lowest to highest. Surgeons were presented with the preoperative scans, the target, and the 5 selected surgical pathways (without knowledge of the cost function values).

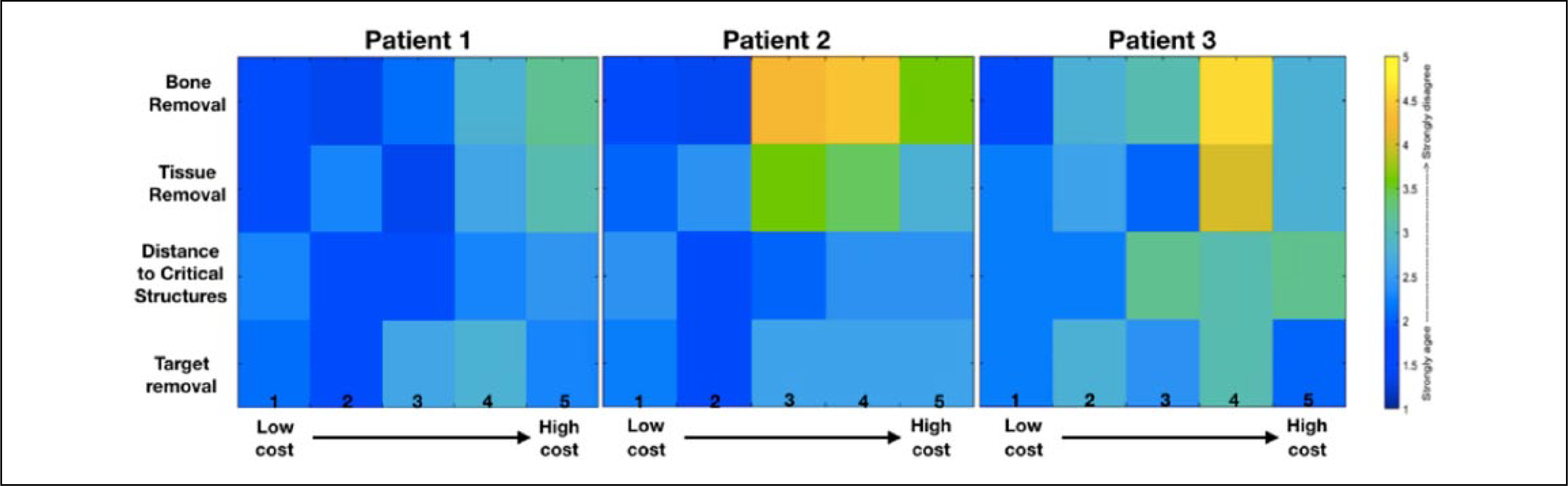
A questionnaire was administered to 5 expert skull base surgeons from the University of Washington and Harborview Medical Centers (Seattle, WA), and they were asked to assess a given pathway on a Likert scale (strongly agree = 1 to strongly disagree = 5). For a selected case, the surgeons were asked to rate their agreement with the following statements: (1) “The amount of bone removal in this path is clinically feasible and does not cause significant risk.” (2) “The amount of soft tissue removal/retraction in this path is clinically feasible.” (3) “Considering the target location, the path has reasonable distance to the critical structures—optic nerve or extraocular muscles.” (4) “The degree of access for the target removal is reasonable with this path.”

The results showed that surgeons selected lower-cost pathways (based on the cost function) as the more reasonable approach to treat the defined target. Specifically, 90% to 95% of all the surgeons’ responses to statements were strongly agree or agree for the first 2 lowest-cost pathways identified by the algorithm in case 1. The other 2 cases were in agreement: 85% to 90% and 65% to 80% of the cases (Figure 3).

Figure 3.

Surgeons’ responses (strongly agree to strongly disagree) to the studied objectives of the surgical pathways with different cost values.

Comparison of Optimized and Manual Planned Surgical Pathways

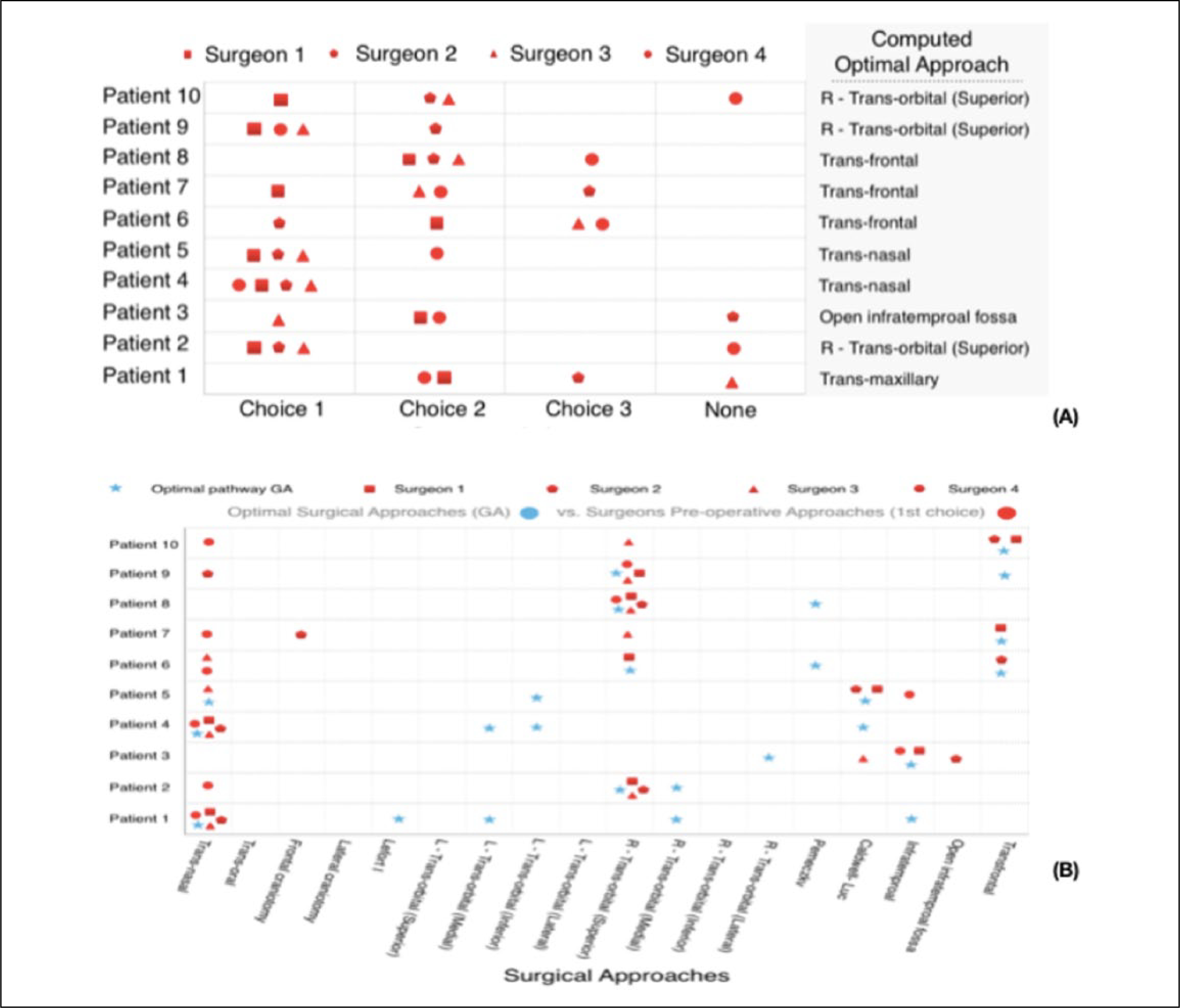
In a second study, the optimized pathways were compared with the surgeons’ manually planned approaches. Four expert surgeons were presented with 10 deidentified preoperative CT scans with manually segmented pathology to serve as the surgical target. The participating surgeons were asked to plan the treatment by selecting their top 3 approaches from a set of 24 pathways described in the literature.^14,23 The approaches were the following: transnasal, transoral, transorbital (superior, inferior, lateral, and medial), transmaxillary (Caldwell-Luc, inferotemporal), frontal craniotomy, pterional craniotomy (lateral craniotomy), open infratemporal fossa (Fisch type C, D), Lefort I, supraorbital minicraniotomy (Perneczky), transfrontal bone (osteoplastic flap, coronal incision). The surgeons were not informed of the computationally derived optimal approaches.

The optimized approach (single pathway) computed by the weighted cost function belonged to the top 3 surgeon-selected approaches in 36/40 (90%) of case evaluations (4 surgeons, 10 cases each). Among these 36 approaches, 31 were the surgeon’s first or second selection. In the 4 patients for which one surgeon’s set of 3 approaches did not contain the computed optimized approach, the optimal approach was identified in the top 3 chosen by the other 3 surgeons (Figure 4A).

Figure 4.

A. Ranking of surgical approaches by surgeons, compared to the computationally derived optimal approach. A symbol is placed where each surgeon ranked the computed optimal in their personal ranking. B. Pareto optimal set of surgical pathways versus surgeon’s first choice for each case.

Furthermore, the Pareto set of optimal surgical pathways, obtained using the multiobjective cost function, were categorized according to the above approaches and were compared to the surgeons’ top 3 selections. The results showed that 70% of surgeons’ top ranked (first choice) approaches were in the Pareto optimal set (Figure 4B).

Comparison of Optimized With Actual Surgical Pathways Performed on the Patient

In a third study, the computed optimized pathways were compared postoperatively with the actual surgical pathways performed on the patients using preoperative and postoperative images. The cases analyzed in this work were classified as “challenging,” requiring multidisciplinary care. For each of these cases, the identified target region contained only those parts of the pathology that were judged difficult to access. The remainder of the lesion was treated as general tissue. If a patient had 2 difficult-to-access regions, at least one of the computed optimized pathways was similar to the actual performed approaches in 85% of cases.

Subjective Evaluation of 2 Simultaneously Optimized Surgical Pathways

Two simultaneous pathways are often used to gain access to clinically challenging targets, which enables multiple approach angles and improved visualization and instrumentation. This was tested for quality and feasibility with the weighted-sum cost function with additional constraints, which were necessary to prevent a duplicate result in spatially similar pathways.

Surgeons were presented with 2D and 3D visualizations of the target location, the 2 jointly optimized pathways, and corresponding metrics: (1) target removal, the number of voxels inside the pathways; (2) angle between the pathways, the angle between the center-lines of 2 pathways; (3) bone removal, the number of bone voxels inside the 2 pathways; (4) tissue removal, the amount of tissue removal inside the 2 pathways; and (5) distance to critical structures, the minimum Euclidean distance of the pathways to optic nerves and extraocular muscles.

For 5 cases depicting skull base pathology, considering the target locations, the surgeons were asked to assess each approach combination for clinical validity and feasibility. The planned pathways were rated as “clinically valid” and “feasible” to access and remove the pathology in all cases (Table 1). In 3 of 5 cases, the surgeons agreed with both surgical approaches in concert. In the other 2 cases, they preferred a different approach for 1 of the 2 pathways. In these 2 cases, the optimized approaches scored better on metrics such as the volume of bone and tissue removal and distance to critical structures compared to the surgeon preferred approach.

Table 1.

Subjective Rating of 3 Surgeons for Simultaneously Optimized Surgical Pathways for 5 Patients.

Data	Approaches	Target Removal (voxels)	Angle Between Pathways (degrees)	Bone removal (voxels)	Tissue Removal (voxels)	Distance to Optic Nerves (mm)	Distance to Extraocular Muscles (mm)	Surgeons Rating
Patient 1	Transnasal Transnasal	945	89.2	0	208	21.4	15.2	Clinically valid
Patient 2	Transnasal Transnasal	1138	42.2	1	300	16.9	12.6	Clinically valid
Patient 3	Transorbital Transorbital	1042	61.75	0	133	8.3	3.0	Clinically valid
Patient 4	Transorbital Transmaxillary	1753	25.27	207	681	11.70	3.0	Clinically valid
Patient 5	Transnasal Transorbital	1672	36.04	91	619	5	4.5	Clinically valid

Discussion

The lack of standardization for surgical pathway selection results in major challenges for the development of new surgical approaches, the ability to accurately study clinical outcomes with fewer variables, and trainee education. Outcome analysis in skull base surgery is challenging because of the lack of objective account of the procedure. Compared to radiation oncology, for example, where a precise dose of radiation is administered to a pre-determined region, a surgical intervention has no quantifiable metric other than postoperative imaging. Defining the preoperative surgical pathway planning as an optimization problem will shift a process that is subjective, difficult to articulate, and variable to a method that is repeatable, understandable, and quantifiable. In this work, a cost function was developed to assign to individual voxels on the preoperative imaging. This was assigned by surgeons for the specific application of skull base surgery and included relevant anatomy.

In validation of the cost function, computationally derived surgical pathways of different cost values for specific target locations were presented to surgeons who agreed that the low-cost surgical pathways were better approaches to treat the target pathway. One exception was that surgeons preferred transnasal approaches (even with a higher cost) over transorbital approaches. This is understandable because transorbital approaches have been introduced only recently and are only performed in advanced skull base treatment centers.

In comparison to the optimized surgical pathways with manual planning using the weighted-sum cost function approach (1 out of 3) surgeons’ top approaches matched with the computationally derived approaches 60% of the time. For the other 40%, it is likely that there was no agreement because of the high frequency of transorbital approaches in the optimization results, which were only recently described for skull base targets. In addition, the surgeons selected the approaches individually. A different approach pathway may have been selected by the surgeon after discussing the case with a team of surgeons in a tumor board meeting.

Furthermore, 70% of surgeons’ first manually selected approaches to treat the target was in the Pareto optimal set obtained by optimizing the multiobjective cost function. This suggests that the optimized approaches were clinically valid and that the multiple objectives and constraints were reasonable.

In comparison to the optimized and actual surgical pathways performed on the patients, the actual approaches were similar to the optimized pathways except for 1 patient. In this case, the computed optimized approaches were transfrontal (using weighted-sum and Pareto optimal set) and transorbital (only on Pareto optimal set). However, the surgeon’s approach was transnasal initially, but because of a postoperative complication (CSF leak), a transorbital approach was subsequently used for revision. The optimized surgical pathways were reasonable because of the tumor location (immediately posterior to the frontal bone) and a large amount of frontal bone erosion (caused by the tumor). Specifically, the small thickness of eroded frontal bone, low amount of tissue removal (only skin), large target, and large distance to critical structures made the transfrontal approach a low-cost surgical pathway. In this specific case, one reason that the surgeon selected a transnasal approach could be the cosmetic effect of accessing the target by removal of the frontal bone and performing coronal incision in the scalp.

One limitation of this method is how to define and implement the concept of cosmetics in the cost function. The obtained surgical pathways in this study were similar to those described in the literature and some that were only recently described. These approaches are novel and only performed at advanced skull base centers. The model will improve with more data, including a wider variety of target locations. For example, in one case, the computer model suggested a transnasal approach to access midline anterior cranial fossa, and for lateral lesions, it suggested novel transorbital and transoral approaches to the infratemporal fossa. In addition, the expert surgeon participants had different training backgrounds, and it would be interesting to analyze the preoperative planning of a more diverse group of surgeons from different institutions. The effect of different institutions was recognized on surgical skills of surgeons when performing dry-lab manipulation tasks.²⁴ Although different centers will have variable preferences for surgical approaches based on training background of surgeons, in an ideal situation, this surgical bias would be excluded. In this way, an optimized surgical approach—or short list of best approaches—is generated for each individual skull base lesion and patient. If the surgeon is not trained in one of those approaches, and there is not a good alternative, referral to an advanced center may be indicated because skull base pathology is extremely complex to treat and is associated with high morbidity.

The optimized surgical approaches obtained by different methods (single, 2 simultaneously, or Pareto optimal set) had lower cost compared to traditional approaches based on bone removal volume, soft-tissue removal volume, and proximity to critical structures; however, extensive analysis and cadaver testing is required to validate the approaches before using these approaches on the patient. Other methods such as simulation, 3D printing of specific anatomy, and performing the simulated surgeries with the computed pathways on the 3D printed materials or on cadavers can be used to validate the approaches.

As computer methods like those described here become more refined, additional work is needed to provide intraoperative guidance to direct the surgeon to follow the computed pathways. We are encouraged by the results to date that demonstrate that a relatively simple cost function can derive surgical approaches that are clinically valid and even produce surgical approaches that have only recently been described in the literature. These computational methods will not replace the surgeon’s decision making, but it will aid the surgeon and provide excellent visualization and metrics. The algorithmic and quantified approach will provide the research tools to advance the field.