Sample size calculation in three-level cluster randomized trials using generalized estimating equation models

Abstract

Three-level cluster randomized trials (CRTs) are increasingly used in implementation science, where 2fold-nested-correlated data arise. For example, interventions are randomly assigned to practices, and providers within the same practice who provide care to participants are trained with the assigned intervention. Teerenstra et al proposed a nested exchangeable correlation structure that accounts for two levels of clustering within the generalized estimating equations (GEE) approach. In this article, we utilize GEE models to test the treatment effect in a two-group comparison for continuous, binary, or count data in three-level CRTs. Given the nested exchangeable correlation structure, we derive the asymptotic variances of the estimator of the treatment effect for different types of outcomes. When the number of clusters is small, researchers have proposed bias-corrected sandwich estimators to improve performance in two-level CRTs. We extend the variances of two bias-corrected sandwich estimators to three-level CRTs. The equal provider and practice sizes were assumed to calculate number of practices for simplicity. However, they are not guaranteed in practice. Relative efficiency (RE) is defined as the ratio of variance of the estimator of the treatment effect for equal to unequal provider and practice sizes. The expressions of REs are obtained from both asymptotic variance estimation and bias-corrected sandwich estimators. Their performances are evaluated for different scenarios of provider and practice size distributions through simulation studies. Finally, a percentage increase in the number of practices is proposed due to efficiency loss from unequal provider and/or practice sizes.

1 |. INTRODUCTION

A cluster randomized trial (CRT) design is utilized when the randomization at the subject level is not practical. The unit of randomization might be hospitals, clinics, classrooms, and so on. Moons et al showed that the comparison in impact studies is scientifically strongest when a CRT is considered.¹ Using a prediction model on improved health outcomes and cost-effectiveness of care, Moons et al indicated that its impact should be assessed ideally in CRTs.² Dissemination and implementation (D&I) research is an emerging field in health and public health. Implementation strategies are central to D&I research and thus CRT designs have an appealing feature compared with the patient-level randomized trials. Furthermore, CRTs are greatly needed for effectiveness research from efficacy science to real world practice.^3,4 Therefore, there has been growing interest in conducting CRTs.^5–11 Such trials have two levels: study subjects are nested into clusters. As noted, three-level CRTs have been considered as well. For example, interventions are randomly assigned to practices. Providers within the same practice who provide care to participants are trained with the assigned intervention. These CRTs have a three-level structure: providers could be correlated within a practice, and the participants could be correlated within a provider. Another example is a study conducted by Faggiano et al.¹² They investigated the effect of a school-based substance abuse prevention program through a CRT, where schools (“clusters”) were randomly assigned to one of experimental arms. The primary outcomes of the study were behavioral endpoints from the students (“subjects”) with data collected at baseline, 6-month and 18-month follow-up (“evaluations from multiple time points”). As such, measurements across the different time points are correlated within a student and students are correlated within a school. Hereafter we use a CRT with practice, provider, and participant levels as the three-level example.

Sample size calculation plays an important role at the stage of study design for investigators. In the design of two-level CRTs, the cluster sizes are often assumed to be identical across clusters. However, equal cluster sizes are not guaranteed in practice. The relative efficiency (RE) of unequal vs equal cluster sizes has been investigated when testing the treatment effect.^13–16 Consequently, more clusters are needed to cover the efficiency loss due to unequal cluster sizes. In the design of three-level CRTs, the required sample sizes include the number of practices m, practice size (number of providers per practice) n_i, i = 1, · · ·, m and provider size (number of participants per provider) k = 1, · · ·, K_ij. Heo et al considered a mixed-effects linear regression model for continuous outcomes, used a test statistic based on maximum likelihood estimates, and derived a closed form power function and formulae for sample size determination required to detect a treatment effect on outcomes.¹⁷ Within the generalized estimating equations (GEEs) approach, Teerenstra et al proposed a three-level (nested) exchangeable correlation structure that accounts for two levels of clustering and derived a sample size formula for both continuous and binary outcomes assuming equal practice sizes n_i ≡ n and equal provider sizes K_ij ≡ K.¹⁸

In our previous work we utilized GEE models to test the treatment effect in a two-group comparison for continuous, binary, or count data in two-level CRTs.¹⁵ In this article we extend this work to three-level CRTs with an assumption of K_ij ≡ K_i. Given the nested exchangeable correlation structure, we derive the asymptotic variances of the estimator of the treatment effect for different types of outcomes. RE is defined as the ratio of variance of the estimator of the treatment effect for equal provider size and equal practice sizes to unequal provider size and/or unequal practice sizes. A simpler formula of RE with continuous, binary, and count outcomes is obtained. However, using the covariance estimator obtained from GEE can inflate type I error rates when the number of clusters is small.^19–21 Therefore, we also consider three-level CRTs with a small number of practices in a two-group study for all three kinds of outcomes. We use two bias-corrected sandwich estimators, an MD-corrected estimator proposed by Mancl and DeRouen¹⁹ and FG-corrected estimator proposed by Fay and Graubard,²² and derive the variances of both estimators of the treatment effect used in sample size calculation. The same definition of RE is used and REs are investigated for several scenarios of provider and practice size distributions through simulation studies. Finally, we propose the percentage increase in number of practices due to efficiency loss from unequal provider and/or practice sizes.

The outline of this article is as follows. In Section 2, we briefly summarize the GEE methods proposed by Liang and Zeger,²³ introduce the “nested exchangeable” correlation structure, and derive the variance of the estimator of the treatment for three kinds of outcomes (continuous, binary, and count) in a two-group comparison. Section 3 shows the variance of the estimator of the treatment effect in two bias-corrected sandwich estimators for three different kinds of outcomes. Section 4 introduces the REs of unequal vs equal provider and/or practice sizes, presents the simulation designs about provider and practice size distributions and provides the results of REs through simulations. In Sections 5 and 6, we propose the algorithm and illustrate how to increase the number of practices due to efficiency loss through a real example. The last section discusses the limitations and directions for future research.

2 |. STATISTICAL GEE MODEL

Let Y_ijk be a response from participant k = 1, · · ·, K_ij, for provider j = 1, · · ·, n_i in practice i = 1, · · ·, m. Let $X_{ijk}={\left(X_{ijk1},\cdots ,X_{ijkp}\right)}^{\prime }$ be a covariate vector and μ_ijk = E(Y_ijk|X_ijk) be a marginal mean response given X_ijk. The marginal model is $g\left({\mu }_{ijk}\right)={\mathit{X}}_{ijk}^{\prime }\mathit{\beta }$. Let ${\mathit{Y}}_{ij}=\left(Y_{ij1},\cdots ,Y_{ij{K}_{ij}}\right)$, ${\mathit{\mu }}_{ij}=\left({\mu }_{ij1},\cdots ,{\mu }_{ij{K}_{ij}}\right)$, and ${\mathit{X}}_{ij}=\left({\mathit{X}}_{ij1},\cdots ,{\mathit{X}}_{ij{K}_{ij}}\right)$ be the 1 × K_ij response vector, 1 × K_ij marginal mean response vector, p × K_ij covariate matrix of provider j in practice i, respectively. Let ${\mathit{Y}}_i={\left({\mathit{Y}}_{i1},\cdots ,{\mathit{Y}}_{i{\text{n}}_i}\right)}^{\prime }$, ${\mathit{\mu }}_i={\left({\mathit{\mu }}_{i1},\cdots ,{\mathit{\mu }}_{i{\text{n}}_i}\right)}^{\prime }$, and ${\mathit{X}}_i=\left({\mathit{X}}_{i1},\cdots ,{\mathit{X}}_{i{n}_i}\right)$ be the matrices of responses, marginal mean responses, and covariate of the providers in practice i, respectively. The mean of Y_i is denoted by μ_i = E(Y_i) and the variance of Y_i is $\mathrm{Cov}\left({\mathit{Y}}_i\mid {\mathit{X}}_i\right)=\theta {\mathit{A}}_i^{1/2}{\mathit{R}}_{i0}\left({\mathit{\omega }}_0\right){\mathit{A}}_i^{1/2}$, where ${\mathit{A}}_i=\mathrm{diag}\left\{\gamma \left({\mu }_{i11}\right),\cdots ,\gamma \left({\mu }_{i1K}\right),\cdots ,\gamma \left({\mu }_{i{n}_{i}1}\right),\cdots ,\gamma \left({\mu }_{i{n}_{i}K}\right)\right\}$, and a ${\sum }_{j=1}^{n_i}{K}_{ij}\times {\sum }_{j=1}^{n_i}{K}_{ij}$ correlation matrix R_i0(ω₀) describes the correlation of measures within the ith practice with a vector of association parameters denoted by ω₀. Both γ and θ are dependent on the distribution of responses. If Y_ijk is normally distributed, γ(μ_ijk) = 1 and θ is the random error variance σ²; if Y_ijk is binary, γ(μ_ijk) = μ_ijk(1 − μ_ijk) and θ = 1; if Y_ijk is count with a Poisson distribution, γ(μ_ijk) = μ_ijk and θ=1.

Liang and Zeger²³ showed that $\sqrt{m}(\widehat{\mathit{\beta }}-\mathit{\beta })$ is asymptotically multivariate normal with a covariance matrix ${\mathit{V}}_{\mathit{R}}\text{=}\underset{m\to \infty }{\lim }m\left({\mathbf{\Sigma }}_1^{-1}{\mathbf{\Sigma }}_0{\mathbf{\Sigma }}_1^{-1}\right)$, where ${\mathbf{\Sigma }}_1={\mathbf{\sum }}_{i=1}^m{\mathit{D}}_i^{\prime }{\mathbf{V}}_i^{\mathbf{-}1}{\mathit{D}}_i$, ${\mathbf{\Sigma }}_0={\sum }_{i=1}^m{\mathit{D}}_i^{\prime }{\mathbf{V}}_i^{-1}\mathrm{cov}\left({\mathit{Y}}_i\mid {\mathit{X}}_i\right){\mathbf{V}}_i^{-1}{\mathit{D}}_i$, ${\mathit{D}}_i=\partial {\mathit{\mu }}_i/\partial {\mathit{\beta }}^{\prime }$ and V_i is a working covariance matrix of Y_i. In order to obtain the variance matrix V_R, R_i0(ω₀) must be positive definite (PD). Let R_iw(ω) be a ${\sum }_{j=1}^{n_i}{K}_{ij}\times {\sum }_{j=1}^{n_i}{K}_{ij}$ working correlation matrix with a vector of association parameters ω. The working covariance matrix is expressed as ${\mathit{V}}_i=\theta {\mathit{A}}_i^{1/2}{\mathit{R}}_{iw}(\mathit{\omega }){\mathit{A}}_i^{1/2}$ and is unequal to Cov(Y_i| X_i) unless R_iw(ω) = R_i0(ω₀). For simplicity, the working correlation matrix R_iw(ω) is denoted by R_i(ω) from now on.

We implement the three-level exchangeable working correlation structure proposed by Teerenstra et al¹⁸

$${\mathit{R}}_{iw}(r,\rho )=\rho {\mathbf{1}}_{K_i{n}_i\times K_i{n}_i}+(r-\rho ){\mathrm{Bdiag}}_{n_i}\left({\mathbf{1}}_{K_i\times K_i}\right)+(1-r){\mathbf{I}}_{K_i{n}_i\times K_i{n}_i},$$

where r denotes the correlation structure includes correlation among participants within the same provider in the same practice and ρ denotes the correlation among participants with different providers in the same practice. Please note the equal number of participants across providers in practice i, K_ij ≡ K_i, must be assumed in this exchangeable working correlation structure. In order to obtain the variance matrix V_R, given a value of K_i and n_i, PD of R_iw(r, ρ) can be determined if the constraints holds,

$$-\frac{1}{K_i-1}<r<1,-\frac{1+\left(K_i-1\right)r}{K_i\left(n_i-1\right)}<\rho <\frac{1+\left(K_i-1\right)r}{K_i}.$$

here λ₁ = 1−r, λ₂ = 1+(K −1)r −K_𝜌, ${\lambda }_{3i}=1+(K-1)r+K\left(n_i-1\right)\rho$ are the distinct eigenvalues of R_iw(r, ρ). The proof was provided by Web Appendix A in the work of Li et al (https://onlinelibrary.wiley.com/action/downloadSupplement?doi=10.1111%2Fbiom.12918&file=biom12918-sup-0002-SuppData.pdf).²⁴ Teerenstra et al showed that

$${\mathit{R}}_i^{-1}(r,\rho )=-\frac{\rho }{{\lambda }_{3i}{\lambda }_{2i}}{\mathbf{1}}_{K_i{n}_i\times K_i{n}_i}-\frac{r-\rho }{(1-r){\lambda }_{2i}}{\mathrm{Bdiag}}_{n_i}\left({\mathbf{1}}_{K_i\times K_i}\right)+\frac{1}{1-r}{I}_{K_i{n}_i\times K_i{n}_i},$$

The proof was shown in Web Appendix 2 in the work of Teerenstra et al (http://www.biometrics.tibs.org/).¹⁸ This inverse matrix is used to derive the expression of V_R in the following subsections.

For the purpose of sample size calculation at the design stage, we need to assume values for the variance and covariance of Y_i. When V_i is assumed to be the same as cov(Y_i| X_i), Σ₀ = Σ₁ and ${\mathit{V}}_{\mathit{R}}=\underset{m\to \infty }{\lim }m{\mathbf{\Sigma }}_1^{-1}$. Suppose the treatment assignment is coded in the last column of the cluster covariate matrices ${\mathit{X}}_i^{\prime }$ and the corresponding last parameter of β is β_p. Let V_β denote the (p, p)th element of V_R. Thus, $\sqrt{m}\left({\widehat{\mathit{\beta }}}_p-{\mathit{\beta }}_p\right)$ has an asymptotically normal distribution N(0, V_β), equivalently, $\mathrm{Var}\left({\widehat{\beta }}_p\right)=V_{\beta }/m$. For simplicity, p = 2. Specifically, the coefficients β₁ is the intercept, β₂ is the treatment effect. The design matrix is ${\mathit{X}}_{i\text{trt}}=\left(\begin{array}{l}{\mathbf{1}}_{1\times K_i{n}_i}\hfill \\ {\mathbf{1}}_{1\times K_i{n}_i}\hfill \end{array}\right)$ for ith cluster assigned to the treatment group, and ${\mathit{X}}_{i\text{cont}}=\left(\begin{array}{l}{\mathbf{1}}_{1\times K_i{n}_i}\hfill \\ {\mathbf{0}}_{1\times K_i{n}_i}\hfill \end{array}\right)$ for ith cluster assigned to the control group, respectively. The cluster allocations of the treatment and control groups are, m_trt = mπ and m_cont = m(1 − π), where π is the group allocation. The hypotheses of interest are H₀: β₂ = 0 vs H₁: β₂ = β_b, where β_b ≠ 0.

2.1 |. Continuous outcome

We use an identity link function on the continuous outcome, that is, ${\mathit{\mu }}_i={\mathit{X}}_i^{\prime }\beta$, and V_i = σ²R_i(r, ρ). With this setting, ${\mathit{D}}_i=\partial {\mathit{\mu }}_i/\partial {\mathit{\beta }}^{\prime }={\mathit{X}}_i^{\prime }$

$${\mathbf{\Sigma }}_1=\sum _{i=1}^m{\mathit{D}}_i^{\prime }{\mathbf{V}}_i^{-1}{\mathit{D}}_i=\frac{1}{{\sigma }^2}\sum _{i=1}^m{\mathit{X}}_i{\mathit{R}}_i^{-1}{\mathit{X}}_i^{\prime }=\frac{1}{{\sigma }^2}\left(\begin{array}{cc}\sum _{i\in \mathrm{trt}}\frac{K_i{n}_i}{{\lambda }_{3i}}+\sum _{i\in \text{cont}}\frac{K_i{n}_i}{{\lambda }_{3i}}& \sum _{i\in \mathrm{trt}}\frac{K_i{n}_i}{{\lambda }_{3i}}\\ \sum _{i\in \mathrm{trt}}\frac{K_i{n}_i}{{\lambda }_{3i}},& \sum _{i\in \mathrm{trt}}\frac{K_i{n}_i}{{\lambda }_{3i}}\end{array}\right),$$ (1)

where i ∈ trt denotes all practices assigned to the treatment group, and i ∈ cont denotes all practices assigned to the control group. The key steps of proofs are shown in Appendix 1. Similar to the proof in Shih’s paper,²⁵ we can show $V_{\beta }=\frac{{\sigma }^2}{\pi (1-\pi )}\frac{m}{\sum _{i=1}^m\frac{K_i{n}_i}{{\lambda }_{3i}}}$. If they are equal practice sizes n_i ≡ n and equal provider sizes K_i ≡ K, then λ₂ = 1 + (K − 1)r − K_ρ, λ₃ = 1 + (K − 1)r + K(n − 1)ρ and

$$V_{\beta }=\frac{{\sigma }^2{\lambda }_3}{\pi (1-\pi )Kn}.$$ (2)

The sample size formula for number of practices when assuming equal provider and practice size is $m=\frac{{\sigma }^2{\lambda }_3}{\pi (1-\pi )Kn}\frac{{\left(z_{1-\alpha /2}+z_{\text{power}}\right)}^2}{{\beta }_b^2}$, where α is a pre-specified significance level, and z_α is the 100×α percentile of a standard normal distribution. Please note that Equation (2) is same as the formula in sect. 4.3 in the work of Teerenstra et al for three-level data.¹⁸ When K = 1, a two-level CRT or longitudinal study, it reduces to Equation (4) in Shih’s paper.²⁵

2.2 |. Binary outcome

We consider the logit model: ${\mathit{\mu }}_i={\mathit{p}}_i=\exp \left({\mathit{X}}_i^{\prime }\mathit{\beta }\right)/\left(1+\exp \left({\mathit{X}}_i^{\prime }\mathit{\beta }\right)\right)$. Here, $p_{ijk}=p_0=\exp \left({\beta }_1\right)/\left(1+\exp \left({\beta }_1\right)\right)$, for all practices in the control group and j = 1,· · ·, n_i; and p_ijk = p₁ = exp(β₁ +β₂)/(1+exp(β₁ +β₂)), for all practices in the treatment group and j = 1, · · ·, n_i. The logarithm of odds ratio for the response $\log \left(\frac{p_1/p_0}{\left(1-p_1\right)/\left(1-p_0\right)}\right)$ equals β₂. Therefore, the null hypothesis H₀: β₂ = 0 is equivalent to p₀ = p₁. Under this scenario, ${\mathit{D}}_i=\partial {\mathit{\mu }}_i/\partial {\mathit{\beta }}^{\prime }=p_0\left(1-p_0\right)\left({\mathbf{1}}_{K_i{n}_i\times 1},{\mathbf{0}}_{K_i{n}_i\times 1}\right)$ for the practices in the control group, denoted by D_icont, and ${\mathit{D}}_i=p_1\left(1-p_1\right)\left({\mathbf{1}}_{K_i{n}_i\times 1},{\mathbf{1}}_{K_i{n}_i\times 1}\right)$ for the practices in the treatment group, denoted by D_itrt, and V_i = p_i(1 − p_i)R_i(r, ρ). Thus,

$${\mathbf{\Sigma }}_1=\left(\begin{array}{cc}{p}_1\left(1-p_1\right)\sum _{i\in \text{trt}}\frac{K_i{n}_i}{{\lambda }_{3i}}+p_0\left(1-p_0\right)\sum _{i\in \text{cont}}\frac{K_i{n}_i}{{\lambda }_{3i}},& p_1\left(1-p_1\right)\sum _{i\in \mathrm{trt}}\frac{K_i{n}_i}{{\lambda }_{3i}}\\ p_1\left(1-p_1\right)\sum _{i\in \mathrm{trt}}\frac{K_i{n}_i}{{\lambda }_{3i}},& p_1\left(1-p_1\right)\sum _{i\in \mathrm{trt}}\frac{K_i{n}_i}{{\lambda }_{3i}}\end{array}\right),$$ (3)

and

$$V_{\beta }=\frac{m}{{\sum }_{i=1}^m\frac{K_i{n}_i}{{\lambda }_{3i}}}\left(\frac{1}{\pi p_1\left(1-p_1\right)}+\frac{1}{(1-\pi )p_0\left(1-p_0\right)}\right).$$

If n_i ≡ n and K_i ≡ K, then

$$V_{\beta }=\frac{{\lambda }_3}{Kn}\left(\frac{1}{\pi p_1\left(1-p_1\right)}+\frac{1}{(1-\pi )p_0\left(1-p_0\right)}\right).$$ (4)

The sample size formula when assuming equal provider and practice size is $m=\frac{{\lambda }_3}{Kn}\left(\frac{1}{\pi p_1\left(1-p_1\right)}+\frac{1}{(1-\pi )p_0\left(1-p_0\right)}\right)\frac{{\left(z_{1-\alpha /2}+z_{\text{power}}\right)}^2}{{\beta }_b^2}$, where ${\beta }_b=\log \left(\frac{p_1/p_0}{\left(1-p_1\right)/\left(1-p_0\right)}\right)$. Please note that Equation (2) is same as the formula in sect. 4.4 in the work of Teerenstra et al,¹⁸ and reduces to Equation (6) when K = 1 in Shih’s paper.²⁵

2.3 |. Count data

We consider the log linear model to analyze the count data, ${\mathit{\mu }}_i=\exp \left({\mathit{X}}_i^{\prime }\mathit{\beta }\right)$, ${\mathit{D}}_i=\partial {\mathit{\mu }}_i/\partial {\mathit{\beta }}^{\prime }={\mathit{X}}_i^{\prime }\exp \left({\mathit{X}}_i^{\prime }\mathit{\beta }\right)$, and

$${\mathit{A}}_i=\mathrm{diag}\left\{\exp \left({\mathit{X}}_{i11}^{\prime }\mathit{\beta }\right),\cdots ,\exp \left({\mathit{X}}_{i1K_i}^{\prime }\mathit{\beta }\right),\cdots ,\exp \left({\mathit{X}}_{i{n}_i}^{\prime }\mathit{\beta }\right),\cdots ,\exp \left({\mathit{X}}_{i{n}_i{K}_i}^{\prime }\mathit{\beta }\right)\right\}.$$

Specifically, ${\mathit{D}}_{i\text{cont}}=e^{{\beta }_1}{\mathit{X}}_{i\text{cont}}^{\prime }$ and ${\mathit{A}}_{i\text{cont}}=e^{{\beta }_1}{\mathit{I}}_{K_i{n}_i\times K_i{n}_i}$ for the subjects in the control group, and ${\mathit{D}}_{i\text{trt}}=e^{{\beta }_1+{\beta }_2}{\mathit{X}}_{i\text{trt}}^{\prime }$ and ${\mathit{A}}_{i\text{trt}}=e^{{\beta }_1+{\beta }_2}{\mathit{I}}_{K_i{n}_i\times K_i{n}_i}$ for the subjects in the treatment group.

$${\mathbf{\Sigma }}_1=\sum _{i=1}^m{\mathit{D}}_i^{\prime }{\mathbf{V}}_i^{-1}{\mathit{D}}_i=e^{{\beta }_1+{\beta }_2}\sum _{i\in \mathrm{trt}}{\mathit{X}}_{itrt}{\mathbf{R}}_i^{-1}{\mathit{X}}_{itrt}^{\prime }+e^{{\beta }_1}\sum _{i\in \text{cont}}{\mathit{X}}_{i\text{cont}}{\mathbf{R}}_i^{-1}{\mathit{X}}_{i\text{cont}}^{\prime }=\left(\begin{array}{cc}{e}^{{\beta }_1+{\beta }_2}\sum _{i\in \mathrm{trt}}\frac{K_i{n}_i}{{\lambda }_{3i}}+e^{{\beta }_1}\sum _{i\in \text{cont}}\frac{K_i{n}_i}{{\lambda }_{3i}},& e^{{\beta }_1+{\beta }_2}\sum _{i\in \mathrm{trt}}\frac{K_i{n}_i}{{\lambda }_{3i}}\\ e^{{\beta }_1+{\beta }_2}\sum _{i\in \mathrm{trt}}\frac{K_i{n}_i}{{\lambda }_{3i}},& e^{{\beta }_1+{\beta }_2}\sum _{i\in \mathrm{trt}}\frac{K_i{n}_i}{{\lambda }_{3i}}\end{array}\right),$$ (5)

and

$$V_{\beta }=\frac{m}{e^{{\beta }_1}{\sum }_{i=1}^m\frac{K_i{n}_i}{{\lambda }_{3i}}}\left(\frac{1}{\pi e^{{\beta }_2}}+\frac{1}{1-\pi }\right).$$

If n_i ≡ n and K_i ≡ K, then

$$V_{\beta }=\frac{{\lambda }_3}{Kn{e}^{{\beta }_1}}\left(\frac{1}{\pi e^{{\beta }_2}}+\frac{1}{1-\pi }\right).$$ (6)

Correspondingly, the sample size formula is $m=\frac{{\lambda }_3}{Kn{e}^{{\beta }_1}}\left(\frac{1}{\pi e^{{\beta }_b}}+\frac{1}{1-\pi }\right)\frac{{\left(z_{1-\alpha /2}+z_{\text{power}}\right)}^2}{{\beta }_b^2}$. Under the assumptions of K = 1, equal practice size n and equal allocation π = 0.5, Equation (4) reduces to $\frac{2[1+(n-1)\rho ]}{n{e}^{{\beta }_1}}\left(\frac{1}{e^{{\beta }_b}}+1\right)$, same as Equation (19) developed by Amatya et al.²⁶ For practical purposes, t_α with m − 2 degrees of freedom is substituted for z_α in all sample size formulas.

3 |. BIAS-CORRECTED SANDWICH ESTIMATORS

The empirical sandwich estimator is consistent even if the working covariance matrix is not the true covariance matrix of Cov(Y_i| X_i).²³ However, this robust covariance estimator in the GEE approach works well only for the large number of clusters. The GEE performance for small clusters has been investigated and simulations have shown that the empirical sandwich estimator tend to be liberal.^19,27–30 Paik²⁹ and Feng et al³⁰ showed that the empirical sandwich estimator tends to underestimate the variance of regression coefficients to a varying degree when the number of clusters is less than 50. Therefore, bias-corrected sandwich estimators have been proposed to improve the performance in the GEE approach.^{19,20,22,31,32} Li and Redden reviewed these estimators for binary outcomes in two-level CRTs with a small number of clusters.³³ Their simulations suggest that no bias-corrected sandwich estimator is universally better than the others when the Wald t-test is used in the CRTs with few clusters and considerable variation of cluster sizes. Lu et al recommended the Wald z-test with MD-corrected sandwich estimator in the GEE analyses for the small number of clusters,³⁴ however, the results showed that the MD-corrected sandwich estimator should be used with caution because the Wald z-test maintains the type I error rate only when the number of clusters is greater than 20.³³ Overall, there is no consensus about using these bias-corrected estimators in two-level CRTs. All these bias-corrected sandwich estimators apply the adjustment when estimating the variance matrix V_R. For example, Morel et al approximated variance matrix through using the maximum of 1 and a trace function.³¹ Only MD-corrected¹⁹ and FG-corrected²² sandwich estimator can be derived mathematically, specifically, though the matrix computation. Therefore, we consider these two corrected sandwich estimators for all three types of outcomes in three-level CRTs in the following subsections.

3.1 |. MD-corrected sandwich estimator

Mancl and DeRouen¹⁹ proposed reducing the bias of the sandwich estimator and the variance of $\widehat{\mathit{\beta }}$ is approximated $V_{\text{MD}}={\mathbf{\Sigma }}_1^{-1}{\mathbf{\Sigma }}_{\text{MD}}{\mathbf{\Sigma }}_1^{-1}$. When we apply this estimator to the three-level data, ${\mathbf{\Sigma }}_{\text{MD}}$ is given by.

$${\mathbf{\Sigma }}_{\text{MD}}=\sum _{i=1}^m{\mathit{D}}_i^{\prime }{\mathbf{V}}_i^{-1}{\left({\mathit{I}}_{K_i{n}_i\times K_i{n}_i}-{\mathit{H}}_i\right)}^{-1}\mathrm{cov}\left({\mathit{Y}}_i\mid {\mathit{X}}_i\right){\left({\mathit{I}}_{K_i{n}_i\times K_i{n}_i}-{\mathit{H}}_i\right)}^{-1}{\mathbf{V}}_i^{-1}{\mathit{D}}_i,$$

where the matrix $H_i={\mathit{D}}_i{\mathbf{\Sigma }}_1^{-1}{\mathit{D}}_i^{\prime }{\mathbf{V}}_i^{-1}$ is an expression for the leverage of the ith cluster. For the purpose of sample size calculation at the design stage, we assume cov(Y_i| X_i) = V_i as usual. Thus, the above expression ${\mathbf{\Sigma }}_{\text{MD}}$ becomes ${\sum }_{i=1}^m{\mathit{D}}_i^{\prime }{\mathbf{V}}_i^{-1}{\left({\mathit{I}}_{K_i{n}_i\times K_i{n}_i}-{\mathit{H}}_i\right)}^{-1}{\mathit{V}}_i{\left({\mathit{I}}_{K_i{n}_i\times K_i{n}_i}-{\mathit{H}}_i\right)}^{-1}{\mathbf{V}}_i^{-1}{\mathit{D}}_i$. We substitute the values of D_i, V_i, and ${\mathbf{\Sigma }}_1$ for each type of outcome in Section 2. For example, for continuous outcomes, ${\mathit{D}}_i={\mathit{X}}_i^{\prime }$, ${\Sigma }_1$ is denoted by Equation (1), and V_i = σ²R_i(r, ρ). For the practices in the control group, through some matrix computation, ${\mathit{H}}_i=a_i{\mathbf{1}}_{K_i{n}_i\times K_i{n}_i}$, where $a_i=\frac{1}{{\lambda }_{3i}c}$, $c=\sum _{i\in \text{cont}}\frac{K_i{n}_i}{{\lambda }_{3i}}$, and then

$${\left({\mathit{I}}_{K_i{n}_i\times K_i{n}_i}-{\mathit{H}}_i\right)}^{-1}={\mathit{I}}_{K_i{n}_i\times K_i{n}_i}+\frac{a_i}{1-a_i{K}_i{n}_i}{\mathbf{1}}_{K_i{n}_i\times K_i{n}_i}.$$

Furthermore, after more matrix computation, we have

$${\mathit{D}}_i^{\prime }{\mathbf{V}}_i^{-1}{\left({\mathit{I}}_i-{\mathit{H}}_i\right)}^{-1}{\mathit{V}}_i{\left({\mathit{I}}_i-{\mathit{H}}_i\right)}^{-1}{\mathbf{V}}_i^{-1}{\mathit{D}}_i=r_i\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right],$$

where $r_i=\frac{K_i{n}_i}{{\sigma }^2{\lambda }_{3i}{\left(1-K_i{n}_i{a}_i\right)}^2}$. Similarly, for the practices in the treatment group, we have

$${\mathit{D}}_i^{\prime }{\mathbf{V}}_i^{-1}{\left({\mathit{I}}_i-{\mathit{H}}_i\right)}^{-1}{\mathit{V}}_i{\left({\mathit{I}}_i-{\mathit{H}}_i\right)}^{-1}{\mathbf{V}}_i^{-1}{\mathit{D}}_i=s_i\left[\begin{array}{ll}1\hfill & 1\hfill \\ 1\hfill & 1\hfill \end{array}\right],$$

where $s_i=\frac{K_i{n}_i}{{\sigma }^2{\lambda }_{3i}{\left(1-K_i{n}_i{b}_i\right)}^2}$, $b_i=\frac{1}{{\lambda }_{3i}t}$, and $t=\sum _{i\in \mathrm{trt}}\frac{K_i{n}_i}{{\lambda }_{3i}}$. Therefore, MD-corrected estimator ${\mathbf{\Sigma }}_1^{-1}{\mathbf{\Sigma }}_{\text{MD}}{\mathbf{\Sigma }}_1^{-1}$ is simplified as

$${\mathbf{\Sigma }}_1^{-1}\left[\begin{array}{cc}\sum _{i\in \mathrm{cont}}{r}_i& \sum _{i\in \mathrm{trt}}{s}_i\\ \sum _{i\in \mathrm{trt}}{s}_i& \sum _{i\in \mathrm{trt}}{s}_i\end{array}\right]{\mathbf{\Sigma }}_1^{-1}.$$

Its (2, 2)th element, the variance of the estimator of the treatment effect, is expressed as

$$\mathrm{Var}\left({\widehat{\beta }}_2\right)={\sigma }^2\left\{\frac{1}{c^2}\sum _{i\in \mathrm{cont}}\frac{K_i{n}_i}{{\lambda }_{3i}{\left(1-K_i{n}_i{a}_i\right)}^2}+\frac{1}{t^2}\sum _{i\in \mathrm{trt}}\frac{K_i{n}_i}{{\lambda }_{3i}{\left(1-K_i{n}_i{b}_i\right)}^2}\right\}$$

for continuous outcomes.

When the outcome is binary, ${\mathit{D}}_i=p_0\left(1-p_0\right)\left({\mathbf{1}}_{K_i{n}_i\times 1},{\mathbf{0}}_{K_i{n}_i\times 1}\right)$ for the practices in the control group, ${\mathit{D}}_i=p_1\left(1-p_1\right)\left({\mathbf{1}}_{K_i{n}_i\times 1},1_{K_i{n}_i\times 1}\right)$ for the practices in the treatment group, ${\mathbf{\Sigma }}_1$ is given by Equation (3), and V_i = p_i(1 − p_i)R_i(r, ρ). Through the similar steps, we have $r_i=\frac{p_0\left(1-p_0\right)K_i{n}_i}{{\lambda }_{3i}{\left(1-K_i{n}_i{a}_i\right)}^2}$, and $S_i=\frac{p_1\left(1-p_1\right)K_i{n}_i}{{\lambda }_{3i}{\left(1-K_i{n}_i{b}_i\right)}^2}$. Finally,

$$\mathrm{Var}\left({\widehat{\beta }}_2\right)=\frac{1}{p_0\left(1-p_0\right)c^2}\sum _{i\in \mathrm{cont}}\frac{K_i{n}_i}{{\lambda }_{3i}{\left(1-K_i{n}_i{a}_i\right)}^2}+\frac{1}{p_1\left(1-p_1\right)t^2}\sum _{i\in \mathrm{trt}}\frac{K_i{n}_i}{{\lambda }_{3i}{\left(1-K_i{n}_i{b}_i\right)}^2};$$

For count data, ${\mathit{D}}_i={\mathit{X}}_i^{\prime }\exp \left({\mathit{X}}_i^{\prime }\mathit{\beta }\right)$, ${\mathbf{\Sigma }}_1$ is denoted by Equation (5), and ${\mathit{V}}_i={\mathit{A}}_i^{1/2}{\mathit{R}}_i(r,\rho ){\mathit{A}}_i^{1/2}$. Through the similar steps, we have $r_i=\frac{e^{{\beta }_1}{K}_i{n}_i}{{\lambda }_{3i}{\left(1-K_i{n}_i{a}_i\right)}^2}$, $S_i=\frac{e^{{\beta }_1+{\beta }_2}{K}_i{n}_i}{{\lambda }_{3i}{\left(1-K_i{n}_i{b}_i\right)}^2}$, and

$$\mathrm{Var}\left({\widehat{\beta }}_2\right)=\frac{1}{e^{{\beta }_1}{c}^2}\sum _{i\in \mathrm{cont}}\frac{K_i{n}_i}{{\lambda }_{3i}{\left(1-K_i{n}_i{a}_i\right)}^2}+\frac{1}{e^{{\beta }_1+{\beta }_2}{t}^2}\sum _{i\in \mathrm{trt}}\frac{K_i{n}_i}{{\lambda }_{3i}{\left(1-K_i{n}_i{b}_i\right)}^2}.$$

If we assume equal practice size n_i = n and equal provider size K_i ≡ K for all i, then a_i ≡ a = [Knm(1−π)]⁻¹ and b_i ≡ b = [Knmπ]⁻¹,

$$\mathrm{Var}\left({\widehat{\beta }}_2\right)=\frac{{\sigma }^2{\lambda }_{3}m}{Kn}\left\{\frac{(1-\pi )}{{(m(1-\pi )-1)}^2}+\frac{\pi }{{(m\pi -1)}^2}\right\}$$

for continuous outcomes;

$$\mathrm{Var}\left({\widehat{\beta }}_2\right)=\frac{{\lambda }_{3}m}{Kn}\left\{\frac{(1-\pi )}{p_0\left(1-p_0\right){(m(1-\pi )-1)}^2}+\frac{\pi }{p_1\left(1-p_1\right){(m\pi -1)}^2}\right\}$$

for binary outcomes; and

$$\mathrm{Var}\left({\widehat{\beta }}_2\right)=\frac{{\lambda }_{3}m}{Kn{e}^{{\beta }_1}}\left\{\frac{(1-\pi )}{{(m(1-\pi )-1)}^2}+\frac{\pi }{e^{{\beta }_2}{(m\pi -1)}^2}\right\}$$

for count data.

3.2 |. FG-corrected sandwich estimator

Fay and Graubard²² corrected the bias by adding a scale factor to the working variance in the sandwich estimator. The variance of $\widehat{\mathit{\beta }}$ is calculated in a FG-corrected estimator by ${\mathit{V}}_{\text{FG}}={\mathbf{\Sigma }}_1^{-1}{\mathbf{\Sigma }}_{\text{FG}}{\mathbf{\Sigma }}_1^{-1}$, where

$${\mathbf{\Sigma }}_{\text{FG}}=\sum _{i=1}^m{\mathit{L}}_i{\mathit{D}}_i^{\prime }{\mathbf{V}}_i^{-1}\mathrm{cov}\left({\mathit{Y}}_i\mid {\mathit{X}}_i\right){\mathbf{V}}_i^{-1}{\mathit{D}}_i{\mathit{L}}_i,$$

L_i is a p × p diagonal matrix with jjth element equal to ${\left[1-\min \left(d,{\mathit{Q}}_i^{jj}\right)\right]}^{-1/2}$, ${\mathit{Q}}_i={\mathit{D}}_i^{\prime }{\mathbf{V}}_i^{-1}{\mathit{D}}_i{\Sigma }_1^{-1}$ and d is a constant defined by the user which guarantees that each diagonal element of L_i is less than or equal to 2. Fay and Graubard²² arbitrarily chose d = 0.75 and their simulations showed that the bound of d = 0.75 is rarely reached.

Again we assume cov(Y_i| X_i) = V_i at the design stage, ${\mathbf{\Sigma }}_{\text{FG}}={\sum }_{i=1}^m{\mathit{L}}_i{\mathit{D}}_i^{\prime }{\mathbf{V}}_i^{-1}{\mathit{D}}_i{\mathit{L}}_i$. Similarly, we substitute the expressions of D_i, V_i, and ${\mathbf{\Sigma }}_1$ for each type of outcome in Section 2. If the ith cluster is in the control group, then after some matrix computation,

$${\mathit{Q}}_i=\frac{K_i{n}_i}{c{\lambda }_{3i}}\left[\begin{array}{cc}1& -1\\ 0& 0\end{array}\right],$$

and the diagonal matrix ${\mathit{L}}_i=\left[\begin{array}{cc}{l}_i^{11}& 0\\ 0& 1\end{array}\right]$. Similarly, we have ${\mathit{Q}}_i=\frac{K_i{n}_i}{t{\lambda }_{3i}}\left[\begin{array}{ll}0\hfill & 1\hfill \\ 0\hfill & 1\hfill \end{array}\right]$ and ${\mathit{L}}_i=\left[\begin{array}{cc}1& 0\\ 0& l_i^{22}\end{array}\right]$ if the ith cluster is in the treatment group; where $l_i^{11}={\left[1-\min \left(d,\frac{K_i{n}_i}{c{\lambda }_{3i}}\right)\right]}^{-1/2}$, and $l_i^{22}={\left[1-\min \left(d,\frac{K_i{n}_i}{t{\lambda }_{3i}}\right)\right]}^{-1/2}$. Let $w_{11}=\sum _{i\in \mathrm{cont}}\frac{K_i{n}_i}{{\lambda }_{3i}}{\left(l_i^{11}\right)}^2$, $w_{12}=\sum _{i\in \text{trt}}\frac{K_i{n}_i}{{\lambda }_{3i}}{l}_i^{22}$, $w_{22}=\sum _{i\in \mathrm{trt}}\frac{K_i{n}_i}{{\lambda }_{3i}}{\left(l_i^{22}\right)}^2$. For continuous outcomes, again, from mathematical computation, we simplify the ${\mathbf{\Sigma }}_{\text{FG}}$ as $\frac{1}{{\sigma }^2}\left[\begin{array}{cc}{w}_{11}+t& w_{12}\\ w_{12}& w_{22}\end{array}\right]$. The (2, 2)th element of ${\mathbf{\Sigma }}_1^{-1}{\mathbf{\Sigma }}_{\text{FG}}{\mathbf{\Sigma }}_1^{-1}$ is

$$\mathrm{Var}\left({\widehat{\beta }}_2\right)=\frac{v_{11}}{o^2}-\frac{2}{o}\left(\frac{1}{o}+\frac{1}{e}\right)v_{12}+{\left(\frac{1}{o}+\frac{1}{e}\right)}^2{v}_{22},$$ (7)

where $o=c={\sum }_{i\in \mathrm{cont}}\frac{K_i{n}_i}{{\lambda }_{3i}}$, $e=t={\sum }_{i\in \mathrm{trt}}\frac{K_i{n}_i}{{\lambda }_{3i}}$, v₁₁ = σ²(w₁₁ + t), v₁₂ = σ²w₂₂, and v₂₂ = σ²w₂₂.

When we assume equal practice size n_i = n and equal provider size K_i ≡ K for all i, then $o_{\text{eq}}=c_{\text{eq}}\equiv \frac{Knm(1-\pi )}{{\lambda }_3}$, $e_{\text{eq}}=t_{\text{eq}}\equiv \frac{Knm\pi }{{\lambda }_3}$, $l_i^{11}=l^{11}\equiv {\left[1-\min \left(d,\frac{1}{m(1-\pi )}\right)\right]}^{-\frac{1}{2}}$, and $l_i^{22}=l^{22}\equiv {\left[1-\min \left(d,\frac{1}{m\pi }\right)\right]}^{-\frac{1}{2}}$. Let $w_{11}^{\text{eq}}=\frac{Kmn(1-\pi )}{{\lambda }_3}{\left(l^{11}\right)}^2$, $w_{12}^{\text{eq}}=\frac{Kmn\pi }{{\lambda }_3}{l}^{22}$, and $w_{22}^{\text{eq}}=\frac{Kmn\pi }{{\lambda }_3}{\left(l^{22}\right)}^2$. The formula of the estimator of the treatment effect under equal size setting is given by

$$\mathrm{Var}\left({\widehat{\beta }}_2\right)=\frac{v_{11}^{\text{eq}}}{o_{\text{eq}}^2}-\frac{2}{o_{\text{eq}}}\left(\frac{1}{o_{\text{eq}}}+\frac{1}{e_{\text{eq}}}\right)v_{12}^{\text{eq}}+{\left(\frac{1}{{\text{o}}_{\text{eq}}}+\frac{1}{e_{\text{eq}}}\right)}^2{v}_{22}^{\text{eq}},$$ (8)

where $v_{11}^{\text{eq}}={\sigma }^2\left(w_{11}^{\text{eq}}+t_{\text{eq}}\right)$, $v_{12}^{\text{eq}}={\sigma }^2{w}_{12}^{\text{eq}}$, and $v_{22}^{\text{eq}}={\sigma }^2{w}_{22}^{\text{eq}}$.

For binary and count outcomes, we make the similar derivation and have the same Equations (7) and (8) for the variance of the estimator of the treatment effect. However, the notations are different and detailed in Table 1.

TABLE 1.

Notations

	Continuous	Binary	Count
o	c	p0(1 − p0)c	$e^{{\beta }_1}c$
e	t	p1(1 − p1)t	$e^{{\beta }_1+{\beta }_2}t$
v11	σ2(w11 + t)	p0(1 − p0)w11 + p1(1 − p1)t	$e^{{\beta }_1}{w}_{11}+e^{{\beta }_1+{\beta }_2}t$
v12	σ2w12	p1(1 − p1)w12	$e^{{\beta }_1+{\beta }_2}{w}_{12}$
v22	σ2w22	p1(1 − p1)w22	$e^{{\beta }_1+{\beta }_2}{w}_{22}$
oeq	ceq	p0(1 − p0)ceq	$e^{{\beta }_1}{c}_{\text{eq}}$
eeq	teq	p1(1 − p1)teq	$e^{{\beta }_1+{\beta }_2}{t}_{\text{eq}}$
$v_{11}^{\text{eq}}$	${\sigma }^2\left(w_{11}^{\text{eq}}+t_{\text{eq}}\right)$	$p_0\left(1-p_0\right)w_{11}^{\text{eq}}+p_1\left(1-p_1\right)t_{\text{eq}}$	$e^{{\beta }_1}{w}_{11}^{\text{eq}}+e^{{\beta }_1+{\beta }_2}{t}_{\text{eq}}$
$v_{12}^{\text{eq}}$	${\sigma }^2{w}_{12}^{\text{eq}}$	$p_1\left(1-p_1\right)w_{12}^{\text{eq}}$	$e^{{\beta }_1+{\beta }_2}{w}_{12}^{\text{eq}}$
$v_{22}^{\text{eq}}$	${\sigma }^2{w}_{22}^{\text{eq}}$	$p_1\left(1-p_1\right)w_{22}^{\text{eq}}$	$e^{{\beta }_1+{\beta }_2}{w}_{22}^{\text{eq}}$

$c={\sum }_{i\in \mathrm{cont}}\frac{K_i{n}_i}{{\lambda }_{3i}}$, $t={\sum }_{i\in \mathrm{trt}}\frac{K_i{n}_i}{{\lambda }_{3i}}$, $l_i^{11}\equiv {\left[1-\min \left(d,\frac{k_i{n}_i}{c{\lambda }_{3i}}\right)\right]}^{-\frac{1}{2}}$, $l_i^{22}\equiv {\left[1-\min \left(d,\frac{k_i{n}_i}{t{\lambda }_{3i}}\right)\right]}^{-\frac{1}{2}}$, $w_{11}={\sum }_{i\in \mathrm{cont}}\frac{k_i{n}_i}{{\lambda }_{3i}}{\left(l_i^{11}\right)}^2$, $w_{12}={\sum }_{i\in \mathrm{trt}}\frac{k_i{n}_i}{{\lambda }_{3i}}{l}_i^{22}$, $w_{22}={\sum }_{i\in \mathrm{trt}}\frac{k_i{n}_i}{{\lambda }_{3i}}{\left(l_i^{22}\right)}^2$, $c_{\text{eq}}\equiv \frac{Knm(1-\pi )}{{\lambda }_3}$, $t_{\text{eq}}\equiv \frac{Knm\pi }{{\lambda }_3}$, $l^{11}\equiv {\left[1-\min \left(d,\frac{1}{m(1-\pi )}\right)\right]}^{-\frac{1}{2}}$, $l^{22}\equiv {\left[1-\min \left(d,\frac{1}{m\pi }\right)\right]}^{-\frac{1}{2}}$, $w_{11}^{\text{eq}}=\frac{Kmn(1-\pi )}{{\lambda }_3}{\left(l^{11}\right)}^2$, $w_{12}^{\text{eq}}=\frac{Kmn\pi }{{\lambda }_3}{l}^{22}$, $w_{22}^{\text{eq}}=\frac{Kmn\pi }{{\lambda }_3}{\left(l^{22}\right)}^2$.

4 |. RE OF UNEQUAL VS EQUAL PRACTICE AND PROVIDER SIZES

In two-level CRTs, RE is defined as relative variance of the treatment effect when comparing equal to unequal cluster sizes.^14,15,35 Here, let Ω_equal denotes a design with equal practice size n_i = n and equal provider size K_i ≡ K, and let Ω_unequal denotes a design with unequal practice size n_i and/or unequal provider size K_i, i = 1, · · ·, m. The RE of unequal vs equal practice and provider sizes for the treatment effect, $\mathrm{RE}\left({\widehat{\beta }}_2\right)$, is defined as

$$\mathrm{RE}\left({\widehat{\beta }}_2\right)=\frac{\mathrm{Var}\left({\widehat{\beta }}_2\mid {\mathbf{\Omega }}_{\text{equal}}\right)}{\mathrm{Var}\left({\widehat{\beta }}_2\mid {\mathbf{\Omega }}_{\text{unequal}}\right)}.$$ (9)

For any type of outcome in Section 2, where the variances are asymptotically estimated,

$$\mathrm{RE}\left({\widehat{\beta }}_2\right)=\frac{[1+(K-1)r+K(n-1)\rho ]}{Kn}\frac{1}{m}\sum _{i=1}^m\frac{K_i{n}_i}{1+\left(K_i-1\right)r+K_i\left(n_i-1\right)\rho }.$$ (10)

When K_i ≡ K = 1,it reduces to a two-level CRT and the formula is the reciprocal of the design effect.^36,37

For both corrected estimators, REs have no consistent formula for the different types of outcomes. Obviously, it is straightforward to numerically calculate $\mathrm{RE}\left({\widehat{\beta }}_2\right)$ from Section 3.1 for an MD-corrected estimator, and Section 3.2 for an FG-corrected estimator. Please note that σ² for continuous outcomes and $e^{{\beta }_1}$ for count data are canceled from the RE calculation. The RE evaluations are investigated for various number of practices m, practice size, and provider size distributions as a function of correlation coefficients (r, ρ). The following sections focus on continuous outcomes. The results for binary and count data are similar and are shown in Appendix Tables 4 and 5.

4.1 |. Simulation designs

In our work with two-level CRTs,¹⁵ we considered six patterns of probabilities of cluster size, and we now consider the same scenarios for distributions of practice (provider) size in three-level CRTs. Figure 1 demonstrates the probabilities p_i, i = 1, · · ·, 20 of practice size for six patterns, where practice size follows a multinomial distribution, $N=mn={\sum }_{i=1}^m{n}_i$ and ${\sum }_{i=1}^m{p}_i=1$. For convenience of the following discussion, we sort the ith practice with the distribution probability p_is, i = 1, · · ·, m, by a non-decreasing order such that p₁ ≤ p₂ ≤ · · · ≤ p_m. Six patterns of (p₁, · · ·, p_m) are discussed under the design Ω_unequal.

FIGURE 1.

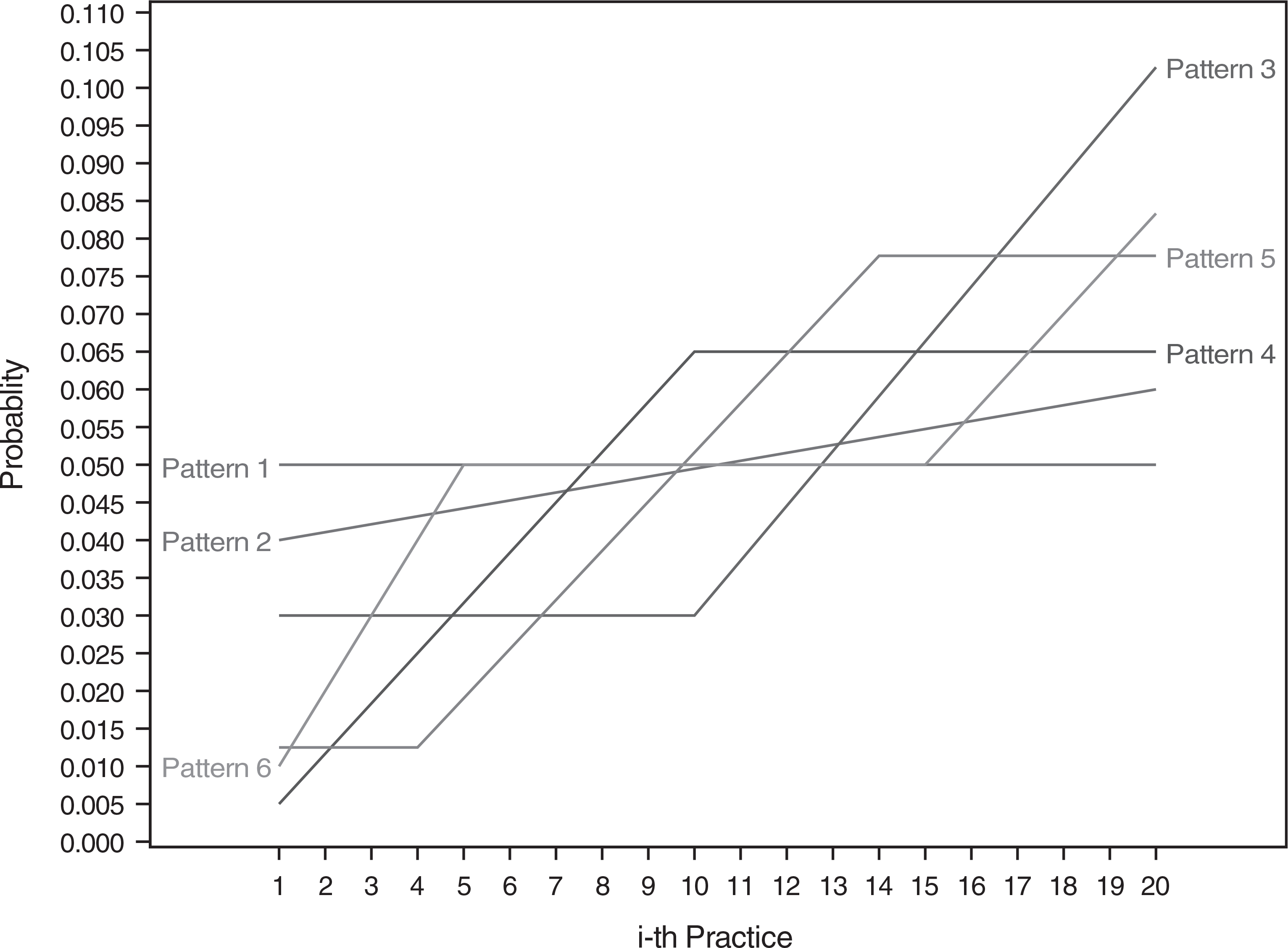
Six basic patterns of probabilities (p₁, · · ·, p_m)

Constant: p₁ = p₂ · · · = p_m

1. Monotonically increasing: p₁ <p₂ <· · ·<p_m;

2. Constant followed by monotonically increasing: p₁ =· · ·= p_l < p_l+1 <· · ·< p_m;

3. Monotonically increasing followed by constant: p₁ <· · ·< p_l = p_l+1 =· · ·=p_m;

4. Constant, monotonically increasing followed by constant: $p_1=p_2\cdots =p_{l_1}<p_{l_1+1}<\cdots <p_{l_2}=\cdots =p_m$;

5. Monotonically increasing, constant followed by monotonically increasing: $p_1<p_2\cdots <p_l=p_{l_1+1}=\cdots =p_{l_2}<\cdots <=p_m$;

Similarly, we consider these six patterns of provider sizes, which are assumed to follow a multinomial distribution with $mK={\sum }_{i=1}^m{K}_i$. $\mathrm{RE}\left({\widehat{\beta }}_2\right)$ is computed through simulation studies with these six patterns which function as the basic setting about the distribution of practice (provider) size.

Appendix Table 1 shows the values of (p₁, · · ·,p_m) for the simulation design with m = 6, while m = 100 was used in Liu et al.¹⁵ Appendix 2 provides the details of $p_i^{\prime }s$ calculations for each pattern. Provided the values of (p₁, · · ·,p_m) are available, we simulate the practice sizes n_i and provider size K_i, i = 1, · · ·, m from a multinomial distribution with mn and mK, and probabilities (p₁, · · ·,p_m), separately. For all the scenarios, the required parameters for (p₁, · · ·,p_m) calculation are shown in Appendix Table 2.

To investigate the RE in three-level CRTs based on GEE models, we consider the following factors: (1) the number of practices m, equal practice size n, and equal provider size K; (2) the values of p₁, · · ·,p_m, equivalently, the pattern of p₁, · · ·,p_m; (3) the association parameter (r,ρ) in the “nested exchangeable” correlation structure. We consider three scenarios about the number of practices: small, medium, and large; e.g. m = 6, 20, 50, respectively. Given a fixed number of practices, we investigate two scenarios for both practice size and provider size; e.g. n = 10, 20; K = 5, 20. For example, a CRT with m = 6, n = 10, and K = 5 has a total sample size of N = 300. All six patterns of practice size and provider size in Figure 1 are used for each study design.

Even if the intracluster correlation coefficients may be small for most CRTs,^38,39 the association parameter (r,ρ) both ranged from 0 to 0.95 with steps of 0.01 considered for illustration purposes. Given the practice size n_i and provider size K_i, the PD of R_i(r,ρ) is checked for each pair (r,ρ). If R_i(r,ρ) is not PD, the pair (r,ρ) is excluded from RE calculation. 1000 simulation samples are generated for each design. REs are calculated for all samples, and mean, SD, minimum and maximum of REs are obtained at each pair (r,ρ) correspondingly. To investigate the RE based on GEE models for a small number of practices, we consider m=6 and 20 only and assume an equal allocation (π = 0.5). Fay and Graubard²² arbitrarily chose d = 0.75, but we set different values of d: 0.1 and 0.75 to see whether they make any differences in RE (eg, $m=6,0.1<\frac{1}{m(1-\pi )}<0.75$ when the practice sizes are equal and an equal allocation of π = 1/2.)

4.2 |. Simulation results

Please note that ${\sum }_{i=1}^m{K}_i{n}_i=Knm$ cannot be guaranteed. For each combined pattern, we only show the simulation results when the mean total sample size among 1000 samples lies within the range of (0.975 × Knm, 1.025 × Knm). For example, m = 50, n = 20, and K = 20, (19 500, 20 500) was used as a selection criteria. Table 2 presents mean (min, max) of coefficient of variation (CV)s of practice size n_i, provider size K_i and cluster size (K_in_i), the minimum of mean RE and corresponding (r, ρ)s, and median of mean RE among 1000 samples for number of practices m = 50.

1. For the scenario of m = 50, n = 20, and K = 20, all minimums of mean REs are larger than 93%. When the pattern of practice size is 1, the maximum and minimum of minimums are 0.981 and 0.941, respectively and they are reached when the patterns of provider size are 1 and 2. Across six patterns of practice size, the minimum is 0.936 when the pattern of practice size is 2 and the pattern of provider size is 1; For three remaining scenarios in terms of n and K, the minimums of minimums are 0.898, 0.922, and 0.892, respectively and all of them are reached when the pattern of either practice size or provider size is 2.

2. The minimum of mean RE decreases if the CV of practice size increases under the fixed CV of provider size or if the CV of provider size increases under the fixed CV of practice size. However, when the CV of cluster size is the largest, the corresponding minimum is not the smallest. For example, the largest mean CV of cluster size in the scenario of m = 50, n = 20, and K = 20 is 0.61 but its minimum of mean RE is 0.947 and it is not the minimum of minimums. We also find that the minimum of mean RE decreases by 3–4% when the provider sizes decreases from 20 to 5 for a fixed m, n and any same pattern of practice size and provide size; In addition, the minimum of mean RE decreases by 1–3% when the practice sizes decreases from 20 to 10 for a fixed m, K and any same pattern of practice size and provide size.

TABLE 2.

Minimum and Median of mean RE from asymptotic estimator

								Mean REa
Number of practices (m)	Practice size (n)	Provider size (K)	Pattern (n)	CV of practice size mean (min, max)	Pattern (K)	CV of provider size mean (min, max)	CV of cluster size mean (min, max)	(r, ρ), Minimumb	Medianb
50	20	20	1	0.22 (0.15, 0.30)	1	0.22 (0.15, 0.29)	0.32 (0.22, 0.45)	(0.08, 0.01), 0.981	0.997
					2	0.47 (0.38, 0.56)	0.53 (0.41, 0.67)	(0.06, 0), 0.941	0.996
					3	0.35 (0.26, 0.44)	0.42 (0.30, 0.57)	(0.05, 0), 0.970	0.997
					4	0.26 (0.18, 0.34)	0.35 (0.24, 0.47)	(0.06, 0.01), 0.978	0.997
					5	0.28 (0.21, 0.36)	0.36 (0.24, 0.51)	(0.05, 0.01), 0.977	0.997
					6	0.49 (0.36, 0.62)	0.55 (0.37, 0.74)	(0.04, 0), 0.954	0.996
			2	0.47 (0.39, 0.56)	1	0.22 (0.16, 0.30)	0.53 (0.39, 0.66)	(0.11, 0.01), 0.936	0.985
			3	0.35 (0.27, 0.43)	1	0.22 (0.15, 0.30)	0.43 (0.31, 0.55)	(0.12, 0.01), 0.964	0.994
					4	0.26 (0.19, 0.33)	0.48 (0.35, 0.61)	(0.09, 0.01), 0.961	0.993
			4	0.26 (0.18, 0.33)	1	0.22 (0.16, 0.30)	0.35 (0.25, 0.48)	(0.09, 0.01), 0.977	0.996
					3	0.35 (0.27, 0.45)	0.48 (0.38, 0.64)	(0.01, 0.01), 0.965	0.995
					4	0.26 (0.19, 0.33)	0.40 (0.28, 0.53)	(0.05, 0.01), 0.973	0.996
					5	0.28 (0.21, 0.36)	0.42 (0.31, 0.55)	(0.04, 0.01), 0.971	0.996
					6	0.49 (0.38, 0.63)	0.60 (0.41, 0.83)	(0, 0.01), 0.957	0.995
			5	0.28 (0.20, 0.35)	1	0.22 (0.15, 0.29)	0.37 (0.26, 0.49)	(0.10, 0.01), 0.974	0.995
					4	0.26 (0.17, 0.34)	0.42 (0.32, 0.54)	(0.06, 0.01), 0.971	0.995
			6	0.49 (0.37, 0.60)	1	0.22 (0.15, 0.30)	0.55 (0.38, 0.74)	(0.16, 0.01), 0.949	0.991
					4	0.26 (0.18, 0.34)	0.61 (0.42, 0.79)	(0.14, 0.01), 0.947	0.991
50	20	5	1	0.22 (0.15, 0.30)	1	0.44 (0.31, 0.56)	0.50 (0.36, 0.68)	(0.04, 0.01), 0.940	0.993
				0.22 (0.17, 0.28)	2	0.58 (0.46, 0.70)	0.63 (0.49, 0.79)	(0.05, 0.01), 0.906	0.990
					3	0.51 (0.34, 0.67)	0.56 (0.37, 0.76)	(0.04, 0.01), 0.925	0.992
				0.22 (0.15, 0.30)	4	0.45 (0.32, 0.60)	0.51 (0.38, 0.66)	(0.04, 0.01), 0.936	0.992
					5	0.47 (0.33, 0.60)	0.53 (0.37, 0.67)	(0.04, 0.01), 0.933	0.992
				0.22 (0.15, 0.30)	6	0.60 (0.44, 0.86)	0.65 (0.46, 0.96)	(0.03, 0.01), 0.912	0.991
			2	0.47 (0.39, 0.56)	1	0.44 (0.31, 0.56)	0.67 (0.51, 0.92)	(0.02, 0.01), 0.898	0.977
			3	0.35 (0.27, 0.43)	1	0.44 (0.29, 0.56)	0.58 (0.42, 0.86)	(0.04, 0.01), 0.924	0.988
					4	0.46 (0.31, 0.58)	0.62 (0.43, 0.92)	(0.03, 0.01), 0.921	0.987
			4	0.26 (0.18, 0.32)	1	0.44 (0.30, 0.56)	0.52 (0.38, 0.73)	(0.04, 0.01), 0.936	0.991
				0.26 (0.18, 0.32)	3	0.51 (0.37, 0.65)	0.61 (0.42, 0.78)	(0.02, 0.01), 0.923	0.990
					4	0.45 (0.31, 0.59)	0.55 (0.39, 0.73)	(0.03, 0.01), 0.934	0.991
					5	0.47 (0.32, 0.59)	0.57 (0.42, 0.74)	(0.02, 0.01), 0.931	0.990
					6	0.60 (0.41, 0.80)	0.70 (0.47, 1.01)	(0.01, 0.01), 0.908	0.989
			5	0.28 (0.21, 0.35)	1	0.44 (0.29, 0.57)	0.53 (0.36, 0.77)	(0.04, 0.01), 0.933	0.991
					4	0.45 (0.30, 0.59)	0.57 (0.39, 0.77)	(0.02, 0.01), 0.931	0.990
			6	0.49 (0.38, 0.60)	1	0.44 (0.29, 0.57)	0.68 (0.40, 1.31)	(0.05, 0.01), 0.908	0.985
					4	0.45 (0.31, 0.59)	0.73 (0.50, 1.36)	(0.04, 0.01), 0.906	0.985
50	10	20	1	0.31 (0.21, 0.45)	1	0.22 (0.15, 0.30)	0.39 (0.29, 0.52)	(0.03, 0.01), 0.965	0.990
					2	0.47 (0.39, 0.56)	0.59 (0.45, 0.73)	(0.01, 0.01), 0.922	0.987
					3	0.35 (0.26, 0.45)	0.48 (0.36, 0.63)	(0.02, 0.01), 0.950	0.989
					4	0.26 (0.17, 0.32)	0.41 (0.31, 0.55)	(0.03, 0.01), 0.961	0.990
					5	0.28 (0.21, 0.36)	0.43 (0.31, 0.59)	(0.02, 0.01), 0.958	0.989
					6	0.49 (0.35, 0.64)	0.60 (0.36, 0.84)	(0.01, 0.01), 0.938	0.988
			2	0.51 (0.40, 0.61)	1	0.22 (0.16, 0.28)	0.56 (0.43, 0.70)	(0.04, 0.01), 0.925	0.972
			3	0.42 (0.31, 0.53)	1	0.22 (0.15, 0.28)	0.48 (0.34, 0.66)	(0.04, 0.01), 0.948	0.983
					4	0.26 (0.19, 0.33)	0.53 (0.40, 0.71)	(0.03, 0.01), 0.944	0.983
			4	0.34 (0.23, 0.45)	1	0.22 (0.16, 0.30)	0.41 (0.30, 0.54)	(0.03, 0.01), 0.960	0.988
					3	0.35 (0.27, 0.45)	0.54 (0.39, 0.72)	(0.01, 0.01), 0.944	0.987
					4	0.26 (0.19, 0.33)	0.46 (0.35, 0.61)	(0.02, 0.01), 0.956	0.988
					5	0.28 (0.21, 0.37)	0.48 (0.36, 0.61)	(0.01, 0.01), 0.953	0.987
					6	0.49 (0.36, 0.64)	0.65 (0.45, 0.91)	(0, 0.01), 0.932	0.986
			5	0.36 (0.25, 0.47)	1	0.22 (0.15, 0.30)	0.43 (0.28, 0.58)	(0.03, 0.01), 0.958	0.987
					4	0.26 (0.18, 0.33)	0.48 (0.35, 0.63)	(0.02, 0.01), 0.953	0.986
			6	0.54 (0.36, 0.70)	1	0.22 (0.15, 0.29)	0.59 (0.39, 0.84)	(0.05, 0.01), 0.933	0.979
					4	0.26 (0.18, 0.34)	0.64 (0.44, 0.89)	(0.04, 0.01), 0.929	0.978
50	10	5	1	0.31 (0.22, 0.40)	1	0.44 (0.32, 0.56)	0.55 (0.39, 0.74)	(0.05, 0.02), 0.928	0.982
				0.31 (0.24, 0.40)	2	0.58 (0.43, 0.73)	0.67 (0.45, 0.96)	(0.05, 0.02), 0.897	0.976
				0.31 (0.23, 0.40)	3	0.51 (0.34, 0.69)	0.61 (0.40, 0.91)	(0.05, 0.02), 0.914	0.979
				0.31 (0.22, 0.45)	4	0.45 (0.31, 0.60)	0.57 (0.39, 0.78)	(0.05, 0.02), 0.925	0.981
					5	0.46 (0.30, 0.60)	0.57 (0.38, 0.79)	(0.05, 0.02), 0.923	0.980
				0.31 (0.23, 0.40)	6	0.61 (0.43, 0.82)	0.70 (0.49, 1.02)	(0.04, 0.02), 0.899	0.977
			2	0.51 (0.40, 0.60)	1	0.43 (0.34, 0.53)	0.70 (0.52, 0.99)	(0.03, 0.02), 0.892	0.961
			3	0.42 (0.31, 0.53)	1	0.44 (0.31, 0.56)	0.63 (0.45, 0.86)	(0.04, 0.02), 0.912	0.973
				0.42 (0.31, 0.53)	4	0.45 (0.31, 0.60)	0.66 (0.50, 0.92)	(0.03, 0.03), 0.910	0.972
			4	0.34 (0.23, 0.45)	1	0.44 (0.31, 0.57)	0.57 (0.41, 0.83)	(0.04, 0.02), 0.924	0.979
					3	0.51 (0.35, 0.68)	0.66 (0.47, 0.93)	(0.01, 0.03), 0.911	0.976
					4	0.45 (0.31, 0.59)	0.60 (0.42, 0.79)	(0.01, 0.03), 0.922	0.978
					5	0.46 (0.32, 0.59)	0.62 (0.42, 0.90)	(0.01, 0.03), 0.920	0.977
					6	0.60 (0.42, 0.81)	0.75 (0.51, 1.23)	(0.02, 0.02), 0.897	0.975
			5	0.36 (0.26, 0.47)	1	0.44 (0.33, 0.57)	0.58 (0.40, 0.82)	(0.04, 0.02), 0.922	0.978
				0.36 (0.27, 0.46)	4	0.45 (0.32, 0.60)	0.62 (0.42, 0.88)	(0.02, 0.03), 0.919	0.977
			6	0.54 (0.36, 0.70)	1	0.44 (0.32, 0.56)	0.72 (0.46, 1.08)	(0.06, 0.02), 0.898	0.968
				0.54 (0.36, 0.70)	4	0.45 (0.32, 0.60)	0.77 (0.46, 1.14)	(0.05, 0.02), 0.896	0.967

^aThe mean RE among 1000 simulations is calculated for each (r, ρ).

^bThe minimum, maximum, and median of mean RE including the corresponding (r, ρ)s are identified across all values of (r, ρ).

Table 3 reports the results from bias-corrected estimators when the number of practice is small, for example,. m= 6 and 20. Within a pattern of practice size, the smallest minimum is obtained at the pattern 5 of either practice size or provider size for any scenario.

1. The number of practice is 20: For the scenario of m = 20, n = 20, and K = 20, the minimums of minimums of mean REs for MD-corrected, FG-corrected estimators with d = 0.1, and FG-corrected estimators with d = 0.75 are 0.853, 0.904, and 0.865, respectively.; For the scenario of m = 20, n = 20, and K = 5, the minimums for these three corrected estimators are 0.818, 0.870, and 0.830, respectively; For the scenario of m = 20, n = 10, and K = 20, the minimums of these three corrected estimators are 0.837, 0.890, and 0.854, respectively; For the scenario of m = 20, n = 10, and K = 5, the minimums of these three corrected estimators are 0.818, 0.874, and 0.834, respectively.

2. The number of practice is 6: For the scenario of m = 6, n = 20, and K = 20, the minimums of minimums of mean REs for MD-corrected, FG-corrected estimators with d = 0.1, and FG-corrected estimators with d = 0.75 are 0.308, 0.797, and 0.510, respectively. They are reached when the pattern of provider size is either 5 or 6; For the scenario of m = 6, n = 20, and K = 5, the minimums for these three corrected estimators are 0.276, 0.782, and 0.476, respectively; For the scenario of m = 6, n = 10, and K = 20, the minimums of these three corrected estimators are 0.289, 0.789, and 0.495, respectively; For the scenario of m = 6, n = 10, and K = 5, the minimums of these three corrected estimators are 0.339, 0.802, and 0.500, respectively.

3. The minimums of mean RE for MD-corrected and FG-corrected estimators are stable when the number of practice is 20. However, they dropped unreasonably for a smaller number of practice, m = 6. Therefore, we suggest using FG-corrected estimators with d = 0.1 in the sample size calculations.

TABLE 3.

Minimum and Median of mean RE from bias-corrected estimators

								Mean REd MD-corrected estimators		Mean REd FG-corrected estimators with d = 0.1		Mean REd FG-corrected estimators with d = 0.75
m	n	K	PN (n)	CVa	PN (K)	CVb	CVc	(r, ρ)e Minimum	Mediane	(r, ρ)e Minimum	Mediane	(r, ρ)e Minimum	Mediane
20	20	20	1	0.22 (0.11, 0.34)	1	0.22 (0.12, 0.35)	0.32 (0.17, 0.46)	(0.02, 0) 0.968	0.997	(0.06, 0.01) 0.986	0.998	(0.03, 0) 0.973	0.997
					2	0.25 (0.10, 0.38)	0.34 (0.17, 0.53)	(0.02, 0) 0.963	0.997	(0.05, 0.01) 0.984	0.998	(0.02, 0) 0.968	0.997
					3	0.56 (0.31, 0.72)	0.61 (0.34, 0.87)	(0.02, 0) 0.889	0.996	(0.05, 0) 0.940	0.997	(0.03, 0) 0.902	0.996
					4	0.47 (0.37, 0.59)	0.53 (0.37, 0.69)	(0.05, 0) 0.891	0.994	(0, 0.01) 0.934	0.995	(0.06, 0) 0.901	0.994
					5	0.58 (0.46, 0.70)	0.63 (0.48, 0.79)	(0.05, 0) 0.853	0.994	(0.07, 0) 0.906	0.995	(0.05, 0) 0.865	0.994
					6	0.40 (0.29, 0.54)	0.47 (0.26, 0.68)	(0.03, 0) 0.924	0.996	(0, 0.01) 0.959	0.997	(0.04, 0) 0.932	0.996
			2	0.25 (0.12, 0.38)	1	0.22 (0.13, 0.35)	0.34 (0.18, 0.55)	(0.03, 0) 0.964	0.996	(0.06, 0.01) 0.983	0.997	(0.03, 0) 0.970	0.996
					2	0.25 (0.13, 0.38)	0.40 (0.20, 0.61)	(0.03, 0) 0.962	0.996	(0.03, 0.01) 0.981	0.997	(0.04, 0) 0.970	0.996
			3	0.55 (0.42, 0.73)	1	0.22 (0.12, 0.34)	0.60 (0.36, 0.89)	(0.02, 0) 0.896	0.985	(0.13, 0.01) 0.936	0.988	(0.26, 0.01) 0.910	0.985
			4	0.46 (0.36, 0.56)	1	0.22 (0.12, 0.33)	0.52 (0.38, 0.69)	(0.16, 0.01) 0.904	0.974	(0.10, 0.01) 0.931	0.979	(0.16, 0.01) 0.911	0.974
			5	0.58 (0.45, 0.70)	1	0.22 (0.11, 0.35)	0.63 (0.44, 0.82)	(0.20, 0.01) 0.865	0.966	(0.10, 0.01) 0.904	0.973	(0.18, 0.01) 0.875	0.966
			6	0.40 (0.25, 0.56)	1	0.22 (0.12, 0.33)	0.46 (0.28, 0.66)	(0.22, 0.01) 0.935	0.985	(0.10, 0.01) 0.955	0.988	(0.15, 0.01) 0.939	0.985
20	20	5	1	0.22 (0.11, 0.34)	1	0.43 (0.25, 0.67)	0.49 (0.23, 0.84)	(0.09, 0) 0.920	0.993	(0.06, 0.01) 0.948	0.995	(0, 0.01) 0.927	0.993
				0.22 (0.11, 0.33)	2	0.45 (0.27, 0.70)	0.51 (0.25, 0.91)	(0.08, 0) 0.915	0.993	(0.04, 0.01) 0.945	0.994	(0.01, 0.01) 0.923	0.993
				0.22 (0.11, 0.32)	3	0.64 (0.38, 1.00)	0.68 (0.39, 1.02)	(0.08, 0) 0.855	0.989	(0.04, 0.01) 0.904	0.991	(0.12, 0) 0.871	0.989
				0.23 (0.14, 0.32)	4	0.56 (0.41, 0.70)	0.62 (0.41, 0.81)	(0.11, 0) 0.871	0.989	(0.09, 0.01) 0.912	0.991	(0.01, 0.01) 0.883	0.989
				0.23 (0.15, 0.32)	5	0.64 (0.49, 0.85)	0.69 (0.49, 0.92)	(0.11, 0) 0.840	0.987	(0.06, 0.01) 0.891	0.989	(0.13, 0) 0.856	0.987
				0.22 (0.13, 0.32)	6	0.52 (0.33, 0.84)	0.58 (0.32, 0.94)	(0.08, 0) 0.889	0.991	(0.04, 0.01) 0.925	0.993	(0, 0.01) 0.900	0.991
			2	0.25 (0.13, 0.38)	1	0.43 (0.25, 0.66)	0.51 (0.26, 0.89)	(0.07, 0) 0.915	0.992	(0.02, 0.01) 0.945	0.994	(0.01, 0.01) 0.923	0.992
					2	0.45 (0.25, 0.68)	0.55 (0.31, 0.95)	(0, 0.01) 0.912	0.991	(0.02, 0.01) 0.942	0.993	(0, 0.01) 0.918	0.991
			3	0.55 (0.42, 0.71)	1	0.43 (0.25, 0.66)	0.72 (0.43, 1.17)	(0.06, 0) 0.844	0.978	(0.03, 0.01) 0.897	0.982	(0.08, 0.01) 0.865	0.978
			4	0.46 (0.37, 0.56)	1	0.43 (0.25, 0.66)	0.66 (0.43, 0.97)	(0.02, 0.01) 0.854	0.966	(0.02, 0.01) 0.897	0.972	(0.02, 0.01) 0.863	0.967
			5	0.58 (0.45, 0.70)	1	0.43 (0.24, 0.67)	0.75 (0.48, 1.20)	(0.03, 0.01) 0.818	0.958	(0, 0.01) 0.870	0.965	(0.03, 0.01) 0.830	0.958
			6	0.40 (0.25, 0.56)	1	0.43 (0.24, 0.67)	0.61 (0.39, 1.06)	(0, 0.01) 0.882	0.979	(0.04, 0.01) 0.918	0.983	(0, 0.01) 0.890	0.979
20	10	20	1	0.31 (0.18, 0.49)	1	0.22 (0.11, 0.34)	0.39 (0.21, 0.64)	(0.03, 0) 0.954	0.989	(0.03, 0.01) 0.972	0.993	(0.06, 0.01) 0.960	0.989
					2	0.25 (0.13, 0.38)	0.41 (0.23, 0.63)	(0.01, 0) 0.949	0.989	(0.03, 0.01) 0.969	0.992	(0.05, 0.01) 0.957	0.989
					3	0.55 (0.40, 0.73)	0.64 (0.39, 0.95)	(0.02, 0) 0.874	0.987	(0, 0.01) 0.926	0.990	(0.02, 0) 0.891	0.987
					4	0.47 (0.38, 0.59)	0.58 (0.40, 0.89)	(0.05, 0) 0.876	0.983	(0.02, 0.01) 0.913	0.987	(0.05, 0) 0.889	0.983
					5	0.58 (0.46, 0.71)	0.68 (0.46, 0.91)	(0.03, 0) 0.837	0.983	(0.01, 0.01) 0.890	0.986	(0.05, 0) 0.854	0.983
					6	0.40 (0.29, 0.54)	0.52 (0.32, 0.76)	(0.04, 0) 0.909	0.986	(0.01, 0.01) 0.940	0.990	(0.04, 0) 0.920	0.986
			2	0.34 (0.19, 0.51)	1	0.22 (0.11, 0.34)	0.41 (0.21, 0.64)	(0.02, 0) 0.950	0.988	(0.03, 0.01) 0.968	0.991	(0.05, 0.01) 0.955	0.988
					2	0.25 (0.13, 0.38)	0.46 (0.25, 0.70)	(0.03, 0) 0.949	0.987	(0.02, 0.01) 0.965	0.991	(0.04, 0.01) 0.951	0.987
			3	0.59 (0.40, 0.79)	1	0.22 (0.11, 0.34)	0.63 (0.36, 0.92)	(0.01, 0) 0.884	0.966	(0.05, 0.01) 0.922	0.973	(0.12, 0.01) 0.895	0.967
			4	0.48 (0.39, 0.62)	1	0.22 (0.11, 0.32)	0.54 (0.37, 0.68)	(0.08, 0.01) 0.901	0.964	(0.03, 0.01) 0.930	0.973	(0.08, 0.01) 0.908	0.965
			5	0.58 (0.47, 0.71)	1	0.22 (0.11, 0.32)	0.63 (0.49, 0.79)	(0.10, 0.01) 0.868	0.952	(0.03, 0.01) 0.908	0.963	(0.10, 0.01) 0.877	0.953
			6	0.44 (0.30, 0.63)	1	0.22 (0.11, 0.32)	0.50 (0.33, 0.76)	(0.12, 0.01) 0.922	0.975	(0.04, 0.01) 0.946	0.981	(0.08, 0.01) 0.927	0.975
20	10	5	1	0.31 (0.18, 0.47)	1	0.43 (0.24, 0.74)	0.55 (0.28, 0.95)	(0.03, 0.01) 0.905	0.981	(0.03, 0.02) 0.937	0.985	(0.03, 0.01) 0.911	0.981
					2	0.45 (0.26, 0.82)	0.56 (0.32, 1.03)	(0.01, 0.01) 0.898	0.980	(0.05, 0.02) 0.934	0.985	(0.04, 0.01) 0.907	0.981
				0.31 (0.18, 0.49)	3	0.64 (0.38, 0.94)	0.73 (0.42, 1.30)	(0.06, 0) 0.839	0.974	(0.04, 0.02) 0.892	0.979	(0.02, 0.01) 0.855	0.974
				0.31 (0.21, 0.45)	4	0.56 (0.40, 0.71)	0.66 (0.42, 0.92)	(0.10, 0) 0.857	0.974	(0.08, 0.02) 0.903	0.979	(0.04, 0.01) 0.869	0.974
				0.32 (0.19, 0.46)	5	0.64 (0.49, 0.94)	0.74 (0.48, 1.13)	(0.12, 0) 0.824	0.969	(0.10, 0.02) 0.880	0.975	(0.07, 0.01) 0.842	0.970
				0.31 (0.18, 0.47)	6	0.53 (0.32, 0.80)	0.64 (0.39, 1.11)	(0.02, 0.01) 0.872	0.977	(0.05, 0.02) 0.914	0.982	(0.05, 0.01) 0.883	0.977
			2	0.33 (0.19, 0.50)	1	0.43 (0.24, 0.74)	0.56 (0.30, 1.05)	(0.02, 0.01) 0.898	0.979	(0.04, 0.02) 0.934	0.984	(0.02, 0.01) 0.907	0.979
					2	0.45 (0.26, 0.82)	0.60 (0.33, 1.13)	(0.01, 0.01) 0.894	0.978	(0.04, 0.02) 0.931	0.983	(0.06, 0.01) 0.904	0.978
			3	0.59 (0.40, 0.79)	1	0.43 (0.24, 0.74)	0.75 (0.43, 1.29)	(0.06, 0) 0.832	0.955	(0.05, 0.02) 0.888	0.963	(0.06, 0.01) 0.847	0.956
			4	0.48 (0.39, 0.62)	1	0.43 (0.26, 0.64)	0.67 (0.46, 0.96)	(0.01, 0.01) 0.851	0.953	(0.03, 0.02) 0.898	0.962	(0.05, 0.01) 0.865	0.954
			5	0.58 (0.47, 0.71)	1	0.43 (0.26, 0.62)	0.75 (0.48, 1.11)	(0.01, 0.01) 0.818	0.940	(0.03, 0.02) 0.874	0.952	(0.01, 0.01) 0.834	0.941
			6	0.44 (0.30, 0.63)	1	0.43 (0.25, 0.65)	0.64 (0.36, 1.14)	(0.03, 0.01) 0.868	0.965	(0.02, 0.02) 0.912	0.972	(0.03, 0.01) 0.879	0.965
6	20	20	1	0.22 (0.03, 0.46)	1	0.21 (0.03, 0.49)	0.31 (0.04, 0.67)	(0, 0) 0.870	0.997	(0.04, 0) 0.979	0.998	(0, 0) 0.911	0.997
					2	0.36 (0.12, 0.63)	0.42 (0.08, 0.85)	(0, 0) 0.773	0.997	(0.04, 0) 0.956	0.997	(0, 0) 0.842	0.997
					3	0.54 (0.28, 0.84)	0.58 (0.12, 1.07)	(0, 0) 0.633	0.996	(0.03, 0) 0.917	0.996	(0, 0) 0.733	0.996
					4	0.54 (0.32, 0.82)	0.59 (0.36, 0.90)	(0, 0) 0.543	0.991	(0.07, 0) 0.875	0.992	(0, 0) 0.686	0.991
					5	0.74 (0.55, 0.92)	0.78 (0.54, 1.11)	(0, 0) 0.308	0.989	(0.07, 0) 0.797	0.990	(0, 0) 0.510	0.989
					6	0.81 (0.50, 1.16)	0.83 (0.30, 1.37)	(0, 0) 0.421	0.994	(0.04, 0) 0.838	0.995	(0, 0) 0.551	0.995
			2	0.36 (0.08, 0.64)	1	0.21 (0.03, 0.49)	0.42 (0.12, 0.88)	(0, 0) 0.770	0.992	(0.23, 0.01) 0.959	0.993	(0, 0) 0.840	0.992
			3	0.54 (0.18, 0.86)	1	0.21 (0.03, 0.49)	0.58 (0.17, 1.10)	(0, 0) 0.633	0.985	(0.29, 0.01) 0.921	0.986	(0.01, 0) 0.732	0.985
			4	0.53 (0.37, 0.69)	1	0.21 (0.03, 0.49)	0.57 (0.34, 0.85)	(0.01, 0) 0.573	0.946	(0.10, 0.01) 0.891	0.960	(0.01, 0) 0.700	0.951
			5	0.73 (0.51, 0.95)	1	0.21 (0.03, 0.48)	0.76 (0.48, 1.12)	(0.01, 0) 0.327	0.918	(0.12, 0.01) 0.814	0.936	(0.01, 0) 0.522	0.925
			6	0.82 (0.44, 1.15)	1	0.21 (0.03, 0.49)	0.83 (0.43, 1.41)	(0.02, 0) 0.422	0.963	(0.32, 0.01) 0.842	0.967	(0.01, 0) 0.547	0.964
6	20	5	1	0.22 (0.04, 0.46)	1	0.41 (0.13, 0.85)	0.47 (0.11, 1.14)	(0, 0) 0.722	0.994	(0, 0.01) 0.937	0.994	(0, 0) 0.804	0.994
				0.22 (0.03, 0.46)	2	0.49 (0, 1.02)	0.54 (0.14, 1.08)	(0, 0) 0.650	0.993	(0.01, 0.01) 0.918	0.993	(0, 0) 0.752	0.993
					3	0.61 (0.13, 1.29)	0.65 (0.13, 1.27)	(0, 0) 0.546	0.990	(0.09, 0) 0.887	0.991	(0, 0) 0.667	0.990
				0.22 (0.03, 0.42)	4	0.58 (0.18, 1.03)	0.62 (0.19, 1.14)	(0, 0) 0.541	0.988	(0.17, 0) 0.882	0.989	(0, 0) 0.677	0.988
				0.21 (0.04, 0.44)	5	0.74 (0.40, 1.14)	0.77 (0.47, 1.29)	(0, 0) 0.359	0.983	(0.15, 0) 0.824	0.985	(0, 0) 0.534	0.984
				0.22 (0.03, 0.46)	6	0.83 (0.36, 1.39)	0.85 (0.35, 1.58)	(0, 0) 0.406	0.986	(0.09, 0) 0.824	0.987	(0, 0) 0.538	0.986
			2	0.36 (0.08, 0.64)	1	0.41 (0.13, 0.85)	0.55 (0.10, 1.18)	(0, 0) 0.642	0.987	(0.04, 0.01) 0.915	0.988	(0, 0) 0.743	0.988
			3	0.54 (0.18, 0.86)	1	0.41 (0.13, 0.85)	0.67 (0.15, 1.38)	(0, 0) 0.534	0.979	(0.04, 0.01) 0.881	0.981	(0, 0) 0.653	0.980
			4	0.53 (0.37, 0.69)	1	0.41 (0.13, 0.81)	0.68 (0.35, 1.16)	(0.01, 0) 0.462	0.936	(0.02, 0.01) 0.854	0.954	(0.01, 0) 0.611	0.943
			5	0.73 (0.51, 0.95)	1	0.41 (0.13, 0.81)	0.85 (0.43, 1.37)	(0.01, 0) 0.276	0.905	(0, 0.01) 0.782	0.928	(0.01, 0) 0.476	0.914
			6	0.82 (0.44, 1.15)	1	0.41 (0.13, 0.85)	0.88 (0.24, 1.65)	(0, 0) 0.369	0.954	(0.13, 0.01) 0.806	0.961	(0.03, 0) 0.505	0.957
6	10	20	1	0.31 (0.06, 0.65)	1	0.21 (0.03, 0.49)	0.37 (0.07, 0.82)	(0, 0) 0.809	0.989	(0.06, 0.01) 0.964	0.991	(0, 0) 0.871	0.989
					2	0.36 (0.12, 0.63)	0.47 (0.08, 0.99)	(0, 0) 0.720	0.988	(0.04, 0) 0.947	0.990	(0, 0) 0.805	0.988
					3	0.54 (0.28, 0.84)	0.61 (0.16, 1.19)	(0, 0) 0.597	0.986	(0.04, 0) 0.909	0.988	(0, 0) 0.705	0.987
					4	0.54 (0.32, 0.82)	0.63 (0.38, 1.03)	(0, 0) 0.502	0.975	(0.07, 0) 0.864	0.980	(0, 0) 0.651	0.977
				0.30 (0.06, 0.65)	5	0.74 (0.55, 0.92)	0.81 (0.53, 1.29)	(0, 0) 0.289	0.970	(0.07, 0) 0.789	0.975	(0, 0) 0.495	0.972
				0.31 (0.06, 0.65)	6	0.81 (0.50, 1.16)	0.85 (0.25, 1.52)	(0, 0) 0.404	0.982	(0.04, 0) 0.830	0.985	(0, 0) 0.539	0.983
			2	0.42 (0.11, 0.80)	1	0.21 (0.03, 0.49)	0.47 (0.09, 1.02)	(0, 0) 0.721	0.978	(0.08, 0.01) 0.942	0.982	(0, 0) 0.803	0.979
			3	0.57 (0.19, 1.02)	1	0.21 (0.03, 0.49)	0.60 (0.19, 1.22)	(0, 0) 0.603	0.963	(0.10, 0.01) 0.907	0.970	(0.01, 0) 0.711	0.966
			4	0.54 (0.35, 0.85)	1	0.21 (0.03, 0.49)	0.57 (0.32, 0.96)	(0.01, 0) 0.586	0.943	(0.07, 0.01) 0.898	0.958	(0.01, 0) 0.704	0.949
			5	0.69 (0.42, 0.96)	1	0.22 (0.06, 0.48)	0.73 (0.40, 1.18)	(0.03, 0) 0.393	0.911	(0.04, 0.01) 0.842	0.933	(0, 0) 0.563	0.919
			6	0.81 (0.32, 1.32)	1	0.21 (0.03, 0.49)	0.83 (0.35, 1.48)	(0.03, 0) 0.424	0.932	(0.13, 0.01) 0.837	0.945	(0.01, 0) 0.548	0.937
6	10	5	1	0.31 (0.06, 0.65)	1	0.41 (0.13, 0.85)	0.52 (0.12, 1.27)	(0, 0) 0.676	0.980	(0, 0.02) 0.923	0.984	(0, 0) 0.768	0.982
					2	0.49 (0, 1.02)	0.58 (0.14, 1.23)	(0, 0) 0.609	0.978	(0.04, 0.01) 0.904	0.982	(0, 0) 0.718	0.980
					3	0.61 (0.13, 1.29)	0.69 (0.16, 1.42)	(0, 0) 0.515	0.972	(0.05, 0.01) 0.872	0.977	(0, 0) 0.640	0.974
				0.31 (0.06, 0.59)	4	0.58 (0.18, 1.03)	0.66 (0.27, 1.27)	(0, 0) 0.508	0.968	(0.11, 0.01) 0.870	0.975	(0.01, 0) 0.649	0.971
				0.30 (0.09, 0.63)	5	0.74 (0.40, 1.14)	0.79 (0.45, 1.40)	(0, 0) 0.342	0.959	(0.09, 0.01) 0.808	0.967	(0, 0) 0.518	0.962
				0.31 (0.06, 0.65)	6	0.83 (0.36, 1.39)	0.87 (0.23, 1.72)	(0, 0) 0.386	0.963	(0.02, 0.01) 0.811	0.970	(0, 0) 0.520	0.966
			2	0.42 (0.11, 0.80)	1	0.41 (0.13, 0.85)	0.59 (0.12, 1.31)	(0, 0) 0.602	0.968	(0, 0.01) 0.902	0.975	(0, 0) 0.712	0.970
			3	0.57 (0.19, 1.02)	1	0.41 (0.13, 0.85)	0.69 (0.20, 1.48)	(0, 0) 0.509	0.951	(0, 0.01) 0.867	0.961	(0.01, 0) 0.630	0.955
			4	0.54 (0.35, 0.85)	1	0.40 (0.13, 0.74)	0.67 (0.32, 1.19)	(0, 0) 0.503	0.931	(0.08, 0.02) 0.863	0.950	(0.02, 0) 0.629	0.939
			5	0.69 (0.42, 0.96)	1	0.43 (0.13, 0.77)	0.82 (0.39, 1.40)	(0, 0) 0.339	0.894	(0.13, 0.02) 0.810	0.923	(0.03, 0) 0.500	0.905
			6	0.81 (0.32, 1.32)	1	0.41 (0.13, 0.85)	0.88 (0.20, 1.67)	(0, 0) 0.369	0.917	(0.04, 0.01) 0.802	0.935	(0.05, 0) 0.511	0.924

K: provider size; m: number of practices; n: practice size; PN: pattern.

^aCV of practice size, mean (min, max).

^bCV of provider size, mean (min, max).

^cCV of cluster size, mean (min, max).

^dThe mean RE among 1000 simulations is calculated for each (r, ρ).

^eThe minimum and median of mean RE including the corresponding (r, ρ)s are identified across all values of (r, ρ).

Proposed Algorithm

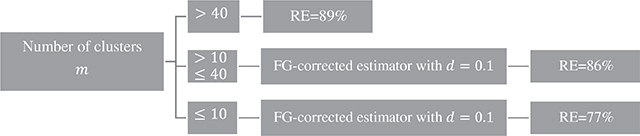
Appendix Table 3 presents the results for a smaller practice size n = 5 while Appendix Tables 4 and 5 show the results for a binary outcome (p₀ = 0.2 and p₁ = 0.3) and a count outcome (β_b = 1.5), respectively. Even if we set the different values of p₀ and p₁ in the binary outcome and of β_b in the count outcome, the findings remain consistent across the simulation settings. Suppose we use an asymptotic estimator to calculate RE for m = 20 or 6, shown in Appendix Table 6, all minimums of mean REs are larger than 86% for m = 20 and 82% for m = 6.When comparing REs between asymptotic and bias-corrected estimations, we find that RE from an asymptotic estimator underestimates the efficiency loss for smallest number of practices. In summary, the worst scenario gives 11% efficiency loss (RE = 89%) for the large number of practices, m = 50, 13% (RE = 87%) for the smaller number of practices, m = 20, and 23% (RE = 77%) for the smallest number of practices, m = 6, respectively.

5 |. PROPOSED ALGORITHM

Sections 2 and 3 provide the required number of practices when assuming equal practice size for continuous, binary, and count outcomes, respectively. Teerenstra et al¹⁸ also proposed the required number of practices with the assumptions of equal practice sizes and K_ij ≡ K for continuous and binary outcomes from a t-distribution with m − 2 of freedom. For practical purposes they suggest substituting z_αfor the t_α and multiply the result by the factor (m + 1)/(m − 1). When unequal practice sizes occur—the most common situation—we should increase the number of practices in order to compensate for efficiency loss due to unequal practice sizes.

For simplicity and to be conservative, we approximate RE in the way shown in the proposed diagram. If m > 40, then 13% (=1/0.89−1) more practices is needed since REs from asymptotic estimation are at least 0.89. If m ≤ 10, then we must sample 30% more practices using an FG-corrected estimator with d = 0.1; If 10 < m ≤ 40, then sampling 15% more practices are needed from an FG-corrected estimators with d = 0.1 to cover the efficiency loss;

Table 4 illustrates the adjustment in number of practices for a continuous outcome with β₂ = 0.2 and σ = 1. The numbers m in the fifth column are calculated from Section 2 at the type I error of 5% and 80% power, while the remaining columns are adjusted by the algorithm mentioned above. It also shows that increasing provider size has a little effect on the sample size calculation of the number of practices.

TABLE 4.

Number of practices adjustments with β_b = 0.2 and σ = 1

K	(r,ρ)	n	φ	m	Asymptotic	FG-corrected with d=0.1
3	(0.2, 0.01)	50	2.87	16		20
		150	5.87	12		14
	(0.2, 0.1)	50	16.1	86	98
		150	46.1	82	94
4	(0.2, 0.01)	50	3.56	14		18
		150	7.56	10		12
	(0.2, 0.1)	50	21.2	84	96
		150	61.2	82	94
5	(0.2, 0.01)	50	4.25	14		18
		150	9.25	10		12
	(0.2, 0.1)	50	26.3	84	96
		150	76.3	80	90
6	(0.2, 0.01)	50	4.94	14		18
		150	10.94	10		12
	(0.2, 0.1)	50	31.4	84	96
		150	91.4	80	90

6 |. AN EXAMPLE

In our work with three-level CRTs,⁴⁰ we take the Helping Hands trial (Netherlands Organization for Health Research and Development ZonMw, grant number 80–007028-98–07101) as an example to present the optimal designs with a given budget. Here, we still use it to show the revised sample size through the algorithm proposed in this article. The trial aimed to change nurse behavior through two strategies, where the state-of-the-art strategy is derived from the literature including education, reminders, feedback, and targeting adequate products and facilities, and the extended strategy contains all elements of the state-of-the-art strategy plus activities aimed at influencing social influence in groups and enhancing leadership. This study randomized the wards to either one strategy and the primary endpoint is adherence to hygiene guidelines, where the multiple evaluations of nurses’ guideline adherence were observed. From 60% in the state-of-the-art strategy to 70% in the extended strategy for the primary endpoint was expected.

The evaluations of adherence to hygiene guidelines are nested within nurses and nurses are nested within wards. All nurses in a ward receiving the same strategy can be considered exchangeable. Teerenstra et al¹⁸ supposed that these evaluations are exchangeable within a nurse since the evaluations “measure” hygiene behavior of a nurse. They supposed the constant behavior of nurse (r = 0.6) and intra-ward coefficient correlation ρ = 0.03. Using n = 15 and K = 3, they calculated the total number of wards m = 58. From our proposed algorithm, we suggest enrolling 66 = (58/0.89) wards when unequal number of nurses across wards.

7 |. DISCUSSION

The sample size formulas for three-level CRTs have been derived in recent years reflecting the increasing interest in evaluation of interventions in real world settings.^17,18 Teerenstra et al¹⁸ considered a GEE approach, introduced a nested exchangeable correlation structure and derived a sample size formula assuming the equal cluster sizes and same number of evaluations within a subject for both continuous and binary outcomes. However, the assumption of equal cluster sizes is not realistic. Researchers defined the RE of unequal vs equal cluster sizes as the ratio of variance of the estimator of the treatment effect for equal to unequal cluster sizes in two-level CRTs.^13–16 In practice, the researchers have no clear picture about the cluster size distribution, and thus the minimum of RE from the various cluster size distribution in simulation studies are considered to increase the number of clusters for efficiency loss due to unequal cluster sizes. In our previous work we proposed an adjusted sample size from relative efficacy derived from GEE models in two-level CRTs.¹⁵ In this article, we use the same definition of RE and then evaluate the performances of REs in three-level CRTs to test the treatment effect in a two-group comparison. The three outcomes of continuous, binary, or count data are discussed simultaneously based on GEE models. The variances of the estimator of the treatment effect are derived for three different types of outcome given the nested exchangeable correlation structure.

To our knowledge, there is no sample size formula for count data in three-level CRTs. We assume equal practice sizes and provider sizes and thus derive the explicit sample size formula, shown following Equation (4). Second, we find the formulas of REs from asymptotic estimation are the same for continuous, binary, and count data using GEE models. That is, RE is not dependent on the type of outcome. Furthermore, $\mathrm{RE}\left({\widehat{\beta }}_2\right)$ is independent of cluster allocation π, the parameters β₁ and β₂. These findings are the same as in two-level CRTs.¹⁵ Third, we also consider two bias-corrected estimators for CRTs with finite practices, for example,. m ≤ 40. REs formulas are different for three types of outcomes and there is no closed-form for REs. They depend on cluster allocations π and the efficacy measure β₂. Fourth, even if λ_3i depends on K besides n_i given a pair of (r, ρ), K has minimal effect on REs for both asymptotic and bias-corrected estimators. Finally, we find that the minimums of mean RE for MD-corrected and FG-corrected estimators are stable when the number of practice is 20. However, they dropped unreasonably for a smaller number of practice, m = 6. Therefore, we suggest using FG-corrected estimators with d = 0.1 in the sample size calculations.

There are several limitations to this approach. The first limitation is that the covariates are not considered in the sample size calculation. The sample size formulas including covariates in the GEE model are definitely more complicated than those in sections 2. Liu and Liang⁴¹ also showed that the performance of the sample size formula is sensitive to the distribution of the covariates. The next limitation is that our proposed RE is investigated based on the nested exchangeable correlation structure only. It is suitable when the lowest level units are exchangeable within the middle level units and the middle level units are exchangeable within the highest level units.¹⁸ Teerenstra et al¹⁸ provided more examples where this structure is reasonable. This assumption may not hold in some scenarios. However, the sample size formulas from GEE models used an exchangeable working correlation structure in two-level CRTs^25,36 and thus the nested exchangeable correlation structure is acceptable for three-level CRTs as well. In addition, Breukelen et al proposed a uniform, positively skewed, negatively skewed, bimodal and unimodal distribution of cluster size in a two-level CRT.¹⁴ They showed that a bimodal distribution has the lowest minimum RE. We assume that practice (provider) sizes follow multinomial distributions and consider only six patterns of the distribution after the sorting of the distribution probabilities. However, more complicated patterns with combinations of these six may occur in practice. Therefore, our $\mathrm{RE}\left({\widehat{\beta }}_2\right)$ may be underestimated for some complicated patterns. This is the third limitation. The fourth limitation is that we assume that practice sizes and provider sizes are independent, and they follow multinomial distributions with $mn={\sum }_{i=1}^m{n}_i$ and probabilities (p_1n, · · ·,p_mn), and $mK={\sum }_{i=1}^m{K}_i$ and probabilities (p_1n, · · ·,p_mk), respectively. Under this assumption, ${\sum }_{i=1}^m{K}_i{n}_i=Knm$ cannot be guaranteed. However, we only consider the scenarios in which the mean total sample size among 1000 samples lies within the range of (0.975 × Knm, 1.025 × Knm) such that it is very close to Knm. The last limitation is that two-group comparison is considered. In practice, researchers may consider more than two groups for comparisons. These could be future research directions.

In conclusion, this article discusses efficiency loss based on GEE models in three-level CRTs and proposes the adjustment of number of practices when unequal practice sizes and provider size occur for both large and small number of cluster studies. We believe that this investigation is very useful and practical, especially for designing three-level CRTs with any outcome types.

DATA AVAILABILITY STATEMENT

Data sharing is not applicable to this article as no new data were created or analyzed in this study.