Development of Martini 2.2 parameters for N-glycans: a case study of the HIV-1 Env glycoprotein dynamics

Abstract

N-linked glycans are ubiquitous in nature and play key roles in biology. For example, glycosylation of pathogenic proteins is a common immune evasive mechanism, hampering the development of successful vaccines. Due to their chemical variability and complex dynamics, an accurate molecular understanding of glycans is still limited by the lack of effective resolution of current experimental approaches. Here, we have developed and implemented a reductive model based on the popular Martini 2.2 coarse-grained force field for the computational study of N-glycosylation. We used the HIV-1 Env as a direct applied example of a highly glycosylated protein. Our results indicate that the model not only reproduces many observables in very good agreement with a fully atomistic force field but also can be extended to study large amount of glycosylation variants, a fundamental property that can aid in the development of drugs and vaccines.

Introduction

It is of general agreement that glycosylation plays critical roles in a wide range of biological processes, from cellular signaling and structural stability to immune system interactions (Spiro 2002; Mitra et al. 2006; Marth and Grewal 2008; Solá and Griebenow 2009; Lannoo and Van Damme 2015; Stanley et al. 2015). The site-specific diversity of glycan occupancy and of glycoform content leads to the diversification of both structure and function of a single glycoprotein. Thus, this energetically expensive process becomes one of the most rewarding evolutionary steps from a biological standpoint.

Many organisms rely on this process for their survival. For instance, in Archaea, glycans enhance the stability of the proteins in order to optimally perform under the harsh conditions of their habitats (Yurist-Doutsch et al. 2008; Calo et al. 2010; Eichler 2013). The “shielding” of key viral surface proteins by glycosylation is a common approach to evade the immune system of more complex eukaryote organisms (Marth and Grewal 2008; Behrens et al. 2016; Valguarnera et al. 2016; Bagdonaite and Wandall 2018). Such shielding of the proteins allows the organisms not only to survive inside the host but is also a very effective mechanism for avoiding future attacks from a more mature immune response. For instance, many viruses make use of such evasive processes, parasitizing the constitutive glycosylation machinery of the cellular target (Pancera et al. 2014; Bagdonaite and Wandall 2018).

From the biophysical perspective, glycosylation modifies several physical aspects of proteins (Mitra et al. 2006; Solá and Griebenow 2009; Gavrilov et al. 2015; Lee et al. 2015). In fact, the addition of glycan moieties can affect the thermodynamics and kinetics of the folding pathway of a protein, favoring a particular state or enhancing the stabilization of a particular configurational ensemble (Jayaprakash and Surolia 2017). The vast extent of hydrogen network created by glycans allows proteins to be resilient to temperature or chemical denaturation. Carbohydrates can also enhance the interaction with cellular receptors by retaining specific contacts with the proteins of interest (Marth and Grewal 2008).

Despite the role of glycosylation and its impact on protein function, a clear picture of the glycan architecture and dynamics at molecular resolution is not yet accessible. Techniques like cryo-electron microscopy (cryo-EM) can capture the large ensemble of glycan dynamics at low filtering thresholds but remain noisy and lack the required resolution for detailed atomistic information (Ward and Wilson 2017). Others like X-ray diffraction or mass spectrometry (MS) are unable to provide dynamic information (Davis and Crispin 2010; Go et al. 2017). On the other hand, high-resolution methods (e.g., NMR) are mostly limited to small molecules and are not very effective for larger protein–glycan ensembles. Thus, there is an urgent need for developing new methods that can capture the dynamical complexity of glycans at higher resolutions.

Computational simulations like molecular dynamics (MD) can provide relevant atomic level information. In fact, several force fields have been developed for studying carbohydrates. Fully atomistic implementations based on widely used force fields like AMBER (Kirschner et al. 2008; Tessier et al. 2008; Demarco 2015), CHARMM (Guvench et al. 2008, 2011; Mallajosyula et al. 2015; Alessandri et al. 2019), GROMOS (Huang et al. 2011) and OPLS (Jorgensen et al. 1996) are available and offer a large variety of biomolecules, which can be coupled with carbohydrates. A couple of them possess integrated and automated web platforms for setting up glycoproteins with all the required ingredients for a successful simulation (Jo et al. 2017) (www.glycam.org). Development of such tools has provided a vast collection of relevant data, which has increased our knowledge in glycobiology.

A common limitation with computer simulations, especially when applying fully atomistic representations (AA), is the size and complexity of the system under study. If combined with large computational requirements, such approaches become limited to only users with access to special infrastructures. One way to deal with this kind of shortcomings is the use of reductive models (Ingolfsson et al. 2014). A reductive model aims to reproduce a set of physical properties while reducing the effective number of particles in the system, resulting in a more efficient exploration of the energy landscape. Such approaches have been widely used and have been beneficial for studying large complex systems (Ingolfsson et al. 2014).

Encouraged by this concept, we have implemented parameters for the simulation of a large variety of asparagine-linked glycans (N-glycans). These models are based on the widely used Martini (Marrink et al. 2007) coarse-grained (CG) force field and retain consistency when combined with other molecules that are part of the force field. As a test case, we study the HIV-1 Env protein as an example of a densely glycosylated protein (Lasky et al. 1986). Direct comparison to fully atomic simulations using CHARMM36 clearly shows that the CG parameters are able to reproduce many properties. However, given the simplicity of the model, we have investigated the effect of different N-glycan variants and how this is transmitted to the overall Env architecture. Overall, our results suggest that the new N-glycan CG parameters can be used and extended for studying other glycoproteins, either by themselves or in combination with other biomolecules without the burden of large computational resources.

Results

Parametrization of N-glycans

In this section, we provide a general description of the parameters implemented specifically for the N-glycan topologies. A more thorough formulation of the Martini force field can be found in the original works (Marrink et al. 2007; Lopez et al. 2009), specially describing the functions of bonded potentials as well as a full description of the beads self-interaction matrix.

Similar to the original work for the adaptation of parameters for carbohydrates (Lopez et al. 2009), our procedure started by properly describing the internal dynamics of the molecules in combination with the proper calibration of the octanol–water partition coefficient (LogPo-w). Reproducing the internal dynamics of single carbohydrate units was not a difficult task. Distributions of internal AA bonded terms were easily adapted into the CG models, and as can be seen (Figure S1B), they are in very good match. In particular cases (N-acetylglucosamine, neuraminic acid), it was necessary to implement exclusions between particles defining internal angles due to the compact geometry of carbohydrates. This procedure allows the system to run without numerical instabilities even at larger time-steps (40 fs); however, we decided to set the integration speed at 30 fs time-steps.

Defining the bonded terms for larger glycans was a more complex task. First, we found that using a simple building block approach was unable to fully reproduce many angles and torsions, key property for the proper projection of the different monosaccharide subunits (e.g., glycosidic bond orientation). This issue became more noticeable when trying to connect branched glycans (e.g., Man-9). Therefore, we proceeded to independently fit both angles and torsions for each of the glycans as populated from their corresponding AA simulations. With respect to this, long AA simulations proved that most of the distributions are unimodal, which can be obtained with good accuracy, even for complicated topologies.

Second, connecting consecutive monomeric subunits can lead to the generation of a variety of alternative parameters sets, as exemplified in Figure S1D. However, some of them can lead to higher numerical instabilities at larger time-steps (Bulacu et al. 2013). Therefore, we have chosen sets in which narrow angle distributions are mostly populated. Thus, most of the angles and torsions in the topologies are modulated using higher force constants in order to match the narrow distributions observed at AA level. This approach will avoid singularities for over-restrained angles reaching values close to 180° (Bulacu et al. 2013). An alternative that was not tested is the use of a restrictive bending potential (Reb) (Bulacu et al. 2013), which can alleviate this effect. Nevertheless, the selected bonded terms were able to properly reproduce both dynamics and configurations of the more complex glycans, while allowing larger time-steps integration.

CG bead polarity was selected based on the direct comparison of LogPo-w to values obtained from AA simulations. Figure 2A clearly shows a very good fit (R² = 0.98), suggesting that Martini and CHARMM are very consistent in the preferential partitioning of molecules between different organic phases. An extra step was required for the proper calibration of the aggregation propensity. AA simulations of saturated (0.1 M) carbohydrate solutions were used as a calibration standard, for which the CG models were directly compared. As discussed before (Stark et al. 2013; Javanainen et al. 2017; Schmalhorst et al. 2017; Alessandri et al. 2019), Martini has consistently shown an artificial tendency for aggregation, more noticeable in larger polymers. Generation of new bead types (increase of the interaction matrix) can potentially overcome this problem, by specifically compensating interactions within the molecules (finer mapping schemes). However, this approach is part of the future release of the Martini force field, so further recalibration of the nonbonded matrix of Martini 2.2 is not part of the scope of this work. Instead, we focus on improving the excessive aggregation by balancing the content of “ring” beads along the topology of the sugars. The final bead selection leaded to the construction of the plot provided in Figure 2B for the set of calibrated monosaccharides. With the exception of N-acetylglucosamine, most of the carbohydrates form aggregates of relatively similar sizes, even at high concentrations (0.1 M). Another important feature to highlight is the larger aggregation clusters formed by neuraminic acid (~25 molecules per aggregate), which is captured by both the AA and the CG model.

Fig. 2.

CG N-glycan model correlates with several CHARMM36 glycan calculated properties. (A) Correlation of LogPo-w for representative monomeric subunits (P-value = 2.50e−05). Glucose, trehalose and maltose LogPo-w were also calculated in order to show consistency with the previous calibrated parameters. (B) Cluster size quantification of monomeric subunits in bulk solutions. Simulations of carbohydrate saturated (0.1 M) solutions were run (see Methods) in order to estimate the aggregation propensity based on cluster size measurements. Cluster size quantification for galactose was not added as it was found statistically similar to cluster size calculated for mannose. (C) AA–CG correlation of aggregation propensity for large N-glycans (P-value = 2.13e−05). Aggregation propensity is estimated as the average number of clusters found in the simulation of saturated (0.1 M) glycan solutions. Black dot corresponds to the CG average cluster for all glycans using purely regular Martini beads (stronger interactions) in the topology. (D) Specific intermolecular interactions for Man-9 N-glycan 0.1 M solutions (P-value = 3.02e−09). Man-9 glycans are topologically defined as independent subregions and their total average number of contacts calculated. The small inset corresponds to correlation for contacts below 600. Quantification for other glycan derivatives is provided in >Figure S2. This figure is available in black and white in print and in colour at Glycobiology online.

Monosaccharide polymerization leads to larger branched glycans, with the correspondent decrease of bead polarity within the regions of connection. Therefore, such chemical change has to be captured as well by the CG model through new iterations of bead rebalancing. A final set of beads was reached that consistently retains the monosaccharide’s LogPo-w and a balanced aggregation propensity at saturated concentration of solutions for polymerized sugars (Figures 2C and >S2A). In fact, after calculating the average number of aggregates in the simulation box (see Methods), it is clear that the CG allows a clear distinction between the relatively higher solubility of the high mannoses (Man-5/9) derivates, in contrast to the lower solubility of the fucosylated (F-) glycans. It is interesting to highlight that the CG even allows (at some extent) a marked distinction among the solubilities for the different high mannose derivatives, otherwise incorrectly captured by using only regular beads (Figure 2C black dot).

It is worth asking the question whether glycans within the aggregates are specifically interacting through certain topological regions. Thus, we have dissected the specific interaction patterns of the large glycans in the simulations. An example is provided in Figure 2D for the Man-9 derivative. First, the molecule was topologically classified in four different regions, shown in the small inset. Each region corresponds to a subset of monosaccharides, which are independently connected from the main root. Thus, their concerted number of interactions are responsible for maintaining the overall stability of the aggregates. Clearly, the larger number of contacts are found within pairs 1–1, 2–2 and 3–3 in the AA and CG, respectively. The higher correlation with the AA counterpart suggests that the reductive CG model is able to capture higher detailed interactions within complicated topologies. Additional analysis of other Man derivatives (>Figure S2B–E) suggests that the CG model correctly reproduces the specific interactions within the monomeric subunits, regardless of topology and polymerization. This result not only confirms that the CG is able to preserve a proper geometry of the molecule but also able to balance the proper intermolecular interactions through a careful compensation by the use of “ring” beads. Access to the full set (15 molecules) can be obtained directly from the Martini force field website (http://cgmartini.nl).

Glycan dynamics of the HIV Env protein

After verifying that the new CG glycan model successfully performs well in bulk solutions, our next step was to get insights into their behavior when interacting with a protein model. Given the world-wide relevance and complexity of HIV as a public health threat and the importance of its envelope protein glycosylation topology in immunogen design (Doores 2015), we chose this as a good target for studying. Past AA simulations have provided several insights into the interplay between the HIV1 envelope protein and its highly glycan content (Yang et al. 2017; Ferreira et al. 2018). However, conclusions are still hampered by the time-scales that can be reached and the excessive computational requirements. A good example is the difficult connection between simulations and large ensemble data coming out from Cryo-EM experiments (Chakraborty et al. 2020). Therefore, the new Martini glycan model can potentially fill the gap with information within energetic regions that can be hardly accessible by fully AA simulations.

Given the excessive computational demands for generating relevant time-scale information out from AA simulations, we have restricted our MD AA calculations to a particular glycosylated Env protein (see Methods) as a comparison target for the CG model. However, we have explored the effects of glycan modification using different high mannose variants at the CG resolution. Following are results that highlight our outcomes.

We have directly compared the internal degrees of motion of the Env backbone scaffold, by means of the root mean square fluctuation (RMSF). Figure S3A clearly shows the good agreement between the CG model and the AA counterpart. It is even remarkable that regions pertaining the variable (V) loops retain the same fluctuation patterns. Thus, although Martini by itself it is not able to properly retain the secondary structure of large protein ensembles, this can be achieved by a proper implementation of internal elastic bands (see Methods). We next move to investigate properties extracted from the glycosidic part. The general effect on hydrodynamic property is shown in Figure S3B. Glycans contribute to nearly half the mass of the Env glycoprotein (Lasky et al. 1986), thus it is clear that this extra mass stemming from glycosylation, as well as the length of these glycans on the Env protein, can directly influence its radius of gyration. Notably, the CG model is able to distribute the mass along the Env in a similar pattern as observed for the AA simulations. Thus, and besides the roughness of the CG model, its underestimation of 0.1 nm can still be considered as a very good agreement.

Dynamics for each glycosylation site was also analyzed. After fitting the whole trajectory with respect to the Env backbone, the RMSF for each of the glycans in the protein were extracted and presented in Figure S3C. As expected, the CG model enhances the dynamics of the glycans, in most cases up to 2-folds with respect to the AA model. Thus, the different models do not show a very strong correlation for independent positions, which can be attributed to configurations that are hardly visited by the AA counterpart. Due to high conformational heterogeneity and flexibility of the glycans (Yang et al. 2017), the shorter time-scales in the AA simulations prevent a robust sampling of available conformation space, which can be overcome by the smoother energy landscape of the CG resolution. In fact, each AA replicate (1.5 us each) does not converge similarly for each position, suggesting larger uncertainties in the results. Regardless, we move forward and investigate the effect on dynamics for different glycan derivatives. Thus, the plot provided in Figure S3D suggests that in general, there is no particular effect across Man 5–7 derivatives. There is, however, a noticeable effect for Man-8, specially at the regions pertaining the gp41 domain. Surprisingly, addition of an extra mannose (Man-9) seems to restore the dynamics within this region. It is possible that the extra mannose sterically affects stabilizing contacts, otherwise favorable for the Man-8 derivative.

We asked the question whether a generalizable pattern can be extracted from this information. Results are provided in Figure 3A, highlighting the variation in dynamics for each glycan position, as a consequence of glycosylation branching. Thus, and based on this analysis, several positions were observed to emerge as regions dynamically affected. Remarkably, these positions are not closer in sequence, but topologically related and most importantly within specific regions of the protein. For instance, the Apex region of the envelope highlights the presence of glycans in position 156 and 197. The equatorial region of the protein is represented by positions 295, 448 and 462. Finally, and consistently with the AA simulations, glycans in the gp41 regions are remarkably variable. As presented later, we observe that glycan contacts within these regions are specially affected by the length of the sugar, a property that can also be dynamically captured.

Fig. 3.

Dynamical and structural properties of N-glycosylated HIV Env protein. (A) Standard deviation (SD) of the root mean square fluctuation (RMSF) for N-glycans. SD is based on RMSF variation among several glycan derivatives (Man-5–Man-9) for all the glycosylation positions, which are topologically shown in the right inset. Color code correlates with glycans showing higher variability. (B) AA–CG comparison of total protein surface area accessible to solvent (SASA) as a function of Man-9 glycan coverage. Values are provided as exposure fraction and averaged among the total ensemble time (6.6 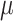s AA and 300 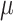s CG). (C) Fraction of total protein exposure as a function of N-glycan derivative. Values were used to calculate residue-specific SASA variation and projected into the 3D HIV Env model. Red color highlights the most variable SASA positions. (D) Region-targeted SASA for the PG9 and VRC34 epitope localization. Values were calculated as in (B). (E) SASA correlation map for residues pertaining the PG9 epitope (see text). Residual-SASA was computed for all CG N-glycosylated derivates (Man-5–Man-9) and color coded according to their correlation. Residues in red are strongly positively correlated; residues in blue are strongly negatively correlated. This figure is available in black and white in print and in colour at Glycobiology online.

HIV-1 Env shielding

Addition of the glycosylation mass results on the masking of regions in the protein, a property that has immunological consequences and therefore coined “glycan shield.” Literature agrees on the relevant consequences of this glycan shield, especially on the development of reactive antibodies (Abs) (Pancera et al. 2014; Stewart-Jones et al. 2016; Wagh et al. 2018, 2020). However, there is no rational tool that allows integration of glycan derivatives and the resulting immunological response. We see the CG model potentially appealing in this respect, and therefore we focus on investigating the effect of glycan content on protein exposure. Figure 3B provides a comprehensive view of glycan shield on the topology of the Env. First, we directly compare the solvent accessible surface area (SASA) calculated from the AA simulations for the Man-9 glycan to the corresponding CG model. Note here that we needed to calibrate a proper CG SASA bead (see Methods) in order to compensate for the differences in resolutions (Figure S3E). Besides the good agreement, both models reveal a total coverage of ~35% of the Env protein surface, which clearly explains the difficulty on eliciting effective Abs. A more thorough analysis allowed as to understand the extend of the agreement between the AA and CG simulations. This information is provided in Figure S3F, in which the SASA value for fully glycosylated Env protein was decomposed in per residue SASA for either the AA or CG models. Although in general solvent accessibility is greater for the CG case, the per residue profile is overall consistent between the two levels of resolution, with a Pearson correlation r = 0.75 (P < 0.05).

SASA analysis carried with other CG glycan derivatives (Figure 3C) suggests that a remarkable reduction of glycan shielding is observed for shorter glycans (e.g., Man-5). With an averaged exposure of 80% of the protein surface, it is noticeable that the addition of one extra sugar into the glycan can produce significant difference. Thus, we can conclude that it is not only the total mass content, but the particular geometry that the new molecule adopts once a new sugar unit is added. Again, this difference is more noticeable for the Man-5 glycan. We also asked the question whether a relevant feature can be extracted out from exposed residues and if this can be directly correlated with topological regions within the Env. Thus, we dissected the SASA for each residue present in the protein as provided in Figure S3G. Clearly, the variance observed along the sequence is not homogenous; however, it is not clear if there is a structural component that can be attached to it. Projection of this variance is provided in Figure 3C, within the 3D structure of the Env protein. Interestingly, regions with larger SASA variability are topologically distributed within the same regions of high glycan dynamics, suggesting that glycan diversity may be only relevant in particular regions of the protein. Moreover, it is clear that there are perpetual “hidden surfaces” of the protein, independent of the glycan type.

Next, we asked the question whether this predicted SASA “hot spots” could have important immunological connotations. In fact, we noticed that several of the predicted highly dynamic glycans are indeed localized within regions, which have been previously determined as target for Abs. Thus, glycan 156 is localized within the PG9 epitope domain, and glycan 197 is situated such that it can affect the shield here by interglycan interactions (Behrens et al. 2016; Chakraborty et al. 2020), while 88, 611 and 637 are topologically close to the VRC34 binding region. Both the PG9 and VRC34 are broadly neutralizing antibody (Walker et al. 2009; Shen et al. 2020) lineages of HIV-1, with the former binding to the V1/V2 apex region and the later targeting the fusion peptide region of Env. Our AA-CG comparison reveals that Man-9 glycans largely shield the exposure of both immunogenic regions (Figure 3D). Remarkably, the CG model not only agrees on the average value but provides a broader distribution, again highlighting the enhanced sampling of the model. We next evaluate specific regions of exposures within these two domains. A residue-based SASA for PG9 and VRC34 binding regions is provided in Figure S4A and B, respectively. The good agreement for the residual SASA in case of PG9 (r = 0.7, P < 0.05) and VRC34 (r = 0.65, P < 0.05) not only suggests that the Martini glycan model provides an overall excellent estimation of topological burial but provides good resolution at the single residue level. Thus, this result encourages for exploring the effect of other glycan derivatives within these two particular regions.

Residue-based SASA analysis is provided in Figure 3E for the PG9 epitope. We evaluated the effect of glycan length (Man-9/Man-5) on the per-residue exposure and provide a correlation matrix for all the residues pertaining this region. We noticed that several residues are positively correlated in their exposure (e.g., 167–169, 170–173), while a large amount are clearly negatively correlated, even when they are topologically close. Thus, it is clear that in PG9, glycan length does not affect all the residues in this region in a similar manner and suggests a very important feature that is dependent on the glycan structure. This is perhaps also because of the long and variable V1 and V2 loops around the PG9 epitope on which the surrounding glycans are located. The dynamic nature of the loops may somewhat mask the effects of glycan lengths on shielding. Surprisingly, we found that the residual exposure in the more structured VRC34 epitope (Figure S4D) is largely positively correlated with glycan length (Figure S4C), which could be explained by the larger flexibility of the glycans within this region.

Glycan contacts and network

Finally, it is important to probe the interactions among the superficial glycans, and its connectivity mechanism within the different regions of the Env in order to elucidate the global topology of the glycan shield (Doores 2015; Stewart-Jones et al. 2016; Ferreira et al. 2018; Berndsen et al. 2020). We have previously implemented (Chakraborty et al. 2020) a graph-directed approach to describe the shield as a topological network. We use a similar definition for the CG glycan ensembles on Env to obtain the glycosylation network and observe how variations in glycan size can perturb the shield.

The glycan network for the CG Man-9 model is given in Figure 4A. In the network, each glycan forms a node, and two glycans that sample overlapping volumes in space are connected by an edge, which is weighted by the fraction of overlap. Thus, these edges give a measure of the occurrence of interactions between the involved nodes. The network can be divided into three spatial regions: (i) a densely connected equatorial region, with the network being sparser at the (ii) apex and at the (iii) base including gp41. The equatorial region includes the known high mannose patch (Pritchard et al. 2015) (HMP) and hosts glycans with high eigencentrality (Figure 4A), being so densely connected. Given the slow dynamics shown by our analyzed AA model, we decided to compare the CG network to our previous model (Chakraborty et al. 2020) where we had used a high-throughput enhanced atomistic modeling (HTAM) based on simulated annealing. The overall topology closely resembles what was previously obtained (Figure S5A). There is also a very strong correlation between the eigencentralities (Figure 4B), with r = 0.87 (P < 0.05). To better understand how the glycan shield topology is different between the CG and atomistic models, we calculated the network adjacency matrix difference (Figure S5A). We observe that the CG adjacency or interglycan volume overlap is higher than HTAM for 48 glycan pairs, and lower than HTAM for 27 pairs. This indicates that the CG glycans can generally sample larger volumes in space even compared to simulated annealing of glycans in HTAM. This becomes even more evident in and around the apex V1/V2 loop glycans (glycans 88 to 197).

Fig. 4.

Glycan network for high Man. Man-9 network comparison between CG and previously published high-throughput atomistic model (HTAM). (A) Glycan network in CG Man-9 model. Nodes are individual glycans, colored by eigencentrality or relative importance. Network represented as 2D force-directed layout. (B) Eigencentrality values of glycans, compared between CG and HTAM. Glycan IDs are in HXB2 numbering. Suffix “_2” denotes glycan from neighboring protomer. (C) Variance plot of contact prevalence among different intraprotomeric glycan variants. Large variability is denoted by red squares. (D) Structural projection of glycans with larger contact variability. Color scales correlate with variability plot. (E) Glycan contact variability for interprotomeric interaction. Only variability larger than 30% of the scale bar are denoted in green circles. This figure is available in black and white in print and in colour at Glycobiology online.

As expected, much of the connectivity is reduced, and the network gets reshuffled as the size of the glycans is reduced from Man-9 (Figure S5). We calculated the reduction in glycan network of shorter glycans (Figure S5B–E) as compared to Man-9 network (Figure 4A) topology. Due to the smaller glycan sizes, the network edges reduce in number and weight. The edge lost or reduced by at least 10% in weight are shown in Figure S5B–E. While Man-9 has 87 edges (Figure 4A), 25 of them are reduced/lost in both Man-8 and Man-7, Man-6 is reduced in 29 edges and Man-5 has the sparsest network with 33 edges reduced/lost. Among the first interactions to leave the network are those at the apex and those involving interprotomer interactions, while the dense equatorial edges have reduced overlap. In the Man-5 network, finally it is mainly the glycans around V4 and the high-mannose patch that persist as before.

In addition to the glycan network analysis, we also add a quantification of glycan–glycan interaction prevalence as provided in Figure 4C and based on the different set of glycan derivatives (Man-9/Man-5) using the N-glycan CG model. Large contact variability is denoted by red squares in the heat map, representing glycan contacts that get more affected by the mannose derivative replacement. As expected, regions with low variability corresponds to regions in which the Env shows perpetual protein burial (e.g., contact prevalence retained). In fact, we found that even for the shorter N-glycan (Man-5) derivatives (Figure S6), it is possible to find a relevant number of contacts, overall maintaining a network of interconnected glycans. As seen in Figure S6, such interconnection is strengthened by the length and increased branching of the glycan. Most of these high contact glycans are those in HMP and around V4 (363–448 and their interactions with 262, 295, 332). They are the same that were found to be more resistant to enzymatic digestion (Berndsen et al. 2020), possibly because of the crowded interactions. We also provide a representative configuration in which the glycans showing higher contact variability are highlighted, easily depicting a topological representation of such network (Figure 4D).

Similarly, we have also calculated glycan contacts pertaining to interprotomeric interactions within the Env (Figure 4E). In particular, this analysis suggests that most of the interconnectivity comes through the Apex region (residue 160, 185e and 156) and also highlighted in the variance plot provided in Figure 4E. Surprisingly, the variability was found stronger within protomers 1–2 and 2–3, suggesting that the glycans are not interacting symmetrically in the whole ensemble. Nevertheless, it is clear that glycan variability is more relevant at the intraprotomeric level, at least for high mannose derivatives.

Discussion

We have provided a set of parameters for the simulations of N-glycans, consistent with the general Martini philosophy. We have followed the general Martini protocol for the generation, optimization and implementation of the CG topologies. However, we have to emphasize that the new Martini N-glycan is consistent with the glycan model implemented in the CHARMM36 force field. We have not evaluated the potential differences/implications with other AA force fields, which have been commonly used in the past for the generation of Martini parameters (e.g., GROMOS (Huang et al. 2011), GLYCAM (Kirschner et al. 2008)). However, given the recognized use of CHARMM in scientific production, we believe there should not be any negative impact.

In agreement with the original parametrization for carbohydrates (Lopez et al. 2009), monosaccharides were implemented using a 3-bead-triangle shape configuration. This type of CG topology projection seems to be the most effective for reducing aliphatic/aromatic rings into Martini CG beads. Its benefit was retained even when extending the topologies for highly polymerized glycans. Thus, the connection between triangular shapes is advantageous in order to reduce highly stressed topologies due to complicated geometries.

Unfortunately, we did not find a proper mechanism to implement a “building-block” approach, which could facilitate the automated construction of other glycan derivatives. Finer deviations in angles and torsions can dramatically affect the geometry and aggregation properties of molecules, in this particular case of the glycans. This effect, which has been thoroughly described in the past (Alessandri et al. 2019), seems to be an inherent problem of topologically complicated molecules/mappings. As a consequence, we find that the most optimal approach to retain most of the properties is to independently adjust the bonded terms for each glycan. We accept this mechanism is not optimal for the fast generation of other glycan types; however, a recently published method (Empereur-Mot et al. 2020) can be directly combined with a machine learning pipeline in order to accelerate the process of generating new topologies.

Another limitation is the precise use of ring bead types for balancing the aggregation propensity. We appreciate that this parameterization protocol requires an iterative “time-consuming” process in which beads need a recalibration when moving toward larger polymerized carbohydrates. Besides other approaches (Stark et al. 2013; Schmalhorst et al. 2017) for fixing the artificial aggregation propensity in Martini, we believe that the use of ring bead types is the most harmless mechanism in order to alleviate this limitation. These beads are already balanced in terms of self-interactions, partitioning and water solubilization; therefore, they preserve an overall consistency with the rest of the force field. Recently, some advances have been made toward MARTINI parameterization of N-glycans, which required introduction of some new bead types and distance-dependent elastic networks to maintain geometry of long glycans (Shivgan et al. 2020). Implementation of new bead types in Martini 3 should alleviate many of the aforementioned limitations and should only require an adjustment to the proposed CG N-glycan model for Martini 2.2, while preserving the bonded terms.

Based on our results, the new N-Glycan Martini model shows very good agreement when compared to the behavior observed with the CHARMM36 (Guvench et al. 2008, 2011; Mallajosyula et al. 2015) glycan force field. Configurations, partitioning between organic phases, aggregation propensities and specific self-contacts were used as targets for comparison, overall showing very good consistency. However, some limitations still remain as a consequence of particle reduction. For instance, and similar to the original carbohydrate parametrization, ring puckering cannot be fully reproducible. Transitions between chair-envelope and boat are inevitably averaged within the 3-bead mapping. While we do not see a very dramatic internal effect in the rings, it can potentially affect the orientation of glycosidic bonds.

In this work, the majority of glycosidic bonds () parametrized for N-glycans mostly exhibit one single torsion when projected into the CG representation. However, sugars connected by 1–6 linkages are prone to exhibit bimodal distributions, which are not easily captured by the CG parameters. In these particular cases, the CG ff aims to represent the most populated torsion, which is clearly limited by the underlying AA dynamics. Thus, it is important to be cautious when representing the glycans in a different energetic state, for instance bound to an Ab.

Finally, the simplicity of the model allows the exploration of large glycan variability and its impact on protein glycosylation. We have used the heavily glycosylated HIV Env protein as a study case. The large variability in glycan content makes it almost impossible to look at every different glycosylation position in the Env using standard fully atomistic representations. Thus, when combined with slow dynamics, study of large glycosylated complexes requires prohibitive amounts of computational resources for obtaining biological-relevant information. We have shown that CG representation alleviates this limitation by providing data pertaining to five different high mannose derivatives, capturing their dynamics within hundreds of microseconds. Such time-scales allow the description of glycan effect on protein “shielding,” glycan dynamics as well as glycan contacts and internal networking. Surprisingly, glycan dynamics as well as protein coverage obtained from our simulations were found to correlate within Env regions for which Abs have been previously targeted, suggesting that the immune system responds to these properties in order to produce effective Abs. In fact, previous work (Wagh et al. 2020) has shown how relevant the glycans are in these positions for the proper recognition and interaction with Abs. In the future, we will focus into understanding this process by setting up a lager glycosylation variability library and its correlation with known neutralizing Abs. Outcomes from this study can potentially provide computational tools for the rational design of vaccines at large scale. They can also potentially be extended to include O-glycans, which generally have the same constituent sugars. Due to the significance of such dense glycan shielding in a number of different enveloped viruses including influenza (Wang et al. 2009), Ebola (Lennemann et al. 2014) and SARS (Lennemann et al. 2014), these glycan parameters will act as critical tools for large-scale structural simulations to aid vaccine design. Moreover, critical roles of glycosylation in the recent COVID-19 threat from SARS-COV2 (Watanabe et al. 2020) and other major illnesses such as mucin-mediated cancer (Chugh et al. 2015) will largely benefit from this study.

Material and Methods

Mapping and parametrization of N-glycans

In line with the original parametrization protocol (Lopez et al. 2009), representation of single ring hexose units is efficiently provided by three CG beads connected in triangular shape. Allowing this CG projection provides three important advantages: (i) overall numerical stability when running at larger time-steps, (ii) even distribution and direct 4-1 mapping of heavy atom masses within the CG beads and (iii) easy expansion when connecting branched termini. Therefore, contrary to the original parametrization (Lopez et al. 2009), carbohydrate branching is possible with retention of monomeric subunits in triangular shapes. An example mapping scheme is provided in Figure S1A for mannose as well as for highly branched glycans (e.g., Man-9) (Figure S1C), overall highlighting topology preservation. Similar mapping schemes were used for deriving other type of glycans, as well as branches.

Internal dynamics of glycans are preserved through a set of bonds, angles and dihedrals consistent with the original publication (Lopez et al. 2009), which were iteratively fitted from distributions obtained from atomistic simulations. Such distributions were obtained by first creating pseudo-CG trajectories using the center of mass of the appropriate fine-grained particles (Rzepiela et al. 2010):

Thus, the number of atoms P are effectively reduced within the position dictated by the vector and a CG trajectory can be extracted.

Nonbonded interactions are dictated by the different bead types integrated in the self-interaction matrix of Martini. A good representation of the molecule requires two main choices to be made for the selection of a particular bead type. First, when combined, the overall polarity of the molecule requires a balanced contribution, which should provide a close match to a partition coefficient between different environments (organic phases) (Marrink et al. 2007). In our case, bead selection was decided based on the octanol–water partition coefficients (LogP_O-W), which were also computed from AA simulations.

The second selection criteria rely on the reproduction of bulk properties, which will largely dictate the aggregation propensity of the molecule. As discussed elsewhere (Stark et al. 2013; Javanainen et al. 2017; Schmalhorst et al. 2017; Alessandri et al. 2019), imbalanced mapping schemes combined with weak force constants in the bonded terms and lack of charge screening by the water model are largely responsible for artificial aggregation of molecules as reported before (Stark et al. 2013; Javanainen et al. 2017; Schmalhorst et al. 2017). Modification of the Lennard-Jones (LJ) potential has been provided as an approach to alleviate this problem (Stark et al. 2013; Schmalhorst et al. 2017). However, this method requires a large recalibration of the original interaction matrix resulting in the generation of new bead types. A second more generalizable approach is the effective use of the originally parametrized “ring” bead types. These bead types are reserved to properly represent uneven mapping schemes, in which a reduced number of atomic particles hardly match a 4-1 mapping. As a result, ring bead types interact with reduced strength and when properly combined, unwanted aggregation can be prevented (see results), while still retaining the proper organic partitioning. We have used this approach in order to balance the loss of atomic particles, especially when glycosidic bonds fuse monomeric subunits. As a result, the generated topologies fully retain consistency with the rest of molecules in Martini, while avoiding further modification of the original LJ balance.

The future release of an updated Martini 3 force field (http://cgmartini.nl/index.php/martini3beta) is expected to introduce a new set of recalibrated bead types, which will deal with the aforementioned limitations. However, the overall mapping scheme as well as bonded terms applied for the parametrization of N-glycans should be transferable making the construction of N-glycans easy for the upcoming release of the force field.

System setup of carbohydrate solutions

Bulk systems of AA carbohydrates were generated with the Glycan Reader and Modeler module (Park et al. 2019) of CHARMM-GUI web (Jo et al. 2017) interface using the CHARMM carbohydrate (Guvench et al. 2008, 2011; Mallajosyula et al. 2015) force field. The large set of single carbohydrate topologies is provided in Figure 1. This set ranges from small ring monosaccharides to large polymerized high mannose derivatives and antenna-added types (e.g., fucosylated glycans). The selection was based upon a thorough revision of published data (Behrens et al. 2016; Cao et al. 2017; Go et al. 2017) related to glycosylation derivatives of the HIV-1 envelopes, one of the most diversely glycosylated proteins known so far. For each case, a tetrahedral box of 1000 nm³ containing 0.1 M solute was constructed. Solutes were randomly placed into the box, and systems were solvated using a CHARMM modified version of the TIP3 (Jorgensen et al. 1983) water model. Excess charge was neutralized and an overall ionic strength of 150 mM was set into the system using K⁺/Cl⁻ ions. Systems were energy minimized and equilibrated for short time (20 ns) using the GROMACS 5.4.1 MD engine (Páll et al. 2014). The last frame after equilibration was later transformed into AMBER-formatted topology using the gromber tool of ParmEd from AmberTools 16 (Salomon-Ferrer et al. 2013). The same initial frames were also mapped into pseudo-CG configurations, which were used for the CG simulations. CG mapping was performed using a modified version of GROMACS 3.1 (Rzepiela et al. 2010), which can be obtained from the Martini website (http://cgmartini.nl/index.php/tools2/resolution-transformation).

Fig. 1.

Schematic representation of N-glycan library parametrized in this work. Large interconnected glycans are based on five different monomeric subunits and their glycosidic bonds are highlighted. This set only covers the most representative high mannoses and fucosylated glycans based on a survey of mass spectrometry data. However, interconnectivity can be modified in order to parametrize less populated glycans. Man-9: high mannose 9, Man-8: high mannose 8, Man-7: high mannose 7, Man-6: high mannose 6, Man-5: high mannose 5, FA2: complex fucosylated glycan with two antennae, FA3: complex fucosylated glycan with three antennae, FA4: complex fucosylated glycan with four antennae, FA2B: complex fucosylated glycan with two antennae (FA3 isomer), FH: complex fucosylated hybrid glycan. Color scheme as well as monosaccharide symbols follow the SNFG (Symbol Nomenclature for Glycans) (Varki et al. 2015). This figure is available in black and white in print and in colour at Glycobiology online.

In order to calculate the LogP_O-W for all the monomeric carbohydrates, we need to simulate the annealing of the molecules between water and a water-saturated octanol phase, respectively. Therefore, each carbohydrate was first inserted in a tetra clinic simulation box of 5 nm edge. The box was then solvated with either pure water molecules or an octanol saturated solution (90% octanol and 10% water). After energy minimization and equilibration of the box volume, configurations were taken for the calculation of the molecular annihilation. Similar to the case of bulk solutions, some frames were transformed into CG resolution for its respective evaluation of the partition coefficient.

System setup for HIV-1 Env glycoproteins

Five random configurations of BG505 SOSIP (Sanders et al. 2013) Env glycoprotein were selected from a previously generated ensemble (Berndsen et al. 2020). In short, for each of these five structures, the underlying BG505 protein scaffold was built by homology modeling from PDB structures 4ZMJ and 5CEZ, with the missing loops modeled ab initio. Man-9 N-glycans were added at 28 N-glycosylation sites (Behrens et al. 2016) on each trimer (84 glycans total) in a template-free fashion with random orientations. The entire glycoprotein system was then minimized and relaxed with 1000 steps of conjugate gradient minimization and five rounds of simulated annealing between 1300K and 300K in eight steps. The CHARMM36 forcefield was used to represent the interactions between the atoms of the system. All modeling was done using MODELLER (Eswar et al. 2006) and ALLOSMOD (Guttman et al. 2013) suites.

The five selected glycoprotein models were set up for production runs by solvating in cubic water boxes with TIP3P water model, having 15Å padding from the glycoprotein periphery. The system was neutralized by adding K⁺ and Cl⁻ atoms at 150 mM concentration. Each system had ~500,000 atoms. Solvation and addition of ions were performed using VMD 1.9.3 (Humphrey et al. 1996a).

A Martini CG model of the HIV Env glycoprotein was constructed based on the coordinates extracted from the AA simulation. First, the AA protein scaffold was converted into a CG model using the ./martinize script, which can be downloaded from the Martini website (http://cgmartini.nl/index.php/tools2/resolution-transformation) and is part of the backward suite (Wassenaar et al. 2014). The protein was represented using the Martini 2.2 protein force field (De Jong et al. 2013). Secondary structure was mimicked using a set of bonded terms, which are assigned based on the nature of the secondary arrangement. Long elastic bands were used in order to retain the tertiary and quaternary conformation of the whole Env complex, except within regions corresponding to the variable loops (V regions). Then, each N-glycan of the AA model was transformed into CG N-glycans using the ./backward script (http://cgmartini.nl/index.php/tools2/resolution-transformation) and added into the protein CG topology. Different high mannose variants were constructed by deleting the correspondent monomeric subunit from the Man-9 topology. Different bonded terms were also derived in order to connect the glycans to their asparagine moieties. Such parameters were directly derived from independent AA simulations of N-acetylglucosamine monomers attached to asparagine amino acids (both nonfucosylated and fucosylated). We found that the correspondent AA dynamics can be captured by one bond and two angles, which are provided in the parameters set.

Atomistic MD simulations of glycan solutions

Bulk simulations of AA carbohydrates were carried using the AMBER 16 software (Le Grand et al. 2013). Water molecules are rigidified with SETTLE (Miyamoto and Kollman 1992), and other covalent bond lengths involving hydrogen are constrained with SHAKE (Miyamoto and Kollman 1992) (tolerance 1/4 106 nm). Lennard-Jones (LJ) interactions are evaluated using an atom-based cutoff with forces switched smoothly to zero between 1.0 and 1.2 nm. Coulomb interactions are calculated using the smooth particle-mesh Ewald method (Darden et al. 1993) with Fourier grid spacing of 0.08–0.10 nm and fourth order interpolation. Simulation in the NPT ensemble is achieved by isotropic coupling to Monte Carlo barostat (Le Grand et al. 2013) at 1.01325 bar with compressibility’s of 4.5 105 bar1; temperature coupling is achieved using velocity Langevin dynamics at 310 K with a coupling constant of 1 ps. The integration time step is 4 fs, which is enabled by hydrogen mass repartitioning. Nonbonded neighbor lists are built to 1.4 nm and updated heuristically. Simulations were run for 10 s and trajectories were saved each 100 ps for analysis.

Simulations for the calculation of the LogP_O-W (see later) partition coefficient were carried using GROMACS 5.4.1 (Páll et al. 2014). A total of 80 independent simulations (40 different per solvation) were run for 0.5 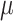s in order to accurately calculate the partition coefficient value.

Atomistic MD simulations of HIV-1 Env

AA simulations of the five glycosylated Env systems were carried out with NAMD version 2.13 (Phillips et al. 2005) using the CHARMM36 forcefield (Huang et al. 2017). The protein segment of the Env glycoprotein utilized the CHARMM36m correction (Huang et al. 2017). First, a 20,000-step steepest descent minimization was performed with gradual release of restraints. Initially, all glycoprotein heavy atoms were restrained to relax the water and ions around Env, and then the restraints were limited to the protein backbone. In the final 5000 steps, all restraints were removed. This was followed by heating to 300K temperature over 100 ps. A 20 ns equilibration run was performed in the NVT ensemble. Finally, more than 1s simulation production run (cumulative 6.6 μs) was performed for each system in the NPT ensemble Nosé–Hoover method (Martyna et al. 1994) in which Langevin dynamics is used to control fluctuations in the barostat (Feller et al. 1995). Periodic boundary conditions were applied, with a 10Å switching distance and 12Å cutoff distance for nonbonded interactions. The particle-mesh Ewald method (Darden et al. 1993) was used to calculate long-range electrostatic interactions. The SHAKE algorithm (Miyamoto and Kollman 1992) was used to constrain bond lengths of hydrogen-containing bonds, allowing for a time step of 2 fs.

Coarse-grained MD simulations

All CG simulations were carried with GROMACS 5.4.1 (Páll et al. 2014). Simulations used a 30 fs time-step for updating forces. Reaction-field electrostatics was used with a Coulomb cutoff of 1.1 nm (De Jong et al. 2016) and dielectric constants of 15 or 0 within or beyond this cutoff, respectively. A cutoff of 1.1 nm was also used for calculating Lennard-Jones interactions, using a scheme that shifts the Van der Waals potential to zero at this cutoff. Simulations were thermally coupled to 310 K using the Velocity rescaling (Bussi et al. 2007) thermostat. Isotropic pressure coupling was set for all systems at 1 bar using a Berendsen et al. (1984) barostat with a relaxation time of 12.0 ps. Bulk carbohydrate solutions were run for 20 s while simulations of the HIV envelope were run for 300 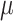s. The later, however, were run using 10 independent replicates of 30 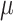s each.

Contrary to AA simulations, CG does not require the partial decoupling of the Coulombic component (LJ beads) (Marrink et al. 2007); thus, 20 independent runs were required for calculating the Martini LogPo-w values. In each case, a total of 1 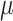s was collected for its analysis with the bar tool implemented in GROMACS (see later).

Water–octanol partition coefficient calculation

To properly calculate the LogPo-w, we first need to identify the solvation free energy differences in the water (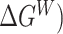 and water-saturated octanol ( phases, respectively. Calculation of the solvation free energy can be accurately computed by gradually vary the solute–solvent interactions from zero (vacuum) to full strength (in solution) so the total potential of the system can be described in terms of a coupling factor 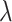. In order to avoid the generation of unwanted forces during the calculation, the solvation free energy was computed in two consecutive substeps: first the electrostatic component was decoupled from the system using a soft-core potential (Páll et al. 2014):

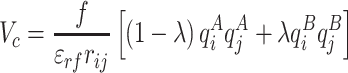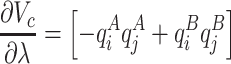Where 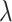was varied between 0 and 1 using 20 evenly distributed values (20 different runs). This step was followed by the decoupling the LJ interactions:

Notice that the transition could be also expressed as a function of and . However, in practice, the difference is not large and the free energy itself does not depend on the pathway. The Bennet acceptance method (Bennett 1976) was then used to calculate the energy difference between two adjacent 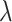values:

G is the free energy and U is the potential energy corresponding to the solvent–solute interaction. And the brackets (< >) denote the ensemble average of the system affected by the 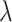value. The value C has to be self-consistently calculated form the recorded energy differences between the two simulation runs. Finally, the LogPo-w value can be calculated from the computed 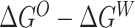difference:

Analysis

Residue-wise root mean square fluctuations (RMSFs) of Env protein were calculated as an average over the backbone atoms. Fluctuations were measured from the mean structures calculated using all trajectories in each system. RMSFs of the glycans were calculated using all the heavy atoms of the glycans. Radius of gyration was calculated using the “rgyr” function in VMD (Humphrey et al. 1996b), from the center of mass of each system, and weighted by the atomic masses. Solvent accessible surface area (SASA) for AA simulations were calculated with a probe size of 0.14 nm radius, corresponding to a water molecule. Probe size for CG simulations was calibrated against the AA measurements, to compensate for the differences in resolution. The CG probe size was varied between 0.14 and 0.56 in seven steps to scan for the closest match with AA results for average protein exposure at 0.14 nm. Best match was found at 0.32 nm (Figure S3E), and it was used as the CG solvent bead radius for SASA calculations. All these analyses were performed using VMD 1.9.3 (Humphrey et al. 1996b) package implemented via TCL scripts. SASA correlation heatmaps were calculated as following: First, a matrix is constructed where computed SASA values for each residue is tabulated against the different glycan derivative. Thus, a final X^*Y matrix is obtained where X and Y correspond to the total number of residues and glycan derivatives, respectively. The correlation was calculated using the numpy libraries as part of python 3.8 and plotted using matplotlib.

N-glycan cluster analysis was carried using the gmx clustsize inbuilt tool in GROMACS. Briefly, A 3D spatial analysis is carried in order to identify molecular contacts between defined solutes (e.g., Man-9). We used a cutoff of 0.55 nm in order to account for the CG beads and analysis was carried out at every time step. Glycan–glycan overlap network topology was calculated as discussed in a previous work (Chakraborty et al. 2020). Briefly, the interglycan overlap was calculated as the total fraction of heavy atoms for atomistic (all particles for CG) from two neighboring glycan ensemble that come within 5 Å of each other. An overlap greater than or equal to 50% of heavy atoms from two neighboring glycans is assigned as 1. This overlap function is used to define the adjacency matrix for the network analysis. Each glycan functions as a node of the graph, and two nodes are connected by an edge if there is at least 10% overlap. The edge length is inversely proportional to the overlap value, that is, the larger the overlap, the closer two nodes (glycans) are in the graph. Only those glycans from the neighboring protomers are considered, which have an interprotomer edge. All graph theory and network analyses were performed using Python and Matlab_R2018a package (Mathworks 2018). Eigencentrality of the nodes gives a measure of relative importance or centrality of each of the glycans on the network and is calculated from the eigenvector of the adjacency matrix, corresponding to the highest eigenvalue.

Funding

This work was funded by the DOE/LDRD grant ER 20190441ER on “Understanding Glycan Dynamics and heterogeneity for effective HIV vaccine development.” SC was funded by grants from the NIH (UM1 AI100645 and UM1 AI144371) and also partially supported by the Center for Nonlinear Studies, LANL. Computational resources were made available by LANL Institutional computing.

Conflict of interest statement

None declared.