A simple mathematical tool to forecast COVID-19 cumulative case numbers

Abstract

Objective

Mathematical models are known to help determine potential intervention strategies by providing an approximate idea of the transmission dynamics of infectious diseases. To develop proper responses, not only are more accurate disease spread models needed, but also those that are easy to use.

Materials and methods

As of July 1, 2020, we selected the 20 countries with the highest numbers of COVID-19 cases in the world. Using the Verhulst–Pearl logistic function formula, we calculated estimates for the total number of cases for each country. We compared these estimates to the actual figures given by the WHO on the same dates. Finally, the formula was tested for longer-term reliability at t = 18 and t = 40 weeks.

Results

The Verhulst–Pearl logistic function formula estimated the actual numbers precisely, with only a 0.5% discrepancy on average for the first month. For all countries in the study and the world at large, the estimates for the 40th week were usually overestimated, although the estimates for some countries were still relatively close to the actual numbers in the forecasting long term. The estimated number for the world in general was about 8 times that actually observed for the long term.

Conclusions

The Verhulst–Pearl equation has the advantage of being very straightforward and applicable in clinical use for predicting the demand on hospitals in the short term of 4–6 weeks, which is usually enough time to reschedule elective procedures and free beds for new waves of the pandemic patients.

1. Introduction

The COVID-19 pandemic caused enormous changes to the delivery of healthcare across the world, and the routine practice of clinical physicians has been substantially affected.1, 2, 3, 4, 5, 6 Mathematical models are known to help determine potential intervention strategies by providing an approximate idea of the transmission dynamics of infectious diseases.7, 8, 9, 10 To predict the course of epidemics, various complex mathematical concepts and models have been developed, including the following: the epidemic exponential growth rate (mainly the susceptible-infectious-recovered [SIR] model),11, 12, 13 susceptible-exposed-infectious-recovered (SEIR) model,^{12 ,} 14, 15, 16, 17 exponential growth rate and basic reproduction number (parametric approach, nonparametric approach), the autoregressive integrated moving average (ARIMA) model,¹⁸ least squares estimation, maximum likelihood estimation, and mechanistic and phenomenological models.¹⁹ However, working with these models is the purview of highly specialized professionals. To estimate the pandemic growth rate, an adequate mix of medical and advanced mathematical knowledge is required. To develop proper responses, not only are more accurate disease spread models needed, but also those that are easy to use.^{13 , 20} Few studies have been published in search for a straightforward mathematical model that can be easily used by clinicians to forecast the approximate rate of COVID-19 spread, and unfortunately, none of these few models published are as simple as expected.^{18 , 20 , 21} Therefore, it may be useful for clinicians and healthcare managers working daily in hospitals to have access to fundamental formulas that can easily predict the course of the epidemic based on its current state of evolution.

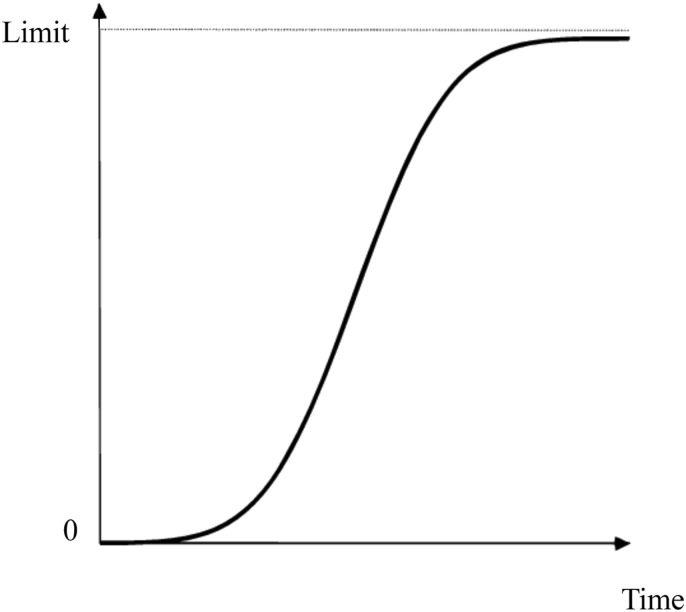
To put it simply, most epidemics are known to grow exponentially in the first stage of an outbreak.²² For this, epidemic curves can be mathematically studied, and the trajectory of the spreading infection can be drawn according to the number of cases in units of time, such as days, weeks, or months. The logistic function curve fits well with the pace of the pandemic over time, both with an early exponential rise and an eventual flattening as the population gains herd immunity.^{13 ,} 23, 24, 25 (Fig. 1 ) Pierre François Verhulst (1804–1849), a Belgian mathematician, studied the law of population growth and showed that its curve increases with a convex curvature and then continues to increase towards a limit but with a concave curvature.^{23 , 25 , 26} Over time, a stable population will reach a saturation level, which is the limit, and the total number of events will not increase higher than this limit.¹² Verhulst–Pearl's exponential growth model has formed the basis for other models. Using this formula simply, if the population of a country and the cumulative number of infected cases in two subsequent time units (t₀ and t₁) in the given country are known, it is possible to estimate the cumulative number of cases at future time points (t₂, t₃, t₄, and so on).

Fig. 1.

The logistic function curve.

We conducted this study to reveal whether Verhulst–Pearl's exponential growth model could be proposed as a simple, reliable formula to predict the cumulative case numbers of the COVID-19 pandemic, and whether it is applicable in neurosurgery for the prediction of the demand on hospitals.

2. Materials and methods

From the situation report dated July 1, 2020, on the World Health Organization's (WHO's) website,²⁷ we chose the 20 countries with the highest numbers of COVID-19 cases in the world ( Table 1 ). We retrieved the latest population figures in millions and the population densities per square meter of these countries from their Wikipedia pages and recorded them (The Wikimedia Foundation, Inc, San Francisco, CA, United States). The motivation behind using Wikipedia as a source for this information was that those pages are updated with the latest data on the countries' populations. We also recorded the world's total population for a comparison. The total number of COVID-19 cases and the total number for these 20 countries and for the world were obtained from the WHO situation report dated July 1, 2010, and recorded as time t = 0.²⁷ Similarly, we found the total numbers of COVID-19 cases from the WHO status report dated July 8, 2020,²⁸ a week later, and recorded them as time t = 1. Then, using the Verhulst–Pearl logistic function formula, we calculated the total case estimates for each country and the world for July 15, July 22, and July 29, 2020 and recorded them as times t = 2, t = 3, and t = 4, respectively. We then compared our estimates with the numbers from the relevant dates of the WHO status reports on July 15, July 22, and July 29, 2020.29, 30, 31 We divided our estimation numbers by actual numbers and examined how much they deviated from the number 1. Finally, the formula was tested for longer-term reliability at t = 18 and t = 40 weeks. The complete data for the actual numbers can be found on the WHO website at https://covid19.who.int/WHO-COVID-19-global-data.csv.³²

Table 1.

Basic Information for the calculations.

	Country	Population	Density/km2	1 July 2020 Total Case Number t = 0	8 July 2020 Total Case Number t = 1	b	e-c
1	USA	328,239,523	33.6	2,573,393	2,923,432	127	0.879
2	Brazil	210,147,125	25	1,368,195	1,623,284	152	0.842
3	Russian Federation	146,748,590	8.4	654,405	700,792	223	0.933
4	India	1352642280	407	585,493	742,417	2309	0.788
5	United Kingdom	67,886,004	270.7	312,658	286,353	216	1.092
6	Peru	32,824,358	23	282,365	305,703	115	0.924
7	Chile	17,574,003	24	279,393	301,019	62	0.927
8	Spain	47,431,256	94	249,271	252,130	189	0.989
9	Italy	60,317,116	201.3	240,578	241,956	250	0.994
10	Iran	83,183,741	48	227,662	245,688	364	0.926
11	Mexico	128,649,565	61	220,657	261,750	582	0.842
12	Pakistan	212,228,286	244.4	213,470	237,489	993	0.898
13	Turkey	83,154,997	105	199,906	207,897	415	0.961
14	Germany	83,166,711	232	194,725	197,341	426	0.986
15	Saudi Arabia	34,218,169	15	190,823	217,108	178	0.878
16	France	67,081,000	104	157,194	159,909	426	0.983
17	South Africa	59,622,350	42.4	151,209	215,855	393	0.699
18	Bangladesh	161,376,708	1,106	145,483	168,645	1108	0.862
19	Canada	37,971,020	3.92	103,918	105,935	354	0.981
20	Qatar	2,795,484	176	96,088	100,945	28	0.953
	World	7,800,000,000	14.7	10,357,662	11,669,259	752	0.887

2.1. Mathematical model

The single, simple formula we used in this study is an application of the Verhulst–Pearl logistic function:²⁶

$N=\frac{Populationofcountry\ast }{1+b{e}^{-ct}}$ (* world population, if calculations are made for the whole world).where N represents the cumulative number of infected cases at time t, e represents a mathematical constant approximately equal to 2.71828, c is the constant of integration, and b is the exponential function base (the rate of change). The result is defined as a logistic curve, which is S-shaped (Fig. 1).

We can explain this formula using an example. Let the cumulative number of infected cases at time t₀ be 600 and the size of population be 90,000. If the cumulative number of infected cases reaches 1,800 one week later (t₁), the cumulative number of infected cases at t₄ (forth week) can be estimated as follows:

When t = 0 $600=\frac{\mathrm{90,000}}{1+b{e}^{-c0}}$ then $600=\frac{\mathrm{90,000}}{1+b}$ thus b=149

When t = 1 $1800=\frac{\mathrm{90,000}}{1+149e^{-c1}}$ $1800=\frac{\mathrm{90,000}}{1+149e^{-c}}$ hence e ^-c = $\frac{49}{149}$

When t = 4 $N=\frac{\mathrm{90,000}}{1+149{(\frac{49}{149})}^t}$ $N=\frac{\mathrm{90,000}}{1+149{(\frac{49}{149})}^4}$ ≈ 32,000

This means that after four weeks, the total number infected people will reach approximately 32,000.

In the classical population growth scenario, the Verhulst-Pearl logistic equation comprises three assumptions.³³ First, all individuals are equivalent, i.e., the addition of every new individual reduces the actual rate of increase by the same fraction at every density. Second, reproductive rate and carrying capacity are unchangeable constants. Third, no time lag exists in the response of the actual rate of increase per individual to changes in population density. In the pandemic scenario, herd immunity is an assumption, i.e., it is assumed that each individual can be infected only once, then becomes immune afterwards. It also is assumed that population size does not change and that no migrations, deaths, or births occur. In addition, it is assumed that no change in the reproduction rate occurs regardless of virus mutations or protective measures taken.

2.2. Data collection and statistical analysis

The Statistical Package for Social Sciences (SPSS v.20 IBM, Armonk, New York) was utilized to record and analyze the data. Variables included patient demographics: cumulative case numbers, ratio of the estimated values/actual numbers for cumulative cases, and country populations. Descriptive analyses were done to determine frequencies, mean, mode, maximum and minimum values, standard deviation, and standard error of the mean.

3. Results

On July 1, 2020, the countries that had the highest numbers of cumulative COVID-19 cases were the following, in descending order: the USA, Brazil, the Russian Federation, India, the United Kingdom, Peru, Chile, Spain, Italy, Iran, Mexico, Pakistan, Turkey, Germany, Saudi Arabia, France, South Africa, Bangladesh, Canada, and Qatar (cumulative case numbers: maximum = 2,573,393, minimum = 96,088, mean = 422,344) (Table 1). The actual cumulative case numbers on July 1 and July 8, which were the bases of the estimates of the following weeks, are shown in Table 1.

3.1. Short-term estimates

When the estimates for July 15, 2020 (t = 2) were calculated using the data from July 1 (t = 0) and July 8 (t = 1) and divided by the actual numbers of July 15, 2020, the mean was 1.005 (range: 0.899–1.039) (Table 2 ). This shows that the formula estimated the actual numbers with only a 0.5% discrepancy on average. We noticed that the total number of cases in the United Kingdom suddenly decreased from 313,487 on July 2, 2020 to 283,761 on July 3, 2020. This change occurred because the United Kingdom revised its historical data, leading to a negative number of new cases and an overall decrease in cases for the country. When we removed the United Kingdom from the list, the mean ratio of the estimated number/actual number was 1.01 for July 15, 2020. Then the result showed, on average, only a 1% discrepancy between the estimated and observed numbers. The estimates for two countries, Italy and Peru, deviated from the actual numbers by less than 0.1%. The estimates for July 15 for three countries, Pakistan, Saudi Arabia, and South Africa, were less accurate. However, the discrepancies in the estimates for those three countries were still minimal and were equal to or less than 3.9%.

Table 2.

The actual-estimate cumulative case numbers and their ratios for July 15, 2020 in the 20 countries.

	Country	15 July 2020 Total Case Number t = 2	15 July 2020 Estimated Total Case Number by the Formula	15 July 2020 Estimated/Actual Ratio
1	USA	3344783	3320581	0,992
2	Brazil	1884967	1925835	1,021
3	Russian Federation	746369	750862	1,006
4	India	936181	942804	1,007
5	The United Kingdom	291377	262108	0,899
6	Peru	330123	330258	1
7	Chile	319493	324303	1,015
8	Spain	256619	255006	0,993
9	Italy	243344	243410	1
10	Iran	262173	265085	1,011
11	Mexico	304435	310522	1,019
12	Pakistan	255769	264162	1,032
13	Turkey	214993	216549	1,007
14	Germany	199726	199963	1,001
15	Saudi Arabia	237803	247241	1,039
16	France	162390	162660	1,001
17	South Africa	298292	308125	1,032
18	Bangladesh	190057	195465	1,028
19	Canada	108155	105945	0,979
20	Qatar	104533	105889	1,012

When the same calculations were performed for July 22, 2020 (t = 3), the mean ratio of the estimated cumulative case number divided by the actual cumulative case number was found to be 1.017 (1.065 excluding the United Kingdom), and the range was 0.813–1.154 (Table 3 ). This means that the formula estimated the actual numbers with only a 1.7% error on average. The mean value came closer to 1 when the UK was included, but this was a paradox and resulted from the buffering effect of the UK on excessively diverging values in the opposite direction from those of other countries, as the UK revised and reduced the number of historical cases. The estimates for three countries, Italy, Peru, and Germany, deviated from the actual cumulative case numbers by less than 0.1%, which showed greater certainty. The formula estimated the case numbers of five countries (the United Kingdom, Pakistan, Saudi Arabia, Bangladesh, and Brazil) for July 22 less accurately than it did for other countries.

Table 3.

The actual-estimate cumulative case numbers and their ratios for July 22, 2020 in the 20 countries.

	Country	22 July 2020 Total Case Number t = 3	22 July 2020 Estimated Total Case Number by the Formula	22 July 2020 Estimated/Actual Ratio
1	USA	3805524	3777209	0,992
2	Brazil	2118646	2284207	1,078
3	Russian Federation	789190	804984	1,020
4	India	1192915	1196181	1,002
5	The United Kingdom	295821	240730	0,813
6	Peru	357681	357953	1
7	Chile	334683	349383	1,043
8	Spain	266194	257778	0,968
9	Italy	244752	245191	1.001
10	Iran	278827	280642	1,006
11	Mexico	349396	334676	0,957
12	Pakistan	267428	294761	1,102
13	Turkey	221500	225169	1,016
14	Germany	202799	203192	1,001
15	Saudi Arabia	255825	281399	1,099
16	France	166511	165509	0,993
17	South Africa	381798	440667	1,154
18	Bangladesh	210510	227099	1,078
19	Canada	111124	110092	0,990
20	Qatar	104533	110931	1,032

When the same calculations were performed for July 29, 2020 (t = 4), the mean ratio of the estimated cumulative case number/actual cumulative case number was found to be 1.068 (range: 732–1.367) (Table 4 ).

Table 4.

The actual-estimate cumulative case numbers and their ratios for July 29, 2020 in the 20 countries.

	Country	29 July 2020 Total case Number t =4	29 July 2020 Estimated Total case Number by the Formula	29 July 2020 Estimated/Actual Ratio
1	USA	4263531	4288470	1,005
2	Brazil	2442375	2706337	1,108
3	Russian Federation	828990	862414	1,040
4	India	1531669	1517640	0,990
5	The United Kingdom	300696	220308	0,732
6	Peru	389717	387079	0,993
7	Chile	349800	376316	1,075
8	Spain	280610	260611	0,928
9	Italy	246488	246494	1,000
10	Iran	296273	328064	1,107
11	Mexico	395489	438329	1,108
12	Pakistan	276288	328171	1,187
13	Turkey	227982	234305	1,027
14	Germany	206926	206062	0,995
15	Saudi Arabia	270831	320095	1,181
16	France	172148	168545	0,979
17	South Africa	459761	628927	1,367
18	Bangladesh	229185	263386	1,149
19	Canada	114597	112340	0,980
20	Qatar	109880	116478	1,060

The estimation for the total world numbers was nearly exact for July 15, and the estimated numbers differed very little in the short term in general. The estimated/actual ratios were 0.08% for cumulative cases (Table 5 ).

Table 5.

The actual and estimate cumulative case and death numbers in the World in general for short-term.

World Population = 7,800,000,000 Density = 14.7
		Actual Total Case Number	Actual Total Death Number	Estimated Total Case Number	Estimated Total Death Number	Ratio (Estimated /Actual) (Case)	Ratio (Estimated/Actual) (Death)
1 July 2020	(t = 0)	10357662	508055	–	–	–	–
8 July 2020	(t = 1)	11669259	539906	–	–	–	–
15 July 2020	(t = 2)	13150645	574464	13162335	573740	1.0008	0.9987
22 July 2020	(t = 3)	14765256	612054	14854313	609756	1.0060	0.9962
29 July 2020	(t = 4)	16558289	656093	16738197	648001	1.0100	0,9870

3.2. Longer-term estimates at t = 18 weeks

Four months after the first estimation week t = 2, we tested the formula's precision for the worldwide cumulative case number estimation for t = 18 weeks (November 5, 2020) and found a number 80% greater than the actual number (the estimate is higher than the actual number). This may suggest that the estimates for the long term may be misleading. However, it may also suggest that fewer cases have been diagnosed worldwide than estimated even though the second wave of the pandemic has continued in Europe since the summer months. The cumulative case number estimates for t = 18 weeks were more accurate for Turkey, Peru, and the Russian Federation (5%, 25%, and 30% discrepancy, respectively) than the total case estimates for all countries. It is worth noting that Turkey revised the number of cases in November 2020. Turkey did not report the number of asymptomatic cases after July 29, 2020 until revision. As of November 25, 2020, those who were positive for the polymerase chain reaction (PCR) test were added to the number of patients even though they were asymptomatic. Asymptomatic cases from July 29 to December 10 were also added to the number of patients and updated in Turkey.

3.3. Longer-term estimates at t = 40 weeks

For all countries in the study and the world at large, the estimates for the 40th week were not as accurate as in the first month (Table 6 ). The estimated number for the world in general was about 8 times that actually observed. In twelve countries, as in the world in general, the estimated numbers were higher than the observed. However, in some countries this difference was relatively close to the respective estimates (Russian Federation, Iran, Qatar, and Peru). In contrast, the difference was much pronounced in some countries (India, Bangladesh, Saudi Arabia, South Africa, and Mexico). These countries had significantly less case observations than anticipated at the longer term. Eight countries had many more case observations than anticipated. Of these, Italy, France, and the UK were the most prominent. (However, it is necessary to remember that the UK revised the case numbers at the time we obtained the reference values). In Fig. 2 , the curves of the estimated and observed cumulative case numbers in selected 6 countries in short- and long-term are demonstrated as an overview. The complete data of this chart are shown in Table 7 .

Table 6.

The actual-estimate cumulative case numbers and their ratios for April 07, 2021 in the 20 countries.

	Country	07 April 2021 Total case Number t = 40	07 April 2021 Estimated Total case Number by the Formula	07 April 2021 Estimated/Actual Ratio
1	USA	30475874	190011326	6,234
2	Brazil	13013601	182736630	14,041
3	Russian Federation	4606162	9827278	2,133
4	India	12801785	1158404820	90,48
5	The United Kingdom	4358882	9303	0,002
6	Peru	1590209	5591373	3,516
7	Chile	1037780	4415578	4,254
8	Spain	3325600	387193	0,116
9	Italy	3686707	305745	0,082
10	Iran	1963394	4673243	2,380
11	Mexico	2251705	80911676	35,933
12	Pakistan	696184	14748317	21,184
13	Turkey	3579185	972292	0,271
14	Germany	2910445	341855	0,117
15	Saudi Arabia	394169	17369642	44,066
16	France	4807569	311714	0,064
17	South Africa	1552853	59622350	38,395
18	Bangladesh	651652	41293937	63,368
19	Canada	1014373	223385	0,220
20	Qatar	185261	551377	2,976

Fig. 2.

Estimated and observed cumulative case numbers in selected 6 countries in short- and long-term. In the short-term of about 2–3 months, estimated numbers were close to the observed numbers in all of the countries. In the longer-term (up to ten months), an overestimation was observed in some countries such as India, Peru, Russian federation and USA, and an underestimation was observed in some countries such as Italy and Turkey. However, in some countries such as Russian Federation and Peru, error in the prediction was relatively low even in the longer-term. (The countries in the chart were listed in alphabetical order.)

Table 7.

Forty-week estimated and observed cumulative case numbers of selected (as example) 6 countries, of which diagrammatic representations are shown in Fig. 2.

Week	Date	Countrya
		India		Italy		Peru		Russian F.		Turkey		USA
		Estimate	Observed	Estimate	Observed	Estimate	Observed	Estimate	Observed	Estimate	Observed	Estimate	Observed
0	1-Jul-20	–	585493	–	240578	–	282365	–	654405	–	199906	–	2573393
1	8-Jul-20	–	742417	–	241956	–	305703	–	700792	–	207897	–	2923432
2	15-Jul-20	942804	936181	243410	243344	330258	330123	750862	746369	216549	214993	3320581	3344783
3	22-Jul-20	1196181	1192915	245191	244752	357953	357681	804984	789190	225169	221500	3777209	3805524
4	29-Jul-20	1517640	1531669	246494	246488	387079	389717	862414	828990	234305	234712	4288470	4263531
5	5-Aug-20	1925348	1908254	247914	248419	418376	433100	923954	866627	243752	288774	4869597	4678610
6	12-Aug-20	2442400	2329638	249404	251237	452314	483133	989857	902701	253614	344130	5528638	5039709
7	19-Aug-20	3097987	2767273	250903	254636	488963	541493	1060426	937321	263873	399865	6275141	5393138
8	26-Aug-20	3929035	3234474	252411	261174	528533	600438	1135998	970865	274517	456364	7120217	5682811
9	2-Sep-20	4982192	3769523	253929	270189	571249	652037	1216888	1005000	285650	513985	8076245	5968380
10	9-Sep-20	6316319	4370128	255455	280153	617351	691575	1303498	1041007	297201	572660	9156977	6248989
11	16-Sep-20	8005576	5020359	256990	289990	667097	733860	1396214	1079519	309218	631120	10377641	6496246
12	23-Sep-20	10143210	5646010	258535	300897	720762	772896	1495456	1122241	321718	689912	11755031	6779609
13	30-Sep-20	12846178	6225763	260089	313011	778639	808714	1601675	1176286	334722	747992	13307582	7077015
15	7-Oct-20	16260709	6757131	261652	330263	841042	829999	1715349	1248619	348249	805387	15055434	7380326
15	14-Oct-20	20568894	7239389	263224	365467	908305	851171	1836988	1340409	362320	863719	17020445	7728436
16	21-Oct-20	25996305	7651107	264806	434449	980781	870876	1967137	1447335	376957	923463	19226183	8124633
17	28-Oct-20	32820534	7990322	266398	564778	1058850	890574	2106372	1563976	392183	985368	21697840	8611256
18	4-Nov-20	41380298	8313876	267998	759829	1142909	906545	2255308	1693454	408021	1048388	24462092	9193765
19	11-Nov-20	52084394	8591730	269609	995463	1233382	923527	2414600	1836960	424495	1112740	27546857	9990620
20	18-Nov-20	65419243	8912907	271229	1238072	1330716	938268	2584942	1991998	441631	1181903	30980950	11085184
21	25-Nov-20	81953001	9222216	272859	1455022	1435383	950557	2767070	2162503	459454	1268523	34793613	12276834
22	2-Dec-20	102333224	9499413	274498	1620901	1547877	963605	2961767	2347401	477993	1461758	39013899	13385755
23	9-Dec-20	127274001	9735850	276148	1757394	1668719	975116	3169861	2541199	497275	1686431	43669905	14755996
24	16-Dec-20	157527526	9932547	277807	1870576	1798453	986130	3392231	2734454	517331	1898447	48787838	16245376
25	23-Dec-20	193834864	10099066	279476	1977370	1937646	998475	3629806	2933753	538189	2062960	54390930	17895109
26	30-Dec-20	236851968	10244852	281155	2067487	2086887	1008908	3883570	3131550	559884	2178580	60498205	19147627
27	6-Jan-21	287050889	10374932	282844	2181619	2246787	1021058	4154559	3308601	582446	2270101	67123149	20643544
28	13-Jan-21	344603224	10495147	284514	2303263	2417974	1037350	4443869	3471053	605911	2346285	74272319	22428591
29	20-Jan-21	409262743	10595660	286253	2400598	2601095	1068802	4752654	3633952	630314	2399781	81943976	23884299
30	27-Jan-21	480274236	10689527	287973	2485956	2796809	1102795	5082129	3774672	655693	2442350	90126837	25050308
31	3-Feb-21	556340752	10777284	289703	2570608	3005784	1142716	5433571	3901204	682084	2492977	98799047	26055512
32	10-Feb-21	635676017	10858371	291443	2655319	3228695	1191221	5808319	4012710	709529	2548195	107927488	26832826
33	17-Feb-21	716150026	10937320	293194	2739591	3466216	1238501	6207778	4112151	738068	2602034	117467536	27433718
34	24-Feb-21	795508001	11030176	294955	2832162	3719014	1286757	6633416	4200902	767744	2655633	127363358	27883560
35	3-Mar-21	871617473	11139516	296726	2955434	3987745	1332939	7086767	4278750	798602	2723316	137548796	28345585
36	10-Mar-21	942687791	11262707	298509	3101093	4273043	1374467	7569427	4351553	830088	2807387	147948852	28827195
37	17-Mar-21	1007416606	11438734	300301	3258770	4575514	1418974	8083057	4418436	864049	2911642	158481728	29208890
38	24-Mar-21	1065043237	11734058	302105	3419616	4895724	1472790	8629380	4483471	898735	3061520	169061308	29594849
39	31-Mar-21	1115316668	12149335	303919	3561012	5234191	1533121	9210175	4545095	934799	3277880	179599942	30033063
40	7-Apr-21	1158404820	12801785	305745	3686707	5591373	1590209	9827278	4606162	972292	3579185	190011326	30475874

^aCountries were listed alphabetically.

In Fig. 3 , when examining the curves of the worldwide observed numbers and estimated cumulative case numbers during the 40 weeks between July 2020 and April 2021 it can be easily seen that the formula quite accurately predicted the observed numbers for the first four months (from July to October 2020). However, the estimates for November and December 2020 were slightly above the observed figures. This overestimation has become increasingly apparent after January 2021. This may not be surprising, as this period coincides with the start and gradual acceleration of vaccination around the world.

Fig. 3.

Global estimated and observed cumulative case numbers.

4. Discussion

Our model using the simple Verhulst–Pearl logistic function equation proves to be in perfect agreement with the real data for forecasting the pandemic progress in the short but not long term, probably because vaccination had begun or perhaps because of the assumptions of the model which may not fit well with the COVID-19 pandemic. Several other authors also reported using the Verhulst–Pearl logistic function in predicting cumulative case numbers from the COVID-19 pandemic.^{13 ,} 34, 35, 36 Mahanty et al.³⁶ compared two nonlinear growth models (Verhulst and Gompertz) and the susceptible-infectious-recovered model (SIR) to predict active COVID-19 cases in India, Pakistan, Italy, Germany, Brazil, and Myanmar, and found that the Verhulst model's fitting effect is better than that of the Gompertz and SIR models. Niazkar et al.³⁷ used the three mathematical prediction models (a recursive-based method, the Boltzmann function-based model, and Beesham's prediction model) to forecast COVID-19 case and death numbers in Iran and Turkey. They concluded that these models failed to predict the first 10–20 days of data, although the recursive-based method was more effective than the others. Postnikov¹³ reported that the SIR model, being sequentially reduced to the Verhulst equation, could provide an accurate description of the COVID-19 epidemic for a period of about three months in various countries, including Italy, the U.S., China, and Russia.

Whether static, deterministic, or dynamic stochastic models are used, studies generally covered one- to three-month periods. Therefore, we were unable to make comparisons with other studies in the literature in the longer term, although our study covers a 10-month period. However, for the short term, the model we used provided estimation results that were similar to those of the dynamic stochastic complex models. Three main parameters limit the ability to predict the long-term growth of the COVID-19 pandemic.³⁸ First, the extent of protective immunity is still unclear. Second, the extent of transmission and immunity among asymptomatic or minimally symptomatic individuals, as it is more common in children, is unknown. Third, it is nearly impossible to measure and model contact rates between susceptible and contagious individuals in various lockdown or reopening scenarios. It is possible that the Verhulst-Pearl model does not work in the longer term just because of its inherent assumptions, which may not fit with the COVID-19 pandemic. However, short-term forecasts of a few weeks based on the logistics growth model can give very reliable results. Due to changes in the external environment, such as modifications in government control policies and new treatment methods, the mathematical models will not necessarily be accurate for long-term estimates, and therefore, the model parameters should be updated to provide reliable long-term forecasts.²² This can be explained by the S-shape of the logistic function curve, which is convex in the early stages of a pandemic unlike the concave curvature seen in the later periods. In other words, when the curve approaches the limit (the saturation of transmission), the change over time will be less. Some published research suggests that mathematical models provide more accurate results at the early exponential growth stage of outbreaks, perhaps because any precautions have not yet been taken.¹³ Since we have been interested in the long-term course of the pandemic leading to a potential herd immunity rather than the very short-term course, we used “week” instead of “day” for the time t-value in the formula, although we were aware that mathematical models were more accurate for short term daily forecasts and weekly forecasts are more prone to error as Arora et al. noted.³⁹

To get an idea of whether the simple model we used in this study is as reliable as the complex models, we compared it with two published studies, one using the Susceptible, Infected and Recovered (SIR) model⁴⁰ and the other using recurrent neural networks, and long short-term memory (LSTM) based model.³⁹ In the first of these studies, using the SIR model with correction factor, Malavika et al.⁴⁰ estimated the cumulative numbers of cases in India as 58912, 81709 and 102974 for 8, 15 and 22 May 2020, respectively. The cumulative numbers of cases reported by WHO for India on the same dates are 56342, 81970 and 118447, respectively, and when we compare them with their respective estimates, we get 1.045, 0.996, and 0.869, respectively. In the other compared study, Arora et al.³⁹ conducted a research on predicting the number of new coronavirus positive cases in India for one day to one week beforehand, using recurrent neural networks and long short-term memory based model. They reported that their model was quite accurate for 1–3 day forecasts, but the error increased for weekly forecasts. The prediction/actual ratios for 7 and 14 May 2020 in their study were 1.005 and 1.002 respectively. In our study, the prediction/actual ratios we found for India on 15, 22 and 29 July are 1,007 (936181/942804), 1,002 (1192915/1196181), and 0,990 (1531669/1517640) respectively. Thus, our forecasting seems to be as reliable as that of Malakavi et al. and Arora et al. Both of these studies were conducted in the pre-vaccination period covering a 2 to 3-week period using daily initial references. In contrast, our study provides estimates for a longer period of 40 weeks, including the vaccination period, using weekly rather than daily initial references for practical purposes.

Appropriately measuring the transmission dynamics of infectious diseases is a function of the calendar period.⁴¹ The most commonly used determinant of the transmission potential is the basic reproduction number, which is defined as the expected number of secondary cases arising from a typical primary case throughout its entire course of infection in a fully susceptible population.42, 43, 44 One of the methods to estimate the reproduction number is to use the growth rate of the cumulative incidence of cases during the exponential growth phase of the pandemic.⁴⁴ As can be expected, an exponential growth model estimates parameters more precisely during a pandemic's exponential growth phase.⁴⁵

All mathematical models are a simplifications of reality.⁴⁶ However, when these simplifications have little effect on the characteristics of the epidemic of interest, it can lead to a satisfactory result. Therefore, the Verhulst–Pearl equation is valid and useful in solving a simple optimal growth problem.^{25 , 26 , 47} Of course, it is not flawless; the Verhulst model is a deterministic model (not a process wherein the random variable exists) and does not include any stochastic (randomly determined) components. Stochastic effects make the invasion threshold challenging to discern.⁴⁸ For example, the number of individuals susceptible to infection and the reproduction number decreases as the outbreak progresses.⁴⁹ The fluctuations on the level of the limit (in other words, endemic disease die-outs or the population saturation point or carrying capacity, similar to that of the increase of a country's population, is not unlimited in terms of herd immunity) cannot be explained by the Verhulst–Pearl model.⁵⁰ However, while adding more complexity to a mathematical model increases the realism, it often makes analysis difficult for an ordinary clinician, and more parameters increase the uncertainty.

Using the mathematical formula in this study, we can predict when the pandemic will end around the world. For herd immunity in the community, typically 60–90% of the population must be immunized via infection or vaccination.^{51 , 52} This percentage is called the herd immunity threshold. The basic reproduction number (R₀) is the most important parameter in calculating the herd immunity threshold and refers to the average number of infected people caused by a single infectious person.^{53 , 54} Although it is not yet known what this rate is for COVID-19, it is estimated to be between 50 and 83%; deducted from that, the R₀ value has been reported to be between 2 and 6 in COVID-19.^{51 , 52 , 54 , 55} This means that when 50–83% of the population becomes immune to the COVID-19 disease, herd immunity will be theoretically achieved (calculated from the formula: herd immunity threshold R = 1- 1/R₀).^{53 , 54 , 56} Hence, assuming there are no reinfections in COVID-19 disease and a lifelong immunity is obtained, and the R₀ value is an average of 4 (i.e., 75% of the population must be infected for herd immunity), we found that 75% (approximately 5.8 billion) of the world population will be infected and immunized 64 weeks (1.10.2021) after t₀ time (1.7.2020) in our study, and thus, herd immunity will be reached. This finding supports claims that herd immunity against COVID-19 cannot be achieved without unacceptably high case fatality rates, even if we assume that the death rate is 2%.⁵² If the immunity gained by ongoing vaccination is considered, it may be possible to achieve herd immunity earlier. These estimates are for the whole world and, because there is heterogeneity in transmission, much better scenarios can be expected for an individual country based on the individual transmission dynamics including their specific R₀ value and mortality rate, which are themselves dependent on many other factors, including age, genetic factors, socioeconomic factors, healthcare system, behavioral factors, use of personal protective equipment, and the spatial distribution of people.⁵³

As herd immunity and a constant force of infection are assumptions in the Verhulst-Pearl exponential growth model we used, this static model has some weaknesses in forecasting the COVID-19 pandemic in the longer term. With the COVID-19 pandemic, the herd immunity threshold seems highly unlikely due to factors such as the emergence of new variants, vaccine hesitancy, limited use of vaccines for children, and uncertainty about the extent to which vaccinated people are infected and spread the virus.⁵⁷ In the model used in our study, it was assumed that each individual could have only one COVID-19 infection, regardless of age, gender, or any other variable. In reality, we now know that it is possible to become infected more than once with COVID-19 and even that the virus might have a potential to reactivate after a latent period,⁵⁸ but we also know that this is not a very common situation, at least not during our study period. Therefore, we think that the herd immunity assumption may not have affected our study's overall results too much.

In contrast to the Verhulst-Pearl exponential growth model's static nature, dynamic models simulate changes in infectious strength and the infectious pathogen's dynamics.^{57 , 59} Dynamic models are highly sophisticated and complex models, but they need detailed knowledge of transmission routes and infectiousness. Therefore, these models' results still might contain much uncertainty. However, the Verhulst-Pearl exponential growth model is deterministic, i.e., if the state of the system at a certain point in time is known, all future states can be determined by solving the relevant model.⁵⁹ Thus, when a rapid investigation is required, analysis using the Verhulst-Pearl exponential growth model, without taking potential stochastic effects into account, may be an option that provides initial results and an idea of the general sequence of events.^{57 , 60} Therefore, large populations in stable environments often are modelled with deterministic models, while stochastic models are more useful in demonstrating the system's inherent variability for small population sizes.^{59 , 60} Thinking in deterministic terms is a way of generating concepts and trying to determine the most probable course of events, even if it excludes stochastic dynamics from the model.⁶⁰

Where does our investigation leave us in terms of the allocation of medical resources in general and neurosurgical planning in particular? The COVID-19 pandemic prompted the application of new priority guidelines for patients requiring neurosurgery interventions. As a result, most elective surgeries have been delayed. Furthermore, patients who need surgery have been avoiding admission to hospitals or have been delaying their treatment as much as possible because they are afraid of being infected by SARS-CoV-2.1, 2, 3 ^{, 24 , 61 , 62}

A European survey from the EANS Ethico-Legal Committee highlighted how the COVID-19 pandemic led to a rationing of neurosurgical care in 80% of the responding countries.³ While the study demonstrated a correlation between the resources available before the pandemic and the ability to uphold neurosurgical services, it also highlighted the collateral damage that prioritization and rationing may have on the population served by the neurosurgical centers participating in the survey. When forced to ration resources due to a pandemic event, an accurate estimation of its evolution would be extremely useful. COVID-19 is expected to evolve into multiple waves, and forecasts on bed availability might mean the difference between being offered surgical or conservative treatment for individual neurosurgical patients. Neurosurgery is under a higher economic burden than many other medical branches in terms of both the cost of patient treatment and the training of residents and medical students interested in neurosurgery63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73 The fair and effective use of resources has become even more important during the pandemic, which seems to be lasting longer than initially thought. Therefore, it is imperative that neurosurgery clinics and neurosurgical societies organize longer-term work patterns and training programs, including professional congresses.

As well as the direct effects of the epidemic, attempts to control it have profound economic consequences.^{55 , 70 , 71} This continuing situation, the length of which is unknown, has caused many government to make economic decisions. Economic decisions have a tremendous influence on the character of life in a society.⁷⁴ Therefore, a reliable estimation of the course of the pandemic will help physicians design more effective plans and arrangements for their patients and the training of residents.

4.1. Limitations

Despite numerous speculations about the epidemiological course of the pandemic, identifying the correct prediction is difficult. We made this study based on figures we obtained from the WHO's sources. However, the WHO warned that the completeness of the indicators varies by countries and regions, and that the decrease in cases shown over time should be interpreted with the trend in country participation, that delays in reporting may be observed, and that the number of cases depends on detection and testing strategies that vary between countries and over time. Therefore, due to variable information collection and reporting, it is more appropriate to analyze each country/region independently.

The benefit of this algorithm, although limited to a short time horizon, is its relative simplicity. Essentially, methods for modeling viral disease dynamics are often more complex, including intrahost, interhost, and environmental factors and involving a large number of stochastic processes. The simple design of the formula we used has not been validated for long time periods. It is just a way of projecting current trends into the near future. However, although this mathematical approach is not complex, its application still requires a basic knowledge of mathematics.

5. Conclusions

The Verhulst–Pearl equation is a valid and useful tool to solve a simple optimal growth problem. Unlike complex mathematical models that increase accuracy, this equation makes the analysis easy for an ordinary clinician. When forced to ration resources due to a pandemic event, an accurate estimation of its evolution would be extremely useful. This model has the advantage of being very simple and applicable in neurosurgery for predicting the demand on hospitals in the short term of 4–6 weeks, which is usually enough time to reschedule elective procedures and free beds for new waves of the pandemic patients. However, the reliability of the formula in long-term estimates is uncertain.

Conflict-of-interest disclosure

The authors declare no competing financial interests and no sources of funding and support, including any for equipment and medications.

Ethical issues

The ethical issues for this study involving human subjects have been carefully considered in line with the Declaration of Helsinki (1964).

Financial support

None

Authors’ contributions

• Naci Balak: Conception of the idea, data collection, analysis design and performance results interpretation, writing the text, literature search, text revision

• Deniz Inandenizlukuslu@marmara.edu.tr Analysis performance, literature search, text revision, critical review of the intellectual content,

• Mario GanauMario.Ganau@alumni.harvard.edu Data analysis and design, interpretation of the results, literature search, text revision, critical review of the intellectual content,

• Cesare Zoiagioiaoffice@gmail.com Data analysis and design, interpretation of the results, literature search, text revision, critical review of the intellectual content,

• Sinan Sönmezssonmez@marmara.edu.tr Literature search, text revision, critical review of the intellectual content,

• Batuhan Kurtbatuhan@marmara.edu.tr Literature search, text revision, critical review of the intellectual content,

• Ahmet Akgülahmetakgul@marmara.edu.tr Literature search, Text revision, critical review of the intellectual content

• Müjgan Tezmtez@marmara.edu.tr Data analysis, literature search, text revision, critical review of the intellectual content, supervision of the course of the project and the article