Computational study of non-conductive selectivity filter conformations and C-type inactivation in a voltage-dependent potassium channel

Li et al. carry out molecular dynamics simulations of the K⁺ channels Shaker and KcsA to test whether a structural constriction of the non-conductive selectivity filter is a universal mechanism of C-type inactivation in K⁺ channels.

Abstract

C-type inactivation is a time-dependent process of great physiological significance that is observed in a large class of K⁺ channels. Experimental and computational studies of the pH-activated KcsA channel show that the functional C-type inactivated state, for this channel, is associated with a structural constriction of the selectivity filter at the level of the central glycine residue in the signature sequence, TTV(G)YGD. The structural constriction is allosterically promoted by the wide opening of the intracellular activation gate. However, whether this is a universal mechanism for C-type inactivation has not been established with certainty because similar constricted structures have not been observed for other K⁺ channels. Seeking to ascertain the general plausibility of the constricted filter conformation, molecular dynamics simulations of a homology model of the pore domain of the voltage-gated potassium channel Shaker were performed. Simulations performed with an open intracellular gate spontaneously resulted in a stable constricted-like filter conformation, providing a plausible nonconductive state responsible for C-type inactivation in the Shaker channel. While there are broad similarities with the constricted structure of KcsA, the hypothetical constricted-like conformation of Shaker also displays some subtle differences. Interestingly, those are recapitulated by the Shaker-like E71V KcsA mutant, suggesting that the residue at this position along the pore helix plays a pivotal role in determining the C-type inactivation behavior. Free energy landscape calculations show that the conductive-to-constricted transition in Shaker is allosterically controlled by the degree of opening of the intracellular activation gate, as observed with the KcsA channel. The behavior of the classic inactivating W434F Shaker mutant is also characterized from a 10-μs MD simulation, revealing that the selectivity filter spontaneously adopts a nonconductive conformation that is constricted at the level of the second glycine in the signature sequence, TTVGY(G)D.

Introduction

The function of potassium (K⁺) channels is to regulate the flow of K⁺ ions across cell membranes in response to various external stimuli. To this end, different aspects of K⁺ channel function, such as open-channel conductance, selectivity, activation gating, and inactivation, are finely adapted to the different tissues where they operate. Of great physiological importance for cellular excitability, C-type inactivation is a general kinetic process observed in a large class of K⁺ channels, whereby prolonged activation by an external stimulus leads to a spontaneous reduction of K⁺ current, reflecting a decreased probability of the conductive state. C-type inactivation plays a critical role in pacing cardiac action potentials and in regulating neuronal firing, and impaired inactivation can lead to a variety of cardiac and neurological disorders (Aldrich et al., 1979; Adelman et al., 1995; Perrin et al., 2008).

The pH-activated KcsA bacterial K⁺ channel serves as an important prototypical model to guide our understanding of C-type inactivation of K⁺ channels at the atomic level. Strong evidence from functional measurements (Cordero-Morales et al., 2006; Chakrapani et al., 2011; Cordero-Morales et al., 2011), x-ray crystallography (Zhou et al., 2001; Cuello et al., 2010a; Cuello et al., 2010b; Tilegenova et al., 2017), NMR spectroscopy (Weingarth et al., 2014), and MD simulations (Pan et al., 2011; Ostmeyer et al., 2013; Li et al., 2017; Li et al., 2018) indicate that C-type inactivation in the KcsA channel is associated with a structural constriction of the selectivity filter occurring at the level of the central glycine residue in the signature sequence, TTVGYGD (bold and underlined letter indicates which residue is the constricted site in channel). The conductive-to-constricted transition of the selectivity filter is allosterically enhanced by the opening of the intracellular activation gate, which indirectly sets the inactivation rate (Li et al., 2018). However, although a number of crystal structures have been determined for voltage-activated K⁺ channel (K_v) and other K⁺ channel families over the past decades, none display a KcsA-like constricted filter. Additional pieces of information contribute to the emerging picture. For example, a recent computational study indicates that C-type inactivation in the hERG channel is associated with a constricted-like conformation of the selectivity filter (Li et al., 2021). Furthermore, a study of the MthK channel concluded that its selectivity filter remains in a canonical conductive conformation in crystal structures even at very low K⁺ concentrations, but that it can ultimately adopt a constricted conformation in the complete absence of bound ions (Boiteux et al., 2020). Therefore, different lines of evidence suggest that the constricted (or constricted-like) conformation of the selectivity filter of K⁺ channels ought to be accessible in general. Nonetheless, whether filter constriction is a universal mechanism of C-type inactivation in K⁺ channels has not clearly been established, and it remains somewhat controversial (Hoshi and Armstrong, 2013; Pau et al., 2017).

As the phenomenon of C-type inactivation was most clearly documented with functional measurements in the case of voltage-activated Shaker K⁺ channel from Drosophila melanogaster (the Shaker channel; Hoshi et al., 1990, 1991; Yellen et al., 1994; Baukrowitz and Yellen, 1995; Kurata and Fedida, 2006; Panyi and Deutsch, 2006; Sadovsky and Yifrach, 2007; Pless et al., 2013; Pau et al., 2017; Szanto et al., 2020), it is critical to ultimately return to these systems to ascertain the validity of the conclusions drawn from studies of the KcsA channel model system. Much has been learned about C-type inactivation in the Shaker channel using site-directed mutagenesis and electrophysiological studies (Yellen et al., 1994; Baukrowitz and Yellen, 1995; Olcese et al., 1997; Pless et al., 2013; Pau et al., 2017), although whether inactivation is due to filter constriction, dilation, or sub-stochiometric ion occupancy is still debated (Hoshi and Armstrong, 2013; Pau et al., 2017). A striking example is the classic W434F Shaker mutant, which abolishes ion conduction without affecting the gating charge associated with voltage activation (Perozo et al., 1993). Although the structural basis of its functional behavior is unknown, it is generally assumed that the W434F Shaker mutant is predominantly in a C-type inactivated state (Yang et al., 1997). Furthermore, a number of studies also suggest that there is an allosteric coupling between the selectivity filter and the intracellular activation gate of the Shaker channel (Panyi and Deutsch, 2006; Sadovsky and Yifrach, 2007; Szanto et al., 2020), but whether the constriction of the selectivity filter is strictly controlled by the opening of the intracellular gate as in the case of the KcsA channel is still an open question.

In view of the high similarity between the pore domains of Shaker and KcsA (almost 40% sequence identity), and by analogy with the well-documented case of the KcsA channel (Cuello et al., 2010a; Li et al., 2018), our working hypothesis is that the molecular mechanism of the C-type inactivation process in the Shaker channel broadly relates to some constriction of the selectivity filter that is allosterically coupled to the opening of the intracellular activation gate. The goal of the present effort is to explore the validity of this hypothesis using MD simulations based on a model of the pore domain of the Shaker channel in the open state. Specific efforts are made to characterize the conformational preference of the selectivity filter using free energy landscape calculations. For the sake of completeness, the rapidly inactivating W434F mutant of Shaker was also characterized using a very long MD simulation.

Materials and methods

The atomic model of the Shaker channel was constructed based on the pore domain of the crystal structure (Long et al., 2007; Protein Data Bank [PDB] accession no. 2R9R) of K_v1.2/K_v2.1. It has a canonical conductive selectivity filter and represents an open structure with the width as 18 Å measured by the Cα–Cα cross-subunit distances of S479 (the equivalent residue of T112 in KcsA) along the transmembrane helix S6. Considering the sequence identity of the pore domain between K_v1.2 and the Shaker channel is 87%, the nonconserved residues of K_v1.2 were substituted by Shaker-like amino acids to build the pore domain of the WT Shaker channel, while keeping the rotamer of the remaining residues as the original crystal structure. An atomic model of the WT KcsA channel was constructed based on its crystal structure (Cuello et al., 2010b; PDB accession no. 3F7V). It represents a fully open structure (width as 23 Å measured by the Cα–Cα cross-subunit distances of T112 along the second transmembrane helix TM2) with a constricted selectivity filter. The model of the Shaker W434F mutant was built with W434 substituted by phenylalanine (F), and the KcsA E71V mutant was built with E71 substituted by valine, both of which were respectively based on the WT models by using the VMD psfgen plugin (Humphrey et al., 1996). For all MD simulations, both the Shaker and KcsA channels were embedded in a bilayer of 3POPC:1POPG lipids and solvated in 150 mM KCl using the web service CHARMM-GUI (Jo et al., 2008; Jo et al., 2009). Most residues were assigned their standard protonation state at pH 7. The total number of atoms in the MD systems is on the order of 45,000 (pore domain of the Shaker channel) or 41,000 (KcsA).

The CHARMM force field PARAM36 for protein (Best et al., 2012; Huang et al., 2017), lipids (Klauda et al., 2010), and ions (Beglov and Roux, 1994) was used. Explicit water was described with the TIP3P model (Jorgensen et al., 1983). All the simulations were performed under NPT (constant numbers of particle N, pressure P, and temperature T) conditions at 310 K and 1 atm, and periodic boundary conditions with electrostatic interactions were treated by the particle mesh Ewald method (Darden and Pedersen, 1993) and a real-space cutoff of 12 Å. The simulations use a time step of 2 fs, with bond distances involving hydrogen atoms fixed using the SHAKE algorithm (Ryckaert et al., 1977). After minimization and equilibrations with harmonic positional restraints (Table S1), the equilibrated systems were simulated either using NAMD version 2.13 (Phillips et al., 2005) or the special-purpose computer Anton (Shaw et al.; 10.1145/1654059.1654099). The conformational change of the selectivity filter was monitored by following the cross-subunit distance between the glycine (G77 for KcsA, and G444 for Shaker) Cα atoms of the two pairs of diagonally opposed monomers.

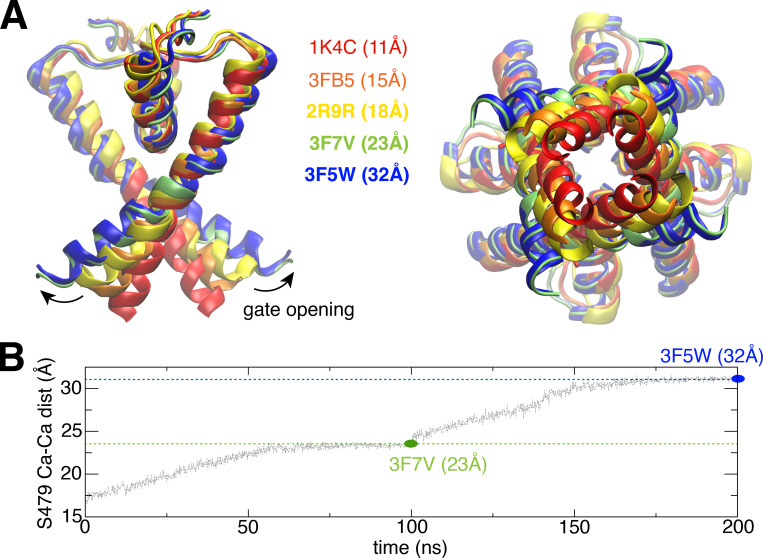
To achieve wider opening of the intracellular gate of the Shaker channel, we designed a mechanistically relevant and system-specific reaction coordinate, i.e., the RMSDs of S6 helices, by using the equivalent TM2 helices from two open structures (PDB accession nos. 3F7V and 3F5W) of KcsA as references, to induce the gate opening stepwise during 200-ns MD simulation (Fig. 2 B). In this bias simulation, the selectivity filter was restrained by using constricted selectivity filter conformation of KcsA as reference. Such a bias simulation provides a series of structures with both constricted selectivity filter and differential opening degrees of the intracellular gate and allows us to test the stability of the constricted selectivity filter in those structures. Then 15 structures were selected from this bias simulation trajectory with a range of opening degrees of the intracellular gate (from 22 to 32 Å; Fig. 2 B) as initial seeds, to perform equilibrium simulations while only restraining the intracellular gate opening (at S479 Cα atoms). These simulations were extended to at least 400 ns to assess the stability of the constricted selectivity filter conformation in the Shaker channel.

Figure 2.

TMD simulation drives the intracellular gate of the Shaker channel open progressively in a stepwise manner.(A) Overlap the K_v1.2/K_v2.1 structure with KcsA structures, to show how to trigger further opening of the intracellular gate by using two KcsA structures (PDB accession nos. 3F7V and 3F5W) as references. (B) Stepwise bias MD simulations to trigger gate opening. The first 100-ns simulation is performed by using 3F7V as a target reference. The second 100-ns simulation is performed by using 3F5W as target reference. dist, distance.

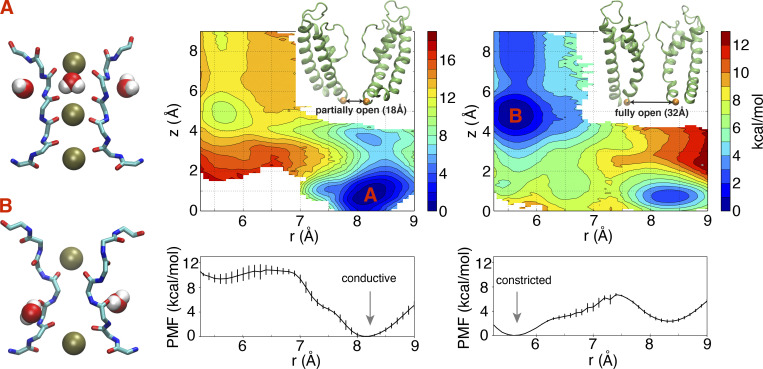
2-D potential of mean force (PMF) calculations were performed using NAMD 2.13 (Phillips et al., 2005) with respect to the two coordinates that were validated in our previous computational studies for the other potassium channels (KcsA and hERG; Ostmeyer et al., 2013; Li et al., 2017, 2018, 2021). One reaction coordinate r describes the width of the selectivity filter and is defined as the average cross-subunit distance between the Cα atoms of glycine (G77 for KcsA, and G444 for Shaker), whereas the other reaction coordinate z indicates the position of the external K⁺ ion along the z axis relative to the center of the selectivity filter. The region of interest in the (r, z) space was covered by a grid of equally spaced umbrella sampling (US) windows. To improve the statistical sampling, the US calculations were performed using Hamiltonian replica-exchange MD (US/H-REMD; Sugita and Okamoto, 2000; Jiang et al., 2012). For the Shaker channel, two sets of 2-D–PMF calculations were performed in two states, respectively, with partially open (18 Å) and wide-open (32 Å) gates. Some initial coordinates for the US windows were taken from the unbiased trajectories, and initial coordinates for the missing windows were obtained by driven MD simulations along the reaction coordinates to the space of the missing windows. Different from previous studies (Ostmeyer et al., 2013), there is no restraint on water molecules to access or leave the inactivating water binding site behind the selectivity filter, and all of the 85 windows were extended to ∼120 ns. For the KcsA channel, the data for WT are from our previous study (Li et al., 2018), and the initial coordinates of the mutant E71V for the 85 US windows were mutated based on WT. All windows for KcsA E71V were extended to 300 ns (only the last 100 ns was used for PMF calculation). The total aggregate simulation time for all US/H-REMD calculations is 42 µs. Exchange attempts were made every 500 steps (or 1 ps of simulation time), and neighboring windows were swapped if the Metropolis Monte Carlo exchange probability was satisfied. Windows were unbiased using the weighted histogram analysis method (Kumar et al., 1992; Roux, 1995), which only required that the US windows were generated according to Boltzmann statistics. Besides 2-D–PMF for (r, z) space, different 2-D–PMFs were constructed. One 2-D–PMF is for two coordinates (Ψ, r), in which Ψ is the backbone dihedral angle Ψ for Val in the selectivity filter (V76 for KcsA, and V443 for Shaker). SDs (Fig. 4) are calculated based on separation of the sampling collected from the 120 ns for each window, in which 20–40 ns, 40–60 ns, 60–80 ns, 80–100 ns, and 100–120 ns are treated as five sets of sampling. The first 20 ns is excluded from the calculation as it is not fully equilibrated.

Figure 4.

2-D–PMF to assess the conformational preferences of the selectivity filter with partially and wide-open intracellular gates based on a model of the pore domain of the Shaker channel. The horizontal reaction coordinate r describes the width of the selectivity filter and is defined as the average cross-subunit pinching distance between the Cα atoms of G444. The vertical reaction coordinate z indicates the position of the external K⁺ ion along z axis relative to the center of the selectivity filter. The lower panel is the 1-D–PMF along horizontal reaction coordinate r, with integration of the vertical reaction coordinate z. The typical conformations for two free energy basins (A and B) are shown in stick representation for protein and van der Waals representation for both water and K⁺ ions. The conductive filter conformation is the most stable when the gate is partially open (18 Å) as in the x-ray structure PDB accession no. 2R9R. The constricted filter conformation is the most stable when the gate is wide open (32 Å) as in the x-ray structure PDB accession no. 3F5W. The 2-D–PMF with a gate opening of 18 Å previously appeared in (Li et al., 2021).

The stability of the constricted conformation of the selectivity filter obtained via simulations based on the CHARMM force field was examined with a 1 µs simulation based on the AMBER force field and the AMBER program. The initial system was created from the coordinates obtained at the end of the CHARMM simulation of the Shaker pore domain with constricted filter. The system was converted to the proper format using the CHARMM-GUI's force field converter (Jo et al., 2008; Lee et al., 2020) for the AMBER force field ff14sb for protein (Maier et al., 2015), LIPID17 for lipids (Gould, I.R., A.A. Skjevik, C.J. Dickson, B.D. Madej, R.C. Walker, personal communication), Joung and Cheatham (2008) for ions, and TIP3P for water (Jorgensen et al., 1983). The generated AMBER scripts provided by CHARMM-GUI (Jo et al., 2008) were used in the subsequent equilibration and production runs using a real-space cutoff of 12 Å. The 1-µs trajectory was generated using the graphics processing units version of the PMEMD MD simulation engine of AMBER20 (Le Grand et al., 2013; Salomon-Ferrer et al., 2013; Case et al., 2021).

Online supplemental material

Fig. S1 shows differential conformational preferences of the Shaker channel with different opening degrees. Fig. S2 shows simulations of the constricted conformation generated using the AMBER force field with the PMEMD MD engine of AMBER. Fig. S3 shows 2-D–PMF explicitly along the two distances between the Cα atoms of G444 of diagonally opposed subunits A and C (r₁), and B and D (r₂) for the Shaker channel at 32 Å opening. Fig. S4 shows a stable constricted conformation of the selectivity filter in KcsA E71V mutant. Table S1 lists MD simulations in the present study (PMF calculation is not included).

Figure S1.

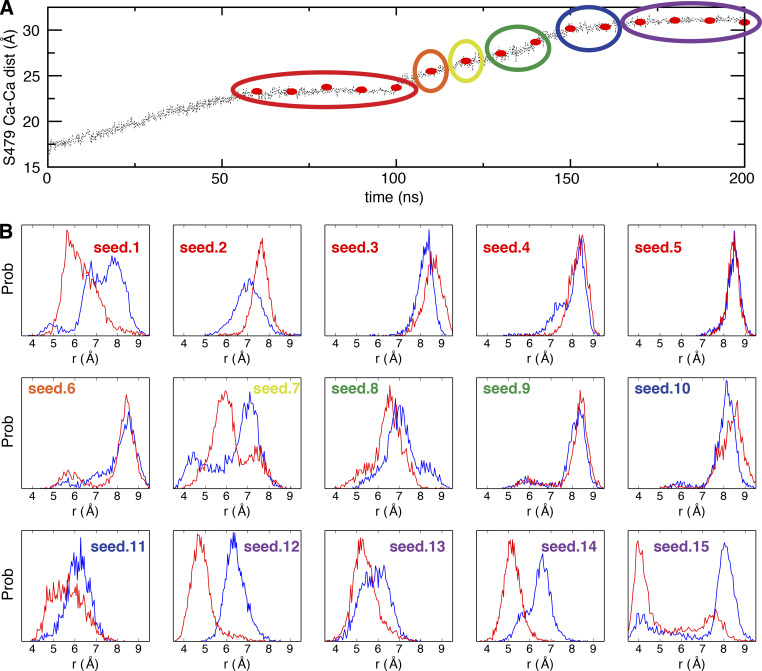
Differential conformational preferences of the Shaker channel with different opening degrees. (A) 15 snapshots (red dot) were selected from the bias MD trajectory as initial seeds for unbiased MD simulations. The initial seeds were clustered into six groups (circled) based on the opening degree. (B) The probability density histograms of the G444 Cα–Cα distance of two pairs of diagonally opposed monomers A and C (red) and B and D (blue) in 15 unbiased MD simulations with opening degree of the intracellular gate restrained. dist, distance; prob, probability.

Figure S2.

Simulations of the constricted conformation generated using the AMBER force field with the PMEMD MD engine of AMBER. Evolution of the constriction starting from the CHARMM-generated conformation. The AMBER-compatible topology and coordinates file were produced by the CHARMM-GUI's force field converter, and the simulation was performed using the AMBER scripts provided by CHARMM-GUI. dist, distance; FF, force field.

Figure S3.

2-D–PMF explicitly along the two distances between the Cα atoms of G444 of diagonally opposed subunits A and C (r₁) and B and D (r₂) for the Shaker channel at 32 Å opening.

Figure S4.

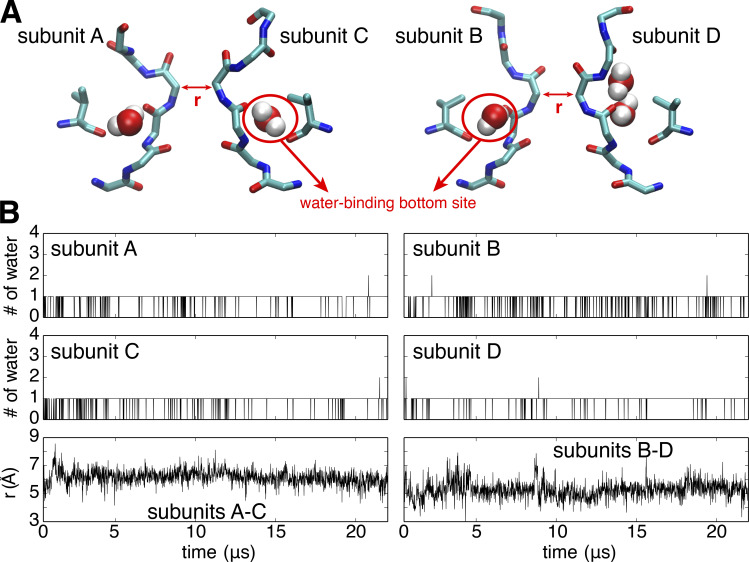
A stable constricted conformation of the selectivity filter in the KcsA E71V mutant. Top: Representative conformation of the selectivity filter and water molecules bound behind the filter. Bottom: Time series of the number of water molecules occupying the water-binding bottom site within each subunit (upper and middle panel) and the cross-subunit distance between the Cα atoms of G77 of diagonally opposed subunits A and C (lower left) and B and D (lower right) during the 21-µs simulations in the wide-open channel.

Results

Conductive filter is stable with partially open intracellular gate

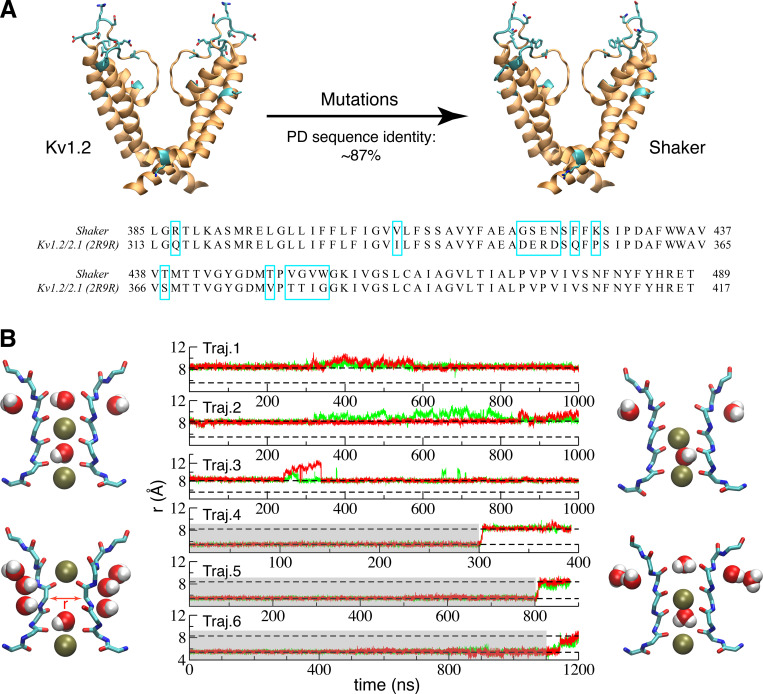
In view of the very high sequence identity (87%) of the pore domain between K_v1.2 and the Shaker channels, it is legitimate to assume that a reliable homology model can be constructed with high confidence (Šali, 1995). A model of the pore domain of the Shaker channel was constructed from the crystallographic x-ray structures of the K_v1.2/K_v2.1 chimera channel PDB accession no. 2R9R (Long et al., 2007), by direct substitution of the nonconserved residues (Fig. 1 A) while keeping the remaining residues in their original rotameric state. Three independent simulations based on this model (trajectories 1–3) maintained a conductive conformation on a microsecond time scale (Fig. 1 B). A second model, in which the selectivity filter was the constricted conformation, was generated using the constricted filter from the low-K⁺ KcsA crystal structure (1K4D). The model also included the inactivating water and ions in the filter. Three additional simulations (trajectories 4–6) were started from this model with a constricted filter. The filter was restrained in this conformation for a period of time (highlighted in gray) to allow complete relaxation of the nearby residues. However, in all three trajectories, the filter rapidly reverted back to a conductive conformation after removing the restraints (Fig. 1 B).

Figure 1.

Simulation of a model of the pore domain of the Shaker channel with partially open intracellular gate.(A) A Shaker model was built up based on the pore domain of the crystal structures (PDB accession no. 2R9R) of K_v1.2/K_v2.1 by mutating a few nonconserved residues (cyan). The nonconserved residues are also highlighted in cyan box in sequence alignment. Based on previous results (Li et al., 2018), the width of 18 Å measured by the Cα–Cα cross-subunit distances of S479 (the equivalent residue of T112 in KcsA) in the 2R9R x-ray structure suggests that it most likely corresponds to a partially open structure. (B) Time series of the cross-subunit distance (r) between the Cα atoms of G444 of diagonally opposed monomers A and C (green) and B and D (red) for six simulations started from the partially open Shaker model. Trajectories (Traj.) 1–3 were started from conductive filter without restraint. In all three trajectories, the filter remained in the conductive conformation. Trajectories 4–6 were initially restrained with their filter in the constricted conformation (highlighted in gray), in which the filters all returned to the conductive conformation once the restraints were released. Two levels representing conductive and constricted states are illustrated with a dashed line. Typical starting (left) and final (right) conformations of the selectivity filter are shown for the two sets of trajectories.

These results provide evidence that the selectivity filter in the partially open Shaker structure predominantly favors the conductive conformation. This is consistent with our previous study on KcsA in which the partially open KcsA (∼17 Å measured by the Cα–Cα cross-subunit distances of T112) preferred the conductive filter conformation (Li et al., 2018). The width of the intracellular gate in the 2R9R x-ray structure of the K_v1.2/K_v2.1 chimera channel is 18 Å, as measured by the Cα–Cα cross-subunit distances of S479. Our previous study of the KcsA channel showed that constriction of the selectivity filter is strongly coupled to the intracellular gate opening: the partially open state of KcsA was prone to maintain a canonical conductive conformation of the selectivity filter, whereas the selectivity filter of fully open structure (>23 Å) had a strong preference to adopt a constricted conformation. In view of these results, it appears necessary to consider the conformational stability of the filter in the context of different openings of the intracellular activation gate.

Constricted structure is formed with wide-open intracellular gate

To help capture conformations of the channel with a constricted filter, we explored a series of models of the pore domain of Shaker in which the opening of the intracellular gate was progressively increased. The opening of the gate in these models was based on available x-ray structures of KcsA with different gate conformation (Cuello et al., 2010b). Two open structures (PDB accession nos. 3F7V and 3F5W) of KcsA, with the Cα–Cα cross-subunit distances of T112 respectively at 23 Å and 32 Å, were used as references to augment the opening of the intracellular gate in our model of the Shaker channel in a stepwise manner (Fig. 2). To be consistent with KcsA in previous study (Li et al., 2018), structure with intracellular gate open to 23 Å is hereafter referred as “fully open,” and structures open >30 Å are referred as “wide open.” The modeling initially relied on a targeted MD (TMD) procedure. The targets are defined from the two wide-open x-ray structures of KcsA. The TMD is pulling the TM helices (S6) to drive the gate open (only the RMSD of S6 helices is included in the colvar module for this bias simulation). A total of 15 initial “seed” conformations were selected with different degrees of opening of the intracellular gate, spanning a range from 23 to 32 Å (Fig. S1 A) to perform extended equilibrium simulations with restraint on the gate opening in the Shaker channel. The modeling initially relied on a TMD procedure. Started from these initial seeds, the simulations were extended to at least 400 ns to test the stability of the constricted conformation of the selectivity filter only with the restraint to keep the same opening degree of the intracellular gate. The conformational state of the selectivity filter was monitored by following the cross-subunit distance between the Cα atoms of G444 from diagonally opposed subunits (Fig. 3). The distance is ∼8 Å for the conductive conformation, and ∼5 Å for the constricted conformation. The degree of opening of the intracellular gate clearly affects the dynamical conformation of the selectivity filter. Some of the simulations with an intracellular gate open from 23 to 30 Å display transient returns to a conductive filter conformation, while it remains constricted in some simulations (seeds 1, 7, and 8). In contrast, the filter remains constricted for at least a pair of subunits (Fig. S1) in simulations with a gate open by >30 Å. A model with a somewhat exaggerated intracellular gate opening of 32 Å was finally chosen to capture the filter in a highly stable constricted conformation. This choice doesn’t imply that the filter constriction is possible only when the opening of the gate is 32 Å. The purpose of this modeling strategy is to elicit the maximum effect on the filter by exploiting the allosteric gate–filter coupling.

Figure 3.

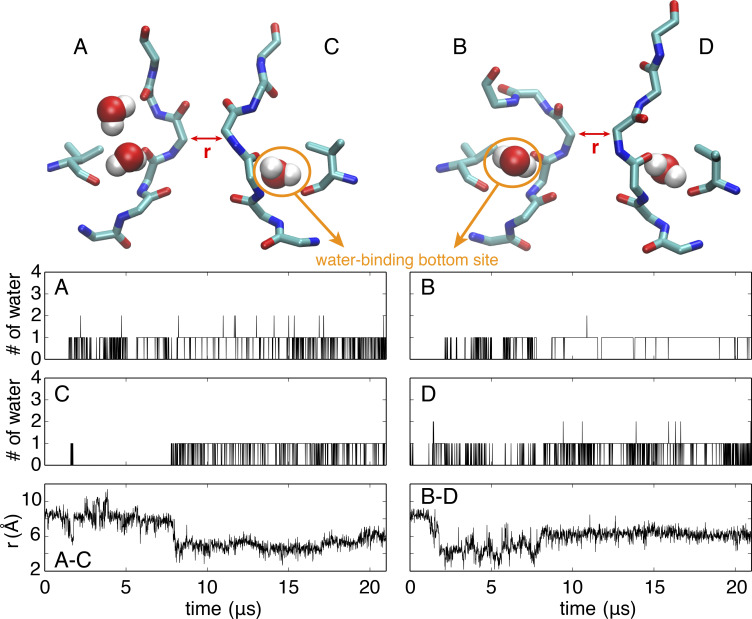
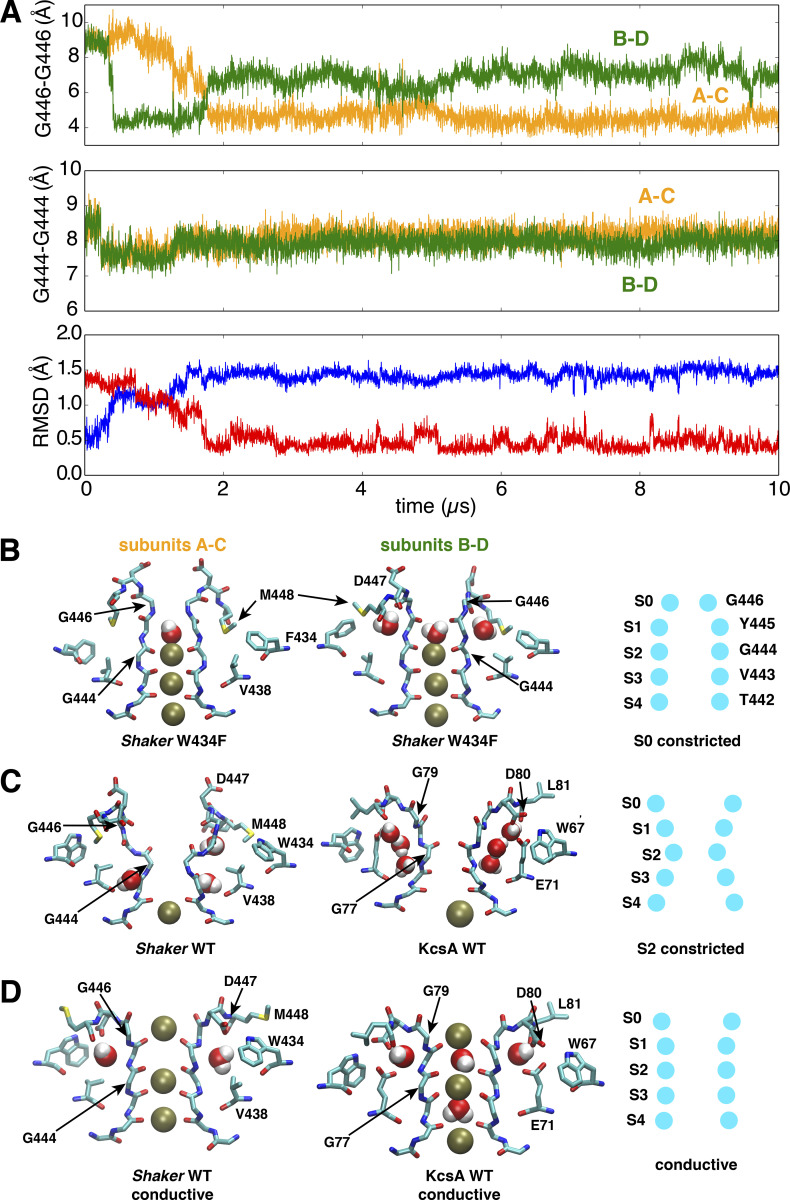
MD simulation of the Shaker channel with an opening of 32 Å for the intracellular gate yields a stable constricted conformation of the selectivity filter. The four channel subunits are labeled A, B, C, and D in clockwise order seen from the extracellular side. (A) Representative conformation of the selectivity filter and water molecules bound behind the filter. (B) Time series of the number of water molecules occupying the water-binding bottom site within each subunit (upper and middle) and the cross-subunit distance between the Cα atoms of G444 of diagonally opposed subunits A and C (lower left) and B and D (lower right) during the 22-µs simulations in the wide-open channel.

To further ascertain the stability of the selectivity filter with this wide-open intracellular gate, one MD simulation was extended to 22 µs without any restraint in the vicinity of the selectivity filter. As shown in Fig. 3, the G444 Cα–Cα cross-subunit distances remained ∼5.5 Å throughout the whole trajectory, indicating that the constricted conformation is stable. Of interest, a small number of water molecules spontaneously bind in a pocket located behind the selectivity filter during the long simulation of the Shaker channel. It was previously shown that such “inactivating” water molecules significantly contribute to stabilize the constricted structure in KcsA (Ostmeyer et al., 2013; Li et al., 2017; Li et al., 2018). Interestingly, it was recently observed that the application of extracellular D₂O slowed entry into the slow inactivated state in Shaker-IR mutants (Szanto et al., 2021), consistent with the computational results. For all four subunits, there is mainly a single water molecule bound at the bottom of the pocket behind the selectivity filter (hereafter referred as the “bottom site”). Occasionally, additional water molecules make brief transient visits behind the filter, as observed with the D subunit in Fig. 3. The uninterrupted binding of inactivating water molecules in the pocket behind the constricted filter is generally indicative of the stability of the constricted structure of Shaker.

The model of the pore domain with wide-open intracellular gate displays a strong kink at I470 and a slight unwinding of the helix S6 near its C terminus. The position of the kink is near the highly conserved “PVP” motif that provides a flexible element thought to be essential for channel gating (Bright et al., 2002; Imbrici et al., 2009). Thus, the kink of the S6 is not necessarily an artifact but could be required for the function. Moreover, it is likely that the unwinding of the S6 terminus is caused by the absence of the S4–S5 linker in the present pore domain simulations.

Before proceeding with further analysis, it is important to briefly address the issue of the atomic force field used to generate the MD simulations. In this regard, it is worth asking how much the observed structural behavior of the selectivity filter is dependent on the CHARMM force field used in the present simulations (Jorgensen et al., 1983; Beglov and Roux, 1994; Klauda et al., 2010; Best et al., 2012; Huang et al., 2017). To address this issue, an additional MD simulation of the constricted conformation of the selectivity filter obtained via simulations based on the CHARMM force field was generated using the AMBER force field (Jorgensen et al., 1983; Joung and Cheatham, 2008; Maier et al., 2015; Gould, I.R., A.A. Skjevik, C.J. Dickson, B.D. Madej, R.C. Walker, personal communication) and the MD simulation engine of AMBER20 (Le Grand et al., 2013; Salomon-Ferrer et al., 2013; Case et al., 2021). This independent simulation shows that the conformation of the filter is indeed highly stable during a 1-µs simulation (Fig. S2) despite the change of force field. The agreement between the simulations using CHARMM or AMBER force field regarding the stability of the constricted filter conformation in the Shaker channel pore model is reassuring and increases our confidence in the computational results.

Free energy landscape to assess filter conformational preference

Free energy landscapes were calculated to quantitatively assess the propensity of the constricted and conductive conformations of the selectivity filter in the Shaker channel as a function of the intracellular gate opening. 2-D–PMFs were calculated using US/H-REMD simulations as a function of the Cα–Cα cross-subunit distance of G444 in the filter (r) and the position of the external K⁺ ion along the pore axis (z) for a partially open state (∼18 Å) and a wide-open state (∼32 Å). These two coordinates, the cross-subunit distance and the K⁺ ion position, provide an effective means to efficiently characterize the conformational free energy landscape of the selectivity filter in KcsA (Ostmeyer et al., 2013; Li et al., 2017; Li et al., 2018). The results are shown in Fig. 4.

The 2-D–PMFs provide an opportunity to clarify the classic observation that high external K⁺ concentration slows C-type inactivation in Shaker (Labarca and Mackinnon, 1992; López-Barneo et al., 1993), which is reproduced with the KcsA channel (Cordero-Morales et al., 2006). In the present simulations, this phenomenon manifests itself through the dependance of the 2-D–PMF on the position of the outermost K⁺ ion (Fig. 4). According to the 2-D–PMF, the propensity to adopt a conductive-like conformation decreases as the K⁺ ion bound to the site S2 moves along the z axis toward the extracellular solution. A high external K⁺ ion concentration, in effect, leads to a higher occupancy of the S2 site, thus stabilizing the conductive conformation. Similar computational results were previously obtained for the KcsA channel (Li et al., 2018).

The calculated 2-D–PMFs also show the relative population shift between the conductive and constricted conformations as a function of intracellular gate opening (Fig. 4). When the intracellular gate is only partially open (18 Å), there is a local free energy basin around r = 8.2 Å, corresponding to a stable conductive state. In contrast, when the intracellular gate is wide open (32 Å), there is a free energy minimum at r = 5.5 Å, corresponding to a stable constricted state (Fig. 4). Thus, with a wide-open intracellular gate, the selectivity filter would be expected to tend to spontaneously interconvert from the conductive to the constricted conformation. The conclusion from the free energy landscapes is consistent with the results from the unbiased simulations shown in Figs. 1 and 3, where the partially open Shaker channel tends to be conductive, and the wide-open channel keeps a stable constricted filter through the 22-µs trajectory.

As observed previously in the case of the KcsA channel (Li et al., 2018), the conformational preference of the selectivity filter is allosterically dependent on the degree of opening of the intracellular gate. When the opening of the gate is small, the conductive conformation of the filter is favored. As shown in the Fig. 4, the local minimum for the constricted conformation becomes markedly deeper as the opening of the intracellular gate increases. Experimentally, Shaker inactivates to ∼20% of the peak current after 18 s (Olcese et al., 1997). This translates into a small free energy difference of ∼0.8 kcal/mol between the conductive and inactivated states. To maximize our ability to characterize a stable constricted filter, we relied on a model with intracellular gate opening of 32 Å. Given that there exists a crystallographic KcsA structure with a gate opening of 32 Å (PDB accession no. 3F5W), the degree of opening in this Shaker model is somewhat large but not unrealistic. While a smaller intracellular gate opening (such as 23 Å) would be expected to yield qualitatively similar observations, the wide gate opening used here (32 Å) serves our purpose because it deepens and clearly marks the free energy well of the constricted conformation in the free energy landscape.

Unique features in the new constricted structure of Shaker

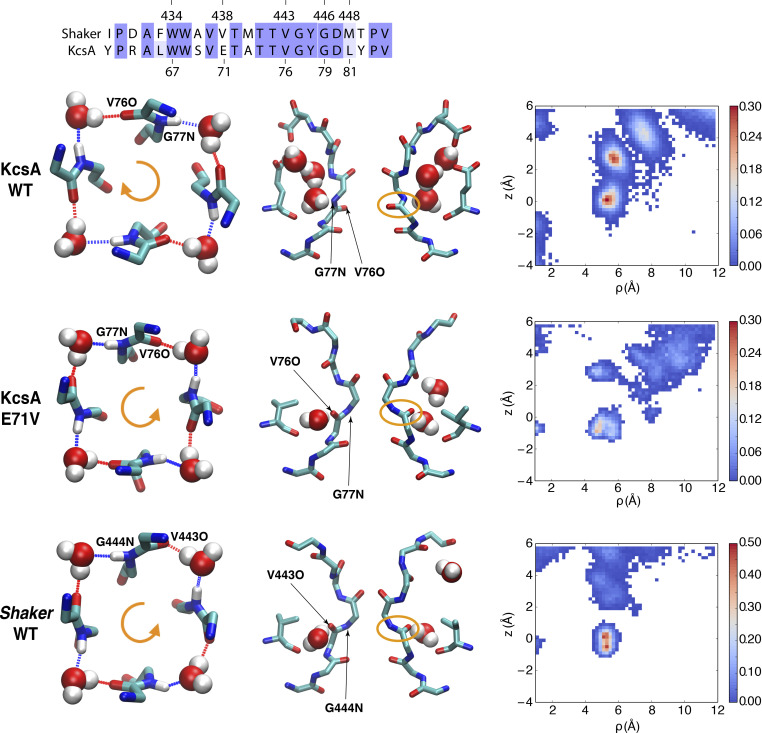
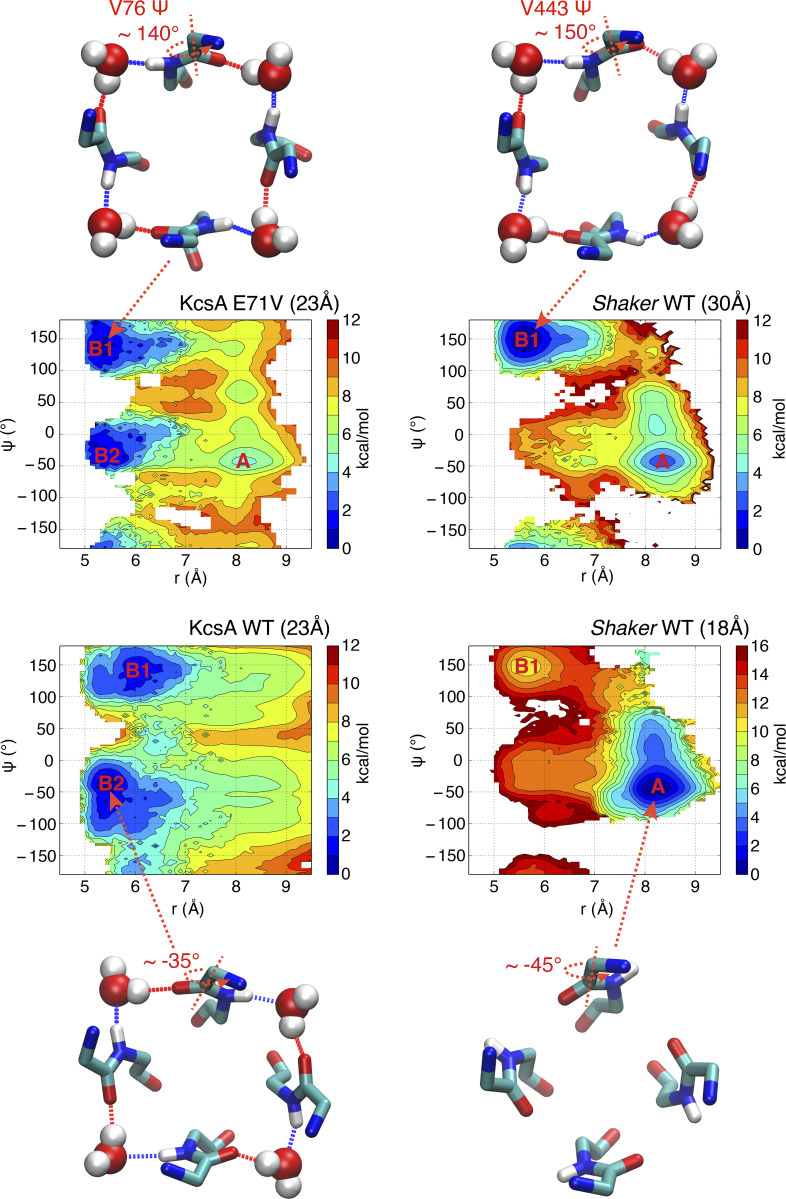
While the constricted conformations of the selectivity filter in Shaker and KcsA are broadly similar, some subtle but important differences are noteworthy. First, the number of inactivating water molecules binding to the pocket located behind the constricted selectivity filter of each subunit is different between KcsA and Shaker. In KcsA, the binding of three inactivating water molecules to fill the space behind the constricted filter within all four subunits (Fig. 5) is a hallmark of the constricted structure (Zhou et al., 2001; Ostmeyer et al., 2013; Weingarth et al., 2014; Li et al., 2017; Tilegenova et al., 2017; Li et al., 2018). In the simulation of the constricted Shaker channel, however, there is only one water molecule bound stably at the bottom site of the inactivating water binding pocket (Figs. 3 and 5). The occupancy map of water molecules shows that water molecules occasionally access the space of the inactivating water binding pocket above the bottom site, but do not bind there stably (Fig. 5). The predominant binding of a single water molecule within each subunit also contributes to the stability of the constricted structure of Shaker (though additional molecules can be brief transient visits). However, it is weaker than the effect of three inactivating water molecules on KcsA, as the latter could form a much larger hydrogen bond network (Ostmeyer et al., 2013; Li et al., 2017), consistent with the observation that the recovery rate of KcsA is much slower than that of the Shaker channel (Hoshi et al., 1991; Ostmeyer et al., 2013). A second critical difference is that the orientation of the backbone carbonyl group of the valine residue along the filter (TVGYG) is different in the constricted conformation of KcsA and Shaker. Compared with KcsA, the carbonyl oxygen of the corresponding valine is flipped and points to the opposite direction in the Shaker channel (Fig. 5). In both KcsA and Shaker, the filter backbone and water molecules bound at the bottom site form a ring-like hydrogen bond network. However, as shown in the top view of Fig. 5, the donor-to-acceptor direction of the backbone and water hydrogen bond ring is clockwise in KcsA, whereas it is counter-clockwise in Shaker.

Figure 5.

Different constricted structures for Shaker and KcsA. Top: Sequence alignment of Shaker and KcsA for the pore helix and the selectivity filter; 15 residues are identical out of a total of 23 residues. Below the sequence alignments are shown typical constricted conformations of the filter, with a top view (left column) and side view (middle column), as well as 2-D water occupancy map (right column) for different channels. Those are WT KcsA (first middle panel), KcsA E71V mutant (second middle panel), and Shaker (bottom). The top view of the filter only shows water molecules in bottom site of four subunits, and the backbone of V76 and G77 in KcsA (or the equivalent V443 and G444 in Shaker). For the 2-D occupancy map of the water molecules behind the selectivity filter, the horizontal reaction coordinate ρ is defined as the distance of the oxygen atom of water molecule with the center of the selectivity filter along the x-y plane. The vertical reaction coordinate z indicates the position of water molecules along the z axis relative to the center of the selectivity filter.

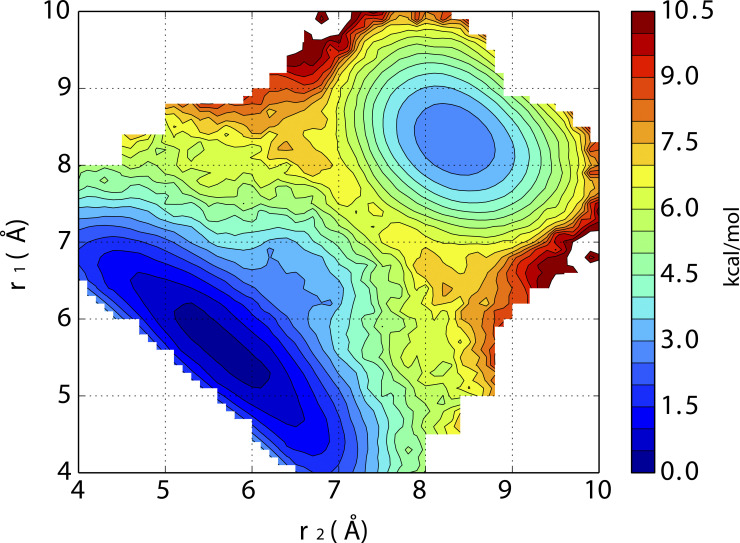
While the variable used to monitor the constriction of the filter in the 2-D–PMFs of Fig. 4 corresponds to the mean distance between two diagonally opposed subunits, it is possible to extract more information from the simulations. For instance, the MD data accumulated in the 2-D–PMFs can be projected explicitly along the two distances between the Cα atoms of G444 of diagonally opposed subunits A and C (r₁), and B and D (r₂), as reported previously (Li et al., 2017; Li et al., 2018; Li et al., 2021). This is useful to distinguish between asymmetric and almost symmetric structures and determine whether moderate r values arise from an asymmetric pinching and dilation, or by the filter being in the conductive conformation. The analysis (shown in Fig. S3) indicates that the conductive conformation (∼8.5 Å in the 2-D–PMF) does not comprise asymmetric constricted and dilated conformations of the filter. In addition, the free energy minimum corresponding to the constricted filter covers some asymmetric regions (one distance is 5.2 Å, and the other is 6.2 Å), but the symmetric constricted filter (∼5.5 Å) is dominant. A similar free energy minimum is energetically prohibited in the hERG channel (Li et al., 2021) and G77^d-Ala KcsA mutant (Li et al., 2017). Thus, the constricted conformation of the filter of Shaker appears to be essentially symmetric.

A molecular determinant of constricted structures

The S5-P-S6 pore domain of Shaker corresponds to the entire TM1-P-TM2 structure of KcsA. For a total of 93 residues, there are 31 identical residues and 15 similar residues, for a global sequence homology of 49%. Focusing on the pore helix and the selectivity filter shows that 15 residues are identical out of a total of 23 residues (see the sequence alignment in Fig. 5). The glutamic acid at position 71 along the pore helix in KcsA is one of the nonconserved residues that is closest to the selectivity filter. The corresponding residue at the corresponding position in Shaker (438) is a valine. It is known that the residue at this position has a significant impact on the C-type inactivation and the modal behavior of the KcsA channel (Cordero-Morales et al., 2006; Cordero-Morales et al., 2007). It is worth noting that the functional behavior of the Shaker V438E mutant is not known, because it cannot be probed experimentally in oocytes due to a lack of expression. To determine whether the residue at this position plays a key role in determining the features of the constricted conformation of the selectivity filter, the free energy landscape of the Shaker-like KcsA mutant E71V was calculated using MD simulations. Started with a fully open structure (23 Å) with a conductive filter, a constricted conformation of the E71V mutant is spontaneously formed as the WT in our previous study (Li et al., 2018), and it is maintained until the end of these extended (21-µs) MD simulations (Fig. S4).

Remarkably, the simulation of the KcsA E71V mutant with constricted filter recapitulates many of the most distinctive features observed in the simulation of the constricted Shaker (Fig. 5). First, the backbone carbonyl of V76 in the constricted of KcsA E71V is flipped as in the constricted Shaker, while it points toward the pore lumen in the constricted WT KcsA. Second, there is a single inactivating water molecule at the bottom site of the pocket in the constricted KcsA E71V, as in the constricted Shaker, while there are three stable inactivating water molecules in the constricted WT KcsA. Finally, the inactivating water molecule bound to the bottom site of the pocket in the constricted KcsA E71V forms a donor-to-acceptor hydrogen-bonded ring with the backbone of the filter in the counterclockwise direction as in the constricted Shaker, instead of the clockwise direction observed in WT KcsA (Fig. 5).

To quantitatively verify the impact of residue E71 (V438 in Shaker) on the propensity of V76 (V443 in Shaker) backbone in the constricted structure, the 2-D–PMF was calculated for KcsA E71V mutant in a fully open state (∼23 Å) and is compared with WT KcsA and the Shaker channel. The 2-D–PMF was calculated along reaction coordinates (r, z), and it is projected along two coordinates (Ψ, r) for analysis, in which Ψ is the backbone dihedral angle Ψ for valine in the selectivity filter (V76 for KcsA, and V443 for Shaker; Fig. 6). The shift of local free energy basin (A) from approximately −45° in a partially open state (18 Å) to ∼150° in a wide-open state (32 Å) just represents the conductive-to-constricted transition in Shaker (Fig. 6, right). Both WT and E71V mutant of KcsA in a fully open state adapt constricted structure, and there are two minimums (B1 and B2) for both constricted WT and E71V (Fig. 6). But the slightly deeper minimum in V76 backbone dihedrals is almost opposite that in WT (∼140° versus −35°), which is highly consistent with the observation of V76 carbonyl oxygen flipping in MD simulations. More importantly, the free energy basin of KcsA E71V mutant is located at a very similar position to that of wide-open Shaker, confirming that the residue 71 is the most likely molecular determinant of the observed differences in the constricted structures.

Figure 6.

2-D–PMF to assess the conformational preferences of different constricted structures. The horizontal reaction coordinate r describes the width of the selectivity filter and is defined as the average cross-subunit pinching distance between the Cα–Cα atoms of G444 in Shaker or G77 in KcsA. The vertical reaction coordinate Ψ indicates the backbone Ψ dihedral angle of the valine in the center of the selectivity filter. The typical conformations for free energy basins are shown in stick for protein and van der Waals representation for water molecules from the top view.

A nonconductive filter conformation of the W434F mutant

The classic mutant W434F is known to almost abolish ion conduction due completely to its predominant preference of a C-type inactivated state (Perozo et al., 1993; Yang et al., 1997). To elucidate the structural basis of its functional behavior, the mutation W434F was introduced into the Shaker pore model, and simulated for 10 µs in its partially open state (∼18 Å). During the trajectory, the W434F mutant made a rapid transition to a constricted conformation spontaneously. The selectivity filter constricts within 1 µs, and adopts a constricted conformation, which remained stable during the following 8 µs, as indicated by the backbone RMSDs of the filter shown in Fig. 7. Compared with the WT Shaker constricted structure, there are three unique properties of the constricted structure of the W434F mutant. First, as shown in Fig. 7, the filter of W434F constricts at the level of the second glycine in the signature sequence, TTVGYGD (G446), near the outermost binding site S0. As shown in Fig. 7, this is in contrast with the constriction of the WT channel, which occurs at the level of the central glycine in the signature sequence, TTVGYGD (G444), near the binding site S2. A cross-subunit distance between the G446 Cα atoms of diagonally opposed subunits drops to ∼4.5 Å, not allowing the K⁺ ions permeate through the filter. Whereas the cross-subunit distances between G444 Cα atoms always maintain at 8 Å, and there is a K⁺ ion bound at the S2 site through the whole trajectory (Fig. 7). Second, the constriction of mutant W434F at the S0 site is remarkably asymmetric, with one distance declining to ∼4.5 Å and the other one fluctuating around 7 Å. Third, the filter constriction of the W434 mutant occurs when the channel is only partially open (∼18 Å). This is notably distinct from the WT Shaker channel that only constricts when its intracellular gate is much more open. The constricted conformation observed here differs from the results of a previous simulation study of the W366F mutation in the K_v1.2/K_v2.1 chimera channel (Kondo et al., 2018). While this study reported changes near the inner mouth of the filter over a 300 ns trajectory, we observe a constriction at the level of the outer site S0 that remains stable over a period of 10 µs. Even though both studies relied on the CHARMM force field, such differences may be due to the sequence of the pore domain and the length of the simulations. A comparison of the conductive selectivity filter of both KcsA and WT Shaker, the classically S2-constricted selectivity filter (KcsA and WT Shaker), and the S0-constricted selectivity filter from the Shaker W434F mutant is provided in Fig. 7, schematically highlighting the main differences.

Figure 7.

A stable conformation constricted at the extracellular S0 site of the selectivity filter in a model of the pore domain of the W434F Shaker mutant.(A) Time series of the cross-subunit distance between the Cα atoms of diagonally opposed subunits, respectively, for G446 to monitor the conformation of S0 site (upper) and G444 to monitor the conformation of S2 site (middle), and the RMSD of the selectivity filter backbone (lower) by using the initial (blue) or last (red) conformation as reference. (B) Side views of the last snapshot of the selectivity filter at the end of the 10-µs trajectory for the subunits A and C (left) or B and D (middle) of the W434F Shaker mutant. A scheme (right) is shown to highlight the selectivity filter conformation constricted at the S0 (G446) site. (C) Side views of the selectivity filter for constricted Shaker WT (left) and WT KcsA (middle). Both are constricted at the S2 site as shown in the scheme (right). (D) Side views of the selectivity filter for conductive Shaker WT (left), WT KcsA (middle), and the scheme (right). The simulation of the W434F mutant was performed with a model with an intracellular gate opening of ∼18Å.

The substitution of W434 by a phenyalanine breaks the highly conserved hydrogen bond between W434 and D447, which allows the D447 flip toward the extracellular bulk. This is a phenomenon also observed in a previous computational study for W434 substituted by unnatural amino acid (Lueck et al., 2016). Following the upward flipping of D447, its neighboring residue M448 moves downward to dock in the region among F434, W435, and Y445. The downward docking of the M448 side chain, favored by the reduced bulkiness of W434F compared with WT, is consistently observed in two diagonally opposite subunits, and it induces an asymmetric constriction of the filter at the extracellular entrance S0 site (Fig. 7). Once the two M448 side chains are docked, a cross-subunit distance between the G446 Cα atoms of diagonally opposed subunits drops to ∼4.5 Å, much shorter than the equivalent distance (5.5 Å) in the symmetric constricted structure of KcsA. The 4.5 Å distance makes it energetically unfavorable to form a symmetric constricted conformation in the W343F mutant, due to the repulsion among the G446 Cα atoms from four subunits. This is why transitions are observed for two pairs of (A–C and B–D) diagonal subunits in the first 2 µs, either A–C or B–D drops to 4.5 Å at different periods of the trajectory, but the two distances are never 4.5 Å simultaneously.

In contrast to model of the WT Shaker channel, the transition toward the constricted conformation adopted by the W434F mutant does not appear to be under the strict allosteric control of the intracellular gate for two reasons. First, the W434F mutant spontaneously constricts even when the intracellular gate is only partially open, whereas this trend is much weaker for the WT pore domain. Second, the W434F mutant constricts at the level of the second glycine (G446) near the outermost S0 site, whereas the WT pore domain constricts at the level of the central glycine (Gly444 equivalent to G77 in KcsA) near the S2 binding site. Compared with the S2 site constriction, which is allosterically coupled to the intracellular gate via the T441 (equivalent to T74 in KcsA), the S0 site does not appear to have direct coupling with T441 and other residues in the allosteric coupling network. This might allow the selectivity filter of the W434F mutant to constrict regardless of the intracellular gate conformation, yielding an inactivation rate that is faster than that of the WT channel.

Discussion

The basic premise of the present study is that C-type inactivation reflects first and foremost the occurrence of a nonconductive constricted conformation (or set of conformations) of the selectivity filter—a process that takes place within the pore domain. This “pore-centric” view of C-type inactivation is supported by many observations, for example, the fact that the phenomenon of C-type inactivation is recapitulated by the bacterial KcsA channel, which lacks any voltage-sensing domains (VSDs; Cordero-Morales et al., 2006; Cordero-Morales et al., 2007; Cuello et al., 2010a; Chakrapani et al., 2011; Cordero-Morales et al., 2011). Undoubtedly, a multitude of additional factors external to the pore domain can influence inactivation (lipids, VSD conformation, etc.), and understanding all those factors will ultimately be important. Nevertheless, our view is that a reductionist approach focused on the characterization of the nonconducting conformation(s) of the pore domain by itself can help capture the most salient features of C-type inactivation of the Shaker voltage-activated channel. The free energy landscape computational methodology used here is fairly similar to that of previous studies of the constricted state in the KcsA channel (Ostmeyer et al., 2013; Li et al., 2017; Li et al., 2018), and more recently the hERG channel (Li et al., 2021). Our central hypothesis is that the molecular mechanism of the C-type inactivation process in the Shaker channel relates to a constriction of the selectivity filter that is allosterically coupled to the opening of the intracellular activation gate opening.

Prior to discussing the main results, it is also important to acknowledge the limitations of a computational approach. MD simulations represent the interactions within the molecular system on the basis of an approximate potential function (a force field) constructed from simple analytical functions, which can affect the results. The most important question is whether the choice of force field has a critical impact on the structural behavior of the selectivity filter. Interestingly, the studies of the constricted conformation in the MthK channel by Boiteux et al. (2020) as well as Furini and Domene (2020) suggest that the main factor that controls the constricted conformation of the selectivity filter is the presence of bound ions. Thus, one may suspect that the strength of the interaction between backbone carbonyl oxygens and the K⁺ ion is perhaps the dominant factor that indirectly affects the conformational preference between constricted and conductive structures. This could explain the apparent disagreement between different force fields regarding the propensity of the constricted state (Furini and Domene, 2020). Encouragingly, the constricted conformation obtained from a simulation based on the CHARMM force field appears to be stable for >1 µs simulation based on the AMBER force field (Fig. S2). This result suggests that the main conformational features revealed by the present simulations are not markedly dependent on the force field. While there are subtle differences between the conformational energy among the most widely used force fields, this observation is consistent with the general experience suggesting that current force fields can capture the overall shape of the potential energy surface of proteins, even though the relative stability of different conformational states may not be in quantitative agreement. Nonetheless, it is prudent to focus on the most salient qualitative trends displayed by the computations in trying to draw our conclusions.

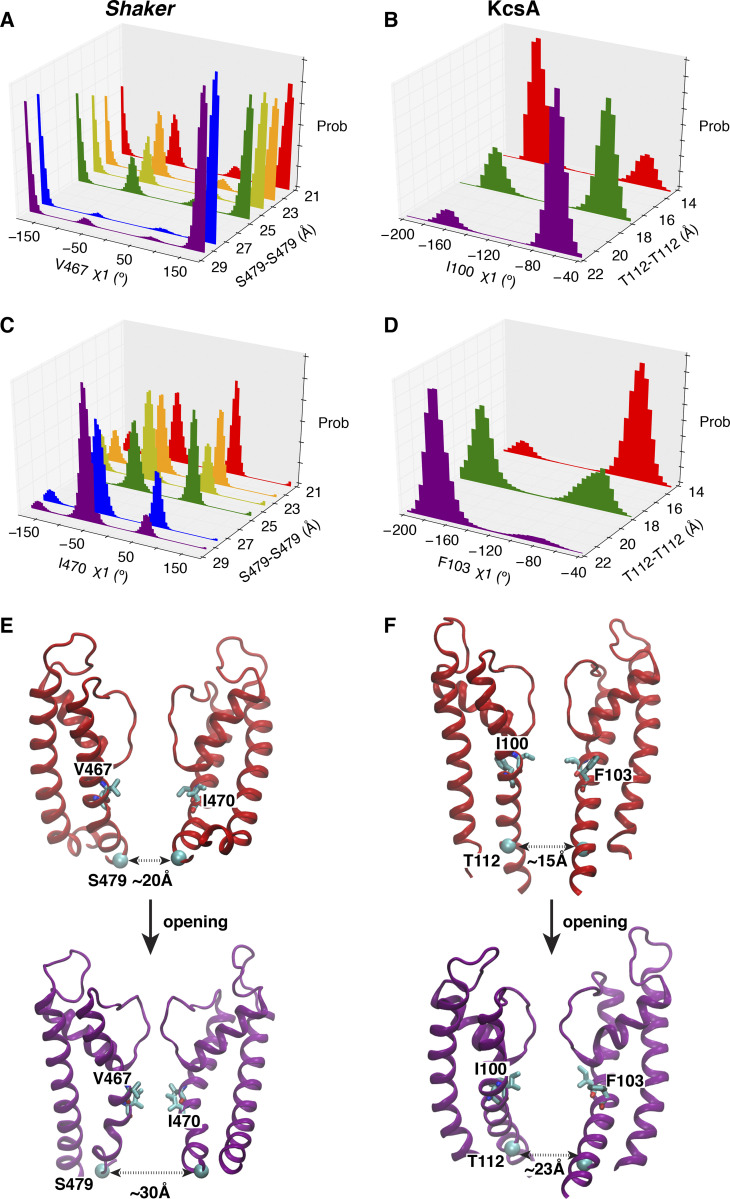
The free energy landscape calculations together with the unbiased MD trajectories indicate that the filter prefers the constricted conformation when the intracellular activation gate is wide open, but prefers to remain in the conductive conformation when the intracellular gate is partially open. This shows that the selectivity filter of Shaker is allosterically controlled by the opening of the intracellular gate, a coupling mechanism also observed in KcsA (Cuello et al., 2010a; Pan et al., 2011; Li et al., 2018). The rotameric distributions of key residues responsible for allosteric coupling confirm that the constricted filter in the Shaker channel is stabilized by the wide opening of the gate, according to a mechanism similar to that previously identified in KcsA (Li et al., 2018). Upon a gradual widening of the intracellular gate from partially to fully open, there are correlated side-chain reorientations of two residues (I100 and F103) beneath the selectivity filter critical for the gate coupling, as shown from the shifts between the bimodal distributions of the χ1 side-chain dihedral angels (Fig. 8). As shown in Fig. 8, MD simulations of Shaker are clustered into six groups according to the degrees of opening of the intracellular gates that are measured at the residue S479 (Shaker) and T112 (KcsA). The gate opening degree shows a correlation with the reorientations of V467 and I470 (equivalent to I100 and F103 in KcsA). In the cluster with the most open gate, there is only one dominant peak for χ1 dihedral angles in both V467 and I470 (Fig. 8, A and C). All of these results suggest that KcsA and Shaker share a similar gating allosteric coupling, whereby the wide opening of the intracellular gate favors the constriction of the filter. It is noted that both V467 and I470 in Shaker are less bulky than the corresponding residues in KcsA (I100 and F103). In KcsA, these residues affect the allosteric gate–filter coupling (Cuello et al., 2010a; Pan et al., 2011). The smaller side chains at these positions could be one of the structural reasons responsible for the smaller propensity to adopt a constricted filter in Shaker, and the fact that a larger opening of the intracellular gate (32 Å) is preferred to form a similar stable constricted filter in Shaker as KcsA (23 Å) in MD simulations.

Figure 8.

The rotameric redistributions of key residues responsible for allosteric coupling upon gate opening in both Shaker and KcsA. (A–D) The rotamer density histograms of key residues for multiple ensembles to represent the different opening degrees from partially to wide open of the intracellular gate. The simulations for Shaker are trajectories 8–23 (Table S1), and the trajectories for KcsA are trajectories 1–10 in a previous study (Li et al., 2018). (E and F) Typical structures to show the process from partially to wide open of the intracellular gate for Shaker (left) and KcsA (right). prob, probability.

The constricted structural model from KcsA and Shaker highlights the flexibility of the selectivity filter and its sensitivity to the surrounding residues, especially to the key residue along the pore helix equivalent to E71 in KcsA. In the constricted structure of WT KcsA, E71 helps coordinate three inactivating water molecules to fill the space behind the constricted filter. Its carbonyl oxygen coordinates with the water molecule in the bottom site, whereas the side chain coordinates with the other two water molecules. The Shaker-like E71V mutation substitutes a hydrophilic side chain with a hydrophobic one, and thus disables the stable binding of water molecules in the pocket except the bottom site. With only one bound inactivating water molecule, the filter of Shaker adopts a different constricted conformation stabilized by alternative contacts. Multi-microsecond MD simulations converge toward a stable constricted filter for a model of the pore domain of the Shaker channel. The computations provide intriguing and suggestive atomic details about the constricted conformation, i.e., the flipping of the valine backbone in the filter and the presence of a single inactivating water molecule within each subunit. Yet, according to computations, the Shaker-like KcsA mutant (E71V) reverts back to a constricted structure more similar to Shaker, highlighting the importance of this residue on the constricted conformation.

Unexpectedly, the Shaker W434F mutant adopts a distinct constricted selectivity filter in the simulations. Rather than the typical constriction at the S2 site near the center of the selectivity filter observed for KcsA and the WT Shaker channel, the W434F is pinched at the outermost S0 binding site. Compared with very recent publications for K2P channels (Lolicato et al., 2020), W434F Shaker mutant shows intriguing similarities of the filter constriction with K2P channels. First, all of them are constricted asymmetrically. Second, they are all constricted at the extracellular mouth (S0 and S1 binding sites) of the selectivity filter. More interestingly, the N82 of the TASK2 channel shows very similar dynamical behavior as the M448 in the W434F Shaker mutant, in the sense that the downward moving of the N82 constricts the S0 site (Li et al., 2020). The similar pattern on filter constriction is due to the sequence similarity between the W434F Shaker mutant and TASK2 channel. To be more specific, the residue 434 equivalent in the P1 domain of K2P channels is also phenylalanine, rather than tryptophan in most K⁺ channels. This critical W-to-F substitution allows the sidechain of another residue (M448 in W434F Shaker mutant, and N82 in TASK2) to be docked behind the filter for the constriction at the S0 site, enabling a stable constriction at the S0 site (as shown in Fig. 7). Compared with the normal constriction near the S2 site in WT Shaker and KcsA channels allosterically controlled by the intracellular gate opening, the constriction at the outermost end of the filter appears to have no direct link to the allosteric coupling. Independent of the intracellular gate opening, the W434F mutant is able to constrict when the channel is just partially open. The unique properties of the constricted conformation of the W434F mutant may partly explain the strong and fast C-type inactivation observed in functional measurements.

The time scales of C-type inactivation can go up to several seconds (Yellen et al., 1994; Baukrowitz and Yellen, 1995; Olcese et al., 1997; Pless et al., 2013; Pau et al., 2017); thus, a short-lived transient constriction of the selectivity filter cannot represent the C-type inactivated state. A long-lived conformational state is necessary to explain the C-type inactivation functional phenotype. In the KcsA channel, three water molecules behind the selectivity filter make a significant contribution to the slow recovery of the channel from C-type inactivation (Ostmeyer et al., 2013). In the WT Shaker channel, there is one water molecule bound at the bottom site of the inactivating water pocket behind the selectivity filter within each subunit. As shown in Fig. 5, water molecules from four subunits could form a hydrogen bond network with the backbone of V443 and G444, which significantly stabilizes the constricted conformation for WT Shaker. In contrast, in the W434F Shaker mutant, the downward movement of the M448 (following the D447 upward flip) allows it to be docked in the space behind the top part of the selectivity filter and enable a stable constriction at the S0 site (as shown in Fig. 8). Similarly, in the hERG channel, the side chain rotation of F627 filling the space behind the selectivity filter could also stabilize the constriction at the S2 site (Li et al., 2021). Thus, there are some common features for the filter constriction among K⁺ channels, but there are also important differences regarding which part of the filter is constricted and how it is stabilized.

Our computations support the notion that a constricted-like conformation similar to that of KcsA can occur for the filter of the voltage-activated Shaker channel. However, there are also subtle differences. For instance, the handedness of the constriction in Shaker appears to be opposite that of KcsA (Figs. 5 and 6). Furthermore, the conformation of constricted Shaker is essentially fourfold symmetric, as in KcsA (Cuello et al., 2010a; Cuello et al., 2010b; Li et al., 2018). This is in contrast to the striking twofold symmetry displayed by the constricted hERG channel (Li et al., 2021), TASK2 channel (Lolicato et al., 2020), Gly77 d-Ala mutant of the KcsA channel (Li et al., 2017), and the W434F Shaker mutant channel. Furthermore, both the W434F Shaker mutant and TASK2 constrict at the extracellular mouth of the filter, whereas the constriction occurs near the central glycine in the case of KcsA, Shaker, and hERG. Despite these variations, constriction of the selectivity filter yields a nonconductive conformation, consistent with the functional phenotype of C-type inactivation displayed by these channels.

While the broad picture emerging from computational studies (Ostmeyer et al., 2013; Li et al., 2017; Li et al., 2018; Li et al., 2021) is that the existence of some physical constriction of the filter in K⁺ channels is plausible (even though some of the details appear to vary from channels to channels), such a conformation has not yet been observed in available experimental structures of K_v channels (Long et al., 2005; Long et al., 2007; Chen et al., 2010; Tao et al., 2010; Pau et al., 2017; Matthies et al., 2018), a fact that begs for some explanation. A number of microscopic factors could have affected our chance to capture such structures experimentally. For example, a recent study suggests that the lack of constricted x-ray structure for the bacterial MthK channel might be explained by the high binding affinity of the ions for the selectivity filter. The constricted conformation itself is accessible and not forbidden for the MthK channel (Boiteux et al., 2020). Furthermore, according to our studies of KcsA (Li et al., 2018), a conductive filter is probably favored when the intracellular gate is partially open due to the strong allosteric gate–filter coupling. This suggests that capturing an inactivated structure might require increasing both the allosteric coupling and the opening of the intracellular gate. Importantly, computational studies indicate that the constricted conformation of a number of K⁺ channels could be asymmetric (Li et al., 2017; Lolicato et al., 2020; Li et al., 2021). Determination of a conformation with such a break of symmetry in a fourfold symmetric protein could present additional challenges for x-ray and cryo-EM studies. At this point, confirmation that C-type inactivation in K_vs is caused by a physical constriction of the selectivity filter awaits direct experimental structural evidence.

Supplementary Material

Table S1

lists MD simulations in the present study.

Data availability

All data are available in the main text or the supplementary materials or upon request to the authors.