Highlights
-
•
Deep learning resulted in excellent VMAT dose predictions for prostate cancer.
-
•
The network was trained on image triplets, outperforming 2D based dose predictions.
-
•
A novel workflow to convert predictions into deliverable plans was implemented.
Keywords: Deep learning, Dose prediction, Volumetric modulated arc therapy, Machine learning, Deliverable treatment plans, Radiotherapy
Abstract
Background and purpose
Radiation therapy treatment planning is a manual, time-consuming task that might be accelerated using machine learning algorithms. In this study, we aimed to evaluate if a triplet-based deep learning model can predict volumetric modulated arc therapy (VMAT) dose distributions for prostate cancer patients.
Materials and methods
A modified U-Net was trained on triplets, a combination of three consecutive image slices and corresponding segmentations, from 160 patients, and compared to a baseline U-Net. Dose predictions from 17 test patients were transformed into deliverable treatment plans using a novel planning workflow.
Results
The model achieved a mean absolute dose error of 1.3%, 1.9%, 1.0% and ≤ 2.6% for clinical target volume (CTV) CTV_D100%, planning target volume (PTV) PTV_D98%, PTV_D95% and organs at risk (OAR) respectively, when compared to the clinical ground truth (GT) dose distributions. All predicted distributions were successfully transformed into deliverable treatment plans and tested on a phantom, resulting in a passing rate of 100% (global gamma, 3%, 2 mm, 15% cutoff). The dose difference between deliverable treatment plans and GT dose distributions was within 4.4%. The difference between the baseline model and our improved model was statistically significant (p < 0.05) for CVT_D100%, PTV_D98% and PTV_D95%.
Conclusion
Triplet-based training improved VMAT dose distribution predictions when compared to 2D. Dose predictions were successfully transformed into deliverable treatment plans using our proposed treatment planning procedure. Our method may automate parts of the workflow for external beam prostate radiation therapy and improve the overall treatment speed and plan quality.
1. Introduction
Treatment planning for external beam radiation therapy (EBRT) involves many manual steps, such as choosing the correct beam angles, energy, and shapes. For intensity-modulated radiation therapy (IMRT) and volumetric modulated arc therapy (VMAT), a trial-and-error process of choosing and altering dose-volume criteria is used to optimize a treatment plan. This manual iteration continues until most, or all pre-defined, clinical goals are satisfied, which can take several hours, depending on patient anatomy and planner experience. Furthermore, more advanced treatment techniques and an increasing number in cancer patients leads to a higher workload, limiting the time available for EBRT treatment planning. This can be a restrictive factor, which might lead to variations in plan quality.
A possible way to improve and automate the optimization and treatment planning process is to use state-of-the-art, machine learning-based algorithms and models. Several research groups are making progress incorporating these new technologies into the EBRT process, to accelerate and improve the treatment planning workflow [1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11], [12]. The field of radiation therapy is likely to face tremendous changes regarding patient workflow, availability of artificial intelligence (AI)-based decision supportive tools and treatment planning efficiency and consistency [13], [14], [15].
Nguyen et al. [1] used a 2D U-Net architecture [16] to predict IMRT dose distributions for prostate cancer patients, based on segmentation masks containing the planning target volume (PTV) and organs at risk (OAR). They later refined the model by adding dense connections into a 3D architecture, leading to a more accurate dose prediction [2]. Other studies tried to predict IMRT dose distributions by incorporating dose-volume histogram (DVH) features into the model, or evaluating different architectures, e.g., ResNet-anti-ResNet and generative adversarial networks (GAN) [2], [3], [4], [5], [6], [7], [8].
McIntosh et al. [9] presented the first machine learning driven framework to predict VMAT dose distributions using a texture filter bank and a contextual Atlas Regression Forest (cARF) algorithm. In addition, they used dose mimicking to transform dose predictions into deliverable treatment plans [9], [10]. Further studies presented on VMAT dose prediction adapted more modern, deep learning-based approaches for automatic feature extraction [2], [11], [12].
Most of the studies focused on IMRT dose prediction, while only a few studies predicted VMAT dose distributions [2], [9], [11], [12]. More important, except for a few cases, the predicted dose was not transformed into a clinical and deliverable treatment plan [5], [10].
This work aimed to evaluate a densely connected deep learning model, based on a modified U-Net architecture, able to predict VMAT dose distributions for prostate cancer patients. In addition, the impact of providing volumetric information by triplet-based training, i.e., combining three consecutive image slices and corresponding segmentations [17], was investigated. Finally, to transform dose predictions into deliverable treatment plans, a novel treatment planning workflow was tested and evaluated using a commercially available treatment planning system (TPS).
2. Material and method
2.1. Dataset description
The used dataset consisted of DICOM computed tomography (CT) images, radiotherapy (RT) structure sets and RT dose information derived from 160 prostate cancer patients, treated with ultra-hypofractionated VMAT plans (42.7 Gy in seven fractions, three days per week for 2.5 weeks, single arc, 360 degrees) between 2018 and 2019 [18]. Eighteen patients with hip prosthesis were excluded from the study population, while 125 patients were used as the training dataset. 17 randomly chosen patients defined the test dataset, which was never used for model training or optimization. A table of patient characteristics is given in Supplementary Table S1. The study was approved by the Regional Ethics Board of Lund, Sweden (EPN Lund, Dnr 2013/742).
2.2. Preprocessing
For each patient, the RT structure set, CT images, and dose distribution were exported from the TPS (Eclipse, Varian Medical Systems, USA). Raw CT pixel values were transformed to Hounsfield Units (HU), truncated between −1000 and +400 and per-sample-normalized between 0 and 1. Dose distributions were normalized using the prescription dose of 42.7 Gy. RT structures were transformed to binary masks, where the PTV, rectum, bladder, left femoral head (LFH), right femoral head (RFH) and body were chosen as the relevant structures for VMAT dose prediction. CT volumes and binary structures were resampled to a voxel size of using linear and nearest neighbor interpolation, respectively. Furthermore, matrix dimensions were changed to pixels.
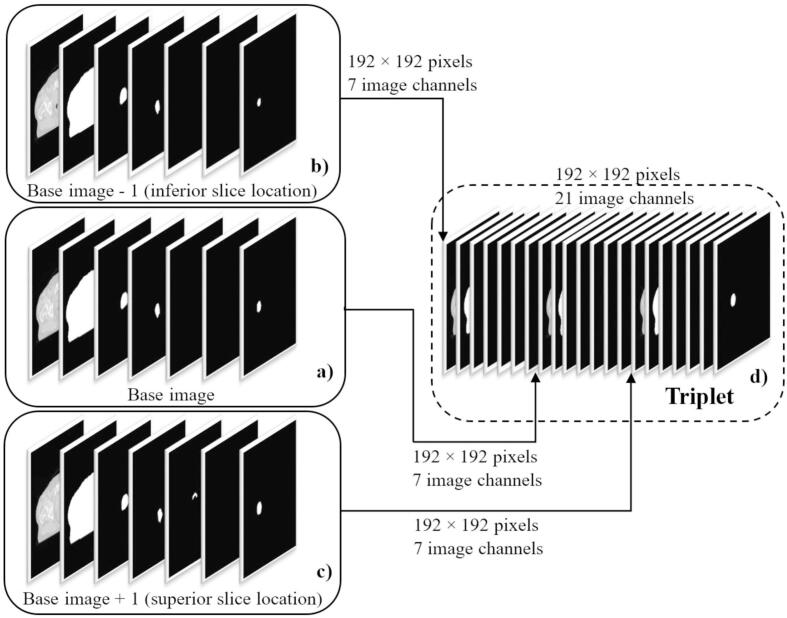
To allow our model to learn volumetric features, training was performed using image triplets (Fig. 1), which can be considered volumetric, but not per se fully 3D. We therefore refer to the method subsequently as “2.5D” training. A triplet combines three consecutive 2D CT slices and their corresponding binary segmentations. Comparable to a three-channel color image (RGB), a CT image slice and its corresponding PTV, body and OAR segmentation structures were combined into an image with 7 separate channels (base image, Fig. 1a, channel 1–7: CT, body, PTV, rectum, bladder, LFH, RFH). Two additional 7 channel images were created using the 2D CT slice and its corresponding segmentations inferior (base image - 1, Fig. 1b) and superior (base image + 1, Fig. 1c) to the base image. All three, 7-channel images, were then concatenated along the channel axis, forming a final triplet with a total of 21 channels (Fig. 1d). The code used in this work can be downloaded from our GitHub repository (https://github.com/MLRadfys/Deep-Learning-Dose-Prediction).
Fig. 1.
Triplets generated from three, spatially consecutive, computed tomography (CT) images and their corresponding target, body, and organs at risk (OAR) segmentation structures. To generate an image triplet, a base image was formed (a), by stacking a 2D CT slice as well as its corresponding body, target, and OAR binary segmentation masks (of the current slice) into 7 different image channels (channels 1–7: CT, body, PTV, rectum, bladder, left femoral head, right femoral head). This preprocessing step was repeated for the 2D CT image and the corresponding segmentations inferior (base image − 1) (b) and superior (base image + 1) (c) to the actual slice location of the base image. All three, 7-channel images (base image − 1, base image, base image + 1), were then concatenated along the channel axis, to form a final image triplet with a dimension of pixels and a total of 21 channels (d).
2.3. Model architecture
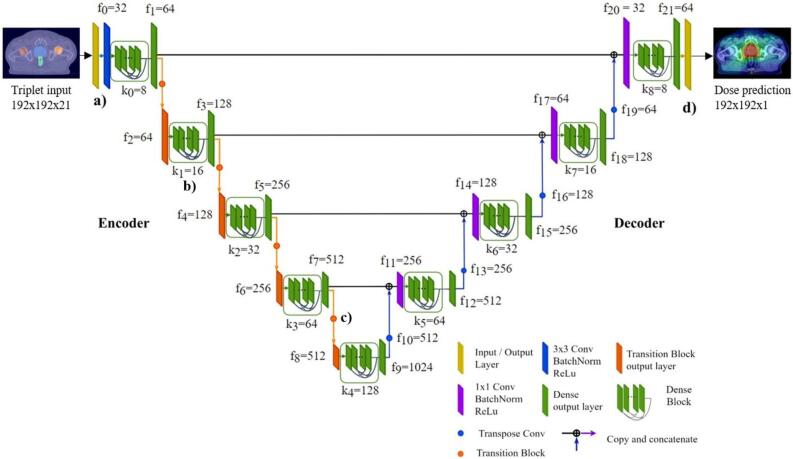
Our proposed modified U-Net architecture consisted of a densely connected encoder and decoder part with batch normalization layers, Rectified Linear Unit (ReLU) activation and transition blocks for upsampling purposes [19], [20], [21]. Triplets with a size of were used as the input to the encoder, where w is the image width, h the height of the image, and c the number of image channels (Fig. 2a). Dense layers [21] were embedded in dense blocks (Fig. 2b), where feature maps of previous layers become the input to the next layer. This addresses the problem of vanishing gradients and improves feature propagation throughout the network [22]. Dense and transition blocks (Fig. 2c) used in this study were designed as suggested by the DenseNet paper published by Huang et al. [21]. For each triplet input, providing volumetric information, a 2D dose distribution prediction with a size of was generated using a final convolutional kernel operation (Fig. 2d). A detailed description of the model architecture is provided in the Supplementary Section.
Fig. 2.
Architecture of the proposed densely connected U-Net used to predict volumetric modulated arc therapy (VMAT) dose distributions for prostate cancer patients. Triplets consisting of computed tomography (CT) images and their corresponding binary segmentation masks of the planning target volume (PTV), body and organs at risk (OAR) were used as the input data to the model (a). Densely connected layers in the encoder and decoder part (b) were used to improve feature propagation and to avoid vanishing gradients. After feature extraction using a series of convolutional operations and transition layers used for downsampling purposes (c), densely connected upsampling operations transformed the latent space representation to a final VMAT dose distribution prediction (d).
2.4. Model training
For this study, a baseline model was trained in 2D, using an encoder-decoder U-Net architecture introduced by Ronneberger et al. [16]. In addition, the original U-Net model as well as our suggested densely connected U-Net were trained in 2.5D. Training was performed for 500 epochs using 5-fold-cross validation and a batch size of 16. The Adam optimizer [23] with a learning rate of lr=0.0001 was used to minimize the mean squared error (MSE) loss between predictions and clinical dose distributions. Data augmentation in form of random image translation , horizontal flipping and rotations was used to reduce overfitting [24], [25].
2.5. Treatment planning workflow
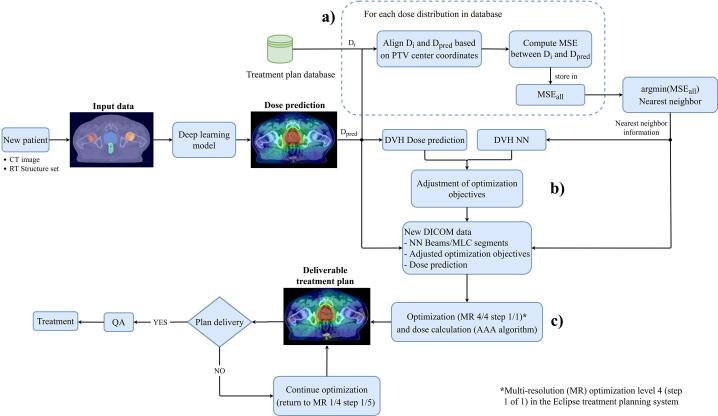
To transform predicted dose distributions into deliverable treatment plans, a nearest neighbor (NN) search was performed, by computing the mean squared error (MSE) between a dose prediction matrix and the clinical dose distribution matrices in the training dataset (Fig. 3a). The MSE, used as a similarity measure is given by:
| (1) |
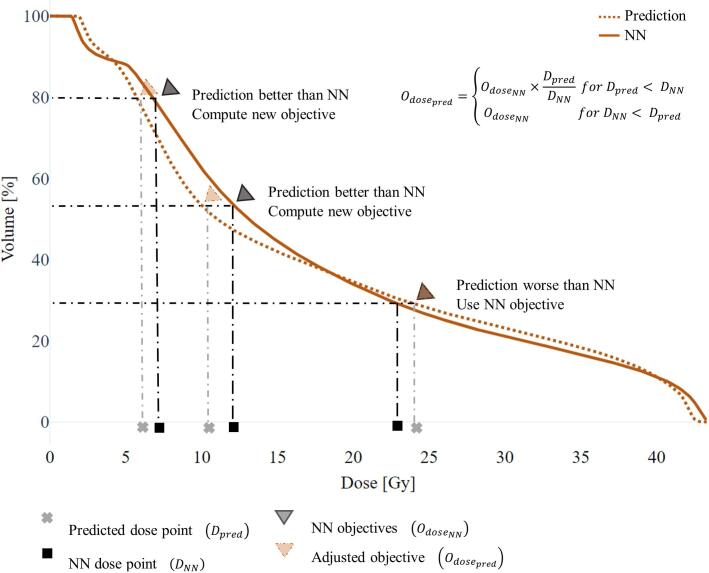
where represents the observed dose values, the predicted dose values and the number of data points. PTV center coordinates were matched prior to any computation. Calculation of the MSE was performed using the scikit image library [26]. Beams, optimization objectives and multileaf collimator (MLC) segments were derived from the NN, and the predicted dose was compared to the NN dose, to adjust dose optimization criteria to fit the best of the two (Fig. 3b, Fig. 4). For OARs, new dose optimization objectives were calculated by:
| (2) |
where is the new dose objective, the objective from the NN, the dose value at the NN DVH volume point defined by , and the predicted dose value at the same DVH volume point as . For target volumes, adjustments could be performed in the same manner, but for . Volume optimization criteria were not adjusted.
Fig. 3.
Proposed treatment planning workflow used to transform predicted volumetric modulated arc therapy (VMAT) dose distributions into deliverable treatment plans. Triplets containing computed tomography (CT) images and binary segmentation masks were used as the input to the densely connected U-Net model, to predict a dose distribution. A nearest neighbor (NN) search was then performed to establish suitable beams and dose-volume criteria (a). Derived optimization criteria were adjusted, based on the dose distribution prediction and the NN dose distribution (b). To generate a deliverable treatment plan, a short dose optimization, starting at the last multi-resolution (MR) level 4 (step 1/1) of the Eclipse TPS, was performed, using the dose prediction as the underlying distribution (c).
Fig. 4.
Optimization parameter adjustment shown for an arbitrary organ at risk (OAR) structure. To find optimization parameters for a predicted dose distribution, the nearest neighbor (NN) dose-volume histogram (DVH) was compared to the dose prediction DVH. Adjustments were made for all OARs, in case the dose prediction was better than the NN dose. No adjustments were made, when the NN dose was better than the predicted dose.
Once the criteria for all structures were established, a short optimization using the predicted dose distribution was performed, starting at the last multi-resolution (MR) level 4 (step 1/1) using the Eclipse TPS (Fig. 3c). The predicted dose distribution, combined with the NN beams and the adjusted optimization parameters, served as the optimization starting point. This process is similar to fine-tuning the segments of the accelerators MLC, to match the predicted dose distribution. All deliverable treatment plans were generated for a TrueBeam accelerator (Varian Medical System, Palo Alto, USA) and an energy of 6 MV, Flattening Filter Free (FFF). Dose calculations were performed using the Anisotropic Analytical Algorithm (AAA). In continuation, we will refer to treatment plans generated by our suggested treatment planning workflow as deliverable treatment plans, and to clinical plans used for training as the ground truth (GT).
2.6. Plan delivery and evaluation
All deep learning-based treatment plans were delivered to a Delta4 phantom and evaluated using multiple DVH parameters: clinical target volume (CTV_D100%), planning target volume (PTV_D98%, PTV_D95%), rectum (Rec_D30%, Rec_D15%, Rec_D10%), left femoral head (FH_Sin_D2%), right femoral head (FH_DX_D2%), bladder (Bladder_Dmean) and body (Body_D0.1%). Dose prediction and treatment plan quality were evaluated by calculating the mean percentage dose error between the dose distributions predicted by the baseline 2D U-Net and the GT, the 2.5D densely connected U-Net and the GT, and between the deliverable treatment plans and the GT. The mean percentage dose error is given by:
| (3) |
where is the dose distribution predicted by a deep learning model, the GT dose distribution derived from a clinical treatment plan, and is a scalar value of the prescribed dose.
2.7. Statistical hypothesis testing
A two-sided Wilcoxon signed-rank test with a significance level of 0.05 was performed on the Bladder_Dmean, Body_D0.1%, FH_Sin_D2% and FH_DX_D2% predictions of the 2D baseline model and the 2.5D densely connected U-Net. For target (PTV_D95%, PTV_D98% CTV_D100%) and rectum (Rec_D30%, Rec_D15%, Rec_D10%) structures, a Bonferroni correction for multiple testing was applied, and a significance level of 0.017 was used.
3. Results
3.1. DVH parameter evaluation
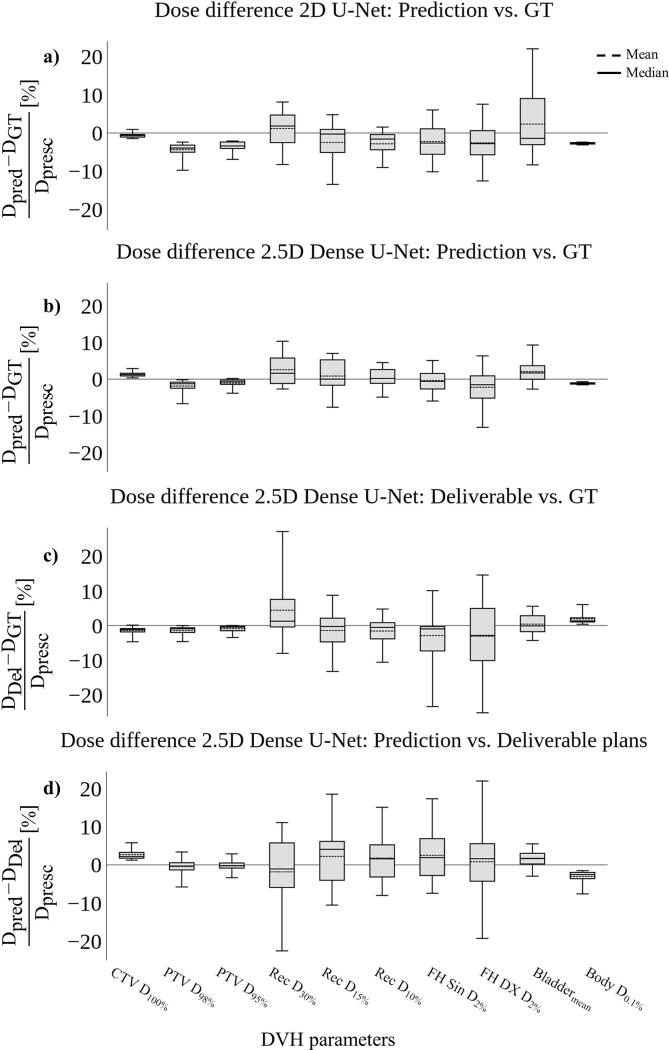
The baseline model trained in 2D predicted dose to the PTV and CTV volumes within a mean percentage dose error of 4.4%, while the dose difference error in OAR and body structures remained within a mean percentage dose error of 2.8% and 2.7%, respectively (Fig. 5a). The densely connected U-Net trained in 2.5D maintained a mean percentage dose error within 1.9% for both, the CTV and the PTV volume (Fig. 5b). For OAR and body structures, the mean percentage dose error remained within 2.6% and 1.1%, respectively. The dose difference error for PTV and CTV between the dose distributions of the deliverable treatment plans and the GT stayed within 1.4%, while most OAR structures stayed within 3%, except for the Rec_D30% structure, which resulted in a mean percentage error of 4.4% (Fig. 5c). The body structure stayed within a mean percentage error of 1.9%. A more detailed summary of the mean percentage dose errors for all evaluated DVH parameters is reported in Supplementary Table S2.
Fig. 5.
Dose difference comparison shown as the mean percentage dose error evaluated for multiple dose-volume histogram (DVH) parameters for n = 17 test patients. In general, 2D dose distribution predicted by the baseline U-Net model led to a poor dose coverage of the target volume (a). The densely connected model trained in 2.5D resulted in an overall lower dose difference for the target, body, and most of the organs at risk (OAR) structures, when compared to the 2D model (b). The mean percentage dose error stayed within 2.6%, 1.1% and 1.9% for OAR, body, and target structures respectively, whereas dose distributions predicted by the 2D baseline U-Net stayed within 3.4%, 2.7% and 4.4% for OAR, body, and target. Using our proposed treatment panning workflow, dose predictions derived from the densely connected U-Net could successfully be transformed into deliverable treatment plans, staying within a mean percentage dose error of 4.4%. Dose coverage of the target volume, body dose and the dose in most of the OARs were close to the ground truth (GT) dose distributions (c). The mean percentage dose error between the predicted dose distributions of the 2.5D densely connected U-Net and the deliverable treatment plans was found to be 2.5%, 3.1% and 2.7% for OAR, body, and target volumes, respectively (d).
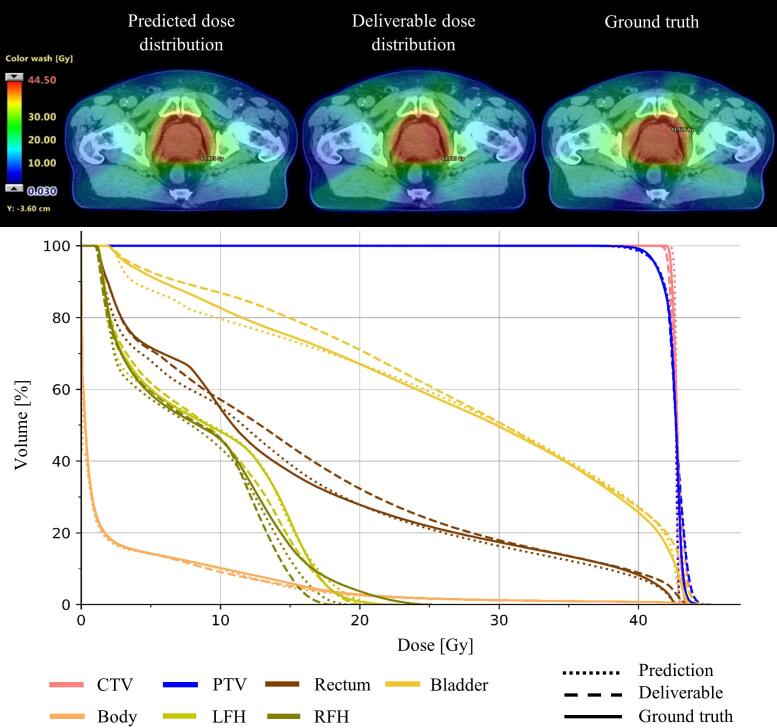
An example dose distribution predicted by the densely connected U-Net for one of the test patients is shown in Fig. 6. The predicted dose distribution is shown in the axial plane together with the corresponding DVH curve, the dose distribution of the deliverable treatment plan generated by our proposed treatment planning workflow and the GT dose distribution. Both, the prediction, and the deliverable dose distribution resulted in DVH curves similar to the GT.
Fig. 6.
Example dose distribution predicted by the 2.5D densely connected U-Net shown for one of the patients from the test dataset, as well as the deliverable dose distribution, optimized based on the model’s dose prediction, and the ground truth (GT). All dose distributions are shown in the axial plan together with their corresponding dose-volume histogram (DVH) curves. Both, model prediction and the deliverable dose distribution resulted in a DVH similar to the clinical GT distribution.
3.2. Model evaluation
The improved performance of the densely connected U-Net trained in 2.5D, was also reflected in model training. Using 5-fold cross validation, the baseline U-Net trained in 2D reached a mean (± SD) MSE loss of , which could be improved to a mean (± SD) MSE loss of , by training the same model architecture in 2.5D. The densely connected U-Net trained in 2.5D, achieved the lowest mean (± SD) MSE value of . Model training took about 15 h per fold, while the mean prediction time for a test patient was about 6.6 s once a model was loaded.
3.3. Dose delivery analysis
The dose verification measurements using the Delta4 phantom, resulted in a passing rate of 100%, global gamma (3%, 2 mm, cutoff of 15%), for all test patients.
3.4. Statistics
The Wilcoxon signed-rank test performed on the predictions of the 2D U-Net and the 2.5D densely connected U-Net resulted in a statistically significant difference for target structures (PTV_D95%, PTV_D98% CTV_D100%), Rec_D15%, Rec_D10%, FH_Sin_D2% and Body_D0.1%. There was no statistically difference for Bladder_Dmean, FH_DX_D2% and Rec_D30%.
4. Discussion
In this study, we presented a densely connected U-Net, able to predict 3D VMAT dose distributions for prostate cancer patients. In contrast to previous studies, where model training was performed in 2D [1], [4], [7], [11], [12], we suggested a 2.5D training approach using image triplets. In addition, we presented a, to the best of our knowledge, novel treatment planning workflow using a commercially available TPS, to transform model predictions into deliverable treatment plans.
Model and dose distribution evaluation was performed using the mean percentage dose error for multiple DVH parameters. Compared to the 2D baseline model, the mean percentage dose error for our densely connected U-Net trained in 2.5D was lower for almost all presented DVH parameters, showing that dose prediction accuracy could be improved by adding nearby, volumetric information through triplets. The predictions of the 2D baseline U-Net resulted in a dose difference between the CTV and the PTV, which might not be achievable, due to physical limitations of clinical linear accelerators. The dose difference between CTV and PTV was reduced using the 2.5D densely connected U-Net, and completely removed by transforming predictions into deliverable treatment plans. The overall better performance of the densely connected U-Net was also observed from the cross-validation result, where the 2.5D densely connected U-Net led to the smallest MSE. The baseline U-Net trained in 2.5D was not further investigated regarding dose prediction performance and treatment plan generation, as our 2.5D densely connected U-Net resulted in a lower MSE value.
Widely varying dose planning practices and the use of different treatment planning guidelines often result in different training datasets with diverging quality, making a direct comparison to previous studies challenging. Nevertheless, to some extent, the dose prediction results of our densely connected U-Net trained on triplets are comparable with the results of Ma et al. [11], who trained a 2D deep learning model on segmentation structures, as well as a modified model, where dosimetric features in form of PTV only plans where incorporated into the convolutional neural network. Ma et al. [11] found that the average dose difference between the GT treatment plans and the 2D model’s predictions were within 3.7% and 4.3% for PTV_D95% and Bladder_Dmean, respectively. For the improved model trained on segmentations and dosimetric PTV features, average dose differences of 2.1% and 3.5% for PTV_D95% and Bladder_Dmean were reported. Our 2.5D densely connected U-Net performed somewhat better, resulting in dose differences within an average error of 1% and 2.1% for PTV_D95% and Bladder_Dmean, respectively.
To transform dose predictions into clinical and deliverable treatment plans, we tested a novel nearest neighbor treatment planning workflow. All deliverable treatment plans were generated based on the model’s predictions and successfully delivered to a Delta4 phantom. A somewhat larger standard deviation for Rec_D30% and the FH structures could be observed in the deliverable treatment plans, which might be based on the overall low priority of these structures according to the used clinical protocol (see Supplementary Table S3), leading to more variations.
McIntosh et al. [10] suggested a dose mimicking algorithm based on voxel objectives, to transform dose predictions into deliverable treatment plans. In our work, DVH-based optimization parameters were used, which might result in a plan with a somewhat different dose, particularly in the low-dose volume. Nevertheless, after a short optimization, where MLC segments are finely tuned to deliver the predicted dose distribution, our method allows for further plan optimization, which might improve the overall treatment plan quality and decrease variances of the treatment planning process. The ability to continue optimizing could be advantageous compared to the dose mimicking approach used by McIntosh et al. [10]. This hypothesis remains to be tested though, as an in-depth analysis of differences and merits of either of the methods is beyond the scope of this work. Even though our presented treatment planning workflow can be used to transform dose predictions into deliverable VMAT prostate treatment plans, our study comprises some limitations. The workflow between the dose prediction model and the TPS is not fully automated yet, and some manual interventions, e.g., DICOM import and setting new optimization objectives, are needed. We also believe that high quality plans should continuously be added to the space of the nearest neighbor search, to potentially find more suitable dose-volume criteria for a specific patient and improve the overall treatment plan quality.
Before clinical implementation, a quality assurance (QA) method to discover suboptimal dose predictions should be developed. For the deliverable treatment plans, generated based on the predicted dose, a routine plan QA should be sufficient, as these plans are finalized using a clinical TPS.
In future projects we would like to explore other areas, e.g., fully 3D training, the direct prediction of MLC sequences, Monitor Units (MU) and dose volume criteria, as well as the predictions of multiple plan suggestions, to improve our methods.
In conclusion, a densely connected U-Net trained in 2.5D, able to predict VMAT dose distributions was presented. Predictions were transformed into deliverable treatment plans using a novel planning workflow. By evaluating the quality of our dose distribution predictions, the treatment plan optimization workflow as well as the final QA delivery, our work indicates that our method can be used in a clinical setting. Our suggested deep learning-based method shows great potential and might refine the overall treatment planning workflow for prostate cancer patients, by accelerating the treatment planning process.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
This work was supported by “Allmänna sjukhusets I Malmö Stiftelse för bekämpande av cancer”; Fru Berta Kamprads stiftelse för utforskning och bekämpning av cancersjukdomar, Lund, SUS foundations, Region Skåne.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.phro.2021.07.008.
Appendix A. Supplementary data
The following are the Supplementary data to this article:
References
- 1.Nguyen D., Long T., Jia X., Lu W., Gu X., Iqbal Z. A feasibility study for predicting optimal radiation therapy dose distributions of prostate cancer patients from patient anatomy using deep learning. Sci Rep. 2019;9(1) doi: 10.1038/s41598-018-37741-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Nguyen D., Jia X., Sher D., Lin M.-H., Iqbal Z., Liu H. 3D radiotherapy dose prediction on head and neck cancer patients with a hierarchically densely connected U-net deep learning architecture. Phys Med Biol. 2019;64(6):065020. doi: 10.1088/1361-6560/ab039b. [DOI] [PubMed] [Google Scholar]
- 3.Ma J, T. B, Nguyen D, Folkerts, Jia X, Lu W, et al. Individualized 3D Dose Distribution Prediction Using Deep Learning. AIRT: Artificial Intelligence in Radiation Therapy; 2019 Oct 17; Shenzhen, China. Springer International Publishing; 2019. p. 110–118.
- 4.Fan Jiawei, Wang Jiazhou, Chen Zhi, Hu Chaosu, Zhang Zhen, Hu Weigang. Automatic treatment planning based on three-dimensional dose distribution predicted from deep learning technique. Med Phys. 2019;46(1):370–381. doi: 10.1002/mp.2019.46.issue-110.1002/mp.13271. [DOI] [PubMed] [Google Scholar]
- 5.Konaxis C, Bol HG, Lagendijk WJJ, Raaymakers WB. Fast automated IMRT sequencing using deep-learned dose from generative adversarial networks. ESTRO: European Society for Radiotherapy and Oncology; 2019 Apr 26–30; Milan, Italy Milan, Italy. Ireland: Elsevier; 2019. p. 220–1.
- 6.Murakami Yu, Magome Taiki, Matsumoto Kazuki, Sato Tomoharu, Yoshioka Yasuo, Oguchi Masahiko. Fully automated dose prediction using generative adversarial networks in prostate cancer patients. PLoS ONE. 2020;15(5):e0232697. doi: 10.1371/journal.pone.0232697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Daoud B., Ki Morooka, Miyauchi S., Kurazume R., Mnejja W., Farhat L. Dose Distribution Prediction for Optimal Treamtment of Modern External Beam Radiation Therapy for Nasopharyngeal Carcinoma. Springer International Publishing; Shenzhen, China. Switzerland: 2019. pp. 128–136. [Google Scholar]
- 8.Kajikawa T, Kadoya N, Ito K, Takayama Y, Chiba T, Tomori S, et al. A convolutional neural network approach for IMRT dose distribution prediction in prostate cancer patients. J Radiat Res 2019;60:685-93. https://doi.org/10.1093/jrr/rrz051. [DOI] [PMC free article] [PubMed]
- 9.McIntosh Chris, Purdie Thomas G. Contextual atlas regression forests: multiple-atlas-based automated dose prediction in radiation therapy. IEEE Trans Med Imaging. 2016;35(4):1000–1012. doi: 10.1109/TMI.2015.2505188. [DOI] [PubMed] [Google Scholar]
- 10.McIntosh C., Welch M., McNiven A., Jaffray D.A., Purdie T.G. Fully automated treatment planning for head and neck radiotherapy using a voxel-based dose prediction and dose mimicking method. Phys Med Biol. 2017;62:5926–5944. doi: 10.1088/1361-6560/aa71f8. [DOI] [PubMed] [Google Scholar]
- 11.Ma Ming, Kovalchuk Nataliya, Buyyounouski Mark K, Xing Lei, Yang Yong. Incorporating dosimetric features into the prediction of 3D VMAT dose distributions using deep convolutional neural network. Phys Med Biol. 2019;64(12):125017. doi: 10.1088/1361-6560/ab2146. [DOI] [PubMed] [Google Scholar]
- 12.Willems S., Crijns W., Sterpin E., Haustermans K., Maes F. Feasibility of CT-Only 3D Dose Prediction for VMAT Prostate Plans Using Deep Learning. Springer International Publishing; Shenzhen, China. Switzerland: 2019. pp. 10–17. [Google Scholar]
- 13.Thompson Reid F., Valdes Gilmer, Fuller Clifton D., Carpenter Colin M., Morin Olivier, Aneja Sanjay. Artificial intelligence in radiation oncology: a specialty-wide disruptive transformation? Radiother Oncol. 2018;129(3):421–426. doi: 10.1016/j.radonc.2018.05.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang C, Zhu X, Hong JC, Zheng D. Artificial Intelligence in Radiotherapy Treatment Planning: Present and Future. Technol Cancer Res Treat 2019;18:1533033819873922. https://doi.org/10.1177/1533033819873922. [DOI] [PMC free article] [PubMed]
- 15.Chamunyonga Crispen, Edwards Christopher, Caldwell Peter, Rutledge Peta, Burbery Julie. The impact of artificial intelligence and machine learning in radiation therapy: considerations for future curriculum enhancement. J Med Imaging Radiat Sci. 2020;51(2):214–220. doi: 10.1016/j.jmir.2020.01.008. [DOI] [PubMed] [Google Scholar]
- 16.Ronneberger O, Fischer P, Brox T. U-Net: Convolutional Networks for Biomedical Image Segmentation. MICCAI: Medical Image Computing and Computer-Assisted Intervention; 2015 Oct 5-9; Munich, Germany. Switzerland: Springer International Publishing; 2015.
- 17.Benson E, Rier L, Millican I, Pritchard S, Costigan C, Pound M, et al. The effect of depth context in the segmentation of the colon in MRI volumes. 2020:2020.03.06.20027722. https://doi.org/10.1101/2020.03.06.20027722.
- 18.Widmark Anders, Gunnlaugsson Adalsteinn, Beckman Lars, Thellenberg-Karlsson Camilla, Hoyer Morten, Lagerlund Magnus. Ultra-hypofractionated versus conventionally fractionated radiotherapy for prostate cancer: 5-year outcomes of the HYPO-RT-PC randomised, non-inferiority, phase 3 trial. Lancet. 2019;394(10196):385–395. doi: 10.1016/S0140-6736(19)31131-6. [DOI] [PubMed] [Google Scholar]
- 19.Ioffe S, Szegedy C. Batch normalization: accelerating deep network training by reducing internal covariate shift. In: Francis B, David B, editors. ICML: Proceedings of the 32nd International Conference on Machine Learning; 2015 July 6–11; Lille, France. Lille: PMLR; 2015. p. 448–56.
- 20.Nair V, Hinton GE. Rectified linear units improve restricted boltzmann machines. In: Johannes F, Thorsten J, editors. ICML: Proceedings of the 27th International Conference on Machine Learning; 2010 June 21-24; Haifa, Israel. Madison: Omnipress; 2010. p. 807–14.
- 21.Huang G., Liu Z., Weinberger Q.K. Densely Connected Convolutional Networks. IEEE; Honolulu, USA. New Jersey: 2017. pp. 2261–2269. [Google Scholar]
- 22.Atienza R. 1st ed. Packt Publishing; Birmingham: 2018. Advanced Deep Learning with Keras: Apply Deep Learning Techniques, Autoencoders, GANs, Variational Autoencoders, Deep Reinforcement Learning, Policy Gradients, and More. [Google Scholar]
- 23.Kingma D., Adam Ba.J. A Method for Stochastic Optimization. arxiv.org; San Diego, USA. New York: 2015. pp. 1–41. [Google Scholar]
- 24.O'Gara S, McGuinness K. Comparing Data Augmentation Strategies for Deep Image Classification. IMVIP: Irish Machine Vision and Image Processing Conference; 2019 Aug 28-30; Dublin, Ireland. Ireland: IMVIP; 2019.
- 25.Shorten C., Khoshgoftaar T.M. A survey on image data augmentation for deep learning. J. Big Data. 2019;6:60. doi: 10.1186/s40537-019-0197-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.van der Walt S., Schonberger J.L., Nunez-Iglesias J., Boulogne F., Warner J.D., Yager N. Scikit-image: image processing in Python. PeerJ. 2014;2:e453. doi: 10.7717/peerj.453. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.