Coevolutionary transitions emerging from flexible molecular recognition and eco-evolutionary feedback

Summary

Highly mutable viruses evolve to evade host immunity that exerts selective pressure and adapts to viral dynamics. Here, we provide a framework for identifying key determinants of the mode and fate of viral-immune coevolution by linking molecular recognition and eco-evolutionary dynamics. We find that conservation level and initial diversity of antigen jointly determine the timing and efficacy of narrow and broad antibody responses, which in turn control the transition between viral persistence, clearance, and rebound. In particular, clearance of structurally complex antigens relies on antibody evolution in a larger antigenic space than where selection directly acts; viral rebound manifests binding-mediated feedback between ecology and rapid evolution. Finally, immune compartmentalization can slow viral escape but also delay clearance. This work suggests that flexible molecular binding allows a plastic phenotype that exploits potentiating neutral variations outside direct contact, opening new and shorter paths toward highly adaptable states.

Graphical abstract

Highlights

• •A scale-crossing framework identifies key determinants of viral-immune coevolution
• •Fast specific response influences slow broad response by shaping antigen dynamics
• •Antibody footprint shift enables breadth acquisition and viral clearance
• •Model explains divergent kinetics and outcomes of HCV infection in humans

Biological sciences; Immunology; Immune system evolution; Microbiology; Evolutionary processes; Mathematical biosciences

Introduction

Among the many viruses that inhabit every species on the planet, some evolve as fast as the adaptive immunity of their host. These rapidly evolving intruders share unusual characteristics (Murin et al., 2019): They evade immune detection by putting on diverse and variable disguises (e.g., via high genetic variability) and divert immune focus by presenting multiple competing antigenic targets.

Despite strong similarity in evasion tactics employed, courses and outcomes of evolution may differ markedly among viruses. A dramatic example is that HIV persists indefinitely in any infected individual, while HCV can be spontaneously cleared in around 30% of those invaded (Thomas et al., 2009), even though the genetic diversity of HCV in a chronically infected person is comparable to or higher than that of HIV (McNearney et al., 1992; Martell et al., 1992; Simmonds et al., 1993; Pybus et al., 2001; Chen et al., 2003; Simmonds, 2004; Forbi et al., 2014; Teimoori et al., 2019). In addition, broadly neutralizing antibodies (bnAbs)—capable of recognizing a vast array of mutant strains—evolve against both viruses (Burton and Hangartner, 2016; Flyak et al., 2018), presenting a potential solution to counter rapid viral evolution. Yet, HIV bnAbs often emerge years into infection and confer little protection (Piantadosi et al., 2009; Gray et al., 2011), whereas HCV bnAbs are found to arise earlier and contribute to viral clearance (Bailey et al., 2017; Kinchen et al., 2018). Such variability in the path and fate suggests that transitions between distinct regimes may be controllable and that long routes of immune adaptation could be shortened if key determinants of possible outcomes were identified.

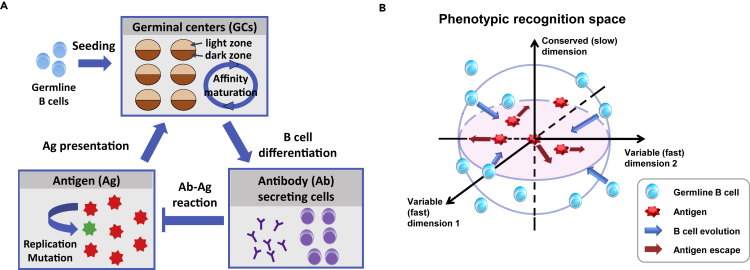
Viral dynamics and outcomes cannot be understood without considering host immunity. B cells constitute the evolving branch of the adaptive immune system and produce a dynamic Ab repertoire. They undergo an accelerated evolutionary process named affinity maturation (AM) (Eisen and Siskind, 1964) in microenvironments called germinal centers (GCs) (Victora and Nussenzweig, 2012); therein cycles of competition, proliferation, and somatic hypermutation (∼10⁶ fold faster than mutations in normal tissue cells [Di Noia and Neuberger, 2007]) result in increasingly stronger binders to the recognized antigen (Ag). Different from most vaccines that remain genetically stable, infecting viruses mutate during AM and engage lymphocytes in mutual selection (Figure 1A): B cells are selected for enhanced binding to Ags sampled into GCs from circulation, while viruses are selected for reduced recognition by circulating Abs (secreted B cell receptors [BCRs]) output from all GCs combined. An enduring co-adaptation relies on genetic novelty in virus and Ab populations, generated and maintained by rapid mutation at comparable rates. Driven by stochastic mutation and selection, an ensemble of coevolving trajectories form in an infected individual.

Figure 1.

Model: from physical space to recognition space

(A) Overview of model compartments, where key agents engage in cycles of stochastic reactions: Affinity maturation (AM) — B cell proliferation and mutation in the dark zone followed by affinity-dependent selection in the light zone — in multiple germinal centers (GCs) seeded by germline B cells, differentiation of mature B cells into antibody (Ab)-secreting cells that exit GCs, replication-mutation-selection of antigens (Ags) in circulation, and sampling and presentation of Ags into GCs that fuel further AM.

(B) Shape-space representation of BCR-Ag interaction and coevolution. Germline B cells (blue ovals) are distributed on or outside the founder hypersphere (blue circles delineating cross-sections), enclosing the Ags (red stars). Single mutations manifest as jumps (colored arrows) with Gaussian distributed step size. B cells move slowly in conserved dimensions where Ags are fixed at the origin (vertical), while moving fast in variable dimensions along which Ags may escape (horizontal). A 3D binding subspace (n_b=3) is illustrated with two variable (fast) dimensions and one conserved (slow) dimension. B cells (Ags) that get closer to (farther from) the Ags (B cells) are preferentially selected.

Important advances are being made to trace viral-immune coevolution during natural infection. Measurements with ever higher throughput and resolution provide a wealth of information across scales, ranging from the origin and pattern of phylogeny (Liao et al., 2013; Wibmer et al., 2013; Bhiman et al., 2015; Zanini et al., 2015; Hadfield et al., 2018), time series of functional traits (e.g., Ab potency and breadth) (Gao et al., 2014; Bonsignori et al., 2016; Escolano et al., 2016; Anthony et al., 2017) and GC dynamics (Tas et al., 2016), to structure and key mutations at and near the binding interface between an Ag epitope and an Ab paratope (West et al., 2014; Wang et al., 2016; Burton and Hangartner, 2016). Three chief observations specifically motivate our model framework. First, not every part of the B cell repertoire is equally accessible; in particular, bnAbs tend to have significantly lower germline frequencies than strain-specific Abs (Abbott et al., 2018), reflecting the fact that conserved residues in the epitope (targets of bnAbs) are fewer and harder to access than variable elements (Julien et al., 2013; Louie et al., 2018). Second, mutational paths toward bnAbs vary in length. Although most bnAbs discovered so far accumulate a large number of genetic alterations (Klein et al., 2013), some broad Abs effective at controlling infections are generated with relatively few somatic mutations (Goo et al., 2014; Simonich et al., 2016). This raises the question of how much AM is needed for bnAbs to emerge and what distinguishes short paths from long ones. Third, clonal diversity and composition vary widely among GCs (Tas et al., 2016), suggesting that spatial segregation of B cells may serve a functional role in the face of moving targets.

Mathematical models have long shed light on the competitive dynamics of AM with a single Ag (Kepler and Perelson, 1993; Oprea and Perelson, 1997; Meyer-Hermann et al., 2001; Figge et al., 2008; Zhang and Shakhnovich, 2010; Amitai et al., 2017), with quantitative insight gained by supplementing modeling with parameter inference (Molari et al., 2020). Recent works have reported features of Ab evolution against multiple related Ags, with a particular interest in how Ag characteristics (number, dose, complexity) and temporal patterns (in series or combination) impact the chance of evolving cross-reactive Abs (Chaudhury et al., 2014; Wang et al., 2015; Childs et al., 2015; Shaffer et al., 2016; Wang, 2017; Sprenger et al., 2020). This line of research is primarily motivated by the discovery of bnAbs against a variety of highly mutable pathogens, such as HIV, HCV, influenza, and malaria, all lacking an effective universal vaccine. In these in silico vaccination studies, Ags are preset and do not respond to AM.

Comparatively fewer studies have considered host-pathogen coevolution (Kamp and Bornholdt, 2002; Luo and Perelson, 2015; Cobey et al., 2015; Nourmohammad et al., 2016); these works often assume constant size of both populations (with recent exceptions (Bradde et al., 2017; Bonsma-Fisher et al., 2018; Jiang and Wang, 2019; Marchi et al., 2021)). This assumption is typical in theoretical evolutionary biology and presumably suitable for the chronic stage of infections, and yet it precludes outcomes other than viral persistence, and neglects potential feedback between ecological dynamics and evolution in a host. Such feedback arises because B cells not only sample and follow the antigenic environment, but also govern the absolute and relative fitness of distinct viral strains. Consequently, Abs arising early and becoming dominant quickly modify the shared “Ag resource” that itself adapts, thereby influencing what future Abs can evolve. Furthermore, existing approaches rarely explore the possibility that physical dynamics of receptor-antigen binding (e.g., locating best complementarity) may strongly impact the efficacy of Ab repertoire.

Here, we present a computational framework of coevolution that addresses these gaps and accounts for notable observations, emphasizing how physical dynamics on the molecular level give rise to evolutionary transitions on much larger scales. We consider Ab cross-reactivity and flexible binding footprint (Zhou et al., 2015; Bonsignori et al., 2016), variation in adaptation rate along different lineages, as well as feedback to and from population dynamics. Instead of modeling particular viruses, we predict conditions under which diverse evolutionary trends emerge, and determine ways in which features of trajectories and diversity patterns at early times inform outcomes.

The main findings are as follows. First, we identify the conservation level and initial diversity of Ag as key determinants of evolutionary outcomes. Second, we find that BCR mutations outside the direct contact region can potentiate Ab footprint shift toward sites of viral vulnerability, thus enabling clearance. Such flexibility of molecular recognition expands the search space and opens new paths of accelerated adaptation. Third, we show that functional consequences of GC compartmentalization depend on Ag variability. Our results stress the importance of considering adaptive dynamics of “Ag resource” when evaluating the viability and efficiency of immune control. We discuss how this understanding suggests new ways to enhance immune efficacy and shortcut long routes to desired outcomes.

Results

Coevolution model

We develop a computational model of B cell AM driven by a coevolving viral population (Figure 1A). To study the effect of population subdivision on collective dynamics, we consider segregation of B cells into a variable number of GCs, independently seeded by germline clones and evolving in parallel. Ab-secreting cells output from all GCs combined accumulate in circulation and remove the viruses they encounter and match. Meanwhile, circulating viruses replicate and diversify; those that, by chance, either avoid matching Abs or acquire escape mutations grow in number. A random subset of Ag is transported into each GC, presented to B cells, and fuels further rounds of AM. B cells that bind and internalize more Ag compete better for limited T cell help while the losers apoptose. Surviving cells either recycle to mature more or differentiate and exit GCs, thereby closing the loop of reactions between B cell and Ag populations.

We simulate the stochastic processes during AM (see STAR Methods for steps) based on rules and parameters derived from experimental studies of GC reactions (Berek and Milstein, 1987; Allen et al., 2007; Victora et al., 2010; Tas et al., 2016) (see supplemental information). Our model is a coarse-grained one that leaves out migration of B cells within and between GCs (Pereira et al., 2010; Bende et al., 2007) and abstracts the molecular contexts of receptor-antigen binding. Nonetheless, this simplification allows us to focus on a few new features that shape evolutionary dynamics and outcomes in essential ways.

Phenotypic description of BCR-Ag interaction and evolution

To describe joint dynamics and feedback of B cell and Ag populations, we extend the classic shape-space model by Perelson and Oster (Perelson and Oster, 1979) to consider evolving phenotypic distributions. BCRs and Ags are points in a common n-dimensional Euclidean vector space named shape space. Dimensions represent groups of amino acids comprising the binding interface between an Ag epitope and a BCR paratope; contiguous dimensions correspond to spatially proximal residue groups. Coordinates describe biochemical properties relevant for binding affinity. This geometric representation captures the specificity of BCR-Ag interaction: A small distance depicts high complementarity, hence, strong binding, whereas a large separation reflects poor match, thus, weak binding.

Residues in a viral eptiope vary in accessibility to BCR: Conserved elements essential for viral fitness and function are often surrounded and partially masked by highly variable residues (and covered by glycans) (Julien et al., 2013; Burton and Hangartner, 2016). Consequently, strain-specific B cells that target easy-to-access variable residues evolve to enhance affinity at a fast pace, whereas cross-reactive B cells directed at poorly accessible conserved residues tend to improve slowly. In this sense, spatial accessibility of binding targets dictates the adaptation rate of elicited clonal lineages.

Guided by these observations, we describe the variability of adaptation rate in a phenomenological manner: B cells move fast in dimensions along which Ags can mutate and evade recognition (n_v fast/variable dimensions), but move slowly in dimensions where Ags are fixed at the origin (n_c=n−n_v slow/conserved dimensions). The corresponding difference in mutation effect is encoded by a difference in the jump step size in shape space (see supplemental information). As illustrated in Figure 1B, germline B cells (blue ovals), starting on or outside a founder hypersphere centered at the origin (where the infecting virus resides), evolve to approach Ags (red stars) in all directions, while viruses can only move along fast/variable dimensions, attempting to escape the chase by facing it.

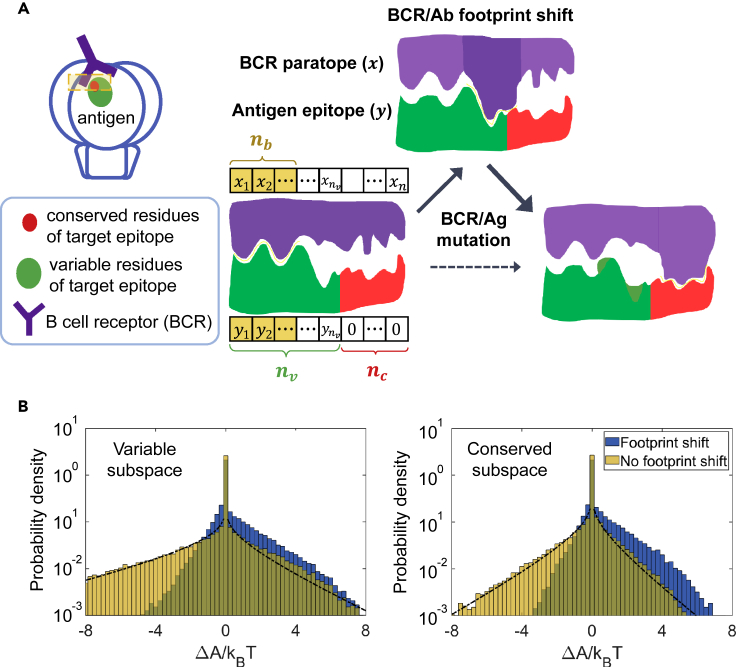
Binding affinity and footprint shift

Structural studies (Sethi et al., 2006; Liao et al., 2013; Zhou et al., 2015; Bonsignori et al., 2016; Huang et al., 2016) indicate that not all the residues constituting a viral Ag epitope are in contact with a particular BCR paratope. Rather, BCRs specific for the same epitope may bind different, yet partially overlapping, portions of it, due to differences in BCR conformation or approach angle. This joint binding surface on the Ag defines the epitope. Hence, the footprint of a particular BCR spans only a fraction of the epitope; in our shape space, BCR-Ag binding takes place in a subspace. Further, once in proximity, a BCR may search across the epitope surface for best complementarity and settle therein once located, as commonly seen in molecular recognition (Baron and McCammon, 2013). This translates to comparing the Ag-BCR Euclidean distance among all subspaces (comprising n_b contiguous dimensions) and taking the minimum; this operation picks out the best match from (n−n_b+1) potential binding sites.

To be specific, we define the local binding affinity A_l (in units of k_BT) between a BCR$\overrightarrow{x}$ and an Ag $\overrightarrow{y}$ as follows

$$A_l\left(\overrightarrow{x},\overrightarrow{y}\right)\equiv A_{\text{max}}-\frac{1}{n_b}\left|\right|\overrightarrow{x}-\overrightarrow{y}|{|}_l^2$$ (Equation 1)

Here $l\in \left\{\mathrm{1,2},\cdots ,n-n_b+1\right\}$ indexes the starting dimension of a n_b-dimensional binding subspace (i.e., the l-th binding footprint); A_max denotes the maximum affinity at perfect match. The global affinity is identified as

$$A\left(\overrightarrow{x},\overrightarrow{y}\right)\equiv \underset{l}{\text{max}}{A}_l\left(\overrightarrow{x},\overrightarrow{y}\right)=A_{\text{max}}-\frac{1}{n_b}\underset{l}{\text{min}}\left|\right|\overrightarrow{x}-\overrightarrow{y}|{|}_l^2$$ (Equation 2)

Hence, a higher affinity indicates a smaller mismatch in conformation; minimization of mismatch reflects a dynamic search for the optimal binding footprint labeled by $l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{y}\right)\equiv {\text{argmax}}_l{A}_l\left(\overrightarrow{x},\overrightarrow{y}\right)$.

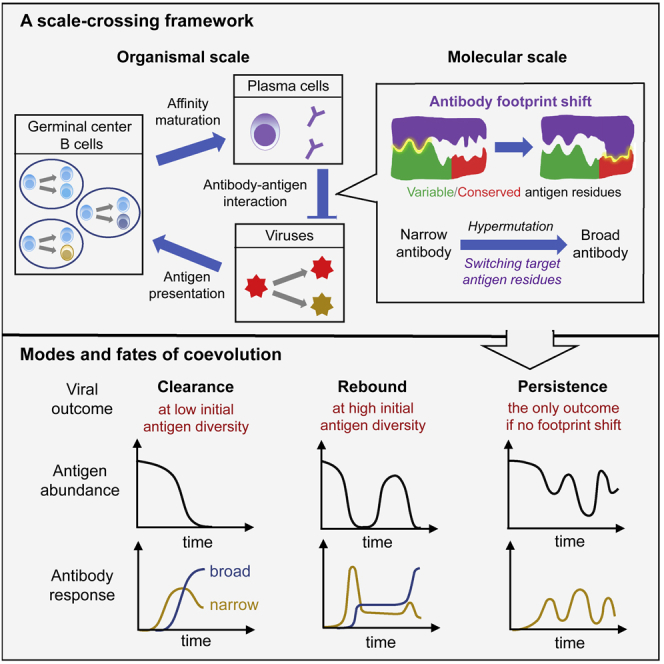
This notion of binding subspace endows Abs with desired properties, such as flexibility in binding target and state-dependent effect of mutations (i.e., epistasis). Importantly, this representation captures the observed shift of Ab/BCR binding footprint on viral epitope during HIV-Ab coevolution (Bonsignori et al., 2016; Zhou et al., 2015), which correlates the precision of targeting to conserved residues with breadth development. As shown schematically in Figure 2A, as mutations induce conformational changes in BCR (purple shape) and/or the variable region of Ag (green shape), the optimal binding footprint (yellow interface) may shift toward increasingly conserved regions of the viral epitope (red shape), under conditions to be discussed below.

Figure 2.

Shift of binding footprint alters the distribution of mutation effect

(A) Binding affinity between Ag epitope $\overrightarrow{y}$ and BCR paratope $\overrightarrow{x}$ is determined by the binding footprint—the binding site with the best complementarity (i.e. the n_b-dimensional subspace in which the shape-space distance is shortest). An initial configuration (lower left) has strongest binding in first n_b dimensions (yellow boxes); adjacent dimensions represent spatially proximal residue groups, here in total n_v (n_c) variable (conserved) ones. Upon mutation in BCR or Ag (change in purple or green shape), whether within or outside the current contact region (yellow interface), footprint may shift (top and lower right). Favorably, shift occurs from variable (green) via mixed to conserved (red) parts of the epitope (solid arrows); direct shift to conserved regions is unlikely (dashed arrow).

(B) Distribution of mutation effect shown for binding of germline B cells to the founder virus, with footprint in variable (left) or conserved (right) subspace before mutation, and footprint shift being allowed (blue) or inhibited (yellow) upon mutation. The black curve indicates the theoretical distribution for fixed footprint; see supplemental information for derivation. n_c=3, n_v=5, and n_b=3.

Footprint shift influences the distribution of mutation effect $P\left(\text{Δ}A\right)$ in two ways: First, when a deleterious mutation ($\text{Δ}{A}_{l^{\text{∗}}}<0$) occurs inside current optimal subspace $l^{\text{∗}}$ and lowers the affinity $A_{l^{\text{∗}}}$, switch to a different subspace in which $A_l>A_{l^{\text{∗}}}+\text{Δ}{A}_{l^{\text{∗}}}$ will buffer against large detrimental effect. Second, when a beneficial mutation ($\text{Δ}{A}_l>0$) occurs outside current optimal subspace ($l\ne l^{\text{∗}}$) such that $A_l+\text{Δ}{A}_l>A_{l^{\text{∗}}}$, switch into this subspace will enhance affinity; without footprint shift, this apparently “neutral” mutation would be wasted. Thus, as shown in Figure 2B for founder B cells and the infecting virus (contrasting blue and yellow histograms), shift of binding footprint leads to fewer and smaller deleterious mutations (a shortened negative tail), along with more frequent beneficial mutations of larger sizes (an expanded positive wing). This turns out to be key to speeding up B cell adaptation and enabling viral clearance.

Based on the conservation level of the optimal binding subspace, we classify GC B cells and Ab-secreting plasma cells into B (broad) type and N (narrow) type, which, respectively, have greater than and at most n_b−1 conserved dimensions when averaged over encountered Ags.

Ecological dynamics influence mutual selection

A GC B cell $\overrightarrow{x}$ is able to successfully acquire Ag in GC cycle t with the following probability

$$P_G\left(\overrightarrow{x},t\right)=\frac{C_{Ag}\left(t\right){\sum }_{\overrightarrow{y}\in \mathcal{Y}}{e}^{A\left(\overrightarrow{x},\overrightarrow{y}\right)}}{1+C_{Ag}\left(t\right){\sum }_{\overrightarrow{y}\in \mathcal{Y}}{e}^{A\left(\overrightarrow{x},\overrightarrow{y}\right)}},$$ (Equation 3)

where $C_{Ag}\left(t\right)$ is the concentration of Ag presented on follicular dendritic cells (FDCs) in a GC, assumed to be proportional to the virus population size at time t in circulation; this neglects the time lag due to Ag transport and presentation. $\mathcal{Y}$ denotes the set of FDC Ags scanned by B cell $\overrightarrow{x}$ in cycle t. Competition for limited T cell help is incorporated by keeping the top 70% potent B cells in each cycle (Shaffer et al., 2016). Conversely, a virus $\overrightarrow{y}$ in circulation is neutralized by Abs secreted by plasma cells it has encountered in generation t with the following probability

$$P_V\left(\overrightarrow{y},t\right)=\frac{C_{pla}\left(t\right){\sum }_{\overrightarrow{x}\in \mathcal{X}}{e}^{A\left(\overrightarrow{x},\overrightarrow{y}\right)}}{1+C_{pla}\left(t\right){\sum }_{\overrightarrow{x}\in \mathcal{X}}{e}^{A\left(\overrightarrow{x},\overrightarrow{y}\right)}}.$$ (Equation 4)

Here, $C_{pla}\left(t\right)$ represents the concentration of plasma cells in cycle t, among which a random subset $\mathcal{X}$ encounter virus $\overrightarrow{y}$. Therefore, through time-dependent concentrations of binding substrates (Ags and plasma cells), population dynamics directly influence two-way selection pressure which, in turn, drives changes in population size and composition, thereby creating a feedback loop between ecology and evolution.

A central feature of our shape space is that both the virus and B cell populations evolve in a larger state space than where selection acts (i.e., n_v, n > n_b). In particular, while BCRs mutate in the full space (n dimensions), mutual selection is only based on binding affinity within a subspace (n_b dimensions). Hence, B cells can enhance receptor potency without increasing selective pressure on the virus. This, therefore, allows mutations that are not immediately beneficial but may potentiate future adaptation to accumulate more efficiently than if all dimensions contribute to binding.

Antigenic determinants for coevolutionary outcomes

Three phases

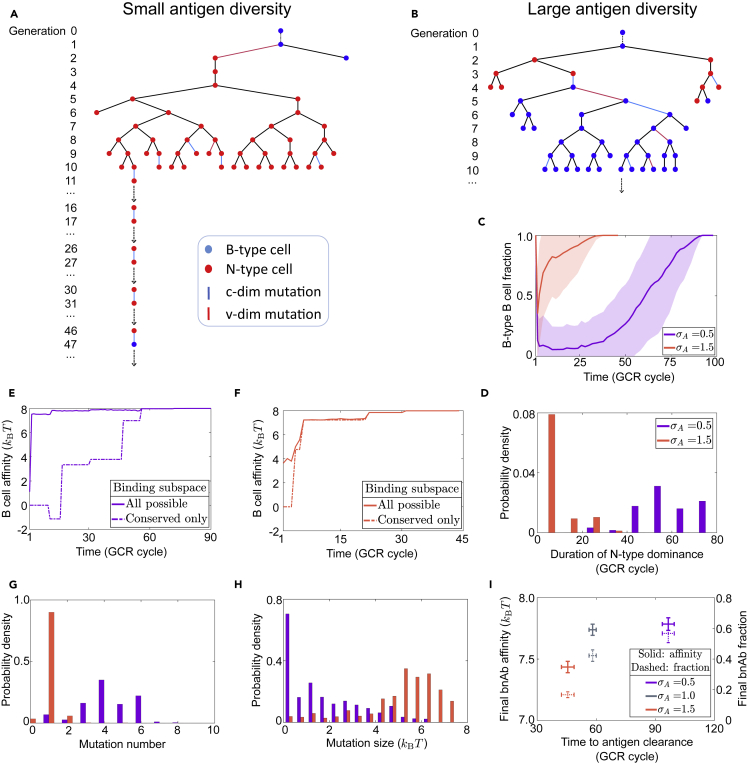
Infections are founded by viral strains centered at the origin of our shape space (with a Gaussian distribution); germline B cells are isotropically distributed on a founder hypersphere in their respective optimal binding subspace. Following estimates based on immunological data (Smith et al., 1997), we choose the shape-space dimensionality to be n=8, in which n_b=3 dimensions constitute each binding subspace, corresponding to the portion of engaged residues among those comprising the epitope (see supplemental information). In the studied parameter range, a total time span of 200 GC cycles is sufficient to distinguish outcomes.

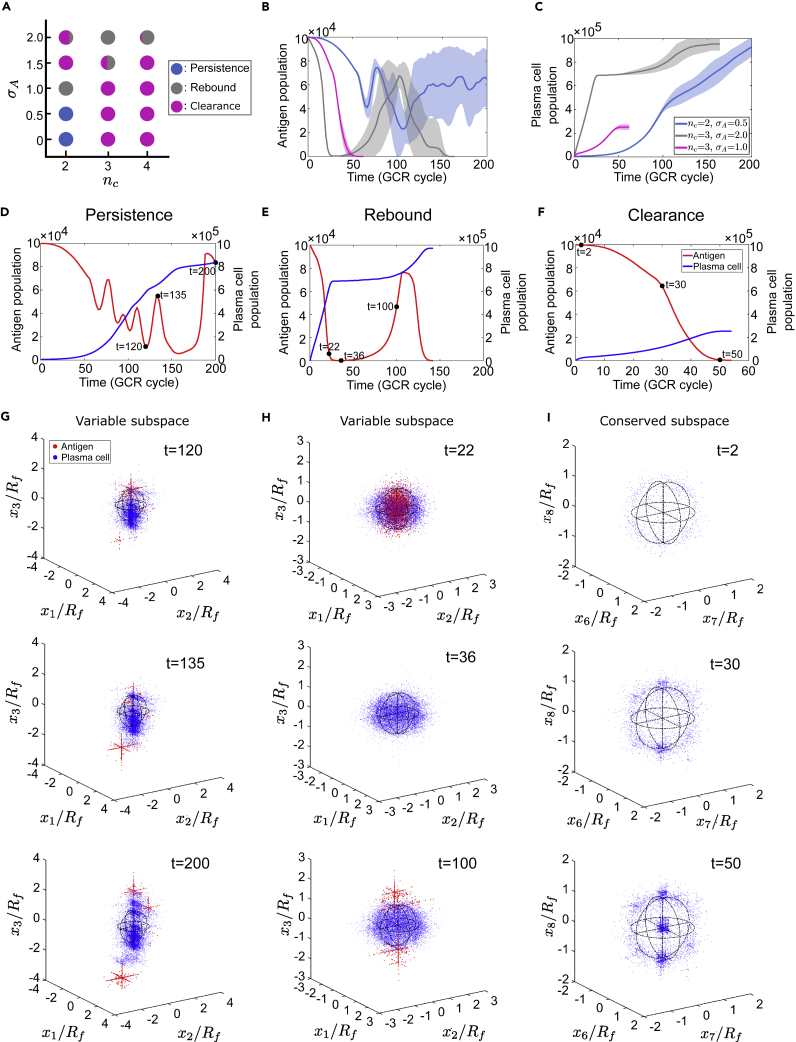
Our model produces dynamics and phenotypic patterns consistent with natural infection of highly mutable viruses (Figure 3). Stochastic simulations identify three distinct outcomes observed in nature—viral/Ag persistence, rebound, and clearance—at different combinations of two control parameters, the number of conserved dimensions, n_c and phenotypic diversity of Ag when they first activate immune responses, σ_A. A phase diagram delineates dynamical regimes (Figure 3A): Viral persistence (blue), as commonly observed for rapidly mutating pathogens (e.g., HIV and HCV), occurs at low epitope conservation (small n_c, n_c<n_b) and modest initial Ag diversity (small σ_A); sufficiently conserved epitopes (n_c≥n_b) combined with moderate Ag diversity at immune activation result in viral clearance (magenta), often associated with acute infections (e.g., influenza and Ebola). More unexpected is the rebound phase (gray) at large initial Ag diversity. Although viral persistence occurs in the majority of chronic infections, a recent study of HCV-Ab coevolution has identified clearance and rebound in different individuals; in both cases bnAbs emerge (Bailey et al., 2017).

Figure 3.

Distinct coevolutionary outcomes and patterns emerge at different combinations of initial antigen diversity and epitope conservation

(A) Phase diagram of three coevolution outcomes: Viral clearance (magenta), rebound (grey), and persistence (blue). At high initial Ag diversity (large σ_A), both clearance and rebound could happen in repeated simulations (each hybrid symbol indicating the proportion of occurrence among 100 runs).

(B and C) Population trajectories of Ags (B) and plasma cell (C) in three phases, shown with mean ± SD (shade) from 10 simulations in each case. Here and after, we measure time in units of GCR cycles; one GCR cycle corresponds to 6 to 12 hr in real time.

(D–I) Representative population trajectories and shape-space configurations of Ags (red) and plasma cell (blue) in each phase.

(D, G) Persistence; n_c=2, σ_A=0.5. (E, H) Rebound; n_c=3, σ_A=2. (F, I) Clearance; n_c=3, σ_A=1. Snapshots in a binding subspace of n_b=3 dimensions are taken at time points marked by black dots in (D–F). (G) and (H) illustrate Ag escape in a variable subspace; (I) demonstrates Ag clearance by bnAbs in a conserved subspace. For visual clarity, a random subset of 5% of plasma cell and 25% of Ags are shown. Shape-space coordinates are scaled by the radius R_f of the B cell founder hypersphere; black circles delineate the cross-sections of founder sphere with three orthogonal planes intersecting at the origin.

Figures 3B and 3C present dynamics of virus and plasma cell populations, respectively, demonstrating defining features of three phases. Figures 3G–3I display characteristic phenotypic patterns developed in the shape space (at time points marked by black dots in Figures 3D–3F), distinguishing outcomes since early times. In the persistence phase (Figure 3D), sustained oscillations in Ag abundance (red), characteristic of predator-prey cycles, are accompanied by a steady accumulation of plasma cells (blue) from GC output. The viral-immune mutual engagement in a Red-Queen state is made vivid through density profiles at several instants during oscillations (Figure 3G): In a variable subspace, a deforming cloud of plasma cells (blue) is chasing after Ag clusters (red), which escape increasingly farther from the infecting strain at the origin that focuses past B cell response (Figure S2).

In the rebound phase, an initially very diverse viral population rapidly falls to a low abundance (below 10% of the initial size or capacity, but above the extinction threshold at 0.1% capacity) and subsequently recovers, forming a population bottleneck; the resulting lack of Ag stimulation for GC reaction yields a plateau in plasma cell counts (Figure 3E). Notably, during the Ag bottleneck, the plasma cell distribution resembles the founder hypersphere, even after Ags reemerge outside the enclosure (Figure 3H bottom panel), indicating very little AM prior to viral rebound. Only after escape mutants build up in number, GC reaction, and plasma cell differentiation resume. Note that even after recovering from the bottleneck, Ags may still be cleared if the epitope is sufficiently conserved. This stage proceeds in a similar manner as in the clearance phase (Figures 3F and 3I). Starting from a small variance, diversifying Ags drive rounds of AM through which B cells evolve from targeting variable residues (Figure 3I top panel) to recognizing a mixed region (middle panel, condensing at opposing poles of the founder sphere), and finally focusing onto conserved residues (bottom panel, high concentration at the origin of a fully conserved subspace). This shift in binding target toward viral vulnerability results in a monotonic decline of Ag population to below the extinction threshold (Figure 3F, red curve).

Characterizing broad and narrow responses

To understand the emergence of diverse trajectories and patterns, we examine how n_c and σ_A jointly control the transition between distinct regimes (Figure 4). While n_c governs the prevalence of germline B cells targeting conserved and variable residues (i.e., precusor frequency of broad and narrow clones), σ_A decides their relative accessibility (phenotypic distance) to Ags. As to be shown below, these parameters control the efficacy and timing of strain-specific and cross-reactive responses which, in turn, determine evolutionary outcomes.

Figure 4.

Transitions between distinct phases are governed by the timing and efficacy of strain-specific and cross-reactive B cell responses

Representative trajectories of Ag population (black) and average BCR-Ag binding probability (colored) for broad (B-type, colored solid; P_B) and narrow (N-type, colored dotted; P_N) B cell lineages under different combinations of epitope conservation (n_c) and initial Ag diversity (σ_A). Parameter choices correspond to the phase diagram in Figure 3A; panels A to E have decreasing initial antigen diversity, σ_A=2,1.5,1,0.5,0, respectively. In each panel, the number of conserved sites increases from left to right, n_c=2,3,4, respectively. When n_c=2 (n_c<n_b, left column), there is no contribution from B-type lineages (i.e. P_B=0), since fully conserved binding subspace does not exist.

To characterize these components, we divide the set $\mathcal{X}$ of plasma BCRs into two subsets, ${\mathcal{X}}_B$ and ${\mathcal{X}}_N$, based on the number of conserved dimensions $c\left(\overrightarrow{x},\overrightarrow{y}\right)$ in the optimal binding subspace between a BCR $\overrightarrow{x}$ and a given Ag $\overrightarrow{y}$: ${\mathcal{X}}_B\equiv \{\overrightarrow{x}\in \mathcal{X}|c(\overrightarrow{x},\overrightarrow{y})=n_b\};{\mathcal{X}}_N\equiv \mathcal{X}\backslash {\mathcal{X}}_B$. Thus, for any BCR $\overrightarrow{x}\in {\mathcal{X}}_B$, it binds Ag $\overrightarrow{y}$ mostly strongly in a fully conserved subspace; ${\mathcal{X}}_B$ is empty if n_c < n_b, since all subspaces contain at least one variable dimension. Accordingly, we can rewrite the probability of Ag removal (Equation 4) as $P_V\left(\overrightarrow{y},t\right)\equiv P_B\left(\overrightarrow{y},t\right)+P_N\left(\overrightarrow{y},t\right)$, where $P_S\left(\overrightarrow{y},t\right)=C_{pla}\left(t\right)\sum _{\overrightarrow{x}\in {\mathcal{X}}_S}\text{exp}\left[A\left(\overrightarrow{x},\overrightarrow{y}\right)\right]/\left\{1+C_{pla}\left(t\right)\sum _{\overrightarrow{x}\in \mathcal{X}}\text{exp}\left[A\left(\overrightarrow{x},\overrightarrow{y}\right)\right]\right\}$, with S=B,N. Therefore, P_B and P_N, when averaged over circulating Ags $\left\{\overrightarrow{y}\right\}$, characterize the efficacy of broad and narrow lineages, respectively.

Figure 4 shows typical trajectories of Ag population size (black) and concomitant strength of B-type (P_B; color, solid) and N-type (P_N; color, dashed) plasma cells for different pairs of n_c and σ_A (columns and rows). In cases where both types exist (n_c ≥ n_b, right two columns) narrow clones arise first and suppress Ag population; broad clones only emerge and expand as narrow lineages decline in efficacy, signifying viral escape. Hence, the peak in P_N indicates a shift in dominance from strain-specific to cross-reactive response.

Initial antigen diversity governs clearance-to-rebound transition

A greater Ag diversity at GC onset (larger σ_A) may reflect a longer lag between infection and activation of responsive B cells that initiate the GC reaction; during the lag, the founder virus diversifies. In our shape space, compared to the founder virus at the origin, a mutated Ag binds more weakly to some B cells but more strongly to others, as long as it remains enclosed by B cells. Similar behavior has been observed in experiment where the same Ag mutations weaken affinity to certain Abs but enhance binding to others (Moore et al., 2012; Huang et al., 2016; Bonsignori et al., 2017), consistent with Ags being corralled by B cells early in infection.

Less intuitively, increasing Ag diversity results in higher mean affinity of strain-specific (N-type) germline B cells without affecting cross-reactive (B-type) cells (see supplemental information text and Figure S1), leading to faster Ag removal by specific clones at early times. This implies that Ag diversity at the response onset (judged by the start of decline in Ag population) controls the access of narrow and broad clones to Ag “resource”, thereby affecting the rate of Ag consumption. Indeed, as σ_A increases, a faster fall in Ag population follows an earlier and steeper rise in P_N (Figure 4 right column, bottom to top), but this also leads to weaker P_B upon viral escape, since broad clones have shorter time to evolve. Thus, through feedback between population dynamics and mutual selection, initial Ag diversity has a complex influence on B cell responses; not only does it affect the efficacy of narrow and broad clones at their peak time, it also tunes the timing of Ag escape and the ensuing expansion of broad lineages that ultimately determine evolutionary outcomes.

Such eco-evolutionary feedback manifests most dramatically as a rapid viral rebound following a deep population bottleneck, when initial Ag diversity is large (Figure 4A). A modest Ag diversity, instead, results in monotonic clearance. These phases appear to capture distinct kinetics of clearance and rebound in HCV-infected individuals (Bailey et al., 2017) and suggest Ag diversity at response onset as a predictor of outcomes. The key lies in the level of AM reached before Ag population falls too small to sustain GC reaction. Specifically, if Ag diversity starts modest, both narrow and broad clones begin with weak affinity and evolve toward viruses at similar antigenic distance. By the time narrow clones start to wane while broad clones are just on the rise, Ags are still relatively abundant. Consequently, broad lineages continue to gain both abundance and breadth as diversifying Ags favor their selection. This, in turn, increasingly limits viral growth, yielding a monotonic drop to extinction. Throughout this process, Ags remain inside B cell enclosure (Figure S3); as the Ag cloud is consumed from the surface inward, a density gradient is generated, providing an “attractant” field that guides B cells toward the founder virus.

In contrast, at large initial diversity, “pioneer” viruses near the frontier of the Ag cloud are close to the B cell founder hypersphere; while being able to escape B cell enclosure with few mutations, these mutants risk being recognized by strain-specific clones as they transect across the frontline. As a result, Ag removal is so rapid that B cells have hardly evolved when escape mutants emerge outside the founder hypersphere (almost unchanged B cell distribution, Figures 3H and S4; rapid rise and fall of P_N, Figure 4A). Meanwhile, Ag population is already too small to sustain GC reaction and AM essentially comes to a halt (Figure 4A right panel, flat P_B due to lack of AM). This thus allows escape mutants to expand unchecked, leading to a significant rebound. With a delay, this renewed supply of mutated Ag boosts AM and selects broad lineages that evolve to acquire breadth and eventually clear the virus (Figure S5).

Epitope conservation determines the timing of viral rebound

When conserved residues make up a larger portion of the epitope (increasing n_c; Figure 4, left to right), narrow response rises more slowly and reach a lower maximum, while broad response, uncompromised by viral escape, gains stronger dominance toward viral clearance (n_c ≥ n_b). In the absence of fully conserved targets, infections persist (n_c < n_b, left column). At intermediate values of σ_A (Figure 4B), dynamics and outcomes exhibit a non-monotonic trend as n_c increases: Monotonic viral clearance occurs either when N-type clones are sufficiently potent early on so they remove Ags before escape mutants arise (left panel, n_c < n_b), or when B-type lineages have time to mature and clear Ags following their escape from narrow lineages (right panel, n_c > n_b). In between (n_c ∼ n_b), however, neither narrow nor broad clones are effective at clearing Ags but they suppress each other; rapid Ag removal by specific clones leaves little time and stimuli to support breadth development, thus, viral rebound ensues.

Interestingly, increasing n_c leads to a shallower Ag population bottleneck and yet a slower rebound (Figure 4A, left to right; Figure 5, yellow to green). This behavior reflects a separation of timescales between the dominance of clones with different binding targets: Weaker binding to variable residues early on reduces Ag removal thus yielding a shallower bottleneck, whereas stronger binding to conserved residues later delays Ag revival; two stages are separated by Ag escape before which little AM has taken place. Note that for a given n_c, just as one would expect, a deeper bottleneck indeed lasts longer (Figure 5, same color, going up and to the left). These results indicate that the conservation level of the viral epitope determines the size and duration of Ag population bottleneck, and hence the timing of viral rebound.

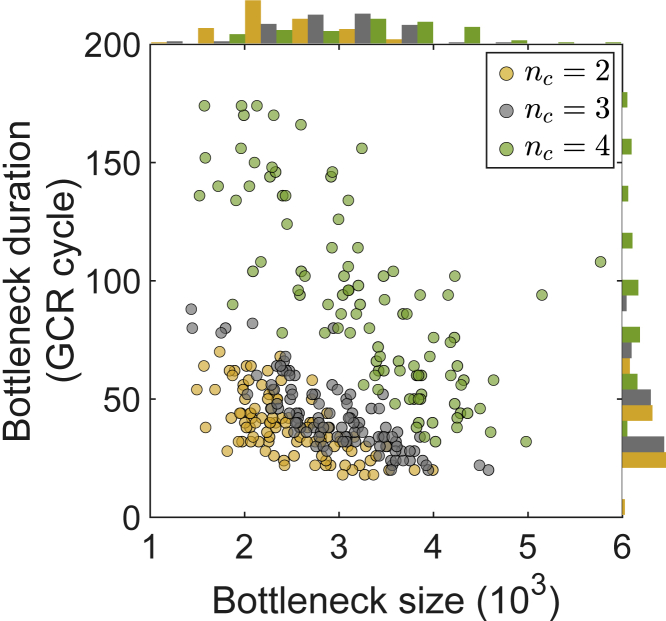
Figure 5.

Epitope conservation controls the size and duration of antigen population bottleneck in rebound phase

Stronger epitope conservation (larger n_c) yields a shallower yet longer-lasting Ag population bottleneck. Bottleneck starts when Ag population first drops to below 10% capacity and ends when it recovers to above this level. Bottleneck size is defined by the time-averaged Ag count during the bottleneck. 100 simulations (scatters) are performed for each n_c value; corresponding histograms are shown along the sides. Initial Ag diversity σ_A=2.

Flexible molecular recognition drives viral extinction and bnAb development

Footprint shift enables viral clearance

The clearance regime per se is not a surprise, if immune adaptation can outpace viral evolution via faster or larger mutations. It becomes more surprising as we rule out this possibility by choosing mutation parameters that support stable persistence. In fact, predator-prey cycles would be the only outcome even for a relatively conserved epitope, if binding footprint were fixed (Figures 6A and S6). Ab footprint shift toward conserved viral residues has been observed during HIV-bnAb development (Bonsignori et al., 2016; Zhou et al., 2015), but how this occurs through coevolution is unclear.

Figure 6.

Footprint shift enables bnAb development and viral clearance

(A) Ag population trajectories with (red) and without (black) shift in BCR binding footprint. Ag clearance only occurs if footprint shift is allowed.

(B) Evolved B cells are grouped based on binding footprint of their germline ancestors against the founder virus; color indicates the number of conserved dimensions in the optimal binding subspace. Data are collected at t=100 (no footprint shift) or when Ag population drops to 10% capacity (with footprint shift). B cells that initially target a fully conserved region (blue) only survive under footprint shift. (A) and (B) are based on the same set of simulations and data are plotted as mean ± SD.

(C and D) Typical trajectories of GC composition (fraction of three cell groups defined in panel B), when footprint is fixed (C) or adjustable (D). n_c=4, σ_A=1.

Figure 6B demonstrates that footprint shift retains descendants of broad germline clones with fully conserved targets (blue bar), such that they can persist to make up a substantial fraction of GC populations and clear the virus (Figure 6D, blue band). In contrast, without a flexible footprint (Figure 6C), broad clones are quickly outcompeted by strain-specific ones and lost once for all. Note, even in this case, despite that highly specific clones (red band) dominate early on, lineages with relatively cross-reactive ancestors (purple band) steadily grow and dominate at later times as Ags diversify. But, because truly broad clones are permanently lost, GC populations only chase after escape viral mutants, leaving an oscillatory signature in Ag population trajectories (Figure 6A, black curve). Therefore, Ab footprint shift enhances Ag removal by preserving broad precusors and promoting expansion of cross-reactive descendants.

Footprint shift opens novel pathways toward broad response

One might wonder, how can slowly evolving cross-reactive clones persist, in the face of strain-specific competitors that are more numerous, potent and faster evolving? Our model suggests an intriguing possibility: Physical optimization of binding—via adjusting BCR footprint—not merely speeds up adaptation of intrinsically slow clones, but allows for a plastic phenotype along a lineage. That is, a shift between binding targets of different conservation levels amounts to switch between states with different environmental sensitivity. Therefore, even if outcompeted early on, cross-reactive (B-type) clones can “regenerate” from strain-specific (N-type) ancestors, enabling sustained adaptation to diversifying Ags.

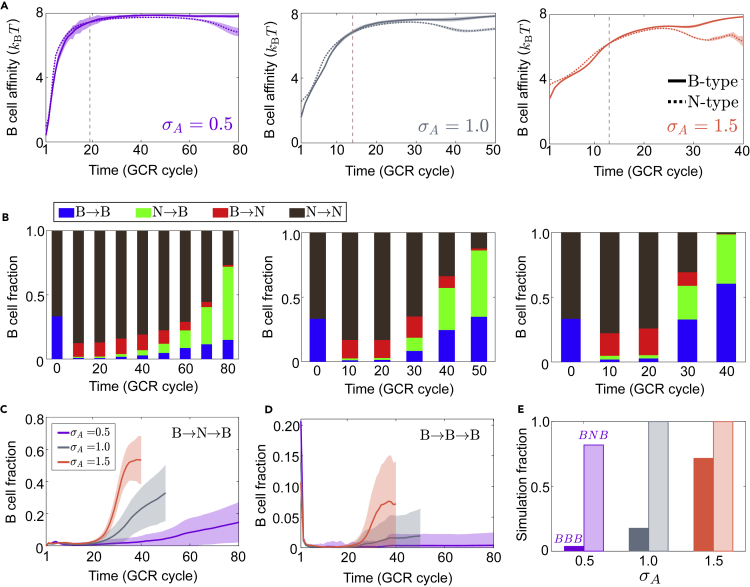
To quantify this intuition, we track the phenotypic identity of surviving B cells over the course of coevolution. Figure 7B presents the time-dependent ensemble-averaged composition based on initial identity X (against founder virus) and current identity Y (against FDC Ags encountered in current GC cycle) of individual cells; hence X→Y represents current Y-type clones descending from an X-type germline precusor — one of four types of identity switch (B→B, N→B, B→N, N→N). Over a wide range of initial Ag diversity, a common pattern emerges: Shortly after the response begins, B→B (blue) drops rapidly while B→N (red) and N→N (coffee) grow; subsequently, N→B (green) and B→B (blue) rise to dominance, while B→N and N→N fall minor. Accordingly, footprint shift opens multiple coexisting novel pathways toward broad clones, with N→N→B and B→N→B being more prevalent than B→B→B.

Figure 7.

Footprint shift opens novel pathways toward broad response.

(A) Affinity trajectories of B-type (solid) and N-type (dotted) clones under different initial Ag diversity. Vertical dashed lines mark the time since when the mean affinity of B-type exceeds that of N-type.

(B) Temporal evolution of ensemble-averaged GC composition based on initial and current identity of individual cells, e.g., N→B represents current B-type clones descending from an N-type germline ancestor; see Figure S8 for absolute B cell counts of each switch type. (A, B) Left to right: σ_A=0.5,1,1.5.

(C and D) Fraction of BNB (C) and BBB (D) cells until viral clearance; see Figure S9 for prevalence of other pathways.

(E) Fraction of simulations (GC ensembles) containing BBB or BNB lineages. Opaque: BBB, transparent: BNB. In all panels, data are collected from the same 50 simulations for each σ_A value; purple for σ_A=0.5, gray for σ_A=1, and red for σ_A=1.5. n_c=4. Data in panels (A, C and D) are plotted as mean ± SD.

While cross-reactivity can be good for evolvability (capacity to adapt), it takes time and the right conditions to itself evolve. These unexpected pathways suggest that spontaneous (but not random) phenotype switch of individual cells—enabled by physical dynamics—allows a cell population to fulfill conflicting demands through a separation of timescales: Switch to N-type early on meets the short-term need for GC survival under severe selection pressure, and switch to B-type later sustains long-term adaptation toward greater breadth and potency. Both switches are achieved by target shift that confers largest affinity gain available. This is further supported by time-dependent distributions of mutation effect in fast (variable) and slow (conserved) dimensions (Figure S7): Early in response, a larger number of beneficial mutations of bigger size exist in fast dimensions, hence switch to N-type is favorable; at later times, adaptive changes of appreciable size continue to be available in slow dimensions, while mutations in fast dimensions can no longer improve affinity, thus, switch to B-type is selected. Consistently, crossing of mean affinities of B- and N-type cells occurs right at the start of N→B switch (Figure 7A, vertical line). Therefore, evolution drives footprint shift and conversely, footprint shift opens new pathways and facilitates adaptation.

Interestingly, initial Ag diversity influences the relative abundance of pathways enabled by footprint shift (Figures 7, S8, and S9). At small σ_A, N→B pathway dominates (Figures 7B and S8 left, green bar), whereas large σ_A favors B→N→B pathway (Figures 7B and S8 right, blue bar), indicating higher initial Ag diversity better preserves broad precusors. Both pathways may contribute to the experimental observation that a fraction of strain-specific precusors later gain breadth (Liao et al., 2013; Doria-Rose et al., 2014; MacLeod et al., 2016; Bonsignori et al., 2017). In practice, B→N→B might be observed as N→B due to the brief presence of broad precusors. Among pathways that both start and end with broad clones, B→N→B is more abundant than B→B→B, in terms of the fraction of cells in a single metapopulation (one simulation of subdivided GCs; see statistics in Figures 7C and 7D) and the fraction of metapopulations containing either pathway (Figure 7E).

Footprint shift exploits potentiating variations

It is apparent from Figure 7C that increasing initial Ag diversity σ_A (purple to red) accelerates the expansion of BNB lineages in GC populations, leading to faster viral clearance. To address how σ_A affects the pace and efficacy of the BNB pathway, we trace the mutational history along BNB lineages that survive until viral elimination, contrasting small and large σ_A (Figure 8). Here, a lineage includes a germline B cell and all its descendants; Figures 8A and 8B depict two typical lineage trees where nodes represent B cells colored by phenotypic identity (red for N-type, blue for B-type), links colored red/blue indicate affinity-altering mutations occurring in variable/conserved dimensions, and black arrows in the latest generation mark B-type clones whose offspring last until virus depletion.

Figure 8.

Increasing initial antigen diversity speeds up expansion of BNB lineages at the cost of bnAb efficacy

(A and B) Example B cell lineage trees typical of the BNB pathway under small (σ_A=0.5) and large (σ_A=1.5) initial Ag diversity. A BNB lineage stems from a B-type founder (blue node in generation 0) and undergoes an N-type dominated intermediate stage (takeover of red nodes) before switching back to B-type dominance (regrowth of blue nodes). Shown are long-lived lineages responsible for viral clearance, where the black arrow at the latest generation indicates the branch that lasts to the very end. Full tree structures are presented only up to generation 10. The extended branch in (A) contains the earliest reappearing B-type clone (at cycle 47) and mutations in conserved dimensions (blue links) leading to it.

(C and D) Fraction of B-type cells (mean ± SD, panel (C)) and histogram for the duration of N-period (N-type fraction being above 50%, panel (D) along long-lived BNB lineages for σ_A=0.5 (purple) and σ_A=1.5 (red)), respectively.

(E and F) B cell affinity along the longest-lived branch (marked in A and B) until Ag clearance. Shown are the optimal affinity among all binding subspaces (solid) and that among fully conserved subspaces only (dashed).

(G and H) Number (G) and size (H) of beneficial mutations in conserved subspaces during the N-period. (C, D) and (G, H) are all based on the same 50 simulations for each σ_A value.

(I) BnAb efficacy, quantified by mean affinity to conserved targets (solid), final fraction among plasma cells (dotted) and time to clear Ag (x axis) at different initial Ag diversity. A bnAb has an optimal binding affinity to conserved targets of at least 6k_BT. n_c=4. Data are plotted as mean ± SD from repeated simulations.

With small σ_A (Figure 8A), a B-type founder switches to N-type and remains N-type for extended time before switching back to B-type. When σ_A is large (Figure 8B), the intermediate N-period is very brief before B-type clones take over. This contrast in N-period duration is clearly seen from the trajectories of B-type fraction in a lineage (Figure 8C) and the statistics of N-period duration across lineages in many populations (Figure 8D).

What drives an earlier N→B switch at a higher initial Ag diversity? Recall that at larger σ_A, N-type clones have higher affinity early on and produce plasma cells more rapidly, leading to faster Ag removal (Figures 4B–4D, right column). Rapid reduction in viral population, in turn, makes it even harder to generate escape mutants, resulting in sooner extinction. Hence, when σ_A is large, few beneficial mutations in conserved dimensions would suffice to clear the virus. Meanwhile, only clones that improve fast enough can survive the fierce competition for rapidly diminishing Ags. Taken together, at higher σ_A, fewer but larger beneficial mutations accumulate in conserved subspaces within a shorter time (Figures 8G and 8H), resulting in sooner dominance of B-type clones and faster viral elimination.

To illustrate how footprint shift facilitates accumulation of adaptive changes that collaborate with breadth development, we present in Figures 8E and 8F the optimal affinity of a B cell (to encountered FDC Ags) among all possible binding subspaces (solid line) and among conserved subspaces only (dashed line), along the long-lived branch marked in panels A and B, respectively. This clearly shows that breadth-conferring mutations accumulated in conserved subspaces are conditionally neutral: They are neutral under the current condition of selection (mutated residues being outside current contact region) but exhibit significant gain in efficacy under new conditions (strongly diversified Ags). In this way, evolving in a non-selecting environment allows “neutral” establishment of breadth-enhancing mutations (stepwise affinity changes, Figures 8E and 8F, dashed); even occasional affinity-reducing mutations can be buffered when σ_A is small (Figure 8E dashed curve, dip at an early time). This is because modestly diverse Ags induce weak specific response, thus having prolonged availability which, in turn, tolerates slow adaptation of broad clones and permits a wider range of paths (Figure S10A versus B).

Although a larger σ_A results in faster Ag clearance, this gain in speed comes at a cost: Ab quality is compromised due to limited evolution, since strong selection pressure (due to rapid Ag consumption) disfavors slow accumulation of breath-conferring mutations. As shown in Figure 8I, both the affinity (solid) and prevalence (dashed) of bnAbs (affinity to conserved targets being at least 6k_BT) fall with increasing σ_A (hastened AM, purple to red; also see Figure S11). An intermediate σ_A may balance speed and efficacy (gray, σ_A=1); time to clearance is halved with modest reduction in bnAb affinity (relative to σ_A=0.5).

Functional role of B cell compartmentalization depends on antigen variability

GCs are dynamic microstructures where B cells evolve and Abs diversify. Multiphoton imaging combined with single-cell sequencing reveals that multiple GCs form in parallel during an immune response, housing modest B cell populations varying in clonal dynamics and diversity (Tas et al., 2016). A natural question is: What is the evolutionary advantage, if any, of segregating into many small populations, relative to assembling few large compartments?

Theoretical and experimental works have suggested that population subdivision could promote or inhibit adaptation depending on the level of epistasis (Kryazhimskiy et al., 2012; Bitbol and Schwab, 2014); most of these studies consider a constant environment. What if the environment responds to system evolution? Our framework accounts for collective evolution of subdivided populations (GCs) coupled by shared adaptive environments (evolving Ags) and, therefore, lets us examine functional consequences of GC compartments on viral outcomes. It turns out that the answer depends on epitope conservation: population subdivision can slow down viral escape if Ag epitope is highly variable (n_c<n_b; Figure 9B, red to purple), but may also delay clearance if the binding target is relatively conserved (n_c>n_b; Figure 9A).

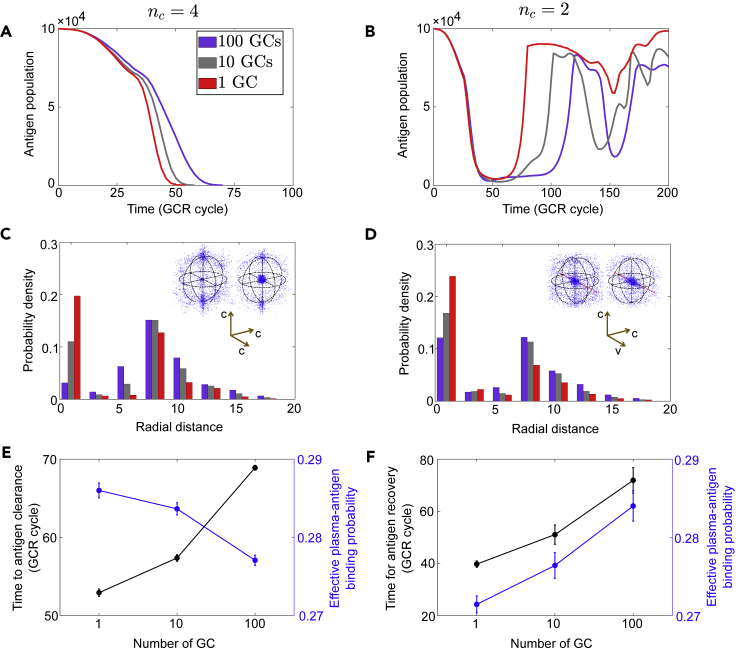
Figure 9.

GC compartmentalization slows viral clearance or rebound depending on epitope conservation

Population subdivision has different functional consequences in the presence (left column, n_c>n_b) and absence (right column, n_c<n_b) of fully conserved binding targets.

(A and B) A typical trajectory of Ag population for each value of GC number.

(C and D) Radial distribution of plasma cells in the optimal binding subspace. Data are collected from simulations in (A) and (B), respectively, at the time when Ag population drops to 10% capacity in the single-GC case. Insets show shape-space patterns for one GC (right) and 100 GCs (left). Blue/red dots: plasma cells/Ags; black circles indicate the B cell founder hypersphere. The same color scheme applies to panels (A–D).

(E and F) Time to clearance (E) or rebound (F) (black) and time-averaged effective plasma-Ag binding probability (blue) for different numbers of GCs. Time for Ag recovery (F) spans between population size falling below 10% capacity and rising above 50% capacity. 20 simulations are performed for each GC number and data are plotted as mean ± SD. σ_A=1.

In both clearance and persistence regimes, moderately diverse Ags create an effective attractant gradient, drawing B cells toward the founder virus at the origin. If a fully conserved binding target exists (n_c>n_b), Ags will remain fixed in the corresponding subspace. Sooner clearance then solely relies on a faster and stronger convergence of B cells toward the origin; this happens to fewer larger GCs, as seen from the radial distribution of plasma cells strongly peaked near the origin (Figure 9C, red histogram for a single GC) and the shape-space snapshots (insets: left, 100 GCs; right, 1 GC). This behavior results from global competition for limited T cell help and rapid increase in selection pressure with decreasing Ag abundance. Consequently, a large effective population size reduces the drift load so that plasma cells are on average closer to the global fitness optimum (fixed at the origin). Thus, as B cells coalesce into fewer larger GCs, Ab efficacy (quantified by time- and population-averaged binding probability between plasma cells and Ags; see supplemental information) rises and the time to clearance falls (Figure 9E).

Conversely, if Ags are highly variable (n_c<n_b), BCRs effective against all variants no longer exist, and the optimal location in the shape space for Ag neutralization is no longer fixed but moving with the evolving Ag distribution. In this case, few large B cell populations, rapidly concentrated to the origin early on, are slow to redirect themselves when Ag mutants emerge outside B cell enclosure (Figure 9D); the resulting plasma cells are therefore ineffective at neutralizing mutant Ags, yielding a rapid rebound following the bottleneck (Figure 9B). With many modest GCs, however, B cells carrying beneficial mutations are distributed across GCs and expand to dominate locally. As such, population subdivision facilitates the generation and maintenance of clonal diversity, enhancing the “mobility” of the collective response. As a result, Abs produced are better able to contain viral mutants and slow the escape (Figure 9F).

In sum, few large GCs speed up global optimization toward a fixed target, whereas many small GCs allow efficient clonal relocation in response to moving targets. Presumably, having a range of GC sizes can strike a balance in meeting these needs. In addition, GC-to-GC communication (e.g., via reactivation of migrating memory cells (Bende et al., 2007) or Ab feedback (Zhang et al., 2013)) might provide a mechanism for regulating the effective population size.

Discussion

Highly mutable viruses are capable of repeatedly evading the host immune response by coevolving with it. Despite comparable pace to diversify and similar tactics to adapt, diverging courses and outcomes may result. Identifying major antigenic determinants for the path and fate is key to predicting hence controlling the evolutionary future. This is in urgent need, as an expanding variety of rapidly adapting pathogens (notably HIV, HCV, influenza, and malaria) defy universal vaccines.

Our stochastic model of coevolution describes the joint dynamics of virus and immunity in a host, accounting for strongly coupled ecological and evolutionary components. We show that distinct viral outcomes (persistence, clearance, and rebound) observed in different individuals emerge from a feedback between physical dynamics involved in molecular recognition and ecological dynamics of co-adapting populations, linked by affinity-dependent mutual selection. Without considering this feedback, clearance and rebound will not be possible.

We identify two antigenic properties that jointly control transitions between distinct regimes–conservation level of viral epitope (n_c) and Ag diversity at the onset of immune response (σ_A). These factors determine the accessibility of different parts of the B cell repertoire and, consequently, control the pace and efficacy of antibody response. By shaping the adaptive dynamics of the antigen “resource”, fast arising narrow response governs when and what broad response may subsequently evolve.

Recent studies (Bailey et al., 2017; Kinchen et al., 2018) report bnAb-mediated clearance of HCV infection in two human subjects without treatment. In particular, one subject (designated C117, clearance subject) exhibits monotonic decline in viral load to extinction, while the other (designated C110, rebound subject) experiences a significant viral resurgence prior to eventual clearance. The contrasting viral kinetics in clearance and rebound phases as predicted by our model closely resemble those reported in the data. More importantly, our work provides a mechanistic explanation for this pronounced difference. Our model predicts that for a sufficiently conserved epitope (n_c≥n_b), as initial Ag diversity exceeds a critical value, monotonic viral clearance transitions to a distinctive rebound; a higher antigen diversity at the onset of antibody response leads to a faster initial decline in viral load. Indeed, phylogenetic and genetic distance analyses (Bailey et al., 2017; Kinchen et al., 2018) indicate that the rebound subject was infected with a larger diversity of viral strains than the clearance subject; moreover, a faster fall of viral load was observed in the former. In addition, our model suggests that a faster decline of antigen population in early infection should result in a retarded accumulation of antibody breadth, because depletion of Ag stimuli halts AM, impeding the emergence and evolution of broad response. This may explain the slower development of plasma breadth in the rebound subject (Kinchen et al., 2018). Finally, model predicts that the rapid fall in viral load leading to extinction (in the clearance phase) is mediated by broad antibodies, whereas the sharp drop toward Ag population bottleneck (in the rebound phase) is caused primarily by strain-specific antibodies. This is supported by data (Kinchen et al., 2018): plasma samples collected from the clearance subject show similar neutralization profiles (patterns of relative potency against a panel of HCV strains) to that of bnAbs. In contrast, plasma of the rebound subject is of much lower neutralization efficacy than bnAbs prior to the viral bottleneck, indicating the dominance of specific antibodies (from which viruses escape).

We propose that flexible molecular recognition allows for plastic phenotypes: A BCR can search across a continuum of potential binding targets on the viral protein and dock at the site of best complementarity; conservation level of thus identified binding target naturally defines B-cell phenotype — broad clones primarily target conserved residues whereas narrow clones chiefly bind variable elements. Provided such flexibility in recognition, phenotype can spontaneously switch in a way that mitigates the tension in response to changing selective forces. Related concepts have been discussed in the context of tradeoff evolution in changing environments (Tikhonov et al., 2020). More broadly, our result suggests that physical dynamics may alter evolutionary constraints, a mechanism expected to apply to other systems where biomolecular binding mediates selection, such as the emergence of drug resistance and evolution of gene regulatory elements.

While a fixed binding target results in viral persistence in line with previous studies, our work suggests that a flexible binding footprint of BCRs enables clearance of antigenically complex pathogens. On one hand, B cells can utilize affinity-enhancing mutations outside current contact region while buffering affinity reduction within the contact, thus enhancing the rate and size of favorable changes. On the other hand, target switch allows strain-specific ancestors to generate cross-reactive descendants, enabling persistent adaptation to diversifying Ags.

Shift of BCR footprint opens unexpected pathways of breadth evolution that can be searched for using longitudinal phenotypic assays: The BNB pathway preserves broad precusors via an intermediate period of narrow phenotypes, whereas the NB pathway expands the range of precursors to strain-specific clones that later acquire breadth-conferring mutations. During the N-period, beneficial variations accrue in conserved dimensions, which potentiate later switch to broad phenotypes. Importantly, these conditionally neutral mutations do not exacerbate selection pressure on the virus, thus prolonging the availability of Ag stimuli. In this sense, “regeneration” of B-type clones relies on BCRs evolving in a larger state space than where selection directly acts, so that lineages slowly accumulating potentiating variations stand a chance to persist.

Last but not least, our result suggests that compartmentalizing AM into multiple GCs—evolving separately but driving viral evolution collectively—may strike a balance between quickly finding an effective solution against conserved antigens and maintaining clonal diversity to fend off faster mutating pathogens.

Our approach employs an extended shape-space depiction of flexible molecular recognition. Different from classic models, our shape-space dimensions represent residue groups constituting the viral epitope; this representation abstracts away atomic details while retaining features that emphasize the biomolecular basis of host-pathogen interactions: First, receptors engage Ags in binding subspaces (actual contacts) but evolve in the full space (potential binding surface). Second, speed of adaptation varies among phenotypic dimensions, reflecting distinct accessibility and mutability of different parts of the epitope. Apart from inheriting desired properties of the Fisher’s geometric model (Tenaillon, 2014), including epistasis and drift load, our coevolution model incorporates moving fitness optima (mutating Ag targets) and hence a dynamic distribution of mutation effect for a given receptor. In addition, the “corralling” geometry with founder B cells enclosing viral Ags captures a slowing bnAb evolution amid sustained viral evolution (Sheng et al., 2016), as well as viral rebound kinetics (Moore et al., 2009; Bailey et al., 2017).

This framework broadly applies to coevolutionary processes in which binding affinity constitutes a physical phenotype and evolution proceeds on similar timescales as ecological dynamics—an under-explored regime of eco-evolutionary dynamics. Our results offer a number of vaccine lessons: (1a) Create a diversity background early on such that lineages of different origins can succeed at various stages toward highly adapted states. (1b) Maintain a search space larger than the exact target, to encourage potentiating variations that may appear neutral but can confer future advantage. In practice, these principles recommend presentation of vaccine constructs with peripheral variable residues, in addition to the conserved core of the target epitope. (2) Supply Ags at a modest yet sustained level, because strong stimulation and rapid Ag consumption hasten AM and yield predominantly low-quality B cells (Cirelli et al., 2019). (3) Apply time-dependent selection pressure that first allows access to diverse ancestors and paths and later filters out inferior lineages, keeping only those capable of sustained adaptation under increasingly more severe selection; dynamic protocols can potentially shorten paths to desired outcomes (Wang and Dai, 2019; Sachdeva et al., 2020).

Limitations of the study

Immunization experiments indicate that memory B cells can be activated by antigen, reenter GCs, and go through further AM (Schwickert et al., 2007; Dogan et al., 2009; McHeyzer-Williams et al., 2015). Such memory reentry behavior has also been speculated for chronic infections (Mesin et al., 2016; Victora and Mouquet, 2018). Of particular interest is how memory reentry impacts GC dynamics and maturation outcome. Extending our model (see supplemental information for details), we find that reactivated memory cells, either by joining ongoing GCs (Figure S14) or by seeding new ones (Figure S15), can facilitate the development of broad antibodies and, in turn, reduce the likelihood and amplitude of viral rebound and accelerate viral clearance.

In the meantime, IgM antibodies, secreted by short-lived plasma cells and not subject to GC reactions, take part in Ag removal before IgG antibodies emerge from AM. We show that an addition of IgM antibodies not only enhances Ag removal toward the viral population bottleneck, but it also aids in corralling escape mutants during rebound (Figure S16); both lead to a higher chance of viral clearance in regimes with mixed outcomes. In addition to B cells, T cells and innate immune cells likely play a role in clearing viruses. Their influence is partially reflected in the initial Ag distribution: Founder viruses are driven to diversify by other immune pressures before B cell response comes into play. However, not enough knowledge is yet available for modeling the full dynamics including T cell and innate responses, which may well interact with B cell dynamics in complex ways.

Our model leaves out a number of biological factors of realism, including Ag transport and recycling, cell migration within and between GCs, immune exhaustion and latent viral reservoir, whose effects deserve focused future studies. Our model assumes optimal regulation of binding, sharp selection in T-help competition, and perfect conservation of core residues; relaxing these assumptions could improve biological precision though is unlikely to alter qualitative conclusions.

This work provides a caricature of viral-immune coevolution that highlights how physical and ecological dynamics interplay to drive non-intuitive system-level behaviors. We hope that it serves as a starting point for studying rapid eco-evolutionary dynamics, mediated by biomolecular interactions, with feedback across scales.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Code for antibody-antigen coevolution model	This paper	https://gist.github.com/JamesShengGH/67ac134d3f631f4f7cf0fe660d0ff763
Software and algorithms
MATLAB R2019a	MathWorks®	https://www.mathworks.com/

Resource availability

Lead contact

Further information and requests should be directed to and will be fulfilled by the lead contact, Shenshen Wang (shenshen@physics.ucla.edu).

Materials availability

This study did not generate new unique reagents.

Data and code availability

The code of our coevolution model can be accessed from GitHub at https://gist.github.com/JamesShengGH/67ac134d3f631f4f7cf0fe660d0ff763.

Method details

Mutation of B cell receptor and antigen

Upon each single mutation in a BCR, one coordinate is chosen from n dimensions uniformly at random ($k\in \left\{\mathrm{1,2},\cdots ,n\right\}$) and changed by an amount that follows a zero-mean Gaussian distribution

$$x_k\to x_k+\delta x_k;\delta x_k\sim \mathcal{N}\left(0,{\text{Δ}}_{B,k}^2\right).$$ (Equation 5)

For a mutation in an Ag, one coordinate randomly chosen from n_v variable dimensions ($k\in \left\{\mathrm{1,2},\cdots ,n_v\right\}$) is altered according to

$$y_k\to y_k+\delta y_k;\delta y_k\sim \mathcal{N}\left(0,{\text{Δ}}_{Ag}^2\right).$$ (Equation 6)

Here the width of the Gaussian distributions characterizes the average magnitude of change in the trait value caused by a mutation. This mutation step size differs between dimensions; specifically, ${\text{Δ}}_{B,k\ge n_v+1}<{\text{Δ}}_{B,k\le n_v}={\text{Δ}}_{Ag}$, i.e., on average, mutations in the conserved/slow dimensions ($k\ge n_v+1$) have smaller effect than those in the variable dimensions ($k\le n_v$), reflecting a lower accessibility of the conserved core than surrounding variable elements in the target epitope (Julien et al., 2013; Wyatt and Sodroski, 1998).

Simulating coevolution

Step 0: Initialization

• (i)Generation of germline B cells

We assume that each of the germline B cells, upon activation by the founder virus (at the shape-space origin), binds to its target antigen on the founder virus (an optimal binding subspace labeled by $l^{\text{∗}}$) with an equal affinity $A_{l^{\text{∗}}}=0$ (i.e., meeting the activation threshold). According to Equation 1, each germline B cell generated in this way resides on a founder hypersphere of dimension n_b and radius $R_f=\sqrt{n_b{A}_{max}}$ in its optimal binding subspace; A_maxdenotes the maximum affinity at perfect match. Collectively, germline B cells enclose initial antigens (see (iii) for their generation), as illustrated in Figure 1B. In SI, we consider germline B cells with a range of affinities for the founder virus, and show that the qualitative results remain while the likelihood of viral clearance increases in place of viral rebound (Figure S17).

By definition, in any binding subspace other than the optimal one ($l^{\prime }\ne l^{\text{∗}}$), local binding affinity $A_{l^{\prime }}$ would be no greater than zero. Thus, we draw B-cell coordinates outside each cell’s respective optimal subspace (i.e., outside the binding footprint) so that $-A_{l^{\prime }}$ follows an exponential distribution with meanλ=2, mimicking declining probabilities radially outward from the founder hypersphere. In SI, we vary the value of λ and find that increasing λ impedes the development of both narrow and broad antibody responses and slows viral clearance (Figure S18), since footprint shift becomes less likely to yield an affinity gain or buffer an affinity loss.

• (ii)GC compartmentalization

Distribute 5000 germline B cells thus generated randomly and evenly among a total number of N_GC germinal centers, where they replicate without mutation until reaching the overall capacity K_b=10⁶.

• (iii)Generation of initial antigens

Ags begin to diversify ever since the founder virus is transmitted. By the time first responsive B cells become activated, a cloud of variant Ags surrounding the infecting strain is developed. To model different levels of Ag diversity at the beginning of GC reactions, Ag coordinates in the variable dimensions are drawn from a Gaussian distribution centered at the origin with a width σ_A. Ag population starts at the capacity K_a=10⁵.

Step 1: Population dynamics of GC B cells

• (i)Ag presentation in GCs: Ags are transported from circulation into each GC and presented on FDCs, providing stimuli for B cell affinity maturation. In total K_a,GC=10⁵ Ags are distributed evenly among GCs. In each GC cycle, FDC Ags are updated with a random subset of current plasma Ags.
• (ii)Ag binding and internalization: In each GC cycle, a B cell randomly encounters 100 FDC Ags and internalizes them with a probability given by Equation 3. Note that different B cells may encounter different sets of FDC Ags. The time-dependent Ag concentration is given by

$$C_{Ag}\left(t\right)=C_{Ag,0}\frac{N_{Ag}\left(t\right)}{K_a},$$ (Equation 7)

where N_Ag(t) represents the Ag population size at cycle t and K_a=10⁵ the Ag carrying capacity.

• (iii)Competition for limited T cell help: Rank surviving B cells in each GC by their affinity averaged over encountered FDC Ags, and keep the top fraction $f_{Tfh}$ while removing the rest that fail to receive T cell signal and apoptose.
• (iv)Memory differentiation: A fraction p_mem=5% of the remaining B cells differentiate into memory cells and leave GC.
• (v)Plasma cell differentiation: Among the remaining B cells whose average affinity is above a threshold A_pla=4k_BT, a fraction p_pla=5% differentiate into plasma cells and leave GC.
• (vi)B cell replication and mutation: Each remaining B cell divides into two daughter cells that independently mutate with a probability μ=0.5. If a mutation occurs, there is a chance of p_let=0.3 that it is lethal and the daughter B cell is removed from GC. With a probability of p_sil=0.5, the mutation is silent and the daughter cell retains the shape-space coordinates of the parent cell. Otherwise the mutation alters affinity (Shlomchik et al., 1998; Shannon and Mehr, 1999; Zhang and Shakhnovich, 2010; Wang et al., 2015; Shaffer et al., 2016); one of the shape-space coordinates will change according to Equation5.
• (vii)GC reseeding: A GC ends when it either perishes or exceeds the initial population size K_b/N_GC (Wang et al., 2015; Shaffer et al., 2016). A new GC is seeded in the next cycle; reseeding includes generation and replication of germline B cells as well as sampling of FDC Ags. This step ensures a constant number of ongoing GCs.

Step 2: Accumulation of plasma and memory cells

We treat both memory and plasma cells as antibody-secreting cells that accumulate in the plasma compartment and drive viral evolution, without explicitly accounting for differentiation of memory cells into plasma cells upon Ag activation. In SI, we study the influence of GC reentry or reseeding by activated memory cells and the effect of IgM antibodies secreted by short-lived plasma cells. It has been reported that humans can maintain circulating memory B cells for many decades after first exposure (Yu et al., 2008). Hence, we ignore the intrinsic decay of antibody-secreting cells; instead, cells in excess of a carrying capacity K_p=10⁶ of the plasma compartment are randomly picked and removed.

Step 3: Population dynamics of antigens

• (i)Neutralization: In every GC cycle, each Ag encounters antibodies secreted by 100 randomly chosen antibody-secreting cells. An Ag is neutralized and removed from the simulation according to the probability given by Equation 4. Different Ags may encounter antibodies produced by different subsets of antibody-secreting cells, which exhibit a time-dependent concentration

$$C_{pla}\left(t\right)=C_{pla,0}\frac{N_{pla}\left(t\right)}{K_p},$$ (Equation 8)

where N_pla(t) denotes the population size of plasma and memory cells combined at cycle t, and K_p is the carrying capacity of these antibody-secreting cells.

• (ii)Replication and mutation: Once every two GC cycles, surviving Ags replicate; during replication, they mutate at a rate of $0.01\text{∗}\left(2\text{∗}{n}_v/n\right)$/virion/generation, so that when n_v=n/2, it matches the observed rate (Luo and Perelson, 2015). Upon mutation, the shape-space coordinates of Ags are altered according to Equation6.
• (iii)Carrying capacity: Excess Ags beyond the capacity K_a are randomly chosen and removed.

Step 4: Iteration

Repeat steps 1–3 until (a) Ag population falls below an extinction threshold K_low=100, or (b) a maximum duration of T_max=200 GC reaction cycles is reached.

Parameter choice

The parameters used in the simulation are given in Table S1.

Dimensionality of binding subspace

There potentially is strong variability in what portion of the antigen-binding region of a B cell receptor (BCR) determines its footprint on an antigen (Ag). When choosing the dimensionality n_b of the binding subspace, we took a structural study (Sethi et al., 2006) as a reference, where binding configurations of a germline antibody with diverse epitopes on multiple peptides were reported. Out of 26 antibody residues involved in binding with these peptides, on average only 11 residues determine the footprint. This led us to a choice with a similar proportion, i.e. n_b/n∼11/26, or n_b=3 given n=8.

Energy scale and mutation step size

Since the absolute value of the expected affinity of a naive repertoire varies among pathogens and among epitopes of the same pathogen, we choose to set the affinity of germline B cells for its target antigen to be at the activation threshold (set as zero affinity) so affinity maturation can initiate. Like in (Shaffer et al., 2016), we choose the maximum affinity A_max to be 8k_BT, so that the equilibrium constant exp(A/k_BT) for binding to the founder virus increases by roughly 3000-fold through affinity maturation. The mutation step size Δ is chosen such that a single mutation can typically change the BCR-Ag binding affinity by 1–2 k_BT.

Antigen population size

We set Ag carrying capacity to 10⁵, which is large enough to capture the variety of viral load kinetics in vivo (Coffin and Swanstrom, 2013) while being computationally efficient. With a proper choice of the concentration coefficients C_Pla,0 and C_Ag,0, observed viral-load variations up to three orders of magnitude were reproduced in simulations.

Distribution of mutation effect without footprint shift

Below we derive the theoretical distribution of mutation effect in the main text (Figure 2, black curve). We consider the change in binding affinity between germline B cells and the founder virus at the shape-space origin, due to a single affinity-altering mutation. Each germline B cell targets the founder virus in one of the n−n_b+1 possible binding subspaces. Cells targeting the same subspace are uniformly distributed on the surface of a n_b-dimensional hypersphere centered at the origin in that subspace, with a radius $R_f=\sqrt{n_b{A}_{max}}$. We set n=8, n_b=3, and A_max=8, so R_f≈4.9.

Each affinity-altering mutation changes the shape-space coordinate in one randomly chosen dimension k. Mutation step size δx_k follows a centered Gaussian distribution, $\delta x_k\sim \mathcal{N}\left(0,{\text{Δ}}_{B,k}^2\right)$, where Δ_B,k=2 for mutations in variable dimensions (k=1,2,3,…,n_v), and Δ_B,k=1 for those in conserved dimensions (k=n_v+1,…,n).

Without footprint shift, mutations outside a germline B cell’s target binding subspace has no effect on affinity (i.e., ΔA=0). A mutation in the target binding subspace, which occurs with probability n_b/n, will change the cell’s coordinate x_k in dimension k. The resulting change in affinity can be calculated based on Equation 1 in the main text

$$\text{Δ}A\left(x_k,\delta x_k\right)=-\frac{{\left(x_k+\delta x_k\right)}^2-x_k^2}{n_b}$$ (Equation 9)

$$=-\frac{2x_k\cdot \delta x_k+{\left(\delta x_k\right)}^2}{n_b}$$

One can express $x_k$ in terms of ΔA and δx_k, i.e., $x_k\left(\text{Δ}A,\delta x_k\right)=-\frac{n_b\text{Δ}A}{2\delta x_k}-\frac{\delta x_k}{2}$.

The probability density of affinity change P(ΔA) can be written in general as follows:

$$P\left(\text{Δ}A\right)=\frac{n_b}{n}{\int }_{-\infty }^{\infty }g\left(\delta x_k\right)h_X\left[x_k\left(\text{Δ}A,\delta x_k\right)\right]\text{d}\delta x_k$$ (Equation 10)

Here, the prefactor ensures that only mutations in the target subspace are considered, $g\left(\delta x_k\right)=\frac{1}{\sqrt{2\pi }{\text{Δ}}_{B,k}}\text{exp}\left(-\frac{\delta x_k^2}{2{\text{Δ}}_{B,k}^2}\right)$ is the Gaussian distribution of mutation step size, and h_X(x_k) is the probability density function of the coordinates of unmutated germline B cells.

To derive h_X(x_k), we consider a spherical coordinate system in the 3-dimensional binding subspace and let the polar axis be along the dimension k in which the mutation takes place. Denoting by θ the polar angle of a germline B cell’s coordinates before mutation, we have $x_k=R_f\text{cos}\theta$. Since germline B cells targeting this subspace are uniformly distributed on the founder hypersphere, we have

$$\text{Pr}(\theta <\text{Θ}<\theta +\text{d}\theta )=\frac{{\int }_0^{2\pi }\text{sin}\theta \text{d}\theta \text{d}\varphi }{4\pi }=\frac{\text{sin}\theta \text{d}\theta }{2}$$ (Equation 11)

which is normalized for $\theta \in [0,\pi ]$. The probability density $h_X\left(x_k\right)$ for $x_k\in [-R_f,R_f]$ thus reads

$$h_X\left(x_k\right)=\text{Pr}(\theta <\text{Θ}<\theta +\text{d}\theta )/\left|d{x}_k\right|$$ (Equation 12)

$$=\frac{\text{sin}\theta }{2}{\left(R_f\text{sin}\theta \right)}^{-1}$$

$$=\frac{1}{2R_f}$$

That is, germline coordinates are uniformly distributed on the interval $x_k\in [-R_f,R_f]$ and vanish outside this range, since germline B cells are right on the surface of the founder hypersphere.

Substituting the expressions of $g\left(\delta x_k\right)$ and $h_X\left(x_k\right)$ into Equation10, we arrive at

$$P\left(\text{Δ}A\right)=\frac{n_b}{2R_{f}n\sqrt{2\pi }{\text{Δ}}_{B,k}}{\int }_{-\infty }^{\infty }\text{exp}\left(-\frac{\delta x_k^2}{2{\text{Δ}}_{B,k}^2}\right)I\left(-R_f\le -\frac{n_b\text{Δ}A}{2\delta x_k}-\frac{\delta x_k}{2}\le R_f\right)\text{d}\delta x_k$$ (Equation 13)

Here, $I\left(Y\right)$ is the indicator function that takes value 1 if the condition Y is satisfied and takes value 0 otherwise.

Dependence of germline B cell affinity on initial antigen diversity

Below we show that the average binding affinity of germline B cells to initial antigens increases with antigen diversity, σ_A, and the number of variable dimensions, n_v. Considering Langmuir binding isotherm, we calculate the “log-mean-exponential” affinity between a founder B cell $\overrightarrow{x}$ and initial antigens {$\overrightarrow{y}$}, i.e., $\text{ln}\langle \text{exp}\left[A\left(\overrightarrow{x},\overrightarrow{y}\right)\right]{\rangle }_{\left\{\overrightarrow{y}\right\}}$.

From Equation 2 in the main text, we have

$$\langle \text{exp}\left[A\left(\overrightarrow{x},\overrightarrow{y}\right)\right]{\rangle }_{\left\{\overrightarrow{y}\right\}}=\text{exp}\left(A_{max}\right)\langle \text{exp}[-{\sum }_{k=l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{y}\right)}^{l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{y}\right)+n_b-1}\frac{{\left(x_k-y_k\right)}^2}{n_b}]{\rangle }_{\left\{\overrightarrow{y}\right\}}$$ (Equation 14)

$$=\text{exp}\left(A_{max}\right)\langle {\prod }_{k=l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{y}\right)}^{l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{y}\right)+n_b-1}\text{exp}[-\frac{{\left(x_k-y_k\right)}^2}{n_b}]{\rangle }_{\left\{\overrightarrow{y}\right\}},$$

where$l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{y}\right)$ denotes the starting dimension of the optimal binding subspace between a germline B cell $\overrightarrow{x}$ and an antigen $\overrightarrow{y}$. When initial antigen diversity is moderate, we can assume that the optimal subspaces (binding footprints) of germline B cells for diverse initial antigens are the same as those for the founder virus at the origin, i.e., $l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{y}\right)=l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{0}\right)$ for all $\overrightarrow{y}$. Note this is only exact when ${\sigma }_A=0$ and yields an affinity no greater than the actual value by imposing a non-optimal binding subspace for finite ${\sigma }_A$.

As described in the STAR Methods section in the main text, the probability distribution $g\left(y_k\right)$ of the Ag coordinate in any variable dimension is Gaussian and becomes a Dirac delta function in conserved dimensions. Thus, we can write $g\left(y_k\right)=\frac{1}{\sqrt{2\pi }{\sigma }_k}\text{exp}\left(-\frac{y_k^2}{2{\sigma }_k^2}\right)$, where ${\sigma }_k={\sigma }_A$, if $1\le k\le n_v$; ${\sigma }_k\to 0$, if $n_v+1\le k\le n$.

Equation14 now becomes

$$\langle \text{exp}\left[A\left(\overrightarrow{x},\overrightarrow{y}\right)\right]{\rangle }_{\left\{\overrightarrow{y}\right\}}\approx \text{exp}\left(A_{max}\right)\langle {\prod }_{k=l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{0}\right)}^{l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{0}\right)+n_b-1}\text{exp}[-\frac{{\left(x_k-y_k\right)}^2}{n_b}]{\rangle }_{\left\{\overrightarrow{y}\right\}}$$ (Equation 15)

$$=\text{exp}\left(A_{max}\right){\prod }_{k=l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{0}\right)}^{l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{0}\right)+n_b-1}{\int }_{-\infty }^{\infty }\text{exp}[-\frac{{\left(x_k-y_k\right)}^2}{n_b}]g\left(y_k\right)d{y}_k$$

$$=\text{exp}\left(A_{max}\right)\text{exp}[-{\sum }_{k=l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{0}\right)}^{l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{0}\right)+n_b-1}\frac{x_k^2}{2{\sigma }_k^2+n_b}]{\prod }_{k=l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{0}\right)}^{l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{0}\right)+n_b-1}\frac{1}{\sqrt{1+\frac{2{\sigma }_k^2}{n_b}}}$$

Since all germline B cells have equal affinity against the founder virus, it follows that

$$A\left(\overrightarrow{x},\overrightarrow{0}\right)=A_{max}-{\sum }_{k=l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{0}\right)}^{l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{0}\right)+n_b-1}\frac{x_k^2}{n_b}\equiv 0$$ (Equation 16)

Hence,

$${\sum }_{k=l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{y}\right)}^{l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{y}\right)+n_b-1}{x}_k^2\simeq n_b{A}_{max}$$ (Equation 17)

for any initial antigen $\overrightarrow{y}$.

Considering target subspaces (binding footprints) being fully conserved or fully variable, i.e. ${\sigma }_k=0$ or ${\sigma }_k={\sigma }_A$ for all k (mixed subspace yielding a value bounded by these limits), the log-mean-exponential affinity from Equation15 becomes

$$\text{ln}\langle \text{exp}\left[A\left(\overrightarrow{x},\overrightarrow{y}\right)\right]{\rangle }_{\left\{\overrightarrow{y}\right\}}=A_{max}-{\sum }_{k=l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{0}\right)}^{l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{0}\right)+n_b-1}[\frac{x_k^2}{2{\sigma }_k^2+n_b}+\frac{1}{2}\text{ln}\left(1+\frac{2{\sigma }_k^2}{n_b}\right)]$$ (Equation 18)

$$=A_{max}-[\frac{A_{max}}{1+\frac{2{\sigma }_k^2}{n_b}}+\frac{n_b}{2}\text{ln}\left(1+\frac{2{\sigma }_k^2}{n_b}\right)]$$

where we have used Eq.17. Note there is no explicit dependence on $\overrightarrow{x}$, because both the germline B cells and initial antigens are isotropic in a fully conserved or fully variable subspace.

When ${\sigma }_k={\sigma }_A>0$, it follows from Eq.18

$$\frac{\text{d}}{\text{d}{\sigma }_A}[\text{ln}\langle \text{exp}[A\left(\overrightarrow{x},\overrightarrow{y}\right)\left]{\rangle }_{\left\{\overrightarrow{x},\overrightarrow{y}\right\}}\right]=4{\sigma }_A[\frac{n_b{A}_{max}}{{\left(2{\sigma }_A^2+n_b\right)}^2}-\frac{n_b}{2}\frac{1}{2{\sigma }_A^2+n_b}]$$ (Equation 19)

$$=\frac{4{\sigma }_A{n}_b}{{\left(2{\sigma }_A^2+n_b\right)}^2}[A_{max}-\frac{1}{2}(2{\sigma }_A^2+n_b)]>0$$

as long as ${\sigma }_A<\sqrt{A_{max}-n_b/2}$, which holds for the parameters used in our simulations, A_max=8, n_b=3, and σ_A≤2. That is, the log-mean-exponential affinity between germline B cells and initial antigens indeed increase with increasing σ_A. In addition, since σ_k ≡ 0 in conserved dimensions, germline B cells targeting variable subspaces have a higher binding affinity than those targeting conserved subspaces if σ_A>0. Thus, increasing the number of variable dimensions, n_v, will increase the fraction of the former and, in turn, lead to higher overall affinity of the germline population.

It is worth pointing out that the result that average initial BCR-Ag affinity increases with σ_A reflects a simple geometric fact: As the the distribution widens around the shape-space origin, they are getting closer to the enclosing B cell founder hypersphere from inside (though remaining within the enclosure). Such geometric fact does not require the affinity function to be quadratic in shape-space distances. A more general definition of affinity reads

$$A_l\left(\overrightarrow{x},\overrightarrow{y}\right)\equiv A_{max}-\frac{1}{n_b}{\sum }_{k=l}^{l+n_b-1}|x_k-y_k{|}^q$$ (Equation 20)

It follows that Eq.15 now becomes

$$\langle \text{exp}\left[A\left(\overrightarrow{x},\overrightarrow{y}\right)\right]{\rangle }_{\left\{\overrightarrow{y}\right\}}\approx \text{exp}\left(A_{max}\right){\prod }_{k=l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{0}\right)}^{l^{\text{∗}}\left(\overrightarrow{x},\overrightarrow{0}\right)+n_b-1}{\int }_{-\infty }^{\infty }\text{exp}\left[-\frac{|x_k-y_k{|}^q}{n_b}\right]g\left(y_k\right)d{y}_k$$ (Equation 21)

Results for q=1,2,3 are shown in Figure S1.

Effective plasma-antigen binding probability

To characterize the overall efficacy of B cell response in viral suppression, we define an effective plasma-antigen binding probability, P_eff(t_i,t_f), on the time interval [t_i,t_f]. Specifically, P_eff(t_i,t_f) determines the total fold change in antigen population size, N_Ag, between t_i and t_f:

$$N_{Ag}\left(t_f\right)=N_{Ag}\left(t_i\right)\text{∗}{\left(1-P_{\text{eff}}\right)}^{t_f-t_i}\text{∗}{2}^{\frac{t_f-t_i]}{2}}$$ (Equation 22)

Here, 1−P_eff indicates the effective probability of Ag survival in one cycle, and $2^{\frac{t_f-t_i}{2}}$ accounts for Ag replication once every other cycle (assuming first replication occurs at t_i).

The actual dynamics is described by

$$N_{Ag}\left(t_f\right)=N_{Ag}\left(t_i\right)\text{∗}\prod _{t=t_i}^{t_f-1}[1-\langle P_V\left(\overrightarrow{y},t\right){\rangle }_{\overrightarrow{y}}]\text{∗}{2}^{\frac{t_f-t_i}{2}}$$ (Equation 23)

where$P_V\left(\overrightarrow{y},t\right)$ is the probability that Ag $\overrightarrow{y}$ will be neutralized by plasma BCR and $\langle \cdot {\rangle }_{\overrightarrow{y}}$ indicates an average over all Ags present at cycle t. Equating Eq.22 and Eq.23 leads to

$$P_{\text{eff}}\left(t_i,t_f\right)=1-{\left\{\prod _{t=t_i}^{t_f-1}\left[1-\langle P_V\left(\overrightarrow{y},t\right){\rangle }_{\overrightarrow{y}}\right]\right\}}^{\frac{1}{t_f-t_i}}$$ (Equation 24)

Therefore, a larger P_eff(t_i,t_f) indicates a higher efficiency of antigen removal in a given time span [t_i,t_f].

Availability of beneficial BCR mutations in slow (conserved) and fast (variable) dimensions

Figure S7presents the distribution of mutation effect in fast (variable) and slow (conserved) dimensions, for lineages with a B-type ancestor that survive until Ag clearance (like in Figure 8). Mutation effect $\text{Δ}A$ is measured by mutation-induced changes in log-mean-exponential affinity of a B cell to encountered FDC Ags, i.e.,

$$\text{Δ}A=\text{log}\langle \text{exp}\left[A\left({\overrightarrow{x}}^{\text{′}},\overrightarrow{y}\right)\right]\rangle -\text{log}\langle \text{exp}\left[A\left(\overrightarrow{x},\overrightarrow{y}\right)\right]\rangle$$ (Equation 25)

Here $\overrightarrow{x}$ and ${\overrightarrow{x}}^{\text{′}}$ are shape-space coordinates of a B cell before and after mutation, respectively; $\langle \cdot \rangle$ denotes an average over FDC Ags {$\overrightarrow{y}$} that B cell $\overrightarrow{x}$ encounters prior to mutation. In the case without footprint shift (yellow, “No FS”), binding footprints between B cells and FDC Ags remain unchanged after mutation.

As seen in Figure S7, at earlier times, affinity improvement is larger for mutations in fast dimensions, because of a larger mutation step size ${\text{Δ}}_{B,v}$. Affinity improvement is further enhanced by footprint shift (blue compared to yellow). These factors, combined with the fact that initial BCR-Ag binding is stronger in fast dimensions when σ_A>0, drive B→N switch for higher affinity. However, beneficial mutations in slow dimensions remain available, while those in fast dimensions are quickly depleted, partly because Ags can escape BCR recognition in fast dimensions, but not in slow dimensions. This allows B cells to continuously improve affinity through mutations in conserved dimensions and, in turn, drives N→B switch in surviving lineages. Taken together, a B→N→B pathway toward breadth develops.

Memory reentry into GCs promotes bnAb development and enhances viral clearance

Experiment has suggested that memory B cells can be activated by antigen, reenter GCs, and go through further affinity maturation. In particular, memory cells can either join ongoing GC reactions, or seed new GCs as founders. Since the exact conditions of memory activation and GC reentry are not well understood, we study both scenarios. In both cases, our model predicts that memory reentry promotes the development of broad antibody response and, in turn, reduces the likelihood and amplitude of viral rebound and accelerates viral clearance.

Memory cells reenter ongoing GCs

At each GC reaction cycle, a memory cell $\overrightarrow{x}$ in the plasma has the following probability to be activated and join a randomly picked ongoing GC:

$$P_M\left(\overrightarrow{x},t\right)=\frac{C_{Ag}\left(t\right){\sum }_{\overrightarrow{y}\in \mathcal{Y}}{e}^{A\left(\overrightarrow{x},\overrightarrow{y}\right)}}{1+C_{Ag}\left(t\right){\sum }_{\overrightarrow{y}\in \mathcal{Y}}{e}^{A\left(\overrightarrow{x},\overrightarrow{y}\right)}}\cdot \alpha$$ (Equation 26)

Here, the Langmuir isotherm determines the probability that the memory cell becomes activated by a random subset $\mathcal{Y}$ of plasma Ag it encounters during cycle t. The constant $\alpha \in \left[\mathrm{0,1}\right]$ denotes the fraction of activated memory cells that reenter an ongoing GC. The actual value of α is unknown, and we examine the extreme case of strong memory reentry ($\alpha =1$) that sets an upper bound of the effect in our extended model.

With reactivated memory cells joining ongoing GCs, a notable change in the coevolutionary outcome is that viral rebound turns into clearance, if the Ag epitope is sufficiently conserved for bnAbs to develop, i.e. n_c≥n_b (Figure S14A versus Figure 3A; see Figure S14 B for clearance time and Figure S14Cfor viral load trajectories). While the total number of antigen-removing cells in the plasma falls due to memory reentry (Figure S14D), the overall quality of the plasma rises since memory cells are of lower affinity than plasma cells (Figure S14E).

On the one hand, the neutralization efficacy of narrow lineages (P_N) is lower (Figure S14F, dashed lines), due primarily to the reduced size of the plasma pool (despite an increase in their average binding affinity due to removal of memory cells; Figure S14E). On the other hand, broad lineages that arise following viral escape gain in binding potency (P_B) compared to without memory reentry (Figure S14F, solid lines, $t\gtrsim 20$). This is because as memory cells reenter GCs and go through further affinity maturation, both the quality and abundance of broad clones increase in the plasma pool. As a result, rapid clearance without rebound becomes more likely (Figures S14B and S14C).

Memory cells seed new GCs

Once a GC collapses and vacates the follicle, a new one can be seeded therein. Assume a fraction β of the founders are memory cells randomly drawn from the plasma pool and the rest are germline B cells.

The effect of memory reseeding is most pronounced and interesting when (1) Ag population goes through a bottleneck so GC reseeding will occur, and (2) n_c≥n_b so broad antibody response can develop (P_B > 0). As the memory-founder fraction β increases from zero (fully naive reseeding) to one (fully memory reseeding), the proportion of trajectories exhibiting monotonic clearance without rebound increases from 20% to 100% when n_c=4 and σ_A=2; the proportion increases from 40% to 100% when n_c=3 and σ_A=1.5. No monotonic clearance is observed when and σ_A=2, even with memory reseeding.

As we show in Figure S15, a larger fraction of memory founders (larger β) leads to an increasing likelihood that viral load remains below 10%of the initial level following the bottleneck (panel A), since broad antibody response evolves faster during the bottleneck (panel C) and more effectively suppresses or even prevents viral resurgence. This is intuitively expected: Since memory cells have gone through earlier rounds of affinity maturation, on average, newly seeded GCs begin with a larger breadth than if starting anew from germline founders. Consequently, virus populations get cleared within a shorter time (panel B). Note that a higher level of naive reseeding (smaller β) results in a greater variability of clearance time (panel B).

IgM antibodies aid in virus removal prior to population bottleneck and following escape

Apart from GC B cells, another antigen-consuming agent is IgM antibodies; they are secreted by short-lived plasma cells that do not go through affinity maturation. These low-affinity IgM antibodies may remove viruses before IgG antibodies are produced by GC reactions.

To study their influence on coevolutionary dynamics and outcomes, we introduce 10⁵ IgM plasma cells (10% of plasma capacity), whose shape-space coordinates were generated the same way as germline B cells, before GC reactions start. We find that the addition of non-evolving IgM antibodies leads to a higher fraction of monotonic viral clearance against rebound in regimes of mixed outcomes (Figures S16A and S16B). This is achieved in two ways. First, with IgM antibodies, the overall efficacy of specific antibodies (P_N) increases initially (Figure S16D), driving a faster decline in viral load (Figure S16C). Second, the drop in P_N following viral escape is reduced (Figure S16D); unlike IgG antibodies that are drawn to the founder viruses (via a self-generated antigen gradient in shape space), IgM antibodies remain in the corralling configuration and, consequently, can intercept escape mutants.

The neutralization efficacy of broad lineages (P_B) slightly decreases in the presence of IgM antibodies (Figure S16D), since the latter effectively dilute broad plasma cells, making it less likely that viruses encounter broad antibodies in the plasma. Nonetheless, the overall effectiveness of narrow and broad responses combined is enhanced both before and during viral bottleneck, thereby promoting viral clearance.

Alternative positioning of germline B cells

So far we have assumed that all germline B cells have the same binding affinity for the founder virus—against the optimal antigen target. For any non-optimal binding target, the initial BCR-Ag binding affinity is lower and the amplitude of deviation is assumed to follow an exponential distribution with mean λ (see STAR Methods→Simulating coevolution→Step 0). Below we show that qualitative results of coevolutionary dynamics and outcomes remain valid for alternative assumptions for germline B cell affinity (Figures S17 and S18). In particular, we allow a range of founder affinities and vary the germline potency against non-optimal binding targets. We find that both changes only quantitatively modify the likelihood and speed of viral clearance.

Differential germline affinities

To allow a range of affinities of germline B cells for the founder virus, we performed simulations in which founder B cells {$\overrightarrow{x}$} assume Gaussian-distributed affinities {$\text{Δ}A\left(\overrightarrow{x}\right)$}, with $\text{Δ}A\left(\overrightarrow{x}\right)\sim \mathcal{N}\left(\mathrm{0,1}\right)$ sampled independently for each cell $\overrightarrow{x}$. Accordingly, the fixed radius of the founder hypersphere, $R_f=\sqrt{n_b{A}_{max}}$, is now replaced by a cell-specific value $R_f\left(\overrightarrow{x}\right)=\sqrt{n_b\left(A_{max}-\text{Δ}A\left(\overrightarrow{x}\right)\right)}$.

With differential founder affinities, coevolutionary outcomes remain unchanged qualitatively (Figure S17A vs Figure 3A), yet the proportion of monotonic viral clearance against rebound is elevated. Because the most potent clones, now of higher affinity than in the case of identical germline affinity, are preferentially expanded by selection, both narrow and broad clones reach higher efficacy in removing viruses more rapidly (Figure S17D). As a result, the success rate of monotonic clearance is enhanced (Figures S17A and S17B) and the mean time to viral extinction shortened (Figures S17B and S17C).

Varying germline potency against non-optimal binding sites

Next, we vary the affinity of germline B cells against the founder virus at non-optimal binding sites (i.e. in non-optimal binding subspaces) by varying λ. As λ increases, lower affinity for the non-optimal targets makes it less likely that footprint shift can buffer deleterious mutations within the contact or catch beneficial mutations outside. Consequently, not only that narrow response becomes less effective (Figure S18B, dashed line), but the efficacy of subsequent broad response rises more slowly (Figure S18B, solid line). Therefore, bnAb development via footprint shift weakens and viral clearance by bnAbs slows (Figure S18A).

Published: August 20, 2021