Evaluating IMRT and VMAT dose accuracy: Practical examples of failure to detect systematic errors when applying a commonly used metric and action levels

Abstract

Purpose:

This study (1) examines a variety of real-world cases where systematic errors were not detected by widely accepted methods for IMRT/VMAT dosimetric accuracy evaluation, and (2) drills-down to identify failure modes and their corresponding means for detection, diagnosis, and mitigation. The primary goal of detailing these case studies is to explore different, more sensitive methods and metrics that could be used more effectively for evaluating accuracy of dose algorithms, delivery systems, and QA devices.

Methods:

The authors present seven real-world case studies representing a variety of combinations of the treatment planning system (TPS), linac, delivery modality, and systematic error type. These case studies are typical to what might be used as part of an IMRT or VMAT commissioning test suite, varying in complexity. Each case study is analyzed according to TG-119 instructions for gamma passing rates and action levels for per-beam and/or composite plan dosimetric QA. Then, each case study is analyzed in-depth with advanced diagnostic methods (dose profile examination, EPID-based measurements, dose difference pattern analysis, 3D measurement-guided dose reconstruction, and dose grid inspection) and more sensitive metrics (2% local normalization/2 mm DTA and estimated DVH comparisons).

Results:

For these case studies, the conventional 3%/3 mm gamma passing rates exceeded 99% for IMRT per-beam analyses and ranged from 93.9% to 100% for composite plan dose analysis, well above the TG-119 action levels of 90% and 88%, respectively. However, all cases had systematic errors that were detected only by using advanced diagnostic techniques and more sensitive metrics. The systematic errors caused variable but noteworthy impact, including estimated target dose coverage loss of up to 5.5% and local dose deviations up to 31.5%. Types of errors included TPS model settings, algorithm limitations, and modeling and alignment of QA phantoms in the TPS. Most of the errors were correctable after detection and diagnosis, and the uncorrectable errors provided useful information about system limitations, which is another key element of system commissioning.

Conclusions

: Many forms of relevant systematic errors can go undetected when the currently prevalent metrics for IMRT/VMAT commissioning are used. If alternative methods and metrics are used instead of (or in addition to) the conventional metrics, these errors are more likely to be detected, and only once they are detected can they be properly diagnosed and rooted out of the system. Removing systematic errors should be a goal not only of commissioning by the end users but also product validation by the manufacturers. For any systematic errors that cannot be removed, detecting and quantifying them is important as it will help the physicist understand the limits of the system and work with the manufacturer on improvements. In summary, IMRT and VMAT commissioning, along with product validation, would benefit from the retirement of the 3%/3 mm passing rates as a primary metric of performance, and the adoption instead of tighter tolerances, more diligent diagnostics, and more thorough analysis.

I. INTRODUCTION

Several well-known tenets of quality are (1) to strive to “build quality in” the system; (2) to reduce variability wherever possible; and (3) to continually improve quality, thus reducing the reliance on costly mass inspection of the final product.^1–4 These ideas are traditionally associated with manufacturing, but are applicable to modern radiation oncology, which can be fairly described as the mass production of highly conformal radiation dose deposited in the patients. The evaluation of the treatment planning and delivery system's dosimetric accuracy is a task critical at many stages, including: (1) product design, (2) system commissioning, and (3) patient-specific quality assurance (QA).

Of particular importance are product design (which includes product validation) and system commissioning, both of which are “upstream” processes that ultimately have influence on every patient. As such, these are the most critical stages to identify and minimize systematic errors and inherent limitations, with the goal to continually work to minimize these imperfections, i.e., to “build quality in.” However, the much more frequent and work-intensive task of patient-specific dose quality assurance often receives more attention in terms of time, energy, and resources. Moreover, there seems to be a growing interest in per-fraction dose QA, which would be yet another inspection, this one with even higher frequency than patient-specific dose QA. One could argue that per-patient and per-fraction QA are somewhat analogous to the “mass inspection” cited often by Deming and others as being less useful than building quality in and minimizing variation^2,3 We might therefore ask ourselves important questions, such as: (1) Are products designed and validated with sufficiently stringent tests of accuracy?, and (2) Given the vital importance of design validation by the manufacturer and system commissioning by the end user, do they get the deserved attention in terms of tight tolerances and continual improvement?

Let us first consider commissioning. The AAPM TG-119 report defined IMRT commissioning as “the initial verification by phantom studies that treatments can be planned, prepared, and delivered with sufficient accuracy.”⁵ The task group designed a representative suite of test plans covering a range of simple to complex modulation patterns. The aim was to “test the overall accuracy of the IMRT system” by analyzing differences which may be caused by measurement uncertainty, limitations in the accuracy of treatment plan system (TPS) dose calculations, and/or limitations in the dose delivery mechanisms. The goal of commissioning is to verify sufficient accuracy, and as such we should strive to detect as many sources of systematic error as possible, eliminate (or reduce the impact of) as many errors as possible, and understand/quantify residual errors. To achieve this, the dose comparison metrics employed must be sufficiently sensitive.^2–4 However, there is a growing body of literature confirming that common dose comparison metrics—in particular the ubiquitous ^6–8 3%/3 mm gamma analysis⁹ passing rate—may lack the sensitivity to detect many forms of systematic error (either real, or induced for the purpose of sensitivity analyses).^10–15

The 3%/3 mm gamma passing rate metric is commonly used for a range of dosimetric QA tasks—from product validation to system commissioning to per-patient and per-fraction dose QA. Continued application of this common metric is promulgated by original publications¹⁶ and, more importantly, guidance reports on system commissioning, most notably TG-119.⁵ Though many of the recent studies on the insensitivity of these common metrics focused on applications in patient-specific dose QA, it is logical to assume that if these metrics are insensitive when used for patient-specific analysis, they would be equally insensitive during the more critical stages of product accuracy validation and commissioning. Insensitive metrics equate to loose tolerances, and quality theory warns that loose tolerances increase variation and allow persistence of “special cause” errors (i.e., correctable systematic errors), while adherence to tight tolerances reduces variation via detection and elimination of systematic error.^1–4 The introduction of statistical process control in the TG-119 report is to be applauded, but there are potential pitfalls of basing IMRT/VMAT dose distribution evaluations primarily on TG-119 metrics and action levels, as pointed out by Cadman.¹⁷

This is not just an academic concern. Despite widespread IMRT treatments at modern radiation therapy centers, accurate dosimetric commissioning of an IMRT system remains a challenge. In the most recent report from the Radiological Physics Center (RPC), only 82% of the institutions passed the end-to-end test with the anthropomorphic head and neck phantom.¹⁸ That test has rather lenient dose difference and distance-to-agreement (DTA) criteria of 7% and 4 mm. Only 69% of the irradiations passed the narrowed TLD dose criterion of 5%. Logical questions follow, such as: (1) Are these failures a result of loose tolerances imposed by manufacturers during product validation?; (2) Are these failures in part due to lack of rigor in commissioning the TPS and delivery systems?; and (3) How high can conventional gamma passing rates be in the presence of pervasive, clinically relevant systematic sources of inaccuracy?

The purpose of this study is to make a case for tighter tolerances and more in-depth and stringent analysis of dose differences—especially for critical upstream tasks such as product validation and system commissioning—by examining an instructive selection of real-world cases. Each case illustrates a unique systematic error that escaped detection by commonly used methods, but was readily detected with alternative analyses of the same data. These representative examples were all observed within the past three years across a range of modern TPS and delivery systems. By examining case-by-case, we identify failure modes and their corresponding means for detection, diagnosis, and risk mitigation. In the process, we investigate if there are different methods and more sensitive metrics that could be employed to improve the many critical processes requiring dose difference analysis.

II. MATERIALS AND METHODS

II.A. Review of TG-119 passing rate metrics and action levels

It is a common practice in radiation therapy to compare measured vs calculated dose in a phantom, and many single-point and array dosimeters exist for this purpose. The differences between the measured (“meas”) dose distributions and their calculated (“calc”) counterparts are frequently compared using gamma analysis.^9,19 This method combines percent dose difference with distance-to-agreement (DTA) evaluation for each point on the dose grid, thus quantifying discrepancies in both low and high dose-gradient with a single number. If the combined criteria are met, the gamma value for any given point is ≤1.0, and the fraction of such points in the population of analyzed points is referred to as the passing rate. Gamma passing rates are a key feature in the AAPM task group report on IMRT Commissioning.^5,20 In the TG-119 report, statistical methods were used to recommend passing rate action levels of 88% and 90% for composite dose gamma analysis (i.e., cumulative dose from all fields, delivered in their treatment geometries) and individual field dose gamma analysis (planar dose acquired normal to beam axis at depth in phantom), respectively.

Whenever gamma passing rates are used, it is imperative to clearly document the user-definable parameters: dose difference threshold and normalization (global or local) method, DTA threshold, and lower dose analysis cutoff. Also important (if only because available as a feature with some dosimetry systems) is to specify if an additional “measurement uncertainty” factor was included in the comparison, as this can affect the gamma passing rate. The “measurement uncertainty”²¹ is a vendor-specific correction that allows for a more lenient absolute dose comparison criterion; it was used in TG-119²⁰ and is analyzed in detail in Sec. IV. In the TG-119 report, the following critical parameters were used to come up with the 88% and 90% action level recommendations:²⁰

• •Absolute dose comparison;
• •3% dose difference threshold;
• •Global normalization method for percent dose differences (i.e., use of prescription or maximum dose as the denominator to compute percent dose differences);
• •3 mm DTA threshold;
• •10% lower dose threshold;
• •Measurement uncertainty turned “on” for diode array measurement analysis.

In this work, the corresponding dose difference/DTA specifications will be referred to as “3%G/3 mm” where the “G” stands for global normalization. A more sensitive combination of parameters using 2% dose difference with local dose difference normalization and 2 mm DTA criterion will be called “2%L/2 mm” with the “L” identifying the local percent difference normalization method.

II.B. Case study descriptions

We present real-world examples from the commissioning and QA of external beam photon systems. These cases were observed in practice at various institutions and do not describe any errors induced solely for study purposes. There were many instructive examples from which to choose; for the sake of conciseness, we selected a representative subset of seven case studies that span multiple combinations of TPS, linac, energy, delivery modality, and types of systematic error ultimately diagnosed (Table I).

TABLE I.

Details of the case studies, including TPS, linac, energy, MLC type, delivery modality, and type of error.

ID	TPS	Linac/MV/MLC	Delivery modality	Error type
1	Pinnacle	Elekta 6 MV 80-leaf (10 mm)	IMRT (step and shoot)	TPS model setting
2	MSK	Varian 6 MV 120-leaf	IMRT (dynamic)	TPS model setting
3	Eclipse	Varian 15 MV 120-leaf	IMRT (dynamic)	TPS input data
4A	Monaco	Elekta 6 MV 80-leaf (4 mm)	IMRT (step and shoot)	TPS algorithm
4B	Monaco	Elekta 6 MV 80-leaf (4 mm)	VMAT (1 arc)	TPS algorithm
5	Pinnacle	Varian 6 MV 120-leaf	VMAT (2 arc)	TPS algorithm
6	Pinnacle	Elekta 10 MV 80-leaf	Open field	TPS phantom setting
7	Eclipse	Varian 6 MV 120-leaf	VMAT (2 arc)	TPS phantom setting

II.C. Specific QA devices and analysis methods used in this study

Standard, commercially available QA devices and methods were used in this study, each of which has been well described in literature, including 2D diode arrays,^22,23 EPID-based dosimetry,^24–27 biplanar, ^28–30 and helical ^31–33 quasi-3D diode arrays, and volumteric measurement-guided dose reconstruction (MGDR).^{11–13,34–37} Table II summarizes which methods were used in each case. Specific tools included MapCHECK, MapCHECK2, EPIDose, ArcCHECK, and 3DVH (Sun Nuclear Corporation, Melbourne, FL) and Delta4 (Scandidos AB, Uppsala, Sweden). Additional analysis methods used to augment gamma passing rates are summarized in Table II and described in detail in Table III.

TABLE II.

Passing rate method (per beam planar or composite), dosimeters, and analysis methods employed for each case study.

ID	Passing rate	Dosimeter(s)	Advanced diagnostic methods
1	Per-beam 2D	MapCHECK2	Dose profiles; 3D MGDR
2	Per-beam 2D	EPIDose	2%L/2 mm error pattern; 3D MGDR
3	Per-beam 2D	MapCHECK	2%L/2 mm error pattern; dose profiles; EPID-based
4A	Composite 3D	ArcCHECK	2%L/2 mm error pattern; dose profiles; 3D MGDR
4B	Composite 3D	ArcCHECK	2%L/2 mm error pattern; 3D MGDR
5	Composite 3D	Delta4; ArcCHECK	2%L/2 mm error patterns; dose profiles; 3D MGDR
6	Composite 3D	ArcCHECK	2%L/2 mm error pattern; ion chamber; 3D MGDR
7	Composite 3D	ArcCHECK	2%L/2 mm error pattern; 3D MGDR; dose grid inspection

TABLE III.

Descriptions of the analysis methods used to help identify the errors.

Method	Description
Ion chamber	Measure absolute dose in region of interest with micro-chamber (if possible). This method is useful if there is a large enough region of consistent and unidirectional dose bias
Dose profiles	Plot absolute dose profiles, planned vs measured, through region(s) of interest
2%L/2 mm error pattern	Employ a sensitive metric and examine patterns of error in the dose distribution
EPID-based	Use EPID input to predict high-density dose planes for more thorough analysis than sparse arrays. The specific tool used in this study was EPIDose. This implementation of EPID-based dosimetry reconstructs planar dose in a phantom for comparison with TPS-calculated dose, as opposed to comparing EPID images generated by a separate algorithm, which does not audit the TPS dose calculation (Ref. 25)
3D measurement guided dose reconstruction (MGDR)	Use measurement-guided dose reconstruction technique to use QA measurements to estimate 3D dose with the TPS voxel resolution, either on a phantom dose or on the patient CT dataset. The specific tool used in this study was 3DVH
Dose grid inspection	Use graphical tools to inspect the TPS dose grid, including extents, resolution, and volume filled by nonzero dose voxels

II.D. Regarding QA measurement and reconstruction methods

The focus of this paper is on interpretation of results when comparing measurements with calculations, rather than on any particular dosimetry system. Although specific devices and reconstruction methods familiar and available to the authors were used in this study, the findings are applicable to any valid dose measurement/reconstruction method. We note that a “valid” system should produce volumetric dose on a phantom with reasonable accuracy (validated at the 2%/2 mm level or better against independent dosimeters) and spatial resolution (ideally ≤ 2.5 mm).³⁵ It should be noted that even validated methods—both current and future—will have limitations where perhaps their accuracy or sensitivity are challenged. There will be pros and cons to each approach and it is possible (and perhaps likely) that no single approach will excel at detecting all potential sources of error.

III. RESULTS

III.A. Summary of conventional passing rate metrics using TG-119 instructions

Table IV summarizes the gamma analysis passing rates for each case study using TPS calculations vs direct measurements in phantom. For Case Studies 1–3, the passing rates were calculated per beam and averaged over all beams in the plan. The means of 99.2, 99.4, and 99.3% (range 96.7% to 100%) were all well above the published TG-119 action level threshold (90%) for per-beam planar analysis in phantom. Case Studies 4–7 were analyzed as 3D composite doses, i.e., all beams planned and delivered at the treatment beam geometries then analyzed as a 3D dose grid vs measurements in phantom. Strictly speaking, the TG-119 published action level for composite dose (88%) applies to fixed-gantry IMRT. However, it was demonstrated that VMAT gamma passing rates for the TG-119 datasets were not statistically significantly different from the IMRT ones,³⁸ and the same criteria can be applied. Each of the studied cases demonstrated 3%G/3 mm passing rates well exceeding 88% (range 93.9% to 97.8%).

TABLE IV.

Observed passing rates using the TG-119 instructions, i.e., 3%G/3 mm, 10% dose threshold, and (when available) measurement uncertainty turned “on.”

ID	Observed passing rates (%)	Details
1	99.2 ± 0.7 (1SD, range 98.1–99.8)	Mean over 7 IMRT beams
2	99.4 ± 1.2 (96.7–100)	Mean over 7 IMRT beams
3	99.3 ± 0.6 (98.9–100)	Mean over 5 IMRT beams
4A	96.6	Composite plan dose, 5 IMRT beams
4B	95.9	Composite plan dose, 1 VMAT beam
5	93.9a, 94.7b	Composite plan dose, 2 VMAT beams
6	97.8	Composite plan dose, 1 open field
7	100	Composite plan dose, 2 VMAT beams

^a AC.

^b Delta4.

III.B. Case-by-case analyses

Case studies are examined one by one with a supporting figure per case study (Figs. 1–7) and another figure illustrating the impact of applying corrections for some of the errors (Fig. 8).

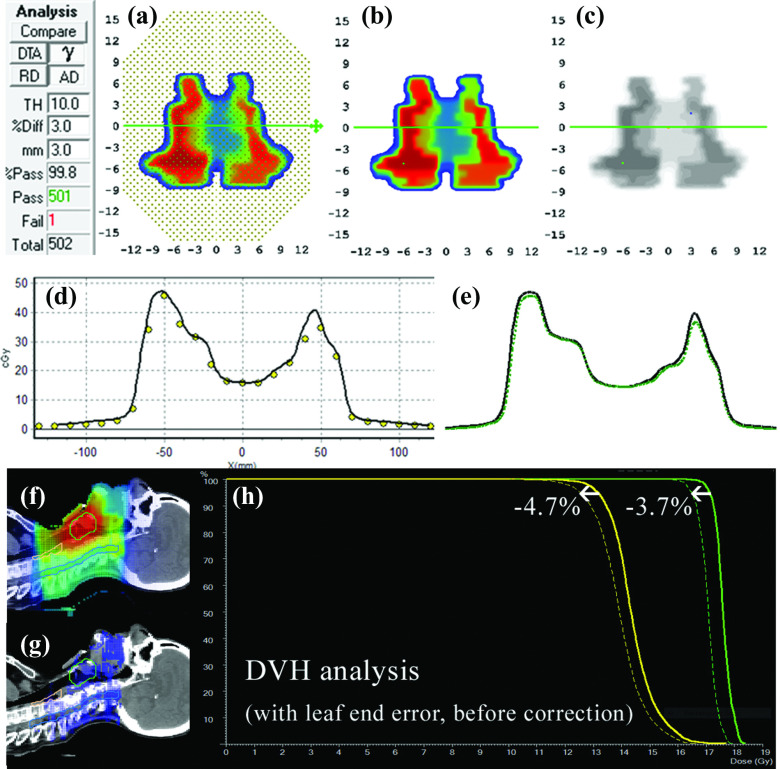
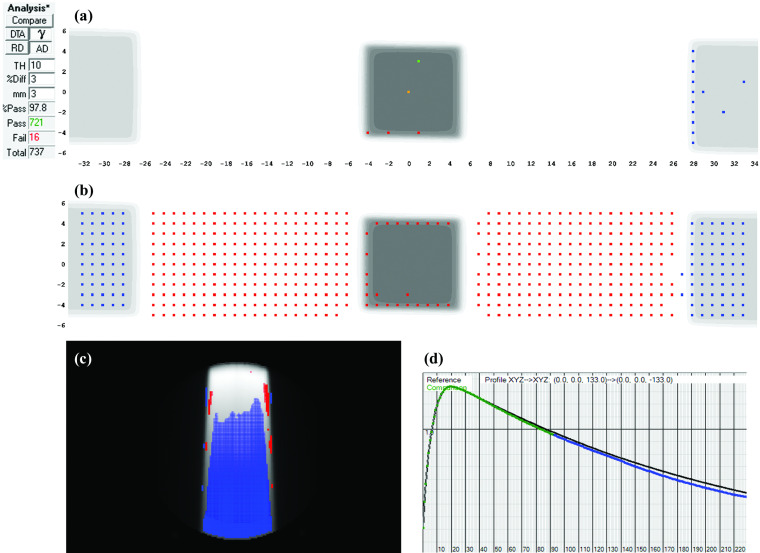
FIG. 1.

Absolute dose planes at 10 cm depth, 100 cm source-detector-distance (SDD) shown for (a) measured and (b) calculated dose. (c) 3%G/3 mm gamma failing points. (d) Dose profiles, dots represent calibrated diode measurements and solid lines the interpolated TPS profiles and (e) with measured profile (dotted) up-sampled using a commercial method (Refs. 12 and 13, and 34). (f) Patient sagittal planar dose from TPS and (g) with 3DVH-esimated error showing lower estimated patient dose as dose difference, and (h) as shifts in DVH curves for two target volumes.

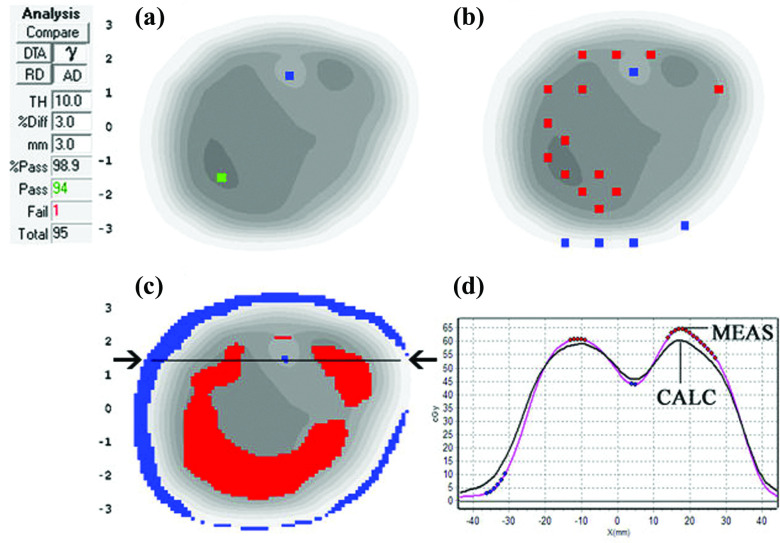
FIG. 2.

Absolute dose planes at 5 cm depth, 100 cm SDD for (a) measured and (b) calculated dose. (c) 3%G/3 mm gamma with failing points shown as the shaded region over the calculated plane in grayscale. (d) 2%L/2 mm gamma failing points showing a clear pattern of meas < calc, i.e., shaded regions showing gamma failing points. (e) Patient coronal TPS plane, (f) 3DVH-estimated dose differences (3DVH–TPS), and (g) estimated DVH errors showing lower MGDR target dose compared to planned.

FIG. 3.

(a) 3%G/3 mm gamma failing points and (b) 2%L/2 mm gamma failing points based on a diode array at 5 cm depth, 100 cm SDD. In both (a) and (b), the visible dots represent failing points. (c) 2%L/2 mm gamma failing points for EPIDose analysis at same virtual depth and (d) dose profile through the horizontal line indicated by the arrows in panel (c), with the black line extracted from the TPS dose grid and the line with dots highlighted from the measurement.

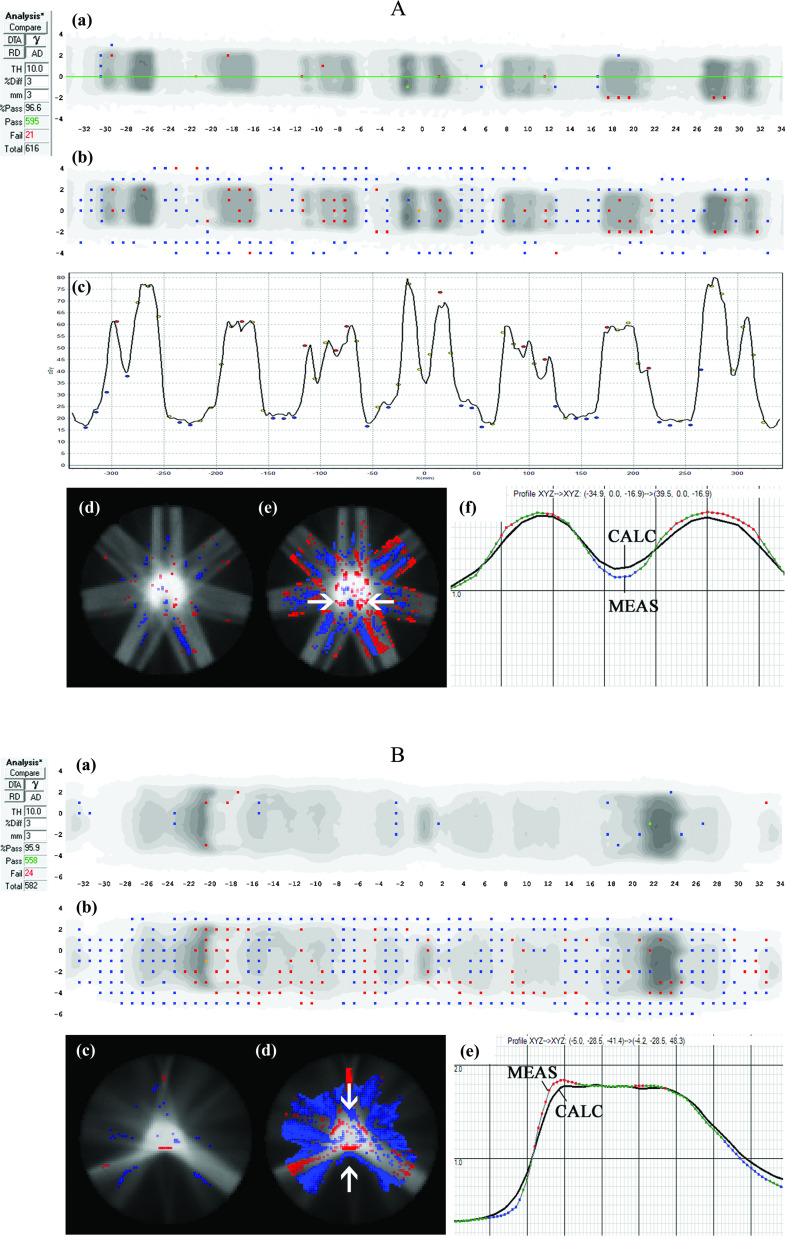
FIG. 4.

Case Study A (top): Seven-beam IMRT plan. (a) 3%G/3 mm gamma failing points over the ArcCHECK detector surface and (b) the same data highlighting points failing 2%L/2 mm gamma analysis. In panels (a) and (b), the visible dots represent failing points. (c) Dose profile over the central (Y = 0 mm) quasi-circular circumference of detectors (location of profile shown by the horizontal line in panel (a) showing meas > calc in peaks and meas < calc in valleys of dose, with the black line a profile interpolated through the TPS dose grid and the dots representing dose measured by the point detectors. (d) 3D MGDR reconstructed dose vs TPS dose for central axial plane, showing points failing 3%G/3 mm gamma analysis, and (e) the same data analyzed with 2%L/2 mm which introduces sensitivity enough to highlight the dose gradient differences. In panels (d) and (e), shaded regions indicate MGDR > calc or MGDR < calc. (f) Dose profile through the horizontal line indicated with arrows in panel (a), also showing the dose gradient differences, with the solid line representing the TPS dose and dotted line the reconstructed measurement. (b) Case Study B: The same TPS model as Case Study A of Fig. 4 analyzed for a single arc VMAT plan. (a) 3%G/3 mm gamma failing points over the ArcCHECK detector surface and (b) the same data highlighting points failing 2%L/2 mm gamma analysis. In panels (a) and (b), the visible dots represent failing points. (c) 3D MGDR reconstructed dose vs TPS dose for central axial plane, showing points failing 3%G/3 mm gamma analysis and (d) the same data analyzed with 2%L/2 mm which introduces sensitivity high enough to highlight the dose gradient differences. (e) Dose profile through the horizontal line indicated with arrows in panel (a), also showing the dose gradient differences, with the black line the TPS dose and dotted line the reconstructed measurement.

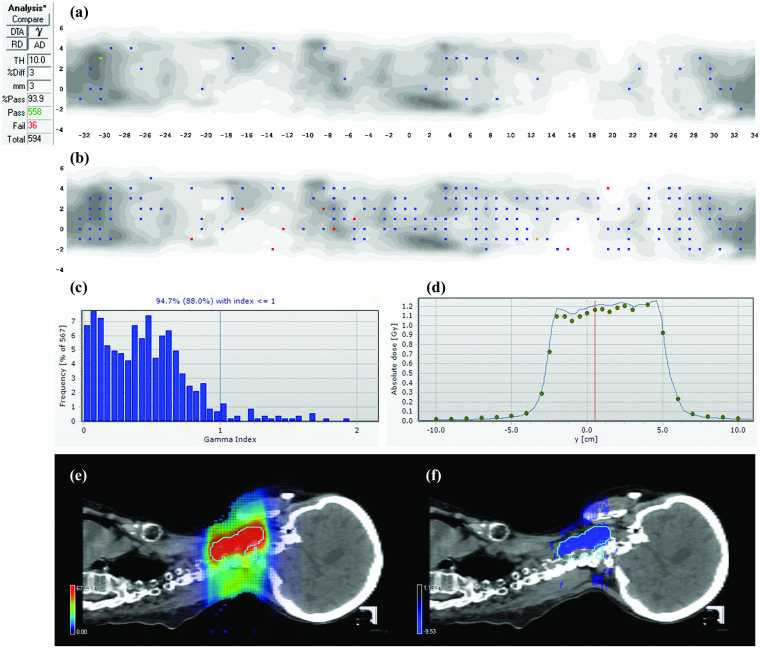
FIG. 5.

Two-arc VMAT plan. (a) 3%G/3 mm gamma failing points on the ArcCHECK detector surface and (b) the same data highlighting points failing 2%L/2 mm gamma analysis. (c) Gamma histogram generated for the same plan using a different 3D dosimeter (Delta4) showing the 94.7% passing rate and (d) absolute dose profiles in the Delta4 illustrating meas < calc over the entire high dose region. (e) TPS dose distribution and (F) 3D MGDR reconstructed dose vs TPS dose for a sagittal plane through the high dose region, showing the clear bias of meas < calc as the shaded region.

FIG. 6.

An open 10 × 10 cm² beam incident on a homogeneous PMMA cylindrical phantom. (a) 3%G/3 mm gamma failing points over the ArcCHECK detector surface and (b) the same data highlighting points failing 2%L/2 mm gamma analysis, where now the meas < calc bias at the beam exit surface becomes visually evident. (c) 3D MGDR reconstructed dose vs TPS dose for central axial plane, showing points failing 2%L/2 mm gamma analysis confirming the meas < calc trend that increases with depth, and (d) the central axis depth dose profiles of TPS (black line) vs MGDR (two-tone shaded line that is below the TPS depth dose line).

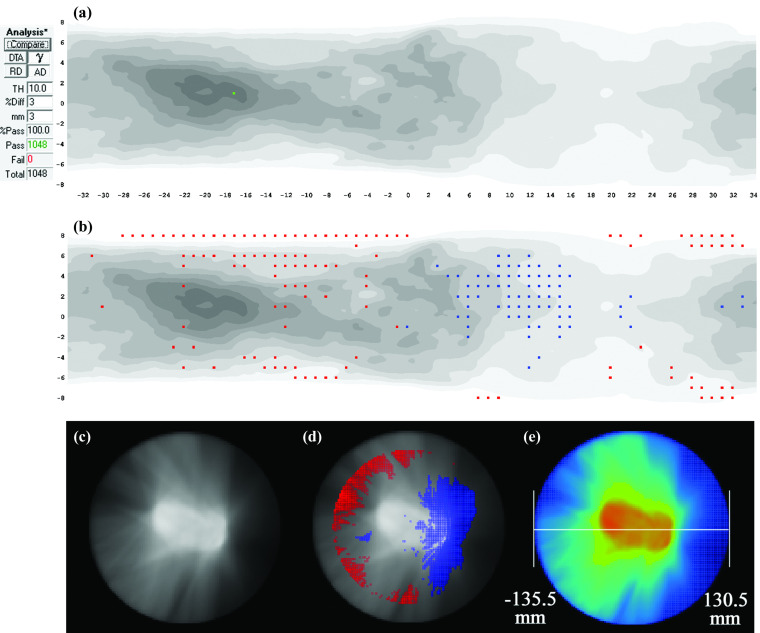
FIG. 7.

Two-arc VMAT plan delivered on a uniform cylindrical phantom. (a) 3%G/3 mm gamma failing points over the ArcCHECK detector surface and (b) the same data highlighting points failing 2%L/2 mm gamma analysis, where now a trend is visualized where meas > calc on the left side of the phantom and meas < calc on the right side, as indicated by shaded regions. (c) 3D MGDR reconstructed dose vs TPS dose for central axial plane, showing points failing 3%G/3 mm gamma analysis showing 100% passing rate, then (d) reanalyzed using 2%L/2 mm confirming the clear error pattern. (e) Analysis of the virtual phantom geometry in the TPS confirms that the beam isocenter was not centered in the phantom model but rather was shifted about 2.75 mm laterally.

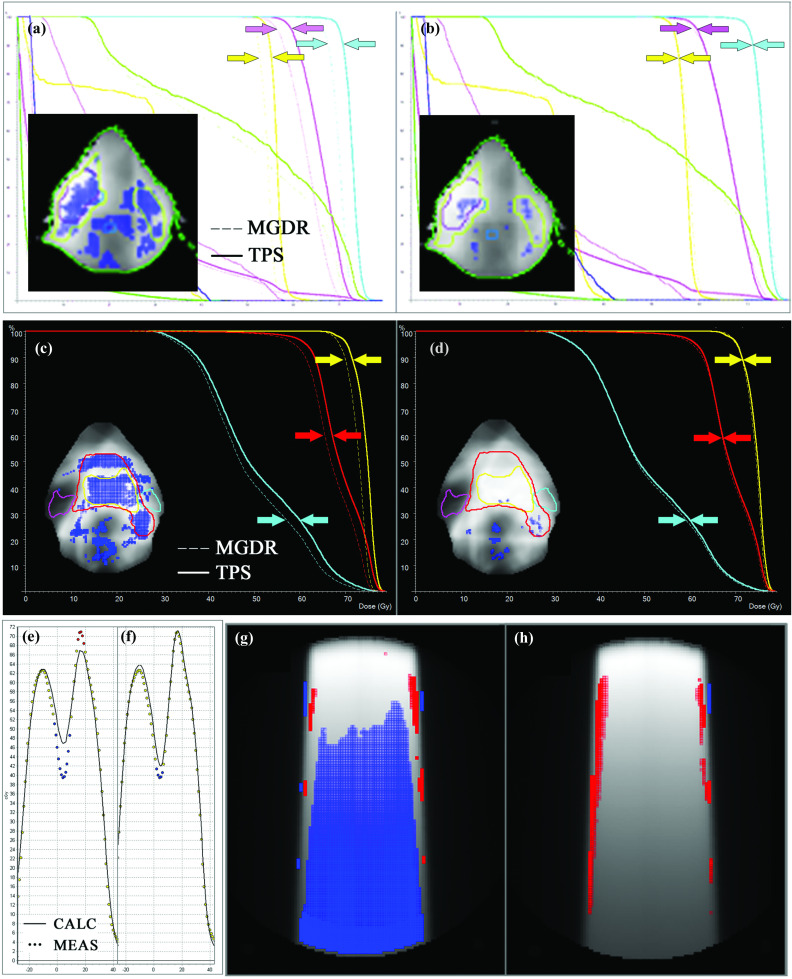
FIG. 8.

[(a) and (b)]: Before (a) and after (b) detection and removal of leaf-end error described by Case Study 1, exhibited for a different head and neck case to illustrate the systematic improvement in dose difference and DVH impact. Arrows have been added to three PTV curves to highlight convergence. [(c) and (d)]: Before (c) and after (d) application of the correct T and G effect by the TPS as described by Case Study 2. Arrows for two PTV curves and the ipsilateral parotid have been added to highlight convergence. [(e) and (f)]: Before (e) and after (f) improving the beam model by rescanning profiles with a small diode detector to eliminate the volume averaging effects of the original scans made with ion chamber. [(g) and (h)]: Phantom dose comparison (TPS vs measured) before (g) and after (h) correction of the QA phantom density configuration in the TPS.

III.B.1. Case Study 1: Incorrect TPS settings for leaf-end modeling

This case presented a 99.2% MapCHECK 3%G/3 mm passing rate (averaged over all beams) for a head and neck IMRT boost plan. However, volumetric MGDR estimates showed a reduction in target dose on the order of 4%, and the predicted DVH error is certainly noticeable (Fig. 1). In troubleshooting, it was noticed that the measured dose profiles were consistently slightly “inside” the calculated profiles and at first a geometric scaling error during QA measurement was suspected. Eventually, it was found that the leaf-end modeling (MLC offset table in the TPS) was not set correctly, causing the TPS to calculate each segment slightly too wide (on the order of 1 mm) which had an additive effect that was quite large over many segments. This was causing the trend of meas < calc and was a real error, easily rectified by adjusting the leaf end offset table. After this correction was made to the TPS and the patient plan and QA were redone [Note: It is important that anytime an improvement/correction is made in the TPS algorithm or beam model, the patient plan should be reoptimized and calculated, not just the QA dose. To do the latter without the former defeats the purpose], the problem was eliminated, i.e., the measured dose profiles and MGDR results came right in line with the TPS calculations. In particular, the D95 differences were decreased to less than 1% (compared to 3.7% and 4.7% before the correction). A thorough analysis of this error and the impact of correction was done for multiple head and neck plans³⁹ show that passing rates of 3D patient dose (again, MGDR vs TPS) improved by 5% after the correction and D95 values were brought to within 1%, indicating that the correction improved accuracy over all plans due to the systematic nature of the error. As an example of this systematic improvement, see the DVH curves in panels (a) and (b) in Fig. 8 before and after correction for a different head and neck patient.

III.B.2. Case Study 2: Setting in TPS causes failure to account for tongue-and-groove effects

Conventional 3%G/3 mm passing rates were high (99.4% average over all beams) but MGDR showed a noteworthy trend of meas < calc in estimated patient dose, on the order of 2%–4% in the target volumes (Fig. 2). More sensitive 2%L/2 mm analysis showed a cold (blue) horizontal striping pattern in dose difference, an indicator of tongue-and-groove (T and G) effect not being accounted for in the TPS model, causing the TPS to overestimate dose. Because this was a dynamic MLC IMRT plan, the effect was pronounced, as evidenced by the DVH in Fig. 2(g). In this particular TPS (Memorial Sloan-Kettering in-house system), the T and G is governed by the per-beam fluence spatial resolution (set to either 1 or 2 mm), and in this case the lower resolution (2 mm) used was not adequate to model T and G. After turning “on” the T and G correction in the TPS by improving the fluence resolution to 1 mm, the meas < calc dose differences dissipated both in per beam 2%L/2 mm analysis and also in the 3D MGDR. [Note: Any TPS corrections that are dependent on a fluence or dose resolution parameter require that the patient plan and dose calculation, not just the QA dose calculation, be redone. If one were to generate a more accurate dose only for the sake of QA and not implement it in the actual patient dose calculation is not a valid process, because the patient dose generated by the TPS will still be incorrect due to the error even though the QA results will improve.] The 4.2% and 2.4% D95 errors (Fig. 2) were reduced to less than 2% and 1%, respectively. This error (and other examples) are described and analyzed in a publication by Chan et al.¹⁵ Figure 8 panels (c) and (d) illustrate the impact of using the correct setting in the TPS to capture the T and G effect.

III.B.3. Case Study 3: TPS beam model with dose gradient errors due to inaccurate (volume-averaged) dose profiles entered into beam model

The 3%G/3 mm passing rate was 99.3% averaged over all beams in the plan, but inspection of dose profiles and 2%L/2 mm analysis showed clear, systematic dose gradient errors with the TPS underestimating dose in “peaks” and overestimating dose in “valleys” (Fig. 3). Measurements were repeated with a higher resolution EPID-based dosimeter (EPIDose), which yielded consistent error patterns. The error here was due to the fact that the dose profiles used for beam modeling were acquired with a Farmer chamber and were thus blurred due to volume-averaging, a problem quantified previously by Arnfield et al. using high-resolution film dosimetry.⁴⁰ Refining the TPS beam model by using profiles scanned with a diode detector reduced this gradient error [Fig. 8, panels (e) and (f)].

III.B.4. Case Study 4 (A and B): Inherent dose gradient errors in TPS beam model/algorithm

A 7-beam IMRT plan was analyzed via composite dose to a cylindrical phantom with a 3%G/3 mm passing rate of 96.6% [see Fig. 4, Case Study A]. However, MGDR showed a striping pattern of “hot” (meas > calc) and “cold” (meas < calc) regions, correlating with the underlying dose pattern. [MGDR reconstruction resolution always matches the TPS dose grid resolution, which in this case was 3 mm and is most commonly 2–3 mm.] In particular, (1) high dose peaks showed meas > calc, with local differences ranging from 2.6% to 31.5% sampled over all diodes in local peaks on the dose profile, with the magnitude of the error depending on the relative sharpness of the peak (sharper peaks had larger errors); (2) low dose valleys showed meas < calc, with local differences ranging from 3.5% to 15.5% sampled over all diodes in local valleys; and (3) high, sloping gradients showed hot/cold interfaces along the gradients. [Note: Differences were minimized by observing all permutations of small shifts and rotations (± 2 mm, ± 2°) of the phantom, to ensure the trend was not due to misalignment.] This error was fully reproducible for both IMRT and VMAT plans, and Case Study B of Fig. 4 shows results for a representative VMAT plan. In this case, there were only two local peaks, and the TPS underestimation of dose vs direct measurement in these regions ranged from 1.7% to 14.8%. TPS overestimations in local valleys were, similar to the IMRT example, on the order of 3% to 13%.

The range of local dose discrepancies assayed with MGDR in 3D were similar in degree to those observed directly at the diodes’ locations, as expected given that those measurements guided the reconstruction. The error patterns are consistent with a dose gradient error where the TPS profiles are too smooth (similar in symptoms, but not cause, to Case Study 3). In this case, the TPS employed vendor-supplied dose models that were not adjustable by the end user. Therefore, the issue is assumed to be a TPS algorithm limitation, but its detection and quantification during commissioning is still useful and important, because the data can be passed back to the manufacturer in a manner clearly illustrating the problem, and hopefully used for future product refinement.

III.B.5. Case Study 5: TPS underestimation of dose for narrow MLC segments in a complex VMAT plan

In this VMAT case, 3%G/3 mm analysis showed passing rates comfortably above the TG-119 action levels (Fig. 5). Passing rates were similar with two different dosimetry arrays (94.7% with the Delta4 and 93.9% with the ArcCHECK). However, further analysis estimated a reduction of dose in the high dose region of roughly 5.5% (meas < calc). Individual dose profiles and 2%L/2 mm analysis showed data consistent with this trend. After drill down analysis of this reirradiation head and neck plan, it was found that the vast majority of VMAT segments in both arcs were very narrow, often on the order of a few mm in width. This is a stress test for the TPS model, which systematically overestimates the dose for such narrow segments. Normally, such segments make up a relatively small portion of the field and the error is negligible, but in this highly modulated case they dominated the dose calculation, resulting in an additive effect. Mitigation in this case was to study and quantify this TPS limitation and avoid this situation in clinical treatment planning when possible. It is not clear at this point what, if any, model adjustments could/should be made. Agreement could be improved by lowering the MLC transmission parameter, but that would bring it further away from the measured value and could be considered “tampering” with the system.³ There is a reluctance to do this based on overall good dosimetric agreement for other cases.^28,32,35,37

III.B.6. Case Study 6: Incorrect QA phantom density set in TPS

Systematic errors can also occur in QA phantom configuration, either real (i.e., phantom alignment, dosimeter calibration, etc.) or virtual (how the virtual phantom is configured in the TPS). In this case, a simple 10 × 10 cm² field on the ArcCHECK phantom gave a high 3%G/3 mm passing rate of 97.8% even with the wrong phantom density in the TPS (Fig. 6). The calculated doses at the exit diodes were ∼8% high compared to measurements, but it should be noted that this is still within 3% error with global normalization despite the large local error. The meas < calc trend with depth was easily seen using 2%L/2 mm analysis and studying the error pattern, and also by performing dose reconstruction on the whole phantom volume. In this case, an ion chamber reading at the phantom center was 3.8% lower than the TPS, consistent with the observations using the diode array and MGDR. The source of the error was an erroneous assignment in the TPS of an electron density of 1.11 relative to water for the uniform PMMA phantom, which should have been set equal to 1.147. This low density setting subsequently caused the TPS calculations to the virtual phantom to be too high, with the percent error increasing with depth.

This systematic error in the assignment of density to the virtual phantom in the TPS was affecting all QA calculations, even though the error was not related to a TPS beam model or algorithm error. Such an error, left undiagnosed and uncorrected, can invite unwarranted tampering with the dosimetry device calibration or, worse, with the beam model. Correcting the TPS's configuration of the PMMA volume's density removed the problem, leaving only real errors (such as beam edge gradients) to be analyzed as seen in Fig. 8 [panels (g) and (h)].

III.B.7. Case Study 7: QA phantom misalignment in the TPS calculation

This was also a case of a systematic error related to the virtual QA phantom configuration in the TPS. Despite a perfect 100% passing rate at the 3%G/3 mm level, MGDR showed an asymmetric trend of meas > calc on the phantom's left half and meas < calc on the phantom's right half (Fig. 7). Switching analysis to 2%L/2 mm confirmed this trend even at the individual diodes. The physical phantom setup on the couch was carefully verified, thus suggesting the source of the error might be an alignment error in the virtual QA phantom, i.e., the isocenter placed in DICOM coordinates not coinciding with the exact center of the phantom model. By inspecting the extents of the calculated dose grid, it was found that the plan isocenter in fact did not coincide with the center of the virtual phantom; rather, it was shifted 2.75 mm in the lateral direction. This was easily rectified but could have negatively impacted the overall commissioning process integrity had it remained hidden by the 3%G/3 mm gamma passing rate. If that same phantom were to be used for per-patient QA, the error would systematically occur in all per-patient comparisons, possibly yielding false positives or artificially low passing rates.

IV. DISCUSSION

IV.A. Root causes of insensitivity of 3%G/3 mm gamma analysis

It is worthwhile to hone in on different aspects and components of the conventional gamma analysis criteria to learn about their relative contributions to the metric's insensitivity. In particular, we focus on the dose difference normalization method, DTA threshold, and the application of a common measurement uncertainty correction.

IV.A.1. Global normalization of percent dose difference

Normalization of the dose difference to a high global value—typically either the measured maximum or the prescribed dose—hides errors in the lower dose regions. This choice of dose difference quantification is often justified by “clinical relevance.” There is certain validity to this argument for the patient-specific tests. However, for the validation and commissioning measurements, it is imperative to clearly understand the TPS performance across the range of dose levels, and local dose difference normalization provides an unbiased metric for such analysis. In addition, global normalization makes for a counter-intuitive dependence of the passing rates on the low dose cutoff threshold for analysis. Decreasing that threshold may lead to an increase in the passing rate despite the fact that the dose calculations are often challenged in low-dose regions. An example of the global normalization contributing the most to insensitivity of 3%G/3 mm gamma is Case Study 4b. In this case, if 3% local is used instead of 3% global (all else being equal), the passing rate drops from 95.9% to 75.3%. If the 3% criterion is left as global and the DTA criterion is turned off, the passing rate falls only to 85.7%, suggesting that the global dose difference normalization is the major contributor to insensitivity of the gamma analysis in this case.

IV.A.2. Distance-to-agreement threshold

An example of the DTA threshold contributing the most to insensitivity of 3%G/3 mm gamma is illustrated by beam #1 of Case Study 1. In this case, if 3% local is used instead of 3% global (all else being equal), the passing rate decreases only slightly, from 99.4% to 98%. However, if the 3% criterion is left as global and the DTA criterion is turned off, the passing rate falls to 72.7%, indicating that the distance tolerance of 3 mm is now the major contributor to insensitivity of the gamma analysis. A 3 mm DTA threshold is quite large compared to 1 mm positioning capabilities of the modern accelerators.⁴¹ Consider a simple anecdote that is easily tested: if one were to shift an entire conformal dose distribution by 3 mm, it would by definition pass gamma comparison with the original one at 100% level if a 3 mm DTA were used; however, local dose errors in the dose gradient regions—and subsequent DVH errors—would be substantial.

IV.A.3. Measurement uncertainty

The “measurement uncertainty” factor is offered in one dosimetry analysis software package²¹ as the means to take into account measurement errors introduced by the dosimeter. We can speculate that it was introduced assuming that the precision of the existing dosimetry arrays is similar in magnitude to the error being measured, rather than the metrologically optimal order of magnitude below it.⁴² This factor was applied in TG-119 for diode array measurements.^5,20 Using it adds extra leniency to the already liberal 3%G allowance. For gamma calculated over a 3D grid, the impact is to add another 1% allowance to the threshold, thus the passing criterion for dose difference is labeled as 3% but is actually 4%; for 2D planar analysis, the magnitude is roughly the same.²¹ Application of the measurement uncertainty is biased in one direction—to improve passing rates—and this could be considered an incorrect implementation, because statistically speaking, a true “uncertainty” would on average cause as many passing points to fail as it would failing points to pass.

When global dose difference normalization was used, turning the measurement uncertainty “on” was observed to raise the passing rate anywhere from 0.5% to 5%, with the biggest impact on IMRT per beam planar analyses. For example, beam #1 of Case Study 3 has a 3%G/3 mm passing rate of 98.9% with the measurement uncertainty “on” and falls to 94.7% if it is turned “off.” Although the data in Table IV for the MapCHECK and ArcCHECK diode arrays are presented with measurement uncertainty “on” as per the TG-119 instructions, turning it “off” would not alter the conclusions. All passing rates would remain comfortably above TG-119 action levels. “Measurement uncertainty” has a much bigger impact if local dose difference normalization is used instead of global. In beam #1 of Case Study 3, for example, the 2%L/2 mm passing rate is 95.7% if the uncertainty is “on” but drops almost 10% to 86.0% when that parameter is toggled off.

Overall, the “measurement uncertainty” is an extra correction that, as implemented, always results in increased passing rates. It also adds variability to the presentation of gamma analysis results for inter-institutional studies and/or publications, as it is not always clearly defined whether this correction was turned “on.”

IV.B. More sensitive metrics and methods, using the same input data

In the cases presented here, the same raw measured data used for insensitive 3%G/3 mm analyses proved more useful if other, more sensitive, analysis methods were used. Thus the problem resides not with the data but rather with the sensitivity of the commissioning metrics. Especially useful were (1) changing gamma analyses thresholds to 2%L/2 mm to study the visual patterns of dose differences that steer the human eye towards intuitive narrowing down of potential sources of error; (2) carefully examining absolute dose profiles and again studying patterns, especially dose levels and dose gradients; and (3) reconstructing full volumetric dose, especially when 2%L/2 mm dose difference patterns, dose profiles, or DVHs are analyzed, all of which are rather sensitive and specific to common sources of error.^11–13,15

IV.C. Universal applicability for other measurement methods/devices

The observations of this study about metrics and interpreting results are applicable to all methods that produce accurate 3D dose measurements and/or reconstructions. In this paper, we specifically used 3DVH for volumetric dose reconstruction because it is a tool available and familiar to us. It is generally accurate at the 2%/2 mm level,^12,34,35 though some minor discrepancies attributed to the detector spacing were noted by Carrasco et al.¹² It has also been analyzed by direct comparison vs polymer gel measurements showing consistent results both in dosimetry and in sensitivity, i.e., both 3DVH and the polymer gel detected consistent differences vs TPS in terms of target dose uniformity and high-gradient target-OAR interfaces under stringent VMAT conditions.⁴³ The method should be validated further for very small targets possible for example in cranial stereotactic radiosurgery, where the diode detector density may become a limiting factor despite the condensed sensing methodology used to estimate data in between directly sampled detector locations. As an interesting side note, the diode-based approach that ultimately detected the sub-mm leaf end modeling errors in Case Study 1, probably could not have detected the tongue-and-groove error as the EPID-based method of Case Study 2, due simple to how the error patterns manifest in relation to the detector locations and density. This reinforces our earlier point that perhaps no specific method will be able to efficiently detect all potential sources of error, as each specific method has pros and cons in terms of accuracy and sensitivity.

There are of course other methods of 3D dosimetry, such as measurements using radiochromic plastics which have excellent direct measurement density and requisite accuracy/precision.^44–46 In addition to these other currently available methods, there will be continued introduction of new methods and evolution (i.e., improvements) in current methods of 2D and 3D dosimetry. In reality, it is probable that a truly comprehensive commissioning of system would require a suite of specific tools and methods and a specially designed set of rigid test cases that specifically probe for potential errors. No matter what the specific method, the conclusions of this work are universally applicable to any and all methods that are appropriately validated under stringent accuracy criteria.

IV.D. Moving forward in terms of dose error evaluation

Overreliance on insensitive metrics—such as the 3%G/3 mm gamma passing rate—could allow systematic errors to go undetected and is contrary to the basic tenets of quality enumerated in the Introduction. It hinders “building quality in” because both manufacturers and medical physicists may erroneously believe their system is of higher quality than it actually is based on the numerically high passing rates. This also by definition violates the goal to strive for tight tolerances and inhibits driving down variation. Continual improvement is likewise hamstrung, as meeting proposed action levels based on insensitive metrics gives a false sense that there is nothing to improve.

While attempts are being made to rationalize tolerance levels for dose distribution agreement in IMRT/VMAT,^47–49 so far there is no consensus as to what is acceptable or recommended. The results of this work suggest that more sensitive metrics—perhaps 2%L/2 mm gamma analysis or new comparison metrics altogether—could be more useful in the commissioning process to maximize dosimetric accuracy. In terms of 2%L/2 mm gamma analysis, it may not always be possible to achieve an appealing passing rate of >90%,⁴⁹ but having a spread continuum of evaluation results, as opposed to a cluster next to the maximum 100% value, would provide a more useful statistical backdrop to fine-tune the system. Metrics showing higher sensitivity and specificity^{11–13,15,46} might also be introduced into product validation and commissioning stages to complement dose difference analysis. Also, qualitative examination of dose difference patterns using very tight tolerances can be instructive, because consistent, reproducible patterns are traits of systematic error.

It would be an interesting study to return to the RPC data and, if possible, reassess TPS and delivery commissioning under more stringent methods and metrics. It is possible, for example, that the many systematic imperfections that can go undetected when a system is commissioned only to 3%G/3 mm gamma passing rate tolerances play a major role in the highly variable performance levels observed in the RPC head and neck credentialing.¹⁸ As evidenced in this current work, very large systematic errors (on the order of up to 5% errors in target dose and up to 31% absolute dose local errors) occur even if conventional methods yield very high 3%G/3 mm passing rates.

IV.E. Knock-on consequences of 3%G/3 mm gamma analysis

Using 3%G/3 mm gamma passing rates as a basis of gauging “sufficient accuracy” as per TG-119 has knock-on effects outside of commissioning. One such effect is that it is often used as the de facto standard to “validate” a new or modified product. For example, even very recently 3%G/3 mm passing rates have been quoted to prove the accuracy of TPS dose algorithms,⁵⁰ delivery systems,⁵¹ or dosimetry devices.⁵²

In this work, we show a variety of clear examples of the metric's insensitivity, supporting the argument that it is inappropriate as a sole basis for commissioning. The same conclusion can be made for the yet further upstream task of product validation by medical device manufacturers and their clinical partners. However, if we were to move towards more sensitive metrics and tighter tolerances for commissioning, these new methods would likely be applied by the manufacturers during product design and validation, too. This would encourage the manufacturers to “design quality in” in a way that the end user cannot, i.e., at the product design level, which is preferred because then all users benefit from the higher quality and reduced variation.

IV.F. A word on variation

In modern radiation therapy, there are many possible combinations of TPS, delivery system, and QA/dosimetry equipment. Each individual device has its own unique limitations and complexities, and these variations are compounded when combined with the variations inherent to the other components of the radiotherapy system. Ideally all products would, over time, continually improve to meet higher benchmarks of quality in all aspects, growing more reliable and less variable. Certain manufacturers are making strides, for example, to reduce the variability in their delivery machines so much that a high quality, standard beam dataset for each machine model could replace the costly and variable process of beam scanning with water tanks. However, when it comes to inter-vendor competition, it is quite common to see technological variation created and exploited for the purpose of product differentiation, thus the free market itself encourages and guarantees a certain degree of natural variation.

However, product variation should not be confused with the process variation (in particular when commissioning and validating products), the latter of which would benefit from across-the-board improvement and standardization. TG-119 was a strong first effort for the first decade of IMRT, but its performance metrics, based on what was deemed achievable at the time, are too lax to effectively audit today's systems. The time has come for updated guidance on evaluating IMRT/VMAT dosimetric accuracy, with more sensitive metrics, more useful benchmarks, and less variation in dosimetry methods.

V. CONCLUSIONS

Supporting the hypothesis expressed by Cadman¹⁷ that the ubiquitous 3%G/3 mm gamma analysis metric is not sensitive enough to provide optimal results in IMRT/VMAT commissioning, we presented a set of real-world cases where using more sensitive metrics resulted in identification of systematic dosimetric errors that otherwise could have gone unnoticed. Some of these errors were easily correctable by the user, while others could at least be reported to the manufacturer as a documented shortcoming of the TPS algorithm. Overreliance on the insensitive metric is counterproductive to quality improvement and can lead to the sense of complacency among the clinical physicists. Use of this metric also enables manufacturers to release products that may not be validated with sufficient rigor, hindering them from designing error out of the system before commercial release. Therefore, adoption of more sensitive metrics/tighter tolerances enables continual improvement of the accuracy of radiation therapy dose delivery not only at the end user level, but also at the level of product design by the manufacturer. Adoption of sensitive metrics and tighter tolerances fit the larger goal to better standardize the methods and processes of commissioning and product validation, with the ultimate goal to increase quality and remove variation to the point of removing reliance on mass inspection.