An Interval-Valued Intuitionistic Hesitant Fuzzy Methodology and Application

Abstract

Using advantages of interval-valued intuitionistic hesitant fuzzy sets (IVIHFS) for describing the hesitant and intuitionistic decisions of experts and identifying the limitations of previous research works about optimization techniques, this paper introduces a new optimization technique and provides a new computational algorithm, applicable in various real life multiobjective optimization problem (MOOP) of engineering and management sectors, and for this, a new operation between IVIHFSs is first introduced. On the basis of this concept, a stepwise computational algorithm is constructed, and it is an extension of both fuzzy and intuitionistic fuzzy optimization techniques. Finally, the proposed algorithm is illustrated using a production planning problem, and the obtained results are compared with the existing optimization techniques.

Introduction

Several versions of optimization technique have been extensively studied in literature for the engineering and management perspective. The ordinary linear programming provides a platform for the development and analysis of an optimization technique under certain or uncertain environments. The values of parameters in classical techniques of optimization were taken as a fixed number. Due to the occurrence of uncertainty and hesitation in many real-life MOOP, it is very tough and challenging to deal via conventional techniques. It is also pointed out that in many real-life problems of engineering and management, the values of the constraint coefficients are either vague or ambiguous due to the incomplete information or unknown resource limits. Therefore, there is a demand of a realistic and effective computational algorithm. The main contributions of the present paper that may make it popular are given below:

• The IVIHFS is one of the recent extensions of fuzzy sets and some limited articles of IVIHFS are available in literature. Here, I explain an IVIHFS based on current adverse circumstance: the physical distancing during COVID-19.

• A new interval valued intuitionistic hesitant fuzzy operation is introduced in this paper.

• The Pareto optimality in interval-valued intuitionistic hesitant fuzzy sense is introduced in this paper.

• I developed a new optimization technique to deal MOOP with uncertainty and hesitation.

• A set of possible interval-valued membership and non membership degrees are defined to tackle uncertainty and hesitation of MOOP rather than single fixed degrees.

• Profit obtained from proposed method is more than the some existing methods.

• Obtained decisions are more realistic and unbiased due to several expert opinions.

• Proposed optimization technique is generalization of both fuzzy and intuitionistic fuzzy optimization techniques.

• Proposed algorithm searches for a better optimal solution with maximum membership and minimum non membership degrees.

• The IVIHFS would be a very useful tool to deal any real-life problem in context of uncertainty and hesitation.

The present paper is organized as follows: in “Literature Review”, the literature review will be presented; some basic definitions related to fuzzy sets will be given in “Preliminaries”; the illustration of IVIHFS and some operations will be presented in “The Interval-Valued Intuitionistic Hesitant Fuzzy Sets” and “Development of Computational Algorithm”, the proposed optimization technique will be developed; in “Computational Algorithm” , the stepwise procedure of the proposed algorithm will be presented; in “Illustration of the Proposed Computational Algorithm”, the proposed algorithm will be implemented in industrial problem; Finally, the conclusions and future research directions will be placed in “Conclusions” and “Future Scope,” respectively.

Literature Review

Zadeh [43] has investigated the fuzzy set (FS) to deal various types of real-life problems with uncertainty and vagueness. Later, Zimmermann [47] has developed a solution methodology for the linear programming problem with several objective functions that was based on the intersection property of fuzzy objective and constraints. Evans and Steuer [10] have proposed a necessary and sufficient condition for a point to be an efficient solution of MOLPP, and some lemma and theorems were stated. Further, for the solution of MOLPP a revised simplex algorithm is developed. Hannan [12] has carried out a novel research work to demonstrate how fuzzy or imprecise goal of the decision maker may be incorporated into a standard goal programming formulation, and the new problem can then be solved using the properties of piecewise linear and continuous functions and by goal programming deviational variables. Further, for this, a methodology for the solution of fuzzy goal programming problem is presented. The main objective of this paper was to find an efficient solution of the MOLPP with fuzzy goals. It was Zionts and Wallenius [48] who have proposed a practical man-machine interactive programming for the solution of optimization problem under some restrictions containing multiple objective functions on feasible space that was a convex set over which the concave objective functions were maximized. Charnes and Cooper [7] presented a survey on recent development of goal programming and multiple objective optimization problems that incudes goal and interval programming with some definitions and examples of goal functionals. Recently, various computational algorithms have been developed based on various types of optimization techniques, for example Cheng [8], Tarabia [34], Brikaa [6], Wu [39], Uddin [36] and Yang [42]. Shih et al. [32] presented a method to find optimal solution of multiobjective programming in interval-valued fuzzy environment where crisp multiobjective programming was converted into an interval-valued fuzzy programming using interval-valued fuzzy membership functions for each crisp inequalities. Recently, Arya [2] and Sen [31] have further studied fuzzy sets.

Due to the occurrence of uncertainty and hesitation about value of parameters of a real life problem, the decision maker and experts face difficulties and that cannot be unheeded. It was Atanassov [3] who has introduced the concept of intuitionistic fuzzy sets (IFS) which is a very important generalization of Zadeh’s theory of fuzzy sets. In an IFS, an element is characterized by both membership and non-membership degrees with respect to a set. Angelov [1] has investigated an optimization technique that was based on the intersection property of intuitionistic fuzzy sets, called an intuitionistic fuzzy optimization technique, and it finds a better optimal solution of an optimization problem after fuzzy optimization technique. Recently, Mahajan [23, 24] and Senthil et al. [16–19] have studied IFS and applied it in several real-life optimization problems. An interval-valued intuitionistic fuzzy set (IVIFS) is a further extension of IFS and is investigated by Atanassov and Gargov [4] in which the membership and nonmembership degrees of an element are, respectively, represented by intervals in [0, 1] rather than fixed real numbers between 0 and 1. IVIFS with interval membership and non-membership has a successful application in modeling and decision making of various engineering and management problems. Further, it is pointed out that the membership degree may slightly differ as assigned by experts and, therefore, one may encounter a kind of uncertainty in various decision making of engineering and management problems that was unheeded by existing versions of fuzzy sets.

Torra and Narukawa [35] have introduced the concept of hesitant fuzzy sets that is an extension of ordinary fuzzy sets that can be considered as a useful tool allowing more possible degrees of an element to a set. The degree of an element in hesitant fuzzy sets is a subinterval of [0, 1]. Recently, it became one of the common interests for several researchers [26–30, 37, 45, 46] in the various sectors. The interval-valued intuitionistic hesitant fuzzy sets were initially introduced by Zhang [44] and currently studied by several researchers [13, 20, 21, 25, 33, 38]. An IVIHFS is a set in which an element has a set of several of possible membership and non-membership functions, and these are two main vehicles of an IVIHFS. Later, the researchers have utilized IVIHFS in the various decision making problems of engineering and management. Only limited research work has been carried out based on newly invented set, and is no work concerning MOOP with IVIHFS done yet. Often a production planning problem (PPP) is mathematically formulated as a MOOP and it may provide a suitable framework in certain or probabilistic environments. In PPP, the value of parameters are assigned by experts on basis of incomplete or unobtainable information. In such condition, classical MOOP methodologies do not deal properly. An IVIHFS involving interval-valued hesitant membership and non-membership degrees can be a fit tool. Bharati and Singh [5] studied interval-valued intuitionistic fuzzy sets and investigated new computational algorithm which is an extension of both fuzzy and intuitionistic fuzzy optimization techniques. And its validity and superiority are explained by an illustrative example, and a comparison with existing algorithms is tabulated. Recently Freen et al. [11, 15] have presented comparative study and application of neutrosophic sets for multiobjective nonlinear programming problems. The present paper may provide a computational insight into several real-life optimization problems that are encountered in engineering and management sectors, since in many existing optimization techniques, the fuzzy sets or their other versions were used to address the uncertainty and hesitation of a real life problems. Also, in these techniques, the value of aspiration level of objective was expressed by a single membership or single membership and non-membership degree. But, the single membership or non-membership of aspiration level of MOOP are conflicting, and, therefore, the existing optimization techniques do not deal MOOP in a proper way. In this paper, I study an IVIHFS, and propose an interval-valued intuitionistic hesitant fuzzy optimization technique. Further, using proposed technique, I develop a new computational algorithm, and further, the developed algorithm can be implemented in various real-life MOOP of engineering and management sectors. The proposed technique is an extension of both fuzzy and intuitionistic fuzzy optimization techniques. Finally, the developed algorithm is illustrated by a production planning problem, and the obtained results are compared with the results of the existing optimization techniques.

Preliminaries

Multiple Objective Optimization Problem

A mathematical representation of multiple objective optimization problem with K objectives, m constraints and n variables, is given as follows:

$$\begin{array}{cc}& \text{Maximize}Z=\{f_1,f_2,\dots ,f_K\}\hfill \\ \hfill & \text{Such that}{g}_i(x)\le 0\hfill \\ \hfill & i=1,2,\dots ,m\hfill \\ \hfill & x_j\ge 0,j=1,2,\dots ,n.\hfill \\ \hfill \end{array}$$ 1

The set $\mathrm{\Omega }=\{x:g_i(x)\le 0,x_j\ge 0;i=1,2,\dots ,m;j=1,2,\dots ,n\}$ is called a basic feasible space of the problem (1).

Pareto-Optimal Solution

A basic feasible solution $x_0\in \mathrm{\Omega }$ is called a Pareto-optimal solution of the problem (1) if and only if there is no $x\in \mathrm{\Omega }$ such that $f_k(x)\ge f_k(x_0)\forall k$ and $f_{k_0}(x)>f_{k_0}(x_0)$ for at least one $k_0.$

Fuzzy Sets

Zadeh [43] Let X be a collection of objects denoted generically by x; then a fuzzy set A in X is a set of ordered pairs: $A=\{(x,{\mu }_A(x)):x\in X\},$ where ${\mu }_A:X⟶[0,1],$ is called membership function.

Fuzzy Optimization Technique

Zimmermann [47] A fuzzy optimization technique (FOT) to the multiple objective optimization problem (1) can be expressed as follows:

$$\begin{array}{cc}& \text{Maximize}\kappa \hfill \\ \hfill & \text{Such that}\kappa \le {\mu }_k(x),k=1,2,...,K\hfill \\ \hfill & g_i(x)\le 0\hfill \\ \hfill & i=1,2,\dots ,m\hfill \\ \hfill & x_j\ge 0,j=1,2,\dots ,n.\hfill \\ \hfill \end{array}$$ 2

Intuitionistic Fuzzy Sets

Atanassov [3]: Let X be a universal set. An intuitionistic fuzzy set A in X is a set of form $A=\{x,{\mu }_A(x),{\nu }_A(x)\}$, where ${\mu }_A:X\to [0,1]$ and ${\nu }_A:X\to [0,1]$ define the degree of membership and degree of non-membership of the element $x\in X$, respectively, and for every $x\in X,0\le {\mu }_A(x)+{\nu }_A(x)\le 1$. The value of ${\pi }_A(x)=1-{\mu }_A(x)-{\nu }_A(x)$ is called the degree of non-determinacy (or uncertainty) of the element $x\in X$ to the intuitionistic fuzzy set A. If ${\pi }_A(x)=0$, then an intuitionistic fuzzy set becomes fuzzy set and takes the form $A=\{x,{\mu }_A(x),1-{\mu }_A(x)\}$.

Angelov [1]: An intuitionistic fuzzy optimization technique (IFOT) to the multiple objective optimization problem (1) can be expressed as follows:

$$\begin{array}{cc}& \text{Maximize}(\kappa -\tau )\hfill \\ \hfill & \text{Such that}\kappa \le {\mu }_k(x),k=1,2,...,K\hfill \\ \hfill & \tau \ge {\nu }_k(x),k=1,2,...,K\hfill \\ \hfill & \kappa +\tau \le 1\hfill \\ \hfill & \kappa \ge \tau ,\tau \ge 0\hfill \\ \hfill & g_i(x)\le 0\hfill \\ \hfill & i=1,2,\dots ,m\hfill \\ \hfill & x_j\ge 0,j=1,2,\dots ,n.\hfill \\ \hfill \end{array}$$ 3

The Interval-Valued Intuitionistic Hesitant Fuzzy Sets

It is sometimes difficult to construct the precise membership and non membership functions of an element to the set. To overcome this difficulty, the notion of hesitant interval-valued intuitionistic fuzzy sets was initiated by [44].

Hesitant Interval-Valued Intuitionistic Fuzzy Sets

Let X be a fixed set; then a hesitant interval-valued intuitionistic fuzzy sets is represented as $H=\{(x,h_A(x))|x\in X\},$ where $h_A(x)$ is a set of some interval-valued intuitionistic fuzzy sets in X, denoting the possible membership degree intervals and non-membership degree intervals of the element $x\in X$ to the set A. $h_A$ is called hesitant element that is used by Xia and Xu [41] in their research works.

Illustration of the Interval-Valued Intuitionistic Hesitant Fuzzy Sets

An IVIHFS is a very recent tool that addresses the uncertainty and hesitation of several real-life problems and, therefore, it is very necessary to explain it. For this, suppose X represents set of 10,00,000 peoples of a country, and if I ask about number of people who follow Physical Distancing during COVID-19 pandemic. Then the natural answers that I may get are the following: [3,000,000; 4,000,000], [3,500,000; 4,000,000], etc. And similarly the number of people who do not follow Physical Distancing are the following: [50,000, 100,000], [60,000, 80,000], etc. In the same manner, let $X=\{x_1,x_2,\dots ,x_N\}$ be the set of N people in a country. And let the number of people who follow Physical Distancing during COVID-19 pandemic be different according different experts. According to first expert let $E^1$ be $[m_l^{E_1}(x),m_r^{E_1}(x)]$ and number of people who do not follow be $[n_l^{E_1}(x),n_r^{E_1}(x)].$

According to second expert $E^2$ be $[m_l^{E_2}(x),m_r^{E_2}(x)]$ and number of people who do not follow be $[n_l^{E_2}(x),n_r^{E_2}(x)].$

According to third expert let $E^3$ be $[m_l^{E_3}(x),m_r^{E_3}(x)]$ and number of people who do not follow be $[n_l^{E_3}(x),n_r^{E_3}(x)].$ similarly,

According to $k\text{th}$ expert let $E^k$ be $[m_l^{E_k}(x),m_r^{E_k}(x)]$ and number of people who do not follow be $[n_l^{E_k}(x),n_r^{E_k}(x)].$

Then $[m_l^{E_1}(x),m_r^{E_1}(x)]+[n_l^{E_1}(x),m_r^{E_1}(x)]\le N$.

$\Rightarrow \frac{[m_l^{E_1}(x),m_r^{E_1}(x)]+[n_l^{E_1}(x),m_r^{E_1}(x)]}{N}\le 1,$ since $N>0,$ following inequalities makes sense.

$\Rightarrow \left[\frac{[m_l^{E_1}(x),m_r^{E_1}(x)]}{N}\right]+\left[\frac{[n_l^{E_1}(x),n_r^{E_1}(x)]}{N}\right]\le 1$.

$\Rightarrow \left[\frac{m_l^{E_1}(x)}{N},,,\frac{m_r^{E_1}(x)}{N}\right]+\left[\frac{n_l^{E_1}(x)}{N},,,\frac{n_r^{E_1}(x)}{N}\right]\le 1$.

Similarly,

$\left[\frac{m_l^{E_2}(x)}{N},,,\frac{m_r^{E_2}(x)}{N}\right]+\left[\frac{n_l^{E_2}(x)}{N},,,\frac{n_r^{E_2}(x)}{N}\right]\le 1$

$\left[\frac{m_l^{E_3}(x)}{N},,,\frac{m_r^{E_3}(x)}{N}\right]+\left[\frac{n_l^{E_3}(x)}{N},,,\frac{n_r^{E_3}(x)}{N}\right]\le 1$

$⋮$

$⋮$

$\left[\frac{m_l^{E_k}(x)}{N},,,\frac{m_r^{E_k}(x)}{N}\right]+\left[\frac{n_l^{E_k}(x)}{N},,,\frac{n_r^{E_k}(x)}{N}\right]\le 1.$

Therefore,

$\{x\in X:⟨[\frac{m_l^{E_1}(x)}{N},\frac{m_r^{E_1}(x)}{N}],[\frac{n_l^{E_1}(x)}{N},\frac{n_r^{E_1}(x)}{N}]⟩;⟨[\frac{m_l^{E_2}(x)}{N},\frac{m_r^{E_2}(x)}{N}],[\frac{n_l^{E_2}(x)}{N},\frac{n_r^{E_2}(x)}{N}]⟩$; $\cdots ⟨[\frac{m_l^{E_k}(x)}{N},\frac{m_r^{E_k}(x)}{N}],[\frac{n_l^{E_k}(x)}{N},\frac{n_r^{E_k}(x)}{N}]⟩\}$ is a hesitant interval-valued intuitionistic fuzzy set.

Let $H_1,$ and $H_2$ be two hesitant interval-valued intuitionistic fuzzy sets and $h_1\in H_1,h_2\in H_2$. Then, some popular operations among HIVIFS are as follows:

• (i)$H^c=\{h^c:h\in H\}$
• (ii)$H_1\cup H_2=\{h_1\cap h_2:h_1\in H_1,h_2\in H_2\}$, where $h_1\cup h_2=\{[max({\mu }_{h_1}^L,{\mu }_{h_2}^L),max({\mu }_{h_1}^U,{\mu }_{h_2}^U)],[min({\nu }_{h_1}^L,{\nu }_{h_2}^L),min({\nu }_{h_1}^U,{\nu }_{h_2}^U)]\}$
• (iii)$H_1\cap H_2=\{h_1\cap h_2:h_1\in H_1,h_2\in H_2\}$, where $h_1\cap h_2=\{[min({\mu }_{h_1}^L,{\mu }_{h_2}^L),min({\mu }_{h_1}^U,{\mu }_{h_2}^U)],[max({\nu }_{h_1}^L,{\nu }_{h_2}^L),max({\nu }_{h_1}^U,{\nu }_{h_2}^U)]\}$

An optimal solution that is obtained from a single objective may or may not satisfy all the conflicting objectives simultaneously. But it is impossible to obtain a solution that simultaneously optimizes all of the objective and satisfies all the restrictions, called the Pareto-optimal solutions. Mathematically, for the hesitant intuitionistic fuzzy optimization, the Pareto-optimal solutions can be defined in the following manner:

A basic feasible solution $x_0$ is called a Pareto-optimal solution for (1) if there does not exist another x such that $f_k(x)\ge f_k(x^0)$ with ${\mu }_k^{E^l}(f_k(x))\ge {\mu }_k^{E^l}(f_k(x^0))$ and ${\nu }_k^{E^l}(f_k(x))\le {\nu }_k^{E^l}(f_k(x^0)),\forall k=1,2,\cdots ,K;l=1,2,\cdots ,N_0$ and $f_{k_0}(x)>f_{k_0}(x^0)$ with ${\mu }_{k_0}^{E^{n_0}}(f_{k_0}(x))>{\mu }_{k_0}^{E^{n_0}}(f_{k_0}(x^0))$ and ${\nu }_{k_0}^{E^{n_0}}(f_{k_0}(x))<{\nu }_{k_0}^{E^{n_0}}(f_{k_0}(x^0))$ for at least one $k_0\in \{1,2,...,K\};n_0\in \{1,2,...,N_0\}.$

Development of Computational Algorithm

In this paper, before developing a new algorithm based on interval-valued intuitionistic hesitant fuzzy optimization technique, I define a new operation ($S\widehat{K}B$ operation) of IVIHFSs.

New Operation of Interval-Valued Intuitionistic Hesitant Fuzzy Sets

For this, let $S=\{x:[({\mu }_{\mathit{SL}}^{E^l},{\mu }_{\mathit{SU}}^{E^l})]\},{\mu }_{\mathit{SL}}^{E^1}<{\mu }_{\mathit{SL}}^{E^2}<\cdots <{\mu }_{\mathit{SL}}^{E^{N_0}};{\mu }_{\mathit{SU}}^{E^1}<{\mu }_{\mathit{SU}}^{E^2}<\cdots <{\mu }_{\mathit{SU}}^{E^{N_0}}$ and $B=\{x:[({\mu }_{\mathit{BL}}^{E^l},{\mu }_{\mathit{BU}}^{E^l})]\},{\mu }_{\mathit{BL}}^{E^l}<{\mu }_{\mathit{BL}}^{E^2}<\cdots <{\mu }_{\mathit{BL}}^{E^{N_0}};{\mu }_{\mathit{BU}}^{E^1}<{\mu }_{\mathit{BU}}^{E^2}<\cdots <{\mu }_{\mathit{BU}}^{E^{N_0}};\forall l=1,2,...,N_0$ be two interval-valued hesitant fuzzy sets.

Then, $S\widehat{K}B=\{x:[min({\mu }_{\mathit{SL}}^{E^l},{\mu }_{\mathit{BL}}^{E^l}),min({\mu }_{\mathit{SU}}^{E^l},{\mu }_{\mathit{BU}}^{E^l})],[max({\nu }_{\mathit{SL}}^{E^l},{\nu }_{\mathit{BL}}^{E^l}),max({\nu }_{\mathit{SU}}^{E^l},{\nu }_{\mathit{BU}}^{E^l})]\},\forall l=1,2,...,N_0$.

Formation of Interval-Valued Intuitionistic Hesitant Fuzzy Goal

In multiobjective optimization, if an imprecise aspiration level is introduced to each of the objectives then these fuzzy objectives are termed as fuzzy goals. Let $g_k^o,k=1,2,\dots ,K$ be the aspiration level assigned to the $k\text{th}$ objective $f_k(x)$. Then the interval-valued intuitionistic hesitant fuzzy fuzzy goals are the following:

• (i)$f_k(x)⪆g_k^o,k=1,2,\dots ,K$ for maximization type of MOOP.
• (ii)$f_k(x)⪅g_k^o,k=1,2,\dots ,K$ for minimization type of MOOP,

where $``{⪆}^{\prime \prime }$ and $``{⪅}^{\prime \prime }$ are interval-valued intuitionistic hesitant fuzzy versions of “$\ge$” and “$\le$,” respectively. These are called “essentially less or equal to” and “essentially greater than or equal to,” respectively.

Formation of Interval-Valued Intuitionistic Hesitant Fuzzy Multiobjective Goal Programming

An interval-valued intuitionistic hesitant fuzzy multiobjective goal programming can be obtained by the problem (1) and can be defined in the following manner:

$$\begin{array}{cc}& \text{Find}X=\{x_1,x_2,\dots ,x_n\}\hfill \\ \hfill & \text{Such that}{f}_k⪆g_k^o,k=1,2,\dots ,K\hfill \\ \hfill & g_i(x)\le 0\hfill \\ \hfill & i=1,2,\dots ,m\hfill \\ \hfill & x_j\ge 0,j=1,2,\dots ,n,\hfill \\ \hfill \end{array}$$ 4

where $g_k^o$ is goal for $k\text{th}$ objective of the MOOP.

Construction of Interval-Valued Intuitionistic Hesitant Fuzzy Membership Functions

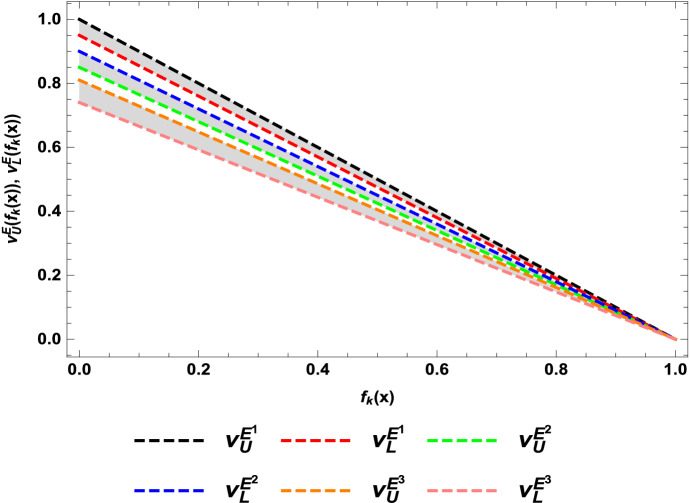
Now I will construct the interval-valued intuitionistic hesitant fuzzy membership function for the $k\text{th}$ fuzzy goal and for this, let ${\mu }_L^{E^1}(f_k(x)),{\mu }_U^{E^1}(f_k(x))$ denote a set of possible interval-valued membership functions (see Fig. 1) and let ${\nu }_L^{E^l}(f_k(x))$, ${\nu }_U^{E^l}(f_k(x))$, $l=1,2,\dots ,N_0.$ denote a set of possible interval-valued non membership functions (see Fig. 2), respectively, and these are defined as follows:

Fig. 1.

Hesitant interval-valued membership functions

Fig. 2.

Hesitant interval-valued non membership functions

Lower Hesitant Fuzzy Membership Functions

The lower hesitant membership function ${\mu }_L^{E^1}(f_k(x)),k=1,2,\dots ,K.$ for the $k$th interval-valued intuitionistic hesitant fuzzy goal $f_k⪆g_k^o,k=1,2,\dots ,K$ can be expressed as follows:

$$\begin{array}{cc}\hfill {\mu }_L^{E^1}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\le L_k^{\mu }\hfill \\ {\alpha }_1\eta \frac{f_k(x)-L_k^{\mu }}{U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le U_k^{\mu }\hfill \\ 1,\mathit{if}{f}_k(x)\ge L_k^{\mu }\hfill \end{array}\right)\hfill \end{array}$$ 5

$$\begin{array}{cc}\hfill {\mu }_L^{E^2}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\le L_k^{\mu }\hfill \\ {\alpha }_2\eta \frac{f_k(x)-L_k^{\mu }}{U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le U_k^{\mu }\hfill \\ 1,\text{if}{f}_k(x)\ge L_k^{\mu }.\hfill \end{array}\right)\hfill \\ \hfill & ...\hfill \end{array}$$ 6

$$\begin{array}{cc}\hfill {\mu }_L^{E^{N_0}}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\le L_k^{\mu }\hfill \\ {\alpha }_{N_0}\eta \frac{f_k(x)-L_k^{\mu }}{U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le U_k^{\mu }\hfill \\ 1,\text{if}{f}_k(x)\ge L_k^{\mu }\hfill \end{array}\right).\hfill \end{array}$$ 7

Upper Hesitant Fuzzy Membership Functions

Let upper and lower bounds for the hesitant fuzzy membership functions be ${\mu }_k^U(f_k(x)),{\mu }_k^L(f_k(x)),k=1,2,...,K.$ Then upper hesitant fuzzy membership functions for each objectives are presented and its shape is presented in Fig. 2 as follows:

$$\begin{array}{cc}\hfill {\mu }_U^{E^1}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\le L_k^{\mu }\hfill \\ {\alpha }_1\frac{f_k(x)-L_k^{\mu }}{U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le U_k^{\mu }\hfill \\ 1,\text{if}{f}_k(x)\ge L_k^{\mu },\hfill \end{array}\right)\hfill \end{array}$$ 8

$$\begin{array}{cc}\hfill {\mu }_U^{E^2}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\le L_k^{\mu }\hfill \\ {\alpha }_2\frac{f_k(x)-L_k^{\mu }}{U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le U_k^{\mu }\hfill \\ 1,\text{if}{f}_k(x)\ge L_k^{\mu }\hfill \end{array}\right)\hfill \\ \hfill & ...\hfill \\ \hfill & ...\hfill \end{array}$$ 9

$$\begin{array}{cc}\hfill {\mu }_U^{E^{N_0}}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\le L_k^{\mu }\hfill \\ {\alpha }_{N_0}\frac{f_k(x)-L_k^{\mu }}{U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le U_k^{\mu }\hfill \\ 1,\text{if}{f}_k(x)\ge L_k^{\mu },\hfill \end{array}\right)\hfill \end{array}$$ 10

where $0\le {\alpha }_1,{\alpha }_2,...,{\alpha }_{N_0}\le 1$.

Lower hesitant fuzzy non membership functions

Let upper and lower bounds for the hesitant fuzzy non membership functions be ${\mu }_k^U(f_k(x)),{\mu }_k^L(f_k(x)).$ Then the lower hesitant fuzzy non membership functions for each objectives are presented below and can be visualized in Fig. 3.

$$\begin{array}{cc}\hfill {\nu }_L^{E^1}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\ge \varphi \times U_k^{\mu }\hfill \\ {\alpha }_1\xi \frac{f_k(x)-L_k^{\mu }}{\varphi \times U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le U_k^{\mu }\hfill \\ 1,\text{if}{f}_k(x)\le L_k^{\mu }\hfill \end{array}\right)\hfill \end{array}$$ 11

$$\begin{array}{cc}\hfill {\nu }_L^{E^2}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\ge \varphi \times U_k^{\mu }\hfill \\ {\alpha }_2\xi \frac{f_k(x)-L_k^{\mu }}{\varphi \times U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le \varphi \times U_k^{\mu }\hfill \\ 1,\text{if}{f}_k(x)\le L_k^{\mu }\hfill \end{array}\right)\hfill \\ \hfill & ...\hfill \\ \hfill & ...\hfill \end{array}$$ 12

$$\begin{array}{cc}\hfill {\nu }_L^{E^{N_0}}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\ge U_k^{\mu }\hfill \\ {\alpha }_{N_0}\xi \frac{f_k(x)-L_k^{\mu }}{\varphi \times U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le \varphi \times U_k^{\mu }\hfill \\ 1,\text{if}{f}_k(x)\le L_k^{\mu }\hfill \\ \text{where}0\le {\alpha }_1,{\alpha }_2,...,{\alpha }_{N_0}\le 1.\hfill \end{array}\right)\hfill \end{array}$$ 13

Fig. 3.

Hesitant interval-valued intuitionistic fuzzy function

Upper Hesitant Fuzzy Non Membership Functions

$$\begin{array}{cc}\hfill {\nu }_U^{E^1}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\ge \varphi \times U_k^{\mu }\hfill \\ {\alpha }_1\frac{f_k(x)-L_k^{\mu }}{\varphi \times U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le U_k^{\mu }\hfill \\ 1,\text{if}{f}_k(x)\le L_k^{\mu }\hfill \end{array}\right)\hfill \end{array}$$ 14

$$\begin{array}{cc}\hfill {\nu }_U^{E^2}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\ge \varphi \times U_k^{\mu }\hfill \\ {\alpha }_2\frac{f_k(x)-L_k^{\mu }}{\varphi \times U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le \varphi \times U_k^{\mu }\hfill \\ 1,\text{if}{f}_k(x)\le L_k^{\mu }\hfill \end{array}\right)\hfill \\ \hfill & ...\hfill \\ \hfill & ...\hfill \end{array}$$ 15

$$\begin{array}{cc}\hfill {\nu }_U^{E^{N_0}}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\ge U_k^{\mu }\hfill \\ {\alpha }_{N_0}\frac{f_k(x)-L_k^{\mu }}{\varphi \times U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le \varphi \times U_k^{\mu }\hfill \\ 1,\text{if}{f}_k(x)\le L_k^{\mu },\hfill \end{array}\right)\hfill \end{array}$$ 16

where $0\le {\alpha }_1,{\alpha }_2,...,{\alpha }_{N_0}\le 1.$

Let $D={\bigcap }_{k=1}^K\widetilde{f_k}$ be a hesitant interval-valued intuitionistic fuzzy decision. Then using $S\widehat{K}B$ operation, I can express an interval-valued intuitionistic hesitant fuzzy degree $\{[{\mu }_D^L(x),{\mu }_D^U(x)],[{\nu }_D^L(x),{\nu }_D^U(x)]\}=\{[({\mu }_L^{E^l}(f_1(x))\wedge {\mu }_L^{E^l}(f_2(x)),\dots \wedge {\mu }_L^{E^1}(f_K(x)),{\mu }_U^{E^l}(f_1(x))\wedge {\mu }_U^{E^1}(f_2(x))),\dots ,\wedge {\mu }_U^{E^1}(f_K(x)))],$

$[({\nu }_L^{E^l}(f_1(x))\vee {\nu }_L^{E^l}(f_2(x)),\dots \vee {\nu }_L^{E^1}(f_K(x)),{\nu }_U^{E^l}(f_1(x))\vee {\nu }_U^{E^1}(f_2(x))),\dots ,\vee {\nu }_U^{E^1}(f_K(x)))]\},$ $\forall l=1,2,\dots ,N_0,$ where $[{\mu }_D^L(x),{\mu }_D^U(x)]=\{[min({\mu }_L^{E^l}(f_1(x)),{\mu }_L^{E^l}(f_2(x)),\dots ,{\mu }_L^{E^1}(f_K(x))),min({\mu }_U^{E^l}(f_1(x)),{\mu }_U^{E^1}(f_2(x)),\cdots ,{\mu }_U^{E^1}(f_K(x)))],$ and $[{\nu }_D^L(x),{\nu }_D^U(x)]=[max({\nu }_L^{E^l}(f_1(x)),{\nu }_L^{E^l}(f_2(x)),\dots ,{\nu }_L^{E^1}(f_K(x))),max({\nu }_U^{E^l}(f_1(x)),{\nu }_U^{E^1}(f_2(x)),\dots ,{\nu }_U^{E^1}(f_K(x)))]\}\forall l=1,2,\dots ,N_0.$

Now, the hesitant interval-valued intuitionistic fuzzy optimization technique for MOOP (1) is presented as follows:

$$\begin{array}{cc}& \text{Maximize}{\mu }_U^{E^l}(f_k(x)),\forall l=1,2,\dots ,N_0\hfill \\ \hfill & \text{Maximize}{\mu }_L^{E^l}(f_k(x)),\forall l=1,2,\dots ,N_0\hfill \\ \hfill & \text{Minimize}{\nu }_U^{E^l}(f_k(x)),\forall l=1,2,\dots ,N_0\hfill \\ \hfill & \text{Minimize}{\nu }_L^{E^l}(f_k(x)),\forall l=1,2,\dots ,N_0\hfill \\ \hfill & \text{Such that}{\mu }_U^{E^l}(f_k(x))\ge {\mu }_L^{E^l}(f_k(x)),\forall l=1,2,\dots ,N_0\hfill \\ \hfill & {\mu }_U^{E^l}(f_k(x))\ge {\nu }_U^{E^l}(f_k(x)),\forall l=1,2,\dots ,N_0\hfill \\ \hfill & {\nu }_U^{E^l}(f_k(x))\ge {\nu }_L^{E^l}(f_k(x)),\forall l=1,2,\dots ,N_0\hfill \\ \hfill & {\mu }_L^{E^l}(f_k(x))\ge {\nu }_L^{E^l}(f_k(x)),\forall l=1,2,\dots ,N_0\hfill \\ \hfill & {\mu }_U^{E^l}(f_k(x))+{\nu }_U^{E^l}(f_k(x))\le 1,\forall l=1,2,\dots ,N_0\hfill \\ \hfill & g_i(x)\le 0,i=1,2,\dots ,m\hfill \\ \hfill & x_j\ge 0,j=1,2,\dots ,n.\hfill \end{array}$$ 17

Now for the simplification of problem (17), I introduce new variables as follows:

${\kappa }_L^l,{\kappa }_U^l,{\tau }_L^l,{\tau }_U^l,\forall l=1,2,\dots ,N_0.$

${\kappa }_L^l=min({\mu }_L^{E^l}(f_1(x)),{\mu }_L^{E^l}(f_2(x)),\dots ,{\mu }_L^{E^1}(f_K(x))),\forall l=1,2,\dots ,N_0$

${\kappa }_U^l=min({\mu }_U^{E^l}(f_1(x)),{\mu }_U^{E^1}(f_2(x)),\dots ,{\mu }_U^{E^1}(f_K(x))),\forall l=1,2,\dots ,N_0$

${\tau }_L^l=max(({\nu }_L^{E^l}(f_1(x)),{\nu }_L^{E^l}(f_2(x)),\dots ,{\nu }_L^{E^1}(f_K(x))),\forall l=1,2,\dots ,N_0$

${\tau }_U^l=max(({\nu }_U^{E^l}(f_1(x)),{\nu }_U^{E^l}(f_2(x)),\dots ,{\nu }_U^{E^1}(f_K(x))),\forall l=1,2,\dots ,N_0.$

The main objective of the problem is to maximize membership function and minimize non membership function under given circumstances. Therefore, I can restate the above problem (35) as follows:

$$\begin{array}{cc}& \text{Maximize}{\kappa }_L^l,l=1,2,\dots ,N_0,\hfill \\ \hfill & \text{Maximize}{\kappa }_U^l,l=1,2,\dots ,N_0,\hfill \\ \hfill & \text{Minimize}{\tau }_L^l,l=1,2,\dots ,N_0,\hfill \\ \hfill & \text{Minimize}{\tau }_U^l,l=1,2,\dots ,N_0.\hfill \\ \hfill & \text{Such that}\hfill \\ \hfill & {\mu }_L^{E^l}(f_k(x))\ge {\kappa }_L^l,l=1,2,\dots ,N_0;k=1,2,\dots ,K\hfill \\ \hfill & {\mu }_U^{E^l}(f_k(x))\ge {\kappa }_U^l,l=1,2,\dots ,N_0;k=1,2,\dots ,K\hfill \\ \hfill & {\nu }_L^{E^l}(f_k(x))\le {\tau }_L^l,l=1,2,\dots ,N_0;k=1,2,\dots ,K\hfill \\ \hfill & {\nu }_U^{E^l}(f_k(x))\le {\tau }_U^l,l=1,2,\dots ,N_0;k=1,2,\dots ,K\hfill \\ \hfill & {\kappa }_U^l\ge {\kappa }_L^l,l=1,2,\dots ,N_0\hfill \\ \hfill & {\tau }_U^l\ge {\tau }_L^l,l=1,2,\dots ,N_0\hfill \\ \hfill & {\kappa }_U^l\ge {\tau }_U^l,l=1,2,\dots ,N_0\hfill \\ \hfill & {\tau }_L^l\ge 0,l=1,2,\dots ,N_0\hfill \\ \hfill & g_i(x)\le 0\hfill \\ \hfill & i=1,2,\dots ,m\hfill \\ \hfill & x_j\ge 0,j=1,2,\dots ,n.\hfill \end{array}$$ 18

Problem (18) can be further modified in the following manner:

$$\begin{array}{cc}& \text{Maximize}\frac{{\sum }_{l=1}^{N_0}({\kappa }_L^l-{\tau }_L^l)+({\kappa }_U^l-{\tau }_U^l)}{N_0}\hfill \\ \hfill & \text{Such that}\hfill \\ \hfill & {\mu }_L^{E^l}(f_k(x))\ge {\kappa }_L^l,l=1,2,\dots ,N_0;k=1,2,\dots ,K\hfill \\ \hfill & {\mu }_U^{E^l}(f_k(x))\ge {\kappa }_U^l,l=1,2,\dots ,N_0;k=1,2,\dots ,K\hfill \\ \hfill & {\nu }_L^{E^l}(f_k(x))\le {\tau }_L^l,l=1,2,\dots ,N_0;k=1,2,\dots ,K\hfill \\ \hfill & {\nu }_U^{E^l}(f_k(x))\le {\tau }_U^l,l=1,2,\dots ,N_0;k=1,2,\dots ,K\hfill \\ \hfill & {\kappa }_U^l\ge {\kappa }_L^l,l=1,2,\dots ,N_0\hfill \\ \hfill & {\tau }_U^l\ge {\tau }_L^l,l=1,2,\dots ,N_0\hfill \\ \hfill & {\kappa }_U^l\ge {\tau }_U^l,l=1,2,\dots ,N_0\hfill \\ \hfill & {\tau }_L^l\ge 0,l=1,2,\dots ,N_0\hfill \\ \hfill & g_i(x)\le 0\hfill \\ \hfill & i=1,2,\dots ,m\hfill \\ \hfill & x_j\ge 0,j=1,2,\dots ,n,\hfill \end{array}$$ 19

where the hesitant fuzzy membership functions for each objectives are presented and visualized in Fig. 1 as follows:

Remark (i)

If ${\mu }_L^{E^l}(f_k(x))={\mu }_U^{E^l}(f_k(x))=\kappa ,l=1,2,\dots ,N_0$ and ${\nu }_L^{E^l}(f_k(x))={\nu }_U^{E^l}(f_k(x))=\tau ,l=1,2,\dots ,N_0,$ then hesitant interval-valued intuitionistic fuzzy technique (19) become an intuitionistic fuzzy optimization technique (20) which have been extensively studied and implemented in various sectors of optimization.

$$\begin{array}{cc}& \text{Maximize}\kappa -\tau \hfill \\ \hfill & \text{Such that}\hfill \\ \hfill & \mu (f_k(x))\ge \kappa \hfill \\ \hfill & \nu (f_k(x))\le \tau \hfill \\ \hfill & \kappa \ge \tau \hfill \\ \hfill & \tau \ge 0\hfill \\ \hfill & g_i(x)\le 0,i=1,2,\dots ,m\hfill \\ \hfill & x_j\ge 0,j=1,2,\dots ,n.\hfill \\ \hfill \end{array}$$ 20

Remark (ii)

If ${\mu }_L^{E^l}(f_k(x))={\mu }_U^{E^l}(f_k(x))=\kappa ,l=1,2,\dots ,N_0$ and ${\nu }_L^{E^l}(f_k(x))={\nu }_U^{E^l}(f_k(x))=0,l=1,2,\dots ,N_0,$ then hesitant interval-valued intuitionistic fuzzy technique (19) becomes a fuzzy optimization technique (21) which has been extensively studied and implemented in various sectors of optimization.

$$\begin{array}{c}\hfill \text{Maximize}\kappa \\ \hfill \text{Such that}\\ \hfill \mu (f_k(x))\ge \kappa \\ \hfill \kappa \ge 0\\ \hfill g_i(x)\le 0,i=1,2,\dots ,m\\ \hfill x_j\ge 0,j=1,2,\dots ,n.\\ \hfill \end{array}$$ 21

Computational Algorithm

Step 1:

Taking the first objective function from set of k objectives of the problem, solve it as a single objective subject to the given constraints. Find the value of objective functions and decision variables.

Step 2:

From values of these decision variables compute values of remaining $(k-1)$ objectives.

Step 3:

Repeat the step 1 and step 2 for remaining $(k-1)$ objective functions.

Step 4:

Tabulate values of objective functions thus obtained from step 1, step 2 and step 3 to form a Table 1 known as positive ideal solution.

Step 5:

From step 4, obtain the lower bounds and upper bounds for each objective functions, where $f_k^{\ast }$ and $f_k^{,}$ are the maximum, minimum values respectively.

Step 6

Here, I denote and define upper and lower bounds by $U_K^{\mu }=max(Z_K(X_r))$ and $L_K^{\mu }=min(Z_K(X_r)),1\le r\le p$, respectively, for each uncertain and imprecise objective functions of MOOP problems.

Step 7:

Set upper and lower bounds for each objective for degree of acceptance and degree of rejection corresponding to set of solutions obtained in step 4.

$U_k^{\mu }=\text{Max}(f_k(X_r))$ and $L_k^{\mu }=\text{Min}(f_k(X_r)),1\le r\le K$.

For non-membership function:

$U_k^{\nu }=\varphi U_k^{\mu }$ where $1\le \varphi \le 3$ called hesitancy index and $L_k^{\nu }=L_k^{\mu }.$

Step 8:

In this step, I apply hesitant interval-valued intuitionistic fuzzy optimization technique for MOOP problem, and I get equivalent linear programming problem.

$$\begin{array}{cc}& \text{Maximize}\frac{{\sum }_{l=1}^{N_0}({\kappa }_L^l-{\tau }_L^l)+({\kappa }_U^l-{\tau }_U^l)}{N_0}\hfill \\ \hfill & \text{Such that}\hfill \\ \hfill & {\mu }_L^{E^l}(f_k(x))\ge {\kappa }_L^l,l=1,2,\dots ,N_0;k=1,2,\dots ,K\hfill \\ \hfill & {\mu }_U^{E^l}(f_k(x))\ge {\kappa }_U^l,l=1,2,\dots ,N_0;k=1,2,\dots ,K\hfill \\ \hfill & {\nu }_L^{E^l}(f_k(x))\le {\tau }_L^l,l=1,2,\dots ,N_0;k=1,2,\dots ,K\hfill \\ \hfill & {\nu }_U^{E^l}(f_k(x))\le {\tau }_U^l,l=1,2,\dots ,N_0;k=1,2,\dots ,K\hfill \\ \hfill & {\kappa }_U^l\ge {\kappa }_L^l,l=1,2,\dots ,N_0\hfill \\ \hfill & {\tau }_U^l\ge {\tau }_L^l,l=1,2,\dots ,N_0\hfill \\ \hfill & {\kappa }_U^l\ge {\tau }_U^l,l=1,2,\dots ,N_0\hfill \\ \hfill & {\tau }_L^l\ge 0,l=1,2,\dots ,N_0\hfill \\ \hfill & g_i(x)\le 0\hfill \\ \hfill & i=1,2,\dots ,m\hfill \\ \hfill & x_j\ge 0,j=1,2,\dots ,n.\hfill \end{array}$$ 22

Table 1.

Positive ideal solution

Maximum	$f_1$	$f_2$	$f_3$	...	$f_k$	X
Maximum $f_1$	$f_1^{\ast }$			...		$X_1$
Maximum $f_2$		$f_2^{\ast }$		...		$X_2$
Maximum $f_3$			$f_3^{\ast }$	...		$X_3$
...				...	...	...
Maximum $f_k$				...	$f_k^{\ast }$	$X_k$
Minimum	$f_1^{\prime }$	$f_2^{\prime }$	$f_3^{\prime }$	...	$f_k^{\prime }$

Here, every uncertain constraint is represented by a set of possible interval-valued membership and interval-valued non membership functions, and these are defined in the following.

Lower Hesitant Fuzzy Membership Functions

Let upper and lower bounds for the hesitant fuzzy membership functions be ${\mu }_k^U(f_k(x)),{\mu }_k^L(f_k(x)),k=1,2,...,K.$ Then hesitant fuzzy membership functions for each objectives are presented below and visualized in Fig. 1 as follows:

$$\begin{array}{cc}\hfill {\mu }_L^{E^1}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\le L_k^{\mu }\hfill \\ {\alpha }_1\eta \frac{f_k(x)-L_k^{\mu }}{U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le U_k^{\mu }\hfill \\ 1,\text{if}{f}_k(x)\ge L_k^{\mu }\hfill \end{array}\right)\hfill \end{array}$$ 23

$$\begin{array}{cc}\hfill {\mu }_L^{E^2}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\le L_k^{\mu }\hfill \\ {\alpha }_2\eta \frac{f_k(x)-L_k^{\mu }}{U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le U_k^{\mu }\hfill \\ 1,\text{if}{f}_k(x)\ge L_k^{\mu }\hfill \end{array}\right)\hfill \\ \hfill & ...\hfill \\ \hfill & ...\hfill \end{array}$$ 24

$$\begin{array}{cc}\hfill {\mu }_L^{E^{N_0}}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\le L_k^{\mu }\hfill \\ {\alpha }_n\eta \frac{f_k(x)-L_k^{\mu }}{U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le U_k^{\mu }\hfill \\ 1,\text{if}{f}_k(x)\ge L_k^{\mu },\hfill \end{array}\right)\hfill \end{array}$$ 25

where $0\le {\alpha }_1,{\alpha }_2,...,{\alpha }_{N_0}\le 1,0\le \eta \le 1.$

Upper Hesitant Fuzzy Membership Functions

Let upper and lower bounds for the hesitant fuzzy membership functions be ${\mu }_k^U(f_k(x)),{\mu }_k^L(f_k(x)),k=1,2,...,K.$ Then hesitant fuzzy membership functions for each objectives are presented and visualized in Figure. 1 as follows:

$$\begin{array}{cc}\hfill {\mu }_U^{E^1}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\le L_k^{\mu }\hfill \\ {\alpha }_1\frac{f_k(x)-L_k^{\mu }}{U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le U_k^{\mu }\hfill \\ 1,\text{if}{f}_k(x)\ge L_k^{\mu }\hfill \end{array}\right)\hfill \end{array}$$ 26

$$\begin{array}{cc}\hfill {\mu }_U^{E^2}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\le L_k^{\mu }\hfill \\ {\alpha }_2\frac{f_k(x)-L_k^{\mu }}{U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le U_k^{\mu }\hfill \\ 1,\text{if}{f}_k(x)\ge L_k^{\mu }\hfill \end{array}\right)\hfill \\ \hfill & ...\hfill \\ \hfill & ...\hfill \end{array}$$ 27

$$\begin{array}{cc}\hfill {\mu }_U^{E^{N_0}}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\le L_k^{\mu }\hfill \\ {\alpha }_{N_0}\frac{f_k(x)-L_k^{\mu }}{U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le U_k^{\mu }\hfill \\ 1,\text{if}{f}_k(x)\ge L_k^{\mu },\hfill \end{array}\right)\hfill \end{array}$$ 28

where $0\le {\alpha }_1,{\alpha }_2,\dots ,{\alpha }_{N_0}\le 1.$

Lower Hesitant Fuzzy Non Membership Functions

Let upper and lower bounds for the hesitant fuzzy non membership functions be ${\mu }_k^U(f_k(x)),{\mu }_k^L(f_k(x)).$ Then hesitant fuzzy non membership functions for each objectives are presented and visualized in Fig. 2 as follows:

$$\begin{array}{cc}\hfill {\nu }_L^{E^1}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\ge \varphi \times U_k^{\mu }\hfill \\ {\alpha }_1\xi \frac{f_k(x)-L_k^{\mu }}{\varphi \times U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le U_k^{\mu }\hfill \\ 1,\text{if}{f}_k(x)\le L_k^{\mu }\hfill \end{array}\right)\hfill \end{array}$$ 29

$$\begin{array}{cc}\hfill {\nu }_L^{E^2}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\ge \varphi \times U_k^{\mu }\hfill \\ {\alpha }_2\xi \frac{f_k(x)-L_k^{\mu }}{\varphi \times U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le \varphi \times U_k^{\mu }\hfill \\ 1,\text{if}{f}_k(x)\le L_k^{\mu }\hfill \end{array}\right)\hfill \\ \hfill & ...\hfill \\ \hfill & ...\hfill \end{array}$$ 30

$$\begin{array}{cc}\hfill {\nu }_L^{E^{N_0}}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\ge U_k^{\mu }\hfill \\ {\alpha }_n\xi \frac{f_k(x)-L_k^{\mu }}{\varphi \times U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le \varphi \times U_k^{\mu }\hfill \\ 1,\text{if}{f}_k(x)\le L_k^{\mu },\hfill \end{array}\right)\hfill \end{array}$$ 31

where $0\le {\alpha }_1,{\alpha }_2,...,{\alpha }_{N_0}\le 1,0\le \xi \le 1,1\le \varphi \le 3.$

Upper Hesitant Fuzzy Non Membership Functions

$$\begin{array}{cc}\hfill {\nu }_U^{E^1}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\ge \varphi \times U_k^{\mu }\hfill \\ {\alpha }_1\frac{f_k(x)-L_k^{\mu }}{\varphi \times U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le U_k^{\mu }\hfill \\ 1,\text{if}{f}_k(x)\le L_k^{\mu }\hfill \end{array}\right)\hfill \end{array}$$ 32

$$\begin{array}{cc}\hfill {\nu }_U^{E^2}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\ge \varphi \times U_k^{\mu }\hfill \\ {\alpha }_2\frac{f_k(x)-L_k^{\mu }}{\varphi \times U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le \varphi \times U_k^{\mu }\hfill \\ 1,\text{if}{f}_k(x)\le L_k^{\mu }\hfill \end{array}\right)\hfill \\ \hfill & ...\hfill \\ \hfill & ...\hfill \end{array}$$ 33

$$\begin{array}{cc}\hfill {\nu }_U^{E^{N_0}}(f_k(x))=& \left\{\begin{array}{c}0,\text{if}{f}_k(x)\ge U_k^{\mu }\hfill \\ {\alpha }_n\frac{f_k(x)-L_k^{\mu }}{\varphi \times U_k^{\mu }-L_k^{\mu }},\text{if}{L}_k^{\mu }\le f_k(x)\le \varphi \times U_k^{\mu }\hfill \\ 1,\text{if}{f}_k(x)\le L_k^{\mu },\hfill \end{array}\right)\hfill \end{array}$$ 34

where $0\le {\alpha }_1,{\alpha }_2,...,{\alpha }_{N_0}\le 1,0\le \xi \le 1$.

Illustration of the Proposed Computational Algorithm

Production Planning Problem

Consider a park of six machine types whose capacities are to be devoted to production of three products. A current capacity portfolio is available, measured in machine hours per weak for each machine capacity unit priced according to machine type. The necessary data in Table 2 are summarized as follows:

Table 2.

Physical parameter values

Machine type	Machine hours	Unit price	Products
			$x_1$	$x_2$	$x_3$
Milling	1400	0.75	12	17	0
Lather	1000	0.60	3	9	8
Grinder	1750	0.35	10	13	15
Jig Saw	1325	0.50	6	0	16
Drill press	900	1.15	0	12	7
Band Saw	1075	0.65	9.5	9.5	4
Total capacity cost	4658.75

Let $x_1,x_2,x_3$ denote three products; then the complete mathematical formulation of the above mentioned problem as a multiobjective linear programming problem is given as follows:

Maximize $\left(\begin{array}{c}{f}_1(x)\\ f_2(x)\\ f_3(x)\end{array}\right)=\left(\begin{array}{c}50x_1+100x_2+17.5x_3\\ 92x_1+75x_2+50x_3\\ 25x_1+100x_2+75x_3\end{array}\right)$

Such that $\left(\begin{array}{ccc}12& 17& 0\\ 3& 9& 8\\ 10& 13& 15\\ 6& 0& 16\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right)\le \left(\begin{array}{c}1400\\ 1000\\ 1750\\ 1325\\ \end{array}\right)$

$\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right)\ge \left(\begin{array}{c}0\\ 0\\ 0\end{array}\right),$ where

$f_1(x):$ represents profit

$f_2(x):$ represents quality

$f_3(x):$ represents worker satisfaction.

Stepwise procedure of the proposed computational algorithm are presented as follows:

Step 1:

Profit, quality and worker satisfaction are three conflicting objectives that cannot be achieved simultaneously. Instead of trying to search an optimal solution such that every objective is optimal (usually impractical), we try to search for an optimal compromise solution where the global evaluation of the synthetic membership degree of optimum for all objectives is maximum and here reflects the decision maker’s consideration of all criteria contained in the multiobjective functions. Based on the global evaluation obtained, we can formulate a single objective linear programming to multiobjective programming problems. The single objective linear programming problem corresponding to given MOLPP is given as follows:

$$\begin{array}{cc}\hfill \text{Maximize}& f_1(x)=50x_1+100x_2+17.5x_3\hfill \\ \hfill & \text{Such that}\hfill \\ \hfill & 12x_1+17x_2\le 1400\hfill \\ \hfill & 3x_1+9x_2+8x_3\le 100\hfill \\ \hfill & 10x_1+13x_2+15x_3\le 1750\hfill \\ \hfill & 6x_1+16x_3\le 1325\hfill \\ \hfill & 12x_2+7x_3\le 900\hfill \\ \hfill & 9.5x_1+9.5x_2+4x_3\le 1075\hfill \\ \hfill & x_1,x_2,x_3\ge 0.\hfill \end{array}$$ 35

Solving single objective linear programming problem (35), I found the following optimum solutions: $x_1=44.93,x_2=50.63,x_3=41.77,{(f_1)}_1=8041.14.$

Step 2:

With these decision variables, computed values of other remaining objective functions are as follows: ${(f_2)}_1=10020.33,{(f_3)}_1=9319.25.$

Step 3:

Step 1 and Step 2 are repeated for other objective functions $f_2,f_3.$

Step 4:

I collect all the optimal solutions obtained from Step 1 and 2 that are placed in Positive Ideal Table 3.

Step 5:

The positive ideal solutions of the considered problem are tabulated in Table 3.

Step 6:

In this step, I calculate lower and upper bounds for each objective functions as follows:

$L_1^{\mu }=5452.63,U_1^{\mu }=8041.14$

$L_2^{\mu }=10020.33,U_2^{\mu }=10950.59$

$L_3^{\mu }=9355.90,U_3^{\mu }=5903.00$

Step 7:

In this step, we construct linear membership function for each objective function (see, Appendix A).

Similarly, we construct linear nonmembership function for each objective function (see, Appendix A).

Step 8:

Solving a hesitant interval-valued intuitionistic fuzzy programming problem for $\varphi =1.2,$ I get the optimal solution, and stop the process. Left and right sides of Fig. 4 show the membership and nonmembership degrees of the obtained solutions (Tables 4 and 5) respectively.

Table 3.

Positive ideal solution

	$f_1$	$f_2$	$f_3$	X
Maximum $f_1$	8041	10020.33	9319.25	$X_1$
Maximum $f_2$	5452.63	10950.59	5903.00	$X_2$
Maximum $f_3$	7983.60	10056.99	9355.90	$X_3$

Fig. 4.

Lower and upper membership and nonmembership degrees

Table 4.

Basic feasible solutions based on proposed algorithm

$x_1^{\ast }$	$x_2^{\ast }$	$x_3^{\ast }$
57.9909	35.1484	47.5441

Table 5.

Optimal values of objectives obtained by various algorithms

S. no.	$(x_j,f_k)$	FS	IFS	IVIFS	HFS	IVIHFS
1.	$f_1$	6826.79	7217.97	7769.64	7845.72	7246.41
2.	$f_2$	10514.18	10359.73	10141.91	10110.95	10348.50
3.	$f_3$	8060.69	8498.59	9116.10	9201.25	8530.42

Conclusions

The interval-valued intuitionistic hesitant fuzzy sets are useful to express intuitionistic fuzzy and hesitant decisions of experts simultaneously. The paper introduces a new set theoretic operation between interval-valued intuitionistic hesitant fuzzy sets. Further, using its advantage, an interval-valued intuitionistic hesitant fuzzy optimization technique is constructed. I also develop a new computational algorithm based on proposed interval-valued intuitionistic hesitant fuzzy optimization technique, and the applicability of this algorithm is illustrated using a production planning problem. queryPlease consider rephrasing the following sentences: The...the sum of all objectives of proposed algorithm is more than some existing algorithms too. The Fig. 5, the profit obtained from proposed algorithm is more than some existing methods, and Fig. 6, the sum of all objectives of proposed algorithm is more than some existing algorithms too.

Fig. 5.

Comparison of results

Fig. 6.

Comparison of sum of objective value

Future Scope

Multiobjective optimization as one of the most used and well-known decision making techniques,; the interesting philosophy and high applicability of MOOP in handling real-world decision making problems with multi objective structures made it very useful and widespread. This leads to further development of MOOP for different decision making problems. Also, present approach is developed based on a newly invented set and hence it can be extended in the following directions:

• The proposed solution concept may be used in nonlinear optimization problems with uncertainty and hesitation.

• It may be implemented in various types of multiple objective transportation and assignment problems.

• Using proposed algorithm one may to get a better solution of the problems of the agricultural, industrial and health management sectors, etc.

• It may be extended to deal multiple objective fractional programming problems.

• It may be implemented in Game theory with uncertainty and hesitation for better decision.

Appendix A

The membership functions for each objectives are given below:

$$\begin{array}{cc}\hfill {\mu }_L^{E^1}(50x_1+100x_2+17.5x_3)=& \left\{\begin{array}{c}0,\text{if}50x_1+100x_2+17.5x_3\le 5452.63\hfill \\ 0.96\eta \frac{50x_1+100x_2+17.5x_3-5452.63}{8041.14-5452.63},\hfill \\ \text{if}5452.63\le 50x_1+100x_2+17.5x_3\le 8041.14\hfill \\ 1,\text{if}50x_1+100x_2+17.5x_3\ge 5452.63\hfill \end{array}\right)\hfill \end{array}$$ 36

$$\begin{array}{cc}\hfill {\mu }_U^{E^1}(50x_1+100x_2+17.5x_3)=& \left\{\begin{array}{c}0,\text{if}50x_1+100x_2+17.5x_3\le 5452.63\hfill \\ 0.96\frac{50x_1+100x_2+17.5x_3-5452.63}{8041.14-5452.63},\hfill \\ \text{if}5452.63\le 50x_1+100x_2+17.5x_3\le 8041.14\hfill \\ 1,\text{if}50x_1+100x_2+17.5x_3\ge 5452.63\hfill \end{array}\right)\hfill \end{array}$$ 37

$$\begin{array}{cc}\hfill {\mu }_L^{E^2}(50x_1+100x_2+17.5x_3)=& \left\{\begin{array}{c}0,\text{if}50x_1+100x_2+17.5x_3\le 5452.63\hfill \\ 0.98\eta \frac{50x_1+100x_2+17.5x_3-5452.63}{8041.14-5452.63},\hfill \\ \text{if}5452.63\le 50x_1+100x_2+17.5x_3\le 8041.14\hfill \\ 1,\text{if}50x_1+100x_2+17.5x_3\ge 5452.63\hfill \end{array}\right)\hfill \end{array}$$ 38

$$\begin{array}{cc}\hfill {\mu }_U^{E^2}(50x_1+100x_2+17.5x_3)=& \left\{\begin{array}{c}0,\text{if}50x_1+100x_2+17.5x_3\le 5452.63\hfill \\ 0.98\frac{50x_1+100x_2+17.5x_3-5452.63}{8041.14-5452.63},\hfill \\ \text{if}5452.63\le 50x_1+100x_2+17.5x_3\le 8041.14\hfill \\ 1,\text{if}50x_1+100x_2+17.5x_3\ge 5452.63\hfill \end{array}\right)\hfill \end{array}$$ 39

$$\begin{array}{cc}\hfill {\mu }_L^{E^3}(50x_1+100x_2+17.5x_3)=& \left\{\begin{array}{c}0,\text{if}50x_1+100x_2+17.5x_3\le 5452.63\hfill \\ \eta \frac{50x_1+100x_2+17.5x_3-5452.63}{8041.14-5452.63},\hfill \\ \text{if}5452.63\le 50x_1+100x_2+17.5x_3\le 8041.14\hfill \\ 1,\text{if}50x_1+100x_2+17.5x_3\ge 5452.63\hfill \end{array}\right)\hfill \end{array}$$ 40

$$\begin{array}{cc}\hfill {\mu }_U^{E^3}(50x_1+100x_2+17.5x_3)=& \left\{\begin{array}{c}0,\text{if}50x_1+100x_2+17.5x_3\le 5452.63\hfill \\ \frac{50x_1+100x_2+17.5x_3-5452.63}{8041.14-5452.63},\hfill \\ \text{if}5452.63\le 50x_1+100x_2+17.5x_3\le 8041.14\hfill \\ 1,\text{if}50x_1+100x_2+17.5x_3\ge 5452.63\hfill \end{array}\right)\hfill \end{array}$$ 41

$$\begin{array}{cc}\hfill {\mu }_L^{E^1}(92x_1+75x_2+50x_3)=& \left\{\begin{array}{c}0,\text{if}92x_1+75x_2+50x_3\le 10020.33\hfill \\ 0.96\eta \frac{92x_1+75x_2+50x_3-10020.33}{10950.59-10020.33},\hfill \\ \text{if}10020.33\le 92x_1+75x_2+50x_3\le 10950.59\hfill \\ 1,\text{if}92x_1+75x_2+50x_3\ge 10020.33\hfill \end{array}\right)\hfill \end{array}$$ 42

$$\begin{array}{cc}\hfill {\mu }_U^{E^1}(92x_1+75x_2+50x_3)=& \left\{\begin{array}{c}0,\text{if}92x_1+75x_2+50x_3\le 10020.33\hfill \\ 0.96\frac{92x_1+75x_2+50x_3-10020.33}{10950.59-10020.33},\hfill \\ \text{if}10020.33\le 92x_1+75x_2+50x_3\le 10950.59\hfill \\ 1,\text{if}92x_1+75x_2+50x_3\ge 10020.33\hfill \end{array}\right)\hfill \end{array}$$ 43

$$\begin{array}{cc}\hfill {\mu }_L^{E^1}(92x_1+75x_2+50x_3)=& \left\{\begin{array}{c}0,\text{if}92x_1+75x_2+50x_3\le 10020.33\hfill \\ 0.96\eta \frac{92x_1+75x_2+50x_3-10020.33}{10950.59-10020.33},\hfill \\ \text{if}10020.33\le 92x_1+75x_2+50x_3\le 10950.59\hfill \\ 1,\text{if}92x_1+75x_2+50x_3\ge 10020.33\hfill \end{array}\right)\hfill \end{array}$$ 44

$$\begin{array}{cc}\hfill {\mu }_U^{E^2}(92x_1+75x_2+50x_3)=& \left\{\begin{array}{c}0,\text{if}92x_1+75x_2+50x_3\le 10020.33\hfill \\ 0.98\frac{92x_1+75x_2+50x_3-10020.33}{10950.59-10020.33},\hfill \\ \text{if}10020.33\le 92x_1+75x_2+50x_3\le 10950.59\hfill \\ 1,\text{if}92x_1+75x_2+50x_3\ge 10020.33\hfill \end{array}\right)\hfill \end{array}$$ 45

$$\begin{array}{cc}\hfill {\mu }_L^{E^3}(92x_1+75x_2+50x_3)=& \left\{\begin{array}{c}0,\text{if}92x_1+75x_2+50x_3\le 10020.33\hfill \\ \eta \frac{92x_1+75x_2+50x_3-10020.33}{10950.59-10020.33},\hfill \\ \text{if}10020.33\le 92x_1+75x_2+50x_3\le 10950.59\hfill \\ 1,\text{if}92x_1+75x_2+50x_3\ge 10020.33\hfill \end{array}\right)\hfill \end{array}$$ 46

$$\begin{array}{cc}\hfill {\mu }_U^{E^3}(92x_1+75x_2+50x_3)=& \left\{\begin{array}{c}0,\text{if}92x_1+75x_2+50x_3\le 10020.33\hfill \\ \frac{92x_1+75x_2+50x_3-10020.33}{10950.59-10020.33},\hfill \\ \text{if}10020.33\le 92x_1+75x_2+50x_3\le 10950.59\hfill \\ 1,\text{if}92x_1+75x_2+50x_3\ge 10020.33\hfill \end{array}\right)\hfill \end{array}$$ 47

$$\begin{array}{cc}\hfill {\mu }_L^{E^1}(25x_1+100x_2+75x_3)=& \left\{\begin{array}{c}0,\text{if}25x_1+100x_2+75x_3\le 5903.00\hfill \\ 0.96\eta \frac{25x_1+100x_2+75x_3-5903.00}{9355.90-5903.00},\hfill \\ \text{if}5903.00\le 25x_1+100x_2+75x_3\le 9355.90\hfill \\ 1,\text{if}25x_1+100x_2+75x_3\ge 5903.00\hfill \end{array}\right)\hfill \end{array}$$ 48

$$\begin{array}{cc}\hfill {\mu }_U^{E^1}(25x_1+100x_2+75x_3)=& \left\{\begin{array}{c}0,\text{if}25x_1+100x_2+75x_3\le 5903.00\hfill \\ 0.96\frac{25x_1+100x_2+75x_3-5903.00}{9355.90-5903.00},\hfill \\ \text{if}5903.00\le 25x_1+100x_2+75x_3\le 9355.90\hfill \\ 1,\text{if}25x_1+100x_2+75x_3\ge 5903.00\hfill \end{array}\right)\hfill \end{array}$$ 49

$$\begin{array}{cc}\hfill {\mu }_L^{E^2}(25x_1+100x_2+75x_3)=& \left\{\begin{array}{c}0,\text{if}25x_1+100x_2+75x_3\le 5903.00\hfill \\ 0.98\eta \frac{25x_1+100x_2+75x_3-5903.00}{9355.90-5903.00},\hfill \\ \text{if}5903.00\le 25x_1+100x_2+75x_3\le 9355.90\hfill \\ 1,\text{if}25x_1+100x_2+75x_3\ge 5903.00\hfill \end{array}\right)\hfill \end{array}$$ 50

$$\begin{array}{cc}\hfill {\mu }_U^{E^3}(25x_1+100x_2+75x_3)=& \left\{\begin{array}{c}0,\text{if}25x_1+100x_2+75x_3\le 5903.00\hfill \\ \frac{25x_1+100x_2+75x_3-5903.00}{9355.90-5903.00},\hfill \\ \text{if}5903.00\le 25x_1+100x_2+75x_3\le 9355.90\hfill \\ 1,\text{if}25x_1+100x_2+75x_3\ge 5903.00\hfill \end{array}\right)\hfill \end{array}$$ 51

The nonmembership functions for each objectives are given below:

$$\begin{array}{cc}\hfill {\nu }_L^{E^1}(50x_1+100x_2+17.5x_3)=& \left\{\begin{array}{c}0,\text{if}50x_1+100x_2+17.5x_3\ge \varphi \times 8041.14\hfill \\ 0.96\xi \frac{\varphi \times 8041.14-50x_1+100x_2+17.5x_3}{\varphi \times 8041.14-5452.63},\hfill \\ \text{if}5452.63\le 50x_1+100x_2+17.5x_3\le \varphi \times 8041.14\hfill \\ 1,\text{if}50x_1+100x_2+17.5x_3\le 5452.63\hfill \end{array}\right)\hfill \end{array}$$ 52

$$\begin{array}{cc}\hfill {\nu }_U^{E^1}(50x_1+100x_2+17.5x_3)=& \left\{\begin{array}{c}0,\text{if}50x_1+100x_2+17.5x_3\ge \varphi \times 8041.14\hfill \\ 0.96\frac{\varphi \times 8041.14-50x_1+100x_2+17.5x_3}{\varphi \times 8041.14-5452.63},\hfill \\ \text{if}5452.63\le 50x_1+100x_2+17.5x_3\le \varphi \times 8041.14\hfill \\ 1,\text{if}50x_1+100x_2+17.5x_3\le 5452.63\hfill \end{array}\right)\hfill \end{array}$$ 53

$$\begin{array}{cc}\hfill {\nu }_L^{E^2}(50x_1+100x_2+17.5x_3)=& \left\{\begin{array}{c}0,\text{if}50x_1+100x_2+17.5x_3\ge \varphi \times 8041.14\hfill \\ 0.98\xi \frac{\varphi \times 8041.14-50x_1+100x_2+17.5x_3}{\varphi \times 8041.14-5452.63},\hfill \\ \text{if}5452.63\le 50x_1+100x_2+17.5x_3\le \varphi \times 8041.14\hfill \\ 1,\text{if}50x_1+100x_2+17.5x_3\le 5452.63\hfill \end{array}\right)\hfill \end{array}$$ 54

$$\begin{array}{cc}\hfill {\nu }_U^{E^2}(50x_1+100x_2+17.5x_3)=& \left\{\begin{array}{c}0,\text{if}50x_1+100x_2+17.5x_3\ge \varphi \times 8041.14\hfill \\ 0.98\frac{\varphi \times 8041.14-50x_1+100x_2+17.5x_3}{\varphi \times 8041.14-5452.63},\hfill \\ \text{if}5452.63\le 50x_1+100x_2+17.5x_3\le \varphi \times 8041.14\hfill \\ 1,\text{if}50x_1+100x_2+17.5x_3\le 5452.63\hfill \end{array}\right)\hfill \end{array}$$ 55

$$\begin{array}{cc}\hfill {\nu }_L^{E^3}(50x_1+100x_2+17.5x_3)=& \left\{\begin{array}{c}0,\text{if}50x_1+100x_2+17.5x_3\ge \varphi \times 8041.14\hfill \\ \xi \frac{\varphi \times 8041.14-50x_1+100x_2+17.5x_3}{\varphi \times 8041.14-5452.63},\hfill \\ \text{if}5452.63\le 50x_1+100x_2+17.5x_3\le \varphi \times 8041.14\hfill \\ 1,\text{if}50x_1+100x_2+17.5x_3\le 5452.63\hfill \end{array}\right)\hfill \end{array}$$ 56

$$\begin{array}{cc}\hfill {\nu }_U^{E^3}(50x_1+100x_2+17.5x_3)=& \left\{\begin{array}{c}0,\text{if}50x_1+100x_2+17.5x_3\ge \varphi \times 8041.14\hfill \\ \frac{\varphi \times 8041.14-50x_1+100x_2+17.5x_3}{\varphi \times 8041.14-5452.63},\hfill \\ \text{if}5452.63\le 50x_1+100x_2+17.5x_3\le \varphi \times 8041.14\hfill \\ 1,\text{if}50x_1+100x_2+17.5x_3\le 5452.63\hfill \end{array}\right)\hfill \end{array}$$ 57

$$\begin{array}{cc}\hfill {\nu }_L^{E^1}(92x_1+75x_2+50x_3)=& \left\{\begin{array}{c}0,\text{if}92x_1+75x_2+50x_3\ge \varphi \times 10950.59\hfill \\ 0.96\xi \frac{\varphi \times 10950.59-92x_1+75x_2+50x_3}{\varphi \times 10950.59-10020.33},\hfill \\ \text{if}10020.33\le 92x_1+75x_2+50x_3\le \varphi \times 10950.59\hfill \\ 1,\text{if}92x_1+75x_2+50x_3\le 10020.33\hfill \end{array}\right)\hfill \end{array}$$ 58

$$\begin{array}{cc}\hfill {\nu }_U^{E^1}(92x_1+75x_2+50x_3)=& \left\{\begin{array}{c}0,\text{if}92x_1+75x_2+50x_3\ge \varphi \times 10950.59\hfill \\ 0.96\frac{\varphi \times 10950.59-92x_1+75x_2+50x_3}{\varphi \times 10950.59-10020.33},\hfill \\ \text{if}10020.33\le 92x_1+75x_2+50x_3\le \varphi \times 10950.59\hfill \\ 1,\text{if}92x_1+75x_2+50x_3\le 10020.33\hfill \end{array}\right)\hfill \end{array}$$ 59

$$\begin{array}{cc}\hfill {\nu }_L^{E^2}(92x_1+75x_2+50x_3)=& \left\{\begin{array}{c}0,\text{if}92x_1+75x_2+50x_3\ge \varphi \times 10950.59\hfill \\ 0.98\xi \frac{\varphi \times 10950.59-92x_1+75x_2+50x_3}{\varphi \times 10950.59-10020.33},\hfill \\ \text{if}10020.33\le 92x_1+75x_2+50x_3\le \varphi \times 10950.59\hfill \\ 1,\text{if}92x_1+75x_2+50x_3\le 10020.33\hfill \end{array}\right)\hfill \end{array}$$ 60

$$\begin{array}{cc}\hfill {\nu }_U^{E^2}(92x_1+75x_2+50x_3)=& \left\{\begin{array}{c}0,\text{if}92x_1+75x_2+50x_3\ge \varphi \times 10950.59\hfill \\ 0.98\frac{\varphi \times 10950.59-92x_1+75x_2+50x_3}{\varphi \times 10950.59-10020.33},\hfill \\ \text{if}10020.33\le 92x_1+75x_2+50x_3\le \varphi \times 10950.59\hfill \\ 1,\text{if}92x_1+75x_2+50x_3\le 10020.33\hfill \end{array}\right)\hfill \end{array}$$ 61

$$\begin{array}{cc}\hfill {\nu }_L^{E^3}(92x_1+75x_2+50x_3)=& \left\{\begin{array}{c}0,\text{if}92x_1+75x_2+50x_3\ge \varphi \times 10950.59\hfill \\ \xi \frac{\varphi \times 10950.59-92x_1+75x_2+50x_3}{\varphi \times 10950.59-10020.33},\hfill \\ \text{if}10020.33\le 92x_1+75x_2+50x_3\le \varphi \times 10950.59\hfill \\ 1,\text{if}92x_1+75x_2+50x_3\le 10020.33\hfill \end{array}\right)\hfill \end{array}$$ 62

$$\begin{array}{cc}\hfill {\nu }_U^{E^3}(92x_1+75x_2+50x_3)=& \left\{\begin{array}{c}0,\text{if}92x_1+75x_2+50x_3\ge \varphi \times 10950.59\hfill \\ \frac{\varphi \times 10950.59-92x_1+75x_2+50x_3}{\varphi \times 10950.59-10020.33},\hfill \\ \text{if}10020.33\le 92x_1+75x_2+50x_3\le \varphi \times 10950.59\hfill \\ 1,\text{if}92x_1+75x_2+50x_3\le 10020.33\hfill \end{array}\right)\hfill \end{array}$$ 63

$$\begin{array}{cc}\hfill {\nu }_L^{E^1}(25x_1+100x_2+75x_3)=& \left\{\begin{array}{c}0,\text{if}25x_1+100x_2+75x_3\ge \varphi \times 9355.90\hfill \\ 0.96\xi \frac{\varphi \times 9355.90-25x_1+100x_2+75x_3}{\varphi \times 9355.90-5903.00},\hfill \\ \text{if}5903.00\le 25x_1+100x_2+75x_3\le \varphi \times 9355.90\hfill \\ 1,\text{if}25x_1+100x_2+75x_3\le 5903.00\hfill \end{array}\right)\hfill \end{array}$$ 64

$$\begin{array}{cc}\hfill {\nu }_U^{E^1}(25x_1+100x_2+75x_3)=& \left\{\begin{array}{c}0,\text{if}25x_1+100x_2+75x_3\ge \varphi \times 9355.90\hfill \\ 0.96\frac{\varphi \times 9355.90-25x_1+100x_2+75x_3}{\varphi \times 9355.90-5903.00},\hfill \\ \text{if}5903.00\le 25x_1+100x_2+75x_3\le \varphi \times 9355.90\hfill \\ 1,\text{if}25x_1+100x_2+75x_3\le 5903.00\hfill \end{array}\right)\hfill \end{array}$$ 65

$$\begin{array}{cc}\hfill {\nu }_L^{E^2}(25x_1+100x_2+75x_3)=& \left\{\begin{array}{c}0,\text{if}25x_1+100x_2+75x_3\ge \varphi \times 9355.90\hfill \\ 0.98\frac{\varphi \times 9355.90-25x_1+100x_2+75x_3}{\varphi \times 9355.90-5903.00},\hfill \\ \text{if}5903.00\le 25x_1+100x_2+75x_3\le \varphi \times 9355.90\hfill \\ 1,\text{if}25x_1+100x_2+75x_3\le 5903.00\hfill \end{array}\right)\hfill \end{array}$$ 66

$$\begin{array}{cc}\hfill {\nu }_U^{E^2}(25x_1+100x_2+75x_3)=& \left\{\begin{array}{c}0,\text{if}25x_1+100x_2+75x_3\ge \varphi \times 9355.90\hfill \\ 0.98\frac{\varphi \times 9355.90-25x_1+100x_2+75x_3}{\varphi \times 9355.90-5903.00},\hfill \\ \text{if}5903.00\le 25x_1+100x_2+75x_3\le \varphi \times 9355.90\hfill \\ 1,\text{if}25x_1+100x_2+75x_3\le 5903.00\hfill \end{array}\right)\hfill \end{array}$$ 67

$$\begin{array}{cc}\hfill {\nu }_L^{E^3}(25x_1+100x_2+75x_3)=& \left\{\begin{array}{c}0,\text{if}25x_1+100x_2+75x_3\ge \varphi \times 9355.90\hfill \\ \frac{\varphi \times 9355.90-25x_1+100x_2+75x_3}{\varphi \times 9355.90-5903.00},\hfill \\ \text{if}5903.00\le 25x_1+100x_2+75x_3\le 9355.90\hfill \\ 1,\text{if}25x_1+100x_2+75x_3\le 5903.00\hfill \end{array}\right)\hfill \end{array}$$ 68

$$\begin{array}{cc}\hfill {\nu }_U^{E^3}(25x_1+100x_2+75x_3)=& \left\{\begin{array}{c}0,\text{if}25x_1+100x_2+75x_3\ge \varphi \times 9355.90\hfill \\ \frac{\varphi \times 9355.90-25x_1+100x_2+75x_3}{\varphi \times 9355.90-5903.00},\hfill \\ \text{if}5903.00\le 25x_1+100x_2+75x_3\le 9355.90\hfill \\ 1,\text{if}25x_1+100x_2+75x_3\le 5903.00\hfill \end{array}\right)\hfill \end{array}$$ 69

where $1\le \varphi \le 3.$

Declarations

Conflict of Interest

Author of this paper declare that I have no conflict of interest.

Ethical Approval

This article does not contain any studies with human participants or animals performed by any of the author.