Dense neuronal reconstruction through X-ray holographic nano-tomography

Abstract

Imaging neuronal networks provides a foundation for understanding the nervous system, but resolving dense nanometer-scale structures over large volumes remains challenging for light (LM) and electron microscopy (EM). Here, we show that X-ray holographic nano-tomography (XNH) can image millimeter-scale volumes with sub-100 nm resolution, enabling reconstruction of dense wiring in Drosophila melanogaster and mouse nervous tissue. We performed correlative XNH and EM to reconstruct hundreds of cortical pyramidal cells, and show that more superficial cells receive stronger synaptic inhibition on their apical dendrites. By combining multiple XNH scans, we imaged an adult Drosophila leg with sufficient resolution to comprehensively catalog mechanosensory neurons and trace individual motor axons from muscles to the central nervous system. To accelerate neuronal reconstructions, we trained a convolutional neural network to automatically segment neurons from XNH volumes. Thus, XNH bridges a key gap between LM and EM, providing a new avenue for neural circuit discovery.

Introduction

Mapping the structure of the nervous system provides a foundation for understanding its function. However, comprehensive mapping at the scale of neuronal circuits requires imaging with both high resolution and large fields of view (FOV). Electron microscopy (EM) has sufficient resolution, but obtaining 3D EM volumes of even small neural circuits requires collecting millions of EM images across thousands of thin sections, and therefore can be prohibitively costly in terms of time and resources^1–4. Conventional light microscopy (LM) is limited in spatial resolution due to the diffraction limit (~250 nm, although super-resolution^5,6 and expansion microscopy^7,8 techniques can exceed this), and thus requires sparse fluorescent labeling to resolve individual cells. Furthermore, visible light does not easily penetrate tissue, requiring physical sectioning or tissue clearing for thick samples (> 1 mm). As a result, the comprehensive set of cells comprising most neural circuits remains unknown. Thus, an imaging modality capable of resolving densely packed neurons over millimeter-scale tissue volumes could enable more complete characterization and understanding of neural circuits.

High energy X-rays (>10 keV) have the potential to image thick specimens with high spatial resolution due to their strong penetration power and sub-nanometer wavelength. Attenuation-based X-ray microscopy techniques offer volumetric imaging of millimeter-scale samples, but these techniques rely on sparse labeling due to limited contrast⁹. Phase-contrast imaging techniques, such as X-ray interferometry^10–12, X-ray ptychography^13,14, single distance free-space propagation imaging^15,16, and X-ray holography^17–21 have brought substantial improvements to image quality, but have yet to achieve the combination of resolution, FOV, and contrast required for reconstruction of densely-stained neuronal morphologies. Thus, until now, tracing of individual neuron morphologies from X-ray image data has been possible only through sparse labeling^9,16,22.

Here, we demonstrate X-ray imaging of densely-stained neural tissue at resolutions down to 87 nm across millimeter-sized volumes, enabling reconstruction of the main branching patterns of neurons within the imaged volume. To achieve this, we employed X-ray holographic nano-tomography (XNH)^23,24 and made improvements by customizing sample preparation, incorporating cryogenic imaging, and optimizing phase retrieval approaches. We show that targeted EM can be used to measure synaptic connectivity of neurons previously reconstructed via XNH. We used this correlative approach in mouse cortex to quantify how the balance of inhibitory and excitatory inputs onto apical dendrites varies by pyramidal cell type (i.e. layer). XNH imaging also allows reconstruction of structures that are difficult to physically section, such as the adult Drosophila leg. We present an XNH dataset of an intact leg in which we reconstructed internal structures, such as muscle fibers and sensory receptors, and traced their associated motor and sensory neurons back to circuits in the fly’s central nervous system. Finally, we applied a convolutional neural network to automatically reconstruct neurons from XNH data. These results establish XNH as a key technique for biological imaging, which bridges the gap between LM and EM (Fig. 1a) to enable dense reconstruction of neuronal morphologies on the scale of neuronal circuits.

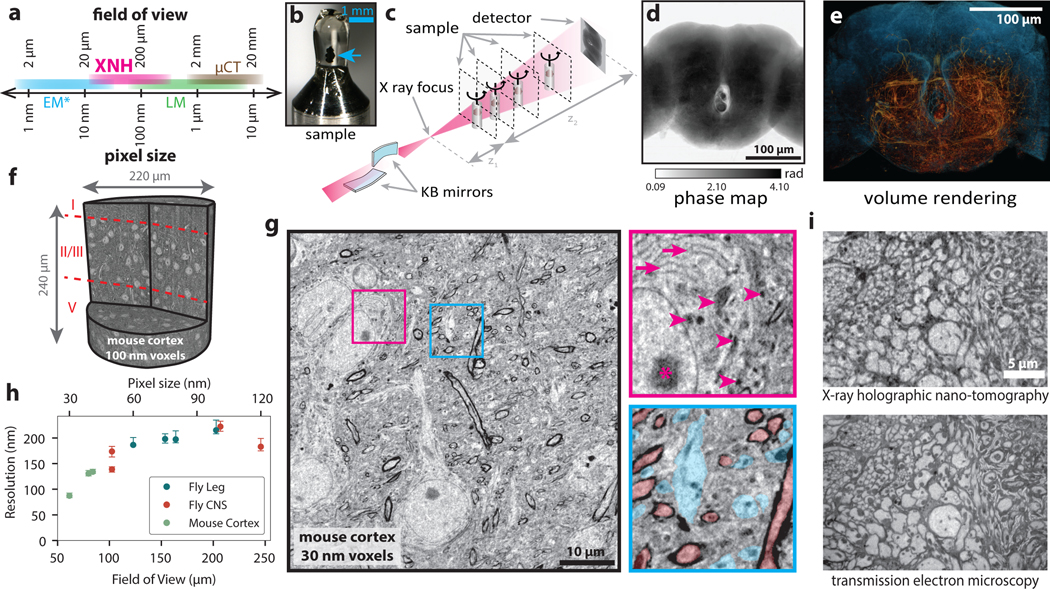
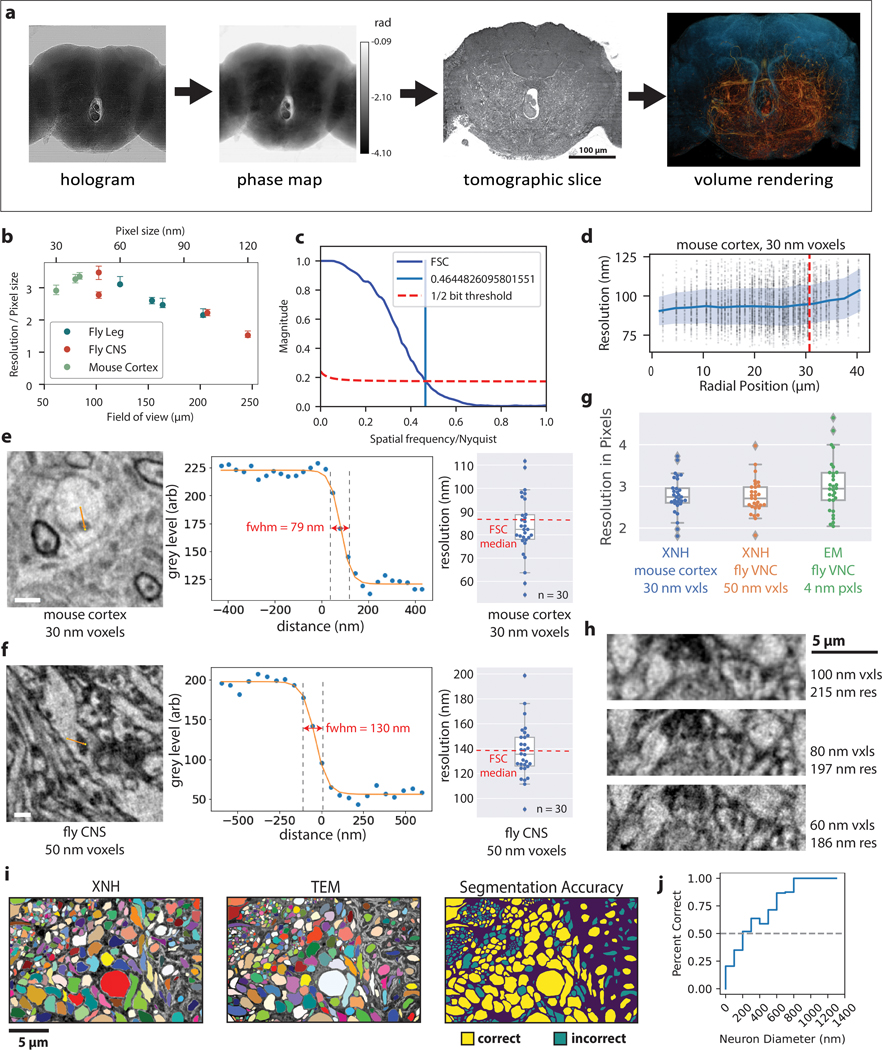
Figure 1: X-ray Holographic Nano-Tomography (XNH) Technique and Characterization.

(a) Schematic depicting pixel and FOV sizes for XNH imaging, along with comparisons to other modalities (assumes a 4 Mpixel detector). Note that EM imaging is generally performed on thin sections or surfaces, while XNH, LM, and micro computed tomography (μCT) can penetrate thicker tissue samples. (b) A Drosophila brain (blue arrow) embedded in resin and mounted for XNH imaging. (c) Imaging setup: the X-ray beam is focused to a spot using two Kirkpatrick-Baez mirrors and traverses the sample before hitting the detector. Holographic projections of the sample (a result of free-space propagation of the coherent X-ray beam) are recorded for each angle as the sample is rotated over 180° (see Extended Data Fig. 1a, Methods) (d) Phase map of the sample shown in Fig. 1b, calculated by computationally combining holograms recorded at 4 different distances from the beam focus. Computed pixel values indicate phase in radians. (e) 3D rendering of XNH volume of the central fly brain (120 nm voxels). The tissue outline is shown in blue, while neurons are highlighted in orange. (f) 3D rendering of an XNH volume of mouse posterior parietal cortex (100 nm voxels). Boundaries between cortical layers are shown in red. (g) Virtual slice through a higher-resolution XNH volume of mouse primary somatosensory cortex (30 nm voxels). Insets: detailed views showing ultrastructural features including mitochondria (magenta arrowheads), endoplasmic reticulum (magenta arrows), nucleolus (magenta asterisk), large dendrites (cyan) and myelinated axons (red). Insets are 10 μm in width. (h) Measured resolution (obtained using Fourier Shell Correlation, see Methods, Supplementary Table 1) for different XNH scans plotted as a function of voxel size and FOV. Datapoints and error bars show mean ± IQR of subvolumes sampled from each XNH scan. Number of subvolumes used for each scan is shown in Supplementary Data Table 1. (i) Comparison of XNH (50 nm voxels) and transmission electron microscopy (12 nm pixels, 100 nm section thickness) images of the same sample, the prothoracic leg nerve of an adult Drosophila.

Results

XNH imaging of central and peripheral nervous systems

We imaged samples of mouse cortex and adult Drosophila brain, ventral nerve cord, and leg at the ID16A beamline of the European Synchrotron (ESRF). The positioning of the sample relative to the focal spot and the detector allows the voxel size and field of view (FOV) to be flexibly adjusted (Fig. 1a). Figure 1b–e shows XNH imaging and the resulting 3D rendering of the central brain of an adult Drosophila (120 nm voxels), in which large individual neuronal processes can be resolved (Extended Data Fig. 1a, Supplementary Video 1, Methods). Figure 1f shows a rendering of an XNH scan from mouse cortex (100 nm voxels), in which cell bodies and larger dendrites can be resolved across multiple cortical layers. Figure 1g shows a virtual slice from a higher-resolution mouse cortex scan (30 nm voxels, Supplementary Video 2). At this resolution, many ultrastructural features are resolved, including mitochondria, endoplasmic reticulum, dendrites, and myelinated axons (Fig. 1g, insets, arrows). However, identification of these ultrastructural features depends in part on prior knowledge of their 3D structure – for example, the tubular shape of mitochondria and dendrites.

To quantify the spatial resolution of XNH image volumes, we used Fourier Shell Correlation (FSC)²⁵ (Methods). We performed scans with voxel sizes between 30 and 120 nm, and measured spatial resolutions between 87 and 222 nm (Fig. 1h, Extended Data Fig. 1b–d,h Supplementary Data Table 1, Supplementary Videos 1–4). We verified these values using an independent edge-fitting measurement (Extended Data Fig. 1e–g).

To verify that XNH images faithfully reproduce tissue ultrastructure, we collected thin-sections of samples after XNH imaging and imaged the same regions at higher lateral resolution with EM (Fig. 1i). We found that the majority of the larger neurites (> 200 nm in diameter) in the EM image could be accurately identified from XNH (Extended Data Fig. 1i,j). This confirms that XNH image volumes contain sufficient membrane contrast and spatial resolution to resolve and reconstruct dense populations of large-caliber neurons (generally long-distance connections) without specific labeling. However, thin processes (such as axon collaterals and distal dendritic branches) are currently difficult to resolve with XNH alone. Although the focus of this study is densely stained tissue (i.e. label-free), we also demonstrated that XNH imaging is compatible with specific labeling of genetically-defined cell types (Extended Data Fig. 5a).

Correlative XNH and EM for connectomic analysis

Pyramidal cells constitute the majority of neurons in the cerebral cortex and are vital for cortical function, but mapping their synaptic inputs is challenging because their dendrites extend several hundreds of micrometers. In particular, apical dendrites (ADs) ascend to layer I, where they integrate long-range excitatory and local inhibitory inputs²⁶ (Fig. 2a), but it is not known in detail how AD connectivity differs across pyramidal cell types. A recent study using large-scale EM revealed that ADs from superficial (layer II/III) pyramidal cells receive proportionally more inhibition than deep-layer (layer V) cells²⁷. However, this study relied on relatively small sample sizes (n ≈ 20 cells per sample) due to the FOV limitations of EM. Here, we combined large FOV XNH (100 nm voxels) with targeted serial section transmission EM²⁸ on the same sample to characterize hundreds of pyramidal cell ADs in posterior parietal cortex (PPC), an area known to be involved in perceptual decision-making²⁹. We first acquired two partially-overlapping XNH scans of mouse PPC that span layers I-V (~8 hours of imaging time), then imaged a synapse-resolution EM dataset from the bottom of layer I that contains the initial bifurcations of pyramidal ADs (~150 hours of imaging time) (Fig. 2a–d, Extended Data Fig. 2a–b, Methods). All 3234 cells within the XNH volumes were identified as excitatory pyramidal cells, inhibitory interneurons, or glia based on morphology and subcellular features³⁰ (Extended Data Fig. 2c). We observed a particularly high density of neuronal somata (both excitatory and inhibitory) concentrated at the top of layer II (designated layer IIa here) (Fig. 2e), which is consistent with histological data (Extended Data Fig. 2d).

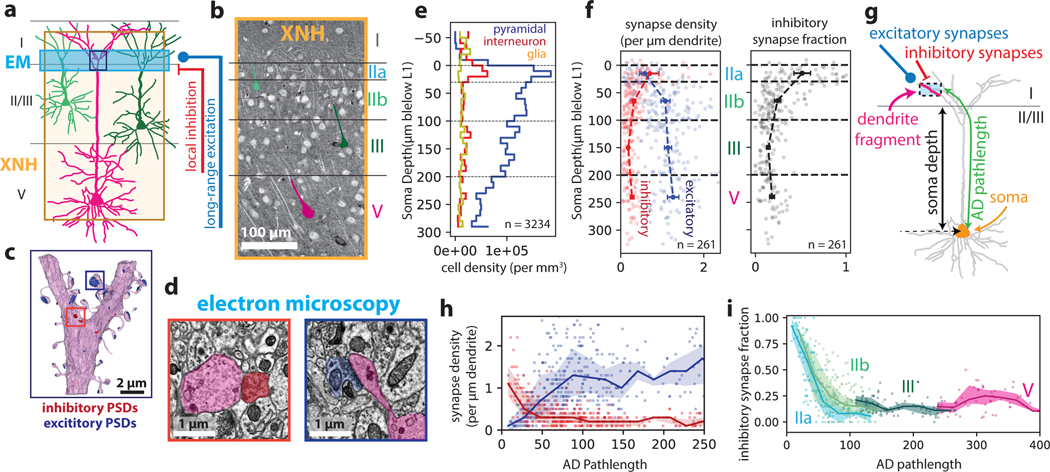
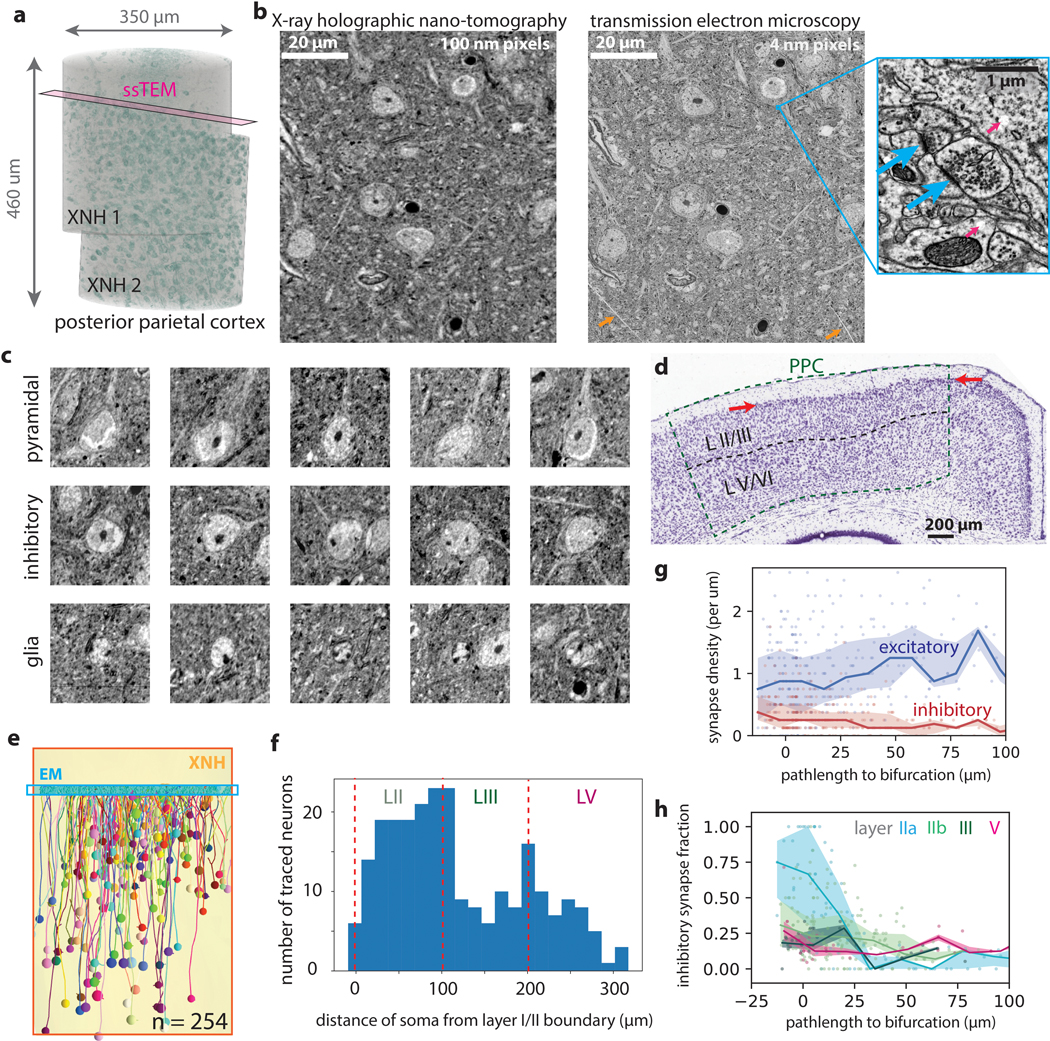
Figure 2: Correlative XNH - EM analysis of the connectivity statistics of pyramidal apical dendrites in posterior parietal cortex (PPC).

(a) Experimental approach: XNH imaging covers superficial and deep layers of PPC with sufficient resolution to resolve cell bodies and apical dendrites (ADs). Targeted 3D EM volume captures the layer I/II interface region, enabling analysis of synaptic inputs onto the apical dendrites near their initial bifurcations. (b) Virtual slice of XNH data (4 μm coronal section, max projection). Cell somata and apical dendrites are visible. Example layer II/III (green) and V (magenta) pyramidal cells are highlighted. (c) 3D EM reconstruction of an AD bifurcation with excitatory (targeting spines, blue) and inhibitory (targeting shafts or spine necks, red) synaptic inputs. (d) Example EM images of inhibitory (red) and excitatory (blue) synapses onto the apical dendrite. (e) Density of cell somata as a function of soma depth (μm below the layer I/II interface), classified as excitatory pyramidal cells (blue), inhibitory interneurons (red) or glia (yellow) (see Extended Data Fig. 2c). The top of layer II (~30 μm) contains a high density of both excitatory and inhibitory neurons. n = 3234 neurons. (f) Left: Synapse density plotted as a function of soma depth (μm below the layer I/II boundary). Excitatory and inhibitory synapses densities shown in blue and red, respectively. Right: Inhibitory synapse fraction plotted as a function of soma depth. Small markers correspond to one neuron. Large markers and error bars indicate mean and 95% confidence interval for each layer calculated via bootstrap analysis. n = 39, 99, 75, 38 neurons for layer IIa, IIb, III and V, respectively. (g) Schematic of dendrite-fragment connectivity analysis. Apical dendrites within the EM volume were divided into fragments 10 μm in length. For each fragment, the density of synapses was recorded along with the pathlength distance from the soma (AD pathlength). (h) Synapse densities (excitatory in blue, inhibitory in red) plotted as a function of pathlength to soma. Each marker corresponds to a 10 μm-long dendrite fragment. Lines and shaded areas indicate binned average (20 μm bins) and interquartile range. (i) Inhibitory synapse fraction plotted as a function of pathlength to soma. Each marker corresponds to one dendrite fragment, colored based on soma type. Lines and shaded areas indicate binned average and interquartile range (mean ± SE) for each soma type.

We traced ADs in the XNH data from pyramidal cell bodies in layers II, III and V up to the layer I/II boundary and identified the same ADs in the aligned EM dataset (n = 261 cells, Extended Data Fig. 2e–f, Methods). We annotated all synaptic inputs onto the ADs within the EM volume (i.e. the bottom of layer I, near the initial bifurcations), labeling each as excitatory (targeting dendritic spines) or inhibitory (targeting dendritic shafts or spine necks) (Fig. 2d)²⁶. We found that layer IIa cells receive more inhibitory synapses and fewer excitatory synapses near the initial bifurcations than do deeper layer cells (Fig. 2f), consistent with previous EM analysis²⁷.

We hypothesized that the increased inhibitory synapse fraction onto ADs of layer IIa cells was due to the proximity of their somata to the initial AD bifurcations, since pyramidal cell bodies receive strong inhibitory input from basket cell interneurons and proximal AD trunks generally have fewer spines²⁶. To test this, we measured the relationship between inhibitory fraction and distance from the soma (Fig. 2g–i, Methods). We found that over the first ~100 μm of path length from the soma, the fraction of inhibitory input onto ADs dropped dramatically. Interestingly, this drop was steepest for layer IIa cells (Fig. 2i, Extended Data Fig. 2g,h), such that the transition from inhibition-dominated to excitation-dominated input was spatially compressed for layer IIa cells.

This multi-scale approach combining XNH and EM in the same tissue sample enabled us to identify three unique properties of layer IIa cells: higher soma density, inhibition-dominated synaptic balance near the initial bifurcations of the ADs, and spatially-compressed transitions from inhibition-dominated to excitation-dominated input on the apical dendrite tufts. These distinct structural properties likely underlie unique functional properties and suggest that association cortex has pyramidal cell specializations beyond the canonical layer structure. Future work will be needed to determine the computational role of these layer IIa cells and whether similar cells exist in other cortical areas.

Millimeter-scale XNH imaging of a Drosophila leg at single-neuron resolution

The Drosophila leg and ventral nerve cord (VNC) are model systems for studying limb motor control^31–33, but we currently lack a detailed map of the sensory and motor neurons that innervate the fly leg. Leveraging the capability of XNH to penetrate mm-scale samples without physical sectioning, we imaged an intact Drosophila front leg (coxa, trochanter, femur, and first half of the tibia segments) and the region of the VNC that controls this leg’s movements (Fig. 3a–c, Extended Data Fig. 3a, Supplementary Data Table 2, Supplementary Video 4). By stitching 10 XNH scans together into a single 3D volume covering over 1.4 mm along the leg’s main axis (Fig. 3c, Extended Data Fig. 3b), we obtained a comprehensive, high-resolution view of the leg’s structure, revealing not only motor and sensory neurons but also muscle fibers and sensory organs.

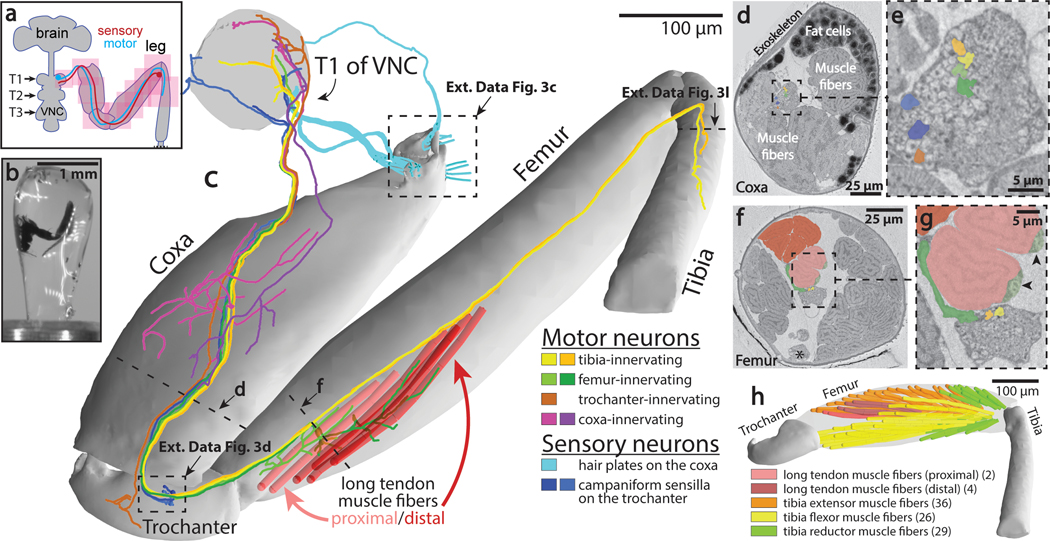
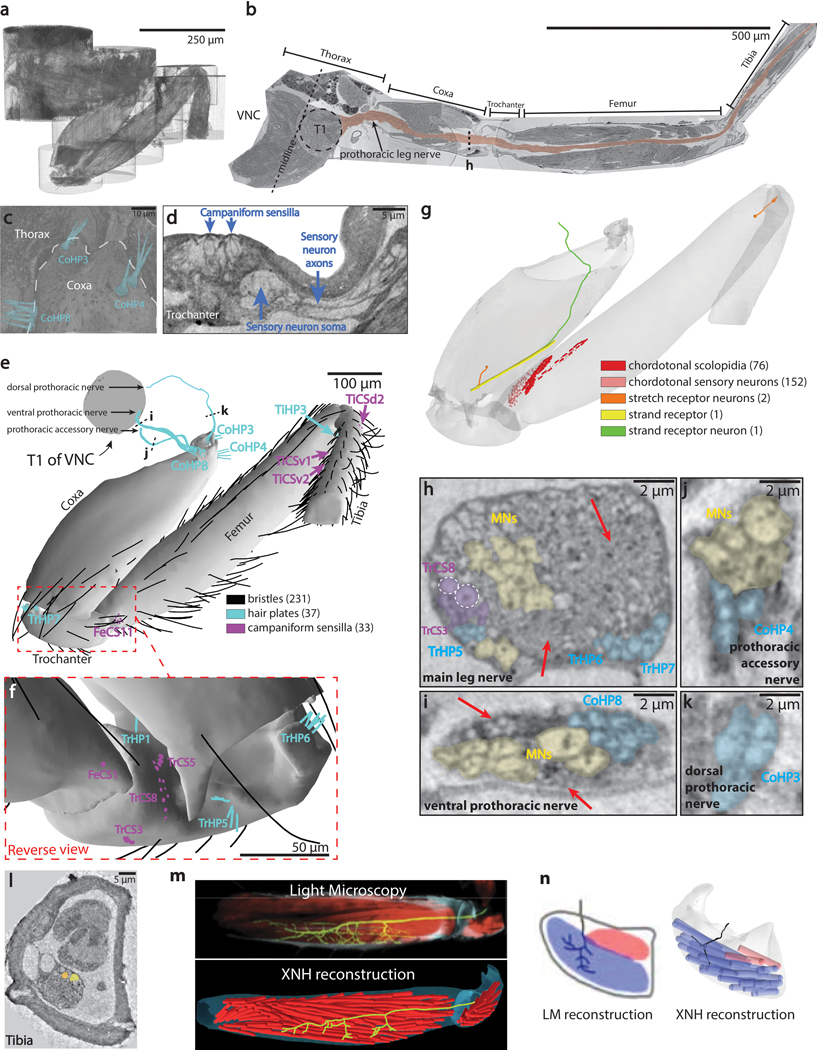
Figure 3: Millimeter-scale imaging of a Drosophila leg at single-neuron resolution.

(a) Schematic of XNH imaging strategy. Ten partially-overlapping XNH scans (Supplementary Data Table 2) were used to capture a front leg’s coxa, trochanter, femur, and half of the tibia, plus the prothoracic neuromere (T1) of the VNC that controls this leg’s movements. The final leg segment, the tarsus, contains no muscles and was not imaged. (b) Photograph of a leg sample after heavy-metal staining, resin embedding, and mounting for XNH imaging. (c) Rendering of reconstructed leg segments, sensory neurons, motor neurons, and muscle fibers. Individual neurons were reconstructed from their target structures in the leg (sensory receptors or muscle fibers) into the VNC. (d-g) Cross-sections through the coxa and femur at locations indicated by dotted lines in (c). Color code is the same as in (c). (d) The arrangement of neurons, muscle fibers, and fat cells in the coxa. (e) Detailed view of nerve from (d). (f) The six long tendon muscle fibers in the femur are organized as a group of two and a group of four, which attach to the long tendon at different locations (see (c)). Asterisk indicates the femoral chordotonal organ, a proprioceptive sensory structure (see Extended Data Fig. 3g)³¹. (g) Detailed view of nerve from (f). Arrowheads indicate swellings of motor neuron axons, likely sites of neuromuscular junctions. Visible here are two swellings from the only motor neuron that innervates these two fibers (light green, see (c)). A different motor neuron (dark green, see (c)) branches off of the leg nerve, traveling past the proximal fibers to innervate the distal fibers. (h) Muscle fibers of the femur. The 97 fibers identified in the femur using XNH is nearly triple that reported previously using fluorescence microscopy³⁸.

First, we comprehensively mapped the sensory organs and their associated sensory neurons in the leg (Supplementary Data Table 3). Our count of organs on the surface of the leg was quantitatively consistent with previous studies that employed scanning EM to visualize these structures³⁴ (Extended Data Fig. 3c–f). In contrast, we identified more internal sensory structures (Extended Data Fig. 3g) than were previously detected with genetic driver lines³⁵. Since XNH is equally capable of resolving surface and internal structures, we were able to complete an exhaustive list of the mechanosensory organs in the fly’s coxa, trochanter, femur, and first half of the tibia (Supplementary Data Table 3).

Next, we reconstructed axons of different classes of sensory neurons to map their projections into the VNC. In doing so, we found systematic variation in the axon diameter of different sensory neuron types, suggesting that some types of sensory signals (namely those from coxal hair plates and trochanteral campaniform sensilla) are conducted to the VNC faster³⁶ or more reliably³⁷ than others (Fig. 3c, Extended Data Fig. 3h–k). Our reconstructions revealed that while most sensory axons enter the VNC through the main leg nerve, the three different coxal hair plates project their axons into the VNC through three different nerves (Fig. 3c, cyan, Extended Data Fig. 3c,e). These results reveal a topographic organization for how these differently positioned (and therefore differently tuned) mechanoreceptors project their signals into the central nervous system.

We then turned to motor structures, reconstructing muscle fibers, tendons, and motor neurons. Motor neurons and muscle fibers had large diameters (1–2 μm and 8–16 μm respectively), enabling straightforward reconstruction throughout the dataset (Fig. 3c–h, Extended Data Fig. 3l). We identified 97 muscle fibers in the femur (Fig. 3h), significantly exceeding the 33 to 40 fibers reported previously using fluorescence microscopy³⁸. Because XNH imaging also resolves the tendons that connect the muscle fibers to the exoskeleton, we were able to unambiguously define muscle groups by identifying muscle fibers that attach to the same tendon (Fig. 3c,h). For example, we found that six muscle fibers in the femur attach to the long tendon, rather than three as previously reported³⁸. Two of the six (light red fibers) attach at the proximal tip of the long tendon and are innervated by a single motor neuron (Fig. 3c,g, light green), whereas the other four (dark red fibers) attach more distally and are innervated by two different motor neurons (one shown in Fig. 3c,g, dark green). This demonstrates that these two muscle fiber groups are under distinct neural control despite connecting to the same tendon. By comparing our reconstructions of motor neuron axons to single-neuron LM images, we were able to identify individual neurons in this dataset that have previously been studied in functional³⁹ or developmental contexts⁴⁰ (Extended Data Fig. 3m–n). These results highlight how a set of overlapping XNH scans can reveal the precise structural relationships between neurons, sensory receptors, and muscle fibers crucial for adaptive control of limb movements.

Automated Segmentation of Neuronal Morphologies using Convolutional Neural Networks

While XNH imaging of millimeter-sized circuits can be accomplished in timescales of hours, manual tracing of neurons can take months. To address this bottleneck, we applied machine-learning algorithms to accelerate neuron reconstruction from XNH image data. We adapted an EM segmentation pipeline⁴¹ and applied it to an XNH image volume of a fly VNC encompassing the majority of a T1 neuromere and part of the front leg nerve (Fig. 4a, Extended Data Fig. 4a, Supplementary Video 2, Methods). This pipeline uses a 3D U-NET convolutional neural network (CNN) (Extended Data Fig. 4b) to make membrane predictions (in the form of an affinity graph, Fig. 4b–c) from XNH image data. Subsequently, voxels are agglomerated into distinct neuron objects based on the predicted affinities (Fig. 4d–e). The resulting neuronal reconstructions (Fig. 4f) contain 3D geometrical information, such as axon and dendrite caliber, that is usually absent from manual tracing.

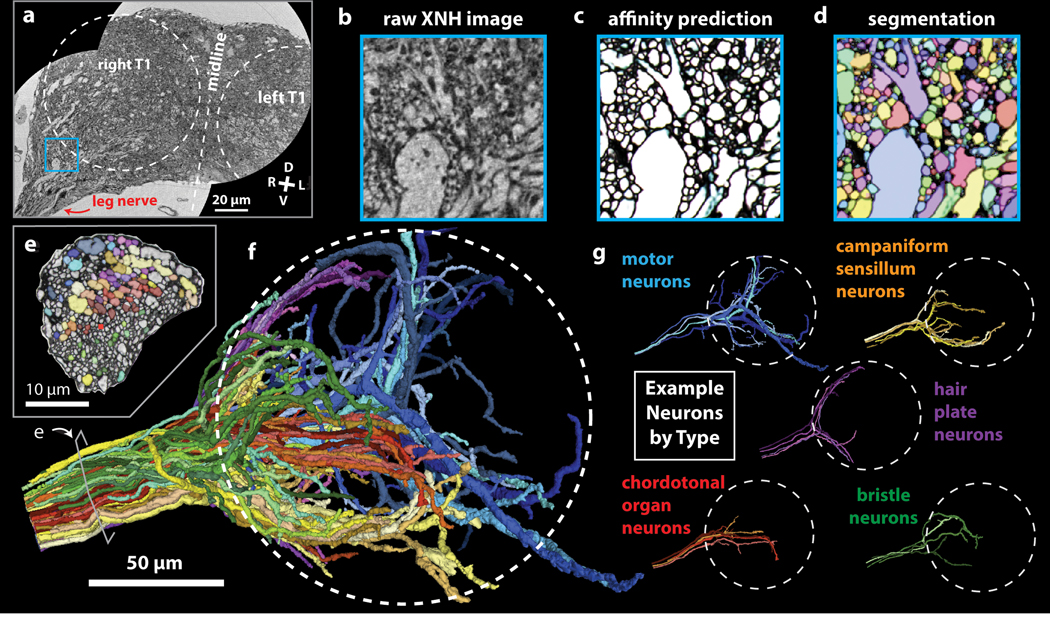
Figure 4: Automated Segmentation of Neuronal Morphologies using Convolutional Neural Networks (CNNs).

(a-b) Raw XNH image data, recorded from the T1 neuromeres of an adult Drosophila VNC. V, ventral; D, dorsal; R, right; L, left. (c) Predicted affinities output by a 3D U-NET (Extended Data Figure 4b) corresponding to the region shown in (b). The affinities quantify how likely it is that each voxel is part of the same neuron as neighboring voxels in z, y and x directions (plotted as RGB). In isotropic XNH data, affinities in different cardinal directions are usually similar, leading to images that appear mostly grayscale. The dark (low affinity) voxels are the basis for membrane predictions. (d) Segmentation corresponding to data shown in (b) and affinities shown in (c). Each neuron is agglomerated into a 3D morphology based on the affinities. In this visualization, each neuron has a unique color. (e) Cross-section of the main leg nerve showing motor and sensory axons reconstructed via automated segmentation. Coloring corresponds to neuron type, revealing spatial organization of neurons within the nerve. (f) 3D visualization of 100 automatically segmented neurons in the Drosophila VNC. Coloring corresponds to neuron types determined based on 3D morphology. Dotted circle indicates boundary of the T1 neuropil associated with control of the front leg. (g) Example morphologies of VNC neuron subclasses (only four example neurons per type shown for clarity).

Accessing large populations of neuronal morphologies by segmentation of XNH data can reveal how circuits are organized. Leveraging this automated segmentation pipeline, we reconstructed 100 neurons that enter the VNC via the main leg nerve and identified them as motor or sensory neuron subtypes based on their axon caliber and main branching patterns^31,40,42,43 (Fig. 4e–g, Supplementary Video 5, Methods). We observed that axons are spatially organized in the nerve, such that neurons of the same morphological subtype tend to also have their axons physically clustered within the nerve (Fig. 4e–f). Furthermore, these reconstructions constitute a database of neuron morphologies that can be corresponded with LM and EM data. For example, by examining the main branching patterns of the largest-diameter motor neuron, we were able to identify it as a fast tibia flexor motor neuron³⁹ that is known to receive direct synaptic input from campaniform sensillum neurons²⁸ (Extended Data Fig. 4c).

To quantify segmentation accuracy, we compared the segmentation to manual tracing of selected neurons, counting the number of split errors (in which different pieces of a neuron are erroneously labeled as separate neurons) and merge errors (in which two different neurons are erroneously joined) (Extended Data Fig. 4d–e). Tuning the segmentation parameters to minimize merge errors while still maintaining an acceptable number of split errors resulted in ~0.75 mergers and ~13 splits per neuron (Extended Data Fig. 4f, Methods). Generally, split errors were found in the most distal branches where the processes became thin, whereas the main branches were segmented with lower error rates. Nevertheless, we found that fixing segmentation errors via proofreading (merging ~13 fragments) was much faster than reconstruction via tracing (placing ~500 nodes).

These results suggest that automated segmentation of XNH data can be used to rapidly reconstruct morphologies for dense populations of neurons. Segmentation networks can also be transferred to different types of tissue; by adding a small amount of cortex-specific training data, we adapted the network to segment XNH data from mouse cortex (Extended Data Fig. 4g–k). Continued progress in neuron segmentation from EM data will likely also benefit segmentation of XNH data, and new approaches for automatic transfer learning may make it possible to generalize EM segmentation algorithms to XNH without needing substantial new training data⁴⁴.

Discussion

Applications of XNH to neural circuits

We demonstrate that X-ray holographic nano-tomography (XNH) enables imaging of neural tissue with sufficient resolution and field of view (FOV) to densely reconstruct individual neurons across millimeter-sized volumes. The resolutions achieved here enable reconstruction of the main dendritic and axonal branches of neurons, but smaller branches are not yet resolved. That said, these resolutions are sufficient for many applications, because a neuron’s main branches often clearly indicate its cell type⁴⁵. In this fashion, we were able to identify pyramidal neuron cell types in mouse cortex (Fig. 2) and to differentiate sensory and motor neurons in the fly VNC (Fig. 3–4).

Given these results, XNH is poised to help address several fundamental questions in neuroscience. For instance, what are all the cellular components in a neuronal circuit, and how are those components arranged? Because heavy metals stain all cells, XNH represents an unbiased approach to mapping neural circuits that can reveal cell types that have previously gone undetected. Because genetic expression is not required, XNH can map millimeter-sized neural circuits in any animal, enabling comparative studies of neural circuit structure across species. With high imaging throughput, multiple samples can be imaged to reveal differences between individuals, developmental stages, or disease models. With the large FOV, projectomes (i.e. atlases of all large-caliber axonal projections between brain regions) can be rapidly mapped to provide a detailed framework for how information flows between brain regions. Projectomes have previously been painstakingly assembled using large-scale EM or built up from sparse fluorescent labeling^46,47, but now the entire brain of smaller model organisms can be mapped in a typical beamline experiment (1–2 weeks) with XNH. Finally, compatibility with EM enables local synaptic connectivity to be studied in the same sample following XNH. This combined approach allows relatively small EM volumes to reveal new patterns of synaptic connectivity for different cell types.

Approaches for volumetric imaging

The penetration power and sub-nanometer wavelength of high-energy X-rays makes them an ideal illumination probe for imaging thick (mm scale), metal-stained tissue samples with nanometer resolution. For neural tissue, phase contrast imaging at X-ray energies above 17 keV provides over a thousand-fold increase in contrast over attenuation contrast⁴⁸. The technique we utilize here, XNH, combines the advantages of phase contrast with today’s smallest and brightest high-energy X-ray focus²³ to reach resolutions needed for resolving individual neurons.

XNH imaging is much faster than volumetric EM in part because EM is typically performed at ~100x smaller voxel size. In principle, low-resolution serial blockface EM (with voxel sizes comparable to XNH) can achieve imaging rates only ~2–3 times slower than XNH^27,49. However, EM imaging of large samples is fundamentally limited by the need for physical sectioning, requiring either destructive sectioning (serial blockface EM) or painstaking collection of thousands of thin sections (serial section EM). With destructive sectioning it is not feasible to survey large volumes quickly at lower resolution, followed by high resolution imaging of subregions of interest, but this is possible with a combined XNH-EM approach (Fig. 2). Furthermore, not all samples can be reliably thin-sectioned – for example, the fly leg (Fig. 3) sections poorly due to the material properties of the exoskeleton. Thus, XNH offers unique capabilities for non-destructive mapping of large circuits in both the central and peripheral nervous systems.

Since XNH is a wide-field imaging technique, teravoxel-sized datasets can be rapidly acquired within days of imaging, enabling a range of applications requiring high-resolution imaging of large FOVs. This aspect sets XNH apart from X-ray ptychography, another phase contrast technique capable of high resolution imaging of biological tissues^13,50. Ptychography is a scanning technique – thus data collection is slower. Furthermore, samples typically need to be smaller than ~100 μm in thickness for ptychography.

In all wide-field imaging modalities, the ratio of FOV to voxel size is determined by the size of the detector (effectively 2048 × 2048 for this work), but this ratio can be increased by using larger detectors or detector arrays. XNH offers additional flexibility because samples can be larger than the FOV of a single scan, and multiple sub-volumes can be imaged and stitched together to extend tissue coverage at high resolution. This allows users to select the optimal voxel size to ensure sufficient resolution for neuron reconstruction while maximizing imaging throughput.

Outlook

Although XNH imaging can be implemented using a commercial X-ray source¹⁹, synchrotron sources are more suitable for obtaining high quality data. Access to these facilities is usually granted via research proposals and thus is free for academic researchers. There are more than 50 synchrotron sources worldwide and an increasing number of these are developing coherent imaging beamlines that could support XNH imaging.

It is worth noting that the resolutions achieved here (87–222 nm) are still far from the theoretical limits for hard X-rays, which have sub-nanometer wavelengths. In practice, XNH resolution is limited by focusing optics, mechanical stability and precision of stage movements, sample warping and performance of reconstruction algorithms, rather than by fundamental physical limits. Similarly, we expect continued improvements in imaging speed. Data collection can be accelerated by using faster and larger detectors, faster actuators, and increased coherent photon flux. The upgrade of the European Synchrotron (to be completed in mid-2020), along with planned improvements to X-ray optics and detectors, may enable faster imaging with the ability to resolve the thinnest neuron branches and the synapses between them, opening an array of applications in mapping neuronal circuit connectivity.

Accession codes

Raw XNH data is available in publicly-accessible repositories under the following accession codes:

1. BossDB (https://bossdb.org/)

https://bossdb.org/project/kuan_phelps2020

1. WebKnossos (https://webknossos.org/)

XNH_ESRF_mouseCortex_30nm

XNH_ESRF_mouseCortex_40nm

XNH_ESRF_drosophilaBrain_120nm

XNH_ESRF_drosophilaVNC_50nm

XNH_ESRF_drosophilaLeg_75nm

1. 3. ESRF (https://data.esrf.fr/public/10.15151/ESRF-DC-217728238)

DOI: doi.esrf.fr/10.15151/ESRF-DC-217728238

Methods

Experimental Animals

Experimental procedures were approved by the Harvard Medical School Institutional Animal Care and Use Committee and performed in accordance with the Guide for Animal Care and Use of Laboratory Animals and the animal welfare guidelines of the National Institutes of Health. Mice (Mus musculus) used in this study were C57BL/6J-Tg(Thy1-GCaMP6s)GP4.3Dkim/J, male, 32 weeks and C57BL/6, male, 28 weeks, ordered through Jackson Laboratory (The Jackson Laboratory, Bar Harbor, ME). Mice were housed up to 4 per home cage at normal temperature and humidity on reverse light cycle, and relocated to clean cages every two weeks.

Flies (Drosophila melanogaster) used in this study were 1–7 day old female adults with the w1118 genetic background. The transgenic approach for labeling GABAergic nuclei (used in Fig. 3 and Extended Data Fig. 5) is described below.

See Life Sciences Reporting Summary for more details.

Sample preparation

Tissue samples were prepared for XNH imaging using protocols for electron microscopy (EM), including fixation, heavy metal staining, dehydration, and resin embedding^4,51. For heavy metal staining, we used an enhanced rOTO protocol⁵¹ for all mouse samples and some of the fly samples. For other fly samples, we modified the protocol to increase⁴ or decrease heavy metal staining, but these variations did not have a large effect on XNH image quality. Following staining, samples were dehydrated in a graded ethanol series and embedded in either TAAB Epon 812 (Canemco) or LX112 (Ladd Research Industries) resin. Resin-embedded samples were polymerized at 60ºC for 2–4 days. Polymerized samples were trimmed down to a narrow (1 to 2 mm diameter) rod using either an ultramicrotome or a fine saw, then glued to an aluminum pin. To smooth rough surfaces on the samples, which introduce noise into the XNH images, mounted samples were covered in a small droplet of resin, and the droplet was polymerized at 60ºC for 2–4 days.

For labeling APEX2-expressing cells (see below), we performed 3,3’-diaminobenzidine (DAB) staining after fixation and before heavy metal staining. Briefly, the nervous system from an adult female was dissected, fixed (2% glutaraldehyde, 2% formaldehyde solution in 100mM sodium cacodylate buffer with 0.04% CaCl2) at room temperature for 75 minutes then moved to 4ºC for overnight fixation in the same solution. The following day, the sample was washed in cacodylate buffer, then 50mM glycine in cacodylate buffer, then cacodylate buffer again. To stain APEX2-expressing cells, the sample was incubated with 0.03% DAB in cacodylate buffer for 30 minutes, then H₂O₂ was added directly to the incubating samples to reach an H₂O₂ concentration of 0.003%⁵². The reaction was allowed to continue for 30 minutes, after which the sample was washed in cacodylate buffer and inspected for visible staining product. Clusters of small brown puncta corresponding to the labeled nuclei were faintly visible (Extended Data Fig. 1g, top panel). The DAB and H₂O₂ incubations were repeated once more to increase the staining intensity. The sample was subsequently stained with 3-amino-1,2,4-triazole-reduced osmium⁴ and uranyl acetate, then dehydrated and embedded in LX112 resin.

We found that heavy-metal staining, typical for EM studies⁵¹, improves membrane contrast in XNH images. However, heavy-metal staining also increases X-ray absorption, causing heating and warping of the sample and thereby degrading image resolution. To counteract sample warping, we imaged in cryogenic conditions and optimized X-ray dosage to maximize signal but avoid excessive heating⁵³. Samples that had major alignment artifacts due to warping or damage during X-ray imaging were excluded from further analysis.

We determined that with optimal imaging conditions even unstained tissue can generate sufficient contrast to trace large neurons (Extended Data Fig. 1h, Supplementary Video 6). The unstained sample (Extended Data Fig. 5b, Supplementary Video 6) was fixed in Karnovsky’s fixative, dehydrated in ethanol, cleared with xylene, and embedded in paraffin. The embedded sample was trimmed down to a narrow (1 to 2 mm diameter) rod using a scalpel, and inserted into a hollow aluminum pin with a 0.8 mm inner diameter for imaging.

Generation of Nuclear-APEX2 Flies

Based on the similarity between XNH and EM images, we reasoned that genetic labeling strategies previously developed for EM such as APEX2^52,54 could be adapted for XNH. We developed a fly reporter line that targets the peroxidase APEX2⁵⁴ to cell nuclei (Methods), and demonstrated that labeled neurons could be identified in XNH datasets (Extended Data Fig. 5a).

To target APEX2 to the nucleus, we fused a targeting sequence consisting of a methionine and 38 amino acids of the Stinger sequence (MSRHRRHRQRSRSRNRSRSRSSERKRRQRSRSRSSERRR) to APEX2. The targeting sequence was first cloned into the pENTR vector and subsequently cloned by recombination using the Gateway system into a destination vector (gift from Dr. Frederik Wirtz-Peitz) containing UAS-attR-sbAPEX2–3xMyc. The resulting UAS-NLS-APEX2-Myc construct was used to generate a transgenic line by direct injection using φC31 site-specific integration at the attP40 docking site on chromosome two.

To test whether APEX2 labeled cells could be identified via XNH imaging, we labeled GABAergic nuclei with APEX2. Fly lines containing the transgenes Gad1-p65AD, UAS-CD8-GFP and elav-Gal4DBD, UAS-CD8-GFP (gifts from Dr. Haluk Lacin) were crossed with the nuclear-APEX2 fly described above to generate flies with genotype w; elav-Gal4DBD, UAS-CD8-GFP / UAS-NLS-APEX2-Myc; Gad1-p65AD, UAS-CD8-GFP / +. The nervous system from a 5–6 day old adult female fly was prepared for XNH imaging as described above.

To automatically detect APEX2-labeled cell nuclei in XNH images, a 3D random forest pixel classifier was created, trained, and deployed using ilastik⁵⁵. For training, a sparse set of pixel labels was interactively annotated for background pixels and labeled cell body pixels.

See Life Sciences Reporting Summary for more details.

Experimental setup and data acquisition

XNH imaging was performed at beamline ID16A at the European Synchrotron in Grenoble, France. The end-station of the beamline is placed 185 m from the undulator source for improved coherence. The X-ray beam was focused using fixed curvature, multilayer coated Kirkpatrick-Baez mirrors into a spot measuring about 15 nm at X-ray energy of 33.6 keV²³ and 30 nm at 17 keV. The photon flux was on the order of 1–4 × 10¹¹ ph/s.

The sample stage and X-ray focusing optics were placed in a vacuum chamber (pressure ~10⁻⁸ mbar) and a liquid nitrogen based cryogenic system was integrated inside the stage, keeping the sample at 120 K during imaging. For cryogenic imaging, the samples were transferred into the vacuum chamber with a Leica cryo-shuttle. The samples were placed on a high-precision rotation stage⁵⁶ downstream of the beam focus, and intensity projections (i.e. holograms) were recorded using a FReLon 4096 × 4096 pixel CCD detector⁵⁷ with 2x binning, lens-coupled to a 23 μm thick GGG:Eu scintillator.

After traversing the sample, the beam was allowed to propagate and generate self-interference patterns (i.e. holograms). The resulting intensity was recorded on the detector placed 1.2 m downstream of the sample. The divergent beam gives geometrical magnification M = (z₁ + z₂)/z₁ with z₁ = focus-to-sample distance and z₂ = sample-to-detector distance. Therefore, the pixel size and the corresponding FOV are proportional to z₁ when the detector position is fixed (Fig. 1b). For each scan, four tomographic series of projections (rotations of the sample over 180º) were recorded at different focus-to-sample distances. To eliminate ring artifacts in tomographic reconstructions, the samples were laterally displaced at each rotation angle by a randomly-determined distance of up to 25 pixels using high-precision piezoelectric actuators²⁴. For each tomographic scan of the mouse cortex, 1800 projections were recorded with exposure times of 0.1 s at X-ray energy 17 keV and 0.35 s at 33.6 keV. For the Drosophila scans at 17 keV, 2000 projections were collected with 0.2 s exposure times.

Image reconstruction

The recorded holograms were initially preprocessed to compensate for distortions and noise specific to the optics and detector, and normalized with the empty beam²⁴. For each rotation angle, the four holograms corresponding to different propagation distances were aligned and brought to the same magnification. Normally, the holograms are cropped to the smallest FOV, corresponding to the targeted pixel size. In order to obtain an extended FOV, the information from the three larger FOVs at lower resolutions was integrated in the reconstruction as well.

From these sets of aligned holograms, phase maps were obtained through an iterative algorithm^21,58–60. The initial approximations of the amplitude and phase were obtained through a method based on⁶¹, adapted for multiple propagation distance holograms⁵⁹. For regularization we used the ratio between the refractive index decrement δ and the absorption index β corresponding to Osmium (δ/β = 27 for X-ray energy 33.6 keV and δ/β = 9 for 17 keV). This regularization was used only to obtain the starting point of the iterative approach and only affects low spatial frequencies. At each iterative step, the amplitude term was kept constant and the phase term was updated. Typically, 10 iterations were sufficient for the phase term to converge. Computation time was approximately 15 minutes per phase map (single CPU node). Computation of the phase maps was done in parallel by treating the holograms for each rotation angle independently.

Lastly, a 3D image volume of the tissue was generated by combining the phase maps from all angles into a tomographic reconstruction using filtered back-projection⁶². Iterative CT approaches and regularization were not used here. Since we acquire and combine four sets of angular projections at four different geometrical magnifications, we can use the lower resolution – larger FOV information to reconstruct extended FOV tomograms. In this case the reconstructed volume is larger than the detector size (Supplementary Data Table 1), however, the image quality degrades gradually towards the edges of the extended field since less information is available (Extended Data Fig. 1d).

Resolution Measurements

While the voxel size is directly determined by the sample positioning, the effective resolution depends on multiple factors, including the focal point size and the coherence properties of the X-ray beam, mechanical stability, detector characteristics, sample composition and image reconstruction approach. To measure the effective resolution, we used Fourier Shell Correlation and Edge-Fitting independently (see below), and found the results to be consistent.

Fourier Shell Correlation

To perform Fourier Shell Correlation (FSC)²⁵, we split the data into two independently-acquired image volumes (see below) and measured the normalized cross-correlation coefficient between the two volumes over corresponding shells (size 6) in Fourier space. The intersection between the FSC line and the ½-bit threshold⁶³ was used to determine the resolution (Extended Data Fig. 1c).

The two image volumes were generated independently from half of the phase maps (even and odd phase projections were separated). FSC was applied by comparing chunks from the two image volumes at corresponding locations. The size of these chunks was varied to find a size at which the FSC metric was stable, which occurred at chunk sizes of ~200³ voxels or larger. Measurements on larger chunks (up to 1000³ voxels) remained stable, but took longer to compute. Computation was performed on evenly spaced chunks across the volume, excluding the regions containing only empty resin. Once the resolutions for all chunks were measured, the median and IQR were calculated (Fig. 1h, Extended Data Fig. 1b).

For characterization of resolution within a single scan (Extended Data Fig. 1d), FSC was performed on image cubes containing 100³ voxels, and each cube was plotted separately.

Edge-Fitting

For measuring resolution by edge-fitting, line paths perpendicular to sharp edges in the image volumes were annotated manually using CATMAID (Extended Data Fig. 1e,f, left)^45,64. The image intensity along these line paths were then calculated using the pyMaid python API (https://github.com/schlegelp/pyMaid). The points along the line paths were fit to the sigmoid function:

$$p_3+\frac{p_0}{2}\left(1-tanh\left(\frac{x-p_1}{p_2}\right)\right)$$

Where $x$ is the length along the line path and $p_{1–4}$ are free parameters determined by nonlinear regression. (Extended Data Fig. 1e,f, middle).

Given a fit to an edge, the measured resolution is given by:

$$res=asech\left(\frac{2}{\sqrt{2}}\left|p_2\right|\right)$$

The fits to each line path were inspected and poor fits were refit with different initial parameters or removed. Edge-fitting was used in the 30 nm mouse cortex dataset (Extended Data Fig. 1e) and the 50 nm Drosophila VNC dataset (Extended Data Fig. 1f). For each dataset, 30 measurements were taken (Extended Data Fig. 1e,f, right). For purposes of comparison, we also applied edge-fitting measurements to electron microscopy images of thin-sections of Drosophila VNC (Extended Data Fig. 1g, 4 nm pixels, 45 nm thick section).

Variability in Measured Resolution

In XNH data, resolution is generally better for scans with smaller voxel size (Fig. 1h). However, measured resolution was significantly larger than the voxel size, between 1.5 to 3.5 times the voxel size. In EM images of nervous tissue, the ratio of measured resolution to pixel size is similar (Extended Data Fig. 1g). As the voxel size is reduced, the resolution per voxel deteriorates (Extended Data Fig. 1b). This is due to a combination of factors, such as more challenging conditions for phase retrieval and tomographic reconstruction and higher risk of sample warping during the scan. The photon flux density increases with smaller voxel sizes, so limiting the radiation dose and imaging at cryogenic temperatures are more critical.

Sample to sample differences also affect the resolution. Sample density can affect beam absorption and heating, and the location of the field of view relative to the mounting pin can affect heat dissipation. For one sample (fly leg), we imaged the same field of view with different voxel sizes, and found that the measured resolution improved monotonically with smaller voxel size (Extended Data Fig. 1h).

We found that the measured resolution is approximately uniform across the scan volumes (i.e. the tomographic reconstruction does not introduce major anisotropy in the image quality) (Extended Data Fig. 1d). However, the resolution near the axis of rotation (the center of the cylinder) appears slightly better. Also, areas in extended field of view (areas outside the detector size, beyond red line in Extended Data Fig. 1d) exhibit slightly degraded resolution. There may also be variation in measured resolution intrinsic to the evaluation method. For example, regions of empty resin (devoid of structure) within a sample exhibit poor resolution when measured by FSC. These regions were excluded from FSC calculations (Fig. 1h, Extended Data Fig. 1b, Supplementary Data Table 1).

Post-Hoc EM imaging

After completing XNH imaging, samples were re-embedded in a block of resin and trimmed for thin-sectioning. Serial thin sections (45–100 nm) were cut using a 35 degree diamond knife (Diatome) and collected onto LUXFilm-coated copper grids (Luxel Corp.). Sections were imaged on a JEOL 1200EX transmission electron microscope (80 kV accelerating potential, 1500x mag), and images were acquired with a 20 MPix camera system (AMT Corp.) at 4–12 nm pixels.

For the fly VNC sample, several thin sections including the main leg nerve were collected and imaged with TEM (Fig. 1i). The XNH image volume was rotated to match the orientation of the transmission EM (TEM) sections using Neuroglancer (https://github.com/google/neuroglancer). The TEM image of the leg nerve was elastically aligned to a single matching image taken from the XNH dataset using AlignTK (https://mmbios.pitt.edu/aligntk-home). Neurons in corresponding images from XNH and EM were independently segmented using the manual annotation software ITK-snap⁶⁵ (www.itksnap.org) (Fig. 1i, Extended Data Fig. 1i). The segmentation generated from the EM image was taken as ground truth, and the accuracy of the XNH segmentation was calculated by comparing it to the EM segmentation. For each neuron, segmentation was considered correct if the number of overlapping pixels shared between the EM and XNH segmentation was greater than half of the number of pixels for the neuron in both XNH and EM segmentations (Extended Data Fig. 1i, right). The size of each neuron was approximated as the diameter of the largest circle centered at the neuron’s center of mass that could fit entirely within the neuron (Extended Data Fig. 1j). Note that this analysis used only 2D image data – additional 3D information would likely improve performance.

For the posterior parietal cortex sample, a 3D EM dataset in posterior parietal cortex (Fig. 2) was collected and imaged using the GridTape pipeline for automated serial section transmission EM⁶⁶. To find the region of tissue imaged with XNH, 1 μm thick histological sections were collected and compared with XNH virtual slices. 250 thin sections (~45 nm thick) were collected onto GridTape for a total of 11 μm total thickness. For each section, an ROI overlapping with the XNH imaged region was imaged using a customized JEOL 1200EX TEM outfitted with a reel-to-reel GridTape stage. Total EM imaging time was approximately 150 hours. In the EM images, the tissue ultrastructure, including chemical synapses, remained well-preserved after XNH imaging (Extended Data Fig. 2b, inset, arrows). The EM images also contained small cracks (orange arrows) and bubbles (inset, pink arrows), which may have resulted from XNH imaging. These minor artifacts did not affect our ability to analyze the data, but it is possible that they can be reduced or eliminated by modifying XNH imaging protocols. However, more correlative XNH-EM data is needed to understand the origin of microcracks and nanobubbles.

The EM images were stitched together and aligned into a continuous volume using the software AlignTK (https://mmbios.pitt.edu/software#aligntk). The XNH datasets were aligned to the EM volume via an affine transformation based on manually annotated correspondence points (annotated using BigWarp https://imagej.net/BigWarp). Data annotation (tracing of apical dendrite morphologies and annotation of synapses) was done with CATMAID^45,64.

Image Volume Stitching

For each pair of XNH scan volumes with overlapping FOVs, correspondence points identifying the same feature in each scan were annotated manually using the ImageJ plugin BigWarp⁶⁷ (https://imagej.net/BigWarp). Translation-rotation-scaling matrices were calculated based on least-squares fitting of these correspondence points (~10–20 pairs per image volume) using custom MATLAB code, then applied to each image volume using the ImageJ plugin BigStitcher⁶⁸. To avoid blurring from misalignments in regions where two scans overlap, image volumes were combined without blending in overlapping regions (custom Python code).

Data analysis – Posterior Parietal Cortex

Manual tracing of neurons was performed by a team of 2 annotators using CATMAID^45,64. All cell somata within the XNH volume were identified manually and classified as non-neuronal, pyramidal neuron, or inhibitory neuron (Fig. 2e, Extended Data Fig. 2c)^30,69,70. For a subset of pyramidal neurons distributed across layers II, III, and V, the apical dendrites were traced in the XNH volume up towards the superficial layers until they intersected the EM volume (Fig. 2b, Fig. S2e). The same apical dendrites were then identified in the EM volume based on their location and shape (Fig. S2b). Within the EM volume, all incoming synapses to the apical dendrite were annotated as excitatory (targeting dendritic spines) or inhibitory (targeting dendritic shafts or spine necks) (Fig. 2d). Presynaptic axons, which were resolvable in the EM data but not the XNH data, were not traced. Pyramidal cells were classified as layer II, III, or V based on the distance of their cell body from the layer I/II boundary, which was estimated as a plane above which the density of cell somata drops dramatically (Fig. 2b, Extended Data Fig. 2a). All tracing was reviewed independently by a second annotator to ensure accuracy.

To calculate synapse densities, we wrote custom python code utilizing the pyMaid python API (https://github.com/schlegelp/pyMaid) to access the CATMAID database. The calculate synapse densities for a given AD (Fig. 2f), the total number of inhibitory or excitatory synapses found in the EM volume was divided by the total pathlength of the AD within the EM volume. For these analyses the location of the excitatory synapses was defined as the location of the base of the spine neck, and only the dendrite trunk (excluding the spines) was used for calculating the dendrite pathlength. The inhibitory synapse fraction was defined as (# inhibitory synapses / total # of synapses). To calculate synapse densities as a function of AD pathlength (Fig. 2h–i, Extended Data Fig. 2g–h), each AD was split into fragments 10 μm in length, and the synapse densities were calculated for each fragment individually. The AD pathlength was defined as the along-the-arbor distance from the center of the dendrite fragment to the soma (Fig. 2h–i) or initial bifurcation (Extended Data Fig. 2g–h).

Data analysis – Drosophila leg and VNC

Sensory receptors, muscle fibers, and neurons were annotated manually using CATMAID^45,64. Sensory receptors and muscle fibers were large enough to be clearly resolved in the XNH volume (50–75 nm voxels). Larger axons were also clearly resolved throughout the leg and VNC (motor neurons, coxal hair plate neurons, trochanteral campaniform sensilla neurons), but other smaller axons (bristle neurons in particular) were too small to be accurately traced. 3D visualizations were produced using ITK-SNAP (Fig. 2c), the 3D viewer widget in CATMAID (Fig. 3, Extended Data Fig. 2e, Extended Data Fig. 3e,f,g,m,n, Extended Data Fig. 4d, ), Neuroglancer (Fig. 4, Extended Data Fig. 4j,k), Paraview (Fig. 1e, Extended Data Fig. 3a) or Fiji (Fig. 1f, Extended Data Fig. 3c).

Automated Segmentation

We used an automated segmentation workflow based on a segmentation pipeline for TEM data⁴¹. The pipeline consists of two major steps: affinity prediction and agglomeration. In the affinity prediction step, a 3D U-Net convolutional neural network (CNN) was used to predict an affinity graph from the image data. The value of the affinity graph at any given voxel represents a pseudo-probability that adjacent voxels (in the x, y, and z axes) are part of the same object. Adjacent voxels crossing object boundaries should have low affinity values, whereas voxels within neurons should have high affinity to the voxels surrounding them (including voxels contained in organelles or other subcellular structures).

Network Training

To expedite training a CNN on XNH data, we leveraged a CNN first trained on ground truth EM volumes from the CREMI challenge (https://cremi.org/), followed by training augmentation with corrected segmentation predicted on XNH data. We began by training an initial network on the CREMI ground truth data (4 nm x 4 nm x 40 nm) downsampled to match the voxel size of the XNH data (50 nm x 50 nm x 50 nm). We deployed this CREMI-trained network on a training volume of XNH data (320 × 320 × 300 voxels) and used Armitage/BrainMaps (Google) to correct the voxelwise segmentation for a sparse set of neurons. The network was then deployed on two more training volumes (200 × 200 × 200 voxels, one in the main leg nerve, one in the T1 neuropil) which were densely traced (via skeletonization, not voxel-wise) by human annotators (using CATMAID). Skeleton tracing was used in lieu of voxel-wise error-correction because it can be completed in much less time and is less likely to introduce human errors in the training volumes. The tracing in these training volumes was used to correct errors in the candidate segmentation, and the corrected training volumes were then used to train the network further, resulting in the final network. The final network was then deployed on the entire dataset. Deploying the network on a server that has 40 CPU cores and ten NVIDIA GTX 2080 Ti’s across the full dataset (1792 × 3584 × 3200 voxels) took less than 10 minutes.

Neuron reconstruction and proofreading

We developed a proofreading workflow based on Neuroglancer (https://github.com/google/neuroglancer) to rapidly reconstruct and error correct neurons from automated segmentation. Although split and merge errors exist in the automated segmentation, such errors are usually easy for humans to recognize in 3D visualizations of reconstructed neurons. Thus, proofreading automated segmentation results is much faster than manual tracing.

For reconstruction/proofreading, a blocked segmentation methodology (in which the volume was divided into independent blocks of 256³ voxels) was used. Neurons were seeded by selecting a neuron fragment (contained within a single block) in the main leg nerve, and sequentially grown by adding neuron fragments in adjacent blocks. During each growth step, the 3D morphology of the neuron was visualized and checked for errors. When merge errors occur, the blocks containing the merge are “frozen” to prevent growth from the merged segment. When a neuron branch stops growing (has no continuations), the proofreader inspects the end of the branch to check from missed continuations (split errors). In this way, both split and merge errors can be corrected. In the fly VNC XNH dataset, neurons took about 10–30 min each to reconstruction/proofread.

Neuron classification

Neurons were classified as motor neurons or sensory neuron subtypes by based on their location in the nerve and 3D morphology^40,42,43,71. The reconstructed neurons are likely missing branches or continuations where they become too small to be resolved XNH. However, in most cases, the large-scale branching patterns were sufficient to classify the neurons. 166 neurons were reconstructed from seeds within the main leg nerve, out of which 66 were not clearly classified into a subtype and were excluded from Fig. 4f and Extended Data Fig. 4c. These unclassified neurons tended to be small fragments that do not extend significantly into the VNC, typically because they became too small to be reliably segmented (see also Extended Data Fig. 1i–j).

Segmentation error quantification

To access the accuracy of automated segmentation, we manually traced 90 neurons from the XNH data (CATMAID) and compared them to the automated segmentation results. For each neuron, a list of all skeleton node (manually placed) – segmentation fragment ID (automatically generated) pairs was generated. In a perfect segmentation, all skeleton nodes for a given skeleton would correspond to the same segmentation ID. For each manually-generated skeleton (neuron), a split error was counted for each extra segmentation ID associated with nodes in that skeleton. Split errors that did not change the topology of the neuron were not counted. For each segmentation ID, a merge error was counted for each segmentation fragment that was paired with skeleton nodes from multiple different neurons. To accuracy the count the number of such merge errors, the blocked segmentation was used (see Neuron Reconstruction and Proofreading above). This way, if two neurons are merged in two different places, it will count as two merge errors. It is worth noting that in this calculation, merge errors are only counted between the subset of neurons for which we performed manual skeletonization. Therefore, if portions of nearby un-skeletonized neurons were merged into the segmentation of a skeletonized neuron, that error would not be detected here. Visual inspection of the segmentation results suggest that this type of error is not overly common, but nevertheless the counts of merge errors reported here are likely an underestimate of the true rate of merge errors. It is important to note that in the neurons shown in Fig. 4f and Extended Data Fig. 4c, most split and merge errors were corrected via reconstruction/proofreading.

Statistics and Reproducibility

The quality of XNH reconstructions depended on imaging settings and sample characteristics, and was generally reproducible for a given set of parameters. For example, 8 XNH scans of the same fly leg sample were recorded with the same imaging parameters with similar results (Supplementary Data Table 2). The 11 datasets reported in Fig. 1h, Supplementary Data Table 1, and Supplementary Videos are a representative sample of XNH reconstruction quality over a range of imaging and sample parameters. Scans acquired during exploratory experiments which yielded poor quality data were not included for data analysis.

For statistical analysis in Fig. 2, the number of annotated neurons (n = 261) was calculated to ensure that a large number of sample points (> 30) exist in each of the 4 sublayers (IIa, IIb, III, V). No a priori statistical power calculations were performed to determine sample size but our sample sizes are larger than those reported in previous publications (ref. 27). For bootstrap analysis of variance (Fig. 2f), 1000 synthetic samples were generated from each layer (layer IIa, layer IIb, layer III, and layer V) by randomly selecting datapoints with replacement until the number matched the original dataset size. Then the mean synapse density or inhibitory synapse fraction was calculated for all 1000 synthetic samples. The plotted 95% confidence intervals plotted in Fig. 2f are the 2.5^th and 97.5^th percentile values from this distribution of synthetic sample means. This bootstrap analysis is a non-parametric test and does not assume normality or equal variances.

EM micrographs shown in Fig. 1i and Extended Data Fig. 1i are representative images. 10 similar thin-sections were prepared and imaged with similar quality, although some sections showed physical damage sustained during the sectioning process. EM micrographs shown in Fig. 2d and Extended Data Fig. 2b are representative images. More than 2 million images with similar quality were recorded from this sample using automated EM, although some regions exhibited small cracks and bubbles, which may have been caused by prior XNH imaging.

This study involved detailed anatomical analysis of nervous tissue samples. In most analyses, were examined fundamental organizational principles of neuronal morphology and connectivity, rather than comparing experimental and control samples. Therefore, randomization was not necessary. Our data was not allocated into groups, thus blinding was not applicable; Data collection and analysis were not performed blind to the conditions of the experiments.

See Life Sciences Reporting Summary for more details.

Extended Data

Extended Data Figure 1: X-ray Holographic Nano-Tomography (XNH) Technique and Characterization.

(a) Overview of XNH imaging and preprocessing. Left: Holographic projections of the sample (a result of free-space propagation of the coherent X-ray beam) are recorded for each angle as the sample is rotated over 180°, then normalized with the incoming beam. Center left: Phase projections are calculated by computationally combining four normalized holograms recorded with the sample placed at different distances from the beam focus. Center right: Virtual slices through the 3D image volumes are calculated using tomographic reconstruction. Right: The resulting XNH image volume can be rendered in 3D and analyzed to reveal neuronal morphologies. (b) Quantification of resolution of XNH scans measured using Fourier Shell Correlation (FSC), normalized by each scan’s pixel size. At larger pixel sizes, the resolution per pixel improves, though the resolution itself is worse (see Fig. 1h). Datapoints and error bars show mean ± IQR of subvolumes sampled from each XNH scan. Number of subvolumes used for each scan is shown in Supplementary Data Table 1. (c) Representative FSC curve shown with the half-bit threshold. The intersection between the FSC curve and the threshold is the measured resolution. (d) Quantification of resolution within the 30 nm mouse cortex scan. Each dot represents an FSC measurement of a 100 voxel³ cube. Blue line and shaded band represent binned averages and standard deviation, respectively. The x-axis is the radial position of the center of the cube (distance from the axis of rotation). The red dotted line indicates the boundary of the scan – data points to the right of the line are from extended field of view regions (Methods). (e-f) Edge-fitting measurements of spatial resolution. Although FSC is commonly used to quantify resolution in many imaging modalities including X-ray imaging, its implementation is somewhat controversial⁶³. To ensure that FSC measurements were accurate, we also used an independent measure of resolution based on fitting sharp edges in the images (see Methods), which produced values consistent with those measured via FSC. Left: Example features used for edge-fitting resolution measurement. For both (e) mouse cortex and (f) fly central nervous system, mitochondria were primarily selected because they have dark contrast and sharp boundaries. Center: Example line scan (image intensity values along the orange lines in the feature images). The measured resolution is parameterized from a best-fit to a sigmoid function (Methods). Right: Distribution of edge-fitting resolution measurements for many features distributed throughout the image volumes. n = 30 features measured as shown; boxes shows median and IQR and whiskers show range excluding outliers beyond 1.5 IQR from the median. The median resolution measured via FSC is shown for comparison. (g) Comparison of edge-fitting resolution measurements for two XNH scans and high-resolution transmission EM images. EM data was acquired from a ~40 nm thick section of Drosophila VNC tissue, imaged with 4 nm pixels. Resolution is plotted in units of pixels. n = 30 features for each dataset; boxes shows median and IQR and whiskers show range excluding outliers beyond 1.5 IQR from the median. (h) Comparison of XNH images acquired from the same FOV in the same sample (fly leg) at different voxel sizes. Within this range, the resolution improves monotonically, but not linearly, with voxel size. (i) Comparison of XNH and EM segmentations. The XNH and EM images shown in Fig. 1i were independently segmented. Colored patches in the left two images represent different neurons in the segmentation. The EM segmentation was taken as ground truth, and the XNH segmentation for each neuron was evaluated. The right-most image shows correct and incorrectly segmented neurons. (j) Quantification of XNH segmentation accuracy. The proportion of correctly segmentation neurons is plotted as a function of neuron size. Neurons larger then 200 nm diameter were segmented correctly more than 50% of the time. Note that this analysis used only 2D image data – additional 3D information would likely improve performance. In addition to the size of the neurons, the membrane contrast is also an important factor in accurately segmenting neurons in XNH. In a few cases, membranes between two axons were not clearly visible in XNH, causing them to be erroneously merged (i). Motor neurons in the leg nerve were also challenging to segment because they contain complex glial wrappings that are not always clearly resolved in XNH (i, right size of images).

Extended Data Figure 2: Correlative XNH - EM analysis of the connectivity statistics of pyramidal apical dendrites in posterior parietal cortex (PPC).

(a) 3D rendering of two aligned and stitched XNH datasets in mouse posterior parietal cortex. Cell somata are colored in green (based on voxel brightness). Magenta plane indicates location of serial EM dataset. (b) Aligned XNH virtual slice (left) and EM image (right) of the same region of cortical tissue (horizontal section). After XNH imaging and thin sectioning, the ultrastructure of the tissue remains well preserved, allowing identification of synapses (inset right, arrows). The EM images also showed small cracks (orange arrows) and bubbles (inset, pink arrows), which may have been caused by XNH imaging. (c) Examples of pyramidal neurons (top), inhibitory interneurons (middle) and glia (bottom) from the XNH data. Cells types were identified by classic ultrastructural features^30,69,70. Pyramidal cells were identified by their prominent apical dendrites, while glia were identified from the relative lack of cytoplasm in the somata and the presence of multiple darkly stained chromatin bundles near the edges of the nuclei. Images are 40 × 40 μm virtual coronal slices (100 nm thick). (d) Histological slice of Nissl stained coronal section including posterior parietal cortex from the Allen Brain Atlas (http://atlas.brain-map.org/). Higher density of cells is evident at the top of layer II (consistent with Fig. 2e). (e) Rendering of cells included in connectivity analysis. Apical dendrites were traced in the XNH data (yellow) from somata (colored spheres) up to the layer I/II boundary where we collected an EM volume (cyan). Although the EM volume only contains short (< 50 μm) fragments of each AD, combining data across hundreds of neurons allowed us to map synaptic I/E balance over hundreds of micrometers of path length (Fig. 2h–i). (f) Histogram of locations (cortical depth) of traced cells used for analysis of synaptic inputs onto apical dendrites. (g) Synapse densities (excitatory in blue, inhibitory in red) plotted as a function of pathlength to the initial bifurcation (as opposed to cell soma in Fig. 2i–j). Each marker corresponds to one dendrite fragment 10 μm long. Lines and shaded areas indicate binned average (20 μm bins) and interquartile range (mean ± SE). (h) Inhibitory synapse fraction plotted as a function of pathlength to the initial bifurcation. Each marker corresponds to one dendrite fragment colored based on the soma type. Lines and shaded areas indicate binned average and interquartile range (mean ± SE) for each soma type individually.

Extended Data Fig. 3: Millimeter-scale imaging of a Drosophila leg at single-neuron resolution.

(a) 3D rendering of the dataset after individual scans were stitched together to form a continuous volume. (b) The image volume was computationally unfolded (ImageJ) to reveal the entire 1.4mm length of the main leg nerve. (c) Volume rendering of the three hair plates that sense the thorax-coxa joint. The clusters are positioned differently within the joint, implying that they are sensitive to different joint angle ranges. (d) Cross-section through the group of eight campaniform sensilla on the trochanter, revealing the underlying sensory neurons and their axons (blue, see Fig. 3c). (e-g) Locations of sensory receptors in the leg. See also Supplementary Data Table 3. (e) Anterior view of external sensory structures. TiCSv1 and TiCSv2 are on the reverse (ventral) side of the tibia. (f) Posterior view of the trochanter, where large number of external mechanosensory structures reside. (g) Partially-transparent view of the leg revealing internal sensory structures (see Supplementary Data Table 3). Coxal stretch receptor: a previous report identified stretch receptor neurons in each of the distal leg segments (femur, tibia, and tarsus) that sense joint angles and are required for proper walking coordination³⁵. We identified a neuron in the coxa whose morphology is consistent with the other stretch receptors and was possibly missed previously due to incomplete fluorescent labeling. This demonstrates that each major joint in the fly leg, and not only the distal joints, are monitored by a single stretch receptor neuron. Coxal strand receptor: we identified a single strand receptor in the coxa, innervated by a single sensory axon for which no cell body was visible in the leg. Strand receptor neurons are unique sensory neurons that have a cell body in the VNC instead of the leg⁷², but this type of neuron has only been previously identified in locusts and other orthopteran insects⁷³. In this reconstruction, the strand receptor neuron’s axon enters the VNC through the accessory nerve, but could not be reconstructed back to its cell body in the VNC. (h-k) Axons of some sensory neurons were large enough to reconstruct at the 150–200 nm resolution achieved here. Sensory neurons innervating coxal hair plates (cyan) and some trochanteral campaniform sensilla (blue) had axons with large diameters, similar in size to motor neuron axons (yellow). In contrast, axons of all chordotonal and bristle neurons were narrower. (h) Cross-section through the main leg nerve at the location indicated in (b). Axons from different sensory clusters bundle together. Two TrCS8 neurons have unusually large diameters (1050 nm and 850 nm, white circles; see Fig 3c for full reconstruction of these axons). The remaining TrCS neurons have axon diameters of 430 ± 140 nm. Motor neurons (yellow) have diameters of 1–2 μm. The unresolved axons (areas indicated by red arrows) are chordotonal neurons and bristle neurons. (i) Cross-section through the ventral prothoracic nerve at the location indicated in (e). Axons from CoHP8 sensory neurons (blue, axon diameters of 1030 ± 90 nm) travel in this nerve, which also contains seven motor neuron axons (yellow), five of which innervate muscles in the coxa (left, axon diameters of 1140 ± 130 nm), and two of which innervate muscles in the thorax (left, axon diameters of 1880 and 2150 nm). The unresolved axons (red arrows) are likely bristle neurons. (j) Cross-section through the prothoracic accessory nerve at the location indicated in (e). Axons from CoHP4 sensory neurons (cyan, axon diameters of 1140 ± 240 nm) travel in this nerve. Shown here is a cross-section through one of two major branches of the prothoracic accessory nerve. This branch also contains five motor neuron axons (yellow, axon diameters 1610 ± 240 nm). (k) Cross-section through the dorsal prothoracic nerve at the location indicated in (e). Axons from CoHP3 sensory neurons (cyan, axon diameters of 1380 ± 20 nm) enter the VNC through this nerve. Shown here is the branch of the dorsal prothoracic nerve containing only the CoHP3 axons. Panels (h-k) are slices through reconstructed XNH volumes with 75nm pixel size, subsequently Gaussian blurred with an 0.3 pixel radius. Axon diameters are reported as mean ± SD. (l) Cross-section through the tibia. The nerve is substantially smaller than in Fig. 3d–g as only a subset of leg neurons extend into the tibia. (m) Top: Morphology of a single motor neuron axon (green dye fill) innervating muscle fibers (red phalloidin stain ) in the femur (image from Azevedo et al.³⁹). Each fly has a single motor neuron with this recognizable morphology^39,40. Bottom: XNH reconstruction of a motor neuron axon having the same recognizable morphology as the neuron as shown in the top panel. Red cylinders represent individual muscle fibers. (n) Left: Morphology of the motor neuron LinB-Tr2 (image from Baek & Mann 2009⁴⁰, Copyright 1999 Society for Neuroscience). This motor neuron is born from Lineage B, the second largest lineage of motor neurons. Right: XNH reconstruction of motor neuron axon having the same recognizable morphology as the neuron shown in the left panel. The thin terminal branches were not resolved in the XNH reconstruction.

Extended Data Figure 4: Automated Segmentation of Neuronal Morphologies using Convolutional Neural Networks (CNNs).

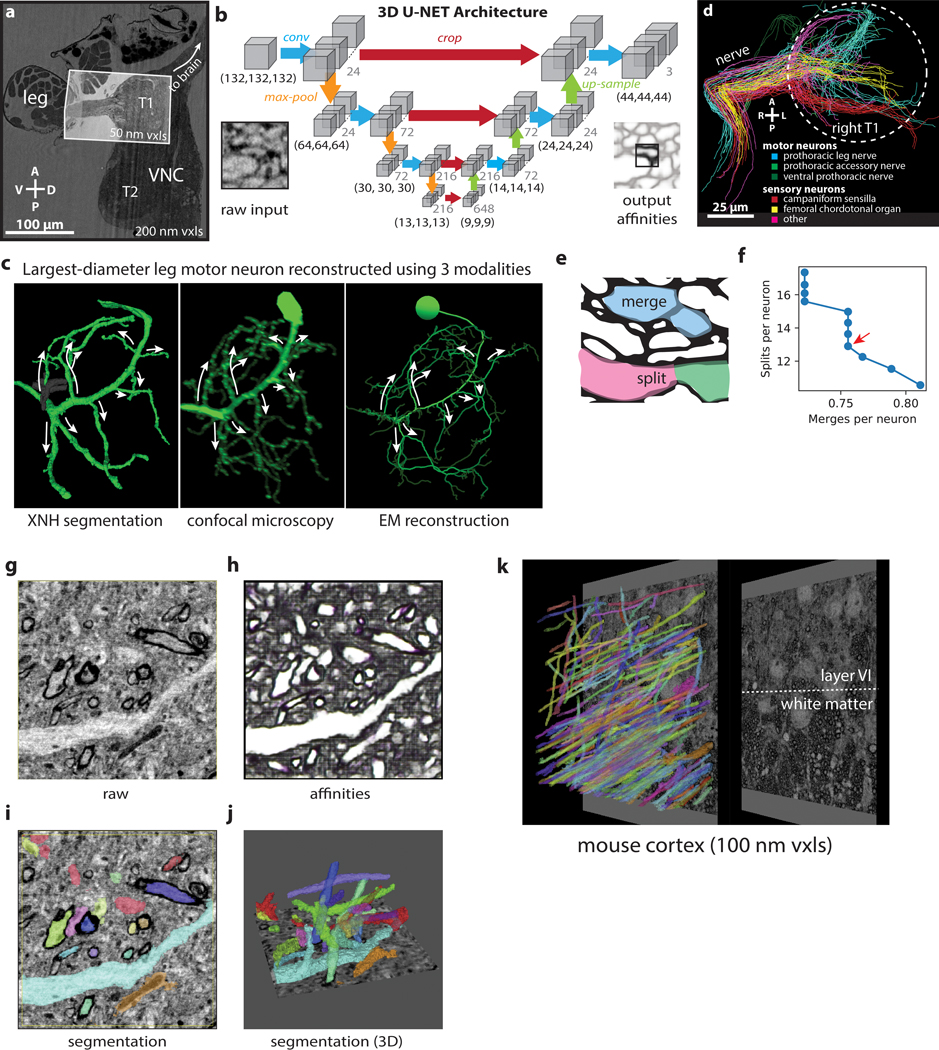
(a) Overview of XNH image volume encompassing the anterior half of the VNC and the first segment of a front leg of an adult Drosophila (200 nm voxels). A smaller, higher resolution (50 nm voxels) volume centered on the prothoracic (T1) neuromere of the VNC and including the initial segment of the leg nerve was used for automatic segmentation. (b) Schematic of U-NET CNN architecture used for automated segmentation (adapted from ⁴¹). Each blue arrow represents two successive convolutions. (c) Morphological comparison of the motor neuron with the largest-diameter branches out of all front leg motor neurons, reconstructed from three different flies using different modalities. Arrows indicate the largest-diameter branches, which match well across the three reconstructions. Left: Reconstruction using automated segmentation of XNH images. Gray segment indicates a merge error that was corrected during proofreading (Methods). Middle: Reconstruction from LM images of a dye-filled motor neuron labeled by 81A07-Gal4. This motor neuron controls the tibia flexor muscle and produces the largest amount of force of any fly leg motor neuron yet identified³⁹. Adapted from Azevedo et al.³⁹. Right: Skeleton reconstruction from EM images. Adapted from Maniates-Selvin et al⁷¹. (d) Population of 90 neurons used for evaluating segmentation error rates. Skeletons were categorized based on their morphologies (as in Fig. 4f) ^40,42,43. White circle indicates the boundary of the T1 neuropil. A, anterior; P, posterior. (e) Examples of merge and split errors. True membrane locations are shown in black. Errors usually result from incorrect prediction of which voxels correspond to membranes. (f) Average error rates of segmentation for the 90 neurons shown in (f). Automated segmentation is parametrized by an agglomeration threshold amounts to a trade-off between split and merge errors. Data points indicate split and merge error rates for different agglomeration thresholds (Methods). The ideal segmentation minimizes the time needed to identify and fix split and merge errors during proofreading (red arrow). Merge error calculations based on comparisons to sparse manual tracing are likely an underestimate of the true number of merge errors. Note that the human-annotated, ground truth segmentation of XNH data excludes some areas where features are too small to resolve; thus these error metrics for XNH segmentation may not be directly comparable to what has been reported for EM. (g-j) Automated segmentation of XNH data in mouse cortex (primary somatosensory, layer 5, 30 nm voxels). (g) Raw data (h) Affinities (zyx corresponding to RGB colors). (i) selected segmentation labels corresponding to (e). (j) Selected 3D renderings of segmented neuron fragments. (k) Large FOV segmentation of myelinated axons in the white matter below mouse parietal cortex. Segmentation of such myelinated axons can enable tracing of long-range inputs between brain areas at single-cell resolution.

Extended Data Figure 5: Additional staining approaches for XNH imaging.

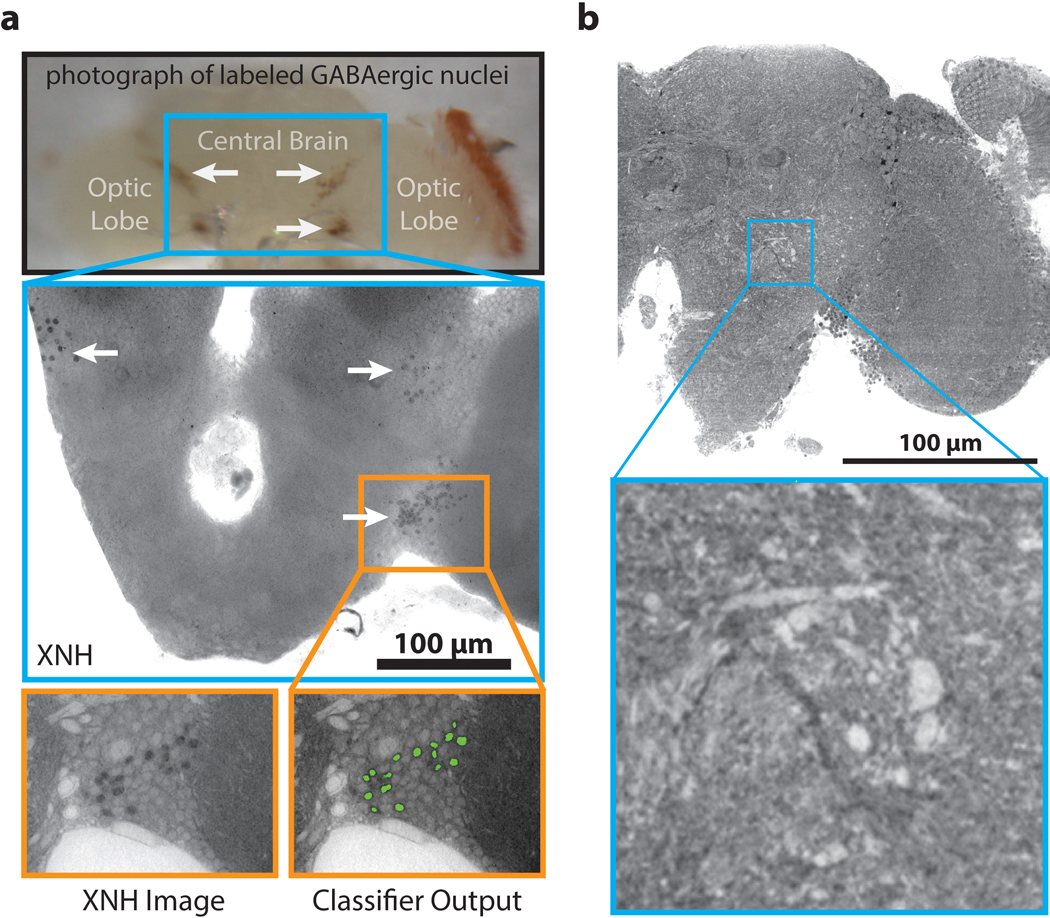
(a) Top: Photograph of fly brain with GABAergic nuclei labeled with APEX2 (arrows). Middle: XNH images (120 nm pixels, 15 μm thick minimum intensity projection) of the same fly brain after heavy metal staining, showing clusters of dark, APEX2 labeled GABAergic cell nuclei (arrows). Bottom: XNH virtual slice (120 nm thick) and output from an automated Random Forest image classifier trained to detect labeled cells (green). (b) XNH data (105 nm voxels) of a Drosophila brain that did not undergo heavy metal staining. Even in unstained soft tissue, phase-contrast imaging provides enough signal that single neurons can still be resolved. FOV encompasses the optic lobe and half of the central brain. See Supplementary Video 6 and Methods.