Basic Reproduction Numbers for a Class of Reaction-Diffusion Epidemic Models

Abstract

We study the basic reproduction numbers for a class of reaction-diffusion epidemic models that are developed from autonomous ODE systems. We present a general numerical framework to compute such basic reproduction numbers; meanwhile, the numerical formulation provides useful insight into their characterizations. Using matrix analysis, we show that the basic reproduction numbers are the same for these PDE models and their associated ODE models in several important cases that include, among others, a single infected compartment, constant diffusion rates, uniform diffusion patterns among the infected compartments, and partial diffusion in the system.

1. Introduction

Mathematical modeling and analysis provide a powerful theoretical tool for epidemiological study. Both ordinary differential equations (ODE) and partial differential equations (PDE) are extensively used. In particular, mathematical models based on reaction-diffusion equations have been frequently employed to investigate the transmission and spread of infectious diseases.

During the development of a PDE epidemic model, an ODE system is often established first to describe the spatially homogeneous dynamics of disease transmission. Then, diffusion terms are added to study the spatial spread of the disease. A diffusion process represents the random movement and dispersal of hosts/pathogens over the spatial domain, normally without a directional preference. Incorporation of such spatial movement, generally associated with location-dependent diffusion rates, into epidemiological, ecological and other biological models emphasizes the spatial heterogeneity of population dynamics (Cantrell and Cosner 1991, 2003), particularly with regard to disease transmission and spread.

There have been many studies devoted to reaction-diffusion epidemic models. For example, existence and well posedness of solutions are analyzed in Kim et al. (2013) and Yamazaki and Wang (2016), equilibrium analyses are conducted in Wang et al. (2015), Wu and Zou (2018), and Yu and Zhao (2016), traveling waves are investigated in Wang et al. (2015), Wang et al. (2016), and Zhao et al. (2018), and realistic epidemic simulations are carried out in Bertuzzo et al. (2010) and Rinaldo et al. (2012). Particularly, basic reproduction numbers for such epidemic systems are studied in Allen et al. (2008), Thieme (2009), Wang and Zhao (2012), and Magal et al. (2019). The basic reproduction number, typically denote by ${\mathcal{R}}_0$, is a critical quantity to measure the transmission risk of an infectious disease. It quantifies the expected number of secondary infections produced by one infective individual in a completely susceptible population, and often characterizes the threshold behavior of an epidemic; i.e., the disease would be eradicated if ${\mathcal{R}}_0<1$ and the disease would persist if ${\mathcal{R}}_0>1$. For ODE epidemic models, ${\mathcal{R}}_0$ is generally defined as the spectral radius of the next-generation matrix Diekmann et al. (1990) and van den Driessche and Watmough (2002), and its calculation follows a standard procedure. For PDE models such as a reaction-diffusion system, the definition and calculation of the basic reproduction number are typically more intriguing. Allen et al. (2008) introduced a variational formula to characterize ${\mathcal{R}}_0$ for a simple SIS model with diffusion terms. Wang and Zhao (2012) defined ${\mathcal{R}}_0$ for reaction-diffusion type systems as the spectral radius of a next-infection operator, using the theory of principal eigenvalues. Thieme (2009) also introduced a theoretical framework to define ${\mathcal{R}}_0$ as the spectral radius of a resolvent-positive operator. More recently, Magal, Webb, and Wu (2019) investigated a vector-host disease model involving diffusive and convective terms, where ${\mathcal{R}}_0$ is found as the spectral radius of a product of four multiplicative operators that include, in particular, two associated with the corresponding ODE model. Other studies related to reaction-diffusion type epidemic models and their basic reproduction numbers can be found in Bertuzzo et al. (2010), Chen and Shi (2020), Ge et al. (2017), Lou and Zhao (2011), Peng and Zhao (2012), Rinaldo et al. (2012), Song et al. (2019), Wang et al. (2015), Wu and Zou (2018), Yamazaki and Wang (2016), and Yu and Zhao (2016).

For most of these PDE epidemic models, the calculation of their basic reproduction numbers requires special efforts since the standard next-generation matrix technique for ODE systems is no longer applicable; instead, the process involves evaluations of various operators defined in infinite-dimensional spaces. Thus, a nontrivial numerical procedure is typically required to achieve this goal.

Since most of such reaction-diffusion type models are associated with meaningful ODE systems that represent spatially homogeneous disease dynamics, it is natural to ask what is the relationship between the ${\mathcal{R}}_0$ of the PDE system and that of the associated ODE system. At present, there are very few studies devoted to address this question. It was shown in Wang and Zhao (2012) that when the diffusion rates are positive constants and the next-generation matrices of the PDE system are independent of the spatial location, the ${\mathcal{R}}_0$ of the PDE system is the same as that of the corresponding ODE system. The authors in Wang et al. (2016) compared the values of the basic reproduction numbers associated with a class of PDE and ODE cholera models using both asymptotical and numerical means; in particular, they found that the ${\mathcal{R}}_0$ of the PDE system approaches the ${\mathcal{R}}_0$ of the ODE system when the (constant) diffusion rates approaches infinity. The authors in Magal et al. (2019) rigorously analyzed the relationship between the PDE-based ${\mathcal{R}}_0$ and the ODE-based ${\mathcal{R}}_0$ for a vector-host model, and established the limits of zero and infinite diffusion rates. Meanwhile, a SEIRS reaction-diffusion model with constant diffusion rates was analyzed in Song et al. (2019) and the monotonicity, asymptotic property, and lower and upper bounds of ${\mathcal{R}}_0$ for this PDE model were established. In a more recent study Chen and Shi (2020), the authors investigated the asymptotic profiles of ${\mathcal{R}}_0$ for a reaction-diffusion epidemic system with constant diffusion rates. They proved that when the diffusion rates tend to zero, ${\mathcal{R}}_0$ approaches the maximum value of the local reproduction number on the spatial domain; when the diffusion rates tend to infinity, ${\mathcal{R}}_0$ approaches the spectral radius of an averaged next-generation matrix. Despite these findings, our understanding of the general connection; i.e., how the ${\mathcal{R}}_0$ of a PDE system is related to that of the corresponding ODE system, remains limited.

In the present paper, we aim to partially address this issue by calculating and analyzing the basic reproduction numbers for a class of reaction-diffusion epidemic models which are developed from underlying autonomous ODE systems. To emphasize spatial heterogeneity, we allow the diffusion rates to be spatially dependent, as various physical studies (see, e.g., Sauty 1980; Sposito et al. 1986; Taylor 1953) have demonstrated that the diffusion rates could vary significantly with respect to spatial locations. Our work also differs from most of the prior studies in the following aspects: (1) instead of analyzing the asymptotic profiles when the constant diffusion rates tend to zero or infinite, we aim to explore a more general relationship between the basic reproduction number of the underlying ODE model and that of the PDE model with variable diffusion rates; (2) our work is inspired by, and builds on, numerical analysis of the operator eigenvalue problem that defines the basic reproduction number of the PDE system. We present a general numerical method to evaluate the value of ${\mathcal{R}}_0$ for such a PDE system, reducing the infinite-dimensional operator eigenvalue problem to a finite-dimensional matrix eigenvalue problem. This approach represents a significant extension of the numerical technique presented in Wang et al. (2016), which is focused on a special type of cholera models, to more general PDE epidemic models. Starting from there, we analyze the relationship between the PDE-based ${\mathcal{R}}_0$ and ODE-based ${\mathcal{R}}_0$, and derive several sufficient conditions under which the two basic reproduction numbers equal each other. These scenarios cover several important types of epidemic models. Throughout this paper, we employ only elementary numerical analysis and matrix theory in our discussion.

We organize the remainder of this paper as follows. In Sect. 2, we present our reaction-diffusion epidemic systems as well as their associated ODE systems, and list necessary assumptions. In Sect. 3, we describe the details of our numerical method for calculating the basic reproduction numbers of the PDE models. In Sect. 4, we state and prove several results regarding the relationship between the basic reproduction numbers of the PDE and ODE models. In Sect. 5, we present a few specific examples to demonstrate our findings. In Sect. 6, we conclude the paper with some discussion.

2. Models and Assumptions

Let n be a positive integer. We consider a vector-valued variable U with n components that combines, in general, the populations of the hosts and pathogens. Specifically, U (t, x) = (u₁(t, x), …, u_n(t, x))^T, where each u_i(t, x) denotes the density of the population in compartment i at time t and position x. In this study, we will focus our attention on the one-dimensional spatial domain [0, 1]. We consider the following reaction-diffusion epidemic system

$$\{\begin{array}{l}\frac{\partial U}{\partial t}=\frac{\partial }{\partial x}\left(D(x)\frac{\partial U}{\partial x}\right)+\mathcal{F}(U)-\mathcal{V}(U),\hspace{1em}t>0,\hspace{1em}x\in [0,1];\hfill \\ \frac{\partial U}{\partial x}(t,0)=\frac{\partial U}{\partial x}(t,1)=0,\hspace{1em}t>0,\hfill \end{array}$$ (1)

together with appropriate initial conditions. In this model,

$$D(x)=\text{diag}\left(d_1(x),\dots ,d_n(x)\right)$$

denotes the diffusion rates at location x, and we assume that D(x) is continuously differentiable on [0, 1]. Meanwhile,

$$\mathcal{F}(U)={\left({\mathcal{F}}_1(U),\dots ,{\mathcal{F}}_n(U)\right)}^T$$

where ${\mathcal{F}}_i$ denotes the appearance rate of newly infected individuals in compartment i, and

$$\mathcal{V}(U)={\mathcal{V}}^{-}(U)-{\mathcal{V}}^{+}(U)={\left({\mathcal{V}}_1^{-},\dots ,{\mathcal{V}}_n^{-}\right)}^T-{\left({\mathcal{V}}_1^{+},\dots ,{\mathcal{V}}_n^{+}\right)}^T={\left({\mathcal{V}}_1,\dots ,{\mathcal{V}}_n\right)}^T$$

where ${\mathcal{V}}_i^{+}$ denotes the transfer rate of individuals into compartment i by all other means, and ${\mathcal{V}}_i^{-}$ the transfer rate of individuals out of compartment i. The compartments in U can be divided into infected and uninfected compartments. Without loss of generality, we may assume U_I = (u₁, …, u_m)^T denotes all the infected compartments, where 1 ≤ m < n. Consequently, we define the set of all disease-free steady states as

$$U_s=\left\{U\ge 0:u_i=0,i=1,\dots ,m\right\}.$$

Before we proceed, we write system (1) in another form

$$\{\begin{array}{l}\frac{\partial U}{\partial t}=D(x)\frac{{\partial }^{2}U}{\partial x^2}-C(x)\frac{\partial U}{\partial x}+\mathcal{F}(U)-\mathcal{V}(U),\hspace{1em}t>0,\hspace{1em}x\in [0,1];\hfill \\ \frac{\partial U}{\partial x}(t,0)=\frac{\partial U}{\partial x}(t,1)=0,\hspace{1em}t>0.\hfill \end{array}$$ (2)

If we impose the constraint

$$C(x)=-\frac{\text{d}}{\text{d}x}D(x),$$ (3)

then system (2) is equivalent to the reaction-diffusion system (1). In what follows, we intend to discuss the slightly more general PDE system (2), where the results can be easily interpreted back to the original system (1) under the condition (3).

We note that if system (2) is homogeneous in space; i.e., U = (u₁(t), …, u_n(t))^T, then the PDE model (2) is reduced to the following ODE model

$$\frac{\text{d}U}{ \text{d}t}=\mathcal{F}(U)-\mathcal{V}(U),\hspace{1em}t>0.$$ (4)

Based on the setting in van den Driessche and Watmough (2002) for ODE epidemic models, we present the following standard assumptions:

• (A1)${\mathcal{F}}_i(U)$, ${\mathcal{V}}_i^{+}(U)$ and ${\mathcal{V}}_i^{-}(U)$ are non-negative and continuously differentiable for 1 ≤ i ≤ n.
• (A2)If u_i = 0, then ${\mathcal{V}}_i^{-}=0$, 1 ≤ i ≤ m.
• (A3)${\mathcal{F}}_i=0$ for i > m.
• (A4)If U ∈ U_s, then ${\mathcal{F}}_i={\mathcal{V}}_i^{+}=0$, i = 1, …, m.

  Each of these assumptions has its biological meaning: (A1) follows from the simple fact that the number of transfer of individuals must be non-negative; (A2) means that there is no individual transferred out from an empty compartment; (A3) states that no new infection happens in the uninfected compartments; and (A4) indicates that a disease-free compartment remains disease-free for all the time.

  Suppose that $U^0=\left(0,\dots ,0,u_{m+1}^0,\dots ,u_n^0\right)$ is a disease-free steady state of model (4), where we assume that U⁰ is spatially independent. Then, the basic reproduction number for the ODE system (4) is defined as the spectral radius of the next-generation matrix (van den Driessche and Watmough 2002); i.e.,

  $${\mathcal{R}}_0^{\text{ODE}}=\rho \left(F{V}^{-1}\right),$$ (5)

  where F and V are m × m constant matrices with (i, j) entry $F_{ij}=\frac{\partial {\mathcal{F}}_i}{\partial u_j}\left(U^0\right)$ and $V_{ij}=\frac{\partial {\mathcal{V}}_i}{\partial u_j}\left(U^0\right)$, respectively. Following the framework in Wang and Zhao (2012), we let T(t) be the solution semigroup on $C\left([0,1],{ℝ}^m\right)$ associated with the following linear reaction-diffusion equation:

  $$\{\begin{array}{l}\frac{\partial U_I}{\partial t}=D_I(x)\frac{{\partial }^2{U}_I}{\partial x^2}-C_I(x)\frac{\partial U_I}{\partial x}-V{U}_I,\hspace{1em}t>0,\hspace{1em}x\in [0,1];\hfill \\ \frac{\partial U_I}{\partial x}(t,0)=\frac{\partial U_I}{\partial x}(t,1)=0,\hspace{1em}t>0,\hfill \end{array}$$ (6)

  where U_I = (u₁, …, u_m)^T, D_I (x) = diag(d₁(x), …, d_m(x)) and C_I (x) = diag(c₁(x), …, c_m(x)). We assume the distribution of the initial infections is U_m(x) = (u₁(x), …, u_m(x))^T. Then, T(t)(U_m(x)) represents the distribution of these infections after time t > 0. Hence, the distribution of new infections at time t > 0 is FT(t)(U_m(x)), and thereby the distribution of the total new infections is

  $${\int }_0^{+\infty }FT(t)\left(U_m(x)\right)\text{d}t.$$

  Thus, the next-generation operator L, which maps the initial infection distribution to the distribution of the total infective individuals generated during the infection period, can be defined as follows,

  $$L:U_m(x)\mapsto F{\int }_0^{+\infty }T(t)\left(U_m(x)\right)\text{d}t.$$ (7)

  Accordingly, the basic reproduction number for the PDE model (2) is the spectral radius of the operator L; i.e.,

  $${\mathcal{R}}_0^{\text{PDE}}=\rho (L).$$ (8)

  Meanwhile, denote

  $$\Gamma =D_I(x)\frac{{\partial }^2}{\partial x^2}-C_I(x)\frac{\partial }{\partial x}-V.$$ (9)

  Clearly, for any t > 0 and a solution ϕ(t, x) of equation (6),

  $$\underset{s\to 0+}{\text{lim}}\frac{T(s)\varphi (t,x)-\varphi (t,x)}{s}=\underset{s\to 0+}{\text{lim}}\frac{\varphi (t+s,x)-\varphi (t,x)}{s}=\frac{\partial \varphi }{\partial t}(t,x)=\Gamma (\varphi ).$$

  Hence, Γ is the generator of the C₀-semigroup T(t) on $C\left([0,1],{ℝ}^m\right)$. Note that T(t)is a positive semigroup since $T(t)C\left([0,1],{ℝ}_{+}^m\right)\subset C\left([0,1],{ℝ}_{+}^m\right)$ for all t ≥ 0. Let σ(Γ) denote the spectrum of the operator Γ. It then follows from (Thieme 2009, Theorem 3.12) that

  $${(\lambda I-\Gamma )}^{-1}(\varphi )={\int }_0^{+\infty }{e}^{-\lambda t}T(t)(\varphi )\text{d}t,\hspace{1em}\forall \lambda >s(\Gamma ),\varphi \in C\left([0,1],{ℝ}^m\right),$$ (10)

  where s(Γ) = sup{Reλ : λ ∈ σ(Γ)} is the spectral bound of Γ. Since the internal evolution of individuals in the infectious compartments is dissipative and exponentially decays in many cases because of the loss of infected members from natural and disease-induced mortalities, we may assume
• (A5)−V is cooperative and s(Γ) < 0.

Thus, fixing λ = 0 in equation (10), we obtain

$$L(\varphi )=F{\int }_0^{+\infty }T(t)(\varphi )\text{d}t=-F{\Gamma }^{-1}(\varphi ),$$ (11)

or L = −FΓ⁻¹. We state two additional assumptions regarding the PDE model (2). First, we set a minimal diffusion rate at all spatial locations; i.e.,

• (H1)There exists a constant d₀ such that d_i(x) ≥ d₀ > 0 for any x ∈ [0, 1] and 1 ≤ i ≤ m.

  Second, for ease of presentation, we assume

• (H2)V = diag(υ₁, …, υ_m) with υ_i > 0, i = 1, …, m.

Many common epidemic models, such as SIR, SEIR, and patchy models (see Sect. 5), satisfy the condition (H2). In case V is not in a diagonal form, it is often possible to re-define the new infection vector, say $\tilde{\mathcal{F}}(U)$, and the transfer vector, say $\tilde{\mathcal{V}}(U)$, in the ODE system (4) such that the associated matrix $\tilde{V}$ is diagonal and that $\frac{\text{d}U}{ \text{d}t}=\mathcal{F}-\mathcal{V}=\tilde{\mathcal{F}}-\tilde{\mathcal{V}}$. It then can be shown that ρ(FV⁻¹) and $\rho \left(\tilde{F}{\tilde{V}}^{-1}\right)$ are equivalent in characterizing the disease threshold; i.e., they are simultaneously higher than (or equal to, or lower than) unity (van den Driessche and Watmough 2002).

3. Numerical Formulation

Let λ be an eigenvalue of L such that L(ϕ(x)) = λϕ(x) for some eigenvector ϕ(x) = (ϕ₁(x), …, ϕ_m(x))^T. Then,

$$-F{\Gamma }^{-1}(\varphi (x))=\lambda \varphi (x).$$ (12)

Suppose that ψ(x) = −Γ⁻¹(ϕ(x)), where ψ(x) = (ψ₁(x), …, ψ_m(x))^T, then −Γ(ψ(x)) = ϕ(x); i.e.,

$$-\left(d_i(x){\nabla }^2{\psi }_i(x)-c_i(x)\nabla {\psi }_i(x)-v_i{\psi }_i(x)\right)={\varphi }_i(x),\hspace{1em}1\le i\le m.$$ (13)

For a sufficiently large integer N > 0, let x_k = k/N, d_ik = d_i(x_k), c_ik = c_i(x_k), ψ_ik = ψ_i(x_k), and ϕ_ik = ϕ_i(x_k) for k = 0, 1, …, N. Applying the standard centered difference scheme to Eq. (13) on the spatial domain [0, 1], we obtain

$$-\left(d_{ik}\frac{{\psi }_{i,k+1}-2{\psi }_{ik}+{\psi }_{i,k-1}}{1/N^2}-c_{ik}\frac{{\psi }_{i,k+1}-{\psi }_{i,k-1}}{2/N}-v_i{\psi }_{ik}\right)\approx {\varphi }_{ik},$$ (14)

or

$$-N\left(d_{ik}N-\frac{c_{ik}}{2}\right){\psi }_{i,k+1}+\left(2d_{ik}{N}^2+v_i\right){\psi }_{ik}-N\left(d_{ik}N+\frac{c_{ik}}{2}\right){\psi }_{i,k-1}\approx {\varphi }_{ik}$$ (15)

for all 0 ≤ k ≤ N, and ψ_i,−1 = ψ_i1, ψ_i,N+1 = ψ_i,N−1 by the Neumann boundary conditions. Combine these N + 1 approximate equations in a matrix form as follows

$$A_i{\Psi }_i\approx {\Phi }_i,$$ (16)

where $A_i=\left[\begin{array}{llll}{a}_{i0}-2d_{i0}{N}^2\hfill & \hfill & \hfill & \hfill \\ b_{i1}^{+}{a}_{i1}\hfill & b_{i1}^{-}\hfill & \hfill & \hfill \\ \ddots \hfill & \ddots \hfill & \ddots \hfill & \hfill \\ \hfill & b_{i,N-1}^{+}\hfill & a_{i,N-1}\hfill & b_{i,N-1}^{-}\hfill \\ \hfill & \hfill & -2d_{in}{N}^2\hfill & a_{iN}\hfill \end{array}\right]$, ${\Psi }_i=\left[\begin{array}{l}{\psi }_{i0}\hfill \\ {\psi }_{i1}\hfill \\ ⋮\hfill \\ {\psi }_{i,N-1}\hfill \\ {\psi }_{iN}\hfill \end{array}\right]$, and ${\Phi }_i=\left[\begin{array}{l}{\varphi }_{i0}\hfill \\ {\varphi }_{i1}\hfill \\ ⋮\hfill \\ {\varphi }_{i,N-1}\hfill \\ {\varphi }_{iN}\hfill \end{array}\right]$ with $b_{ik}^{+}=-N\left(d_{ik}N+\frac{c_{ik}}{2}\right)$, $b_{ik}^{-}=-N\left(d_{ik}N-\frac{c_{ik}}{2}\right)$, and a_ik = 2d_ik N² +υ_i for all 0 ≤ k ≤ N.

Let us define

$$N^{*}=\text{max}\left\{N_i:i=1,\dots ,m\right\},\hspace{1em}\text{where}{N}_i=\frac{\underset{0\le x\le 1}{\text{max}}|c_i(x)|}{2d_0}.$$ (17)

Then, N > N* implies that $N>\frac{\left|c_i(x)\right|}{2d_i(x)}$ for any x ∈ [0, 1], thus $b_{ik}^{+}<0$ and $b_{ik}^{-}<0$.

Next, we show that for each i = 1, ⋯, m, the matrix A_i is invertible and υ_i is a lower bound of the eigenvalues of A_i.

Lemma 3.1

Let $M_k=\left[\begin{array}{cccc}{x}_1& {\alpha }_1& & \\ {\beta }_1& x_2& \ddots & \\ & \ddots & \ddots & {\alpha }_{k-1}\\ & & {\beta }_{k-1}& x_k\end{array}\right]$, where $x_j\in ℝ$ and αjβj > 0 for all j, then M_k is diagonalizable and all eigenvalues of M_k are real.

Proof

Since α_jβ_j > 0, we can define $s_j=\frac{{\alpha }_j}{\left|{\alpha }_j\right|}=\frac{{\beta }_j}{\left|{\beta }_j\right|}$, 1 ≤ j ≤ k. Denote

$$B_k=\left[\begin{array}{llll}{x}_1\hfill & s_1\sqrt{{\alpha }_1{\beta }_1}\hfill & \hfill & \hfill \\ s_1\sqrt{{\alpha }_1{\beta }_1}\hfill & x_2\hfill & \ddots \hfill & \hfill \\ \hfill & \ddots \hfill & \ddots \hfill & S_k-1\sqrt{{\alpha }_{k-1}{\beta }_{k-1}}\hfill \\ \hfill & \hfill & s_{k-1}\sqrt{{\alpha }_{k-1}{\beta }_{k-1}}\hfill & x_k\hfill \end{array}\right].$$

Then, B_k is a real symmetric matrix and thereby B_k is diagonalizable and all eigenvalues of B_k are real. Choose a nonsingular diagonal matrix

$$P_k=\text{diag}\left(1,\sqrt{\frac{{\alpha }_1}{{\beta }_1}},\sqrt{\frac{{\alpha }_1{\alpha }_2}{{\beta }_1{\beta }_2}},\cdots ,\sqrt{\frac{{\alpha }_1\cdots {\alpha }_{k-1}}{{\beta }_1\dots {\beta }_{k-1}}}\right).$$

One can verify that $M_k=P_k^{-1}{B}_k{P}_k$. Thus, we complete the proof. □

Lemma 3.2

Let N > N*, where N* is defined in Eq. (17). If ${\lambda }_{A_i}$ is an eigenvalue of A_i, then ${\lambda }_{A_i}$ is real and ${\lambda }_{A_i}\ge v_i$, 1 ≤ i ≤ m.

Proof

Note that for any k, $b_{ik}^{+}$ and $b_{ik}^{-}$ are negative when N > N*. Then, $\left|b_{ik}^{+}\right|+\left|b_{ik}^{-}\right|=2d_{ik}{N}^2$. Hence, by the Gershgorin Circle Theorem, there exists a p ∈ {0, 1, …, N} such that

$$\left|{\lambda }_{A_i}-a_{ip}\right|\le 2d_{ip}{N}^2=a_{ip}-v_i,$$

which indicates that $\text{Re}\left({\lambda }_{A_i}\right)\ge v_i$. It follows from Lemma 3.1 that ${\lambda }_{A_i}\in ℝ$ and hence ${\lambda }_{A_i}\ge v_i$. □

Denote $\Psi ={\left({\Psi }_1^T,\dots ,{\Psi }_m^T\right)}^T$, $\Phi ={\left({\Phi }_1^T,\dots ,{\Phi }_m^T\right)}^T$, and

$$A=\text{diag}\left(A_1,\dots ,A_m\right).$$

Then, A is invertible and Ψ ≈ A⁻¹ Φ by Eq. (16). It follows from Eq. (12) that

$$F\psi (x)=-F{\Gamma }^{-1}(\varphi (x))=\lambda \varphi (x),$$ (18)

which yields

$$\left(F\otimes I_{N+1}\right)\Psi =\lambda \Phi$$ (19)

for any integer N > 0, where I_N+1 is the (N + 1) × (N + 1) identity matrix and ⊗ denotes the Kronecker product that is defined as follows: for any r × s matrix M = (m_ij) and p × q matrix Q,

$$M\otimes Q=\left[\begin{array}{lll}{m}_{11}Q\hfill & \cdots \hfill & m_{1s}Q\hfill \\ ⋮\hfill & \ddots \hfill & ⋮\hfill \\ m_{r1}Q\hfill & \cdots \hfill & m_{rs}Q\hfill \end{array}\right].$$

Substituting Ψ ≈ A⁻¹ Φ into equation (19), our numerical formulation thus leads to

$$\left(F\otimes I_{N+1}\right)A^{-1}\Phi \approx \lambda \Phi .$$ (20)

We are now ready to state the following result.

Theorem 3.1

$${\mathcal{R}}_0^{\text{PDE}}=\underset{N\to \infty }{\text{lim}}\rho \left(\left(F\otimes I_{N+1}\right)A^{-1}\right).$$ (21)

Proof

From the basic theory in numerical analysis (Richtmyer and Morton 1994; Thomas 1995), the solution of Eq. (20) (or, Eq. 14) converges to the solution of Eq. (12) (or, Eq. 13) when N → ∞. Hence, for sufficiently large N, an eigenvalue of the operator L = −FΓ⁻¹ is an approximation to an eigenvalue of the matrix (F ⊗ I_N+1)A⁻¹, and vice versa. Moreover, for any ε > 0, we have

$$\left|\rho \left(\left(F\otimes I_{N+1}\right)A^{-1}\right)-\rho (L)\right|<\epsilon$$

for sufficiently large N. Letting ε → 0, we obtain ${\mathcal{R}}_0^{\text{PDE}}=\rho (L)={\text{lim}}_{N\to \infty }\rho \left(\left(F\otimes I_{N+1}\right)A^{-1}\right)$. □

Essentially, our numerical formulation reduces the original operator eigenvalue problem (12) to a matrix eigenvalue problem (20), which is not only useful for practical evaluation (there are many efficient numerical techniques currently available for computing matrix eigenvalues (Golub and Van Loan 1996; Saad 2011)), but also provides important insight into the property of ${\mathcal{R}}_0^{\text{PDE}}$.

4. ${\mathcal{R}}_0$ Analysis

In what follows, we conduct an analysis of ${\mathcal{R}}_0^{\text{PDE}}$ and its relationship to ${\mathcal{R}}_0^{\text{ODE}}$ using our result in (21). We first introduce the following lemmas.

Lemma 4.1

For all N > N*, $\rho \left(A_i^{-1}\right)=1/v_i$, 1 ≤ i ≤ m.

Proof

It follows from Lemma 3.2 that $\rho \left(A_i^{-1}\right)\le 1/v_i$. It suffices to show that υ_i is an eigenvalue of A_i; i.e., det(υ_i I_N+1 − A_i) = 0. Note that, the summation of the k-th row of the matrix υ_i I_N+1 − A_i is $v_i-a_{ik}-b_{ik}^{+}-b_{ik}^{-}=-2d_{ik}{N}^2+2d_{ik}{N}^2=0$ for all 0 ≤ k ≤ N. Thus, the statement holds true. □

Lemma 4.2

Assume that, X = (x_ij) is an m × m matrix and Y_ij (1 ≤ i, j ≤ m) are n × n matrices. If there exists a nonsingular matrix P such that P⁻¹Y_ij P = D_ij for all i, j = 1, …, m, where $D_{ij}=\mathit{\text{diag}}\left(y_{ij}^{(1)},\dots ,y_{ij}^{(n)}\right)$, then

$$\text{det}\left[\begin{array}{lll}{x}_{11}{Y}_{11}\hfill & \cdots \hfill & x_{1m}{Y}_{1m}\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill \\ x_{m1}{Y}_{m1}\hfill & \cdots \hfill & x_{mm}{Y}_{mm}\hfill \end{array}\right]=\prod _{k=1}^n\text{det}\left[\begin{array}{lll}{x}_{11}{y}_{11}^{(k)}\hfill & \cdots \hfill & x_{1m}{y}_{1m}^{(k)}\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill \\ x_{m1}{y}_{m1}^{(k)}\hfill & \cdots \hfill & x_{mm}{y}_{mm}^{(k)}\hfill \end{array}\right].$$

Proof

Note that,

$$\left[\begin{array}{lll}{x}_{11}{Y}_{11}\hfill & \cdots \hfill & x_{1m}{Y}_{1m}\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill \\ x_{m1}{Y}_{m1}\hfill & \cdots \hfill & x_{mm}{Y}_{mm}\hfill \end{array}\right]=\left(I_m\otimes P\right)\left[\begin{array}{lll}{x}_{11}{D}_{11}\hfill & \cdots \hfill & x_{1m}{D}_{1m}\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill \\ x_{m1}{D}_{m1}\hfill & \cdots \hfill & x_{mm}{D}_{mm}\hfill \end{array}\right]\left(I_m\otimes P^{-1}\right)$$

and the determinants of the left and right matrices satisfy

$$\text{det}\left(I_m\otimes P\right)\text{det}\left(I_m\otimes P^{-1}\right)={(\text{det}P)}^m{\left(\text{det}{P}^{-1}\right)}^m=1.$$

We now only need to calculate the determinant of the middle matrix. Apply Laplace expansion by choosing rows {1, n + 1, …, (m − 1)n + 1} to obtain

$$\begin{gathered} \text{det}\left[\begin{array}{lll}{x}_{11}{D}_{11}\hfill & \cdots \hfill & x_{1m}{D}_{1m}\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill \\ x_{m1}{D}_{m1}\hfill & \cdots \hfill & x_{mm}{D}_{mm}\hfill \end{array}\right]=\text{det}\left[\begin{array}{lll}{x}_{11}{y}_{11}^{(1)}\hfill & \cdots \hfill & x_{1m}{y}_{1m}^{(1)}\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill \\ x_{m1}{y}_{m1}^{(1)}\hfill & \cdots \hfill & x_{mm}{y}_{mm}^{(1)}\hfill \end{array}\right] \\ \text{det}\left[\begin{array}{lll}{x}_{11}{D}_{11}^{(1)}\hfill & \cdots \hfill & x_{1m}{D}_{1m}^{(1)}\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill \\ x_{m1}{D}_{m1}^{(1)}\hfill & \cdots \hfill & x_{mm}{D}_{mm}^{(1)}\hfill \end{array}\right], \end{gathered}$$

where $D_{ij}^{(1)}=\text{diag}\left(y_{ij}^{(2)},\dots ,y_{ij}^{(n)}\right)$. Similarly, keep applying Laplace expansion by choosing rows {1, n, …, (m − 1)(n − 1) + 1} for the latter matrix, and one can easily obtain

$$\text{det}\left[\begin{array}{lll}{x}_{11}{D}_{11}\hfill & \cdots \hfill & x_{1m}{D}_{1m}\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill \\ x_{m1}{D}_{m1}\hfill & \cdots \hfill & x_{mm}{Y}_{mm}\hfill \end{array}\right]=\prod _{k=1}^n\text{det}\left[\begin{array}{lll}{x}_{11}{y}_{11}^{(k)}\hfill & \cdots \hfill & x_{1m}{y}_{1m}^k\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill \\ x_{m1}{y}_{m1}^{(k)}\hfill & \cdots \hfill & x_{mm}{y}_{mm}^{(k)}\hfill \end{array}\right],$$

which completes the proof. □

Lemma 4.3

If Z and W −Z are both n×n non-negative matrices, then ρ(W) ≥ ρ(Z).

Proof

Let Z = (z_ij) and W = (w_ij), i, j = 1, …, n. Then w_ij ≥ z_ij ≥ 0. Hence, for any integer k ≥ 1, it is easy to see that if we denote W^k = (p_ij) and Z^k = (q_ij), then p_ij ≥ q_ij, i, j = 1, …, n, and thereby

$${\Vert W^k\Vert }_2^2=\sum _{i,j=1}^n{\left|p_{ij}\right|}^2\ge \sum _{i,j=1}^n{\left|q_{ij}\right|}^2={\Vert Z^k\Vert }_2^2.$$

Thus, $\rho (W)=\underset{k\to \infty }{\text{lim}}{\Vert W^k\Vert }_2^{1/k}\ge \underset{k\to \infty }{\text{lim}}{\Vert Z^k\Vert }_2^{1/k}=\rho (Z)$. □

Now, we state our main results in the following three theorems.

Theorem 4.1

Let (A1)–(A5) and (H1)–(H2) hold.

1. Assume that, ${\left\{A_i\right\}}_{i=1}^m$ for system (2) is a commuting family. Then, ${\mathcal{R}}_0^{PDE}\le {\mathcal{R}}_0^{ODE}$

2. If F is a triangular matrix, then ${\mathcal{R}}_0^{PDE}={\mathcal{R}}_0^{ODE}$. Particularly, if m = 1, then. ${\mathcal{R}}_0^{PDE}={\mathcal{R}}_0^{ODE}$

Proof

1. It is clear that when N > N*, ${\left\{A_i\right\}}_{i=1}^m$ is a family of diagonalizable matrices by Lemma 3.1. The commuting property ensures that ${\left\{A_i\right\}}_{i=1}^m$ are simultaneously diagonalizable (Horn and Johnson 1985). It follows from Lemma 3.2 that we can write

   $$Q{A}_i^{-1}{Q}^{-1}=\text{diag}\left({\alpha }_{i1},\dots ,{\alpha }_{i,N+1}\right)$$

   with some nonsingular matrix Q for any N > N*, where 0 < α_ik ≤ 1/υ_i for i = 1, …, m and k = 1, …, N + 1. Hence, it follows from Lemma 4.2 that

   $$\text{det}\left(\lambda I_{m(N+1)}-\left(F\otimes I_{N+1}\right)A^{-1}\right)=\prod _{k=1}^{N+1}\text{det}\left(\lambda I_m-O_k\right),$$ (22)

   where $O_k=\left[\begin{array}{lll}{F}_{11}{\alpha }_{1k}\hfill & \cdots \hfill & F_{1m}{\alpha }_{mk}\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill \\ F_{m1}{\alpha }_{1k}\hfill & \cdots \hfill & F_{mm}{\alpha }_{mk}\hfill \end{array}\right]$ for 1 ≤ k ≤ N + 1. Thus, equation (22) yields

   $$\rho \left(F\otimes I_{N+1}\right)A^{-1})=\text{max}\left\{\rho \left(O_k\right):k=1,\dots ,N+1\right\}.$$ (23)

   Note that, F is non-negative by assumptions (A1) and (A4), then O_k and FV ⁻¹ − O_k are both non-negative, and thus ρ(O_k) ≤ ρ(FV⁻¹) by Lemma 4.3. Therefore, $\rho \left(F\otimes I_{N+1}\right)A^{-1})\le \rho \left(F{V}^{-1}\right)={\mathcal{R}}_0^{\text{ODE}}$. Taking the limit N → ∞, we obtain ${\mathcal{R}}_0^{\text{PDE}}\le {\mathcal{R}}_0^{\text{ODE}}$.
2. This directly follows from Lemma 4.1 that

   $$\rho \left(\left(F\otimes I_{N+1}\right)A^{-1}\right)=\underset{1\le i\le m}{\text{max}}\left\{\rho \left(F_{ii}{A}_i^{-1}\right)\right\}=\underset{1\le i\le m}{\text{max}}\left\{F_{ii}/v_i\right\}=\rho \left(F{V}^{-1}\right)$$

   for any integer N sufficiently large.

Remark 4.1

The second part of Theorem 4.1 states, as a special case, that if the reaction-diffusion model (2) has only one infected compartment, then its basic reproduction number is identical to that of the underlying ODE model.

Next, we characterize the sufficient and necessary conditions such that ${\left\{A_i\right\}}_{i=1}^m$ is a commuting family.

Theorem 4.2

Let N > N*. The matrix set ${\left\{A_i\right\}}_{i=1}^m$ associated with system (2) is a commuting with system (2) is a commuting family if and only if there exist constants δ_i, σ_i, and continuous functions d(x), c(x) such that d_i(x) = δ_id(x), c_i(x) = σ_ic(x), and δ_iσ_j = δ_jσ_i, 1 ≤ i, j ≤ m.

Proof

We can rewrite $A_i=N^2{H}_i+\frac{N}{2}{G}_i+v_i{I}_{N+1}$ for i = 1, …, m, where

$$H_i=\left[\begin{array}{llll}2d_{i0}-2d_{i0}\hfill & \hfill & \hfill & \hfill \\ -d_{i1}2d_{i1}\hfill & -d_{i1}\hfill & \hfill & \hfill \\ \ddots \hfill & \ddots \hfill & \ddots \hfill & \hfill \\ \hfill & -d_{i,N-1}\hfill & 2d_{i,N-1}\hfill & -d_{i,N-1}\hfill \\ \hfill & \hfill & -2d_{iN}\hfill & 2d_{iN}\hfill \end{array}\right],$$

$$G_i=\left[\begin{array}{lllll}0\hfill & 0\hfill & \hfill & \hfill & \hfill \\ -c_{i1}\hfill & 0\hfill & c_{i1}\hfill & \hfill & \hfill \\ \hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill & \hfill \\ \hfill & \hfill & -c_{i,N-1}\hfill & 0\hfill & c_{i,N-1}\hfill \\ \hfill & \hfill & \hfill & 0\hfill & 0\hfill \end{array}\right].$$

Then, A_i A_j − A_j A_i = 0 is equivalent to

$$N^2\left(H_i{H}_j-H_j{H}_i\right)+\frac{N}{2}\left(H_i{G}_j+G_i{H}_j-H_j{G}_i-G_j{H}_i\right)+\frac{1}{2}\left(G_i{G}_j-G_j{G}_i\right)=0.$$ (24)

One can verify that

$$H_i{H}_j-H_j{H}_i=\left[\begin{array}{llllll}2h_{ij}^{(0)}-4h_{ij}^{(0)}\hfill & 2h_{ij}^{(0)}\hfill & \hfill & \hfill & \hfill & \hfill \\ 2h_{ij}^{(0)}{\eta }_{ij}^{(0)}\hfill & -2h_{ij}^{(1)}\hfill & h_{ij}^{(1)}\hfill & \hfill & \hfill & \hfill \\ -h_{ij}^{(1)}2h_{ij}^{(1)}\hfill & {\eta }_{ij}^{(1)}\hfill & -2h_{ij}^{(2)}\hfill & h_{ij}^{(2)}\hfill & \hfill & \hfill \\ \ddots \hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill & \hfill \\ \hfill & -h_{ij}^{(N-3)}\hfill & 2h_{ij}^{(N-3)}\hfill & {\eta }_{ij}^{(N-3)}\hfill & -2h_{ij}^{(N-2)}\hfill & h_{ij}^{(N-2)}\hfill \\ \hfill & \hfill & -h_{ij}^{(N-2)}\hfill & 2h_{ij}^{(N-2)}\hfill & {\eta }_{ij}^{(N-2)}\hfill & -2h_{ij}^{(N-1)}\hfill \\ \hfill & \hfill & \hfill & -2h_{ij}^{(N-1)}\hfill & 4h_{ij}^{(N-1)}\hfill & -2h_{ij}^{(N-1)}\hfill \end{array}\right],$$

where $h_{ij}^{(k)}=d_{ik}{d}_{j,k+1}-d_{jk}{d}_{i,k+1}$, and ${\eta }_{ij}^{(k)}=-2h_{ij}^{(k)}+2h_{ij}^{(k+1)}$, k = 0, …, N − 1

$$H_i{G}_j-H_j{G}_i=\left[\begin{array}{ccccccc}2p_{ij}^{(0)}& 0& -2p_{ij}^{(0)}& & & & \\ -2f_{ij}^{(1)}& p_{ij}^{(1)}& 2f_{ij}^{(1)}& -p_{ij}^{(1)}& & & \\ q_{ij}^{(2)}& -2f_{ij}^{(2)}& p_{ij}^{(2)}-q_{ij}^{(2)}& 2f_{ij}^{(2)}& -p_{ij}^{(2)}& & \\ & \ddots & \ddots & \ddots & \ddots & \ddots & \\ & & q_{ij}^{(N-2)}& -2f_{ij}^{(N-2)}& p_{ij}^{(N-2)}-q_{ij}^{(N-2)}& 2f_{ij}^{(N-2)}& -p_{ij}^{(N-2)}\\ & & & q_{ij}^{(N-1)}& -2f_{ij}^{(N-1)}& -q_{ij}^{(N-1)}& 2f_{ij}^{(N-1)}\\ & & & & 2q_{ij}^{(N)}& 0& -2q_{ij}^{(N)}\end{array}\right],$$

$$G_i{H}_j-G_j{H}_i=\left[\begin{array}{lllllll}0\hfill & 0\hfill & 0\hfill & \hfill & \hfill & \hfill & \hfill \\ 2p_{ij}^{(0)}\hfill & -2p_{ij}^{(0)}+q_{ij}^{(2)}\hfill & -2q_{ij}^{(2)}\hfill & q_{ij}^{(2)}\hfill & \hfill & \hfill & \hfill \\ -p_{ij}^{(1)}\hfill & 2p_{ij}^{(1)}\hfill & -p_{ij}^{(1)}+q_{ij}^{(3)}\hfill & -2q_{ij}^{(3)}\hfill & q_{ij}^{(3)}\hfill & \hfill & \hfill \\ \hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill & \hfill \\ \hfill & \hfill & -p_{ij}^{(N-3)}\hfill & 2p_{ij}^{(N-3)}\hfill & -p_{ij}^{(N-3)}+q_{ij}^{(N-1)}\hfill & -2q_{ij}^{(N-1)}\hfill & q_{ij}^{(N-1)}\hfill \\ \hfill & \hfill & \hfill & -p_{ij}^{(N-2)}\hfill & 2p_{ij}^{(N-2)}\hfill & -p_{ij}^{(N-2)}+2q_{ij}^{(N)}\hfill & -2q_{ij}^{(N)}\hfill \\ \hfill & \hfill & \hfill & \hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right],$$

where $p_{ij}^{(k)}=d_{ik}{c}_{j,k+1}-d_{jk}{c}_{i,k+1}$, $q_{ij}^{(k)}=d_{ik}{c}_{j,k-1}-d_{jk}{c}_{i,k-1}$, and $f_{ij}^{(k)}=d_{ik}{c}_{jk}-d_{jk}{c}_{ik}$, k = 0, …, N, and

$$G_i{G}_j-G_j{G}_i=\left[\begin{array}{lllllll}0\hfill & 0\hfill & 0\hfill & \hfill & \hfill & \hfill & \hfill \\ 0\hfill & -r_{ij}^{(1)}\hfill & 0\hfill & r_{ij}^{(1)}\hfill & \hfill & \hfill & \hfill \\ -r_{ij}^{(1)}\hfill & 0\hfill & r_{ij}^{(1)}-r_{ij}^{(2)}\hfill & 0\hfill & r_{ij}^{(2)}\hfill & \hfill & \hfill \\ \hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill & \hfill \\ \hfill & \hfill & -r_{ij}^{(N-3)}\hfill & 0\hfill & r_{ij}^{(N-3)}-r_{ij}^{(N-2)}\hfill & 0\hfill & r_{ij}^{(N-2)}\hfill \\ \hfill & \hfill & \hfill & -r_{ij}^{(N-2)}\hfill & 0\hfill & r_{ij}^{(N-2)}\hfill & 0\hfill \\ \hfill & \hfill & \hfill & \hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right],$$

where $r_{ij}^{(k)}=c_{ik}{c}_{j,k+1}-c_{jk}{c}_{i,k+1}$, k = 1, …, N − 2. Consider the (1, 2) element and the (N + 1, N) element of the matrix in Eq. (24), we have $N^2\left(4h_{ij}^{(0)}\right)=N^2\left(4h_{ij}^{(N-1)}\right)=0$. Summing up all the elements of each row into the first column, it is easy to see that

$$\{\begin{array}{l}{N}^2\left(h_{ij}^{(1)}\right)=0,\hfill \\ N^2\left(h_{ij}^{(k)}-h_{ij}^{(k-1)}\right)=0,k=2,\dots ,N-2,\hfill \\ N^2\left(h_{ij}^{(N-2)}\right)=0.\hfill \end{array}$$

Thus, $h_{ij}^{(k)}=0$; i.e.,

$$d_{ik}{d}_{j,k+1}=d_{jk}{d}_{i,k+1}$$ (25)

for all 0 ≤ k ≤ N − 1. Since d₁(x) > 0, x ∈ [0, 1], then for any rational number $\frac{k}{N}\in [0,1)$, 0 ≤ k ≤ N − 1, it follows from equation (25) that

$$\frac{d_j\left(\frac{k}{N}\right)}{d_1\left(\frac{k}{N}\right)}=\frac{d_j\left(\frac{k-1}{N}\right)}{d_1\left(\frac{k-1}{N}\right)}=\cdots =\frac{d_j(0)}{d_1(0)},\hspace{1em}j=1,\dots ,m.$$

Note that, $\frac{d_j(x)}{d_1(x)}$ is continuous on [0, 1], hence $\frac{d_j(x)}{d_1(x)}=\frac{d_j(0)}{d_1(0)}$ for all x ∈ [0, 1]. Let d(x) = d₁(x) and ${\delta }_j=\frac{d_j(0)}{d_1(0)}$. Then for any 1 ≤ j ≤ m, we obtain

$$d_j(x)={\delta }_{j}d(x).$$ (26)

Accordingly, H_i H_j − H_j H_i = 0 and equation (24) becomes

$$N\left(H_i{G}_j+G_i{H}_j-H_j{G}_i-G_j{H}_i\right)+\frac{1}{2}\left(G_i{G}_j-G_j{G}_i\right)=0.$$ (27)

For k = 2, …, N, consider the (k, k − 1) element and the (k, k + 1) element of the matrix in equation (27), we obtain $f_{ij}^{(k-1)}=p_{ij}^{(k-2)}$ and $f_{ij}^{(k-1)}=q_{ij}^{(k)}$, respectively. Hence,

$$H_i{G}_j-H_j{G}_i+G_i{H}_j-G_j{H}_i=\left[\begin{array}{lllllll}2p_{ij}^{(0)}\hfill & 0\hfill & -2p_{ij}^{(0)}\hfill & \hfill & \hfill & \hfill & \hfill \\ 0\hfill & {\theta }_{ij}^{(1)}\hfill & 0\hfill & -{\theta }_{ij}^{(1)}\hfill & \hfill & \hfill & \hfill \\ -{\theta }_{ij}^{(1)}\hfill & 0\hfill & {\theta }_{ij}^{(1)}+{\theta }_{ij}^{(2)}\hfill & 0\hfill & -{\theta }_{ij}^{(2)}\hfill & \hfill & \hfill \\ \hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill & \hfill \\ \hfill & \hfill & -{\theta }_{ij}^{(N-3)}\hfill & 0\hfill & {\theta }_{ij}^{(N-3)}+{\theta }_{ij}^{(N-2)}\hfill & 0\hfill & -{\theta }_{ij}^{(N-2)}\hfill \\ \hfill & \hfill & \hfill & -{\theta }_{ij}^{(N-2)}\hfill & 0\hfill & {\theta }_{ij}^{(N-2)}\hfill & 0\hfill \\ \hfill & \hfill & \hfill & \hfill & 2p_{ij}^{(N-2)}\hfill & 0\hfill & -2p_{ij}^{(N-2)}\hfill \end{array}\right],$$

where ${\theta }_{ij}^k=p_{ij}^{(k)}-p_{ij}^{(k-1)}$, k = 1, …, N – 2. It follows from the (k, k + 2) element and the (k + 2, k) element of the matrix in equation (27) that

$$\{\begin{array}{l}N\left(-2p_{ij}^{(0)}\right)=0,\hfill \\ N\left(-{\theta }_{ij}^{(k)}\right)+\frac{1}{2}{r}_{ij}^{(k)}=0,k=1,\dots ,N-2,\hfill \\ N\left(-{\theta }_{ij}^{(k)}\right)-\frac{1}{2}{r}_{ij}^{(k)}=0,k=1,\dots ,N-2,\hfill \\ N\left(2p_{ij}^{(N-2)}\right)=0.\hfill \end{array}$$

Thus, $r_{ij}^{(k)}=0$ and $p_{ij}^{(k)}=0$; i.e.,

$$c_{ik}{c}_{j,k+1}=c_{jk}{c}_{i,k+1},\hspace{1em}{d}_{ik}{c}_{j,k+1}=d_{jk}{c}_{i,k+1}$$ (28)

for k = 0, 1, …, N − 2. Note that, d_i(x) = δ_id(x); it follows from equation (28) that

$$c_i\left(\frac{k+1}{N}\right)=\frac{{\delta }_i}{{\delta }_1}{c}_1\left(\frac{k+1}{N}\right),\hspace{1em}k=0,1,\dots ,N-2.$$

Hence, for 1 ≤ i ≤ m, c_i(x) = σ_ic₁(x) for all x ∈ [0, 1], where ${\sigma }_i=\frac{{\delta }_i}{{\delta }_1}$. In addition, ${\delta }_i{\sigma }_j=\frac{{\delta }_i{\delta }_j}{{\delta }_1}={\delta }_j{\sigma }_i$, 1 ≤ i, j ≤ m. The proof is thus complete. □

Remark 4.2

The conditions in Theorem 4.2 are stated in terms of system (2) without the constraint (3), which would be more general than the original reaction-diffusion system (1). If Eq. (3) is considered, then the conditions in Theorem 4.2 can be obviously simplified and only d_i(x) = δ_id(x), 1 ≤ i ≤ m, are needed.

Based on Theorem 4.2, we can in fact show that ${\mathcal{R}}_0^{\text{PDE}}={\mathcal{R}}_0^{\text{ODE}}$ if ${\left\{A_i\right\}}_{i=1}^m$ is a commuting family.

Theorem 4.3

Let (A1)–(A5) and (H1)–(H2) hold. Suppose that there exist continuous functions d(x) and c(x) such that d_i(x) = δ_id(x) and c_i(x) = σ_ic(x) for 1 ≤ i ≤ m, where the constants δ_i, σ_i satisfy δ_iσ_j = δ_jσ_i for all 1 ≤ i, j ≤ m, then ${\mathcal{R}}_0^{PDE}={\mathcal{R}}_0^{ODE}$.

Proof

On one hand, we have ${\mathcal{R}}_0^{\text{PDE}}\le {\mathcal{R}}_0^{\text{ODE}}$ by Theorems 4.1 and 4.2. On the other hand, we note that d_ik = δ_id(x_k) ≔ δ_id_k and c_ik = σ_ic(x_k) ≔ σ_ic_k. Then, for any 1 ≤ i ≤ m,

$$\frac{A_i-v_i{I}_{N+1}}{{\delta }_i}=\left[\begin{array}{llll}2d_0{N}^2\hfill & -2d_0{N}^2\hfill & \hfill & \hfill \\ -N\left(d_{1}N+\frac{c_1{\sigma }_i}{2{\delta }_i}\right)\hfill & 2d_1{N}^2\hfill & -N\left(d_{1}N-\frac{c_1{\sigma }_i}{2{\delta }_i}\right)\hfill & \hfill \\ \hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill & \hfill \\ \hfill & \hfill & -N\left(d_{N-1}N+\frac{c_{N-1}{\sigma }_i}{2{\delta }_i}\right)\hfill & 2d_{N-1}{N}^2-N\left(d_{N-1}N-\frac{c_{N-1}{\sigma }_i}{2{\delta }_i}\right)\hfill \\ \hfill & \hfill & \hfill & -2d_N{N}^{2}2d_N{N}^2\hfill \end{array}\right]$$

Since $\frac{{\sigma }_i}{{\delta }_i}=\frac{{\sigma }_j}{{\delta }_j}$ for all 1 ≤ i, j ≤ m, we obtain that

$$\frac{A_i-v_i{I}_{N+1}}{{\delta }_i}=\frac{A_j-v_j{I}_{N+1}}{{\delta }_j},\hspace{1em}1\le i,j\le m.$$

Denote this identical matrix by A₀. It is clear to see that A₀ is diagonalizable for all N > N* by Lemma 3.1. Note that, the summation of each row of matrix A₀ is 0, and hence, 0 is the smallest eigenvalue of A₀ by Lemma 3.2. We assume those eigenvalues are 0 ≤ λ₁ ≤ ⋯ ≤ λ_N. Then, there exists a nonsingular matrix P such that

$$A_i=P^{-1}\text{diag}\left(v_i,v_i+{\delta }_i{\lambda }_1,\dots ,v_i+{\delta }_i{\lambda }_N\right)P.$$

Thus,

$$P{A}_i^{-1}{P}^{-1}=\text{diag}\left(\frac{1}{v_i},\frac{1}{v_i+{\delta }_i{\lambda }_1},\dots ,\frac{1}{v_i+{\delta }_i{\lambda }_N}\right).$$

It follows from the proof of Theorem 4.1(1) that O₁ = FV⁻¹ and from Lemma 4.3 that ρ(O₁) ≥ ρ(O_k) for 2 ≤ k ≤ N + 1. Consequently, equation (23) yields

$$\rho \left(F\otimes I_{N+1}\right)A^{-1})=\rho \left(F{V}^{-1}\right)$$ (29)

for all N > N*. Letting N → ∞, we obtain ${\mathcal{R}}_0^{\text{PDE}}={\mathcal{R}}_0^{\text{ODE}}$. □

Remark 4.3

Again, the conditions in Theorem 4.3 are stated in terms of system (2). If we impose the constraint (3) and consider the original system (1), then the following results immediately follow from Theorem 4.3. These results cover several special, but important, scenarios of reaction-diffusion epidemic models: (i) constant diffusion rates (Remark 4.4); (ii) uniform diffusion patterns among the infected compartments (Remark 4.5); (iii) partial diffusion in the system (Corollary 4.2). In each of the following scenarios, the basic reproduction number ${\mathcal{R}}_0^{\text{PDE}}$ for the reaction-diffusion system (1) and the basic reproduction number ${\mathcal{R}}_0^{\text{ODE}}$ for its ODE counterpart are the same.

Corollary 4.1

If there exist constants δ_i and a continuous function d(x) such that d_i(x) = δ_id(x) for all i = 1, …, m in system (1), then ${\mathcal{R}}_0^{PDE}={\mathcal{R}}_0^{ODE}$.

Remark 4.4

In particular, if the diffusion rates of all the infected compartments are positive constants in system (1), then ${\mathcal{R}}_0^{\text{PDE}}={\mathcal{R}}_0^{\text{ODE}}$.

Remark 4.5

In particular, if d_i(x) = d_j(x) for 1 ≤ i, j ≤ m in system (1), then ${\mathcal{R}}_0^{\text{PDE}}={\mathcal{R}}_0^{\text{ODE}}$.

Corollary 4.2

If d_i(x) = 0 for i = 1, …, m − 1 and d_m(x) ≥ d₀ > 0 in system (1), then ${\mathcal{R}}_0^{PDE}={\mathcal{R}}_0^{ODE}$.

Remark 4.6

Although the assumption (H1) does not hold in Corollary 4.2, we note that A_i = υ_i I_N+1, since d_i(x) = c_i(x) = 0, for 1 ≤ i ≤ m − 1. Meanwhile, for any N > N*, it follows from the proof of Theorem 4.1(1) that there exists 1 ≤ k ≤ N +1 such that α_mk = 1/υ_m. Hence, we obtain the matrix O_k = FV⁻¹, which yields ${\mathcal{R}}_0^{\text{PDE}}={\mathcal{R}}_0^{\text{ODE}}$.

5. Examples

We provide a few examples below to illustrate some common reaction-diffusion epidemic models that have the same basic reproduction numbers as those of their ODE counterparts. Sect. 5.1 presents a SIR model which has a single infected compartment; Sect. 5.2 presents two SIR-B models where one is partially diffusive and the other has constant diffusion rates; Sect. 5.3 presents a patchy model where the matrix F is in a triangular form; Sect. 5.4 presents a SEIR model which has a uniform diffusion pattern in the infected compartments. Some numerical simulation results are also presented.

5.1. SIR Model

Let us consider the following SIR model with diffusion, which is an extension of the reaction-diffusion SIR system presented in Kim et al. (2013):

$$\frac{\partial S}{\partial t}=\frac{\partial }{\partial x}\left(d_S(x)\frac{\partial S}{\partial x}\right)+\Lambda -\alpha SI-\mu S,\hspace{1em}x\in [0,1],t>0;$$

$$\frac{\partial I}{\partial t}=\frac{\partial }{\partial x}\left(d_I(x)\frac{\partial I}{\partial x}\right)+\alpha SI-\mu I-\gamma I,\hspace{1em}x\in [0,1],t>0;$$

$$\frac{\partial R}{\partial t}=\frac{\partial }{\partial x}\left(d_R(x)\frac{\partial R}{\partial x}\right)+\gamma I-\mu R,\hspace{1em}x\in [0,1],t>0;$$

$$\frac{\partial S}{\partial x}(t,0)=\frac{\partial I}{\partial x}(t,0)=\frac{\partial R}{\partial x}(t,0)=0,\hspace{1em}t>0;$$

$$\frac{\partial S}{\partial x}(t,1)=\frac{\partial I}{\partial x}(t,1)=\frac{\partial R}{\partial x}(t,1)=0,\hspace{1em}t>0;$$

$$S(0,x)=S_0(x),I(0,x)=I_0(x),R(0,x)=R_0(x),\hspace{1em}x\in [0,1].$$ (30)

Here, S, I, and R are the numbers of susceptible, infected, and recovered individuals, respectively, and d_S(x), d_I(x) and d_R(x) are their associated diffusion rates. The parameters Λ, α, μ, and γ represent the recruitment rate, transmission rate, natural death rate, and disease recovery rate, respectively.

Apparently, system (30) admits a disease-free steady state $(S,I,R)=\left(\frac{\Lambda }{\mu },0,0\right)$, and I is the only infection compartment; i.e., m = 1. Note that, $F=\frac{\alpha \Lambda }{\mu }$ and V = μ + γ. From Theorem 4.1(2), we know that the basic reproduction number of the PDE system (30) is the same as that of its ODE system:

$${\mathcal{R}}_0^{\text{PDE}}=\rho \left(F{V}^{-1}\right)=\frac{\alpha \Lambda }{\mu (\mu +\gamma )}.$$

A numerical test is performed to demonstrate our numerical method based on Eq. (21). Figure 1 plots the values of our numerical calculation of ρ(F ⊗ I_N+1)A⁻¹) versus N for the model (30). We set the diffusion rate of the infected individuals as d_I (x) = sin(50x) + 0.04x + 1 in this test. Since ${\mathcal{R}}_0^{\text{ODE}}=\rho \left(F{V}^{-1}\right)$ does not depend on N, it is represented by a horizontal line in the graph. We observe that when N is sufficiently large, the numerical values of ${\mathcal{R}}_0^{\text{PDE}}$ (i.e., ρ(F ⊗ I_N+1)A⁻¹)) agree almost perfectly with ${\mathcal{R}}_0^{\text{ODE}}$, and this pattern continues for all N > 210. This is consistent with our result in Eq. (29).

Fig. 1.

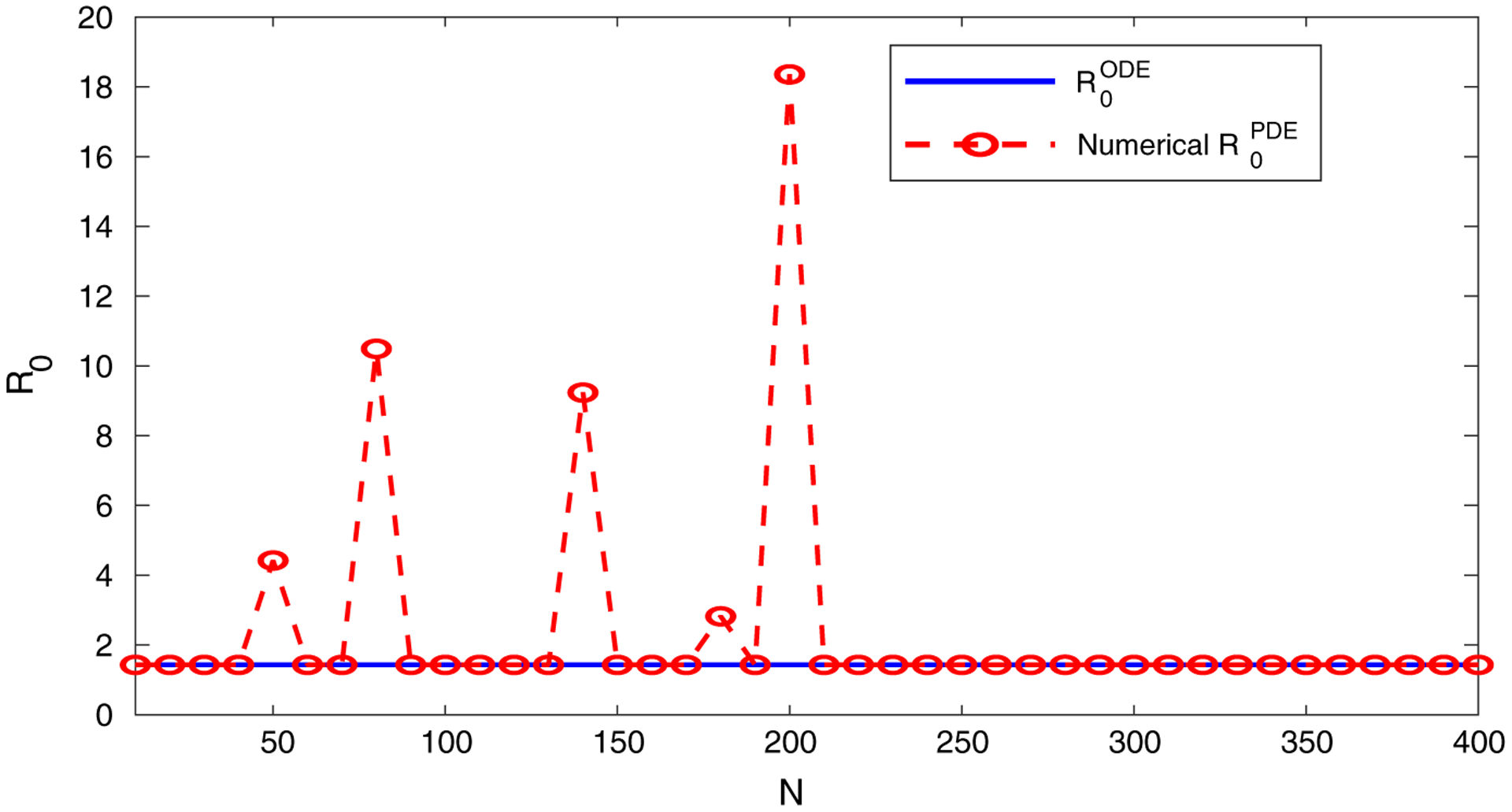
Comparison between ${\mathcal{R}}_0^{\text{ODE}}$ and the numerical values of ${\mathcal{R}}_0^{\text{PDE}}$ as N increases, for the SIR model (30). Here, ${\mathcal{R}}_0^{\text{ODE}}\approx 1.43$ is independent of N. The numerical values of ${\mathcal{R}}_0^{\text{PDE}}$ are based on the calculation of ρ(F ⊗ I_N+1)A⁻¹)

5.2. SIR-B Models

SIR-B models, where ‘B’ refers to the bacterial compartment, have been used to study the transmission dynamics of waterborne bacterial infections, particularly cholera (Tien and Earn 2010; Posny and Wang 2014; Mukandavire et al. 2011). Such a disease is typically transmitted through both the indirect (i.e., environment-to-human) and direct (i.e., human-to-human) routes. In addition, suppose that the waterborne bacteria undergo diffusion in a river that is simply represented by a one-dimensional spatial domain [0, 1]. We thus obtain the following PDE system

$$\frac{\partial S}{\partial t}=\Lambda -(\alpha I+\beta B)S-\mu S;$$

$$\frac{\partial I}{\partial t}=(\alpha I+\beta B)S-(\mu +\gamma )I;$$

$$\frac{\partial R}{\partial t}=\gamma I-\mu R;$$

$$\frac{\partial B}{\partial t}=\frac{\partial }{\partial x}\left(d_B(x)\frac{\partial B}{\partial x}\right)+\xi I+rB\left(1-\frac{B}{K}\right)-\tau B,$$ (31)

for t > 0, x ∈ [0, 1] with Neumann boundary conditions and appropriate initial conditions. In this model, B represents the concentration of the bacterial pathogen in the contaminated water; α and β denote the direct and indirect transmission rates, respectively; ξ is the rate of contribution, such as shedding, from an infected individual to the bacterial population in the aquatic environment; r is the bacterial intrinsic growth rate, K is the carrying capacity of the bacterial growth, and τ is the bacterial removal rate.

The model (31) is a partially diffusive PDE system in the sense that the diffusion process is only incorporated into the bacterial movement. The infection compartments are I and B. The disease-free equilibrium is $(S,I,R,B)=\left(\frac{\Lambda }{\mu },0,0,0\right)$ and thereby

$$F=\left[\begin{array}{cc}\frac{\alpha \Lambda }{\mu }& \frac{\beta \Lambda }{\mu }\\ \xi & r\end{array}\right]\hspace{1em}\text{and}\hspace{1em}V=\left[\begin{array}{cc}\mu +\gamma & 0\\ 0& \tau \end{array}\right].$$

From Corollary 4.2, the basic reproduction number of system (31) is

$${\mathcal{R}}_0^{\text{PDE}}=\rho \left(F{V}^{-1}\right)=\frac{1}{2}\left(\frac{\alpha \Lambda }{\mu (\mu +\gamma )}+\frac{r}{\tau }+\sqrt{{\left(\frac{\alpha \Lambda }{\mu (\mu +\gamma )}-\frac{r}{\tau }\right)}^2+\frac{4\xi \beta \Lambda }{\mu \tau (\mu +\gamma )}}\right).$$ (32)

Again, to verify our computational approach based on Eq. (21) and to provide a numerical evidence on the relationship between ${\mathcal{R}}_0^{\text{PDE}}$ and ${\mathcal{R}}_0^{\text{ODE}}$, we plot ρ(F ⊗ I_N+1)A⁻¹) versus N in Fig. 2 for the model (31). We set the bacterial diffusion rate as d_B(x) = sin(100x) + 1.13. We observe a pattern similar to that in Fig. 1. Specifically, for all N > 80, the numerical values of ${\mathcal{R}}_0^{\text{PDE}}$ (i.e., ρ(F ⊗ I_N+1)A⁻¹)) coincide with ${\mathcal{R}}_0^{\text{ODE}}$, consistent with our prediction in Eq. (29).

Fig. 2.

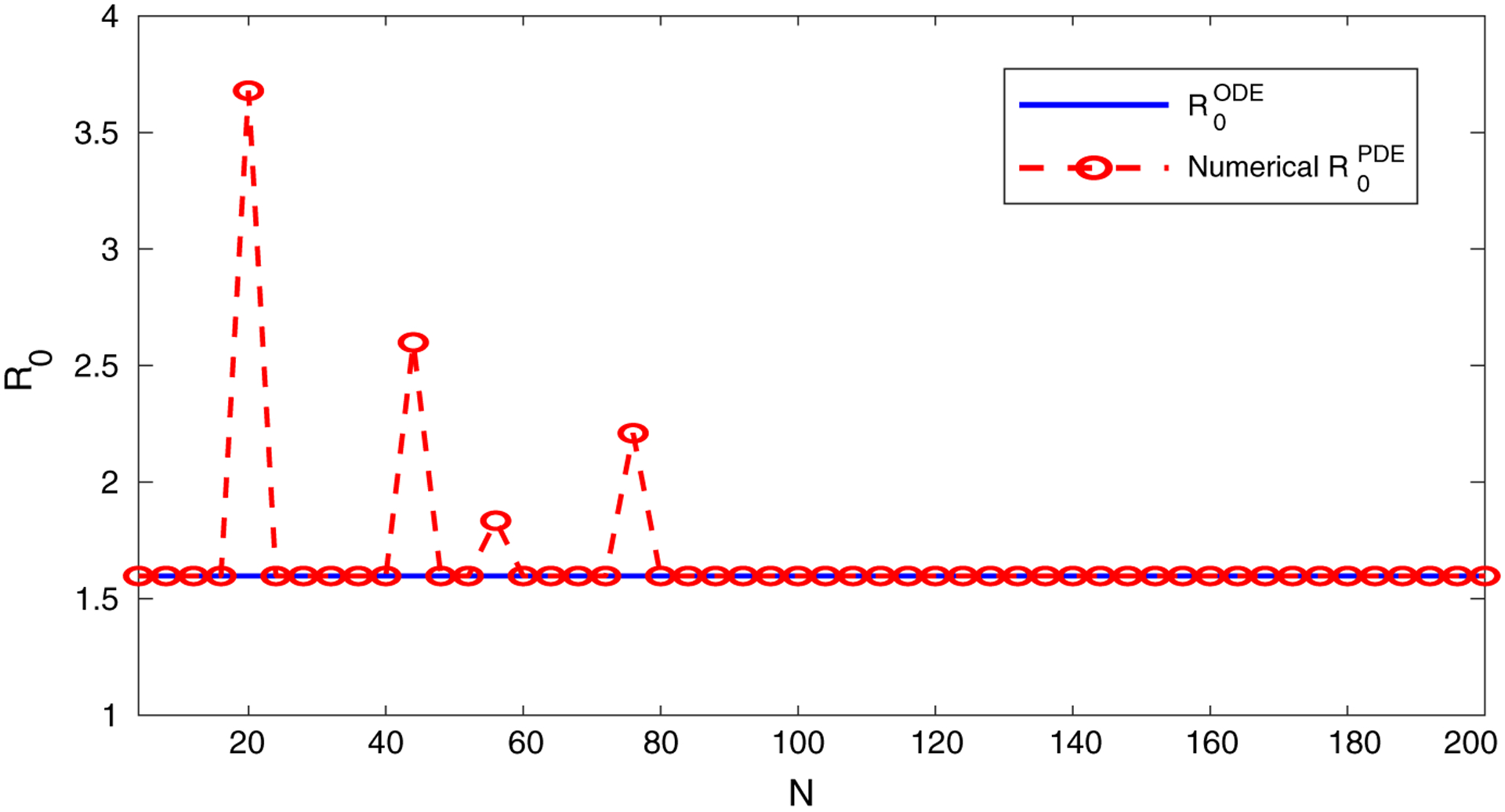
Comparison between ${\mathcal{R}}_0^{\text{ODE}}$ and the numerical values of ${\mathcal{R}}_0^{\text{PDE}}$ as N increases, for the SIR-B model 31). Here, ${\mathcal{R}}_0^{\text{ODE}}\approx 1.60$ is independent of N. The numerical values of ${\mathcal{R}}_0^{\text{PDE}}$ are based on the calculation of ρ(F ⊗ I_N+1)A⁻¹)

On another setting, let us consider the movement of the human hosts as well on the same spatial domain. We assume that all the human hosts and pathogenic bacteria go through a diffusion process and that the diffusion is homogeneous in space so that all the diffusion rates are positive constants. Then, system (31) is modified as

$$\frac{\partial S}{\partial t}=d_S\frac{{\partial }^{2}S}{\partial x^2}+\Lambda -(\alpha I+\beta B)S-\mu S;$$

$$\frac{\partial I}{\partial t}=d_I\frac{{\partial }^{2}I}{\partial x^2}+(\alpha I+\beta B)S-(\mu +\gamma )I;$$

$$\frac{\partial R}{\partial t}=d_R\frac{{\partial }^{2}R}{\partial x^2}+\gamma I-\mu R;$$

$$\frac{\partial B}{\partial t}=d_B\frac{{\partial }^{2}B}{\partial x^2}+\xi I+rB\left(1-\frac{B}{K}\right)-\tau B,$$ (33)

for t > 0 and x ∈ [0, 1]. With the constant diffusion rates, one can apply Remark 4.4 to obtain that the basic reproduction number for the reaction-diffusion system (33) is just the same as given in equation (32).

5.3. Patchy Model

Next, we consider a patchy setting which is a natural extension of the brucellosis patchy model studied in Yang et al. (2017). We assume an environment of n patches, where each patch consists of susceptible and infected individuals and where the disease can spread from patch i to patch j for 1 ≤ i < j ≤ n through unidirectional migration. We additionally consider a diffusion process of the susceptible and infected individuals over the spatial domain [0, 1]. Thus, we may formulate the following reaction-diffusion system with Neumann boundary conditions and appropriate initial conditions:

$$\frac{\partial S_i}{\partial t}=\frac{\partial }{\partial x}\left(d_{S_i}(x)\frac{\partial S_i}{\partial x}\right)+{\Lambda }_i+\sum _{j<i}{\theta }_{ji}{S}_j-\left({\alpha }_i{I}_i+\sum _{j>i}{\theta }_{ij}+{\mu }_i\right)S_i;$$

$$\frac{\partial I_i}{\partial t}=\frac{\partial }{\partial x}\left(d_{I_i}(x)\frac{\partial I_i}{\partial x}\right)+{\alpha }_i{S}_i{I}_i+\sum _{j<i}{\delta }_{ji}{I}_j-\left(\sum _{j>i}{\delta }_{ij}+{\gamma }_i+{\mu }_i\right)I_i,$$ (34)

for i = 1, ⋯ , n. Here, θ_ij and δ_ij denote the migration rates of susceptible and infected individuals from patch i to patch j, respectively; Λ_i, α_i, μ_i and γ_i denote the recruitment rate, transmission rate, natural death rate, and disease recovery rate, respectively, for patch i (1 ≤ i ≤ n).

The infection compartments for this model are obviously I_i for 1 ≤ i ≤ n. The disease-free equilibrium is

$$x_0={\left(0,0,\dots ,0,S_1^0,\dots ,S_n^0\right)}^T$$

with $S_1^0=\frac{{\Lambda }_1}{{\mu }_1}$ and $S_i^0=\frac{{\Lambda }_i+\sum _{j<i}{\theta }_{ji}{S}_j^0}{\sum _{j>i}{\theta }_{ij}+{\mu }_i}$ for i = 2, ⋯ , n. Consequently,

$$F={\left[F_{ij}\right]}_{n\times n}\hspace{1em}\text{with}\hspace{1em}{F}_{ij}=\{\begin{array}{ll}{\delta }_{ji},\hfill & i>j,\hfill \\ {\alpha }_i{S}_i^0,\hfill & i=j,\hfill \\ 0,\hfill & i<j,\hfill \end{array}$$

and

$$V=\text{diag}\left(\sum _{j>1}{\delta }_{1j}+{\gamma }_1+{\mu }_1,\cdots ,{\delta }_{n-1,n}+{\gamma }_{n-1}+{\mu }_{n-1},{\gamma }_n+{\mu }_n\right).$$

Since the matrix F is triangular, Theorem 4.1(2) applies and the basic reproduction number of system (34) is given by

$${\mathcal{R}}_0^{\text{PDE}}=\rho \left(F{V}^{-1}\right)=\text{max}\left\{\frac{{\alpha }_1{S}_1^0}{\sum _{j>1}{\delta }_{1j}+{\gamma }_1+{\mu }_1},\cdots ,\frac{{\alpha }_{n-1}{S}_{n-1}^0}{{\delta }_{n-1,n}+{\gamma }_{n-1}+{\mu }_{n-1}},\frac{{\alpha }_n{S}_n^0}{{\gamma }_n+{\mu }_n}\right\}.$$

5.4. SEIR Model

SEIR models investigate disease transmission in a population consisting of the susceptible, exposed, infected, and recovered individuals. Here, we consider a SEIR model slightly modified from (van den Driessche and Watmough 2002, Example 4.1). We assume that exposed individuals progress to the infected group at rate υ, exposed individuals recover at rate γ₁ and enter the recovered class, and infected individuals recover at rate γ₂ among whom a portion p (0 ≤ p ≤ 1) enters the exposed class and the other portion 1 − p enters the recovered class. We further assume that the two infected compartments (E and I) have the same movement pattern; namely, their diffusion rates are the same: d_E(x) = d_I (x) = d(x). We then obtain the following reaction-diffusion system associated with this SEIR model:

$$\frac{\partial S}{\partial t}=\frac{\partial }{\partial x}\left(d_S(x)\frac{\partial S}{\partial x}\right)+\Lambda -\alpha SI-\mu S;$$

$$\frac{\partial E}{\partial t}=\frac{\partial }{\partial x}\left(d(x)\frac{\partial E}{\partial x}\right)+\alpha SI+p{\gamma }_{2}I-\left(\mu +v+{\gamma }_1\right)E;$$

$$\frac{\partial I}{\partial t}=\frac{\partial }{\partial x}\left(d(x)\frac{\partial I}{\partial x}\right)+vE-\left(\mu +{\gamma }_2\right)I;$$

$$\frac{\partial R}{\partial t}=\frac{\partial }{\partial x}\left(d_R(x)\frac{\partial R}{\partial x}\right)+{\gamma }_{1}E+(1-p){\gamma }_{2}I-\mu R,$$ (35)

for x ∈ [0, 1] and t > 0. There is only one disease-free equilibrium

$$(S,E,I,R)=\left(\frac{\Lambda }{\mu },0,0,0\right),$$

and

$$F=\left[\begin{array}{ll}0\hfill & \frac{\alpha \Lambda }{\mu }+p{\gamma }_2\hfill \\ v\hfill & 0\hfill \end{array}\right],\hspace{1em}V=\left[\begin{array}{ll}\mu +v+{\gamma }_1\hfill & 0\hfill \\ 0\hfill & \mu +{\gamma }_2\hfill \end{array}\right].$$

By Remark 4.5, the basic reproduction number for system (35) is given by

$${\mathcal{R}}_0^{\text{PDE}}=\rho \left(F{V}^{-1}\right)=\sqrt{\frac{v\left(\alpha \Lambda +p\mu {\gamma }_2\right)}{\mu \left(\mu +{\gamma }_2\right)\left(\mu +v+{\gamma }_1\right)}}.$$

6. Conclusion

We have presented a numerical approach that can be applied to the calculation of the basic reproduction numbers for a variety of reaction-diffusion type epidemic models. Essentially, our method transfers the computation of the spectral radius associated with an infinite-dimensional operator to the computation of the principal eigenvalue associated with a finite-dimensional matrix. Such a representation of ${\mathcal{R}}_0$ enables us to analyze and compare the basic reproduction numbers for the PDE system and its corresponding ODE system, based solely on elementary numerical analysis and matrix theory. We have found, in particular, that ${\mathcal{R}}_0^{\text{PDE}}={\mathcal{R}}_0^{\text{ODE}}$ under a range of conditions that cover several important cases, including the presence of a single infected compartment, constant diffusion rates, uniform diffusion patterns among the infected compartments, and partial diffusion in the system.

In general, the calculation of the basic reproduction number for a PDE system is not a simple procedure, due to the involvement of operator analysis and eigenvalue computation. Consequently, it becomes a nontrivial task to quantify the disease transmission risk represented by such a PDE model. Our results show that for a number of important epidemic scenarios involving reaction-diffusion equations, the task of ${\mathcal{R}}_0$ computation is simplified and replaced by that of the corresponding ODE system; i.e., ${\mathcal{R}}_0^{\text{PDE}}={\mathcal{R}}_0^{\text{ODE}}$. These scenarios include some common SIR, SEIR, SIR-B, and patchy models. Our findings help us to gain essential understanding of the disease transmission thresholds for these models, while saving unnecessary computational efforts.

We have assumed that the underlying ODE system is autonomous with constant parameters, though the diffusion rates in our model are location-dependent and emphasize spatial heterogeneity. In case, the ODE system has spatially varying parameters, our numerical method can still be applied with minimal adjustment, but our analysis will need some modification. Particularly, the definition of ${\mathcal{R}}_0^{\text{ODE}}$ would depend on the spatial location x, and so a simple relationship between ${\mathcal{R}}_0^{\text{PDE}}$ and ${\mathcal{R}}_0^{\text{ODE}}$ may not exist in general. This will provide one interesting direction in our future research. We will also explore the computation, comparison, and analysis of the basic reproduction numbers for more general reaction-convection-diffusion type epidemic models, including those that are defined on multi-dimensional spatial domains and those that do not satisfy the conditions prescribed in Theorem 4.3.