Dynamics of a stochastic delay differential model for COVID-19 infection with asymptomatic infected and interacting people: Case study in the UAE

Abstract

Public health science is increasingly focusing on understanding how COVID-19 spreads among humans. For the dynamics of COVID-19, we propose a stochastic epidemic model, with time-delays, Susceptible–Infected–Asymptomatic–Quarantined–Recovered (SIAQR). One global positive solution exists with probability one in the model. As a threshold condition of persistence and existence of an ergodic stationary distribution, we deduce a generalized stochastic threshold ${\mathcal{R}}_0^s<{\mathcal{R}}_0$. To estimate the percentages of people who must be vaccinated to achieve herd immunity, least-squares approaches were used to estimate ${\mathcal{R}}_0$ from real observations in the UAE. Our results suggest that when ${\mathcal{R}}_0>1$, a proportion $max(1-1/{\mathcal{R}}_0)$ of the population needs to be immunized/vaccinated during the pandemic wave. Numerical simulations show that the proposed stochastic delay differential model is consistent with the physical sensitivity and fluctuation of the real observations.

Introduction

Since the confirmation of the first cases of COVID-19 in the UAE on 29 January 2020, when an infected family of four members: mother, father, nine-year-old girl and grandmother visited the Emirates on January 16th. The first sought treatment on January 23rd after the grandmother developed flu-like symptoms. The rest members of the family subsequently developed the disease. Since then, various preventive measures and techniques to ensure prompt identification and follow up of confirmed cases and their contacts to control the spread of diseases have been imposed by the UAE [1]. In this paper, we propose a new compartmental stochastic epidemic model with time-delays describing the transmission of COVID-19 in the UAE. It takes account on the asymptomatic people and the strategies involving hospital isolation of the confirmed infected person, quarantine of people contacting them, and home containment of all population to restrict mobility. The model also takes into account the potential environmental factors such as temperature and humidity along with international travel and lack of proper social consciousness for isolation as causes of the spread of COVID 19.

Numerical modeling of infectious and transmission diseases has an essential role in the epidemiological aspect of disease control [2], [3], [4], [5], [6], [7]. Several useful papers have been formulated to develop mathematical models in various countries to analyze the complex transmission pattern for COVID-19. In [8], the authors provided age-structured compartmental SEIR (susceptible, exposed, infected and recovered) framework that accounts for specific distributions of different characteristic times, as well as the population structure in the region. In [9], the authors discussed a deterministic model with fractional order of COVID-19 dynamics with quarantine, isolation, and environmental viral load. In [10], the authors analyzed some environmental factors such as atmospheric humidity, temperature, geographic location of the countries, humidity, etc., that impact the worldwide spread of the COVID-19. Currently, there are many mathematical models used to explain disease processes of COVID-19, for more details, refer the reader to [11], [12], [13], [14], [15], [16].

Scientists keep an eye on the developments in the virus, including transformations to the spikes on the surface of the virus [17]. Recent studies, along with genetic analyses of the virus, are supporting researchers realize how changes to the virus might influence how it expands and what occurs to people who are contaminated with it. Various variants of the virus that causes COVID-19 are spreading out globally [18], [19], [20]. These variants appear to be spread more efficiently and speedily than other variants, which may cause to more cases of COVID-19. An increment in the number of cases will bring more pressure on medical management systems. Up to this time, studies indicate that antibodies generated through vaccination with currently authorized vaccines identify these variants [21], [22], and studies are still ongoing in this field.

In fact there is a difficulty in predicting number of patients, by using deterministic epidemic models, especially with different confinement measures taken by different countries, as well as changes in the virus characteristics. The main aim in this work is to propose an epidemic model describing the transmission of COVID-19 (SARS-CoV-2 virus) in the UAE, using a Susceptible–Infected–Asymptomatic–Quarantined–Recovered (SIAQR) model with time-delays, where the parameters are stochastically perturbed to consider the difficulty in detecting patients, and other difficulties. In this model, we incorporate the isolation of infected people, and take into account the people (asymptomatic infected) moving freely and are infected but do not have symptoms and added the measure of the quarantine of the people interacting with an affected individual. We also investigate reality of the proposed model by fitting it to real observations for COVID-19 cases in the UAE. The stochastic best-fit model to the COVID-19 infected populations gives an extra degree of realism in comparison with its corresponding deterministic model. We experimentally estimate the severity of the disease, ${\mathcal{R}}_0$, in order to determine the percentages that should be vaccinated to achieve herd immunity.

The organization of the paper is as follows: In “Stochastic epidemic model with time-delays”, we introduce the deterministic and the stochastic models. In “Global positive solution”, the existence and uniqueness of the global positive solution for the model is discussed. We analyze a stationary distribution and ergodicity of the stochastic model in “Stationary distribution and ergodicity”. “Numerical simulations and fitting model to observations” presents numerical simulations for supporting theoretical results related to dynamical behavior of the model and a comparison is presented between real data and the obtained findings. We then conclude in “Conclusion”.

Stochastic epidemic model with time-delays

We examine transmission dynamics of the novel coronavirus through a mathematical model agreeing to the component of the virus transmittal [23], [24]. We classify the total population $N\left(t\right)$ in five groups: Susceptible individuals $S\left(t\right)$; Infected individuals $I\left(t\right)$ (confirmed infected); Asymptomatic infected people $A\left(t\right)$; Quarantined individuals $Q\left(t\right)$; and Recovered people $R\left(t\right)$. The following deterministic delay differential equations (DDEs) describes the transmission dynamics of COVID-19 (see Fig. 1)

$$\dot{S}\left(t\right)=\Lambda -d_{S}S\left(t\right)-\alpha \beta S\left(t\right)I(t-{\tau }_1)-\beta S\left(t\right)A\left(t\right)+\xi Q\left(t\right),$$$$\dot{I}\left(t\right)=\theta Q\left(t\right)+\delta A\left(t\right)-(\mu +d_0+d_I)I\left(t\right),$$$$\dot{A}\left(t\right)=\beta S\left(t\right)A\left(t\right)-(\delta +\lambda +d_A)A\left(t\right),$$$$\dot{Q}\left(t\right)=\alpha \beta S\left(t\right)I(t-{\tau }_1)-(\xi +\theta +d_Q)Q\left(t\right),$$$$\dot{R}\left(t\right)=\mu I(t-{\tau }_2)+\lambda A\left(t\right)-d_{R}R\left(t\right).$$ (1)

Equation of died people can be expressed as

$$\dot{D}\left(t\right)=d_{I}I.$$

We assume that the population is closed then we can compute $D=N-S\left(t\right)+I\left(t\right)+A\left(t\right)+Q\left(t\right)+R\left(t\right)$, where $N$ is the total accumulative population. The time-lag or time-delay ${\tau }_1$ ($3$–$14$ days) stands for the incubation period [25]; While ${\tau }_2$ is considered to justify time needed for the infected individuals to become recovered. Presence of time-delays in the model supplements the dynamics of the system, as they may create periodic solutions for various values [3]. The suggested SIAQR model fulfills the following hypothesis: (1) All the parameters in the model are positive, with biological meaning defined in Table 1; (2) real asymptomatic patients will remain asymptomatic up to recovery and do not spread the infection; (3) patients who are for a short time asymptomatic are considered on symptomatic ones; (4) the second infection is not examined within the study; (5) the UAE health system is not overwhelmed; (6) natural birth of $I,Q,R$ rate are not factors.

Fig. 1.

The diagram of model (1), shows the transition between compartments.

Table 1.

Main parameters of the SIAQR model.

Parameters	Description
$\Lambda$	The birth rate
$d_S,d_A,d_Q,d_R$	Natural death rates of $S,A,Q,R$, respectively
$d_I$	Disease death rate
$d_0$	Additional disease caused rate suffered by the infectious individuals
$\beta$	Contact/transmission rate
$\alpha$	Contact rate of susceptible people with a confirmed infected individuals
$\xi$	The rate of quarantined population that are negatively diagnosed
$\theta$	The proportion of quarantined population that are diagnosed positively
$\delta$	The rate of asymptomatic people that becoming symptomatic
$\mu$	The rate of recovered of infective individuals
$\lambda$	The rate of recovered of asymptomatic individuals

We use the next-generation matrix approach [26] to estimate the basic reproduction number

$${\mathcal{R}}_0=\frac{\beta \Lambda }{d_S(\delta +\lambda +d_A)}.$$

If ${\mathcal{R}}_0<1$, system (1) has a unique disease-free equilibrium ${\mathcal{E}}_0=(\frac{\Lambda }{d_S},0,0,0,0)$, which is a global attractor in the first octant. If ${\mathcal{R}}_0>1$, then system (1) has two equilibria, a disease-free equilibrium ${\mathcal{E}}_0$ and an endemic equilibrium ${\mathcal{E}}^{\ast }=(S^{\ast },I^{\ast },A^{\ast },Q^{\ast },R^{\ast })$, such that ${\mathcal{E}}_0$ is unstable and ${\mathcal{E}}^{\ast }$ is a global attractor in the interior of the first octant, where $S^{\ast }=\frac{\Lambda /d_S}{{\mathcal{R}}_0}$, $I^{\ast }=\frac{d_S({\mathcal{R}}_0-1)}{\beta (\alpha +K_1-\xi \alpha /(\xi +\theta +d_Q))}$, $A^{\ast }=K_1{I}^{\ast }$, $Q^{\ast }=\frac{\alpha \beta \Lambda }{d_S(\xi +\theta +d_Q){\mathcal{R}}_0}{I}^{\ast }$, and $R^{\ast }=K_2{I}^{\ast }$, such that $K_1=\frac{(\mu +d_0+d_I)(\xi +\theta +d_Q)-\left(\theta \alpha (\delta +\lambda +d_A)\right)}{\delta (\xi +\theta +d_Q)}$, $K_2=\frac{\mu +\lambda K_1}{d_R}$.

In reality, epidemic models are unavoidably influenced by environmental white noise which is an vital component in nature, since it can give an extra degree of reality compared to their undisturbed counterparts. Numerous researchers have examined the impact of stochasticity on epidemic models [27], [28], [29], [30], [31]. Stochastic perturbation variables have a considerable affect on the disease drive of all sorts of virus infections to humans. Taking this into thought empowers to show uncertainty into deterministic natural models to uncover the natural inconstancy impact, whether it could be an environmental perturbation in parameters or random noise within the differential systems.

Therefore, we replace a parameter, e.g., $d_S$ by $d_S-\nu dW$, where $W$ is a Brownian motion defined on the complete probability space($\Omega ,\mathcal{F},{\left\{\mathcal{F}\right\}}_{t\ge t},\mathbb{P}$) with a filtration ${\left\{\mathcal{F}\right\}}_{t\ge 0}$ satisfying the usual conditions and $\nu$ is the intensity of the noise. For more realistic situation of the development process of the disease, we incorporate the effect of randomization by introducing perturbation on the natural death rate with white noise into each equation of model (1). The modified stochastic DDEs model takes the form

$$dS=(\Lambda -d_{S}S\left(t\right)-\alpha \beta S\left(t\right)I(t-{\tau }_1)-\beta S\left(t\right)A\left(t\right)+\xi Q\left(t\right))dt+{\nu }_{1}S\left(t\right)d{W}_1,$$$$dI=(\theta Q\left(t\right)+\delta A\left(t\right)-(\mu +d_0+d_I)I\left(t\right))dt+{\nu }_{2}I\left(t\right)d{W}_2,$$$$dA=(\beta S\left(t\right)A\left(t\right)-(\delta +\lambda +d_A)A\left(t\right))dt+{\nu }_{3}A\left(t\right)d{W}_3,$$$$dQ=(\alpha \beta S\left(t\right)I(t-{\tau }_1)-(\xi +\theta +d_Q)Q\left(t\right))dt+{\nu }_{4}Q\left(t\right)d{W}_4,$$$$dR=(\mu I(t-{\tau }_2)+\lambda A\left(t\right)-d_{R}R\left(t\right))dt+{\nu }_{5}R\left(t\right)d{W}_5.$$ (2)

Here,

$$S\left(\kappa \right)={\psi }_1\left(\kappa \right),I\left(\kappa \right)={\psi }_2\left(\kappa \right),A\left(\kappa \right)={\psi }_3\left(\kappa \right),$$$$Q\left(\kappa \right)={\psi }_4\left(\kappa \right),R\left(\kappa \right)={\psi }_5,$$$$\kappa \in [-\tau ,0],\tau =max\{{\tau }_1,{\tau }_2\}.$$ (3)

${\psi }_i\left(0\right)>0$ and ${\psi }_i\left(\kappa \right)$, $i=1,\dots ,5$, are nonnegative continuous initial functions on $[-\tau ,0]$.

Global positive solution

To study the dynamical behaviors of the epidemic stochastic model (2), we firstly need to investigate whether the solution is global and positive. In this case, the system coefficients (2) must satisfy linear growth and Lipschitzian conditions, so that a positive solution is obtained. Using the Lyapunov operator, we can demonstrate this.

Theorem 1

If the coefficients of system(2)are locally Lipschitz continuous, then for any given initial condition (3) there is a unique positive solution $(S\left(t\right),I\left(t\right),A\left(t\right),Q\left(t\right),R\left(t\right))$ of system (2) on $t\ge -\tau$ , and the solution will remain in ${\mathbb{R}}_{+}^5$ a.s. (almost surely).

Proof

Define a ${\mathcal{C}}^2-$ function $V(S,I,A,Q,R):{\mathbb{R}}_{+}^5\to {\mathbb{R}}_{+}$ by

$$V(S,I,A,Q,R)=V(.)=(S-1-lnS)+(I-1-lnI)+(A-1-lnA)+(Q-1-lnQ)+(R-1-lnR)+\alpha \beta {\int }_t^{t+{\tau }_1}I(s-{\tau }_1)ds+\mu {\int }_t^{t+{\tau }_2}I(s-{\tau }_2)ds.$$ (4)

Due to It$\hat{o}$’s formula on $V(.)$

$$dV(.)=\mathcal{L}Vdt+{\nu }_1(S-1)d{W}_1\left(t\right)+{\nu }_2(I-1)d{W}_2\left(t\right)$$$$+{\nu }_3(A-1)d{W}_3\left(t\right)+{\nu }_4(Q-1)d{W}_4\left(t\right)$$$$+{\nu }_5(R-1)d{W}_5\left(t\right).$$ (5)

Where

$$\mathcal{L}V=(1-\frac{1}{S})[\Lambda -d_{S}S-\alpha \beta SI(t-{\tau }_1)-\beta SA+\xi Q]$$$$+(1-\frac{1}{I})[\theta Q+\delta A-(\mu +d_0+d_I)I]$$$$+(1-\frac{1}{A})[\beta SA-(\delta +\lambda +d_A)A]$$$$+(1-\frac{1}{Q})[\alpha \beta SI(t-{\tau }_1)-(\xi +\theta +d_Q)Q]$$$$+(1-\frac{1}{R})[\mu I(t-{\tau }_2)+\lambda A-d_{R}R]$$$$+\alpha \beta I\left(t\right)-\alpha \beta I(t-{\tau }_1)+\mu I\left(t\right)-\mu I(t-{\tau }_2)$$$$+\frac{{\nu }_1^2+{\nu }_2^2+{\nu }_3^2+{\nu }_4^2+{\nu }_5^2}{2}\le \Lambda +d_S+d_A+d_Q+d_0+d_I+d_R+\xi +\theta +\mu +\delta +\lambda -(\beta +d_S)S$$$$+(\alpha \beta -(d_0+d_I))I$$$$-d_{Q}Q+(\beta -d_A)A-d_{R}R+\frac{{\nu }_1^2+{\nu }_2^2+{\nu }_3^2+{\nu }_4^2+{\nu }_5^2}{2}.$$ (6)

Assume that $\beta \le max\{\frac{d_0+d_I}{\alpha },d_A\}$. Hence, we have

$$\mathcal{L}V\le \Lambda +d_S+d_A+d_Q+d_0+d_I+d_R+\xi +\theta +\mu +\delta +\lambda$$$$+\frac{{\nu }_1^2+{\nu }_2^2+{\nu }_3^2+{\nu }_4^2+{\nu }_5^2}{2}\le \mathcal{M},$$ (7)

where $\mathcal{M}$ is a positive constant. It follows that $\mathcal{L}V(.)$ is bounded. Since the following proof is standard and it is similar to the method in the literature [32], so it is omitted. Therefore, the proof is completed.

Stationary distribution and ergodicity

Ergodic property of a stochastic SIAQR model means that the stochastic model has a unique stationary distribution which expects the persistence of the disease in the future under some conditions on the intensity of white noise, that is the stochastic model fluctuate in a surroundings of the endemic equilibrium of the corresponding deterministic model.

Lemma 1 [33] —

The Markov process $X\left(t\right)$ has a unique ergodic stationary distribution $\mu (.)$ if there exist a bounded domain $\mathcal{U}\subset {\mathbb{R}}^d$ with regular boundary $\Gamma$ and

• (A.1) there is a positive number $\mathcal{M}$ such that ${\sum }_{i,j=1}^d{\lambda }_{ij}\left(x\right){\xi }_i{\xi }_j\ge \mathcal{M}{\left|\xi \right|}^2,x\in \mathcal{U},\xi \in {\mathbb{R}}^d$ .
• (A.2) there exists a nonnegative ${\mathcal{C}}^2$ -function $V$ such that $\mathcal{L}V$ is negative for any ${\mathbb{R}}^d\setminus \mathcal{U}$ .

In this section, we define

$${\mathcal{R}}_0^s=\frac{\Lambda \theta \alpha \lambda {\beta }^2}{{\hat{d}}_S{\hat{d}}_I{\hat{d}}_A{\hat{d}}_Q{\hat{d}}_R},$$ (8)

where

$${\hat{d}}_S=d_S+\frac{{\nu }_1^2}{2},{\hat{d}}_I=d_I+\mu +d_0+\frac{{\nu }_2^2}{2},{\hat{d}}_A=d_A+\delta +\lambda +\frac{{\nu }_3^2}{2},$$

$${\hat{d}}_Q=d_Q+\xi +\theta +\frac{{\nu }_4^2}{2},{\hat{d}}_R=d_R+\frac{{\nu }_5^2}{2}.$$

Theorem 2

If ${\mathcal{R}}_0^s>1$ and $\Lambda >\frac{{\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2}{2}$ . Then for any initial value $(S\left(0\right),I\left(0\right),A\left(0\right),Q\left(0\right),R\left(0\right))\in {\mathbb{R}}_{+}^5$ , there is a stationary distribution $\mu (.)$ for system (2) and the system is ergodic.

Proof

According to Lemma 1 on the existence of the stationary distribution, we will verify that $(A.1)$ and $(A.2)$ hold, the diffusion matrix of system (2) is

$$\Lambda (S,I,A,Q,R)=\left(\begin{array}{ccccc}\hfill {\nu }_1^2{S}^2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\nu }_2^2{I}^2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\nu }_3^2{A}^2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\nu }_4^2{Q}^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\nu }_5^2{R}^2\hfill \end{array}\right).$$

Let $\mathcal{U}$ be any bounded domain in ${\mathbb{R}}_{+}^5$, then there exists a positive constant

$${\mathcal{M}}_0=\underset{(S,I,A,Q,R)\in {\overline{\mathcal{U}}}_{\sigma }}{min}\{{\nu }_1^2{S}^2,{\nu }_2^2{I}^2,{\nu }_3^2{A}^2,{\nu }_4^2{Q}^2,{\nu }_5^2{R}^2\},$$

such that

$$\sum _{i,j=1}^5{\lambda }_{ij}(S,I,A,Q,R){\xi }_i{\xi }_j={\nu }_1^2{S}^2{\xi }_1^2+{\nu }_2^2{I}^2{\xi }_2^2+{\nu }_3^2{A}^2{\xi }_3^2+{\nu }_4^2{Q}^2{\xi }_4^2+{\nu }_4^2{R}^2{\xi }_5^2\ge {\mathcal{M}}_0{\left|\xi \right|}^2,$$

for any $(S,I,A,Q,R)\in {\overline{\mathcal{U}}}_{\sigma },\xi =({\xi }_1,{\xi }_2,{\xi }_3,{\xi }_4,{\xi }_5)\in {\mathbb{R}}_{+}^5$. Thus, we have verified that condition $(A.1)$ of Lemma 1 is satisfied. We then prove condition $(A.2)$ of Lemma 1.

Next, we define a nonnegative ${\mathcal{C}}^2-$function $\mathcal{G}:{\mathbb{R}}_{+}^5\to {\mathbb{R}}_{+}$ by

$$\mathcal{G}(S,I,A,Q,R)=\mathcal{G}(.)=\mathcal{B}[-lnS-{\rho }_{1}lnI-{\rho }_{2}lnA-{\rho }_{3}lnQ$$$$-{\rho }_{4}lnR+\alpha \beta {\int }_t^{t+{\tau }_1}I(s-{\tau }_1)ds]$$$$+\alpha \beta {\int }_t^{t+{\tau }_1}I(s-{\tau }_1)ds-lnQ-lnS-lnR$$$$+\frac{1}{\zeta +1}{(S+I+A+Q+R)}^{\zeta +1},$$ (9)

where,

$${\rho }_1=\frac{\Lambda \theta \alpha \lambda {\beta }^2}{{\hat{d}}_I^2{\hat{d}}_A{\hat{d}}_Q{\hat{d}}_R},{\rho }_2=\frac{\Lambda \theta \alpha \lambda {\beta }^2}{{\hat{d}}_I{\hat{d}}_A^2{\hat{d}}_Q{\hat{d}}_R},$$

$${\rho }_3=\frac{\Lambda \theta \alpha \lambda {\beta }^2}{{\hat{d}}_I{\hat{d}}_A{\hat{d}}_Q^2{\hat{d}}_R},{\rho }_4=\frac{\Lambda \theta \alpha \lambda {\beta }^2}{{\hat{d}}_I{\hat{d}}_A{\hat{d}}_Q{\hat{d}}_R^2}.$$

Denote ${\mathcal{G}}_1(S,I,A,Q,R)=-lnS-{\rho }_{1}lnI-{\rho }_{2}lnA-{\rho }_{3}lnQ-{\rho }_{4}lnR+\alpha \beta {\int }_t^{t+{\tau }_1}I(s-{\tau }_1)ds$, ${\mathcal{G}}_2(S,I)=-lnS+\alpha \beta {\int }_t^{t+{\tau }_1}I(s-{\tau }_1)ds$, ${\mathcal{G}}_3(S,I,A,Q,R)=\frac{1}{\zeta +1}{(S+I+A+Q+R)}^{\zeta +1}$. Noting that $\mathcal{G}(.)$ is not only continuous, but also tends to $+\infty$ as $(S,I,A,Q,R)$ approaches to the boundary of ${\mathbb{R}}_{+}^5$ and $\Vert (S,I,A,Q,R)\Vert \to \infty$. Therefore, $\mathcal{G}$ must have a minimum point $(S\left(0\right),I\left(0\right),A\left(0\right),Q\left(0\right),R\left(0\right))$ in the interior of ${\mathbb{R}}_{+}^5$. Define a ${\mathcal{C}}^2$-function $\tilde{\mathcal{G}}(.):{\mathbb{R}}_{+}^5\to {\mathbb{R}}_{+}$ as

$$\tilde{\mathcal{G}}(.)=\mathcal{B}{\mathcal{G}}_1+{\mathcal{G}}_2+{\mathcal{G}}_3-lnQ-lnR-\mathcal{G}(S\left(0\right),I\left(0\right),A\left(0\right),Q\left(0\right),R\left(0\right)),$$ (10)

where $(S,I,A,Q,R)\in (\frac{1}{k_0},k_0)\times (\frac{1}{k_0},k_0)\times (\frac{1}{k_0},k_0)\times (\frac{1}{k_0},k_0)\times (\frac{1}{k_0},k_0)$ and $k_0>1$ is a sufficiently large integer. Additionally, $\zeta >1$ is a constant satisfying $\Lambda >\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)$. Choose a positive constant $\mathcal{B}$ big enough such that

$$-\mathcal{B}\chi +\Phi \le -2,$$ (11)

where $\chi =\frac{\Lambda \theta \alpha \lambda {\beta }^2}{{\hat{d}}_I{\hat{d}}_A{\hat{d}}_Q{\hat{d}}_R}-(d_s+\frac{{\nu }_1^2}{2})>0$ since ${\mathcal{R}}_0^s>1$, and $\Phi =max\{{\Phi }_1,{\Phi }_2\}$. We have

$${\Phi }_0=\underset{(S,I,A,Q,R)\in {\mathbb{R}}_{+}^5}{sup}\{-\frac{1}{2}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]$$$$\times {(S+I+A+O+R)}^{\zeta +1}$$$$+\Lambda {(S+I+A+O+R)}^{\zeta }\}<\infty .$$$${\Phi }_1=\underset{(S,I,A,Q,R)\in {\mathbb{R}}_{+}^5}{sup}\{-\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)I^{\zeta +1}$$$$+\mathcal{B}\beta A+\xi +\theta +d_Q+d_R+d_S$$$$+\alpha \beta I+\beta A+\frac{{\nu }_1^2+{\nu }_2^2+{\nu }_3^2}{2}+{\Phi }_0]\}<\infty .$$$${\Phi }_2=\underset{(S,I,A,Q,R)\in {\mathbb{R}}_{+}^5}{sup}\{-\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)A^{\zeta +1}$$$$+\xi +\theta +d_Q+d_R+d_S$$$$+\alpha \beta I+\beta A+\frac{{\nu }_1^2+{\nu }_2^2+{\nu }_3^2}{2}+{\Phi }_0]\}<\infty .$$$${\Phi }_3=\underset{(S,I,A,Q,R)\in {\mathbb{R}}_{+}^5}{sup}\{\mathcal{B}\beta A+\mathcal{B}\alpha \beta I+{\Phi }_0+\xi +\theta +d_Q+\frac{{\nu }_4^2}{2}+d_R+\frac{{\nu }_5^2}{2}$$$$+\alpha \beta I+\beta A+d_S+\frac{{\nu }_1^2}{2}-\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]$$$$\times (I^{\zeta +1}+A^{\zeta +1})\}<\infty .$$ (12)

Hence,

$$\mathcal{L}\tilde{\mathcal{G}}=\mathcal{B}\mathcal{L}{\mathcal{G}}_1+\mathcal{L}{\mathcal{G}}_2+\mathcal{L}{\mathcal{G}}_3+\mathcal{L}(-lnQ)+\mathcal{L}(-lnR).$$ (13)

By It$\hat{o}$’s formula to ${\mathcal{G}}_1$, we get

$$\mathcal{L}{\mathcal{G}}_1=\frac{-\Lambda }{S}-\frac{\xi Q}{S}-\frac{{\rho }_1\theta Q}{I}-\frac{{\rho }_1\delta A}{I}-{\rho }_2\beta S-\frac{{\rho }_3\alpha \beta SI(t-{\tau }_1)}{Q}$$$$-\frac{{\rho }_4\mu I(t-{\tau }_2)}{R}-\frac{{\rho }_4\lambda A}{R}$$$$+d_S+{\rho }_1(\mu +d_0+d_I)+{\rho }_2(\delta +\lambda +d_A)+{\rho }_3(\xi +\theta +d_Q)$$$$+{\rho }_4{d}_R+\frac{{\nu }_1^2}{2}+\alpha \beta I$$$$+\beta A+\frac{{\rho }_1{\nu }_2^2}{2}+\frac{{\rho }_2{\nu }_3^2}{2}+\frac{{\rho }_3{\nu }_4^2}{2}+\frac{{\rho }_4{\nu }_5^2}{2}.$$ (14)

Therefore, we can obtain that

$$\mathcal{L}{\mathcal{G}}_1\le -5\sqrt[5]{\Lambda \theta \alpha \lambda {\beta }^2{\rho }_1{\rho }_2{\rho }_3{\rho }_4}+d_S+\frac{{\nu }_1^2}{2}+{\rho }_1(\mu +d_0+d_I+\frac{{\nu }_2^2}{2})$$$$+{\rho }_2(\delta +\lambda +d_A+\frac{{\nu }_3^2}{2})$$$$+{\rho }_3(\xi +\theta +d_Q+\frac{{\nu }_4^2}{2})+{\rho }_4(d_R+\frac{{\nu }_5^2}{2})+\alpha \beta I+\beta A\le -\frac{\Lambda \theta \alpha \lambda {\beta }^2}{\widehat{d_I}\widehat{d_A}\widehat{d_Q}\widehat{d_R}}+d_S+\frac{{\nu }_1^2}{2}+\beta A+\alpha \beta I≔-\chi +\beta A+\alpha \beta I,$$ (15)

and

$$\mathcal{L}{\mathcal{G}}_2=-\frac{\Lambda }{S}-\frac{\xi Q}{S}+\alpha \beta I+\beta A+d_S+\frac{{\nu }_1^2}{2},$$ (16)

$$\mathcal{L}{\mathcal{G}}_3={(S+I+A+Q+R)}^{\zeta }[\Lambda -d_{S}S-(d_0+d_I)I-d_{A}A-d_{Q}Q-d_{R}R]$$$$+\frac{\zeta }{2}{(S+I+A+Q+R)}^{\zeta -1}\times [{\nu }_1^2{S}^2+{\nu }_2^2{I}^2+{\nu }_3^2{A}^2+{\nu }_4^2{Q}^2+{\nu }_5^2{R}^2],$$ (17)

choose $\Lambda =min\{d_S,d_0+d_I,d_A,d_Q,d_R\}$, we obtain that

$$\mathcal{L}{\mathcal{G}}_3\le {(S+I+A+Q+R)}^{\zeta }[\Lambda -\Lambda (S+I+A+Q+R)]$$$$+\frac{\zeta }{2}{(S+I+A+Q+R)}^{\zeta +1}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)\le \Lambda {(S+I+A+Q+R)}^{\zeta }-{(S+I+A+Q+R)}^{\zeta +1}$$$$\times (\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2))\le {\Phi }_0-\frac{1}{2}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]{(S+I+A+Q+R)}^{\zeta +1}\le {\Phi }_0-\frac{1}{2}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]$$$$\times (S^{\zeta +1}+I^{\zeta +1}+A^{\zeta +1}+Q^{\zeta +1}+R^{\zeta +1}).$$ (18)

Additionally, we have

$$\mathcal{L}(-lnQ)=-\frac{\alpha \beta SI(t-{\tau }_1)}{Q}+\xi +\theta +d_Q+\frac{{\nu }_4^2}{2},$$$$\mathcal{L}(-lnR)=-\frac{\mu I(t-{\tau }_2)}{R}-\frac{\lambda A}{R}+d_R+\frac{{\nu }_5^2}{2}.$$ (19)

Substituting (15)–(19) into (13),

$$\mathcal{L}\tilde{\mathcal{G}}\le -\mathcal{B}\chi +\mathcal{B}\beta A+\mathcal{B}\alpha \beta I+{\Phi }_0+\alpha \beta I+\beta A+d_S+\frac{{\nu }_1^2}{2}$$$$-\frac{1}{2}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]\text{(}{S}^{\zeta +1}$$$$+I^{\zeta +1}+A^{\zeta +1}+Q^{\zeta +1}+R^{\zeta +1}\text{)}$$$$-\frac{\alpha \beta SI(t-{\tau }_1)}{Q}+\xi +\theta +d_Q+\frac{{\nu }_4^2}{2}-\frac{\mu I(t-{\tau }_2)}{R}$$$$-\frac{\lambda A}{R}+d_R+\frac{{\nu }_5^2}{2}-\frac{\Lambda }{S}-\frac{\xi Q}{S}\le -\mathcal{B}\chi +\mathcal{B}\beta A+\mathcal{B}\alpha \beta I+{\Phi }_0-\frac{\alpha \beta SI(t-{\tau }_1)}{Q}+\xi +\theta +d_Q$$$$+\frac{{\nu }_4^2}{2}-\frac{\mu I(t-{\tau }_2)}{R}-\frac{\lambda A}{R}$$$$-\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]\text{(}{S}^{\zeta +1}$$$$+I^{\zeta +1}+A^{\zeta +1}+Q^{\zeta +1}+R^{\zeta +1}\text{)}$$$$+d_R+\frac{{\nu }_5^2}{2}-\frac{\Lambda }{S}-\frac{\xi Q}{S}+\alpha \beta I+\beta A+d_S+\frac{{\nu }_1^2}{2}$$$$-\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)](I^{\zeta +1}+A^{\zeta +1}).$$ (20)

Define a bounded closed set

$$\mathcal{U}=\text{{}(S,I,A,Q,R)\in {\mathbb{R}}_{+}^5:\epsilon \le S\le \frac{1}{\epsilon },\epsilon \le I\le \frac{1}{\epsilon },\epsilon \le A\le \frac{1}{\epsilon },$$$${\epsilon }^3\le Q\le \frac{1}{{\epsilon }^3},{\epsilon }^2\le R\le \frac{1}{{\epsilon }^2}\text{}},$$ (21)

for $\epsilon >0$, such that

$$-\frac{\Lambda }{\epsilon }+{\Phi }_3\le -1.$$ (22)

$$-\mathcal{B}\chi +\mathcal{B}\alpha \beta \epsilon +{\Phi }_1\le -1$$ (23)

$$-\mathcal{B}\chi +\mathcal{B}\beta \epsilon +{\Phi }_2\le -1$$ (24)

$$-\frac{\alpha \beta }{\epsilon }+{\Phi }_3\le -1$$ (25)

$$-\frac{\mu }{\epsilon }+{\Phi }_3\le -1$$ (26)

$$-\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]\frac{1}{{\epsilon }^{\zeta +1}}+{\Phi }_3\le -1$$ (27)

$$-\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]\frac{1}{{\epsilon }^{3\zeta +3}}+{\Phi }_3\le -1$$ (28)

$$-\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]\frac{1}{{\epsilon }^{2\zeta +2}}+{\Phi }_3\le -1.$$ (29)

In order to be more intuitive, we divide ${\mathbb{R}}_{+}^5\setminus \mathcal{U}={\cup }_{i=1}^{10}{\mathcal{U}}_i$, into the following ten regions:

$${\mathcal{U}}_1=\{(S,I,A,Q,R)\in {\mathbb{R}}_{+}^5;0<S<\epsilon \},$$$${\mathcal{U}}_2=\{(S,I,A,Q,R)\in {\mathbb{R}}_{+}^5;0<I<\epsilon \},$$$${\mathcal{U}}_3=\{(S,I,A,Q,R)\in {\mathbb{R}}_{+}^5;0<A<\epsilon \},$$$${\mathcal{U}}_4=\{(S,I,A,Q,R)\in {\mathbb{R}}_{+}^5;0<Q<{\epsilon }^3,S\ge \epsilon ,I\ge \epsilon \},$$$${\mathcal{U}}_5=\{(S,I,A,Q,R)\in {\mathbb{R}}_{+}^5;0<R<{\epsilon }^2,I\ge \epsilon \},$$$${\mathcal{U}}_6=\{(S,I,A,Q,R)\in {\mathbb{R}}_{+}^5;S>\frac{1}{\epsilon }\},$$$${\mathcal{U}}_7=\{(S,I,A,Q,R)\in {\mathbb{R}}_{+}^5;I>\frac{1}{\epsilon }\},$$$${\mathcal{U}}_8=\{(S,I,A,Q,R)\in {\mathbb{R}}_{+}^5;A>\frac{1}{\epsilon }\},$$$${\mathcal{U}}_9=\{(S,I,A,Q,R)\in {\mathbb{R}}_{+}^5;Q>\frac{1}{{\epsilon }^3}\},$$$${\mathcal{U}}_{10}=\{(S,I,A,Q,R)\in {\mathbb{R}}_{+}^5;R>\frac{1}{{\epsilon }^2}\}.$$ (30)

To prove $\mathcal{L}\tilde{\mathcal{G}}\le -1$ for any $(S,I,A,Q,R)\in {\mathbb{R}}_{+}^5\setminus \mathcal{U}={\cup }_{i=1}^{10}{\mathcal{U}}_i$, we consider 10 Cases as in Appendix which contains the rest of the proof. Thus, Condition $(A.2)$ of Lemma 1 holds.

Numerical simulations and fitting model to observations

In this section, some numerical simulations are given to validate the theoretical results, using Milstein’s higher order method [34], [35] to numerically solve SDDEs (2) and DDE23 Matlab Package [36] to solve the undisturbed model (1). The reality of the proposed model is also investigated, in the next subsection, by fitting the deterministic model to real observations of COVID-19 recorded cases in the UAE [37], given in Table 2.

Table 2.

Number of recorded COVID-19 cases in UAE, from October 2020 to May 2021 [37].

Month	Average number of recorded infected population in UAE
October 2020	38,418.00
November 2020	36,245.00
December 2020	38,339.00
January 2021	94,569.00
February 2021	87,933.00
March 2021	70,766.00
April 2021	58,902.00
May 2021	54,756.00

Choose the initial value $(S\left(0\right),I\left(0\right),A\left(0\right),Q\left(0\right),R\left(0\right))=(0.99,0.0093,0.0003,0.0002,0.0002)$ with parameters values:

$$\Lambda =0.09,\alpha =0.08,\beta =1.919,\xi =0.02,$$$$\delta =0.26,d_S=0.09,\theta =0.0985,$$$$\mu =0.001,d_I=0.001,\lambda =0.3,d_0=0.09,$$$$d_A=0.09,d_R=0.2,d_Q=0.09.$$ (31)

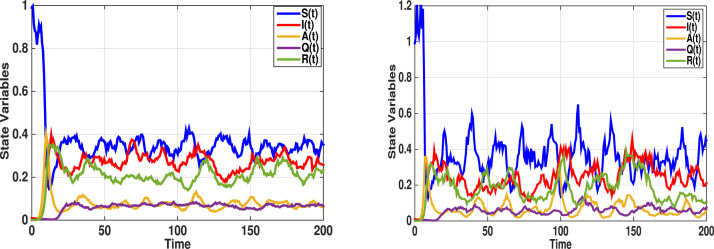
Fig. 2 displays the prediction of the persistence of the disease. We assume that the incubation period ${\tau }_1=7$ (days) and the time necessary for the infected individuals to become recovered ${\tau }_2=10$ (days). Choose ${\nu }_1=0.05$, ${\nu }_2=0.05$, ${\nu }_3=0.1$, ${\nu }_4=0.05$ and ${\nu }_5=0.1$. Hence, conditions:

$${\mathcal{R}}_0^s=3.304>1,0.09=\Lambda >\frac{{\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2}{2}=0.005$$

Given these data, Theorem 2 is satisfied, and therefore, we conclude the existence of the stationary distribution and ergodicity for the stochastic model (2). Fig. 2 (left) shows that system (2) admits a unique ergodic stationary distribution $\mu (.)$. To further clarify the impact of the stochastic perturbation on the stochastic model (2), we increase the intensities to ${\nu }_1=0.1$, ${\nu }_2=0.15$, ${\nu }_3=0.1$, ${\nu }_4=0.15$ and ${\nu }_5=0.1$, Fig. 2 (right); By direct calculations

$${\mathcal{R}}_0^s=2.718>1,0.09=\Lambda >\frac{{\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2}{2}=0.01125.$$

The stochastic model (2) still has a stationary distribution, nevertheless the magnitude oscillations become stronger.

Fig. 2.

Numerical simulations of SDDEs model (2) with ${\tau }_1=7$ and ${\tau }_2=10$, other parameter values are given in (31). When ${\mathcal{R}}_0^s>1$, the disease is persistent and the model has a unique ergodic stationary distribution. Left banner shows the stationary distribution for low level intensity of white noise with ${\nu }_1=0.05$, ${\nu }_2=0.05$, ${\nu }_3=0.1$, ${\nu }_4=0.05$ and ${\nu }_5=0.1$; While in the right banner the intensity of white noise increased to ${\nu }_1=0.1$, ${\nu }_2=0.15$, ${\nu }_3=0.1$, ${\nu }_4=0.15$ and ${\nu }_5=0.1$. The stochastic model (2) has a unique stationary distribution, nevertheless the magnitude oscillations become stronger.

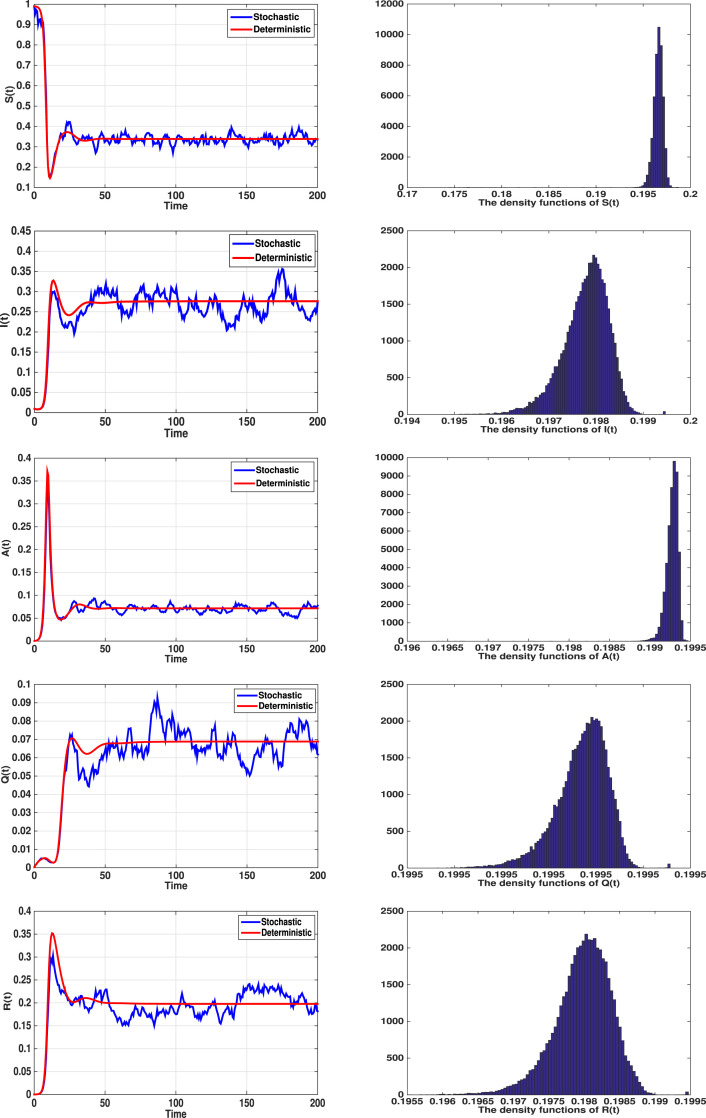
Fig. 3 displays the dynamics of systems (1), (2), with time-delays ${\tau }_1=7$ and ${\tau }_2=10$; The left column shows numerical simulations of SDDEs (2) and corresponding undisturbed one (1). The intensity of white noise increased to ${\nu }_1=0.1$, ${\nu }_2=0.05$, ${\nu }_3=0.05$, ${\nu }_4=0.05$ and ${\nu }_5=0.05$. The stationary distribution, where ${\mathcal{R}}_0^s>1$, illustrates that the solution of the stochastic model (2) fluctuate in a surroundings of the endemic equilibrium ${\mathcal{E}}^{\ast }$ of the corresponding undisturbed model (1).

Fig. 3.

Left column shows the numerical simulations of SDDEs (2) and corresponding undisturbed model (1), with ${\tau }_1=7$ and ${\tau }_2=10$, other parameter values are given in (31). When ${\mathcal{R}}_0^s>1$, the stochastic model has a unique ergodic stationary distribution, fluctuate around ${\mathcal{E}}^{\ast }$. The right column displays the histogram of the probability density functions.

Fitting deterministic model (1) to observations

Using real observations of COVID-19 in the UAE, produced by WHO from October 2020 to May 2021 [37] , we estimate the corresponding parameters in the proposed deterministic model (1). We then adopt the criterion of least squares approach (discussed in [3], [38]) to fit a system of DDEs to real data.

Given a set of real data ${\{t_i,Y_i\}}_{i=1}^M$, such as in Table 2, and a mathematical model (1). The objective function (weighted least squares function)

$${\Phi }_W\left(\mathbf{p}\right)=\sum _{i=1}^5\sum _{j=1}^M{[y^i(t_j,\mathbf{p})-Y_j^i]}^2{w}_{ij}.$$ (32)

Here, $y^i,i=1,\dots ,5$ represent the variables $S,I,A,Q,R$; $\mathbf{p}$ are the model parameters to be estimated. Thus, we then try to attain the optimum parameter $\hat{\mathbf{p}}$ that satisfies $\Phi \left(\hat{\mathbf{p}}\right)\le {min}_p\Phi \left(\mathbf{p}\right)\equiv {max}_p\mathcal{L}\left(\mathbf{p}\right)$. Where $\mathcal{L}\left(\mathbf{p}\right)$ is the likelihood function [38], [39]. However, estimation of the parameters appear in the deterministic SIAQR model (1) is considered as an optimization problem that should consider the following steps:

• 1.We guess an initial value ${\mathbf{p}}_{\mathbf{0}}$ of the parameter estimates;
• 2.We then solve the system with the current values of the parameters using a suitable scheme of the deterministic model (1);
• 3.The parameter values are then adjusted by a minimization routine such as OPTIMTOOL in Matlab;
• 4.When no further reduction in the value $\Phi \left(\mathbf{p}\right)$ is possible, the best fit parameter values have been found;
• 5.Determine whether the chosen set of parameter values is acceptable or not.

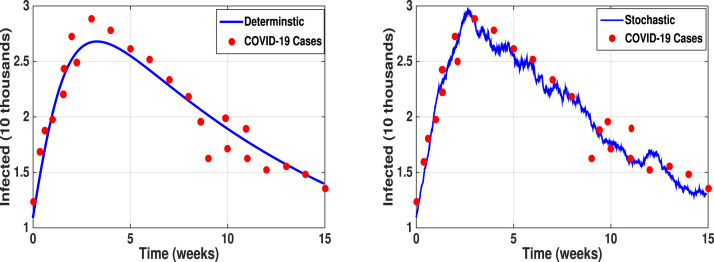
We estimate the fundamental parameters that govern the reproduction number ${\mathcal{R}}_0$. In Case I, Fig. 4 (left) shows the simulation of the best-fit model to the COVID-19 infected populations in the UAE from December 2020 to May 2021 weekly. Using the above mentioned scheme and given initial guess the parameter estimates are $\hat{\lambda }=0.6269$, $\hat{\delta }=0.16$, $\hat{\Lambda }=0.1026$. During this outbreak, the corresponding estimated $\widehat{{\mathcal{R}}_0}=3.882>1$. We assume the other parameter values as $\alpha =0.1$ $\beta =0.2$, $\xi =0.04$, $\theta =0.35$, $d_S=0.006$, $d_I=0.04$, $d_0=0.01$, $d_R=0.5$ and $d_Q=0.01$.

Fig. 4.

Case I: Shows the best fit model prediction (1) to COVID-19 cases during the outbreak period December 2020–May 2021. Parameter estimates are $\hat{\lambda }=0.6269$, $\hat{\delta }=0.085$, $\hat{\Lambda }=0.1026$. The corresponding estimated $\widehat{{\mathcal{R}}_0}=3.882>1$.

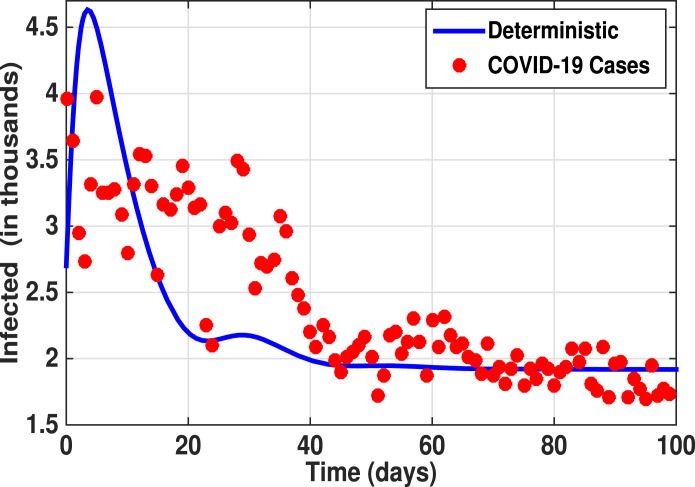
Fig. 5 (Case II) shows the simulation of the best-fit model to the COVID-19 infected populations daily in the UAE from February to May 2021. Parameter estimates are $\widehat{d_A}=0.0165$, $\hat{\mu }=0.0286$, $\hat{\lambda }=0.7035$. The corresponding estimated $\widehat{{\mathcal{R}}_0}=2.545>1$, Such that the infection is persistent. We assume the other parameter values as $\Lambda =0.7$, $\alpha =0.1$ $\beta =0.2$, $\xi =0.02$, $\theta =0.35$, $d_S=0.06$, $d_I=0.04$, $d_0=0.01$, $d_R=0.4$ and $d_Q=0.01$.

Fig. 5.

Case II: Shows the best fit model prediction (1) to COVID-19 cases from February 2021–May 2021. Parameter estimates are $\widehat{d_A}=0.0165$, $\hat{\mu }=0.0286$, $\hat{\lambda }=0.7035$. The corresponding estimated $\widehat{{\mathcal{R}}_0}=2.545>1$.

Fig. 6 shows the simulations of the stochastic best-fit model to the COVID-19 infected populations in the UAE from February to May 2021. Here, we consider the parameter values as in Fig. 5, with ${\nu }_1=0.05$, ${\nu }_2=0.05$, ${\nu }_3=0.01$, ${\nu }_4=0.01$ and ${\nu }_5=0.01$.

Fig. 6.

Shows stochastic model (2) prediction (blue curve) to COVID-19 cases (red curve) from February to May 2021 per days. With ${\nu }_1=0.05$, ${\nu }_2=0.05$, ${\nu }_3=0.01$, ${\nu }_4=0.01$ and ${\nu }_5=0.01$. The stochastic perturbations improve the consistency of the model with the real data. It is consistent with the physical sensitivity and fluctuation of the real observations. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

We arrive at the following Remarks:

Remark 1

COVID-19 can be reduced in severity, by prior vaccination (immunization) or the timely use of specific antiviral agents. Vaccination is then operated by reducing the pool of susceptible individuals, and when this is reduced sufficiently, an infectious disease cannot spread within the population. It is not, of course, necessary to vaccinate everyone to prevent an epidemic: immunizing someone not only protects that person but confers some protection to the population in general. To eradicate an endemic infection or prevent a novel epidemic, a proportion $(1-1/{\mathcal{R}}_0^s)\equiv max(1-1/{\mathcal{R}}_0)$ of the population needs to be successfully immunized [40]. In case of the current COVID-19 pandemic, assuming that ${\mathcal{R}}_0=2.545>{\mathcal{R}}_0^s$, then we would need to immunize $max60.07\text{\%}$ of the population, this value can be reduced or increased for different forms of SIR epidemic models.

Remark 2

Stochastic epidemic model, with time-delays, gives an extra degree of authenticity in comparison with its comparing deterministic show. It is consistent with the physical sensitivity and fluctuation of the real observations.

Conclusion

The effect of environmental factors on the spread of COVID-19 is of experimental and theoretical importance in understanding the disease dynamics. In this work, we proposed a stochastic delay differential model (SIAQR) to investigate the dynamics of the ongoing COVID-19, taking into account the classification of different phases of its spread in population. We proved the unique and global positive solution of the system with probability one. Persistence and existence of an ergodic stationary distribution is also investigated. Estimates ${\mathcal{R}}_0^s<{\mathcal{R}}_0$ can give better insights about the transmissibility of infection in a certain country. Real observations of infected cases, during and after the lock down from the UAE (for the spread of COVID-19 during a period of six months) have been considered to fit such data with the suggested models.

In using the present stochastic SIAQR model for the dynamics of COVID-19, the main objective is to take into account all of the environmental factors that have a significant impact on its spread. We stochastically perturbed the COVID-19 model parameters using a normal distribution in order to account for the uncertainty in estimates and simulate the difficulties in detecting patients, various isolation measures taken by different countries, and changes in virus characteristics. Periodicity of the outbreaks is likely to occur as a result of the presence of time-delay in the transmission terms.

The severity of the COVID-19 outbreak in the UAE or other country is indicated by ${\mathcal{R}}_0$. The values of ${\mathcal{R}}_0$ are estimated from real observations in order to determine the percentages that must be vaccinated to achieve herd immunity. Our results suggest that when ${\mathcal{R}}_0=3.882$, a proportion at most 74.2% of the population needs to be vaccinated to reduce the infection of the disease. However, when ${\mathcal{R}}_0=2.545$, a proportion at most 60.07% of the population can only be vaccinated. The numerical simulations show that the proposed stochastic delay differential model is consistent with the physical sensitivity and fluctuation the real observations, and gives an extra degree of realism, compared with its corresponding deterministic model.

The authors conclude that the stochastic SIAQR model is a procedure to figure out epidemiological characteristics of COVID-19. Our proposed model adds new understandings into epidemiological situations under the effect of the environmental noise in the COVID-19 epidemic models. The consolidation of environmental perturbations and time-lag, in the epidemic model, has a significant impact on the persistence and possible extinction of the disease and improves the dynamics of the system.

Compliance with ethics requirements

This article does not contain any study with human or animal subjects.

CRediT authorship contribution statement

F.A. Rihan: Conceptualization, Supervision, Validation, Writing – review & editing. H.J. Alsakaji: Writing – original draft, Visualization, Software, Methodology.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix. Rest of Proof Theorem 2

Case 1: For any $(S,I,A,Q,R)\in {\mathcal{U}}_1$

$$\mathcal{L}\tilde{\mathcal{G}}\le \mathcal{B}\beta A+\mathcal{B}\alpha \beta I+{\Phi }_0+\xi +\theta +d_Q+\frac{{\nu }_4^2}{2}+d_R+\frac{{\nu }_5^2}{2}-\frac{\Lambda }{S}+\alpha \beta I+\beta A$$$$+d_S+\frac{{\nu }_1^2}{2}-\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)](I^{\zeta +1}+A^{\zeta +1})\le -\frac{\Lambda }{S}+{\Phi }_3\le -\frac{\Lambda }{\epsilon }+{\Phi }_3\le -1,$$ (33)

condition (22) implies $\mathcal{L}\tilde{\mathcal{G}}\le -1$ for any $(S,I,A,Q,R)\in {\mathcal{U}}_1$

Case 2: For any $(S,I,A,Q,R)\in {\mathcal{U}}_2$

$$\mathcal{L}\tilde{\mathcal{G}}\le -\mathcal{B}\chi +\mathcal{B}\beta A+\mathcal{B}\alpha \beta I-\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)I^{\zeta +1}$$$$+\xi +\theta +d_Q+d_R+d_S$$$$+\alpha \beta I+\beta A+\frac{{\nu }_1^2+{\nu }_2^2+{\nu }_3^2}{2}+{\Phi }_0]\le -\mathcal{B}\chi +\mathcal{B}\alpha \beta I+{\Phi }_1\le -\mathcal{B}\chi +\mathcal{B}\alpha \beta \epsilon +{\Phi }_1\le -1,$$ (34)

from conditions (11), (23), we get $\mathcal{L}\tilde{\mathcal{G}}\le -1$ for any $(S,I,A,Q,R)\in {\mathcal{U}}_2$.

Case 3: For any $(S,I,A,Q,R)\in {\mathcal{U}}_3$

$$\mathcal{L}\tilde{\mathcal{G}}\le -\mathcal{B}\chi +\mathcal{B}\beta A+\mathcal{B}\alpha \beta I-\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)I^{\zeta +1}$$$$+\xi +\theta +d_Q+d_R+d_S$$$$+\alpha \beta I+\beta A+\frac{{\nu }_1^2+{\nu }_2^2+{\nu }_3^2}{2}+{\Phi }_0]\le -\mathcal{B}\chi +\mathcal{B}\beta A+{\Phi }_2\le -\mathcal{B}\chi +\mathcal{B}\beta \epsilon +{\Phi }_2\le -1,$$ (35)

which is obtained from (11), (24). Consequently, $\mathcal{L}\tilde{\mathcal{G}}\le -1$ for any $(S,I,A,Q,R)\in {\mathcal{U}}_3$.

Case 4: For any $(S,I,A,Q,R)\in {\mathcal{U}}_4$

$$\mathcal{L}\tilde{\mathcal{G}}\le \mathcal{B}\beta A+\mathcal{B}\alpha \beta I+{\Phi }_0+\xi +\theta +d_Q+\frac{{\nu }_4^2}{2}+d_R+\frac{{\nu }_5^2}{2}$$$$-\frac{\alpha \beta SI(t-{\tau }_1)}{Q}+\alpha \beta I+\beta A$$$$+d_S+\frac{{\nu }_1^2}{2}-\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)](I^{\zeta +1}+A^{\zeta +1})\le -\frac{\alpha \beta SI(t-{\tau }_1)}{Q}+{\Phi }_3\le -\frac{\alpha \beta {\epsilon }^2}{{\epsilon }^3}+{\Phi }_3\le -\frac{\alpha \beta }{\epsilon }+{\Phi }_3\le -1.$$ (36)

Therefore, from (25) one obtains $\mathcal{L}\tilde{\mathcal{G}}\le -1$ for any $(S,I,A,Q,R)\in {\mathcal{U}}_4$.

Case 5: For any $(S,I,A,Q,R)\in {\mathcal{U}}_5$

$$\mathcal{L}\tilde{\mathcal{G}}\le \mathcal{B}\beta A+\mathcal{B}\alpha \beta I+{\Phi }_0+\xi +\theta +d_Q+\frac{{\nu }_4^2}{2}+d_R$$$$+\frac{{\nu }_5^2}{2}-\frac{\mu I(t-{\tau }_2)}{R}+\alpha \beta I+\beta A$$$$+d_S+\frac{{\nu }_1^2}{2}-\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)](I^{\zeta +1}+A^{\zeta +1})\le -\frac{\mu I(t-{\tau }_2)}{R}+{\Phi }_3\le -\frac{\mu \epsilon }{{\epsilon }^2}+{\Phi }_3\le -\frac{\mu }{\epsilon }+{\Phi }_3\le -1.$$ (37)

Hence, from (26) $\mathcal{L}\tilde{\mathcal{G}}\le -1$ for any $(S,I,A,Q,R)\in {\mathcal{U}}_5$.

Case 6: For any $(S,I,A,Q,R)\in {\mathcal{U}}_6$

$$\mathcal{L}\tilde{\mathcal{G}}\le -\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]S^{\zeta +1}+\mathcal{B}\beta A$$$$+\mathcal{B}\alpha \beta I+{\Phi }_0+\xi +\theta +d_Q+\frac{{\nu }_4^2}{2}$$$$+d_R+\frac{{\nu }_5^2}{2}+\alpha \beta I+\beta A+d_S+\frac{{\nu }_1^2}{2}$$$$-\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)](I^{\zeta +1}+A^{\zeta +1})\le -\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]S^{\zeta +1}+{\Phi }_3\le -\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]\frac{1}{{\epsilon }^{\zeta +1}}+{\Phi }_3\le -1,$$ (38)

from condition (27), we obtain $\mathcal{L}\tilde{\mathcal{G}}\le -1$ for any $(S,I,A,Q,R)\in {\mathcal{U}}_6$.

Case 7: For any $(S,I,A,Q,R)\in {\mathcal{U}}_7$

$$\mathcal{L}\tilde{\mathcal{G}}\le -\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]I^{\zeta +1}+\mathcal{B}\beta A+\mathcal{B}\alpha \beta I$$$$+{\Phi }_0+\xi +\theta +d_Q+\frac{{\nu }_4^2}{2}$$$$+d_R+\frac{{\nu }_5^2}{2}+\alpha \beta I+\beta A+d_S+\frac{{\nu }_1^2}{2}$$$$-\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)](I^{\zeta +1}+A^{\zeta +1})\le -\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]I^{\zeta +1}+{\Phi }_3\le -\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]\frac{1}{{\epsilon }^{\zeta +1}}+{\Phi }_3\le -1.$$ (39)

Therefore, from (27) $\mathcal{L}\tilde{\mathcal{G}}\le -1$ for any $(S,I,A,Q,R)\in {\mathcal{U}}_7$.

Case 8: For any $(S,I,A,Q,R)\in {\mathcal{U}}_8$

$$\mathcal{L}\tilde{\mathcal{G}}\le -\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]A^{\zeta +1}+\mathcal{B}\beta A+\mathcal{B}\alpha \beta I$$$$+{\Phi }_0+\xi +\theta +d_Q+\frac{{\nu }_4^2}{2}$$$$+d_R+\frac{{\nu }_5^2}{2}+\alpha \beta I+\beta A+d_S+\frac{{\nu }_1^2}{2}$$$$-\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)](I^{\zeta +1}+A^{\zeta +1})\le -\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]A^{\zeta +1}+{\Phi }_3\le -\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]\frac{1}{{\epsilon }^{\zeta +1}}+{\Phi }_3\le -1,$$ (40)

which follows from (27). Thus, $\mathcal{L}\tilde{\mathcal{G}}\le -1$ for any $(S,I,A,Q,R)\in {\mathcal{U}}_8$.

Case 9: For any $(S,I,A,Q,R)\in {\mathcal{U}}_9$

$$\mathcal{L}\tilde{\mathcal{G}}\le -\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]Q^{\zeta +1}+\mathcal{B}\beta A+\mathcal{B}\alpha \beta I$$$$+{\Phi }_0+\xi +\theta +d_Q+\frac{{\nu }_4^2}{2}$$$$+d_R+\frac{{\nu }_5^2}{2}+\alpha \beta I+\beta A+d_S+\frac{{\nu }_1^2}{2}$$$$-\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)](I^{\zeta +1}+A^{\zeta +1})\le -\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]Q^{\zeta +1}+{\Phi }_3\le -\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]\frac{1}{{\epsilon }^{3\zeta +3}}+{\Phi }_3\le -1.$$ (41)

Therefore, it follows from (28) that $\mathcal{L}\tilde{\mathcal{G}}\le -1$ for any $(S,I,A,Q,R)\in {\mathcal{U}}_9$.

Case 10: For any $(S,I,A,Q,R)\in {\mathcal{U}}_{10}$

$$\mathcal{L}\tilde{\mathcal{G}}\le -\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]R^{\zeta +1}+\mathcal{B}\beta A+\mathcal{B}\alpha \beta I$$$$+{\Phi }_0+\xi +\theta +d_Q+\frac{{\nu }_4^2}{2}$$$$+d_R+\frac{{\nu }_5^2}{2}+\alpha \beta I+\beta A+d_S+\frac{{\nu }_1^2}{2}$$$$-\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)](I^{\zeta +1}+A^{\zeta +1})\le -\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]R^{\zeta +1}+{\Phi }_3\le -\frac{1}{4}[\Lambda -\frac{\zeta }{2}({\nu }_1^2\vee {\nu }_2^2\vee {\nu }_3^2\vee {\nu }_4^2\vee {\nu }_5^2)]\frac{1}{{\epsilon }^{2\zeta +2}}+{\Phi }_3\le -1.$$ (42)

Hence, from (29) one gets $\mathcal{L}\tilde{\mathcal{G}}\le -1$ for any $(S,I,A,Q,R)\in {\mathcal{U}}_{10}$. The above cases lead to $\mathcal{L}\tilde{\mathcal{G}}\le -1$ for any $(S,I,A,Q,R)\in {\mathbb{R}}_{+}^5\setminus \mathcal{U}$.