Fast gap-affine pairwise alignment using the wavefront algorithm

Abstract

Motivation

Pairwise alignment of sequences is a fundamental method in modern molecular biology, implemented within multiple bioinformatics tools and libraries. Current advances in sequencing technologies press for the development of faster pairwise alignment algorithms that can scale with increasing read lengths and production yields.

Results

In this article, we present the wavefront alignment algorithm (WFA), an exact gap-affine algorithm that takes advantage of homologous regions between the sequences to accelerate the alignment process. As opposed to traditional dynamic programming algorithms that run in quadratic time, the WFA runs in time O(ns), proportional to the read length n and the alignment score s, using $O(s^2)$ memory. Furthermore, our algorithm exhibits simple data dependencies that can be easily vectorized, even by the automatic features of modern compilers, for different architectures, without the need to adapt the code. We evaluate the performance of our algorithm, together with other state-of-the-art implementations. As a result, we demonstrate that the WFA runs 20–300× faster than other methods aligning short Illumina-like sequences, and 10–100× faster using long noisy reads like those produced by Oxford Nanopore Technologies.

Availability and implementation

The WFA algorithm is implemented within the wavefront-aligner library, and it is publicly available at https://github.com/smarco/WFA.

1 Introduction

Pairwise alignment of biological sequences is a core component of many bioinformatics tools. In genomics, it is an essential building block for read mapping (Langmead and Salzberg, 2012; Li, 2013; Marco-Sola et al., 2012), variant detection (DePristo et al., 2011), de novo genome assembly (Simpson et al., 2009), multiple sequence alignment (Notredame et al., 2000) and many other methods. Moreover, it can be adapted to different protocols and applications (e.g. DNA-seq, RNA-seq or bisulfite analysis) using different distance functions (e.g. mismatch, edit, gap-linear or gap-affine), modifying the alignment scope (e.g. global, semi-global or local alignment) or adjusting the scoring penalties. Nevertheless, all these variations share the same algorithmic core.

Over the last decade, the volume of biological data generated by sequencing technologies has increased exponentially. Besides, third-generation technologies, such as those developed by PacBio and Oxford Nanopore Technologies (ONT), can yield sequences longer than 20K bases; more than 100× longer than those produced by the extensively used Illumina sequencers. This presses for the development of faster algorithms that can keep up with the data production pace and scale with longer read lengths produced by newer sequencing technologies.

In its most common formulation, the pairwise alignment problem is solved using some variation of the Needleman–Wunsch (NW) algorithm (Needleman and Wunsch, 1970) for gap-linear penalties or the Smith–Waterman–Gotoh (SWG) algorithm (Gotoh, 1982) for gap-affine penalties. These solutions are based on dynamic programming (DP) and consist on first computing the recurrence equations on a DP matrix, and then tracing back the optimal alignment. As a result, they require quadratic time and memory on the length of the sequences.

Over the years, these algorithms have been extensively studied, and many different techniques and heuristics have been developed to accelerate DP computations. The most successful optimizations focus on vectorization strategies (Daily, 2016) (including bit-parallel encodings Loving et al., 2014), banded computations (Suzuki and Kasahara, 2017) and cut-off techniques (Gusfield, 1997). Notwithstanding these efforts, the quadratic execution time of classical approaches quickly becomes the bottleneck, and these methods fail to scale with longer read lengths. Besides, intrinsic dependencies on the DP recurrences limit the effectiveness of vectorization approaches; what is more, they require ad hoc implementations for each different SIMD instruction set. In many cases, practical implementations tend to apply heuristics that can miss the optimal alignment at the expense of faster execution times. Interestingly, all these algorithms are oblivious to the similarities between the sequences. That is, they perform the same computations whether the sequences are highly divergent or completely identical.

1.1 Previous work

Over the years, alignment algorithms for the edit distance have been largely studied and optimized due to its simplicity. As a result, many efficient libraries and tools like Edlib (Šošić and Šikić, 2017) [implementing Myers’s bit-vector algorithm (Myers, 1999)], or DAligner (Myers, 2014) [implementing Myers’s O(ND) difference algorithm (Myers, 1986)] are now available. However, the edit distance fails to capture critical properties of the difference between biological sequences. For that reason, gap-affine distance is commonly preferred, and thus many research efforts have been invested on accelerating the SWG algorithm.

Many of the SWG optimization techniques are focused on exploiting intra-sequence parallelism using tailored vectorization strategies. In this way, Wozniak (1997) first proposed to compute DP cells along the minor diagonal in parallel. Then, Rognes (Rognes and Seeberg, 2000) proposed to vectorize along the query sequence, introducing the query profile technique. Later on, Farrar (2007) proposed to reorganize computations in a striped fashion. Farrar’s method dominated over all other approaches until Daily presented the prefix-scan method (Daily et al., 2015), which in practice outperforms all previous methods. Meanwhile, focusing on further exploiting instruction-level parallelism, the BitPAl algorithm (Loving et al., 2014) was presented as a natural extension of Myers’s bit-vector algorithm restricted to gap-linear penalties. Although it requires generating tailored code for each different set of penalties, it represents an interesting method for computing the alignment distance (i.e. not the full alignment) if all the penalties are fixed and known in advance.

Recently, Suzuki and Kasahara (2018) proposed a differential encoding of the DP matrix that effectively reduces the size required to store each DP cell to further exploit SIMD operations. Combined with an adaptive-band, that adjusts its size according to the scores computed so far, they developed the Gaba library (Suzuki and Kasahara, 2017). Because of its good performance, this algorithm was re-implemented in the KSW2 library, which is currently used within the core of the Minimap2 mapper (Li, 2018).

Over the past decade, many libraries implementing efficient SWG algorithms have been developed due to its critical role in several bioinformatics tools and pipelines. The SSW library (Zhao et al., 2013) was one of the first libraries to offer an efficient implementation of the SWG using Farrar’s striped algorithm. Later on, the Parasail library (Daily, 2016), that implements several intra-sequence vectorization strategies, was published. But also, the SeqAn (Rahn et al., 2018) developers have put many efforts into incorporating high-performance and parallel implementations of the SWG among its many algorithms. At the same time, all these libraries implement additional optimizations that can further enhance the presented methods. For instance, the integer saturation strategy, which first computes the alignment using a small integer type, and recomputes the alignment in case an overflow/underflow is detected. In addition, these libraries implement several coarse-grain parallelization techniques that allow performing various independent alignments in parallel. But also, they include tailored implementations for specific SIMD instruction sets than can yield shorter execution times.

Last, it should be noted that there are many other lines of research for accelerating the SWG involving hardware accelerators; including Graphics Processing Units (Chacón et al., 2014; Liu et al., 2013), Field-Programmable Gate Arrays (Li et al., 2007), Cell Broadband Engine (Szalkowski et al., 2008), Xeon Phi processor (Liu et al., 2014) and even custom hardware designs (Hasan et al., 2008).

1.2 Our contribution

In this article, we present the wavefront alignment algorithm (WFA) for exact pairwise alignment of sequences. This novel alignment method progressively computes partial alignments of increasing score until the optimal solution is reached. In this way, the WFA algorithm exploits similarities between sequences to accelerate the computation of the optimal alignment. As a result, its time complexity O(ns) depends on the sequence length n and the optimal alignment score s. This allows scaling with sequence length provided that the error-rate between the sequences remains moderate. We demonstrate that the WFA algorithm outperforms other state-of-the-art methods, while requiring less memory.

2 Materials

In the following sections, we describe the main concepts behind the WFA algorithm. First, we introduce the concept of furthest-reaching points and wavefronts, and then we redefine the recurrent equations of the SWG algorithm in terms of wavefronts. Finally, we prove that the first wavefront that reaches the bottom-right corner of the DP matrix corresponds to the optimal pairwise alignment between the sequences.

2.1 Pairwise global alignment of sequences

Let the query $q=q_0{q}_1\dots q_{n-1}$ and the text $t=t_0{t}_1\dots t_{m-1}$ be strings of length $\left|q\right|=n$ and $\left|t\right|=m$, respectively (Table 1). We define the pairwise global alignment problem in terms of computing the alignment [or edit path, Myers (1986)] from (0, 0) to (n, m) with minimum penalty score, allowing matching bases, substitutions and gaps (i.e. insertions and deletions). Under the gap-affine model, the alignment penalty score is computed based on $\{a,x,o,e\}$, where a and x correspond to the penalty of matching or mismatching two bases, respectively, and the gap-penalty function is expressed as the linear function $g(n)=o+n·e$ (where n is the length of the gap). As stated before, this problem is commonly solved using some variation of the SWG algorithm (Gotoh, 1982). Eq. 1 shows the recurrence relations of the DP matrix used in the SWG algorithm.

$$\{\begin{array}{cc}{I}_{v,h}\hfill & =\min \{M_{v,h-1}+o+e,I_{v,h-1}+e\}\hfill \\ D_{v,h}\hfill & =\min \{M_{v-1,h}+o+e,D_{v-1,h}+e\}\hfill \\ M_{v,h}\hfill & =\min \{I_{v,h},D_{v,h},M_{v-1,h-1}+s(q_{v-1},t_{h-1})\}\hfill \end{array}.$$ (1)

Table 1.

Notations

Symbol	Description
q, t	Strings: $q=q_0{q}_1\dots q_{n-1},\hspace{0.17em}t=t_0{t}_1\dots t_{m-1}$
$p=\{a,x,o,e\}$	Gap-affine penalty scores
M, I, D	SWG alignment matrices
${\mathcal{F}}_{s,k}$	Furthest-reaching (f.r.) point on diagonal k with score s
${\tilde{M}}_{s,k}$	Offset in the diagonal to the corresponding f.r. point ${\mathcal{F}}_{s,k}$
$\widetilde{I_s},\hspace{0.17em}\widetilde{D_s},\hspace{0.17em}\widetilde{M_s}$	Components of the wavefront WFs
WFs	Wavefront of score s
${\tilde{M}}^{hi}$	Index of the rightmost diagonal in the component
${\tilde{M}}^{lo}$	Index of the lowest diagonal in the component
WFmin	Minimum wavefront length
WFdiff	Maximum difference distance

Despite its general formulation, in practice, the majority of applications use strictly positive penalties, i.e. $x,o,e>0$. And, as in other methods, we focus on the match-mismatch model where the mismatch between every two different bases always has the same penalty, x. That is, function s(v, h), for $0\le v<n$ and $0\le h<m$, evaluates to a if $q_v==t_h$ and x otherwise. In addition, our method fixes the match score to zero (a = 0) to enable exploiting similarities between the sequences and accelerate the alignment process. As we demonstrate later, this allows defining a much simpler and faster method for gap-affine alignment.

2.2 Wavefront furthest-reaching diagonals

Restricted to the edit distance, the so-called diagonal-transition algorithms (Landau and Vishkin, 1989; Ukkonen, 1985) exploited the fact that DP diagonals have monotonically increasing scores. In particular, Myers’ O(nd) algorithm (Myers, 1986), implemented at the core of the Linux diff-tool, computes the longest common subsequence of two sequences taking advantage of stretches of matching characters along the diagonals. Our algorithm extends these ideas to the gap-affine model.

For each score s and diagonal k, the furthest-reaching (f.r.) point ${\mathcal{F}}_{s,k}$ denotes the DP-cell, on diagonal k and with score s, that is more far-off from the beginning of the diagonal. Note that a point $p=(v,h)$, in the diagonal $k=h-v$, is further than other $p\prime =(v-1,h-1)$ ($p\prime <p$) in the same diagonal. Then, we define ${\tilde{I}}_{s,k},\hspace{0.17em}{\tilde{D}}_{s,k}$ and ${\tilde{M}}_{s,k}$ as the offset in the diagonal to the f.r. point ${\mathcal{F}}_{s,k}$ for each of the three SWG matrices I, D and M, respectively. So, for a given score s, we define the s-wavefront (WF_s) as the set of all the f.r. points with score s; that is, the set of offsets ${\tilde{I}}_{s,k},\hspace{0.17em}{\tilde{D}}_{s,k}$ and ${\tilde{M}}_{s,k}$, for all k. Likewise, we denote $\widetilde{I_s},\hspace{0.17em}\widetilde{D_s}$ and $\widetilde{M_s}$, the components of the wavefront WF_s. Assuming each component of a wavefront is represented using a vector of offsets centred over the main diagonal (k = 0), let ${\tilde{M}}^{hi}$ denote the index of the rightmost diagonal in the component, and ${\tilde{M}}^{lo}$ the index of the lowest.

Our goal is to compute the minimum s such that any of the f.r. points of WF_s reaches (n, m). We notice that for any s, the f.r. points of WF_s can only be originated from points whose score is s – o, s – e or s – x; or from a previous point with score s solely followed by matches along the diagonal. Considering only insertions, deletions and mismatches; we can redefine Eq. 1 in terms of offsets to f.r. points (Eq. 2).

$$\begin{array}{cc}\hspace{1em}\hspace{1em}{\tilde{I}}_{s,k}\hfill & =\max \{\begin{array}{cc}{\tilde{M}}_{s-o-e,k-1}\hfill & (\text{Open} \text{insertion})\hfill \\ {\tilde{I}}_{s-e,k-1}\hfill & (\text{Extend} \text{insertion})\hfill \end{array}\}+1\hfill \\ \hspace{1em}\hspace{1em}{\tilde{D}}_{s,k}\hfill & =\max \{\begin{array}{cc}{\tilde{M}}_{s-o-e,k+1}\hfill & (\text{Open} \text{deletion})\hfill \\ {\tilde{D}}_{s-e,k+1}\hfill & (\text{Extend} \text{deletion})\hfill \end{array}\}\hfill \\ \hspace{1em}\hspace{1em}{\tilde{M}}_{s,k}\hfill & =\max \{\begin{array}{cc}{\tilde{M}}_{s-x,k}+1\hfill & \left(\text{Substitution}\right)\hfill \\ {\tilde{I}}_{s,k}\hfill & \left(\text{Insertion}\right)\hfill \\ {\tilde{D}}_{s,k}\hfill & \left(\text{Deletion}\right)\hfill \end{array}\},\hfill \end{array}$$ (2)

with initial condition ${\tilde{M}}_{0,0}=0$

Essentially, Eq. 2 states that we can compute the set of f.r. points of WF_s using $W{F}_{s-o},\hspace{0.17em}W{F}_{s-e}$ and $W{F}_{s-x}$. For example, in order to compute the f.r. point ${\tilde{D}}_{s,k}$, we only have to consider which f.r. point brings the resulting offset further: a newly opened deletion ${\tilde{M}}_{s-o-e,k+1}$, or an extended one ${\tilde{D}}_{s-e,k+1}$ (both coming from one diagonal above). Similarly, as to compute the f.r. point ${\tilde{M}}_{s,k}$, we only need to compare offsets between the f.r. points corresponding to an insertion ${\tilde{I}}_{s,k}$, a deletion ${\tilde{D}}_{s,k}$ and a mismatch from ${\tilde{M}}_{s-x,k}$. Then, we consider matches, and we take advantage of the fact that a = 0. For that, we extend all the previously computed points by Eq. 2, as far as possible, following matching characters along the diagonal.

Lemma 2.1. The resulting points of applying  Eq. 2  and extending them, following matching characters along the diagonal, are the f.r. points for the score s, that is WF_s.

Proof. Suppose that point $p\in W{F}_s$ (originated by point q from a previous $W{F}_{s\prime },\hspace{0.17em}s\prime =s-p,p\in \{x,o,e\}$) is not the f.r. point on the diagonal k. Then, there must exist a point $p\prime$ that is f.r. on that diagonal $(p\prime >p)$. For that $p\prime$, there must exist a point $q\prime$ (with a score $s\prime$) that generated $p\prime$ (perhaps, after extension by accounting matches on the diagonal). However, $q\prime$ cannot be the f.r. point on the diagonal (i.e. does not belong to $W{F}_{s\prime }$), otherwise, it would have generated p. Therefore, $q\prime <q$ and thus, it follows that $p\prime \le p$, in the best case (f.r point), $p\prime =p$. □

It follows from Lemma 2.1 that the optimal alignment corresponds to the sequence of wavefronts from WF₀ to WF_s, being WF_s the wavefront with the smallest s that contains a f.r. point that reaches (n, m).

2.3 Wavefront algorithm

Using Lemma 2.1 and staring with ${\tilde{M}}_{0,0}=0$, the WFA algorithm (Algorithm 1) progressively computes wavefronts of increasing score until the cell (n, m) is reached.

First, for each score s, the algorithm extends the points ${\tilde{M}}_{s,k}$ following matching characters along the diagonals, using WF_EXTEND(${\tilde{M}}_s,q,t$) (Algorithm 2). Then, it checks whether any of the resulting f.r. points of wavefront WF_s reaches (n, m). If not, the algorithm proceeds to compute the next wavefront $W{F}_{s+1}$ using WF_NEXT($\tilde{D},\tilde{I},\tilde{M},q,t,s$) (Algorithm 3, which applies Eq. 2), and iterates again.

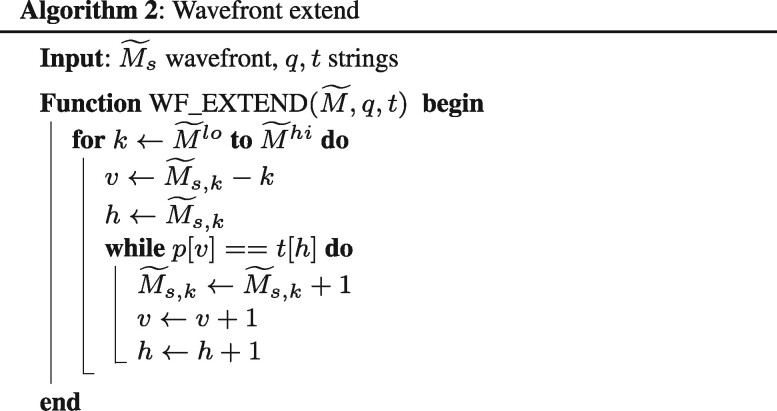
In the case of global alignment, the algorithm starts with a unitary wavefront (${\tilde{M}}_{0,0}$). As the algorithm iterates, the length of the wavefronts increases according to Eq. 3. That is, each new wavefront grows to span over one more diagonal on each end (i.e. ${\tilde{M}}_s^{hi}$ and ${\tilde{M}}_s^{lo}$) compared to the wavefronts it depends on. As a result, the size of each subsequent wavefront increases proportional to the alignment score between the sequences. Hence, the algorithm requires $O(s^2)$ memory to store all wavefronts.

$$\begin{array}{cc}{\tilde{M}}_s^{hi}\hfill & ={\tilde{I}}_s^{hi}={\tilde{D}}_s^{hi}=\max \{{\tilde{M}}_{s-x}^{hi},{\tilde{M}}_{s-o-e}^{hi},{\tilde{I}}_{s-e}^{hi},{\tilde{D}}_{s-e}^{hi}\}+1\hfill \\ {\tilde{M}}_s^{lo}\hfill & ={\tilde{I}}_s^{lo}={\tilde{D}}_s^{lo}=\max \{{\tilde{M}}_{s-x}^{lo}{\tilde{M}}_{s-o-e}^{lo}{\tilde{I}}_s^{s-e},{\tilde{D}}_s^{s-e}\}-1.\hfill \end{array}$$ (3)

Also, note that extending a wavefront (WF_EXTEND function) is bounded by the number of diagonal matching characters ($\max \{n,m\}$) and the length of the wavefront. Similarly, the function WF_NEXT computes each next wavefront in time proportional to the wavefront length. Therefore, the running time of the WFA algorithm, to compute an alignment of score s, is bounded in the worst case by $O(\max \{n,m\}·s)$, or O(ns) assuming that the sequences have the same length.

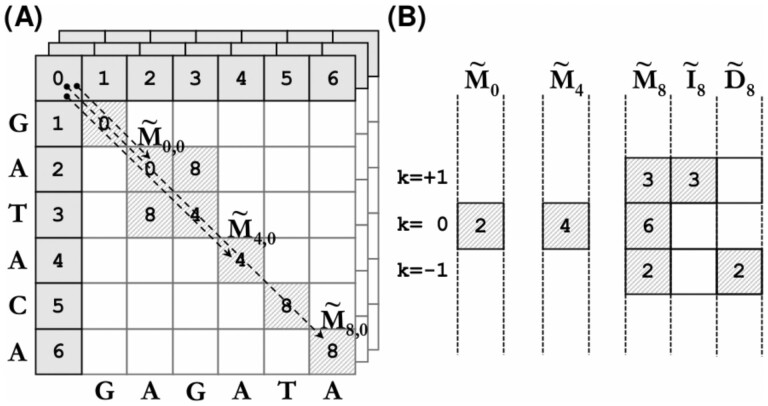
Figure 1 shows an example of computing a global gap-affine alignment using a DP matrix and the WFA algorithm. The figure demonstrates that the WFA only needs to compute a minimal number of DP cells to find the optimal alignment. The WFA explores the cells of the DP matrix by increasing score, like seeking for the minimum cost path from (0, 0) to (n, m). In this way, the algorithm effectively computes an adaptive band without previous knowledge of the alignment error between the sequences. Moreover, it performs this seemingly irregular computation using simple and regular operations over the wavefronts. Furthermore, the algorithm only requires to store a few wavefronts before reaching the bottom right cell of the DP matrix. Considering the penalties used in Figure 1, the only score values that can appear in the DP matrix, before reaching the optimal alignment at s = 8, are s = 0 and s = 4. For that reason, the WFA only needs to store the wavefronts WF₀, WF₄ and WF₈. And, unlike the DP matrix, these wavefronts avoid storing runs of cells with the same score (byproduct of the matches along the diagonal).

Fig. 1.

(A) DP matrices (i.e. M, D and I) depicting the only cells computed by the WFA in order to align $q=“\text{GATACA}”$ against $t=“\text{GAGATA}”$ using the penalties $\{x=4,o=6,e=2\}$. The arrows show the f.r. points of the main diagonal in matrix M (i.e. ${\tilde{M}}_{0,0},\hspace{0.17em}{\tilde{M}}_{4,0}$ and ${\tilde{M}}_{8,0}$). (B) Equivalent representation using wavefronts (i.e. WF₀, WF₄ and WF₈)

Once the algorithm computes a wavefront that reaches (n, m), and therefore, the optimal alignment between the sequences, it can retrieve back the path that leads from (0, 0) to (n, m) (i.e. backtrace). As opposed to DP-based algorithms, the WFA’s backtrace is performed across the wavefronts’ offsets instead of using the DP matrix scores. On each step of the backtrace, the function determines which f.r. point, from the previous wavefronts, originated the current offset. The difference between the actual offset and the source is the total amount of matching characters between the two positions. For example, in Figure 1, offset ${\tilde{M}}_{8,0}=6$ has been generated from the f.r. point ${\tilde{M}}_{4,0}=4$. The difference between the two offsets corresponds to the matches from (5, 5) to (6, 6), both included.

2.4 Adaptive wavefront reduction

As the WFA algorithm iterates, wavefronts of increasing score span over more and more diagonals. While some of the f.r. points quickly advance towards the solution, others are left behind on their diagonal as they are unlikely to lead to the optimal solution. As a consequence, the WFA algorithm invests a substantial amount of time processing unpromising paths. For that reason, we propose a heuristic version of the algorithm (WFA-Adapt) that removes f.r. points from outer diagonals that are extremely far behind compared to other points in the same wavefront.

In this way, the WFA-Adapt performs a wavefront pruning (Algorithm 4) after performing each wavefront extension. It determines the distance d_k of each diagonal f.r. point to the (n, m) cell. Then it computes the minimum $d_{\text{min}}={\min }_k\left\{d_k\right\}$ and discards outer diagonal points that are more than WF_diff cells behind it (i.e. $d_k-d_{\text{min}}>W{F}_{\text{diff}}$). Despite its simplicity, computing each d_k distance for all the f.r. points of the wavefront carries a non-negligible toll on the total running time of the algorithm. For that reason, we define a minimum wavefront length WF_min required to trigger the reduction (WF_REDUCE).

In practice, the WFA-Adapt heuristic successfully removes distant f.r. points unlikely to be part of the optimal alignment. Therefore, the span of the wavefront is focused on the diagonals closer to the alignment solution, further reducing the amount of memory required by the algorithm. In a way, similar pruning techniques are implemented into DP-based algorithms. These banded methods avoid computing paths beyond a band of diagonals. Unlike those methods, our wavefront reduction method prunes based on the potential of the diagonal to lead to the optimal solution, without previous knowledge of the error between the sequences whatsoever.

Nonetheless, it is important to highlight that the WFA-Adapt method is no longer exact and might miss some optimal solutions; unlike the WFA. In practice, for a reasonable selection of $(W{F}_{\text{min}},W{F}_{\text{diff}})$, this is rarely the case, even when aligning long noisy sequences.

2.5 Efficient computation of wavefronts

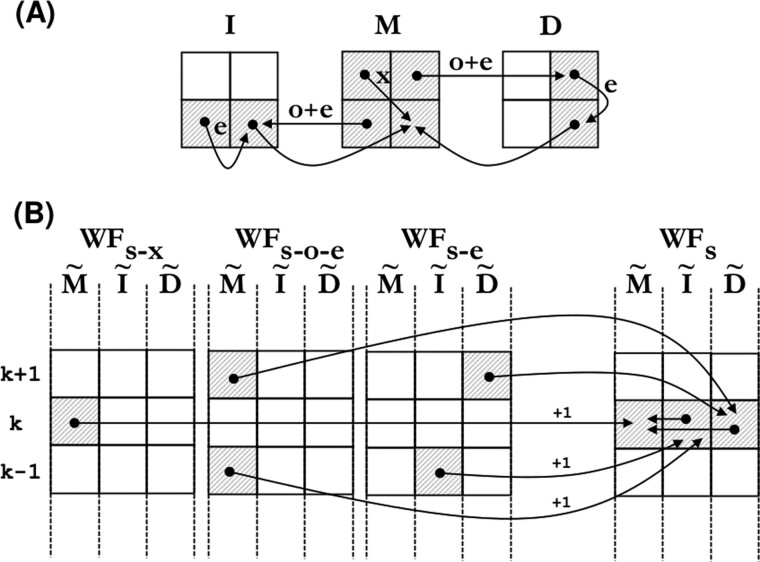
As opposed to traditional DP-based algorithms, the core functions of the wavefront algorithm depict simple data dependencies (Fig. 2). This allows the implementation of effective fine-grain parallelization techniques to accelerate the computation of each wavefront.

Fig. 2.

(A) Dependencies between DP cells when computing another cell using gap-affine penalties. (B) Dependencies between wavefronts as to compute one element of the next wavefront (Algorithm 3)

In the case of the WF_NEXT function, the automatic vectorization features of modern compilers can easily detect the dependencies between wavefronts and transparently issue SIMD instructions to significantly accelerate the computation. This represents a major advantage over other methods that rely on specific SIMD intrinsics and custom implementations. These tools not only have limited portability to different computer architectures but also require complicated, time-consuming and error-prone implementations. In contrast, our approach allows transparent vectorization of the algorithm for any SIMD instruction-set and architecture supported by the compiler.

In the same way, the function WF_EXTEND can be accelerated by means of exploiting bit-level parallelism techniques. That is, instead of comparing characters along the diagonal one at a time, we perform comparisons in blocks of eight characters (i.e. packed in a 64-bit computer word). In this way, the algorithm performs parallel comparisons and extends each diagonal up to eight positions per step. Taking into account that spurious matches between blocks of eight characters are very unlikely to occur, this technique prevents the inner loop of WF_EXTEND from iterating more than once in most cases. Otherwise, it means that the function has detected a stretch of matches which, in turn, favors the overall performance of the algorithm.

Note that, depending on the penalties selected, some (or even all) of the wavefronts required to compute a wavefront might not exist. That means that there is no possible combination of penalties that can generate the current score. In those cases, the number of operations involved in WF_NEXT gets reduced. Hence, our implementation contains different specializations of this function to accelerate those cases where some source wavefronts are not needed, and thus the complexity can be reduced.

Notably, the WFA encodes the offsets to the f.r. points on each diagonal, not the actual score values. Therefore, the representation range of each wavefront element is bounded by the length of the sequences, and not by the maximum score possible. In most cases, the WFA can conveniently encode offsets using 16-bit integers (for sequences up to 2¹⁶ characters), or even 8-bit integers (for Illumina-like sequences, no longer than 255 bases). This succinct representation not only allows saving memory but also allows using wider SIMD instructions that can operate over more elements at once. In turn, this further enhances the efficiency of our WFA implementation.

3 Results

We evaluate the performance of our implementation of the WFA and WFA-Adapt algorithms, together with other widely used libraries that implement optimized versions of well-known pairwise alignment algorithms.

3.1 Experimental setup

We select the widely used Parasail library (Daily, 2016) that implements the diagonal method by Wozniak (Wozniak, 1997) (ParaDiag), the striped approach proposed by Farrar (Farrar, 2007) (ParaStrip), the prefix-scan algorithm (Daily et al., 2015) (ParaScan) and the classical banded heuristic method (ParaBand). Also, we evaluate the gap-affine implementation of the SeqAn library (Rahn et al., 2018), the bit-parallel implementation for non-unitary penalties (Loving et al., 2014) (BitPAl) and the adaptive band algorithm from Suzuki (Suzuki and Kasahara, 2018) (Gaba). In addition, we evaluate the performance of the highly optimized SIMD algorithms KSW2-Z2 (ksw2_extz2_sse), and KSW2-D2 (ksw2_extd2_sse), from the KSW2 library, used within Minimap2 (Li, 2018). On top of that, we present the performance results of the Edlib (Šošić and Šikić, 2017) library as a base line for comparison. Because Edlib is restricted to compute the edit-distance alignment, its execution is remarkably fast.

For the purpose of the evaluation, all the methods have been configured to generate global alignments. These methods are grouped in three categories: ‘Gap-affine (Exact)’ (WFA, KSW2-Z2, SeqAn, ParaStrip, ParaScan and ParaDiag) for exact algorithms that use gap-affine penalties, ‘Gap-affine (Banded)’ (WFA-Adap, Gaba and ParaBand) for approximate algorithms that use gap-affine penalties, and ‘Others’ (Edlib, BitPAl and KSW2-D2) for exact methods that use other penalty models. Note that the gap-affine banded methods are approximated and not guaranteed to find the optimal alignment. Similarly, note that the algorithms ParaBand and BitPAl only compute the alignment score (not the full alignment) and the latter is restricted to linear-gap penalties.

We discarded other methods from the evaluation as their running time was exceedingly long or because their recall was substantially below par. This is the case of other KSW2 algorithms (like the approximate versions), other edit distance methods [e.g. BPM (Myers, 1999) or DAligner (Myers, 2014)] or custom implementations for hardware accelerators (which fall beyond the scope of this article).

We choose two real datasets: 100 000 sequences from an Illumina HiSeq 2000 of 100 bp (Accession number ERX069505), and 25 000 ONT MinION sequences from (Bowden et al., 2019) (Accession numbers ERR3278877–ERR3278886). Also, we simulate several datasets of various lengths (i.e. 100, 1K, 10K and 100K bases), with different error rates (i.e. d = 1, 2, 5, 10 and 20% error rate) by means of randomly adding mismatches and indels. For every dataset, we select as many sequences as needed, so that each of them contains a total of 10 million bp.

All tests are executed on an Intel Xeon Platinum 8160 equipped with 96 GB of RAM, running SuSE Linux Enterprise Server. For each method, we measure execution time and memory consumed. In addition, we verify the results using a basic SWG implementation in order to compute the recall of each method.

3.2 Evaluation on real data

Table 2 shows the time performance results obtained for all the algorithms evaluated using both real and simulated datasets. On real datasets, the WFA performs many times faster than other methods. In particular, aligning HiSeq sequences, our method is 200–300× faster compared to traditional DP algorithms, and 20–40× faster than the adaptive-band methods. Similarly, when aligning ONT sequences, the WFA performs 28–200× and 6–7× times faster than DP algorithms and adaptive-band methods, respectively. Moreover, it is several times faster than methods that only compute the alignment score. Furthermore, the WFA-Adapt refinement attains an extra 1.6× speedup over the original WFA when aligning long ONT reads.

Table 2.

Time performance of pairwise alignment algorithms

				100			1K			10K			100K
		HiSeq	ONT	d = 1%	d = 5%	d = 20%	d = 1%	d = 5%	d = 20%	d = 1%	d = 5%	d = 20%	d = 1%	d = 5%	d = 20%
Gap-affine (Exact)	WFA	0.06	2.46	0.09	0.37	1.55	0.14	0.93	6.93	0.43	7.28	66.00	8.49	102.00	2542.00
	KSW2-Z2	2.42	15.23	2.41	2.79	3.06	16.43	16.47	16.64	188.40	188.40	189.00	2146.00	2136.00	2139.00
	SeqAn	18.18	180.60	18.28	19.17	22.64	184.80	190.80	213.60	n/a	n/a	n/a	n/a	n/a	n/a
	ParaStrip	77.40	530.40	77.40	75.60	70.80	603.60	602.40	572.40	n/a	n/a	n/a	n/a	n/a	n/a
	ParaScan	12.03	69.00	11.85	11.89	11.99	75.00	75.00	75.00	746.40	747.00	747.00	n/a	n/a	n/a
	ParaDiag	17.80	130.20	17.53	17.58	17.66	141.60	141.60	141.60	n/a	n/a	n/a	n/a	n/a	n/a
Gap-affine (Banded)	WFA-Adap	0.07	1.51	0.09	0.50	2.20	0.16	0.68	2.75	0.17	0.68	3.00	0.26	1.53	6.97
	Gaba	1.26	error	1.28	1.33	error	0.68	0.74	error	0.60	0.81	error	0.72	0.76	error
	ParaBand	3.71	8.26	3.75	3.89	4.17	4.04	4.51	5.34	4.87	6.39	8.87	8.11	11.81	20.43
Others	Edlib	1.75	2.28	1.73	1.82	1.94	1.95	2.03	2.73	3.67	4.50	7.39	6.95	19.34	error
	BitPAl	0.47	2.18	0.47	0.47	0.47	2.27	2.31	2.33	21.44	21.44	21.47	212.40	212.40	212.40
	KSW2-D2	2.87	18.13	2.86	3.23	3.49	19.56	19.64	19.81	219.60	219.60	220.20	2385.00	2380.00	2452.00

Note: Running time in seconds obtained by the different pairwise alignment algorithms on real and simulated datasets. Penalties used for all tests $\{x=4,o=6,e=2\}$ correspond to the ones used by BWA-MEM. Alignment algorithms have been grouped in three categories: ‘Gap-affine (Exact)’ for exact algorithms that use gap-affine penalties, ‘Gap-affine (Banded)’ for approximate algorithms that use gap-affine penalties, and ‘Others’ for exact algorithms that use other distance models (i.e. edit distance or linear-gap penalties). On simulated datasets, results are broken down by error rate. Experiments whose running time exceeded 2 hours are marked as ‘n/a’. Likewise, runs that consistently failed are labelled with ‘error’. Note that WFA-Adapt was executed using WF_min = 10 and WF_diff = 50.

3.3 Evaluation on simulated data

When aligning simulated datasets, WFA methods consistently outperform other algorithms. Overall, WFA and adaptive-band methods are faster than classical DP algorithms. In particular, as the read length increases, Parasail and SeqAn’s implementations require impractical running times. Notably, BitPAl and ParaBand running times remain reasonably low, but alas, their results are limited to the alignment score. Altogether, these methods prove to be completely insensitive to the error between the sequences. For that reason, WFA and WFA-Adapt methods achieve remarkable speedups when the error rate remains moderate (i.e. d = 1–5%). For instance, compared to ParaBand, WFA methods run up to 13× and 78× faster for error rates of 1 and 5%, respectively; and up to 138× and 814× faster compared to BitPAl for the same error rates.

On the other hand, WFA methods prove to be generally faster and more accurate than adaptive-band methods. Although these adaptive algorithms prove to be superior to classical approaches, WFA and WFA-Adapt methods scale better with both the sequence length and the error rate. In particular, executions of the KSW2 library consistently take between 2× and 510× longer than the WFA. In the demanding scenario of aligning reads of 100K bases at just 1% of divergence rate, WFA-Adapt runs more than three orders of magnitude faster than the KSW2 algorithms. It is important to note that KSW2-D2 uses 2-piece affine model (Gotoh, 1990), that is why it is slower than KSW2-Z2 which uses the 1-piece/standard model.

In general, as the error rate increases, adaptive-band methods either take longer to finish, like KSW2-Z2 and KSW2-D2, or become insensitive reporting suboptimal alignments, like Gaba. Table 3 presents a summary of time and recall results obtained using two broadly used penalty schemes; that is, those used by the ubiquitous mappers BWA-MEM (Li, 2013) and Bowtie2 (Langmead and Salzberg, 2012). In the case of the Gaba algorithm, executions times seem to decrease as the sequence length increases. Nonetheless, this is the result of aggressive heuristics that, in the end, cause a significant drop in the total recall (∼5%) or fail to align noisy sequences (e.g. aligning ONT sequences). Notably, only the WFA methods could successfully align all datasets of 100K bases, whereas other methods took an unreasonable amount of time or failed. Moreover, WFA-Adapt could finish all the executions in less than 7 seconds achieving the maximum possible recall; that is, reporting 100% of the optimal alignments.

Table 3.

Accuracy of pairwise alignment algorithms

		HiSeq		ONT		l = 1K, d = 5%		l = 10K, d = 5%
		Time	Recall	Time	Recall	Time	Recall	Time	Recall
BWA-MEM	WFA	0.06	100	2.46	100	0.93	100	7.28	100
	WFA-Adap	0.07	100	1.51	99.8	0.68	100	0.68	100
	Gaba	1.26	100	error	error	0.74	95.2	0.81	94.8
	KSW2-Z2	2.42	100	15.23	100	16.47	100	188.4	100
	KSW2-D2	2.87	100	18.13	100	19.64	100	219.6	100
Bowtie2	WFA	0.07	100	4.80	100	1.60	100	12.05	100
	WFA-Adap	0.08	100	3.18	99.8	1.32	100	1.25	100
	Gaba	1.26	100	error	error	0.74	95.4	0.66	95.4
	KSW2-Z2	2.40	100	15.21	100	16.46	100	190.8	100
	KSW2-D2	2.91	100	18.16	100	19.66	100	220.8	100

Note: Time (in seconds) and recall (as percentage of the total sequences aligned) for error-sensitive algorithms. Two different penalty schemes were used: first corresponding to the default values used by BWA-MEM (i.e. $x=4,o=6,e=2$), and second matching Bowtie2’s end-to-end alignment scores (i.e. $x=6,o=5,e=3$).

In practice, the WFA algorithm seems barely sensitive to the sequence length, but to the alignment score between the sequences. In turn, this is subject to the penalty scores chosen for the alignment. Table 3 reflects how the performance of the WFA methods is affected by different choices of penalty scores. Although the running times remain remarkably low, selecting penalties that increase the final alignment score can negatively impact the performance of the algorithm; in this case, increasing the alignment time up to 2× in the worst case.

3.4 Memory footprint

Table 4 presents the overall memory consumption of the algorithms evaluated. These results experimentally confirm the reduced memory footprint required by the WFA methods. Moreover, as the read length and error rate increases, the WFA-Adapt method uses 19–36× times less memory than other methods. This not only results in a significant reduction on the overall memory used but also relieves the pressure put in the memory hierarchy by traditional DP-based algorithms.

Table 4.

Memory consumption of pairwise alignment algorithms

			l = 100		l = 1K		l = 10K
	HiSeq	ONT	d = 1%	d = 20%	d = 1%	d = 20%	d = 1%	d = 20%
WFA	0.5	3.1	0.4	0.4	1.4	4.2	6.2	269.6
KSW2-Z2	0.4	5	0.3	0.3	4.3	5	384.7	387.1
SeqAn	0.3	2.6	0.4	0.4	2.9	1.4	n/a	n/a
ParaStrip	6.7	7.9	68.5	15.6	6	13.1	n/a	n/a
ParaScan	6.8	7.9	68.5	15.4	6.2	12.8	196.1	202.6
ParaDiag	6.8	7.2	15.6	15.3	5.1	12	n/a	n/a
WFA-Adap	0.4	2	0.4	0.5	0.9	1.5	6.1	10.7
Gaba	0.7	Error	0.7	Error	4.3	Error	640.9	Error
ParaBand	0.4	0.3	0.5	0.4	0.4	0.5	0.5	0.5
Edlib	0.3	0.4	0.3	0.3	0.3	0.3	0.4	0.4
BitPAl	0.4	0.5	0.5	0.3	0.3	0.4	0.6	0.7
KSW2-D2	0.3	4.7	0.4	0.3	4.3	4.6	384.8	388.5

Note: Memory usage (MB) of each alignment algorithm for different sequence length and error rate.

4 Discussion

In this article, we presented a novel algorithm for gap-affine pairwise alignment. Our method exploits the similarities between the sequences to deliver exact alignments while outperforming in time and memory other state-of-the-art algorithms. To this end, our algorithm computes alignments of increasing score using a succinct diagonal-transition representation. As a result, the WFA algorithm runs in O(ns) time and memory; being n the sequence length, and s the alignment score between the sequences.

To date, adaptive-band algorithms dominated over other approaches. In practice, these methods seek to heuristically delimit the alignment path to avoid computing DP cells whose score is too high. Compared to them, the WFA algorithm naturally computes cells of the DP matrix by increasing score without introducing further complexities. Due to its simplicity, the WFA algorithm can be easily vectorized using SIMD instructions, as opposed to traditional DP-based algorithms. Moreover, data dependencies can be automatically understood by modern compilers in order to transparently issue SIMD instructions for any supported vectorial architecture. Furthermore, when aligning moderately long sequences (i.e. less than 255 bases), the WFA can encode diagonal offsets using 8-bit integers, which not only enhances SIMD performance but also further reduces the memory footprint.

In addition, the WFA algorithm poses no constrain on the alphabet size, nor requires any preprocessing step in advance. Besides, the progressive computation of alignments of increasing score allows the WFA to implement exact cut-offs techniques. And yet, this method does not require any prior estimation of the alignment score between the sequences whatsoever. Also, note that the optimizations presented in this article are focused on intra-sequence parallelization. Consequently, all the experiments were executed using a single thread. Nevertheless, the WFA can be used together with many inter-sequence paralellization techniques in order to exploit the multi-threading capabilities of modern processors. And, although the WFA algorithm has been presented using the gap-affine scoring model, it can be easily adapted to more other scoring models, like the linear-gap model or the piece-wise affine model (Gotoh, 1990; Miller and Myers, 1988). Likewise, it can be adapted to semi-global alignment by adjusting the initial conditions of Eq. 2 and the exit condition on Algorithm 1. But also, it can even be used for finding overlaps and local alignments in the spirit of mappers like DAligner (Myers, 2014).

Undoubtedly, pairwise alignment will remain as a central and critical building-block of many bioinformatics applications. For that reason, our algorithm represents a fast and scalable solution for many sequence analysis tools to cope with the ever-increasing yields of sequencing technologies. In this way, the WFA approach will pave the way for the design of better alignment algorithms in years to come.

Funding

This research was supported by the European Unions’s Horizon 2020 Framework Programme under the DeepHealth project [825111], by the European Union Regional Development Fund within the framework of the ERDF Operational Program of Catalonia 2014-2020 with a grant of 50% of total cost eligible under the DRAC project [001-P-001723], by the MINECO-Spain (contracts TIN2017-84553-C2-1-R and TIN2015-65316-P) and by the Catalan government (contracts 2017-SGR-313, 2017-SGR-1328 and 2017-SGR-1414). M.M. was partially supported by the Spanish Ministry of Economy, Industry and Competitiveness under Ramón y Cajal fellowship number RYC-2016-21104.

Conflict of Interest: none declared.