COTAN: scRNA-seq data analysis based on gene co-expression

Abstract

Estimating the co-expression of cell identity factors in single-cell is crucial. Due to the low efficiency of scRNA-seq methodologies, sensitive computational approaches are critical to accurately infer transcription profiles in a cell population. We introduce COTAN, a statistical and computational method, to analyze the co-expression of gene pairs at single cell level, providing the foundation for single-cell gene interactome analysis. The basic idea is studying the zero UMI counts’ distribution instead of focusing on positive counts; this is done with a generalized contingency tables framework. COTAN can assess the correlated or anti-correlated expression of gene pairs, providing a new correlation index with an approximate p-value for the associated test of independence. COTAN can evaluate whether single genes are differentially expressed, scoring them with a newly defined global differentiation index. Similarly to correlation network analysis, it provides ways to plot and cluster genes according to their co-expression pattern with other genes, effectively helping the study of gene interactions, becoming a new tool to identify cell-identity markers. We assayed COTAN on two neural development datasets with very promising results. COTAN is an R package that complements the traditional single cell RNA-seq analysis and it is available at https://github.com/seriph78/COTAN.

INTRODUCTION

Single cell RNA sequencing technology was first implemented in 2009 (1). Since then scRNA-seq provided an unprecedented insight into tissue cellular heterogeneity (2) and developmental processes (3–5). Currently, there are several techniques to isolate and sequence single cells (6–10). Different methods have their own strengths and weaknesses and exhibit great variability in the number of cells analyzed and in the length of sequenced RNA. Although the most appropriate choice depends on the biological question of interest (11), droplet based techniques are the most commonly used, because of their high-throughput, acceptable sensitivity, good precision and affordable cost per cell (12,13).

Single cell transcriptomes can describe known cell identity states and uncover new ones. This is frequently achieved by clustering cells with consistent gene expression (14,15) or more recently by cell lineage and pseudotime reconstruction (16). The typical pipeline requires to log-transform and normalize raw read counts, yielding ‘expression levels’, and to perform multivariate analysis on the latter (17,18). Unfortunately, the intrinsic low efficiency of scRNA-seq (8,9,12) precludes the detection of weakly expressed genes in many cells, in particular in droplet based experiments. This has a critical effect on the analysis of expression levels, causing the appearance of dropout artefacts (19,20), and often restricting the analysis to tools based on zero-inflation and imputation (21–23).

However, the introduction of Unique Molecular Identifiers (24) greatly reduces amplification noise, and the resulting UMI counts typically fit simple probabilistic models, thus allowing approaches not based on normalization (19).

Building on the opportunity given by the presence of UMIs and improving further the multinomial assumption verified in (19), we developed COTAN, CO-expression Tables ANalysis, a statistical framework and method of analysis, which uses UMI count matrices without normalization and does not depend on zero-inflation. Rather, COTAN focuses on zeros and their joint distribution to directly infer gene relations.

We tested COTAN on two neural development datasets as benchmarks of two of the main droplet based techniques Drop-seq (8) and 10× Genomics Chromium (9): a mouse cortex Drop-seq dataset (4) and a mouse hippocampal 10× dataset (25). Indeed, brain embryonic structures display high cell diversity, with dividing multipotent progenitor cells, newborn neurons differentiating with many distinct identities and glial cells, all co-existing in a mixed cell population. This makes them particularly suited for scRNA-seq studies aiming to depict cell identity states and relationships between gene expressions.

On these datasets COTAN can effectively assess co-expression and disjoint expression of gene pairs, also in case of very low UMI counts, yielding for each pair a correlation test p-value and a signed coefficient of co-expression (COEX).

Notably, Pearson and Spearman correlation are more noisy and cannot be used directly for the study of gene expression relationships, which instead is often carried out indirectly, through cell clustering and subsequent differential expression analysis between clusters. In fact, the numerous available tools show significant differences especially when poorly expressed genes are not filtered out (26). The two-step nature of these methods might introduce biases or loss of information, especially for genes with low expression. Moreover, the mutual exclusion for the expression of two genes can be hard to assess in this way.

As a second feature, COTAN can investigate whether single genes are constitutive or differentially expressed in the population, by scoring them with a global index of differentiation (GDI).

As a third feature, COTAN can help detecting cell-identity markers and studying gene interactions. In fact COEX may be used in a way similar to how correlation is used in gene network analysis (27), but instead of building a network adjacency matrix, we propose a novel dimensionality reduction of the gene space and a related gene cluster analysis.

MATERIALS AND METHODS

Mathematical framework

To ease the reading, the mathematical theory is only drafted in the main paper. A more elaborate discussion can be found in the Supplementary Material. The companion mathematical paper (28) contains further theoretical materials, including: a detailed explanation of the models for UMI counts and probability of zero UMI counts; an alternative estimation framework based on the square root variance-stabilizing transformation; a proof that the dispersion parameter can be uniquely determined; a proof that under null hypothesis, COEX has approximately Gaussian distribution; an extension of GPA to deal with differential expression.

UMI count model

For each gene g and cell c, let R_g,c denote the UMI count. For a uniform population of cells, it is reasonable to assume that these are negative binomial random variables, also known as Gamma-Poisson, meaning that R ∼ Poisson(Λ) with Λ ∼ gamma(η, θ). Our model is based on the assumption that cells also have a variable UMI detection efficiency (UDE) ν_c, which modulates the UMI count by

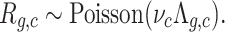For a uniform population of cells, Λ_g,c and R_g,c should all be independent, conditional on ν_c. On the other hand, for a mixed population of cells, Λ_g,c will be complicate mixtures of gamma distributions, independent in c but not in g. The subsequent Poisson samplings yielding R_g,c will still be independent. These assumptions correspond to the large numbers approximation of the multinomial model proposed in (19) and are in line with similar models discussed in (29).

There is an arbitrary factor in the definition of ν and Λ, so we impose that the average of ν_c is 1. In this way, Λ_g,c has the same scale as R_g,c for the average cell, and hence it may be viewed as a sort of normalized virtual expression. It is considered a positive random variable, with mean λ_g not depending on c, with unknown distribution, and independent in c. Then E[R_g,c|Λ_g,c] = ν_cΛ_g,c, and the expected UMI count is given by 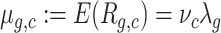, so in particular higher UDE yields a higher average library size.

We estimate the model’s parameters ν_c and λ_g in a simple linear way (for details see Parameter estimation in Supplementary material). Accuracy and precision of estimators were evaluated on synthetic datasets with heterogeneous cell types, for which the true values of ν and λ were known (see Supplementary Figure S1 and Synthetic datasets in Supplementary material).

We stress that UDE is not supposed to depend on the genes, and in fact the workflow includes a step to check this important assumption on the data (see Software pipeline).

Occurrence of zero UMI counts

The estimate of μ_g,c = λ_gν_c is the starting point to approximate the probability that R_g,c = 0. In general the population of cells is not uniform, so we cannot fix any specific model for the distribution of R_g,c. Instead we make the assumption that this probability takes a simple form, depending on one additional parameter a_g,

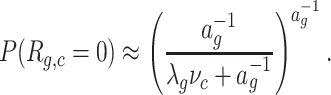(1)

This family of functions corresponds to the probability of zero for a negative binomial distribution with mean μ_g,c and dispersion a_g (X has dispersion a if 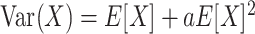). We stress that we are not assuming R_g,c to have negative binomial distribution, but just that P(R_g,c = 0) depends on c and g as in (1).

In fact the value of a_g is not estimated as the dispersion of R_g,c, but by fitting the observed number of cells with zero UMI counts (see Estimate fora_g in the Supplementary material). If the population is uniform, then R_g,c would really be negative binomial with average λ_gν_c and dispersion a_g (though in that case it would be better to estimate a_g as the dispersion). In all other cases λ_g and a_g encode information on the occurrence of zero counts for all cell types, encompassing types expressing and not expressing g.

Then, given any two genes g₁ and g₂ and under the null hypothesis that their expressions 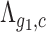and 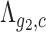are independent, the expected number of cells for which both genes have zero UMI counts is simply 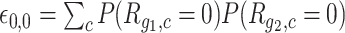and can be estimated with Equation (1). This is used as expected counts in the contingency tables in Gene-pair analysis section.

Software pipeline

We developed and tested COTAN on datasets obtained with droplet based techniques and in particular on 10× datasets and Drop-seq datasets. Figure 1 illustrates the pipeline, which is detailed in this section. Analysis requires and starts from a matrix of raw UMI counts, after removing possible cell doublets or multiplets and low quality or dying cells (with too high mitochondrial RNA percentage).

Figure 1.

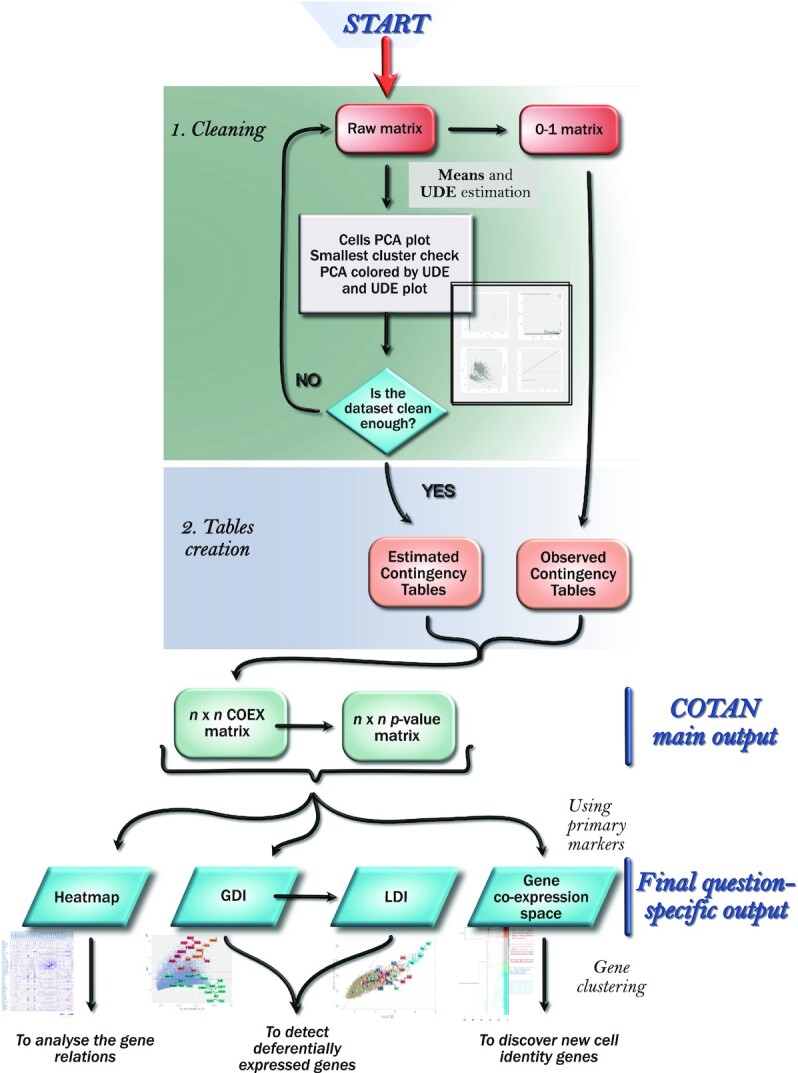
Pipeline diagram.

Data cleaning

The first step consists in removing genes that are not significantly expressed (default threshold is to require one or more reads in at least 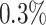of cells) or unwanted (such as the mitochondrial ones).

There is then an iterative procedure to filter out outlier cells (such as blood cells in a brain cortex dataset). In each iteration the UDE is estimated for all cells and UMI counts are simply normalized dividing by its value. Cells are then clustered by Mahalanobis distance (two clusters, A and B, complete linkage clustering) and represented on the plane of the first two principal components. The clustering algorithm detects outlier cells which will fall into the smallest cluster B (Supplementary Figure S8A). A subsequent plot displays the most abundant genes expressed in B, to allow the user to check if they are peculiar in any way (Supplementary Figure S8C). The user may choose to drop the cells in B and do another iteration, or to stop the procedure, when the PCA plot does not show obvious outliers (Supplementary Figure S8B–D).

After the last iteration two final quality checks are performed on the estimated UDE of cells. Firstly the PCA plot colored by UDE should not show a clear separation of cells with high and low UDE (Supplementary Figure S9A). In fact, COTAN builds on the assumption that UDE is not gene-dependent (see UMI count model) and if the PCA plot is polarized by UDE, this assumption might be false. Secondly, the plot of sorted UDE values will show if the efficiency drops markedly for a small fraction of cells. If this is the case, we usually want to exclude cells below the elbow point (see Supplementary Figure S9B and C; we remark that UDE values are normalized to have average 1, so there is no absolute threshold for efficiency to be acceptable). If cells are removed, another estimation iteration is due.

Tables implementation

Two genome-wide procedures compute the number of cells (observed and expected) in each of the conditions needed by gene-pair analysis (GPA, see Gene-pair analysis below and GPA theory in Supplementary material).

For each couple of genes, COTAN needs to build the 2 × 2 contingency table of zero/non-zero UMI counts. If n is the number of genes in the sample, the totality of observed values of these tables consist in n × n × 2 × 2 integers. In our implementation, four n × n matrices store the number of cells in each of the four conditions (expressing both genes, only the first one, only the second one or none). Constitutive genes that show non-zero UMI count in every cell cannot be used and are removed in this step (saving a list of them).

The expected values of the same 2 × 2 contingency tables are estimated as described in Occurrence of zero UMI counts and stored again as four n × n matrices corresponding to the same four conditions. In the implementation, the estimation of the dispersion parameters a_g is determined by simple bisection. In the case of the genes that would require a negative dispersion, because 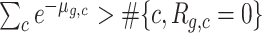, we choose instead to impose a zero dispersion model (Poisson distribution) with increased mean (1 + b_g)λ_g, yielding 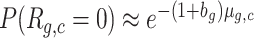(see also Estimate fora_g in the Supplementary material). This choice is consistent with the intended universality of the approach, because no distribution of Λ_g,c would give a negative dispersion and because λ_g is anyway an estimated quantity and therefore noisy. The positive parameter b_g is encoded as −a_g so that one single parameter can account for both cases. The fraction of genes with negative a_g is reported. In the typical dataset, about 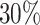of all genes fall in this case, with values of b_g no larger than 0.15 and average under 0.02. These genes are typically constitutive genes with low GDI and UMI count compatible with a negative binomial distribution.

Main output

For each pair of genes, the software computes the GPA test statistics S, the corresponding χ²(1) p-value, and the COEX index (see Statistical inference on co-expression in Supplementary material). These are saved in three n × n matrices, and the primary output of COTAN analysis consists of the latter two.

Computation time

The time required for the analysis is approximately proportional to the number of cells in the dataset. The most demanding step is the estimation of dispersion parameters, but since it is very sensible to the number of cores used, it can become much faster when many cores are available. As a reference, a dataset with 5000 cells was analyzed in about 3 min on 11 cores of an Intel(R) Dual Xeon(R) Silver 4214 at 2.20 GHz with 64GB of RAM.

Seurat pipeline

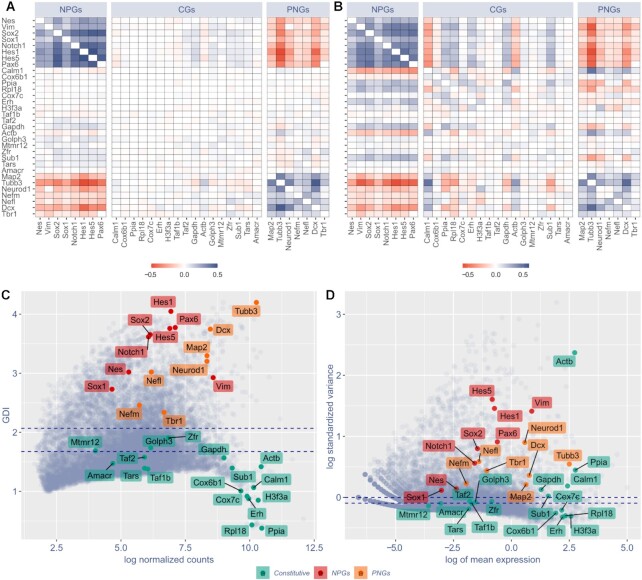
Seurat (3.1.0) workflow was performed on E16.5 hippocampal dataset (25) following the Guided Clustering Tutorial www.satijalab.org/seurat/v3.1/pbmc3k_tutorial.html (accessed 20 February 2020), with modifications. Data import (CreateSeuratObject) was done using min.cells 3 and min.features 200. The selected range for the number of features was between 200 and 4000; the maximum allowed fraction of mitochondrial genes per cell was 7.5%. Normalization was done using the default parameters. The correlation was then calculated on the whole Seurat normalized data matrix and the heatmap was plotted subsetting this (Figure 2B). Figure 2D was plotted by calling the function FindVariableFeatures with selection method VST.

Figure 2.

GPA and GDI are able to discriminate constitutive genes (CGs) from neural progenitor genes (NPGs) and pan-neuronal genes (PNGs). (A) COTAN GPA of selected genes. Cell color encodes COEX index: blue indicates genes showing joint expression, red indicates genes showing disjoint expression. White indicates independence, meaning that one or both genes are constitutive, or that the statistical power is too low to detect co-expression. Since the co-expression of a gene with itself is irrelevant, the diagonal is made artificially white. (B) Pearson correlation matrix of the same selected genes as in (A), using Seurat (34) normalized expression levels (obtained following the website vignettes – Guided Clustering Tutorial). (C, D) Comparison between COTAN global differentiation index (GDI, C) and Seurat highly variable features (D) analysis. Red labels indicate NPGs, orange labels PNGs, green labels CGs. Dotted blue lines correspond to the median (lowest) and the third quartile (highest). All plots refer to E16.5 mouse hippocampal cells (25) and genes are selected to be characteristic of NPGs, PNGs and constitutive genes with both high and low typical expression.

RESULTS

Overview

High throughput scRNA-seq methods allow the study of large cell populations, at the cost of suffering low expression levels. In fact read counts can be so scarce as to inhibit the analysis with traditional approaches of many relevant genes (see Supplementary Figure S3). On the other hand COTAN, after parameter estimation, encodes UMI counts as zero/non-zero. This choice is a critical feature of the method, with the aim to increase its sensitivity for genes with low expression level.

There are a few key concepts in COTAN (see also Materials and Methods). They are drafted here to build a terminology for the subsequent sections, and then detailed in the Supplementary Material.

Gene-pair analysis

Gene-pair analysis (GPA) is the core of COTAN’s computations. It works on couples of genes, by comparing the proportion of cells with zero UMI counts for both genes, with the expected number under the hypothesis that the detections of the two genes are independent. This independence holds in particular whenever one of the two genes is actually expressed in all cells (whether or not it is detected). If instead the expression of both genes correlates with the same cell identity states, then there will be evidence against independence. See GPA theory in Supplementary material.

GPA outputs the p-value for this test and a co-expression index (COEX) with values in the [−1, 1] range, which estimates the deviation from the proportion which was expected under independence (positive for co-expression and negative for disjoint expression). The mathematical derivation of this p-value is not rigorous, so its properties were tested on negative datasets where it was found to be more robust than standard correlation analysis on expression levels (see in Supplementary material Negative dataset analysis and Supplementary Figure S4).

The full potential of GPA is realized when it is performed genome-wide, between all pairs of genes, as this allows to extract very detailed information, as exemplified below.

Differentiation indices

Genome-wide GPA tests can be used to score single genes according to their propensity to show either joint or disjoint expression against other genes.

Fixing a gene g and looking at the distribution of the p-values of g against all other genes (Supplementary Figure S5), one can compute the global differentiation index (GDI) of g, which is low (typically below 1.5, see Supplementary Figure S2) for constitutive genes and high for differentially expressed genes, thus allowing a systematic procedure for detecting the latter type in the transcriptome.

If the same approach is restricted to the p-values of g against genes in a subset V (i.e. of genes related to some function), we get instead the local differentiation index relative to V (LDI), which is more specialized and sensitive than GDI for most applications (Supplementary Figure S6).

See also Filtering differentially expressed genes in the Supplementary material.

Co-expression space

The genome-wide COEX matrix can be used to embed genes in what we call co-expression space: a multidimensional representation of genes which is particularly powerful for investigating relations between differentially expressed genes. This is reminiscent of correlation network analysis (30), in that a nonlinear transformation is applied to a correlation matrix (COEX in our case) to recover a notion of distance between genes.

The geometry of this space is based on co-expression patterns: genes are close to each other when their activation is synchronized through different cell types and far apart otherwise. This allows genes to be effectively clustered by co-expression and represented in plots, after dimensionality reduction. See also Filtering differentially expressed genes in the Supplementary material.

Workflow

We implemented COTAN as an R package available on GitHub.

The tool should be applied on post-quality-control UMI counts (after doublets and dying cells have been removed). There are two required steps to get the main output matrices, and then several options are available depending on the question to be investigated (see Figure 1).

The first step is the model parameters estimation. In particular, the parameters needed by the model are the UDE for the cells and the mean and dispersion for the expression of genes (denoted by ν_c, λ_g and a_g, see Mathematicalframework). The estimation of UDE allows to make cell expression roughly comparable and hence the user has the choice to filter out cells with uncommon expression, with an iterative estimating-cleaning-estimating procedure (see Data cleaning).

At the end a plot is displayed to assess the most important assumption of the model, namely that UDE is not correlated with cell differentiation in the sample (see UMI count model and Software pipeline).

The second step, tables creation, begins by computing the probability of zero UMI counts for each cell–gene combination, given the estimated parameters. These probabilities allow to devise the GPA test, which is based on generalized 2 × 2 contingency tables (also indicated as co-expression tables) which collect the joint occurrence of zero UMI counts for two genes (see GPA theory, in Supplementary material).

Operatively, for each gene pair, COTAN constructs the observed and expected co-expression tables and then performs the GPA, computing p-value and COEX. See also Tables implementation and Main output.

The two genome-wide matrices of COEX and p-values are COTAN’s main output. Both are n × n, symmetric matrices, where n is the number of genes.

Starting from there, several possibilities are available. COEX can be directly plotted as a heatmap, for all genes or for a selection. One can compute the differentiation indices (GDI and LDI) of genes to restrict attention to those whose expression manifestly depends on cell identity states. Finally, by restricting the COEX matrix to a rectangular submatrix and through a suitable nonlinear transformation, one can embed the genes in the co-expression space and then perform cluster analysis and dimensionality reduction.

GPA and GDI of mouse hippocampus

We assayed COTAN on a scRNA-seq dataset of embryonic hippocampus (25), focusing on a collection of selected Constitutive Genes (CGs) (31), Neural Progenitor Genes (NPGs) (32,33) and Pan-Neuronal Genes (PNGs) (32,33). COTAN’s GPA effectively discriminated between CGs, showing COEX near zero against all genes, and NPGs or PNGs, having positive or negative COEX when tested against one another (Figure 2A). Notably, each NPG positively correlated with other NPGs and negatively with PNGs, and vice-versa, indicating COTAN capability to correctly infer joint or disjoint expression of two genes at single cell level.

We compared COEX to correlations coefficients computed on gene expression levels, obtained by Seurat (34). Figure 2A and B compare heatmaps of COEX and Pearson correlation (Spearman correlation being slightly worse). COEX proved more accurate in discriminating between CGs, NPGs and PNGs, indicating COTAN as better suited in analyzing the co-expression of couples of genes at single cell level. To make the comparison more quantitative, we computed the average of the absolute value of these indices for the two cases of no correlation and correlation. For pairs of genes with at least one CG, the average of absolute values of COEX was 0.0136, while it was 0.0488 and 0.0526 for Pearson and Spearman correlation indices. For the pairs with no CG gene, it was respectively 0.213, 0.236 and 0.223. This is confirmed by correlation p-values (obtained from GPA over 2252 cells for COTAN and from Fisher information over 2080 cells for correlations), with false positive rates (p-value < 10⁻⁴, out of 391 cases) of 1.8%, 29.2% and 31.51% respectively for COTAN, Pearson and Spearman. False negative were 13, 12 and 15 out of 105 cases respectively (see also Supplementary Figure S4 for comparison on negative datasets).

We then compared GDI to the highly variable feature analysis of Seurat (34). GDI efficiently discriminates between CGs, which lay below the median (with two exceptions, Golph3 and Zfr), and NPGs and PNGs, located above the third quartile (Figure 2C). While, highly variable features analysis of Seurat (Figure 2D) was much less precise in discriminating between CGs and cell identity genes (compare Figure 2D to C) with, for example, the two neuronal markers Dcx and Map2 close to Gadph and Sub1.

Gene clustering of mouse cortex

Correlation analysis approaches are commonly used to identify cell clusters with consistent global gene expression. Conversely, gene network analysis tools (27) such as WGCNA (30) use correlation to build co-expression networks and from them infer gene clusters. COTAN does something similar, using COEX as a correlation matrix and building on it to determine clusters of genes. It does not construct a co-expression network as an intermediate step and instead directly groups together genes with similar co-expression patterns against selected genes in the sample.

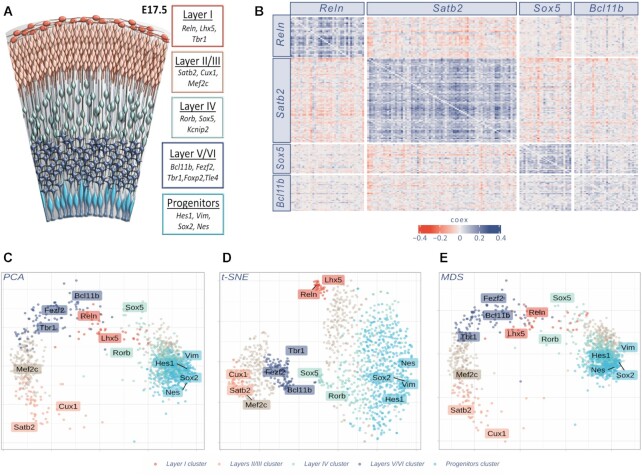
We used COTAN to investigate a dataset of mouse embryonic cortex (4), because the molecular identity of its many cell types is well described (32). We firstly selected from literature (32) robust primary markers for layer I (Reln), layers II/III (Satb2), layer IV (Sox5) and layers V/VI (Bcl11b), see Figure 3A. Then, for each marker we selected its most correlated genes. We used COEX > 0 for all genes and GPA p-value <0.0001 for Satb2, Reln and Sox5, and GPA p-value <0.001 for Bcl11b. This allowed determining a total of 170 secondary layer markers, after removing seven overlapping genes. For all these genes, we plotted an ordered symmetric heatmap of GPA COEX values, grouping the secondary marker genes by the primary marker used to select them (Figure 3B).

Figure 3.

Gene clustering in scRNA-seq analysis. (A) The six layers of differentiated neurons and progenitor cells of late embryonic cortex are depicted in different colors, together with known markers of cell identity (32,40). (B) GPA heatmap of the 170 genes showing strong joint expression with the genes indicated in labels: Reln, Satb2, Sox5 and Bcl11b respectively markers of layers I, II/III, IV and V/VI. The heatmap shows the reciprocal relationship between all genes pairs; significant joint expression is indicated with blue (positive COEX values) while significant disjoint expression is indicated in red (negative COEX values). (C, D) and (E) Different dimensionality reduction plots (Principal Component Analysis, t-distributed Stochastic Neighbour Embedding and Multidimensional Scaling, respectively) of 1235 genes (10% highest LDI). t-SNE plot was performed using initial dimensions 20, maximum iterations 3000, perplexity 30, eta = 200 and theta = 0.4. Colors identify clusters as specified in Investigating marker genes with cluster analysis. Labels correspond to the ten primary markers, together with four other known layer identity markers (Tbr1, Mef2c, Nes and Sox2) as additional landmarks. All plots refer to E17.5 mouse cortex cells (4).

COTAN showed to be well suited to evaluate the co-expression of gene pairs genome-wide. The comparison between groups highlighted an impressive consistency of co-expression inside each group and robust disjoint expression between different groups, with the only exception of Sox5 and Bcl11b groups, which resulted as co-expressed. We believe that the Reln, Satb2 and Sox5/Bcl11b groups represent genuine gene signatures of distinct cortical cell identity and that similar signatures can be found by unbiased approaches.

To refine these results and further investigate gene relations, we considered the co-expression space. In accordance with the recommendations of the method, we restricted the genes for the pattern comparison to a comprehensive set V of layer-associated markers (see Supplementary Figure S7). In analogy to other methods (35) the analysis was guided by few key genes: to build V we selected a shortlist of ten known primary markers of cortical layer identity (32) (Reln and Lhx5 for layer I, Satb2 and Cux1 for layers II/III, Rorb and Sox5 for layer IV, Bcl11b and Fexf2 for layers V/VI and Vim and Hes1 for progenitor cells), together with the top 25 genes most correlated with each of them, for a total of 181 secondary markers, after removing overlapping genes.

For all genes in the dataset, we computed the LDI relative to the genes in V and used it to filter the 10% genes with the highest values, in order to get a meaningful graphical representation and better input data for the subsequent cluster analysis (Supplementary Figure S7).

These differentially expressed genes were embedded inside the co-expression space, where cluster analysis (by Ward’s hierarchical method) and dimensionality reduction were performed (Figure 3C–E). For these plots, genes were colored according to the cluster analysis results (detailed below).

Notably, each gene cluster shows univocal correspondence with all the primary markers of one of the major cortical cell identities at the developmental stage of analysis, proving COTAN ability to gather genes with similar nature regarding cell identity.

Investigating marker genes with cluster analysis

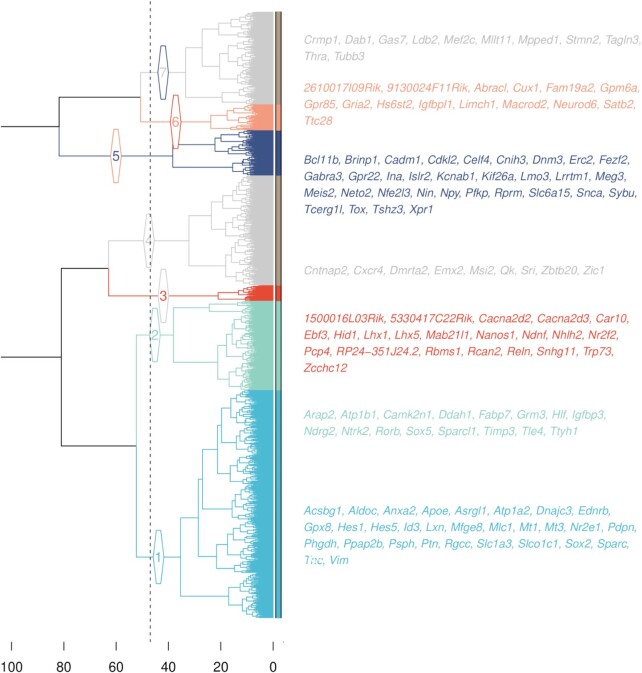
The cluster analysis of the previous section used Ward’s minimum variance hierarchical method (36), based on the distance matrix of the co-expression space. The resulting tree presents a natural cutting gap at seven clusters (possible alternatives being at 2, 4 or 5 clusters—see Figure 4).

Figure 4.

Hierarchical clustering of genes. The dotted line denotes the height of the tree cut forming seven clusters. Branches and leaves colors indicate cluster identity: cluster 1, in light blue, indicates progenitor identity, cluster 2, in aquamarine, indicates layer IV identity, cluster 3, in red, indicates layer I identity, cluster 5, in dark blue, indicates layers V/VI identity and cluster 6, in pink, denotes layers II/III identity. The two clusters in gray (4 and 7) do not contain primary markers and are likely inconsistent with projection neuron identity. The gene names reported are the ones identified as secondary markers (see Gene clustering of mouse cortex).

Each of the five pairs of primary markers was found undivided in a different cluster. From them we assigned the identity of the five clusters and in particular: cluster 1, containing Vim and Hes1, was identified as a set of genes related to progenitors identity; cluster 2, containing Sox5 and Rorb, was identified as genes related to layer IV identity; cluster 3, containing Reln and Lhx5, was identified as genes related to layer I identity; cluster 5, containing Bcl11b and Fezf2, was identified as genes related to layer V/VI identity; finally, cluster 6, containing Cux1 and Satb2, was identified as genes related to layer II/III identity.

The last two clusters did not contain any primary marker. To assess their identity we performed a gene enrichment analysis on the Enrichr web site (37,38). We found that cluster 4 is enriched in septofimbrial nucleus genes, and cluster 7 is enriched in nucleus accumbens genes (in the Allen Brain Atlas up-regulated genes dataset—data tables attached as supplementary files—ABA_up_table_cl4_enrichr.csv and ABA_up_table_cl7_enrichr.csv).

To test the ability of COTAN gene clustering to detect new markers, we compared the five identified clusters with data reported in the literature (5). Results are summarized in Table 1, where we also included the output of the modules identification performed by WGCNA (30), to get a comparison with a common method for gene network analysis and clustering. Of the 48 markers used or identified in (5), 5 are not expressed in the dataset, 10 fell outside the 10% genes selected by LDI and the other 33 entered clustering. We further excluded 6 genes that belonged to the ten primary markers (and are hence clustered correctly by construction). The agreement in the layer assignment was remarkable, with only 5 out of 27 genes assigned to different clusters. In particular two (Htra1 and Plxna4) were assigned to layers different from those identified in (5), and three were assigned to the clusters not associated to layers.

Table 1.

Number of layer markers found by Loo et al. (5) with their respective layer according to the original paper (columns) and according to COTAN and WGCNA (rows). Bold text denotes consistent identification by the two methods. Plxna4 in purple, see text. The second table has the same data as the first one, but excluding all genes belonging to the set V of secondary markers, as these were selected by co-expression with the primary markers and hence their assignment to the correct clusters might be favored by the method. The third table shows the four modules identified by WGCNA. Two of them included the primary markers of layer I and progenitor cells and were so identified. The third one contained no primary marker and five markers by Loo et al. (5). The fourth one included no marker. Several marker genes were outside all four modules

		Markers from Loo et al. (5)
		Layer I	Layers II/III	Layers V/VI	Progenitor
Markers detected by COTAN	Layer I	4
	Layers II/III		3	1
	Layer IV				1
	Layers V/VI			7
	Progenitor				8
	Other cluster			1	2
Markers outside V detected by COTAN	Layer I
	Layers II/III		2	1
	Layer IV				1
	Layers V/VI			5
	Progenitor				5
	Other cluster			1	2
Markers detected by WGCNA	Layer I	2
	Progenitor				7
	Other module 1				5
	Other module 2
	Not in a module	1	4	9	2

It must be noted that the dataset (4) that we analyzed and that of Loo et al. (5) refer to different developmental stages (E17.5 and E14.5 respectively) and this might be a reason for some discrepancies. Consider for example Plxna4, which is a known marker for layers V/VI, and that our analysis assigned instead to layers II/III. A comparison with ISH Allen Brain Atlas in Supplementary Figure S10 shows that Plaxna4 transcript is localized principally in layers V/VI at early stages, but it actually co-localizes with layers II/III at later stages. (Plxna4 was the only one among the five incoherently labelled genes, with known cortical expression pattern in the Allen Brain Atlas database.)

COTAN identified a much higher number of layer markers compared to the conventional methods applied in (5) (see supplementary file STable1.csv). Among all possible new layer markers detected by COTAN, we analyzed the ones presenting nucleic acid binding gene ontology (GO:0003676). Complete tables are attached as supplementary files (STable1.csv and STable2.csv). Supplementary Figure S11 shows the E18.5 ISH collection of the genes available from Allen Brain Atlas website. Most of the genes show ISH pattern consistent with layer identity as identified by COTAN, with few exceptions.

In conclusion, gene co-expression space can extract specific information from the dataset serving as a suitable base for gene clustering and novel cell identity marker identification.

DISCUSSION

We introduced COTAN, a novel method for the analysis of scRNA-seq data with UMI counts. COTAN is based on a flexible model for the probability of zero UMI counts and a generalized contingency table framework for zero/non-zero UMI counts for couples of genes.

We described the application of COTAN to datasets of mouse embryonic hippocampus and cerebral cortex, that show high and documented cell identity diversity.

We found that COTAN is well suited to identify gene pairs which are jointly or disjointly expressed in the sample. This is graphically summarized through heatmap plots (as in Figures 2A and 3B) or numerically with two quantities: an approximate p-value (for a test on independence) and the COEX index, which is a signed measurement of co-expression (positive and blue in the heatmaps for joint expression; negative and red, when the expression of one gene tends to exclude the expression of the other).

COTAN can quantitatively and directly extricate gene relationships, also for lowly expressed genes.

Building on the p-values, COTAN can compute for each gene new scores (GDI and LDI) to assess which genes are differentially expressed. The GDI is a useful tool to detect differentially expressed genes, similarly to Seurat’s variable features, but with constitutive genes and not-constitutive genes more separated (as shown in Figure 2). In addition, with the LDI it is possible to focus this analysis on specific biological features, uncovering information that may be hidden or confounded by whole genome approaches.

Finally, exploiting all the information in the matrix of COEX for many genes (through the co-expression space), COTAN can cluster genes with consistent differential expression at single cell level, allowing to confirm previously known cell-identity markers and enabling the discovery of new ones.

It should be noted that COTAN is most useful when the population of cells is not too heterogeneous, because if there are too many cell types then most genes will be differentially expressed. In those cases the interpretation of results might become difficult.

In conclusion, COTAN is a novel approach that lays the groundwork to directly infer single-cell gene interactome and relationship, and represents an alternative to indirect approaches (30,39) in the panorama of single cell data analysis methods.

DATA AVAILABILITY

Data analysis in this paper was based on two public datasets, as described below. For GPA and GDI of mouse hippocampus we analyzed the cells from time point E16.5 of the mouse dentate gyrus dataset with GEO number GSE104323 (25). Cells removed during cleaning were 33 out of 2285. For Gene clustering of mouse cortex we analyzed the cells from time point E17.5 of the mouse embryonic cortex dataset with GEO number GSM2861514 (4). Cells removed during cleaning were 17 out of 880.

The COTAN package is publicly available on GitHub at https://github.com/seriph78/COTAN. All data and analysis described in this manuscript are available as a repository at https://github.com/seriph78/Cotan_paper or as a web site at https://seriph78.github.io/Cotan_paper/.

SUPPLEMENTARY DATA

Supplementary Data are available at NARGAB Online.

FUNDING

AIRC [project [to MHC] (grant number IG 23539).

Conflict of interest statement. None declared.