Abstract
Advanced perfusion‐weighted imaging (PWI) methods that combine gradient echo (GE) and spin echo (SE) data are important tools for the study of brain tumours. In PWI, single‐shot, EPI‐based methods have been widely used due to their relatively high imaging speed. However, when used with increasing spatial resolution, single‐shot EPI methods often show limitations in whole‐brain coverage for multi‐contrast applications. To overcome this limitation, this work employs a new version of EPI with keyhole (EPIK) to provide five echoes: two with GEs, two with mixed GESE and one with SE; the sequence is termed “GESE‐EPIK.” The performance of GESE‐EPIK is evaluated against its nearest relative, EPI, in terms of the temporal signal‐to‐noise ratio (tSNR). Here, data from brain tumour patients were acquired using a hybrid 3T MR‐BrainPET scanner.
GESE‐EPIK resulted in reduced susceptibility artefacts, shorter TEs for the five echoes and increased brain coverage when compared to EPI. Moreover, compared to EPI, EPIK achieved a comparable tSNR for the first and second echoes and significantly higher tSNR for other echoes.
A new method to obtain multi‐echo GE and SE data with shorter TEs and increased brain coverage is demonstrated. As proposed here, the workflow can be shortened and the integration of multimodal clinical MR‐PET studies can be facilitated.
Keywords: EPIK, gradient echo/spin echo, image distortion, MR‐PET, multi‐contrast
1. INTRODUCTION
Dynamic magnetic resonance imaging using a contrast agent is a methodology often used to evaluate perfusion in tumours or stroke and to study blood–brain‐barrier disruption in tumours, using dynamic susceptibility contrast (DSC) and dynamic contrast enhanced (DCE) methods. In DSC, the changes in T 2 */T 2 are tracked and related to cerebral blood flow (CBF) and volume (CBV), while in DCE the changes in T 1 are monitored and related to permeability and the extravascular‐extracellular space (EES), that is, to the volume transfer constant (K trans) and the ESS volume fraction (v e). It has been shown that parametric images extracted from both DSC and DCE are relevant for the characterisation of tumours (Artzi et al., 2015). However, current clinical methodology used to acquire these parametric images is based on two independent pulse sequences—one for DSC and one for DCE (Bergamino, Bonzano, Levrero, Mancardi, & Roccatagliata, 2014; Ostergaard, 2005; Shiroishi et al., 2015; Yankeelov & Gore, 2009). These sequences are single‐shot, gradient echo (GE) EPI and spoiled GE, respectively. Importantly, for this application, images acquired with the two sequences need to be coregistered, and herein lies two of the biggest confounds: geometric distortions and signal dropout are sequence dependent. The use of single‐shot pulse sequences for DSC GE‐EPI suffers from errors due to contrast agent leakage. This is often addressed with a preload injection prior to the actual measurement, which requires increased measurement time and an additional contrast agent injection (Boxerman et al., 2012; Boxerman, Schmainda, & Weisskoff, 2006; Knutsson et al., 2014; Paulson & Schmainda, 2008). This approach reduces uncertainties, but does not completely eliminate them (Quarles, Ward, & Schmainda, 2005). Conversely, T 1‐weighted imaging using spoiled GE is used for DCE, which requires balancing a trade‐off between temporal resolution and spatial resolution/brain coverage (Bergamino et al., 2014).
In order to overcome the need for two independent sequences and to address some of the associated drawbacks, methods based on double‐echo GE‐EPI sequences have been proposed (Vonken, van Osch, Bakker, & Viergever, 1999). By combining both echoes, the T 1‐shortening resulting from contrast agent extravasation can be corrected. This approach is potentially of great importance for avoiding a prebolus injection, thereby reducing the amount of injected gadolinium (Quarles et al., 2005; Vonken et al., 1999), as well as reducing measurement times. Moreover, the two echoes can also be combined to extrapolate the signal at zero echo time and consequently obtain a DCE time series (Vonken et al., 1999). The work presented in (Quarles, Gore, Xu, & Yankeelov, 2012) compared the DCE kinetic parameters obtained from double‐echo DSC and independent DCE measurement using small animals and found good agreement between the two measurements. Furthermore, the use of a double‐echo sequence also showed good agreement in permeability and perfusion measurements in phantom studies (Kim et al., 2004).
A more thorough and versatile investigation of tumours, including obtaining information about the vasculature, can be carried out by combining GE and spin echo (SE) signals. For this purpose, a method using a refocusing pulse after the first two GEs to obtain an additional image including spin‐echo contrast has been proposed (Schmiedeskamp et al., 2012). The method is the so‐called GE, spin‐echo (GESE) DSC method or spin and gradient‐echo (SAGE; Skinner et al., 2014). GESE DSC has been successfully demonstrated in humans in different organs (Skinner et al., 2014) and small animals (Stokes, Skinner, & Quarles, 2014). Despite the lower signal‐to‐noise ratio (SNR) of the SE when compared to the GE in this sequence, SE imaging is more sensitive to capillary‐sized vascular structures than GE imaging because the GE is sensitive to all vessel sizes (Dennie et al., 1998). Using vessel size imaging (VSI) it has been shown that information can be derived from simultaneously acquired GE and SE data (Donahue et al., 2000; Kiselev, Strecker, Ziyeh, Speck, & Hennig, 2005; Tropres et al., 2001), where the calculated vessel sizes have been previously validated with histology (Kellner et al., 2015; Lemasson et al., 2013). Nevertheless, similar to the GE contrast, it is also necessary to correct T 1 contrast agent leakage effects in SE imaging in order to avoid quantification errors (Emblem et al., 2013; Schmiedeskamp, Straka, Newbould, et al., 2012; Stokes & Quarles, 2016).
The recently proposed multi‐echo approaches using GE and SE information to evaluate tumours have clinical potential due to the fact that they inherently provide information on perfusion, permeability and vessel architecture (Schmiedeskamp, Straka, Newbould, et al., 2012). However, this approach is also hindered by limitations such as susceptibility artefacts and geometric distortions resulting from the single‐shot EPI readout. In particular, these limitations can significantly hamper the quantification of perfusion measures in tumours located near the air cavities, thereby reducing diagnostic applicability. Additionally, with multi‐echo approaches employing a higher number of echoes, a trade‐off between temporal resolution, brain coverage and spatial resolution needs to be taken into consideration. Moreover, in previous works (Schmiedeskamp, Straka, Newbould, et al., 2012; Stokes & Quarles, 2016), the arterial input function (AIF) was defined manually which is a time‐consuming procedure and is prone to inter‐user variability. Here, an automatic method to obtain an AIF, exploiting multi‐echo information, based on thresholds of quantity‐of‐merit to define the best AIF has been used (Newton, Pruthi, Stokes, Skinner, & Quarles, 2016) in order to reduced unwanted variance.
The work presented here demonstrates a new, alternative method for GESE‐DSC using EPI with keyhole (EPIK). Single‐contrast, GE EPIK (Shah & Zilles, 2004a and 2004b) had been previously validated at both 1.5T (Zaitsev, Zilles, & Shah, 2001) and 3T (Yun, Reske, Vahedipour, Warbrick, & Shah, 2013; Yun & Shah, 2017) Moreover, dual‐contrast EPIK has also been demonstrated in a proof‐of‐concept to study dynamic contrast‐enhanced perfusion with application to tumours (Zaitsev et al., 2005). When compared to single‐shot EPI, EPIK has been proven to provide a higher temporal resolution, a sharper point spread function (PSF) and enhanced robustness against susceptibility distortions and signal dropout, while maintaining the capability to track dynamic signal changes in fMRI or perfusion MRI. By virtue of the fact that EPIK is a multi‐shot technique, it achieves these apparently contradictory goals by employing a keyhole region which is acquired in each shot and a sparse region which under‐samples k‐space in any given shot. A higher bandwidth in the phase‐encode direction is thus ensured, leading to robustness against signal dropout as well as an increase in the temporal resolution. Dynamic processes can be followed with high fidelity by virtue of a sliding window which uses only lines acquired in the last n shots, for example, 3 as employed here.
The original GE‐EPIK scheme has been extended to a GESE version to provide five echoes: two with GEs, two with mixed GESE and one with SE (i.e., GESE‐EPIK). GESE‐EPIK can be accelerated using parallel imaging and partial Fourier techniques to achieve an even higher spatial resolution and better brain coverage. Furthermore, the present work also employs an automated analysis pipeline using clustering of multi‐echo data to define an AIF. This approach was tested in a cohort of brain tumour patients in a hybrid MR‐PET study. The automated analysis pipeline enabled parametric images to be obtained with minimal user interaction, thus improving reproducibility and reducing workload. These attributes are highly desirable features in clinical applications. The automated pipeline, described briefly in the Appendix, includes the processing of PET data, which indicates its applicability for any type of DSC‐MRI performed in the hybrid MR‐PET system.
2. MATERIALS AND METHODS
2.1. Accelerated GESE‐EPIK
The EPIK scheme combines a more frequent sampling of the central portion of k‐space, often termed the “keyhole,” with a continuous, interleaved update of high spatial‐frequency information along with a sliding window. Figure 1a shows the schematic representation of the k‐space trajectory illustrative of a three‐shot EPIK sequence. Each measurement scans the central k‐space region (k‐space keyhole) completely with Δk y = 1/FOV, while scanning the peripheral k‐space regions (k‐space sparse) sparsely with Δk y’ = 3/FOV. Using the notation M p(i), where Mp labels shots and i is an index for k‐space, the sequence of measurements for peripheral k‐space runs as follows: M1(1), M2(2), M3(3i), M4(1), M5(2), …. That is, the first line numbers to be sampled in the first, second, and third scans are 1, 2, and 3, respectively. The line number becomes 1 again at the fourth scan. The missing k‐space lines, for any given k‐space, (see Figure 1a) can be completed by sharing the peripheral data from three consecutive scans. Here, the keyhole region was set as 1/4 of the entire k‐space. In this way, the total number of phase encoding lines required in EPIK is 1/2 (i.e., 1/4 + [3/4]/3) of that for an otherwise comparable EPI sequence. When a fourth scan is acquired, the data from the first scan are discarded and thus the periphery is updated by the application of this sliding window. This “discard and update” feature of EPIK is extremely important as it ensures that new data are introduced in a short timescale, thereby reducing temporal correlations in the images very significantly; as long as the update is faster than the dynamic changes under investigation, the changes can be tracked with high fidelity.
FIGURE 1.
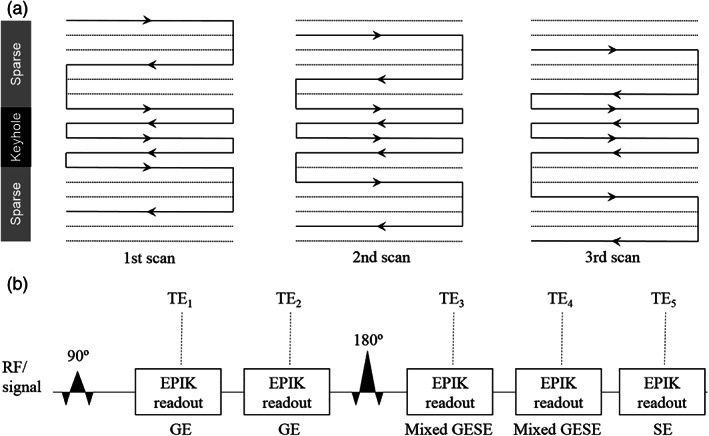
(a) A schematic depiction of the 3‐shot EPIK k‐space trajectory used as a basis for further development. The solid and dotted lines indicate the k‐space line positions to sample or skip, respectively, at each temporal scan. The lines in the keyhole region are sampled in every measurement. (b) Schematic sequence representation for GESE‐EPIK with five echoes: Two with GEs, two with mixed GESE and one with SE
The original EPIK scheme was further developed here to offer five echoes (GESE‐EPIK) as shown in Figure 1b. A 90° pulse was applied and two GEs (TE1/TE2) were acquired, followed by a refocusing 180° RF pulse. Three more echoes were then acquired (TE3/TE4/TE5), whereby the third and fourth are mixed GESE echoes and the last echo is an SE. The GESE‐EPIK scheme was accelerated by partial Fourier (6/8) and parallel imaging techniques (R = 2). In this way, the total number of phase encoding lines is reduced to 3/16 of a comparable, full k‐space EPI sequence. For this work, the above configuration was deployed on a 3T MR‐BrainPET (Siemens Medical Solutions, Erlangen, Germany) scanner with an eight‐channel phased‐array, receive coil from the manufacturer; a 16‐rung birdcage coil was used for RF transmission.
2.2. Image reconstruction
For the correction of even‐odd line phase differences, three nonphase‐encoded navigator echoes were acquired in GESE‐EPIK. To ensure that the phase increases smoothly when sharing data from the sparse regions, echo time shifting (ETS) was integrated in the accelerated GESE‐EPIK acquisition (Butts, Riederer, Ehman, Thompson, & Jack, 1994). The final reconstructed images for accelerated GESE‐EPIK were obtained by first performing line‐sharing for the sparse region of EPIK, then applying GRAPPA reconstruction (Griswold et al., 2002; Schmiedeskamp, Straka, Newbould, et al., 2012) to the under‐sampled k‐space lines, and lastly, by computing the partial‐Fourier‐missing k‐space lines with the projection onto a convex sets (POCS) algorithm (Haacke, Lindskogj, & Lin, 1969).
2.3. Temporal signal‐to‐noise analysis
In order to evaluate the temporal SNR (tSNR) of GESE‐EPIK, a measurement with 100 repetitions was acquired with a healthy volunteer using GESE‐EPIK and GESE‐EPI (without administration of contrast agent). For this measurement, the in‐plane resolution of both sequences was fixed to 2.50 × 2.50 mm2 (matrix size: 96 × 96) and the slice thickness was 3 mm. A TR of 1,500 ms was used and the minimum echo time possible in each sequence was employed (EPIK: TE 1/TE 2/TE 3/TE 4/TE 5 = 11/27/50/66/80 ms; EPI: TE 1/TE 2/TE 3/TE 4/TE 5 = 12/35/65/88/109 ms). The same acceleration factors—e.g., twofold parallel imaging and a partial Fourier of 6/8—were used in both EPIK and EPI. It is noted here that any acceleration technique that is EPI‐compatible is also EPIK‐compatible therefore the choice of the above parameters is exemplary only. Further, the maximum possible number of slices achievable by each imaging sequence was employed; this was 14 for EPIK and 10 for EPI representing a 40% increased coverage for EPIK for the same TR. The tSNR maps for each measurement were computed by calculating the ratio of the signal average (S) to the signal standard deviation (σ) per voxel over time (i.e., tSNR = S/σ). The tSNR ratios for EPIK and EPI were calculated in order to compare the performance of the two sequences.
2.4. MRI acquisitions
Perfusion weighted images were acquired using the GESE‐EPIK and GESE‐EPI as described above. The employed imaging parameters were also the same as above. For each subject, Gadoteric acid (Dotarem Guerbet) was injected with a dose of 0.1 mmol/kg of body weight and 100 volumes were acquired in order to track dynamic signal changes induced by the contrast agent for each sequence; 0.1 mmol/kg of contrast agent was injected prior to GESE‐EPIK and prior to GESE‐EPI. The injection was performed automatically with a power injector (Injektron 82 MRT Medtron AG) at a flow rate of 5 mL/s. The clinical protocol consisted of T 1‐ and T 2‐weighted anatomical imaging (precontrast), perfusion‐weighted imaging (PWI) using both sequences (contrast injection) and T 1‐weighted imaging (postcontrast). During each injection, GESE‐EPIK and GESE‐EPI data were acquired whereby the EPIK measurements preceded the EPI measurements.
2.5. Subjects
For sequence comparison, data were acquired from a young healthy volunteer only; no contrast agent was administered. For the clinical study, eight patients with brain tumours participated. For the healthy volunteer and the patients, following a complete description of the study, written informed consent was obtained prior to scanning. The local institutional review board (IRB: RWTH Aachen University, Germany) approved the study protocols, screening questionnaires, and consent forms.
2.6. Postprocessing and image analysis
2.6.1. Signal conversion
In order to obtain the ΔR 2* signal time courses from GESE‐EPIK, the first two echoes were combined to account for T 1 effects in accordance with previous work (Vonken et al., 1999):
where, S TE1 0 and S TE2 0 are the baseline signals and S TE1(t) and S TE2(t) are the time series of the first and second echoes, respectively. Furthermore, the first two echoes can be also combined to obtain a T 1‐weighted signal by extrapolating the signal to TE = 0 (Quarles et al., 2012; Vonken et al., 1999):
In the case of ΔR 2, T 1 should be also considered (Schmiedeskamp, Straka, Newbould, et al., 2012; Stokes & Quarles, 2016). In this work, due to its simplicity and fast computation, the analytical solution proposed in (Stokes & Quarles, 2016) was employed. Thus, to calculate ΔR 2, the extrapolated signal to TE = 0 was used:
2.6.2. Arterial input function estimation
To obtain parametric images, an AIF is required (Calamante, 2013). To achieve this, the steps and cluster algorithm proposed by Yin, Sun, Yang, and Guo (2015) was adapted to the multi‐contrast approach and applied to the T 1‐insensitive ΔR 2* data (Bleeker et al., 2011; Murase, Kikuchi, Miki, Shimizu, & Ikezoe, 2001; Newton et al., 2016; Shi & Malik, 2000). A detailed description of how the AIF was estimated is described in the Appendix.
2.6.3. Parametric images calculation
Seven parametric images were computed from the GESE‐EPIK data. After defining the required AIF, CBV was computed for both ΔR 2* and ΔR 2 corrected for leakage. CBF was calculated using the maximum of the tissue impulse response function from the circular singular value decomposition (SVD) for each ΔR 2* and ΔR 2. Mean transit time (MTT) was derived as the ratio between the CBF and CBV (Willats & Calamante, 2013). Vessel size weighted images were obtained based on the ratio between the integrals of ΔR 2* and ΔR 2 (Kiselev et al., 2005; Schmiedeskamp, Straka, Newbould, et al., 2012). All data analysis was performed using MATLAB (MathWorks, Natick, MA).
2.7. PET acquisition
Simultaneously with the MR measurements, a [18F]‐FET PET scan was carried out in the hybrid instrument. To enable this, an intravenous injection of 3 MBq of [18F]‐FET/kg of body weight was injected (Filss et al., 2014). PET data were reconstructed using OP‐OSEM3D software with four subsets and 32 iterations, and the images were normalised and corrected for attenuation, scatter, dead time and randoms. The reconstructed images have an isotropic voxel size of 1.25 mm3 with a matrix size of 256 × 256 × 153. Note that, the BrainPET is a head only high‐resolution PET insert with an isotropic centre resolution of 3 mm (Herzog et al., 2011).
2.8. Tumour delineation
[18F]‐FET PET was used as the clinical reference to delineate the tumour volume‐of‐interest (VOI) in the summed image from 20 to 40 min p.i. by a 3D auto‐contouring process using a tumour‐to‐brain ratio (TBR) of ≥1.6 (Pauleit et al., 2005). Based on the tumour VOI, region analysis was performed on the PWI data.
3. RESULTS
3.1. tSNR analysis
Figure 2 shows the computed tSNR maps from a healthy subject. A representative slice for both EPI and EPIK is shown for each of the five echo times. For the later echoes, the increased tSNR of EPIK over EPI is more evident due to higher signal levels resulting from the shorter echo times inherent in the EPIK acquisition scheme. In addition, EPIK facilitated the acquisition of four slices more than EPI for the same TR.
FIGURE 2.
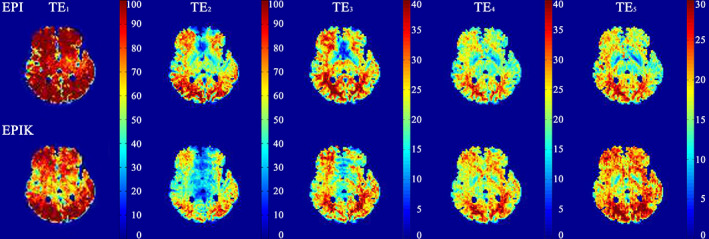
A representative slice illustrating the tSNR of EPIK and EPI for the five different echoes
Figure 3 shows the ratio of tSNR between EPIK and EPI for the same slice. For the first echo (see the leftmost figure), the tSNR of EPIK is slightly reduced when compared to EPI, presenting whole brain tSNR ratio histogram at 0.8; note that the TE for EPIK/EPI was 11/12 ms. For the second echo, the tSNR of EPIK is also slightly reduced compared to that of EPI, with the histogram peak presenting at 0.85. For the other later echoes, the tSNRs of EPIK are significantly higher than those obtained with EPI, with a histogram peak of 1.26 for the last echo; in some regions of the brain the tSNR of EPIK is three times higher than that of EPI, which is a direct consequence of the use of shorter TEs in EPIK. Furthermore, from the first and second echo results, it was observed that the tSNRs of EPIK were much higher than those of EPI, particularly around the frontal regions; for other brain regions, the tSNRs were similar for both methods. This result underscores the fact that signal dropout caused by the susceptibility differences in the frontal regions was much less in EPIK than in EPI.
FIGURE 3.
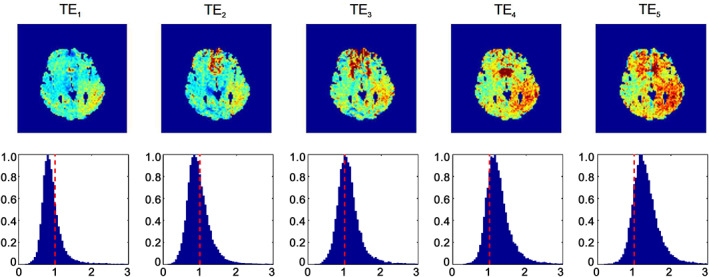
Illustration of the tSNR ratio of EPIK and EPI. From left to right: The echo number increases from 1 to 5, whereby the last echo is a spin echo. On the top row, the tSNR ratio for a representative slice is shown and on the bottom row, the tSNR ratio histogram for the whole brain is depicted
3.2. Reconstructed images and contrast tracking
Figure 4a shows the reconstructed images for all five echoes from EPIK at baseline (top row) and at peak contrast passage (bottom row). Figure 4b, shows the time course of the signal intensity depicting the arrival of the contrast agent in a single, representative grey matter voxel. For all echo times, it was possible to clearly track the dynamic signal changes induced by the contrast agent, even though a higher signal drop was found in earlier echoes when compared to the later echoes. These results are in agreement with the results obtained with the standard EPI technique proposed by Schmiedeskamp, Straka, Newbould, et al. (2012). However, the EPIK data presented here have a higher spatial resolution, significantly better brain coverage, fewer susceptibility artefacts and higher SNRs due to the shorter echo times that are achievable with EPIK. A specific slice location was chosen to best demonstrate the reduced susceptibility artefacts in EPIK. Figure 5 depicts the reconstructed slice from EPI and EPIK. A substantial reduction of geometric distortions (i.e., signal drop‐out due to susceptibility differences) can be observed in the EPIK acquisition and is marked by the white arrows.
FIGURE 4.
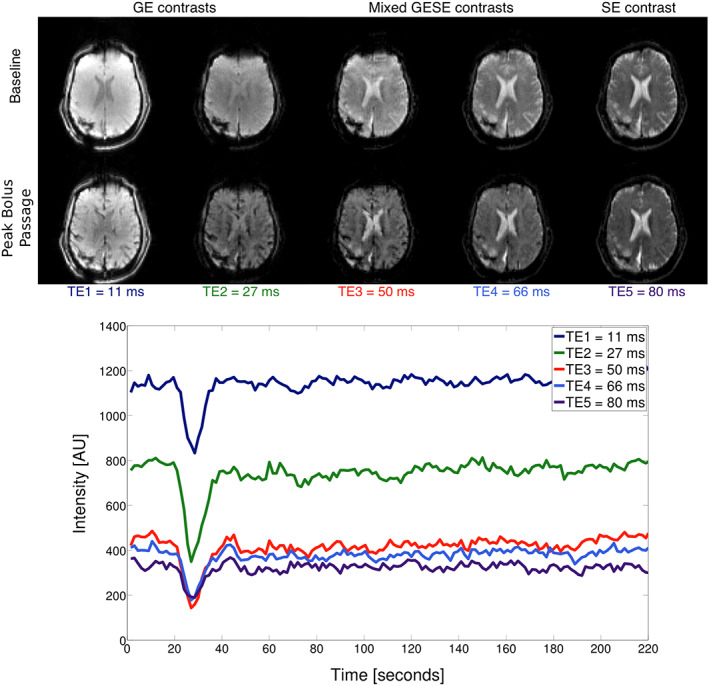
(a) GESE‐EPIK images with GE, mixed GESE and SE contrast. The top row shows the five echo images at the baseline and the bottom row shows the images at the peak bolus passage. (b) Signal intensity time course for the different echoes showing the arrival of the contrast agent bolus
FIGURE 5.
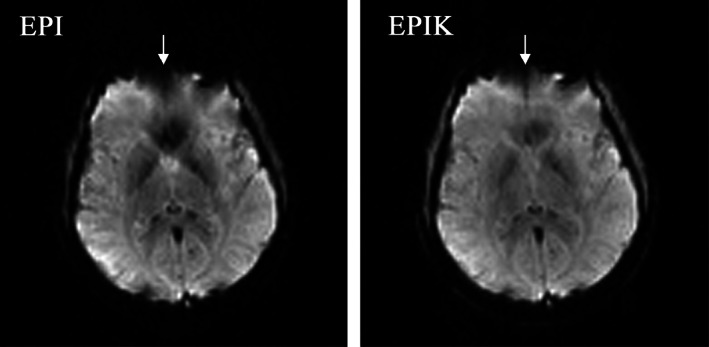
Reconstructed image from (a) EPI and (b) EPIK. The selected slice depicts the performance of EPIK in the reduction of susceptibility artefacts. The differences are marked with the white arrows
3.3. Multi‐contrast data
By using a combination of the echoes, it is possible to obtain several contrasts based on T 2*‐ and T 2‐weighted curves corrected for the T 1 effect. Figure 6 (left) presents the T 2*‐weighted time series for the first echo, where it can be observed that the leakage effect due to T 1 exists; this effect is mitigated following the correction procedure as described above. The same effect is observed in the T 2‐weighted time series but with a lower amplitude. Based on the combination of the first two echoes, DCE contrast can be obtained by interpolating to zero echo time. Figure 6 (right) presents the zero echo time interpolated signal enhancement for a pixel in healthy tissue and one in the tumour.
FIGURE 6.
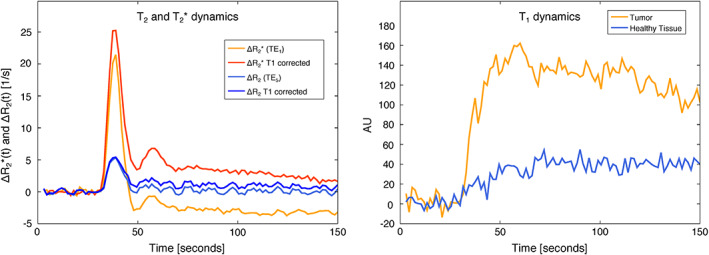
Left: the T 2*‐ and T 2‐weighted time course data with and without T 1 correction are depicted. Right: The T 1‐weighted time course is presented
3.4. MR‐PET and parametric images
Figure 7 presents tumour delineation based on the PET data as well as on the GESE‐EPIK parametric images for a randomly chosen subject (subject 4). These results were obtained using the AIF determination method described in the Appendix. The values of CBF from the GE data are higher than those from the SE data. The same effect was observed for the CBV data. The hottest voxels from the FET‐PET image are not in agreement with the maximum value of the perfusion weighted images either in GE and SE, suggesting that the two contrasts present different information. In addition, vessel size images are also presented where it is possible to observe different vessel organisation in the tumour when compared to contralateral areas.
FIGURE 7.
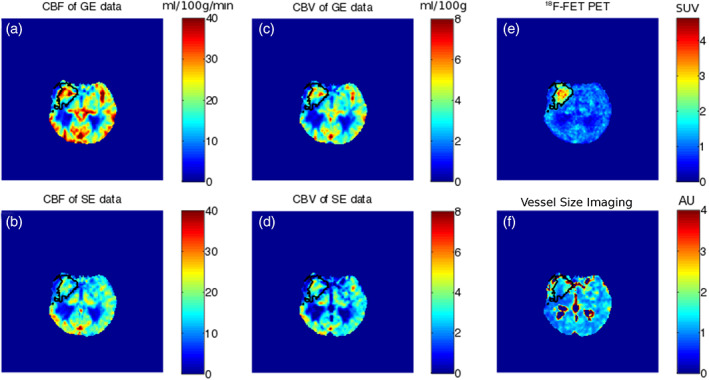
Multi‐parametric images obtained in this study to evaluate vessel distribution. (a,b) CBF for GE and SE data, (c,d) CBV for GE and SE data, (e) PET data and (f) vessel size image
4. DISCUSSION
The work presented here demonstrates a significantly improved methodology to obtain advanced perfusion measurements using multi‐echo, GESE‐EPIK. To address the trade‐off between the spatial/temporal resolution and brain coverage, the proposed protocol uses multi‐echo, GESE‐EPIK in order to obtain much better brain coverage than EPI and with shorter TEs for the five echoes under clinical constraint. Furthermore, the multi‐echo sequence also allows one to perform leakage correction for both GE and SE, reducing the number of injections and/or amount of contrast agent injected. The method was tested and demonstrated in a healthy subject (no contrast agent injected) before being used on patients in a 3T hybrid MR‐PET scanner using an automatic pipeline to determine the AIF.
In contrast to the original, FLASH‐based keyhole imaging technique (Feinberg & Oshio, 1994), which only acquires peripheral k‐space data once during the measurement, one important feature of EPIK is its continuous update of the periphery of the k‐space (Yun & Shah, 2017). In EPIK, only small parts of peripheral k‐space are shared for a very limited number of scans. This fact implies that the correlation of k‐space through the time‐series images is not substantial, meaning that dynamic contrast changes can be followed with high fidelity. Crucially, the keyhole regions are updated at every scan, which preserves most of the SNR and features for every scan. In our early work (Yun et al., 2013; Yun & Shah, 2017), the issue of autocorrelation in the data was thoroughly investigated with an MRI simulator as well as with real fMRI data and was found to be nonsignificant. Considering the fact that the behaviour of the signal changes in DSC‐MRI is also relatively smooth, as with the BOLD signal changes in our previous work, the impact of autocorrelation was not significant. From the sequence point of view, when compared to conventional multi‐echo and single‐shot EPI methods used in the literature (Schmiedeskamp, Straka, Newbould, et al., 2012; Skinner et al., 2014), EPIK enabled the acquisition of data with a higher spatial and temporal resolution, shorter echo times and an increased number of slices, which is mainly attributed to its sampling strategy in combination with partial Fourier encoding. If partial Fourier encoding is employed with EPI, the shorter echo time advantage of EPIK would be partly negated but at the expense of a somewhat lower SNR for EPI; the temporal resolution advantage of EPIK would remain given that, for the example presented here, three EPIK images can be acquired in the time it takes EPI to acquire two. It is possible that the slightly reduced tSNR ratio at earlier echoes in EPIK is due to the fact that EPIK is more sensitive to motion (Zaitsev et al., 2001). Nevertheless, the slight reduction of tSNR did not lead to any substantial impact on the tracking of dynamic signal changes (see Figure 4). On the contrary, at the later echoes (third, fourth, and fifth echoes), where much shorter TEs were achieved in EPIK than in EPI, significantly higher tSNRs was observed in EPIK. The advantage of the shorter TE in EPIK is more evident in the later echoes, where the tSNR benefit can be, maximally, three times higher for the last echo (Figure 3). For the sake of completeness, it is noted here that the “sparse factor” in EPIK can also be optimised in relation to the timescale of the dynamic process to be captured; this could, potentially, lead to even shorter TEs. Furthermore, as a consequence of longer readout durations, single‐shot EPI images are more prone to severe image distortions. By acquiring a reduced number of lines using EPIK, the readout durations are shorter and the distortions are also concomitantly reduced. This was experimentally verified, once again, for the first and second echoes where EPIK suffers less signal dropout around the frontal lobes, while EPI showed significantly lower tSNR (see Figure 3). An alternative method to reduce the readout time and echo time is to use a multi‐shot approach, as already suggested in the multi‐echo GE DSC context (Newbould et al., 2007). The method proposed here differs from the multi‐shot approach as it uses the keyhole paradigm to sample the central k‐space area in each repetition. Compared to a standard multi‐shot approach, GESE‐EPIK as proposed here is less sensitive to motion artefacts (the central line of k‐space is sampled in each shot) and has a higher SNR/unit time because the fully‐sampled keyhole dominates the SNR.
In order to achieve clinical relevance, the proposed GESE‐EPIK sequence uses a temporal resolution that is currently the “standard” in clinics with a TR of 1,500 ms and a moderate parallel imaging factor of two; this is to be compared to a longer TR of 1,800 ms and parallel imaging factor of three that is used in EPI (Bjornerud, Sorensen, Mouridsen, & Emblem, 2011; Schmiedeskamp, Straka, Newbould, et al., 2012) leading to a higher g‐factor penalty. Maintaining similar brain coverage (14 slices; 3 mm slice thickness), even though a reduced parallel imaging factor was used by taking advantage of partial Fourier and EPIK schemes, the spatial resolution was increased from 2.85 × 2.85 mm2 (SAGE matrix size: 86 × 86 and a parallel imaging acceleration factor of 3) to 2.50 × 2.50 mm2 (GESE‐EPIK matrix size: 96 × 96 and a parallel imaging acceleration factor of 2). With GESE‐EPIK, the advantageous volume coverage, when compared to EPI, can still be improved further in order to obtain full brain coverage. This can be achieved by using multiband excitation and refocusing pulses as suggested in Eichner et al. (2014). It is important to note that any acceleration technique that can be applied to EPI can also be applied to EPIK, and thus the differential advantages of EPIK over EPI will remain.
Parametric images obtained by contrast bolus tracking are influenced by both T 1 effects and definition of the AIF. In order to address the issue of T 1 effects, the method proposed by Stokes and Quarles (2016) was used here. The simplified analytical method is considerably faster than the nonlinear fitting approach (Schmiedeskamp, Straka, Newbould, et al., 2012), making it advantageous for processing data in a clinical setting. It also considers the slice profile, constant over the acquisition (Schmiedeskamp, Straka, & Bammer, 2012; Stokes & Quarles, 2016), for the calculation of ΔR 2* and ΔR 2. In this work, five echoes, with considerably shorter TEs for the latter three echoes, were obtained to demonstrate the flexibility of the proposed GESE‐EPIK method. In order to address AIF definition, the automated clustering method proposed by Yin, Sun, et al., 2015 was employed due to its relatively fast computation speed and high accuracy (Yin, Sun, et al. (2015); Mouridsen, Christensen, Gyldensted, & Ostergaard, 2006; Yin, Yang, & Guo, 2015). In the original algorithm, the slice with the middle cerebral artery (MCA) was used to define the AIF. However, with a reduced number of slices, depending on the location of the tumour, it is not guaranteed that the exact MCA plane will be acquired. In order to account for such limitations, not only a single slice, but also a group of slices near the MCA was considered in the constraining steps and the cluster algorithm. This could potentially introduce errors due to the inclusion of more voxels than using just the slice of interest. Nevertheless, the metric used to choose between the AIF clusters takes into account the sharpness, time to peak and peak value (PV) of the curves in order to avoid an erroneous AIF. This methodology was applied in tumour patients assuming a normal vascular structure and needs further validation in case of stroke where proximal arterial occlusion can occur. Methods that avoid using an AIF could also be a possible alternative to the proposed method (Eichner et al., 2014; Enmi et al., 2012). The investigation thereof is, however, beyond the scope of this work.
In this work, parametric images were calculated in an automated fashion (see Supporting Information Figure S1), which is crucial for clinical practice as it reduces user variability. By including PET data in the pipeline, multimodal approaches can be fully exploited, which is an important factor given the increasing availability of hybrid MR‐PET instrumentation in the clinic. With EPIK, an integer fraction (EPIK: 2.5 × 2.5 mm2) of the in‐plane voxel size of the BrainPET scanner (PET: 1.25 × 1.25 mm2) is obtained while, at the same time, achieving better brain coverage than that possible using methods presented in the literature (Schmiedeskamp, Straka, Newbould, et al., 2012). Matching to a multiple of the in‐plane pixel size of the PET data will help to facilitate multimodal approaches by employing image combination and avoiding interpolation errors. The 3T BrainPET scanner used in this work is a high‐resolution scanner and is not widely available, but the methodology presented here is fully compatible with commercially available hybrid MR‐PET scanners. Here, the in‐plane resolution of EPIK is similar to the desired BrainPET resolution (3 mm3). In general, commercially available MR‐PET scanners have lower resolution (~5 mm3) than the brain‐dedicated machine used here (~3 mm3); in such a case EPIK would provide, comparatively, much higher resolution than PET.
The combined MR‐PET analysis of brain tumours has been shown to be highly relevant for the characterisation of tumour grade (Sacconi et al., 2016). In particular, PWI has been used as a complementary method to PET (Sacconi et al., 2016). Depending on the tumour type, PWI has been shown to provide different information that is not in agreement with the clinical standard for brain tumours, the [18F]‐FET PET scan [40, 42, 52], (Tropres et al., 2001; Sari, Erlandsson, & Thielemans, 2015; Stokes, Skinner, & Quarles, 2014), and in our Institute (Cicone et al., 2015; Filss et al., 2014). The introduction of the proposed GESE‐EPIK sequence, which provides extra information regarding the microvasculature, will be further explored and compared with [18F]‐FET PET (Figure 7), whereby the matched voxel size will help to reduce interpolation errors. In addition, the reduced distortions and signal dropout inherent to EPIK also presents advantages, not only in standalone MRI studies, but also in combined MR‐PET studies. Reduced distortions at 3T have been demonstrated in our early work (Yun et al., 2013; Yun & Shah, 2017). In the present study, this was also verified by the results showing GESE‐EPIK has a higher tSNR, particularly for the frontal regions in the first and second echo data. This was in line with our previous work and might yield new directions with which to investigate the efficacy of therapies by means of vessel architecture (Stokes & Quarles, 2016). Furthermore, the multi‐echo capability of GESE‐EPIK allows computation of a T 1‐corrected time series data that points in the direction of obviating the need for a prebolus injection to correct for leakage effects (Figure 6). This is of great importance, in particular for the region of the tumour where the blood‐brain barrier is disrupted, and might allow for a reduction in measurement time or the introduction of new sequences in the clinical protocols. In addition to the standard PWI metrics, obtaining DCE time courses opens up the possibility of calculating the permeability characteristics of the tumour (Calamante, 2013; Caldeira et al., 2015; Schmiedeskamp et al., 2013; Schmiedeskamp, Straka, & Bammer, 2012; Skinner, Moots, Ayers, & Quarles, 2016). Combination of GESE‐EPIK and MR‐PET data, such as combined AIF estimation (Caldeira et al., 2015; Poulin et al., 2013; Silva et al., 2015), PET modelling (Erlandsson et al., 2015; Sari, Erlandsson, & Thielemans, 2015) and angiogenic modelling (Hutterer, Hattingen, Palm, Proescholdt, & Hau, 2015) can be further investigated using GESE‐EPIK and the high‐resolution, hybrid BrainPET, avoiding co‐registration and interpolation errors.
In conclusion, the GESE‐EPIK sequence was implemented and validated at 3T in a normal healthy volunteer, in the absence of contrast agent injection, and was subsequently used in a cohort of brain tumour patients, including administration of a contrast agent, to exploit the hybrid MR‐PET capabilities of the 3T BrainPET scanner. The GESE‐EPIK approach outperforms GESE‐EPI in terms of achieving shorter echo times for the five echoes; the TEs of the last echoes were 80 and 109 ms for EPIK and EPI, respectively. The use of shorter TEs in EPIK led to a shorter “required minimum TR” for each slice and hence, resulted in a larger number of slices in EPIK for a given overall TR; the number of slices achieved by EPIK and EPI was 14 and 10, respectively. EPIK also demonstrated reduced susceptibility artefacts around the frontal regions, which is in line with our early work (Yun et al., 2013; Yun & Shah, 2017; Zaitsev et al., 2001). For the third, fourth, and fifth echo data, the tSNRs of EPIK were significantly higher than from those of EPI, which was a direct consequence of the use of shorter TEs in EPIK. The suggested hybrid imaging approach presents a method that allows one to obtain higher resolution EPIK data in combination with high‐resolution BrainPET data. The multi‐echo GESE‐EPIK sequence opens up possibilities to obtain multimodal permeability, perfusion and metabolic tumour analysis when combined with hybrid MR‐PET data.
CONFLICT OF INTEREST
None of the authors have any actual or potential conflict of interest.
Supporting information
Figure S1 Processing steps proposed to obtain the arterial input function. The 1st step is motion correction to correct for slight motion. The 2nd step is the echo correlation to avoid the noise floor. Then, in the 3rd step to increase vessel sensitivity, an AUC threshold is considered. To correct for pulsation, a curve smoothness criteria is included in the 4th step. Prior to performing the cluster algorithm and defining the AIF, partial volume correction is also considered.
Figure S2 Left: the derived AIF is depicted from the selected voxels (see figure on the right). Right: voxel locations are near the MCA and these are recommended for the determination of the AIF.
ACKNOWLEDGEMENTS
The authors thank Dr. Christian Fills, Dr. Gabriele Stoffels, Lutz Tellmann, Silke Frensch, Suzanne Schaden, Kornelia Frey for assistance with the MR‐PET study. The authors also thank Dr. Liliana Caldeira for fruitful discussions. Claire Rick is thanked for her editorial input and proofreading of the manuscript.
NJS is funded in part by the Helmholtz Alliance ICEMED—Imaging and Curing Environmental Metabolic Diseases, through the Initiative and Network Fund of the Helmholtz Association.
AUTOMATED ESTIMATION OF AIF
In the present work, AIF estimation was performed with an automated procedure. It consists of six steps as described below and schematically illustrated in Supporting Information Figure S1.
In order to avoid motion in the time series, the data were motion corrected by applying a rigid transformation using SPM12. Thereafter, only the slices near the MCA were considered.
In order to avoid the noise floor, the time curves that presented a relatively high Pearson correlation coefficient (higher than 0.95) between the first and the second echo were considered (Newton et al., 2016). This step is only possible when two echoes are available in multi‐contrast approaches.
In order to be sensitive to vessels, a threshold based on the area under the curve (AUC) of time signal, P AUC, was applied, whereby curves with a high AUC were excluded (Murase et al., 2001).
In order to avoid physiological pulsations, a curve smoothness criterion was considered from the remaining curves. Here, a threshold, P rough, was applied such that curves with larger integral values were no longer considered (Murase et al., 2001). In our approach, the threshold P AUC and P rough were 0.90 and 0.30, respectively.
In order to account for partial volume effects, a simplified version of the method published by Bleeker et al. (2011) was used. For this purpose, the first passage of the contrast agent was fitted to a gamma function and the AUC of the 1st contrast agent passage, AUC1st, was compared to the baseline signal level as defined in an early work (Yin, Sun, et al. (2015)). The ratio between the baseline signal level and AUC1st was then calculated and the pixels with values 20% above and below the mean were excluded.
The remaining pixels were used as input in the Ncut algorithm (Shi & Malik, 2000). Here, the number of clusters was set as 5 and the AIF cluster was chosen from the metric (M) that relates the PV, time‐to‐peak (TTP) and full‐width‐half‐maximum (FWHM), M = PV/(TTP × FWHM; Murase et al., 2001). Supporting Information Figure S2 presents the determined AIF location and shape from a representative subject.
Shah NJ, da Silva NA, Yun SD. Perfusion weighted imaging using combined gradient/spin echo EPIK: Brain tumour applications in hybrid MR‐PET. Hum Brain Mapp. 2021;42:4144–4154. 10.1002/hbm.24537
Funding information Helmholtz Alliance ICEMED , Grant/Award Number: HA‐314; Helmholtz Association
REFERENCES
- Artzi, M., Blumenthal, D. T., Bokstein, F., Nadav, G., Liberman, G., Alzenstein, O., & Ben Bashat, D. (2015). Classification of tumor area using combined DCE and DSC MRI in patients with glioblastoma. Journal of Neuro Oncology, 121, 349–357. [DOI] [PubMed] [Google Scholar]
- Bergamino, M., Bonzano, L., Levrero, F., Mancardi, G. L., & Roccatagliata, L. (2014). A review of technical aspects of T1‐weighted dynamic contrast‐enhanced magnetic resonance imaging (DCE‐MRI) in human brain tumors. Physica Medica, 30, 635–643. [DOI] [PubMed] [Google Scholar]
- Bjornerud, A., Sorensen, A. G., Mouridsen, K., & Emblem, K. E. (2011). T1‐ and T2*‐dominant extravasation correction in DSC‐MRI: Part I—Theoretical considerations and implications for assessment of tumor hemodynamic properties. Journal of Cerebral Blood Flow and Metabolism, 31, 2041–2053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bleeker, E. J., van Osch, M. J., Connelly, A., van Buchem, M. A., Webb, A. G., & Calamante, F. (2011). New criterion to aid manual and automatic selection of the arterial input function in dynamic susceptibility contrast MRI. Magnetic Resonance in Medicine, 65, 448–456. [DOI] [PubMed] [Google Scholar]
- Boxerman, J. L., Prah, D. E., Paulson, E. S., Machan, J. T., Bedekar, D., & Schmainda, K. M. (2012). The role of preload and leakage correction in gadolinium‐based cerebral blood volume estimation determined by comparison with MION as a criterion standard. AJNR American Journal of Neuroradiology, 33, 1081–1087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boxerman, J. L., Schmainda, K. M., & Weisskoff, R. M. (2006). Relative cerebral blood volume maps corrected for contrast agent extravasation significantly correlate with glioma tumor grade, whereas uncorrected maps do not. AJNR American Journal of Neuroradiology, 27, 859–867. [PMC free article] [PubMed] [Google Scholar]
- Butts, K., Riederer, S. J., Ehman, R. L., Thompson, R. M., & Jack, C. R. (1994). Interleaved echo planar imaging on a standard MRI system. Magnetic Resonance in Medicine, 31, 67–72. [DOI] [PubMed] [Google Scholar]
- Calamante, F. (2013). Arterial input function in perfusion MRI: A comprehensive review. Progress in Nuclear Magnetic Resonance Spectroscopy, 74, 1–32. [DOI] [PubMed] [Google Scholar]
- Caldeira, L., Yun, S. D., da Silva, N., Filss, C., Scheins, J., Tellmann, L., … Shah, N. J. (2015). Simultaneous acquisition of dynamic PET‐MRI: Arterial input function using DSC‐MRI and [18F]‐FET. European Journal of Nuclear Medicine and Molecular Imaging Physics, 2, A70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cicone, F., Filss, C. P., Minniti, G., Rossi‐Espagnet, C., Papa, A., Scaringi, C., … Langen, K. J. (2015). Volumetric assessment of recurrent or progressive gliomas: Comparison between F‐DOPA PET and perfusion‐weighted MRI. European Journal of Nuclear Medicine and Molecular Imaging, 42, 905–915. [DOI] [PubMed] [Google Scholar]
- da Silva, N. A., Caldeira, L., Herzog, H., Tellmann, L., Filss, C., Langen, K. J., & Shah, N. J. (2015). Automatic derivation of an MR‐PET image‐based input function for quantification of 18F‐FET. European Journal of Nuclear Medicine and Molecular Imaging Physics, 2, A27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dennie, J., Mandeville, J. B., Boxerman, J. L., Packard, S. D., Rosen, B. R., & Weisskoff, R. M. (1998). NMR imaging of changes in vascular morphology due to tumor angiogenesis. Magnetic Resonance in Medicine, 40, 793–799. [DOI] [PubMed] [Google Scholar]
- Donahue, K. M., Krouwer, H. G., Rand, S. D., Pathak, A. P., Marszalkowski, C. S., Censky, S. C., & Prost, R. W. (2000). Utility of simultaneously acquired gradient‐echo and spin‐echo cerebral blood volume and morphology maps in brain tumor patients. Magnetic Resonance in Medicine, 43, 845–853. [DOI] [PubMed] [Google Scholar]
- Eichner, C., Jafari‐Khouzani, K., Cauley, S., Bhat, H., Polaskova, P., Andronesi, O. C., … Setsompop, K. (2014). Slice accelerated gradient‐echo spin‐echo dynamic susceptibility contrast imaging with blipped CAIPI for increased slice coverage. Magnetic Resonance in Medicine, 72, 770–778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emblem, K. E., Mouridsen, K., Bjornerud, A., Farrar, C. T., Jennings, D., Borra, R. J., … Sorensen, A. G. (2013). Vessel architectural imaging identifies cancer patient responders to anti‐angiogenic therapy. Nature Medicine, 19, 1178–1183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enmi, J., Kudomi, N., Hayashi, T., Yamamoto, A., Iguchi, S., Moriguchi, T., … Iida, H. (2012). Quantitative assessment of regional cerebral blood flow by dynamic susceptibility contrast‐enhanced MRI, without the need for arterial blood signals. Physics in Medicine and Biology, 57, 7873–7892. [DOI] [PubMed] [Google Scholar]
- Erlandsson, L. M., Liljeroth, M., Atkinson, D., Arridge, S., Ourselin, S., & Hutton, B. (2015). Improved parameterestimation with combined PET‐MRI kinetic modelling. European Journal of Nuclear Medicine and Molecular Imaging Physics, 2, A25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feinberg, D. A., & Oshio, K. (1994). Phase errors in multi‐shot echo planar imaging. Magnetic Resonance in Medicine, 32, 535–539. [DOI] [PubMed] [Google Scholar]
- Filss, C. P., Galldiks, N., Stoffels, G., Sabel, M., Wittsack, H. J., Turowski, B., … Langen, K. J. (2014). Comparison of 18F‐FET PET and perfusion‐weighted MR imaging: A PET/MR imaging hybrid study in patients with brain tumors. Journal of Nuclear Medicine, 55, 540–545. [DOI] [PubMed] [Google Scholar]
- Griswold, M. A., Jakob, P. M., Heidemann, R. M., Nittka, M., Jellus, V., Wang, J., … Haase, A. (2002). Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magnetic Resonance in Medicine, 47(6), 1202–1210. [DOI] [PubMed] [Google Scholar]
- Haacke, E. M., Lindskogj, E. D., & Lin, W. (1969). A fast, iterative, partial‐fourier technique capable of local phase recovery. Journal of Magnetic Resonance, 92, 126–145. [Google Scholar]
- Herzog, H., Langen, K. J., Weirich, C., Rota Kops, E., Kaffanke, J., Tellmann, L., … Shah, N. J. (2011). High resolution BrainPET combined with simultaneous MRI. Nuklearmedizin, 50, 74–82. [DOI] [PubMed] [Google Scholar]
- Hutterer, M., Hattingen, E., Palm, C., Proescholdt, M. A., & Hau, P. (2015). Current standards and new concepts in MRI and PET response assessment of antiangiogenic therapies in high‐grade glioma patients. Neuro Oncology, 17, 784–800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kellner, E., Breyer, T., Gall, P., Müller, K., Trippel, M., Staszewski, O., … Mader, I. (2015). MR evaluation of vessel size imaging of human gliomas: Validation by histopathology. Journal of Magnetic Resonance Imaging, 42(4), 1117–1125. [DOI] [PubMed] [Google Scholar]
- Kim, E. J., Kim, D. H., Lee, S. H., Huh, Y. M., Song, H. T., & Suh, J. S. (2004). Simultaneous acquisition of perfusion and permeability from corrected relaxation rates with dynamic susceptibility contrast dual gradient echo. Magnetic Resonance Imaging, 22, 307–314. [DOI] [PubMed] [Google Scholar]
- Kiselev, V. G., Strecker, R., Ziyeh, S., Speck, O., & Hennig, J. (2005). Vessel size imaging in humans. Magnetic Resonance in Medicine, 53, 553–563. [DOI] [PubMed] [Google Scholar]
- Knutsson, L., Lindgren, E., Ahlgren, A., van Osch, M. J., Bloch, K. M., Surova, Y., … Wirestam, R. (2014). Dynamic susceptibility contrast MRI with a prebolus contrast agent administration design for improved absolute quantification of perfusion. Magnetic Resonance in Medicine, 72, 996–1006. [DOI] [PubMed] [Google Scholar]
- Lemasson, B., Valable, S., Farion, R., Krainik, A., Remy, C., & Barbier, E. L. (2013). In vivo imaging of vessel diameter, size, and density: A comparative study between MRI and histology. Magnetic Resonance in Medicine, 69, 18–26. [DOI] [PubMed] [Google Scholar]
- Mouridsen, K., Christensen, S., Gyldensted, L., & Ostergaard, L. (2006). Automatic selection of arterial input function using cluster analysis. Magnetic Resonance in Medicine, 55, 524–531. [DOI] [PubMed] [Google Scholar]
- Murase, K., Kikuchi, K., Miki, H., Shimizu, T., & Ikezoe, J. (2001). Determination of arterial input function using fuzzy clustering for quantification of cerebral blood flow with dynamic susceptibility contrast‐enhanced MR imaging. Journal of Magnetic Resonance Imaging, 13, 797–806. [DOI] [PubMed] [Google Scholar]
- Newbould, R. D., Skare, S. T., Jochimsen, T. H., Alley, M. T., Moseley, M. E., Albers, G. W., & Bammer, R. (2007). Perfusion mapping with multiecho multishot parallel imaging EPI. Magnetic Resonance in Medicine, 58, 70–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newton, A. T., Pruthi, S., Stokes, A. M., Skinner, J. T., & Quarles, C. C. (2016). Improving perfusion measurement in DSC‐MRI through the use of multi‐echo information for AIF determination. AJNR American Journal of Neuroradiology, 37, 1237–1243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shiroishi, M. S., Castellazzi, G., Boxerman, J. L., D'Amore, F., Essig, M., Nguyen, T. B., … Law, M. (2015). Principles of T2*‐weighted dynamic susceptibility contrast MRI technique in brain tumor imaging. Journal of Magnetic Resonance Imaging, 41, 296–313. [DOI] [PubMed] [Google Scholar]
- Ostergaard, L. (2005). Principles of cerebral perfusion imaging by bolus tracking. Journal of Magnetic Resonance Imaging, 22, 710–717. [DOI] [PubMed] [Google Scholar]
- Pauleit, D., Floeth, F., Hamacher, K., Riemenschneider, M. J., Reifenberger, G., Muller, H. W., … Langen, K. J. (2005). O‐(2‐[18F]fluoroethyl)‐L‐tyrosine PET combined with MRI improves the diagnostic assessment of cerebral gliomas. Brain, 128, 678–687. [DOI] [PubMed] [Google Scholar]
- Paulson, E. S., & Schmainda, K. M. (2008). Comparison of dynamic susceptibility‐weighted contrast‐enhanced MR methods: Recommendations for measuring relative cerebral blood volume in brain tumors. Radiology, 249, 601–613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poulin, E., Lebel, R., Croteau, E., Blanchette, M., Tremblay, L., Lecomte, R., … Lepage, M. (2013). Conversion of arterial input functions for dual pharmacokinetic modeling using Gd‐DTPA/MRI and 18F‐FDG/PET. Magnetic Resonance in Medicine, 69, 781–792. [DOI] [PubMed] [Google Scholar]
- Quarles, C. C., Gore, J. C., Xu, L., & Yankeelov, T. E. (2012). Comparison of dual‐echo DSC‐MRI‐ and DCE‐MRI‐derived contrast agent kinetic parameters. Magnetic Resonance Imaging, 30, 944–953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quarles, C. C., Ward, B. D., & Schmainda, K. M. (2005). Improving the reliability of obtaining tumor hemodynamic parameters in the presence of contrast agent extravasation. Magnetic Resonance in Medicine, 53, 1307–1316. [DOI] [PubMed] [Google Scholar]
- Tropres, I., Grimault, S., Vaeth, A., Grillon, E., Julien, C., Payen, J. F., … Decorps, M. (2001). Vessel size imaging. Magnetic Resonance in Medicine, 45, 397–408. [DOI] [PubMed] [Google Scholar]
- Sacconi, B., Raad, R. A., Lee, J., Fine, H., Kondziolka, D., Golfinos, J. G., … Jain, R. (2016). Concurrent functional and metabolic assessment of brain tumors using hybrid PET/MR imaging. Journal of Neuro Oncology, 127, 287–293. [DOI] [PubMed] [Google Scholar]
- Sari, H., Erlandsson, K., & Thielemans, K. (2015). Incorporation of MRI‐AIF information for improved kinetic Modelling of dynamic PET data. IEEE Transactions on Nuclear Science, 62, 612–618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmiedeskamp, H., Andre, J. B., Straka, M., Christen, T., Nagpal, S., Recht, L., … Bammer, R. (2013). Simultaneous perfusion and permeability measurements using combined spin‐ and gradient‐echo MRI. Journal of Cerebral Blood Flow and Metabolism, 33, 732–743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmiedeskamp, H., Straka, M., & Bammer, R. (2012). Compensation of slice profile mismatch in combined spin and gradient‐echo echo‐planar imaging pulse sequences. Magnetic Resonance in Medicine, 67, 378–388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmiedeskamp, H., Straka, M., Newbould, R. D., Zaharchuk, G., Andre, J. B., Olivot, J. M., … Bammer, R. (2012). Combined spin‐and gradient‐Echo perfusion‐weighted imaging. Magnetic Resonance in Medicine, 68, 30–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah, N. J., & Zilles, K. Magnetic resonance imaging method. U.S. Patent No. 6,707,299 B2. 2004a.
- Shah, N. J., & Zilles, K. Imaging process in the spatial frequency space and useful for examining the properties of object. U.S. Patent No. 6,781,372. 2004b.
- Shi, J., & Malik, J. (2000). Normalized cuts and image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 22, 888–905. [Google Scholar]
- Skinner, J. T., Moots, P. L., Ayers, G. D., & Quarles, C. C. (2016). On the use of DSC‐MRI for measuring vascular permeability. AJNR American Journal of Neuroradiology, 37, 80–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skinner, J. T., Robison, R. K., Elder, C. P., Newton, A. T., Damon, B. M., & Quarles, C. C. (2014). Evaluation of a multiple spin‐ and gradient‐echo (SAGE) EPI acquisition with SENSE acceleration: Applications for perfusion imaging in and outside the brain. Magnetic Resonance Imaging, 32, 1171–1180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stokes, A. M., & Quarles, C. C. (2016). A simplified spin and gradient echo approach for brain tumor perfusion imaging. Magnetic Resonance in Medicine, 75, 356–362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stokes, A. M., Skinner, J. T., & Quarles, C. C. (2014). Assessment of a combined spin‐ and gradient‐echo (SAGE) DSC‐MRI method for preclinical neuroimaging. Magnetic Resonance Imaging, 32, 1181–1190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vonken, E. J., van Osch, M. J., Bakker, C. J., & Viergever, M. A. (1999). Measurement of cerebral perfusion with dual‐echo multi‐slice quantitative dynamic susceptibility contrast MRI. Journal of Magnetic Resonance Imaging, 10, 109–117. [DOI] [PubMed] [Google Scholar]
- Willats, L., & Calamante, F. (2013). The 39 steps: Evading error and deciphering the secrets for accurate dynamic susceptibility contrast MRI. NMR in Biomedicine, 26, 913–931. [DOI] [PubMed] [Google Scholar]
- Yankeelov, T. E., & Gore, J. C. (2009). Dynamic contrast enhanced magnetic resonance imaging in oncology: Theory, data acquisition, analysis, and examples. Current Medical Imaging Reviews, 3, 91–107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin, J., Sun, H., Yang, J., & Guo, Q. (2015). Automated detection of the arterial input function using normalized cut clustering to determine cerebral perfusion by dynamic susceptibility contrast‐magnetic resonance imaging. Journal of Magnetic Resonance Imaging, 41, 1071–1078. [DOI] [PubMed] [Google Scholar]
- Yin, J., Yang, J., & Guo, Q. (2015). Automatic determination of the arterial input function in dynamic susceptibility contrast MRI: Comparison of different reproducible clustering algorithms. Neuroradiology, 57, 535–543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yun, S. D., Reske, M., Vahedipour, K., Warbrick, T., & Shah, N. J. (2013). Parallel imaging acceleration of EPIK for reduced image distortions in fMRI. NeuroImage, 73, 135–143. [DOI] [PubMed] [Google Scholar]
- Yun, S. D., & Shah, N. J. (2017). Whole‐brain high in‐plane resolution fMRI using accelerated EPIK for enhanced characterisation of functional areas at 3T. PLoS One, 12, e0184759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaitsev, M., D'Arcy, J., Collins, D. J., Leach, M. O., Zilles, K., & Shah, N. J. (2005). Dual‐contrast echo planar imaging with keyhole: Application to dynamic contrast‐enhanced perfusion studies. Physics in Medicine and Biology, 50, 4491–4505. [DOI] [PubMed] [Google Scholar]
- Zaitsev, M., Zilles, K., & Shah, N. J. (2001). Shared k‐space echo planar imaging with keyhole. Magnetic Resonance in Medicine, 45, 109–117. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1 Processing steps proposed to obtain the arterial input function. The 1st step is motion correction to correct for slight motion. The 2nd step is the echo correlation to avoid the noise floor. Then, in the 3rd step to increase vessel sensitivity, an AUC threshold is considered. To correct for pulsation, a curve smoothness criteria is included in the 4th step. Prior to performing the cluster algorithm and defining the AIF, partial volume correction is also considered.
Figure S2 Left: the derived AIF is depicted from the selected voxels (see figure on the right). Right: voxel locations are near the MCA and these are recommended for the determination of the AIF.


