Elastic scattering spectroscopy for early detection of breast cancer: partially supervised Bayesian image classification of scanned sentinel lymph nodes

Abstract.

Sentinel lymph node biopsy is a standard diagnosis procedure to determine whether breast cancer has spread to the lymph glands in the armpit (the axillary nodes). The metastatic status of the sentinel node (the first node in the axillary chain that drains the affected breast) is the determining factor in surgery between conservative lumpectomy and more radical mastectomy including axillary node excision. The traditional assessment of the node requires sample preparation and pathologist interpretation. An automated elastic scattering spectroscopy (ESS) scanning device was constructed to take measurements from the entire cut surface of the excised sentinel node and to produce ESS images for cancer diagnosis. Here, we report on a partially supervised image classification scheme employing a Bayesian multivariate, finite mixture model with a Markov random field (MRF) spatial prior. A reduced dimensional space was applied to represent the scanning data of the node by a statistical image, in which normal, metastatic, and nonnodal-tissue pixels are identified. Our results show that our model enables rapid imaging of lymph nodes. It can be used to recognize nonnodal areas automatically at the same time as diagnosing sentinel node metastases with sensitivity and specificity of 85% and 94%, respectively. ESS images can help surgeons by providing a reliable and rapid intraoperative determination of sentinel nodal metastases in breast cancer.

1. Introduction

Breast cancer is the most common malignancy in women in the western world, with a reported incidence of up to one in eight women. The ability to provide the best treatment for breast cancer depends on establishing whether or not the cancer has spread to the axillary lymph nodes.

Traditionally, the presence of axillary lymph node metastases has been determined by axillary lymph node dissection (ALND), which is a surgical procedure that removes all the lymph nodes under the armpit. However, this has associated complications, particularly lymphoedema (persistent swelling of the arm) and shoulder dysfunction.

In recent years, sentinel lymph node biopsy (SLNB) has become the standard diagnostic procedure to determine whether breast cancer has spread to the axillary lymph nodes. The sentinel node is the first node in the axillary chain to be invaded by cancer spreading from the breast. It has been well documented that if cancer cannot be detected in the sentinel node, the chance of there being any cancer in nodes further down the chain draining the breast is exceedingly small, and thus there is no need to resect the rest of the axillary nodes.¹ Avoidance of axillary chain excision markedly reduces the risk of complications associated with full clearance.^2,3 Thus, SLNB has become the standard of clinical care for patients with early breast cancer.⁴

To get the maximum benefit from sentinel node biopsy, it is important to be able to intraoperatively determine whether or not cancer is present in the node. Conventional intraoperative analysis is undertaken by either touch-imprint cytology⁵ or frozen-section histology.^6,7 Both methods require sample preparation and interpretation of the findings by an experienced pathologist. A real-time optical method for determining sentinel node involvement, with no requirement for the presence of a pathologist, would provide significant benefits to patients undergoing surgery for breast cancer while reducing the costs to the health-care system.

Elastic scattering spectroscopy (ESS) is a special subset of a broader class of optical methods called diffuse reflectance spectroscopy (DRS).⁸ Whereas the source–detector separation for DRS is unspecified and can be large (as in the regime where the approximations of the diffusion equation are upheld), with the ESS method, the source–detector separation is small: significantly smaller than the reduced mean-free-path for scattering. As such, the approximations of the diffusion equation do not apply. With ESS, the details of the scattering phase function are important, and higher moments of the phase function (or full Mie theory calculations) must be included to properly describe the ESS reflectance. Thus, ESS is sensitive to changes in the details of the cellular and subcellular architecture that affect scattering, whereas DRS, in general, is not. The sizes, refractive indices, and structures of the subcellular components (e.g., nucleus, nucleolus, and mitochondria) are known to change when cells become malignant.⁹ Employing multivariate statistical techniques on the recorded optical spectra may enable rapid ex vivo examination of freshly excised nodes, yielding computer-generated diagnosis without tissue processing and pathologist interpretation.

Conventional, “manually” measured ESS spectra can invoke considerable experimental variations caused by angle or pressure of the handheld fiber-optic probe. Although it is possible to ameliorate the effect of this variability by statistical preprocessing of the data,¹⁰ it remains a source of “noise” in such measurements. To physically avoid this problem and to produce more reliable measurements for rapid intraoperative diagnosis of sentinel node metastases, an automated two-dimensional (2-D) ESS scanning device was developed to take measurements from the entire cut surface of the excised nodes. Instead of basing the diagnosis on a number of point measurements, this application-specific ESS scanner examines the full area of the node by taking measurements at 400 points (pixels) in a $20\times 20$ grid of 0.5-mm increments, and has the ability to produce diagnostic images of the surface of any tissue sample that can be optically scanned to assess the cancer risk. The assumption is that more complete optical sampling of the tissue surface under examination should increase the accuracy of diagnosis.

However, additional problems arise in the analysis and interpretation of the ESS-scanned measurement data. The commonly used supervised-classification methods, e.g., linear discriminant analysis (LDA), require “ground truth” data to train the algorithm. Since the typical histology data for sentinel lymph nodes is on a per-node basis, there is no site-specific reference pathology available for individual pixels in the scanned image. This leads to problems when deriving a classification algorithm for pixels. We do, however, have manual measurements on totally normal and totally metastatic nodes from an earlier phase of this research.¹¹ An obvious approach is to use the manual measurement data to train a classification algorithm for use with the scanner data. However, apart from the normal and metastatic classes, the scan also includes a third class, which corresponds to the nonnodal area surrounding the node, possibly contaminated by blood or lipids. There are no training data available for this nonnodal class, which varies considerably from node to node and can lead to confounding spectral signatures. Using the two-class discriminant algorithm developed from manual data, the spectra from background usually result in a score indicative of cancer. The nonnode area may thus be misclassified as metastatic and impede the correct recognition of normal and metastatic nodes. In our earlier work^12,13 using the two-class discriminant algorithm, there was a need to remove nonnodal areas from the image by visual inspection and the final image was not convincing due to misclassified pixels. To avoid an unacceptable number of false positives arising from the misclassification of individual pixels, a cluster-of-nine rule was used in the previous work¹³ that a node is declared to be metastatic only if there is a cluster of at least nine contiguous pixels (of a $3\times 3$ grid), all classified as metastatic, but it did not clean up the image.

Beyond dealing with the problem described above, there is also an interesting opportunity arising in the ESS scanning data analysis. Since the scanner generates a spectral image, it should be possible to use a smoothness assumption about the image to improve the classification of individual pixels.

To solve the problems and make use of the advantage of having an image, a partially supervised Bayesian multivariate finite-mixture image classification model with a Markov random field (MRF) spatial prior, described in detail elsewhere,¹⁴ has been employed to recognize the nonnodal area automatically at the same time as distinguishing normal from metastatic tissue. The basic idea is that the classification of the points in the image is done by clustering, using a mixture model and guided by prior information from manual data as well as spatial correlation from adjacent points in the image.

The model fitting is implemented in two stages. The first stage fits a Bayesian multivariate finite-mixture model, based on dimension-reduced spectral data, taking no account of the spatial correlation in the image. This generates a preliminary solution. The second stage, with spatial correlation taken into account between contiguous pixels in the image, aims at generating a more realistic image.

2. Materials and Methods

2.1. Elastic Scattering Spectroscopy Scanning Device

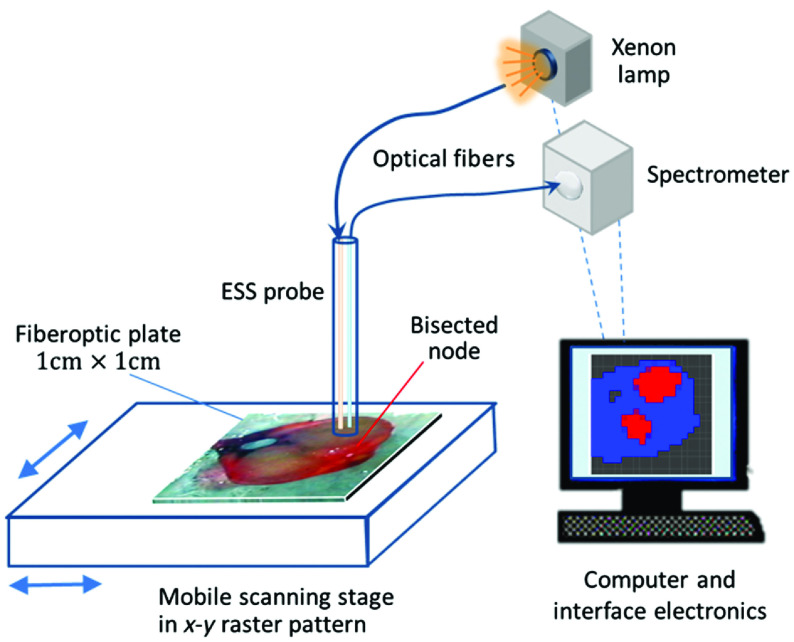
In the project of which this work forms part, ESS is being developed as a technique to discriminate between lymph nodes that contain metastatic tissue and lymph nodes that are normal. In the first phase of the work, spectra were collected from nodes using a handheld probe.¹¹ In further development, an automated 2-D ESS scanning device (an optical scanner) was constructed to take measurements from the entire cut surface of a node.¹³ The ESS scanner instrumentation consists of a xenon arc lamp, a static fiber-optic ESS probe, a mobile sample stage, a spectrometer, and a computer to control the various components and record the spectra (see Fig. 1).

Fig. 1.

Schematic diagram of ESS scanning device system. The bisected node is scanned through a fiber-optic plate above it by moving the scanning stage under a fixed ESS probe in an $x\text{-}y$ raster pattern to create a $20\times 20$ grid of spectra at 0.5-mm intervals.

After excision, nodes are bisected along their long axis. The cut surface of the node is placed under a specially designed thin fiber-optic plate (also called a microchannel plate) attached to a motorized stage that translates in the horizontal plane under a stationary ESS probe, incrementally in two axes, in an $x\text{-}y$ raster scanning pattern (Fig. 1) to enable a fine grid of ESS measurements of the cut surface of the node. The probe is optically coupled to the fiber-optic plate with a drop of immersion oil. Prior to use, the system response is calibrated against a standard diffuse reflector as a spectral-response reference (Spectralon) through the fiber-optic plate. A $10\times 10\mathrm{mm}$ area of the cut surface of each node is scanned, pixel-by-pixel, with the plate being translated to each measurement position but held stationary during each 10-ms measurement.

A $20\times 20\text{\hspace{0.17em}\hspace{0.17em}pixel}$ ESS measurement image is generated by the system, i.e., 400 pixels, each of size $0.5\times 0.5\mathrm{mm}$. The 0.5-mm step sizes on the ESS scanner would detect a lymph node metastasis which is 0.4 mm across and thus has the potential to detect micrometastasis (cancer deposit of 0.2 to 2 mm).¹² More explanation will be given later in Sec. 4. For each node, a low-magnification microphotograph is taken of the area to be scanned. This area usually includes some part of the fiber-optic plate not contacting the node. These photographs are used later to compare with the images generated by our model for the purpose of assessing one aspect of the model’s success.

2.2. Spectral Acquisition

All spectra were recorded as a ratio to a reference spectrum taken from a spectrally flat diffuse-reflecting material (Spectralon™), thus rendering the data independent of the spectral response of the system. Each spectrum is recorded at $p=1801$ wavelengths in the near–UV–visible–NIR region of 320 to 919 nm.

Two spectral datasets, manual measurements and scanning measurements, were collected in two phases of the study. Ethics committee approval was obtained for this study. In the first phase, spectra were measured by placing the optical probe manually at up to 16 sites on the cut surface of the bisected excised node. A total of 3213 spectra taken manually from 339 normal and 30 totally metastatic nodes excised from 205 patients were gathered in order to develop an algorithm to distinguish cancer from normal nodal tissue. Each node was assessed and assigned as normal or metastatic by histological experts, and this assignment was applied to all the points for the node. No spectra from the background area are available in this dataset.

In the second phase of the study, to assess nodes more comprehensively, an independent set of spectra from a total of 117 nodes, including 65 normal nodes and 52 partially or totally metastatic nodes from 81 patients were scanned, giving a $20\times 20\text{\hspace{0.17em}\hspace{0.17em}pixel}$ image with $n=400$ spectra for each node. The cut surface of the node with bisected shape is placed under a square fiber optic plate as shown in Fig. 1, and in most cases the scanning data contain not only the areas from the normal or metastatic classes but also nonnodal areas, possibly contaminated by blood or lipid. No training set from the first phase manual data is available for this nonnodal class. The reference pathology is only provided on a per-node basis and is not available for individual pixels in the image.

The scanned data from the 117 nodes were randomly split into two sets with half of the nodes in each class being placed in the first set and half in the second set. The first set, including 33 normal nodes and 26 partially or totally metastatic nodes, was used as a training set to tune the parameters of the classification rules, as described in Sec. 2.3.5. The second set was not used until after the diagnostic classification rules had been selected and trained with those tuning parameters fixed. This set, including 32 normal nodes and 26 partially or totally metastatic nodes was then used as an independent test set for prospective prediction, as described in Sec. 2.3.5.

2.3. Statistical Analysis

2.3.1. Preliminary data processing

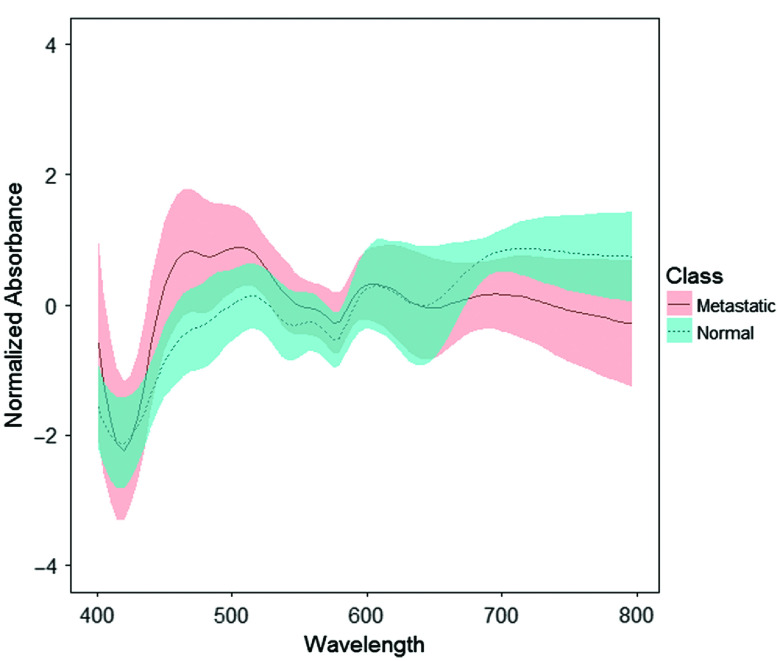
Standard data preprocessing was carried out on spectra from both manual measurements and scanning measurements to improve signal quality.^10,11,15 This involved spectral smoothing using the Savitzky–Golay filter,¹⁶ cropping the noisy ends of the spectra before 400 nm and after 800 nm and normalizing using the standard normal variate method.¹⁷ The mean spectra of the manual measurements from normal and metastatic nodes after standard preprocessing are shown in Fig. 2.

Fig. 2.

Mean spectra of the manual measurements from normal (blue dashed line) and completely metastatic (red solid line) nodes after standard preprocessing. The shaded regions represent one standard deviation of the spectral variability.

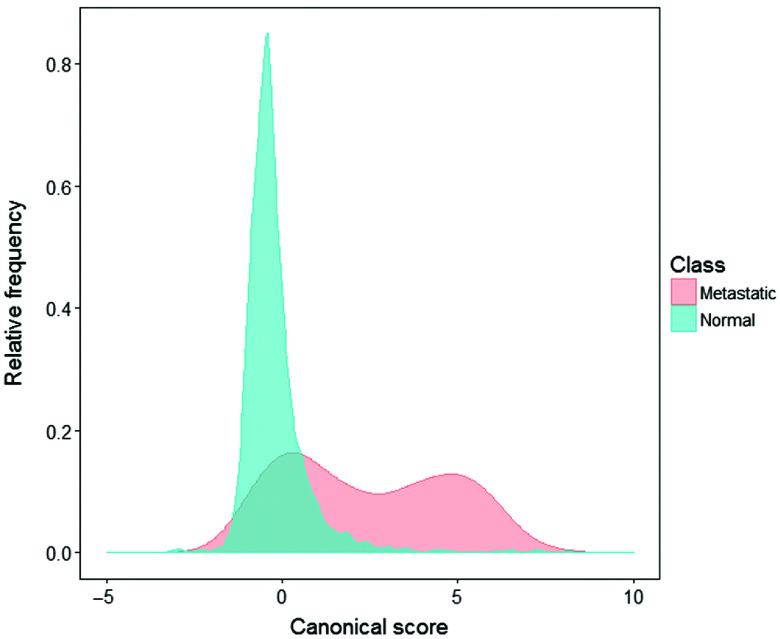
A preliminary analysis on the manual measurement data was first carried out by a principal component analysis followed by a LDA to find the canonical variate, the direction maximizing the discrimination between normal and metastatic nodes. Leave-out-one-site cross-validation was undertaken to assess the accuracy of the LDA analysis on a per-site basis. Figure 3 shows the distribution of canonical scores from normal (blue) and metastatic spectra (red) in the manual measurement data derived from an LDA, using 20 principal components. There are two dominant peaks, the first at a score of $\sim 0$, corresponding to normal nodes and some parts of metastatic nodes, and the second at $\sim 4$, corresponding to metastatic nodes only. Scores from metastatic nodes have a bimodal distribution. It may be that despite the selection of totally metastatic nodes, there remains a mix of normal and metastatic spectra, presumably related to remaining normal structures within the metastatic nodes. Ideally, it would be helpful to exclude from our manual data those spectra taken from normal sites of metastatic node. In reality, it is quite hard to avoid such bimodal problem because each node is assessed as a whole by histological experts and there is no reference pathology available for specific site of the node; or it may be that the metastatic areas are genuinely highly variable from node to node.¹³ Our Bayesian image classification model could deal with this problem caused by the variable component in the mixture and this will be illustrated in examples as described in Sec. 3.

Fig. 3.

Distribution plot of LDA canonical scores of normal (blue) and metastatic (red) spectra from manual measurement data. The frequency is plotted as a proportion of each class.

2.3.2. Discriminant dimension reduction

Before implementing the multivariate image classification model, the discriminant dimension reduction method^14,18 was applied to project the high-dimensional spectra from each nodal scan onto a low-dimensional space specific to that node. The method constructs an external variable and a small number of internal variable(s). The external variable was constructed by projecting the scanned node data onto the direction of the canonical variable derived from LDA applied to the first $k_{\mathrm{ext}}$ PC scores of the manual data. This external variable, common to all nodes, ensures that the main diagnostic information is preserved in the dimension reduction. To allow the method to adapt to each individual node, the internal variable(s) were then constructed by extracting the first $k_{\mathrm{int}}$ PCs of the spectra of a given node in a subspace orthogonal to the direction of the external variable. By using the external variable, we impose one dimension derived from the manual data (not derived from the node in question), which we believe can separate normal from metastatic tissues. Adding internal variables derived from the node of interest retains the variability specific to this node. The dimension-reduced scanned data of each node thus contain one external variable and one or more internal variable(s), with dimensions reduced from $n\times p$ ($n=400$, $p=1801$) to $n\times k(k=1+k_{\mathrm{int}})$. The manual data were then also projected onto the space spanned by the directions of the external and internal variables for the node of interest. Along these directions, means and variances derived from normal and metastatic spectra were calculated to be used in the priors for normal and metastatic components in Sec. 2.3.3.

External and internal variables were constructed on each scanned node for a grid of values of $k_{\mathrm{ext}}$, the number of principal components constructing the external variable by using LDA, and $k_{\mathrm{int}}$, the number of internal variable(s). Here $k_{\mathrm{ext}}$ ranging from 5 to 20 was used to construct the external variable, which maximizes the discrimination between normal and metastatic nodes in the manual data, and $k_{\mathrm{int}}$ ranges from 1 to 5.

2.3.3. Bayesian multivariate finite mixture model application (first stage)

A partially supervised image classification algorithm employing a Bayesian multivariate finite-mixture model was then applied to the $k$-dimensional data to model the three unknown classes (normal, metastatic, and nonnodal) in the images from the scanned measurements. The modeling is done separately for each node.

In this initial stage, the spatial correlations are ignored, and we suppose that the spectra from the node $x_1,\dots ,x_n$ are $k$-dimensional random observations generated independently from a mixture of normal, metastatic, and nonnodal classes. The multivariate $t$ distribution was chosen for the $j$’th class density of the mixture ($j=1$, 2, 3, for normal, metastatic, and background group, respectively), so that with probability ${\pi }_{ij}$ $x_i$ belongs to the $j$’th class and $x_i\sim t({\mu }_j,{\mathrm{\Sigma }}_j,{\nu }_j)$ with mean vector ${\mu }_j$, scale matrix ${\mathrm{\Sigma }}_j$, and degrees of freedom ${\nu }_j$. Since the nonnodal area is more likely to appear on the fringe, ${\pi }_{ij}$ depends on a position parameter ${\alpha }_{ij}$ in a way that gives the pixels on the corner or edge a higher probability of being a nonnodal component than those in the center of the image.¹⁴

The Bayesian approach used here allows us to incorporate prior information on the parameters of the mixture components into the model. Using the means and variances derived from the manual measurements as described in Sec. 2.3.2, an extended normal inverse Wishart prior $p({\mu }_j,{\mathrm{\Sigma }}_j)$^19,20,14 provides different priors for different components in the mixture and allows different weights to be given to this prior in different dimensions of the scanned data.

Since, in the Bayesian posterior density, both class membership of each observation and the parameters of each class are unknown and are strongly interdependent, the model fitting in the first stage was implemented by an iterated expectation-maximization (EM) algorithm.²¹ This gives estimates of the parameters ${\mu }_j$ and ${\mathrm{\Sigma }}_j$ of the three multivariate $t$ distributions and a class label $y_i$ for each pixel. This estimated configuration becomes the starting point for the second stage of the fitting.

In principle, it is also possible to estimate ${\nu }_j$, the degrees of freedom of the multivariate $t$ distribution, as part of the EM fitting. But in our application, we simply searched over a grid for the degrees of freedom ${\nu }_{s1}$ in the first stage and ${\nu }_{s2}$ in the second stage, with values ranging from 4 to 20 as described in Sec. 3.

2.3.4. Markov random field spatial prior (second stage)

In the second stage, spatial interactions between neighboring or nearby pixels modeled by an MRF prior^22,23 were then imposed on the Bayesian multivariate finite mixture model. Following the suggestion of Besag,²⁴ ${\pi }_{ij}$, the conditional prior probability of pixel $i$ having class label $j$, given the class labels of all other pixels, is defined as a spatial prior¹⁴ in the following way:

$${\pi }_{ij}={\alpha }_{ij}\exp \{-\beta {\gamma }_{ij}(y)\},$$

where ${\gamma }_{ij}(y)$ is the proportion of neighbors of pixel $i$ having class memberships with a value different to $j$ based on the current image configuration $y$. (Here, the neighbors refer to a second order neighborhood, that is, the eight pixels surrounding each single pixel of the image). $\beta$ is a smoothing parameter ranging from 0 to 30, the size of which decides the local smoothness; and ${\alpha }_{ij}$ is the same position parameter as in the first-stage model, giving higher probability to nonnodal pixels at the edge of the image.

Due to the dependence structure introduced by the MRF in this stage, implementing the E-step of the EM algorithm is nontrivial. Thus, the restoration maximization (RM) algorithm²⁵ was used to fit this Bayesian multivariate $t$-mixture model with the locally dependent MRF prior, starting from the image configuration reached in the first stage. The result of the fitting is a new estimated configuration that has more smoothness than the one produced by the first stage fitting.

2.3.5. Image classification performance assessment

Image classification rules were derived from the dimension-reduced scanned data for the training set with various combinations of $k_{\mathrm{ext}}$, $k_{\mathrm{int}}$, ${\nu }_{s1}$, ${\nu }_{s2}$, and $\beta$. In order to search for optimal combinations of these parameters, instead of an exhaustive searching of all the possible combinations, a more restricted approach was adopted. First, we varied combinations of $k_{\mathrm{ext}}$ and $k_{\mathrm{int}}$ for a restricted number of values of ${\nu }_{s1}$, ${\nu }_{s2}$, and $\beta$, and then we fixed $k_{\mathrm{ext}}=20$ to construct the external variable and $k_{\mathrm{int}}=1$ to construct one internal variable, the values that gave the best results in this limited search. The scanned data of each node were thus reduced from 1801-dimensions to two-dimensions with one external variable and one internal variable. The classification rules derived from various combinations of ${\nu }_{s1}$, ${\nu }_{s2}$, and $\beta$, with $k_{\mathrm{ext}}=20$ and $k_{\mathrm{int}}=1$, were then applied to all the scanned nodes from the training set to generate a set of classification results.

Since reference pathology is not available for individual pixels of the images, but only for each node as a whole, the classification was carried out on a per-node basis. To define conditions for classifying each node as metastatic or nonmetastatic, we simply counted the number of positive (metastatic) pixels in the node. With spatial correlation among adjacent pixels of the image being considered, the likelihood of scattered false-positive pixels occurring over a node is low. Hence, we classify a node as metastatic if it has even one pixel (usually, a contiguous group) thus classified, and the classification accuracy was measured by sensitivity and specificity using one positive pixel as a threshold. The classification accuracy was also measured by AUC, the area under the receiver operating characteristic (ROC) curve,²⁶ which plots the sensitivity versus the false-positive rate (1-specificity) and is generated by varying the threshold number of positive pixels required to classify the node as positive, i.e., metastatic. Clinicians are also interested in the predictive values of test results. To avoid unnecessary axillary clearance by reducing false-positive rate, population positive predictive value (PPV) is of more interest in the long-term assessment of the model. PPV measures the probability that a patient with a positive test does, in fact, have the disease of interest. However, considering that the training data set in this study is small, maximizing specificity gives a more stable diagnostic result, and so we will focus on optimizing specificity. To test the robustness of the final model, predictions were made for the separate test set described in Sec. 2.2. The same spectral pretreatment procedures as used for the training set were implemented on these data, followed by an application of the optimal classification model derived from the training data described in Sec. 2.2, using the optimal combination of parameters $k_{\mathrm{ext}}$, $k_{\mathrm{int}}$, ${\nu }_{s1}$, ${\nu }_{s2}$, and $\beta$, also learned from the training data.

The main measure of performance is, of course, a successful classification of the node as normal or metastatic, but success of the modeling can also be assessed by comparing the produced ESS image with the picture of the node. The ESS image was generated by plotting a $20\times 20$ matrix of pixels with the following color codes: black indicates the pixels classified as nonnodal component; for normal or metastatic component, we used the posterior probability of the pixel belonging to the metastatic component to generate a color between red (representing metastatic) and blue (representing normal) for each pixel. This image was compared by eye with the photograph of the node to assess the method’s success in reconstructing its shape.

All the computations and analyses were performed using the $R$ statistical language and software environment²⁷ for statistical computing and graphics.

3. Results

The classification accuracy results using the scanned nodes from the training set for the various combinations of ${\nu }_{s1}$ and ${\nu }_{s2}$ and $\beta$ with fixed values of $k_{\mathrm{ext}}=20$ and $k_{\mathrm{int}}=1$ are shown in Table 1.

Table 1.

The classification accuracy results using training set with various combinations of ${\nu }_{s1}$ and ${\nu }_{s2}$ (degrees of freedom of $t$ in the first and second stage algorithms, respectively) and $\beta$ (the smoothness parameter) with $k_{\mathrm{ext}}=20$ and $k_{\mathrm{int}}=1$.

${\nu }_{s1}$	${\nu }_{s2}$	$\beta$	Accuracy
			Sensitivity (%)	Specificity (%)	AUC
4	4	5	88	64	0.90
4	4	10	85	82	0.90
4	4	15	85	94	0.91
4	4	20	77	97	0.88
4	4	25	77	97	0.88
4	4	30	77	97	0.88
4	10	5	88	61	0.89
4	10	10	88	67	0.90
4	10	15	85	82	0.90
4	10	20	85	88	0.90
4	10	25	81	91	0.89
4	10	30	77	91	0.87
4	20	5	88	61	0.90
4	20	10	88	64	0.89
4	20	15	88	70	0.90
4	20	20	85	70	0.89
4	20	25	85	82	0.90
4	20	30	85	88	0.91
10	10	5	85	42	0.81
10	10	10	85	55	0.83
10	10	15	81	70	0.84
10	10	20	77	76	0.83
10	10	25	73	79	0.82
10	10	30	69	79	0.80
10	20	5	88	42	0.82
10	20	10	85	52	0.83
10	20	15	85	61	0.84
10	20	20	81	61	0.83
10	20	25	77	67	0.82
10	20	30	77	73	0.82
20	20	5	92	36	0.82
20	20	10	88	42	0.82
20	20	15	88	48	0.83
20	20	20	81	55	0.80
20	20	25	81	61	0.81
20	20	30	81	67	0.82

Our experiments show that good classification results can be achieved by different options. Using lower degrees of freedom for the $t$ distribution and higher values of the smoothness parameter $\beta$ tends to give higher specificity. Although the model with higher degrees of freedom, ${\nu }_{s2}=10$ or 20, together with higher value of $\beta$ gives high specificity as well, its sensitivity is lower.

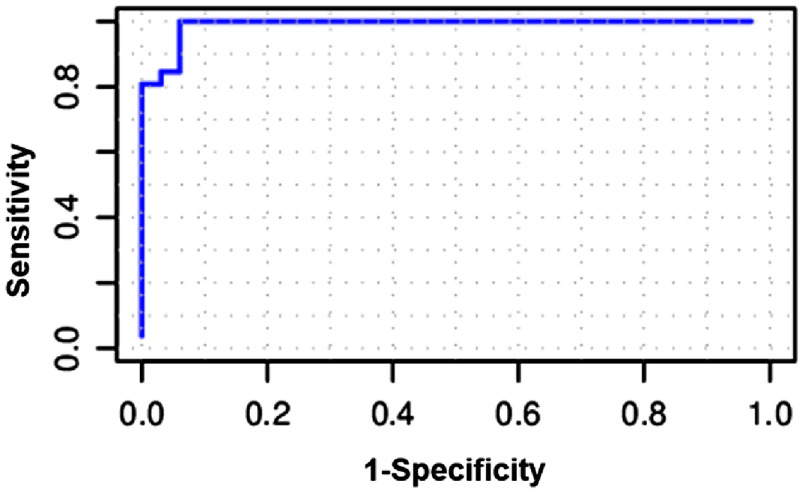
Instead of simply choosing the class label with the highest probability to define the condition of each pixel, the following approach was taken to meet the criterion of finding the highest sensitivity for a desired specificity. The cutoff probability for a pixel being metastatic can be adjusted to obtain as high specificity as possible, and then to seek the highest sensitivity to avoid unnecessary axillary clearance, which is irreversible. By choosing 0.97 as a cutoff for individual pixels and then doing the classification on per-node basis as described in Sec. 2.3.5, we can arrive at a specificity of 94% with a sensitivity of 85% and an AUC of 0.91 for the optimal model, using $k_{\mathrm{ext}}=20$, $k_{\mathrm{int}}=1$, ${\nu }_{s1}=4$, ${\nu }_{s2}=4$, and $\beta =15$ as given in Table 1. When $\beta$ increases to 20, we can even achieve a specificity of 97% with a sensitivity of 77%, compared with the specificity and sensitivity of 96% and 69% for a related but slightly different dataset reported by Austwick et al.¹³ The ROC curve for the optimal model is shown in Fig. 4.

Fig. 4.

ROC curve for the optimal image classification model ($k_{\mathrm{ext}}=20$, $k_{\mathrm{int}}=1$, ${\nu }_{s1}=4$, ${\nu }_{s2}=4$, and $\beta =15$).

The optimal model was then applied to the independent test set of 58 nodes, and it gave prediction results with sensitivity of 85% and specificity of 91%.

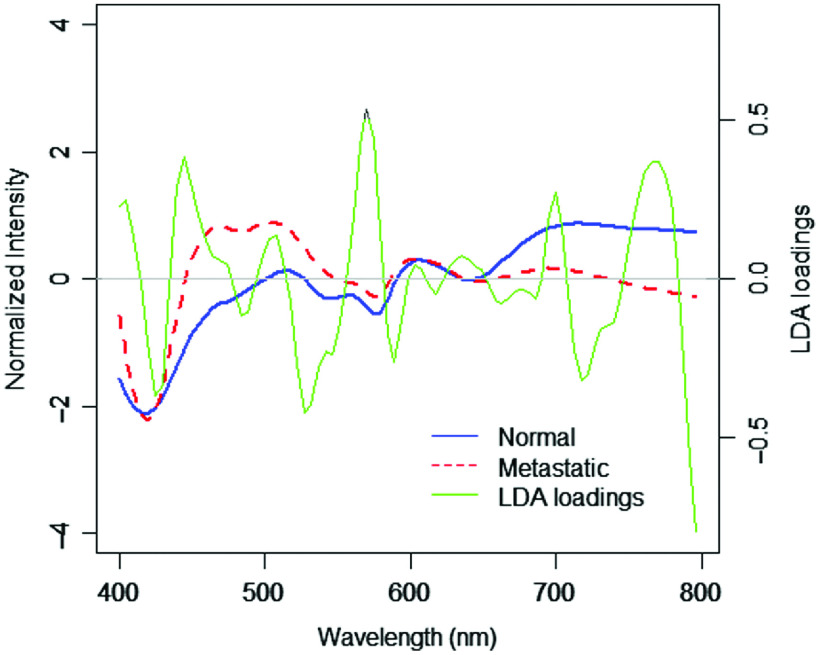
The model works best in a reduced two-dimensional space, spanned by the directions of the external and internal variables. The direction of the external variable separates the normal and metastatic classes. LDA loading used to construct the external variable, shows the contribution at each wavelength to the classification, and thus allows some interpretation of spectral features. In Fig. 5, the LDA loading is derived from an LDA on the first 20 PC scores of the manual data. The high peaks in the LDA loading at around 540 and 580 nm are associated with absorption dips of ${\mathrm{HbO}}_2$ at 542 and 577 nm in the spectra of metastases due to increase in Hb presence. One prominent peak in the LDA loading at around 760 nm corresponding to clear differences between the mean spectra of normal and metastatic nodes is consistent with a lowered oxygen saturation of hemoglobin in dysplastic tissue, as has been noted in various research groups.^28,29 It is known that cancers and precancerous tissues are characterized by increased blood content and decreased hemoglobin saturation.^30,31 These may be some interpretation of spectral features related to the differences between normal and metastatic breast tissues along the axis of external variable. The internal variable then captures the remaining features of each individual node, particularly the nonnodal component.

Fig. 5.

LDA loading for discrimination between normal and metastatic nodes in the manual data. The LDA loading is shown in green, with the mean spectra for the two types superimposed (normal in blue solid line and metastatic in red dotted line).

In a reduced dimensional space, the two-stage image classification model works well and the final images of the model are convincing. Some examples of the images of partially or totally metastatic nodes and normal nodes generated by this optimal model are shown in Fig. 6. In the first stage, guided by the position parameter and the priors from manual data, the three classes in the mixture are almost recognized. The image configuration (in the middle column) shows a rough match to the photograph (in the left column), with some nonnodal spots on the corner or edge being misclassified as metastatic or normal. In the second stage, with spatial smoothness taken into account, the isolated pixels are cleared up, and those misclassified nonnodal pixels all recover (as shown in the right column). The resulting image becomes smoother and exhibits a better match to the photograph. The last two rows of Fig. 6 give examples of a node including only normal and nonnodal components. Due to the variability of metastatic areas, some normal areas may be misclassified as metastatic in the first stage. With spatial information involved those misclassified normal pixels may recover in the second stage. In this situation, the stage 2 is particularly helpful to correctly classify the normal node so as to avoid unnecessary axillary node clearance. The model thus shows its flexibility in capturing features from individual nodes and shows its robustness to the uncertainty of metastatic component.

Fig. 6.

Examples of the constructed images from three partially or totally metastatic nodes (first, second, and third rows) and two totally normal nodes (fourth and fifth rows) using the two-stage image classification model in a reduced two-dimensional space. The left column shows the photographs of the nodes (the red dotted line circles the area suspected of containing metastasis as visually detected by experienced clinicians). The middle and right columns are the first stage and second stage resulting images of the scanned nodes, with posterior probability scores plotted as colors. Red corresponds to spectra indicative of metastases, blue corresponds to spectra indicative of normal lymph tissue, and black corresponds to nonnodal spectra.

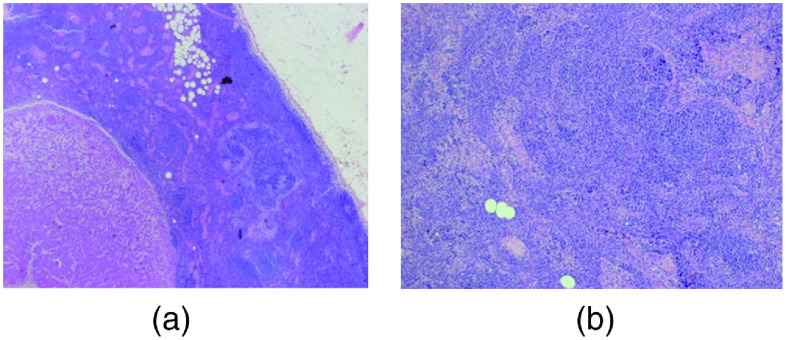
Based on standard histopathological analysis with hematoxylin and eosin (H&E) staining, the pathological diagnostic correlations with ESS were made on a per-node basis. Figure 7 shows exemplary H&E histology images, representative of disease states, albeit not correlated to specific ESS measurement sites.

Fig. 7.

Exemplary H&E histology images of (a) a partially metastatic node showing regional metastasis (lower left) and normal lymphatic tissue (middle), and (b) a normal lymph node.

4. Conclusion and Discussions

In this paper, a partially supervised image classification algorithm based on a Bayesian multivariate mixture model with MRF spatial prior was applied to represent a scanned node diagnostic image for rapid and automatic detection of metastatic sentinel lymph nodes based on an ESS scanning system. With details of the model introduced in another paper,¹⁴ this paper focuses on model selections, interpretation, and evaluation of overall classification performance, in particular taking into consideration the clinical care for patients.

The spectral data are high-dimensional and are projected onto a low-dimensional space before constructing an image classification model. The model works best with the two axes (of external and internal variables), which are function-specific and interpretable. Typically, the external axis derived from the manual data, not derived from the node in question, can separate the normal and metastatic classes; the internal axis derived from the spectra on the node we are interested in allows the model to capture the remaining features of each individual node, particularly the nonnodal component.

Based on the low-dimensional data, this partially supervised image classification model is fitted in two stages. In the first stage, the classification is guided by the prior knowledge of the classes, and a rough image is generated in this stage. In the second stage, an MRF spatial prior is then incorporated into the model to represent the continuity of the image, so as to improve the image classification.

A traditional supervised classification method is not suitable here as the required training data for the nonnodal class is not available and it may not be feasible to acquire such training data in the future due to its considerable variability. This partially supervised image classification model has shown significant benefits in the following aspects. With the position parameter and spatial smoothness of the image taken into account, this model could capture sufficient features to successfully recognize the variable nonnodal area automatically and, hence, enhance the discrimination between normal and metastatic nodes. One particular advantage of this approach is that it will continue to work without retraining if someone decides to change the material used for the background. The classification rule is simple that we classify a node as metastatic if it has even one pixel thus classified, without need for the cluster-of-nine rule. The most attractive points of this model are that it can achieve good classification accuracy and can generate a realistic image for a rapid diagnosis without the need for tissue preparation or expert interpretation. This is crucial for real-time intraoperative diagnosis of sentinel node metastases in breast cancer. As a general method, this model may also be applied to other situations for both noise/background recognition and multigroup tissue classification.

Furthermore, this work has the potential to make an important contribution to the detection of small regions of cancerous cells within sentinel lymph node. Since the reference pathology is not available for individual pixels of the image, but only for each node as a whole, the classification was currently carried out on a per-node basis. However, classification can be carried out on a single pixel basis. In the previous paper,¹³ the cluster-of-nine rule was used. For simplicity, we assume a tumor has circular cross section. With 0.5-mm increment of ESS measurements, metastases with a radius of less than $0.7\mathrm{mm}$ (the distance between pixels on the diagonals) will not be sufficient to declare a node as positive for cancer. The nine-pixel criterion puts a lower limit on detectable tumors of over 1 mm in diameter. In this paper, the probability of individual pixel being metastatic is used to generate ESS image. With spatial correlation taken into account between adjacent pixels in the image, the likelihood of scattered false-positive pixels occurring over a node is low. We therefore classify a node as metastatic if it has even one pixel is classified as metastatic. That is, the model can detect cancer in a single pixel. For ESS measurements with 0.5-mm increment, metastases with a radius of 0.25 mm would be sufficient to declare a node as positive for cancer. So even some micrometastases (cancer deposit 0.2 to 2 mm) in a small area may be detected. The detection of lymph nodal micrometastatic tumor cells provides an accurate assessment of tumor staging and has powerful prognostic implications in breast cancer.³² The early detection of smallest metastases could identify the patients who are most likely to benefit from adjuvant therapy. This work will make essential contribution to assessing the smallest metastases that ESS is able to detect.

The ESS scanned measurement with 0.5-mm resolution is sufficient to detect clinically relevant lymph nodes as the management of breast cancer patients with sentinel lymph node metastases is changing in light of the American College of Surgeons Oncology Group (ACOSOG) Z0011 trial results.³³ Also, our diagnostic algorithm maximizes specificity to avoid unnecessary ALNDs to improve its clinical significance.

The ESS scanner was designed to produce a spatial diagnosis. It would have been ideal to compare the ESS resulting diagnostic images directly with coregistered corresponding H&E histology images. Unfortunately, this was not possible for two reasons: (1) as part of the study protocol, all bivalved scanned nodes were sent for routine histopathological processing and examination by the pathologist, without alteration of the standard histopathology procedure; hence, under that protocol, the diagnostic correlations with ESS were made solely on a per-node basis, without site-specific correlation; and (2) the ESS images are widefield maps, covering an area of 30 to $60{\mathrm{mm}}^2$, with effective resolution of $\sim 1\mathrm{mm}$, whereas the scale of diagnostic histology images (with resolutions of $\sim 1\mu \mathrm{m}$) yields a field of view that is two to three orders-of-magnitude smaller. As such, comparative images for whole nodes were not practical. We note that it would have violated clinical protocol to further dissect the excised nodes during the surgical procedures (to enable histology that was site-correlated with individual ESS measurements). Therefore, in prior publications by our group,^12,13 the training phase in development of the diagnostic algorithm was accomplished by only using spectra that were recorded from nodes deemed to be entirely normal or entirely replaced by cancer. In the testing phase, partially metastatic nodes were included, with diagnosis on a per-node basis. In our future work, we hope to obtain H&E-stained slides that involve multiple sections and are at a higher resolution so as to enable spatial correlation with ESS diagnostic images. Such histological correlation would be instructive in assessing the site-specific metastases and nontumor sites in the metastatic node that ESS is able to detect and would thus strengthen the evaluation of the diagnostic accuracy of SLNB in breast cancer.

Although this image classification model achieves good classification performance assessed by sensitivity and specificity, there is still some scope for improving on it. Since the cancer in a node that is missed during the ESS analysis will still be detected on subsequent routine histology examination, the sensitivity of 85% is certainly good enough for this application to produce some reduction in second operations. The specificity of 94% sounds good with only 6% false-positive rate, but it may not be good enough when examining PPV. Assuming a population prevalence of 20% and the same values of sensitivities and specificities, this choice of parameters would lead to a PPV of 78%. This means that 22% of the cases detected as positive are actually false positives, leading to unnecessary surgical axillary dissection. In this study, probably due to the small data set, it was difficult to obtain a PPV above 90%. To further assess the effectiveness of the diagnostic test, we would like to carry out a prospective clinical study and analysis for future work on a larger number of patients in favor of PPV.

Biography

Biographies for the authors are not available.

Disclosures

The authors have no relevant financial interests in this article and no potential conflicts of interest to disclose.