Quantum stochastic resonance of individual Fe atoms

Magnetic atoms on surfaces exhibit quantum stochastic resonance that synchronizes the atoms’ dynamics to a harmonic drive voltage.

Abstract

Stochastic resonance, where noise synchronizes a system’s response to an external drive, is a wide-reaching phenomenon found in noisy systems spanning from the dynamics of neurons to the periodicity of ice ages. Quantum tunneling can extend stochastic resonance to the quantum realm. We demonstrate quantum stochastic resonance for magnetic transitions in atoms by inelastic electron tunneling with a scanning tunneling microscope. Stochastic resonance is shown deep in the quantum regime, where spin-state fluctuations are driven by tunneling of the magnetization, and in a semiclassical crossover region, where thermally excited electrons drive transitions between ground and excited states. Inducing synchronization by periodically modulating transition rates provides a general mechanism to determine real-time spin dynamics ranging from milliseconds to picoseconds.

INTRODUCTION

Noise has been a constant challenge to effective measurement and analysis, yet it can be harnessed to both interact and controllably modify the behavior of a wide variety of systems. One such case is stochastic resonance (SR), which can be found in harmonically driven stochastic bistable systems with an inherent noise source (1–3). SR can be observed in the periodicity of glaciation (4, 5), in the charge carrier dynamics of microstructure devices (6, 7), and even in the dynamic behavior of neurons (8). Understanding and applying SR to quantum systems, where the dynamics do not rely on thermal activation over a barrier and where the stochasticity can arise from nonequilibrium dissipative processes, open new possibilities for manipulating and controlling quantum systems (3, 9–13). Quantum SR has mostly been a theoretical prediction (3, 12, 13), with only recent experiments showing evidence thereof in driven quantum dot microstructures (7).

SR is possible in harmonically driven stochastic bistable systems with an inherent noise source. It manifests as a frequency-dependent synchronization between the system’s switching and the drive. The switching statistics attain a maximum when the drive frequency is close to the characteristic rate of the noise-induced transitions between the two stable states, thus revealing behavior reminiscent of a resonance even in the absence of a resonator (14). This synchronization may increase the signal-to-noise ratio of a measurement (3, 15), profoundly change the system’s time evolution (14), or reveal dynamics that would otherwise be hidden in the noise (6).

Here, we show, using a scanning tunneling microscope (STM), that the spin dynamics of a single Fe atom undergo quantum SR when excited by a modulated voltage. SR is manifested by a frequency-dependent synchronization of the atom’s spin-state transitions to this oscillating voltage. Figure 1A schematically depicts the atom’s spin state when phase-locked to the voltage drive. At low temperatures, quantum tunneling of the magnetization causes the iron atom to switch spontaneously and stochastically between two magnetic states. Voltage-dependent inelastic electron tunneling from the STM tip modulates the spin transition rates, causing the spin-state evolution to phase-lock most efficiently to the oscillatory drive voltage when the drive frequency and the characteristic time scale of the fluctuations match. At higher temperatures, an additional scattering channel opens and marks the crossover to the semiclassical regime of SR (11). A notable consequence of the frequency-dependent synchronization between spin-state fluctuations and voltage drive is a drive-frequency-dependent change in the average current. This relationship can be exploited to resonantly interact with magnetically unstable atomic structures, making tunneling transitions on the megahertz to gigahertz scale observable.

Fig. 1. Driven spin dynamics of Fe (N site) atoms on Cu₂N.

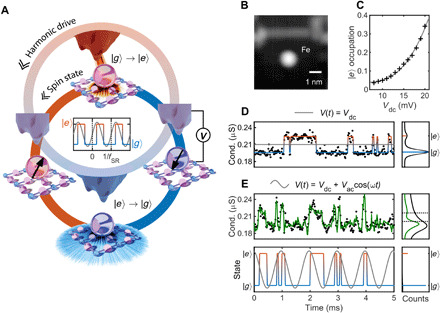
(A) Illustration of the spin state’s excitation and relaxation cycle (lower circle) when phase-locked to a harmonic drive voltage (upper circle). First, the atom (red sphere; top) is excited by high-energy electrons scattering from the tip to the substrate (red streaks); then, the atom (red sphere; left) is in the excited state (arrow pointing upward); next, the surface electron scattering (blue streaks; bottom) results in a relaxation to the ground state; and, last, the atom (blue sphere; right) is in the ground state (arrow pointing downward). The inset shows the SR when the cycle is synchronized to a harmonic drive. (B) Constant current topography of the Fe atom [I_set = 100 pA and V_set = −100 mV, color scale from low (black) to high (white)]. (C) Average occupation of the excited spin state; measured (crosses) and fit by a power law function (solid line). (D) Telegraph noise of the atom’s conductance (black points) observed when applying a constant bias voltage (V_dc = 15 mV) between tip and sample. The corresponding spin state is indicated by a solid line (blue to red). Right: Histogram of the conductance. (E) Measured time trace of the atom’s conductance as a function of time, unfiltered (black) and filtered (green). Bottom trace shows the corresponding spin state (blue to red). Histograms show the distribution of the full conductance/state trace. V_dc = 15 mV, V_ac = 5 mV, and ω = 1 kHz. The drive signal is shown in gray. All measurements are performed at magnetic field B = 500 mT, temperature T = 0.5 K, and setpoint current I_set = 3 nA.

RESULTS AND DISCUSSION

First, we characterize this mechanism by performing real-time measurements of the response of the atom’s spin states to a static bias voltage (V_dc) (Fig. 1D). The Fe atom on the fourfold symmetric N site of copper nitride (Cu₂N; Fig. 1B) has millisecond spin lifetimes when the magnetic field is applied along the spin’s easy axis and it switches spontaneously between two spin states (16–20). These states can be distinguished with a spin-polarized tip as the tip-atom conductance is spin dependent due to tunneling magnetoresistance (21). Hence, time traces of the tunnel current at fixed tip-sample distance yield real-time observations of the spin state (for details, see fig. S2). These slow spin transitions enable real-time resolution that is typically not possible for magnetic atoms on surfaces. They show frequent transitions between two states that occur at voltages well below the first inelastic excitation threshold (21 mV; see fig. S1), consistent with a classically forbidden transition across the magnetic anisotropy barrier. Note that, in this work, we limit the discussion to this subthreshold regime. The occupation of the excited state increases with voltage, while the transition energies of the spin states do not, indicating a voltage-dependent excitation rate (Fig. 1C). The exponent of a power law fit (α = 2.9 ± 0.2) indicates that higher energy states contribute substantially to the excitation mechanism (22, 23). Controlling the atom’s spin transition rates using the externally applied voltage provides a means to drive the SR.

We now introduce a harmonic drive voltage V_ac that modulates the excitation probability periodically in time. Figure 2A shows the spin state’s response at three different drive frequencies, demonstrating that the switching can synchronize to the applied periodic drive, seen as the spin undergoing one cycle of excitation and relaxation in one period of the drive. This is most prominent at approximately 1 kHz.

Fig. 2. Spin-state synchronization.

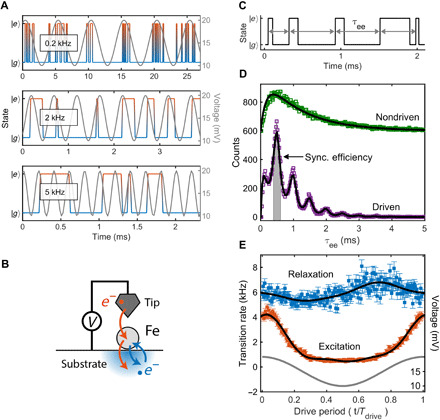
(A) Measured time traces of the atom’s spin state (blue to red) for different driving frequencies (V_ac = 5 mV and V_set = 15 mV). (B) Schematic description of the scattering processes responsible for the excitation (red arrows) and relaxation (blue arrows) of the Fe atom’s spin state. (C) Schematic spin-state evolution with time (black line), with the time τ_ee between excitation events shown with arrows. (D) Event histogram of τ_ee for a constant bias voltage (nondriven, green) and for a driving harmonic signal with a frequency of 2 kHz (driven, purple). The ratio of gray-shaded counts to total counts is the synchronization efficiency. The histogram for the constant bias voltage case is fit with a hypoexponential function (black), while the histogram for the driven case (black) was calculated analytically using the rates in (C). (E) Time-dependent excitation (red) and relaxation (blue) rates are plotted over one period, and the black line is the fit used as input to the SR model (see Methods for details). The corresponding voltage is shown in gray. T_drive = 0.5 ms, B = 500 mT, T = 0.5 K, I_set = 3 nA, V_set = 15 mV, and V_ac = 5 mV.

SR manifests in a profound modification of the switching statistics, which can be quantified by making a histogram (Fig. 2D) of the times between excitations (Fig. 2C, τ_ee, gray arrows). With a static bias voltage applied (nondriven case), the counts exhibit a hypoexponential distribution, in agreement with the expectation of a nonresonant stochastic process governed by telegraph noise (with Poisson-distributed excitation and relaxation processes with different characteristic times) (24). With a 2-kHz drive signal of 5-mV amplitude added to the constant bias voltage (driven case), the counts peak at integer multiples of the excitation period T_drive = 0.5 ms. The peak at T_drive is almost three times larger than the nondriven case, and counts for times above 1 ms are strongly suppressed. The transitions are now synchronized to the oscillating drive. As the counts deviate from a hypoexponential distribution, either the excitation or the relaxation (or both) is no longer Poisson-distributed. Thus, driving fundamentally changes the dynamics of the spin.

The individual switching events in the time traces (Fig. 1D) occur much faster than the time between successive spin-state transitions, so it is reasonable to assume that the conditional probability of a transition out of a state, given that it is occupied, depends only on the instantaneous values of the drive voltages. Since spin correlations have extremely short lifetimes (20, 23, 25), we can consider that no correlations between spin and electron bath exist on the time scale of the N site Fe atom spin switching; therefore, we model all transitions as Markovian, i.e., memoryless. In this Markovian limit, transition rate theory is applicable (15), and the theoretical methods used to characterize quantum SR in (13) can be generalized to calculate the switching time distribution nonperturbatively for any prescribed periodic time dependence of the conditional probabilities (see Methods). Unlike in conventional SR, the individual spin states could couple differently to their environment (tunneling current and electron spin scattering from the bath), which would effectively make the spin states experience different levels of noise. To account for this possibility, we model the excitation and relaxation rates separately.

We extract the conditional transition rates directly from the measured time traces by evaluating the probability to switch between spin states per unit time, relative to the drive cycle (Fig. 2E). We find the relaxation rate to be constant, but the excitation rate is voltage dependent and thus varies throughout the drive cycle. Figure 2B shows a schematic description of the two mechanisms responsible for this effect. The spin transitions in the Fe atom depend only on the attempt rate and the transition matrix element between the states. The transition matrix element is an intrinsic property of the spin and not readily modifiable, but the attempt rate may be modulated. While relaxation is dominated by scattering with bath electrons and therefore remains constant over one period of the drive, excitation is mediated by voltage-dependent inelastic electron tunneling from the tip via the Fe atom to the substrate and is thereby controllable with the applied voltage.

With the conditional relaxation and excitation rates as the only inputs and no fitting parameters, the theory quantitatively reproduces the experimentally obtained switching time distribution in Fig. 2D (driven case). This confirms the prediction that modulating only one of the transition rates in a quantum system induces SR, in contrast to conventional SR where the barrier height between states is modulated (12). This demonstrates that the voltage-dependent synchronization of the Fe atom’s dynamics is caused by quantum SR.

To quantify the degree of synchronization of the Fe atom’s spin to the harmonic drive, we define the synchronization efficiency as the number of counts in the harmonic peak in the switching time distribution normalized by the total number of counts (see gray area highlighted in Fig. 2D). The plot of synchronization efficiency versus frequency in Fig. 3A has a prominent resonant peak centered at 1.4 kHz. Note that this peak arises solely from the statistics of the system and it does not rely on a resonator (14).

Fig. 3. Signature of quantum SR.

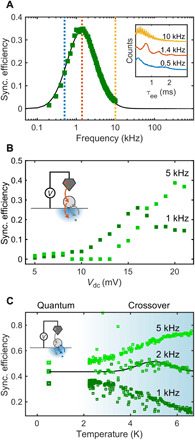
(A) Synchronization efficiency (green) versus drive frequency, with a log-normal fit (black line). Error bars are comparable to marker size. The inset shows the corresponding event histograms at the frequencies indicated by the vertical dotted lines. T = 0.5 K and V_set = 15 mV. (B) Synchronization efficiency versus V_dc for 1 and 5 kHz (green and light green markers, respectively). The inset shows a schematic description of the scattering process. (C) Synchronization efficiency versus temperature for 1, 2, and 5 kHz (dark green, green, and light green markers, respectively; offset for clarity). The inset shows the relevant scattering process. The color gradient indicates the crossover from quantum to semiclassical SR. The black line is a guide to the eye. B = 500 mT, I_set = 3 nA, V_ac = 5 mV, and V_set = 15 mV.

An important characteristic of SR is its strong dependence on the time scale of the noise. In our experiment, we can independently tune two noise sources (26). First, thermal noise, which induces spin transitions by scattering with thermally excited bath electrons, can be adjusted via the sample temperature. Second, nonthermal noise, which induces spin transitions by inelastic tunneling with electrons from the tip, can be controlled via the bias voltage. This constitutes a quantum noise source as it does not vanish when temperature goes toward zero.

By sweeping the applied voltage V_dc at constant drive frequency (Fig. 3B), we tune the Fe atom’s excitation rate from evolving slower than the drive to evolving faster. A clear maximum in synchronization efficiency is observed at 16 mV for a 1-kHz drive. Increasing the drive frequency to 5 kHz shifts the maximum to higher voltages.

Keeping V_dc constant and increasing the temperature yields thresholding behavior (Fig. 3C). The synchronization efficiency remains constant for all measured frequencies up to 2.5 K. For temperatures beyond 2.5 K, with a 1-kHz drive, the synchronization efficiency decreases with increasing temperature; at 2 kHz, a maximum is found at ~4.5 K; and at 5 kHz, it continually increases over the observed temperature range.

This behavior is consistent with the crossover regime between quantum and semiclassical SR, where thermal excitations and quantum tunneling become comparable. At low temperatures, the SR is generated by the quantum noise of electron tunneling for which the synchronization efficiency peaks at 1.4 kHz. Above 2.5 K, thermally excited electrons begin to participate in the scattering and increase the spin switching rate, moving the SR away from its quantum limit.

SR actively modifies the ground-state occupation as a function of drive frequency (Fig. 4A); the dependence is well approximated by a Lorentzian line shape centered at 0 Hz. Because of the difference in conductance between the ground and excited states when observed with a spin-polarized tip, the time-averaged tunnel current directly maps the frequency-dependent occupation n_g via the relation: $\overline{I}=[n_{\mathrm{g}}{\mathrm{\sigma }}_{\mathrm{g}}(\mathrm{\eta })+(1-n_{\mathrm{g}}){\mathrm{\sigma }}_{\mathrm{e}}(\mathrm{\eta })]V_{\text{dc}}$, where V_dc is the DC bias voltage, η is the spin polarization of the tip, and σ_g and σ_e are spin polarization–dependent conductivities of the ground and excited states, respectively. This unlocks access to the stochastic dynamics of quantum spins that evolve at time scales faster than the real-time limit of the STM.

Fig. 4. Modulating time-independent observables.

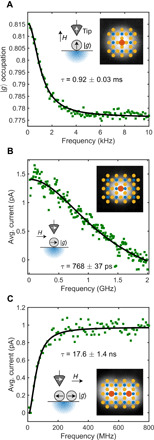
(A) Average occupation of the nitrogen site atom’s ground state as a function of the driving frequency along with a Lorentzian fit (black line), B = 500 mT. (B) Time-averaged spin-polarized current measured on a copper site atom with easy axis parallel to the external magnetic field, B = 1.5 T (C) Time-averaged spin-polarized current measured on an antiferromagnetically coupled Fe dimer oriented parallel to the external magnetic field, B = 2 T. Insets for all three panels show a constant current topography acquired at I_set = 100 pA and V_set = 100 mV, with a corresponding overlay of the atomic structure (Cu, orange; N, blue; Fe, red). Each panel also includes a schematic description showing the relative orientation of the nanostructure’s ground state (light gray), the spin-polarized tip (dark gray), and the external magnetic field (H).

We apply this to an Fe atom adsorbed on a different binding site with increased transverse magnetic anisotropy (27), which markedly increases the transition rate between the ground and excited states. Consequently, the SR shifts by six orders of magnitude in frequency, from kilohertz to gigahertz (Fig. 4B), and establishes that the spin fluctuates at a characteristic time scale of 768 ps.

Beyond the time scale of fluctuations, these measurements also give insight into the details of the spin states involved. The reversed sign of the Lorentzian when measuring on an antiferromagnetic dimer of Fe atoms (Fig. 4C) shows that the excited state has a higher conductance than the ground state, which, together with the increased time constant, indicates that the two atoms are switching collectively.

The ability to detect SR by measuring variations of the time-averaged occupation of states extends this approach to a variety of spin-based (17, 28–31) and charge-based (32) atomic-scale quantum systems with ultrafast dynamics. Increasing the measurement bandwidth from the 2 GHz demonstrated here to 90 GHz [which has been demonstrated previously in the STM (33)] would resolve subpicosecond spin dynamics. We posit that this approach allows for the study of dynamics at the fundamental time scale of electron scattering on surfaces (23), as the measurement time scale approaches the rate at which bath electrons reach a new steady state after a scattering event. In this limit, the behavior at high frequencies can yield insight into the fundamental processes governing the conditional transition probabilities in any quantum system where transition rates between discrete states can be modulated by an external drive voltage and may reveal the emergence of correlation-induced non-Markovian dynamics, the stabilization of dissipative coherence (9), the coherent destruction of tunneling (10), or the effect of driving-induced quantum coherence (11).

METHODS

Experimental methods

Low-temperature scanning tunneling microscopy experiments were performed in a sub-Kelvin Unisoku ³He vector magnetic field [(2,2,9) T] STM, type USM 1300 ³He. The sample preparation was performed in ultrahigh vacuum, where we prepared a Cu(100) single crystal with repeated Ar⁺ sputtering (ion energy of 1 keV) and annealing (850 K) cycles. A monolayer of Cu₂N (27) was grown by N₂ sputtering (ion energy of 1 keV) at a N₂ partial pressure of 5 × 10⁻⁶ mbar and consecutive annealing to 600 K. The sample was precooled to approximately 20 K, and Fe atoms were deposited by positioning the cold sample in a low flux of Fe vapor from a Knudsen cell for 8 s.

Atom manipulation

Fe atoms were placed on the nitrogen adsorption site and the copper adsorption site using vertical atom manipulation (34) with a Pt/Ir tip. The Fe atom is directly dropped onto the N site of the Cu₂N surface (16). For the adsorption on the Cu site, the atom is hopped from the N site toward the Cu site. The nitrogen adsorption site yields a larger apparent height compared to the copper site, which itself can be occupied by hopping the atom in the four different directions defined by the crystal symmetry using a small voltage pulse. A spin-averaging tip does not reveal any inelastic excitation thresholds in dI/dV spectra. We obtain a spin-polarized STM tip by picking up a cluster of Fe atoms. The magnetic field is applied along the out-of-plane direction. The dI/dV spectra recorded with a spin-polarized tip reveal an excitation localized at 21 mV that is affected by the applied magnetic field (fig. S1). Below 21 mV, an initial lowering of the conductance is observed followed by a sharp peak for larger bias magnitude. We attribute this to spin pumping into a long-lived excited state. Between 5 and 20 mV, increased current noise is observed in the spectrum. This noise results from stochastic switching of the Fe atom’s magnetic moment induced by tunneling of the magnetization between excited and ground states that can occur below the excitation threshold. Here we limit the discussion to the subthreshold regime as excitations occur on a time scale that can readily be resolved.

Spin Hamiltonian

We use an effective spin Hamiltonian model and describe electron spin scattering up to second order in the atomic spin to calculate the conductance spectrum of the Fe atom on the nitrogen site of the copper nitride surface (35). By allowing for a small transition probability between the two lowest lying states, we can explain the spontaneous switching that is observed below the first inelastic excitation threshold. The Fe atom’s magnetic moment is expressed in terms of an effective S = 2 spin model. Orbital angular momentum contributions are modeled by the magnetocrystalline anisotropy terms of the Hamiltonian and a Landé g factor of 3. This yields the spin Hamiltonian

$$\widehat{H}=B_2^0{\widehat{O}}_2^0+B_4^0{\widehat{O}}_4^0+B_4^4{\widehat{O}}_4^4+g{\mathrm{\mu }}_{\mathrm{B}}\widehat{\mathbf{S}}\bullet \mathbf{B}$$

where $B_p^q$ and ${\widehat{O}}_k^q$ are the Stevens operators and their associated coefficients that can be nonzero for the fourfold symmetry of the N binding site. $\widehat{\mathbf{S}}$ is the Fe atom’s spin operator, B is the magnetic field, and μ_B is the Bohr magneton. Fit coefficients that yield best agreement between spin Hamiltonian model and measured dI/dV spectra are listed in fig. S1. This fit yields qualitative results, and it reproduces both the dip at approximately the Zeeman splitting of a spin 2 atom in a 500-mT magnetic field (see right panel for state diagram), and the first allowed transition at 21 mV (marked with a yellow arrow). Both features result from spin pumping into the long-lived excited state that modifies the dI/dV (22, 25). The large uncertainty in the second two Steven’s operator coefficients is due to the dI/dV being a static measurement and points to the need for a dynamic measurement/modeling technique.

Event recognition and data analysis

The switching of the Fe atom between different spin states can be detected by a change in conductance of a spin-polarized tunnel current with z feedback turned off (25). At constant bias, this spin-state switching directly transduces into tunnel current switches with each current value corresponding to a specific spin state due to the spin polarization of the tip. When applying an oscillating voltage to the tunnel junction, the current is modulated not only by the spin-state switching but also by the oscillating bias voltage. A direct discrimination between ground and excited states in terms of a switching in the current amplitude is no longer possible. By recording the applied bias voltage synchronous with the tunnel current, the voltage oscillation can be demodulated. The demodulated signal then contains only the fluctuations of the tunnel current induced by the spin-state switching.

This process is schematically depicted in fig. S2. First, the modulated voltage (A1) yields a modulated tunnel current (A2). These two measured quantities readily allow the time-dependent conductance (A3) to be determined. By subtracting the voltage multiplied with the average set point conductance from the current and dividing by the average voltage, the conductance can be determined in a more noise-robust manner than simple division. This approximation is correct up to second order in spin-induced conductance changes. Persisting noise from the time trace is filtered (A4) by a time-domain convolution filter that is optimized to filter out instrument-specific noise peaks (fig. S2B). We checked that this convolution filter does not introduce spurious signals by reference measurements without an oscillating voltage applied. Last, a Schmitt trigger threshold function can be used on this dataset to extract the switching between spin states and generate an event trace (A5) that directly shows the time that the Fe atom spends in the excited and ground states. The thresholds are chosen by generating a histogram of the conductance trace (as in the top right panel of Fig. 1E) and by setting the thresholds at one-fifth of the peak width below the excited-state peak and one-fifth of the peak width above the ground-state peak. This was found to optimize between spurious event recognition (from instrument noise crossing the threshold when it is too low) and to ensure that no real events are missed (if the threshold is too high).

Figure S2C shows a comparison between the power spectral density for the raw conductance trace and the event trace after filtering and applying the trigger threshold, verifying that both the filter function and thresholding preserve the Lorentzian power spectrum of the spin switching.

Conditional transition rates

The conditional transition probabilities are the only input needed for the SR model and need to be determined experimentally from the measured transition rates. The conditional transition rate is the function W_ab(t) that gives the probability to make a transition from state a to state b in a time dt as W_ab(t)dt. To obtain these transition rates, the full-time trace of length t_meas is mapped to $\raisebox{1ex}{$t_{\text{meas}}$}\!\left/ \!\raisebox{-1ex}{$T$}\right.$ segments, where T is the modulation period. By then defining M bins within T, we can count how often the spin switching occurred in each of the M bins in each segment. Considering that there were c_ai transitions per $\raisebox{1ex}{$\mathit{dt}$}\!\left/ \!\raisebox{-1ex}{$T$}\right.$ per t_meas, where $\mathit{dt}=\raisebox{1ex}{$T$}\!\left/ \!\raisebox{-1ex}{$M$}\right.$, this yields the discrete form of the time-dependent rates R_ab(t)

$$R_{\mathit{ab}}(t=i\bullet \mathit{dt})=c_{\mathit{ai}}\frac{M}{t_{\text{meas}}}$$

where c_ai is the count of transitions out of state a in the ith bin. R_ab(t = i ∙ dt) is then divided by the time-dependent occupation of state a n_a(t = i ∙ dt), which has also been binned in the same M bins, yielding the conditional transition rate

$$W_{\mathit{ab}}(t=i\bullet \mathit{dt})=\raisebox{1ex}{$R_{\mathit{ab}}(t=i\bullet \mathit{dt}) $}\!\left/ \!\raisebox{-1ex}{$n_a(t=i\bullet \mathit{dt})$}\right.$$

For a sufficiently large M, W_ab(t = i ∙ dt) can be linearly interpolated to yield the conditional transition rate at any arbitrary time within the period. The statistical error resulting from the binning of both the transitions and the occupation was accounted for in generating the error bars in Fig. 2E. Bins were chosen such as to minimize this error.

Synchronization efficiency

Throughout this work, we quantify the strength of SR using the synchronization efficiency. This is calculated by comparing the relative area of the window around the modulation period ±¹/₄ period (shaded in gray in Fig. 2D) in a histogram of the time between switching events, to all other measured times between switching events. Thus, the synchronization efficiency measures how well a full cycle of excitation and relaxation is matched to the harmonic drive signal. It is a direct measure of the synchronization effect that is at the heart of the SR process (14) and allows direct comparison of the SR as a function of all relevant parameters: frequency, voltage-controlled noise, and temperature-controlled noise (Fig. 3). For reference, fig. S4 shows the SR in signal-to-noise ratio as a function of noise amplitude (controlled via voltage).

Spin switching transduction via SR

To measure the dynamics of the copper site Fe atom (Fig. 4B) and those of the antiferromagnetically coupled Fe dimer (Fig. 4C), a lock-in amplifier and a high-frequency voltage source are used. The drive-induced spin switching is much faster than the bandwidth of the transimpedance amplifier (Femto DLPCA-200), and only its effect on the integrated current can be detected. The drive voltage is generated using a Keysight M8195A Arbitrary Waveform Generator, applied directly to the tip lead of the STM. To measure the resulting rectified current, the drive voltage is applied for the first half of the lock-in cycle and off for the second half. This makes the lock-in output proportional to the drive-induced rectified current and allows it to be separated from the current caused by the constant DC voltage. The amplitude at the junction is held constant by accounting for the attenuation of the transfer line (36). The lock-in frequency is 691 Hz, well below the 1-kHz cutoff of the transimpedance amplifier in 10⁹ gain mode. Because of the spin polarization of the STM tip and the differing conductivities of the ground and excited states for both structures, the rectified current corresponds to the relative occupation of the ground and excited states.

Theoretical methods

The theoretical calculations use methods developed to characterize systems exhibiting SR in (12, 13). In the theory, it is assumed that it is appropriate to describe the system’s dynamics in terms of transitions between two states, with the conditional probabilities of these transitions having no dependence on the length of time that the system has been in its current state. Defining W_slow(t) and W_fast(t) to be the conditional rates of transitions out of the ground state g and the excited state e given that the appropriate state is occupied, n_g(t) and n_e(t), the probabilities that the system is in state g and state e, respectively, satisfy the differential equation

$$\frac{d{n}_e}{\mathit{dt}}=W_{\text{slow}}(t)n_g(t)-W_{\text{fast}}(t)n_e(t)$$ (1)

$$=W_{\text{slow}}(t)-[W_{\text{fast}}(t)+W_{\text{slow}}(t)]n_e(t)$$

where the second line follows because n_e(t) + n_g(t) = 1.

In (13), it is demonstrated that when W_slow(t) and W_fast(t) are periodic in time with period T, at long times, the solution to Eq. 1 approaches a function n_e(t) that is also periodic with period T. The explicit form of function n_e(t) is

$$n_e(t)=\frac{1}{1-e^{-\langle W\rangle T}}{\displaystyle {\int }_0^T}d{t}^{*}{W}_{\text{slow}}(t-t^{*})e^{-\langle W\rangle t^{*}}h(t-t^{*},t)$$

where

$$h(t_1,t_2)=\text{exp}[-{\displaystyle {\int }_{t_1}^{t_2}}d{t}^{*} \mathrm{\delta }W(t^{*})]$$

$$W(t)=W_{\text{slow}}(t)+W_{\text{fast}}(t),\text{and} \mathrm{\delta }W(t)=W(t)-\langle W\rangle$$

The experimental measurements of time-independent observables shown in Fig. 4 can be compared to the time average of n_e(t). The methods from (12, 13) can be extended to obtain theoretical predictions for the time between excitations τ_ee and are shown in Fig. 2 in terms of the time-dependent conditional probabilities W_slow(t) and W_fast(t). Defining the synchronization Q(τ) as the probability density that the time between successive slow transitions is τ and Y_slow(τ) as the probability of a transition from the ground state to excited state occurs at a time τ relative to the drive, we find

$$\begin{array}{c}Q(\mathrm{\tau })={\displaystyle {\int }_0^T}{\mathit{dt}}_0{Y}_{\text{slow}}(t_0){\displaystyle {\int }_{t_0}^{t_0+\mathrm{\tau }}}{\mathit{dt}}_1 \text{exp} [-{\displaystyle {\int }_{t_0}^{t_1}}d{t}^{\prime }{W}_{\text{fast}}(t^{\prime })]W_{\text{fast}}(t_1)\\ \text{exp}[-{\displaystyle {\int }_{t_1}^{t_0+\mathrm{\tau }}}d{t}^{″}{W}_{\text{slow}}(t^{″})]W_{\text{slow}}(t_0+\mathrm{\tau })\end{array}$$

This equation can be understood by noting that the first (slow) transition from the ground state to the excited state takes place at time t₀ relative to the drive and therefore occurs with probability Y_slow(t₀). Then, there is a fast transition back down to the ground state at time t₁: The conditional probability that this fast transition happens at time t₁, given that the first transition was at time t₀, is the product of the probability that it did not happen between t₀ and t₁ and the probability that it did happen between time t₁ and t₁ + δt₁. The conditional probability that the next transition from the ground state to excited state occurs at time t₀ + τ is analogous; it is the product of the probability that the transition did not happen between time t₁ and t₀ + τ and the probability that it did happen between time τ and τ + dτ [which is W_slow(t₀ + τ)dτ].

The function Y_slow(t) is simply related to n_g(t)

$$Y_{\text{slow}}(t)=n_g(t) W_{\text{slow}}(t)/N$$

where N is the normalization constant

$$N={\displaystyle {\int }_0^T}\mathit{dt} n_g(t)W_{\mathit{\text{slow}}}(t)$$

Figure 2B compares the experimentally measured synchronization probability to the theoretical calculation of this probability using the measured values of the voltage-dependent transition rates (Fig. 2C).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/33/eabg2616/DC1