Abstract
Understanding causality is of crucial importance in biomedical sciences, where developing prediction models is insufficient because the models need to be actionable. However, data sources, such as electronic health records, are observational and often plagued with various types of biases, e.g. confounding. Although randomized controlled trials are the gold standard to estimate the causal effects of treatment interventions on health outcomes, they are not always possible. Propensity score matching (PSM) is a popular statistical technique for observational data that aims at balancing the characteristics of the population assigned either to a treatment or to a control group, making treatment assignment and outcome independent upon these characteristics. However, matching subjects can reduce the sample size. Inverse probability weighting (IPW) maintains the sample size, but extreme values can lead to instability. While PSM and IPW have been historically used in conjunction with linear regression, machine learning methods –including deep learning with propensity dropout– have been proposed to account for nonlinear treatment assignments. In this work, we propose a novel deep learning approach –the Propensity Score Synthetic Augmentation Matching using Generative Adversarial Networks (PSSAM-GAN)– that aims at keeping the sample size, without IPW, by generating synthetic matches. PSSAM-GAN can be used in conjunction with any other prediction method to estimate treatment effects. Experiments performed on both semi-synthetic (perinatal interventions) and real-world observational data (antibiotic treatments, and job interventions) show that the PSSAM-GAN approach effectively creates balanced datasets, relaxing the weighting/dropout needs for downstream methods, and providing competitive performance in effects estimation as compared to simple GAN and in conjunction with other deep counterfactual learning architectures, e.g. TARNet.
Keywords: Causal AI, Causal inference, Deep learning, Biomedical informatics, Generative adversarial networks, Propensity score, Treatment effect, Electronic health record, Big data
1. Introduction
In many research domains –especially in medicine and social science– it is challenging to distinguish conditional association from causation, yet such distinction is crucial for developing models that can be used to evaluate interventions, i.e. how actions can causally lead to desired effects. A typical causal inference scenario in medicine is to determine whether a treatment is effective with respect to an health outcome (e.g., lipid-lowering medications to reduce the risk of cardiovascular disease). The randomized controlled trial (RCT) randomly assigns treatments to individuals, making the treatment independent of individuals’ characteristics and guaranteeing that if an effect on an outcome is found, it can only be attributed to the treatment [23]. Nonetheless, performing RCT experiments is not always possible due to ethical concerns or operational grounds, e.g., it would not be ethical to assign and force individuals randomly to smoking for assessing if it caused lung cancer. Therefore, in many real-world situations, observational data are the only resource.
In observational studies, the knowledge on the data generation process or the space of variables involved in such process is limited. Hence, observational datasets can be contaminated with different biases, arising in various steps of the data generation process, and thus, impeding the way to infer causal claims [17]. Types of these biases include confounding (i.e., missing the true cause of an outcome but including spurious features correlated with the cause) and colliders (i.e., mistakenly including effects of an outcome as predictors), and other more complex configurations such as M-shaped or butterfly bias [3].
Therefore, inferring causal effects from observational data is problematic, and requires proper handling of possible biases on top of applying regression techniques. When analyzing the effect of a treatment intervention on a health outcome, propensity score matching (PSM) is often used to make the treatment independent from other pre-treatment covariates –in effect, balancing the existing data to resemble an RCT [18]. The propensity score π(x) represents the probability of receiving a treatment T = 1 (assuming that the alternative is no treatment T = 0) conditioned on the pre-treatment covariates X, denoted as
| (1) |
The propensity score can be estimated using any regression method –often, regularized logistic regression is used [26]. Then, through PSM, the original dataset is re-balanced by matching pairs of treated/untreated individuals (i.e., cases vs. controls) by their propensity scores. Several algorithms can be used for the PSM process, such as k-nearest neighbor or caliper matching [2]. However, PSM often leads to exclusion of instances, and can evidently decrease the sample size or feature space. Thus, in real-world problems, (i) the number of controls often exceeds the number of cases, and (ii) the propensity score distribution of the case population can be seemingly shifted from the control population. Instead of PSM, other techniques such as inverse probability weighting (IPW) can be used, but they can also pose problems due to extreme values of the weights [6]. In general, PSM, IPW and related methods hinge upon the potential outcomes statistical framework [18, 19], which represents the observed (factual) and unobserved/potential (counterfactual) outcomes given a treatment, used to calculate causal treatment effects, both at the individual level and at the population (average) level.
Machine learning approaches have been used in the potential outcomes framework, e.g. Bayesian additive regression trees [7] and random forests [27]. The increasing availability of large amounts of electronic health record (EHR) also led to the flourishing of deep learning for causal inference [9], exploiting nonlinear approaches related to PSM and IPW. Notable examples include Treatment-Agnostic Representation Network (TARNet) [21], Dragonnet [22], and the Deep Counterfactual Network with Propensity-Dropout (DCN-PD) [1]. In TARNet, a two-heads multitask model was developed for estimating a binary treatment outcome, where each sample is assigned a specific weight indemnifying the imbalance between the treated and the control groups. During training, only parameters of one head of the network are updated, according to the treatment assignment indicator of the sample. Dragonnet was a modified TARNet which exploited targeted regularization using propensity scores. In DCN-PD, a doubly-robust model [4] was utilized, where a feed-forward network and a multitask network were developed to estimate the propensity score and the individual treatment effects, respectively. Then, a dropout probability of the network for each sample was calculated from its propensity score, and such dropout probability was used to regularize the network [25].
1.1. Contribution
In this work, we aim at addressing the problem of sample size reduction by PSM, without recurring to weighting schemes, to provide a general data re-balancing method applicable to any learning method downstream. We propose a novel deep learning approach –the Propensity Score Synthetic Augmentation Matching using Generative Adversarial Networks (PSSAM-GAN)– which leverages GAN [5] to generate data samples that can cover the treatment propensity space. In other words, PSSAM-GAN artificially creates treatment matches for unmatched controls (or vice versa). Deep generative models have been increasingly employed for causal inference problems, e.g. the Generative Adversarial Nets for Inference of Individualized Treatment Effects (GANITE) [29], Causal Effect Variational Autoencoder (CEVAE) [13], and Causal-GAN [11]. To the best of our knowledge, this is the first time GAN are not used directly for counterfactual prediction, but for separating the prediction task from the bias-handling. We here provide a generative model for data re-balancing, apt to aid not only with outcome prediction, but also with parameter inference.
After generating the unmatched samples with PSSAM-GAN, a semi-supervised method can be used to train a given multitask regression model, used to estimate average or individual treatment effects (through counterfactual prediction). In the experiments conducted here –using a semi-synthetic dataset from an RCT on perinatal intervention, and two real-world datasets on work interventions and antibiotic treatments– we show that PSSAM-GAN effectively creates balanced data, and favorably compares to the regularization approaches of DCN-PD and TARNet. In fact, PSSAM-GAN enables the application of a broader set of methods, not necessarily doubly-robust, guaranteeing the upstream handling of group assignment bias.
2. Methods
2.1. Problem formulation
We use the potential outcomes framework [18,19]. Thus, we consider a population sample of N individuals who can be prescribed a treatment T (binary, for simplicity), have a set of pre-treatment background covariates X, and have a measured health outcome Y. We denote each subject i as the tuple . For each individual i the potential outcomes are represented as and when applying treatments Ti = 0 and Ti = 1, respectively. The individualized treatment effect (ITE) τ(x) for an individual i with feature vector Xi = x is defined as the difference in the mean potential outcomes under both treatment interventions (i.e., treated vs. not treated), conditional on the observed covariate vector x
| (2) |
Since an individual cannot be on and off treatment at the same time, i.e. one cannot obtain both potential outcomes from a person, we cannot calculate τ(x) directly. Only one outcome (factual) can be observed, while the other (counterfactual) is missing. If the potential outcomes are independent of the treatment assignment, conditionally on the background variables, i.e. {Y1, Y0} ⊥T|X, the assumption of strongly ignorable treatment assignment (SITA) is met [8,15]. Under the assumption of SITA, we can calculate ITE as follows: .1 Further, under SITA and by averaging over the distribution of X, we can calculate the average treatment effect (ATE) τ01 as follows:
| (3) |
ITE and ATE can be calculated with x being equally matched in treatment/control groups but stratification becomes infeasible as the dimension of x increases. With the help of PSM/IPW, through the conditional probability π(x) one can balance the probability of receiving T given X = x across the two comparison groups.
2.2. Proposed framework
The objective of PSSAM-GAN is to improve PSM by generating synthetic samples that can be paired to unmatched instances, covering the covariate space that would be otherwise lost, and re-balancing the dataset.
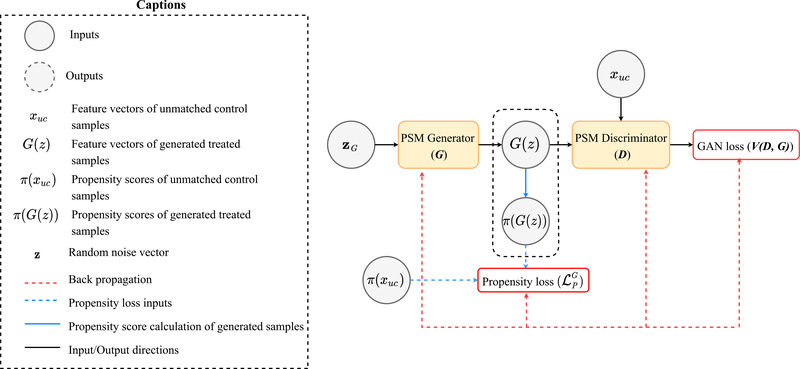
We outline the PSSAM-GAN procedure in Fig. 1. First, a regular PSM is performed on the original dataset. Second, a GAN is used to generate synthetic data, whose propensity scores would pair with the unmatched instances, leftover by PSM. Third, a semi-supervised learning approach assigns labels (i.e., outcomes) to the GAN-generated data. Finally, the synthetic data are collated to the original dataset and this balanced dataset can be used with regular learning algorithms.
Fig. 1.
Schematic of the PSSAM-GAN framework.
2.2.1. Propensity score matching
We calculate the propensity score vector π(X) for the dataset using a given regression method. Among the possible off-the-shelf choices, e.g. Bayesian additive regression trees, neural networks, logistic regression or LASSO, we used the neural network configuration used in the propensity network part of DCN-PD [1]. This choice gives more flexibility than logistic regression or LASSO in calculating propensity scores because it is able to address nonlinear or nonparallel treatment assignments. We then pair the treated and control samples according to their propensity scores. Here, we use a nearest-neighbor matching with replacement, which has been shown to provide a good bias-variance trade-off [2]. After matching, we pass the unpaired instances on to the GAN. For simplicity, we assume from now on that the unmatched instances are all controls (since with EHR usually the selection is in treatment assignment). Nonetheless, the GAN can generate samples to match also the leftover treated.
2.2.2. Generation of synthetic samples
Next, we use a GAN to generate a number of treated samples using the propensity score distribution of the unmatched controls as a guide. The GAN consists of two feed-forward networks, a generator and a discriminator, trained in the classical adversarial manner, such that the generator learns the true data distribution p(x) and fools the discriminator by producing fake samples. The standard optimization function to train a GAN with data distribution as p(x) and random noise as p(z) follows [5]:
| (4) |
The primary objective of the generator G in PSSAM-GAN is to learn the distribution of the unmatched control pdata(xuc) such that it can fool the discriminator. To accomplish this, the generator is given a random noise as input. Along with this, an additional constraint to the generator is that the generated samples must have a similar propensity scores as the unmatched control ones. To achieve this, we introduce the following propensity loss that implements the propensity score constraint:
| (5) |
where and π(G(z(i))) are the propensity scores of the ith unmatched control and generated treated sample. As a result, G will output a full feature vector of a sample whose propensity scores will be as close as the unmatched control ones; at this point we set T=1 to consider them as treated. We show the architecture of the GAN block of PSSAM-GAN in Fig. 2. With the two objective functions of above, the generator G is iteratively optimized with m mini-batches as follows:
| (6) |
where is the ith unmatched control sample, and β > 0 is a hyperparameter. Similarly to GANITE [29], β has to be tuned during the experiments, to manage the relative weighting between the generator loss and the propensity loss.
Fig. 2.
Architecture of the generative adversarial network used in PSSAM-GAN to generate synthetic (treated) samples to be paired with the unmatched (control) samples by the propensity score matching.
The discriminator D in PSSAM-GAN is a standard discriminator whose primary objective is to differentiate the real unmatched control and fake generated samples. The discriminator D is optimized with m mini-batches as follows:
| (7) |
2.2.3. Synthetic labeling
The GAN generates unlabeled instances. In principle, outcome assignment based on nearest-neighbor match could be used, but rather than the sole comparison of π(X), one should match on X, thus needing a specific distance function. Another, more general-purpose option is semi-supervised learning [30]. Here, we employed multitask regression by TARNet and DCN-PD, using the regularizer, to infer the outcome labels Y for the generated samples. In this way, we were able to obtain both a factual and counterfactual outcomes, and then use either one based on treatment assignment. Of note, we tested the label assignment using the original dataset and also only the PSM-induced subset.
2.2.4. Downstream model learning
The original dataset is merged with the synthetic one into a balanced final dataset, which is used to train a multitask regression model such as TARNet or DCN-PD. Note that when creating the augmented dataset, some duplicates from the initial PSM stage can be included. Models are then evaluated in terms of ITE/ATE using a holdout test set which was never used in any previous step.
Algorithm 1 describes the different phases of PSSAM-GAN algorithm to obtain the final model. Note that by removing the propensity loss in Eq. 5, it is possible to obtain a simple GAN, consistent with the one proposed in [5]. The simple GAN will be compared with the proposed PSSAM-GAN in the experimental settings, showing the performance gain provided by incorporating the propensity loss equation.
2.3. Experimental setup
2.3.1. Datasets
Evaluating causal inference algorithm on real-world data is always difficult because of the problem of underlying unmeasured bias and missing counterfactual outcomes. Nonetheless, these data are crucial for evidence-based validation. In this work, we used both semi-synthetic (i. e., real factual outcomes and simulated counterfactuals) and real data.
The semi-synthetic dataset is derived from the Infant Health and Development Program (IHDP), a real RCT for improving health outcomes of premature infants (https://www.icpsr.umich.edu/web/HMCA/studies/9795). The original data was artificially modified to induce bias, by selecting only one ethnic group (non-white) in one intervention arm, while the other included all. Then, a nonlinear surface outcome function was designed to fit a given treatment effect, providing counterfactual outcomes. The final dataset consists of 747 subjects –139 treated and 608 controls– with 25 covariates associated with each subject [7].
Next, we use the Jobs dataset [12,24], which includes two population samples subject to work interventions and income survey: the LaLonde’s National Supported Work Demonstration (NSWD) experimental sample (297 treated, 425 control) and the Population Survey of Income Dynamics (PSID) comparison group (2,490 control). This is real data that does not involve any alteration or simulation. There were 482 (15%) subjects unemployed by the end of the study. The treatment variable was job training and the outcomes were post-training income and employment status. A binary classification task was set up as described in [21]. Both IHDP and Jobs have been used widely as benchmarks in causal inference studies (https://www.fredjo.com/).
Algorithm 1.
PSSAM-GAN: Propensity Score Synthetic Augmentation Matching using Generative Adversarial Networks.
| Input: Training set X = {(x(1), t(1), y(1)),…, (x(n), t(n), y(n)) }, loss function L(., .), hyperparameter β > 0, generator network G with initial parameters θg, discriminator network D with initial parameters θd, epochs K |
| 1. Perform neural network-based propensity score π(X) calculation and matching between the treated samples (t = 1) and control samples (t = 0) using the nearest neighbor algorithm with replacement |
| 2. Separate out the unmatched control samples from the matched ones |
| 3. for epochs = 1, 2, … ,Ks do |
| 4. Sample minibatch of m noise samples where |
| 5. Sample minibatch of m unmatched control samples from the distribution pdata(xuc) |
| 6. Update the discriminator D by ascending its stochastic gradient: |
| 7. Sample minibatch of m noise samples where |
| 8. Update the generator G by descending its stochastic gradient: |
| 9. end for |
| 10. Remove the discriminator D and get the generated samples from the generator G and assign them as treated |
| 11. Train a multitask regression model with the original training set X to obtain outcome labels for the generated treated samples |
| 12. Merge the original dataset with the synthetic data into an augmented balanced dataset |
| 13. Train a multitask regression model with the augmented dataset |
Next, we use a collection of bacterial samples (Staphylococcus aureus) sequenced by Multilocus sequence typing (MLST) with associated information on antibiotic resistance (https://pubmlst.org/), which was previously used to identify genetic resistance signatures [16]. This is a novel, real dataset. Bacteria acquire resistance to antibiotics through various genetic mechanisms, e.g. mutations or horizontal gene transfer, but configurations for housekeeping genes are usually limited to few, specific point mutations. Therefore, the propensities of treatment resistance or susceptibility for most mutations in housekeeping genes should be similar. However, much larger discriminative value of housekeeping mutations was found, which could be explained by selection bias [16]. The S. aureus dataset included 2006 samples, over 3000 housekeeping mutation variables, and the methicillin antibiotic treatment.
2.3.2. Deep learning modules’ settings
For the GAN module, we use a 3-layer feed-forward neural network for both the generator and discriminator with LeakyRelU [28] activations in the hidden layers. The generator includes between 17 and 25 hidden units in each layer (tuned for each dataset), whereas the discriminator included 25 hidden unites. The generator/discriminator learning rates and the hyperparameter β were set to 0.0002 and 1.0, respectively. The GAN was trained for 10,000 epochs (Ks) with a mini-batch size (m) of 64. The parameters of the generator (θg) and discriminator (θd) were updated by the Adam optimizer [10].
We evaluated PSSAM-GAN under different multitask regression configurations, varying weighting and dropout schemes: (i) DCN-PD; (ii) DCN without PD; (iii) DCN with constant dropout probability of 0.5 for all layers and all training examples; (iv) TARNet; and (v) the GAN without the propensity loss (defined by Eq. 5). The methods were trained both with the original dataset and with the augmented balanced dataset which included the synthetic instances. DCN-PD employs an alternate training strategy where either treated or control samples are used when the epoch number is even or odd, respectively. In TARNet, each sample is weighted, and the mini-batches are sampled randomly [21].
We ran the DCN and PD network for 400 and 50 epochs, respectively, in both the semi-supervised step and the final regression module. The learning rates of the DCN and PD were 0.0001 and 0.001 respectively. For TARNet, the model was trained for 3000 epochs in both the semi-supervised learning and final regression. We set the learning rate, the λ L2 regularizer (for the parameters of hypotheses layers), and the batch size to 0.0001, 0.00001, and 100, respectively. We used the default parameters and training settings for DCN-PD [1] and TARNet [21]. PSSAM-GAN was implemented using Pytorch (https://pytorch.org/). All the experiments were performed on an i7 Macbook Pro, with 16GB RAM, mounting Catalina OS. The code is available under the MIT license on GitHub at: https://github.com/Shantanu48114860/PSSAM-GAN.
2.3.3. Validation and performance metrics
When comparing PSSAM-GAN with DCN-PD and TARNet for the Jobs dataset, we followed the original papers’ train/test split setup for continuity in interpreting the results, noting that some of the original procedures have been re-coded here in Pytorch. For the IHDP dataset, we trained the models on 80% of the data and tested on 20%, as described in [1], and repeated this for 1000 iterations. For the Jobs dataset, we selected 10% of the data as the test set, and repeated the procedure for 10 iterations [21].
In terms of performance metrics, for IHDP – according to [7,21,29] – using the expected Precision in Estimation of Heterogeneous Effect (ϵPEHE) and the ATE, we evaluated and the error on the true ATE, i.e. ϵATE. Unlike IHDP, there are no counterfactual outcomes in the Jobs dataset, so the performance metrics used were Policy Risk (Rpol(π)) and ϵATT, which is the error on the ATE in the treated group. The detailed formulae are given as follows:
| (8) |
| (9) |
| (10) |
where ,
Ti = {x(n) : ti(n) = 1}, and E is the subset of RCT.
3. Results
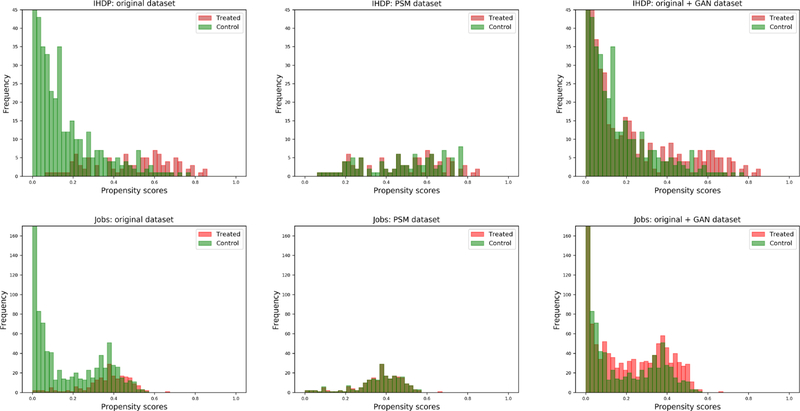
The GAN module produced synthetic instances for the unmatched controls covering the whole propensity score space in both datasets. Fig. 3 shows the distributions of the propensity scores, stratified by treatment group, for the original dataset, the PSM-filtered data (only treated samples matched to their controls using nearest neighbor), and then the final dataset that merged the GAN’s synthetic samples with the original data. The original score distributions are highly imbalanced and show substantial distribution shift between treated and control samples; the PSM-filtered distributions are balanced, but included a smaller sample size over a narrower score interval. Instead, the GAN-augmented dataset not only covers a larger propensity score interval, but also show that the stratified treated/controls distributions are very similar.
Fig. 3.
Histograms of the propensity score distributions for IHDP (top) and Jobs (bottom) datasets, stratified by treatment/control group. From left to right, the panels show the original dataset before PSM, the matched dataset after PSM and the dataset augmented with PSSAM-GAN framework.
Table 1 shows the mean ± st.dev performance metrics on both IHDP and Jobs dataset when applying the PSSAM-GAN framework and comparing it with the regular weighting/dropout deep learning models. Note that the point estimates for DCN(-PD) and TARNet may be slightly different from the referenced papers because we re-implemented some of the procedural steps using Pytorch. Nonetheless, the confidence intervals are consistent with prior literature. PSSAM-GAN improves performance over the other approaches, including the simple GAN, and results show that best and near-best results can be achieved without weighting or dropout regularization schemes. The advantage of PSSAM-GAN over the simple GAN is evident across both the IHDP and Jobs datasets, and consistent with any of the downstream methods used. This is due to the incorporation of the propensity loss in Eq. 5, which ensures that the synthetically generated treated samples have propensity scores closer to the control samples, including those who were unmatched. In addition, PSSAM-GAN had superior performance over DCN-PD and TARNet by 33% (without applying PD regularization) and 5%, respectively, in the IHDP dataset, whilst showed a more moderate improvement in the Jobs (1–2% for both performance indices). Of note, the moderate improvement in the Jobs dataset is not unexpected, as it was previously shown that the average gain of TARNet over ordinary least square was minimal (not significant) for the policy risk (Rpol(π)) and there was no gain for ϵATT [21]. In our experiments, we found that the increment in performance obtained with PSSAM-GAN was highly unlikely due to chance, as in all but one tests the null hypothesis of no difference was not supported [14]. The p-values reported in Table 1 refer to ϵATE and ϵATT, while for the other two measures they were all below 0.0001.
Table 1.
Performance on the out-of-sample test sets (mean ± st.dev) of the PSSAM-GAN framework vs. a simple GAN setup, and the regular weighting/dropout deep learning models, on the IHDP and Jobs datasets.
| IHDP |
Jobs |
|||||
|---|---|---|---|---|---|---|
| ϵATE | p-value | ϵATT | p-value | Rpol(π) | ||
|
| ||||||
| DCN-PD | 1.77 ± 0.09 | 0.18 ± 0.18 | 0.3294 | 0.08 ± 0.07 | 0.0192 | 0.29 ± 0.05 |
| DCN (Dropout probability: 0.5) | 2.08 ± 0.12 | 0.43 ± 0.17 | <0.0001 | 0.11 ± 0.05 | <0.0001 | 0.29 ± 0.05 |
| TARNet | 1.13 ± 0.03 | 0.21 ± 0.13 | <0.0001 | 0.13 ± 0.07 | <0.0001 | 0.29 ± 0.06 |
| PSSAM-GAN | ||||||
| + DCN | 1.18 ± 0.03 |
0.19 ± 0.09 | 0.0041 | 0.07 ±0.04 | ref. | 0.29 ± 0.05 |
| + DCN-PD | 1.82 ± 0.14 | 0.52 ± 0.38 | <0.0001 | 0.07 ± 0.07 | 1.0000 | 0.29 ± 0.05 |
| + DCN (Dropout probability: 0.5) | 2.07 ± 0.12 | 0.45 ± 0.21 | <0.0001 | 0.09 ± 0.08 | <0.0001 | 0.29 ± 0.06 |
| + TARNet | 1.07 ±0.02 | 0.17 ±0.10 | ref. | 0.13 ± 0.10 | <0.0001 | 0.27 ±0.03 |
| GAN | ||||||
| + DCN | 1.43 ± 0.04 | 0.19 ± 0.1 | 0.0064 | 0.10 ± 0.07 | <0.0001 | 0.29 ± 0.05 |
| + DCN-PD | 1.98 ± 0.16 | 0.82 ± 0.44 | <0.0001 | 0.08 ± 0.07 | 0.0192 | 0.30 ± 0.05 |
| + DCN (Dropout probability: 0.5) | 2.21 ± 0.13 | 0.44 ± 0.16 | <0.0192 | 0.12 ± 0.07 | <0.0001 | 0.32 ± 0.05 |
| + TARNet | 1.37 ± 0.02 | 0.23 ± 0.09 | <0.0001 | 0.13 ± 0.17 | <0.0001 | 0.30 ± 0.05 |
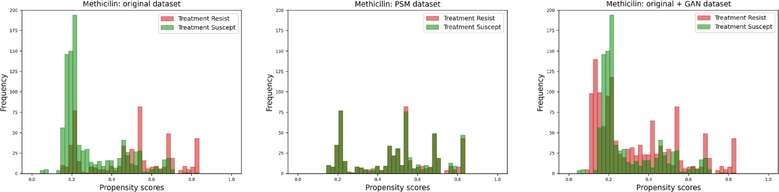
Next, we analyzed the larger bacterial dataset of MLST with respect to antibiotic treatment resistance. Fig. 4 shows the propensity score distributions for methicillin in the original data, in the matched subsets by PSM, and in the augmented space by PSSAM-GAN. As expected, the PSM drops a consistent part of the population, methicillin-susceptible in this case. On the contrary, PSSAM-GAN generates examples that cover the whole spectrum of treatment propensities, yet some of the high scores for methicillin resistance are left unmatched. In fact, we cannot rule out that some of the mutations in the genes sequenced by MLST might be actually causative of methicillin resistance. However, for most of the housekeeping mutations (and here we are using over 3000 sites) this would not be the case, and rather the association with treatment resistance would be due to founder events and hitchhiking mutations, as suggested in a previous study on the same data looking at phylogenetic structure and sampling bias [16]. In fact, the MEGARes database (https://megares.meglab.org/), one of the most comprehensive collections of bacterial genes with known association to antibiotic resistance, lists only 490 single-point mutations of housekeeping genes with confirmed resistance compared to over 7800 resistance entries of other genes across all antibiotics (i.e. 6.2% of known resistance is found in housekeeping genes). On average, housekeeping genes in MEGARes have a median (interquartile range) nucleotide length of 1544 (802–2, 619), thus the expected contribution of single-point mutations to any-antibiotic resistance is only 0.06%.
Fig. 4.
Histograms of the propensity score distributions for the bacterial dataset. From left to right, the panels show the original dataset before PSM, the matched dataset after PSM and the dataset augmented with PSSAM-GAN framework.
4. Discussion
We show that PSSAM-GAN is able to generate synthetic instances that cover the space of propensity scores for unmatched samples, increasing the sample size and richness of the covariate space. In addition, we demonstrate that it compares and combines favorably with the deep learning weighting/dropout schemes of DCN-PD and TARNet (besides being better than a baseline GAN architecture). We note that the provision of balanced datasets offers an operational advantage since other multitask regression learning can be applied without the need to tailor them to handle group assignment imbalance. For instance, PSSAM-GAN could be further integrated with Dragonnet [22].
The utility of PSSAM-GAN in practice can be foreseen in various scenarios, one such being its employment in emulating RCT on observational data, i.e., the target trial framework. The inclusion criteria apt to fulfill the SITA in target trial designs often lead to a case funnel, with substantial drop in sample size from the initial population (which can be large) and possibly imbalanced intervention groups.
Limitations of this contribution include the possible performance fluctuations due to the initial choice of the PSM method and propensity score function. Although propensity-based methods are less problematic than IPW because they do not have to invert weights, skewness of their distribution can still affect model learning and generation of samples. Similarly, performance can vary on the basis of the dropout threshold, as our results showed –error increased using a dropout probability of 0.5. Possible improvement could be achieved by using stable weights [31]. Another possible issue is that the semi-supervised step could be biased by data imbalance, and that the labelling might be inaccurate. Yet, the label assignment step is a pure prediction task and we are not interested in calculating any effect at that point of the procedure; in fact, training with only matched samples (to further reduce bias) did not affect the overall performance.
Here, we explored PSSAM-GAN in the special case of a binary treatment/intervention. One extension to this work is developing and applying it to multiple treatment groups, e.g. using a softmax. Also, in the downstream learning module, when using TARNet, one could generate balanced mini-batches using the perfect-match algorithm, leveraging the augmented-balanced dataset, instead of the weighting scheme [20]. Finally, for high-dimensional datasets, a regularization scheme or dimension reduction (e.g. through a latent space from a sparse autoencoder) could be used to reduce noise.
4.1. Conclusion
In conclusion, PSSAM-GAN is a promising approach to overcome the limitations of PSM- and IPW-based methods, especially addressing the sample size reduction and the weight instability problems. Differently from other approaches, PSSAM-GAN not only provides treatment effect estimation, but also sample generation. PSSAM-GAN is also well suited for high-dimensional studies, e.g. using EHR or genomics. Further, it provides a general-purpose tool apt to be used in conjunction with any multitask regression scheme.
6. Funding
This work was supported in part by the National Institutes of Health [grant numbers R01AI145552; R01AI141810; R21AI138815; R01CA246418; U18DP006512; R21AG068717; and R21CA245858].
Footnotes
Ethics statement
The authors declare to follow and comply to the Code of Ethics of the World Medical Association (Declaration of Helsinki). All data analyzed in this work are de-identified and public domain. See links and references in the methods for data availability.
Declaration of Competing Interest
All authors have no conflicts to declare.
When we generated the proof, this inline equation got distored. Do we need to change it to a numbered equation like equation 3?
References
- [1].Alaa AM, Weisz M, Van Der Schaar M, Deep counterfactual networks with propensity-dropout. arXiv preprint arXiv:1706.05966. [Google Scholar]
- [2].Austin PC, A comparison of 12 algorithms for matching on the propensity score, Stat Med 33 (2014) 1057–1069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Ding P, Miratrix LW, To adjust or not to adjust? sensitivity analysis of m-bias and butterfly-bias, J Causal Inference 3 (1) (2015) 41–57, 10.1515/jci-2013-0021. [DOI] [Google Scholar]
- [4].Dudík M, Erhan D, Langford J, Li L, et al. , Doubly robust policy evaluation and optimization, Statistical Science 29 (4) (2014) 485–511. [Google Scholar]
- [5].Goodfellow IJ, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, Courville A, Bengio Y, Generative adversarial networks, 2014. [Google Scholar]
- [6].Hernan M, Robins J, Causal inference, in: Chapman & Hall/CRC Monographs on Statistics & Applied Probab, Taylor & Francis, 2019. [Google Scholar]
- [7].Hill JL, Bayesian nonparametric modeling for causal inference, Journal of Computational and Graphical Statistics 20 (1) (2011) 217–240. [Google Scholar]
- [8].Imbens GW, The role of the propensity score in estimating dose-response functions, Biometrika 87 (3) (2000) 706–710. [Google Scholar]
- [9].Johansson F, Shalit U, Sontag D, Learning representations for counterfactual inference. International conference on machine learning, 2016, pp. 3020–3029. [Google Scholar]
- [10].Kingma DP, Ba J, Adam: a method for stochastic optimization. arXiv preprint arXiv:1412.6980. [Google Scholar]
- [11].Kocaoglu M, Snyder C, Dimakis AG, Vishwanath S, Causalgan: learning causal implicit generative models with adversarial training. arXiv preprint arXiv:1 709.02023. [Google Scholar]
- [12].LaLonde RJ, Evaluating the econometric evaluations of training programs with experimental data, Am Econ Rev (1986) 604–620. [Google Scholar]
- [13].Louizos C, Shalit U, Mooij JM, Sontag D, Zemel R, Welling M, Causal effect inference with deep latent-variable models. Advances in Neural Information Processing Systems, 2017, pp. 6446–6456. [Google Scholar]
- [14].Nadeau C, Bengio Y, Inference for the generalization error, Mach. Learn. 52 (3) (2003) 239–281, 10.1023/A:1024068626366. [DOI] [Google Scholar]
- [15].Pearl J, Glymour M, Jewell N, Causal inference in statistics: A Primer, Wiley, 2016. [Google Scholar]
- [16].Prosperi M, Azarian T, Johnson JA, Salemi M, Milicchio F, Oliva M, Unexpected predictors of antibiotic resistance in housekeeping genes of staphylococcus aureus. Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, in: BCB ‘19, Association for Computing Machinery, New York, NY, USA, 2019, pp. 259–268, 10.1145/3307339.3342138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Prosperi M, Guo Y, Sperrin M, Koopman JS, Min JS, He X, Rich S, Wang M, Buchan IE, Bian J, Causal inference and counterfactual prediction in machine learning for actionable healthcare, Nature Machine Intelligence 2 (2020) 369–375, 10.1038/s42256-020-0197-y. [DOI] [Google Scholar]
- [18].Rosenbaum PR, Rubin DB, The central role of the propensity score in observational studies for causal effects, Biometrika 70 (1) (1983) 41–55, 10.1093/biomet/70.1.41. [DOI] [Google Scholar]
- [19].Rubin DB, Estimating causal effects of treatments in randomized and nonrandomized studies, J Educ Psychol 66 (5) (1974) 688–701. [Google Scholar]
- [20].Schwab P, Linhardt L, Karlen W, Perfect match: a simple method for learning representations for counterfactual inference with neural networks. arXiv preprint arXiv:1810.00656. [Google Scholar]
- [21].Shalit U, Johansson FD, Sontag D, Estimating individual treatment effect: generalization bounds and algorithms, in: Precup D, Teh YW (Eds.), Proceedings of the 34th International Conference on Machine Learning, Proceedings of Machine Learning Research, 70, PMLR, International Convention Centre, Sydney, Australia, 2017, pp. 3076–3085. [Google Scholar]
- [22].Shi C, Blei D, Veitch V, Adapting neural networks for the estimation of treatment effects. Advances in Neural Information Processing Systems, 2019, pp. 2507–2517. [Google Scholar]
- [23].Sibbald B, Roland M, Understanding controlled trials: why are randomised controlled trials important? BMJ 316 (7126) (1998) 201, 10.1136/bmj.316.7126.201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Smith JA, Todd PE, Does matching overcome lalonde’s critique of nonexperimental estimators? J Econom 125 (1–2) (2005) 305–353. [Google Scholar]
- [25].Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R, Dropout: a simple way to prevent neural networks from overfitting, The journal of machine learning research 15 (1) (2014) 1929–1958. [Google Scholar]
- [26].Tian Y, Schuemie MJ, Suchard MA, Evaluating large-scale propensity score performance through real-world and synthetic data experiments, Int J Epidemiol 47 (6) (2018) 2005–2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Wager S, Athey S, Estimation and inference of heterogeneous treatment effects using random forests, J Am Stat Assoc 113 (523) (2018) 1228–1242. [Google Scholar]
- [28].Xu B, Wang N, Chen T, Li M, Empirical evaluation of rectified activations in convolutional network, CoRR (2015). arXiv:1505.00853. [Google Scholar]
- [29].Yoon J, Jordon J, van der Schaar M, GANITE: estimation of individualized treatment effects using generative adversarial nets. 6th International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, April 30, - May 3, 2018, Conference Track Proceedings, OpenReview.net, 2018. [Google Scholar]
- [30].Zhu X, Goldberg AB, Introduction to semi-supervised learning, Synthesis lectures on artificial intelligence and machine learning 3 (1) (2009) 1–130. [Google Scholar]
- [31].Zubizarreta JR, Stable weights that balance covariates for estimation with incomplete outcome data, J Am Stat Assoc 110 (511) (2015) 910–922, 10.1080/01621459.2015.1023805. [DOI] [Google Scholar]