Abstract
The nearly neutral theory predicts specific relations between effective population size (Ne) and patterns of divergence and polymorphism, which depend on the shape of the distribution of fitness effects (DFE) of new mutations. However, testing these relations is not straightforward, owing to the difficulty in estimating Ne. Here, we introduce an integrative framework allowing for an explicit reconstruction of the phylogenetic history of Ne, thus leading to a quantitative test of the nearly neutral theory and an estimation of the allometric scaling of the ratios of nonsynonymous over synonymous polymorphism () and divergence (dN/dS) with respect to Ne. As an illustration, we applied our method to primates, for which the nearly neutral predictions were mostly verified. Under a purely nearly neutral model with a constant DFE across species, we find that the variation in and dN/dS as a function of Ne is too large to be compatible with current estimates of the DFE based on site frequency spectra. The reconstructed history of Ne shows a 10-fold variation across primates. The mutation rate per generation u, also reconstructed over the tree by the method, varies over a 3-fold range and is negatively correlated with Ne. As a result of these opposing trends for Ne and u, variation in πS is intermediate, primarily driven by Ne but substantially influenced by u. Altogether, our integrative framework provides a quantitative assessment of the role of Ne and u in modulating patterns of genetic variation, while giving a synthetic picture of their history over the clade.
Keywords: effective population size, phylogeny, nearly neutral evolution, codon model
Introduction
Significance
Natural selection tends to increase the frequency of mutants of higher fitness and to eliminate less fit genetic variants. However, chance events over the life of the individuals in the population are susceptible to introduce deviations from these trends, which are expected to have a stronger impact in smaller populations. In the long-term, these fluctuations, called random drift, can lead to the accumulation of mildly deleterious mutations in the genomes of living species, and for that reason, the effective population size (usually denoted Ne, and which captures the relative strength of drift, relative to selection) has been proposed as a major determinant of the evolution of genome architecture and content. A proper quantitative test of this hypothesis, however, is hampered by the fact that Ne is difficult to estimate in practice. Here, we propose a Bayesian integrative approach for reconstructing the broad-scale variation in Ne across an entire phylogeny, which in turns allows for quantifying how Ne correlates with life-history traits and with various measures of genetic diversity and selection strength, between and within species. We apply this approach to the phylogeny of primates, and observe that selection is indeed less efficient in primates characterized by smaller effective population sizes.
Effective population size (Ne) is a central parameter in population genetics and in molecular evolution, impacting both genetic diversity and the strength of selection (Charlesworth 2009; Leffler et al. 2012). The influence of Ne on diversity reflects the fact that larger populations can store more genetic variation, whereas the second aspect, efficacy of selection, is driven by the link between Ne and genetic drift: the lower the Ne, the more genetic evolution is influenced by the random sampling of individuals over generations. As a result, long-term trends in Ne are expected to have an important impact on genome evolution (Lynch et al. 2011) and, more generally, on the relative contribution of adaptive and nonadaptive forces in shaping macroevolutionary patterns.
The nearly neutral theory proposes a simple conceptual framework for formalizing the role of selection and drift on genetic sequences. According to this theory, genetic sequences are mostly under purifying selection; deleterious mutation are eliminated by selection, whereas neutral and nearly neutral mutations are subject to genetic drift and can therefore segregate and reach fixation. The inverse of Ne defines the selection threshold under which genetic drift dominates. This results in specific quantitative relations between Ne and key molecular parameters (Ohta 1995). In particular, species with small Ne are expected to have a higher ratio of nonsynonymous (dN) to synonymous (dS) substitution rates and a higher ratio of nonsynonymous (πN) to synonymous (πS) nucleotide diversity. Under certain assumptions, these two ratios are linked to Ne through allometric functions in which the scaling coefficient is directly related to the shape of the distribution of fitness effects (DFE) (Kimura 1979; Welch et al. 2008).
The empirical test of these predictions raises the problem that Ne is difficult to measure directly in practice. In principle, Ne could be estimated through demographic and census data. However, the relation between census and effective population size is far from straightforward. Consequently, many studies which have tried to test nearly neutral theory have used proxies indirectly linked to Ne. In particular, life-history traits (LHTs, essentially body mass or maximum longevity) are expected to correlate negatively with Ne (Waples et al. 2013). As a result, or are predicted to correlate positively with LHT. This has been tested, leading to various outcomes, with both positive and negative results (Eyre-Walker et al. 2002; Popadin et al. 2007; Nikolaev et al. 2007; Lartillot 2013; Nabholz et al. 2013; Romiguier et al. 2014; Figuet et al. 2016).
More direct estimations of Ne can be obtained from πS since, in accordance with coalescent theory, (with u referring to the mutation rate per site per generation). Thus, one would predict a negative correlation of , and LHT with πS. Such predictions have been tested, and generally verified, in several previous studies (Piganeau and Eyre-Walker 2009; Romiguier et al. 2014; Figuet et al. 2016; Galtier 2016; Chen et al. 2017; James et al. 2017). However, these more specific tests of the nearly neutral theory are only qualitative, at least in their current form, in which Ne is indirectly accessed through πS without any attempt to correct for the confounding effect of the mutation rate u and its variation across species.
New Approaches
In this study, we aim to solve this problem by using a Bayesian integrative approach, in which the joint evolutionary history of a set of molecular and phenotypic traits is explicitely reconstructed along a phylogeny. This method has previously been used to test the predictions of the nearly neutral theory via indirect proxies of Ne (Lartillot 2013; Nabholz et al. 2013). Here, we propose an elaboration on this approach, in which the variation in the mutation rate per generation u is globally reconstructed over the phylogeny by combining the relaxed molecular clock of the model with data about generation times. This in turns allows us to tease out Ne and u from the πS estimates obtained in extant species, thus leading to a complete reconstruction of the phylogenetic history of Ne and of its scaling relations with other traits such as or . Using this reconstruction, we can conduct a proper quantitative test of some of the predictions of the nearly neutral theory and then compare our findings with independent knowledge previously derived from the analysis of site frequency spectra. The approach requires a multiple sequence alignment across a group of species, together with polymorphism data, ideally averaged over many loci to stabilize the estimates, as well as data about LHTs in extant species and fossil calibrations. Here, we apply it to previously published phylogenetic and transcriptome data in primates (Perelman et al. 2011; Perry et al. 2012).
Results
Empirical Phylogenetic Correlation Analysis
We first conducted a general correlation analysis between dS, dN/dS, πS, , and LHTs. Our analysis relies on a multiple sequence alignment of 54 coding genes in 61 primates (adapted from Perelman et al. 2011), combined with data about LHTs taken from the literature (de Magalhaes and Costa 2009; Besenbacher et al. 2019) and polymorphism data from ten primates species (obtained from Perry et al. 2012; Romiguier et al. 2014; Figuet et al. 2016). Of note, these estimates of πS and are based on the global transcriptome data, thus not restricted to the 54 coding genes represented in the multiple sequence alignment (see Materials and Methods for details, Data subsection).
In a first step, these data were analyzed using a previously introduced Bayesian integrative model (Coevol, Lartillot and Poujol 2011). This model is an adaptation of the classical comparative method based on the principle of phylogenetically independent contrasts (Felsenstein 1985) to the problem of estimating the correlation between quantitative traits (such as LHT, πS, and ) and substitution rates (such as dS and dN/dS). The joint evolutionary process followed by all these variables is assumed to be multivariate Brownian:
| (1) |
| (2) |
| (3) |
where are the instant values of the six traits (body mass, age at sexual maturity, longevity, generation time πS, ). This process is parameterized by an 8 × 8 variance–covariance matrix Σ, which captures the correlation structure between rates and traits. The model is conditioned on sequence and trait data, using Markov Chain Monte Carlo (MCMC). Then, the marginal posterior distribution on Σ is used to derive measures of the strength and the slopes of the correlations between rates and traits, using standard covariance analysis and in a way that automatically accounts for phylogenetic inertia. In the following, this Brownian model is referred to as the “phenomenological” model, because it does not entail any specific assumption about the population–genetic relations that might exist between dN/dS, , and Ne.
Based on this first analysis, neither nor dN/dS appear to correlate with LHTs (table 1), except for a positive correlation between and longevity (correlation coefficient r = 0.49). On the other hand, the correlations among molecular quantities are globally in agreement with the nearly neutral predictions, although with rather unequal statistical support. Most notably, shows a clear negative correlation with πS (). As for dN/dS, it also shows a negative correlation with πS (), although with very marginal support (posterior probability of a negative correlation pp < 0.95). The two variables, dN/dS and are also positively correlated with each other (r = 0.42), but again, with marginal support. The weaker correlations observed for dN/dS, compared with the more robust correlation between and πS, could be due either to the presence of a minor fraction of adaptive substitutions or, alternatively, to a discrepancy between the short-term demographic effects reflected in both πS and and long-term trends captured by dN/dS.
Table 1.
Correlation Coefficients between dS, dN/dS, πS, and , Life-History Traits, and Ne
| dS | dN/dS | Mat. | Mass | Long. | π S | Gen. | u | N e | ||
|---|---|---|---|---|---|---|---|---|---|---|
| dS | 0.24 | −0.38 | −0.64** | −0.27 | −0.60 | 0.45 | −0.42 | 0.72** | −0.72** | |
| dN/dS | 0.15 | 0.08 | 0.49 | −0.50 | 0.42 | 0.42 | 0.58* | −0.58* | ||
| Maturity | 0.61** | 0.52** | 0.05 | 0.10 | 0.64** | 0.09 | −0.01 | |||
| Mass | 0.53** | 0.38 | −0.19 | 0.64** | −0.19 | 0.32 | ||||
| Longevity | −0.24 | 0.26 | 0.88** | 0.36 | −0.32 | |||||
| π S | −0.78** | −0.04 | −0.67* | 0.92** | ||||||
| 0.11 | 0.57 | −0.73** | ||||||||
| Gen. time | 0.29 | −0.17 | ||||||||
| u | −0.89** |
Note.—Asterisks indicate strength of support (**pp>0.975, *pp>0.95).
Although not conclusive, the correlation patterns between πS, , and dN/dS are compatible with the hypothesis that the nearly neutral model is essentially valid for primates. The overall lack of correlation with LHT, on the other hand, suggest that there is no clear correlation between effective population size and body size or other related LHTs in this group. Possibly, the phylogenetic scale might be too small to show sufficient variation in LHT that would be interpretable in terms of variation in Ne. Alternatively, Ne might be driven by other life-history characters (in particular, the mating systems), which may not directly correlate with body size. Of note, in those cases where the estimated correlation of dN/dS or with LHTs were in agreement with the predictions of the nearly neutral theory (Eyre-Walker et al. 2002; Popadin et al. 2007; Nikolaev et al. 2007; Lartillot 2013; Nabholz et al. 2013; Romiguier et al. 2014; Figuet et al. 2016), the reported correlation strengths were often weak, weaker than the correlations found directly between πS and and dN/dS (Piganeau and Eyre-Walker 2009; Romiguier et al. 2014; Figuet et al. 2016; Galtier 2016; Chen et al. 2017; James et al. 2017).
Teasing Apart Divergence Times, Mutation Rates, and Effective Population Size
The correlation patterns shown by the three molecular quantities πS, , and suggest that Ne plays a nonnegligible role in their interspecific variation. However, in its current form, this correlation analysis does not give any quantitative insight about the scaling of and as a function of Ne and, more generally, about the quantitative impact of Ne on the evolution of coding sequences. In order to achieve this, an explicit estimate of the key parameter Ne, and of its variation across species, is first necessary. In this direction, a first simple but fundamental equation relates πS with Ne:
| (4) |
In order to estimate Ne from equation (4), an estimation of u is also required. Here, it can be obtained by noting that:
| (5) |
where r is the mutation rate per site and per year and τ the generation time. Assuming that synonymous mutations are neutral, we can identify the mutation rate with the synonymous substitution rate dS, thus leading to:
| (6) |
Finally, combining equations (4) and (6) and taking the logarithm gives:
| (7) |
This expression suggests to apply the linear transformation given by equation (7) to the three variables , and , all of which are jointly reconstructed across the tree by the phenomenological model introduced above, which then gives a global phylogenetic reconstruction of . A similar argument, based on equation (6), gives:
| (8) |
which can be used to obtain a global reconstruction of the mutation rate per generation u. Finally, since the two transformations given by equations (7) and (8) are linear, the correlation patterns between , and the other variables included in the analysis can be recovered by applying elementary matrix algebra to the covariance matrix estimated under the initial parameterization (see Materials and Methods, Ex Post Log-Linear Transformation).
The results of this linearly transformed correlation analysis are gathered in table 1 (last two columns). First, in accordance with the predictions of the nearly neutral theory, and show a negative correlation with Ne ( for and −0.58 for dN/dS). Second, u is inferred to covary negatively with Ne (), suggesting that species with large Ne tend to have a lower u (Lynch et al. 2011). This correlation should be interpreted with caution, however, because these two variables are both estimated partly based on , such that estimation errors on πS will systematically affect them in opposite directions. On the other hand, and perhaps more convincingly, u is negatively correlated with πS (, table 1). Unlike Ne and u, πS and u are empirically independent in the present case (i.e., estimated based on different data sources). This latter correlation thus further strengthens the case that Ne and u have opposite trends. It also suggests that the variation in u is more moderate than the variation in Ne, such that πS remains in the end positively correlated with Ne.
Quantitative Scaling of and as a Function of Ne
Once an explicit estimate of Ne and of its variation is available, the scaling behavior of and as a function of Ne can be quantified. Mathematically, the Brownian process followed by rates and traits, such as given by equation (1), implies the following log-linear relations:
| (9) |
| (10) |
where , for i = 1, 2, are Brownian motions. These last two terms are mathematically equivalent to the residual errors of the linear regression between the independent contrasts of and against . Equivalently:
| (11) |
| (12) |
where , for i = 1, 2. In other words, the slopes of the log-linear relations, β1 and β2, are just the scaling coefficients of and as a function of Ne. These two scaling coefficients can be directly obtained based on the covariance matrix estimated above (see Correlations and Slopes in the Materials and Methods section). Of note, equations (9–12) are just a reformulation of the output of the correlation analysis conducted previously. As such, they do not entail any specific hypothesis about the population–genetic relations between , dN/dS, and Ne. A population–genetic interpretation of these equations is considered in the next subsection.
In the present case, the estimates of β1 and β2 are of similar magnitude, with point estimates of 0.17 and 0.10, respectively (table 2). It is worth comparing these estimates with those that would be obtained if we were using πS directly as a proxy of Ne (i.e., without correcting for u). The slopes of the log-linear scaling of and dN/dS as a function of πS are steeper than those obtained as a function of Ne, with point estimates of 0.29 and 0.13 (table 2), suggesting that the confounding effects of u are not negligible on the evolutionary scale of a mammalian order such as primates and, as such, can substantially distort the scaling relations if not properly taken into account.
Table 2.
Scaling Coefficient of dN/dS and as Functions of Ne and πS, Compared with Estimates of the Shape Parameter β of the Distribution of Fitness Effects
| Method or Source | Point Estimate | Credible/Confidence Interval |
|---|---|---|
| 0.17 | (0.02, 0.3) | |
| 0.10 | (−0.02, 0.22) | |
| 0.29 | (0.12, 0.51) | |
| 0.13 | (−0.12, 0.51) | |
| β (mechanistic model) | 0.27 | (0.22, 0.33) |
| Eyre-Walker et al. (2006) | 0.23 | (0.19, 0.27) |
| Boyko et al. (2008) | 0.18 | (0.16, 0.21) |
| Castellano et al. (2019) | 0.16 | (0.13, 0.17) |
Relation with the Shape of the DFE
Mechanistically, the slope of and as a function of can be interpreted in the light of an explicit mathematical model of the nearly neutral regime. Such mathematical models, which are routinely used in modern Mac-Donald Kreitman tests (Charlesworth and Eyre-Walker 2008; Eyre-Walker and Keightley 2009; Halligan et al. 2010; Galtier 2016), formalize how mutation, selection, and drift modulate the detailed patterns of polymorphism and divergence. In turn, these modulations depend on the shape of the DFE over nonsynonymous mutations (Eyre-Walker and Keightley 2007). Mathematically, the DFE is often modeled as a gamma distribution. The shape parameter of this distribution (usually denoted as β) is classically estimated based on empirical synonymous and nonsynonymous site frequency spectra. Typical estimates of the shape parameter are of the order of 0.15 to 0.20 in humans (Eyre-Walker et al. 2006; Boyko et al. 2008), thus suggesting a strongly leptokurtic distribution, with the majority of mutations having either very small or very large fitness effects.
When the shape parameter β is small, both and are theoretically predicted to scale as a function of Ne as a power-law, with a scaling exponent equal to β (Kimura 1979; Welch et al. 2008), that is:
| (13) |
| (14) |
The relation given by equation (13) was used previously for analyzing the impact of the variation in Ne along the genome in Drosophila (Castellano et al. 2018). Assuming that 1) the sequences follow a purely nearly neutral regime, thus without positive selection; 2) the DFE is constant across primate species; 3) variation in Ne is sufficiently slow, compared with the fixation time of nonsynonymous substitutions, and 4) short-term Ne and long-term Ne are identical, equations (13) and (14) also predict the interspecific variation in and dN/dS as a function of Ne. More specifically, by identifying these two equations with equations (11) and (12), the present argument predicts that the interspecific allometric scaling coefficients β1 and β2 estimated above should both be equal to the shape parameter β of the DFE. In the present case, the two estimates β1 and β2 are indeed congruent with each other, with overlapping credible intervals (table 2). They are also compatible with previously reported independent estimates of the shape parameter of the DFE, such as obtained from site frequency spectra in humans and in other great apes (also reported in table 2).
A Mechanistic Nearly Neutral Phylogenetic Codon Model
Since all of the results presented thus far are compatible with a nearly neutral regime, we decided to construct a mechanistic version of the model directly from first principles. Thus far, a phenomenological approach was adopted, in which the whole set of variables of interest (dS, dN/dS, πS, , and LHT) were jointly reconstructed along the phylogeny, as a multivariate log-normal Brownian process with eight degrees of freedom. Only in a second step were Ne and u extracted from this multivariate process, using log-linear relations. As a result, dN/dS, πS, and are correlated with Ne and u, but they are not deterministic functions of these fundamental variables, such as suggested by equations (6), (7), (13), and (14).
In the mechanistic model now introduced, these deterministic relations are enforced. The Brownian process now has six degrees of freedom (πS, , and the LHT), corresponding to the variables that are directly observed in extant species. Then, equations (6), (7), (13), and (14) are inverted, so as to express r = dS, dN/dS, Ne, and u as time-dependent deterministic functions of this Brownian process (see Materials and Methods, Mechanistic Model). In these equations, the shape parameter β, along with κ1 and κ2 in equations (13) and (14), are structural parameters of the model, representing the DFE, itself assumed to be constant across species. These parameters are estimated along with the covariance matrix, divergence times, and the realization of the process along the phylogeny. The model is conditioned on the same data (sequence alignment, traits, polymorphism) and using the same fossil calibration scheme as for the phenomenological model.
This mechanistic model was implemented in two alternative versions. A first naive version assumes that genetic divergence takes place exactly at the splitting times defined by the underlying species phylogeny. Identifying genetic divergence with species divergence, however, amounts to ignoring the time it takes for coalescence to occur in the ancestral populations. For that reason, an alternative model was considered, based on the argument that the mean coalescence time in the ancestral population at a given ancestral node of the phylogeny is equal to , where Ne is the effective population size and τ the generation time prevailing at or around that node of the species tree. Since Ne and τ are both reconstructed along the entire species phylogeny, it is therefore possible to use the local information about the current value of Ne and τ to account for the extra amount of divergence δt induced by coalescence in the ancestral population when calculating the sequence likelihood (see Materials and Methods). In the following, these two alternative versions of the mechanistic model are called the “naive-phylogenetic” and “mean-coalescent” versions. Of note, the mean-coalescent version is solely invoked to correct mutation rate and time estimates, not dN/dS. In reality, ancestral coalescence is expected to lead to nontrivial patterns of nonsynonymous and synonymous divergence (Mugal et al. 2020), which are ignored here.
Fitting the model on the data returns an estimate of the structural parameters of the DFE as well as a dated tree, annotated with the complete history of the variation in mutation rate and in effective population size along its branches. These different aspects of the output of the analysis are now considered in turn.
Mechanistic Estimate of the Shape Parameter of the DFE
The mechanistic model yields an estimate of β (table 2) that is somewhat higher than the slopes β1 and β2 estimated previously with the phenomenological approach, with a posterior median at 0.27 and a credible interval equal to . The credible interval is smaller than those for β1 and β2, reflecting the fact that the mechanistic model is more constrained. Our estimate of β also appears to be higher than independent estimates obtained from site frequency spectra. Of note, there is some discrepancy among those DFE-based estimates, whose credible intervals do not overlap. However, our estimate is significantly higher than the more recent estimate obtained by jointly analyzing the site frequency spectra across great apes (Castellano et al. 2019), which is probably the most relevant one in the present context. This observation suggests a potential violation of the mechanistic model (see Discussion).
Estimated Mutation Rates
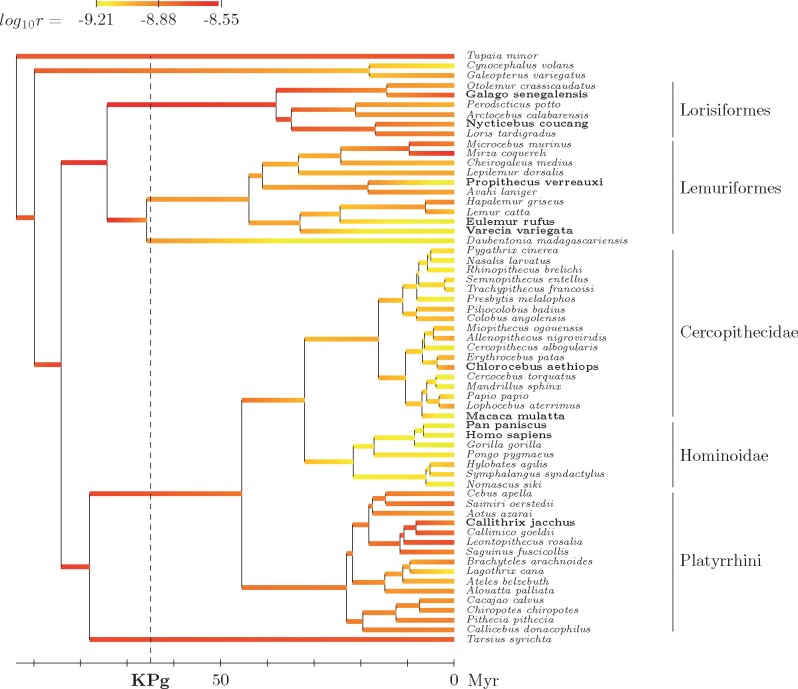
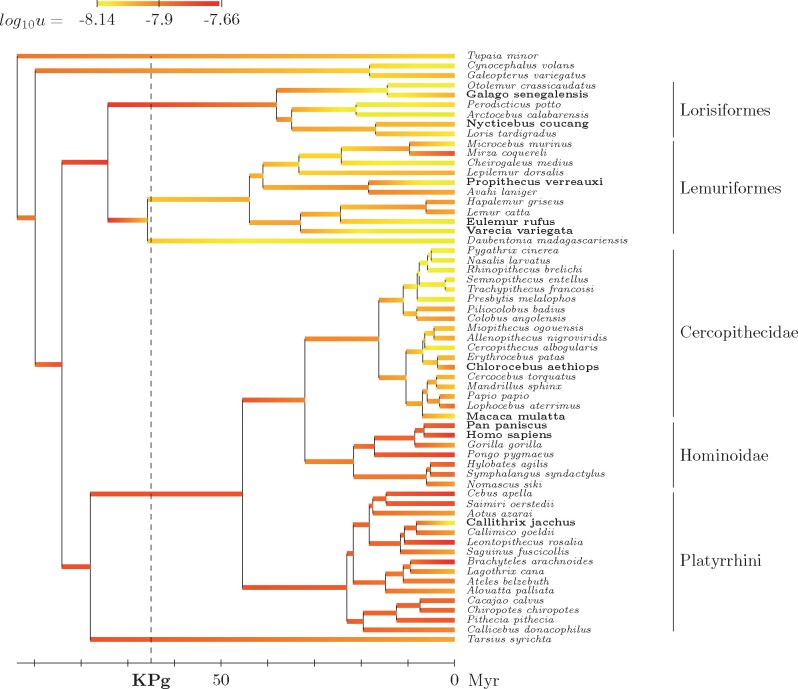
The dated phylogeny, together with the reconstructed history of the mutation rate per year r, is shown in figure 1. Here, the mechanistic model works like a standard molecular dating method, using fossil calibration and a relaxed clock model to tease out times and rates from raw synonymous sequence divergence. Generation time, also reconstructed along the tree by the model, is then used to convert the mutation rate per year r into a mutation rate per generation u (fig. 2). Point estimates (medians) and 95% credible intervals of both r and u for some extant species of interest and a few key ancestors are shown in table 3.
Fig. 1.
Reconstructed phylogenetic history of the mutation rate per year r (posterior median estimate) under the mechanistic model. Species for which transcriptome-wide polymorphism data were used are indicated in bold face.
Fig. 2.
Reconstructed phylogenetic history of the mutation rate per generation u (posterior median estimate) under the mechanistic model. Species for which transcriptome-wide polymorphism data were used are indicated in bold face.
Table 3.
Estimates of Mutation Rate per Year r and Per Generation u (posterior median and 95% credible interval), for Several Extant and Ancestral Species
| Species |
r (per 109 years) |
u (per 108 generation) |
|||
|---|---|---|---|---|---|
| Without anc. pol.a | With anc. pol.b | Without anc. pol.a | With anc. pol.b | Pedigreesc | |
| Homo | 0.81 (0.61, 1.11) | 0.67 (0.50, 0.91) | 2.36 (1.76, 3.21) | 1.95 (1.46, 2.65) | 1.23–1.29 |
| Pan | 0.79 (0.67, 0.93) | 0.67 (0.56, 0.80) | 1.91 (1.61, 2.23) | 1.62 (1.34, 1.92) | 1.26–1.48 |
| Gorilla | 0.73 (0.44, 1.13) | 0.55 (0.32, 0.85) | 1.39 (0.84, 2.15) | 1.05 (0.60, 1.62) | 1.13 |
| Pongo | 0.84 (0.54, 1.20) | 0.73 (0.46, 1.04) | 2.11 (1.36, 3.00) | 1.84 (1.16, 2.59) | 1.66 |
| Macaca | 0.68 (0.54, 0.81) | 0.58 (0.46, 0.71) | 0.95 (0.75, 1.14) | 0.82 (0.64, 1.00) | 0.37 |
| Papio | 0.90 (0.50, 1.59) | 0.71 (0.38, 1.30) | 1.23 (0.77, 1.94) | 0.98 (0.57, 1.59) | 0.55 |
| Aotus | 1.09 (0.63, 1.77) | 1.02 (0.56, 1.74) | 1.16 (0.70, 1.78) | 1.08 (0.61, 1.70) | 0.81 |
| Catarrhini | 0.87 (0.54, 1.45) | 0.91 (0.55, 1.52) | 1.24 (0.83, 1.79) | 1.23 (0.82, 1.85) | |
| Platyrrhini | 1.48 (1.00, 2.15) | 1.42 (0.96, 2.09) | 1.57 (1.18, 2.15) | 1.53 (1.12, 2.06) | |
| Haplorrhini | 2.00 (1.01, 4.07) | 2.09 (0.98, 4.42) | 1.44 (0.88, 2.38) | 1.60 (0.92, 2.84) | |
| Strepsirrhini | 2.57 (1.34, 4.99) | 2.77 (1.29, 5.94) | 1.65 (1.02, 2.73) | 1.88 (1.08, 3.38) | |
| Primates | 2.07 (1.06, 4.24) | 2.20 (1.05, 4.79) | 1.45 (0.87, 2.47) | 1.62 (0.94, 2.93) | |
Naive-phylogenetic method (not accounting for ancestral polymorphism).
Mean-coalescent method (accounting for ancestral polymorphism).
From table 1 of Wu et al. (2020).
The naive-phylogenetic model tends to return higher mutation rates, compared with the mean-coalescent approach, in particular for extant taxa and, more generally, for recent ancestors. For instance, in humans, the mutation rate per year is estimated at when coalescence in the ancestral population is ignored, versus when it is accounted for in the model. This reflects a bias induced by ignoring ancestral coalescence. For instance, the Human–Chimpanzee split is constrained at around 5–7 Myr, but coalescence in the ancestral population can easily go back to 9 Myr, which, if dated at 7 Myr, automatically induces an overestimation of the mutation rate along the branch leading to Humans (Besenbacher et al. 2019).
The estimates obtained here under the mean-coalescent model are intermediate, lower than previously reported phylogenetic estimates but still higher than pedigree-based estimates. For instance, typical phylogenetic estimates for the mutation rate in humans are typically of the order of per year, or per generation, whereas pedigree-based estimates are generally about half these values. Concerning other primates, our estimates are also higher than pedigree-based estimates previously reported for macaques (Wang et al. 2020) and baboons (Wu et al. 2020). On the other hand, they are congruent for Gorilla, Pongo (Besenbacher et al. 2019), and Aotus (Thomas et al. 2018). In the following, only coalescent-aware estimates are further considered.
Across primates, the mutation rate per year r shows a 5-fold variation from to point mutations per year and per nucleotide site (fig. 1). The rate of mutation is relatively high in the ancestor of primates (). On the side of Strepsirrhini, it remains high in Lorisiformes () but is lower in Lemuriformes (). Concerning Haplorrhini, the rate undergoes a net slowdown in Catarrhini (), further accentuated in apes, which are among the slowest evolving primates (). These observations are globally in accordance with previous observations, in particular, emphasizing that the slowdown occurring in apes (Steiper et al. 2004) is in fact in the continuity of a broader process of deceleration more generally across catarrhine primates (Perelman et al. 2011).
Compared with the mutation rate per year, the mutation rate per generation u varies over a more moderate range, showing a 3-fold variation across primates. Moderately high ancestrally (), it shows a convergent decrease in Lorisiformes, Lemuriformes, and Cercopithecidae (reaching below in several species in these three clades), but otherwise, remains more in the range of 1.5 to . At first sight, the mutation rates per year r and per generation u tend to show opposite patterns: slow-evolving lineages, with a low mutation rate per year, tend to have a higher mutation rate per generation (high u). This is particularly apparent for apes (low r, high u) or for Lorisiformes (high r, low u). However, there are some exceptions, of lineages that have both a high r and a high u, most notably Platyrrhini (new world monkeys). More generally, the correlation analysis (table 1) suggests that u and r are positively, not negatively, correlated on average across primates.
Phylogenetic Reconstruction of Ne
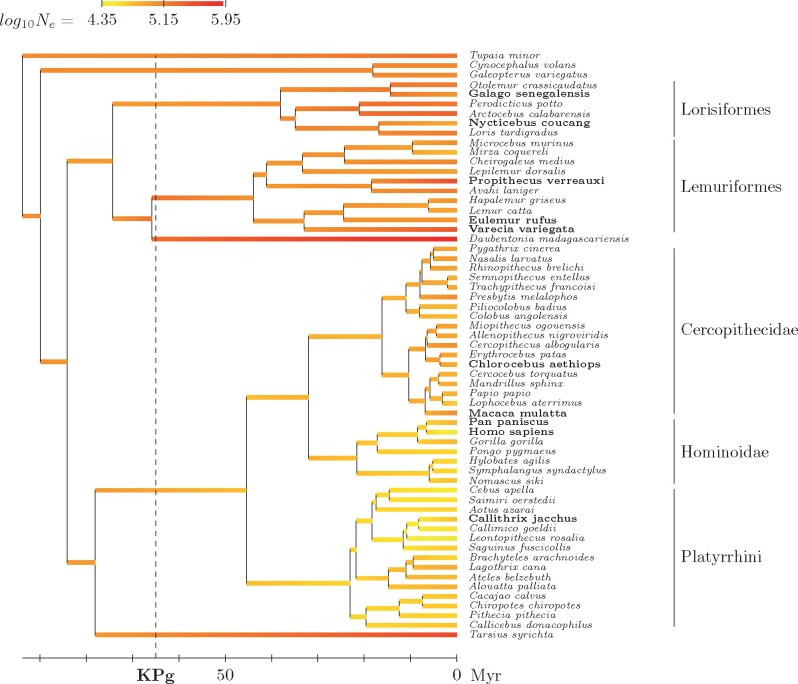
The marginal reconstruction of Ne along the phylogeny of primates returned by the mechanistic model is shown in figure 3 (supplementary fig. 1, Supplementary Material online, for the reconstruction returned by the phenomenological model). More detailed information, with credible intervals, is given in table 4 for several species of interest and key ancestors along the phylogeny.
Fig. 3.
Reconstructed phylogenetic history of Ne (posterior median estimate) under the mechanistic model. Species for which transcriptome-wide polymorphism data were used are indicated in bold face.
Table 4.
Estimates of Effective Population Size (, posterior median, and 95% credible interval) for Several Extant Taxa and Ancestors
| Species | Mechanistic | Mech. w/o anc. pol. | Phenomenological | Uncoupled | Coal.a | hmmcoalb |
|---|---|---|---|---|---|---|
| Homo | 23 (17, 30) | 19 (14, 25) | 19 (12, 36) | 20 (13, 32) | (13, 16) | 8 |
| Pan | 64 (54, 78) | 54 (46, 64) | 67 (45, 101) | 60 (40, 94) | (31, 62) | 30 |
| Gorilla | 64 (25, 170) | 67 (27, 159) | 110 (37, 354) | 47 (20, 108) | (28, 57) | 21 |
| Pongo | 42 (15, 109) | 38 (15, 89) | 52 (20, 131) | 32 (10, 103) | (42, 85) | 19 |
| Homo-Pan | 44 (28, 69) | 43 (28, 66) | 49 (29, 87) | 39 (24, 64) | (10, 47) | 50 |
| Homo-Gorilla | 45 (26, 73) | 46 (28, 74) | 54 (31, 101) | 41 (24, 70) | (27, 61) | 47 |
| Hominidae | 48 (24, 91) | 44 (24, 78) | 52 (26, 104) | 45 (21, 97) | ||
| Hominoidea | 56 (28, 111) | 52 (28, 98) | 63 (31, 139) | 53 (24, 121) | ||
| Cercopithecidae | 64 (34, 114) | 70 (41, 118) | 81 (43, 156) | 72 (36, 147) | ||
| Catarrhini | 67 (33, 137) | 68 (36, 128) | 70 (34, 157) | 57 (26, 128) | ||
| Platyrrhini | 42 (22, 79) | 37 (20, 67) | 32 (16, 60) | 32 (14, 79) | ||
| Simiiformes | 56 (26, 130) | 53 (26, 110) | 43 (18, 97) | 39 (15, 101) | ||
| Tarsius | 392 (80, 2220) | 285 (74, 1477) | 89 (18, 391) | 49 (4, 568) | ||
| Haplorrhini | 96 (40, 240) | 88 (39, 199) | 46 (15, 131) | 45 (14, 149) | ||
| Lorisiformes | 117 (55, 253) | 115 (58, 244) | 53 (16, 135) | 53 (21, 135) | ||
| Lemuriformes | 102 (47, 218) | 97 (48, 197) | 118 (48, 285) | 152 (66, 377) | ||
| Daubentonia | 863 (162, 6174) | 893 (183, 5296) | 739 (142, 5583) | 335 (43, 2796) | ||
| Strepsirrhini | 93 (37, 253) | 84 (36, 200) | 39 (12, 116) | 45 (16, 132) | ||
| Primates | 97 (40, 251) | 88 (39, 200) | 47 (14, 132) | 46 (15, 151) |
From Prado-Martinez et al. (2013), table 1, for extant hominids, and from Rannala and Yang (2003) for ancestral species.
The Ne estimates for the four extant hominids (Homo, Pan, Gorilla, and Pongo) are globally congruent with independent estimates based on other coalescent-based approaches (Prado-Martinez et al. 2013). In particular, for Humans, Ne is estimated to be between 13,000 and 24,000. For other hominids, they tend to be somewhat higher than coalescent-based estimates. Concerning the successive last common ancestors along the hominid subtree, our estimation is also consistent with the independent-locus multispecies coalescent (Rannala and Yang 2003).
The history of Ne shows a clear large-scale structure over the primate phylogeny. Starting with a point estimate at around 100,000 in the last common ancestor of primates, Ne then goes down in Haplorrhini, stabilizing at around 65,000 in Cercopithecidae (old-world monkeys), 50,000 in Hominoidea (going further down more specifically in Humans), and 40,000 in Platyrrhini (new-world monkeys). Conversely, in Strepsirrhini, Ne tends to show higher values, staying at 100,000 in Lemuriformes and going up to 160,000 to 200,000 in Lorisiformes. Finally, rather large effective sizes are estimated for the two isolated species Tarsius and Daubentonia—although the credible intervals are very large (table 4). These estimates may not be so reliable, owing to the very long branches leading to these two species.
The reconstruction of Ne shown in figure 3 mirrors the patterns of dN/dS estimated over the tree (supplementary fig. 2, Supplementary Material online). This is partially expected given the fact that the model relies on the scaling relation between dN/dS and Ne given by equation (14). However, the model integrates other sources of information, in particular, from πS and . In order to get some insight about how each of these variables informs the reconstructed history of Ne, two additional models were considered.
First, an alternative version of the phenomenological model was used (supplementary fig. 3, Supplementary Material online), in which all time-dependent variables are assumed to evolve independently. Under this uncoupled model, Ne is not informed by dN/dS or , but only by and by the estimates of u implied by the relaxed clock and data about generation times. Compared with the mechanistic version just presented, this uncoupled model gives lower Ne estimates most notably for the last common ancestor of primates (30,000, vs. 100,000 under the mechanistic model), but also for the two species Daubentonia and Tarsius (which have a low dN/dS). Conversely, it returns higher Ne estimates in Lemuriformes (which have a high dN/dS compared with Lorisidae).
Interestingly, under the uncoupled model, there is a substantial uncertainty about the estimation of Ne across the tree: the 95% credible intervals span one order of magnitude on average. This uncertainty is reduced under the reconstructions relying on the additional information contributed by dN/dS and , quantitatively, by 30% under the phenomenological, and by 50% under the mechanistic covariant models (table 4). In the end, there is thus on average a factor 5 between the lower and the upper bound of the 95% credible intervals on Ne estimates under the most constrained (mechanistic) model. Concerning the deep branches of the tree, most of this reduction in uncertainty is primarily contributed by dN/dS—which thus gives an idea of how much information is extracted from multiple sequence alignments by these models about ancient population genetic regimes.
Second, as mentioned above, the mechanistic model infers a value of 0.27 for the shape parameter β, which is higher than recent SFS-based estimates, of the order of 0.16. Fixing in the mechanistic model returns a reconstruction of Ne over the phylogeny (supplementary fig. 4, Supplementary Material online) qualitatively similar to that returned by the unconstrained version of the model (fig. 3), although covering a broader range (about 100-fold) than under either the mechanistic or the uncoupled models (about 10- to 30-fold, fig. 3 and supplementary fig. 3, Supplementary Material online). This illustrates the key role of β in calibrating the transfer of information from dN/dS to Ne. According to the scaling relation given by equation (14), when β is small, a large variation in Ne results in a small shift in dN/dS. Thus, conversely, with a smaller β, the empirically observed variation in dN/dS over the tree implies a broader range of Ne variation across primates. In the present case, this argument also suggests an explanation of why the small value of β inferred by SFS is rejected by the mechanistic model—because the variation in Ne implied by the history of dN/dS under such a small value of β would exceed the one implied by the range of πS observed in extant species.
Of note, the Ne estimates are lower under the naive-phylogenetic (supplementary fig. 5, Supplementary Material online) than under the mean-coalescent approach (fig. 3). This difference between the two models is due to the fact that, given πS, any bias in the estimation of u has to be compensated for by an opposite bias of the same magnitude in the estimation of Ne. These discrepancies are relatively minor, however, and the global patterns of the history of Ne along the tree are very similar in both cases.
Finally, the phylogenetic history of the mutation rate per generation u mirrors that of Ne, such that species with smaller Ne tend to have a higher value for u (compare figs. 1 and 2). These opposite patterns of variation, combined with the fact that Ne shows a greater amplitude in its variation across primates compared with u, results in πS being mostly driven by Ne, although with a partial dampening of its overall variation. This joint pattern for Ne and u explains why the regression slopes of and against πS are steeper than those against Ne (table 2).
Discussion
A Bayesian Integrative Framework for Comparative Population Genomics
The question of the role of Ne in the evolution of coding sequences has motivated much work over the years. One main problem that has attracted particular attention is to understand to what extent Ne modulates the ratio of nonsynonymous over synonymous polymorphism () or divergence (). Often, πS has been used as a proxy for Ne. However, πS also depends on u, the mutation rate per generation, which differs between species.
In this context, the main contribution of the present work is to propose a Bayesian integrative phylogenetic framework for conducting such comparative analyses in a way that allows for direct quantitative estimation of Ne and of its impact on molecular evolution across a clade of interest. Relying on an integrated relaxed clock model to calibrate mutation rates, the program leverages an estimate of Ne based on πS, correcting for u. Simultaneously, it conducts a regression analysis, returning an estimate of the scaling exponent of molecular quantities such as dN/dS and , but also potentially other variables or quantitative traits, directly as a function of Ne. As a byproduct, the approach also returns a global reconstruction of the history of effective population size and mutation rate across the phylogeny.
As can be seen from table 2, correcting for variation in mutation rate between species (for u), as opposed to regressing directly against πS, does have an impact on the estimated scaling relations. In the present case, the slopes as a function of πS tend to be steeper than as a function of Ne, a pattern that is more generally expected if species with large Ne also tend to have lower mutation rates per generation, such as previously suggested (Lynch et al. 2011) and confirmed by our correlation analysis (table 1). The approach introduced here should therefore represent a useful methodological contribution in the context of the current discussions on the role played by those scaling coefficients in molecular evolution (James et al. 2017; Castellano et al. 2018, 2019; Galtier and Rousselle 2020).
Estimating Mutation Rates
Conceptually, our approach for extracting Ne is merely a reformulation, in a Bayesian integrative framework, of the classical idea of estimating Ne from πS by factoring out the mutation rate u, itself estimated based on a molecular clock argument. The integrative approach presents several advantages, however. First, it imposes the same assumptions about the molecular clock, relying on the same sequence data and the same global set of fossil constraints, uniformly for all species included in the analysis. Second, it automatically propagates the uncertainty about estimates of u, which themselves incorporate the uncertainty about divergence times, onto the credible intervals eventually reported for Ne or for the slopes of the regressions. Third, these slopes are also automatically corrected for phylogenetic nonindependence. Finally, on purely practical grounds, the application of the method is straightforward, just requiring as its input a multiple sequence alignment for the clade of interest, estimates of πS and for some or all of the extant species and fossil calibrations.
An alternative to the phylogenetic estimation of u is to rely on high-throughput sequencing of pedigrees. As of yet, such estimates are available only for 7 primates (Chintalapati and Moorjani 2020), but this is likely to change in the future. For these 7 species, the phylogenetic estimates obtained here are higher than pedigree-based estimates, thus in line with previous observations. The reasons for this discrepancy are not yet well-understood (Scally and Durbin 2012; Ségurel et al. 2014; Chintalapati and Moorjani 2020). Interestingly, accounting for coalescence in the ancestral populations contributes a lot to making phylogenetic estimates closer to those obtained in the same species by sequencing pedigrees, although not entirely.
In principle, pedigree-based estimates of u could be included in the framework presented here, as additional constraints at the tips of the phylogeny to inform the reconstruction of Ne. However, given the still unexplained mismatch between pedigrees and phylogenies, it is perhaps more meaningful to compare them after the fact, as was done here (table 3), and then further investigate the various entry points in the model, at the level of the relaxed clock, the prior on divergence times, the fossil constraints, that could be responsible for this discrepancy.
Mechanistic Models of Coding Sequence Evolution
Our phylogenetic approach was implemented in two alternative versions, using either a phenomenological or a mechanistic modeling strategy. The phenomenological model implements the idea of conducting comparative regression analyses directly against Ne, such as discussed above. In itself, this approach is agnostic about the underlying selective regimes over proteins and, in particular, is not inherently committed to a nearly neutral interpretation.
The mechanistic model, on the other hand, makes more aggressive assumptions about the underlying selective regime. It is fundamentally a Bayesian phylogenetic implementation of the nearly neutral theory. Accordingly, it assumes that protein-coding sequences are exclusively under purifying selection. Another key assumption of the model, not necessarily implied by the nearly neutral theory, is that the DFE is constant across species. These assumptions give more constraint to the analysis and return more focused estimates. However, the estimate of the shape parameter of the DFE obtained under this model turns out to be significantly higher than some of the estimates based on SFS obtained in humans or in great apes (table 2), suggesting that one of these two assumptions might not be strictly valid.
The question of whether the DFE is constant across species has recently motivated both methodological work for jointly analyzing the site frequency spectra of multiple species (Tataru and Bataillon 2019) and empirical investigations (Castellano et al. 2019; Galtier and Rousselle 2020). These empirical analyses suggest that the shape parameter is rather stable across great apes (Castellano et al. 2019) and more broadly across primates Galtier and Rousselle (2020). The mean of the distribution, on the other hand (usually denoted ), was found to be potentially variable across great apes (Castellano et al. 2019), such that species with larger Ne values also tend to have more strongly deleterious nonsynonymous mutations. The rather steep variation of the population scaled mean as a function of πS observed across metazoans Galtier and Rousselle (2020) might also be interpreted as reflecting an underlying positive covariation of with Ne. Importantly, since dN/dS and scale as , this specific pattern of covariation between the unscaled mean of the DFE and Ne predicts that the regression slopes should be steeper than β. This could explain the high estimate of β obtained here under the mechanistic model. Of note, the scaling of and dN/dS with respect to Ne returned by the phenomenological model are compatible with SFS-based estimates, but this might just be a consequence of the rather large credible intervals obtained in their case.
To further investigate this question, conducting a broader analysis with polymorphism data obtained for a larger number of primate species—and using the same set of coding genes for estimating πS and , on one hand, and dS and dN/dS, on the other hand—would certainly be an important direction to pursue, as it would consolidate the results presented here, which are still preliminary in many respects. In particular, it would yield more precise estimates of the scaling coefficients under the phenomenological model. If this confirms the discrepancy between the interspecific scaling coefficients and SFS-based estimates, then, the assumption of a constant DFE under the mechanistic model could be relaxed, although this would then require incorporating information, not just about mean diversity (πS and ), but also about site frequency spectra in extant species, in order to constrain the estimation.
Concerning the other assumption of the mechanistic model, of an exclusively purifying selection regime, the dN/dS ratio may in fact contain a fraction of adaptive substitutions, susceptible to distort the relation between dN/dS and Ne. The relative importance of adaptive versus nearly neutral substitutions in primates is still debated (Eyre-Walker and Keightley 2009; Galtier 2016; Zhen et al. 2021). In any case, adaptive substitutions might certainly represent an important issue when applying the method to other phylogenetic groups. Here also, the model could be further elaborated, by explicitly including an adaptive component to the total dN/dS. Quite interestingly, the resulting model could then be seen as an integrative multispecies version of the Mac-Donald Kreitman test, returning an estimate of the history of the adaptive substitution rate over the phylogeny—which could then be compared with independent estimates based on pairs of sister species (Charlesworth and Eyre-Walker 2008; Eyre-Walker and Keightley 2009; Halligan et al. 2010; Galtier 2016).
Finally, another potential issue, which concerns both the mechanistic and the phenomenological model, is that short-term Ne (such as reflected by πS) may be strongly dependent on recent demographic events (Charlesworth 2009) and may thus not be identical with long-term Ne (such as reflected by ). This might be one of the reasons why shows a weaker correlation with πS than . A possible improvement of our model in this direction would consist in allowing for an additional level of variability at the leaves, representing the mismatch between long- and short-term Ne. Other sources of variance in extant diversity estimates could also be modeled, in particular, the additional stochasticity contributed by the random genealogy or by the low counts of SNPs. These last two points are probably a minor issue for nuclear exome-wide polymorphism data, such as explored here. In contrast, they could be quite relevant in the case of the small and nonrecombining mitochondrial genome, for which the question of the interspecific scaling behavior of dN/dS and as a function of Ne is also of interest (James et al. 2017).
Evolution of Mutation Rates, Ne, and Life History across Primates
The global phylogenetic history of Ne (fig. 3) and mutation rates (figs. 1 and 2) obtained here offers interesting insights into the macroevolutionary trends in primates, making connections between life-history and molecular evolution. Previous analyses have repeatedly pointed out a slowdown of the molecular clock in apes (Steiper et al. 2004), more broadly in catarrhine primates (Perelman et al. 2011), or even more globally throughout the evolutionary history of the entire order (Steiper and Seiffert 2012), suggesting a trend toward increasing body size and longer generation times in this group. Our reconstruction confirms this global picture, adding another feature, in the form of a global decrease in effective population size, although more specifically in simians (fig. 3). A global picture only in terms of evolutionary trends along a small-versus-large body size axis, however, would be an oversimplification. In particular, dS and dN/dS appear to respond differently to LHT, dS being negatively correlated with body size (table 1) as previously reported (Steiper and Seiffert 2012), whereas dN/dS correlates only with longevity but not with body size, a pattern also observed across mammals (Nikolaev et al. 2007; Lartillot 2013).
The trend in decreasing Ne observed here is primarily driven by the underlying variation in dN/dS. As such, it provides another illustration of the more general result that molecular evolutionary patterns inferred from genetic sequences using phylogenetic methods can be informative about life-history evolution (Lartillot and Delsuc 2012; Romiguier et al. 2013; Figuet et al. 2014; Wu et al. 2017). Compared with previous work, however, an important new contribution of the present work is a quantitative reconstruction, over the phylogeny, directly in terms of the canonical parameters of population genetics, the mutation rate u and the effective population size Ne. Such broad-scale reconstructions, as opposed to focused estimates in isolated extant species, are potentially useful in several respects. First, they provide a basis for further testing some of the key ideas about the role of mutation rate or genetic drift in genome evolution (Lynch et al. 2011; Lefébure et al. 2017). Second, the integrative framework could be augmented with trait-dependent diversification models (Fitzjohn 2010), so as to examine the role of Ne or u in speciation and extinction patterns.
Materials and Methods
Coding Sequence Data, Phylogenetic Tree, and Fossil Calibration
The coding sequences were taken from Perelman et al. (2011) and modified. It consists in a modified subset, codon compliant, based on 54 nuclear autosomal genes in 61 species of primates, and of a total length 15.9 kb. We used the tree topology published by Perelman et al. (itself based on a maximum likelihood analysis), as well as the eight fossil calibrations that were used in this previous study to estimate divergence times. These calibrations were encoded as hard constraints on the molecular dating analysis.
Life-History Traits
We used four LHTs in this study. Adult body mass (as a proxy for body mass, 16 missing values), maximum recorded lifespan (ML, as a proxy for longevity, 19 missing values), and female age of sexual maturity (ASM, 26 missing values) were obtained from the AnAge database (de Magalhaes and Costa 2009). Estimates about generation time were calculated from maximum longevity and age at maturity following a method detailed by UICN (Pacifici et al. 2013):
In the case of great apes, and most notably for Humans, these estimates appear to be too high (48.5 years for Homo, 24.7 for Pan, 23.8 for Gorilla, and 24.1 for Pongo). For these four species, direct estimates of the generation time (29, 24, 19, and 25 years, respectively) were taken from Besenbacher et al. (2019).
Estimation of Polymorphism (πS and )
The estimates of the synonymous nucleotide diversity πS and the ratio of nonsynonymous over synonymous diversity and πS of ten primate species were calculated on the sequence data from Perry et al. (2012), such as reanalyzed by Romiguier et al. (2014) and Figuet et al. (2016). We matched these polymorphism data for the three species Pan troglodytes, Propithecus vereauxi coquereli, and Eulemur mongoz, to Pan paniscus, Propithecus verreauxi, and Eulemur rufus, respectively, from the Perelman et al. multiple sequence alignment.
A first series of analyses were conducted using the estimates of and πS reported by Romiguier et al. (2014). Alternatively, and in order to avoid the artifactual correlations induced between πS and by shared data sampling error, the method of Romiguier et al. (2014) was adapted so as to estimate πS and on different subset of the sites, using the hypergeometric method (James et al. 2017). Specifically, starting from the original fasta file containing the 8 variants for each contig of a given species, coding sites were randomly partitioned into two subsets, with equal probability independently for each site, and the πS and statistics were computed on each subset using the dNdSpiNpiS software program (available at https://kimura.univ-montp2.fr/calcul/softwares.html), with the same options as those used in Romiguier et al. (2014). Finally, the πS estimate from the first half was combined with the estimate obtained on the second half. The results presented in the main document are all based on this hypergeometric method. They are essentially identical to those obtained using the original polymorphism estimates (supplementary table 2, Supplementary Material online).
Models
The Phenomenological Model
The phenomenological model is essentially the one introduced in Lartillot and Poujol (2011), with some minor modifications. The exact structure of the model is given in the manual of Coevol, version 1.5b.
Correlations and Slopes
Given a covariance matrix Σ describing the correlation structure of a Brownian process X, the strength of the correlation coefficient between two entries of X, k, and l, is given by:
The slope of the regression of trait l against trait k is given by:
In both cases, the equation is applied successively on each point obtained from the posterior distribution by MCMC, yielding a collection of values, for either the correlation coefficient or the slope, from which a median point estimate and a credible interval are then computed.
Ex Post Log-Linear Transformation of the Correlation Analysis
In the following, the multivariate process X is specified such that the entries are in the same order as in table 1 (dS, dN/dS, maturity, mass, longevity, πS, , and generation time τ). Based on this vector X, an extended vector Y can be defined, as:
Since and are given by the following log-linear relations:
| (15) |
| (16) |
Y can be expressed as . Here, K is a vector of constants (depending on the time scale), and A is an 8 × 10 matrix:
where I8 is the 8 × 8 identity matrix. Since X is Brownian, parameterized by a covariance matrix ΣX, Y is also Brownian, with (degenerate) covariance structure given by . In practice, we added a new method in Coevol to read the output and apply the linear transformation (from X and ΣX to Y and ΣY) on each sample from the posterior distribution. This gives a reconstruction of Ne (posterior median, credible intervals) and of the correlation matrix ΣY.
Mechanistic Nearly Neutral Model
This alternative model uses the original Coevol framework but introduces additional constraints, such that some of the parameters are deduced through deterministic relations implying other Brownian dependent parameters. Specifically, the Brownian free variables are now:
Then, using equations (6), (7), (11), and (12), the other variables of interest can be expressed as deterministic functions:
This model has three structural free parameters, β, κ1, and κ2, which were each endowed with a normal prior, of mean 0 and variance 1.
The naive-phylogenetic version of the model uses the default approach used in Coevol, that is, assumes a single dated tree T, with branch lengths measured in time. The Brownian multivariate process X runs along this tree, splitting into two independent processes whenever a speciation node is encountered along the phylogeny. Conditional on T and X, the sequences then evolve along that same tree T, using a codon-model in which dS and dN/dS are modulated across branches, such as implied by X (Lartillot and Poujol 2011). For the mean-coalescent version of the model, on the other hand, conditional on T and X, the sequence evolutionary process is assumed to run on a dated tree different from T. Compared with T, the node ages of are all shifted further back into the past by an amount , where Ne and τ are the instant values of effective population size and generation time implied by the process X at the corresponding node in the original tree T, and is the difference between the age of the focal node on T and the age of its oldest daughter node in . This additional constraint is meant to ensure that a node should always be older than its daughter nodes in . Owing to the variation in Ne and τ between successive nodes, this constraint may not be automatically realized, in particular in regions of the tree in which successive splitting times are within coalescence time from each other—precisely those splits that are potentially under a regime of incomplete lineage sorting. In practice, this problem is rarely encountered (less than one node of the whole tree on average under the posterior distribution).
Uncoupled Model
The “uncoupled” model, already implemented in Coevol, is similar to the phenomenological version of the model, except that the variables of interest (dS, dN/dS, πS, , and τ) are modeled as independent Brownian processes along the tree. Equivalently, we use a multivariate Brownian model with a diagonal covariance matrix (see Lartillot and Poujol 2011, for details).
MCMC and Postanalysis
Two independent chains were run under each model configuration. Convergence of the chains was first checked visually (a burnin of approximately 1,000 points, out of 6,000, was taken for the phenomenological model, and of 100 out of 3,100 for the mechanistic model) and quantified using Coevol’s program Tracecomp (effective sample size greater than 500 and maximum discrepancy smaller than 0.10 across all pairs of runs and across all statistics, except for the age of the root of the tree, which typically has a lower effective sample size). We used the posterior median as the point estimate. The statistical support for correlations is assessed in terms of the posterior probability of a positive or a negative correlation. The slope is estimated for each covariance matrix sampled from the distribution, which then gives a sample from the marginal posterior distribution over the slope.
Supplementary Material
Supplementary data are available at Genome Biology and Evolution online.
Supplementary Material
Acknowledgments
We wish to thank Emeric Figuet, Jonathan Romiguier, and Nicolas Galtier for sharing polymorphism data (PopPhyl project) and for their help in rerunning the scripts for analyzing them, Emmanuel Douzery and Frederic Delsuc for editing the multiple sequence alignment of Perelman et al. to make it codon-compliant, and Nicolas Galtier, Laurent Duret, and Thibault Latrille for their input on this work and their comments on the manuscript. This work was funded by French National Research Agency (Grant No. ANR-15-CE12-0010-01/DASIRE). Phylogenetic analyses were conducted using the computing facilities of the CC LBBE/PRABI.
Author Contributions
The modifications of Coevol and the new models presented in this study are primarily attributable to M.B., who also gathered and formatted the data and conducted all analyses, in the context of an internship (master Biosciences of École Normale Supérieure de Lyon). N.L. contributed additional analyses and further elaborations for the revised version. M.B. and N.L. both contributed to the writing of the manuscript.
Data Availability
Coevol (Lartillot and Poujol 2011) is an open source program available on github: https://github.com/bayesiancook/coevol. All models and data used here, along with scripts to rerun the entire analysis, are accessible from this repo. Data and scripts for computing πS and are available from figshare (https://www.doi.org/10.6084/m9.figshare.14784888.v1).
Literature Cited
- Besenbacher S, Hvilsom C, Marques-Bonet T, Mailund T, Schierup MH.. 2019. Direct estimation of mutations in great apes reconciles phylogenetic dating. Nat Ecol Evol. 3(2):286–292. [DOI] [PubMed] [Google Scholar]
- Boyko AR, et al. 2008. Assessing the evolutionary impact of amino acid mutations in the human genome. PLoS Genet. 4(5):e1000083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castellano D, James J, Eyre-Walker A.. 2018. Nearly neutral evolution across the Drosophila melanogaster genome. Mol Biol Evol. 35(11):2685–2694. [DOI] [PubMed] [Google Scholar]
- Castellano D, Macià MC, Tataru P, Bataillon T, Munch K.. 2019. Comparison of the full distribution of fitness effects of new amino acid mutations across great apes. Genetics 213(3):953–966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth B.2009. Fundamental concepts in genetics: effective population size and patterns of molecular evolution and variation. Nat Rev Genet. 10(3):195–205. [DOI] [PubMed] [Google Scholar]
- Charlesworth J, Eyre-Walker A.. 2008. The McDonald-Kreitman test and slightly deleterious mutations. Mol Biol Evol. 25(6):1007–1015. [DOI] [PubMed] [Google Scholar]
- Chen J, Glémin S, Lascoux M.. 2017. Genetic diversity and the efficacy of purifying selection across plant and animal species. Mol Biol Evol. 34(6):1417–1428. [DOI] [PubMed] [Google Scholar]
- Chintalapati M, Moorjani P.. 2020. Evolution of the mutation rate across primates. Curr Opin Genet Dev. 62:58–64. [DOI] [PubMed] [Google Scholar]
- de Magalhaes J, Costa J.. 2009. A database of vertebrate longevity records and their relation to other life-history traits. J Evol Biol. 22(8):1770–1774. [DOI] [PubMed] [Google Scholar]
- Eyre-Walker A, Keightley PD.. 2007. The distribution of fitness effects of new mutations. Nat Rev Genet. 8(8):610–618. [DOI] [PubMed] [Google Scholar]
- Eyre-Walker A, Keightley PD.. 2009. Estimating the rate of adaptive molecular evolution in the presence of slightly deleterious mutations and population size change. Mol Biol Evol. 26(9):2097–2108. [DOI] [PubMed] [Google Scholar]
- Eyre-Walker A, Keightley PD, Smith NGC, Gaffney D.. 2002. Quantifying the slightly deleterious mutation model of molecular evolution. Mol Biol Evol. 19(12):2142–2149. [DOI] [PubMed] [Google Scholar]
- Eyre-Walker A, Woolfit M, Phelps T.. 2006. The distribution of fitness effects of new deleterious amino acid mutations in humans. Genetics 173(2):891–900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Figuet E, et al. 2016. Life history traits, protein evolution, and the nearly neutral theory in amniotes. Mol Biol Evol. 33(6):1517–1527. [DOI] [PubMed] [Google Scholar]
- Figuet E, Romiguier J, Dutheil JY, Galtier N.. 2014. Mitochondrial DNA as a tool for reconstructing past life-history traits in mammals. J Evol Biol. 27(5):899–910. [DOI] [PubMed] [Google Scholar]
- Fitzjohn RG.2010. Quantitative traits and diversification. Syst Biol. 59(6):619–633. [DOI] [PubMed] [Google Scholar]
- Galtier N.2016. Adaptive protein evolution in animals and the effective population size hypothesis. PLoS Genet. 12(1):e1005774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galtier N, Rousselle M.. 2020. How much does Ne vary among species? Genetics 216(2):559–572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halligan DL, Oliver F, Eyre-Walker A, Harr B, Keightley PD.. 2010. Evidence for pervasive adaptive protein evolution in wild mice. PLoS Genet. 6(1):e1000825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- James J, Castellano D, Eyre-Walker A.. 2017. DNA sequence diversity and the efficiency of natural selection in animal mitochondrial DNA. Heredity (Edinb). 118(1):88–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M.1979. Model of effectively neutral mutations in which selective constraint is incorporated. Proc Natl Acad Sci U S A. 76(7):3440–3444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lartillot N.2013. Interaction between selection and biased gene conversion in mammalian protein-coding sequence evolution revealed by a phylogenetic covariance analysis. Mol Biol Evol. 30(2):356–368. [DOI] [PubMed] [Google Scholar]
- Lartillot N, Delsuc F.. 2012. Joint reconstruction of divergence times and life-history evolution in placental mammals using a phylogenetic covariance model. Evolution 66(6):1773–1787. [DOI] [PubMed] [Google Scholar]
- Lartillot N, Poujol R.. 2011. A phylogenetic model for investigating correlated evolution of substitution rates and continuous phenotypic characters. Mol Biol Evol. 28(1):729–744. [DOI] [PubMed] [Google Scholar]
- Lefébure T, et al. 2017. Less effective selection leads to larger genomes. Genome Res. 27(6):1016–1028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leffler EM, et al. 2012. Revisiting an old riddle: what determines genetic diversity levels within species? PLoS Biol. 10(9):e1001388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M, Bobay L-M, Catania F, Gout J-F, Rho M.. 2011. The repatterning of eukaryotic genomes by random genetic drift. Annu Rev Genomics Hum Genet. 12:347–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mugal CF, Kutschera VE, Botero-Castro F, Wolf JBW, Kaj I.. 2020. Polymorphism data assist estimation of the nonsynonymous over synonymous fixation rate ratio ω for closely related species. Mol Biol Evol. 37(1):260–279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nabholz B, Uwimana N, Lartillot N.. 2013. Reconstructing the phylogenetic history of long-term effective population size and life-history traits using patterns of amino acid replacement in mitochondrial genomes of mammals and birds. Genome Biol Evol. 5(7):1273–1290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nikolaev SI, et al. 2007. Life-history traits drive the evolutionary rates of mammalian coding and noncoding genomic elements. Proc Natl Acad Sci U S A. 104(51):20443–20448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohta T.1995. Synonymous and nonsynonymous substitutions in mammalian genes and the nearly neutral theory. J Mol Evol. 40(1):56–63. [DOI] [PubMed] [Google Scholar]
- Pacifici M, Santini L, Di Marco M, Baisero D.. 2013. Generation length for mammals. Nat Conserv. 5:87–94. [Google Scholar]
- Perelman P, et al. 2011. A molecular phylogeny of living primates. PLoS Genet. 7(3):e1001342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perry GH, et al. 2012. Comparative RNA sequencing reveals substantial genetic variation in endangered primates. Genome Res. 22(4):602–610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piganeau G, Eyre-Walker A.. 2009. Evidence for variation in the effective population size of animal mitochondrial DNA. PLoS One 4(2):e4396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popadin K, Polishchuk L, Mamirova L, Knorre D, Gunbin K.. 2007. Accumulation of slightly deleterious mutations in mitochondrial protein-coding genes of large versus small mammals. Proc Natl Acad Sci U S A. 104(33):13390–13395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prado-Martinez J, et al. 2013. Great ape genetic diversity and population history. Nature 499(7459):471–475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rannala B, Yang Z.. 2003. Bayes estimation of species divergence times and ancestral population sizes using DNA sequences from multiple loci. Genetics 164(4):1645–1656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romiguier J, et al. 2014. Comparative population genomics in animals uncovers the determinants of genetic diversity. Nature 515(7526):261–263. [DOI] [PubMed] [Google Scholar]
- Romiguier J, Ranwez V, Douzery EJP, Galtier N.. 2013. Genomic evidence for large, long-lived ancestors to placental mammals. Mol Biol Evol. 30(1):5–13. [DOI] [PubMed] [Google Scholar]
- Scally A, Durbin R.. 2012. Revising the human mutation rate: implications for understanding human evolution. Nat Rev Genet. 13(10):745–753. [DOI] [PubMed] [Google Scholar]
- Ségurel L, Wyman MJ, Przeworski M.. 2014. Determinants of mutation rate variation in the human germline. Annu Rev Genomics Hum Genet. 15(1):47–70. [DOI] [PubMed] [Google Scholar]
- Steiper ME, Seiffert ER.. 2012. Evidence for a convergent slowdown in primate molecular rates and its implications for the timing of early primate evolution. Proc Natl Acad Sci U S A. 109(16):6006–6011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steiper ME, Young NM, Sukarna TY.. 2004. Genomic data support the hominoid slowdown and an Early Oligocene estimate for the hominoid-cercopithecoid divergence Proc Natl Acad Sci U S A. 101(49):17021–17026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tataru P, Bataillon T.. 2019. polyDFEv2.0: testing for invariance of the distribution of fitness effects within and across species. Bioinformatics 35(16):2868–2869. [DOI] [PubMed] [Google Scholar]
- Thomas GWC, et al. 2018. Reproductive longevity predicts mutation rates in primates. Curr Biol. 28(19):3193–3197.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang RJ, et al. 2020. Paternal age in rhesus macaques is positively associated with germline mutation accumulation but not with measures of offspring sociability. Genome Res. 30(6):826–834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waples RS, Luikart G, Faulkner JR, Tallmon DA.. 2013. Simple life-history traits explain key effective population size ratios across diverse taxa. Proc R Soc Lond A. 280(1768):20131339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welch JJ, Eyre-Walker A, Waxman D.. 2008. Divergence and polymorphism under the nearly neutral theory of molecular evolution. J Mol Evol. 67(4):418–426. [DOI] [PubMed] [Google Scholar]
- Wu FL, et al. 2020. A comparison of humans and baboons suggests germline mutation rates do not track cell divisions. PLoS Biol. 18(8):e3000838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu J, Yonezawa T, Kishino H.. 2017. Rates of molecular evolution suggest natural history of life history traits and a post-K-Pg nocturnal bottleneck of placentals. Curr Biol. 27(19):3025–3033.e5. [DOI] [PubMed] [Google Scholar]
- Zhen Y, Huber CD, Davies RW, Lohmueller KE.. 2021. Greater strength of selection and higher proportion of beneficial amino acid changing mutations in humans compared with mice and Drosophila melanogaster. Genome Res. 31(1):110–120. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Coevol (Lartillot and Poujol 2011) is an open source program available on github: https://github.com/bayesiancook/coevol. All models and data used here, along with scripts to rerun the entire analysis, are accessible from this repo. Data and scripts for computing πS and are available from figshare (https://www.doi.org/10.6084/m9.figshare.14784888.v1).