Prepregnancy body mass index and spina bifida: Potential contributions of bias

Abstract

Background:

Epidemiologists have consistently observed associations between prepregnancy obesity and spina bifida in offspring. Most studies, however, used self-reported body mass index (potential for exposure misclassification) and incompletely ascertained cases of spina bifida among terminations of pregnancy (potential for selection bias). We conducted a quantitative bias analysis to explore the potential effects of these biases on study results.

Methods:

We included 808 mothers of fetuses or infants with spina bifida (case mothers) and 7,685 mothers of infants without birth defects (control mothers) from a population-based case–control study, the National Birth Defects Prevention Study (1997–2011). First, we performed a conventional epidemiologic analysis, adjusting for potential confounders using logistic regression. Then, we used 5,000 iterations of probabilistic bias analysis to adjust for the combination of confounding, exposure misclassification, and selection bias.

Results:

In the conventional confounding-adjusted analysis, prepregnancy obesity was associated with spina bifida (odds ratio 1.4, 95% confidence interval: 1.2, 1.7). In the probabilistic bias analysis, we tested nine different models for the combined effects of confounding, exposure misclassification, and selection bias. Results were consistent with a weak to moderate association between prepregnancy obesity and spina bifida, with the median odds ratios across the nine models ranging from 1.1 to 1.4.

Conclusions:

Given our assumptions about the occurrence of bias in the study, our results suggest that exposure misclassification, selection bias, and confounding do not completely explain the association between prepregnancy obesity and spina bifida.

1 |. INTRODUCTION

For over 20 years, epidemiologists have consistently found associations between high prepregnancy body mass index (BMI) and increased risk for neural tube defects, including spina bifida, in offspring (Huang, Chen, & Feng, 2017). The biological mechanisms underlying this association are not yet understood. Folate status differs by BMI, but women with overweight or obesity have higher red blood cell folate levels than women with normal BMI, which should indicate a lower—not higher—risk for spina bifida (Manandhar, Beydoun, & Kancherla, 2020). Impaired glucose control in pregnancy is another hypothesis; obesity increases the risk of type 2 diabetes, and diabetes is a cause of birth defects. Recent research, however, suggests that pregestational diabetes is not a risk factor for isolated spina bifida (Tinker et al., 2020). Other hypotheses under investigation include differences in diet quality, micronutrient status, and oxidative stress between mothers with and without obesity (Carmichael, Rasmussen, & Shaw, 2010).

One hypothesis that has been acknowledged but not quantitatively assessed is that uncontrolled biases in epidemiologic studies could be producing a spurious association between prepregnancy BMI and spina bifida. Many studies of prepregnancy BMI and spina bifida are population-based case–control studies that share important characteristics: a high risk for bias from exposure misclassification and selection bias and no statistical analyses adjusting for these biases.

Exposure misclassification can occur if prepregnancy BMI is calculated from self-reported height and weight. In the United States, adults tend to overreport their height and underreport their weight, leading to a lower reported BMI than their true BMI (Hodge, Shah, McCullough, Gapstur, & Patel, 2020). Accuracy of self-reported BMI may also vary by sociodemographic factors such as age and race/ethnicity (Hattori & Sturm, 2013). Predicting how exposure misclassification will affect the results of epidemiologic studies is challenging without performing formal statistical analyses (Jurek, Greenland, & Maldonado, 2008).

Selection bias can occur if cases are incompletely ascertained among terminations of pregnancy (Howards et al., 2015). In some regions, two-thirds of families opt for termination of pregnancy following prenatal diagnosis of a fetus with spina bifida, meaning a substantial proportion of cases may be inadvertently excluded (Johnson et al., 2012). If the likelihood of termination—and thus inclusion in the study—differs by prepregnancy BMI, selection bias can occur (Cragan & Khoury, 2000). One proposed mechanism is that high prepregnancy BMI decreases the likelihood of prenatal diagnosis of spina bifida via ultrasonography, decreases the likelihood of termination of pregnancy, and increases the probability that the liveborn case will be identified and included in the study (Peek & Nanan, 2009). This hypothesis is supported by studies that have found lower likelihood of prenatal diagnosis of birth defects among mothers with obesity, which makes the fetal anatomy difficult to visualize on ultrasound (Dashe, McIntire, & Twickler, 2009; Pasko, Wood, Jenkins, Owen, & Harper, 2016). This mechanism of selection bias is illustrated in Figure 1.

FIGURE 1.

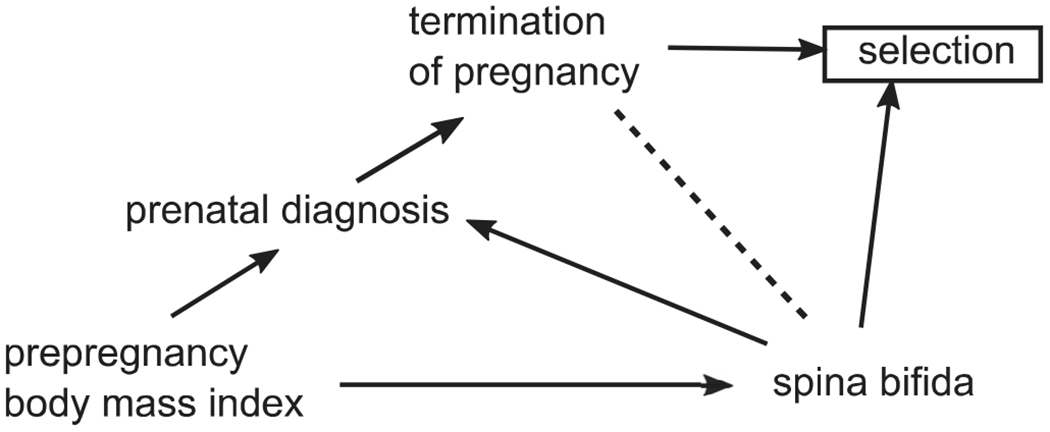
Directed acyclic graph illustrating one possible mechanism of selection bias. Selection bias (collider stratification bias) could occur if selection into the study is driven by prepregnancy body mass index (via differential prenatal diagnosis and termination of pregnancy) and selection based on outcome (via case–control sampling)

To predict how exposure misclassification and selection bias might affect the observed association between prepregnancy BMI and spina bifida, we can conduct a quantitative bias analysis. Quantitative bias analysis refers to a variety of statistical methods used to model how biases like exposure misclassification and selection bias affect study results (Lash, Fox, & Fink, 2009). These bias analyses use information about exposure classification and participation rates to model how bias might be affecting study results. Although detailed data on exposure classification and participation rates are seldom available in epidemiologic studies, these parameters can be estimated through literature review or by making assumptions about how bias might have occurred in the study (Lash et al., 2014). The purpose of bias analysis is not always to estimate the true magnitude of the association, especially if good validation data are unavailable, which would make that task difficult. Valuable contributions of bias analysis also include observing how study results change when making a variety of realistic assumptions about how bias might have occurred in the study, and using these results to decide if bias is a likely explanation for study results.

To explore how bias could be affecting associations between prepregnancy BMI and spina bifida, we performed quantitative bias analyses using data from the National Birth Defects Prevention Study (NBDPS), a population-based case–control study that has similar potential for exposure misclassification and selection bias to many previous studies of prepregnancy BMI and spina bifida. To achieve a large enough sample size for quantitative bias analysis, we updated a previously published analysis from NBDPS with an additional 9 years of data (Waller et al., 2007).

2 |. METHODS

NBDPS is a population-based case–control study of risk factors for major structural birth defects (Reefhuis et al., 2015). Cases were live births, fetal deaths at ≥20 gestational weeks, or terminations of pregnancy at any gestational age with one or more NBDPS-eligible birth defects. They were identified from birth defects surveillance systems in Arkansas, California, Georgia, Iowa, Massachusetts, New Jersey, New York, North Carolina, Texas, and Utah. Clinical geneticists reviewed medical record abstracts to exclude birth defects caused by suspected genetic syndromes (Rasmussen et al., 2003). Controls were live births without major birth defects, randomly selected from hospital birth logs or birth certificates in the same catchment areas as cases. Eligible mothers delivered on or after October 1, 1997, and had due dates on or before December 31, 2011. Six weeks to two years after delivery, mothers completed a computer-assisted telephone interview during which they reported sociodemographic information, height, and prepregnancy weight.

This study followed the U.S. Federal Policy for the Protection of Human Subjects. All participating sites had institutional review board approval and all participants provided informed consent for participation. All analyses were conducted in SAS 9.4 (Cary, NC).

In our analyses, we included mothers who had a fetus or infant with spina bifida but no other major birth defects (case mothers) and mothers of liveborn infants without major birth defects (control mothers). We calculated prepregnancy BMI as self-reported weight in kilograms divided by squared self-reported height in meters. We used four BMI categories in our analyses: underweight (<18.5 kg/m²), normal weight (18.5–24.9 kg/m²), overweight (25.0–29.9 kg/m²), and obesity (≥30 kg/m²). We used categorized instead of continuous BMI as our exposure variable to allow for nonlinear associations between BMI and spina bifida and to facilitate comparisons with previous studies, many of which reported BMI categories.

We excluded mothers aged <18 years at conception because the same BMI categories are not typically used for children. We also excluded mothers enrolled at study sites during periods when cases were not ascertained among terminations of pregnancy because our analysis for selection bias required information on these cases: Georgia (1997–1998), Massachusetts (all years), New Jersey (all years), and New York (1997–1999). We excluded mothers with type 1 diabetes, a risk factor for birth defects, but retained mothers with type 2 diabetes because this variable could be on the causal pathway between prepregnancy BMI and spina bifida. For our analysis of exposure misclassification, we could only find suitable data on BMI reporting accuracy for non-Hispanic white, non-Hispanic black, and Hispanic mothers; we restricted our study population to these three racial and ethnic groups.

Our multivariable models were adjusted for two potential confounders, maternal race/ethnicity and household income, and one study design variable, study site. We obtained these variables from the maternal questionnaire and excluded participants with missing data. We considered maternal age, education, and preconceptional folic acid supplementation as additional covariates; because none appreciably affected results when included in the models, we removed them from the models to prevent nonpositivity (zero cells) in the models (Westreich & Cole, 2010).

We excluded mothers with missing prepregnancy BMI (4%) from all analyses except those in which we conducted bias analyses for exposure misclassification; in those analyses, we could also adjust for missing exposure data. Although including mothers with missing data in some analyses but not others might mean that our populations are not comparable between analyses, a previous study of missing prepregnancy BMI in NBDPS found that results are similar whether adjusting for missing BMI or excluding participants with missing data (Razzaghi et al., 2016).

2.1 |. Conventional analyses

We used logistic regression to estimate unadjusted (crude) and confounder-adjusted odds ratios (ORs) and 95% confidence intervals (CIs) for associations between prepregnancy BMI categories and spina bifida, using the normal weight BMI category as the reference group.

2.2 |. Bias analysis: exposure misclassification

To adjust for exposure misclassification, we chose a previously described method that reweights participants so that the BMI distribution reported by mothers better resembles the BMI distribution that most likely existed in reality (Lyles & Lin, 2010). This type of weighting is conceptually similar to how survey participants are often weighted to account for the difference between the demographics of people who participate and the demographics of the entire population. This method has been previously applied to NBDPS data (Johnson et al., 2018).

To use this method, we needed predictive values—the probability that the BMI category reported by the mother was accurate. We had no such data for NBDPS. Instead, we found data from the National Health and Nutrition Examination Survey (NHANES), a cross-sectional survey representative of the U.S. civilian, noninstitutionalized population (Zipf et al., 2013). To better match the NBDPS population, we restricted the dataset to nonpregnant women aged 18–44 years who participated in NHANES between 1999 and 2010. We also reweighted the age distribution of the NHANES population to match the age distribution of the NBDPS control mothers (Parker, Branum, Axelrad, & Cohen, 2013).

NHANES participants self-reported their height and weight during an initial interview. Within 2 weeks, staff measured participants’ heights and weights; we excluded participants without these measurements. Therefore, both self-reported and measured BMI categories were available for each included participant. For women in each self-reported BMI category (underweight, normal weight, overweight, obesity, and missing data), we calculated the probability that their measured BMI classification was underweight, normal weight, overweight, or obesity. We calculated these predictive values within strata of race/ethnicity and incorporated NHANES’s complex survey sampling design in the calculation (Table 1). The major sources of misclassification in NHANES were women reporting underweight when they were truly normal weight and women reporting overweight when they truly had obesity.

TABLE 1.

Probability of measured body mass index category based on what participants self-reported as their body mass index for three racial and ethnic groups, National Health and Nutrition Examination Survey, 1999–2010

Self-reported body mass index	Measured body mass index	Non-Hispanic white	Non-Hispanic black	Hispanic
Underweight	Underweight	0.78	0.50	0.59
	Normal weight	0.22	0.50	0.41
	Overweight	0	0	0
	Obesity	0	0	0
Normal weight	Underweight	0.03	0.05	0.02
	Normal weight	0.87	0.78	0.79
	Overweight	0.10	0.16	0.18
	Obesity	0	0.01	0.01
Overweight	Underweight	0	0	0
	Normal weight	0.07	0.05	0.09
	Overweight	0.75	0.72	0.71
	Obesity	0.18	0.23	0.20
Obesity	Underweight	0	0	0
	Normal weight	0	0	0.01
	Overweight	0.03	0.03	0.07
	Obesity	0.97	0.96	0.92
Missing	Underweight	0.02	0.01	0.02
	Normal weight	0.25	0.09	0.32
	Overweight	0.17	0.18	0.29
	Obesity	0.56	0.72	0.37

Because we did not know if our NHANES estimates were correct for our study population, we conducted a probabilistic bias analysis. A probabilistic bias analysis is one that assigns a range of predictive values to account for uncertainty. For example, in Table 1 we found that among women reporting that they were underweight, 78% were truly underweight when they were measured. Although we could have treated 78% as the truth, we assumed that in the NBDPS population, the value might be similar but not exactly 78%. In our analyses, we created triangular distributions with the predictive value as the mode (78%, in this example) and +/− 10 percentage points of the mode as the minimum (68%) and maximum (88%) of the distribution. We had little information to guide our choice of width or shape of the distribution, so we chose these values to balance allowing sufficient variability without incorporating so much uncertainty that results would be uninterpretable.

To conduct the probabilistic analysis, we randomly chose 5,000 values from our triangular distributions and used them to calculate 5,000 odds ratios (OR), each time using the predictive value as a weight in the multivariable logistic regression model to adjust for exposure misclassification in addition to confounding. Further details on how this method works and how random error is added into the results have been published previously (Johnson et al., 2018; Lash et al., 2009). Because this analysis does not produce a single OR as its result, we present results as the median odds ratio and the 95% simulation interval (SI). The 95% SI represents the 2.5th and 97.5th percentiles of the ORs, which encompasses 95% of the ORs generated by simulation.

We did not know if case or control mothers more accurately reported their prepregnancy BMI or how any differences might affect results. We made three different assumptions in our analyses: equal accuracy in reporting BMI, case mothers more accurately report BMI, and control mothers more accurately report BMI. Further details along with the predictive values used for each assumption are shown in the Web Appendix.

2.3 |. Bias analysis: selection bias

We adjusted for potential selection bias from two sources: (1) study participation and (2) underascertainment of cases among terminations of pregnancy, which might favor inclusion of mothers with obesity and live births and drive selection bias via the mechanism illustrated in Figure 1. To do this, we used inverse probability of selection weights (IPSWs) in our logistic regression models (Hernán, Hernández-Díaz, & Robins, 2004). As an example of how this method works, imagine that our study included every spina bifida case among live births (probability of selection = 1) but only 1 in every 5 cases among terminations of pregnancy (probability of selection = 0.2). We could fix this imbalance by counting every case among terminations of pregnancy five times instead of once (5 is the inverse probability of selection: 1/0.2 = 5). In this example, the IPSW used in the logistic regression model is 1 for cases among live births and 5 for cases among terminations.

To adjust for selection bias from study participation, we used available information on NBDPS participation rates (our best estimate of the probability of selection): 67% of eligible case mothers and 65% of eligible control mothers participated in NBDPS (Reefhuis et al., 2015). We had no information about how participation differed by the exposure, BMI. We found a study of participation in a Danish pregnancy cohort, which reported that mothers with prepregnancy underweight or obesity were less likely to participate than other mothers (Nohr, Frydenberg, Henriksen, & Olsen, 2006). We used this information to calculate BMI-specific participation rates and then IPSWs for our analysis (see Web Appendix for further details).

To adjust for selection bias from underascertainment of cases among terminations of pregnancy, we first had to address systematic differences in ascertainment. Some NBDPS sites actively ascertained cases among pregnancies ending in termination after prenatal diagnosis throughout the study period, but others used passive ascertaintment at first and began active ascertainment only partway through (Reefhuis et al., 2015). Active ascertainment likely finds more cases (higher selection probability) than passive ascertainment (lower selection probability). We categorized mothers as being enrolled during a time and place of active ascertainment or not and calculated IPSWs separately for each situation.

For each of these two groups, we estimated the selection probabilities for cases among terminations of pregnancy using a previously described method (Howards et al., 2015). Briefly, this method uses multiple pieces of information—the probabilities of prenatal diagnosis given BMI, termination of pregnancy given prenatal diagnosis or not, and selection into the study given the pregnancy ended in live birth or fetal loss—to calculate likely selection probabilities. This information came from both NBDPS and published studies (Finer & Zolna, 2016; Johnson et al., 2012; Jones & Finer, 2012). The full data used for these calculations are shown in the Web Appendix. Using this method, we estimated that 22% of eligible spina bifida-affected pregnancies ending in termination of pregnancy were included in the study among mothers participating during periods of active ascertainment compared to 14% among mothers participating at other times (selection probabilities of 0.22 and 0.14). For simplicity, we assumed 100% selection for pregnancies ending in live birth or fetal loss (selection probability = 1). Although selection bias from underascertainment of stillbirths could occur, selection bias via underascertainment of terminations of pregnancy would likely result in larger biases, both because they are more common and because of potential selection bias through differential prenatal diagnosis by prepregnancy BMI.

We tested three selection bias scenarios. First, we assumed that study participation was the only source of selection bias and these participation rates did not differ by BMI. Second, we added selection bias from underascertainment of cases among terminations of pregnancy. Third, we additionally allowed study selection probabilities to vary by BMI for the control mothers but not the case mothers; we assumed that mothers of children with spina bifida were motivated to participate, whereas control mother participation could be affected by sociodemographic factors for which BMI is a proxy measure (e.g., income and education). Selection probabilities are presented in Table 2. By varying the ratio of selection probabilities between cases and controls across BMI strata, this scenario addresses potential differential selection by both exposure and outcome.

TABLE 2.

Selection probabilities for case and control mothers given self-reported body mass index under three assumptions about occurrence of selection bias in the study

	Assumption 1a		Assumption 2b			Assumption 3c
Self-reported body mass index category	Case mothers	Control mothers	Case mothers (LB, SB)	Case mothers(TOP)d	Control mothers	Cases mothers (LB, SB)	Cases mothers(TOP)d	Control mothers
Underweight	0.67	0.65	0.67	0.67*p	0.65	0.67	0.67*p	0.65*0.84
Normal weight	0.67	0.65	0.67	0.67*p	0.65	0.67	0.67*p	0.65*1.04
Overweight	0.67	0.65	0.67	0.67*p	0.65	0.67	0.67*p	0.65*0.96
Obesity	0.67	0.65	0.67	0.67*p	0.65	0.67	0.67*p	0.65*0.89
Missing	0.67	0.65	0.67	0.67*p	0.65	0.67	0.67*p	0.65*1.00

Abbreviations: LB, live birth; SB, stillbirth; TOP, termination of pregnancy.

^aStudy participation rates are the only source of selection bias.

^bStudy participation rates and underascertainment of cases contribute to selection bias.

^cStudy participation rates and underascertainment of cases contribute to selection bias and study participation rates vary by case–control status and prepregnancy body mass index.

^dp is the selection probability for mothers in sites and years with and without active ascertainment of cases among prenatal diagnoses: p = .22 among mothers enrolled under active ascertainment; p = .14 among mothers who were not.

We conducted probabilistic bias analyses, randomly choosing study selection probabilities and ascertainment selection probabilities 5,000 times from triangular distributions. These distributions had the selection probabilities in Table 2 as the mode; the maximum and minimum were ± 0.05 of the mode. (We also tested a wider distribution [± 0.10], which produced little to no change in results. Results from this analysis are not reported.) We inverted selection probabilities to calculate IPSWs and used these IPSWs as weights in a multivariable logistic regression model to adjust for selection bias and confounding together. We summarized results from the probabilistic analysis as median OR and 95% SI.

2.4 |. Bias analysis: combined biases

In our final analyses, we adjusted for exposure misclassification, selection bias, and confounding together. In total, we examined nine models: combinations of the three exposure misclassification models and the three selection bias models. For each of the 5,000 iterations of probabilistic bias analysis, we multiplied the predictive value weight (exposure misclassification) and IPSW (selection bias) to generate a final multiple-bias-correcting weight for each observation, a method that has been previously described (Johnson et al., 2018). We used this weight in a multivariable logistic regression model and reported results as median OR and 95% SI.

3 |. RESULTS

Of the 1,297 spina bifida case mothers and 11,829 control mothers participating in NBDPS, 808 case mothers and 7,685 control mothers were included. Major reasons for exclusion were ineligible study sites and years (161 cases, 2,266 controls), missing data on household income (89 cases, 666 controls), ineligible race/ethnicity groups (66 cases, 610 controls), and spina bifida cases with multiple major birth defects (111 cases). A participant flow chart is presented in the Web Appendix. Compared to control mothers, case mothers had higher prevalence of prepregnancy obesity, Hispanic ethnicity, and low household income and were more likely to live in California (Table 3).

TABLE 3.

Characteristics of included spina bifida case and control mothers, National Birth Defects Prevention Study, 1997–2011

	Case		Control
	N = 808		N = 7,685
	n	%	n	%
Pregnancy outcome
Live birth	703	87	7,685	100
Fetal death	16	2	0	0
Termination	89	11	0	0
Prepregnancy body mass index category
Underweight	18	2	349	5
Normal weight	343	46	3,744	51
Overweight	186	25	1,776	24
Obesity	203	27	1,529	21
Missing	58		287
Maternal race/ethnicity
Non-Hispanic white	463	57	4,788	62
Non-Hispanic black	58	7	896	12
Hispanic	287	36	2,001	26
Household income
<$50,000	595	74	5,137	67
>$50,000	213	26	2,548	33
Study site
Arkansas	104	13	1,183	15
California	162	20	932	12
Georgia	101	13	954	12
Iowa	127	16	1,115	15
New York	48	6	671	9
North Carolina	72	9	790	10
Texas	108	13	1,039	14
Utah	86	11	1,001	13

In the conventional confounder-adjusted analysis, higher prepregnancy BMI was associated with increased prevalence of spina bifida in a dose–response pattern: OR 1.4 (95% CI: 1.2, 1.7) for obesity versus normal weight, OR 1.1 (95% CI: 0.9,1.4) for overweight, and OR 0.6 (95% CI: 0.3, 0.9) for underweight. Overall, the results from the quantitative bias analyses were similar to those from the conventional analysis and generally showed the same dose–response association between prepregnancy BMI and spina bifida (Figures 2, 3, 4).

FIGURE 2.

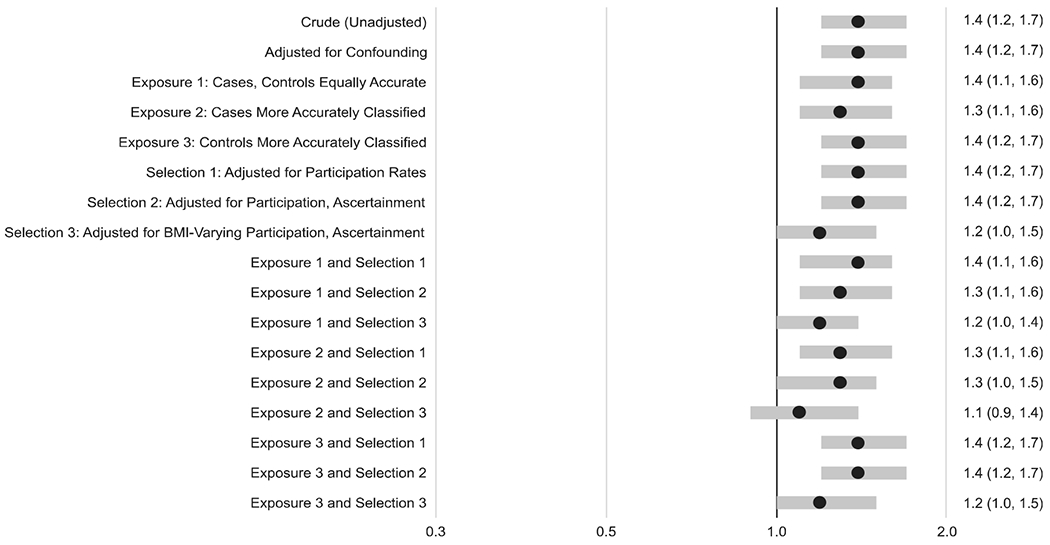
Odds ratios and 95% confidence intervals from conventional analyses and median odds ratios and 95% simulation intervals from bias analyses for the association between prepregnancy obesity (vs. normal weight) and spina bifida. The analyses include one unadjusted model, one adjusted for confounding, three models for exposure misclassification plus confounding, and three adjusting for selection bias plus confounding. The final nine models combine the various assumptions for exposure misclassification, selection bias, and confounding. The assumptions for each model are explained in more detail in the text

FIGURE 3.

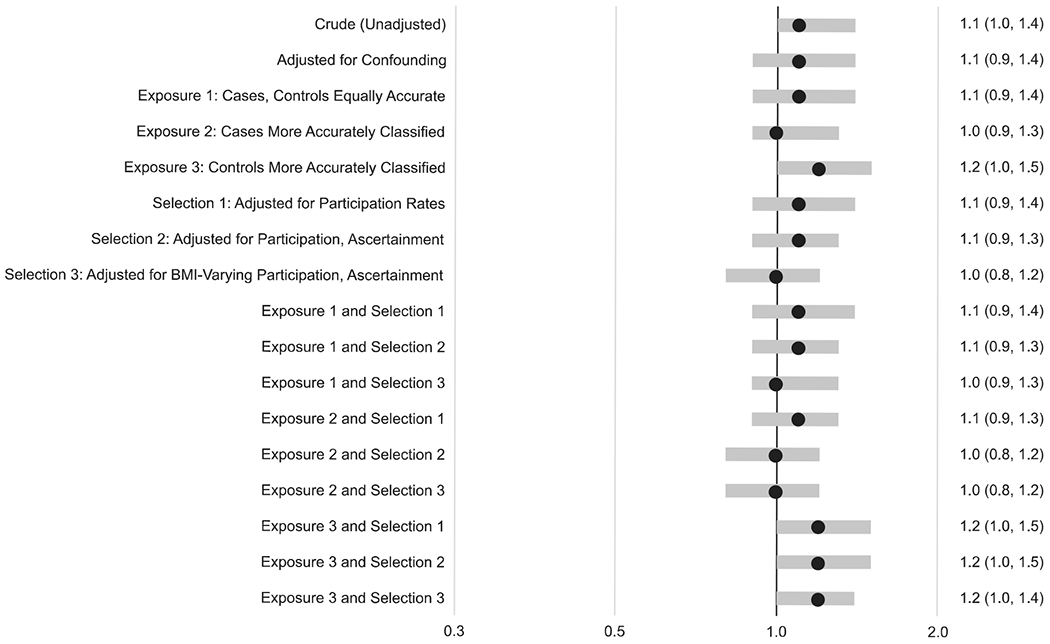
Odds ratios and 95% confidence intervals from conventional analyses and median odds ratios and 95% simulation intervals from bias analyses for the association between prepregnancy overweight (vs. normal weight) and spina bifida for the same series of two conventional models and 15 bias analysis models. The assumptions for each model are explained in more detail in the text

FIGURE 4.

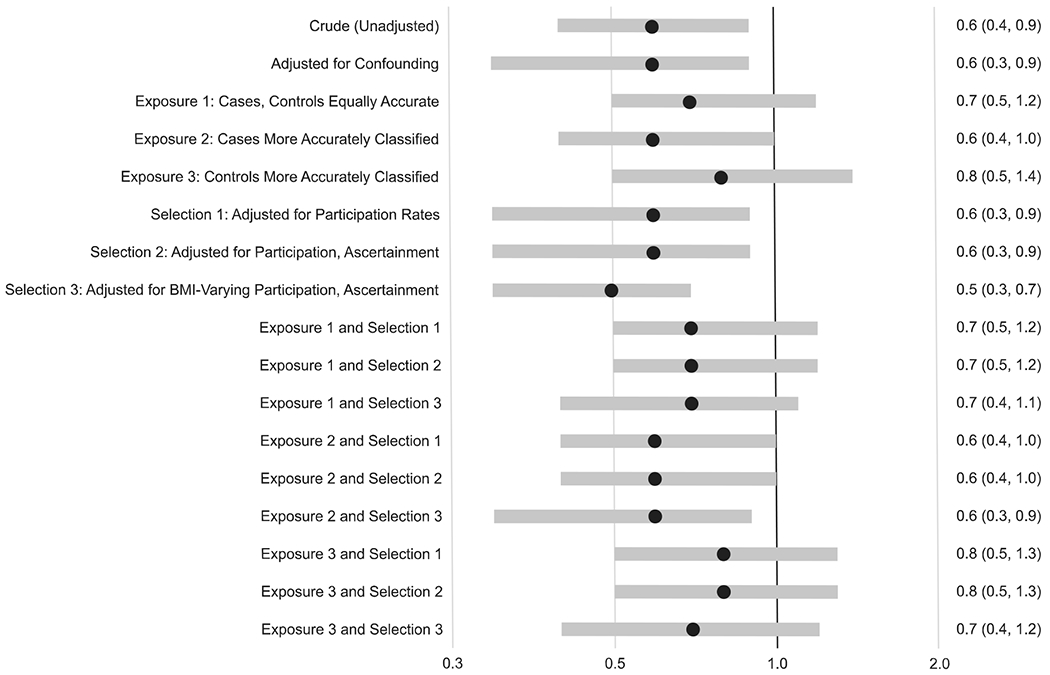
Odds ratios and 95% confidence intervals from conventional analyses and median odds ratios and 95% simulation intervals from bias analyses for the association between prepregnancy underweight (vs. normal weight) and spina bifida for the same series of two conventional models and 15 bias analysis models. The assumptions for each model are explained in more detail in the text

There was one exception: the dose–response pattern was less apparent when we assumed that participation in the study varied by prepregnancy BMI. For example, for the results where cases had more accurate BMI reporting and selection probabilities varied by prepregnancy BMI (labeled “Exposure 2 and Selection 3” in the Figures), the median OR for obesity was 1.1 (95% SI: 0.9, 1.4), for overweight was 1.0 (95% SI: 0.8, 1.2), and for underweight was 0.6 (95% SI: 0.3, 0.9).

4 |. DISCUSSION

Using quantitative bias analysis, we found that exposure misclassification, selection bias, and confounding did not completely explain the association between prepregnancy BMI and spina bifida under most of our assumptions.

Our conventional crude and confounding-adjusted results showed similar dose–response associations to those found in other studies, although many of these studies found stronger associations between obesity and spina bifida than we did. (Huang et al., 2017; Rasmussen, Chu, Kim, Scmid, & Lau, 2008; Stothard, Tennant, Bell, & Rankin, 2009). Differences between our results and the previously published studies could be caused by a variety of study design or population characteristics, including differences in case ascertainment (e.g., inclusion of terminations of pregnancy), folic acid fortification or supplementation in the population, or between-population factors that affect occurrence of prepregnancy obesity. Among these previous studies was an NBDPS analysis using data from 1997 to 2002 (Waller et al., 2007). In our confounding-adjusted analyses, updated through 2011, we found a stronger inverse association between underweight and spina bifida than the previous NBDPS study (OR 0.6 vs. 0.9) but a weaker association with obesity (OR 1.4 vs. 2.1). Differences in inclusion/exclusion criteria and model covariates between the two studies explained much of these differences. When we applied our inclusion/exclusion criteria and models to 1997–2002 data versus 1997–2011 data, we found similar associations for underweight (OR 0.5 vs. 0.6) but the stronger association for obesity persisted (OR 1.8 vs. 1.4). The remaining differences may be explained by changes in the NBDPS catchment areas over time.

In our bias analyses, each of our three assumptions about exposure misclassification gave similar results. For underweight mothers, all three results were attenuated compared to conventional analyses; however, results were based on small numbers and the 95% SIs were wide and overlapped substantially with the conventional OR and 95% CIs. For mothers who were overweight or had obesity, all three provided results similar to the conventional analyses. We only tested three out of a large number of possible assumptions about exposure misclassification, and had we chosen distributions that had less overlap between them, these more varied distributions could have produced different results.

Ours was not the first bias analysis for selection bias; investigators in the previous NBDPS study conducted a similar, but nonprobabilistic, analysis (Waller et al., 2007). They used a selection probability of .5 and found little effect on study results. Similarly, we observed little effect using selection probabilities of .22 and .14 for sites with and without active ascertainment of prenatally diagnosed cases. We saw the greatest effect when we varied selection probabilities by prepregnancy BMI. This result is not surprising because selection bias occurs when both exposure and outcome affect selection; varying selection probabilities by BMI satisfied these two conditions. If selection bias is truly present, our results are compatible with the risk of spina bifida being similar for mothers with normal weight, overweight, and obesity, but lower for mothers who are underweight.

Simultaneous adjustment for exposure misclassification, selection bias, and confounding allowed us to see how results would change when these biases were combined, as opposed to observing their independent effects. We noticed no unusual synergistic effects when combining biases, something we could not predict without conducting a formal bias analysis. Another role of bias analysis is the explicit acknowledgement of uncertainty in the study (Lash et al., 2014). The difficulties we encountered when trying to find data to model the biases in our study should remind analysts of the uncertainty inherent in epidemiologic research that is not often addressed when interpreting results from conventional analyses.

Although we used the best validation data we could find, our data had limitations. For exposure misclassification, we used NHANES data that validated self-reported current weight, not prepregnancy weight, because we could find no other suitable validation data. We also estimated predictive values for the missing BMI category from a small number of NHANES participants with missing data, meaning that our weights could have been imprecisely estimated. For selection bias, we used a Danish study from the same era as NBDPS to estimate selection probabilities conditional on prepregnancy BMI, but we do not know if the results are generalizable to our U.S. population. We chose nine combinations of exposure misclassification and selection bias for our analysis to explore the effects of making different assumptions on occurrence of bias. There likely exist other combinations that would result in different conclusions, but our results were fairly robust across our chosen combinations. These limitations mean that we should not interpret our study results as estimates of the “true” magnitude of the association. Instead, we use these results to illustrate how study results would (or would not) be affected if biases of these magnitudes were occurring in the study. This information can help us to determine if bias is a likely explanation for observed study results.

NBDPS has a large sample size to increase precision and a careful case classification to minimize outcome misclassification. Our analysis adds adjustment for exposure misclassification, selection bias, and confounding. Various other factors could have affected our results, such as misclassification of covariates, other types of selection bias (e.g., underascertainment of cases among live births and stillbirths), residual and unmeasured confounding, effect measure modification, etiologic heterogeneity between spina bifida subtypes, and appropriateness of our complete-case analysis, triangular distributions, and methods to estimate weights. Balancing complexity of the analysis and practicality is a necessary part of bias analysis, and we focused on the sources of bias that we thought might have the greatest effect on study results (Lash et al., 2014).

In summary, the dose–response relationship between prepregnancy BMI and spina bifida largely remained after we accounted for exposure misclassification, selection bias from participation rates, selection bias from case underascertainment, and confounding by select sociodemographic factors, although it was attenuated under certain assumptions about selection bias.

DATA AVAILABILITY STATEMENT

The data used in this study were obtained from the Centers for Birth Defects Research and Prevention. The procedures for accessing these data can be found at https://www.cdc.gov/ncbddd/birthdefects/nbdps-public-access-procedures.html.