Abstract
Purpose
Accurate and efficient spine registration is crucial to success of spine image-guidance. However, changes in spine pose cause intervertebral motion that can lead to significant registration errors. In this study, we develop a geometrical rectification technique via non-linear principal component analysis (NLPCA) to achieve level-wise vertebral registration that is robust to large changes in spine pose.
Methods
We used explanted porcine spines and live pigs to develop and test our technique. Each sample was scanned with pre-operative CT (pCT) in an initial pose, and re-scanned with intraoperative stereovision (iSV) in a different surgical posture. Patient registration rectified arbitrary spinal postures in pCT and iSV into a common, neutral pose through a parameterized moving-frame approach. Topologically encoded depth projection 2D images were then generated to establish invertible point-to-pixel correspondences. Level-wise point correspondences between pCT and iSV vertebral surfaces were generated via 2D image registration. Finally, closed-form vertebral level-wise rigid registration was obtained by directly mapping 3D surface point pairs. Implanted mini screws were used as fiducial markers to measure registration accuracy.
Results
In 7 explanted porcine spines and 2 live animal surgeries (maximum in-spine pose change of 87.5 mm and 32.7 degrees averaged from all spines), average target registration errors (TRE) of 1.70±0.15 mm and 1.85±0.16 mm were achieved, respectively. The automated spine rectification took 3–5 mins, followed by an additional 30 secs for depth image projection and level-wise registration.
Conclusion
Accuracy and efficiency of the proposed level-wise spine registration supports its application in human open spine surgeries. The registration framework, itself, may also be applicable to other intraoperative imaging modalities such as ultrasound and MRI, which may expand utility of the approach in spine registration in general.
Keywords: Spine imaging, image registration, patient registration, stereovision, deep learning networks, NLPCA
1. Introduction
Open spine surgery is performed routinely in patients who require open lumbar decompression, or have symptomatic degenerative lumbar spondylolisthesis, and who have failed conservative treatment and require open posterior lumbar decompression and fusion surgery. According to a recent survey, the total number of spinal fusion procedures carried out worldwide has increased over the past several decades: now more than 400,000 spine fusion cases are performed in the United States [1], alone. Open posterior lumbar interbody fusion is one of the most established procedures and is performed commonly by the majority of spine surgeons [2]. Image-based navigation using pre-operative images is gaining acceptance in spine surgery, especially in fusion procedures [3] because conventional free-hand operations can lead to misplacement of pedicle screws. Compared to conventional approaches, image-guidance improves surgical accuracy in a number of situations [4].
Nevertheless, intraoperative imaging for spine procedures is typically costly and involves radiation. Intraoperative X-ray radiography/fluoroscopy is common when assessing placement of surgical devices [5]. Intra-operative CT (iCT) combined with pre-operative MRI is also possible [6]. Alternatively, radiation-free, low-cost imaging modalities such as ultrasound (US [7,8]) and stereovision (iSV [9]) have shown promise for spine image-guidance. Typically, they are co-registered with pre-operative CT (pCT) to establish patient registration.
Intervertebral mobility degrades spine registration accuracy, especially when a large spine posture change occurs such as between pCT acquisition and surgical intervention (supine vs. prone). Intervertebral motion is also common during surgery due to organ movement [10], where spine pose changes up to 20 mm have been reported that could lead to a registration success rate lower than 60% [11]. An abnormal spinal curvature due to large intervertebral motion also requires correction of spinal deformity [12]. Existing spine registration methods are able to accommodate smaller pose changes and often require an initial registration before accounting for full spinal deformation [13].
More recently, deep learning approaches have also been proposed. They include convolutional neural network (CNN) based on 2D/3D X-ray and CT to estimate vertebral rigid-body transformation [14], and 3D-2D spine vertebral matching using Faster-RCNN to identify correspondences between 3D CT and 2D X-ray [15]. However, they are currently limited to rigid registration for the whole spine and do not yet account for intervertebral motion.
In this study, we develop an automatic spine registration framework based on porcine lumbar spines that is robust to large changes in spinal pose. We aimed at producing level- or piece-wise registrations for each vertebra. Contributions of the work include:
A 2D correspondence alignment framework based on topological depth projection images to accommodate large spine pose changes;
A mix-up technique [16] applied to an auto-encoder-based spine shape analysis network [17], which can improve the robustness of unsupervised learning of arbitrary spine shapes;
A template-based 2D spine segmentation to allow level-wise spine registration.
2. Prior work on spine registration
Point-based Methods.
Existing fiducial-based registration methods require anatomical landmarks or implanted fiducials for spine registration [18]. They achieve sufficient accuracy for short spine segments but suffer from line-of-sight limitations [19].
Image-based Methods.
Most spine registration methods rely on images. Rigid registration remains popular when using intraoperative radiographic/fluoroscopic X-ray. For example, a 2D/3D registration framework estimating patient position has been applied to image-guided radiation therapy [20], and is widely adopted for geometric calibration of robotic C-arms [21]. Multi-stage, locally rigid deformation methods have also emerged to allow 2D/3D registration while accommodating changes in spinal curvature. Nevertheless, manual effort is still required to mark vertebral centers [14].
Free-form deformable techniques such as Demons [22] and Coherent Point Drift (CPD) [23] often achieve improved accuracy over rigid registrations. However, they can cause geometrical distortion if no structural constraints are applied to maintain local vertebral rigidity [6]. A biomechanically constrained, groupwise registration is developed to register US and CT of the lumbar spine [7]. Multimodal joint registration technique using common shape coefficients and modality specific pose coefficients is developed for spine anesthesia guidance [24]. Other spine motion estimation techniques include piecewise registration [25], statistical shape models [26], and multi-vertebrae deformation models [27]. These approaches perform registration locally to preserve vertebral structures, using either explicit vertebral segmentation or implicit rigidity constraints.
3. Methodology
3.1. Overall Strategy
Instead of directly registering spines of arbitrary postures in 3D and relying on a deformation model or an explicit constraint to minimize vertebral distortion [28], we transform spines of arbitrary postures into a common, neutral pose. We refer to this process as spine “shape rectification”. Then, 2D projection images are generated from the rectified spines to encode vertebral topological heights as image intensity values. By tracking how the spine geometry is transformed using point-to-point and point-to-pixel correspondences, vertebral level-wise registration is obtained via a closed form solution between vertebral 3D point pairs.
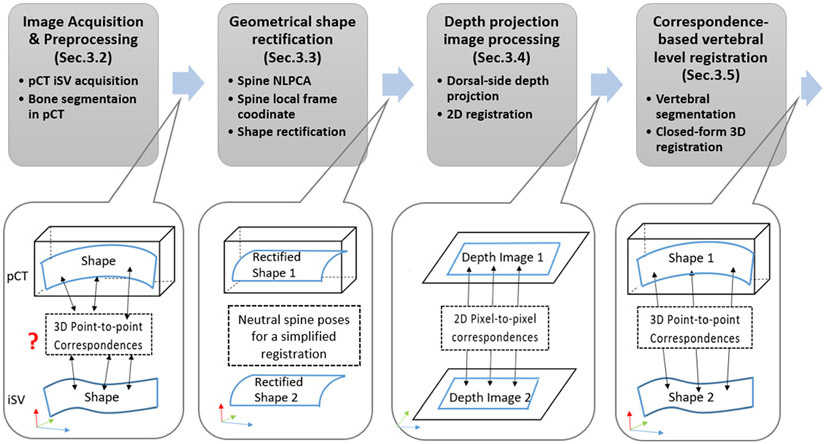
Fig. 1 illustrates our overall registration framework, which involves four main steps: (i) image acquisition and preprocessing; (ii) geometrical shape rectification; (iii) generation of depth projection images; and (iv) correspondence-based 3D registration.
Fig. 1.
Illustration of the spine registration pipeline, which includes four models: (1) pCT and iSV are first acquired and preprocessed; (2) whole spines in pCT and iSV are then rectified into a common, neutral pose via NLPCA; (3) 2D depth projection images are generated to provide 2D registration via image correlation: and (4) level-wise vertebral registration is achieved via and closed-form rigid registration based on invertible point-to-pixel correspondences between segmented vertebral pairs.
3.2. Image acquisition and preprocessing
Spine 3D surface points served as input to our registration pipeline. For CT, Otsu-based global thresholding was used to create a binary mask which was effective because all spines were acquired by the same scanner with the same clinical imaging protocol (thus, image data intensities have minimum local or inter-subject variation). An isosurface was generated, from which mesh nodes served as a point cloud. For iSV, the exposed spine 3D surface was reconstructed [9,29].
3.3. Geometrical shape rectification
The spine longitudinal axis is a prominent feature to define its global orientation. Due to vertebral symmetry, the lateral axis of the transverse process (TP) and the ventral-dorsal axis of the spinous process (SP) determine a local orientation. A typical 3D point cloud of the exposed spine surface, x (either from CT or iSV), represents a non-linear distribution along a manifold Gaussian warped along the spine longitudinal axis. Identifying global and local orientations is analogous to finding the principal surfaces of the point cloud distribution, which can be achieved through a nonlinear principal component analysis (NLPCA). Technical details of NLPCA can be found in [17].
3.3.1. Unsupervised Spine NLPCA
Spine shape analysis network.
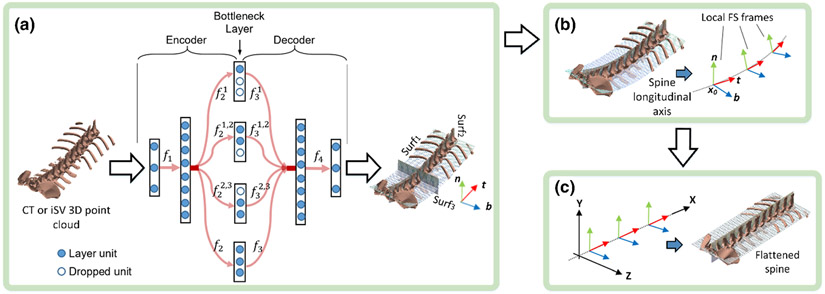
Autoencoders were used to reduce data dimension or feature space. A stacked autoencoder (SAE) learned a compressed representation of the 3D point cloud from which three anatomical axes were identified. In our work, it encodes a 3D point cloud to a few lower dimensional representations (encoder), and reconstructs back to a 3D point cloud as output (decoder). Effectively, the SAE reduces a 3D point-cloud into either 1D or 2D representations to learn the corresponding curvature and surface contour, respectively. Here, the curve corresponded to the longitudinal axis of the spine, while the two surfaces corresponded to those formed by the lateral and longitudinal axes and the ventral-dorsal and longitudinal axes, respectively.
The SAE is a fully connected, five-layer network (with layer sizes of 3, 8, 3, 8, and 3 units, respectively; Fig. 2a). Each unit represents one dimension of the data, which corresponds to either the x, y or z coordinates in the input layer. Layer-wise mapping, fi, is defined as:
| (1) |
where Wi and bi are the network variable matrix and vector to be learned, respectively, and σi(x) = tanh (x) for i=2, 3 (internal hidden layers) and σi(x) = x for i=1, 4 (input and output layers). The network loss function is:
| (2) |
Fig. 2.
Illustration of the spine shape analysis network: an auto-encoder network with fully connected layers of dimensions of 3-8-3-8-3 (a). Subnetworks are forced to drop out during training to apply appropriate optimization constraints. The input and output layers (i.e., the 1st and 5th layers) encode the x, y, and z coordinates, while units in the bottleneck layer represent the first, second, and third principal directions, respectively. After training, the decoder maps regularly sampled, planner point clouds to the corresponding curved principal surfaces (Surf1, Surf2, and Surf3). Local Frenet-Serret frames are established along the spine longitudinal axis (b). Finally, the spine is rectified/flattened using moving frame transformations (c).
Spine longitudinal axis.
First, to identify the major principal component along the spine longitudinal axis, the second and third units (corresponding to the second and third principal components, or the lateral and ventral-dorsal directions, respectively) of the middle subnetwork or “bottleneck” layer (Fig. 2a) are forced to drop out by the following equation to achieve dimension reduction:
| (3) |
where , are obtained by dropping the second and third units of the mapping, f2 and f3, respectively (i.e., removing the corresponding second and third row in W1 and W2 in (1)). This process retrains information only along the major principal component.
Spine lateral and ventral-dorsal directions.
To learn the second principal component along the spine lateral direction, both the 1st and 2nd units are retained (i.e., dropping the 3rd unit). This step allows information to be retained along both the longitudinal and lateral directions, and forms a curved surface. Dropping the 3rd unit leads to:
| (4) |
where and are obtained by dropping the third unit of the mappings, f2, and f3, respectively. Finally, for the third principal component along the spine ventral-dorsal direction, either the 1st and 3rd or 2nd and 3rd units are retained to form a curved surface and identify the third principal component. We choose to retain the 2nd and 3rd unit, or to drop the 1st unit, which leads to:
| (5) |
where and are obtained by dropping the 1st unit of the mappings, f2, and f3, respectively. The combined minimization error norm is finally obtained:
| (6) |
where α1, α2, and α3 could be used to further adjust the relative weights (which were empirically set to 1.0 in this study). Effectively, this norm places the highest weights along the longitudinal axis (three terms, with E1 entirely for this component), and the lowest weights along the ventral-dorsal direction (two terms) [17]. Minimizing the combined error norm leads to a multi-task optimization to satisfy all of the specified constraints, obtaining three principal surfaces (Fig. 2a)
Data augmentation.
The NLPCA framework was found to be effective for pCT spines. However, performance could be unstable for iSV because of unbalanced sampling due to reconstruction artefacts (e.g., holes or spikes around reconstructed surface boundaries), and a smaller field-of-view resulting from limited spine exposure. This issue was mitigated by using a “mix-up” technique [16] to balance the point cloud distribution (Fig. 3). For a random point pair, (x1, x2), a randomly weighted average point, , was introduced into the training dataset:
| (7) |
where μ ∈ (0,1) is independently drawn from a Beta(0.5, 0.5) distribution to ensure that is close to the original x1, x2. We further empirically constrained ∥x1 − x2∥ < 5 mm. This ensured a local data mix-up to preserve a non-convex shape of the spine. The two Beta shape parameters were identical (of 0.5) to suppress overfitting [16].
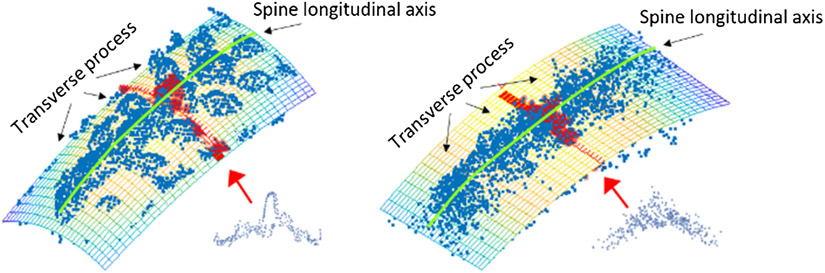
Fig. 3.
Mix-up point augmentation avoids overfitting principal surfaces to local point distribution in iSV (left) by effectively applying a local smoothing filter, which suppresses local shapes while maintaining the global shape representation (right).
Principal surfaces.
After training, a regular planar grid-like point set along each of the three major axes was used as input to the 4 bottleneck layer subnetworks, each of which has 3 units for input (corresponding to the point coordinates). Following the decoder, the three curved principal surfaces, Surf1, Surf2 and Surf3, were obtained (Fig. 2a).
3.3.2. Spine Coordinate System using Moving Frames
The spine is a piece-wise rigid linkage of multiple vertebrae. Its longitudinal axis (i.e., intersection of Surf1 and Surf2) can be approximated by a series of moving frames [30]. Empirically, 30 frames were found to be sufficient, with their origins uniformly distributed along the axis (Fig. 2b). Modeling spine intervertebral motion was achieved by transforming the series of associated moving frames instead of operating directly on the 3D point cloud. Essentially, this approach parameterized the motion of the spine 3D point cloud.
Local coordinate.
Formally, a Frenet-Serret Frame (FS-frame [30]) was defined with its origin at a sampling point, x0 ∈ R3, and its local coordinate axes along tangent (t(x0)), normal (n(x0)), and bi-normal (b(x0)) vectors. Effectively, these local coordinate axes are intersections of surface pairs among Surf1, Surf2, and Surf3, respectively (Fig. 2b). For an arbitrary spine point x, its local coordinate, y, in its nearest frame on x0 can then be determined by the following equation:
| (8) |
Modeling spine posture via local frame transform.
With these local coordinates, each point within the spine point cloud was assigned to its nearest FS-frame (as measured by the distance to the FS-frame origins). This step allowed the spine point cloud to be divided into subsets parametrically controlled by their corresponding FS-frames. An arbitrary whole-spine geometrical posture, or equivalently, the intervertebral motion, can then be approximated by a series of rigid transforms to the local FS-frames. For an arbitrary point on the spine, x, its new coordinate, x′ after a transformation, G, applied to its local FS-frame (with origin x0), is given by
| (9) |
Given that the local coordinatey depends only on the origin, x0, and t, n, and b from the principal surfaces (Eqn. 8) and invariant to transform G, spine vertebral motion or posture can then be represented by the series of local frame transformations.
3.3.3. Spine Shape Rectification
Spine shape rectification was achieved by transforming all FS-frames to match a common global coordinate system, which was chosen as the first frame in the series (i.e., X, Y, Z in Fig. 2c; most caudal). After the transformation, each spine point migrated to a new position under its frame (Eqn. 9). This process led to a “flattened” neutral spine posture. The same rectification was applied to both pCT and iSV. For iSV, multiple reconstructed surfaces (typically three iSV scans for one vertebra) were first combined to capture the entire exposed spine surface along its longitudinal axis.
Spine shape space.
A spine of arbitrary posture can be numerically represented by a set of frame deformations, {G} (Eqn. 9), relative to its rectified posture. Thus, {G} becomes the “coordinate” of the specific spine posture in a shape space. Effectively, this technique using the rectified shape as a common, global shape coordinate extends an earlier spine shape representation [31], where the deformation was encoded by intervertebral transformation matrices.
3.4. Depth projection image processing
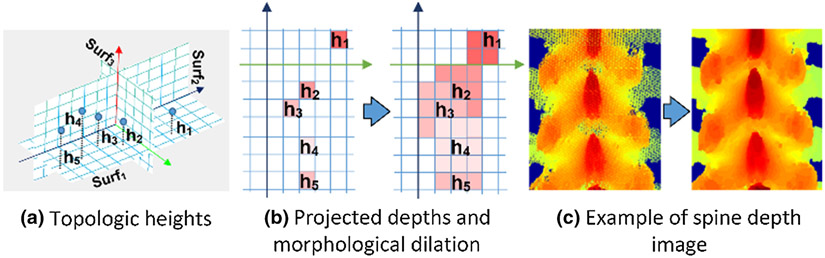
After transforming pCT and iSV data into a common, neutral posture, their 3D topological surfaces were projected into 2D images to further simplify spine registration [28] (Fig. 1). Given that the spine dorsal side was exposed to generate iSV data, the same dorsal-side depth projection was generated from both pCT and iSV. To sample the spine surface and its topological depth values, the XZ plane (i.e., the rectified Surf1 in Fig. 4a) was discretized into a uniform grid (with an isotropic “pixel” resolution of 0.5 mm) to create an image representation of the topological depth information. The gray-scale value of each pixel was then determined as the maximum Y value of enclosed sampling point projections from the dorsal to ventral direction (Fig. 4b left). Projection image undersampling, including holes and unfilled pixels, was corrected by morphological dilation (Fig. 4c). This procedure was performed on both pCT and iSV, which led to their corresponding point-to-pixel, and inversely, pixel-to-point, correspondences.
Fig. 4.
Procedure to generate a depth projection image from a shape-rectified 3D point cloud. The topological surface (a) is encoded by height (i.e., the rectified Surf1). The discretized XZ plane with the height information becomes a depth projection image (b). The resulting depth image (c) captures the geometrical details of the spine surface in which each image pixel corresponds to a 3D point on the spine surface. The projection images encoded rich features of the spinous processes and in the laminar areas (c).
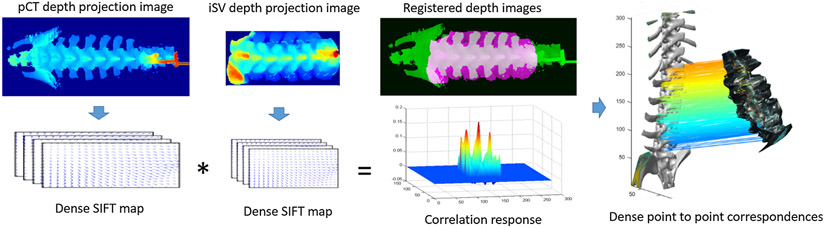
The 2D depth projection images were generated from rectified pCT and iSV spines, therefore, they can be registered rigidly (Fig. 5). Dense SIFT feature maps [32] were used (default settings, with bin size of 8) from which their cross correlations (xcorr.m in Matlab) were calculated by implicitly translating the iSV projection image rigidly along the two image dimensions by a step size of 1 pixel. Each peak in correlation response corresponded to a local registration. The highest peak was found to register pCT and iSV with the correct vertebral level-wise pairing.
Fig. 5.
Two-dimensional registration of depth projection images from rectified pCT and iSV spines using dense SIFT features and linear cross-correlation. Peaks in correlation response represent the matching of different vertebra level positions and the highest peak corresponds to a correct vertebral level pairing.
The resulting registration established the pixel-to-pixel correspondences between pCT and iSV projection images. In combination with the invertible point-to-pixel correspondences between their respective spinal 3D surface points (Fig. 1), point-to-point correspondences between spine surface points in pCT and iSV were obtained. A 3D point-based registration was then readily available in their neutral postures (Fig. 5, right), which served as the basis for subsequent vertebral level-wise 3D registration in the original postures.
3.5. Correspondence-based vertebral level registration
3.5.1. Template-based Vertebral Segmentation
Vertebral segmentation was necessary for level-wise registration. An adaptive template-based scheme [33] was adopted to segment vertebrae from the 2D depth projection images. A 3D volumetric vertebral segmentation was not necessary since subsequent spine registrations were based on surface data from pCT and iSV.
Specifically, a universal template vertebra (L3) was manually segmented from the pCT projection image in a randomly chosen and rectified spine sample. The template was then moved along the longitudinal axis by a typical intervertebral distance to localize the next adjacent vertebral segment via a nonlinear dense SIFT registration. The newly identified vertebra served as an updated template to localize its next adjacent segment. This strategy minimized morphological differences between the two registered neighboring segments. The process was repeated until all lumbar vertebrae (L1–LA, as only available from iSV) were identified.
To segment vertebrae in another spine sample, it was registered rigidly with the initial sample so that the two L3 segments were aligned. The newly identified L3 served as the template to segment other vertebral segments following the same adaptive procedure. Finally, the 2D segmentations were mapped to 3D following the pixel-to-point correspondences obtained from the depth projection (Section 3.4).
3.5.2. Closed-Form Vertebral Rigid Registration
The correspondence point pairs between pCT and iSV (Fig.5 right), p and q, allowed a closed-form rigid registration for an arbitrary vertebral level by minimizing the least squares error [34]:
| (10) |
where pi is the i-th spine point in iSV and qi is the corresponding i-th point in pCT, N is the number of point pairs. Matrix R and vector t are the desired 3D rotational matrix and translation vector, respectively, and they are given by closed-form solutions:
| (11) |
| (12) |
| (13) |
where {λi} and {ξi} are the eigenvalues and eigenvectors of matrix, MTM.
4. Experiments
4.1. Imaging and Tracking Systems
Pre- and intra-operative CT scans were acquired with typical clinical imaging protocol using a Siemens SOMATOM Definition AS scanner, with a typical scanning resolution of 0.27 mm×0.27 mm×0.6 mm. For iSV, a handheld device was developed [29] for intraoperative acquisition. It consisted of two high-resolution (1920×1080) cameras that yielded millimeter reconstruction accuracy (1.2±0.6 mm) based on 324 iSV image pairs and 2553 measurement points from six cadaver porcine spine samples. Each reconstruction took <1 s using a GPU-based optical flow technique to identify stereo correspondences between image pairs, which were used to generate a dense disparity map for iSV surface reconstruction. The HHS device is significantly more portable than an operating microscope used previously [9]. The Medtronic StealthStation S7 was used for tracking and navigation [9]. A patient tracker rigidly attached to the sacrum provided a common reference for the tracked iSV.
4.2. Surgical Procedures
Seven explanted porcine spines and two live pigs (weight range of 35–70 kg) were used to simulate open spinal surgery in humans. For explanted spines, vertebral ligaments were removed similarly to human surgery to expose at least 5 vertebral levels. For each exposed vertebra, 2–5 Leibinger titanium mini-screws (1.5 mm diameter, 3 mm depth) were implanted in spinous and transverse processes, as well as in lamina areas [33]. Then, pCT was acquired after screw implantation. Next, postures of explanted samples were altered manually to induce intervertebral motion prior to iSV acquisitions. Finally, intraoperative CT (iCT) was obtained in the surgical position [33], which served as ground-truth to assess registration accuracy and iSV reconstruction accuracy based on root mean squared (RMS) distances between homologous screw locations.
For live swine experiments, subjects were anesthetized and remained immobile throughout the procedure. They were positioned prone to expose the vertebral bony surfaces, surgically. Similar to the explanted spine procedure, mini-screws were implanted in the exposed spinous and lamina areas. The subjects were closed surgically, and were re-positioned in a supine posture for pCT acquisition. They were re-positioned in a prone posture and the surgical area was re-opened to expose vertebrae for iSV acquisition. Finally, iCT was also captured to allow ground-truth assessment of registration accuracy.
4.3. Registration Results
For all registrations, TREs based on embedded screws were reported. The corresponding level-wise registration transformation was uploaded to the Stealth Station to generate an updated CT (uCT) volume. Since uCT instead of the ground-truth iCT was used for subsequent navigation, we also computed uCT-iCT registration TREs using the same embedded screws for verification. Porcine template was using the method described in Sec. 3.
Table 1 summarizes TREs from level-wise iSV-pCT registrations grouped by each spine sample. We presented the max in-spine displacement to indicate the registration difficulty for each case. The displacement is obtained by manually aligning the sacrum between pCT and iCT then measuring the maximum distance and relative rotation of between the rests of the vertebrae. For live swine tests, these displacements are morphologically realistic displacements while for explanted cases.
Table 1:
Summary of registration accuracy using our rectification-based approach and two baseline methods in terms of TREs (mm) for seven explanted spines and two live animal experiments, along with corresponding iSV reconstruction and spine posture differences.
| Subject ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Avg. |
|---|---|---|---|---|---|---|---|---|---|---|
| Explanted porcine spines | Live animal | |||||||||
| TRE (NLPCA) | 1.48±0.57 | 1.67±0.70 | 1.82±0.80 | 1.86±0.63 | 1.68±0.53 | 1.54±0.76 | 1.82±1.07 | 1.98±0.73 | 1.71±0.65 | 1.73±0.16 |
| TRE (uCT-iCT) | 1.59±0.54 | 1.79±0.28 | NA | 1.64±0.42 | 1.94±0.42 | 1.64±0.38 | 1.96±1.25 | 1.53±0.72 | 1.83±0.74 | 1.74±0.16 |
| TRE (Landmark) | 2.62±0.99 | 2.11±1.06 | 2.53±0.98 | 2.32±1.19 | 2.29±0.79 | 2.54±0.67 | 2.34±1.25 | 2.45±1.19 | 1.96±0.91 | 2.35±0.21 |
| TRE (ICP) | 2.33±1.05 | 2.49±1.22 | 2.21±0.66 | 2.86±1.68 | 2.16±0.79 | 1.91±0.83 | 2.14±0.94 | 2.38±0.89 | 1.78±1.09 | 2.25±0.32 |
| Max in-spine displace. + rotation * | 91.5 (24.5°) | 182.2 (34.0°) | 47.7 (38.6°) | 53.5 (31.8°) | 62.8 (38.9°) | 126.8 (44.8°) | 93.1 (47.1°) | 77.4 (20.1°) | 52.8 (14.2°) | 87.5±43.2 (32.7°±11.2) |
| iSV reconstruction accuracy | 1.05±0.25 | 1.08±0.47 | 0.79±0.40 | 1.42±0.45 | 0.87±0.23 | 1.07±0.17 | 1.21±0.41 | 1.57±0.22 | 1.65±0.37 | 1.19±0.30 |
maximum in-spine displacements and rotations are obtained by rigidly registering the sacrum between pCT and iCT, and they represent the maximum relative change in location for the same vertebra as accumulated from the intervertebral motion of the 5 segments. Pearson correlation between the TRE (NLPCA) and iSV reconstruction accuracy was computed based on level-wise TRE (From L1 to L5).
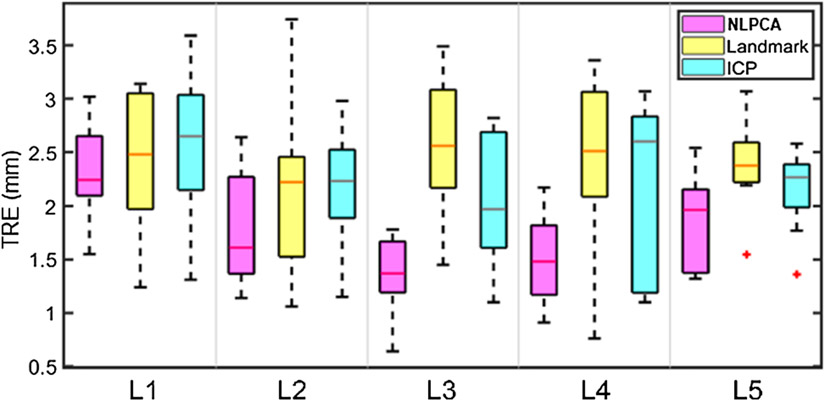
All TREs were < 2 mm, with an average of 1.70±0.15 mm and 1.85±0.19 mm for explanted spines and live animals, respectively. The accuracy was similar to that in uCT-iCT registration, suggesting the same level of registration accuracy in actual surgical navigation using uCT. The iSV reconstruction accuracies for the explanted and live animals were 1.07±0.21 mm and 1.61±0.06 mm, respectively. They were consistently smaller than the two baseline techniques using anatomical landmarks or ICP, either per spine sample (Table 1) or grouped by vertebra across samples (Fig. 6).
Fig. 6.
Comparison of level-wise TREs (pCT-iSV) using the NLPCA approach and two baseline methods using either landmarks or ICP. TREs for each vertebral level are based on all spine samples (N=9).
Grouping results from all spines (N=9), TREs and iSV reconstruction accuracies were correlated statistically (correlation coefficient = 0.30, p<0.05). The relatively low correlation coefficient suggested that other sources of error may exist. For each spine, the maximum posture change (relative to sacrum) in terms of translational displacement and rotational angle were also determined and found to have an average value of 87.5 mm and 16.6 deg, respectively.
Fig. 7 compares iSV-uCT and iSV-iCT alignments for four representative vertebral level-wise registrations. The accurate alignment of mini screws between uCT and ground-truth iCT (bottom) also suggests accurate registration.
Fig. 7.
(Top) Representative vertebral level-wise iSV-pCT registration at a given level (as indicated). For comparison, iSV is aligned with the inherently co-registered iCT acquired at the same stage. Misalignment between iSV and pCT (arrows) indicate apparent vertebral motion. (Bottom) Overlays of uCT (green) and iCT (cyan) for each spine and their cross-sections are also shown, where the alignment of the mini screws indicates accurate iSV-pCT registration. Alignments of mini screws in uCT and iCT are shown in the insets.
Fig. 8 illustrates how a level-wise registration was used for surgical navigation. Using a handheld stylus to identify a specific vertebra of interest (one click), the corresponding level-wise registration was selected in the commercial navigation. A uCT was then presented to provide navigation for the chosen vertebra.
Fig. 8.
A level-wise registration for L4 was uploaded to StealthStation to provide surgical image-guidance in a live pig experiment. The mini screw in the L4 spinous process (yellow box on left) identified by a tracked hand-held stylus is shown to align well with the probe tip in the image space of uCT (right), suggesting an accurate patient registration.
5. Discussion and Conclusion
In this study, we developed an automatic framework to decompose a direct 3D spine intermodality registration into a series of simpler tasks to achieve accurate level-wise registration, which is robust for spines with large pose changes. Based on 7 explanted spines and 2 live animal experiments, the registration pipeline achieved an average TRE of 1.70 mm and 1.85 mm, respectively, with an average maximum relative rotation of 32.7 degrees (Table 1). Computational cost for NLPCA was typically 3–5 min, and the subsequent point-based, closed-form registration required less than 30 seconds. The accuracy and efficiency performance suggest feasibility for applying the pCT-iSV registration framework in human surgeries.
Key to our approach is to rectify a spine of an arbitrary posture into a common, neutral pose using NLPCA. Topological depth features in the rectified spine are then encoded to form a 2D projection image. This transforms 3D spine registration into 2D image correlation. The resulting pixel-to-pixel and the invertible point-to-pixel correspondences enable a level-wise registration in 3D (Fig. 1). In contrast, typical spine registration methods require an exhaustive point-wise correspondence search [6]. An appropriate initialization was also necessary, e.g., by center alignment between point sets or manual initialization [9], or ensuring that pre- and intra-operative spines were in similar postures [6]. These registration techniques are effective for spines with relatively small pose changes but are more difficult with larger pose changes (e.g., supine vs. prone).
Our approach avoids the need for establishing point-wise correspondences directly in 3D, which may explain its smaller TRE relative to conventional ICP-based methods with manual initialization, especially for the explanted spines (mean TRE of 1.70 mm vs. 2.30 mm). The comparison was similar for landmark-based methods (mean TRE of 2.39 mm and 2.21 mm for explanted and live animal spines). The registration robustness depends on the point cloud size. Based on three random spines, we parametrically determined that at least 4 k sampling points were necessary to achieve a success rate >90% (average TRE of 1.33±0.06 mm and 0.91±0.08 mm for pCT and iSV, respectively), with 1.5 min requried to converge.
Cross-modality comparisons.
Recent spine image-based registrations such as a multi-view 2D-3D registration for X-ray has achieved high accuracy (TRE of 0.22 mm) [35]. For CT-to-MRI registration, a modality-independent neighborhood descriptor (MIND) was developed to generate a deformation field for image warping, which achieved a TRE of 1.7 mm [22]. Nevertheless, these registrations relied on high-cost image acquisition systems to capture detailed spinal structures. Further, some registration methods such as MIND are computationally intensive [22].
CT-to-US and CT-to-iSV registrations benefit from low-cost and radiation free intraoperative imaging. They achieve acceptable performance by using point-based and intensity gradient-based techniques [36] or landmark- and ICP-based methods [9]. However, they typically require an initial alignment before registration. The spine registration pipeline we developed in this study performs CT-to-iSV registration automatically without manual intervention for an initial alignment. The pipeline meets clinical accuracy requirement (< 2mm) in both explanted and live animal spines. Eventually, the efficacy of this registration framework can be assessed by comparing surgical outcomes with those from conventional registration methods in live animal procedures in a randomized trial. This work is ongoing and will be reported in the future.
Limitations and future work.
Our registration pipeline requires at least three vertebral segments in iSV to achieve sufficient robustness – a restriction that may limit the technique to larger spine exposures. This limitation is largely related to iSV line-of-sight requirements. Nevertheless, the overall registration framework, itself (Fig. 1), is still applicable to other imaging modalities such as US and MR [27][22], where volumetric image acquisitions are unaffected by size of surgical exposure.
Our results also indicate that iSV-pCT registration accuracy is correlated with iSV surface reconstruction accuracy (p<0.01). Overall, explanted cases had slightly better registration accuracy and lower iSV reconstruction error relative to live animal surgeries (mean TRE of 1.70 mm vs. 1.85 mm and mean iSV reconstruction error of 1.07 mm vs. 1.61 mm, respectively). Further improvements for the iSV surface reconstruction may be desirable.
Although manual effort was involved in the 2D templated-based segmentation, it did not affect the automatic registration framework (it only occurred once). Advanced deep learning segmentation [37] is now available, and may eliminate the need for manual input. Manual selection of vertebra by the surgeon to indicate the desired level-wise image-guidance (albeit no explicit vertebral level labeling is required) was largely a consequence of using the StealthStation, since only a single rigid transformation can be applied at a time with this navigation system. Despite these limitations, the accuracy and efficiency found in 9 porcine spines suggest the technique is applicable to human spine procedures, although iSV spine reconstruction in human procedures is likely to be more complex and needs to be investigated in the future.
Funding
This study was funded by the NIH grant R01 EB025747.
Footnotes
Conflict of Interest
The authors are inventors on patents and patents-pending related to stereovision assigned to the Trustees of Dartmouth College.
Ethical approval
All procedures performed in studies involving animals were in accordance with the ethical standards of the institution or practice at which the studies were conducted.
This article does not contain any studies with human participants performed by any of the authors.
Informed consent
This article does not contain patient data.
Contributor Information
Yunliang Cai, Worcester Polytechnic Institute 100 Institute Rd, Worcester MA 01609, USA.
Shaoju Wu, Worcester Polytechnic Institute 100 Institute Rd, Worcester MA 01609, USA.
Xiaoyao Fan, Dartmouth College Dartmouth-Hitchcock Medical Center 1 Medical Center Dr, Lebanon, NH 03766, USA.
Jonathan Olson, Dartmouth College Dartmouth-Hitchcock Medical Center 1 Medical Center Dr, Lebanon, NH 03766, USA.
Linton Evans, Dartmouth College Dartmouth-Hitchcock Medical Center 1 Medical Center Dr, Lebanon, NH 03766, USA.
Scott Lollis, University of Vermont Medical Center, Burlington, VT 05401 USA.
Sohail K. Mirza, Dartmouth College Dartmouth-Hitchcock Medical Center 1 Medical Center Dr, Lebanon, NH 03766, USA
Keith D. Paulsen, Dartmouth College Dartmouth-Hitchcock Medical Center 1 Medical Center Dr, Lebanon, NH 03766, USA
Songbai Ji, Worcester Polytechnic Institute 100 Institute Rd, Worcester MA 01609, USA.
7 References
- [1].Reisener M-J, Pumberger M, Shue J, Girardi FP, and Hughes AP, 2020, “Trends in Lumbar Spinal Fusion—a Literature Review,” J. Spine Surg, 6(4), p. 752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Lestini W, Fulghum J, and Whitehurst L, 1994, “Lumbar Spinal Fusion: Advantages of Posterior Lumbar Interbody Fusion.,” Surg Technol Int, pp. 3:577–90. [PubMed] [Google Scholar]
- [3].Härtl R, Lam KS, Wang J, Korge A, Kandziora F, and Audigé L, 2013, “Worldwide Survey on the Use of Navigation in Spine Surgery.,” World Neurosurg., 79(1), pp. 162–172. [DOI] [PubMed] [Google Scholar]
- [4].Gelalis ID, Paschos NK, Pakos EE, Politis AN, Arnaoutoglou CM, Karageorgos AC, Ploumis A, and Xenakis T. a, 2012, “Accuracy of Pedicle Screw Placement: A Systematic Review of Prospective in Vivo Studies Comparing Free Hand, Fluoroscopy Guidance and Navigation Techniques.,” Eur. Spine J, 21(2), pp. 247–255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Uneri A, De Silva T, Goerres J, Jacobson M, Ketcha M, Reaungamornrat S, Kleinszig G, Vogt S, Khanna A, Osgood G, Wolinsky J-P, and Siewerdsen J, 2017, “Intraoperative Evaluation of Device Placement in Spine Surgery Using Known-Component 3D-2D Image Registration,” Phys. Med. Biol [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Reaungamornrat S, Wang a S., Uneri a, Otake Y, Khanna a J., and Siewerdsen JH, 2014, “Deformable Image Registration with Local Rigidity Constraints for Cone-Beam CT-Guided Spine Surgery.,” Phys. Med. Biol, 59(14), pp. 3761–3787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Gill S, Abolmaesumi P, Fichtinger G, Boisvert J, Pichora D, Borshneck D, and Mousavi P, 2012, “Biomechanically Constrained Groupwise Ultrasound to CT Registration of the Lumbar Spine.,” Med. Image Anal, 16(3), pp. 662–674. [DOI] [PubMed] [Google Scholar]
- [8].Yan CXB, Goulet B, Chen SJ-S, Tampieri D, and Collins DL, 2012, “Validation of Automated Ultrasound-CT Registration of Vertebrae.,” Int. J. Comput. Assist. Radiol. Surg, 7(4), pp. 601–610. [DOI] [PubMed] [Google Scholar]
- [9].Ji S, Fan X, Paulsen KD, Roberts DW, Mirza SK, and Lollis SS, 2015, “Patient Registration Using Intraoperative Stereovision in Image-Guided Open Spinal Surgery,” IEEE Trans. Biomed. Eng, 62(9), pp. 2177–2186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Agazaryan N, Tenn SE, Desalles AAF, and Selch MT, 2008, “Image-Guided Radiosurgery for Spinal Tumors: Methods, Accuracy and Patient Intrafraction Motion,” Phys. Med. Biol [DOI] [PubMed] [Google Scholar]
- [11].Tomazevic D, Likar B, and Pernus F, 2006, “3-D/2-D Registration by Integrating 2-D Information in 3-D,” IEEE Trans. Med. Imaging [DOI] [PubMed] [Google Scholar]
- [12].Hawes MC, and O’Brien JP, 2006, “The Transformation of Spinal Curvature into Spinal Deformity: Pathological Processes and Implications for Treatment,” Scoliosis. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Jobidon-Lavergne H, Kadoury S, Knez D, and Aubin C. é., 2019, “Biomechanically Driven Intraoperative Spine Registration during Navigated Anterior Vertebral Body Tethering,” Phys. Med. Biol [DOI] [PubMed] [Google Scholar]
- [14].Hille G, Saalfeld S, Serowy S, and Tönnies K, 2018, “Multi-Segmental Spine Image Registration Supporting Image-Guided Interventions of Spinal Metastases,” Comput. Biol. Med [DOI] [PubMed] [Google Scholar]
- [15].Yu H, Fu Y, Yu H, Wei Y, Wang X, Jiao J, Bramlet M, Kesavadas T, Shi H, Wang Z, Wen B, and Huang T, 2019, “A Novel Framework for 3D-2D Vertebra Matching,” Proceedings - 2nd International Conference on Multimedia Information Processing and Retrieval, MIPR 2019, Institute of Electrical and Electronics Engineers Inc., pp. 121–126. [Google Scholar]
- [16].Zhang H, Cisse M, Dauphin YN, and Lopez-Paz D, 2018, “MixUp: Beyond Empirical Risk Minimization,” 6th International Conference on Learning Representations, ICLR 2018 - Conference Track Proceedings. [Google Scholar]
- [17].Scholz M, Fraunholz M, and Selbig J, 2008, “Nonlinear Principal Component Analysis: Neural Network Models and Applications,” Principal Manifolds for Data Visualization and Dimension Reduction, Springer, pp. 44–67. [Google Scholar]
- [18].Murphy MJ, Adler JR,J, Bodduluri M, Dooley J, Forster K, Hai J, Le Q, Luxton G, Martin D, and Poen J, 2000, “Image-Guided Radiosurgery for the Spine and Pancreas,” Comput. Aided Surg, 5(4), pp. 278–288. [DOI] [PubMed] [Google Scholar]
- [19].Holly LT, Bloch O, and Johnson JP, 2006, “Evaluation of Registration Techniques for Spinal Image Guidance.,” J. Neurosurg. Spine, 4(4), pp. 323–8. [DOI] [PubMed] [Google Scholar]
- [20].Otake Y, Armand M, Armiger RS, Kutzer MD, Basafa E, Kazanzides P, and Taylor RH, 2012, “Intraoperative Image-Based Multiview 2D/3D Registration for Image-Guided Orthopaedic Surgery: Incorporation of Fiducial-Based C-Arm Tracking and GPU-Acceleration,” IEEE Trans. Med. Imaging, 31(4), pp. 948–962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Ouadah S, Stayman JW, Gang GJ, Ehtiati T, and Siewerdsen JH, 2016, “Self-Calibration of Cone-Beam CT Geometry Using 3D–2D Image Registration,” Phys. Med. Biol, 61(7), pp. 2613–2632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Reaungamornrat S, De Silva T, Uneri A, Vogt S, Kleinszig G, Khanna AJ, Wolinsky JP, Prince JL, and Siewerdsen JH, 2016, “MIND Demons: Symmetric Diffeomorphic Deformable Registration of MR and CT for Image-Guided Spine Surgery,” IEEE Trans. Med. Imaging, 35(11), pp. 2413–2424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Goerres J, Uneri A, De Silva T, Ketcha M, Reaungamornrat S, Jacobson M, Vogt S, Kleinszig G, Osgood G, Wolinsky J-P, and Siewerdsen JH, 2017, “Spinal Pedicle Screw Planning Using Deformable Atlas Registration,” Phys. Med. Biol, 62(7), pp. 2871–2891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Behnami D, Seitel A, Rasoulian A, Anas EMA, Lessoway V, Osborn J, Rohling R, and Abolmaesumi P, 2016, “Joint Registration of Ultrasound, CT and a Shape+pose Statistical Model of the Lumbar Spine for Guiding Anesthesia,” Int. J. Comput. Assist. Radiol. Surg [DOI] [PubMed] [Google Scholar]
- [25].Cech P, Andronache A, and Wang L, 2006, “Piecewise Rigid Multimodal Spine Registration,” Bildverarbeitung Für Die Medizin 2006, Springer-Verlag, Berlin/Heidelberg, pp. 211–215. [Google Scholar]
- [26].Khallaghi S, Mousavi P, Gong RH, Gill S, Boisvert J, Fichtinger G, Pichora D, Borschneck D, and Abolmaesumi P, 2010, “Registration of a Statistical Shape Model of the Lumbar Spine to 3D Ultrasound Images.,” Med. Image Comput. Comput. Assist. Interv, 13, pp. 68–75. [DOI] [PubMed] [Google Scholar]
- [27].Glocker B, Zikic D, and Haynor DR, 2014, “Robust Registration of Longitudinal Spine CT,” Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics), 8673 LNCS(PART 1), pp. 251–258. [DOI] [PubMed] [Google Scholar]
- [28].Cai Y, Olson JD, Fan X, Evans LT, Paulsen KD, Roberts DW, Mirza SK, Lollis SS, and Ji S, 2016, “Automatic Geometric Rectification for Patient Registration in Image-Guided Spinal Surgery,” Spiedigitallibrary.Org, p. 97860E. [Google Scholar]
- [29].Fan X, Durtschi MS, Li C, Evans LT, Ji S, Mirza SK, and Paulsen KD, “Hand-Held Stereovision System for Image Updating in Open Spine Surgery.” [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Do Carmo MP, 1976, “Differential Geometry of Curves and Surfaces,” Dover phoenix Ed., 2, pp. xiv, 474 p. [Google Scholar]
- [31].Kadoury S, Labelle H, and Paragios N, 2013, “Spine Segmentation in Medical Images Using Manifold Embeddings and Higher-Order MRFs.,” IEEE Trans. Med. Imaging [DOI] [PubMed] [Google Scholar]
- [32].Liu C, Yuen J, and Torralba A, 2011, “SIFT Flow: Dense Correspondence across Scenes and Its Applications,” IEEE Trans. Pattern Anal. Mach. Intell, 33(5), pp. 978–994. [DOI] [PubMed] [Google Scholar]
- [33].Ji S, Fan X, Paulsen KD, Roberts DW, Mirza SK, and Lollis SS, 2015, “Intraoperative CT as a Registration Benchmark for Intervertebral Motion Compensation in Image-Guided Open Spinal Surgery.,” Int. J. Comput. Assist. Radiol. Surg, 10(12), pp. 2009–2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Eggert DW, Lorusso a., and Fisher RB, 1997, “Estimating 3-D Rigid Body Transformations: A Comparison of Four Major Algorithms,” Mach. Vis. Appl, 9(5–6), pp. 272–290. [Google Scholar]
- [35].Schaffert R, Wang J, Fischer P, Maier A, and Borsdorf A, 2019, “Robust Multi-View 2-D/3-D Registration Using Point-To-Plane Correspondence Model,” IEEE Trans. Med. Imaging [DOI] [PubMed] [Google Scholar]
- [36].Brendel B, Winter S, Rick A, Stockheim M, and Ermert H, 2002, “Registration of 3D CT and Ultrasound Datasets of the Spine Using Bone Structures,” Comput. Aided Surg, 7(3), pp. 146–155. [DOI] [PubMed] [Google Scholar]
- [37].Hesamian MH, Jia W, He X, and Kennedy P, 2019, “Deep Learning Techniques for Medical Image Segmentation: Achievements and Challenges,” J. Digit. Imaging, 32(4), pp. 582–596. [DOI] [PMC free article] [PubMed] [Google Scholar]