On the Mechanism of Alkylammonium Ligands Binding to the Surface of CsPbBr₃ Nanocrystals

Abstract

CsPbBr₃ nanocrystals (NCs) suffer from instabilities caused by the dynamic and labile nature of both the inorganic core and the organic–inorganic interface. Surface ligand engineering thus remains an imminent research topic. In this study, classical molecular dynamics simulations with an explicit solvent are used to gain insights into the inherent binding properties of three different alkylammonium ligands—primary dodecylammonium (DA), secondary didodecylammonium (DDA), and quaternary dimethyldi- dodecylammonium (DMDDA). Our simulations uncover three main factors that govern the effective ligand–substrate interactions: (i) the ability of the head-group to penetrate into the binding pocket, (ii) the strength of head-group interactions with the polar solvent, and (iii) the higher barrier for ligand adsorption/desorption in the case of multiple alkyl chains. The interplay between these factors causes the following order of the binding free energies: DDA < DA ≈ DMDDA, while surface capping with DDA and DMDDA ligands is additionally stabilized by the kinetic barrier. These findings are in agreement with previous experimental observations and with the results of presented ligand-exchange experiments, wherein DDA is found to loosely bind to the CsPbBr₃ surface, while DMDDA capping is more stable than capping with the primary oleylammonium ligand. The presented mechanistic understanding of the ligand–NC interactions will aid in the design of cationic ligands that make perovskite NC surfaces more robust.

Since their discovery in 2015,¹ colloidal cesium lead halide (CsPbX₃) perovskite nanocrystals (NCs) have received significant academic attention as an efficient semiconductor material for light emission applications.^2,3 Simplicity of the chemical synthesis, inherently narrow emission from near-band-edge states with high photoluminescence quantum yield (PL QY) without any need of overcoating with a protective inorganic shell make NCs the system of choice for applications in LEDs,⁴⁻¹⁰ displays,¹¹⁻¹⁴ lasers,¹⁵⁻²² and quantum light sources.²³⁻²⁷ Practical deployment of CsPbX₃ NCs is, however, severely hampered by the instability caused by the softness and lability of these materials. In particular, the organic–inorganic interface is the main stumbling block on the way to producing sufficiently robust NCs and materials based on them. Highly dynamic binding exists between the NC surface and capping ligands, typically a pair consisting of an anion (Br^– or oleate, OLA^–) and a cation (oleylammonium, OlAm⁺),²⁸ resulting in rapid ligand desorption upon isolation and purification of colloids. These processes manifest themselves as a loss of colloidal stability and a rapid decrease in PL QY and eventually as a loss of structural integrity and sintering of NCs into bulk polycrystalline materials.

The need for improved structural, chemical, and environmental stability of CsPbX₃ NCs continuously motivates exploration of diverse capping ligands, both experimentally and theoretically.²⁹⁻³⁶ Recent studies have encompassed quaternary dimethyldidodecylammonium (DMDDA) halides,^6,32,37,38 alkylphosphonic acids,³⁹⁻⁴¹ and long-chain zwitterionic ligands,^33,42,43 yielding considerable improvements in obtaining purifiable and stable colloids. However, comprehensive understanding of the NC–ligand–solvent interface and the atomistic origin of the observed differences lags behind.

Ab initio calculations and classical molecular dynamics (MD) simulations can be used to gain mechanistic insights into binding of capping ligands to the NC surfaces.⁴⁴⁻⁵¹ Their atomic resolution makes it possible to obtain a detailed thermodynamic assessment of ligand adsorption on inorganic crystalline surfaces, therefore enabling comparison of the relative efficiencies of different surface passivation strategies. See example in ref (52) of a system iron oxide surface—stearic acid ligand—hydrocarbon solvent. However, the complexity of the system involving inorganic crystal, capping ligand shell, and organic solvent makes this a very challenging task. In fact, thermodynamics of ligand binding to the surface of semiconductor NCs has never been investigated using explicit representations of all three components of the system.

This work presents a combined computational and experimental mechanistic study on the binding of alkylammonium capping ligands to the surface of CsPbBr₃ NCs. We use all-atom classical MD simulations to examine inherent binding properties of three different ligands—primary dodecylammonium (DA), secondary didodecylammonium (DDA), and quaternary dimethyldidodecylammonium (DMDDA) (see Figure 1a)—in a mixture of nonpolar (toluene) and polar (acetone) solvents, the medium which is typically encountered during purification of the NCs. Two factors leading to strong ligand binding are revealed: (i) the ability of the head-group to fit into the binding pocket, and the (ii) weak interaction of the head-group with a polar solvent, which explain strong binding of DA and DMDDA ligands, respectively. In addition, desorption/adsorption of ligands with multiple alkyl tails is found to be hampered by a high free-energy barrier (up to 140 kJ/mol for the DMDDA ligand at 50% surface coverage), adding to kinetic stabilization of the ligand capping layer. Overall, our findings agree with earlier experimental observations that DDA is not able to efficiently bind to the surface of CsPbBr₃ NCs,⁵³ whereas its methylated analogue, DMDDA, has a good affinity to the surface and renders CsPbBr₃ NCs highly stable and robust.^32,37 Reference experiments with these ligands are also consistent with the MD simulations. We then outline that a good cationic ligand can be found among molecules with compact yet fully methylated head-groups and multiple alkyl chains in the backbone.

Figure 1.

Thermodynamics of ligand binding to the surface of CsPbBr₃ at very low surface coverage (σ → 0). (a) Side view on the complete simulation box, containing the slab, a ligand, and a mixed toluene/acetone solvent. Br, Cs, and Pb atoms are depicted in green, yellow, and brown, respectively. One surface Cs ion was substituted with one of the following ligands (from left to right): DA, DDA, and DMDDA. (b) PMF profiles as a function of the distance between the ligand head-group and the center of the slab, and (c–e) corresponding changes in non-bonded potential energy of the system. The shaded regions correspond to the entropic contribution to the free energy. For clarity, all energy curves are superimposed at large distances, where they plateau.

Computational Model

A slab of bulk cubic CsPbBr₃, terminated from both sides with CsBr-rich (100) crystallographic planes, was chosen to represent the idealized surface of the NCs.^54,55 One of these surfaces was then passivated by replacing some of the surface Cs⁺ ions with alkylammonium ligands.⁵⁶ The system was then solvated with a 1:1 (by volume) mixture of toluene and acetone, which are a common solvent/antisolvent combination used for purification of CsPbBr₃ NCs, the step at which damage to the ligand passivation shell is most likely to occur. Our model disregards the possible effects of acid–base equilibria, the influence of various additives or byproducts on NC colloids in order to achieve computational tractability. Further details of the system preparation and MD simulation procedures can be found in the methods section.

First, we consider the case of infinitely low surface coverage, σ → 0, wherein only a single Cs ion on the surface of the slab was substituted with a ligand molecule (see Figure 1a). In this setup, the distance between the closest ligand neighbors is 4.7 nm, the length of the box along x and y directions, which is large enough to consider the adsorbed ligands independent. In order to estimate free-energy change associated with ligand’s binding to the perovskite surface, the potential of mean force (PMF) was computed as a function of the distance between the nitrogen atom of the ligand and the middle atomic plane of the slab (see the methods section for more details).

Degree of Head-Group Substitution has a Complex Effect on Ligand’s Binding

The obtained PMFs, as depicted in Figure 1b, show pronounced minima at short distances that correspond to configurations of ligands bound to the surface. PMF curves plateau at longer distances, pointing to the lack of interactions (apart from long-range electrostatic attraction). At intermediate distances, ca. 1.5 nm, there is a small local minimum in all PMFs, which is attributed to interactions mediated by one acetone molecule. The depth of the main minimum depends on the ligand. The lowest value of free energy, ΔF_bind = −90 kJ/mol, is seen for the DA ligand, which has only one alkyl chain attached to the head group. The shallowest minimum, ΔF_bind = −50 kJ/mol, is measured for the DDA ligand, which differs from DA by having two alkyl chains attached to the same head group. The third ligand, DMDDA, has ΔF_bind = −80 kJ/mol, which falls in between the values observed for the other two systems. The fact that this ligand is the most substituted of all (its head-group has all four hydrogens replaced) suggests that the degree of substitution is not the only parameter controlling the strength of ligand’s binding.

Desolvation as the Key Factor Controlling DA’s Binding

To shed light on the origin of the observed free-energy ranking, we analyzed the simulated systems’ potential energy as a function of the same reaction coordinate. Bonded energy—which originates from bond stretching, angle bending, and torsion angle rotation—does not notably change with decreasing d_slab–N. Instead, the change in non-bonded potential energy (which includes van der Waals and electrostatic interactions), ⟨U_NB⟩(d_slab–N), shows that the bound state is energetically more favorable for all ligands (Figure 1c–e). The corresponding potential energy difference is referred to as the binding energy and can be computed as ΔU_bind = ⟨U_NB⟩_pl – ⟨U_NB⟩_min, where ⟨U_NB⟩_pl and ⟨U_NB⟩_min are the average non-bonded potential energy at the plateau and at the minimum in PMF, respectively. Note that solvent is completely averaged out in the computation of the binding energy. Together with the binding entropy term, −TΔS_bind, binding energy controls the strength of ligand binding through the known thermodynamic relationship ΔF_bind = ΔU_bind – TΔS_bind. Here, we see that the DA ligand exhibits a qualitatively different behavior compared to the other two ligands. While binding of DDA and DMDDA ligands is mostly driven by energy (ΔU_bind ≈ −30 kJ/mol and ≈−60 kJ/mol for DDA and DMDDA, respectively, and entropic contribution is about −20 kJ/mol for both ligands), binding of the DA ligand is rather dominated by entropy (ΔU_bind ≈ −40 kJ/mol, which is less than ≈−50 kJ/mol attributed to the entropy gain).

The large entropic contribution for DA is puzzling and calls for further investigation. It can be seen in Figure 1c that ΔU_bind for this system reaches a value of −40 kJ/mol at d_slab–N = 1.0 nm. The corresponding change in free energy is −60 kJ/mol, which gives the difference attributed to entropy of about −20 kJ/mol. This is similar to the entropy gain observed for the other two ligands, hinting that perhaps a common mechanism is at play in all three systems. One common effect that operates in all studied systems is solvation. Our simulations show that ligands far from the surface strongly interact with polar acetone molecules (Figure 2a). The unoccupied binding pocket is also fully solvated. In contrast, the binding interface becomes desolvated when the ligands approach the surface at a short distance d_slab–N = 1.0 nm. The escape of solvent molecules is accompanied by an increase in entropy, which appears to be the common mechanism facilitating the binding of all three ligands. In contrast to the other two ligands, DA exhibits a unique behavior when d_slab–N is further reduced below 1 nm. While its ΔU_bind remains almost unchanged, the PMF continues to decline. In the final 0.2 nm, it decreases by another 30 kJ/mol before reaching a minimum of −90 kJ/mol. No such behavior is observed either for DDA or DMDDA since these two ligands do not fit into the binding pocket due to geometric constraints and rather stay at the surface (Figure 2c). The unique entropic contribution to the binding of the DA ligand can be attributed to a complete head-group desolvation, which occurs when it penetrates deep into the binding pocket (as schematically illustrated in Figure 2b). Indeed, we observe that all head-groups undergo only partial desolvation upon approaching d_slab–N = 1.0 nm. For instance, DA head-group retains on average 1.1 acetone molecules in the first solvation shell, whereas DDA and DMDDA—0.75 and 0.5 molecules, respectively (Figure 2a). Burial of the DA head-group deeply into the binding pocket leads to a complete desolvation, followed by the estimated entropy change of −TΔS = −20 kJ/mol (see the Supporting Information for the details of calculation). This value is similar to the free-energy drop observed on the PMF, therefore supporting the proposed mechanism.

Figure 2.

(a) Radial distribution functions for N_ligand–O_acetone distances, computed at various separations between the ligand and the slab illustrating partial or complete head-group desolvation upon binding to the surface. (b,c) Typical geometries of a bound state. DA’s head-group undergoes full desolvation and penetrates deep into the binding pocket (b), whereas bulkier DDA’s and DMDDA’s head-groups stay at the surface of the binding site (c). In (c), the residual solvation of ligands is omitted for clarity.

Binding of the Ligands that Do Not Fit into the Binding Pocket

Whereas for DA entropy is important, binding specifics of DDA and DMDDA ligands can be fully explained by the binding energy alone. Indeed, the difference between ΔU_bind for these systems is 30 kJ/mol, which is exactly the free-energy difference (Figure 1). To better understand how this figure comes about, ΔU_bind was decomposed into six contributions: three terms corresponding to the ligand, the slab and the solvent subsystems, plus three cross-terms. All six contributions were then grouped into two terms—ΔU_bind⁽¹⁾, which accounts for the interactions within the slab + ligand subsystem, and ΔU_bind, which contains ligand–solvent, slab–solvent, and solvent–solvent interactions and therefore shows how solvent counteracts ligand’s binding

ΔU_bind⁽¹⁾ and ΔU_bind, as well as different components of the latter are presented in Figure 3a. It is seen that ΔU_bind⁽¹⁾ shows no significant difference between DDA and DMDDA ligands. This rules out the hypothesis that a more favorable interaction with the surface is responsible for the stronger binding of the DMDDA ligand. In contrast, the contribution from solvent-related potential energy, ΔU_bind, shows precisely 30 kJ/mol difference between the two ligands. Among the three components of ΔU_bind⁽²⁾, the change in solvent self-energy, ΔU_bind, was found to be identical for the two ligands. The contribution from ligand–solvent interactions, ΔU_bind^(lig–sol), shows about 10 kJ/mol difference between the two ligands, and the remaining 20 kJ/mol originate from slab–solvent interactions, ΔU_bind. It can be further shown that the difference in the binding strength of DDA and DMDDA ligands is determined mainly by electrostatic interactions with acetone, while other non-bonded energy terms make little or no contribution. This is not surprising given acetone’s polar nature. Since the free DDA ligand readily engages in hydrogen bonding with acetone, unlike to DMDDA, it results in a higher energy penalty when some of these interactions are lost upon binding. This mechanism explains the difference in ΔU_bind^(lig–sol). In contrast, the fact that most of the difference between the two ligands resides in slab–solvent interactions seems counterintuitive at first glance. Detailed examination of the MD trajectories, however, reveals that DDA preserves some close contacts with acetone molecules even in the bound state (Figure 2a). This is clearly seen in Figure 3b, which shows a density map of acetone oxygen atoms just above the surface of the slab. Although the preferred binding sites are near cesium ions, some portion of the solvent molecules are coordinated to the head-group of the ligand. No such molecules are observed for the DMDDA ligand (see Figure 3b, lower panel), which is not able to participate in hydrogen bonding. It is clear, therefore, that DDA competes with surface ions for the interactions with solvent molecules, which is why ⟨U_NB⟩ experiences a larger increase upon binding for the DDA ligand. Either directly or through the indirect competitive mechanism, the energetics of the head-group solvation appears to play a key role in determining the difference between DDA and DMDDA ligands’ binding strength.

Figure 3.

Analysis of the differences between binding of DDA and DMDDA ligands. Panel (a) shows comparison of different non-bonded potential energy contributions to ΔU_bind. The main difference between the two ligands is observed for interactions that involve solvent, more specifically ligand–solvent and slab–solvent interactions. (b) Maps showing the number density of acetone oxygen atoms in the first solvation layer of the slab in the case of DDA (upper panel) and DMDDA (lower panel) ligands bound to the surface. The red circle shows the region where the head-group of the DDA ligand retains its interactions with acetone molecules, leading to an increase in the density of acetone oxygen atoms in the places unfavorable for slab–acetone interactions.

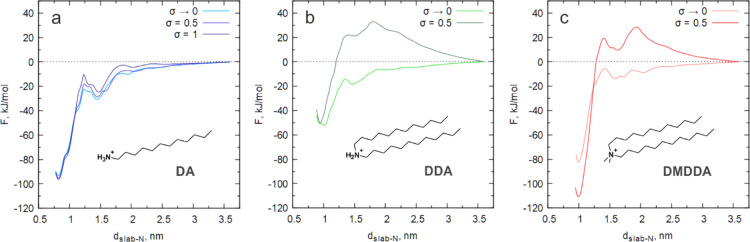
Kinetic Barrier for Ligands with Multiple Tails at Finite Surface Coverage

Next, we examined how the binding of the ligands is affected by an increase in surface coverage. For this purpose, simulation boxes were built with 50% (σ = 0.5) and 100% (σ = 1, only for the DA ligand) binding sites occupied. The symmetric distribution of attachment points, as shown in Figure S1, was used for σ = 0.5. As can be seen in Figure 4a, the binding of the single-chain DA ligand is not affected by the degree of surface coverage. On the contrary, ligands with two alkyl chains show qualitatively different PMF profiles at non-zero surface coverage (Figure 4b,c). Regions of positive free energy are observed at intermediate distances for the DDA and DMDDA ligands, which means an additional barrier for the detachment of a ligand from the surface. In the case of DDA, the height of the barrier, measured as the difference between the highest and the lowest points on PMF, is about 80 kJ/mol, which is quite substantial. For comparison, the binding free energy of the ligand at this surface coverage is not exceeding −50 kJ/mol. For the DMDDA ligand, the desorption barrier is even higher, ca. 140 kJ/mol, significantly exceeding the free-energy penalty that is required to detach a primary alkylammonium ligand. The barrier can also be measured for the adsorption process, yielding approximately the same value of ca. 30 kJ/mol for DDA and DMDDA ligands, while no barrier is found for the DA ligand even at the largest possible surface coverage σ = 1 (grafting density of alkyl chains is the same as for the other two ligands at σ = 0.5). Therefore, the existence of the barrier stems from the pair-wise linking of the alkyl tails at the head-group. The exact mechanism by which the additional tail acts is not clear yet. It could be steric/entropic repulsion between neighboring ligand tails. Alternatively, the tail may interfere with how the head-group of the ligand interacts with the surface. It is clear, though, that the purely excluded volume effect can be ruled out as the binding free energy remains largely unaffected, as shown in Figure 4b,c. In addition, the solvent may be involved as well since the repulsion observed on PMF profiles appears to be long-ranged.

Figure 4.

PMF profiles for the detachment of DA (a), DDA (b), and DMDDA (c) ligands computed at different values of a surface coverage parameter σ. It is apparent that the binding free energy of the DA ligand is independent of σ and stays around −95 kJ/mol. On the other hand, PMF profiles change significantly in the case of DDA and DMDDA, illustrating the influence of ligands, which are already present at the surface.

The long-range nature of the repulsion observed for the double-chain ligands prevents us from the direct interpretation of the binding free energies calculated from the corresponding PMF profiles. Still, it seems that the ligands follow a trend similar to that of σ → 0, with the DDA ligand being loosely bound to the surface and DA and DMDDA ligands showing comparably high values of binding free energy. Together with a high desorption barrier for the DMDDA ligand, this may explain the remarkable stability of DMDDA-capped CsPbBr₃ NC colloids during their purification with polar solvents.

Comparison with Ligand-Exchange Experiments

In order to test theoretical findings, a ligand-exchange experiment was performed, in which the composition of the ligand passivation shell around CsPbBr₃ NCs was evaluated using quantitative ¹H NMR spectroscopy. A hot-injection synthesis with oleylamine (OlAm) and oleic acid (OLA)¹ was used to prepare the starting colloid. Here, protonated OlAm serves as an experimental equivalent of the primary DA ligand. Its binding to the surface of CsPbBr₃ NCs was demonstrated earlier,^28,56 whereas OLA serves as a solubilizing agent to dissolve inorganic Cs₂CO₃ and PbBr₂ salts and as a proton source for OlAm.^28,57,58 The resulting CsPbBr₃ NCs were precipitated from the crude reaction mixture by centrifugation, redispersed in toluene, and used for ligand-exchange experiments, which are schematically shown in Figure 5a.

Figure 5.

(a) Schematic of the ligand-exchange experiment, which was used to study the binding of alkylammonium ligands to the surface of CsPbBr₃ NCs. (b) ¹H NMR spectra of purified NCs after treatment with DDA (top) and DMDDA ligands (bottom). Toluene-d₈ was used as a solvent. (c) Quantitative ¹H NMR spectra of the corresponding samples after digestion in DMSO-d₆. Mesitylene was used as an internal standard.

In a recent report, Bodnarchuk et al. showed that the addition of PbBr₂ together with the DMDDA ligand during the ligand-exchange process improves the PL QY and the shelf life of the resulting NCs.³² This effect was attributed to the restoration of the damaged surface PbBr₆ octahedra. Indeed, results of XPS and inductively coupled plasma-optical emission spectroscopy analyses point toward ABr-rich surface termination of the NCs treated with or without PbBr₂ addition, with the former experiencing 2–3% higher Br/Pb ratios. XPS-derived Cs/Pb ratios, instead, anticorrelate with N/Pb ratios, therefore confirming that DMDDA cations replace Cs⁺ ions on the ABr-rich surface of the NCs.³² We also observe the beneficial effect of including PbBr₂ into a ligand stock solution. It is even more pronounced in the case of DDA treatment, where samples prepared in the absence of PbBr₂ additive do not survive the subsequent purification with antisolvent. We used two cycles of precipitation with acetone (added to a toluene dispersion of NCs) in order to effectively remove excess and liberated ligands after the ligand exchange. Alternatively, ethyl acetate was tested as a less aggressive antisolvent, which allowed us to perform three cycles of purification. The results obtained with this purification protocol are consistent with those discussed below and are presented in the Supporting Information.

Bright-field transmission electron microscopy (BF-TEM) images show that both the DDA- and DMDDA-treated NCs retain their cubic shape without any signs of immediate aggregation, and only a slight decrease in the NC size is observed for both samples (Figure S2). No signs of transformation into the Cs₄PbBr₆ phase during the ligand-exchange experiment were detected with UV–vis spectroscopy (Figure S3). The DDA-treated sample, however, features significantly worse stability compared to the DMDDA-treated one. It quickly precipitates after dilution with hexane or during long-term storage (Figure S4a), which is a sign of loose and highly dynamic ligand binding to the surface. Moreover, DDA-treated NCs deposited on the TEM grid start to sinter after few days of storage under ambient conditions (Figure S4c). No such degradation was observed for the DMDDA-treated samples. ¹H NMR spectra of the treated NCs in toluene-d₈ are presented in Figure 5b (please refer to the Supporting Information for the full-scale spectra and details of the peak assignment). A broad signal shape and a significantly shifted signal position are characteristics of a ligand being in the interaction with the NC surface.^{28,41,59−62} The DDA-treated sample contains a significant fraction of surface-bound original oleyl ligands, which give a broad resonance at 5.64 ppm, together with a small amount of free oleyl species (narrow signal at 5.50 ppm). Broad signals spanning the range from 5 to 3 ppm were assigned to α-CH₂ protons of surface-bound OlAm and DDA ligands. Instead, the DMDDA-treated sample contains only a minor amount of free oleyl species (resonance 9), and the only observed bound ligand is DMDDA, which shows two broad signals at 3.95 and 3.65 ppm corresponding to α-CH₃ and α-CH₂ protons.

In order to quantify ligand composition, the samples were digested in deuterated dimethyl sulfoxide (DMSO-d₆), yielding clear colorless solutions. The corresponding quantitative ¹H NMR spectra are presented in Figure 5c, and the results of quantification are summarized in Tables 1 and 2. In addition, we have estimated the degree of NCs’ surface coverage by the ligands, which were previously confirmed to be bound to the surface. For this purpose, the concentration of the NCs was determined using an experimentally derived molar extinction coefficient.⁶³ The knowledge of NC concentration together with their average size (from BF-TEM images) and a theoretical density of binding sites (2.9 nm^–1) was then used to estimate the concentration of binding sites in the corresponding samples of treated CsPbBr₃ NCs. An estimate of the surface coverage by a specific ligand follows on as a ratio between the experimentally determined concentration of the ligand and the estimated concentration of binding sites.

Table 1. Ligand Composition of the DDA-Treated Sample.

species	concentration (mM)	estimated surface coverage (%)
binding sites	7.4
DDA	1.5–1.8a	20–24
OlAm	3.6–3.0a	49–41
OLA (free)	0.3b

^aFrom integration of the overlapping resonances 1 and 4. The result of quantification depends slightly on the actual assignment of the resonances 2 and 5.

^bFrom integration of the resonance 9 in the spectrum of the NCs before digestion (Figure 5b).

Table 2. Ligand Composition of the DMDDA-Treated Sample.

species	concentration (mM)	estimated surface coverage (%)
binding sites	7.2
DMDDA	3.1a	43
OlAm	0.03b	≤0.5
OLA (free)	0.3c

^aFrom integration of the resonances 6 and 7.

^bFrom integration of the resonance 1.

^cFrom integration of the resonance 9.

In the case of DMDDA-treated samples, the dominant ligand is DMDDA, and surface coverage of CsPbBr₃ NCs with this ligand is estimated to be about 43%, which is close to the value of 50% used in our simulations. Surface coverage with the residual OlAm ligand is calculated from the integration of the signal at 2.90 ppm (the enlarged region, as shown in Figure 5c) to be negligible, less than 0.5%. It is important to note that OlAm accounts for only ca. 10% of the total oleyl-chain content in the digested solution (resonance 9, as shown in Figure 5c). The remaining 90% are therefore attributed to OLA, the characteristic signals of which are difficult to spot due to an overlap with other intense peaks (Figure S9). Integration of the sharp signal at 5.50 ppm in the NMR spectrum of the NCs before digestion (Figure 5b) provides a consistent estimate of the OLA concentration and therefore confirms that OLA does not participate in the binding to the surface of CsPbBr₃ NCs.

Unlike the DMDDA-treated sample, the ¹H NMR spectrum of the DDA-treated sample after digestion in DMSO-d₆ shows comparable quantities of both OlAm and DDA ligands (Figure 5c, upper panel). Complete overlap of the α-CH₂ triplets of the two ligands and a small chemical shift difference between the β-CH₂ quintets prevent their unambiguous assignment. Therefore, the ratio between the two ligands was calculated by comparing integrals of the two β-CH₂ resonances. We find [DDA]/[OlAm] = 0.4 or 0.6, depending on the actual peak assignment. Concentrations of the two ligands were then derived using this ratio and the integral of the mixed resonance 1,4 due to a lower background level in this region of the spectrum (see Table 1). By analogy to the DMDDA-treated sample, the sharp resonance 9, as shown in Figure 5b, was attributed to the residual-free OLA.

Overall, it is apparent that the DDA ligand only partially replaces bound OlAm ligand. Given that the feed ratio of the two ligands was DDA/OlAm = 1.1:1 (see the Supporting Information for details), which is more than 0.4–0.6:1 after purification, we conclude that secondary DDA has lower affinity to the CsPbBr₃ NCs surface than OlAm. Instead, the DMDDA ligand provides stable surface passivation and completely replaces the original OlAm ligand. Similar conclusions follow from ligand-exchange experiments, in which another common antisolvent, ethyl acetate, was employed (see the Supporting Information). Here, the ratio between DDA and OlAm ligands decreases from 0.9:1 (feed) to 0.03:1 after ligand exchange and purification. For comparison, the DMDDA/OlAm ratio increases to 9.5:1 after DMDDA treatment, while the same ligand feed ratio as in the case of DDA treatment was used.

The results of ligand-exchange experiments qualitatively support our computational finding that the secondary DDA ligand does not provide stable passivation of the CsPbBr₃ surface, as compared to the other two ligands. The experiment also shows that passivation with the quaternary DMDDA ligand is more robust than with the primary OlAm. This may be partially related to the kinetic stabilization effect discovered in our computational study. However, fully unambiguous conclusion requires a more elaborate experimental design, in order to distinguish between thermodynamic and kinetic factors. We should also note that there are other factors which may have effect on the results of ligand-exchange experiments and which were not included in our computational model. First, one should be aware of OLA contamination in the starting colloid (Figure S5). Acid–base equilibria of the primary and secondary alkylammonium ligands with the oleate base can reduce effective binding strength of OlAm and DDA ligands compared to DMDDA, which cannot participate in such equilibria. The effect is expected to be stronger for the OlAm ligand than for DDA due to generally higher pK_b of a primary amine compared to a secondary amine. Another factor is the reactivity of unprotonated OlAm and DDA toward atmospheric CO₂, leading to the reversible formation of corresponding alkylcarbamates.^64,65 Overall, the experiment may underestimate inherent binding strength of OlAm and DDA ligands, as well as the difference between them.

In conclusion, we have studied the binding of different alkylammonium ligands to the surface of CsPbBr₃ NCs in a mixed toluene/acetone solvent using MD simulations. At low surface coverage, two factors enhancing the binding strength were unveiled: (a) the ability of the ligand head-group to penetrate into the binding pocket and (b) a weak interaction of the head-group with polar acetone molecules. Ligands that possess either of these properties, such as the primary DA ligand, which has a small head-group capable of entering the binding pocket, or quaternary DMDDA ligand, which has a bulky head-group with minor interactions with acetone, display stronger binding than DDA. At finite surface coverage, the same trends of binding free energies are observed. In addition, the availability of two alkyl chains attached to a single head-group causes a free-energy barrier for the adsorption/desorption of the DDA and DMDDA ligands. No barrier is observed for DA at surface coverages as high as σ = 1. The desorption barrier for the DMDDA ligand is higher than that for the other systems and amounts to ≈140 kJ/mol. Such a high barrier is expected to inhibit the process of ligand detachment from the surface, protecting DMDDA-capped NCs from excessive loss of ligands during the purification steps. Enhancing stability by a kinetic barrier may prove to be an important strategy for CsPbBr₃ NCs as the approaches relying on stronger ligand–NC surface binding may cause damage to the soft inorganic core.^35,66−69

The mechanisms identified in this work can be employed as guiding principles for developing new ligands that impart higher colloidal stability. Some of the discovered requirements to achieve better ligand binding are mutually exclusive, while others can be combined. For example, protection of the head-group from contacts with polar solvents unavoidably leads to the increase in head-group’s bulkiness. However, both head-group types, the compact one and the one protected from energetic contacts with polar solvents, can have several alkyl tails (Chart 1). The compact head-group can be combined with two alkyl chains if the branching point of the primary alkylammonium ligand is located further along the chain (i.e., at the α- or β-carbon, structures 1 and 2 in Chart 1). In the case of protected quaternary alkylammonium head-groups, the freedom of design is higher. The branching point can be located either on the nitrogen itself (DMDDA ligand) or be shifted further along the chain (Chart 1, structures 3 and 4). DMDDA’s head-group can be rendered more compact by involving the two alkyl chains into a pyrrolidinium cycle, thereby chemically constraining their conformational freedom (Chart 1, structure 5). Alternatively, it is possible to design a number of relatively compact and simultaneously fully substituted alkyliminium head-groups, which have only three alkyl substituents at the nitrogen. Some plausible examples of such iminium ligands include imidazolium, triazolium, pyridinium, and formamidinium derivatives, exemplified in Chart 1 (structures 6–9).

Chart 1. Cationic ligands that are expected to yield robust passivation of CsPbBr₃ NCs.

Methods

Simulation Box

Interactions of different ammonium ligands with the surface of perovskite NCs were studied by means of classical MD simulations using a slab of bulk cubic CsPbBr₃ with a size of 8 × 8 × 3.5 unit cells. Based on the available HR-TEM images of CsPbBr₃ NCs^1,70 and taking into account the fact that lead halide octahedral units demonstrate high stability in various layered and other hybrid perovskite-related materials,⁷¹⁻⁷³ the two opposite surfaces of the slab were chosen to be terminated with CsBr-rich (100) planes. CsBr-rich surface termination agrees well with the results of previous experimental and theoretical studies.^32,54,55 One of these surfaces was then passivated with organic ligands by replacing some of Cs⁺ ions with one type of the following ammonium cations—DA, DDA, or DMDDA. Different degrees of surface coverage parameter (σ) were considered, and for σ = 0.5, ligands were distributed according to the symmetric periodic pattern in order to ensure that all the binding positions have equivalent surrounding (Figure S1). The system was then placed in a rectangular simulation box with periodic boundary conditions, and 305 (340 for σ → 0) toluene and 440 (490 for σ → 0) acetone molecules were added to represent common conditions during the purification of the NCs. Two of the simulation box parameters were always kept fixed to eight times the experimental value of the cubic CsPbBr₃ unit cell (8·a = 4.699 nm).⁷⁴ The remaining parameter—box length along z-axis—was either fixed or allowed to change, depending on the simulated thermodynamic ensemble. A typical value of the box length after equilibration was about 8 nm.

The all-atom CHARMM General Force Field (CGenFF 4.0)⁷⁵ was used to model interactions between atoms in the organic part of the system. Topologies of the ligands were generated using CGenFF software.^76,77 Missing dihedral parameters for the DMDDA ligand were replaced by analogous dihedral parameters for DDA and choline molecules. Nonbonded parameters for Cs⁺ and Br^– ions were adopted from ref (78) and for Pb²⁺ ion—from ref (79). No bonded interactions were employed for the ions comprising the slab. The constructed classical perovskite model was tested in simulations of bulk CsPbBr₃ crystal. The results are briefly discussed in the Supporting Information.

Simulation Protocol and PMF Calculation

The complete simulation box was equilibrated for 20 ps in NVT ensemble and then for additional 10 ns in NPT ensemble. The structures were additionally annealed in the case of DDA and DMDDA ligands and surface coverage σ = 0.5. Briefly, the system was first simulated at 300 K in NPT ensemble (1 ns), followed by a simulation at 500 K in NVT ensemble (1 ns), after which cooling to 300 K at the rate of 100 K/ns was performed, finally followed by the equilibration in NPT ensemble (10 ns). This was carried out to facilitate convergence to the proper structure of the ligand layer, given slower conformational dynamics of these two surfactants in the bound state. In all simulations, positions of lead ions in the middle layer of the slab were restrained to the origin of z-axis and to their initial values in x and y directions by applying weak harmonic restraining potential with a force constant of 1000 kJ/(mol·nm²), in order to prevent floating of the slab across the simulation box.

The final well-equilibrated configurations were used as a starting point in the computation of PMF profiles using the umbrella sampling technique.⁸⁰ Harmonic biasing potential with the force constant k = 2000 kJ/(mol nm²) was applied to the nitrogen atom of the target ligand along z-axis. Umbrella windows were evenly distributed between 0.8 and 1.0 nm (depending on the ligand) and 3.5 nm with the increment of 0.1 nm, where the distance is measured from the nitrogen atom to the origin of z-axis (middle atomic plane of the slab). Movements of the nitrogen atom of the target head-group in x and y directions were restrained using weak harmonic potential with the force constant k = 500 kJ/(mol·nm²). We note that the applied potential does not interfere with the internal vibrations, rotations, or conformational changes in the head-group. Starting configurations for each umbrella window were generated with a separate MD run, where the target ligand was pulled (with a rate of 0.002 nm/ps) from its initial position on the surface to a specific distance from the slab. Each window was simulated for 40 ns at 300 K, preceded by 2 ns of equilibration. In cases where insufficient sampling or poor convergence were discovered, additional umbrella windows with stronger biasing potentials [up to 8000 kJ/(mol·nm²)] were added. The unbiased distribution was reconstructed using the weighted histogram analysis method.^81,82 Error analysis was conducted to assess the uncertainty of the obtained PMF curves. First, PMFs were computed as a running average over segments of the trajectories of increasing length. It was found that convergence occurs around 10 ns, after which point the binding free energy experiences variations of ca. 5 kJ/mol depending on the system. Next, the entire trajectory of 40 ns (for each umbrella window) was split into five equal non-overlapping segments, and PMF was computed for each segment separately. The error was estimated as the standard deviation over five measurements to be about 3–7 kJ/mol (depending on the specific system). This level of accuracy is sufficient to prove that observed differences in the binding free energy of the studied systems are statistically significant.

It was found that alkylammonium ligand detaches from the surface of the slab without its bromide counter-ion in all examined systems, leaving the surface negatively charged. For comparison, we computed PMF for the detachment of DA⁺Br^– ion pair by applying artificial half-harmonic restraint on the distance between the nitrogen atom and one of the nearest bromide ions. Detachment of the bromide together with the ligand was found to be ≈45 kJ/mol less favorable in the toluene/acetone mixture.

All reported simulations were performed using GROMACS software package.⁸³ Electrostatic interactions were computed using the smooth particle-mesh Ewald method.⁸⁴

Calculation of Potential Energies and their Components

In order to analyze potential energy as a function of the distance between the ligand and the slab, these two quantities were computed as trajectory averages (⟨U⟩ and ⟨d_slab–N⟩ correspondingly) for each umbrella window. Different pairs of interactions (e.g., bonded vs. nonbonded; ligand–slab, ligand–solvent, etc.) were considered in order to calculate different contributions to ⟨U⟩. Long-range part of electrostatic potential energy was split into different contributions by switching off charges on atoms out of interest and recalculating total long-range electrostatic potential energy for the pregenerated trajectories. Binding energy and its contributions were defined as ΔU_bind⁽ⁱ⁾ = ⟨U_NB⟩_pl – ⟨U_NB⁽ⁱ⁾⟩_min, where ⟨U_NB⟩_pl and ⟨U_NB⁽ⁱ⁾⟩_min are the average non-bonded potential energy at the plateau and at the minimum in PMF, respectively, and upper index (i) is either absent or refers to the name of the corresponding potential energy contribution.

Preparation of Cesium Oleate Stock Solution

200 mg of Cs₂CO₃ (0.613 mmol), 0.6 mL of OLA (1.9 mmol), and 7.5 mL of ODE were loaded into a 20 mL vial inside of a nitrogen-filled glovebox and heated at 100 °C until complete dissolution. The solution was then cooled and stored until needed. Since Cs-OLA precipitates out of ODE at room temperature, it has to be preheated to ca. 100 °C before injection. The list of chemicals is available in the Supporting Information.

Synthesis of CsPbBr₃ NCs

CsPbBr₃ NCs were synthesized, according to a modified version of the procedure published by Protesescu et al.¹ 220 mg of PbBr₂ (0.6 mmol) and 20 mL of dry ODE were loaded into an Ar-filled 100 mL three-neck flask equipped with a thermocouple and connected to a Schlenk line through a reflux condenser. Thermocontroller was set to 180 °C, and 2.0 mL of OLA and 2.0 mL of OlAm were injected into the flask when the temperature had reached 120 °C. At 180 °C, the solution became transparent and colorless. At this point, Cs-OLA stock solution (3.2 mL) was swiftly injected to initiate nucleation of CsPbBr₃ NCs. After 10 s, the reaction mixture was cooled to room temperature with a water/ice bath. The crude solution was centrifuged at 20,100 RCF for 10 min, and the supernatant was discarded. The precipitate was redispersed in toluene (1.2 mL) and centrifuged again (15,200 RCF, 5 min). The obtained solution in toluene was diluted two times and used for characterization and ligand-exchange experiments (referred to as starting colloid).

Synthesis of DDA Bromide

An excess of ca. 48% HBr in water (ca. 1.4 mL) was added dropwise to a stirred solution of DDA (3.54 g) in 20 mL of isopropanol. After 7 h of stirring at room temperature, the obtained suspension was filtered, and the solid was washed with diethyl ether and recrystallized from 25 mL of ethanol. The resulting product was dried under vacuum and stored inside of the nitrogen-filled glovebox (yield—80%).

Preparation of DDA (DMDDA) Stock Solution for Ligand Exchange

0.2 mmol of DDA-Br (or 0.2 mmol of DMDDA-Br) and 0.1 mmol of PbBr₂ were dissolved in 3 mL of toluene under heating. Both ligand solutions start to precipitate after some time at room temperature. In order to obtain again transparent solutions, they should be slightly heated until dissolution, cooled to room temperature, and used immediately for the ligand-exchange experiments.

Ligand-Exchange Experiments

300 μL of DDA (or DMDDA) stock solution was diluted in 1 mL of toluene and added dropwise to 1 mL of starting colloid. After 1 h of stirring at room temperature, the NCs were precipitated with the addition of 2.3 mL of acetone followed by centrifugation (19,800 RCF, 5 min). The obtained precipitate was redispersed in 1 mL of toluene and centrifuged at 6700 RCF for 3 min in order to remove any insoluble contaminations. The NCs were precipitated again with the addition of 1 mL of acetone-d₆ followed by centrifugation and redispersed in 0.5 mL of toluene-d₈. The obtained solution was filtered through a 0.2 μm PTFE filter to make sure that it does not contain any aggregated NCs and used for further characterization [yield of the ligand-exchange experiment after purification—70–80% (based on optically determined CsPbBr₃ concentration⁶³)].

Material Characterization

Samples for optical characterization were diluted with n-hexane and placed into glass cuvettes with 1 cm path length. UV–visible light absorption spectra were recorded with a Jasco V-670 spectrophotometer using pure solvent as a reference. PL spectra were recorded using a Fluorolog iHR 320 Horiba Jobin Yvon spectrofluorometer equipped with a PMT detector. Absolute QY was measured with a Hamamatsu absolute PL QY spectrometer C11347 Quantarus-QY using a 450 nm excitation wavelength. TEM samples were prepared by drop-casting the dilute solutions of the NCs in toluene on Formvar/carbon-coated 200 mesh copper grids. TEM images were obtained using a JEOL JEM-1400 Plus microscope operating at 120 kV. Solution ¹H NMR spectra were recorded on a Bruker 11.7 T (500 MHz) spectrometer equipped with an AVANCE III console and a PABBO probe. ¹H chemical shifts were referenced externally relative to TMS. Quantitative ¹H NMR spectra were recorded with a 5 s delay between scans to allow full relaxation of the magnetization. All concentrations were determined using mesitylene as an internal standard. ¹H NMR spectra of the reference compounds were recorded on a 7 T (300 MHz) Bruker AVANCE II spectrometer with a PABBO probe.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.chemmater.1c01081.

• Validation of the CsPbBr₃ model, estimation of the entropy gain due to the DA’s head-group desolvation, chemicals, surface passivation pattern at σ = 0.5, additional characterization of CsPbBr₃ NCs, full-scale ¹H NMR spectra and details of their peak assignment, and results of ligand-exchange experiments using ethyl acetate antisolvent (PDF)

Author Contributions

All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.