Excited States from State-Specific Orbital-Optimized Pair Coupled Cluster

Abstract

The pair coupled cluster doubles (pCCD) method (where the excitation manifold is restricted to electron pairs) has a series of interesting features. Among others, it provides ground-state energies very close to what is obtained with doubly occupied configuration interaction (DOCI), but with a polynomial cost (compared with the exponential cost of the latter). Here, we address whether this similarity holds for excited states by exploring the symmetric dissociation of the linear H₄ molecule. When ground-state Hartree–Fock (HF) orbitals are employed, pCCD and DOCI excited-state energies do not match, a feature that is assigned to the poor HF reference. In contrast, by optimizing the orbitals at the pCCD level (oo-pCCD) specifically for each excited state, the discrepancies between pCCD and DOCI decrease by 1 or 2 orders of magnitude. Therefore, the pCCD and DOCI methodologies still provide comparable energies for excited states, but only if suitable, state-specific orbitals are adopted. We also assessed whether a pCCD approach could be used to directly target doubly excited states, without having to resort to the equation-of-motion (EOM) formalism. In our Δoo-pCCD model, excitation energies are extracted from the energy difference between separate oo-pCCD calculations for the ground state and the targeted excited state. For a set comprising the doubly excited states of CH⁺, BH, nitroxyl, nitrosomethane, and formaldehyde, we found that Δoo-pCCD provides quite accurate excitation energies, with root-mean-square deviations (with respect to full configuration interaction results) lower than those of CC3 and comparable to those of EOM-CCSDT, two methods with a much higher computational cost.

1. Coupled Cluster for Ground States

The coupled cluster (CC) family of methods¹⁻⁵ is one of the most successful wave function approaches for the description of chemical systems.⁶⁻¹¹ In particular, low-order truncated CC methods, such as CC with singles, doubles, and perturbative triples CCSD(T),^8,12 properly describe weak correlation, while inclusion of higher-order excitations is required for strongly correlated systems.

In CC theory, the exponential excitation operator

1

with

2

(where N is the number of electrons) acts on a (normalized) single Slater determinant |Φ⟩ (such as Hartree–Fock (HF)) to convert it into the exact wave function

3

The nth excitation operator T̂_n is defined, in the second-quantized form, as

4

where c_i and c_a^† are the usual annihilation and creation operators which annihilate an electron in the occupied spinorbital i and create an electron in the vacant spinorbital a, respectively. From here on, i, j, ... are occupied spinorbitals; a, b, ... denote virtual (unoccupied) spinorbitals; and p, q, r, and s indicate arbitrary (orthonormal) spinorbitals.

The Schrödinger equation then reads

5

which can be rewritten as

6

by defining the effective (non-Hermitian) similarity-transformed Hamiltonian

7

Although H̅ is non-Hermitian, the similarity transformation (7) ensures that H̅ has an energy spectrum that is identical to the original Hermitian operator Ĥ. Besides, the exponential structure of the wave operator ensures rigorous size extensivity and is responsible for the comparative high accuracy of the theory at a relatively low computational cost. The cluster amplitudes t_ij...^ab... defined in eq 4 are the quantities to determine.

Truncating T^ to double excitations, that is, T̂ = T̂₁ + T̂₂, with

8a

8b

defines CC with singles and doubles (CCSD), and one gets the single and double amplitudes, t_i^a and t_ij, via the amplitude equations

9a

9b

The (nonvariational) CCSD energy is evaluated by projection

10

in contrast to its variational analogue

11

(where the Rayleigh–Ritz variational principle has been used to determine the energy and the amplitudes) which is a true upper bound to the (exact) full configuration interaction (FCI) energy E_FCI.^13,14 Unfortunately, VCC is computationally intractable. Indeed, even for truncated CC methods such as CCSD, VCC has factorial complexity since the power series expansion of the VCC energy (11) does not naturally truncate, that is, does not terminate before the N-electron limit.

2. CC for Excited States

Excited states can be attained via the equation-of-motion (EOM) formalism¹⁵⁻¹⁹ which consists in diagonalizing the H̅ matrix in the space of excited determinants. If restricted to singly and doubly excited configurations, one obtains the EOM-CCSD method. Loosely speaking, EOM-CCSD can be seen as a configuration interaction (CI) with singles and doubles (CISD) using H̅ instead of Ĥ. However, because H̅ is not Hermitian, its matrix representation is therefore nonsymmetric, unlike the corresponding CI Hamiltonian matrix. EOM-CCSD accurately describes single excitations^20,21 but struggles to model excited states with strong double-excitation character due to the lack of triples and higher excitations.^22,23 This issue can be cured by adding higher excitations but at a significant computational cost.²⁴⁻²⁹

In this paper, inspired by several groups,³⁰⁻³² we will focus on an alternative to EOM-CC and target excited states within the “ground-state” CC formalism described in Section 1 by searching for higher-energy solutions of the conventional CC amplitude equations (see eqs 9a and 9b). Indeed, as illustrated below, the amplitude equations form a set of polynomial equations in the cluster amplitudes, and they are, by definition, highly nonlinear. Therefore, the standard ground-state CC solution resulting from the usual self-consistent iterative procedure is not the only solution to this set of equations. Unfortunately, these higher roots of the CC equations (that we label nonstandard in the following) are hardly attainable in practice, and one must be very cautious when targeting these solutions.

There exist three main factors that, we believe, significantly influence the solution that is reached. First, the set of orbitals used to build the reference Slater determinant |Φ⟩ is rather important. Ground-state HF orbitals are usually employed, but alternative choices are possible, and excited-state HF orbitals [obtained via the maximum overlap method (MOM)³³⁻³⁶ or more fancy algorithms³⁷⁻³⁹ to avoid variational collapse] are getting more and more common.^32,37,40,41 Second, the starting amplitudes that are usually derived from perturbation theory (CCSD guess amplitudes are usually taken as MP2 amplitudes) may influence the outcome of the iterative process. Third, the type of iterative algorithms (usually based on the Newton–Raphson method and supplemented by Pulay’s DIIS method⁴²⁻⁴⁴) must also be carefully chosen so as to target, for example, saddle points instead of minima. Throughout the text, we refer to Newton–Raphson when the full Jacobian (for zeros) or Hessian (for extrema) matrix is employed and to quasi-Newton when they are provided only approximately.

The seminal works of Živković, and Monkhorst were the first to shed some light on the existence conditions of the higher roots of the CC equations.^45,46 Adamowicz and Bartlett studied the attainability of some excited states of the LiH molecule using the dominant determinants of CI expansions as a reference state for a CCSD calculation.⁴⁷ Later, Jankowski et al. investigated the coupled cluster double (CCD) solutions of ¹A₁ symmetry in the H₄ molecule,⁴⁸⁻⁵⁰ evidencing that some nonstandard CC solutions are unphysical. Moreover, they showed that the number of attainable solutions depends on the choice of the reference determinants.⁵⁰

A crucial step in the study of nonstandard CC solutions was the introduction of the homotopy method by Kowalski and Jankowski,^51,52 which allows to find all the solutions of a set of polynomial equations.⁵³ The gist of this method is to create an analytic continuation between a set of equations for which the solutions are known at λ = 0 and the set of equations to be solved at λ = 1. The key difficulty of the homotopy method is to be able to follow distinctly the solutions from λ = 0 to λ = 1. In practice, this “path tracking” is very difficult and computationally expensive. In a subsequent series of papers, Jankowski and Kowalski explored in more detail the structure of the CC solutions using the same homotopy method⁵⁴⁻⁵⁷ (see also refs (58)–⁶⁰). In the meantime, Piecuch and Kowalski published an extensive review along the same lines,³⁰ and we refer the interested reader to this instructive review for additional information.

A few years later, the homotopy method was used to study the Pariser–Parr–Pople model of benzene and [10]-annulene.^61,62 More recently, Mayhall and Raghavachari pointed out that the problem of the CC solution structure still needs to be addressed for real systems, and they investigated the appearance of multiple CCSD solutions for the NiH molecule.³¹ Finally, Lee et al. targeted doubly excited states and double core hole states of small molecules using orbital-optimized non-Aufbau determinants.³²

3. Pair CCD for Ground States

Our primary goal here is to investigate precisely the type and nature of excited states that one can reach (and their actual number) in the simple case of pair CCD (pCCD), which provides a reasonable description of strong correlation for a wide variety of systems.⁶³⁻⁷² pCCD, which was first named the antisymmetric product of 1-reference orbital geminals,⁷³⁻⁸⁰ restricts CCD to the seniority zero subspace, the subspace of all closed-shell determinants.⁸¹ In the present context of closed-shell systems, the seniority number is defined as the number of unpaired electrons in a determinant.⁸² While expanding the wave function in terms of the excitation rank has been proved to be slowly convergent for strongly correlated systems, the seniority zero subspace appears to be efficient at describing such systems.⁸¹ Because the pCCD energy is not invariant with respect to orbital rotations, the orbitals must be optimized to enhance the amount of correlation energy recovered.^65,74,81

pCCD has quite interesting features because it provides, at a mean-field computational cost (disregarding the cost of the two-electron integral transformation), very similar ground-state energies as doubly occupied CI (DOCI), a method with formal exponential scaling.^81,83−88 This surprising observation has been shown to hold for both canonical HF orbitals and energetically optimized orbitals (like pCCD, DOCI is not invariant to the orbitals with respect to which seniority is defined). However, the equivalence between pCCD and DOCI is not strict mathematically speaking,^63,67,89 and significant differences have been revealed for pairing Hamiltonians in particular.⁶⁴ Here, we propose to investigate whether or not this energetic similarity between pCCD and DOCI pertains for excited states in the case of molecular systems.

The pCCD equations can be easily obtained from the usual CCD equations by restricting the excitation manifold to electron pairs, that is,

12

where we have defined, for convenience, the pair operators P_q^† = c_q↑c_q↓^†. For the sake of conciseness, we denote the pair amplitudes t_ii as t_i^a from here on as we will not consider single excitations. By considering the similarly-transformed Hamiltonian H̅ defined in eq 7, we obtain

13a

13b

which yields the following explicit equations:⁶³

14a

14b

where f_p^q are elements of the Fock operator and v_pq = ⟨pq|rs⟩ are two-electron integrals in the spatial orbital basis written following Dirac’s notation.

Equation 14b provides OV quadratic equations in the OV unknown amplitudes t_i^a (where O and V are the numbers of occupied and virtual spatial orbitals, respectively). An upper bound for the number of solutions of a system of polynomial equations is provided by Bézout’s number, which is equal to 2^OV in the present case.^{30,52,55,90,91} In contrast, the number of DOCI solutions is strictly equal to the binomial coefficient .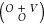

Starting with amplitudes borrowed from second-order “pair” Møller–Plesset

15

the usual approach to solve these equations employs a quasi-Newton algorithm (where the differences of the Fock diagonal elements are taken as an approximate Jacobian matrix) which consists in updating the pCCD amplitudes as

16

where the pCCD residuals r_i^a are given by eq 14b and are only equal to zero at convergence. These equations can be solved in cubic computational cost if one defines an intermediate array to bypass the only quartic step (see the last term in eq 14b).^63,76−78

Unlike CCD, the pCCD energy depends on orbital rotations within the occupied and virtual spaces (besides the occupied–virtual rotations). By variationally optimizing all orbitals, we have what may be called orbital optimized pCCD (oo-pCCD).

For the sake of consistency, we briefly review how to perform orbital optimization^92,93 for a pCCD ansatz.⁶³ To do so, the energy has to be expressed as a functional to be minimized, that is,

17

where the de-excitation operator

18

is introduced. Then, imposing the functional to be stationary with respect to the z-amplitudes, that is, ∂Ẽ/∂z_aⁱ = 0, immediately returns the equations for the t-amplitudes (eq 14b) and thereby for the pCCD energy (eq 14a). Doing the same for the t-amplitudes, that is, ∂Ẽ/∂t_i = 0, gives a new set of (linear) equations to be solved for the z-amplitudes (see ref (63) for its explicit expression).

As commonly done, the orbital rotations are introduced by an exponential unitary operator, e^κ̂, which acts on the right- and left-hand wave functions.⁹⁴ The operator

19

encompasses all unique orbital rotations, and its antihermiticity guarantees the unitarity of e^κ̂ and hence the orthogonality of the rotated orbitals. Next, the energy is expressed as a functional of the orbital rotation operator κ̂, that is,

20

Using matrix representations, stationary points with respect to κ_pq can be found with the Newton–Raphson method, which consist in expanding the energy to the second order around κ = 0

21

where g is the orbital gradient and H is the orbital Hessian, with both evaluated at κ = 0, that is,

22

The approximated energy functional is minimized with the orbital rotation κ = −H^–1·g, which then defines a new second-order approximation. This procedure is repeated until the orbitals become stationary, that is, ||g||_∞ < τ, where τ is a user-defined threshold which has been set to 10^–5 a.u. in the present study.

All the additional equations required to energetically optimize the orbitals can be found in ref (63), particularly the one- and two-body density matrices required to compute the orbital gradient and Hessian matrices.

4. pCCD for Excited States

Excited states can be accessed with a pCCD reference via the EOM formalism as investigated by Boguslawski.^69,71,72 By including single and paired double excitations in the EOM excitation operator, one arrives at the EOM-pCCD + S model.^69,71 Approximately accounting for the nonpair excitations provides a more sophisticated approach, the EOM-pCCD-LCCSD method.⁷² More precisely, the reference is described with a hybrid pCCD and linearized CC approach for the nonpair excitations, while all single and double excitations are included in the EOM excitation operator. Both methods have been used for computing excitation energies of singly and doubly excited states,^{69,71,72,95,96} and very good performance was attained in these applications. However, excitation energies tend to be somewhat overestimated with respect to reference (FCI) values. This takes place because the reference wave functions are built from orbitals optimized for the ground state (for either the HF or pCCD wave function), thus biasing the calculations toward this state.

One of our main goals here is to explore an alternative route for describing doubly excited states, while still making use of the pCCD ansatz. The idea is to perform independent, state-specific oo-pCCD calculations for the ground state and for a specifically targeted doubly excited state. This defines the Δoo-pCCD method, where excitation energies are evaluated from the energy difference between these two separate oo-pCCD calculations. In this way, we hope that our Δoo-pCCD method can provide a more balanced description of correlation effects for both states and thus more accurate excitation energies when compared with more computationally demanding CC alternatives, such as CC3 and EOM-CCSDT.

5. Computational Details

A selected version of DOCI was implemented in quantum package via a straightforward modification of the CI using a perturbative selection made iteratively (CIPSI) algorithm⁹⁷⁻⁹⁹ where only the seniority zero determinants of the FCI space are considered^100−102 (note that the calculation of the second-order perturbative correction is also restricted to the seniority zero subspace¹⁰⁰). A similar modification has been employed by Shepherd et al.⁶⁷ to perform DOCI calculations within FCIQMC.¹⁰³ In our DOCI implementation, the roots are located with the standard Davidson diagonalization method.¹⁰⁴ The pCCD method and the corresponding orbital optimization algorithm were also implemented in quantum package following ref (63). The FCI calculations presented here are also performed with the CIPSI algorithm implemented in quantum package.^97−99,102 Solving the CC equations and optimizing the orbitals for excited states are central to our discussion and are thus discussed in separate sections below. Details regarding the particular applications are also given in their respective sections. Complementary CC3, EOM-CCSDT, and EOM-CCSDTQ calculations were also performed with the CFOUR package.¹⁰⁵

6. Results and Discussion

6.1. Targeting Excited States

When aiming at excited states, important aspects regarding the algorithms for solving the pCCD equations and the orbital optimization should be addressed first. We illustrate these points with pCCD calculations for the helium atom in the small 6-31G basis set made of two basis functions, where the working equations can be solved analytically for the single amplitude t ≡ t_h^l between the highest occupied molecular orbital (HOMO) (h) and the lowest unoccupied molecular orbital (LUMO) (l) orbitals.

The first aspect concerns the updating step of the algorithm (see eq 16), which must be modified to properly target excited states. Once the two canonical HF orbitals are obtained, the pCCD amplitude t is obtained by finding the roots of a single second-order polynomial equation

23

which is shown in Figure 1 (top panel). The first root is located at a small t and corresponds to the ground state (where the HOMO orbital is doubly occupied), whereas the second root appears at a larger t value and corresponds to the doubly excited state (where the LUMO is doubly occupied). As readily seen, eq 16 implicitly assumes that the derivative of the residual with respect to t (the denominator) can be approximated by the orbital energy differences (2f_l^l – 2f_h in our case study). However, this quantity is independent of the amplitudes (and usually positive for a ground-state reference). This assumption clearly breaks down far from the ground-state solution. At a given iteration, t will keep decreasing/increasing when the residual is positive/negative. Therefore, one either converges to the ground state (when the guess amplitude is smaller than the second root) or diverges (when the guess amplitude is larger than the second root).

Figure 1.

Ground and doubly excited states for the helium atom (6-31G basis set), identified as the roots of the pCCD residual polynomial (top panel) or as the stationary points of the integrated residual polynomial (bottom panel).

The picture might become more familiar when the root-finding problem is framed as an optimization problem, also depicted in Figure 1 (bottom panel) for our case study. In this framework, we look for the stationary points, but the equivalent of eq 16 only works properly when looking for minima. The equivalent assumption is that the second derivative is constant and positive, even though it is actually negative close to the maximum. Locating this additional stationary point thus requires information about the actual curvature.

Back to the original root-finding problem, this implies employing the first derivative of the residual as the denominator in eq 16. Doing so is precisely the Newton–Raphson method. For the single-amplitude case, the correct residual derivative is

24

while in eq 16, only the orbital energy differences (2f_l^l – 2f_h) are considered. When the terms involving the two-electron integrals are accounted for, both roots depicted in Figure 1 can be located, each one with a well-defined basin of attraction.

Therefore, the usual updating algorithm can only find the roots where all the residual first derivatives are positive. While this holds in general for the lowest-lying solution, it does not for higher-lying roots. In the latter case, one should provide the Jacobian matrix or at least some descent approximation of it. Here, we have employed the Newton–Raphson method by evaluating and inverting the full Jacobian matrix J of the system of residual equations (see Eq. 14b), that is, J_ia,jb = ∂r_i^a/∂t_j, which in pCCD is given as

25

Then, at each Newton–Raphson step, the pCCD amplitudes are updated as

26

Compared with the usual quasi-Newton approach (see eq 16), the main overhead concerns storing and inverting the Jacobian matrix. On the other hand, its computation comes with a minor cost (and the same scaling) as all the needed contractions are already performed for the residuals. Alternatively, we may approximate the Jacobian matrix by its diagonal, which requires much less memory. Making use of the full or diagonal Jacobian matrix proved to be quite reliable when targeting excited states besides requiring much fewer iterations to converge.

6.2. Orbital Optimization

The orbital optimization procedure represents the second key aspect to address when targeting excited states. Still considering the helium atom in the 6-31G basis set, we present in Figure 2 how the pCCD amplitudes and energies behave as one varies the reference orbitals, which are solely determined by the parameter κ that rotates the HOMO and LUMO HF orbitals (the case depicted in Figure 1 corresponds to κ = 0, where the HOMO HF orbital is doubly occupied). Crossings between the two pCCD solutions are observed around 44 and 134° for both t-amplitudes and energies. In between these points, the reference wave function resembles more the excited state, while the ground state is reached with large t-amplitudes. The bottom panels of Figure 2 highlight the stationary points for the pCCD energy, where the reference orbitals are said to be optimized. In particular, oo-pCCD and FCI deliver the same energies, as should be for a two-electron system.⁶³ For the ground state, this takes place with very slight orbital mixing (κ = 0.11°), while optimized orbitals for the doubly excited state are found at κ = 87.6°, close to double occupation of the LUMO HF orbital (κ = 90°). In contrast, a more significant mixing of the HF orbitals provides a very poor reference (for either state), and pCCD cannot recover from this.

Figure 2.

Amplitudes (top), pCCD total energies E_pCCD (middle), and the difference to the first [E_FCI(1)] and second [E_FCI(2)] FCI energies (bottom) for the lower (red) and higher (blue) pCCD solutions of the helium atom computed with the 6-31G basis set along the single orbital rotation parameter κ between HOMO and LUMO HF orbitals (κ = 0 represents the ground-state HF reference).

For helium, obtaining oo-pCCD solutions is relatively straightforward. However, as the number of orbital rotation parameters increases, one needs a reliable and hopefully black-box optimization protocol. Optimizing orbitals for excited states has proved to be considerably more challenging than for the ground state. While at least one minimum exists for the latter, the former typically appear as saddle points. Additionally, a multitude of local minima and saddle points can be expected, and a correspondence between each stationary point and each physical state does not necessarily exist. One might encounter more than one stationary point that actually represents the same physical state. Alternatively, some of them could be artifacts of the underlying (approximate) level of theory. Furthermore, if the optimization is aimed at a given excited state, there is no way to tell beforehand the order of the corresponding saddle point, not even if it exists. Also, even when we do land in such a point, there is no guarantee that it is the only one describing the targeted state. Finally, one might converge to the ground state when another state was intended, and this collapse to the wrong solution should be avoided when implementing a robust algorithm.

Our previous discussion about how to optimize t-amplitudes for excited states (see Section 6.1) applies in the same way for orbital optimization. When higher-lying pCCD solutions are targeted, some information about the orbital rotation Hessian has to be provided (even if approximate). Here, we have computed the full orbital Hessian and gradients⁶³ during the entire optimization process. We also tried computing only the diagonal Hessian, but convergence deteriorated significantly. Evaluating and storing the full Hessian is affordable for the cases we have considered here, and we have proceeded as such. We further explored the DIIS algorithm,⁴² but this was often unstable for excited states or favored the collapse to the ground state. We stress, however, that the orbital optimization protocol that we have devised here (for either ground or excited states) is computationally feasible only for small molecules. In view of the need to compute and store the full Hessian, our approach would become impractical for larger systems, where more approximate and efficient algorithms should be employed instead. Tailored algorithms have recently allowed orbital optimization within pCCD for ground-state calculations of a model vitamin B12 compound,¹⁰⁶ and adapted versions of such algorithms might be required for oo-pCCD calculations targeting excited states in large systems.

The orbitals were optimized with a modified Newton–Raphson method. At each iteration, the full Hessian is diagonalized and before solving the corresponding linear system, the eigenvalues are modified as follows: the positive ones are increased by a constant positive factor, which effectively damps the next step along the corresponding eigenvector direction. Doing the same for the negative eigenvalues could turn one positive, thereby changing the Hessian structure and guiding the optimization toward a stationary point with an unintended saddle order. Therefore, we have added a constant negative factor to the negative eigenvalues, which damps the step while preserving the Hessian structure. When there are more negative eigenvalues than intended, we step along the gradients corresponding to the largest negative ones. By carefully choosing the damping factors, we were able to converge to a desired stationary point for the states we have targeted here.

At this point, we summarize the complete algorithm employed in our oo-pCCD calculations. Each calculation starts with ground-state HF orbitals, and when doubly excited states are concerned, the corresponding non-Aufbau occupancy is employed. The pCCD equations are solved for the t-amplitudes (eq 14b) with the Newton–Raphson algorithm. With these converged amplitudes, the de-excitation z-amplitudes are obtained with a single Newton–Raphson step (since they appear linearly⁶³). Both sets of amplitudes as well as the one- and two-electron integrals are needed to compute one- and two-body density matrices. These, in turn, are used to compute orbital gradient and Hessian, which provide the orbital rotation parameters according to our modified Newton–Raphson algorithm. This defines a new reference wave function, and the process repeats iteratively until convergence.

6.3. Hydrogen Chains

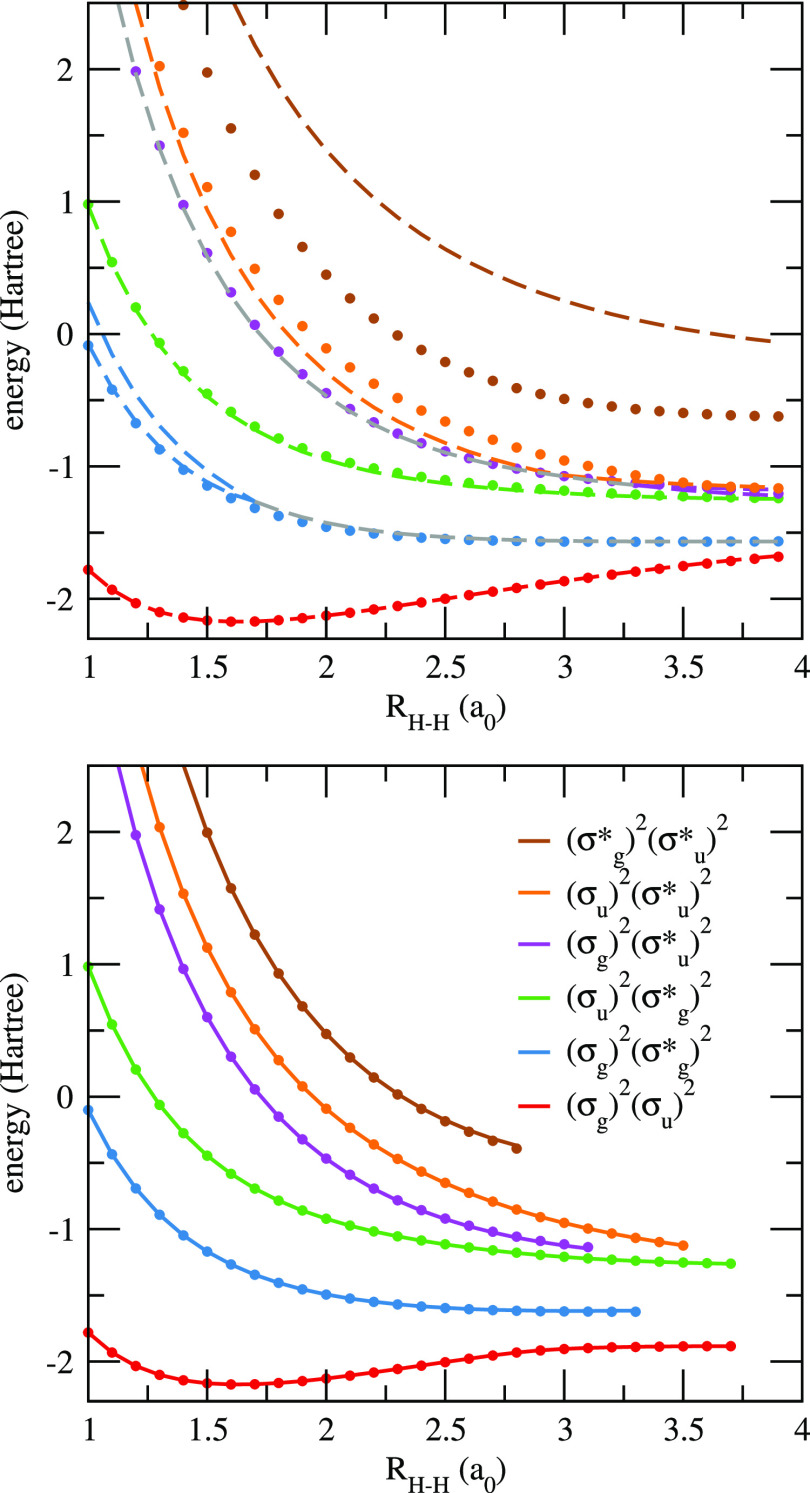
As a first example, we consider the linear H₄ molecule in a minimal basis (STO-6G), and we compute the ground- and excited-state energies of this system at the pCCD and DOCI levels as a function of the distance between the (equally spaced) hydrogen atoms R_H–H. This corresponds to a system with four electrons in four spatial orbitals with the respective symmetries σ_g, σ_u, σ_g^*, and σ_u (in ascending energies).

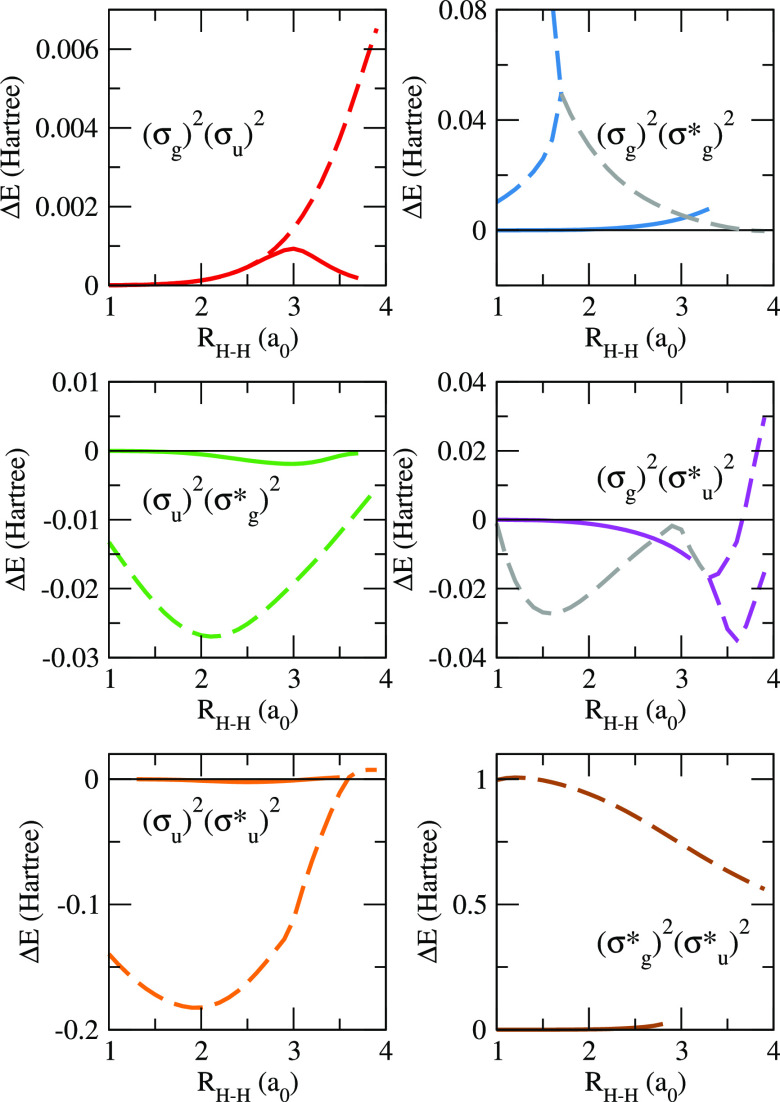
We have considered two scenarios. In the first (top panel of Figure 3), canonical HF orbitals were employed throughout, and both pCCD and DOCI potential energy curves represent different solutions of their corresponding equations. In the second scenario (bottom panel of Figure 3), oo-pCCD calculations were performed for each targeted state, and the same set of optimized orbitals was used to find the matching DOCI root. In order to help our discussion, the differences between pCCD and DOCI energies (with and without orbital optimization) are also shown in Figure 4.

Figure 3.

Ground- and excited-state energies of the linear H₄ molecule in the STO-6G basis obtained with various methods as functions of the distance between the (equally spaced) hydrogen atoms R_H–H. On the top panel, pCCD (dashed lines) and DOCI (markers) energies, both computed with ground-state HF orbitals (gray dashed lines denote the real part of the complex solutions), are shown. On the bottom panel, oo-pCCD (solid lines) and DOCI (markers) energies, both computed with state-specific optimized orbitals, are shown. Raw data are provided in the Supporting Information.

Figure 4.

Differences between oo-pCCD and DOCI energies, both computed with ground-state HF (dashed lines) and state-specific optimized orbitals (solid lines), for the linear H₄ molecule in the STO-6G basis as functions of the distance between the (equally spaced) hydrogen atoms R_H–H. Gray dashed lines correspond to the regions where the pCCD solutions become complex (the real part is used to compute the difference).

The obtained pCCD optimized orbitals are shown in the Supporting Information. Even though they were allowed to break spatial symmetry, only symmetry-preserving orbitals were found for the excited states. This does not constitute a limitation for our purpose of comparing the two methods, yet we might still be missing possible symmetry-broken oo-pCCD solutions.^107,108 In particular, the ground-state orbital Hessian has one negative eigenvalue between 1.4a₀ and 2.7a₀, which indicates the existence of a lower-lying solution with symmetry-broken orbitals.^109−112 Similarly, the number of negative Hessian eigenvalues changes from 3 to 2 when stretching beyond 2.3–2.4a₀ for the second excited state and from 6 to 5 above 1.9–2.0a₀ for the fifth excited state. In contrast, the index is constant for the first, third, and fourth excited states (2, 3, and 3, respectively). While symmetry-broken solutions describing these doubly excited states might still exist, they were not found, suggesting that the potential number of multiple solutions for this small basis set might not be too large.

For the same set of orbitals, pCCD and DOCI ground-state energies are very close, as expected. We notice, however, that orbital optimization improves the comparison at more stretched geometries (see the top left panel of Figure 4). Our results regarding the excited states are much more interesting, revealing several important features about the comparison between pCCD and DOCI. In the first scenario (ground-state HF reference), the striking similarity between pCCD and DOCI energies does not hold for excited states. While the potential energy curves still share a common behavior, significant energy differences are observed by as much as 1 hartree for the quadruply excited state, (σ_g^*)²(σ_u)². Furthermore, the first [(σ_g)²(σ_g^*)²] and the third [(σ_g)²(σ_u)²] doubly excited states can be described by two distinct pCCD solutions each. For the lower-lying one, there are two real solutions close in energy below 1.7a₀, where they merge into a complex conjugate pair. The branching point for the higher-lying state is found at 3.3a₀, but here, the complex solutions are found at shorter distances.

When orbitals are variationally optimized for each state at the pCCD level (see the bottom panel of Figure 3), the scenario is completely different. Now, oo-pCCD and DOCI levels of theory provide quite similar energies for all doubly (and quadruply) excited states, with visually indistinguishable potential energy curves (note that the DOCI calculations are also performed with the pCCD optimized orbitals in this case, such that the two methods are being compared for the same set of orbitals. Another line of comparison would consider separate orbital optimizations for pCCD and DOCI. However, doing so for the latter would be much more computationally demanding, and we did not explore this scenario here). For all states, oo-pCCD represents a massive improvement with respect to pCCD with HF orbitals. The average deviations to the corresponding DOCI results drop by 1 or 2 orders of magnitude, while the maximum deviation amounts to 0.02 hartree, compared with 1 hartree in the case of HF orbitals (see Figure 4). Not only this, but orbital optimization eliminates the double (and complex) solutions previously discussed for the first doubly excited state. While such solutions could arguably be assigned as unphysical, we see that their troubling behavior is as an artifact of the HF reference. Once this constraint is removed and the orbitals are allowed to relax, only single-valued real solutions appear. In general, we thus expect that oo-pCCD can locate physical states where nonoptimized pCCD fails or gives more dubious results.

Our findings can be explained as follows: the deficiencies of the first set of pCCD calculations can be traced back to the ground-state HF orbitals, which represents a poor reference when excited states are concerned. Of course, the argument applies for both pCCD and DOCI, but it is more serious for the former as it lacks higher-order connected excitations (most importantly the connected quadruple excitations). In particular, these missing excitations account for the largely overestimated pCCD energies associated with the quadruply excited state. By optimizing the orbitals at the pCCD level, the reference now provides a qualitatively correct description of each targeted state. In this sense, more electronic correlation is recovered with the paired double excitations for the optimized reference, in comparison with a ground-state HF reference. Therefore, higher-order excitations lose importance in oo-pCCD, and the computed energies are very close to the DOCI results.

We also found that DOCI is much less sensitive to the orbital choice than pCCD. The latter energies change by 0.17 hartree in average, compared with the 0.02 hartree difference observed in the former. Again, this can be understood from the lack of higher-order connected excitations in pCCD, which in turn would be partially accounted for by orbital optimization. On the other hand, all paired excitations are present in DOCI and hence less dependence on the reference.

We notice, however, that oo-pCCD also faced convergence problems when stretching the H–H bonds beyond a certain point. Either the pCCD equations failed to converge for the targeted excited state or the orbital optimization leads to a solution representing another state. This took place for all states, typically at shorter distances as we moved higher in energy. It could be that a stationary point would only be found if the orbitals had been allowed to become complex, but we did not explore this possibility here. Instead, this could be a genuine limitation of projected pCCD in describing physical states at geometries with stronger static correlation. Finally, symmetry-broken orbitals could perhaps be required at larger bond lengths, but no such solutions were found for the excited states.

6.4. Larger Molecules

The goal of this section is to showcase that Δoo-pCCD can provide reliable excitation energies for more realistic molecules. An exhaustive comparison including a larger set of systems and employing different basis sets is beyond the scope of this work. Here, we have considered five molecules with well-known doubly excited states, namely, CH⁺, BH, nitroxyl (HNO), nitrosomethane (H₃C–NO), and formaldehyde (H₂C=O). Following previous studies, we employed a bond length of 2.137 13a₀ for CH^{+25,72,113,114} and of 2.3289a₀ for BH.¹¹⁵ For the remaining molecules, the geometries reported in ref (22) were also adopted here. The frozen-core approximation and the 6-31+G(d) basis set (with spherical Gaussian functions) were employed throughout. For the particular case of CH⁺, we have also considered the basis set presented in ref (113) and employed in subsequent studies.^25,72,114

The set of pCCD optimized orbitals for both ground and doubly excited states can be found in the Supporting Information. These orbitals have been allowed to fully relax and break the molecular point group symmetry, which took place for the doubly excited states of nitroxyl, nitrosomethane, and formaldehyde as well as for the ground state of the latter two. Doing so can further lower the energy at the expense of losing the spatial symmetry of the wave function. We have tried different orbital guesses and damping factors for the orbital optimization, and no other stationary symmetry-broken orbitals were found, suggesting that the potential problem of multiple solutions would be less serious for the cases studied here. An inspection of the orbitals confirms that we describe the 3¹Σ⁺ and 2¹Σ⁺ doubly excited states of BH and CH⁺, respectively, in line with previous results.^{25,72,113−115} Due to the symmetry-broken nature of the orbitals in larger molecules, a precise assignment of the excitation becomes less straightforward but possible nonetheless. By analyzing the differences in the orbital densities of ground and excited states, we can infer the (n)² → (π*)² excitations of formaldehyde, nitroxyl, and nitrosomethane, also in consistency with the existing assignments.²²

Table 1 summarizes the excitation energies for the first excited states with a dominant double-excitation character. While a detailed analysis comprising several levels of theory can be found elsewhere,²² here, the comparison is focused on our pCCD calculations and EOM-CC-based methodologies, having the (extrapolated) FCI as the reference result.²² For CH⁺, BH, and nitroxyl, we managed to find higher-lying solutions of the pCCD amplitude equations, when considering ground-state HF orbitals as reference orbitals. These solutions were assigned to the targeted doubly excited states and are labeled in Table 1 as HF-pCCD. This was achieved by using a very large guess amplitude (typically in the range of ∼10² to 10³) for the intended excitation. At convergence, many other amplitudes attain absolute values larger than 1, yet the one representing the dominant excitation remains the largest. Higher-lying solutions were also found for nitrosomethane and formaldehyde but at significantly higher energies, and it is not clear if they provide a descent representation of the targeted excited state. Overall, the performance of HF-pCCD is quite erratic, with surprisingly decent results for CH⁺ and nitroxyl but qualitatively wrong ones for BH, nitrosomethane, and formaldehyde. This probably reflects the inadequacy of using ground-state HF orbitals as a reference for describing such states.

Table 1. Vertical Excitation Energies ΔE (and Their Corresponding Deviation ΔΔE with Respect to the FCI Reference Energies) Computed with Various Methods for the First Doubly Excited States of Five Molecules^a.

molecule	method	ΔE (eV)	ΔΔE (eV)
CH+b	HF-pCCD	7.74	–0.81
	Δoo-pCCD	8.36	–0.19
	FCIc	8.55	0
	EOM-CCSDTd	8.62	0.07
	EOM-CCSDtd	8.64	0.09
	EOM-oo-pCCD-LCCSDe	8.84	0.29
	EOM-pCCD-LCCSDe	7.61	–0.94
	CC3f	8.78	0.23
CH+	HF-pCCD	7.90	–0.61
	Δoo-pCCD	8.32	–0.19
	FCI	8.51	0
	EOM-CCSDTQ	8.52	0.01
	EOM-CCSDT	8.59	0.08
	CC3	8.75	0.24
BH	HF-pCCD	15.89	8.78
	Δoo-pCCD	7.35	0.24
	FCI	7.11	0
	EOM-CCSDTQ	7.12	0.01
	EOM-CCSDT	7.15	0.04
	CC3	7.30	0.19
HNO	HF-pCCD	5.53	1.02
	Δoo-pCCD	4.49	–0.02
	FCIg	4.51	0
	EOM-CCSDTQg	4.54	0.03
	EOM-CCSDTg	4.81	0.30
	CC3g	5.28	0.77
H3C–NO	Δoo-pCCD	4.66	–0.20
	FCIg	4.86	0
	EOM-CCSDTg	5.26	0.40
	CC3g	5.73	0.87
H2C=O	Δoo-pCCD	11.26	0.40
	FCIg	10.86	0
	EOM-CCSDTQg	10.87	0.01
	EOM-CCSDTg	11.10	0.24
	CC3g	11.49	0.63

^aThe 6-31+G(d) basis set was considered throughout, except for the first entry, where the basis set was presented elsewhere.¹¹³ Total energies are provided in the Supporting Information.

^bBasis set taken from ref (113).

^cResults from ref (113).

^dResults from ref (114).

^eResults from ref (72).

^fResults from ref (25).

^gResults from ref (22).

However, one of the key insights of the present work is that this issue can be largely eliminated by state-specific orbital optimization. The results labeled as Δoo-pCCD in Table 1 stem from the energy difference between two separate oo-pCCD calculations, one for the intended doubly excited state and the other for the ground state. Not only this method correctly locates all the targeted states but also the excitation energies also compare very favorably with FCI. For the set of molecules surveyed with the 6-31+G(d) basis set, the mean absolute error (MAE) is 0.21 eV, the root-mean-square error (RMSE) is 0.24 eV, and the mean signed error (MSE) is 0.05 eV. Δoo-pCCD is thus considerably more accurate than CC3 (an MAE and an MSE of 0.54 eV and an RMSE of 0.61 eV) and comparable to EOM-CCSDT (an MAE and an MSE of 0.21 eV and an RMSE of 0.25 eV). Importantly, the excitation energies are not systematically over- or underestimated with respect to the reference values. In contrast, they tend to be overestimated with EOM-CC methodologies not only for doubly excited states but also for singly excited states.

The above observations regarding accuracy and precision of Δoo-pCCD and EOM-CC methods can be understood based on how the reference wave functions are described and how correlation effects are included in each case. In EOM-CC, the HF Slater determinant serves as the reference for both ground and doubly excited states, thereby creating a bias toward the former. In addition, excitations are introduced exponentially in the cluster operator but linearly in the EOM excitation operator, further favoring the ground state. All in all, electronic correlation is quickly (in the sense of the excitation degree) introduced for the ground state, while the excited states are still recovering from its poor HF reference. This is most critical in the case of EOM-CCSD, which largely overestimates (by ∼1  eV or more) excitation energies of doubly excited states.¹¹⁴ Higher orders of excitation are needed in order to obtain more accurate results, yet still they tend to approach the reference values from above.

The situation for Δoo-pCCD is quite different. Each state has its own reference, with orbitals variationally optimized for a pCCD wave function. We notice that this goes beyond an MOM-based pCCD calculation, where the excited-state optimized orbitals would have mean-field quality. Another key distinction is that Δoo-pCCD provides a unified description of each state, while EOM-based formalisms rely on a formal distinction between them. Therefore, correlation effects should be accounted for at the same pace, regardless of the targeted state. This is exactly what we observe as excitation energies lie either above or below the reference values. This implies that the correlation energy of both ground and excited states is recovered in a balanced way. Furthermore, paired double excitations already account for important electronic correlation of the doubly excited states, given that their orbitals have been optimized. This explains the comparable performances of Δoo-pCCD and EOM-CCSDT. In the latter, lower-order excitations would account for orbital relaxation, while actual correlation would only be introduced with the higher-order terms.

Recent studies with state-specific, orbital-optimized density functional theory have also pointed out encouraging results.^37,40,41 RMSEs lie in the range of 0.15–0.65 eV, depending on the choice of the functional. Bearing in mind the limited set of molecules we explore here, the accuracy of Δoo-pCCD would be comparable to that of the best-performing functional (B97M-V).^37,40

While having a dominant doubly excited character, the states that we have surveyed also present some single-excitation contribution, however not surpassing 5% based on CC3 calculations.²² As long as this percentage is small, the lack of single excitations is not expected to greatly affect the performance of the Δoo-pCCD method. Furthermore, part of this contribution would not correspond to a truly singly excited character but rather to orbital relaxation in the excited state, which in turn is accounted for in Δoo-pCCD. It remains to be seen how the method performs for doubly excited states that have a more considerable singly excited character, as in butadiene and benzene.^22,35,36

7. Conclusions

We have explored excited-state solutions of the pCCD method, a version of CCD where the cluster operator is restricted to paired double excitations. For the helium atom in the 6-31G basis set, we have discussed key aspects regarding the solutions of pCCD and orbital optimization. In particular, we have shown that the Jacobian matrix of the CC residual equations has to be provided (even if approximately) when aiming for excited states. Similarly, the orbital rotation Hessian is needed when performing orbital optimization for excited states.

Our first goal was to establish a connection between pCCD and DOCI for excited states. For this, we have investigated the symmetric dissociation of the linear H₄ molecule with the STO-6G basis set as a function of the distance between the hydrogen atoms. When the reference is described with ground-state HF orbitals, excited-state solutions of pCCD and DOCI no longer match, in contrast to the ground-state case. Such deviations arise because pCCD struggles more than DOCI in recovering electronic correlation due to the missing higher-order connected excitations in the former. However, these higher-order excitations only become important because of the unsuitable starting point provided by the ground-state HF wave function. By variationally optimizing the orbitals (at the pCCD level) for a targeted doubly excited state, the reference is significantly improved, and higher-order excitations become much less relevant. Therefore, when state-specific optimized orbitals were employed, pCCD and DOCI methodologies delivered much closer excited-state energies.

The second goal was to probe the performance of state-specific orbital-optimized pCCD (or Δoo-pCCD) in describing excited states with strong double-excitation character. We have surveyed a set of five molecules with well-characterized doubly excited states. With ground-state HF orbitals, higher roots of pCCD either provide inaccurate excitation energies or fail to locate the targeted state at reasonable energies. Once again, the problem lies on the reference function, rather than on pCCD itself. Orbital optimization brings a dramatic improvement as excitation energies become in much better agreement to the reference (FCI) values, with a performance superior to CC3 and similar to EOM-CCSDT.

Thus, Δoo-pCCD might be considered as an alternative and accurate option for targeting doubly excited states. Although studies on a larger set of molecules and with other basis sets would be recommended, the current initial results on Δoo-pCCD are quite promising. Of course, additional challenges might appear when one considers more chemically challenging situations (larger systems, strong correlation, etc.). Furthermore, it remains to be seen how the method would perform when one employs state-specific HF orbitals instead of the more expensive optimized orbitals at the pCCD level, as has been done here. We hope to report further on these aspects in the near future.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.1c00348.

• State-specific optimized orbitals (PDF)

• Data used to generate the potential energy curves in Figure 3 (TXT)

• Total energies for the entries in Table 1 (TXT)

The authors declare no competing financial interest.