Q-Force: Quantum Mechanically Augmented Molecular Force Fields

Abstract

The quality of molecular dynamics simulations strongly depends on the accuracy of the underlying force fields (FFs) that determine all intra- and intermolecular interactions of the system. Commonly, transferable FF parameters are determined based on a representative set of small molecules. However, such an approach sacrifices accuracy in favor of generality. In this work, an open-source and automated toolkit named Q-Force is presented, which augments these transferable FFs with molecule-specific bonded parameters and atomic charges that are derived from quantum mechanical (QM) calculations. The molecular fragmentation procedure allows treatment of large molecules (>200 atoms) with a low computational cost. The generated Q-Force FFs can be used at the same computational cost as transferable FFs, but with improved accuracy: We demonstrate this for the vibrational properties on a set of small molecules and for the potential energy surface on a complex molecule (186 atoms) with photovoltaic applications. Overall, the accuracy, user-friendliness, and minimal computational overhead of the Q-Force protocol make it widely applicable for atomistic molecular dynamics simulations.

Introduction

Computational chemistry often suffers from a dilemma between reaching high accuracy and high applicability, i.e., simulating large systems for a long time. Quantum mechanical (QM) methods that can treat the intricate quantum nature of electrons (and nuclei) are computationally very demanding, even more so when their time evolution is of interest. Therefore, for many materials science and biophysics applications that require simulating thousands/millions of atoms for nano/microseconds, classical molecular mechanics (MM) following Newton’s law of motion is used instead, at the cost of computational accuracy. Such MM models make use of a set of parameters, known as force fields (FFs), that are based on the topological features of the molecule (e.g., bonds and angles) to approximate its potential energy surface (PES).¹ In this work, an automated toolkit to match the MM PES of the molecule to the QM one is discussed, which allows MM models to approach the accuracy of QM, without additional computational cost after the initial reparametrization.

The traditional approach to making FFs, as it is done by the commonly used GROMOS,²⁻⁵ OPLS,^6,7 CHARMM,⁸⁻¹¹ and AMBER^12,13 FFs, relies on atom types and their assumed transferability: Parameters for a set of small molecules are fitted rigorously to both experimental (e.g., mass densities, enthalpies of vaporization, and free energies of hydration) and QM (e.g., dipole moments, electrostatic potentials, and torsional barriers) data to generate a set of tabulated parameters for each atom type based on their chemical environment (e.g., alkyl carbon, ether carbon, and ester carbon). In this manner, a significant portion of the chemical space can be covered by only tens to hundreds of atom types. This approach is favorable since it allows nonexpert users to generate FFs for their molecules of study with ease and without FF developers needing to attempt the impossible task of parametrizing the whole chemical space in advance. However, the use of atom types clearly sacrifices accuracy in favor of generalization. The popularity of these transferable FFs is not only a testament to the validity of the transferability assumption to some extent, but also to the importance of having a simple procedure to determine FF parameters for any new molecule. The latter allowed them to be available to a much wider scientific community. Automated tools that assign atom types to given molecular structures and provide an FF based on these atom types, such as ATB¹⁴ for GROMOS, CGenFF^15,16 for CHARMM, and LigParGen¹⁷ for OPLS, have been crucial for the widespread use of these transferable FFs.

An alternative approach to the atom-type-based FF parametrization is to derive molecule-specific FF parameters for the molecule under study. This could be done using both experimental and QM data; however, the former is often not available for novel molecules. The idea of parametrizing FFs based on QM is definitely not new and reach back almost 50 years.¹⁸⁻²¹ Thereafter, efforts have been made to parametrize both the intramolecular²²⁻²⁴ and the intermolecular^25,26 FF terms from QM calculations. While such molecule-specific and QM-based FFs have the advantage that for each molecule the best possible FF for a given MM functional form can be created, a disadvantage is that several QM calculations and fitting of every FF parameter must be done for that molecule. This can be a daunting and error-prone task without having automated tools at the disposal. Such tools, however, started to appear in the last decades,²⁷⁻⁴⁵ although their use has not yet come close to rivaling transferable FFs.

An important choice when it comes to designing a tool for molecule-specific automated FFs is the MM functional form. A complex functional form (e.g., QMDFF,⁴⁰ xTB-FF,⁴¹ SFAM,⁴² QuickFF,^34,35 and MEDFF³⁶) yields a highly accurate FF, but it is orders of magnitude more expensive than transferable FFs, which limits their applicability drastically. Moreover, the use of these complex MM functional forms hinders their compatibility to highly optimized and parallelized molecular dynamics (MD) software such as GROMACS,⁴⁶ Tinker-HP,⁴⁷ and AMBER,⁴⁸ which limits their applicability even further. Alternatively, a similar functional form to transferable FFs can be used (e.g., JOYCE/PICKY,²⁷⁻³² QUBEKit,^38,39 PHF,⁴³ ParaMol⁴⁵), which allows MD simulations that are at a comparable computational cost but ideally at a higher accuracy than their transferable FF counterparts.

Aside from the need for an automated toolkit, the main bottleneck for the derivation of molecule-specific FFs is formed by the cost of the QM calculations, in particular of geometry optimizations, Hessian calculations, and relaxed dihedral scans that are needed for the parametrization. As the size of the molecule grows, performing QM calculations on the whole molecule becomes increasingly difficult. This is especially true for dihedral scans since the number of dihedrals to be scanned often grows significantly with the size of the molecule. Therefore, a fragmentation scheme that divides the molecule into chemically meaningful smaller fragments becomes essential when dealing with large molecules (e.g., larger than 50–100 atoms). While such fragmentation schemes have been implemented in some automated toolkits that employ complex functional forms,⁴⁰⁻⁴² approaches that use standard functional forms have been lacking such schemes. Consequently, most of the applications in the field with such approaches have been limited to systems with less than 100 atoms.

Commonly, molecule-specific FF approaches introduce new nonbonded interaction terms or have reparametrized the coefficients of the standard Lennard-Jones (LJ) and/or Coulomb terms. However, for these altered nonbonded interactions, thermodynamic properties (which strongly depend on these interactions), if at all validated, are often done so for pristine systems and not for mixtures. Therefore, it is still an open question how well the thermodynamic properties are preserved when nonbonded interactions are derived in a molecule-specific manner. In contrast, a considerable amount of effort has been put into ensuring that the cross-molecular interactions yield accurate thermodynamic properties in transferable FFs.^1,4,49

The aim of this paper is to introduce Q-Force, a toolkit to augment existing transferable FFs with molecule-specific FF parameters that are derived from QM calculations. The augmentation is done by retaining the nonbonded parameters of these transferable FFs and consequently also their rigorously tested thermodynamic properties. In other words, Q-Force can produce a QM-matched FF for a given molecule that can be combined with other molecules in the user’s choice of FF family (e.g., OPLS, GROMOS, AMBER, CHARMM). Such an approach has the advantage that novel or nonstandard molecules can easily be augmented with Q-Force, while complex molecules which have already been parametrized rigorously (e.g., DNA, RNA, proteins) do not have to be reparametrized. This compatibility allows the easy application of Q-Force to various fields, such as computer-aided drug design, ligand-binding with biomolecules, and searching for novel organic semiconductors. Several applications of Q-Force for the latter case have recently been published.⁵⁰⁻⁵³ The main characteristics of the Q-Force procedure are outlined below:

• Applicability has been an important consideration for Q-Force: it is open source, easily installable, and fully automated, which allows seamless combination with high-throughput methods.

• It can be combined with any existing transferable (or QM-based) FF through the augmentation approach.

• The automated molecular fragmentation scheme allows the treatment of molecules significantly larger than those commonly treated by similar QM-based approaches (>200 atoms). The fragment database also prevents repeated QM calculations when the same fragment is identified in different molecules.

• Significant improvements to the accuracy of the FF with respect to transferable FFs and competitive performance with respect to other QM-based approaches are demonstrated and discussed in the Results and Discussion section.

• The validation of the FF is done on-the-fly: The fitting quality with respect to the QM reference is provided during the run. Therefore, the user always knows how well the fitting procedure has been performed and whether any further action is necessary.

• It can be applied to any organic molecule and FFs can be created for their ground states, ionic states, and/or excited states.

Two major cases where we foresee the use of Q-Force will show significant improvement over the existing transferable FFs are: (1) Complex/nonstandard molecules that are not covered in the initial parametrization (training set) of the transferable FFs. While most simple functional groups are covered in the training set and perform quite well with the transferable FFs, especially (complex) conjugated ring systems and their combinations with different functional groups often require case-by-case treatment and can benefit significantly by their FFs being augmented by QM data. Several examples of such cases are treated in this paper and significant improvements can be seen for the PES for molecule-specific FFs. (2) A frequently used multiscale approach in computational chemistry is to take snapshots from MD trajectories and perform high-level QM calculations on these snapshots. In these cases, using an FF that has the same minimum energy geometry and a closely matched PES to the QM method that will later be used to perform the QM calculations on the snapshots is highly beneficial to avoid spurious results that are caused by the mismatch in geometries.^54,55 This effect has also been shown in a study using Q-Force FFs.⁵¹

The structure of the remainder of the paper is as follows: In the Methods section, after an initial description of the functional form of the Q-Force FF, the steps of the Q-Force procedure (as depicted by the flowchart in Figure 1) will be explained, technical and computational details will be shown, and known limitations of the model will be discussed. In the Results and Discussion section, the performance of the Q-Force FF for several small molecules will be benchmarked to a QM reference as a proof-of-concept and further compared to existing transferable and QM-based FFs. The thermodynamic properties of these FFs are also demonstrated. Then, the importance of QM augmentation of the FF will be demonstrated for nonstandard dihedral profiles, where the performance of transferable FFs is shown to quickly deteriorate. Finally, materials science applications of Q-Force will further evidence the impact of augmenting FFs with accurate QM references on obtaining accurate PESs. The Q-Force toolkit, several examples, and tutorials on its usage are freely available on GitHub (https://github.com/selimsami/qforce).

Figure 1.

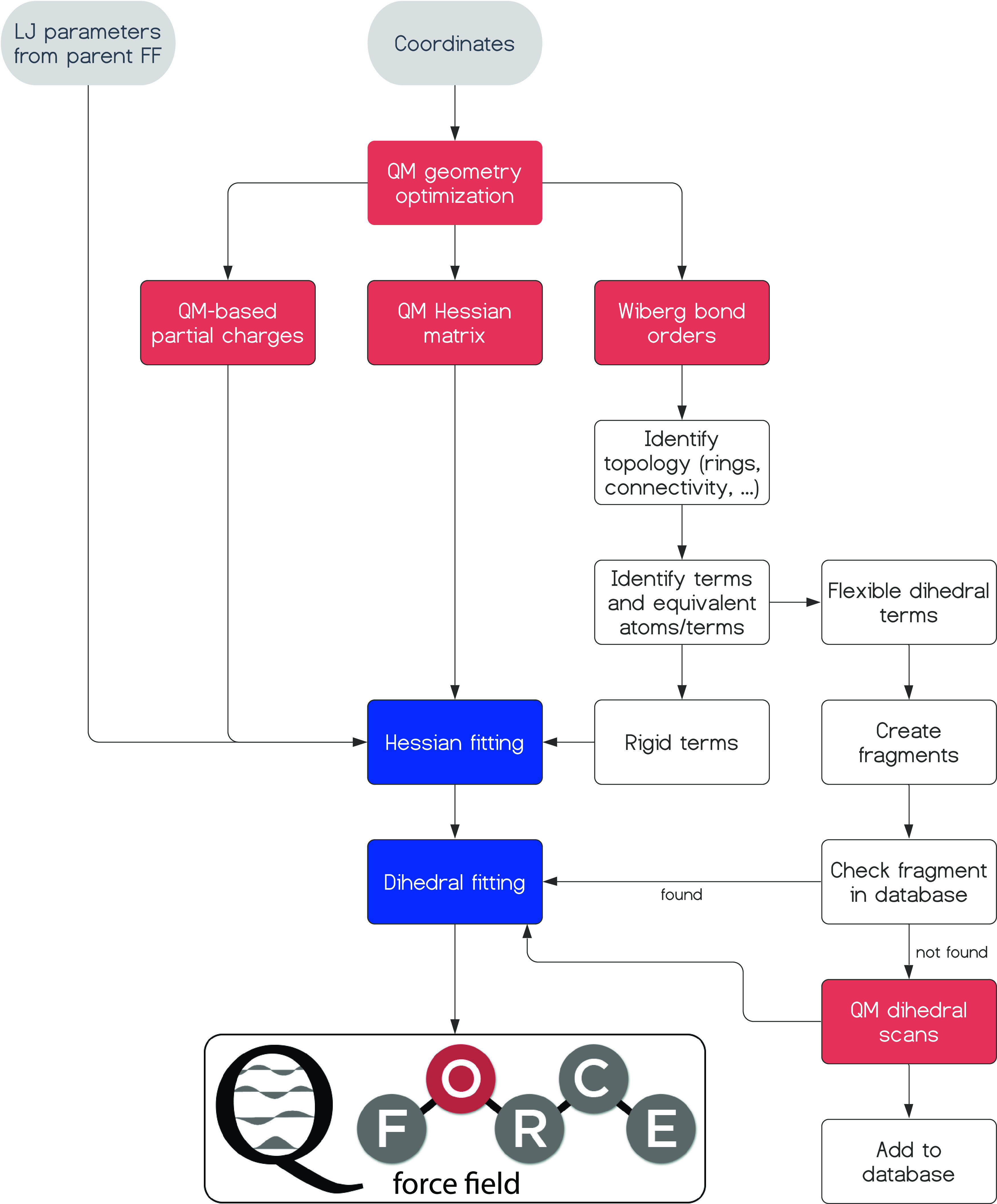
Q-Force flowchart. Gray boxes refer to the input, red ones to the performed QM calculations, and blue ones to the fitting steps. Further description of this flowchart can be found in the text.

Methods

Definition of the Q-Force Force Field

FFs contain terms that describe the interactions within the molecule (intramolecular) and between different molecules (intermolecular). The intramolecular part is composed of bonded interactions between closely neighboring atoms (e.g., bonds, angles, dihedrals) and nonbonded interactions within the molecule. The intermolecular part is composed of nonbonded interactions that occur between different molecules. The total potential energy of the system (V_pot) is given by the sum of these interactions

1

In the following, we describe the functional form of these FF terms that are used in Q-Force. The bond potentials between atom pairs A and B that form a bond AB are treated with the harmonic potential

2

where k_r is the force constant and r₀ is the equilibrium bond length. The bond angle potentials for atom triplets of A, B, and C that form an angle ABC are treated by

3

where the first term is a harmonic angle potential for the ABC angle and the second term is a harmonic bond potential between the A and C atoms that is also known as the Urey–Bradley term.^56,57

For dihedrals, three different functions are employed. For rigid dihedrals, which are proper and improper dihedrals that are constrained to a single minimum (e.g., conjugated rings or double bonds), a harmonic dihedral term given by

4

is used. Inversion dihedrals, which are nonplanar dihedrals (>25°) with a double-well potential (e.g., nonconjugated rings or pyramidal inversions), are represented by

5

For flexible dihedrals, which are dihedrals that have multiple accessible minima (e.g., alkane chain), a Ryckaert–Bellemans type⁵⁸ of dihedral function given by

6

is used, where C_n are the six constants that determine the shape and height of each dihedral profile.

In the case of triplets of colinear atoms (e.g., acetonitrile), identified by an angle larger than 170°, the Urey–Bradley term from eq 3 is skipped to avoid generating linear dependencies. Additionally, the ill-defined dihedral terms containing these atoms are also not generated.

A Coulomb potential given by

7

is used to account for the electrostatic interactions between particle pairs A and B that are more than two bonds apart. By default, the CM5 method⁵⁹ based on Hirschfeld partitioning⁶⁰⁻⁶² is used to determine the atomic charges. These charges are scaled by 1.2 in the case of neutral molecules to account for the condensed-phase polarization.⁶³ CM5 charges have been shown to give consistent⁵⁹ and accurate^63,64 atomic charges for MD applications, as also demonstrated in this work. However, users have the option to use a charge method that better matches their parent FF to increase the compatibility (e.g., RESP charges with Hartree–Fock 6-31G* for GAFF).

A 6–12 LJ potential given by

8

is used to account for the repulsion and dispersion interactions between the particles. As previously described, these terms are inherited from the parent FF. For nonbonded interactions between atom pairs that are three bonds apart (commonly named as 1–4 interactions), the treatment of the parent FF is followed, which can be either scaled-down interactions (e.g., OPLS, AMBER) or special pair interactions (e.g., GROMOS).

Identifying the Topology and FF Terms

The distance matrix of the QM optimized geometry is used to create a graphical representation⁶⁵ of the molecule where atoms are registered as nodes and bonds correspond to the edges between the nodes of the graph. Such a graphical representation allows the determination of all of the bonds, angles, dihedrals, and rings in the molecule with ease and is further useful in the fragmentation procedure that is discussed later. Wiberg bond orders⁶⁶ are used to determine conjugated, double, and triple bonds of the molecule. This information, along with the previously determined topology of the molecule, is then used for determining the FF terms and their categorization into rigid (bonds, angles, rigid dihedrals, inversion dihedrals) and flexible (flexible dihedrals) terms.

While the determination of bonds, angles, and dihedrals in a molecule is quite straightforward, automatic categorization of dihedrals into rigid, inversion, and flexible dihedrals requires further discussion. A rigid dihedral is recognized in the following cases: (1) the bond order between the central atoms of the dihedral is 1.75 or higher, (2) the dihedral is in a ring and it is planar (the deviation from planarity is smaller than 25°), (3) a special type of rigid dihedral is necessary (improper dihedral) when previously mentioned types of rigid dihedrals are not present near an atom that needs to be kept planar (e.g., for a ketone, an improper dihedral will be necessary, while for a phenol it will not be necessary since the oxygen is kept planar by the rigid dihedrals originating in the phenyl ring). In the first two cases, a rigid dihedral term will be added to all combinations of atoms containing the same central atoms and in the last case, a single improper dihedral will be added. For the last two cases, if the deviation from planarity is larger than 25°, then an inversion dihedral with a double-well potential is added. The remainder of the dihedral terms will be recognized as flexible dihedrals. These dihedrals are expected to have multiple accessible energetical minima. These are located in linear chains where a 360° rotation is technically possible. For these dihedrals, a full 360° QM and MM scan is performed for the fitting.

Equivalence of Atoms and FF Terms

Transferable FFs rely on atom types, which categorize atoms based on their chemical environment (e.g., alkyl carbon, ether carbon, ester carbon), to cover a large portion of the chemical space with a relatively small training set. Such an approach provides generality at the cost of accuracy: Atoms with somewhat different environments are mapped to the same atom type even though, for example, not all ether carbons are equivalent.

For molecule-specific FFs, since the best set of parameters is derived for each atom, approximating atoms to predetermined atom types is unnecessary. However, it is beneficial to determine the equivalent atoms and FF terms within the molecule for several reasons: (1) it avoids spurious small differences between chemically equivalent atoms and FF terms; (2) for most molecules, considering the equivalence of FF terms greatly reduces the number of fitting parameters for the Hessian matrix which is beneficial for both the stability of the fitting procedure and for avoiding overfitting; and (3) it prevents duplicate QM dihedral scan calculations for chemically equivalent fragments.

The default approach in Q-Force is to generate an identifier for each atom based on their first four neighbors (this number can be changed or the equivalent atom identification can be turned off by the user). The identifier contains the path to each atom that is up to four bonds apart. The elements of the atoms and the bond types (i.e., single, conjugated, double) of the bonds that are within the path are written to that identifier. The equivalent FF terms are then identified based on the equivalent atoms with special considerations that are not discussed here (e.g., bond terms between two atom pairs, with both pairs having identifiers A and B, are not necessarily equivalent).

Hessian Fitting

After the determination of the rigid FF terms, force constants (k) corresponding to these terms (as shown in eqs 2–4) are determined by a linear least-squares fitting where the squared difference between the QM and MM Hessians given by

9

is minimized with the constraint that force constants have positive values. Here, H_ij refers to the Cartesian Hessian matrix elements. While the force constants (k) of the rigid FF terms are being fitted, the nonbonded (NB) interactions are also accounted for in the MM Hessian matrix but not fitted. Accounting of the nonbonded interactions during the Hessian fitting is essential, especially for molecules with strong intramolecular interactions, as otherwise these nonbonded interactions can affect the parametrization of the bonded terms and the final parameters can be dependent on the minimum at which the Hessian calculation is performed.

A Hessian fitting approach like this has originally been used by Dasgupta et al.²³ and more recently in the QMDFF procedure and has been shown to give accurate harmonic vibrational frequencies. In our implementation, forces are computed analytically and the Hessian is computed numerically with a three-point derivative with displacements of 0.003 Å in both directions. The Hessian terms that are smaller than 10^–4 kJ/mol/Ų are discarded to improve performance and because they have no effect on the results. The calculation and fitting of the MM Hessian is extremely fast, as highly optimized SciPy⁶⁷ routines are used: It takes less than a minute for molecules containing 200 atoms on an average laptop.

Fitting of Flexible Dihedrals

While the Hessian matrix contains all of the necessary information for the parametrization of the rigid FF terms at the optimized geometry, for flexible dihedrals that have multiple minima, the Hessian matrix contains insufficient information. Therefore, relaxed dihedral scans (i.e., at each scan interval, the rest of the geometry is optimized, while the scanned dihedral is frozen) must be performed both at QM and MM levels to determine the corresponding dihedral energy profiles. An MM relaxed scan requires an FF, which is available at this stage of the procedure, as seen in Figure 1 (the rigid bonded terms obtained from the Hessian fitting, partial charges obtained from the QM calculations, and the LJ parameters retained from the parent FF). Then, the difference between the two profiles, ΔV

10

can be fitted to a Ryckaert–Bellemans type of dihedral function (see eq 6) using a least-squares fitting. For the fitting, higher weights (w) are given to data points that are lower in energy using

11

where w scales the residuals during the fitting. This weighting step has minor effects on most of the dihedrals for which a near-perfect fit can be obtained. However, it becomes highly beneficial for more complicated profiles (as exemplified in the results) where a perfect fit cannot be obtained. In these cases, prioritizing the accuracy of the lower energy barriers is sensible as the dynamics are more affected by them (e.g., a 5 kJ/mol error in a 15 kJ/mol barrier is more detrimental than the same error on a 100 kJ/mol barrier—both because of the percent error difference and also because a 100 kJ/mol barrier will be much less frequently visited during a regular MD run). Equation 11, in our experience, has shown to give a good balance between prioritizing lower energies and not neglecting higher energy barriers.

A serial relaxed dihedral scan (i.e., the dihedral angle is scanned consecutively in a single direction), as opposed to single-point calculations at each scan interval, is necessary but not always sufficient to obtain accurate and reliable dihedral energy profiles. A known problem^68,69 with serial relaxed scans is that in some cases, the starting geometry of a given step, which is the optimized geometry of the previous step, can guide the optimization toward a spurious local minimum which makes the profile dependent on the scan direction and causes asymmetries in a dihedral profile that should be symmetrical. Recently, a step-wise wavefront propagation method, called TorsionDrive, in which extra relaxed optimizations are performed in reverse and forward directions, has been shown to avoid these spurious asymmetries, however, at a 3.5–7.5 times increased computational cost.⁶⁹ In Q-Force, the user can conveniently request the symmetrization of such spurious asymmetries, allowing us to reach a similar outcome without any additional computational cost. This approach is exemplified in the Results and Discussion section.

Another source of problem is the coupled dihedrals where considering a single scan could lead to the wrong QM dihedral profile as the reference. In Q-Force, this can be partly alleviated by providing multiple QM scans for a specific dihedral (for example, a reverse scan or a scan where the coupled dihedral is at a different angle), which will then automatically take the lowest energy path along the scan and discard higher-energy configurations. A more rigorous treatment of such dihedrals would be the two-dimensional (2D) dihedral scans and the corresponding CMAP potentials,^1,70,71 and this is currently a work in progress.

Fragmentation and the Fragment Database

As the size of the molecule grows, not only the cost of individual calculations grows, but often so does the number of relaxed dihedral scans that needs to be performed. For example, assuming a 200-atom molecule with 25 flexible dihedrals and 15° scan intervals, one would need to do 600 geometry optimizations on a 200-atom molecule. Clearly, this quickly becomes unfeasible. As these relaxed QM dihedral scans were identified as the computational bottleneck of the procedure, a fragmentation scheme was implemented to construct chemically meaningful fragments for each dihedral that needs to be scanned. This resulted in a drastic lowering of the computational cost and made Q-Force applicable to very large (>200 atoms) molecules. Aside from the computational cost, our experience shows that performing dihedral scans on smaller fragments also makes the spurious asymmetries discussed in the previous subsection less likely to happen.

The automated fragment generation works in the following way: When a flexible dihedral is identified, the first three neighbors of the central atoms of that dihedral are by default taken as part of the fragment. Then, the next atoms are removed and the fragment is capped with a hydrogen atom unless: (1) the bond with the next neighbor has a bond order larger than 1.75; (2) the bond with the next neighbor is part of a ring; (3) the current atom has an electronegativity in Pauling scale larger than 3.0 (to prevent unwanted intramolecular hydrogen bonds, e.g., an O–C bond is not replaced by a O–H). If one of these cases holds true, the next atom is included into the fragment and the same check is done for the neighbors of the new atom. The process is repeated in all paths until either breakable bonds are identified or the end of the paths is reached. Two illustrations to the automated fragment generation are given in Figure 2.

Figure 2.

Two examples of the automatic fragmentation procedure. It is shown that fragments are not terminated in the middle of a ring (left) or when a highly electronegative atom has to be capped with a hydrogen (right).

As identical molecular fragments can exist in multiple molecules, we have also implemented a database (currently only stored locally) where previously scanned fragments (together with the employed computational method) are stored. And if these fragments are ever identified on a new molecule again, the scan results are retrieved from the database, preventing additional calculations. The identification of the fragments is done using the previously discussed graphical representation of the molecule and its fragments. Two fragments are considered identical if they have the same connectivities between the same elements, and with matching bond orders and lone pair electrons. Bond orders are obtained from a Wiberg bond order analysis⁶⁶ and the lone pair electrons are determined from a natural bond orbitals (NBO) analysis.⁷²

Validation on-the-Fly

An important but sometimes lacking ability when using automated and (semi-)black-box procedures is to be aware of when the procedure performs well and when it performs suboptimally. In Q-Force, the validation of the FF is done on-the-fly: In the case of the Hessian fitting, QM and MM vibrational frequencies are plotted and the mean percent error of the MM vibrational frequencies is given. Moreover, MM vibrational modes are also written to a file in a format that can be visualized by VMD⁷³ and be compared to their QM counterparts. In the case of dihedral fitting, for each flexible dihedral, QM and MM dihedral profiles are plotted together and the R² value of the fitting is given as an indication of how well the fitting went. A warning is given if the R² is lower than 0.9 and any fitted data point has an error larger than 2 kJ/mol, prompting the user to check if the results have the desired accuracy. These on-the-fly validations allow users to be always aware of the accuracy of the generated FF to decide whether further action is necessary.

Limitations

Some known, and likely not exhaustive, limitations of the Q-Force procedure are discussed below:

• The choice of the functional form of the Q-Force FF enables treatment of large systems, however, at the same time it limits its accuracy compared to more complex functional form FFs (QMDFF, xTB-FF, etc.). Bond breaking, bond forming, and bond order changes cannot occur with the current functional form. Organometallic complexes and metal clusters are outside the scope of this work. Similarly, electrostatics are currently only treated by point charges and charges cannot polarize each other during the simulation. A polarizable version of the Q-Force FF is currently in progress.

• It is well known that some neighboring flexible dihedral profiles are mutually dependent. In such cases, two-dimensional dihedral profiles can be assigned to neighboring dihedrals, often referred to as CMAP correction.^1,70,71 Identification and special treatment of these co-dependent dihedrals, and CMAP potentials are currently not implemented in Q-Force. However, their implementation is currently in progress.

• The fragmentation scheme has only been implemented for the treatment of flexible dihedrals and not for the calculation of the Hessian matrix. Consequently, treatment of extremely large molecules (>∼500 atoms) might be limited by the computational cost of the geometry optimization and Hessian calculation of the whole molecule (unless a cheaper method, such as DFTB, is used for the parametrization). The problem with fragmentation before a geometry optimization is that it relies on accurate input geometries, and in many cases, it can result in wrong bond orders and consequently wrong bonds being cut during the creation of the fragments.

Technical Details

The default choice for the QM reference is density functional theory with the Perdew–Burke–Ernzerhof (PBE) functional,⁷⁴ 6-31+G* basis set,⁷⁵ and D3-BJ⁷⁶ empirical dispersion correction. The PBE functional is chosen because its Hessian matrix does not need empirical scaling as with some other functionals to match experimental frequencies.⁴⁰ However, the user has the choice to use other functionals and basis sets and scale their Hessian accordingly as the scaling is implemented. For example, for excited states, different functionals may be more preferable.^77,78 Currently, the compatible QM software packages are Gaussian (09 and 16)^79,80 and Q-Chem.⁸¹ Other QM packages can easily be added due to the modular structure of the code. The FF is generated in GROMACS format, which is also readily compatible with OpenMM⁸² and can easily be converted to AMBER or CHARMM formats using the ParmEd software.⁸³

Results and Discussion

Vibrational Analysis of Small Molecules

We first look at how Q-Force performs for small molecules with respect to two very commonly used automated topology builders for transferable FFs, namely, ATB for GROMOS FFs and LigParGen for OPLS FFs. The computation of the vibrational frequencies, modes and IR spectra, and the method used for matching QM and MM vibrational frequencies and modes to each other are described in the Supporting Information. Figure 3a shows results comparing the vibrational frequencies of these two transferable FFs and Q-Force to the QM reference for a molecule set comprising 16 small organic molecules (see the figure caption for the list of the molecules). Q-Force outperforms both transferable FFs for every tested molecule with a mean absolute deviation (MAD) in vibrational frequencies of 3.6% (30.5 cm^–1) compared to OPLS/LigParGen with 7.3% (78.0 cm^–1) and GROMOS/ATB with 12.6% (129.4 cm^–1). This is not particularly surprising as Q-Force was parametrized against the QM reference while the transferable FFs were not. However, it is also important to keep in mind that these transferable FFs have been parameterized for this kind of small molecules—the accuracy of these methods is expected to further decrease for more complex molecules that were not covered in the initial parametrization, as also observed in this work.

Figure 3.

(a) QM vs MM vibrational frequencies for 16 small molecules, with a total of 494 vibrational frequencies for the GROMOS/ATB, OPLS/LigParGen, Q-Force (GROMOS-based) FFs. The red line corresponds to perfect agreement between QM and MM. MADs in vibrational frequencies are 12.9% (134.2 cm^–1) for GROMOS/ATB, 8.4% (89.5 cm^–1) for OPLS/LigParGen, and 4.2% (37.3 cm^–1) for Q-Force. The molecules are propane, isobutane, acetic acid, trans-2-butene, ethanol, acetonitrile, dimethyl ether, methane thiol, pyrazine, thiophene, ethene, benzene, toluene, naphthalene, fluorobenzene, and 1,2-dichloroethane. (b) Normalized occurrence of the overlap between the QM and MM normal modes. A value of 1 corresponds to perfect overlap. The average overlaps between QM and FFs are 0.83, 0.89, and 0.92 for GROMOS, OPLS, and Q-Force, respectively. (c) Experimental (red)⁸⁴ and Q-Force (green) gas-phase IR spectra for a selection of molecules. The maximum intensity is normalized to one.

A closer look at Figure 3a also helps to identify systematic errors in transferable FFs. For example, for the GROMOS/ATB FF, frequencies in the range of 400–700 cm^–1 have been consistently underestimated. Many of these data points correspond to aromatic ring out-of-plane bending modes, resulting in GROMOS aromatic rings being much less planar than they are supposed to be. This behavior has been previously noticed and sometimes these parameters are empirically scaled up to make them “stiffer”.⁵¹ The use of QM-derived FFs such as Q-Force can also help to identify and correct such systematic errors in existing transferable FFs by means of optimizing the parameters of existing atom types and identifying when extra atom types are necessary.

Along with the vibrational frequencies, the vibrational normal modes corresponding to these frequencies are also important to be in agreement with QM. Figure 3b shows the overlap between QM and MM vibrational modes. While all FFs perform quite well for these small molecules, Q-Force is shown to have the highest mean overlap (0.92). Figure 3c shows gas-phase IR spectra corresponding to a selection of molecules for Q-Force (green) and experiments (red). The results show that the Q-Force-based FF is able to qualitatively reproduce the experimental spectra.

While performed on a different set of small molecules, QMDFF and SFAM, which have much more complicated and computational demanding functional forms of the FF, reported MADs of 44⁴⁰ and 66.5 cm^–1,⁴² respectively. QUBEKit³⁹ and PHF,⁴³ on the other hand, with a similar functional form to Q-Force, reported a MAD of 6.3% and 73 cm^–1, respectively. This shows that the Q-Force FF (with a MAD of 4.2% or 37.3 cm^–1) gives, if not better, comparable vibrational frequencies to the existing molecule-specific FFs, even to those with more complex functional forms. A more direct comparison can also be made between the vibrational analysis of thiophene with the Q-Force FF in Figure S1 with another QM-derived FF based on the PICKY protocol present in Figure 3 of ref (32). While both FFs perform very well for this molecule, slightly higher overlaps are observed for the Q-Force FF and the match between the QM and MM vibrational frequencies is higher for Q-Force, particularly at lower frequencies. The better match at lower frequencies hints at the better treatment of the in-ring distortions; however, a more extensive comparison is needed to draw definitive conclusions.

Dihedral Profiles of Small Molecules

After demonstrating the accuracy of the Q-Force vibrational frequencies, the next step toward obtaining accurate MM PESs is having accurate dihedral profiles for the flexible dihedrals. In fact, the performance of the flexible dihedral functions around the global minimum is also evident in the vibrational frequencies shown in Figure 3. The frequencies below ∼300 cm^–1 often correspond to these kinds of low-energy displacements of the flexible dihedrals and they are also shown to be in good agreement with the QM reference. However, since the Hessian contains no information about other possible minima, the complete dihedral profile must be investigated to obtain accurate PESs.

To this end, QM and Q-Force dihedral profiles are compared in Figure 4a for all of the flexible dihedrals of the same 16 small molecules from Figure 3. For all dihedrals, a very good agreement (MAD of 0.21 kJ/mol and a maximum deviation of 1.25 kJ/mol) is obtained between the QM and MD profiles using the automated procedures in Q-Force. This shows that the Q-Force procedure is also able to accurately reproduce the QM dihedral profiles. Moreover, due to the database of dihedral profiles in Q-Force, if these molecules/fragments are identified in another molecule in the future, they would be identified automatically and no new calculations would be necessary.

Figure 4.

(a) QM (dots) vs Q-Force (lines) dihedral profiles obtained through relaxed scans for all of the flexible dihedrals of the molecules in Figure 3, with a total of 11 dihedrals. MAD is 0.21 kJ/mol, and the maximum deviation of any point in any dihedral profile is 1.25 kJ/mol. (b) Dihedral profiles obtained by the Boltzmann inversion (eq 12) of the dihedral distributions in the condensed phase with the Q-Force FF. The data points beyond a 20 kJ/mol barrier are not presented as these are not properly sampled during the simulations. Uniquely, the cyan profile drawn with crosses instead of dots corresponds to a gas-phase simulation (see text for further discussion).

To investigate the dynamics of these dihedrals, the dihedral distributions in condensed-phase simulations were converted to free energy profiles (Figure 4b) through an inverse Boltzmann analysis given by

12

where R is the gas constant, T is the temperature, n_α is the number of occurrences of the angle α, and N is the total number of data points. Comparing the scanned QM and Q-Force dihedral profiles (Figure 4a) with the ones from the MD simulations (Figure 4b), a very good match is observed between the two for all dihedrals, indicating consistency between the fitting procedure and the observed behavior during molecular dynamics. The only noticeable difference between the two is the cyan profile, which corresponds to the rotation of the OH hydrogen in ethanol, and it has a higher barrier in the condensed phase (dots) around 0°. This is a consequence of the hydrogen bonding being less available in the cis configuration (0°) and thus having a high free energy barrier and not a discrepancy due to the Q-Force procedure. This is demonstrated by the agreement of the gas-phase profile for this dihedral (cyan with crosses) with the QM profile.

Thermodynamic Properties

To investigate the effect of the Q-Force procedure on thermodynamic properties, two Q-Force FFs have been generated for each of the 16 molecules discussed earlier. The first set of FFs has inherited both LJ parameters and atomic charges from the parent FF of GROMOS/ATB, having Q-Force only re-parametrize the intramolecular interactions. In the second set, only LJ parameters have been inherited from GROMOS/ATB, while the atomic charges were computed with the CM5 method. CM5 charges were scaled by 1.2 to account for the condensed-phase polarization.⁶³ Similar calculations were also done with two reference FFs, namely, GROMOS/ATB and OPLS/LigParGen.

Table 1 shows MAD of mass density and enthalpy of vaporization with respect to experiments for the four sets of FFs. Additionally, for the two Q-Force FFs, their MAD to the parent GROMOS/ATB FF is also shown. As demonstrated, retaining both the LJ parameters and the atomic charges results in a minimal difference between Q-Force and its parent FF, strongly indicating that the compatibility to the rest of the GROMOS FF library is retained. Switching to CM5 charges, on the other hand, drastically increases this difference, especially for the enthalpy of vaporization. However, as the comparison to the experiment indicates, the increased difference between Q-Force (1.2 × CM5 charges) and GROMOS/ATB seems to be toward a better agreement with experiments, as MAD in both density and enthalpy of vaporization decreases appreciably for the Q-Force (1.2 × CM5 charges) FF.

Table 1. MAD of Density (ρ, g/cm³) and Enthalpy of Vaporization (ΔH_vap, kJ/mol) to Experiment for the Same 16 Small Molecules^a.

force field	ρ	ΔHvap
	MAD to experiment
OPLS/LigParGen	0.029	2.9
GROMOS/ATB	0.052	4.5
Q-Force (q = GROMOS)	0.046	4.7
Q-Force (q = 1.2 × CM5)	0.032	2.7
	MAD to GROMOS
Q-Force (q = GROMOS)	0.012	0.7
Q-Force (q = 1.2 × CM5)	0.031	3.8

^aFor the Q-Force FFs, which uses GROMOS/ATB atom types for the LJ interactions in this study, MAD to GROMOS/ATB is also shown. Data points corresponding to individual molecules are presented in the Supporting Information.

These results show that using the Q-Force procedure with the exactly same nonbonded interactions as the parent FF (Q-Force with GROMOS/ATB charges) will result in very similar thermodynamic properties. This reaffirms that the thermodynamic properties are mostly governed by nonbonded interactions and that FFs augmented with Q-Force can be expected to be compatible in this respect with the parent FF family. Additionally, it has been shown that using QM-based and molecule-specific atomic charges (Q-Force with 1.2 × CM5 charges) can improve the thermodynamic properties relative to the parent FF, as it has done for the set of molecules in this study.

Treatment of Problematic Dihedral Scans

As discussed in the Methods section, serial relaxed dihedral scans can sometimes result in spuriously asymmetric dihedral profiles. This is exemplified in Figure 5 for the 4- and 2-pyridiniophenolate molecules, where the QM profiles (in gray) suffer such asymmetry, especially around the transition region of 90 and 270° even though 0–90, 90–180, 180–270, 270–360° quadrants are expected to be equivalent or mirrored based on the molecular symmetry. The reason behind this asymmetry is that during the scan, the improper dihedrals between the two rings deviate from planarity into a pyramidal structure and are stuck at a local minimum due to the high pyramidal inversion energy barrier until the point where the sharp drop in energy occurs. This clearly indicates a hysteresis effect, possibly due to the neglect of multireference effects in the wavefunction. Evidently, using these asymmetric profiles for the subsequent fitting of the FF parameters would introduce errors. The Q-Force procedure allows the automatic symmetrization of the dihedral profile, taking only the lower-energy data points from the equivalent quadrants, as shown in Figure 5 (in red). A similar molecule with a similar asymmetry problem was studied with the TorsionDrive method⁶⁹ and following their procedure, they have obtained a very similar symmetrized profile. Note that there is no additional computational cost in the approach implemented in Q-Force, unlike the TorsionDrive method, which, while being a more rigorous approach, resulted, for a similar molecule, in an ∼4 times increase in the number of performed relaxed scans.

Figure 5.

QM, symmetrized QM, Q-Force, GROMOS/ATB, and OPLS/LigParGen dihedral profiles for (a) 4-pyridiniophenolate and (b) 2-pyridiniophenolate. The molecules and the scanned dihedral are indicated in the insets.

The fitting of the Q-Force dihedral profiles then makes use of the symmetrized QM profile and as a result, a profile that is symmetrical and in good agreement with the QM profile is obtained for both molecules. The effect of the weighting function from eq 11 can also be seen here: The more important lower-energy points are reproduced with high accuracy at the cost of some level of accuracy for the high-energy points. GROMOS as well as OPLS FFs, both of which clearly were not trained based on these types of molecules, fail drastically to reproduce the dihedral profiles for both molecules. This clearly illustrates the limitation of transferable FFs—that they cannot be expected to work accurately for the type of molecules that were not covered in the original fitting of the FF.

QM vs MM Potential Energy Surfaces

Having shown that the Q-Force procedure leads to both accurate Hessian and dihedral profiles, the next question is whether this accuracy will lead to a good agreement between the QM and MM PESs. To test the PES of the Q-Force FF and the fragmentation procedure on a large molecule, we have chosen the ITIC molecule (186 atoms). This molecule^85,86 and its family of molecules^87,88 have been shown to lead to record power conversion efficiencies for organic photovoltaics applications. For this molecule, 200 snapshots were taken from gas-phase MM simulations of ITIC with two transferable FFs (GROMOS/ATB and OPLS/LigParGen) and the corresponding Q-Force FFs (GROMOS-based, OPLS-based); then, QM single-point energy calculations were performed on these snapshots and the potential energies from the corresponding geometries were compared (Figure 6a). Additionally, Figure 6b shows QM optimized geometries (in red) overlaid with the optimized GROMOS (in blue), OPLS (in orange), and Q-Force (in green) geometries. By visual inspection, a good match can be observed between the Q-Force and QM structures while both transferable FFs show significant deviation, most importantly losing the planarity of the backbone. This is also evident from the root-mean-square deviation (RMSD) between the QM and MM structures, which are 1.5, 3.2, and 0.3 Å for GROMOS, OPLS, and Q-Force, respectively.

Figure 6.

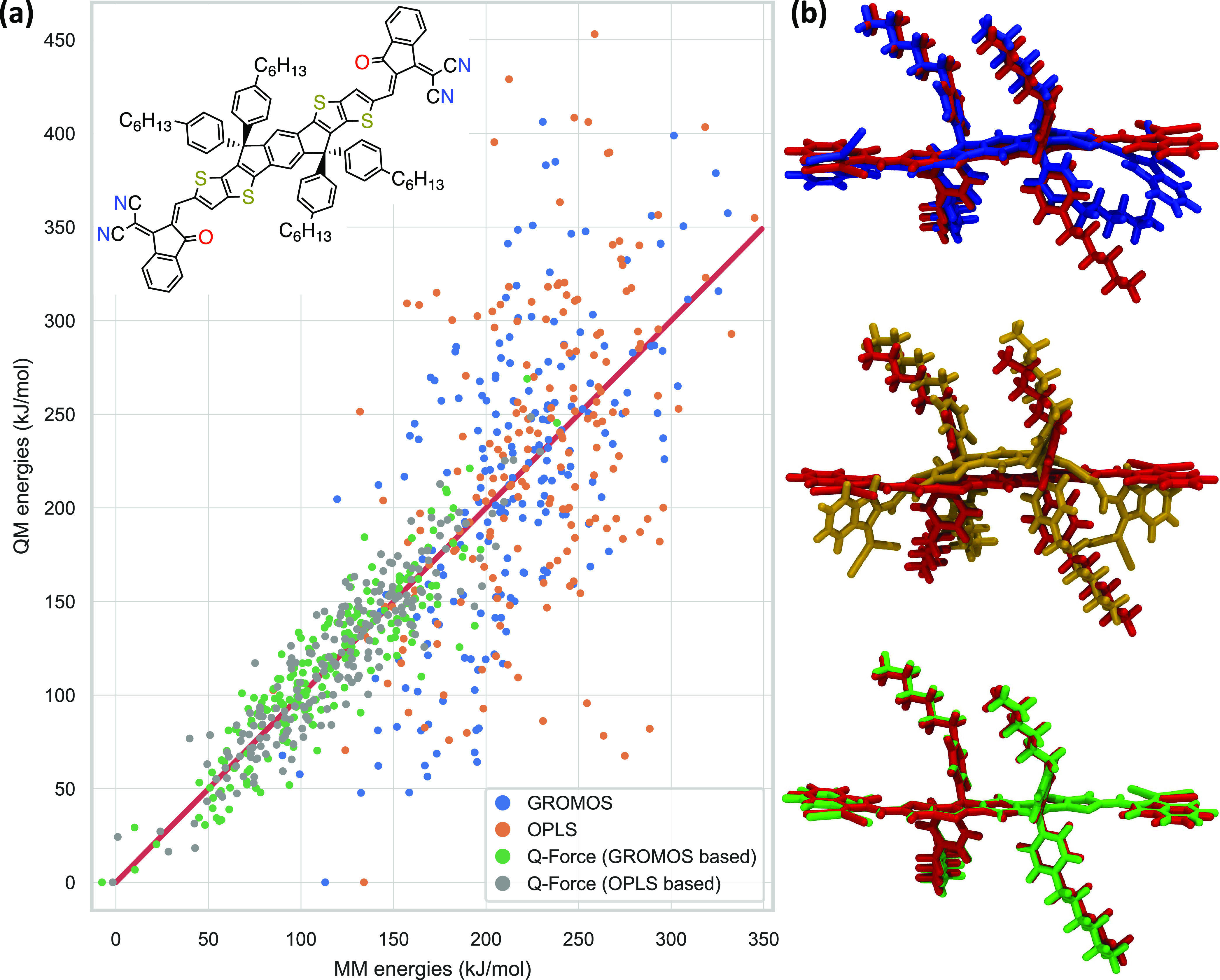
(a) QM vs MM potential energies for the 200 snapshots taken with each FF with the red line indicating a perfect match. The minimum QM energy is set to zero, and the FF energies are shifted to minimize the error with respect to the QM results. MAD between the QM and MD energies are 47.7, 53.6, 14.5, and 13.5 kJ/mol for GROMOS, OPLS, Q-Force (GROMOS-based), and Q-Force (OPLS-based) FFs, respectively. The differences (error) in standard deviation (σ) between QM and FF energies (calculated as 100 × (σ_QM – σ_FF)/σ_QM) are 82, 85, 7, and 5%, respectively. (b) QM optimized ITIC structures (in red) overlaid with the GROMOS (blue), OPLS (orange), and Q-Force (green) optimized structures. The two Q-Force-based FFs had almost indistinguishable structures; therefore, only one is presented here. The results of the Hessian fitting and dihedral profiles for the ITIC molecule are presented in the Supporting Information (Figures S2 and S4).

The results of this approach are shown in Figure 6a. MADs between the QM and MM energies are 47.7, 53.6, 14.5. and 13.5 kJ/mol for GROMOS, OPLS, Q-Force (GROMOS-based), and Q-Force (OPLS-based) FFs, respectively. These results show that Q-Force reproduces the QM PES extremely well with no significant outliers. The differences (error) in standard deviation (σ) between QM and FF energies (calculated as 100 × (σ_QM – σ_FF)/σ_QM) are 82, 85, 7, and 5%, respectively. This indicates that transferable FFs have significantly broader energy distribution, meaning that they visit high-energy configurations that would not have been visited in a QM-based simulation. This is also evident from the QM energies of the snapshots relative to the QM energy of the optimized molecule in Figure S3. While the average relative energies for Q-Force-based FFs (710 and 701 kJ/mol) are very much in line with the available thermal energy for ITIC at 298 K (673 kJ/mol), transferable FFs visit significantly higher-energy configurations (averages: 1036 and 1113 kJ/mol) that are not realistic. Overall, these results demonstrate the ability of Q-Force to sample much more accurate configurations for complex molecules during an MD simulation, compared to the transferable FFs that it has augmented, which is very promising for future applications in both materials science and biophysics.

Importantly, the improvement of the PES with Q-Force comes with no additional computational cost during the MD simulations; as the simulations with three different FFs were completed in comparable amounts of compute time. For the initial parametrization, the geometry optimization and the calculation of the QM Hessian took less than a day on 32 CPUs. Dihedral scans, due to the fragmentation scheme, took significantly less time. Overall, the whole procedure took less than 15 min of manual labor. This demonstrates that much larger systems are within the capabilities of the Q-Force procedure.

Conclusions

In this paper, we presented the Q-Force procedure that has the aim of augmenting existing transferable FFs with QM-based and molecule-specific bonded parameters and atomic charges. The automation of the procedure enables the derivation of the FF parameters in a transparent and reproducible manner and minimizes both (nonsystematic) human error and manual labor. The on-the-fly validation enables the careful evaluation of the quality of the generated FF. The fragmentation of large molecules allows the parametrization of large systems with significantly reduced computational cost, making the treatment of large molecules (>200 atoms) feasible. The procedure can be applied to any organic molecule not only in their ground state but also in their ionic and excited states; work in this direction is currently in progress in our group.

The accuracy of the Hessian fitting procedure was demonstrated with a set of small molecules where the Q-Force procedure obtained a significantly lower MAD in vibrational frequencies with respect to the QM reference compared to transferable FFs GROMOS/ATB and OPLS/LigParGen. For the same set of molecules, the fitting procedure for the flexible dihedral terms was shown to give high accuracy for all dihedrals. These improvements to the intramolecular properties came at no cost to the accuracy of thermodynamic properties, and in fact, the use of Q-Force with scaled CM5 charges has been shown to improve the thermodynamic properties for our test molecule set with respect to the parent transferable FF. For a large molecule (186 atoms), it was demonstrated that having accurate Hessian and dihedral profiles indeed leads to a significantly more accurate PES: The Q-Force-based PES has shown a significantly lower MAD compared to the transferable FFs and unlike those transferable FFs, it has not suffered from systematic underestimation of the QM energies. Such an underestimation will cause the transferable FFs to access the wrong configurations during the MD simulations, which might have significant consequences on the properties of interest.

The Q-Force toolkit, with an intuitive and easy-to-use interface, and together with relevant tutorials, is freely available on GitHub (https://github.com/selimsami/qforce). The functional form of the Q-Force FF bears no additional computational cost after the initial parametrization, making it available to any MD application that was previously treated with transferable FFs. Additionally, as the nonbonded interactions of the parent FF are preserved, compatibility can be expected with molecules already parametrized with the parent FF, such as complex biological molecules (e.g., DNA, RNA). Hence, Q-Force is easily applicable to various materials science and biophysics applications.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.1c00195.

• Supporting figures, MD simulation and analysis details, and the Q-Force documentation (PDF)

• Force fields from MD simulations (ZIP)

The authors declare no competing financial interest.