Constructing a representative in‐silico population for paediatric simulations: Application to HIV‐positive African children

Abstract

Aims

Simulations are an essential tool for investigating scenarios in pharmacokinetics‐pharmacodynamics. The models used during simulation often include the effect of highly correlated covariates such as weight, height and sex, and for children also age, which complicates the construction of an in silico population. For this reason, a suitable and representative patient population is crucial for the simulations to produce meaningful results. For simulation in paediatric patients, international growth charts from the World Health Organization (WHO) and the Centers for Disease Control and Prevention (CDC) provide a reference, but these may not always be representative for specific populations, such as malnourished children with HIV or acutely unwell children.

Methods

We present a workflow to construct a virtual paediatric patient population using WHO and CDC growth charts, suggest piecewise linear functions to adjust the median of the growth charts by sex and age, and suggest visual diagnostics to compare with the target population. We applied this workflow in a population of 1206 HIV‐positive African children, consisting of 19 742 observations with weight ranging from 3.8 to 79.7 kg, height from 55.5 to 180 cm, and an age between 0.40 and 18 years.

Results

Before adjustment, the WHO and CDC charts produced weights and heights higher compared to the observed data. After applying our methodology, we could simulate weight, height, sex and age combinations in good agreement with the observed data.

Conclusion

The methodology presented here is flexible and may be applied to other scenarios where WHO and CDC growth standards might not be appropriate. In addition we provide R scripts and a large ready‐to‐use paediatric population.

What is already known about this subject

• Pharmacometric simulations require a representative population to produce meaningful results.

• World Health Organization (WHO) and Centers for Disease Control and Prevention (CDC) growth charts can be used to construct in silico populations but might not be suitable for populations that deviate from these optimal growth charts.

What this study adds

• A flexible methodology to generate a representative in silico paediatric population can aid pharmacometricians in making better predictions in vulnerable patient populations.

1. INTRODUCTION

Modelling and simulation are increasingly important within pharmacokinetics‐pharmacodynamics to investigate alternative scenarios or support decision making in trial design or public health policy. Besides a model and a relevant outcome (eg, exposure metrics, survival), a realistic target population is required. This means that the covariate values reflect those in the intended use population and that they maintain their respective correlation (eg, weight and height).

Two widely used approaches to accomplish this are (a) nonparametric bootstrapping of historical data (ie, re‐sampling from a real population) and (b) simulating an entirely new population using parametric distributions for relevant covariate values. However, both approaches require a (relatively large) representative population as a starting point to sample from or derive the parametric multivariate distributions.¹ Generating a completely new virtual population has the advantage that the number of patients and their characteristics can be tailored to the experimental purpose. Doing this for a single covariate (eg, weight) is straightforward, but it becomes complicated when multiple correlated covariates are required. For example, predicted fat‐free mass (FFM) is calculated based on sex, weight and height,² so the values of all these individual covariates need be plausible and coherent with one another to generate credible in silico subjects. In children, it is often necessary to include age to describe maturation of clearance, as well as for predicting FFM.³, ⁴

The World Health Organization (WHO)⁵ and Centers for Disease Control and Prevention (CDC) growth charts⁶ provide a reference for weight and height by sex and age for children in optimal conditions. With these charts one can calculate the weight‐ or height‐for age z‐score for a specific child (eqs 1 and 2). The z‐score is a measure of how many standard deviations an individual child is from the median characteristics given their sex (s) and age (a), and is used to evaluate if that child is growing as expected.

$$Z=\frac{{\left(X_{\mathrm{s},\mathrm{a}}/M_{\mathrm{s},\mathrm{a}}\right)}^{L_{\mathrm{s},\mathrm{a}}}-1}{L_{\mathrm{s},\mathrm{a}}\times S_{\mathrm{s},\mathrm{a}}},L\ne 0$$ (1)

$$Z=\frac{\ln \left(X_{\mathrm{s},\mathrm{a}}/M_{\mathrm{s},\mathrm{a}}\right)}{S_{\mathrm{s},\mathrm{a}}},L=0$$ (2)

where L represents the power of the Box‐Cox transformation, M is the median, S is the generalized coefficient of variation, Z is the z‐score (a random variable following a standard normal distribution by construction with a mean of zero and a standard deviation of 1) and X is the characteristic of choice (ie, weight or height). The WHO and CDC growth charts provide sex‐ and age‐specific L, M and S parameters, where in practice L is never 0, to perform the Box‐Cox transformation and a z‐score, where Z ~ N (0, 1).

These growth charts can also be used for simulating children following the distribution described in those charts. However, worldwide not all children grow up in optimal conditions and this can lead to a mismatch between the simulated and observed children. Therefore, the generated population must be adapted to specific groups, such as malnourished paediatric patients, who are more likely to be stunted, wasted or both.⁷ This needs to be accounted for since it could significantly affect simulation outcomes. A scenario where this is highly relevant is the design of weight‐based dosing regimens for antiretrovirals or antituberculosis drugs for African children who are HIV‐positive or infected with tuberculosis, which is the case‐study presented here. We provide a workflow, based on a previous report, to generate a virtual paediatric population and propose a method to adjust for stunting and wasting.⁸

2. METHODS

2.1. Growth charts

Where the WHO chart summarizes global weight data on children until 10 years of age and height data up to 18 years, the CDC characterizes the typical growth of children in the United States up to 18 years of age for both height and weight. In this report we aimed to provide a workflow to generate a global paediatric population and we used the WHO charts where possible. For weight we therefore merged the WHO chart up to 10 years of age with the CDC chart from 10 years onwards. Due to this merge the L, M and S parameters were not continuous and made a jump down‐ or upwards (Supporting Information Figure S1). This was mitigated by adjusting the CDC parameters to the WHO values proportionally. The WHO height chart is comparable with the CDC chart (Supporting Information Figure S2) and was used for the full age range (0‐18 years).

By rearranging eq. 1, one can simulate weight and height for each combination of sex and age using the input from the growth charts and a normal distribution to generate z‐scores. This is shown in eq. 3.

$$X_{\mathrm{s},\mathrm{a}}=M_{\mathrm{s},\mathrm{a}}\times {\left(1+L_{\mathrm{s},\mathrm{a}}\times S_{\mathrm{s},\mathrm{a}}\times Z\right)}^{1/L_{\mathrm{s},\mathrm{a}}}$$ (3)

2.2. Observed patient data

Data from HIV‐positive children included in the ARROW trial was available and used to (a) assess the natural correlation between z‐scores of weight and height (ie, a child that is underweight is more likely to also be smaller than average) using equation 1, (b) compare with the simulated population and (c) adjust the simulated population with a sex‐ and age‐dependent function.⁹ A second cohort of HIV‐positive children below 25 kg from the CHAPAS‐3 trial was used to validate the final virtual patient population.¹⁰

2.3. Adjusted simulated population

The data generated from the reference growth charts was graphically compared with the observed data. To determine a plausible correlation between weight and height in the population of interest, the individual z‐scores weight‐for‐age and height‐for‐age were calculated on the observed data using eq. 1, and their correlation was determined. This correlation was used to generate multivariate normally distributed z‐scores for weight and height where Z ~ N (0, 1).

To adjust for stunting and wasting we first calculated the difference between the observed height and weight and the median (M _s,a‐value provided by the growth charts) by dividing the observed data points by the M _s,a‐value to obtain an adjustment factor. Piecewise linear functions were used to model this adjustment factor over sex and age to obtain a correction function, f(sex, age), basing model selection on the Bayesian Information Criterion (BIC).

The multivariate normally distributed z‐scores, together with the LMS parameters from the growth charts, were used to generate a simulated population using eq. 4:

$$X_{\mathrm{s},\mathrm{a}}=f\left(\mathrm{sex},\mathrm{age}\right)\times M_{\mathrm{s},\mathrm{a}}\times {\left(1+L_{\mathrm{s},\mathrm{a}}\times S_{\mathrm{s},\mathrm{a}}\times Z\right)}^{1/L_{\mathrm{s},\mathrm{a}}}$$ (4)

The weight, height and FFM of the simulated and observed population were graphically compared again. Finally, the simulated population was compared with the CHAPAS‐3 dataset for validation. For this final comparison, simulated and observed patients weighing above 25 kg and above 12 years of age were excluded to emulate the inclusion criteria of CHAPAS‐3.

All analyses were performed in R (version 4.0.0) with R Studio interface (version 1.2.5042) using tidyverse, data.table, gridExtra and ggpubr packages. Piecewise linear functions were derived in NONMEM (version 7.4.2; Icon Development Solutions, Ellicott City, MD, USA) and Perl‐Speaks‐NONMEM (version 4.8.8) with the Pirana (version 2.9.9) interface.¹¹

3. RESULTS

3.1. Growth charts

The United States CDC growth charts generally contain a higher median weight combined with a higher variance and more skewness towards high weights than the WHO growth charts. We therefore adjusted the LMS parameters of the CDC charts to bring them in line with the WHO charts at 10 years. For males the parameters were adjusted downwards by 43%, 3% and 9%, and for females by 29%, 4% and 12% for the L (Box‐Cox transformation), M (median) and S (coefficient of variation) parameters, respectively (Supporting Information Figure S1).

3.2. Observed patient data

The ARROW dataset contained 52 193 matched observations of height and weight in 1206 HIV‐positive children from Uganda and Zimbabwe who were followed up for up to 5 years. We included maximally one measurement every third month for each patient, thus yielding 19 742 observations. The patients had a median (range) age of 8.0 (0.40‐18) years, weight of 21.0 (3.80‐79.7) kg, height of 117 (55.5‐180) cm, weight‐for‐age z‐score of −1.3 (−7.1‐4.2) and height‐for‐age z‐score of −1.9 (−8.4‐3.4); 49% were female. Eighty‐nine per cent of the patients had a weight‐for‐age z‐score below 0 and 95% had a height‐for‐age z‐score below 0, contrasting with 50% that would be expected if the growth charts reflected this population. The correlation between the z‐scores for weight‐for‐age and height‐for‐age was 0.70 (Figure 1). During the simulation step this correlation was used to generate multivariate normally distributed z‐scores for weight and height.

FIGURE 1.

The correlation between height‐ and weight‐for‐age z‐score in the ARROW dataset was 0.70

The CHAPAS‐3 dataset contained 11 221 height and weight observations in 478 HIV‐positive children from Uganda, Zambia and Zimbabwe. Using maximally one measurement every third month for each patient resulted in 4943 measurements with a median (range) age of 4.7 (0.22‐17) years, weight of 16 (4.5‐42.9) kg, height of 101 (58.7‐156) cm, weight‐for‐age z‐score of −0.89 (−6‐2.1) and height‐for‐age z‐score of −1.8 (−7.9‐2.6); 51% were female. Eighty‐three per cent of the patients had a weight‐for‐age z‐score below 0 and 93% had a height‐for‐age z‐score below 0. The correlation between the z‐scores for weight‐for‐age and height‐for‐age was 0.72.

3.3. Adjusted simulated population

Using the growth charts a virtual population was simulated and visually compared with the ARROW dataset (Figure 2, left column). The median, 5^th and 95^th percentiles for the weight, height and FFM of the simulated population are higher than those from the observed data in ARROW, indicating that children in this study had lower weights, heights and FFMs than the typical values.

FIGURE 2.

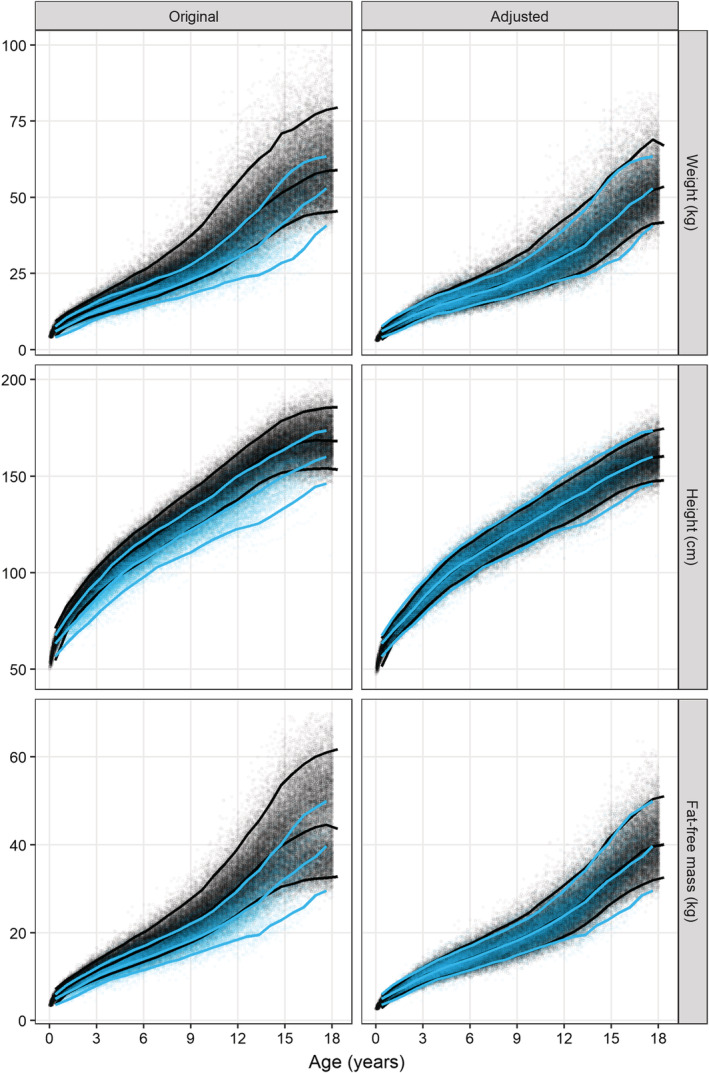
Agreement between the observed (blue dots) and simulated (black dots) distribution of weight (top row), height (middle row) and fat‐free mass (bottom row) before (left column) and after (right column) adjusting the simulated data using the sex‐ and age‐dependent adjustment factor. The lines represent the median, 5^th and 95^th percentile of the observed (blue) and simulated (black) data

The adjustment factor for weight was best described using a piecewise linear function with five breakpoints, two of which are sex‐dependent (Figure 3 and Supporting Information Table S1). The adjustment factor for height was best described by a piecewise linear function with seven breakpoints, three of which are sex‐dependent (Figure 3 and Supporting Information Table S2).

FIGURE 3.

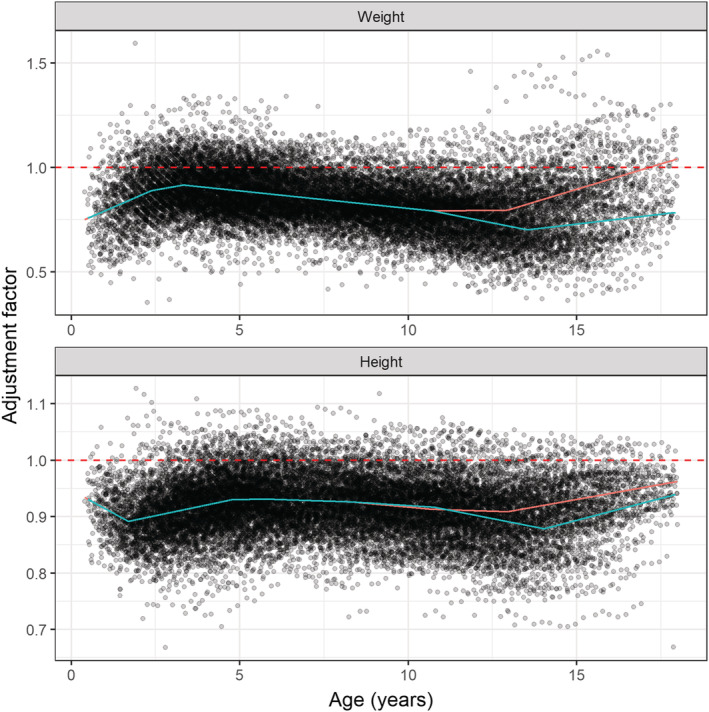
Adjustment factors for patient weight (top) and height (bottom). The lines represent the piecewise linear functions describing the relation between age and the adjustment factor for females (red) and males (blue). The functions are given in Supporting Information Tables S1 and S2. The dashed red line represents the situation where a population is already in line with WHO and CDC growth charts

After adjustment, there was generally good agreement between the observed and simulated medians for weight, height and FFM (Figure 2, right column). More detailed density plots per age group (eg, infants, toddlers and adolescents) of the observed and simulated data before and after adjustment confirm a good agreement in all groups after adjustment (Supporting Information Figure S3). The external validation with the CHAPAS‐3 data also showed good agreement between observed and simulated patients after adjustment of the growth charts (Figure 4).

FIGURE 4.

Agreement between the observed data from the CHAPAS‐3 trial (red dots) and simulated (black dots) distribution of weight (top row), height (middle row) and fat‐free mass (bottom row) before (left column) and after (right column) adjusting the simulated data using the sex‐ and age‐dependent adjustment factor. The lines represent the median of the observed (red) and simulated (black) data

An in silico paediatric population constructed with the final model is available in the Supporting Information. It consists of over 86 000 African HIV‐positive children aged 0 to 18 years (50% female) with 200 patients per age‐month. Additionally, the R‐script is provided to ease the comparison of other populations and the one provided. Finally, the R‐script also allows the input of an alternative correction function or simulation of a new population.

4. DISCUSSION

Paediatric patients are a difficult population to treat because maturation and growth need to be accounted for, both at the start of treatment and during prolonged treatment (eg, tuberculosis and HIV). This population is a moving target due to maturation and growth while children are aging. Malnutrition in some of the populations is not uncommon and these children make some of the most vulnerable patients. Because body size, whether it is weight or fat‐free mass, has a large impact on pharmacokinetic parameters it is crucial that simulations that guide drug development take malnourishment into account and make predictions in an accurate target population.

However, generating a virtual population for use in modelling and simulation with multiple correlated variables can be challenging. Here, we provide a straightforward approach to construct a population using freely available data sources and software, focused on anthropometric measures. Furthermore, we applied this method to a population of HIV‐positive children from Sub‐Saharan Africa and showed that our in silico population is a good representation of the real dataset, making it suitable for simulations. We provide a ready‐to‐use dataset containing children from birth to 18 years old representative for African HIV‐infected children.

When generating and adjusting a simulated population one must carefully consider its proposed use. In this analysis we showed an example aimed at reflecting an HIV‐positive paediatric population that initiates treatment and is then followed up. Therefore, we chose to use one measurement per individual every 3 months, thus reflecting children during chronic treatment with antiretroviral drugs when they are not acutely sick. To create a population that represents unwell (immuno‐compromised) HIV‐infected children initiating treatment for the first‐time, we could have used only the first recorded weight and height.

Our method has some limitations. First, WHO provides a growth chart for a height up to 18 years, but for weight only up to 10 years. Hence, we used the CDC chart for weight in children above 10 years. However, there are differences between these charts. Where WHO charts describe the growth of healthy children under optimal environmental and health conditions measured in selected communities globally,¹² CDC charts describe the growth of children during a certain historical time span. In 2015‐2016, one in five US children between 11 and 19 was obese and this is reflected in the LMS parameters of the CDC tables.¹³ To mitigate this, we adjusted the CDC charts to be in line with WHO before calculating the functions for the adjustment factors. Second, the derived functions to adjust the growth charts are empirical and extrapolation to other populations (eg, tuberculosis or malaria patients, pre‐term neonates) should be done with caution, taking any additional assumptions into account. A graphical comparison, as demonstrated in Figure 4, can be useful to investigate the agreement between a virtual population used for simulation and a target population. Only then one can decide to accept any deviations and proceed with the simulations or readjust the virtual population to better represent the target population.

Choosing a relevant population is an essential step in producing realistic simulation results. To allow for transparent and reproducible science, it is crucial that details about simulation results include a clear description of the population used, ideally making it publicly available. However, when using real patient data, this is not always possible due to data anonymity concerns. The workflow we provided here can be applied to generate in silico populations of interest that agree with an observed population, thus circumventing issues with data anonymity. This way, the population can be shared publicly, which supports full reproducibility of simulation results and reuse of the same population by future investigators.

COMPETING INTERESTS

R.W. and P.D. are supported by PediCAP, which is part of the EDCTP programme supported by the European Union (grant number RIA2017MC‐2023). E.M.S. is supported by PanACEA, which is part of the EDCTP programme supported by the European Union (grant number TRIA2015‐1102‐PanACEA). A.S.W. and M.C. are supported by core support from the Medical Research Council UK to the MRC Clinical Trials Unit (MC_UU_12023/22) through a concordat with the Department for International Development. A.S.W. is also an National Institute for Health Research (NIHR) Senior Investigator. The views expressed are those of the author(s) and not necessarily those of the NHS, the NIHR, the Department of Health or Public Health England (PHE). P.D. receives support from the National Research Foundation (NRF) of South Africa (NRF grant 109 056).

CONTRIBUTORS

R.E.W. participated in design, analysis and interpretation of the data and drafting the manuscript. E.M.S. and P.D. participated in conception, design, analysis and interpretation of the data and revising the manuscript. A.S.W and M.N.C. participated in acquisition of data, analysis and interpretation of the data and revising the manuscript.

Supporting information

TABLE S1 Functions to adjust the median weight from the growth chart by sex and age

TABLE S2 Functions to adjust the median height from the growth chart by sex and age

TABLE S3 Example of how your data should be formatted to investigate the agreement between the generated population and your own

FIGURE S1 LMS parameters for weight from the WHO chart (0–10 years) and the CDC chart (10–18 years) before (top row) and after (bottom row) adjusting

FIGURE S2 LMS parameters for height from the WHO and CDC charts. The L‐parameter in the WHO chart equals 1 for all ages and both sexes, i.e. L equals 1 means that it is not used in equation 1

FIGURE S3 Density plots of weight, height and fat‐free mass of the observed ARROW data (blue) and the simulated data (red) before and after adjusting in eight age groups

Supporting Information

Wasmann RE, Svensson EM, Walker AS, Clements MN, Denti P. Constructing a representative in‐silico population for paediatric simulations: Application to HIV‐positive African children. Br J Clin Pharmacol. 2021;87:2847–2854. 10.1111/bcp.14694

DATA AVAILABILITY STATEMENT

The virtual population and the R‐script to generate this population are available in the Supporting Information.