Computationally efficient measure of topological redundancy of biological and social networks

Abstract

It is well known that biological and social interaction networks have a varying degree of redundancy, though a consensus of the precise cause of this is so far lacking. In this paper, we introduce a topological redundancy measure for labeled directed networks that is formal, computationally efficient, and applicable to a variety of directed networks such as cellular signaling, and metabolic and social interaction networks. We demonstrate the computational efficiency of our measure by computing its value and statistical significance on a number of biological and social networks with up to several thousands of nodes and edges. Our results suggest a number of interesting observations: (1) Social networks are more redundant that their biological counterparts, (2) transcriptional networks are less redundant than signaling networks, (3) the topological redundancy of the C. elegans metabolic network is largely due to its inclusion of currency metabolites, and (4) the redundancy of signaling networks is highly (negatively) correlated with the monotonicity of their dynamics.

I. INTRODUCTION

The concepts of degeneracy and redundancy are well known in information theory. Loosely speaking, degeneracy refers to structurally different elements performing the same function, whereas redundancy refers to identical elements performing the same function¹. In electronic systems, such measures are useful in analyzing properties such as fault tolerance. It is an accepted fact that biological networks do not necessarily have the lowest possible degeneracy or redundancy; for example, the connectivity of neurons in brains suggest a high degree of degeneracy [2]. However, as Tononi et al. observed in their paper [3]:

“Although many similar examples exist in all fields and levels of biology, a specific notion of degeneracy has yet to be firmly incorporated into biological thinking, largely because of the lack of a formal theoretical framework”.

The same comment holds true about redundancy as well. A further reason for the lack of incorporation of these notions in biological thinking is the lack of effective algorithmic procedures for computing these measures for large-scale networks even when formal definitions are available. Therefore, such studies are often done in a somewhat ad hoc fashion, as in Ref. [4]. There do exist notions of “redundancy” in the field of analysis of undirected networks based on clustering coefficients (see e.g., [5]) or betweenness centrality measures (see e.g., [6]). However, such notions are not appropriate for the analysis of biological networks where one must distinguish positive from negative regulatory interactions, and where the study of dynamics is of interest.

II. BRIEF REVIEW OF AN INFORMATION-THEORETIC DEGENERACY AND REDUNDANCY MEASURES

Formal information-theoretic definitions of degeneracy and redundancy for dynamic biological systems were proposed in [3] (see also [7,8]) based on mutual-information contents. These definitions assume access to suitable perturbation experiments and corresponding accurate measurements of the relevant parameters. Thus, they are not directly comparable to the topology-based redundancy measures that we propose in this paper. Nonetheless, we next briefly review these definitions as a way to illustrate some key points of other measures often used in the literature that motivated us to define our new redundancy measure.

The authors of [3] consider a system consisting of n elements that produces a set of outputs $\mathcal{O}$ via a fixed connectivity matrix from a subset of these elements. The elements are described by a jointly distributed random vector X that represents steady-state activities of the components of their system. The degeneracy $\mathcal{D}(X;\mathcal{O})$ of the system is then expressed as the average mutual information $(\mathcal{I})$ shared between $\mathcal{O}$ and the “perturbed” bi-partitions of X summed over all bipartition sizes [Eq. (2b) of [3]], that is,

$$\mathcal{D}(X;\mathcal{O})=\frac{1}{2}\times \sum _{k=1}^n\sum _j({\mathcal{I}}^P\left(X_j^k;\mathcal{O}\right)+{\mathcal{I}}^P\left(X\backslash X_j^k;\mathcal{O}\right)-{\mathcal{I}}^P(X;\mathcal{O})),$$ (1)

where $X_j^k$ is a j^th subset of X composed of k elements and the notation ${\mathcal{I}}^P(\mathcal{A};\mathcal{O})$ denotes the mutual information between a subset of elements $\mathcal{A}$ and an output set $\mathcal{O}$, when $\mathcal{A}$ is injected with a small fixed amount of uncorrelated noise²; see [3,7] for details. One can immediately see a computational difficulty in applying such a definition: the number of possible bipartitions could be astronomically large even for a modest size network. For example, for a network with 100 nodes which is a number smaller than all but one of the networks considered in this paper, the number of bi-partitions is roughly 2¹⁰⁰ > 10³⁰. Measures avoiding averaging over all bi-partitions were also proposed in [3], but the computational complexities and accuracies of these measures remain to be thoroughly investigated and evaluated on larger networks.

In a similar manner, the redundancy $℞(X;\mathcal{O})$ of a system X was defined in [3] as the difference between summed mutual information upon perturbation between all subsets of size up to 1 and $\mathcal{O}$, and the mutual information between the entire system and $\mathcal{O}$ [Eq. (3) in [3]], that is,

$$℞(X;\mathcal{O})=\sum _{j=1}^n{\mathcal{I}}^P\left(X_j^1;\mathcal{O}\right)-{\mathcal{I}}^P(X;\mathcal{O}).$$ (2)

Note that a clear shortcoming of this measure is that it only provides a number, but does not indicate which subset of elements is redundant. Identifying redundant elements is important for the interpretation of results, and may also serve as an important step of the network construction and refinement process, as we will illustrate in our application to the C. elegans metabolic network and the oriented PPI network. Tononi et al. [3] illustrated the above measure on a few model networks as a proof of concept, but large networks clearly necessitate alternate measures that allow efficient calculations.

In this paper we propose a new topological measure of redundancy. A benefit of our new redundancy measure is that we can actually find an approximately minimal network and, in the case of multiple minimal networks of similar quality, a subset of them by enabling a randomization step in the algorithmic procedure. We determine this redundancy value for a number of biological and social networks of large sizes and observe a number of interesting properties of our redundancy measure.

III. MODELS FOR DIRECTED BIOLOGICAL AND SOCIAL NETWORKS

There are two very different levels of models for biological systems. A so-called network topology model (also known as a “wiring diagram” or a “static graph”) provides a coarse diagram or map of the physical, chemical, or statistical connections between molecular components of the network, without specifying the detailed kinetics. In this type of model, a network of molecular interactions is viewed as a graph: Cellular components are nodes in a network, and the interactions between these components are represented by edges connecting the nodes. In this paper, we are mainly concerned with this type of model; exact details are described in Sec. III A.

In the other type of model, a network dynamics model, mathematical rules (e.g., systems of Boolean rules or differential equations) are used to specify the behavior over time of each of the molecular components in the network. Our investigation is not directly concerned with such dynamic models. However, since we will show a correlation of our redundancy measure for the network topology model with a property, namely monotonicity, of an associated network dynamics model, we briefly review this model in Sec. III B.

A. Network topology model

Three common types of molecular biological networks are as follows: transcriptional regulatory networks, metabolic networks, and signaling networks. The nodes of transcriptional regulatory networks represent genes, and edges represent (positive or negative) regulation of a given gene’s expression by proteins associated with other genes. The nodes of metabolic networks are metabolites and the edges represent the enzyme-catalyzed reactions in which these metabolites participate as reactants or products. The nodes of signaling networks are proteins and small molecules, and the edges represent physical or chemical interactions or indirect positive or negative causal effects. A unified formalism to describe all these types of networks uses a directed graph G = (V,E,w) with vertex set V, edge set E, and an edge labeling function w : E ↦ {−1,+1} in which a label of 1 (respectively, −1) represents an positive (respectively, negative) influence. A pathway is then a path P from vertex u to vertex v, and the excitory or inhibitory nature of the pathway is specified by the parity Π_e∈P w(e) ∈ {−1,+1} of such a path P; see Fig. 1 for an illustration.

FIG. 1.

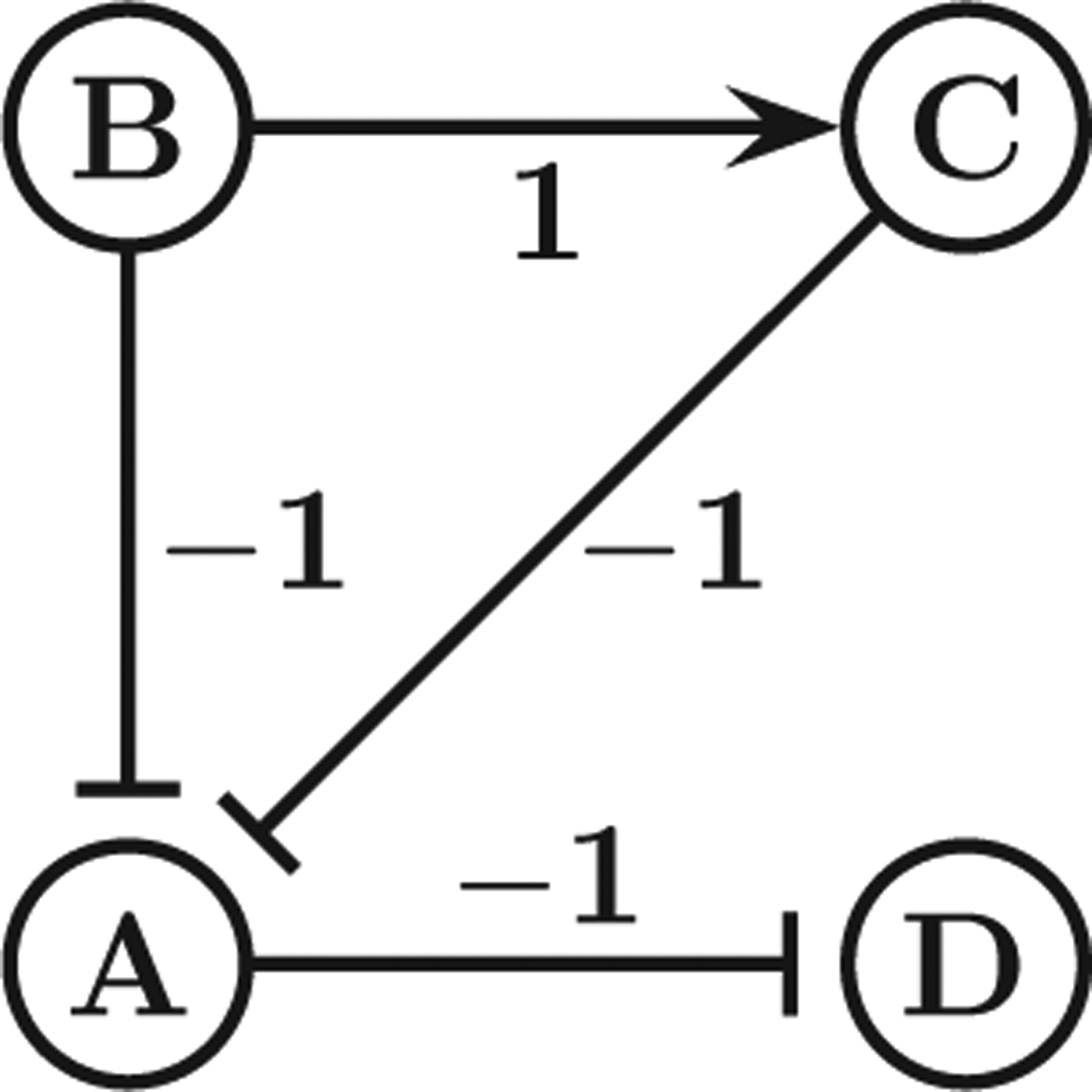
The network topology model for biological networks. The parity of the pathway B → C → A ⊣ D is 1 × (−1) × (−1) = 1.

Our model for directed social interaction networks is simply a directed graph in which edges represent significant relationships between the entities, for example, nodes may represent Web pages and directed edges may represent hyperlinks of one Web page in another. Obviously, we can think of such a model as one of the above type in which all edges are labeled +1 (and, thus all paths have the same parity); this allows us to treat both social and biological networks in a mathematically uniform manner for the purpose of designing and analyzing algorithms.

B. Network dynamics and monotonicity

Consider systems modeled via ordinary differential equations:

$$\frac{d{x}_i(t)}{dt}=f_i\left(x_1(t),x_2(t),\dots ,x_n(t)\right)\text{\hspace{1em}for\hspace{1em}}i=1,2,\dots ,n,$$ (3)

where x_i(t) indicates the concentration of the i^th entity in the model at time t and the f_i’s are functions of n variables. We assume that x(t) = (x₁(t),x₂(t), … ,x_n(t)) evolves in an open subset of ${ℝ}^n$, the f_i’s are differentiable, and solutions are defined for t ⩾ 0. For example, a simple two-species interaction could be described by

$$\frac{d{x}_1}{dt}(t)=3x_1(t)-5x_2(t),$$

$$\frac{d{x}_2}{dt}(t)=x_1(t)+x_2(t).$$

A particularly appealing class of dynamics is that of monotone systems [9,10]. Informally, the dynamics of a monotone system preserves a specific partial order (hierarchy) of its inputs over time. Mathematically, monotonicity can be defined as follows.

Definition 1 [9,10].

Given a partial order ⪯ over ${ℝ}^n$, system (3) is said to be monotone with respect to ⪯ if

$$\forall t⩾0:\left(x_1(0),\dots ,x_n(0)\right)\preccurlyeq \left(x_1(0),\dots ,x_n(0)\right)y_1(0),\dots ,y_n(0))\Rightarrow \left(x_1(t),\dots ,x_n(t)\right)\preccurlyeq \left(y_1(t),\dots ,y_n(t)\right),$$

where (x₁(t), … ,x_n(t)) and (y₁(t), … ,y_n(t)) are the solutions of (3) with initial conditions (x₁(0), … ,x_n(0)) and (y₁(0), … ,y_n(0)), respectively.

We will restrict our attention to orthant orders. These are the partial orders ⪯_s over ${ℝ}^n$, for any given s = (s₁, … s_n) ∈ {−1, 1}ⁿ, defined as (see [10–12])

$$x{⪯}_{s}y\iff \forall i:s_i{x}_i⩽s_i{y}_i.$$

In particular, the “cooperative order” is the partial order ⪯_s for s = (1, 1, … ,1).

Monotone systems constitute a nicely behaved class of dynamical systems in several ways. For example, for these systems pathological behaviors (chaotic attractors) are ruled out. Even though they may have an arbitrarily large dimensionality, monotone systems (under an additional irreducibility assumption) behave in many ways like one-dimensional systems; for example, bounded trajectories generically converge to steady states, and stable oscillatory behaviors do not exist. Monotonicity with respect to orthant orders is equivalent to the nonexistence of negative loops in systems; analyzing the behaviors of such loops is a long-standing topic in biology in the context of regulation, metabolism, and development, starting from the work of Monod and Jacob in 1961 [13]. In this paper, we will define a measure of “degree of monotonicity” for dynamical systems and relate it to our topology-based redundancy measure.

IV. A NEW MEASURE OF REDUNDANCY

We will use the following notations for conciseness:

1. For any two vertices u and υ, $u\stackrel{x}{\Rightarrow }\upsilon$ (respectively, $u\stackrel{x}{\to }\upsilon$) denotes a path (respectively, an edge) from u to v of parity x. We include the empty path $u\stackrel{1}{\to }u$ for each vertex u.

2. For any E′ ⊆ E, reachable (E′) is the set of all ordered triples (u,v,x) such that $u\stackrel{x}{\Rightarrow }\upsilon$ exists in the subgraph (V,E′).

For example, for the network in Fig. 1, $\text{B}\stackrel{1}{\Rightarrow }\text{D}$ exists because of the path B ⊣ A ⊣ D and also because of the path B → C ⊣ A ⊣ D, and reachable ({B → C, A ⊣ D}) = {(A, A, 1), (B, B, 1), (C, C, 1), (D, D, 1), (B, C, 1), (C, C, 1), (A, D, −1),}.

We next state a combinatorial optimization problem that will be needed in order to introduce our new redundancy measure.

• Problem Name: Binary Transitive Reduction (BTR).

• Instance: a directed graph G = (V,E) with a subset of edges E_fixed ⊂ E and an edge labeling function w : E ↦ {−1, 1}.

• Valid Solution: a subgraph G′ = (V,E′) such that

  1. E ⊇ E_fixed and
  2. reachable (E′) = reachable (E).
     (E \ E′ is referred to as a set of “redundant” edges.)

• Goals: minimize |E′|.

Intuitively, the BTR problem prunes pathways for which alternate equivalent pathways exist (see e.g., [14,15]). The set of edges in E_fixed in the definition of BTR represents edges that may not be removed during the algorithm; this is useful in the context when one wishes to reduce a network while preserving specific pathways. For the redundancy calculations performed in this paper, we assume no prior knowledge of direct interactions; thus for the rest of the paper we set E_fixed = ∅. As an illustration, in Fig. 1 if we let E′ = E \ {B ⊣ A} then reachable (E′) =reachable (E) because of the path B → C ⊣ A.

Finding a maximum set of edges that can be removed is nontrivial; in fact, the problem is NP hard [17]. To illustrate the algorithmic difficulties, consider the network shown in Fig. 2. Removal of all the black edges provides a nonoptimal solution of BTR, whereas an optimal solution with about half the edges compared to the nonoptimal solution can be obtained by keeping all the black edges and removing all but two of the gray edges. The special case of BTR with E_fixed = ∅ and w(e) = 1 for all edges e is the so-called classical minimum equivalent digraph problem, and it has been investigated extensively in the context of checking minimality of connectivity requirements in computer networks (see e.g., [17]). Other examples of applications of BTR –type network optimizations include the work by Wagner [18] employing a special case of BTR to determine network structure from gene perturbation data in the context of biological networks and the work by Dubois and Cécile [19] in the context of social network analysis and visualization.

FIG. 2.

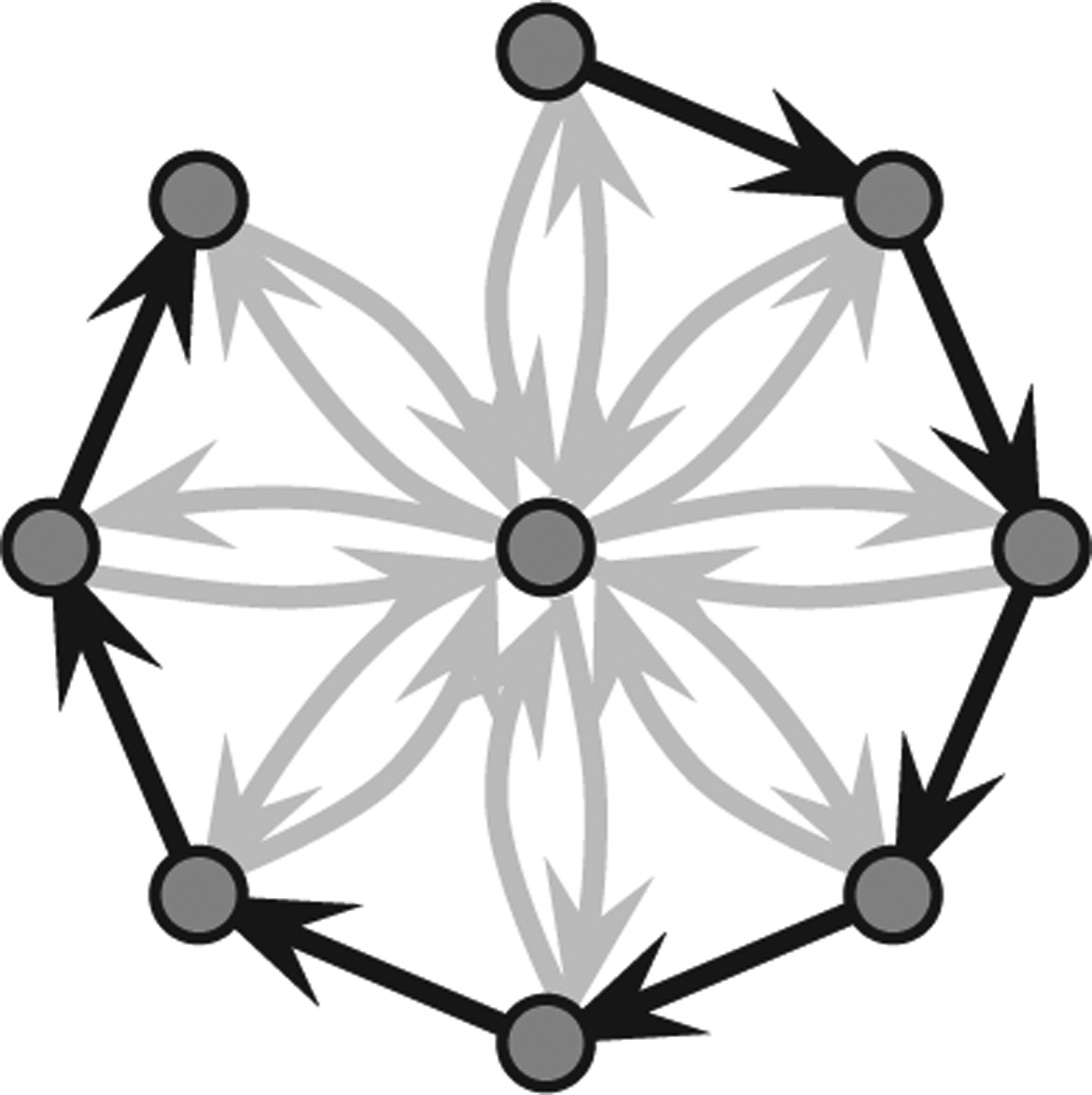
Choosing one wrong edge may cost too much in BTR.

Based on the BTR problem, we propose a new combinatorial measure of redundancy that can be computed efficiently. Note that BTR does not change pathway level information of the network and removes edges from one node to another only when a similar alternate pathway exists, thus truly removing redundant connections. Thus, $\frac{\left|E^{\prime }\right|}{|E|}$ provides a measure of global compressibility of the network and our proposed new redundancy measure ℞_new is defined to be

$${℞}_{\text{new}}=1-\frac{\left|E^{\prime }\right|}{\left|E\right|}.$$ (4)

The |E| term in the denominator of the above definition translates to a “min-max normalization” of the measure [20], and ensures that $0<{℞}_{\text{new}}<1$. Note that the higher the value of ℞_new is, the more redundant the network is.

A. Properties of our topological redundancy measure and applications of a minimal network

Any topological redundancy measure should have a desirable property: The measure must not only reflect simple connectivity properties such as degree sequence or average degree, it must also depend on higher-order connectivity. Our redundancy measure indeed has this property, since paths of arbitrary length are considered for removal of an edge. For a concrete example, consider two graphs shown in Fig. 3; the in-degree and out-degree sequence of each graph is $\underset{\frac{n}{2}+1}{\underbrace{1,1,\dots ,1,1}},\underset{\frac{n}{2}-1}{\underbrace{2,2,\dots ,2}}$, but their redundancy values are drastically different. Similarly, higher average degree does not necessarily imply higher values of redundancy; for example, the network in Fig. 3, when generalized on n nodes, has an average degree below 2 and a redundancy value of roughly 0.33, whereas the graph $K_{\frac{n}{2}\cdot \frac{n}{2}}$ (a completed bipartite graph with each partition having n/2 nodes and all edges directed from the left to the right partition) has an average degree of n/2 but a redundancy value of 0.

FIG. 3.

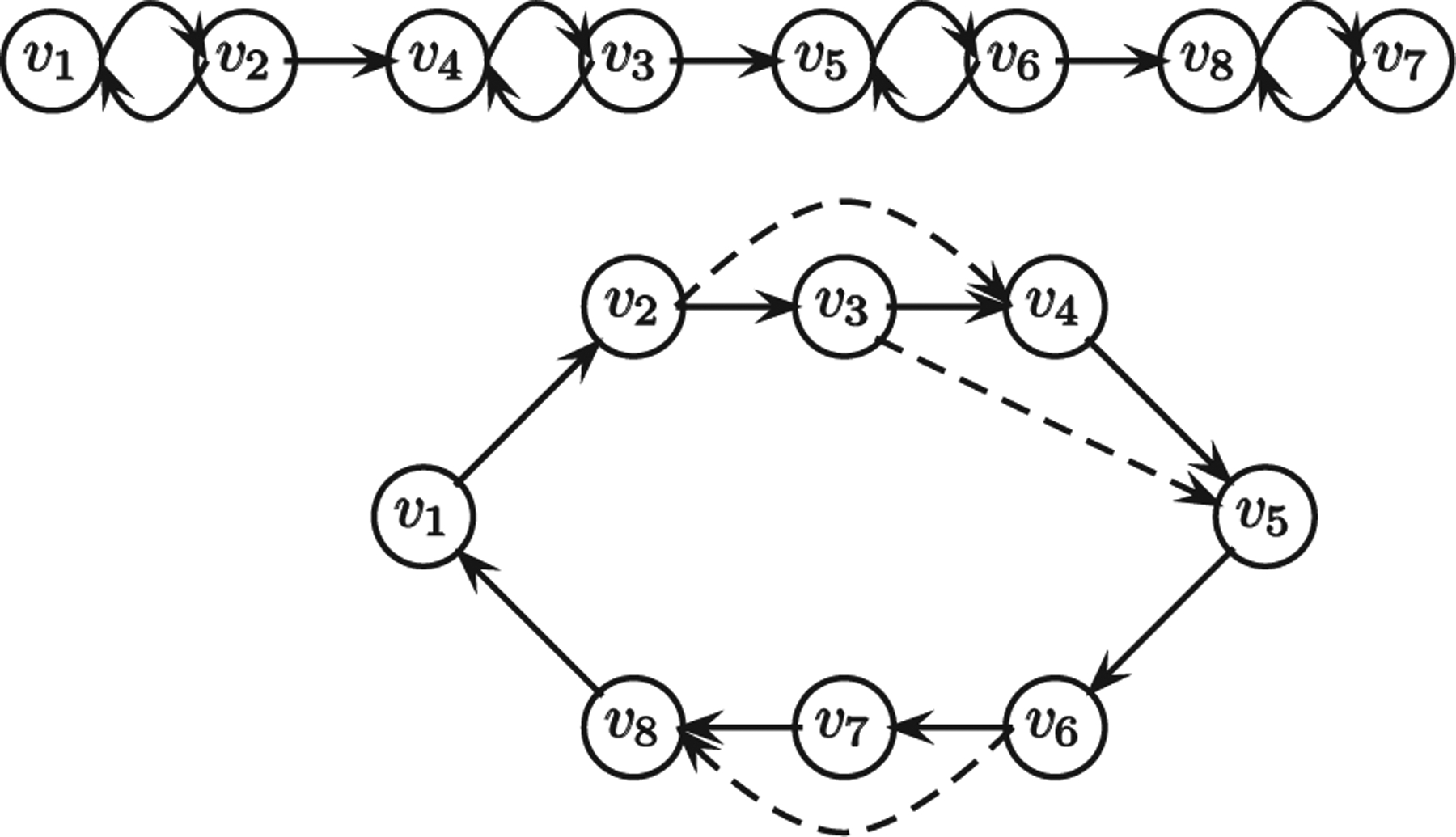
Two n-node graphs with same degree sequence but with different values of *_new, shown for n = 8. The top graph has no redundant edges, thus for it *_new = 0. The dashed edges for the bottom graph can be removed, giving ${*}_{\text{new}}=\frac{3}{11}$.

B. Computing ℞_new

Although solving BTR exactly is an NP-hard problem, it has a rich combinatorial structure that allowed us to design an efficient approximation algorithm. The resulting algorithms were incorporated in our NET-SYNTHESIS software [15] (publicly available at [16]).

Although it is impossible to provide all details of the algorithmic approaches that was used for NET-SYNTHESIS, we provide some high-level details of the algorithm used; the reader can find further details, correctness proofs, and algorithmic analysis in [14,21]. It was proved in [21] that any strongly connected component (SCC) of the given graph G = (V,E), say (V₁,E₁) with V₁ ⊆ V and E₁ = (V₁ × V₁) ∩ E, can be classified as one of the two types: a single parity SCC if, for any two vertices u,v ∈ V₁, $u\stackrel{x}{\Rightarrow }\upsilon$ exists in the SCC for exactly one x from {−1,1}, and a multiple parity SCC if, for any two vertices u,v ∈ V₁, $u\stackrel{x}{\Rightarrow }\upsilon$ exists in the SCC for both x = 1 and x = −1. A high-level view of the algorithmic approach is shown in Fig. 4.

FIG. 4.

A high-level view of the algorithmic approach in NET-SYNTHESIS to perform BTR.

The running time of NET-SYNTHESIS is dominated by Step 2. Theoretically, the worst-case running time of the algorithm is O(n³) when n is the number of vertices in G, but empirically the implementation allows us to calculate ℞_new for networks up to about five to ten thousand nodes, thereby allowing us to compute the redundancy parameter for large networks. We expect that a future improved implementation of BTR will allow the calculation of redundancy values for even larger networks. Regarding optimality of the computed solution, theoretically NET-SYNTHESIS returns a solution that is a 3-approximation [14] (i.e., |E_solution| is no more than three times of that in an optimal solution in the worst case). However, extensive empirical evaluations reported in [14] suggest that in practice |E_solution| is almost always close to optimal (within an extra 10% of the optimal).

C. Illustration of redundancy calculation for a small biological networks

Our results of redundancy calculations on large-size biological and social networks are reported later, in Sec. VII, but here we illustrate the redundancy and minimal network calculations on a biological network that arises from the repetition of a fixed gene regulatory network over a number of cells. This gene regulatory network is formed among products of the segment polarity gene family, which plays an important role in the embryonic development of Drosophila melanogaster. The interactions incorporated in this network include translation (protein production from mRNA), transcriptional regulation, and protein-protein interactions. Two of the interactions are intercellular: Specifically, the proteins wingless and hedgehog can leave the cell they are produced in and can interact with receptor proteins in the membrane of neighboring cells. We select this network for several reasons. First, the core part of the network for a single cell is small, consisting of 13 nodes and 22 edges, which enables analytical calculations of redundancy and visual depiction of redundant edges. Secondly, in spite of its simplicity and regularity, the associated multicell network does exhibit nontrivial redundancies due to the intercellular interactions and the cyclic arrangement of cells. The network for a single cell was first published in [22] and later in slightly modified form in [23,24]. Figure 5 (a) shows the network of [22] with the interpretation of the regulatory role of PTC_m on the reaction CI → CN as PTC_m → CN and PTC_m ⊣ CI . We note that the intercellular interactions are present at the whole cell membrane and not just the right boundary as shown for simplicity in all reconstructions. In a manner similar to that in other papers (e.g.,, see [11]), we build a one-dimensional multicellular version by considering a row of y cells, each of which has separate variables for each of the compounds, letting the cell-to-cell interactions be as in Fig. 5 (a), but acting on both left and right neighbors, and using cyclic boundary conditions; see Fig. 5 (b) for an illustration.

FIG. 5.

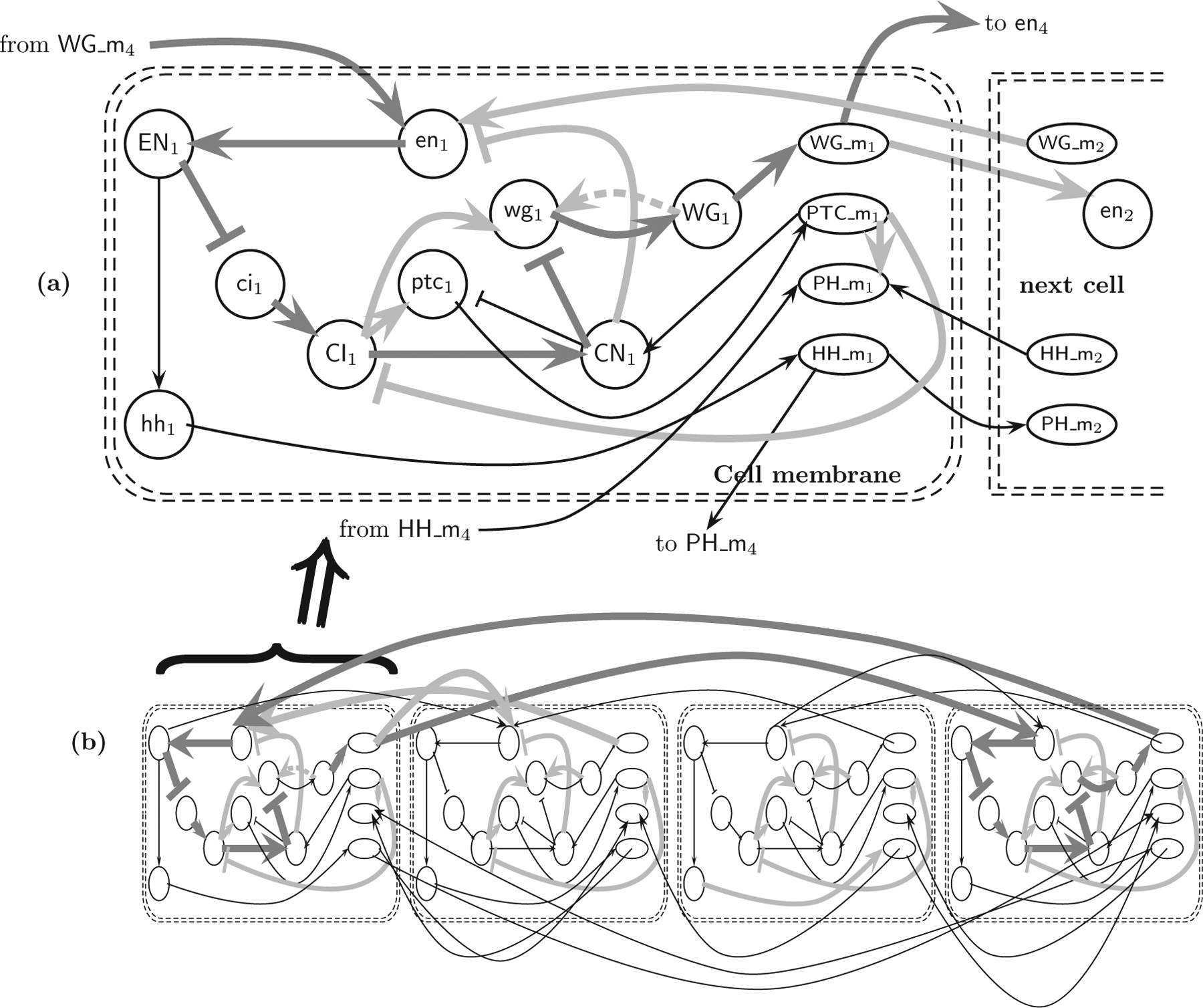
(a) The Drosophila segment polarity network for a single cell, redrawn from [22]. (b) A network of four cells. The redundant edges in each cell are colored light gray. The dark gray edges form an alternate pathway of same parity for the edge WG ₁ → wg ₁.

If the network contains y > 2 cells, then

1. The number of vertices and edges are 13y and 22y, respectively; and

2. NET-SYNTHESIS, after performing BTR , keeps 16y – 2 edges, giving ${℞}_{\text{new}}=\frac{6y+2}{22y}\approx \frac{3}{11}$.

Identifying a molecule in the i^th cell via a subscript i, NET-SYNTHESIS removed the following edges:

1. the two edges WG_m₂ → en₁ and WG_m₁ → en₂, and

2. the set of six edges from each cell i : PTC_m_i → PH_m_i , PTC_m_i ⊣ CI_i, WG_i → wg_i, CN_i ⊣ en_i, CI_i → wg_i, and CI_i → ptc_i.

As can be seen, the redundancies depend in a nontrivial manner on higher-order connections. For example, the light gray edge WG ₁ → wg ₁ is redundant because of the alternate dark gray pathway shown in Fig. 5.

D. Computing the confidence parameter for ℞_new

We apply our redundancy measure on seven biological networks and four social networks (see Table I). For each (social or biological) network G in Table I, except networks (9) and (10), having a redundancy value of ℞_new(G), we generated 100 random networks, and computed the redundancies ${℞}_{\text{new}}\left(G_{{\text{random}}_1}\right)$, ${℞}_{\text{new}}\left(G_{{\text{random}}_2}\right)$, …, ${℞}_{\text{new}}\left(G_{{\text{random}}_{100}}\right)$ of these random networks. We then use a (unpaired) one-sample student’s t test to determine the probability that ${℞}_{\text{new}}\left(G\right)$ can be generated by a distribution that fits the data points ${℞}_{\text{new}}\left(G_{{\text{random}}_1}\right)$, …,${℞}_{\text{new}}\left(G_{{\text{random}}_{100}}\right)$.

Table I.

Network data with sources. If duplicated edges were present in the original network, they were removed in calculation of number of edges.

	Number of nodes (n)	Number of edges (m)	Average degree (m/n)	Brief description and reference
Biological networks
(1)	311	451	1.45		E. coli transcriptional regulatory network constructed by Shen-Orr et al. in [25] for direct regulatory interactions between transcription factors and the genes or operons they regulate; see [41].
(2)	512	1047	2.04		Mammalian network of signaling pathways and cellular machines in the hippocampal CA1 neuron constructed by Ma’ayan et al. [42]; see [43].
(3)	418	544	1.3		E. coli transcriptional regulatory network (updated version of the network constructed by Shen-Orr et al. in [25]); see [26].
(4)	59	135	2.28		T-cell large granular lymphocyte (T-LGL) survival signaling network constructed by Zhang et al. [44]; see [45].
(5)	690	1082	1.56		S. cerevisiae transcriptional regulatory network constructed by Milo et al. [46] showing interactions between transcription factor proteins and genes; see [47].
(6)	651	2040	3.13		C. elegans metabolic network constructed by Jeong et al. [48] and also used by Duch and Arenas in [49].
(7)	786	2453	3.12		An oriented version of an unweighted PPI network constructed from S. cerevisiae interactions in the BIOGRID database by Gitter et al. [50].
Social networks
(8)	198	2742	13.84		Network of Jazz musicians [51].
(9)	1133	10903	9.62		List of edges of the network of e-mail interchanges between members of the University Rovira i Virgili (Tarragona) [52].
(10)	11240	24316	2.16		Network of users of the Pretty-Good-Privacy algorithm for secure information interchange; edges connect users that trust each other [53].
(11)	1169	1912	1.63		Enron e-mail network; available from UC Berkeley Enron Email Analysis [54].

The current implementation of NET-SYNTHESIS runs slowly due to its intensive disk access on networks (9) and (10) in Table I because network (9) is very dense (an average degree of 9.62 on 1133 nodes) and network (10) has a very large number of edges (24 316 edges). Redundancy analysis of a single random graph generated for either of these two networks requires a week or more, and any meaningful statistics would require on the order of 100 random graphs for each network. Due to the prohibitive time requirements we were not able to report p values for these two networks Since the characteristics of various biological and social networks are of different nature, we generate random networks for the various networks using two different methods as explained below.

Ideally, for networks of a particular type, one would prefer to use an accurate generative null model for highest accuracy in p values. For signaling and transcriptional biological networks [networks (1)–(5) in Table I], Ref. [14], based on extensive literature review of similar kinds of biological networks in prior papers, arrived at the characteristics of a generative null model that is described below and used by us for these networks³. One of the most frequently reported topological characteristics of such networks is the distribution of in-degrees and out-degrees of nodes, which exhibit a degree distribution that is close to a power law or a mixture of a power law and an exponential distribution [27–29]. Specifically, transcriptional regulatory networks have been reported to exhibit a power-law out-degree distribution, while the in-degree distribution is more restricted [25,30]. Based on such topological characterizations of signaling and transcriptional networks reported in the literature, Ref. [14] used the following degree distributions for the purpose of generating random networks for the biological transcriptional and signaling networks such as the ones in (1)–(5) in Table I:

1. The number of vertices is the same as the network G whose redundancy value was computed.

2. The in-degree and out-degree distributions of the random networks are as follows:

   • The distribution of in-degree of the networks is exponential, that is, Pr[in-degree =x]= c₁ e^−cx with $\frac{1}{2}<c_1<\frac{1}{3}$ and a maximum in-degree of 12.
   • The distribution of out-degree of the networks is governed by a power law, that is, for x ⩾ 1, Pr[out-degree =x]= c₂ x^−c, for x = 0 Pr[out-degree = 0]⩾ c₂ with 2 < c₂ < 3 and a maximum out-degree of 200.
   • The parameters in the above distribution are adjusted such that the sum of in-degrees of all vertices are equal to the sum of out-degrees of all vertices and the expected number of edges is the same as G.

3. The percentage for activation/inhibition edges in the random network is the same as in G.

Each of the r random networks with these degree distributions are generated using our private implementation of the method suggested by Newman et al. in [31].

For social networks, for the C. elegans metabolic network and for the oriented PPI network [networks (6)–(11) in Table I], in the absence of a consensus on an accurate generative null model, we generated the r random networks using a Markov-chain algorithm [32] in a similar manner as in, say [25], by starting with the real network G and repeatedly swapping randomly chosen pairs of connections in the following manner⁴:

V. MEASURE OF MONOTONICITY FOR BIOLOGICAL NETWORKS

To explain the intuition behind the computation of a monotonicity measure of the dynamics of a biological system, we start by relating the time dynamics of the system with the graph-theoretic model of the network in the following way [10–12]. The time-varying system as defined by Eq. (3) defines a labeled-graph model G = (V,E,w) of the biological network in the following manner:

• V = {x₁, … ,x_n};

• if $\frac{\partial f_j}{\partial x_i}⩾0$ for all x(t)= (x_1(t),x₂(t), … ,x_n(t)) and $\frac{\partial f_j}{\partial x_i}>0$ for some x(t), then (x_i,x_j) ∈ E and w(x_i,x_j) 1;

• if $\frac{\partial f_j}{\partial x_i}⩽0$ for all x(t) and $\frac{\partial f_j}{\partial x_i}<0$ for some x(t), then (x_i,x_j) ∈ E and w(x_i,x_j) = −1.

• (we assume that, for each i and j, either $\frac{\partial f_j}{\partial x_i}⩾0$ for all x or $\frac{\partial f_j}{\partial x_i}⩽0$ for all x.)

As an example, consider the following biological model of testosterone dynamics [33,34]:

$$\begin{gathered} \frac{d{x}_1}{dt}(t)=\frac{A}{K+x_3(t)}-b_1{x}_1(t)\text{,} \\ \frac{d{x}_2}{dt}(t)=c_1{x}_1(t)-b_2{x}_2(t)\text{,} \\ \frac{d{x}_3}{dt}(t)=c_2{x}_2(t)-b_3{x}_3(t). \end{gathered}$$ (5)

The corresponding labeled network for this system is shown in Fig. 6. It is easy to show that (5) is not monotone with respect to ⪯_s, for all possible s. On the other hand, if we remove the term involving x₃ in the first equation, we obtain a system that is monotone with respect to ⪯_s, s (1,1,1). A cause of nonmonotonicity of the system is the =existence of sign-inconsistent paths between two nodes in an undirected version of the network (i.e., the existence of both an activation and an inhibitory path between two nodes when the directions of the edges are ignored). To be precise, define a closed undirected chain in the labeled graph G as a sequence of vertices x_i1, … ,x_ir such that x_i1 = x_ir , and such that for every λ = 1, … ,r − 1 either $\left(x_{i_{\lambda }},x_{i_{\lambda +1}}\right)\in E$ or $\left(x_{i_{\lambda +1}},x_{i_{\lambda }}\right)\in E$. Then, the following result holds [11] see also [35] and [36], page 101].

FIG. 6.

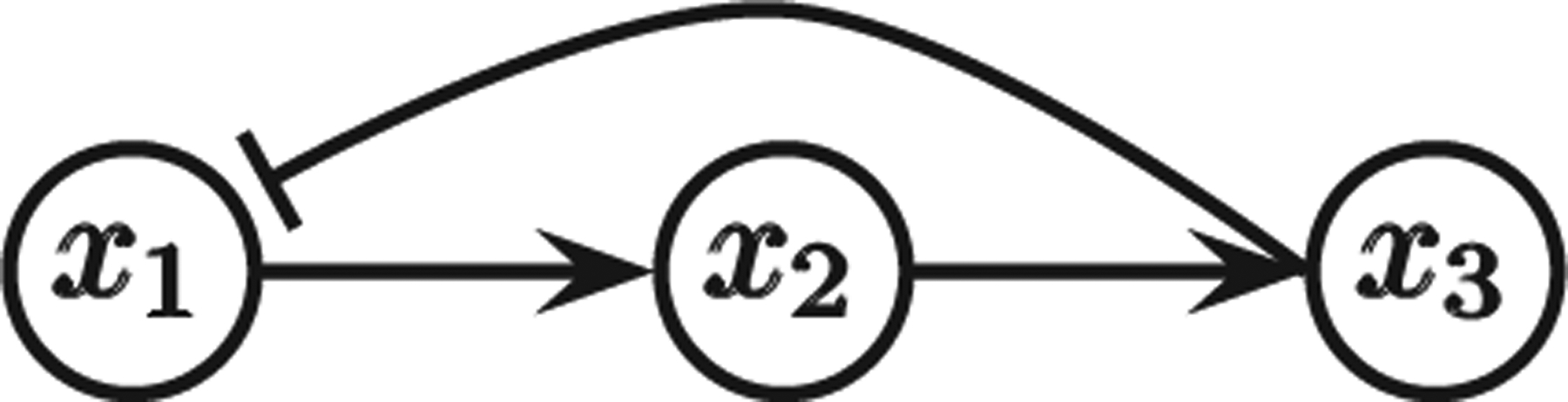
Network for the system in Eq. (5).

Lemma 2 [11] Consider a dynamical system (3) with associated directed labeled graph G. Then, (3) is monotone with respect to some orthant order if and only if all closed undirected chains of G have parity 1.

Note that the combinatorial characterization of monotonicity in Lemma 2 is via the absence of undirected closed chains of parity 1. Thus, in particular, any monotone system has

1. no negative feedback loops, and

2. no incoherent feed-forward loops.

However, some systems may not be monotone even if (a) and (b) hold; see Fig. 7 for an example.

FIG. 7.

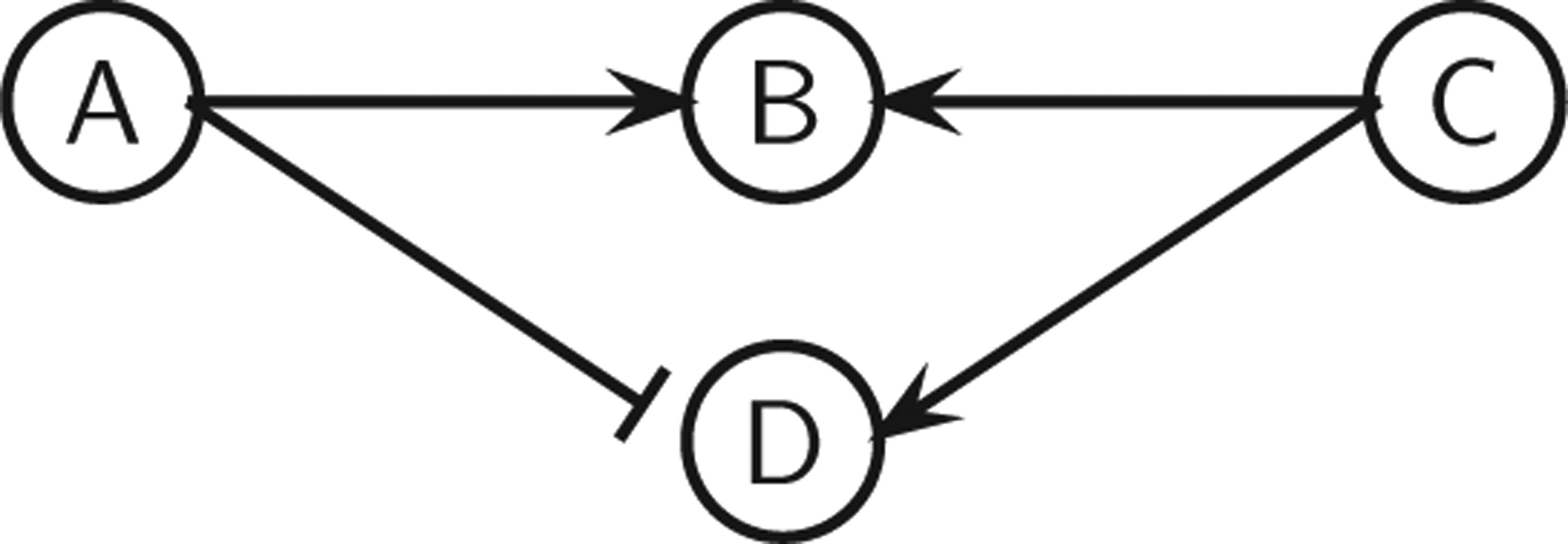
A nonmonotone system with no negative feedback loops and no incoherent feed-forward loops.

Lemma 2 leads in a natural manner to the following sign consistency (SC) problem to determine how monotone a system is [11,37].

• Problem name: Sign Consistency (SC).

• Instance: a directed graph G = (V,E) with an edge labeling function w : E ↦ {−1,1}.

• Valid Solution: vertex labelling function L : V → {−1,1}.

• Goal:maximize |F | where F = {(u,v) w(u,v) = L(u)L(v)} is a set of “consistent” edges.

Similar to our redundancy measure, we define the degree of monotonicity of a network to be

$$\text{M}=\frac{\left|F\right|}{\left|E\right|},$$ (6)

where F is the set of consistent edges in an optimal solution. The |E| term in the denominator of the above definition translates to a min-max normalization of the measure, and ensures that 0 < M < 1. Note that the higher the value of M is the more monotone the network is (cf. [11,37]).

A. Computing M

In [11] a semidefinite-programming (SDP) based approximation algorithm is described for SC that has a worst-case theoretical guarantee of returning at least about 88% of the maximum number of edges. The algorithm was implemented in MATLAB (the MATLAB codes are publicly available at [38]). Other algorithmic implementations of the SC problems are described in [37,39].

B. Computing correlation between M and ℞_new

After obtaining the ordered pair of six values $\left({\text{M}}_1,{℞}_{{\text{new}}_1}\right),\dots ,\left({\text{M}}_6,{℞}_{{\text{new}}_6}\right)$ of M and ℞_new for the first six networks in Table I, we computed the standard Pearson product moment correlation coefficient $r=\frac{{\sum }_{i=1}^6\left({℞}_{{\text{new}}_i}-\overline{{℞}_{\text{new}}}\right)\left({\text{M}}_i-\overline{\text{M}}\right)}{\sqrt{{\sum }_{i=1}^6{\left({℞}_{{\text{new}}_i}-\overline{{℞}_{\text{new}}}\right)}^2\sum {\left({\text{M}}_i-\overline{\text{M}}\right)}^2}}$, where $\overline{{℞}_{\text{new}}}=\frac{{\sum }_{i=1}^6{℞}_{{\text{new}}_i}}{6}$ and $\overline{\text{M}}=\frac{{\sum }_{i=1}^6{\text{M}}_i}{6}$ are the average redundancy and monotonicity values, respectively. The possible values of r always lie in the range [−1,1], and values −1 and 1 signify strongest negative and positive correlations, respectively. A p value for this correlation was calculated by a T test with two-tailed distribution and unequal variance to show the probability of getting a correlation as large as the observed value by random chance when the true correlation is zero.

VI. NETWORK DATA

We selected a total of 11 networks, seven biological ones and four social ones. We selected these networks with the following criteria in mind:

1. The biological networks were selected with an eye toward covering a diverse set of species on the evolutionary scale and toward covering networks of diverse natures (e.g., metabolic, transcriptional); a species tree of the biological organisms for our networks is shown in Fig. 8.

2. The social networks were selected covering interactions in different social environments.

3. The networks span a wide range on size (number of edges ranging from 135 to 24 316) and density (average degree ranging from 1.3 to 13.4) to demonstrate that our new redundancy measure can be computed efficiently for a large class of networks.

Table I provides more details and sources for these networks.

FIG. 8.

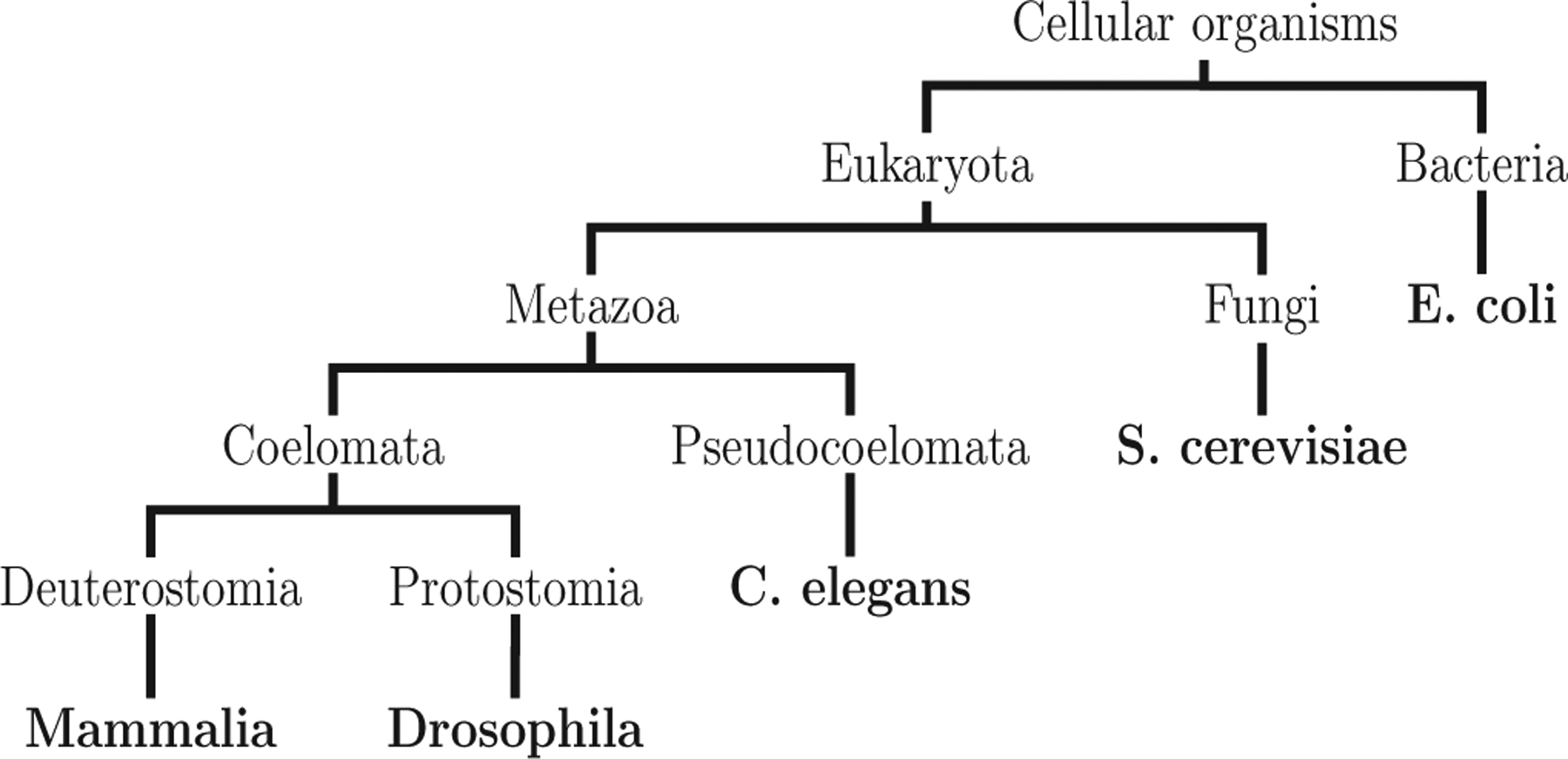
An unweighted species tree of the organisms for our biological networks, constructed using the Taxonomy Browser resources of NCBI [40]. The tree is not drawn to scale.

VII. RESULTS AND DISCUSSIONS

In Table II we show the tabulation of redundancy and, when appropriate, also monotonicity values for our networks. Because of their large sizes, p values for the redundancy measure could not be estimated very reliably for networks (9) and (10) since they require runs on many random networks, each of which would take upward of a week; thus we do not report p values for these networks. The extremely low p values in Table II indicate that the real networks’ redundancy values cannot be generated by a distribution that fits the redundancies of the equivalent random graphs.

Table II.

(a) Topological redundancy and (b) monotonicity values. Higher values of ℞_new (respectively, M) imply more redundancy (respectively, monotonicity). In general, a p value below 10⁻⁴ indicates statistical significance. N/A means not applicable; — indicates p value could not be computed in reasonable time with the current implementation of NET-SYNTHESIS because of its extensive disk access for networks that are too large or dense. Note that the p values depend not only on the average redundancies of the random networks but also on the higher order moments.

	(a) Redundancy			(b) Monotonicity M
Network	℞new	p value	Average redundancy of random networks
Biological networks
(1) E. coli transcriptional	0.062	1.43 × 10−29	0.188	0.796
(2) Mammalian signaling	0.434	4.4 × 10−52	0.576	0.593
(3) E. coli transcriptional	0.068	2.61 × 10−9	0.099	0.862
(4) T-LGL signaling	0.438	1.15 × 10−11	0.350	0.867
(5) S. cerevisiae transcriptional	0.060	9.34 × 10−43	0.228	0.926
(6) C. elegans metabolic	0.669	2.2 × 10−147	0.790	0.444
(7) Oriented S. cerevisiae protein interactions	0.481	3.68 × 10−111	0.593	N/A
Social networks
(8) Jazz musicians network	0.897	1.06 × 10−107	0.929	N/A
(9) E-mail network at University Rovira i Virgili	0.840	–	–	N/A
(10) Secure information interchange user network	0.486	–	–	N/A
(11) Enron e-mail network	0.352	2.14 × 10−68	0.377	N/A

If one prefers, a normalization of the redundancy values of the networks for which randomly generated networks are available can be performed as follows. For each of the nine networks, we first computed the standardized redundancy value for each of the 100 random networks to eliminate sampling bias (for a sample x₁,x₂, … ,x_m with average μ and standard deviation σ, the standardized value of x_i is given by $\frac{x_i-\mu }{\sigma }$). Then, we calculated the standardized range (difference between maximum and minimum) of these 100 standardized redundancy values. Finally, we normalized original redundancy value by dividing them by this standardized range. The resulting normalized values are shown in Table III (for comparison purposes, the normalized redundancy values are scaled so that their summation is exactly the same as the summation of original redundancy values). As can be seen, the ranks of both original and normalized values are almost the same [in the order (5), (1), (3), (11), (2), (4), (7), (6), (8) and (5), (1), (3), (11), (4), (2), (7), (6), (8), respectively] and the relative magnitudes of the values are similar whether one uses the normalized or original values, and thus all of our conclusions are valid in either case. Thus, in the rest of the paper, we use the original redundancy values with the understanding that all of our conclusions are valid for the normalized values as well.

Table III.

Normalization keeps relative magnitudes and ranks of values similar to that in the original.

	Networks
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(11)
Original redundancy ℞new	0.062	0.434	0.068	0.438	0.06	0.669	0.481	0.897	0.352
Normalized redundancy $\widehat{{℞}_{\text{new}}}$	0.048	0.364	0.070	0.319	0.043	0.708	0.497	1.112	0.295

In spite of our somewhat limited set of experiments, our results do point to some interesting hypotheses, which we summarize below.

A. ℞_new can be computed quickly for large networks and is statistically significant

As our simulations show, the new redundancy measure can be computed quickly for networks up to thousands of nodes; for example, typically NET-SYNTHESIS takes from a few seconds up to a minute for networks having up to 1000 nodes or edges. This is a desirable property of any redundancy measure so that it can be used by future researchers as biological and social networks grow in number and size. Moreover, the extremely low p values suggest statistical significance of the new measure.

B. Redundancy variations in biological networks

We focus our attention to the variations of the redundancy values for the five transcriptional/signaling biological networks in our data set and make the following observations.

a. Transcriptional versus signaling networks.

Networks (1), (3), and (6) are transcriptional networks with all having similar low redundancies (0.062, 0.068, and 0.06). On the other hand, network (2) is a signaling network and network (4) is also predominantly signaling, though it includes four transcriptional edges; these two mammalian signal transduction networks have similar midrange redundancies, namely 0.434 and 0.438, respectively. We hypothesize that in general transcriptional networks are less redundant than signaling networks. A straightforward supporting evidence for this is the higher average degree of signaling networks as compared to the transcriptional ones. Transcriptional networks have indeed been reported to have a feed-forward structure with few feedback loops and relatively low cross-talk [55], whereas [42] reports a large strongly connected component for their studied signaling networks (which makes it possible to reach almost any node from any input node).

b. Role of currency metabolites in redundancy of metabolite networks.

Our data source for the C. elegans metabolic network includes two types of nodes, the metabolites and reaction nodes, and the edges are directed either from those metabolites that are the reactants of a reaction to the reaction node, or from the reaction node to the products of the reaction. In this representation, redundant edges appear if both (one of) the reactant(s) and (one of) the product(s) of a reaction appear as reactants of a different reaction, or conversely, both (one of) the reactant(s) and (one of) the product(s) of a reaction appear as products of a different reaction. Because a reaction cannot go forward if one of its reactants is not present, the redundant edges are not biologically redundant and cannot be eliminated. Our result of a surprisingly high redundancy value for the metabolic network nevertheless indicates a high abundance of a pattern, which warrants further investigation.

One possibility we considered is that one of the reactions is essentially a dimerization of a compound and its slightly modified variant. However, we found no strong support for this case. Another possibility is that metabolites that participate in a large number of reactions will have a higher chance to be the reactant or product of such “redundant” edges. There is a biological basis for this possibility in the existence of currency metabolites. Currency metabolites (sometimes also referred to as carrier or current metabolites) are plentiful in normally functioning cells and occur in widely different exchange processes. For example, ATP can be seen as the energy currency of the cell. Because of their wide participation in diverse reactions, currency metabolites tend to be the highest degree nodes of metabolic networks. There is some discussion in the literature on how large the group of currency metabolites is, but the consensus list includes H₂0, ATP, ADP, NAD and its variants, NH4+, and PO4³⁻ (phosphate) [56,57].

Our data source for the C. elegans metabolic network indicates the identity of the 10 highest in-degree nodes (as a group) and the 10 highest out-degree nodes (as a group). Out of the 13 distinct nodes in the aggregate of these two groups, 11 belong in the consensus list of currency metabolites, leaving out co-enzyme A and L glutamate. We found that when we rank the nodes of the network by the number of redundant edges (as found by NET-SYNTHESIS) incident upon them and consider the top 17 nodes in this rank order, they include all the 13 highest degree nodes in the original networks. Thus we can conclude that the topological redundancy of the C. elegans metabolic network is largely due to its inclusion of currency metabolites.

C. Redundancy of social versus biological networks

The results in Table II seem to suggest that social networks are more redundant than biological networks. In fact, the two most redundant networks in the table are the two social networks (8) and (9) which have redundancies about twice that of any biological networks considered, and the remaining two social networks have redundancies comparable to the highest redundancy of the biological networks. We hypothesize that in general this is the case. This hypothesis is perhaps not very surprising in the context of past research as explained below.

The research work of Navlakha and Kingsford [58] suggests that biological networks may grow and evolve quite differently than social networks. In particular, they show that models for biological networks may perform poorly for social networks and vice versa. It is conceivable that different models may give rise to different magnitudes of redundancy.

Some previous research works (see e.g., [59–61]) ascertain that social networks tend to exhibit assortativity (i.e., highly connected nodes tend to be connected with other high degree nodes), whereas biological networks typically show dissortativity (i.e., high degree nodes tend to attach to low degree nodes). It is not difficult to see that such properties may lead to the difference in redundancies for the two types of networks; For example, in Fig. 9 an edge between two nodes of high degree results in removal of a large number of edges. To check the general hypothesis of assortativity for our specific networks, we computed the assortativity coefficient for a network as defined in [60]. This coefficient is calculated in the following manner. First, we ignore the direction of edges obtaining an undirected graph G = (V,E) from the given directed graph. Then, the assortativity coefficient r is computed by the following formula:

$$r=\frac{\frac{1}{\left|E\right|}{\sum }_{\{u,\upsilon \}\in E}{d}_u{d}_{\upsilon }-{\left[\frac{1}{2\left|E\right|}{\sum }_{\{u,\upsilon \}\in E}\left(d_u+d_{\upsilon }\right)\right]}^2}{\frac{1}{2\left|E\right|}{\sum }_{\{u,\upsilon \}\in E}\left[{\left(d_u\right)}^2+{\left(d_{\upsilon }\right)}^2\right]-{\left[\frac{1}{2\left|E\right|}{\sum }_{\{u,\upsilon \}\in E}\left(d_u+d_{\upsilon }\right)\right]}^2},$$

where d_u denotes the degree of a node u. It is known that −1 ⩽ r ⩽ 1, and more negative (respectively, more positive) values of r indicating more disassortativity (respectively, more assortativity) of the given network. As Table IV shows, all biological networks are disassortative, whereas all but one social network are assortative.

FIG. 9.

Adding the edge colored light gray may increase the redundancy of the social network drastically (removed edges shown as dotted).

Table IV.

Values of the assortativity coefficient r and the transitivity coefficient τ. Negative values of r indicate disassortativity whereas positive values of r indicate assortativity.

	Network index
	Biological							Social
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)
r =	−0.149	−0.106	−0.204	−0.089	−0.398	−0.060	−0.1377	+0.02	+0.07	+0.239	−0.44
τ =	0.037	0.010	0.007	0.043	0.005	0.047	0.017	0.255	0.058	–	0.013

Finally, social networks that are related to human behavior are often expected to exhibit a high degree of transitivity [62–64]. For example, the classical work of Leinhardt [64] asserts that the structure of interpersonal relations in children’s groups will progress in consistent fashion from less to more transitive organization as the children become older. Transitivity in this type of behavioral context translates to coherent type 1 feed-forward loops (i.e., feed-forward loops of the form A → B, B → C, and A → C), each of which contains a redundant edge, and thus higher transitivity immediately implies higher redundancy in our context. To check how far this general hypothesis holds for our specific networks, we calculated the transitivity coefficient for our networks. The transitivity coefficient τ of a directed network [65] is given by $\frac{{\mu }_3}{{\mu }_2+{\mu }_3}$ where μ₂ and μ₃ are the number of ordered triplets of vertices that have two and three edges among them, respectively. We used an obvious algorithm to calculate this value; τ could not be calculated within reasonable time for the social network (10) in Table I because of its large number of nodes and edges. As shown in Table IV, all the biological networks have small transitivity coefficients, and among the social networks, network (8) has a value of τ that is significantly more than any of the biological networks.

D. Redundancy, minimality, and orienting PPI networks

Protein interaction networks represent physical interactions among proteins. While many protein interactions have an orientation, the current maps of protein-protein interaction (PPI) networks are often unoriented (undirected) in part due to the limitations of the current experimental technologies such as [66]. Thus, there is an obvious interest in trying to orient these networks by, say, combining causal information at the cellular level. Unfortunately, most versions of the orientation problem is theoretically NP hard [67,68], and thus heuristics for such orientations may either not lead to all pathways of interest or lead to extra spurious pathways that are not supported [50,68].

Our calculation of redundancy values and minimal networks provides a way to gain insight into a predicted orientation of a PPI network and to determine whether the predicted oriented network has a level of redundancy similar to those in known biological networks. Obviously, the lower the value of ℞_new is, the more compact is the construction of the oriented network. However, one must also ensure that the minimal network also contains the right kind of pathways, (e.g., paths in the “gold standard”). To this effect, we describe the results of this approach via the NET-SYNTHESIS software on an oriented PPI network from [50].

We first briefly review the method by which the oriented PPI network used by us was generated. The starting point for the network consisted of all physical interactions among yeast proteins from version 2.0.51 of BIOGRID [69]. Edge weights were assigned based on the type and quantity of experimental support for each interaction, and low-weight edges were removed from the network. The network was oriented so as to maximize the weighted number of length-bounded paths between predetermined sources and targets, which were taken from yeast MAPK signaling pathways. The final set of 2435 edges included all oriented edges that belonged to any path with five or fewer edges between a source and target and edge weights were dropped for subsequent analysis. The sources, targets, PPI filtering, and orientation algorithm are described more fully in [50].

Now we discuss the paths in the nonredundant network (after reduction via NET-SYNTHESIS) that are present in the gold standard. Several of the short source-target paths in this network correspond to known yeast MAPK signaling pathways, specifically the pheromone response and filamentous growth pathways [70]. Figure 10 depicts the union of all linear paths in the nonredundant network that have multiple consecutive edges that match a gold standard path. The paths that matched a gold standard path are highly similar, and the common gold standard edges in these hits are Ste7 → Fus3, Fus3 →, Dig1, and Dig1 → Ste12.

FIG. 10.

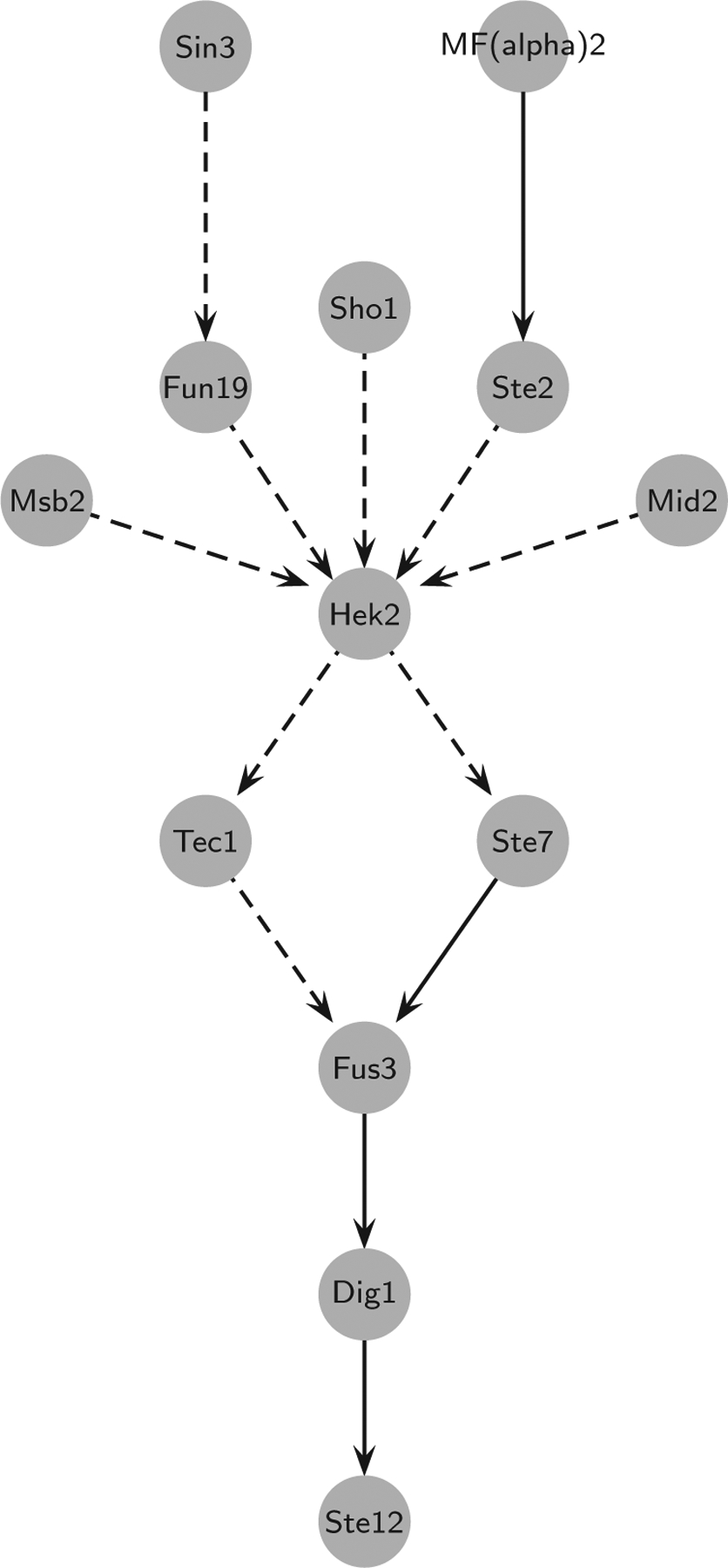
(Color online) Paths in the nonredundant oriented PPI network that match known yeast signaling pathways. Solid edges are present in the gold standard and dashed edges represent novel predictions.

E. Correlation between redundancy and network dynamics

The Pearson correlation coefficient between M and ℞_new is about −0.8 with a p value of 0.0066. Thus, monotonicity is negatively correlated to redundancy (i.e., higher values of redundancy are expected to lead to lower values of monotonicity and vice versa).

As explained before, monotonicity is known to be negatively correlated to negative feedback loops [11,71]. Negative feedback loops also tend to increase the redundancy of signal transduction networks; see Fig. 11 for an illustration. Indeed, strongly connected components with at least one negative feedback loop were called multiple parity components in [21] and played a significant role in redundancy calculations.

FIG. 11.

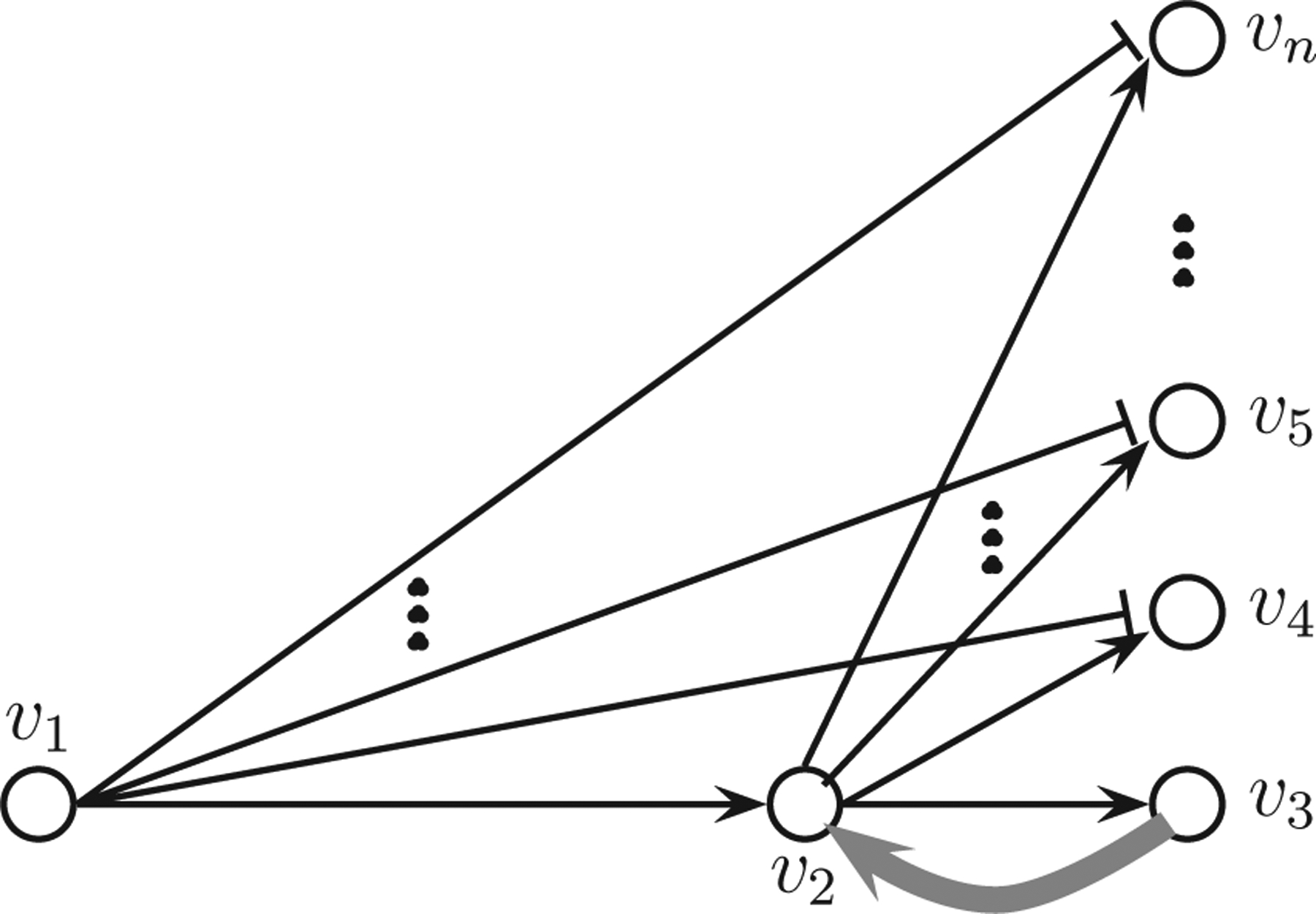
The network shown has no negative feedback loops and no redundant edges. However, if we replace the gray activation edge υ₃ → υ₂ to an inhibition edge υ₃ ⊣ υ₂, a negative feedback loop is created and this makes all the remaining inhibitory edges in the network redundant (e.g., the edge υ₁ ⊣ υ₄ is redundant because of the path υ₁ → υ₂ → υ₃ ⊣ υ₂ → υ₄).

Furthermore, recent results of Kwon and Cho [72] on the correlation between topological properties and robustness of networks are also consistent with the negative correlation that we obtained. The authors of that paper considered a weighted network model in which the state of each node is a real number in the range {−1,1} and the positive and negative weights of the connections represent the strengths of the excitory or inhibitory connections, respectively. A negative (respectively, positive) feedback loop is then defined to be a simple cycle with an odd (respectively, even) number of negative weights in the cycle, and the degree of robustness of a network is then defined by selecting a group of nodes randomly, perturbing the values of their states, and measuring the extent of change of states of various nodes in the network by computing the ratio of state values converging to a same final state to which the original initial state converged (biologically, this concept of robustness means the extent of maintaining the original stable state against given perturbations). Based on extensive simulation results, the authors concluded that networks with fewer negative feedback loops are likely to be more robust in their sense. More robustness with respect to perturbations suggests less influence of one node on another, and consequently fewer alternate pathways of the same nature from a node to another, indicating less redundancy values, whereas fewer negative feedback loops correspond to a higher degree of monotonicity. Thus, their observation is, at least on an intuitive level, consistent with our finding.

F. Significance of a minimal network

It is certainly an interesting question to ask if a topologically minimal network has similar dynamical or functional properties as the original network. Note that the question does not make sense for the four (static) social networks [networks (8), (9), (10), and (11) in Table I], since the individual nodes in these networks usually do not have well-defined functions or dynamics, and one of their most interesting properties, namely connectivity, is preserved in the minimal network. The redundancy issue of the metabolic network [network (6) of Table I] is explained separately in detail in Sec. VII B. There is no associated dynamics with the oriented PPI network [network (7) of Table I]. Thus, this question only applies for the first five biological networks [networks (1), (2), (3), (4), and (5)] in Table I. A dynamic description/model of these networks would characterize dynamic behaviors, such as stability and response to external inputs. When the network has designated outputs or read-outs, such as gene expression rates in transcriptional networks, it may be of interest to characterize the behavior of these outputs as a function of the inputs.

A topologically minimal network has the same input-output connectivity (reachability) as the original and thus the excitory or inhibitory influence between each input-output pair is preserved. It is minimal in the “information theoretic” sense in that any network with the same output behavior must be of at least this size. A correlation of the redundancy measure with the monotonicity of dynamics is explored in Sec. VII E. Will a topologically minimal network also have the same output behavior as the original one for the same input? In general, there is no such guarantee since the dynamics depend on what type of functions (“gate”) are used to combine incoming connections to nodes and the “time delay” in the signal propagation, both of which are omitted in the graph-theoretic representation of regulatory and signal-transduction networks such as (1)–(5) in Table I. For example, consider the two networks shown in Fig. 12 in which network (b) has a redundant connection A → C. The functions of these two circuits could be different, however, depending on the “gate” function used to combine the inputs B → C and A → C in network (b). Due to the shared A → B → C connectivity in the two networks, in both cases node C will be activated if A is continuously supplied. However, while network (a) merely implements a delay between C and A, the coherent type-1 feed-forward loop indicated in (b) is what [73] calls a “sign-sensitive delay element” that filters spikes in signals (low-pass filter) provided that an “AND” gate combines the inputs to node C; one example of such a circuit is that of the Arabinose system in E. coli [74]. In summary, deleting edges may result in functionalities that are not exactly the same.

FIG. 12.

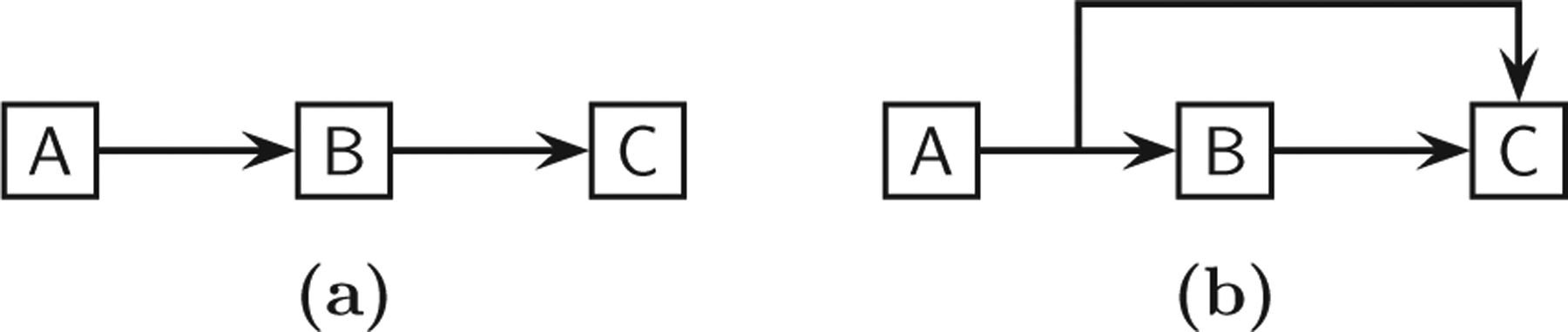
Equivalence of dynamics depends on node functions.

However, despite the fact that a minimal network may not preserve all dynamic properties of the original one, a significant application of finding minimal networks lies precisely in allowing one to identify redundant connections (edges). In this manner, one may focus on investigating the functionalities of these redundant edges (e.g., identifying the manner in which their effect is cumulated with those of the other regulators of their target nodes could be a key step toward understanding the behavior of the entire network).

Thus, the tools developed here are of general interest as they not only provide a quantified measure of overall redundancy of the network, but also allow their identification of redundancies and hence help direct future research toward the understanding of the functional significance of the added links.

VIII. AVAILABILITY OF DATA AND SOFTWARE

Most of the data for the original network as well as those for the random networks used in the calculation of p values for ℞_new are available from our Web site [75]. The NET-SYNTHESIS software for calculating redundancies is available from our Web site [16]. MATLAB codes for computing monotonicity values are available from our Web site [38].

IX. CONCLUSIONS

In this paper we have defined a new combinatorial measure of redundancy of biological and social networks, and have illustrated its efficient computation on several small and large networks. We also noted some interesting hypotheses that one could draw from these results such as:

1. Transcriptional networks are likely to be less redundant than signaling networks.

2. The topological redundancy of the C. elegans metabolic network is largely due to its inclusion of currency metabolites.

3. Social networks are prone to be more redundant than biological networks.

4. Our calculation of redundancy values and minimal networks provides a way to gain insight into a predicted orientation of a protein-protein-interaction (PPI) network and determine whether the predicted oriented network has a level of redundancy similar to those in known biological networks.

5. Our topology-based redundancy measure for biological signaling networks is statistically correlated with some measure of the dynamics of the network, namely higher redundancy is correlated to lower monotonicity and vice versa.

We believe that our fast and accurate computation of redundancy measure will help future researchers to further fine tune the measure and test it on a large-scale basis. An interesting question that has been partially addressed in the past literature but deserves further investigation is to determine the reasons of redundancy of various kinds of biological networks.