Successful Prediction of Human Steady‐State Unbound Brain‐to‐Plasma Concentration Ratio of P‐gp Substrates Using the Proteomics‐Informed Relative Expression Factor Approach

Abstract

In order to optimize central nervous system (CNS) drug development, accurate prediction of the drug’s human steady‐state unbound brain interstitial fluid‐to‐plasma concentration ratio (K_p,uu,brain) is critical, especially for drugs that are effluxed by the multiple drug resistance transporters (e.g., P‐glycoprotein, P‐gp). Due to lack of good in vitro human blood‐brain barrier models, we and others have advocated the use of a proteomics‐informed relative expressive factor (REF) approach to predict K_p,uu,brain. Therefore, we tested the success of this approach in humans, with a focus on P‐gp substrates, using brain positron emission tomography imaging data for verification. To do so, the efflux ratio (ER) of verapamil, N‐desmethyl loperamide, and metoclopramide was determined in human P‐gp‐transfected MDCKII cells using the Transwell assay. Then, using the ER estimate, K_p,uu,brain of the drug was predicted using REF (ER approach). Alternatively, in vitro passive and P‐gp–mediated intrinsic clearances (CLs) of these drugs, estimated using a five‐compartmental model, were extrapolated to in vivo using REF (active CL) and brain microvascular endothelial cells protein content (passive CL). The ER approach successfully predicted K_p,uu,brain of all three drugs within twofold of observed data and within 95% confidence interval of the observed data for verapamil and N‐desmethyl loperamide. Using the in vitro–to–in vivo extrapolated clearance approach, K_p,uu,brain was reasonably well predicted but not the brain unbound interstitial fluid drug concentration‐time profile. Therefore, we propose that the ER approach be used to predict K_p,uu,brain of CNS candidate drugs to enhance their success in development.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

☑ Accurately predicting unbound brain interstitial fluid (ISF) concentrations of CNS drugs is challenging, especially when drugs are substrates of efflux transporters (e.g., P‐glycoprotein). This is one reason why development of CNS drugs has a high attrition rate.

• WHAT QUESTION DID THIS STUDY ADDRESS?

☑ We determined whether the proteomics‐informed relative expression factor (REF) approach can successfully predict the unbound human brain ISF distribution of drugs at steady state or pseudoequilibrium.

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

☑ For the first time, we showed that human K_p,uu,brain, the unbound brain‐to‐plasma concentration ratio, of three selective P‐gp substrates can be successfully predicted using the proteomics‐informed REF approach.

• HOW MIGHT THIS CHANGE CLINICAL PHARMACOLOGY OR TRANSLATIONAL SCIENCE?

☑ Adopting the proteomics‐informed REF approach to predict steady‐state/pseudoequilibrium drug concentrations in the brain ISF should allow improved success in CNS drug development.

Despite more than $1 billion expended per drug candidate, new drugs targeting the central nervous system (CNS) suffer from a high attrition rate, mainly due to lack of efficacy in phase III clinical trials.¹ One potential contributor to this lack of efficacy is that insufficient therapeutic concentrations of the drug are achieved at the target site. This is a particular challenge for CNS drugs as the blood‐brain barrier (BBB) restricts the entry of drugs into the CNS by forming a tight barrier and by actively effluxing drugs via the multiple drug resistance transporters, such as P‐glycoprotein (P‐gp) and breast cancer resistance protein (BCRP), that are highly expressed at the BBB.², ³ For substrates of these transporters, such efflux results in steady‐state unbound drug concentrations in the interstitial fluid of the brain (ISF), where most CNS drugs interact with their targets,⁴ that are lower than the corresponding unbound drug concentration in the plasma. This is reflected by K_p,uu,brain, the unbound brain‐to‐plasma concentration ratio at steady state, < 1. The greater the fraction transported by the efflux transporter (f _t), the lower the K_p,uu,brain.

K_p,uu,brain and ISF concentrations can be directly measured in humans by intracerebral microdialysis.⁵ However, this approach is highly invasive and therefore neither practical nor ethical. Other methods have been proposed to indirectly estimate or predict K_p,uu.brain: measurement of cerebrospinal fluid drug concentrations by lumbar puncture, positron emission tomography (PET) imaging, allometry scaling from studies in preclinical species, and in vitro–in vivo extrapolation (IVIVE) using human primary or immortalized brain microvascular endothelial cells (BMEC). However, all of these have important shortcomings limiting their applicability and/or reliability, namely, validity of extrapolation to brain ISF (cerebrospinal fluid drug concentration), technical and budgetary challenges (PET imaging), validity of the preclinical‐to‐clinical translation (allometry), and primary BMEC availability.⁶, ⁷

Considering this important gap, we and others have proposed a novel and innovative method to predict human K_p,uu,brain using the proteomics‐informed relative expression factor (REF) approach. Briefly, the in vivo human drug K_p,uu,brain is predicted by scaling the in vitro K_p,uu of the drug, measured in cells overexpressing the transporter of interest, using REF. The REF is the abundance of the transporter in the transporter‐expressing cells vs. the human BMEC. These transporter abundances are quantified by quantitative targeted proteomics.⁸ This approach assumes that the affinity of the drug for the transporter of interest in vitro (in cells overexpressing the transporter) is the same as that in vivo while the maximal velocity (V_max) of drug transport differs between in vitro and in vivo only because of difference in transporter abundance. This approach has recently been shown to have relatively good predictions of animal K_p,uu,brain.⁹, ¹⁰, ¹¹ However, its success has not been demonstrated in humans. To apply this approach to humans, brain drug concentration‐time data (obtained by noninvasive PET imaging) of drugs selectively transported at the human BBB (e.g., by P‐gp) need to be available. This study focuses on selective P‐gp substrate drugs, though limited in number, for which such data are available. Therefore, the primary objective of this study was to first predict the human K_p,uu,brain of drugs with varying P‐gp f_t using the REF approach. Then, to verify these predictions using the corresponding PET imaging data in humans obtained by us and others.¹², ¹³, ¹⁴, ¹⁵ Our secondary objective was to use the REF approach to dynamically predict (not just at steady state) human brain ISF drug concentrations. We chose to study three P‐gp substrates that have varying P‐gp f_t values and for which human PET imaging data are available: verapamil (f_t ~ 0.83),¹², ¹⁵ N‐desmethyl loperamide (f_t ~ 0.95),¹³ and metoclopramide (f_t ~ 0.43).¹⁴ Our criteria for successful verification were to predict these K_p,uu,brain values, or to dynamically predict the area under the concentration‐time curve (AUC) in the ISF of the drugs, within twofold of the observed values.

MATERIALS AND METHODS

Materials

See Supplementary Materials.

Methods

Cell culture

On day 0, 6 × 10⁵ Madin‐Darby canine kidney cells knock‐out (KO) for canine P‐gp and overexpressing human P‐gp (MDCK‐hMDR1^cMDR1‐KO)¹⁶, ¹⁷ (kindly provided by Dr Per Artusson, Uppsala University, Sweden) were seeded onto 12 mm, 0.4‐µm polyester Transwell filter inserts (Corning, Kennebunk, ME) and allowed to differentiate for 4 days before use on day 4. The medium was changed on day 3. See Supplementary Materials for details.

Transport experiments

On day 4, confluent cells, grown as a monolayer, were washed twice with prewarmed Hank's balanced salt solution (with calcium and magnesium) buffered at pH 7.4 with 10 mM N‐2‐hydroxyethylpiperazine‐N‐2‐ethane sulfonic acid (HEPES) and incubated for 15 minutes at 37°C in an orbital shaker (New Brunswick Scientific, Edison, NJ) rotating at 120 rpm before use. Assays were performed (in triplicate) with 300 nM [³H]verapamil (1.67 Ci/mmol), 3 µM N‐desmethyl loperamide, or 500 nM metoclopramide, in absence or presence of 5 µM tariquidar (TRQ) (added to both donor and receiver compartments). Transport studies were initiated by adding the drugs in transport buffer to the donor compartment. For A → B transport, the donor is the A compartment (apical, volume 0.5 mL), and the receiver, the B compartment (basal, volume 1 mL). For B → A transport, the donor is the B compartment and the receiver is the A compartment. Drug concentrations were chosen to be in the range where the A > B apparent drug permeability was independent of the drug concentrations as per available¹⁸ or in‐house (not shown) data. Samples were drawn from both donor (5–10 µL) and receiver (100 µL) compartments at multiple timepoints (0–6 hours for [³H]verapamil, 0–2 hours for N‐desmethyl loperamide, and 0–2 hours for metoclopramide). The receiver compartment was replenished by adding 100 µL of incubation medium not containing the substrate. At the end of the experiment, cells were washed three times, lysed, and total protein content measured. Simultaneously, in different wells, control transport experiments were conducted as above with a P‐gp probe drug, quinidine (2 µM), and Lucifer Yellow (50 µM) or [¹⁴C]mannitol (0.1 µCi/mL) as paracellular markers (to evaluate the integrity of the cell monolayer). Four independent transport experiments (passages 2–15) were performed for each drug. See Supplementary Materials for details.

Quantification of test compounds

[³H]verapamil was quantified by scintillation counting (PerkinElmer, Waltham, MA) while unlabeled compounds (verapamil, N‐desmethyl loperamide, and metoclopramide) were quantified by liquid chromatography with tandem mass spectrometry on Acquity ultraperformance liquid chromatography system (Waters, Milford, MA) coupled to an AB Sciex Triple Quad 6500 (SCIEX, Framingham, MA) (see Supplementary Materials for details).

Proteomic quantification of P‐gp abundance in MDCK‐hMDR1^cMDR1‐KO cells

For every experiment, P‐gp total cell membrane abundance (pmol/mg protein) was quantified (in duplicate) in the cell lysates following reduction, alkylation and digestion as previously described (Wang et al. 2015). Surrogate light and heavy peptides NTTGALTTR, chosen based on previously described criteria,¹⁹ were quantified by liquid chromatography coupled with tandem mass spectrometry (See Supplementary Materials for details). P‐gp REF was calculated as follows:

$$\text{REF}=\frac{\text{P - gp}\text{abundance}\text{in}\text{human}\text{brain}\text{tissue}(\text{pmol}/\text{mg}\text{BMEC}\text{protein})}{\text{P - gp}\text{abundance}\text{in}\text{P - gp}\text{expressing}\text{cells}(\text{pmol}/\text{mg}\text{protein})}$$ (1)

where BMEC were isolated from human brains as described before.⁸

IVIVE of K_p,uu,brain

We predicted the in vivo K_p,uu,brain using two methods. Method 1 used the in vitro efflux ratio (ER) (in MDCK‐hMDR1^cMDR1‐KO cells) and scaled it to in vivo to estimate K_p,uu,brain using P‐gp REF (Eq. 1). Since K_p,uu,brain.,is a steady‐state value and a net result of the bidirectional clearances across the BBB, this method cannot provide unique estimates of these clearances (CLs) and therefore cannot allow dynamic predictions of the ISF drug concentration‐time profiles. To obtain the latter, we used method 2 where we first estimated, using a five‐compartment (5C) model, the in vitro intrinsic clearances of drug flux across the MDCK cells in the Transwell assay. Then, these in vitro CLs were extrapolated to in vivo using BMEC protein content (passive diffusion CL) or the REF approach (P‐gp–mediated CL) to estimate both the K_p,uu,brain and ISF drug concentration‐time profiles.

IVIVE of K_p,uu,brain from in vitro ER (method 1)

The in vitro steady‐state ER, in the presence (ER_TRQ(+)) and absence (ER_TRQ(‐)) of tariquidar, was calculated as follows:

$$\text{ER}=\frac{{\text{cA}}_{\text{R,BA}}·{\text{AUC}}_{\text{D,AB}}}{{\text{cA}}_{\text{R,AB}}·{\text{AUC}}_{\text{D,BA}}}$$ (2)

where cA_R,BA and cA_R,AB represent the cumulative amount of compound in the receiver compartment (corrected for drug amount sampled from compartment over the course of the experiment), calculated from the slope of the amount of compound measured in the receiver compartment vs. time multiplied by the duration of the experiment (6 hours for verapamil, 2 hours for N‐desmethyl loperamide, and 1 hour for metoclopramide, timepoints during which the drug appearance in the receiver compartment remained linear), in BA and AB experiments, respectively; AUC_D,AB and AUC_D,BA represent the AUC in the donor compartment, in AB and BA experiments, respectively, calculated using the trapezoidal method. This method for the calculation of ER was preferred over the traditional method (which is based on the donor concentration at time zero) because it corrects for depletion of the drug in the donor compartment.

K_p,uu,brain is equal to the ratio of the unbound CL into the brain and the sum of those exiting the brain. The latter is the sum of efflux unbound CL from the brain back to the blood, the unbound metabolic CL in the brain tissue, and the bulk flow.²⁰ Cerebral metabolism was assumed to be negligible. For small lipophilic drugs such as the ones used in this study (logD_pH7.4 0.79–3.49), we assume that bulk flow << passive diffusion at the BBB. Under these assumptions, K_p,uu,brain can be simplified as the ratio of the unbound CL from the blood into the tissue and that from the brain tissue back to the blood. Thus, ER is inversely related to K_p,uu,brain. When active efflux is present, these two parameters will deviate from unity (ER > 1 or K_p,uu,brain < 1) and K_p,uu,brain can be extrapolated from in vitro to in vivo using REF, as described previously,⁹, ¹⁰, ¹¹ using the following equation:

$${\mathrm{K}}_{\text{p,uu,brain, pred}\left(\text{method 1}\right)}=\frac{1}{\left({\text{ER}}_{\text{TRQ}\left(‐\right)}‐{\text{ER}}_{\text{TRQ}\left(+\right)}\right)·\text{REF}+1}$$ (3)

IVIVE of K_p,uu,brain from in vitro intrinsic CL (method 2)

A 5C model (Figure  1, upper panel) was built in Phoenix 8.1 (Certara, Princeton, NJ) to obtain estimates of intrinsic passive and P‐gp–mediated CL (see Supplementary Materials for the differential equations used). The volume of the cells was estimated as a function of the measured protein amount in each well (5.05 µL/mg total protein + 0.41 µL²¹). The volumes of the apical and basal membranes were assumed to be 5% of V_cell each.²² In this model (Figure  1a), the brain compartment is a combination of the brain ISF and the parenchymal cells, assuming that unbound concentrations in the ISF and the parenchymal cells are the same. Passive CL into and out of the membrane are represented by Cl_int,i and Cl_int,o, respectively, and assumed to be the same. MDCKII cells have been previously shown to present microvilli on their apical membrane, resulting in higher passive CL on the apical vs. the basal membrane. As CL is the product of permeability and surface area, the passive diffusion CL of the drug across the basal membrane (Cl_int,i,2 = Cl_int,o,2) was assumed to be a fraction of that across the apical membrane (Cl_int,i,1 = Cl_int,o,1), as follows:

$${\text{Cl}}_{\text{int},i,2}={\mathrm{f}}_{\text{SA}}·{\text{Cl}}_{\text{int},i,1}$$ (4)

where f_SA was assumed to be 0.12, the ratio of the surface area at the basal (2) vs. apical (1) membrane.²³ The free intracellular fraction of the drug (f_u,c) was assumed to be equal to the free fraction of the drug in the cell lysate (see Supplementary Materials for details).

Figure 1.

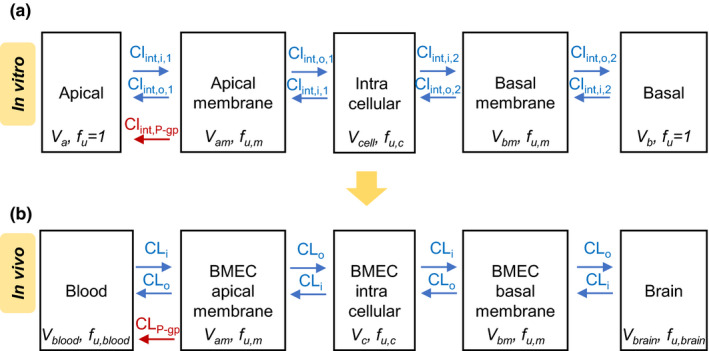
Five‐compartment (5C) models used to estimate in vitro intrinsic clearances and simulate in vivo brain concentrations using the in vitro–to–in vivo extrapolated (proteomics‐informed) clearances. (a) The 5C model, fitted to the in vitro Transwell data (donor, receiver, cell lysate), was composed of the donor and receiver chambers (apical or basal), cell membranes (apical and basal), and intracellular compartment. Volumes of the intracellular cell compartment and membranes were estimated as a function of total protein content in each well. Unbound fraction in the cell (homogenate) was estimated using ultrafiltration. The in vitro passive diffusion intrinsic clearance into and out of the membranes (Cl_int,i and Cl_int,o, respectively) were set as equal and were adjusted for the difference in surface area between the apical (due to presence of microvilli) and basal membrane. (b) The above 5C model was translated to in vivo, except the passive diffusion clearance across the apical and basal membrane was set as equal (microvilli are absent on the luminal membrane of the BBB). BBB, blood‐brain barrier; BMEC, brain microvascular endothelial cells; CL, clearance; CL_i, passive in vivo CL into the membrane; Cl_int,i, passive intrinsic uptake clearance into the membrane; Cl_int,o, passive intrinsic CL out of the membrane; Cl_int,P‐gp, P‐gp (P‐glycoprotein)‐mediated intrinsic clearance; CL_o, unbound in vivo passive diffusion out of the membrane CL; f_u, unbound fraction; f_u,blood, unbound fraction in the blood; f_u,brain, unbound fraction in the brain; f_u,c, unbound intracellular fraction; f_u,m, unbound fraction in membranes; V_a, apical chamber volume; V_am, volume of the apical membrane; V_b, basal chamber volume; V_blood, blood volume; V_bm, volume of the basal membrane; V_brain, brain volume; V_c, BMEC intracellular compartment volume; V_cell, intracellular volume. [Colour figure can be viewed at wileyonlinelibrary.com]

The model was simultaneously fitted to both the A → B and B → A data (donor, receiver, and cell lysate) in the presence of tariquidar to obtain estimates of the unbound fraction in the membrane (f_u,m) and Cl_int,i,1. Then, these parameters were fixed, and the model was simultaneously fitted to the A → B and B → A data in absence of tariquidar to estimate P‐gp–mediated CL (Cl_int,P‐gp). The goodness of fit was evaluated by visual inspection of the simulated and observed data as well as the weighted residuals plots (the Poisson error model was used).

The estimated intrinsic CLs were then extrapolated from in vitro to in vivo using the following equations:

$${\text{CL}}_i={\text{Cl}}_{\text{int},i,1}\left(\frac{\text{mL}/s}{\text{mg}\text{prot}}\right)·\text{BMEC}\text{protein}\text{yield}\left(\frac{\text{mg}\text{prot}}{\mathrm{g}\text{tissue}}\right)·\text{mass}\text{brain}\left(\mathrm{g}\text{tissue}\right)$$ (5)

$${\text{CL}}_{\text{P - gp}}={\text{Cl}}_{\text{int},\text{P - gp}}\left(\frac{\text{mL/s}}{\text{mg}\text{prot}}\right)·\frac{\text{P - gp}\text{abundance}\text{ex}\text{vivo}(\text{pmol/g}\text{tissue})}{\text{P - gp}\text{abundance}\text{in}\text{vitro}\left(\text{pmol/mg}\text{prot}\right)}·\text{mass}\text{brain}\left(\mathrm{g}\text{tissue}\right)$$ (6)

Average BMEC protein yield (0.99 mg/g gray matter) and P‐gp abundance (9.11 pmol/g gray matter) ex vivo values were previously obtained in our lab, using the same proteomic quantification method used to quantify the in vitro cell abundance of P‐gp.⁸ For scaling from gray matter to total brain, based on in‐house data, we assumed that total protein content was reduced fourfold in white matter vs. gray matter, but had the same P‐gp abundance relative to total protein content (as suggested from similar cerebral extraction ratio (cER) in gray and white matters observed by Eyal et al.¹²). The ratio of gray matter–to–white matter was set to 1.3.²⁴

K_{p,uu,brain,pred(method 2)} was then calculated as follows:

$${\mathrm{K}}_{\text{p,}\text{uu,}\text{brain,}\text{pred}\left(\text{method}2\right)}=\frac{{\text{CL}}_i}{{\text{CL}}_o+{\text{CL}}_{\text{P - gp}}}$$ (7)

with CL_i equal to CL_o (unbound passive diffusion CL).

Predictions of unbound concentrations in the ISF from the IVIV extrapolated intrinsic CL using a 5C model (method 2)

Unbound concentrations of verapamil, N‐desmethyl loperamide, and metoclopramide in the ISF were simulated in SAAMII using a 5C model (Figure  1b) and the mean IVIV extrapolated CL_i and CL_P‐gp values (see Supplementary Materials for differential equations). As described previously, blood concentrations measured by PET imaging were used as a forcing function (i.e., as a driving force for movement of drug from blood to the brain across the BBB). In the in vivo model, in contrast to the in vitro model, the passive diffusions on the apical and basal membranes were assumed to be the same because of the absence of microvilli in BMEC.²⁵ See Table  S1 for parameters used for simulation of brain concentration‐time profiles.

Verification of IVIVE approaches using human PET imaging data

We verified our predictions using human observed K_p,uu,brain (K_{p,uu,brain,obs}) values as well as observed brain concentrations obtained from the previously published PET imaging studies.¹², ¹⁴, ²⁶ For verapamil and N‐desmethyl loperamide, K_{p,uu,brain,obs} was calculated from the cER generated by Eyal et al. (in gray matter)¹² and Kreisl et al. (in the composite neocortex),²⁶ as follows:

$${\mathrm{f}}_{t\text{,obs}}=1‐\text{cER}=1‐\frac{K_1}{\text{cBF}}$$ (8)

$${\mathrm{K}}_{\text{p,uu,brain, obs}}=1‐{\mathrm{f}}_t=\text{cER}=\frac{K_1}{\text{cBF}}$$ (9)

Where f_t is the fraction of drug effluxed by transporters at the human BBB. The cER reflects the ability of the brain to extract the compound from the systemic compartment and is defined as the cerebral uptake CL (K₁) divided by the cerebral blood flow (cBF). Of note, identical cER values were previously reported for verapamil in the white and the gray matter,¹² suggesting similar K_p,uu,brain in gray and white matter.

For metoclopramide, a weak substrate of P‐gp, K₁ was not impacted by P‐gp inhibition in humans (using cyclosporine as an inhibitor).¹⁴ Therefore, K_{p,uu,brain,obs} was calculated from the tissue volume of distribution V_T (a PET imaging term equivalent to K_p,brain) as follows:

$${\mathrm{K}}_{\mathrm{p},\text{uu},\text{brain},\text{obs}}={\mathrm{K}}_{\mathrm{p},\text{brain}}·\frac{{\mathrm{f}}_{\mathrm{u},\text{brain}}}{{\mathrm{f}}_{\mathrm{u},\mathrm{p}}}$$ (10)

The observed unbound brain concentration‐time profiles were obtained by correcting the observed total brain concentrations measured by PET imaging¹³, ¹⁴, ¹⁵ for blood content (4.4%)²⁷ and converting total concentrations to unbound using f_u.brain (see Supplementary Materials for details). For all three compounds, concentration‐time profiles of verification data were limited to 20 minutes after PET tracer administration during which metabolism of the drug was minimal. For the 5C model, the simulated unbound brain concentrations were calculated as the sum of the total amount of the drug in the BMEC compartments (apical and basal membranes + intracellular) and the brain compartment divided by the sum of the volume of those four compartments, multiplied by the unbound fraction in brain homogenate (f_u,brain).

Statistical analyses

A Spearman test was used to assess the correlation between the change in in vitro P‐gp abundance and the corresponding active efflux ratios. The 95% confidence intervals of the observed values were calculated from the reported arithmetic mean, standard deviation and sample size of the data set. The Welch’s t‐test was used to detect statistically significant differences between the predicted and observed K_p,uu,brain values. For all tests, the significance threshold was set to P = 0.05.

RESULTS

Human K_p,uu,brain values were well predicted by the ER approach

For all three drugs, the average predicted K_{p,uu,brain,pred(method 1)} (i.e., from the in vitro ER) fell within twofold of the K_{p,uu,brain,obs} obtained in the PET imaging studies (Figure  2). Moreover, the predicted K_{p,uu,brain,pred(method 1)} for verapamil and N‐desmethyl loperamide fell within the 95% confidence interval (CI_95%) of the in vivo K_{p,uu,brain,obs} (Table  1 and Figure  2).

Figure 2.

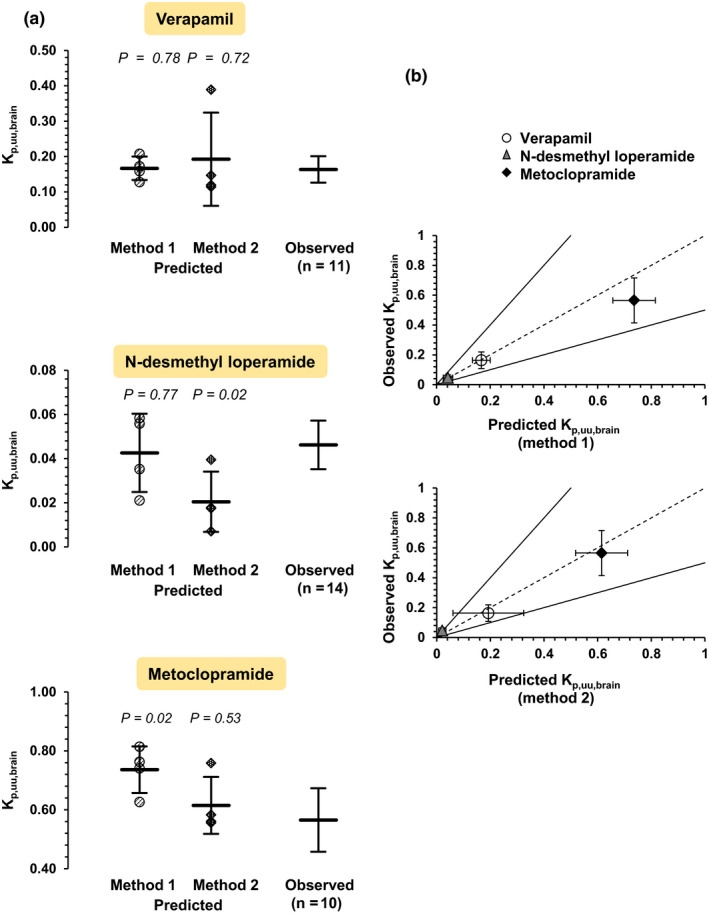
Verification of predictions of K_p,uu,brain values of the three drugs by the observed PET imaging data.¹², ¹³, ¹⁴ (a) Individual predicted K_p,uu,brain values (with mean ± standard deviation of four independent experiments) are shown for method 1 (i.e., from in vitro ER (efflux ratio)) and method 2 (i.e., from in vitro CL (intrinsic clearances)). The average observed values with their CI_95% (95% confidence intervals) are also shown. The predicted K_p,uu,brain using method 1 fell within the CI_95% of the observed in vivo K_p,uu,brain for verapamil and N‐desmethyl loperamide, and there was no statistically significant difference between the predicted and observed values. For metoclopramide, there was a statistically significant difference between the predicted and observed values, and the predicted K_p,uu,brain did not fall within the CI_95% of the observedin vivo K_p,uu,brain. Using method 2, the predicted K_p,uu,brain for verapamil and metoclopramide were within CI_95% of the observed values. Similarly, there was no significant difference between the predicted and observed values for the two drugs. This was not the case for N‐desmethyl loperamide (underestimation greater than twofold and significant difference between predicted and observed values). Statistically significant differences between observed and predicted K_p,uu,brain values were assessed by the Welch’s t‐test. (b) The predicted K_p,uu,brain values using method 1 were within twofold (continuous lines) of the observed values as measured by PET imaging. For method 2, the predicted K_p,uu,brain values were within twofold of observed values for verapamil and metoclopramide but not for N‐desmethyl loperamide (predicted/observed: 0.44). Vertical and horizontal error bars represent the standard deviations of the observed (n = 11 for verapamil, n = 14 for N‐desmethyl loperamide, n = 10 for metoclopramide) and predicted values (n = four experiments), respectively. The dashed line is the line of unity. K_p,uu,brain, steady‐state unbound brain interstitial fluid‐to‐plasma concentration ratio; PET, positron emission tomography. [Colour figure can be viewed at wileyonlinelibrary.com]

Table 1.

Predicted K_p,uu,brain using method 1, i.e., from in vitro ER

Compound	Exp.	ERTRQ(‐)	ERTRQ(+)	ERTRQ(‐) ‐ ERTRQ(+)	REF	Kp,uu,brain,pred(method 1)		Kp,uu,brain,obs (CI95%)	P/O
						Individual	Mean ± SD
Verapamil	1	2.94	0.76	2.18	2.20	0.17	0.17 ± 0.03	0.16 (0.13–0.20)	1.02
	2	2.97	0.76	2.21	2.39	0.16
	3	3.59	0.71	2.88	2.37	0.13
	4	3.73	0.83	2.90	1.32	0.21
N‐desmethyl loperamide	1	18.28	0.86	17.42	0.97	0.056	0.043 ± 0.018	0.046 (0.035–0.057)	0.92
	2	26.21	0.82	25.39	1.83	0.021
	3	55.00	0.98	54.02	0.30	0.058
	4	119.43	0.82	118.61	0.23	0.035
Metoclopramide	1	1.87	0.70	1.17	0.30	0.74	0.74 ± 0.08	0.57 (0.46–0.67)	1.30
	2	1.79	0.92	0.87	0.36	0.76
	3	3.56	1.03	2.53	0.24	0.63
	4	2.98	1.68	1.30	0.18	0.81

CI_95%, 95% confidence interval; ER, efflux ratio; Exp., experiment; K_p,uu,brain, unbound brain‐to‐plasma concentration ratio; P/O, predicted/observed K_p,uu,brain ratio; REF, relative expression factor (measured by targeted proteomics); TRQ, tariquidar.

While the differences in the ERs in the absence and presence of tariquidar in the Transwell assays for verapamil and metoclopramide were relatively consistent between experiments, this was not the case for N‐desmethyl loperamide. Of the three drugs, the difference in ERs for N‐desmethyl loperamide was the largest and therefore most sensitive to changes in P‐gp abundance (Table  1). Indeed, the trend in change in N‐desmethyl loperamide ER was consistent with the change in P‐gp abundance (Table  1 & Figure  2). There was a significant positive correlation (Spearman’s ρ = 0.60; P = 0.04) between change in ER and change in P‐gp abundance (expressed for each drug as fold‐change relative to the lowest P‐gp abundance) when the data for all three drugs were pooled (Figure  3).

Figure 3.

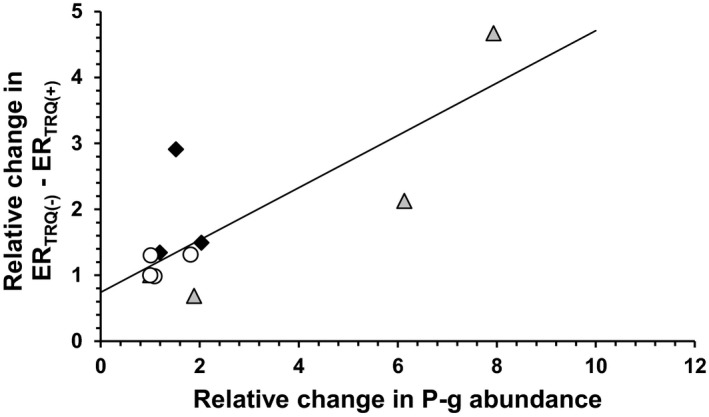
Significant positive correlation (Spearman’s ρ = 0.60, P = 0.04; continuous line) between interexperiment (relative) fold‐change in total P‐gp abundance (in pmol per mg total protein) and the corresponding fold‐change in the difference between efflux ratios in absence (ER_TRQ(‐)) and in presence (ER_TRQ(+)) of tariquidar in the Transwell experiments. The x‐axis data for each drug were expressed relatively to the lowest P‐gp abundance in experiments conducted for a given drug. Empty circles, verapamil; gray triangles, N‐desmethyl loperamide; black diamonds, metoclopramide. P‐gp, P‐glycoprotein. [Colour figure can be viewed at wileyonlinelibrary.com]

Human K_p,uu,brain values were well predicted by the CL approach

The fit of the 5C model to the in vitro data (concentrations in donor and receiver chambers) was acceptable (Figure  4). K_{p,uu,brain,pred(method 2)} values, predicted from the average IVIV extrapolated passive and P‐gp–mediated CL were within twofold of the observed data for all drugs and within CI_95% of the observed values for verapamil and metoclopramide, but not for N‐desmethyl loperamide (underestimation greater than twofold) (Table  2 and Figure  2).

Figure 4.

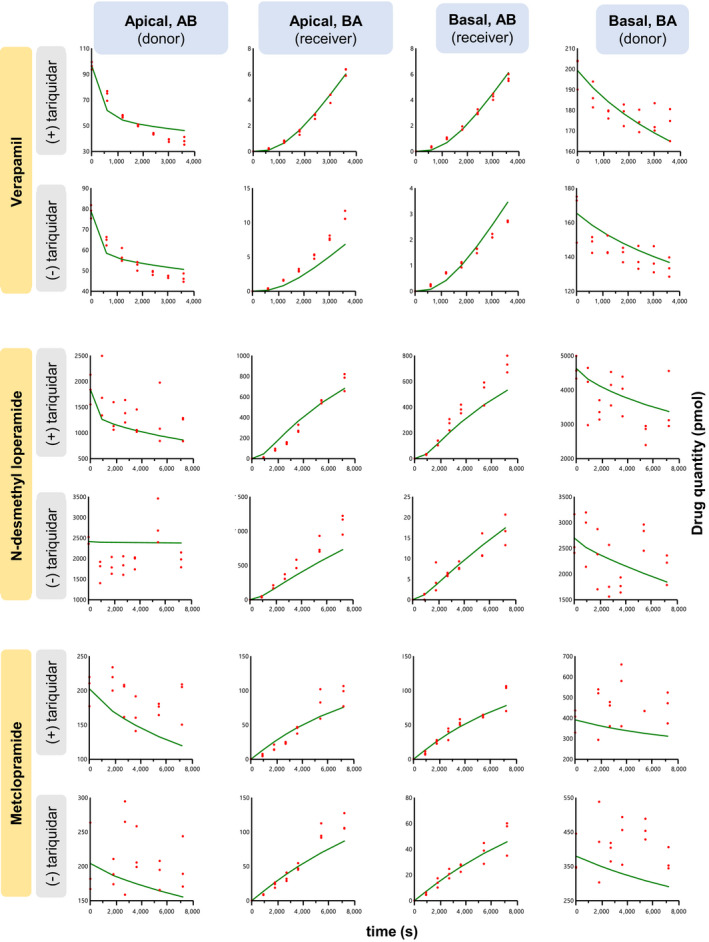
Observed (red dots) in vitro Transwell data (amount, pmol) and the corresponding predicted values (green lines) using the five‐compartmental (5C) model in the absence and presence of tariquidar (P‐gp inhibitor). The model predicted the amount in the receiver compartment well, but, due to the scatter in the data, did not predict as well the amount in the donor compartment (N‐desmethyl loperamide and metoclopramide). Intrinsic in vitro clearances were estimated as follows: Passive diffusion clearances and f_u,m (unbound fraction in membrane) were estimated from (+) tariquidar data sets. After fixing these parameters to these estimates, P‐gp–mediated clearance was estimated from (−) tariquidar data sets. In all instances, parameters were estimated by simultaneously fitting the model to both the A → B and B → A data sets. Experiments at each timepoint were conducted in triplicate. AB, apical‐to‐basal; BA, basal‐to‐apical; P‐gp, P‐glycoprotein; s, seconds. [Colour figure can be viewed at wileyonlinelibrary.com]

Table 2.

Predicted K_{p,uu,brain,pred} using method 2 (5C model)

Compound	Exp.	fu,m	In vitro Clint,i (µl/s/mg prot)	In vitro Clint,P‐gp (µl/s/mg prot)	P‐pg abundance in vitro (pmol/mg prot)	IVIV Extrapolated CLi (mL/min)a	IVIV Extrapolated CLP‐gp (mL/min)a	Kp,uu,brain,pred(method 2) a	Kp,uu,brain,obs (CI95%)	P/O
Verapamil	1	5.99e‐4	3.08	2.43	1.25	179 ± 33	1,014 ± 590	0.19 ± 0.13	0.16 (0.13–0.20)	1.18
	2	4.50e‐4	3.14	6.17	1.15
	3	2.39e‐4	3.97	3.87	1.16
	4	7.51e‐4	2.56	4.28	2.09
N‐desmethyl loperamide	1	4.59e‐4	3.28	19.5	0.97	287 ± 88	18,503 ± 12,011	0.020 ± 0.014	0.046 (0.035–0.057)	0.44
	2	3.41e‐4	0.44	65.1	1.83
	3	1.41e‐4	6.16	150	9.20
	4	5.00e‐4	6.66	476	11.90
Metoclopramide	1	1	5.19	5.36	9.20	279 ± 58	189 ± 83	0.61 ± 0.10	0.57 (0.46–0.67)	1.08
	2	1	3.74	0.99	7.70
	3	1	6.22	5.65	11.69
	4	1	4.76	6.34	15.67

Predicted K_{p,uu,brain,pred} using method 2, i.e., by extrapolating in vitro intrinsic clearances, obtained from fitting the five‐compartmental model to the in vitro Transwell data, to in vivo using the relative expression factor (for P‐gp–mediated CL) and BMEC protein content (for passive CL).

BMEC, brain microvascular endothelial cells; CI_95%, 95% confidence interval; CL, clearance; Cl_i, in vivo passive unbound into membrane (equal to that out of the membrane); Cl_int,i, passive intrinsic uptake clearance into the membrane; Cl_int,P‐gp, P‐gp–mediated intrinsic clearance; Exp., experiment; f_u,m, unbound fraction in membranes; IVIV, in vitro–to–in vivo; K_p,uu,brain, unbound brain‐to‐plasma concentration ratio; P‐gp, P‐glycoprotein; P/O, predicted/observed value; Prot, protein.

^a Mean ± standard deviation.

Unbound ISF concentration‐time profiles were underpredicted using the IVIV extrapolated CL and the 5C model (method 2)

The predicted brain ISF concentrations were lower than the observed values (Figure  5, top panels) and fell outside the 0.5–2 acceptance criteria, indicating that the IVIV extrapolated intrinsic CLs (estimated using the 5C model; method 2) were lower than the observed values. Therefore, we optimized an empirical scaling factor (ESF) that was applied to the IVIV extrapolated CL (both passive and P‐gp‐mediated CL) so that the predicted and the observed concentration‐time curves matched. In doing so, when CL_i∙f_u,p/B:P > cBF and CL_o + CL_P‐gp > cBF /(K_{p,uu,brain,pred(method 2)}∙f_u,p/B:P), the model became perfusion‐limited. Therefore, the total CL at the blood‐apical membrane interface was fixed to cBF (blood to apical membrane) and cBF∙f_u,m/(K_{p,uu,brain,pred(method 2)}∙f_u,p/B:P) (apical membrane to blood), while all other total intercompartmental CL exceeded those values. The impact of different ESFs on unbound brain ISF concentrations profiles are shown in Figure  S1. The optimized ESF that provided the best match of the initial predicted ISF concentrations to the observed values (as determined by visual inspection of simulated and observed profiles) for verapamil, N‐desmethyl loperamide, and metoclopramide were 17, 80, and 12, respectively (Figure  5, lower panels).

Figure 5.

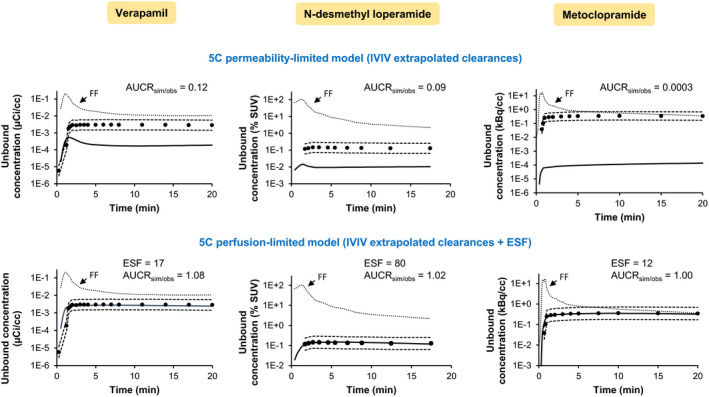
Predicted (continuous line; dashed lines represent twofold acceptable range) and observed (dots) unbound brain concentration‐time profiles of the drugs. The former were predicted using (top panels) IVIV (in vitro–to–in vivo) extrapolated CL and a five‐compartment model including the brain microvascular endothelial cell (BMEC) membranes and intracellular compartments. This method underpredicted the observed profiles at the majority of the timepoints. Consequently, (bottom panels) the IVIV extrapolated clearances of the 5C model were optimized, using an ESF (empirical scaling factor), so that the predicted and observed concentration‐time profiles matched. After applying the ESF, the model became perfusion‐limited. The stippled line, highlighted with an arrow, represents the unbound blood drug concentrations (forcing function, FF) used as input function to predict the unbound brain concentrations. Note that in the 5C model the brain concentrations are a composite of the “brain compartment” (representing the brain interstitial fluid and brain parenchymal cells) and the BMECs’ membranes and intracellular compartments. The unbound brain concentrations were obtained by multiplying the f_u.brain (unbound fraction in brain homogenates) and the total brain concentrations. Observed brain concentration measured by PET imaging¹³, ¹⁴, ¹⁵ were corrected for blood content (4.4%) in the brain. AUCR_sim/obs is the average simulated/observed ratio for the AUC of unbound brain concentrations. For verapamil and metoclopramide, the observed data are from a representative subject while those for N‐desmethyl loperamide are the average of all study subjects (individual data not available). AUC, area under the concentration‐time curve; CL, clearance; min, minutes; kBq, kilobecquerel; PET, positron emission tomography; SUV, standardized uptake value; µCi, microcurie. [Colour figure can be viewed at wileyonlinelibrary.com]

DISCUSSION

In this study, we predicted static K_p,uu,brain as well as dynamic ISF concentrations from in vitro data using the REF approach. Although the static predictions were conducted as described before,⁹, ¹⁰, ¹¹, ²⁸ our study can be distinguished from these previous studies in several ways. First, the compounds used for verification of our approach are selective P‐gp substrates.²⁹, ³⁰, ³¹, ³² Second, to ensure that our transport data were not confounded by endogenous canine P‐gp activity, we used transfected cells where canine P‐gp was knocked‐out. Third, P‐gp abundance in MDCK‐hMDR1^cMDR1‐KO was measured for each independent experiment. We showed that drug ER obtained on different days and REF were inversely related, highlighting the need to measure in vitro P‐gp abundance in each cell transport study (Table  1 and Figure  3). To minimize bias in determination of REF,³³, ³⁴ quantification of P‐gp in MDCK‐hMDR1^cMDR1‐KO cells and BMECs by targeted proteomics was conducted using the same method, within the same lab. Fifth, to verify our predictions of K_p,uu,brain, we used the cER, the cerebral extraction ratio, a parameter estimated from PET imaging, which is independent of the magnitude of drug binding to the brain tissue and therefore not confounded by any errors in determination of this value (this is because it is estimated using the ratio of the uptake CL into the brain K₁ and the cBF; of note the cER of a drug by an organ is identical whether it is based on total drug or unbound drug in the organ). This approach was possible for verapamil and N‐desmethyl loperamide but not for metoclopramide. Metoclopramide’s brain uptake CL (K₁) was not affected by cyclosporin A, a P‐gp inhibitor.¹⁴ Therefore, for metoclopramide, we used the K_p,brain value measured by PET imaging and converted it to K_p,uu,brain using binding information in both plasma and brain tissue, recognizing the pitfalls in accurately estimating these binding values. Finally, unlike other studies, we used the REF approach to IVIV extrapolate the bidirectional clearances of the drugs across the human BBB and dynamically predict the brain ISF concentrations of the drugs.

In our study, we successfully predicted K_p,uu,brain of all three drugs within twofold of the mean observed values, and for verapamil and N‐desmethyl loperamide, within the observed CI_95% of the mean value. These results suggest that steady‐state ISF concentrations can be reliably predicted using REF to scale the in vitro ER obtained from MDCK cells studied in Transwell assays to K_p,uu,brain. To our knowledge, this is the first time that human K_p,uu,brain has been successfully predicted and verified using PET imaging data. Therefore, this approach, together with drug‐receptor interaction data, could be used in the future to guide selection of CNS drugs for development from the preclinical to the clinical phase.

While accurate prediction of K_p,uu,brain is important in drug development, accurate and dynamic prediction of ISF concentration‐time profile, during a dosing interval at steady state, can also be important, for example, where drug efficacy and/or toxicity is determined by the unbound maximum ISF drug concentrations.⁷, ²⁰ To predict brain ISF drug concentrations, accurate prediction of the unbound influx and efflux brain CL is required. To predict these CLs, we IVIV extrapolated P‐gp‐mediated and passive CL using REF and BMEC protein content, respectively. First, to estimate these in vitro CLs, we used a 5C model including cell membranes, which allows the drug to be sequestered in the membranes and is consistent with the “vacuum cleaner” hypothesis of P‐gp transport (supported by our PET imaging studies¹², ¹⁵, ³⁵, ³⁶), which indicates that P‐gp effluxes drugs directly from the apical membrane to blood.²², ³⁷, ³⁸ In contrast to a 3C model (Figure  S2), the 5C model was able to recapitulate the initial rapid drop in the donor drug concentration (Figure  4). Using these IVIV extrapolated CLs (method 2), though the K_p,uu,brain values were reasonably well predicted, the ISF concentrations were considerably underpredicted. These data indicate that the ratio of active‐to‐passive CLs of the drug was well predicted by the REF approach, but not the absolute values of these CLs. This failure could be corrected only with a drug‐specific ESF. The reasons for this failure could be related to differences in physiological environment between in vitro and in vivo, such as endogenous factors (e.g., plasma proteins) and the unstirred water layer,³⁹, ⁴⁰ or assumptions in various parameters used in the 5C model. However, the reasons for this failure cannot be related to a saturation of P‐g in vitro (in vitro drug concentrations were higher than those in the PET studies) as K_p,uu,brain was well predicted from the efflux ratio indicating lack of saturation of P‐gp, either in vivo or in vitro.

Underprediction of transporter‐based drug CL is a well‐acknowledged issue in drug development using traditional scaling approaches which do not account for transporter abundance. Such underprediction has been reduced when using the REF approach. For example, using this approach, we have successfully predicted metformin (an OCT substrate) hepatic uptake CL as well renal secretory CL,⁴¹, ⁴² and hepatic uptake CL of rosuvastatin (an OATP and NTCP substrate)⁴³ within twofold of the observed values; however, these predictions (except for metformin hepatic uptake CL) were close to the lower twofold boundary, indicating that IVIVE of CLs, using the REF approach, needs further refinement.⁴³

There are a few limitations to our approach, First, due to sparse availability of human PET imaging data we could not include other P‐gp–transported drugs in our verification data set nor could we extend our approach to drugs transported by other transporters such as BCRP. However, when such PET imaging data are available, our REF approach could be extended to these drugs, using data from both BCRP and P‐gp‐transfected cell lines. Second, the CL approach (method 2) cannot be prospectively used to predict brain ISF concentrations until it is successful without using an ESF.

Collectively, here we report the first successful prediction of K_p,uu,brain in humans for specific P‐gp substrates using the REF as the sole scaling factor. Our results suggest that the proteomics‐informed REF approach is an accurate and high‐throughput method for prediction of steady‐state / pseudoequilibrium drug concentrations in the brain ISF. We propose that the REF‐scaled ER method (method 1), rather than the IVIV extrapolated CL method (method 2), be used to predict K_p,uu,brain of drugs. Adopting this method should increase success in the development of CNS drugs that are P‐gp substrates.

Funding

This work was funded by the Swiss National Science Foundation through an Early Postdoc. Mobility fellowship awarded to F.S. (grant P2GEP3_188323), and by the University of Washington Research Affiliate Program on Transporters (UWRAPT) through funding from Gilead, Amgen, Merck, Genentech, Biogen, Takeda, Pfizer, and Bristol Myers Squibb.

Conflict of Interest

The authors declared no competing interests for this work.

Author Contributions

F.S. and J.D.U. wrote the manuscript. F.S. and J.D.U. designed the research. F.S. and O.A. performed the research. F.S. and O.A. analyzed data.

Supporting information

Supplementary Material