Fine‐Gray subdistribution hazard models to simultaneously estimate the absolute risk of different event types: Cumulative total failure probability may exceed 1

Abstract

The Fine‐Gray subdistribution hazard model has become the default method to estimate the incidence of outcomes over time in the presence of competing risks. This model is attractive because it directly relates covariates to the cumulative incidence function (CIF) of the event of interest. An alternative is to combine the different cause‐specific hazard functions to obtain the different CIFs. A limitation of the subdistribution hazard approach is that the sum of the cause‐specific CIFs can exceed 1 (100%) for some covariate patterns. Using data on 9479 patients hospitalized with acute myocardial infarction, we estimated the cumulative incidence of both cardiovascular death and non‐cardiovascular death for each patient. We found that when using subdistribution hazard models, approximately 5% of subjects had an estimated risk of 5‐year all‐cause death (obtained by combining the two cause‐specific CIFs obtained from subdistribution hazard models) that exceeded 1. This phenomenon was avoided by using the two cause‐specific hazard models. We provide a proof that the sum of predictions exceeds 1 is a fundamental problem with the Fine‐Gray subdistribution hazard model. We further explored this issue using simulations based on two different types of data‐generating process, one based on subdistribution hazard models and other based on cause‐specific hazard models. We conclude that care should be taken when using the Fine‐Gray subdistribution hazard model in situations with wide risk distributions or a high cumulative incidence, and if one is interested in the risk of failure from each of the different event types.

1. INTRODUCTION

Accurate estimation of the incidence of events that occur over time is crucial when estimating patient prognosis. In survival analysis, a competing event (or risk) is an event whose occurrence precludes the occurrence of the primary event of interest. Applied statisticians and clinical investigators are increasingly aware of the need to account for competing events when estimating the incidence of outcomes over time.¹

When using regression models, there are two primary methods for estimating the cumulative incidence of events in the presence of competing risks. First, the Fine‐Gray subdistribution hazard model allows for modeling the effect of covariates on the CIF.² Second, an analyst can fit cause‐specific hazard models for each of the event types and then combine the resultant models to estimate CIFs for each event type.³, ⁴

While both methods have been described in the statistical literature, our impression is that the former is used substantially more frequently than the latter. Indeed, many authors use the term “competing risk regression model” synonymously with the Fine‐Gray subdistribution hazard model. However, a little‐known limitation of the Fine‐Gray subdistribution hazard model is that, for specific covariate patterns and for certain values of time, the sum of the estimated CIFs for the K different event types is not constrained to be less than or equal to 1. This potential problem of the total failure probability exceeding 1 is not unexpected and not unknown, but it is rarely reported; the only documented case currently known to us appears in the competing risks and multi‐state modeling vignette of the survival package in R by Therneau et al⁵

The objective of this article is to illustrate issues with estimation of covariate pattern‐specific CIFs (ie, when the focus is on subject‐specific estimates of absolute risk) when using the Fine‐Gray subdistribution hazard model. We contrast the use of the subdistribution hazard model with using cause‐specific hazard models for all event types to estimate subject‐specific CIFs. This article is structured as follows: In Section 2, we provide notation and review methods for estimating the CIF in the presence of competing risks. In Section 3, we present a case study using empirical data on patients hospitalized with acute myocardial infarction (AMI) and consider two competing events: cardiovascular and non‐cardiovascular death. In Section 4, we explore the issue of the total failure probability exceeding 1 using mathematical modeling and simulations. In Section 5, we provide a proof that the occurrence of a total failure probability exceeding 1 is a fundamental problem with the Fine‐Gray subdistribution hazard model. Finally, in Section 6, we summarize our findings and place them in the context of the existing literature.

2. APPROACHES TO COMPETING RISK ANALYSIS

Assume a setting with K different types of events (eg, death due to cause 1 vs death due to cause 2, …, vs death due to cause K). Let

$${\lambda }_k(t)=\underset{\mathrm{\Delta }t\to 0}{\lim }\frac{\mathrm{Pr}(t\le T<t+\mathrm{\Delta }t,D=k|T\ge t)}{\mathrm{\Delta }t}$$ (1)

denote the cause‐specific hazard function for the kth event type, where D is a variable denoting the type of event that occurred and T denotes the time of the occurrence of an event. Then

$${\mathrm{\Lambda }}_k(t)=\underset{0}{\overset{t}{\int }}{\lambda }_k(s)\mathit{ds}$$ (2)

denotes the cumulative hazard function for the kth event type. The overall survival function (survival from any of the K different types of events) is equal to

$$S(t)=\exp \left(-\sum _{k=1}^K{\mathrm{\Lambda }}_k(t)\right).$$ (3)

Note that the overall survival function incorporates all the cause‐specific hazard functions. We define the cumulative incidence function (CIF) for the kth event type as

$$F_k(t)=\mathrm{Pr}(T\le t,D=k).$$ (4)

The CIF is estimated as $F_k(t)={\int }_0^t{\lambda }_k(s)S(s)\mathit{ds}$. Thus, the CIF for the kth event type implicitly incorporates the cause‐specific hazard functions for all K event types (through the inclusion of the survival function in the integrand). Competing risk data are frequently subject to right censoring, which occurs when a subject has not failed from any cause at the end of follow‐up. Furthermore, in some settings, the cause of failure may be missing or the failure may be attributable to multiple causes. Methods have been developed to address these specific settings.⁶, ⁷

It is well known that in the presence of competing risks, the use of the Kaplan‐Meier survival function (by censoring on the competing risks) results in biased estimation of the CIF.³, ⁸, ⁹ The reason for this is that the Kaplan‐Meier survival function only incorporates the cause‐specific hazard function for the one type of event under consideration. In contrast to this, the estimator for the CIF incorporates the cause‐specific hazard functions for all the event types. Furthermore, while the sum of the K CIFs is constrained to be at most 1 (${\sum }_{k=1}^K{F}_k(t)\le 1$), the sum of K CIFs estimated using Kaplan‐Meier methods can exceed 1.⁹ This suggests that accurate risk estimation in the presence of competing risks requires knowledge of all the cause‐specific hazard functions.

When using regression models, the Fine‐Gray subdistribution hazard model allows for modeling the effect of covariates on the CIF.² Alternatively, an analyst can fit cause‐specific hazard models.³, ⁴ Using this approach, we have that

$$F_k(t)=\underset{0}{\overset{t}{\int }}{\lambda }_k(s)\exp \left(-\underset{0}{\overset{s}{\int }}({\lambda }_1(u)+\cdots +{\lambda }_K(u))\mathit{du}\right)\mathit{ds}.$$ (5)

While the subdistribution hazard models and fitting all of the cause‐specific hazard models are the most commonly used approaches for estimating cumulative incidence in the presence of competing risks, other methods, including the additive hazard model, have been developed for this purpose.¹⁰, ¹¹, ¹², ¹³ The additive hazard model for cause‐specific hazards has an additional conceptual advantage, namely, that the sum over all cause‐specific hazards, which is the all‐cause hazard, also follows an additive hazards model.

3. CASE STUDY

We consider a case study to compare estimates obtained using Fine‐Gray subdistribution hazard modeling vs estimating CIFs obtained using all the cause‐specific hazard models.

3.1. Data sources

We used data from first phase of The Enhanced Feedback for Effective Cardiac Treatment study,¹⁴ which collected data on patients hospitalized with AMI between April 1, 1999 and March 31, 2001 at 86 hospital corporations in Ontario, Canada. For the current study, data were available on 9479 patients hospitalized with a diagnosis of AMI.

The outcome was time to death, with subjects censored 5 years after the date of hospital admission. Death was categorized as either death due to cardiovascular causes or death due to non‐cardiovascular causes. Outcome ascertainment was through linkage with the provincial death registry. Of the 9479 patients, 2280 (24.1%) died of cardiovascular causes within 5 years of admission, while 1123 (11.8%) died of non‐cardiovascular causes within 5 years of admission. All subjects were followed to either the date of death or 5 years post‐admission, whichever came first.

We considered 33 predictor variables, consisting of demographic characteristics (age, sex); presentation characteristics (cardiogenic shock, acute congestive heart failure/pulmonary edema); vital signs on presentation (systolic blood pressure, diastolic blood pressure, heart rate, respiratory rate); classic cardiac risk factors (diabetes, hypertension, current smoker, dyslipidemia, family history of coronary artery disease); comorbid conditions (cerebrovascular disease/transient ischemic attack, angina, cancer, dementia, peptic ulcer disease, previous AMI, asthma, depression, peripheral vascular disease, previous revascularization, congestive heart failure, hyperthyroidism, aortic stenosis); laboratory tests (hemoglobin, white blood count, sodium, potassium, glucose, urea, creatinine). These predictors are similar to those have been used previously in predicting mortality in patients hospitalized with AMI, which were selected based on discussions with a cardiologist.¹⁵, ¹⁶ Our purpose was to illustrate discrepancies between patient‐specific cumulative incidence probabilities for different modeling approaches and to investigate the problem of “total failure probability exceeding 1”, not to find optimal models for the cause‐specific hazards or subdistribution hazards. We therefore did not attempt to find optimal transformations for the continuous covariates, and did not check for nonlinearities or possible interactions.

3.2. Statistical methods

We regressed the subdistribution hazard of cardiovascular death on the covariates described above. Using the fitted model, we obtained the estimated CIF for each subject in the sample and estimated the probability of cardiovascular death within 1 year, 2 years, 3 years, 4 years, and 5 years. We then repeated this analysis and calculations using non‐cardiovascular death. For each subject, we then added the probabilities of cardiovascular and non‐cardiovascular death at 1 to 5 years to obtain the probability of all‐cause mortality at 1 to 5 years.

We fit two cause‐specific hazard models using the covariates described above. Cause‐specific hazard models for cardiovascular and non‐cardiovascular death were estimated separately. Using the two fitted models, we obtained the estimated CIF for each type of outcome for each subject in the sample. As above, we estimated the probabilities of cardiovascular and non‐cardiovascular death within 1 to 5 years. For each subject, we added the probabilities of cardiovascular and non‐cardiovascular death at 1 to 5 years.

Finally, we fit a Cox proportional hazards model for all‐cause mortality using the covariates described above (note that all‐cause death is comprised of death due to cardiovascular causes and death due to non‐cardiovascular causes). Using the fitted model, we estimated for each subject the probabilities of all‐cause mortality within 1 to 5 years. Note that the five regression models (two Fine‐Gray subdistribution hazard models, two cause‐specific hazard models, one Cox proportional hazard model) all incorporated the same covariates described above, with linear terms for continuous predictors.

3.3. Results

We used a variant of Bland‐Altman plots to compare different estimates of cumulative incidence (Figure 1). We used the estimate from the method based on combining cause‐specific hazards models or on the Cox model for all‐cause mortality as the reference method, and report it on the horizontal axis, rather than the average of the two estimates.¹⁷ We plot the difference between two estimates on the vertical axis. We report the results for cumulative incidence at 5 years in the main body of this article, and report results for cumulative incidence at 1 to 4 years in the supplemental online material. On each plot, we superimposed a horizontal line denoting the mean difference between the two estimates of cumulative incidences across all subjects, and two additional horizontal lines denoting differences that are 1.96 SDs above and below the mean difference. Furthermore, we fit a loess local polynomial regression model in which we regressed the difference in estimates on the estimate obtained using the reference method. The fitted regression model is superimposed on each panel (blue curve). For both cardiovascular and non‐cardiovascular death, while the mean difference between the two methods was approximately 0, the difference between the two methods tended to increase as the estimated incidence from the cause‐specific method increased (blue loess curve).

FIGURE 1.

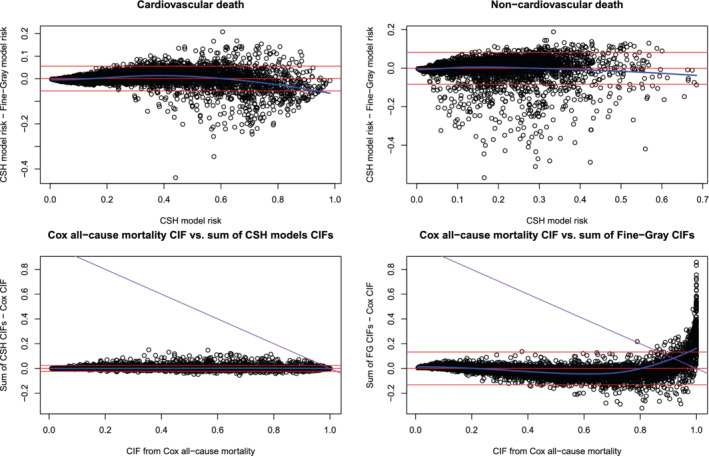
Five‐year cumulative incidence [Colour figure can be viewed at wileyonlinelibrary.com]

The cumulative incidence of all‐cause mortality obtained from a single Cox model compared to that obtained from adding the two CIFs derived from the two cause‐specific hazard models is shown in bottom left panel of Figure 1. On average, the difference between the two methods was 0. Furthermore, the difference between the methods did not vary across the range of estimated incidence obtained from the Cox model for all‐cause mortality. We have superimposed on this panel a line (purple line) such that points above this line have a total failure probability that exceeds 1. All estimated cumulative incidences of all‐cause mortality were less than 1 under both modeling approaches.

The cumulative incidence of all‐cause mortality obtained from a single Cox model compared to that obtained from adding the two CIFs derived from the two Fine‐Gray subdistribution hazard models is shown in the lower right panel of Figure 1. While the mean difference between the two methods was approximately 0, the difference between the two methods tended to increase as the estimated incidence obtained from the Cox model increased. We have superimposed on this panel a line (purple line) such that points above this line have a total failure probability that exceeds 1. Results for estimated cumulative incidence at 1 to 4 years are reported in Figures S1 to S4 in the supplemental online material.

There was a non‐negligible proportion of subjects for whom the estimated probability of all‐cause mortality, as derived from the two Fine‐Gray models, exceeded 1 (the subjects whose points lie above the purple line). For example, when estimating the cumulative incidence of all‐cause mortality within 5 years by combining the two cause‐specific cumulative incidence estimates obtained from the Fine‐Gray model, 4.9% of subjects had a cumulative incidence of all‐cause mortality that exceeded 1.

We explored the characteristics of those subjects for whom the sum of the two cause‐specific probabilities of death (derived from the Fine‐Gray model) within 5 years exceeded 1. We computed the Mahalanobis distance of each subject from the center of the multivariate distribution of the 33 baseline covariates (for the purpose of these computations, binary variables were treated as numeric 1/0 variables). The median Mahalanobis distance for those subjects whose sum of the two cause‐specific probabilities of death within 5 years was less than or equal to 1 was 22.0 (25th and 75th percentiles: 14.3 and 36.7). The median Mahalanobis distance for those subjects whose sum of the two cause‐specific probabilities of death within 5 years exceeded 1 was 70.4 (25th and 75th percentiles: 49.0 and 100.0). Thus, subjects for whom the sum of the two cause‐specific probabilities exceeded 1 tended to be further from the center of the multivariate distribution than were subjects for whom the sum of the two probabilities was less than or equal to 1.

For each subject in the overall sample, we computed the linear predictor for each of the two Fine‐Gray models. For each subject, we then computed the Mahalanobis distance of the vector consisting of the two linear predictors (one for cardiovascular death and one for non‐cardiovascular death) from the center of the multivariate distribution of these vectors. Nonparametric estimates of the density functions of the Mahalanobis distance in those with and without a total failure probability that exceeded 1 are described in Figure 2 (top left panel). The distribution of the Mahalanobis distance was shifted to the right in those with a total failure probability that exceeded 1 compared to those in whom it was less than 1. For those subjects whose sum of the two cause‐specific probabilities of death within 5 years was less than or equal to 1, the median Mahalanobis distance was 1.4 (25th and 75th percentiles: 0.6 and 2.4). For those subjects whose sum of the two cause‐specific probabilities of death within 5 years exceeded 1, the median Mahalanobis distance was 5.2 (25th and 75th percentiles: 4.0 and 7.3). Thus, subjects for whom the sum of the two probabilities exceeded 1 tended to have larger linear predictors than did subjects for whom the two probabilities did not exceed 1. A scatter plot of the two linear predictors is provided in Figure 2 (top right panel and lower two panels). Different colors are used to represent subjects with total event probabilities below and above 1. There is a clear delineation between the two linear predictors of these two groups of subjects.

FIGURE 2.

Difference between those with TFP ≤ 1 and TFP > 1 [Colour figure can be viewed at wileyonlinelibrary.com]

Baseline characteristics are compared between those with and without a total failure probability obtained from the Fine‐Gray models that exceeded 1 (Table 1). For each of the 33 variables, we computed the absolute standardized difference comparing the mean or prevalence of the variable between those with a total failure probability that exceeded 1 and those with a total failure probability that was less than 1 (the standardized difference is the difference in means in units of pooled SD).¹⁸ For the 12 continuous variables, the absolute standardized differences ranged from 0.39 (sodium) to 1.76 (age). Thus, there were meaningful differences in all 12 continuous variables between the two groups. For the 21 binary variables, the absolute standardized differences ranged from 0.02 (peptic ulcer disease) to 0.82 (family history of coronary artery disease). Fifteen of the 21 binary variables had absolute standardized differences that exceeded 0.25. Thus, there were meaningful differences in most covariates between those with a total failure probability greater than 1 and those with a total failure probability less than or equal to 1. In general, those with a total failure probability that exceeded 1 tended to be older, sicker and were more likely to be female than those with a total failure probability that was less than 1. Older, sicker patients are those patients who would tend to have a high risk of both cardiovascular death and non‐cardiovascular death.

TABLE 1.

Comparisons of subjects with total failure probability (TFP) < 1 vs those with TFP ≥ 1

Variable	TFP < 1 (N = 9015)	TFP ≥ 1 (N = 464)	Standardized difference
Age	66.78 ± 13.43	85.48 ± 6.81	1.76
Female	34.9%	55.8%	0.43
Cardiogenic shock	1.0%	12.1%	0.46
Acute congestive heart failure/pulmonary edema	4.8%	22.4%	0.53
Systolic BP	147.94 ± 31.36	124.50 ± 34.53	0.71
Diastolic BP	83.39 ± 18.58	70.34 ± 21.79	0.64
Heart rate	83.43 ± 23.81	104.55 ± 27.28	0.82
Respiratory rate	20.82 ± 5.41	28.54 ± 8.73	1.06
Diabetes	25.3%	45.9%	0.44
Hypertension	45.8%	50.0%	0.08
Current smoker	33.1%	16.6%	0.39
Dyslipidemia	31.7%	9.7%	0.56
Family history of heart disease	31.6%	3.0%	0.82
Cerebrovascular accident/transient ischemic attack	9.2%)	31.5%	0.58
Angina	32.8%	36.0%	0.07
Cancer	2.6%	12.7%	0.39
Dementia	2.9%	24.8%	0.67
Peptic ulcer disease	5.5%	6.0%	0.02
Previous AMI	22.3%	39.0%	0.37
Asthma	5.4%	6.7%	0.05
Depression	6.8%	16.2%	0.30
Peripheral arterial disease	7.1%	19.4%	0.37
Previous revascularization	9.3%	6.0%	0.12
Congestive heart failure	3.9%	25.2%	0.63
Hyperthyroidism	1.2%	3.0%	0.13
Aortic stenosis	1.4%	6.5%	0.26
Hemoglobin	138.72 ± 18.21	113.60 ± 22.03	1.24
White blood count	10.35 ± 4.96	14.27 ± 9.53	0.52
Sodium	138.99 ± 3.80	137.19 ± 5.27	0.39
Potassium	4.09 ± 0.55	4.63 ± 0.80	0.79
Glucose	9.39 ± 5.16	13.24 ± 7.46	0.60
Urea	7.38 ± 4.40	16.87 ± 10.48	1.18
Creatinine	103.13 ± 54.23	213.73 ± 152.16	0.97

Note: Cells contain either mean ± SD (continuous variables) or percent (binary variables).

4. MATHEMATICAL MODELING AND SIMULATIONS TO EXAMINE THE PROBLEM OF TOTAL FAILURE PROBABILITY EXCEEDING 1

In the case study in Section 3, we showed that in an empirical example there was a non‐negligible proportion of subjects for whom the estimated total failure probability exceeded 1. In this section, we explore this issue using mathematical modeling and simulations.

4.1. Mathematical modeling

We assume that there are two type competing events, of which the first if the primary event of interest. For simplicity, we restrict our attention to a single covariate x, but the problem we examine persists for multiple covariates. The Fine‐Gray subdistribution hazard model specifies that the cumulative incidence of event 1, given x, denoted by F ₁(t| x), is given by

$$1-F_1(t|x)={(1-F_{10}(t))}^{\exp ({\beta }_{1}x)},$$ (6)

where F ₁₀(t) is the baseline CIF of event 1 corresponding to x = 0, β ₁ is the regression coefficient, and $e^{{\beta }_{1}x}$ is the subdistribution hazard ratio. When the Fine‐Gray model is fit to both events, the model for the second event is given by

$$1-F_2(t|x)={(1-F_{20}(t))}^{\exp ({\beta }_{2}x)}.$$ (7)

Fix a time point t, and define p ₁ = F ₁₀(t) and p ₂ = F ₂₀(t). Then the total failure probability given x is

$$\mathrm{TFP}(x)=F_1(t|x)+F_2(t|x)=1-{(1-p_1)}^{{\gamma }_1(x)}+1-{(1-p_2)}^{{\gamma }_2(x)},$$

where ${\gamma }_k(x)=e^{{\beta }_{k}x}$, for k = 1, 2, and dependence of TFP(x) on t is removed from the notation. We think of x being a continuous covariate, such as age, blood pressure, or a prognostic score, having been standardized so that its mean equals 0 and its variance equals 1. Figure 3 shows a plot of TFP(x) against x, for p ₁ = p ₂ = 0.45, and for the pair of β ₁ and β ₂ having (a) opposite signs, β ₁ =  −β ₂ = 0.5; (b) the same sign, β ₁ = β ₂ = 0.5. Looking at the opposite signs figure, we see that for |x| > 1.993, we will have that TFP(x) > 1 (the shaded area). If x follows a standard normal distribution, the probability of this happening is 0.046. For the same signs figure, TFP(x) > 1 for x > 0.296, which happens with probability 0.384.

FIGURE 3.

Total failure probability

For the special case of p ₁ = p ₂ and ∣β ₁∣ = ∣β ₂∣, we have, for a sequence of values of p ₁ and β ₁, determined the values of x for which TFP(x) > 1, and, assuming that x follows a standard normal distribution, calculated the probability that TFP(x) > 1. This probability represents the proportion of subjects in the population for which the model‐based total failure probability is greater than 1. Numerical verification revealed that, subject to p ₁ + p ₂ and ∣β ₁∣ + ∣β ₂∣ being constant, this is a best case scenario for the Fine‐Gray model, in the sense that TFP(x) > 1 is least likely to happen. The result is shown in Figure 4. The opposite sign case is shown in the left panel. When the baseline risks are modest, large covariate effects are needed to see TFP(x) > 1, but for higher baseline risks, TFP(x) > 1 is quite likely to occur for modest effect sizes. For the same sign case, shown in the right panel, it can be seen that already for modest baseline risks the problem will be manifest, even for modest covariate effects. R code for these analyses is provided at https://github.com/survival‐lumc/FG‐TotalFailureProbability.

FIGURE 4.

Probability of total failure probability exceeding 1 [Colour figure can be viewed at wileyonlinelibrary.com]

4.2. Monte Carlo simulations

We conducted a set of simulations to explore in greater detail the observations made in the case study. We simulated datasets and applied Fine‐Gray subdistribution hazard models and cause‐specific hazard models to model cause‐specific events. Using the fitted models, we estimated subject‐specific estimates of the probability of the occurrence of events within specified durations of time. We considered two data‐generating processes. The first was based on simulating data from a subdistribution hazard model, while the second was based on cause‐specific hazard models. The description of the methods and the summary of the results are provided in the supplemental online material.

5. A PROOF OF THE FUNDAMENTAL PROBLEM OF THE TOTAL FAILURE PROBABILITY EXCEEDING 1

In the case study in Section 3, we showed that in an empirical example there was a non‐negligible proportion of subjects for whom the estimated total failure probability exceeded 1. Here we will show that this is a fundamental inconsistency problem of the Fine‐Gray subdistribution hazard model.

Theorem 1

Suppose proportional subdistribution hazard models are given for two competing risks, given by

$$F_1(t|x)=1-{(1-F_{10}(t))}^{{\gamma }_1(x)},F_2(t|x)=1-{(1-F_{20}(t))}^{{\gamma }_2(x)},$$

where F ₁₀(t) and F ₂₀(t) are the baseline cumulative incidences of event types 1 and 2, respectively, corresponding to x = 0, and ${\gamma }_1(x)=e^{{\beta }_1(x)}$ and ${\gamma }_2(x)=e^{{\beta }_2(x)}$ are the subdistribution hazard ratios for x of event type 1 and event type 2, respectively. Let t be any time point, for which the baseline cumulative incidences p ₁ = F ₁₀(t) and p ₂ = F ₂₀(t) satisfy 0 < p ₁ < 1, 0 < p ₂ < 1, and p ₁ + p ₂ < 1. If β ₁ and β ₂ are both unequal to 0, then there exists a covariate value x for which the total failure probability, given by

$$\mathrm{TFP}(x)=F_1(t|x)+F_2(t|x)=1-{(1-p_1)}^{{\gamma }_1(x)}+1-{(1-p_2)}^{{\gamma }_2(x)}$$

is strictly greater than 1.

Define q ₁ = 1 − p ₁ and q ₂ = 1 − p ₂, for which we have 0 < q ₁ < 1, 0 < q ₂ < 1, and q ₁ + q ₂ > 1. We need to show that there exists an x such that

$$r(x)=r(x;q_1,q_2,{\beta }_1,{\beta }_2)<1,\text{with}r(x)={q_1}^{{\gamma }_1(x)}+{q_2}^{{\gamma }_2(x)},$$

because TFP(x) = 2 − r(x). We start by noting that both $q_1^{{\gamma }_1(x)}$ and $q_2^{{\gamma }_2(x)}$ are between 0 and 1, and hence that 0 < r(x) < 2 and that r(x) is continuously differentiable in x. Also, for β ₁ > 0, we have that ${\lim }_{x\to \mathrm{\infty }}{q}_1^{{\gamma }_1(x)}=0$ and ${\lim }_{x\to -\mathrm{\infty }}{q}_1^{{\gamma }_1(x)}=1$, while for β ₁ < 0, we have that ${\lim }_{x\to \mathrm{\infty }}{q}_1^{{\gamma }_1(x)}=1$ and ${\lim }_{x\to -\mathrm{\infty }}{q}_1^{{\gamma }_1(x)}=0$. Similar limits hold for event type 2. As a result, if β ₁ and β ₂ have the same sign, we have either ${\lim }_{x\to \mathrm{\infty }}r(x)=0$ (if β ₁ and β ₂ are both positive) or ${\lim }_{x\to -\mathrm{\infty }}r(x)=0$ (if both are negative). In that case, we clearly have r(x) < 1 for sufficiently large positive or negative x.

It remains to consider the case where β ₁ and β ₂ have opposite signs. Suppose first that β ₁ > 0, and consider r(x) for x going to infinity. We have ${\lim }_{x\to \mathrm{\infty }}{q}_1^{{\gamma }_1(x)}=0$ and ${\lim }_{x\to \mathrm{\infty }}{q}_2^{{\gamma }_2(x)}=1$, and as a result ${\lim }_{x\to \mathrm{\infty }}r(x)=1$; we will now show that ${\lim }_{x\to \mathrm{\infty }}{r}^{\prime }(x)=0$ and r ^′(x) > 0 for x sufficiently large. Because r(x) is continuously differentiable, this means that r(x) tends to 1 from below, and therefore that for x sufficiently large, we must have that r(x) < 1. The derivative of r(x) with respect to x is given by

$$r^{\prime }(x)=\log (q_1){\beta }_1{\gamma }_1(x)q_1^{{\gamma }_1(x)}+\log (q_2){\beta }_2{\gamma }_2(x)q_2^{{\gamma }_2(x)},$$

of which the second term clearly tends to 0 as x → ∞. For the first term, we have the conflicting ${\lim }_{x\to \mathrm{\infty }}{q}_1^{{\gamma }_1(x)}=0$ and ${\lim }_{x\to \mathrm{\infty }}{\gamma }_1(x)=\mathrm{\infty }$, or ${\lim }_{x\to \mathrm{\infty }}1/{\gamma }_1(x)={\lim }_{x\to \mathrm{\infty }}{e}^{-{\beta }_{1}x}=0$. By applying L'Hôpital's rule, we see that

$${\lim }_{x\to \mathrm{\infty }}{q}_1^{{\gamma }_1(x)}/e^{-{\beta }_{1}x}={\lim }_{x\to \mathrm{\infty }}\log (q_1){\beta }_1{\gamma }_1(x)q_1^{{\gamma }_1(x)}/(-{\beta }_1{\gamma }_1(x))=-\log (q_1){\lim }_{x\to \mathrm{\infty }}{q}_1^{{\gamma }_1(x)}=0.$$

If β ₁ < 0, then by noticing that r(−x; q ₁, q ₂, −β ₁, −β ₂) = r(x; q ₁, q ₂, β ₁, β ₂) we see that we have r(x) < 1 for sufficiently large negative x. This proves the theorem.

Note that the present theorem only considers a single covariate x. The theorem immediately extends to multivariable models by simply considering the first covariate x ₁ and setting all the other covariates to 0. In that case, a value of x ₁ can be found for which the total failure probability exceeds 1, unless the regression coefficient for x ₁ for 1 or both events equals 0.

6. DISCUSSION AND CONCLUSION

We demonstrated that the use of the Fine‐Gray subdistribution hazard model can result in a cumulative total failure probability problem in a substantial number of patients in real life data analyses. The problem occurs when the estimated subject‐specific cumulative total failure probability exceeds 1 within specified durations of time. This is clearly problematic, as the probability of all‐cause events is necessarily bounded by 1. We provided a proof that this is a fundamental problem with the Fine‐Gray subdistribution hazard model. It is simple to avoid the issue of the sum of estimated CIFs exceeding 1 by fitting both cause‐specific hazard models and combining the estimated cause‐specific hazard functions to estimate cause‐specific CIFs.

An intuitive explanation for the problematic performance of the subdistribution hazard model when considering multiple different events is provided by Beyersmann et al¹⁹ Consider a setting with two different types of events and a subdistribution hazard model for each of the two event types. Let Pr(X _T = 1) and Pr(X _T = 2) denote the proportion of events that are type 1 and type 2 events, respectively, for a reference subject (ie, a subject to whom the baseline subdistribution hazard function pertains) as time approaches infinity. Then, the regression coefficients of the second subdistribution hazard model are completely determined by the regression coefficients of the first subdistribution hazard along with Pr(X _T = 1) and Pr(X _T = 2). However, when fitting the two subdistribution hazard models separately, this constraint is not respected. Thus, in practice, when fitting two subdistribution hazard models, at least one of the fitted models will be incorrect. This will lead to biased estimation of the CIF and possible violation of the constraint that the total event probability be constrained to be less than 1.

In the absence of competing risks, the direction of the regression coefficient (ie, positive vs negative) from a Cox proportional hazards model indicate the direction of the effect of the associated covariate on the risk of the occurrence of the outcome (however the magnitude of the coefficient does not directly indicate the magnitude of the effect on risk). However, in the presence of competing risks, the ability to do so is lost when using cause‐specific hazard models. This property is recovered with the Fine‐Gray subdistribution hazard model.²⁰ Thus, increasing values of a covariate that has a positive regression coefficient in a subdistribution hazard model are associated with an increase in the CIF, while increasing values of a covariate that has a negative regression coefficient are associated with decreases in the CIF. For this reason, the subdistribution hazard model is an “interpretation‐friendly” approach to modeling competing risk data.²¹ In contrast to the “interpretation‐friendly” nature of the subdistribution hazard model, it is difficult to determine the direction of the effect of individual covariates on the CIF when combining the different cause‐specific hazard functions. Formula (5) in Section 1 relating the cause‐specific hazard functions to the CIF is essentially a black box, and one cannot derive a closed‐form expression for the CIF conditional on subject characteristics.²² The use of the Fine‐Gray subdistribution hazard model allows anyone to estimate the absolute risk of an outcome for any covariate pattern provided that the investigator has published or provided the baseline CIF and the regression coefficients. This is more difficult to do when using cause‐specific hazard models.

In some settings, only one of the different event types is of interest, and the other event types are treated as “nuisance” outcomes. For example, information on only the future incidence of cardiac death may be of importance when making some decisions about patient treatment (eg, when deciding whether to initiate certain pharmacological interventions). However, in other settings, information on the risk of all competing events may be important when making other decisions about patient treatment (eg, when making decisions about implantation of implantable cardioverter defibrillators the risk of death from other noncardiac causes is important due to a limited supply of these devices). When presenting patients or decision‐makers with information on the subject‐specific risks of the occurrence of each event type, it is important that these have a sum that is constrained to be less than or equal to 1. This would suggest that in these settings, the use of cause‐specific hazard modeling would be preferable to the use of the subdistribution hazard model. While they were not examined in this current article, other methods, including the additive hazard model, have also been developed for this purpose.¹⁰, ¹¹, ¹², ¹³

In our case study, we observed that those subjects whose estimated total failure probability exceeded 1 tended to be older and sicker than those subjects for whom the estimated total failure probability was less than or equal to 1. The former are those subjects who are high risk of both cardiovascular and non‐cardiovascular death. Based on our case study analyses, we hypothesize that in other applied applications, this issue may be more likely to affect those subjects who are high risk for each of the different competing events. Based on the case study, the mathematical proof, and the simulations, it is clear that this issue is more likely to affect those whose covariates are more extreme and far from the center of the distribution of the covariates.

A limited number of studies have compared risk estimation using the Fine‐Gray model with the use of all the cause‐specific hazard models. Wolbers et al²² compared these two approaches for predicting coronary heart disease (CHD) in older women living in Rotterdam, The Netherlands. They observed that the two methods had comparable calibration for predicting the 10‐year risk of CHD. Calibration was assessed by comparing mean predicted vs observed risk across 10 deciles of predicted risk. Within each decile, the mean predicted risk was comparable between the two methods. However, they did not compare individual risk estimates across the sample of women in the study, nor did they consider estimation of the incidence of the competing risk.

A common aphorism in statistics, attributed to George Box, is that “all models are wrong, but some are useful”.²³ Our findings reflect the truth of this aphorism. The observation that the sum of the estimated cause‐specific absolute risk can exceed 1 (100%) is an indication that at least one of the fitted Fine‐Gray subdistribution hazard model is wrong, as total risk cannot exceed 1 (100%). However, the model can still be useful for at least two reasons. First, as noted above, it allows one to determine which variables are associated with increased or decreased risk. Knowledge of this cannot be extracted from cause‐specific hazard models in the presence of competing risks. Second, when the focus is on a single event type, the subdistribution hazard model allows for estimation of subject‐specific estimates of absolute risk. While there may be bias in some of these estimates, these estimates are still preferable to those obtained using a single Cox proportional hazards model that ignores the presence of competing risks.

Our results do not contradict the recommendation of Latouche and colleagues, who suggested that, in the presence of competing risks, one should present the results for both cause‐specific hazard models and subdistribution hazard models for all event types.²⁴ Our impression is that Latouche and colleagues were focused on studies focused on understanding the relationship between covariates and the occurrence of the different outcomes, while our focus was on estimating the cumulative incidence of each of the different types of events. We demonstrated that there is a fundamental issue with the subdistribution hazard model in that the total failure probability obtained by combining estimates from different subdistribution hazard models is not constrained to be less than or equal to 1. The issue of estimating absolute risk is different from that of understanding etiology and epidemiological associations.

In conclusion, applied analysts need to be aware of this little‐known limitation of the Fine‐Gray subdistribution hazard model in which the sum of the cause‐specific estimates of absolute risk (ie, the total event probability) can exceed 1 (100%) for some subjects and for some times. The use of all of the cause‐specific hazard models allows one to avoid this limitation. When the cumulative incidence of all of the events types is of interest, then, when using the Fine‐Gray subdistribution hazard model, analysts are encouraged to determine the total failure probability for all subjects at clinically meaningful times. Investigators are encouraged to consider the use of all of the cause‐specific hazard models when the focus is on the absolute risk of each of the different types of events.

Supporting information

Data S1. Supporting information

Austin PC, Steyerberg EW, Putter H. Fine‐Gray subdistribution hazard models to simultaneously estimate the absolute risk of different event types: Cumulative total failure probability may exceed 1. Statistics in Medicine. 2021;40:4200–4212. 10.1002/sim.9023

DATA AVAILABILITY STATEMENT

The data sets used for this study were held securely in a linked, de‐identified form and analysed at ICES. While data sharing agreements prohibit ICES from making the data set publicly available, access may be granted to those who meet pre‐specified criteria for confidential access, available at www.ices.on.ca/DAS.