Validation of Wall Shear Stress Assessment in Non-invasive Coronary CTA versus Invasive Imaging: A Patient-specific Computational Study

Abstract

Endothelial shear stress (ESS) identifies coronary plaques at high risk for progression and/or rupture leading to a future acute coronary syndrome. In this study an optimized methodology was developed to derive ESS, pressure drop and oscillatory shear index using computational fluid dynamics (CFD) in 3D models of coronary arteries derived from non-invasive coronary computed tomography angiography (CTA). These CTA-based ESS calculations were compared to the ESS calculations using the gold standard with fusion of invasive imaging and CTA.

In 14 patients paired patient-specific CFD models based on invasive and non-invasive imaging of the left anterior descending (LAD) coronary arteries were created. Ten patients were used to optimize the methodology, and four patients to test this methodology. Time-averaged ESS (TAESS) was calculated for both coronary models applying patient-specific physiological data available at the time of imaging. For data analysis, each 3D reconstructed coronary artery was divided into 2 mm segments and each segment was subdivided into 8 arcs (45^o).TAESS and other hemodynamic parameters were averaged per segment as well as per arc. Furthermore, the paired segment- and arc-averaged TAESS were categorized into patient-specific tertiles (low, medium and high).

In the ten LADs, used for optimization of the methodology, we found high correlations between invasively-derived and non-invasively-derived TAESS averaged over segments (n=263, r=0.86) as well as arcs (n=2104,r= 0.85, p<0.001). The correlation was also strong in the four testing-patients with r=0.95 (n=117 segments, p=0.001) and r=0.93 (n=936 arcs, p=0.001).There was an overall high concordance of 78% of the three TAESS categories comparing both methodologies using the segment- and 76% for the arc- averages in the first ten patients. This concordance was lower in the four testing patients (64% and 64% in segment- and arc-averaged TAESS). Although the correlation and concordance were high for both patient groups, the absolute TAESS values averaged per segment and arc were overestimated using non-invasive vs. invasive imaging [testing patients: TAESS segment: 30.1[17.1–83.8] vs. 15.8[8.8–63.4] and TAESS arc: 29.4[16.2–74.7] vs 15.0[8.9–57.4] p<0.001]. We showed that our methodology can accurately assess the TAESS distribution non-invasively from CTA and demonstrated a good correlation with TAESS calculated using IVUS/OCT 3D reconstructed models.

INTRODUCTION

Coronary artery disease (CAD) continues to be the leading cause of death in the US³. Prevention of ischemic coronary artery disease is challenging as over 50% of patients with acute coronary syndrome (ACS) have no prior symptoms of myocardial ischemia or manifestations of CAD ². The development of coronary events in patients without prior symptoms is commonly caused by the progression and/or disruption of non-calcified plaques and locations with previously no significant obstructive CAD³³.

Local hemodynamic factors, such as endothelial shear stress (ESS), defined as tangential force acting on the endothelial cells, play a major role in the development and progression of atherosclerosis⁹. These ESS-related pathophysiological concepts—as investigated using computational fluid dynamics (CFD)— have been validated in clinical studies applying invasive intravascular coronary imaging modalities such as intravascular ultrasound (IVUS) and optical coherence tomography (OCT)^13,27,39. IVUS and OCT are high-spatial resolution intracoronary modalities (200 μm and 10 μm, respectively) that allow accurate in vivo characterization of atherosclerotic plaque and lumen shape in human coronary arteries. IVUS/OCT-based investigations, provide a significant motivation for this study as they demonstrated the potential of ESS to predict future events independent of coronary morphology^13,39,40. However, these analyses have been based on invasive imaging technologies, which fundamentally limit the application of ESS assessment for clinical decision-making to patients that are already in the catheterization lab for an invasive procedure.

The ability to perform similar ESS analyses based on non-invasive imaging, such as coronary computed tomography angiography(CTA), has the potential to include a much larger number of individuals who can readily undergo non-invasive testing for CAD. In the current standard of care, patients that present with non-acute symptoms of CAD undergo diagnostic non-invasive testing by CTA to decide for either the need of percutaneous coronary intervention or medical treatment. CTA allows for non-invasive evaluation of the entire coronary artery tree including the lumen and vessel wall and thereby the presence, extent and characteristics of atherosclerotic plaque. Despite a lower CTA resolution of ~500 μm, recent studies show that CFD modeling based on CTA images for the assessment of hemodynamic significance of coronary artery stenosis is as accurate as invasive coronary angiography^1,11,29. For example, fractional flow reserve (FFR) defined as the ratio of distal to proximal pressure across the plaque has been shown to be accurately calculated non-invasively based on CTA^30,31.

Therefore, the overall goal of this study was to develop and validate a methodology to study ESS calculated by CFD using non-invasive CTA. Hence, the objectives of this study were to 1) establish a methodology to create 3D CFD models based on invasive and non-invasive imaging of the same arteries and compare the final geometries, and 2) compare and validate ESS calculation based on coronary CTA against calculations based on fusion of CTA with invasive imaging of coronary arteries. Since we showed a high correlation and similar ESS patterns using the two imaging methods, we hereby provide a clinically relevant, non-invasive methodological approach to assess a valuable hemodynamic factor that is applicable, and potentially readily available, for a large group of patients at risk of development and progression of CAD.

METHODOLOGY

Patient Population

For this study a combination of two existing datasets was used. The first part of the dataset consisted of patient data (n=8) that were acquired during a standard patient screening for stable chest pain and percutaneous coronary intervention procedure from the research patient data repository of Massachusetts General Hospital (MGH). Patients that were selected for the current study underwent CTA not more than 90 days before the invasive imaging (IVUS or OCT) and did not have prior coronary interventions, revascularizations or were scheduled for valve replacement. All patients provided written informed consent. This retrospective study was approved by the institutional review board of MGH (Figure 1).

Figure 1.

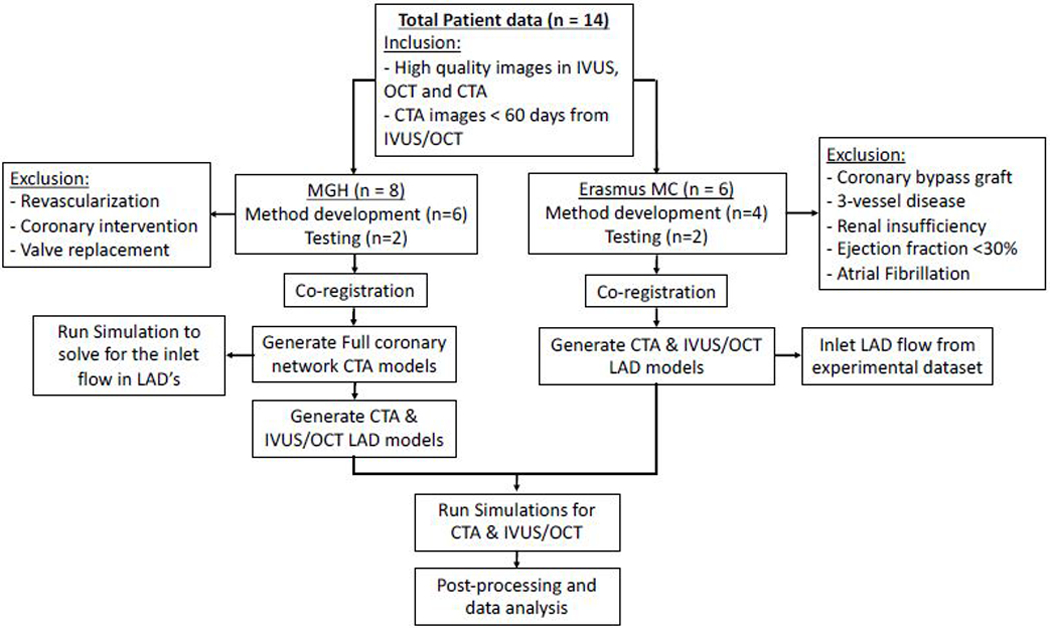
Workflow of the study with 14 total number of patients where 10 is used for methodology development and 4 are used to test the methodology developed. Specifications for each cohort as well as the exclusion criteria are also included.

The second part of the dataset (n=6) comes from a study repository from the Erasmus MC, Rotterdam (EMC). Hemodynamically stable patients with an acute coronary syndrome (ACS) with at least one non-stented non-culprit coronary vessel were invasively imaged using IVUS. Patients were excluded with a history of previous coronary artery bypass graft surgery, 3-vessel disease, renal insufficiency, ejection fraction <30% and atrial fibrillation. Patients included in this study underwent invasive coronary imaging (IVUS) of the non-stented non-culprit coronary vessel and CTA one month after the invasive procedure. All patients provided written informed consent. The study protocol was approved by the local medical ethical committee of the EMC (Figure 1).

Collectively, we selected a total of fourteen patients, eight from MGH, six from EMC. Of these, ten (6 from MGH and 4 from EMC) were used for training and optimizing the methodology during an iterative development phase (referred to as training dataset) and an additional four patients (2 from MGH and 2 from EMC) were used to test the methodology (referred to as the testing dataset). Only the left anterior descending coronary artery (LAD) was studied, so that all patients had a similar branching pattern.

Coronary CTA Imaging Data Acquisition

For the MGH cases, coronary CTA were performed as the standard clinical protocol where patients were prospectively ECG gated scanned with automatic exposure control (tube potential and tube current modulation). CTA was performed using Isovue 370 (iopamidol). Images were reconstructed using 0.6 mm thickness using iterative reconstruction methods.

Similarly, in the patients from EMC, the CT scans were acquired through a prospectively gated protocol with 70–80kV and the tube current was set for automatic exposure control (SOMATOM Force- 192 slice 3^rd generation dual-source CT scanner, Siemens AG, Germany). Kernel Bv40, Slice thickness 3mm increment 1.5mm, Admire 5 setting was used for reconstruction of the images.

IVUS and OCT Imaging Data Acquisition

Coronary angiograms were recorded with full contrast injection before the insertion of a guidewire that is used to advance an IVUS/OCT catheter into the coronary artery. From the MGH data repository, patients were selected who underwent IVUS imaging of their coronary arteries using a Boston Scientific Opticross IVUS catheter with automatic pullback rate of 1 mm/sec or OCT imaging using a frequency-domain(FD)-OCT system (St. Jude Medical, St. Paul, MN). Automated pullback was initiated at a speed of 36/54 mm/sec in concordance with blood clearance.

EMC patients went through a similar protocol as MGH IVUS imaging. However, the images were acquired by an automated pullback (0.5mm/s) with a NIRS-IVUS catheter (TVC Insight Coronary Imaging Catheter, InfraRedX, Burlington, MA, USA). Subsequently, local flow measurements were performed in between side branches in the segment of interest using Doppler velocimetry.

All of the IVUS and OCT images were anonymized and digitally stored.

Co-registration of Invasive and Noninvasive Imaging

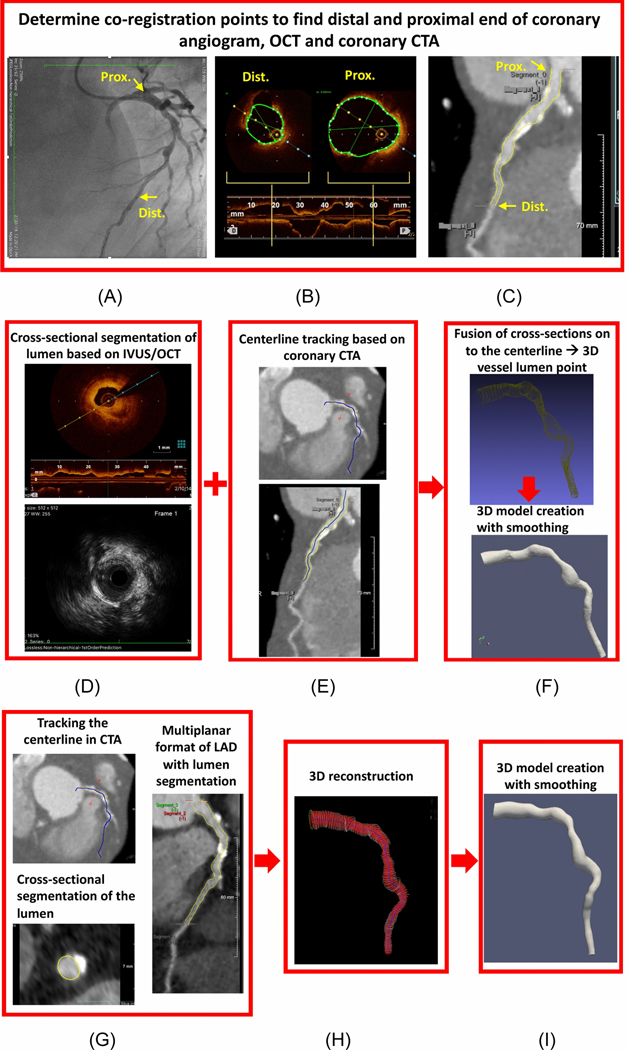
To obtain the correct longitudinal location and circumferential orientation of the IVUS/OCT images while fusing them with CTA, anatomic landmarks such as side branches and bifurcations were used (Figure 2A). Further, we used coronary angiograms acquired at the time of IVUS/OCT to keep track of the location of branches relative to each other. We also used coronary angiograms to ensure that the general shape of the vessel matched the 3D shape reconstructed from CTA. For the training patients, this process was performed and optimized iteratively to ensure that the frames consisting the landmarks in invasive imaging corresponds to the same slice in CTA multiplanar reconstruction cross-sections of the LAD. We further established a method to include the vessel of interest such that it starts and ends immediately after the location where the branch leaves the main artery in all imaging modalities. This allowed for a clearly marked proximal and distal end of the vessel. In addition, in the case of IVUS co-registration, there may be branches censored due to gating. Therefore, we closely looked at both gated and un-gated IVUS images to ensure that there were no branches misidentified in the process of co-registration.

Figure 2.

Illustration for methodology workflow in co-registration of the invasive and noninvasive imaging based on (A) coronary angiogram, (B) intravascular imaging (in this case OCT) (C) and coronary CTA on the multiplanar reconstruction view. Steps involved in 3D model for invasive-based models where first (D) cross-sectional segmentation for the lumen is performed (E) second the centerline based on CTA is extracted (F) cross-sectional lumen cloud points are fused with centerline to create 3D shape and lastly the smoothed 3D LAD model is reconstructed. Steps involved in 3D reconstruction based on coronary CTA where first (G) the centerline is first tracked and coronary lumen is segmented and (H) 3D shape of the vessel is crated based on the segmented contours and (I) the final smoothed 3D reconstructed model is created.

3D reconstruction of coronary artery tree and coronary vessel of interest: CT based image segmentation

In order to create a 3D reconstruction of a full coronary tree, the lumen of each major coronary artery and the ascending aorta was semi-automatically segmented using a commercially available software package (Medis QAngioCT and 3DWorkbench, Leiden, Netherlands). Corrections were made when necessary by an expert reader to ensure accurate segmentation. After anatomical 3D reconstruction of the coronary arteries and the ascending aorta, the vessels were imported into Simvascular⁴² to merge these arteries and create a coronary network (Figure 2B). With this approach the flow information in the vessel of interest could be computed, in case that information was not available. The methods that were applied to solve the hemodynamics in a coronary network was described in detail before⁴¹.

Subsequently, the segment of interest from the LAD was isolated (Figure 2C). To select the segment of interest, co-registration of CTA with invasive imaging (as described in detail below) was of key importance to ensure that also invasive image acquisition was performed on the selected segment. After isolation of the segment of interest the side branches were removed from the CTA segmentation, since the models based on IVUS/OCT do not contain side branches. Therefore, following the conservation of mass law, the total mass flowrate was calculated, adding all the downstream side branches flowrate on to the main vessel. The final 3D reconstruction of the coronary artery was smoothed using a Laplacian smoothing algorithm with 3 iterations and weighing factor of 0.01. We found 3 iterations of smoothing to be an optimum number to preserve the shape and anatomy of the vessel while sharp edges and skewed surfaces are eliminated. Furthermore, 3D centerlines were extracted for the vessel of interest.

Invasive Imaging Lumen Segmentations

IVUS images were gated at the same cardiac phase, so that diameter variations as a result of the cardiac contraction were removed. For the dataset acquired at MGH, IVUS/OCT segmentations of the lumen were manually conducted using an in-house segmentation software at the Vascular Profiling Laboratory at the Brigham and Women’s hospital similar to previous protocol^10,38. We extracted the segmented lumens at each cross-section as point clouds at each gated frame for IVUS and all the OCT frames. We adapted this methodology which enabled us to fuse the contours segmented based on invasive imaging with the 3D centerline extracted from CT²³. The IVUS images for the testing patients acquired at EMC were blindly segmented applying QCU-CMS software (version 4.69, LKEB, Division of image processing, Leiden, The Netherlands) and also exported as point clouds.

3D-Reconstruction of coronary artery: CT fused with IVUS/OCT

In order to create a 3D coronary reconstruction based on the 2D-lumen segmentations from IVUS/OCT, we fused the 2D point clouds extracted in the previous step with the 3D-centerline extracted from CT (Figure 2C–E). As a first step in the fusion process, we interpolated the centerline points such that the number of centerline points was the same as the number of 2D-cross sectional lumen segmentations. Then, the obtained point clouds were isotopically transformed such that the lumen centroid coincided with the CT-based centerline points and the normal to the cross sections were aligned with the local curvature tangent of the centerline. In addition, to ensure correct orientation as well as the rotation of each cross-section we used the landmarks in the co-registration process (as described below) and compared each consecutive cross-section’s normal to ensure their dot-products are positive. In previous studies, the 3D reconstruction of IVUS/OCT-based geometries were performed fusing the centerline extracted from2D orthogonal coronary angiograms. However, in this study we adapted a more recent hybrid methodology fusing the 2D cross-sections based on IVUS/OCT with the 3D centerline extracted from coronary CTA. This methodology have been shown to be as accurate as the former methodology in calculating shear stress and been used other shear stress based studies^19,20. In addition, this methodology was used partly because in our retrospective MGH patients, not all had orthogonal 2D coronary angiograms for the centerline to be readily extracted. Lastly, we used MeshLab, an open source software to create a surface mesh from the point-clouds using a ball-pivoting methodology by Bernardini et al.⁴. Similar to the CTA-based coronary models, the final 3D coronary artery was smoothed using a Laplacian smoothing algorithm with 3 iterations.

It is important to note that ten patients (6 MGH and 4 EMC) were used to optimize the methodology. Therefore, segmentations and model creations were performed iteratively and not fully blinded between the imaging modalities in the process of methodology development. Therefore, segmentations and 3D reconstructions of coronary arteries may have been performed multiple times communicating between the imaging modalities until a consistent method was established through all patients. Hence, addressing imaging artifacts in each imaging modality and methods of co-registration concluded in an iterative process in the training phase. Therefore, we also analyzed a testing data set of four patients (2 EMC, 2 MGH) for which segmentations were done only once and fully blindly where IVUS/OCT segmentations were performed by one reader and CTA segmentations were done by a different reader and the landmarks were communicated only once.

CFD Simulations

In order to calculate the ESS and other hemodynamic parameters, three-dimensional pulsatile CFD simulations of blood flow were performed using patient-specific coronary artery meshes in Simvascular⁴². This software uses a novel second order preconditioning implicit method¹⁷ and is optimized to solve the 3D incompressible Navier-Stokes equations (Eq1a and 1b) in vascular systems reconstructed from image data; where u, ρ, w, v and g stand for flow velocity, blood density, internal sources,

$\frac{\partial \rho }{\partial t}+\nabla \cdot (\rho u)=0$	(Eq 1a)
$\frac{\partial u}{\partial t}+(u.\nabla )u-v{\nabla }^{2}u=-\nabla w+g;$	(Eq 1b)

kinematic viscosity and external source, respectively.

Blood was treated as Newtonian fluid with a density and kinematic viscosity of 1060 kg/m³ and 3.8×10⁻⁶ m²/s, respectively. We assumed blood is a Newtonian fluid as this is valid assumption in arteries larger than capillaries where the shear rate is relatively low for blood to behave as a Newtonian fluid³⁴. Reynolds number were in the laminar region (Table 1) in the coronaries. Mean Reynolds number was defined as $Re=\frac{U_{avg}D}{v}$ where U_avg is the average velocity in the vessel of interest. Therefore, there was no turbulence modeling as the mean ESS was calculated in the 3D reconstructions of coronaries based on a) CT only and b) in their counterparts based on the fusion of CT and invasive imaging (IVUS, OCT).The inflow boundary conditions, in case they were not measured, were calculated using the full coronary network (see above). The detailed description on the mesh generation and the boundary conditions applied for the CFD simulations in the isolated segments and the full coronary network can be found below.

Table 1.

List of patient’s demographics, invasive imaging modality and the parameters used to create the computational models.

	Age (yrs)	Sex	IVUS or OCT	HR (bpm)	BPmean (mmHg)	Avg Qinlet (mL/s)	ReCTA	Reinasive	No. of Elements (CTA)	No. of Elements (invasive)	Max edge size (cm) (CTA)	Max edge size (cm) (invasive)
Patient 1	70	M	OCT	63	99	0.8	143.5	154.2	98096	93230	0.030	0.030
Patient 2	55	F	IVUS	60	85	0.2	35.0	30.1	65221	83265	0.040	0.040
Patient 3	57	M	IVUS	70	99	0.4	65.7	65.9	206364	213869	0.03	0.030
Patient 4	66	M	OCT	64	106	1.4	184.4	177.4	150611	103857	0.030	0.035
Patient 5	64	M	IVUS	78	81	0.6	112.7	103.0	150145	172312	0.030	0.030
Patient 6	73	M	OCT	63	67	1.3	257.5	226.2	93259	106668	0.060	0.064
Patient 7	48	M	IVUS	67	74	1.1	147.0	121.8	130684	175214	0.040	0.040
Patient 8	57	M	IVUS	70	125	4.3	470.5	388.5	78022	113754	0.045	0.045
Patient 9	52	M	IVUS	68	82	0.5	63.3	50.7	125240	172283	0.045	0.045
Patient 10	51	M	IVUS	68	97	0.5	92.3	75.5	126468	113195	0.030	0.035
Patient 11	46	M	OCT	92	84	2.0	362.2	312.0	73870	61132	0.030	0.035
Patient 12	82	M	IVUS	58	77	0.9	190.7	186.1	87515	91351	0.030	0.030
Patient 13	63	M	IVUS	62	77	0.9	109.1	87.3	278431	402344	0.040	0.040
Patient 14	56	M	IVUS	84	103	0.9	105.0	89.2	71832	56398	0.050	0.060

HR= heart rate; Q: flowrate; Re: Reynolds numbers

Mesh generation:

the 3D-reconstructed coronary anatomy was meshed using TetGen³⁶ (an open source tetrahedral mesh generator that uses 3D Delaunay Triangulation with 2 layers of boundary layer mesh). To ensure a fully resolved flow, the Courant-Friedrichs-Lewy number was set to be <1 and a maximum allowable edge size for a given element was specified for the entire mesh not to exceed half of the smallest outflow diameter. At the aortic level, the mesh size was adjusted to be larger to avoid having an unnecessary large number of elements. Local refinements were further performed at locations of bifurcations and stenosis. A mesh convergence test was performed to determine the threshold of element size for each simulation to ensure no more than 1% change in TAESS at locations with luminal narrowing.

Boundary conditions:

For patient-specific boundary condition assignment, depending on the cohort, two different methodologies were applied to impose the inlet flowrate (Q) waveform. For the MGH dataset, the flow was solved using the 3D-coronary network, by providing the inlet flowrate waveform at the aortic valve level. The waveform used was obtained from measurements in a healthy person in the Vascular Model Repository⁴⁵. However, conserving the shape of the waveform, its period was adjusted for the heart rate of the patient and the area under the curve of the waveform was adjusted using the patient specific stroke volume as an input in the coronary network simulations. The stoke volume was calculated by multiplying the end-diastolic left ventricle volume from the coronary CTA scans (using Syngo.via - Siemens Medical Solutions, USA) with the ejection fraction obtained from a recent Echocardiogram (obtained no longer than 30 days from CTA).

The downstream hemodynamics and circulation that were not included in the 3D model were modeled using lumped parameter networks that use electric circuit analogs to prescribe the relationship between flow and pressure in these vessels. These boundary conditions were based on a previously tested algorithms implemented in Simvascular⁴². To ensure we are using the correct flow rate information, the diastolic, systolic, mean pressure, and cardiac output were checked to match the patient-specific measurements at the time of the scan. In addition, other metrics such as percent total coronary outflow with respect to cardiac output and the shape of the right and left coronary waveforms were checked against reported literature data^8,24,25. In the event of more than 10% difference between the clinical measurement and calculated pressure and flowrates, the simulation was repeated by changing the lump network element of resistance and capacitance until a good agreement was reached.

Once the flow was solved through the whole coronary network, the flowrate waveform at the vessel of interest (LAD) was retrospectively calculated as the summation of all the downstream branches flowrates. The calculated total LAD flowrate was thereafter used as an input for a second set of CFD calculations in the models of the isolated LAD arteries (Figure 2H). These latter CFD calculations were performed to assess the detailed hemodynamics parameters for the CTA- and IVUS/OCT-based models. To enable a 1:1 comparison between IVUS/OCT and coronary CTA based ESS calculations, the inlet boundary conditions were kept the same between the models. However, the distal lumped element model resistances for the CTA-based models were scaled according to the outlet cross-sectional area of the IVUS/OCT-based models. With this approach, the differences in ESS between the two models is fully based on the local geometry.

For the EMC patient cohort, the average flowrate was calculated by multiplying the time averaged measured velocity and the cross-sectional area of measurement location. Furthermore, the same general waveform used for MGH patients was scaled and adjusted for the patient-specific average flowrate and heart rate measured at the time of imaging acquisition.

For all the simulations, the shape of the inlet velocity profile was assumed to be parabolic and no-slip boundary conditions were imposed at the walls. The arterial wall was assumed to be rigid as it has been previously shown that wall elasticity in calculation of ESS has a negligible effect for the calculation of ESS in the coronary network¹⁶. Each patient’s hemodynamics were solved for 6 cardiac cycles to reach full convergence and the final results were reported based on the results of the last cardiac cycle calculations. The convergence criteria was set to reach a nonlinear residual <1E-4 and peak flowrate at outlet difference of <1% from the 5^th to 6^th cardiac cycle.

Data Analysis and Hemodynamic Computations

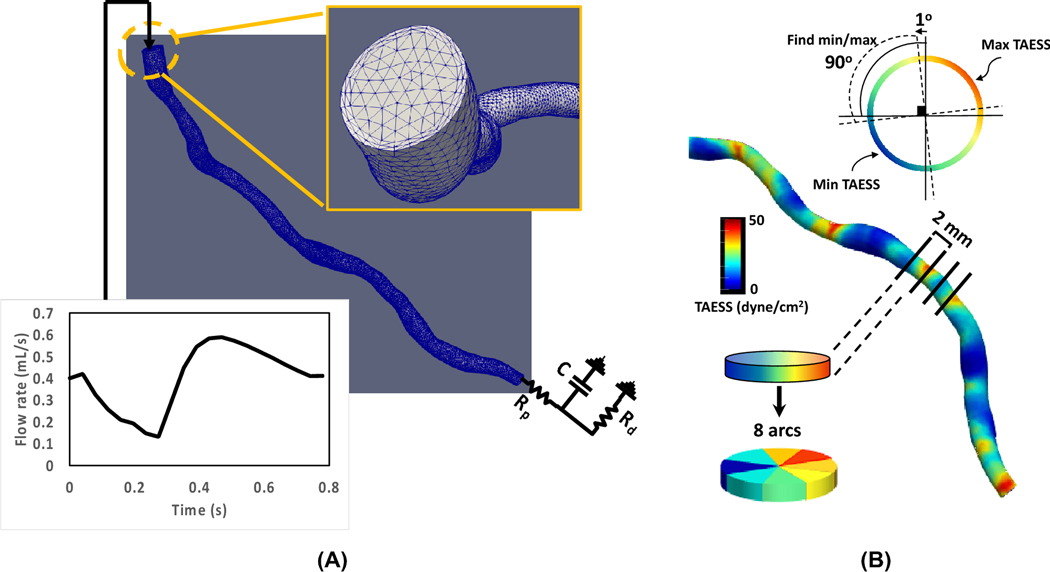
ESS was calculated as a continuous variable at the wall of the coronary segment as the product of viscosity and the gradient of blood velocity at the wall (Table 2). An in-house python-based code using the “vtk package” was used to extract 1) time averaged ESS (TAESS) at each degree arc angle in each cross-section along the centerline for creation of 2D map of TAESS during the cardiac cycle and 2) cross-sectional diameter and area along the centerline of the vessel. For final data analysis, the constructed coronary models were divided into consecutive 2 mm segments and each segment was divided into 45^o arcs along the centerline (Figure 3B). The TAESS was averaged per segment $\left(\overline{TAES{S}_{seg}}\right)$ and per 45° arc $(\left(\overline{TAES{S}_{arc}}\right)$ (see Table 2 for definitions). Previous studies used 3 mm segments to summarize the local hemodynamic characteristics to minimize the variation and noise in calculations^9,13. However, for this study, we chose to compare the TAESS using the 2 mm segments rather than 3 mm segments for a more detailed comparison of the two imaging modalities. Subsequently, the segments and 45° arcs were categorized into low, medium and high TAESS according to the TAESS using patient-specific tertiles following previously reported studies^13,21,23. Furthermore, in each 2 mm segment the local minimum TAESS_min and max TAESS_max were calculated as the 90° arc with the lowest and highest average TAESS within the segment, examining these 90° arcs per 1° around the circumference of the segment following previous studies^6,39,43 (Figure 3B).

Table 2.

list of hemodynamic factors calculated in this study, their meaning and equations that define them.

Eq #	Term	Meaning	Equation
2	${\tau }_w$	Blood velocity gradient at vessel wall	${\tau }_w=\mu {\left.\frac{\partial \overrightarrow{u}}{\partial \overrightarrow{n}}\right|}_{wall}$
3	${\overline{TAESS}}_{seg}$	Area averaged TAESS	${\overline{TAESS}}_{seg}=\frac{\sum _{n=1}^{N_{surface}}TAESS}{N_{surface}}$
4	${\overline{TAESS}}_{Arc}$	45° arc averaged TAESS	${\overline{TAESS}}_{Arc}=\frac{\sum _{n=1}^{N_{arc}}TAESS}{N_{arc}}$
5	$OSI$	Oscillatory shear index	$OSI=0.5\left(1-\frac{\left|{\int }_0^T{\overrightarrow{\tau }}_{w}dt\right|}{{\int }_0^T\left|{\overrightarrow{\tau }}_w\right|dt}\right)$
6	${\overline{OSI}}_{seg}$	Area averaged oscillatory shear index	${\overline{OSI}}_{seg}=\frac{\sum _{n=1}^{N_{surface}}OSI}{N_{surface}}$
7	${\overline{P}}_{seg}$	Time-averaged area-averaged pressure	${\overline{P}}_{seg}=\frac{\sum _{n=1}^{N_{area}}P}{N_{area}}$

$\mu$: dynamic viscosity, $\overrightarrow{u}:$ blood velocity, $\overrightarrow{n}:$ directional vector normal to the wall, N_surface : total number of surface mesh points at the wall, N_arc: total number of surface mesh points at the wall in each 45^o arc, N_area: total number of mesh points at the cross-sectional area

Figure 3.

(A) Boundary conditions used for the left anterior descending 3D reconstructed models where the input flow rate is a waveform adapted from a healthy person in the Vascular Model Repository²¹ such that the waveform is adjusted for the patient-specific mean flow rate as well as the heart rate at the time of patient scans. The distal boundary condition is an RCR lumped element model where the proximal (R_p) and distal (R_d) resistance are adjusted by the mean flow rate and pressure measurements. C stands for capacitance and is kept as the constant value of 4.16×10^-6. The mesh generated for each coronary artery included 2 boundary layers with maximum of 0.5 portion of edge size. (B) Schematics illustrating methods used to calculate segment- and arc-averaged and minimum/maximum TAESS along the artery’s centerline. The minimum and maximum TAESS is determined by finding the minimum/maximum of TAESS in each 90° arc and in the entire cross-section rotating at 1° increments at a time.

Segment averaged oscillatory shear index $\left(\overline{OS{I}_{seg}}\right)$ —characterizing the degree of shear stress reversal in a pulsatile flow— was calculated as the averaged OSI values over the 2-mm segment where $OSI=0.5\left(1-\frac{\left|{\int }_0^T{\overrightarrow{\tau }}_{w}dt\right|}{{\int }_0^T\left|{\overrightarrow{\tau }}_w\right|dt}\right)$. Similarly, time-averaged pressure was averaged over each 2-mm segment. All the time-averaged values reported here were averaged over the last cycle of the simulations. A list of all calculated parameters and their definitions can be found in Table 2.

Statistical Analysis

Continuous parameters were reported in mean ± standard deviation or median(interquartile range [IQR]) and the categorical variables were reported as counts and percentages and compared in a paired analysis. The mean for normally distributed data were tested to be significantly different with a paired t-test and Wilcoxon rank sum test was used for the median in non-normal distributed data. Pearson linear coefficient, r, was calculated to report the correlation between the (hemodynamic) parameters derived between the two imaging modalities. Standard errors of the correlation coefficient were corrected for the fact that the multiple arterial segments within patients were not independent using the “Huber-White” sandwich estimator²². Bland-Altman plots were created to evaluate agreement between the ESS calculations based on CTA and IVUS/OCT. All calculations were two-tailed with p<0.05 considered statistically significant.

RESULTS

Patient Population:

The patients selected were 60.0 ± 10.2 of age and 93% were male.

Continuous TAESS:

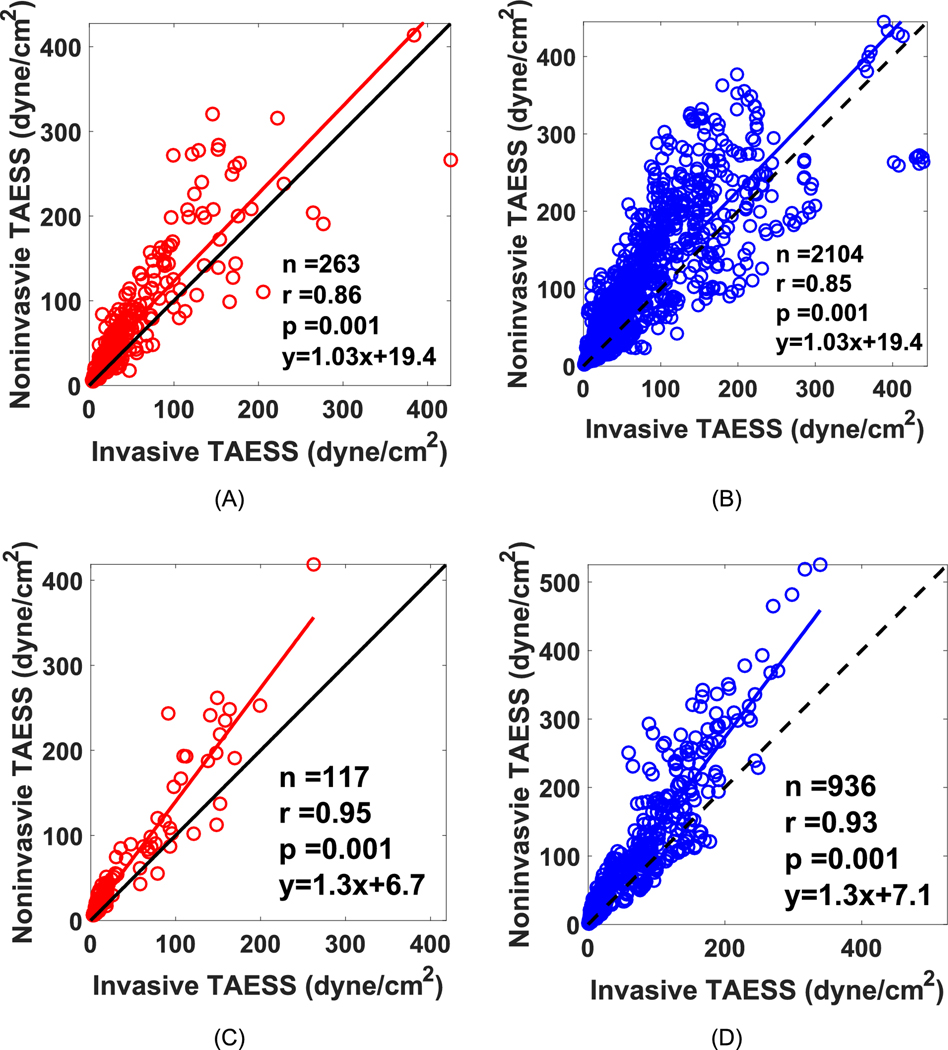
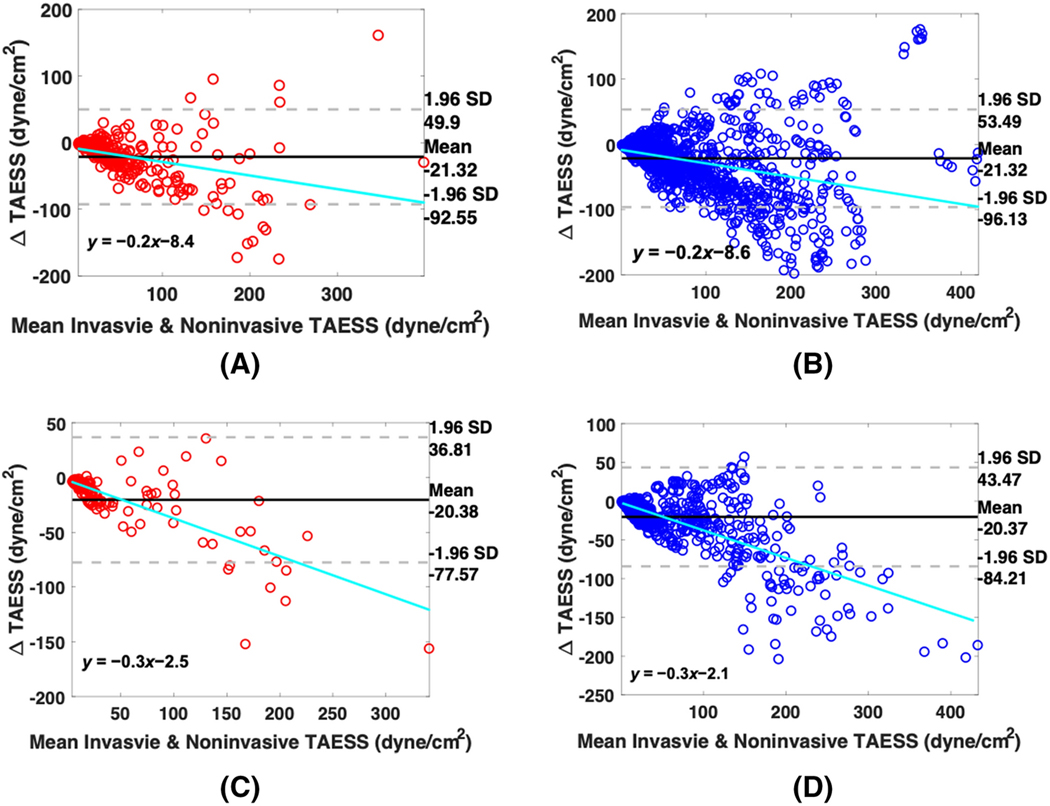
The overall TAESS pattern (in 3D and 2D maps) as obtained using the models based on invasive and non-invasive imaging were very similar. Figure 4 displays a case with a very high correlation, where in Figure 5 an example with moderate correlation is presented. The training dataset consisted of 263 paired segments and the median ${\overline{TAESS}}_{seg}$ was significantly higher as assessed with the non-invasive models compared to the invasive models (50.1[25.8–90.1], 31.7 [19.3–62.4] dyne/cm², p<0.001). Similarly, in a total of 2104 arcs, the arc-averaged TAESS values were 47.7 [24.1–90.0] and 29.9 [18.1–62.4] dyne/cm² (p<0.001) based on non-invasive and invasive models, respectively. There was a strong and significant Pearson correlation found between the two methodologies for ${\overline{TAESS}}_{seg}$ and ${\overline{TAESS}}_{arc}$ [r= 0.86 and r=0.85 (p<0.001)], (Figure 6). Similarly, in the testing patients (117 segments and 936 45° arcs) a high correlation between the two imaging modalities was found for ${\overline{TAESS}}_{seg}$ and ${\overline{TAESS}}_{arc}$ (r=0.95 and 0.93; p=0.001), and similarly as the training patients, the absolute ${\overline{TAESS}}_{seg}$ and ${\overline{TAESS}}_{arc}$ were overestimated using non-invasive imaging (Table 3). The Bland-Altman plots (Figure 7) showed that apart from the observed absolute differences in the TAESS values for both segment- (mean difference: −21.3± 36.3 dyne/cm²) and arc-averaged (mean difference: −21.3±38.2 dyne/cm²) TAESS, the differences were also dependent on the value of the TAESS Similar differences and trends was observed for the testing patients (Figure 7 C–D). TAESS values were not normally distributed (and skewed towards lower values) and thus we reported median values in this study. However, the mean differences between the TAESS values based on two imaging modalities had a normal distribution and hence we reported means and standard deviations in Bland-Altman plots.

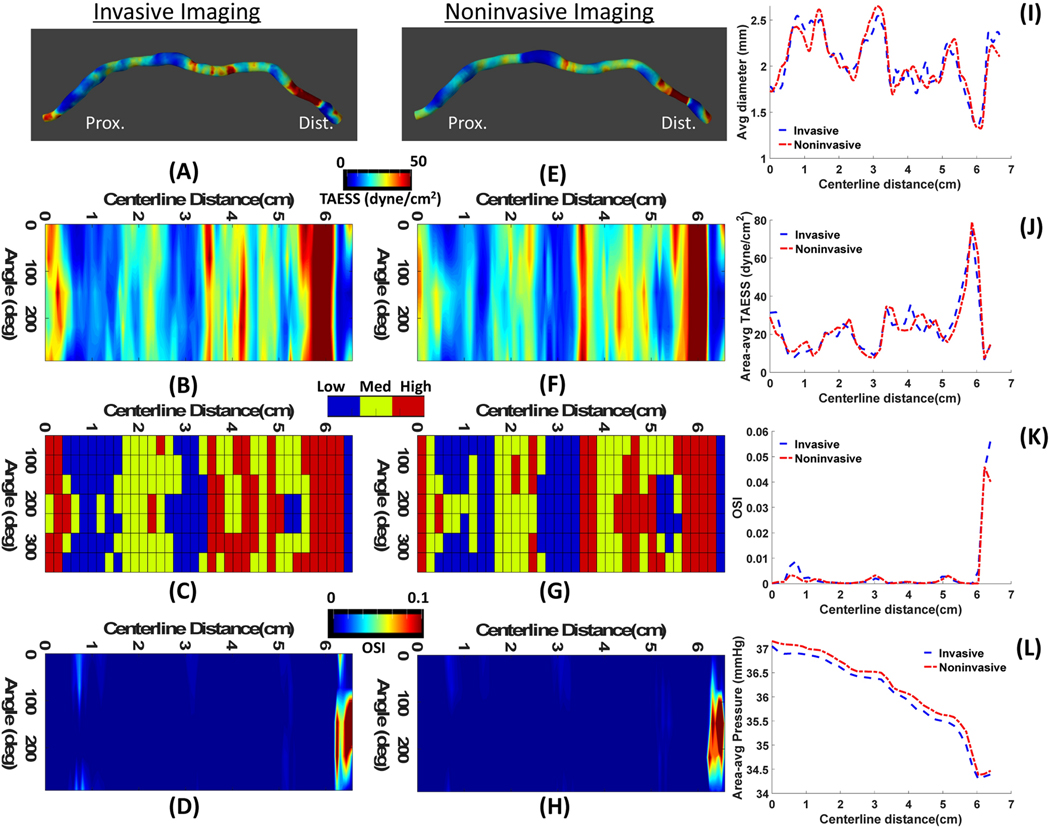
Figure 4.

A representative case (Patient 3) with high agreement between the hemodynamics calculation based on invasive IVUS (A-D) and noninvasive CTA (E-H). 3D map of ESS representations (A,D) where the proximal and distal ends of the vessels are aligned with the 2D map of ESS (B,F) along the centerline of the vessel. Categorical values of ESS (C,G) show low, medium and high at each 45° arc and 2D map of OSI (D,H) values along the centerline are shown. Comparisons of average diameter (I), area averaged TAESS (J), area averaged OSI (K) and area-averaged pressure (L) show a high agreement between IVUS and CTA calculated parameters.

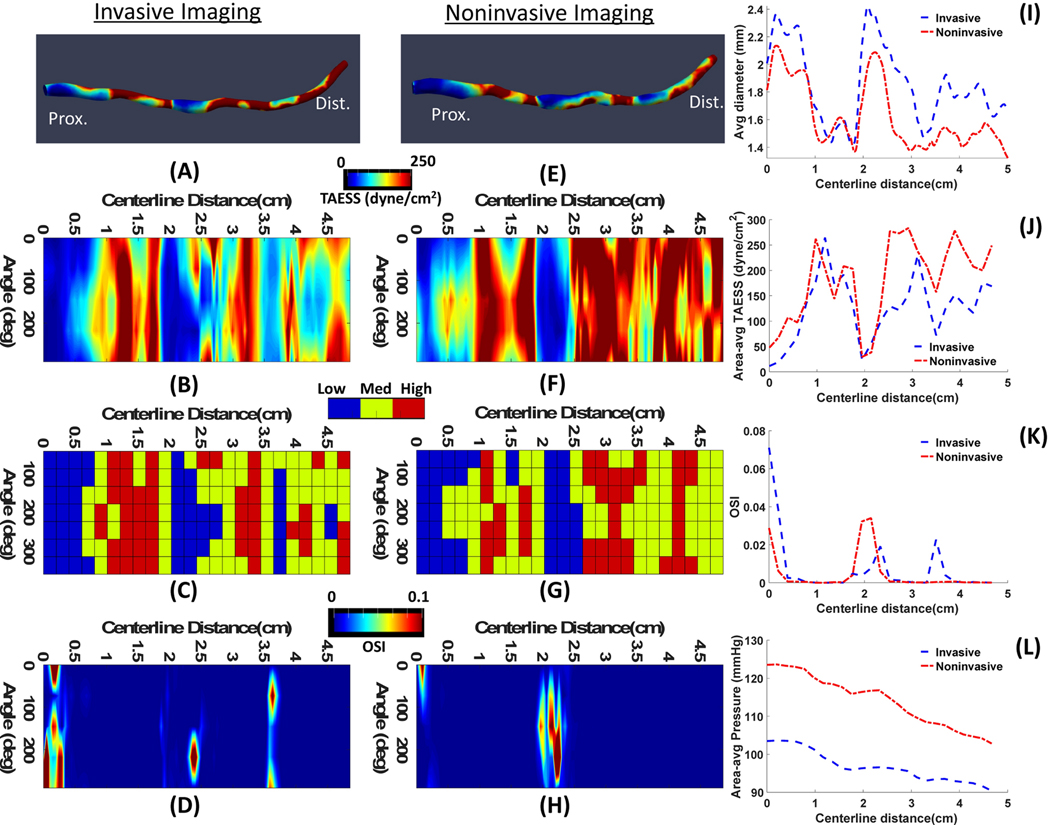
Figure 5.

A representative case (Patient 6) with moderate agreement between the hemodynamics calculation based on invasive OCT(A-D) and noninvasive CTA (E-H). 3D map of ESS representations (A,D) where the proximal and distal ends of the vessels are aligned with the 2D map of ESS (B,F) along the centerline of the vessel. Categorical values of ESS (C,G) show low, medium and high at each 45° arc and 2D map of OSI (D,H) values along the centerline are shown. Comparisons of average diameter (I), area averaged TAESS (J), area averaged OSI (K) and area-averaged pressure (L) show moderate agreement between IVUS and CTA calculated parameters.

Figure 6.

Correlation plots between on TAESS calculations based on invasive and noninvasive imaging for the training dataset showing a high (A) Pearson correlation (r=0.86) for area-averaged TAESS and (B) r=0.85 for arc-averaged TAESS. The linear fit curve has a slope of 1.03 and a y-intercept of 19.4 showing a slightly higher TAESS values for the noninvasive imaging modality. The independent and testing patients show very high correlation between the invasive and noninvasive models for (C) area-averaged and (D) arc-averaged TAESS with a higher TAESS estimation in noninvasive TAESS.

Table 3.

Median[IQR] values for hemodynamics calculated in the training and testing dataset based on invasive (IVUS/OCT) and noninvasive (CTA) imaging.

	Training Data			Testing Data
	CTA Median [IQR]	OCT/IVUS Median [IQR]	p-value	CTA Median [IQR]	OCT/IVUS Median [IQR]	p-value
${\overline{TAESS}}_{seg}$ (dyne/cm2)	50.1[25.8–90.1]	31.7 [19.3–62.4]	<0.001	30.1[17.1–83.8]	15.8[8.8–63.4]	<0.001
${\overline{TAESS}}_{arc}$ (dyne/cm2)	47.7[24.1–90.0]	29.9 [18.1–62.4]	<0.001	29.4[16.2–74.7]	15.0[8.9–57.4]	<0.001
$TAES{S}_{min}$ (dyne/cm2)	16.2[6.7–34.7]	10.3[4.4–19.5]	0.006	13.4[6.1–25.9]	6.0[4.1–17.1]	<0.001
$TAES{S}_{max}$ (dyne/cm2)	90.3[42.8–167.6]	55.3[34.0–117.3]	0.007	51.8[27.4–128.4]	25.6[18.0–120.9]	<0.001
${\overline{OSI}}_{seg}$ (x10−4)	6.3[2.0–34.0]	1.1[2.0–51.0]	0.15	8.5[3.0–24.0]	23.0[7.0–57.0]	<0.001
${\overline{P}}_{seg}$ (mmHg)	84.8[52.5–100.5]	69.2[43.1–87.6]	<0.001	96.3[70.9–98.9]	78.8[78.5–90.3]	<0.001
Dia (mm)	2.2[1.8–2.7]	2.4[2.0–3.1]	<0.001	2.5[1.9–3.0]	3.1[2.2–3.6]	<0.001

${\overline{TAESS}}_{seg}$: segment-averaged time averaged endothelial shear stress; ${\overline{TAESS}}_{arc}$: arc-averaged time averaged endothelial shear stress; $TAES{S}_{min},TAES{S}_{min}$: minimum and maximum time averaged endothelial shear stress in each 2mm segment; ${\overline{OSI}}_{seg}$: segment-averaged oscillatory shear index; ${\overline{P}}_{seg}$: segment-averaged time averaged pressure; Dia: lumen diameter

Figure 7.

Bland-Altman plots to compare the TAESS calculated based on noninvasive-based models versus the gold standard invasive-based models for (A) the area averaged TAESS (B) arc-averaged TAESS in the training cohort and (C) the area-averaged and (D) arc-averaged in the four independent testing patients. $\text{Δ}TESS={\overline{TAESS}}_{invasive}-{\overline{TAESS}}_{non-invasive}$

For the training patients, medians of TAESS_min were significantly different in invasive and non-invasive imaging with values of 10.3[4.4–19.5] and 16.2[6.7–34.7] dynes/cm², respectively. TAESS_max values were also significantly different in the invasive and non-invasive models (55.3[34.0–117.3] vs. 90.3[42.8–167.6] dynes/cm²). In addition, minimum and maximum TAESS had a correlation of 0.82 and 0.86 respectively (p<0.001) between the two models based on invasive and noninvasive imaging. A similar tendency was observed in the testing patients along the entire vessel with significant difference in absolute values of TAESS_min and TAESS_max with a high correlation between the two imaging modalities (r = 0.85 and 0.89 for, TAESS_min and TAESS_max, respectively)

Categorical TAESS:

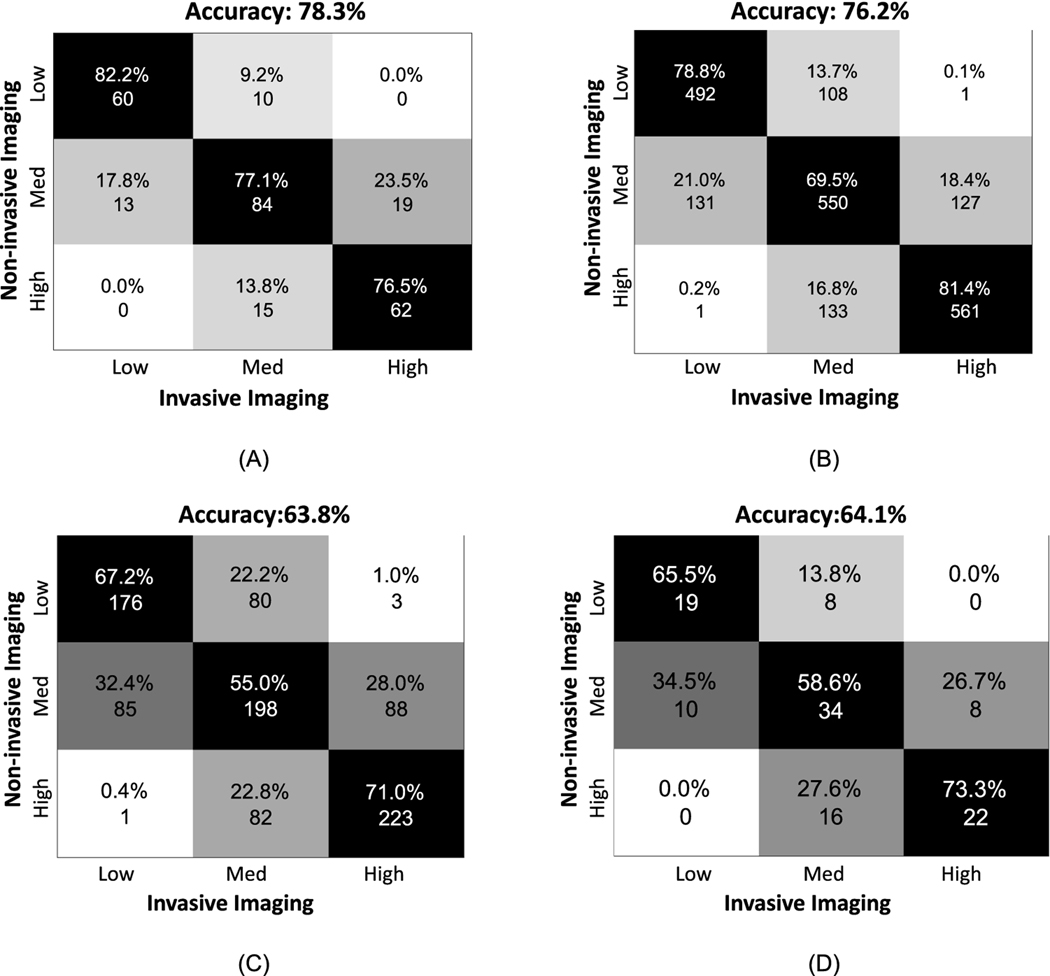
After categorizing the TAESS in three patient-specific tertiles(low, mid, high) for each 2mm-segment and 45°-arc, we found a high agreement between invasive and non-invasive imaging (Figure 8). The confusion matrices shows an overall accuracy of 78.3% for the categorical ${\overline{TAESS}}_{seg}$ values where low, medium and high categories had 82.2%, 77.2% and 76.5% concordance between the two imaging modalities. Similarly, the categorical ${\overline{TAESS}}_{Arc}$ values had an overall accuracy of 76.2% where the low, medium and high categories had an agreement of 78.8%, 69.5% and 81.4%, respectively. The same trend was observed in the testing dataset with a lower overall accuracy of 64.1% and 63.8% in for the segment-averaged and arc-averaged concordance.

Figure 8.

Confusion matrices to demonstrate the agreement between categorical TAESS based in invasive- and no- invasive-based models based on patient-specific tertiles for (A) area-averaged and (B) arc-averaged calculation in the training cohort and (C) area-averaged and (D) arc-averaged calculations in the testing cohort. The testing cohort accuracy is relatively lower than the training cohort models when matching categorical TAESS, however the trend is similar where there is higher accuracy in the low and high categories and the medium category is mis-categorized in the noninvasive-based models.

In both training and testing datasets, the majority of disagreements were observed in the arcs and areas where the non-invasive-based TAESS was labeled as medium (77.1% in training, 55% in testing) and the invasive model labeled as low (17.8% in training, 32.4% in testing) or high (23.5% in training, 28.0% in testing).

Other Hemodynamic Calculations:

The median[IQR] values for OSI and pressure are reported in Table 3. ${\overline{OSI}}_{seg}$ based on non-invasive imaging had a significant moderate Pearson correlation with invasive imaging in the training dataset (r=0.64, p <0.001) and testing dataset (r=0.70, p <0.001). ${\overline{P}}_{seg}$ had a high correlation of (r=0.91, p<0.001) in the training dataset and r=0.85, p<0.001) in the testing dataset.

Lumen diameter:

The median lumen diameter of the LAD arteries as assessed with invasive imaging was 2.4[2.0–3.1] mm and significantly larger than the lumen diameter as measured with coronary CTA (2.2[1.8–2.7] mm (p<0.001)). In the linear regression analysis, we found that also diameter as derived for both imaging methods are highly correlated (Figure S1A) with a significant correlation of 0.93 (p<0.001). The high correlation trend remained very similar for the testing dataset (Figure S1B).

DISCUSSION

In this study a robust methodology was developed and validated to assess TAESS non-invasively using CTA. Therefore, TAESS as assessed with CTA was compared and validated against invasive imaging data from both clinically routine imaging as well as a dataset from a controlled clinical trial. With correct co-registration, accurate segmentation, adjusted boundary conditions as well as optimized smoothing of both imaging modalities, the methodology developed here demonstrates the ability to perform a detailed hemodynamic assessment based on non-invasive CTA. Although the absolute TAESS values were overestimated using CTA-based calculations, the observed patterns had a high concordance, which allows for providing non-invasively derived ESS information as a potential biomarker available for a new group of patients at high risk of plaque progression and future events.

There are a few studies that based ESS calculations solely on coronary CTA imaging with no comparison of invasive imaging. Lee et al²⁹ studied an adverse hemodynamic characteristic including FFR_CT, ESS and axial plaque stress to assess the presence of adverse plaque characteristics resulting in future ACS. In Han et al²¹ high categorical ESS was associated with adverse plaque characteristics independent of stenosis severity. However, in both of these studies, ESS was not studied in detail and was averaged over the length of the lesion discarding the heterogeneity of the local ESS over the stenosis.

Since CTA-based ESS calculations have shown a great potential to serve as a noninvasive method for risk prediction of ACS²⁹,²¹, it is of crucial importance to have access to accurate TAESS measurements. Therefore, we aimed at developing a robust methodology to assess CTA-based TAESS and validated it against IVUS/OCT TAESS in human coronary arteries. A previous study performed by Bulant et al.⁷ showed that the CFD models based on CTA estimated higher TAESS compared to IVUS, similar to our observations. Although we showed a high correlation (r) TAESS calculated between the two imaging modalities, this over estimation of TAESS based on non-invasive imaging is visualized more clearly in Bland-Altman plots (Figure 7) where the systematic bias of on ~−20 dyne/cm2 can be observed on the mean differences in both training and testing patients as well as a proportional difference when a linear regression is performed with a slope of ~−0.2 to −0.3 in the training and testing patients, respectively.

In our study, geometry difference is the main contributor to calculation of different TAESS values between the two geometries. One of the reasons for a higher estimation of TAESS in the CT-based models is the observed difference in measured diameters. CT-based diameters were smaller than invasive imaging and were undermeasured by 30% (as shown in the linear regression analysis in Figure S1A). Our data is consistent with previous studies that compared minimal lumen area where Collet et al¹² and Veselka et al⁴⁴ reported a 25 or 28% f of undermeasurement of CTA lumen diameter as compared to IVUS imaging. In addition, in the FIGURE-OUT (Functional Imaging criteria for GUiding REview of invasive coronary angiOgraphy, intravascular Ultrasound, and coronary computed Tomographic angiography) trial, Doh et al¹⁴. showed a consistent underestimation of minimal luminal diameter and minimal luminal area based on coronary CTA compared to IVUS regardless of vessel size, lesion severity, lesion location, and the presence of calcification. This underestimation of luminal diameter is particularly clinically relevant when the severity of coronary artery disease in patients is assessed using different imaging modalities. Therefore, in our study when calculating the shear stress, this disagreement of luminal measurement becomes clinically relevant. Although lumen size has a major influence in determining TAESS values, it is not the only determinant factor. For example, the shape of the lumen is another important contributing factor. We assume that the cross-sections are circular, however, in some segments, due to the presence of disease, cardiac phase and the curvature of the artery, the lumen shape takes a different form and is not a perfect circular shape. As IVUS/OCT has a higher resolution in capturing these variations, the diameter can be measured accounting for those changes while coronary CTA is not capable of capturing those details. Therefore, shear stress is highly dependent on local geometry such as curvature and presence of plaque resulting in a complex 3D flow structure where TAESS will have a different pattern as compared to a straight cylinder. A list of sources that contribute to the differences in 3D geometry reconstruction and therefore calculation of shear stress is discussed further in this section.

Although Bulant et al. compared TAESS based on non-invasive and invasive imaging, they did not study the local heterogeneity in ESS in great detail. Furthermore, they did not check the agreement between the two imaging modality for categorized TAESS. We showed detailed agreement of segment- averaged as well as arc-averaged between the two imaging modality using standard coronary CTA and IVUS/OCT and showed that our methods can be robustly used in four additional patients. In addition, for clinical implication of CTA we studied categories of low, medium and high TAESS values and demonstrated that there is a high agreement between the relative TAESS values as well. Lastly, it should be mentioned that although our analysis was done for a 2 mm segment which shows a more detailed comparison, we saw a very similar, slightly higher, correlation between the TAESS values for 3mm segments calculated in both the training and testing patients (Supplementary Figure S14).

We found a large range in absolute TAESS values in our study (Table 3). Compared to the reported TAESS values based on IVUS/OCT, the values in our study were generally in the same range as other studies. For example in Stone et al.⁴⁰ values from the PREDICTION trial for the lowest and highest values of local ESS based IVUS imaging were reported as 6.1±3.4 and 60.2±2.9 dyne/cm². In another IVUS-based study, Samady et al.³⁵ reported values for TAESS with low categorical ESS as 5.7±2.3 dyne/cm² and high ESS as 43.9±21.4 dyne/cm². Our results may have higher absolute TAESS values due to removal of side branches which are consistent with the observations in other studies¹⁸, however the wide range in TAESS values did now allow us to conclude clear differences with other studies^9,26,38. It should be noted that each patient-specific physiologic conditions are different from one another resulting in a variability of TAESS values. Therefore, to categorize the shear stress values, the thresholds were chosen based on each patient-specific ranges. However, we repeated the categorical analysis, this time with predefined thresholds based on previous studies^13,28 where low, medium and high categories were defined as TAESS < 10, 10 ≤ TAESS < 25 and TAESS ≥ 25 dynes/cm², respectively, and found that low TAESS is categorized very accurately (75% in training and 100% testing patients) based on invasive vs. noninvasive imaging while medium and high categories are less accurately categorized (66% and 85%, respectively in training patients) compared to the patient-specific tertiles (Figure S15).

In the process of creating computational models using the two approaches applying CTA and IVUS/OCT we have discovered a few issues that may introduce errors in anatomical model creation. The first and most important source of error was a mismatch in co-registration of images between modalities. For example, in gated IVUS images, there may be branches that are not visible on the gated views and this issue could cause a miscount and therefore mismatch of branches. We have observed that even a small miscount in co-registration of IVUS/OCT or slices in CTA results in an incorrect anatomical reconstruction.

The second source of error was the imaging artifacts that influenced the lumen segmentation. As expected, the contrast between lumen and vessel wall was most clear in OCT images. However, the following imaging artifacts could influence our ability to segment the lumen properly: incomplete blood displacement/residual blood artifact- resulting in light attenuation, sew-up⁵ artifacts resulting from rapid wire or vessel movement along one frame and misalignment of the lumen border. We also observed signal-poor regions at sites with oblique incidence of OCT beam which introduced an asymmetric oval cross-sectional area as opposed to a circular cross-section³⁷. This was very apparent in Patient 6 (Figure 5) which represents the poorest performance of hemodynamic comparisons between the invasive and non-invasive imaging modality. For IVUS, similar to OCT, sew-up artifacts may cause uncertainty in lumen border segmentation especially at locations with side branches. In coronary CTA, one of the major segmentation challenges were regions with calcium where the blooming effects artificially causes the lumen to look smaller. Therefore, we segmented the lumen to the best of our ability such that it represents the true lumen size.

The third source of error is the lower image resolution of CTA_. This is especially important for distal segments where the lumen in some cases was not clearly visible. We followed the current clinical and research protocols to exclude the vessels that are <1.5 mm in diameter in distal segments¹¹. Indeed, the minimum reported CTA-based lumen diameter in one of the distal segments is 1.53 mm.

Study Limitations and Future Work

The underlying hypothesis of this work was that coronary CTA, although with 3–10 fold lower resolution than IVUS and OCT imaging can capture the local hemodynamics and detailed flow structures to estimate endothelial shear stress. We selectively included patients with high image quality and excluded patients with large amount of calcified plaques or previous stent placement in the CTA images. Including sub-optimal dataset would conclude a result where CTA may not perform as well as invasive imaging. A future study should be implemented including sub-optimal images to have a more comprehensive analysis of all types of CTA images. Although the time between the imaging acquisitions was up to 90 days, we assumed that the patient-specific cardiovascular hemodynamics and anatomy did not majorly change between the two imaging modalities acquisitions. Since IVUS/OCT are single vessel imaging modalities, our study included no side branches. In addition, this study includes only LAD arteries that contain a high number of branches. Since side branches were majorly important in our methodology as landmarks to match the invasive with non-invasive imaging, a study including right coronary arteries with less side branches should be also implemented to ensure the results can be replicated for this vessel as well. We used a general input waveform and tailored it specific to each patient’s cardiac output and heart rate which introduces a limitation to the patient-specific waveform effect in calculation of ESS. Previous studies based on invasive imaging have shown the association of ESS with future events as well as atherosclerosis progression^13,15,32,39. With the results of this proof of concept study, we showed that non-invasive CTA based 3D models have similar ESS patterns compared to the golden standard of intravascular invasive imaging based models. A future study or retrospective analysis of studies with serial coronary CTA scans should be conducted to assess the ability of coronary CTA CFD models in predicting plaque progression on CTA and the relationship with future events.

Conclusion:

In this methodology development study we demonstrated that our CTA-based models can assess TAESS in great detail. These TAESS have a high correlation with TAESS derived from golden standard of IVUS/OCT based 3D reconstructions. Although CTA-based calculation over-estimated the TAESS, the found patterns were very similar to the ones based on invasive imaging. Therefore, CTA-based ESS studies may be an alternative to capture the same relationship between ESS and plaque morphology as the invasive imaging-based calculations.