Rejoinder: ‘Estimating time-varying causal excursion effects in mobile health with binary outcomes’

1. Introduction

We would like to thank the editor for making this a discussion paper. We are honoured that these three groups of researchers agreed to be discussants. Reading their discussions has been an enjoyable and thought-provoking journey for us. We organize our rejoinder by topic, as some topics have been discussed by multiple discussants.

2. Dependence of the causal excursion effect on treatment protocol

In general, the causal excursion effect in (2) of the main manuscript depends on the randomization probability of past treatment assignments (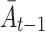), which we refer to as the treatment protocol. This feature distinguishes the excursion effect from most other causal effects in time-varying treatment settings, such as causal effects in marginal structural models or structural nested mean models.

Guo et al. (2021) and Zhang & Laber (2021) provided numerical examples to illustrate this feature of the excursion effect. Guo et al. (2021, Equation 6) considered as one example the following data-generating process:

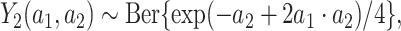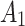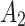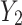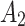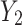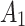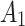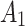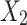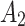where the prior treatment, , interacts with the present treatment, , to affect . They showed that the magnitude and sign of the causal excursion effect of on , which marginalizes over , depends on the randomization probability of . In the second example they considered, there is a three-way interaction between , and on 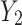, and they showed that the effect modification by 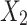of the causal excursion effect of 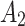can vary depending on the randomization probability of 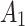. Zhang & Laber (2021) provided two examples where the current treatment interacts with a prior treatment as well as a time-varying covariate, and showed the dependence of the excursion effect on the randomization probability of prior treatments. Zhang & Laber (2021) wrote ‘a large negative causal excursion effect does not mean a treatment is harmful; rather it may mean that the protocol drove patients into states for which treatment appeared harmful.’ We very much agree. Indeed, the comparison between two excursions starting at time 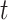is likely to greatly differ by the treatment protocol up to time 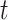; an example is to consider (i) a treatment protocol that is feasible to implement in practice, and (ii) a treatment protocol that is infeasible or excessively onerous. Below we argue that this consequence makes sense in a continual learning setting such as in mobile health.

First, note that this consequence of marginalization occurs in all marginal models; models that don’t condition on all relevant covariates. In Equation (6) of Guo et al. (2021) 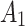  plays the role of a covariate in the analysis of the effect of 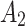on 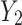. Another related setting is the primary analysis for a factor in a factorial design, where the other factors are averaged over. If there is interaction between factors, then the primary analysis result for one factor will depend on the distribution of the other factors.

As discussed in § 8 of the main manuscript, we view the dependence of the causal excursion effect on the randomization probability of past treatments, the treatment protocol, as a desirable feature. In our mind, the causal excursion effect makes most sense in a continual learning setting. Because the technology is evolving rapidly, mobile health intervention development/optimization requires repeated updating and improvement. We advocate that the treatment protocol at any given time, including when implemented in a micro-randomized trial, be sufficiently realistic that it can be implemented in practice. We mean realistic in the sense that considerations of burden and domain knowledge on effectiveness have been taken into account. Thus, at each stage researchers are interested in answering the question: how would one further improve the current treatment protocol? Causal excursion effects provide an approximation to a gradient in addressing this question; see § 3 below.

Nonetheless, the examples provided by Guo et al. (2021) and Zhang & Laber (2021) clearly illustrate the dependence of the causal excursion effect on the treatment protocol, and highlight the importance of interpreting the causal excursion effect in the context of the treatment protocol. We agree with the discussants that additional analyses, such as effect moderation of the causal excursion effect by prior treatments and time-varying covariates, are often useful to understand the dependence of the causal excursion effect on the treatment protocol. We consider them as secondary and exploratory analyses, which have been routinely carried out in micro-randomized trial analyses. For example, in HeartSteps V1 (Klasnja et al., 2018), a micro-randomized trial for developing push notifications to encourage regular physical activity among sedentary adults, after the primary analysis to assess the marginal excursion effect of the push notification, the researchers conducted a variety of secondary analyses, which included the effect modification by past treatments and past covariates, and how the marginal excursion effect changes over time. They found that the magnitude of the effect changes from positive to not different from 0 around mid-study, suggesting that burden and habituation due to past treatments affects the causal excursion effect. Additional qualitative studies, e.g., via exit interviews, suggested that the decreasing, with time, magnitude of the excursion effect might be due to habituation.

Zhang & Laber (2021) discussed two exploratory analysis approaches to assess the degree of dependence of causal excursion effect on treatment protocol. One approach is to use a partially observable Markov decision process to capture the non-Markov dynamics of patient histories, including past treatments, which can be understood as constructing features that summarize the past effect modifiers. The other approach is to vary the randomization probabilities, or other features of the design, and assess how the causal excursion effect varies accordingly. These are interesting future research topics.

3. Using the causal excursion effect to modify the protocol

Guo et al. (2021) pointed out that due to the dependence of the causal excursion effect on the treatment protocol, modifying the treatment protocol based on the excursion effect can be a challenging task. This is because as the treatment protocol is modified, the causal excursion effect would change accordingly. We very much agree. Below we lay out our current understanding and thoughts on this topic.

Using the treatment regime notation mentioned by Guo et al. (2021) in their § 1, let 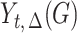be the potential outcome of 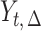under a regime 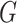. Let 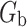be the regime, i.e., the treatment protocol, in the micro-randomized trial. Consider a new candidate regime, 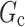. A natural comparison between the two regimes is the log relative risk,

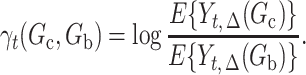(1)

For clarity, we only consider the marginal comparison and do not condition on any effect modifiers 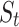. Inverse probability weighting can be used to estimate the numerator in (1) using data collected under 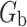; note that to ensure the weights are stable, 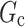cannot be too different from 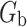. One realistic situation is where 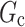represents a small deviation from the treatment protocol 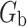. For example, 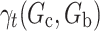represents an approximation to the derivative

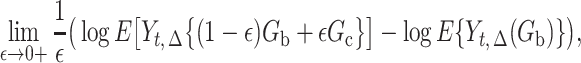(2)

where 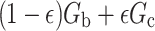is a mixture of the two regimes. Equation (2) represents the relative change in the log expected potential proximal outcome when the regime changes in the direction of 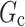. The sign of 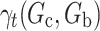as well as how it varies over time, plus expert input and qualitative user studies, inform how to alter the current treatment protocol. A caveat is that these are high-dimensional optimization problems and the gradient at any point in a particular direction may be misleading, e.g., it may lead to a saddle point or a local optimum.

Using the above notation, the causal excursion effect defined in the main manuscript can be written as 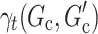, where 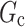is the regime that is the same as the treatment protocol 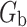up to 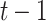, then it assigns the future 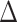treatments deterministically as 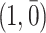, and 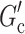is the regime that is the same as the treatment protocol 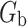up to 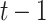, then it assigns the future 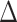treatments deterministically as 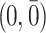. As a result, 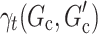can be viewed as an approximation to

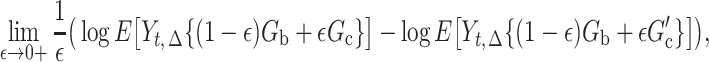i.e., the difference in the relative change in the log expected proximal outcome when the regime changes in the direction of 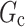versus when the regime changes in the direction of 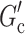. One recent work that leverages the above idea is Liao et al. (2020), where the authors used effect modification analyses of micro-randomized trial data to form a warm-start policy for a reinforcement learning algorithm in a subsequent study.

4. Other points raised by discussants

4.1. Causal excursion effects with different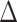

In the main manuscript, the causal excursion effect is defined for a specific 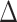, the time window over which the proximal outcome is measured, and 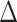is typically predetermined based on domain knowledge. For example, in Sense2Stop (Sarker et al., 2017; Dempsey et al., 2020), a micro-randomized trial for developing stress reduction interventions for people who recently quit smoking, the decision point is per minute and 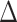is 120 minutes. The particular choice of 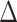was based on the research team’s prior knowledge of the time duration for the intervention effect.

Kim et al. (2021) in their § 3 propose to model the excursion effect for each 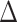separately for a collection of 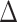s. Such analysis might be used to inform the duration for an intervention to take effect as well as the duration over which the intervention’s effect lasts. We agree that this is a fruitful option for exploratory analysis. However, the warning in (Guo et al., 2021, § 2.2) on history-adjusted marginal structural models indicates that great care must taken to avoid producing model incoherence. We look forward to seeing the work of Kim et al. (2021) in this direction.

4.2. Extension to observational data; efficiency improvement

Both Guo et al. (2021) and Kim et al. (2021) discussed extending the estimating equation (10) of the main manuscript to observational study settings. The estimator 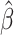solving estimating equation (10) is consistent for the parameter in the marginal excursion effect, 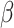in equation (9), if the propensity score 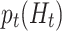can be consistently estimated. However, as Guo et al. (2021) and Kim et al. (2021) pointed out, when is incorrectly modelled, 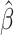will generally not be consistent even if 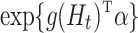is a correct model for the mean potential outcome under no-future-treatment excursion, 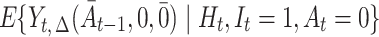. This is due to the fact that the causal excursion effect 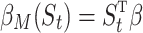is a marginal model; the fully conditional, on 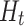, causal effect is not necessarily 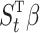. Therefore, even when 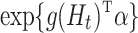is a correct model for 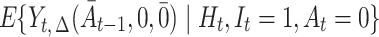, the term 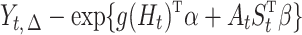in the estimating equation (10) does not generally have conditional expectation zero given 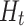. Guo et al. (2021) proposed to subtract the projection of 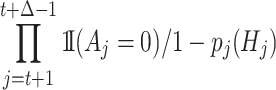onto the scores for treatment to both obtain a doubly robust version and to improve efficiency. Fortunately, for the micro-randomized trials one knows the randomization probability, and the one-sided robustness, consistency under misspecified 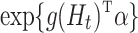, is adequate there. We thank the discussants for pointing this out, and we leave the detailed derivation of a doubly robust version of the estimator for the causal excursion effect for future work.

Of course, the semiparametric locally efficient estimator for the fully conditional, on 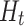, effect with , which was derived in § 4 of the main manuscript based on the results in Robins (1994), has the double robustness property in the sense that it is consistent if either the propensity score model is correct or 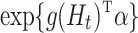is a correct model for 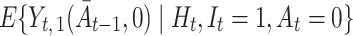. We look forward to the future work of Kim et al. in extending this method to Poisson distributed outcomes.

4.3. Connection and difference between the causal excursion effect and structural models

As we mentioned in § 2.2 of the main manuscript, the causal excursion effect differs from the causal effects considered in marginal structural models and structural nested mean models, and the marginalization aspect of the causal excursion effect is related to the history-restricted version of marginal structural models. Guo et al. (2021), in their Figs. 1–3, rather nicely illustrate the connection and difference between the causal excursion effect and the structural nested mean models and a variety of marginal structural models, including the classic, history-restricted and history-adjusted marginal structural models. We appreciate Guo et al. (2021) making the differences between these effects so clear.

4.4. Identifiability for other types of excursions

In the definition of the causal excursion effect, we considered the two excursions 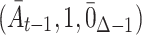and 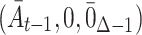. Guo et al. (2021), in their § 1, pointed out that these two are the only static regimes that are identified without further assumptions. Other statistic regimes will have 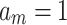for some 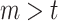, and the average potential outcome under such regimes is generally not identifiable without additional assumptions because of the violation of positivity assumption when 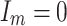with positive probability. We agree with their statement, and appreciate the clarification.

In the Sense2Stop micro-randomized trial that motivated us to consider causal excursion effects with general 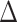, other static regimes were not of scientific interest. If a micro-randomized trial is well designed, regimes such as those that violate the positivity assumption should have been a priori decided to be uninteresting for scientific or ethical reasons. Absent further assumptions, the regimes that are identified by the micro-randomized trial must assign no treatment at time 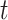whenever 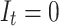. Note that 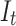can be affected by prior treatments. A rather interesting question is the following. Suppose under the treatment protocol of the micro-randomized trial the probability of 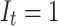is low, and suppose the interest is in estimation of the effect of a new regime that is expected to influence 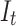so much that 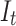will be 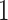with high probability. While this new regime might not violate the positivity assumption, it is likely that the estimator of the effect of this new regime will be quite variable. This can be an area in which it is critical to follow the recommendation of Guo et al. (2021) to extend our current estimator to a doubly robust estimator with improved efficiency.