Effect of crista morphology on mitochondrial ATP output: A computational study

Abstract

Folding of the mitochondrial inner membrane (IM) into cristae greatly increases the ATP-generating surface area, S_IM, per unit volume but also creates diffusional bottlenecks that could limit reaction rates inside mitochondria. This study explores possible effects of inner membrane folding on mitochondrial ATP output, using a mathematical model for energy metabolism developed by the Jafri group and two- and three-dimensional spatial models for mitochondria, implemented on the Virtual Cell platform. Simulations demonstrate that cristae are micro-compartments functionally distinct from the cytosol. At physiological steady states, standing gradients of ADP form inside cristae that depend on the size and shape of the compartments, and reduce local flux (rate per unit area) of the adenine nucleotide translocase. This causes matrix ADP levels to drop, which in turn reduces the flux of ATP synthase. The adverse effects of membrane folding on reaction fluxes increase with crista length and are greater for lamellar than tubular crista. However, total ATP output per mitochondrion is the product of flux of ATP synthase and S_IM which can be two-fold greater for mitochondria with lamellar than tubular cristae, resulting in greater ATP output for the former. The simulations also demonstrate the crucial role played by intracristal kinases (adenylate kinase, creatine kinase) in maintaining the energy advantage of IM folding.

Graphical abstract

Highlights

• •Folding the mitochondrial inner membrane (IM) increases ATP-generating surface, S.
• •Compartments (cristae) created by IM folding restrict internal diffusion of ADP.
• •Flux of ATP synthase, J, is diffusion limited, affected by crista shape and size.
• •ATP output (J x S) is greater for mitochondria with lamellar (vs. tubular) cristae.
• •Diffusion effects are modulated by kinases (adenylate, creatine) inside cristae.

Abbreviations

ANT

adenine nucleotide translocase

EM

electron microscopic

ICS

intracristal space

IM

mitochondrial inner membrane

MICOS

mitochondrial contact site and crista organizing system

OM

mitochondrial outer membrane

PMF

proton motive force

VDAC

Voltage dependent anion selective channel

1. Introduction

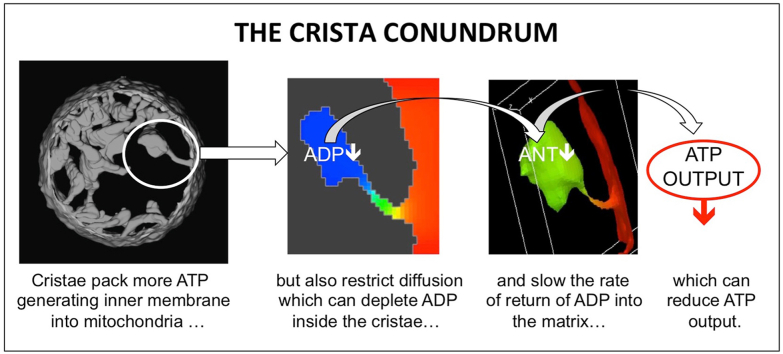
The mitochondrion is the locus of the central process in eukaryotic bioenergetics, the chemiosmotic coupling of substrate oxidation to synthesis of ATP, the cell’s energy currency (Mitchell, 1961). Descended from a single endosymbiotic event over a billion years ago, mitochondria have integrated into numerous cellular metabolic and signaling pathways, and have evolved to optimize their function in each cell type. Mitochondria share a common design: an outer membrane (OM) encasing an inner membrane (IM) that is the scaffold for the respiratory chain and, in turn, encloses a dense matrix of enzymes and ribosomes. The OM surface has a high density of VDAC pores that renders it permeable to solutes smaller than a few kilodaltons (Colombini, 2004; Mannella and Colombini, 1984). Conversely, the IM is impermeable to ions and metabolites (essential to maintain its electrochemical gradient), and contains numerous specific transport proteins. The IM is topologically complex, with numerous folds termed cristae for their crest-like profiles in electron microscopic (EM) images (Palade, 1953; Sjostrand, 1953). Three-dimensional analyses reveal that cristae are membrane invaginations that communicate with the region between the inner and outer membranes (the intermembrane space, IMS) through narrow crista junctions, with openings typically 20–60 ​nm in width (Daems and Wisse, 1966; Mannella et al., 1994; Perkins et al., 1997; Scorrano et al., 2002). The size, shape and packing density of cristae vary among different organisms, among different tissues within the same organism, and even between different regions of the same cells, e.g., (Munn, 1974). Variations are systematic, for example, mitochondria in cells with higher energy demand tend to have larger, more densely packed cristae, presumably to increase ATP production per volume occupied by mitochondria in the cell. Likewise, there is evidence of IM morphing associated with changes in physiological state (reviewed in Mannella et al., 2013; Cogliati et al., 2016), including mitochondrial energization (Hackenbrock, 1966; Mannella, 2006), apoptosis (Scorrano et al., 2002; Heath-Engel and Shore, 2006), and oxidative stress (Deng et al., 2002; Mannella, 2008; Plecita-Hlavata and Jezek, 2016).

The overall size and shape of mitochondria represent a balance struck by organelle fusion and fission, controlled by specific proteins (Scott and Youle, 2010; Huang et al., 2011). Similarly, cristae do not form randomly, e.g., by simple extension and stacking of layers. Rather, cristae are generated and their integrity and shape maintained by mechanisms involving distinct classes of proteins (Friedman et al., 2015; Harner et al., 2016). These include the F₁F₀ ATP synthase (Paumard et al., 2002; Strauss et al., 2008); the mitochondrial contact site complex, MICOS (Harner et al., 2011; Hoppins et al., 2011), which interacts with ATP synthase (Eydt et al., 2017); and Opa1 (Mgm1 in yeast), a highly regulated protein also involved in mitochondrial fusion (Meeusen et al., 2006; Frezza et al., 2006). Thus, the structure of mitochondria has been subject to selective pressure and, by inference, the mitochondrial structure observed in every cell type has evolved to be functionally optimal.

The consequences of mitochondrial design on bioenergetic function merit systematic investigation, given the obvious importance to understanding of cell bioenergetics and diseases with mitochondria involvement, many of which are associated with aberrant mitochondrial structure, e.g., (Munn, 1974; Hoppel et al., 2009; Vincent et al., 2016). In particular, the narrow tubular junctions that interconnect mitochondrial compartments likely represent diffusional bottlenecks for ions, metabolites and soluble proteins (Mannella et al., 1994, 1997). That this may be the case has been demonstrated by reports of lateral proton gradients inside cristae (Rieger et al., 2014; Toth et al., 2020) and of increased mobility of cytochrome c between intracristal and intermembrane spaces following IM remodeling (Scorrano et al., 2002). There is even evidence of dynamic regulation of crista openings in response to metabolic demand (Patten et al., 2014; Dlasková et al., 2019). Similarly, computer modeling of oxidative phosphorylation employing various IM spatial models, idealized and derived from EM tomography, have indicated that concentrations of protons (Song et al., 2013), Ca²⁺ and phosphate (Mannella et al., 2013), and ADP (Mannella et al., 2001; Garcia et al., 2019) can vary significantly between crista and cytosolic spaces. Since the rate of the adenine nucleotide translocase (ANT) depends critically on the ratio of [ADP]/[ATP] on either side of the IM (Klingenberg, 2008), intracristal ADP depletion would slow return of ADP into the matrix and reduce the rate of ATP synthesis (due to lowered matrix levels of ADP).

The extent to which restricted metabolite diffusion inside mitochondria might impact ATP production is especially relevant in tissues such as muscle, where mitochondria respond to high and fluctuating energy demands. Mitochondria of cardiac myocytes contain densely packed tubular or lamellar cristae that yield an IM surface area of 40–60 ​$\mathrm{\mu }$m² per $\mathrm{\mu }$m³ of mitochondrial volume (S_IM/V_MIT ​= ​40−60 ​$\mathrm{\mu }$m⁻¹) which is 2–3 times greater than for liver mitochondria (~20 ​μm⁻¹), as measured by EM morphometry (Smith and Page, 1976; El’darov et al., 2015; Schwerzmann et al., 1986). This study explores the effects of internal metabolite diffusion on mitochondrial ATP output by simulating energy metabolism inside spatial models for cristae of different shape and size. It is found that crista morphology significantly impacts ATP production in a manner that increases with scale and extent of IM folding. The results also illustrate the critically important role of intracristal kinases (such as adenylate and creatine kinases) in maintaining the energy advantage of IM folding.

2. Methods

We have implemented the mathematical model for mitochondrial energy metabolism of Nguyen et al. (2007), which incorporates the Magnus−Keizer model of electron transport and ATP production (Magnus and Keizer, 1998), on the Virtual Cell computational platform (Schaff et al., 1997; CowanMoraru et al., 2012). The “BioModel” (shown schematically in Appendix Fig 1), consists of 24 differential equations for reaction fluxes of the citric acid cycle, electron transfer and ATP synthesis, as well as fluxes for the major ion and metabolite transporters, as defined in equations (1) to (27) of Nguyen et al. (2007). The reaction and transport flux equations incorporate a set of 112 parameters (physical constants, metabolite and ion concentrations, reaction kinetic constants), most of which are defined in Tables 1−6 of Nguyen et al., (2007). The calcium concentration was set to 1.35 ​× ​10⁻⁴ ​mM, and two adjustments were made specific to cardiac muscle mitochondria: the maximum velocity of ATP synthase (V_AS in equation 13 in equation (2) in Appendix) was changed from 1.125 ​× ​10⁻³ ​mM ​ms⁻¹ to 9 ​×10⁻⁴ ​mM ​ms⁻¹ (Wescott et al., 2019), and the calcium permeability of the uniporter was changed from 2.159 msec⁻¹ to 2.59 ​× ​10⁻³ msec⁻¹ (Williams et al., 2013). Initial values for concentrations of ATP and ADP in the mitochondrial matrix were 0.44 ​mM and 0.72 ​mM, corresponding to levels in resting myocytes (Nguyen et al., 2007). Cytosolic ATP and ADP concentrations were set for different simulations, as described below.

An additional rate equation was included in the BioModel not present in Nguyen et al. (2007), a reversible ATP ←→ ADP ​+ ​P_i reaction outside the mitochondrial matrix, intended as a surrogate for the wide range of kinase, ATPase, phosphorylation and related reactions present in different cell types. The velocity of the “surrogate kinase” reaction was represented as a simple mass action formula:

V_SK ​= ​k_f [ATP] ​− ​k_r [ADP][P_i]. (1)

This reaction was tuned in simulations by varying the forward rate constant, k_f, in the range 0.003–0.07 ms⁻¹, while holding the reverse rate constant, k_r, at 1 ​mM ​ms⁻¹. Since [ADP] outside the matrix is usually much smaller than [ATP] and [P_i], lower k_f values render the surrogate kinase reaction closer to equilibrium and more sensitive to local [ADP] (see Section 3.2.2).

The Virtual Cell platform allows assignment of reactions to specific compartments within a spatial model and to the membranes that enclose the compartments, and solves the corresponding partial differential equations at each grid point, allowing for simple diffusion between the pixels or voxels within each compartment. The compartments defined for the mitochondrial models were the matrix space and the space outside the matrix, separated by the mitochondrial inner membrane. The default diffusion coefficient provided by Virtual Cell (10 ​μm²/s) was used for all chemical species except adenine nucleotides (145 ​μm²/s outside matrix, 100 ​μm²/s inside matrix) and Ca²⁺ (530 ​μm²/s outside matrix, 223 ​μm²/s inside matrix) (Vendelin et al., 2000; Donahue and Abercrombie, 1988; Allbritton et al., 1992).

There is ample evidence that respiratory chain components are concentrated on the crista regions of the IM and that ATP synthase occurs primarily on curved IM regions as dimer ribbons, e.g., (Strauss et al., 2008; Gilkerson et al., 2003). While it is possible within the Virtual Cell environment to assign reactions to sub-regions of compartments and membranes, in the current study fluxes of enzymes and transporters were assumed evenly distributed within their respective compartments and membrane surfaces.

The mitochondrial outer membrane (OM) was not explicitly represented in the spatial models, in effect, assuming the OM is not a significant permeability barrier to ions and metabolites. Conditions under which this assumption might not hold, due to partial closure of the VDAC channel (e.g. (Liu and Colombini, 1992; Xu et al., 2001; Rostovtseva and Bezrukov, 2012)) were not explored in the current study.

The boundaries of the Virtual Cell “computing box” were usually 40 ​nm from the periphery of the IM, approximately 20 ​nm outside the location of the missing OM (see Fig. 3). Concentrations of ADP and ATP at the boundaries were set to their initial values outside the matrix ([ADP]°_CYT and [ATP]°_CYT), i.e., steady state solutions yielded these values at the boundaries (in effect, representing the cytosol interface). With the exception of Fig. 1 (see Section 3.1.1), simulations were run using [ATP]°_CYT values of 4.0 ​mM (in the middle of the usual range in mammalian cells of 1–10 ​mM), and [ADP]°_CYT values of 0.037–0.37 ​mM (representing low and high work load, respectively) (Nguyen et al., 2007).

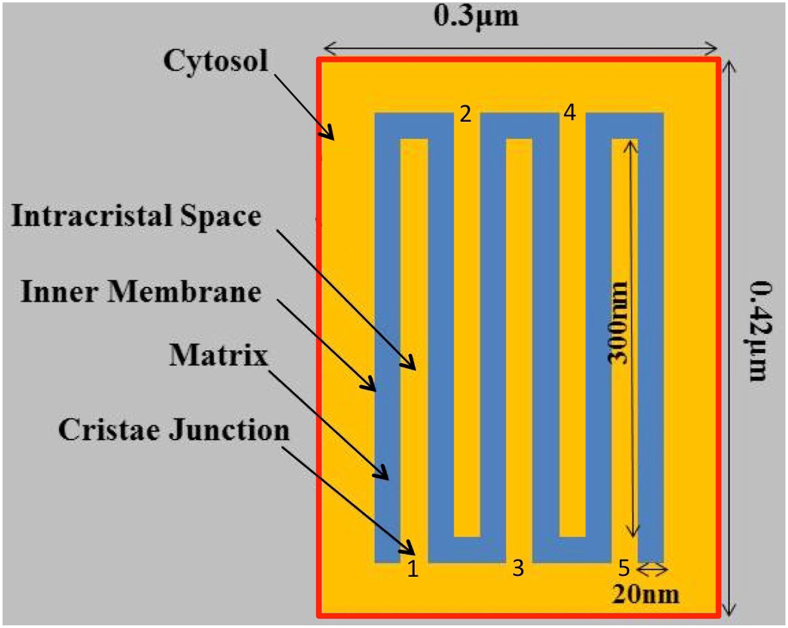
Fig. 3.

Idealized 2D spatial model of a mitochondrion with 5 cristae and no outer membrane. The matrix space is blue and the space outside the matrix (intracristal or cytosolic) is yellow. Cristae are numbered 1 through 5 ​at the crista junction openings.

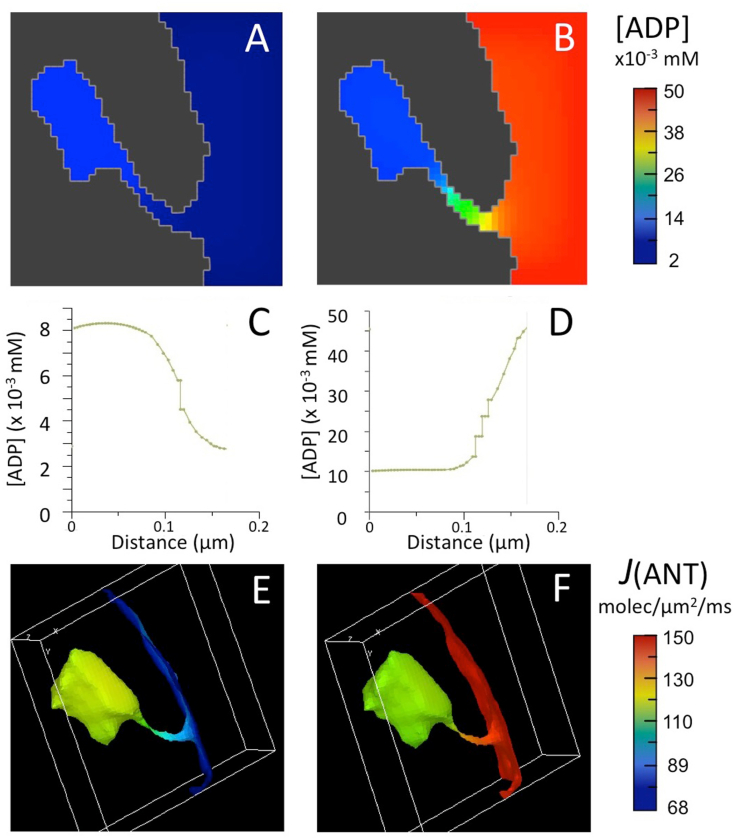
Fig. 1.

Results of computer simulations run with complete BioModel for mitochondrial energy metabolism and 3D spatial model for a crista, as described in text.

(A,B) Maps of ADP concentration, [ADP], outside matrix for initial [ADP] of 0.002 ​mM (A) and 0.05 ​mM (B).

(C,D) Plots of [ADP] from a point distal to the crista junction opening to a point proximal to the opening in (A) and (B), respectively.

(E,F) Maps of ANT flux, J(ANT), on the inner membrane corresponding to the [ADP] maps of (A,B).

Computations were run until steady states were achieved, using variable time steps typically 0.01–0.10 msec (set by the solver) and spatial increments of (5 ​nm)² and (5 ​nm)³ for two- and three-dimensional (2D and 3D) simulations, respectively. Steady state respiratory fluxes of ~10 atoms O/μm²/msec were achieved that fell within the physiological range1. Since the spatial models typically contained 10⁴–10⁵ computing elements, and achieving steady state usually required 10–100 msec of simulation time, runs using the complete BioModel (25 differential equations) were computationally intensive. To speed up computation, a reduced BioModel was used (presented schematically in Fig. 2) that involved only three reactions, surrogate kinase (equation (1) above), ANT and ATP synthase (equations (1) and (2) in Appendix). Use of the reduced BioModel decreased both the number of computations per cycle (22 fewer equations) and the simulation time to reach steady state, by eliminating slow oscillations exhibited by citric acid cycle reactions.

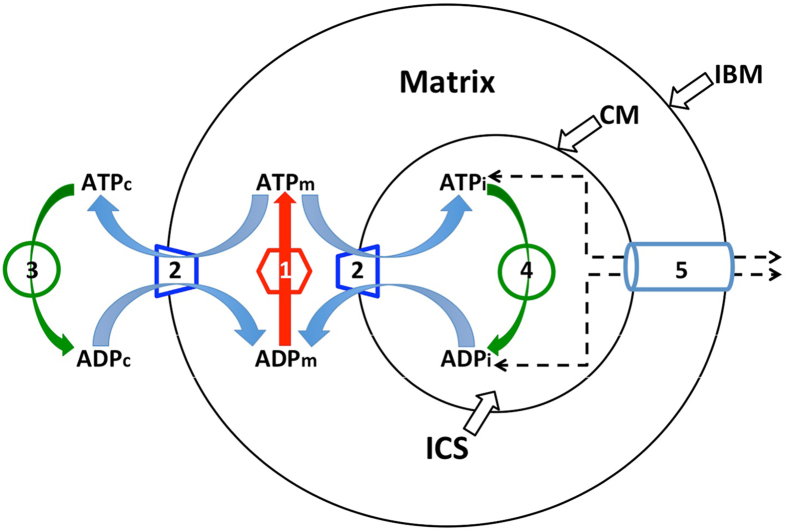
Fig. 2.

Schematic diagram of the “reduced BioModel” for biochemical reactions directly involved in ATP ⇔ ADP “cycling” and transport. There are five processes involved: (1) the ATP synthase, shown as a matrix activity since it occurs on the matrix-facing surface of the inner membrane; (2) the adenine nucleotide translocator, ANT, which can occur either on the peripheral region of the inner membrane (the inner boundary membrane, IBM) or on the internal folds (crista membrane regions, CM, collectively represented as a single crista for simplictly); (3) the surrogate kinase activity in the cytosol and (4) the surrogate kinase activity inside cristae (the intracristal space, ICS, represented as a single compartment for simplicity). Process (5) is an implicit diffusion step, representing restricted movement of adenine nucleotides between cristae and cytosol through crista junctions, collectively represented by a tube connecting IBM and CM. In Virtual Cell, diffusion of metabolites is computed between adjacent volume elements; with the crista junction openings creating diffusional bottlenecks between cytosol and each crista compartment. Subscripts on ADP and ATP: m, matrix; c, cytosol; i, intracristal space.

Fortran code for the Nguyen et al. (2007) model is available at http://www.binf.gmu.edu/jafri/models/models.html. Virtual Cell implementations of the complete model (model code “Energy-production-pathway-complete-model-01132021”) and reduced model (model code “Energy-production-pathway-reduced-model-01132021”), along with the two- and three-dimensional spatial models used in this study, are publicly available at https://vcell.org/.

3. Results

As noted above, internalization of the mitochondrial inner membrane (IM) was a critical early step in the evolution of eukaryotes, increasing the density of ATP-generating machinery while creating diffusion restrictions that could limit the rate of ATP synthesis. The objectives of this study were to use computer modeling to understand the influence of IM morphology on mitochondrial ATP generation and to define factors that exacerbate or compensate for effects of restricted diffusion.

3.1. Effects of inner membrane folding on adenine nucleotide transport

3.1.1. Simulations using complete BioModel

Computer simulations were run with a 3D spatial model for a single crista derived from the EM tomogram of a rat liver mitochondrion, used in a previous study (Mannella et al., 2001). The crista consisted of a flattened cisterna, approximately 300 ​nm across, connected to the peripheral IM by a tubular region, 280 ​nm long and 20–30 ​nm in diameter. Initial concentrations of adenine nucleotides in the matrix were set to typical resting values ([ATP]°_MAT ​= ​0.44 ​mM, [ADP]°_MAT ​= ​0.72 ​$\mathrm{\mu }$M (Nguyen et al., 2007), and the initial cytosolic concentration of ATP was set just above the matrix value: [ATP]°_CYT ​= ​0.56 ​mM. Simulations were run for two values of cytosolic ADP: [ADP]°_CYT ​= ​0.002 ​mM (very low level associated with respiratory state 4) and 0.05 ​mM (typical for a cellular resting state) (Korzeniewski, 2015); and the forward rate constant for the surrogate kinase, k_f, was 0.07 ms⁻¹. As previously observed (Mannella et al., 2001), ~5 fold standing gradients of ADP were established inside the crista at steady state, in this case resulting in ADP sequestration at 0.002 ​mM [ADP]°_CYT and ADP depletion at 0.05 ​mM [ADP]°_CYT (Fig. 1A–D).

The flux of adenine nucleotide translocase, J(ANT), depends critically on local ratios of [ADP] and [ATP] on either side of the IM ((Klingenberg, 2008), also equation (1), Appendix). During these simulations [ATP]_MAT, [ATP]_CYT and [ADP]_MAT remained high and displayed only marginal spatial variations (1–4%) at steady state, in contrast to the steep ADP gradients (~80%) observed inside the crista. Thus, the latter strongly influenced the flux of ANT facing the internal crista space, J(ANT)_ICS. For [ADP]°_CYT ​= ​0.002 ​mM, J(ANT)_ICS attained a maximum value 34% greater than that on the periphery of the IM (facing the cytosol), J(ANT)_CYT (79 vs 59 molecules/μm²/ms) (Fig. 1E). Conversely, for [ADP]°_CYT ​= ​0.05 ​mM, J(ANT)_ICS dropped 13% below J(ANT) _CYT (82 vs 94 molecules/μm²/ms) (Fig. 1F). (Results of simulations are summarized in Table 1.)

Table 1.

Variation in [ADP] and ANT flux inside cristae.

MODEL (FIGURE)	Kf (msec−1)	LCRIS (nm)	[ADP] (mM)		J(ANT) (mol/μm2/ms)
			Proximal	Distal	Proximal	Distal
3D TOMO	0.07	580	.002	.009	68	120
(1)			.050	.010	150	118
2D	0.003	320	.037	.016	110	72
(4)
			.370	.160	114	106
		620	.037	.005	125	38
			.370	.055	122	85
3D LAM	0.003	150	.037	.017	108	76
(5,6)		900	.037	.003	137	22
	0.009	150	.037	.022	104	83
		900	.037	.009	119	56
3D TUB	0.003	150	.037	.028	101	90
(5,6)		900	.037	.003	125	18
	0.009	150	.037	.029	100	92
		900	.037	.008	115	49

Gradients of ADP concentration, [ADP], and ANT flux, J(ANT), were established inside cristae during steady state. Values are presented for [ADP] and J(ANT) at the crista openings (proximal) and at the farthest end of the cristae from the openings (distal) for spatial models with cristae of different length, L_CRIS, and different values of the forward rate constant for the surrogate kinase reaction, k_f. 3D TOMO refers to the three-dimensional crista model extracted from an EM tomogram of a mitochondrion (described in text). The other simulations used idealized 2D and 3D spatial models based on those in Fig. 3, Fig. 5. Numbers in parentheses in first column refer to figures in the text with typical results for that spatial model. Abbreviations: LAM, lamellar cristae; TUB, tubular cristae.

These results (see also below) indicate that cristae define functional micro-compartments, with local steady states distinct from those in the bulk cytosol. When cellular energy demand is low ([ADP]_CYT ​≤ ​0.05 ​mM), the confined crista spaces buffer internal [ADP] (local steady state determined by the surrogate kinase reaction, see Section 3.2.2) and support a relatively constant ANT flux. Because of this “structural buffering”, only the fraction of ANT on the IM periphery (outside cristae) would be responsive to cellular energy demand under these conditions (see Discussion, Section 4.3).

3.1.2. Simulations using reduced BioModel

Systematic studies using larger scale spatial models were expedited by simplifying the BioModel (as explained in Methods, Section 2). The reduced model, shown schematically in Fig. 2, was similar to that used previously (Mannella et al., 2001). It consisted of the biochemical reactions directly involved in ATP ⇔ ADP “cycling” and transport: ATP synthase (labelled 1 in Fig. 2), ANT (labelled 2), and the surrogate kinase (labelled 3 in the cytosol and 4 inside the cristae), along with an implicit diffusion step (labelled 5) for the movement of adenine nucleotides between cristae and cytosol.

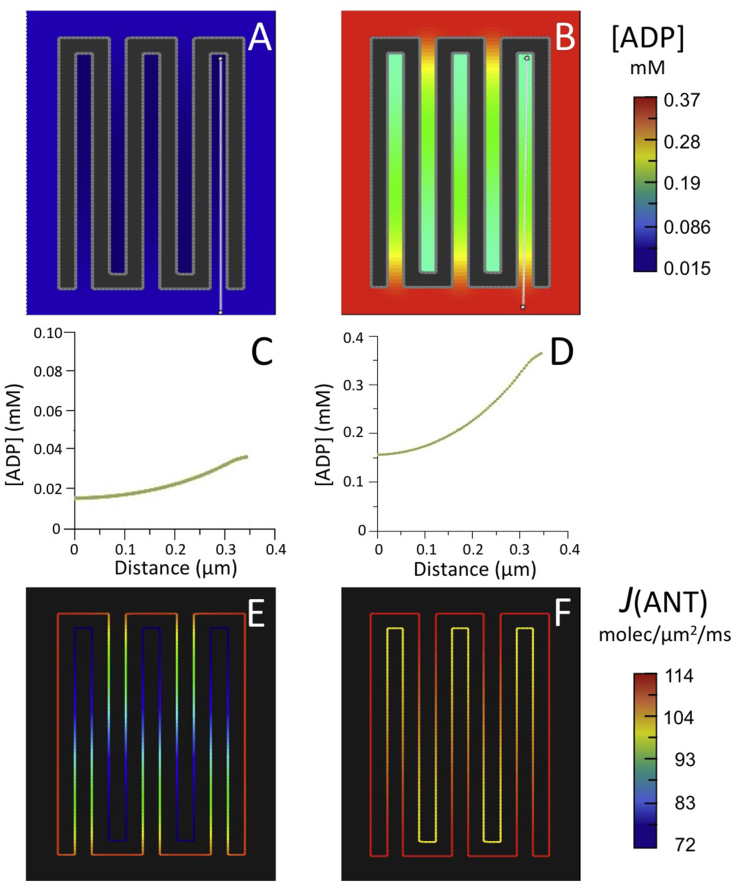
Simulations were run with the reduced BioModel using the two-dimensional (2D) spatial model in Fig. 3, consisting of a continuous IM (outer limits 220 ​nm ​× ​340 ​nm) with five crista invaginations, each 320 ​nm long by 20 ​nm wide (within the range commonly observed in electron tomograms of mammalian mitochondria, e.g. (Perkins et al., 1997; Mannella et al., 1997; Mannella et al., 2001), and separated by a 20 ​nm band of matrix. This geometry approximates the spacing of cristae inside “crowded” mitochondria such as muscle, which typically contain ~50 cristae per 1000 ​nm cross-section, e.g., (El’darov et al., 2015). In effect, this 2D model represents a cross-section through a uniform, infinite column, in this case representing random IM folds akin to a “baffle” model for cristae, e.g. (Frey and Mannella, 2000). While useful as a first approximation (rapid computation times, easily modified and scaled), such 2D models underestimate diffusion-related effects due to bottlenecks (narrow crista junctions) and cannot replicate actual crista morphologies such as tubular and lamellar.

The simulations used a membrane potential of 160 ​mV and the same initial values of [ATP]°_MAT and [ADP]°_MAT as before. [ATP]°_CYT was set to 4.0 ​mM, and [ADP]°_CYT to 0.037 and 0.37 ​$\mathrm{\mu }$M to simulate low and high work load (e.g., resting and contracting muscle), respectively (Nguyen et al., 2007; Korzeniewski, 2015). To compensate for the effect of higher [ATP]°_CYT (4.0 vs. 0.56 ​mM in the previous simulations) on the forward rate of the surrogate kinase reaction, a smaller k_f value was used (0.003 ms⁻¹).

For both values of [ADP]°_CYT, standing ADP gradients were established inside cristae corresponding to decreases of ~50% relative to cytosolic levels (Fig. 4A–D), smaller than observed with the 3D crista model (i.e., a large compartment connected to the outside by a long narrow tube). The corresponding decreases in intracristal ANT flux, J(ANT)_ICS, relative to that on the IM periphery, J(ANT)_CYT, were 37% and 9% for [ADP]°_CYT ​= ​0.037 ​mM and 0.37 ​mM, respectively (Fig. 4E and F and Table 1).

Fig. 4.

Results of computer simulations using the reduced BioModel for mitochondrial energy metabolism (Fig. 2) with (A–F) the 5-crista 2D spatial model of Fig. 3 and (G–L) a larger 15-crista 2D model, as described in text.

(A,B; G,H) Maps of steady state ADP concentration, [ADP], outside matrix for initial [ADP] of 0.037 ​mM (A,G) and 0.370 ​mM (B,H).

(C,D; I,J) Plots of [ADP] along the white lines (from distal to proximal relative to the crista junctions) in the maps of (A,B; G,H), respectively.

(E,F; K,L) Maps of ANT flux, J(ANT), along the inner membrane corresponding to the conditions of (A,B; G,H), respectively.

Simulations were run for the same initial conditions with a larger 2D spatial model, consisting of 15 cristae with lengths (620 ​nm) almost twice as large as in the previous model, typical of cristae that extend across the full width of muscle mitochondria, e.g., (Hoppel et al., 2009; Picard et al., 2012). For both values of [ADP]°_CYT (0.037 and 0.37 ​mM), 7-fold standing gradients of [ADP] developed inside cristae (Fig. 4G–J), more than three times larger than observed with the smaller model. For [ADP]°_CYT ​= ​0.037 ​mM, J(ANT)_ICS dropped by 73% relative to the ANT flux value on the IM periphery, almost twice the drop observed with shorter cristae (Fig. 4K and Table 1). Similarly, for [ADP]°_CYT ​= ​0.37 ​mM, the drop in translocase flux inside the longer cristae (34%) was more than three times that observed with the smaller cristae (Fig. 4L and Table 1.) Clearly, the effects of IM folding on intracristal ADP levels and ANT flux are more significant as crista length increases.

3.2. Crista morphology and kinase activity regulate ATP output

3.2.1. Effects of IM folding on flux of ATP synthase and ATP outout

Computer simulations were employed to quantitate the effect of IM topology on mitochondrial ATP output or production:

qATP ​= ​J(AS) x S_IM (2)

where J(AS) is the flux of ATP synthase (equation (2), Appendix) and S_IM is the surface area of the inner membrane.

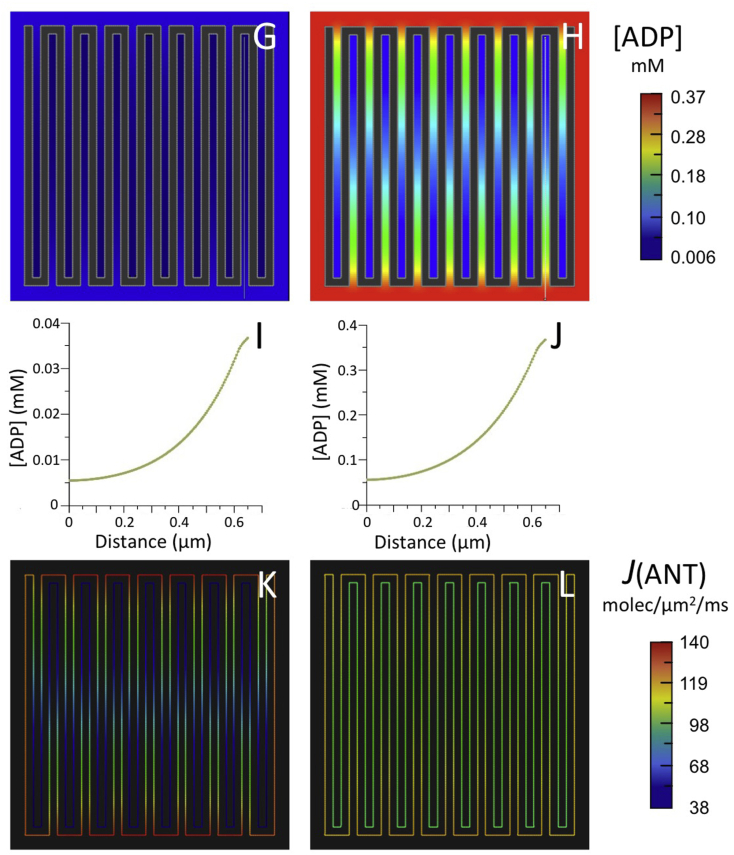
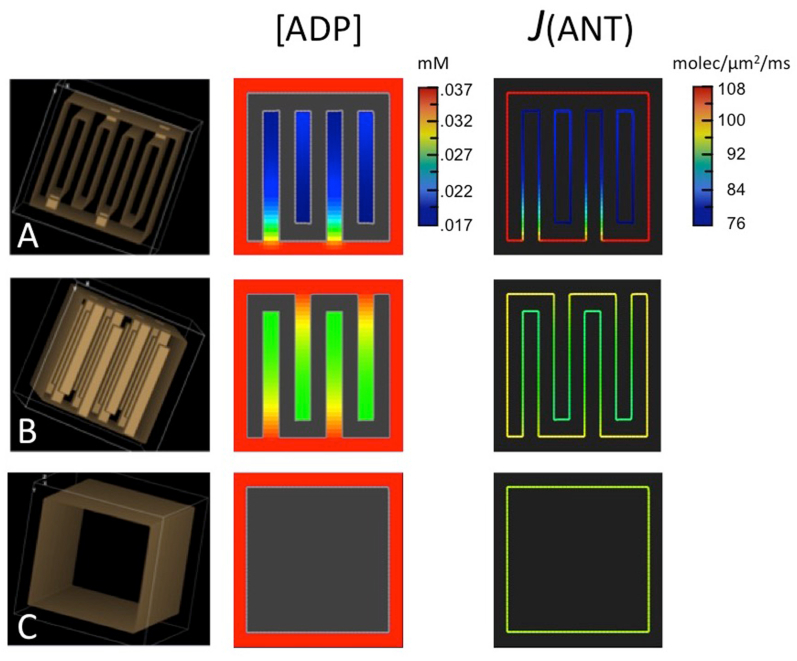
Simulations were run using idealized enclosed 3D spatial models with the three folding motifs shown in Fig. 5: (A) four parallel lamellar cristae (overall dimensions: x ​= ​20 ​nm, y ​= ​150 ​nm, z ​= ​140 ​nm) with single crista junction openings (20 ​× ​20 ​× ​20 ​nm³) alternating on two opposing surfaces; (B) sixteen parallel tubular crista (dimensions: x ​= ​z ​= ​20 ​nm, y ​= ​150 ​nm) that are extensions of single crista junction openings (20 ​× ​20 ​nm²) alternating on two opposing surfaces, and (C) an inner membrane without cristae. To determine effects of scale, the computing voxel in Virtual Cell was increased in the y direction (crista length, L_CRIS) by $3\mathsf{X}$ or $6\mathsf{X}$, and in the z direction (crista width) by $3\mathsf{X}$ 2. The spacing in the x-direction (between the walls of lamellar cristae) was held constant at 20 ​nm. The length of cristae in the largest models approaches that of the longest cristae observed in mitochondria of cardiac and skeletal muscle, e.g. (Hoppel et al., 2009; Picard et al., 2012). The model volume (matrix ​+ ​cristae) varied from 180 ​× ​170 ​× ​180 ​nm³ ​= ​0.0055 ​μm³ to 180 ​× ​1020 ​× ​540 ​nm³ ​= ​0.099 ​μm³, the latter representing approximately one-third and one-sixth the average volumes of rat liver and heart mitochondria, respectively (measured by EM morphometry (Schwerzmann et al., 1986; Laguens, 1971)). Other pertinent geometric parameters for the models are summarized in Table 2.

Fig. 5.

Results of computer simulations run using the reduced BioModel for mitochondrial energy metabolism and 3D spatial models, as described in text. Rows correspond to spatial models with (A) lamellar, (B) tubular and (C) no cristae, respectively, shown in first box of each row. The second and third boxes in each row are slices from 3D maps of ADP concentration, [ADP], outside matrix and of ANT flux, J(ANT), on the inner membrane for each model at steady state.

Table 2.

Geometric parameters of 3D spatial models.

MODEL	SIM/VMIT (μm−1)	SCRIS/SIM	SCRIS/VICS (μm−1)	VICS/NCRIS (× 10−3 ​μm3)
LAM CRIS	64–44	0.50–0.64	118–102	0.42–7.6
TUB CRIS	60–37	0.47–0.56	157–147	0.069–1.25
NO CRIS	32–16	0	0	0

Ranges in values (left to right) correspond to increasing mitochondrial volume. Abbreviations: S, surface area; V, volume; N, number; MIT, mitochondria, CRIS, cristae, IM, inner membrane, ICS, intracristal space, LAM, lamellar, TUB, tubular, MAT, matrix.

Simulations were run with these 3D models using the reduced BioModel and the same initial conditions as for the 2D simulations of Fig. 4, with [ADP]°_CYT ​= ​0.037 ​mM (results summarized in Table 1). At steady state, 2 fold gradients of [ADP]_ICS were established along the short (L_CRIS ​= ​150 ​nm) lamellar cristae, with corresponding drop in J(ANT)_ICS of 30% relative to the translocase flux on the IM periphery (Fig. 5A). When L_CRIS was increased to 900 ​nm, the steady state [ADP]_ICS gradient increased to over 10 fold, with an 84% drop in J(ANT)_ICS. For tubular cristae (Fig. 5B), the steady-state gradient of [ADP]_ICS for L_CRIS ​= ​150 ​nm was 1.4 fold, with a corresponding drop in J(ANT)_ICS of only 10% (vs. 30% for lamellar cristae). However, when L_CRIS was increased to 900 ​nm, the steepness of the [ADP]_ICS gradient (10 fold) and corresponding drop in J(ANT)_ICS (85%) were essentially the same as for lamellar cristae.

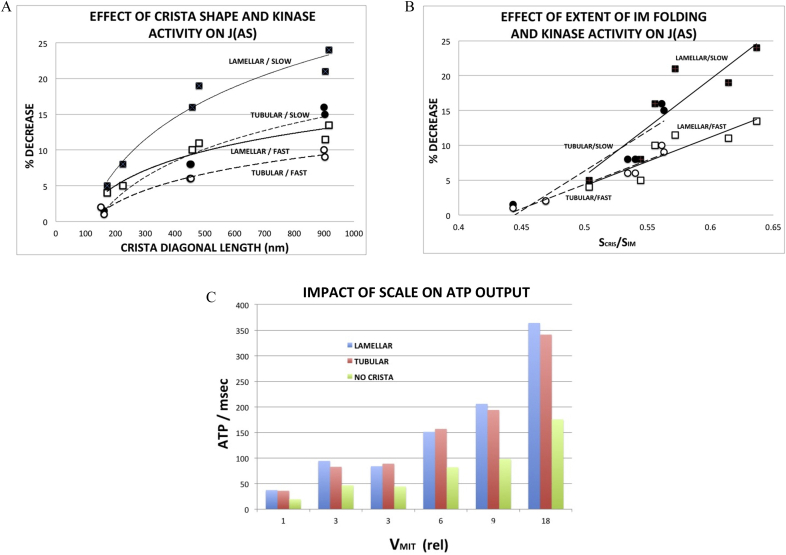
The impact of increasing crista size on the flux of ATP synthase, J(AS), is presented graphically in Fig. 6A and B. The drop in J(AS) (relative to that of the model with no cristae) increased steadily with crista length and was approximately twice as large for lamellar than tubular cristae at the largest dimensions (Fig. 6A, solid symbols). When the decrease in J(AS) is plotted against a measure of the extent of IM folding (surface area of cristae/total IM surface area ​= ​S_CRIS/S_IM, Table 2), the values for tubular and lamellar cristae merge (Fig. 6B, solid symbols). In the range of S_CRIS/S_IM covered by the models (0.45–0.65), the relationship appears linear (R² ​= ​0.86), generally consistent with dependence of J(AS) on the fraction of ANT inside cristae where its flux is reduced by restricted diffusion of ADP.

Fig. 6.

Effects of inner membrane morphology and surrogate kinase activity on (A,B) flux of ATP synthase, J(AS) and (C) ATP output. qATP. Graphs summarize results of computer simulations run with reduced BioModel and 3D spatial models (Fig. 5) of increasing size, as described in text.

(A) Decrease in J(AS) as a function of crista length, calculated as the diagonal from the center of the junction opening to the farthest corner of the crista surface. Data for lamellar crista are represented by ☐ and tubular cristae by ◯; closed symbols correspond to the smaller forward rate constant for the surrogate kinase (k_f ​= ​0.003 ms⁻¹) and open symbols to a three fold larger rate constant (k_f ​= ​0.009 ms⁻¹), labelled “slow” and “fast”, respectively. Solid trend lines correspond to data for lamellar cristae and dashed trend lines for tubular cristae.

(B) Decrease in J(AS) as a function of extent of inner membrane folding; symbols and trend lines as in (A).

(C) ATP output, qATP ​= ​J(AS) × inner membrane area, as a function of relative model volume (largest volume ​= ​0.099 ​μm³). There are two models with three fold volume increase (i.e., V_MIT ​= ​3) relative to the original. Data on left corresponds to model with threefold larger crista width (z × 3); data on right to threefold larger crista length (y × 3).

In all cases, the overall rate of ATP production, qATP ​= ​J(AS) × S_IM, was significantly larger for mitochondrial models with cristae than without, approximately doubled for both lamellar and tubular cristae at all sizes (Fig. 6C). Thus, as expected, the increased surface area provided by inner membrane folding more than compensates for decreased flux of ATP synthase due to restricted diffusion of ADP inside cristae. Despite the lower values of J(AS) for lamellar relative to tubular cristae, ATP production of the two models are roughly equivalent in Fig. 6C, due to the larger IM surface areas (S_IM in equation (2)) of the lamellar models. This has important consequences when results are extrapolated to mitochondrial dimensions observed in tissue like cardiac muscle (see Discussion, section 4.1).

3.2.2. Intracristal kinases modulate impact of IM folding

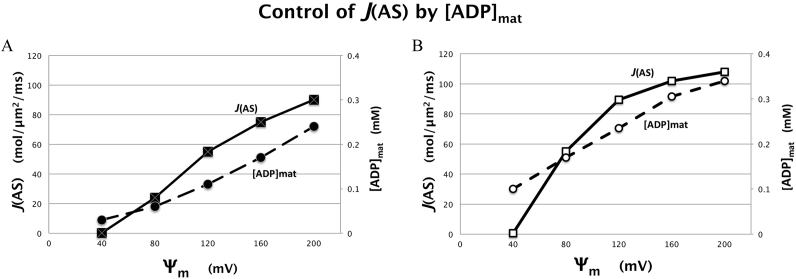
Under the conditions of these simulations, which mimic physiological situations1, steady state ANT flux determines the matrix ADP level which, in turn, sets the flux of ATP synthase, J(AS). This is illustrated in Fig. 7A for simulations using the large 2D spatial model and starting conditions as in Fig. 4, but varying membrane potential, Ψ_m, from 40 to 200 ​mV. As expected J(AS) closely parallels [ADP]_MAT for [ADP]°_CYT ​= ​0.037 ​mM over the full range of Ψ_m. In effect, ATP synthesis is diffusion limited because ANT is diffusion limited, slowed by depletion of intracristal ADP relative to cytosolic levels.

Fig. 7.

Correlation between steady state flux of ATP synthase, J(AS), and the concentration of ADP in the matrix, [ADP]_MAT for computer simulations as in Fig. 4G (15-crista 2D model) for varying membrane potential (Ψ_m, negative sign not shown).

(A) Results for “slow” surrogate kinase reaction (k_f ​= ​0.003 ​ms⁻¹). (B) Results for “fast” surrogate kinase reaction (k_f ​= ​0.07 ​ms⁻¹).

These simulations demonstrated that the surrogate kinase reaction, equation (1), is able to modulate the impact of diffusion limitations on flux of the ATP synthase. Increasing the forward reaction rate constant, k_f, increases ATP ⇔ ADP cycling inside cristae, elevating intracristal [ADP] and J(ANT). The effect is illustrated in Fig. 7B: increasing k_f leads to elevated [ADP]_MAT and, consequently, J(AS) at equivalent values of Ψ_m. Note that, for both kinase levels, J(AS) is very low or zero for membrane potentials at or below 50–60 ​mV, consistent with experimental observations with cardiac muscle mitochondria (Wescott et al., 2019).

The consequences of increased activity of the surrogate kinase on fluxes of ANT and ATP synthase in 3D simulations are summarized in Table 1, Table 3A. For the longest lamellar and tubular cristae (L_CRIS ​= ​900 ​nm), a 3 fold increase in k_f attenuated the decrease in J(ANT) from approximately 85% to 55% (Table 1). For the largest crista-containing mitochondrial models, the decrease in J(AS) relative to the model with no cristae changed from 25% to 14% for lamellar cristae and from 15% to 9% for tubular cristae (Table 3A). By compensating for restricted ADP diffusion, increasing the activity of intracristal kinases as mitochondrial size increases is essential to retain the energetic advantage derived from folding the inner membrane.

Table 3.

Energy penalty for mitochondria with lamellar and tubular cristae.

A) Crista Shape	KINASE (rel)	J(AS) (mol/μm2/ms)	SCRIS (μm2)	ATP OUTPUT q ​= ​J(AS) × SCRIS (mol/ms)	ENERGY PENALTY Δq ​= ​[Jmax(AS) - J(AS)] × SCRIS (mol/ms)	Δq/qmax (%)	q/qo
LAM	SLOW	74.5	4.8	358	118	25	2.0
	FAST	85.5		410	65	14	2.3
TUB	SLOW	84	4.1	344	61.5	15	1.9
	FAST	90		369	37	9	2.1
NONE (o)	SLOW	99	1.8	178	0	0	1
	FAST	99		178	0	0	1

B) Crista Shape	KINASE (rel)	J(AS) (mol/μm2/ms)	SCRIS (μm2)	ATP OUTPUT q ​= ​J(AS) × SCRIS (mol/ms)	ENERGY PENALTY Δq ​= ​[Jmax(AS) - J(AS)] × SCRIS (mol/ms)	Δq/qmax (%)	q/qo
LAM	SLOW	38	37.4	1421	2281	62	4.2
	FAST	67		2506	1197	32	7.4
TUB	SLOW	59	20.4	1204	836	41	3.6
	FAST	74		1510	510	25	4.5
NONE (o)	SLOW	99	3.4	337	0	0	1
	FAST	99		337	0	0	1

Effects of crista morphology and kinase activity on ATP output (q) for lamellar (LAM) and tubular (TUB) spatial models of the mitochondrial inner membrane, relative to a model with no cristae (NONE). Results in Table A (upper) correspond to fluxes of ATP synthase, J(AS), and IM surface areas, S_IM, for the largest 3D spatial models used for computer simulations with the reduced BioModel. Results in Table B (lower) correspond to J(AS) values extrapolated for rat cardiac muscle mitochondria (see text), using the linear regression equations in Fig. 6B. Kinase activities are labelled SLOW and FAST, corresponding to forward reaction constants (k_f) of 0.003 and 0.009 msec⁻¹, respectively. Other abbreviations: mol ​= ​molecules, ms ​= ​millisecond, q_o ​= ​ATP output for the model with no cristae, q_max ​= ​hypothetical q for a model with cristae calculated using J(AS) for the model with no cristae, J^max(AS).

4. Discussion

4.1. Energy penalty associated with IM folding

The internalizing of the mitochondrial inner membrane to form cristae packs more energy transducing machinery into the same volume but also restricts diffusion of key metabolites like ADP (Mannella et al., 1994, 2001; Garcia et al., 2019). These simulations show that, as the extent of IM folding increases, diffusion effects become more significant and, depending on cytosolic ADP levels and relative activity of internal kinases, can limit fluxes of adenine nucleotide transport, J(ANT), and ATP synthesis, J(AS). The attenuation of J(AS) is partially compensated in terms of overall ATP output, qATP, by increased inner membrane surface area relative to models without cristae (q ​= ​J(AS) × S_IM). Thus, each spatial model i can be characterized in terms of an “energy penalty” imposed on ATP output:

Δqⁱ ATP ​= ​q^maxATP - qⁱATP = (J^max(AS) × Sⁱ_IM) - (Jⁱ(AS) × Sⁱ_IM) (3)

where J^max(AS) is the flux of ATP synthase with no internal diffusion restriction, i.e., that of the mitochondrial IM model with the same volume but no cristae. For convenience in the discussion that follows, the “energy penalty” is defined as the percent decrease in ATP output: 100 × ΔqⁱATP/q^maxATP.

Energy penalties associated with the largest lamellar and tubular crista spatial models are summarized in Table 3A. Over the range of kinase activities, the largest lamellar model has an energy penalty of 25–15% versus 17–9% for the equivalent tubular model. As noted, flux attenuation increases with scale in the simulations, expected for diffusion-limited reactions. The average volume of a rat cardiac muscle mitochondrion has been estimated by EM morphometry at 0.57 ​μm³ (Laguens, 1971), and variances in these measurements suggest individual mitochondria may be considerably larger (Picard et al., 2012). Tomographic analysis of rat cardiac muscle mitochondria (Mannella, unpublished) indicates lamellar cristae increase IM surface area 7–14 fold, and tubular cristae 4–5 fold, compared with less than 2 fold in the smaller spatial models used for the simulations. Thus, the potential impact of IM folding on ATP output of actual mitochondria is likely much greater than observed with the models. The results in Table 3A were extrapolated to cylindrical mitochondria with volume 0.42 ​μm³ (0.3 ​μm radius, 1.5 ​μm length), using the linear relationships between percent decrease in J(AS) and extent of IM folding, S_CRIS/S_IM in Fig. 6B. The extrapolations, summarized in Table 3B, project to 62−32% reduction in J(AS) for cardiac muscle mitochondria with lamellar cristae (S_CRIS/S_IM ​~ ​0.9) and 41−25% with tubular cristae (S_CRIS/S_IM ​~ ​0.8), over the range of kinase activities explored. However, the almost two-fold greater IM surface area in mitochondria with lamellar vs. tubular cristae more than compensates for slower fluxes of ATP synthase. ATP production by mitochondria with lamellar cristae was 30−80% above that for tubular cristae, with the differential increasing with increased kinase activity. Note that, in all cases, ATP output for mitochondria with cristae was considerably greater than that for mitochondria without cristae by factors of 4.2–7.4× and 3.6–4.5× for lamellar and tubular morphologies, respectively.

The more pronounced “energy penalty” on ATP synthesis for lamellar compared to tubular cristae may be understood in terms of the geometry of the compartments. The volume (V) “supplied” by a single junction “mouth” (opening) is six times larger and the surface area of the ANT-containing membrane “servicing” (enclosing) that volume (S/V) is 25–30% smaller for lamellar compared to tubular cristae at equivalent scale (Table 2). This conclusion that cristae with higher S/V support greater rates of ATP synthesis is in apparent contradiction to an earlier computational study of the mitochondrial electrochemical potential (or proton motive force, PMF) that reached the opposite conclusion (Song et al., 2013). The focus of the latter study was the influence of crista shape on PMF, in particular proton gradients. Membrane potential, Ψ_m, was a variable (whereas it was held constant in the current study), and external ADP was present in excess, so that effects of ADP diffusion were not considered. A computational study involving both sets of reactions would provide a more comprehensive understanding of the impact of crista morphology on mitochondrial ATP production.

4.2. Cristae as functional micro-compartments

A clear implication from the simulations is that cristae are functional micro-compartments with steady states distinct from those in the bulk cytosol. The concept of metabolic compartmentation within mitochondria is not new. Hypotheses about the role of intramitochondrial kinases to sustain high internal ADP levels needed to export ATP from the matrix were forwarded shortly after discovery of the kinases (Jacobus and Lehninger, 1973), (Gellerich, 1992). Subsequent mathematical modeling studies explored questions related to the role of restricted diffusion on observed regulation of energy metabolism by ADP, e.g., (Aliev and Saks, 1997; Saks et al., 2003; Vendelin et al., 2004; Kay et al., 2000). In these studies, the mitochondrial micro-compartment was generally considered to be the intermembrane space, the peripheral region between the outer and inner membranes. Permeation of adenine nucleotides through the OM was considered diffusion-limiting, a concept that gained favor as evidence grew for partial closure of VDAC pores (Xu et al., 2001; Rostovtseva and Bezrukov, 2012). The approach used in the current study takes mathematical modeling a step further, by simulating energy metabolism within spatial models of specific inner membrane morphologies (i.e., “virtual mitochondrion”). The results provide compelling evidence that functional compartmentation can arise solely from restricted diffusion within the confines of the cristae, independent of the permeability state of the outer membrane, e.g., (Mannella et al., 1997; Klingenberg, 2008; Dzeja and Terzic, 2003; Schlattner et al., 2006). Future studies could examine the combined effects of varying crista morphology and outer membrane permeability on energy metabolism.

4.3. Implications of ANT localization

These modeling studies imply the existence of two functionally distinct populations of ANT, one on the peripheral region of the IM where its flux is regulated by [ADP] in the cytosol (assuming a highly permeable OM) and the other facing inside cristae, where [ADP] is buffered in resting cells. In the example of Fig. 1, the crista compartment kept [ADP] at ~0.01 ​mM under conditions where cytosolic [ADP] varied 25 fold, and intracristal ANT fluxes held steady while peripheral fluxes varied two fold. The simulations assumed uniform distribution of ANT on the IM and, in fact, there is no evidence that ANT is concentrated in particular IM subregions, e.g., its interactome includes proteins located on both cristae and the IM periphery (Lu et al., 2017). In effect, the fraction of ANT inside cristae sets the “idle” for mitochondrial ATP generation. The greater the crista membrane surface area, the less sensitive the “idle” to cell energy demand, which at first glance might seem counter intuitive, i.e., increasing the fraction of ANT on the IM periphery would make ANT a better sensor for energy demand. However, there are benefits to running mitochondrial ATP production at a steady moderate rate, not subject to small variations in cytosolic ADP, to better respond to sudden fluctuations in energy demand, e.g. (Balaban, 2012). The “structural buffering” of intracristal [ADP], and consequently of mitochondrial ATP output, inferred from these simulations is greatest when the ratio of cristal to peripheral IM surface area is highest, as is the case for mitochondria in tissues with high energy demand like brain and muscle. Note that, under conditions of extreme energy depletion such as in contracting muscle, the rise in cytosolic [ADP] results in elevated intracristal [ADP] and more uniform ANT fluxes everywhere on the IM. There is also the possibility of mechanistic interactions between ANT and ATP synthase (e.g., local channeling of ADP at an “ATP synthasome” (Klingenberg, 2008; Chen et al., 2004)) that might override any advantages of locating ANT outside cristae. In a recent computational study that included both differential equation (non spatial) and molecular dynamic (spatial) approaches, it was found that exclusively co-localizing ANT with ATP synthase inside cristae vs. exclusively on the IM periphery significantly affected export of ATP to the cytosol (Garcia et al., 2019). Differences were attributed to changes in gradients of adenine nucleotides created by restricted diffusion through crista junctions. It was inferred that such structural buffering of ATP within cristae might allow mitochondria to better respond to fluctuating energy demands.

4.4. Critical role of intracristal kinases

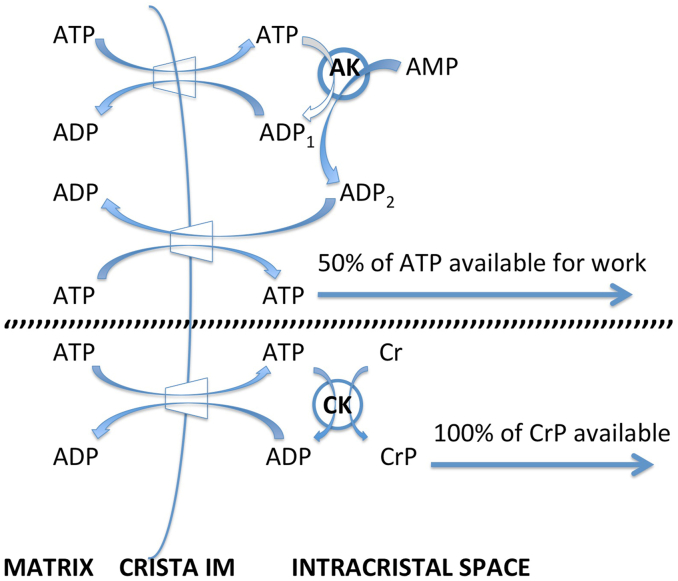
Under the conditions used in this modeling study, which focused on steady state ATP production, flux of ATP synthase is set by matrix [ADP] (Fig. 7). This constraints the rate of ADP phosphorylation at steady state to equal the rate at which ANT returns ADP to the matrix. ADP is recycled locally inside cristae, generated 1:1 by the surrogate kinase reaction from every ATP molecule transported across the IM by ANT, and immediately “antiported” back into the matrix with the release of the next ATP (Fig. 2). As a result, in the models, there is no net release of ATP from cristae into the cytosol. In the cell, mitochondrial kinases function differently (Fig. 8). Adenylate kinase (AK), found in mitochondria of “low energy demand” mammalian tissues like liver, generates 2 ADP for every ATP (+AMP). Thus, half of the ATP transported by ANT into crista compartments is available for diffusion to the cytosol, while the other half is used to replenish the ADP pool needed for local ANT function (Gellerich, 1992; Igamberdiev and Kleczkowski, 2015). Creatine kinase (CK) is present in mitochondria of “high energy demand” tissues like muscle and brain at specific activity three times greater than that of AK in liver (Jacobus and Lehninger, 1973). CK rapidly generates creatine phosphate from ATP at 1:1 stoichiometry, conserving ~100% of the free energy of ATP hydrolysis to do work in the cytosol, while replenishing (1:1) the local intracristal ADP pool, e.g. (Wallimann et al., 1992). Independent of considerations about relative diffusivities and spatial or temporal buffering of “high-energy phosphates” (e.g. (Wallimann et al., 1992)), this may be the single most important rationale for the CK energy shuttle in muscle and brain. When creatine kinase recycles ATP → ADP within cristae, the 50% loss of exportable ATP associated with adenylate kinase is avoided.

Fig. 8.

Diagram for recycling of ADP and ATP inside cristae by adenylate kinase, AK (top scheme) and creatine kinase, CK (bottom). ANT is represented by the trapezoid symbol on the inner membrane, IM. Other abbreviations: Cr, creatine, CrP, creatine phosphate.

More generally, these simulations demonstrate that increasing the activity of intracristal kinases overcomes limitations imposed on mitochondrial ATP output by diffusion of the key metabolite, ADP. Enhancing efficiency of ATP generation may be the primary driver for overexpression of creatine kinase in mitochondria with respiratory chain defects (Stadhouders et al., 1994). From an evolutionary perspective, the adaptation of adenylate kinase (an ancient enzyme (Nguyen et al., 2017) to the intermembrane space of the proto-mitochondrion (the periplasm of the endosymbiont) likely coincided with elaboration of cristae and was essential for retaining the energetic advantage of inner membrane infolding. Creatine kinase is a member of the phosphagen kinase family, with several other members also having mitochondrial isoforms (including arginine and tauromycin kinases) (Mühlebach et al., 1996; Teixeira and Borges, 2012). Since these kinases appeared first in metazoans, they represent a more recent adaptation of mitochondrial energy metabolism that may have allowed mitochondria to increase in size and extent of IM infolding.

The current “virtual mitochondrion” implementation provides useful insights into regulation of mitochondrial energy metabolism by factors such as inner membrane topology but has limitations. One is the use of a single “surrogate kinase” reaction to capture both the recycling of adenine nucleotides in the intracristal space and the consumption of ATP in the cytosol. In principle, specific mitochondrial and cytosolic kinase reactions could be modeled, along with a tunable hydrolysis reaction to represent cell energy consumption. Likewise, effects on mitochondrial energy metabolism caused by variations in crista junction size and frequency could be explored, e.g., to compare with recent experimental observations of possible feedback regulation (Patten et al., 2014; Dlasková et al., 2019). However, idealized 3D spatial models do not capture the size and complexity of cristae in actual mitochondria. Thus, what might be minor trends in the models could translate to highly significant effects in actual mitochondria, as suggested by the (strictly empirical) extrapolation of fluxes and ATP outputs employed above. Full-scale simulations of energy metabolism using models of entire mitochondria derived from EM tomography, as in (Garcia et al., 2019), combined with information about localization of the ATP synthase on curved regions of cristae (e.g. (Strauss et al., 2008)) could elucidate how specific membrane topologies (normal and aberrant) and levels of internal kinases impact ATP production.

CRediT authorship contribution statement

Nasrin Afzal: Investigation, Formal analysis, Software, Methodology, Writing – original draft, Data curation, Visualization. W. Jonathan Lederer: Conceptualization, Funding acquisition, Writing – review and editing. M. Saleet Jafri: Conceptualization, Formal analysis, Resources, Methodology, Data curation, Project administration, Writing – review & editing, Supervision. Carmen A. Mannella: Formal analysis, Validation, Writing – original draft preparation , Writing - review and editing, Visualization, Supervision.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

APPENDIX

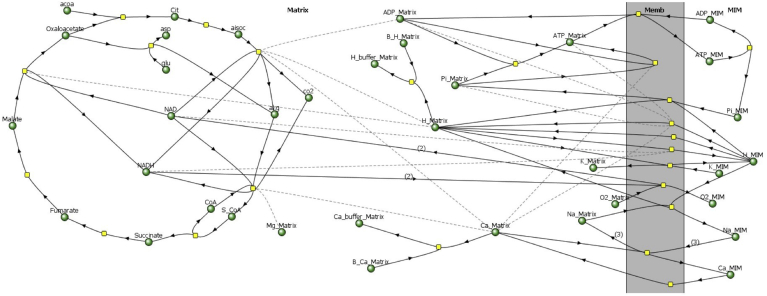
1. Reactions in the Complete BioModel

Fig. 1.

Diagram of the complete BioModel for mitochondrial energy metabolism used for simulations in Virtual Cell. Reaction pathways (solid arrows) are represented in terms of chemical species (metabolites, ions and buffers; green circles), and enzymes or transporters (yellow squares), based on the model of Nguyen et al. (2007). Effectors are connected to enzymes by dashed lines. The reactions occur in two compartments, the Matrix (left) and the space outside the matrix (right, MIM), and on the mitochondrial inner membrane (Memb) that separates them. Other non-standard abbreviations: acoa, acetyl Coenzyme A; aisoc, iso-citrate; akg, α-ketoglutarate; asp, aspartate; B_Ca, Ca²⁺ bound to calcium buffer (Ca_buffer); B_H, H⁺ bound to proton buffer (H_buffer); Cit, citrate; co2, carbon dioxide; glu, glutamate; O2, dioxygen; S_CoA, succinyl Coenzyme A.

2. Flux Equations for Reduced Biomodel

The rate equations for the reduced BioModel, on which most of the results presented in the paper are based, consist of that for the surrogate kinase, equation (1) in the main text, and the following equations for the fluxes of ANT (J_ANT) and ATP synthase (J_AS), as defined in (Nguyen et al., 2007):

$$J_{ANT}=V_{ANT}\frac{1-\frac{{\left[AT{P}^{4-}\right]}_e{\left[AD{P}^{3-}\right]}_m}{{\left[AD{P}^{3-}\right]}_e{\left[AT{P}^{4-}\right]}_m}\exp \left(\frac{-F{\psi }_m}{RT}\right)}{\left\{1+\frac{{\left[AT{P}^{4-}\right]}_e}{{\left[AD{P}^{3-}\right]}_e}\exp \left(\frac{-f_{P}F{\psi }_m}{RT}\right)\right\}\left\{1+\frac{{\left[AD{P}^{3-}\right]}_m}{{\left[AD{P}^{4-}\right]}_m}\right\}}$$ (1)

where V_ANT is the maximum velocity of the translocase, F is the Faraday constant, Ψ_m is the membrane potential, and $f_p$ is the fraction of effective membrane potential for the translocase (set to 0.5 (Magnus and Keizer, 1998)). The ionic forms of ADP and ATP are fractions of the total ATP and ADP concentrations (inside the matrix, m, and external to the matrix, e) as defined in Table 4 of (Nguyen et al., 2007).

$$J_{AS}=V_{AS}\frac{\frac{{\left[ADP\right]}_m}{K_{ADP}}\frac{{\left[P_i\right]}_m}{K_{Pi}}-\frac{{\left[ATP\right]}_m}{K_{ATP}}}{\left(1+\frac{{\left[ADP\right]}_m}{K_{ADP}}\right)\left(1+\frac{{\left[P_i\right]}_m}{K_{Pi}}\right)+\left(\frac{{\left[ATP\right]}_m}{K_{ATP}}\right)}\frac{{\left[{\Psi }_m\right]}^8}{K_{V,ATP}^8+{\left[{\Psi }_m\right]}^8}\left[1-e^{\frac{-{\left[C{a}^{2+}\right]}_m}{K_{Ca,ATP}}}\right]$$ (2)

where V_AS is the maximum velocity of the synthase, K_ADP is the binding constant for ADP, K_ATP is the binding constant for ATP, K_Pi is the binding constant for P_i, K_Ca,ATP is the Ca²⁺ binding constant, and K_V,ATP is the membrane potential yielding half-maximal ATP production.

Appendix A. Supplementary data

The following are the Supplementary data to this article: