Quantum-electrodynamical time-dependent density functional theory within Gaussian atomic basis

Abstract

Inspired by the formulation of quantum-electrodynamical time-dependent density functional theory (QED-TDDFT) by Rubio and co-workers [Flick et al., ACS Photonics 6, 2757-2778 (2019)], we propose an implementation that uses dimensionless amplitudes for describing the photonic contributions to QED-TDDFT electron–photon eigenstates. This leads to a Hermitian QED-TDDFT coupling matrix that is expected to facilitate the future development of analytic derivatives. Through a Gaussian atomic basis implementation of the QED-TDDFT method, we examined the effect of dipole self-energy, rotating-wave approximation, and the Tamm–Dancoff approximation on the QED-TDDFT eigenstates of model compounds (ethene, formaldehyde, and benzaldehyde) in an optical cavity. We highlight, in the strong coupling regime, the role of higher-energy and off-resonance excited states with large transition dipole moments in the direction of the photonic field, which are automatically accounted for in our QED-TDDFT calculations and might substantially affect the energies and compositions of polaritons associated with lower-energy electronic states.

I. INTRODUCTION

Quantum optics effects on atoms have been extensively studied during the last several decades,^1–9 enabling scientists to shift atomic energy levels,^10,11 tune atomic electronic transition rates,^12–14 and generate quantum systems with atom–atom entangled states.^15,16 In contrast, the behavior of molecules in optical cavities attracted a lot of attention only in recent years.^17–23 In particular, several molecules have been shown to couple strongly to a quantized radiation field, causing their electronic states to hybridize with the cavity photon levels to produce superpositions and entanglements.^2,24,25 The study of such entangled states leads to the establishment of the field of polariton chemistry, which focuses on the use of optical cavities to manipulate chemical and photochemical reactivities,^23,26–39 modify the intersystem crossing rates,^{27,28,37,39–41} and enhance organic molecule light emitting efficiencies.^42–50

In principle, a coupled molecule–photon system is best described by the relativistic quantum field theory (QFT).⁵¹ However, to avoid the computational complexity of QFT, many non-relativistic and simplified theories have been developed.⁵² Within the Rabi model, for instance, one adopts a semiclassical approach that combines a non-relativistic quantum mechanical description for the molecule and a classical description of the electromagnetic field.^53–56 The Pauli–Fierz model was introduced to provide consistent treatment of the spontaneous emission.^57,58 Jaynes and Cummings proposed two other similar quantum models, which are known as the Jaynes–Cummings (JC) model and rotating-wave approximation (RWA).^59,60 Within both models, the counter-rotation terms (CRTs) are neglected, which turns out to be a valid approximation for the resonance and near-resonance conditions and weak coupling regimes.^52,59,60

In the study of polariton chemistry, it has been common to restrict the description of each electronic system to a simplified two- or three-state model.^{23,55,56,61–68} The corresponding input parameters (energy levels and coupling elements), on which the models would heavily rely, are obtained from either experiments or first-principles quantum chemistry calculations. Through employing these models, it has been predicted that the coupling of molecular systems to quantized radiation modes could substantially modify the potential energy surfaces and create new conical intersections,^27,28,40,69 suppress or enhance photoisomerization reactions,^47,70–74 increase the charge transfer and excitation energy transfer rates,^52,75–79 accelerate the singlet fission kinetics,^41,80 and even control the chemical reactions remotely.^37,81 These observations open up opportunities to use optical cavities to manipulate chemical and photochemical reactions.

Recently, ab initio quantum mechanical frameworks were proposed to describe interacting electrons and photons.^{51,63,82–93} Specifically, Rubio and co-workers developed quantum-electrodynamical density functional theory (QEDFT)^{82–84,86,89,93–96} and quantum electrodynamics coupled-cluster (QED-CC) theory,^97–99 which inherit an accurate description of the molecular electronic structure from time-dependent density functional theory, coupled-cluster theory, equation-of-motion coupled-cluster theory, and other ab initio electronic structure theories.

In this work, we closely follow the QEDFT method from Rubio and co-workers.^{82–84,86,89,91,93–96} Through a slightly modified matrix formulation of linear-response quantum-electrodynamical time-dependent density functional theory (QED-TDDFT), we obtain a Hermitian TDDFT-Pauli–Fierz (TDDFT-PF) Hamiltonian for coupling molecules and cavity photons. This allows us to systematically examine the effects of CRTs, dipole self-energy (DSE), and the Tamm–Dancoff approximation (TDA) and to compare the polariton energies to different model Hamiltonian results. We expect that as the electron–photon coupling strength increases, there might be (a) a substantial deviation from symmetric Rabi splitting (which arises from the two-state model Hamiltonian) and (b) significant differences in the polariton energy and compositions among various theoretical models.

This work is organized as follows: The TDDFT-PF formula is derived in Sec. II B and in Appendixes A and B (with linear-response and equation-of-motion formulations, respectively), with its no-DSE, RWA, and TDA variations presented in Sec. II C. Section III describes our Gaussian atomic basis implementation within the PySCF software package.¹⁰⁰ Preliminary results on the polariton states of ethene, formaldehyde, and benzaldehyde molecules in the optical cavity are reported in Sec. IV, which is followed by a discussion in Sec. V.

II. THEORY

A. Notation

For a molecule, we will use indices i, j to represent its occupied Kohn–Sham orbitals and a, b to denote its unoccupied (virtual) Kohn–Sham orbitals. The corresponding orbital energies will be written as ɛ_i, ɛ_j, ɛ_a, and ɛ_b. The dipole moment vector in the basis of these orbitals is

$${\mathit{\mu }}_{ai}=\left(⟨a|\widehat{x}|i⟩,⟨a|\widehat{y}|i⟩,⟨a|\widehat{z}|i⟩\right).$$ (1)

We will use A and B to refer to conventional TDDFT coupling supermatrices, while X and Y are TDDFT amplitudes.^101–108

For an optical cavity with M photon modes, its αth mode of frequency is denoted by ω_α. With the long-wavelength approximation, the corresponding fundamental coupling strength,^63,91

$${\mathit{\lambda }}_{\alpha }=\sqrt{\frac{1}{{ϵ}_0}}{S}_{\alpha }({\mathit{r}}_0){\mathit{ϵ}}_{\alpha },\alpha =1,2,\dots ,M,$$ (2)

depends on the transversal polarization vector ϵ_α. For a Fabry–Pérot cavity of volume V_tot = L_xL_yL_z and with mirror planes perpendicular to the z-axis, the dimensionless mode function

$$S_{\alpha }(\mathit{r})=\sqrt{\frac{2}{V_{\text{tot}}}}\sin \left(\frac{\alpha \pi z}{L_z}\right)$$ (3)

is evaluated at a chosen reference point r₀ for the molecular subsystem. When there are N identical and non-interacting molecules with the same orientation, the effective volume of each molecule, $V_{\text{eff}}=\frac{V_{\text{tot}}}{N}$, can be used in Eq. (3).²⁷

For each photon mode, the corresponding displacement coordinate and conjugate moment refer to

$${\widehat{q}}_{\alpha }=\sqrt{\frac{\hslash }{2{\omega }_{\alpha }}}\left({\widehat{b}}_{\alpha }+{\widehat{b}}_{\alpha }^{†}\right),$$ (4)

$${\widehat{p}}_{\alpha }=-i\sqrt{\frac{\hslash {\omega }_{\alpha }}{2}}\left({\widehat{b}}_{\alpha }-{\widehat{b}}_{\alpha }^{†}\right),$$ (5)

with ${\widehat{b}}_{\alpha }^{†}$ and ${\widehat{b}}_{\alpha }$ being the creation and annihilation operators for the mode. For convenience, the dot product of the dipole moment of each virtual-occupied pair and the photon field will be written as

$${\lambda }_{ai}^{\alpha }={\mathit{\mu }}_{ai}\cdot {\mathit{\lambda }}_{\alpha }.$$ (6)

B. QED-TDDFT equation within the Pauli–Fierz Hamiltonian

For a molecule confined in this optical cavity, by making the Born–Oppenheimer approximation and the long-wavelength or dipole approximation in the length gauge, its Pauli–Fierz Hamiltonian can be written as^52,91

$$\widehat{H}={\widehat{H}}_{\text{elec}}+\sum _{\alpha =1}^M\left[\frac{1}{2}{\widehat{p}}_{\alpha }^2+\frac{1}{2}{\omega }_{\alpha }^2{\left({\widehat{q}}_{\alpha }-\frac{1}{{\omega }_{\alpha }}{\mathit{\lambda }}_{\alpha }\cdot ⟨\widehat{\mathit{\mu }}⟩\right)}^2\right]+\sum _{\alpha =1}^M\frac{j_{\alpha }(t)}{{\omega }_{\alpha }}{\widehat{q}}_{\alpha },$$ (7)

where the photon modes interact with the expectation value of molecular dipole moment, $⟨\widehat{\mathit{\mu }}⟩$, and j_α(t) = λ_α · j(t) is the classical external current coupling to the αth cavity mode. Note that, in this “d · E” formula,⁵² the expectation value of the dipole moment, $⟨\widehat{\mathit{\mu }}⟩$, for a time-dependent electronic wavefunction [Eq. (B1)] is coupled with the photon field, which will be essential in the formulation of the DSE term in Eq. (B23).

If the electronic Hamiltonian, ${\widehat{H}}_{\text{elec}}$, is described by the Kohn–Sham density functional theory, the corresponding TDDFT-PF equation is shown in Appendixes A and B to be

$$\begin{array}{ccc}\hfill & \hfill & \left[\begin{array}{cccc}\hfill \mathbf{A}+\mathbf{\Delta }\hfill & \hfill \mathbf{B}+\mathbf{\Delta }\hfill & \hfill \hslash {\mathbf{g}}^{†}\hfill & \hfill \hslash {\tilde{\mathbf{g}}}^{†}\hfill \\ \hfill \mathbf{B}+\mathbf{\Delta }\hfill & \hfill \mathbf{A}+\mathbf{\Delta }\hfill & \hfill \hslash {\mathbf{g}}^{†}\hfill & \hfill \hslash {\tilde{\mathbf{g}}}^{†}\hfill \\ \hfill \hslash \mathbf{g}\hfill & \hfill \hslash \mathbf{g}\hfill & \hfill \hslash \mathit{\omega }\hfill & \hfill 0\hfill \\ \hfill \hslash \tilde{\mathbf{g}}\hfill & \hfill \hslash \tilde{\mathbf{g}}\hfill & \hfill 0\hfill & \hfill \hslash \mathit{\omega }\hfill \end{array}\right]\left[\begin{array}{c}\hfill \mathbf{X}\hfill \\ \hfill \mathbf{Y}\hfill \\ \hfill \mathbf{M}\hfill \\ \hfill \mathbf{N}\hfill \end{array}\right]\hfill \\ \hfill & \hfill & =\hslash {\mathrm{\Omega }}^{\text{TDDFT}-\text{PF}}\left[\begin{array}{cccc}\hfill \mathbf{1}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\mathbf{1}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \mathbf{1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\mathbf{1}\hfill \end{array}\right]\left[\begin{array}{c}\hfill \mathbf{X}\hfill \\ \hfill \mathbf{Y}\hfill \\ \hfill \mathbf{M}\hfill \\ \hfill \mathbf{N}\hfill \end{array}\right].\hfill \end{array}$$ (8)

The derivation in Appendix A closely follows that of Flick et al.’s matrix formulation of linear-response QED-TDDFT,⁹¹ but with two subtle differences. First, a Hermitian Hamiltonian matrix was acquired on the left-hand side of Eq. (8). Second, dimensionless photon amplitudes (M and N) were adopted. In Appendix B, an equivalent equation-of-motion formulation¹⁰⁹ is shown.

In Eq. (8), the electron–electron block contains TDDFT supermatrices, A and B, as augmented by the DSE terms,^52,99

$${\mathrm{\Delta }}_{ai,bj}=\sum _{\alpha =1}^M{\lambda }_{ai}^{\alpha }{\lambda }_{bj}^{\alpha },$$ (9)

while the electron–photon and photon–electron blocks are

$$\hslash g_{bj}^{\alpha }=\hslash {\tilde{g}}_{bj}^{\alpha }=\sqrt{\frac{\hslash {\omega }_{\alpha }}{2}}{\lambda }_{bj}^{\alpha },$$ (10)

whereas the photon–photon block is a diagonal matrix,

$${\omega }_{\alpha \beta }={\delta }_{\alpha \beta }{\omega }_{\alpha }.$$ (11)

Due to the couplings (i.e., the electron–photon and photon–electron blocks), the Ith eigenvector of the TDDFT-PF equation, ${({\mathbf{X}}^I,{\mathbf{Y}}^I,{\mathbf{M}}^I,{\mathbf{N}}^I)}^{\text{T}}$, contains photonic amplitudes (M^I and N^I) in addition to normal electronic amplitudes (X^I and Y^I). The ortho-normalization condition is

$$\sum _{ai}\left(X_{ai}^I{X}_{ai}^J-Y_{ai}^I{Y}_{ai}^J\right)+\sum _{\alpha }\left(M_{\alpha }^I{M}_{\alpha }^J-N_{\alpha }^I{N}_{\alpha }^J\right)={\delta }_{IJ}.$$ (12)

These components could be explained to be the Fourier coefficients of the time-dependent parameters^109–111 (also see Appendixes A and B).

C. A prism of QED-TDDFT methods

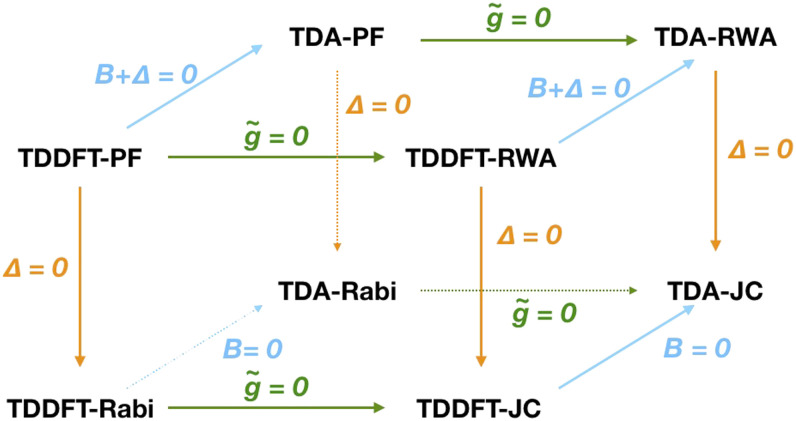
The TDDFT-PF formula [Eq. (8)] can be approximated in a number of ways, as shown in Fig. 1. First, one can invoke the Tamm–Dancoff approximation (TDA),¹⁰³ which sets the B + Δ elements to zero. One then obtains the TDA-PF model,

$$\left[\begin{array}{ccc}\hfill \mathbf{A}+\mathbf{\Delta }\hfill & \hfill \hslash {\mathbf{g}}^{†}\hfill & \hfill \hslash {\tilde{\mathbf{g}}}^{†}\hfill \\ \hfill \hslash \mathbf{g}\hfill & \hfill \hslash \mathit{\omega }\hfill & \hfill 0\hfill \\ \hfill \hslash \tilde{\mathbf{g}}\hfill & \hfill 0\hfill & \hfill \hslash \mathit{\omega }\hfill \end{array}\right]\left[\begin{array}{c}\hfill \mathbf{X}\hfill \\ \hfill \mathbf{M}\hfill \\ \hfill \mathbf{N}\hfill \end{array}\right]=\hslash {\mathrm{\Omega }}^{\text{TDA}-\text{PF}}\left[\begin{array}{ccc}\hfill \mathbf{1}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \mathbf{1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -\mathbf{1}\hfill \end{array}\right]\left[\begin{array}{c}\hfill \mathbf{X}\hfill \\ \hfill \mathbf{M}\hfill \\ \hfill \mathbf{N}\hfill \end{array}\right].$$ (13)

FIG. 1.

A prism of QED-TDDFT methods.

If the DSE addition, Δ, to matrix A is further removed, one obtains the TDA-Rabi model,¹¹²

$$\left[\begin{array}{ccc}\hfill \mathbf{A}\hfill & \hfill \hslash {\mathbf{g}}^{†}\hfill & \hfill \hslash {\tilde{\mathbf{g}}}^{†}\hfill \\ \hfill \hslash \mathbf{g}\hfill & \hfill \hslash \mathit{\omega }\hfill & \hfill 0\hfill \\ \hfill \hslash \tilde{\mathbf{g}}\hfill & \hfill 0\hfill & \hfill \hslash \mathit{\omega }\hfill \end{array}\right]\left[\begin{array}{c}\hfill \mathbf{X}\hfill \\ \hfill \mathbf{M}\hfill \\ \hfill \mathbf{N}\hfill \end{array}\right]=\hslash {\mathrm{\Omega }}^{\text{TDA}-\text{Rabi}}\left[\begin{array}{ccc}\hfill \mathbf{1}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \mathbf{1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -\mathbf{1}\hfill \end{array}\right]\left[\begin{array}{c}\hfill \mathbf{X}\hfill \\ \hfill \mathbf{M}\hfill \\ \hfill \mathbf{N}\hfill \end{array}\right].$$ (14)

If the counter-rotation terms (CRTs), which are shown as $\hslash {\tilde{\mathbf{g}}}^{†}$, are neglected from Eq. (13), it amounts to the rotating-wave approximation (RWA),¹¹²

$$\left[\begin{array}{cc}\hfill \mathbf{A}+\mathbf{\Delta }\hfill & \hfill \hslash {\mathbf{g}}^{†}\hfill \\ \hfill \hslash \mathbf{g}\hfill & \hfill \hslash \mathit{\omega }\hfill \end{array}\right]\left[\begin{array}{c}\hfill \mathbf{X}\hfill \\ \hfill \mathbf{M}\hfill \end{array}\right]=\hslash {\mathrm{\Omega }}^{\text{TDA}-\text{RWA}}\left[\begin{array}{cc}\hfill \mathbf{1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \mathbf{1}\hfill \end{array}\right]\left[\begin{array}{c}\hfill \mathbf{X}\hfill \\ \hfill \mathbf{M}\hfill \end{array}\right].$$ (15)

Finally, if both DSE and CRT are neglected in the TDA-PF formula [Eq. (13)], one arrives at the TDA-Jaynes–Cummings (TDA-JC) model,

$$\left[\begin{array}{cc}\hfill \mathbf{A}\hfill & \hfill \hslash {\mathbf{g}}^{†}\hfill \\ \hfill \hslash \mathbf{g}\hfill & \hfill \hslash \mathit{\omega }\hfill \end{array}\right]\left[\begin{array}{c}\hfill \mathbf{X}\hfill \\ \hfill \mathbf{M}\hfill \end{array}\right]=\hslash {\mathrm{\Omega }}^{\text{TDA}-\text{JC}}\left[\begin{array}{cc}\hfill \mathbf{1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \mathbf{1}\hfill \end{array}\right]\left[\begin{array}{c}\hfill \mathbf{X}\hfill \\ \hfill \mathbf{M}\hfill \end{array}\right].$$ (16)

Clearly, the first-order DSE correction to the energy of the Ith TDA-JC polariton is always positive,

$${\mathrm{\Omega }}_I^{\text{TDA}-\text{RWA}}={\mathrm{\Omega }}_I^{\text{TDA}-\text{JC}}+\sum _{\alpha =1}^M{\left|{\mathit{\lambda }}_{\alpha }\cdot {\mathit{\mu }}_I\right|}^2+\cdots ,$$ (17)

with the transition dipole moment of the Ith polariton being

$${\mathit{\mu }}_I^{\text{TDA}-\text{JC}}=\sum _{ai}{X}_{I,ai}^{\text{TDA}-\text{JC}}{\mathit{\mu }}_{ai}.$$ (18)

In contrast, the leading CRT correction to the TDA-JC energy is second-order and always negative,

$${\mathrm{\Omega }}_I^{\text{TDA}-\text{Rabi}}={\mathrm{\Omega }}_I^{\text{TDA}-\text{JC}}-\sum _{\alpha =1}^M\frac{g_{\alpha ,I}^2}{{\mathrm{\Omega }}_I^{\text{TDA}-\text{JC}}+{\omega }_{\alpha }}+\cdots ,$$ (19)

where

$$g_{\alpha ,I}=\sqrt{\frac{{\omega }_{\alpha }}{2\hslash }}\left({\mathit{\lambda }}_{\alpha }\cdot {\mathit{\mu }}_I^{\text{TDA}-\text{JC}}\right)$$ (20)

is the coupling between the Ith excited state and the αth cavity mode. Note that under the resonance condition (${\mathrm{\Omega }}_I^{\text{TDA}-\text{JC}}={\omega }_{\alpha }$) as well as g_α,I/ω_α ≪ 1, the leading CRT contributions are second-order to g_α,I (and, thus, λ_α). In those cases, the CRT contribution is roughly $\frac{1}{4}$ of the DSE term, but with an opposite sign. This is different from the report from Huo and co-workers,^52,113 who found the CRT contribution to be $-\frac{1}{2}$ times the DSE term. This discrepancy will be explained later in the context of QED-TDDFT results on test molecules.

As shown in Fig. 1, the TDDFT-Rabi, TDDFT-RWA, and TDDFT-JC models can be defined in a similar procedure starting from the TDDFT-PF model. For instance, the TDDFT-JC working equation would be

$$\left[\begin{array}{ccc}\hfill \mathbf{A}\hfill & \hfill \mathbf{B}\hfill & \hfill \hslash {\mathbf{g}}^{†}\hfill \\ \hfill \mathbf{B}\hfill & \hfill \mathbf{A}\hfill & \hfill \hslash {\mathbf{g}}^{†}\hfill \\ \hfill \hslash \mathbf{g}\hfill & \hfill \hslash \mathbf{g}\hfill & \hfill \hslash \mathit{\omega }\hfill \end{array}\right]\left[\begin{array}{c}\hfill \mathbf{X}\hfill \\ \hfill \mathbf{Y}\hfill \\ \hfill \mathbf{M}\hfill \end{array}\right]=\hslash {\mathrm{\Omega }}^{\text{TDDFT}-\text{JC}}\left[\begin{array}{ccc}\hfill \mathbf{1}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\mathbf{1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \mathbf{1}\hfill \end{array}\right]\left[\begin{array}{c}\hfill \mathbf{X}\hfill \\ \hfill \mathbf{Y}\hfill \\ \hfill \mathbf{M}\hfill \end{array}\right].$$ (21)

Clearly, if this equation [or its TDA counterpart in Eq. (16)] is recast in the representation of gas-phase TDDFT (or TDA) eigenstates, it is reduced to the familiar Jaynes–Cummings model, but coupling all the excited states to the photon field.

III. COMPUTATIONAL DETAILS

A. Method implementation

The QED-TDDFT methods are implemented in a modified version of the PySCF software package,¹⁰⁰ and they are also being implemented in the Q-Chem software package.¹¹⁴ Several functionals (such as PBE,¹¹⁵ PBE0,¹¹⁶ B3LYP,^117–119 and ωB97X-D¹²⁰) are supported in our implementation. Only PBE0 results are presented in Sec. IV, while the use of other functionals is found to lead to qualitatively similar results for the test systems. (The PBE functional results are compared to those of PBE0 for the formaldehyde molecule in the supplementary material.) The lowest eigenstates are solved using Davidson’s diagonalization algorithm,¹²¹ which is the default approach for solving TDDFT equations in packages such as PySCF and Q-Chem. The working equation of all eight QED-TDDFT models is solved directly within our PySCF implementation. For TDDFT-PF, for instance, the second and fourth equations in Eq. (8) are both multiplied by −1, leading to an eigenvalue problem of a non-symmetric matrix.

For TDDFT-PF and TDDFT-Rabi equations [Eqs. (8) and (S7)], a compact Hermitian form is shown in Eq. (S18) of the supplementary material, which is equivalent to Eq. (43) of Ref. 91. When pure functionals are used, the matrix A − B contains only diagonal elements, which are virtual-occupied orbital energy differences,^101,122 leading to simple expressions for the electron–electron and electron–photon blocks [see Eqs. (44) and (45) of Ref. 91]. However, for the Hartree–Fock method and hybrid exchange-correlation functionals, A − B would have one or more negative eigenvalues when the self-consistent field (SCF) solution is externally unstable with respect to complex SCF.^123,124 In those cases, one cannot obtain a real ${\left(\mathbf{A}-\mathbf{B}\right)}^{1/2}$ factor and might fail to transform the eigenvalue problem to the compact Hermitian form in Eq. (S18).

All calculations have a comparable cost, in terms of timing, to the corresponding gas-phase TDDFT or TDA calculation. Because the calculation is dominated by the evaluation of matrix–vector products (contraction of trial density matrices with two-electron integrals and the exchange-correlation counterpart), the actual computational time is linearly proportional to the number of trial vectors. In our QED-TDDFT calculations on benzaldehyde, for example, it takes about 4 times more trial vectors to obtain the first 50 solutions to the TDDFT-PF, TDDFT-Rabi, TDDFT-RWA, and TDDFT-JC equations than their TDA counterparts, making them around 4 times more expensive in terms of computational time.

B. Test systems

The ground-state geometries of all the molecules are obtained at the PBE0/6-311++G** level of theory using the Q-Chem software package.¹¹⁴ Planar Fabry–Pérot micro-cavities are chosen with a frequency resonant (or near-resonant) with the first excited states with a significant oscillation strength of each molecule. Namely, a single fundamental coupling strength vector (λ) is set to be parallel to the transition dipole moment of that particular excited state. The coupling strength is tuned by varying the concentration, while the maximum coupling strength is obtained using the estimated volume of each molecule. Note that this assumes that all the molecules have exactly the same orientation in the optical cavity. The coupling strengths λ are represented in atomic units, as $1\mathrm{a}.\mathrm{u}.=1{\sqrt{m}}_{\text{e}}{E}_{\text{h}}/e\hslash$.

Furthermore, we consider only one mode of the radiation field with α = 1 and apply the long-wavelength approximation by setting z to half way between the two mirrors. In the end, S_α(r) in Eq. (3) has a value of $\sqrt{\frac{2}{V_{\text{eff}}}}$ in all our calculations.

Three molecular systems are considered in this work:

• •For the ethene molecule, the effective molecular volume is estimated to be $2331a_0^3$, which corresponds to a maximum coupling strength of λ_max = 0.1038 a.u. The cavity frequency is set to be 6.961 eV, which is resonant with the first TDA excited state in vacuum; and the coupling vector is parallel to the corresponding electronic transition dipole moment.
• •For the formaldehyde molecule, the effective molecular volume is estimated to be $1991a_0^3$, which amounts to a maximum coupling strength of λ_max = 0.1123 a.u. The cavity frequency is set to be 6.777 eV in the TDDFT calculations and 6.784 eV in the TDA calculations, which is in resonant with the second-excited state in the corresponding gas-phase calculations.
• •For the benzaldehyde molecule, the effective molecular volume is estimated to be $73050a_0^3$, with the corresponding maximum coupling strength being λ_max = 0.0185 a.u. The cavity frequency is set to be either in resonance (4.879 eV for TDA, while 4.810 eV for TDDFT) with or 0.02 eV off-resonant (4.899 eV for TDA and 4.830 eV for TDDFT) from the second excitation energy.

IV. RESULTS AND DISCUSSIONS

In this section, some preliminary results are presented. In Subsection IV A, the ethene molecule (C₂H₄) is used as a model system in resonance with the cavity mode to show the equivalence of the Jaynes–Cummings model and the corresponding TDA-JC method. In Subsection IV B, polariton spectra of the formaldehyde molecule (also in resonance with the photon field) are shown at various levels of QED-TDDFT models to systematically analyze the effects of DSE and CRT as well as the TDA approximation. In Subsection IV C, the benzaldehyde molecule is studied as a more practical example of photochrome. The TDA-JC results are compared to the two-state model, while the cavity frequencies are set to be in resonance or off-resonance with the first TDA excitation energy.

A. Ethene

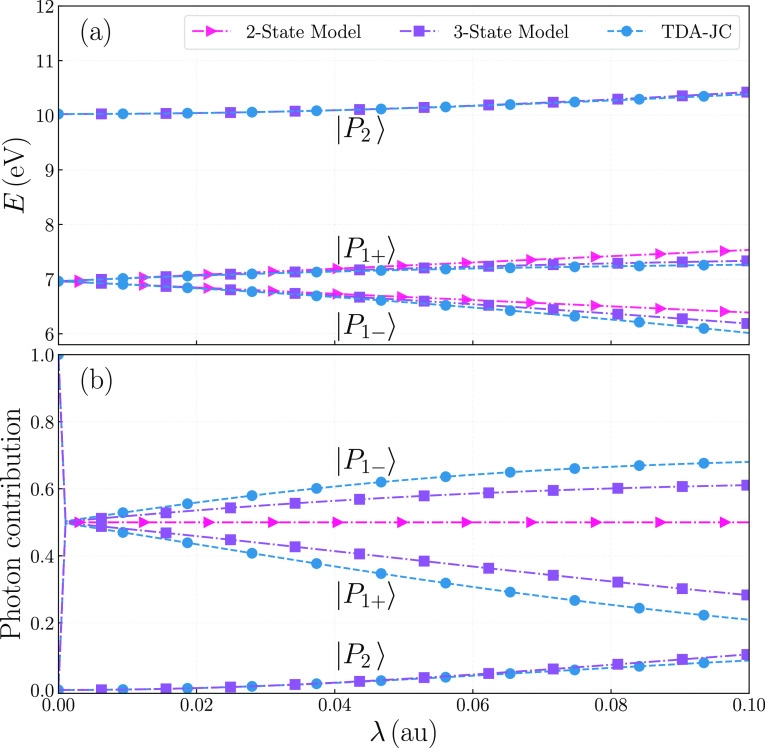
For the ethene molecule, the first excited state in the gas phase has a TDA excitation energy of 6.961 eV and a transition dipole moment in the x-direction. As shown in Fig. 2(a), this state exhibits an expected Rabi splitting into two polariton states upon the application of a resonant radiation field in the x-direction. Within the TDA-JC model, the lower polariton, $\left|P_{1-}\right.⟩$, keeps reducing its energy, while the upper polariton, $\left|P_{1+}\right.⟩$, is subjected to a monotonic increase in its energy. The Rabi splitting is clearly non-symmetric. By the maximum coupling strength, λ = 0.1038 a.u., the lower polariton has a TDA-JC excitation energy of 5.965 eV, which translated to a net reduction of 0.996 eV from its gas-phase value. In contrast, the upper polariton is predicted to have a TDA-JC excitation energy value of 7.270 eV at λ = 0.1038 a.u., which amounts to a net gain of only 0.308 eV.

FIG. 2.

(a) Polariton spectrum of the ethene molecule and (b) photon contribution to each polariton state within the TDA-JC model using the PBE0 functional and 6-311++G** basis set, as a function of coupling strength λ. Solutions to model Hamiltonians with different numbers of states are also presented for a comparison.

A symmetric Rabi splitting of the upper and lower polaritons would be expected for a two-state Jaynes–Cummings model Hamiltonian, which is constructed using gas-phase TDA results according to Eq. (C1). The energy eigenvalues, as expressed in Eqs. (C4) and (C5), are plotted (as pink triangles) against the coupling strength in Fig. 2(a). The energy of the lower polariton within the two-state model decreases linearly with the electron–photon coupling strength (up to a net reduction of 0.595 eV), while that of the upper polariton increases linearly (in a symmetric fashion with respect to the lower polariton). While the two-state model can be considered as an appropriate approximation when the coupling strength is weak, a non-symmetric Rabi splitting at stronger coupling strength within the TDA-JC model would suggest a non-negligible perturbation from one or more higher excited states.

Within our current implementation of QED-TDA and QED-TDDFT methods, all molecules are assumed to adopt the same orientation, whereas an implementation for randomly oriented photochromes is under development and shall be presented in the subsequent publications.¹²⁵ As a direct consequence of this assumption, among higher excited states, only those with a large transition dipole component in the x-direction can perturb the aforementioned polaritons. As shown in Table S1, the next state with a substantial dipole moment in the x-direction is the 13th state with an excitation energy of 10.022 eV. This state [labeled $\left|P_2\right.⟩$ in Fig. 2(a)] could be accounted for through building a three-state Hamiltonian in Eq. (C6). For both $\left|P_{1-}\right.⟩$ and $\left|P_{1+}\right.⟩$ polariton states, their energies within the three-state model are brought much closer to the TDA-JC values in Fig. 2(a), which is a substantial improvement over the two-state model.

Interestingly, upon perturbation from the higher excited states, the $\left|P_{1-}\right.⟩$ and $\left|P_{1+}\right.⟩$ polariton states both get lowered in their energies, hence producing the non-symmetric Rabi splitting. Such energy lowerings can be easily understood within the three-state model, where both polaritons are shown in Eqs. (C10) and (C11) to receive an identical and negative second-order contribution to their energies. To counterbalance these energy changes, the energy of the $\left|P_2\right.⟩$ state (corresponding to the 13th excited state in the gas phase) gains energy with increasing coupling strengths, as demonstrated in Fig. 2(a).

When the polariton “wavefunction” is concerned, Fig. 2(b) showed that, at the weak-coupling limit, $\left|P_{1-}\right.⟩$ and $\left|P_{1+}\right.⟩$ each contains 50% of photon contribution. As the coupling strength increases, however, the TDA-JC $\left|P_{1-}\right.⟩$ state (as well as the one from the three-state model) gradually gains more photon character. An explanation of this again requires us to go beyond the two-state model, which incorrectly predicts a non-varying photon contribution. Indeed, within the three-state model, the lower polariton “wavefunction” in Eq. (C13) contains larger and larger contributions from |g⟩|1⟩ with increasing coupling strengths. In contrast, the TDA-JC upper polariton, |P₁₊⟩, as well as its three-state counterpart gradually lose photon character, and as a compensation, the |P₂⟩ state slowly gains some photon character.

In terms of the photon character of |P₁₋⟩ and |P₁₊⟩ states, the three-state model only qualitatively predicts the trend of the TDA-JC model. To fully reproduce the TDA-JC energies within 0.02 eV, however, it would take at least additional 18 excited states from the gas-phase calculation in the construction of the model Hamiltonian. This reflects the strength of our QED-TDA and QED-TDDFT algorithms: instead of hand-picking excited states that might exert a significant perturbation, these states are automatically accounted for through the Davidson diagonalization procedure.

Our TDA-JC calculations and three-state modeling are carried out with only up to the maximum coupling strength that is allowable by the molecular volume. Theoretically, though, if one goes beyond that limit, the three-state model will show that (a) the photon character of |P₁₋⟩ reaches a peak value before decreasing and (b) the upper polariton, |P₁₊⟩, loses all its photon character and converges its energy to the value computed with Eq. (C18).

B. Formaldehyde

For the formaldehyde molecule, the TDA-JC model [marked as blue dots in Fig. 3(a)] yielded very similar results to that of ethene: the first excited state with a substantial oscillator strength in the gas phase (excitation energy: 6.784 eV, dipole: 0.490 a.u.) undergoes a non-symmetric Rabi splitting in the photon cavity. This happens due to a perturbation from the fourth state (labeled |P₂⟩) with an excitation energy of 7.856 eV and a large transition dipole moment of 0.3728 a.u. in the x-direction.

FIG. 3.

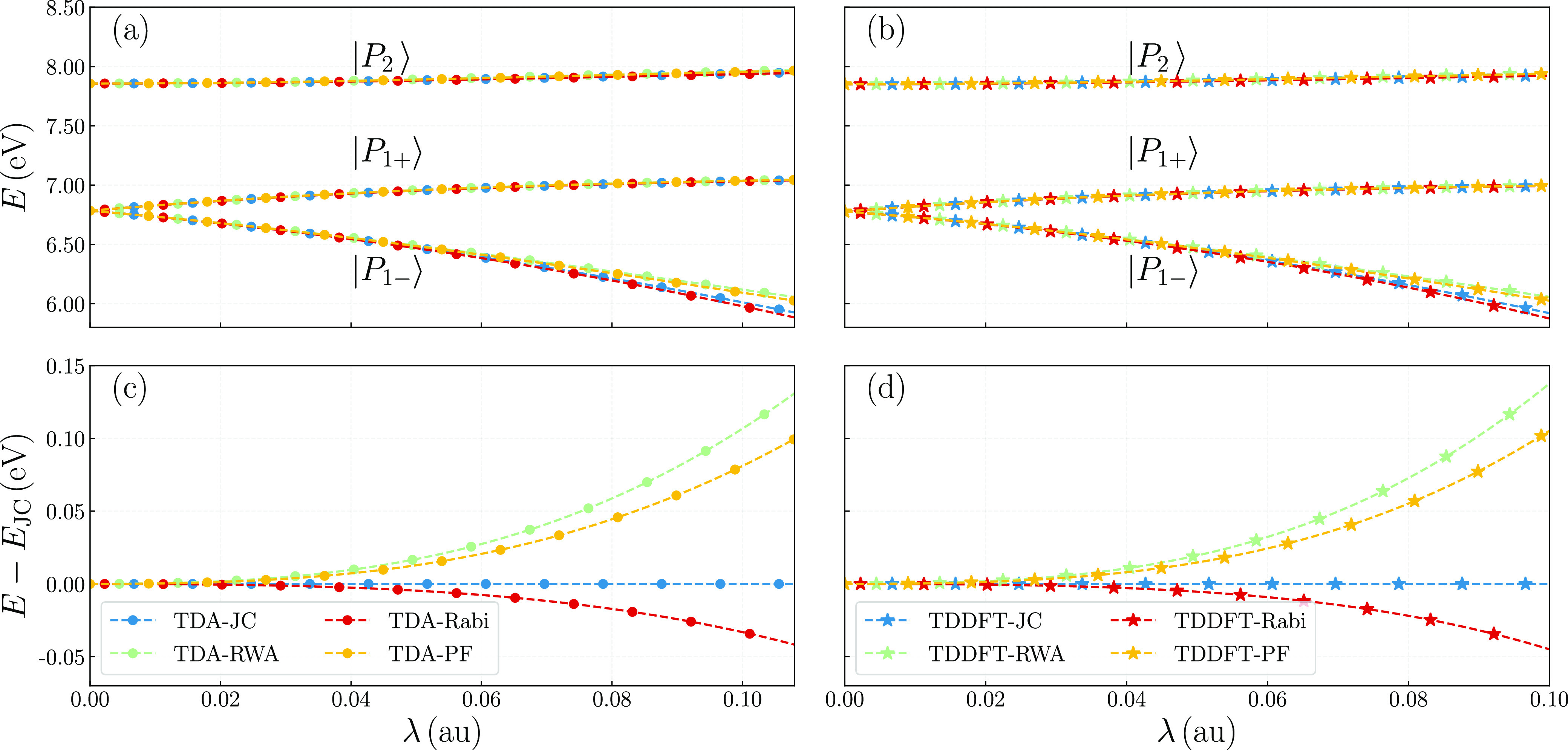
(a) QED-TDA and (b) QED-TDDFT polariton spectra of the formaldehyde molecule using different QED-TDDFT models with the PBE0 functional and 6-311++G** basis set, as a function of coupling strength λ. (c) and (d) highlight the difference in the lower polariton energy from Rabi, RWA, and PF models against corresponding TDA-JC or TDDFT-JC values.

For this molecule, we would shift our attention to a comparison among the JC, Rabi, RWA, and PF variations of QED-TDA or QED-TDDFT methods. As shown in Fig. 3(a), when the coupling strength is small, the four variations produce very similar energy spectra. In fact, at λ = 0.045 a.u., the predicted Rabi splitting differs by no more than 0.02 eV among the four models.

When the coupling strength further increases, the four models yield nearly identical energies for the upper polariton, |P₁₊⟩. However, the predicted energies for the lower polariton, |P₁₋⟩, start to exhibit notable differences [Fig. 3(a)]. This is clearer in Fig. 3(c), which shows the energy differences against the TDA-JC model. The TDA-Rabi model (marked red), which adds the CRT to TDA-JC, lowers the polariton energy in an agreement with the leading perturbative correction in Eq. (19). Meanwhile, the TDA-RWA model (illustrated as green dots) captures the DSE contribution missing in the TDA-JC model and, thus, raises the polariton energy in consistence with Eq. (17). At large λ values, the CRT correction to the TDA-JC model is found to be three to four times smaller than the DSE correction, in terms of the absolute value. For the TDA-PF model [marked yellow in Fig. 3(b)], which adds both CRT and DSE corrections to the TDA-JC model, the CRT only partially canceled the DSE component, leading also to a net energy increase.

At smaller λ values, the CRT correction is found numerically to be exactly $-\frac{1}{4}$ of the DSE correction, which is consistent with our earlier analysis at the end of Subsection II C. Therefore, we also mentioned Mandal et al.’s prediction that the CRT correction is $-\frac{1}{2}$ of the DSE value at resonance.⁵² This discrepancy is caused by a subtle difference in choosing the value of the fundamental coupling strength, λ_α, which is set to be $\sqrt{\frac{2}{{ϵ}_0{V}_{\text{eff}}}}{\mathit{ϵ}}_{\alpha }$ in our work but $\sqrt{\frac{1}{{ϵ}_0{V}_{\text{eff}}}}{\mathit{ϵ}}_{\alpha }$ in Ref. 52. As a result, our DSE correction in Eq. (17) is twice larger. Meanwhile, at resonance and weak coupling, the electron–photon coupling in Eq. (20) can be written as $g_{\alpha ,I}=\sqrt{\frac{{\omega }_{\alpha }}{2\hslash }}\left({\mathit{\lambda }}_{\alpha }\cdot {\mathit{\mu }}_I^{\text{TDA}-\text{JC}}\right)=\sqrt{\frac{{\omega }_{\alpha }}{2\hslash }}\left({\mathit{\lambda }}_{\alpha }\cdot \frac{1}{\sqrt{2}}{\mathit{\mu }}_I^{\text{TDA}}\right)=\sqrt{\frac{{\omega }_{\alpha }}{2\hslash {ϵ}_0{V}_{\text{eff}}}}\left({\mathit{ϵ}}_{\alpha }\cdot {\mathit{\mu }}_I^{\text{TDA}}\right)$, which is exactly the same as Eq. (11) in Ref. 52. This led to an identical CRT correction, $-\frac{\hslash }{2{\omega }_{\alpha }}{g}_{\alpha ,I}^2$. In choosing our value for λ_α, we follow Rubio,^83,91 Subotnik,^65–67,126 and others.^82,98 It would be a reasonable choice when one or more molecules is placed within a horizontal plane equidistant from the two mirrors (z = L_z/2, where the sine wave reaches its maximum value). When the molecular concentration further increases, however, it might be better to follow Huo and co-workers and adopt a reduced λ_α value to reflect a molecular distribution along the photon wavevector (i.e., perpendicular to mirror surfaces).^52,112

While our discussion on the formaldehyde molecule has, so far, focused on QED-TDA calculations, all our observations on the comparison among JC, Rabi, RWA, and PF models would also apply to QED-TDDFT results displayed in Figs. 3(c) and 3(d). Overall, with the leading contribution from CRT and DSE being second-order to the coupling strength, both terms can be ignored for small coupling strengths. Namely, the TDA-JC and TDDFT-JC models can be used to describe polariton states at the weak light–matter interaction regime.^52,113 However, more caution is needed to select an appropriate model in strong and ultra-strong coupling regimes, where the lower polariton energy can become unbounded without the DSE correction.⁵²

C. Benzaldehyde

The TDA-JC results of the benzaldehyde molecule are presented as a more realistic example of the photochrome. (Other QED-TDDFT models are also tested and found to lead to similar results in Table S5.) In particular, the focus is placed on the second-excited state from the gas-phase TDA calculation with an excitation energy of 4.879 eV and a transition dipole of 0.427 a.u. in the xy-plane. In Fig. 4(a), this state is coupled to a resonant Fabry–Pérot mode, while in Fig. 4(b), it is coupled to an off-resonance cavity mode of 4.899 eV (i.e., a detuning of 0.02 eV). Clearly, as the coupling strength λ increases, larger Rabi splittings occur in both resonant and off-resonant cases. Moreover, the energies of both lower and upper polaritons deviate further away from the two-state-predicted values (dotted–dashed lines), in a way similar to the ethene and formaldehyde molecules. Interestingly, for our chosen coupling strengths, the off-resonance results in Fig. 4(b) show slightly smaller differences between the two-state Jaynes–Cummings model and the TDA-JC method. This occurs because, with a detuning of 0.02 eV, the overall Rabi splitting is slightly smaller.

FIG. 4.

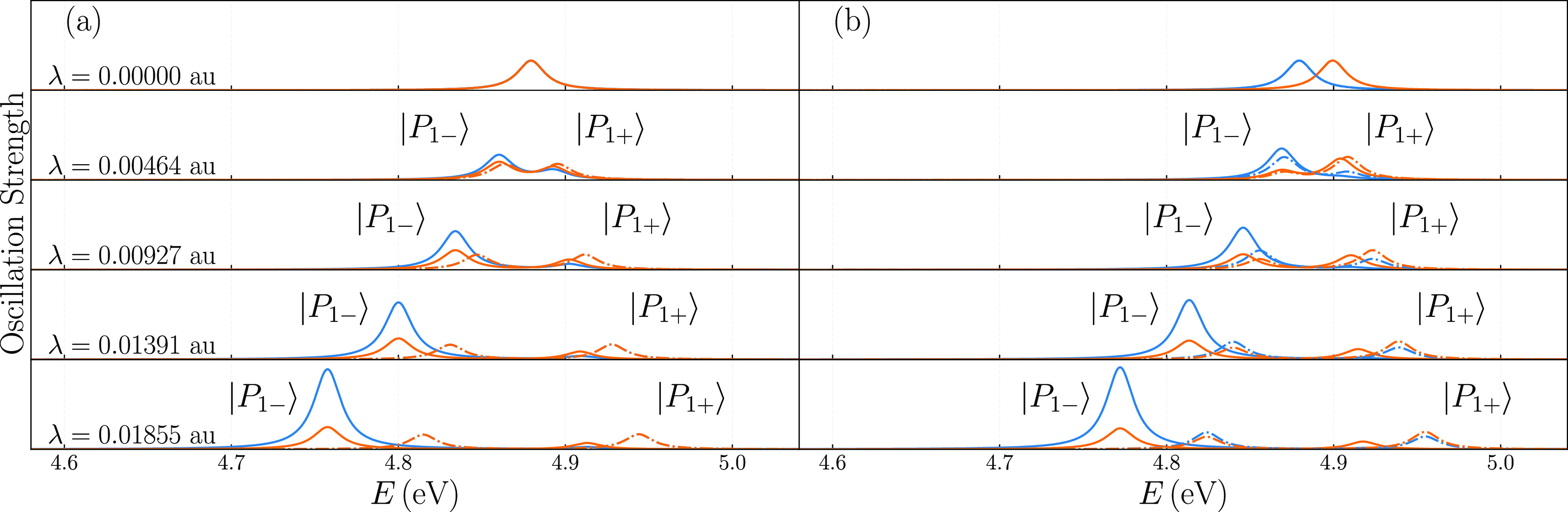
Absorption spectra of the benzaldehyde molecule from TDA-JC (solid lines) and two-state Jaynes–Cummings model (dotted-dashed lines) calculations with different coupling strengths using the PBE0 functional and 6-311++G** basis set. The Fabry–Pérot mode is chosen to be (a) in resonance (4.879 eV) and (b) 0.02 eV off-resonance (4.899 eV) from the gas-phase excited state. The blue and orange lines indicate the electron and photon contributions, respectively. Following Ref. 91, Lorentzian broadening is employed with Δ = 10⁻² eV.

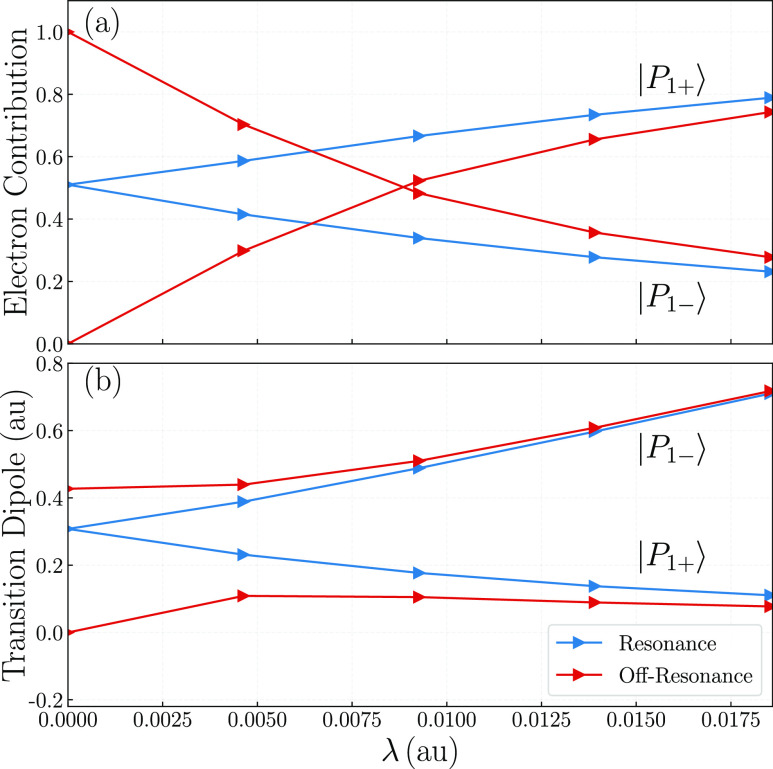
An analysis of the composition of polariton “wavefunction” of benzaldehyde leads to observations similar to the ethene molecule [Fig. 2(b)]. At non-zero coupling strengths, the lower polariton, |P₁₋⟩, is shown in Fig. 5(a) to contain less electron contribution than the photon contribution, while the opposite can be seen for the upper polariton, |P₁₊⟩. Such deviations from the two-state Jaynes–Cummings model, which would predict equal electron and photon contributions for both polaritons in a resonance coupling, can be traced to non-negligible second-order contributions from higher excited states (third, fifth, and 11th states in Table S4, and many more) of gas-phase benzaldehyde. For off-resonance coupling, similar behavior can also be seen in Fig. 5(a), but the lower polariton, |P₁₋⟩, contains more electron contributions (than the resonance case) due to a higher photon energy.

FIG. 5.

(a) Electron contributions and (b) the corresponding norms of transition dipole moments for the lower and upper polaritons of benzaldehyde at different coupling strengths with resonance (blue) and off-resonance (red) photon energies.

At first glance, smaller electronic contribution to the lower polariton with stronger electron–photon coupling, as shown in Fig. 5(a), would appear to contradict Figs. 4(a) and 4(b), where the TDA-JC molecular oscillation strength (marked blue) of the lower polariton actually increases with coupling strength. To resolve such a “contradiction,” it is useful to examine the change in the molecular transition dipoles of the polaritons [as defined in Eqs. (S2) and (S3) in the supplementary material] with varying coupling strengths. Surprisingly, as shown in Fig. 5(b), the transition dipole of the lower polariton increases with larger coupling strength, while the opposite happens to the upper polariton. This can be understood within a three-state model. Specifically, Eq. (C15) indicates that the transition dipole of the lower polariton will be enhanced by those of higher-energy excited states, while the transition dipole of the upper polariton will get weakened by those states [Eq. (C16)]. This is confirmed by Fig. S1, which shows a steady increase in the transition dipole of the lower polariton as more states are included in the Jaynes–Cummings model Hamiltonian and by an opposite trend for the upper polariton in Fig. S1. In the limit of strong couplings (such as λ = 0.018 53 a.u.), the upper polariton state of benzaldehyde should be dominated by the |e₁⟩ state (with the corresponding coefficient being 0.88). However, due to the slow $\frac{1}{{\omega }_2-\omega }$ decay arising from Eqs. (C15) and (C16) and demonstrated in Fig. S1, many higher excited states (with small but non-zero mixing coefficients) combine together to cancel the |e₁⟩ dipole moment. At λ = 0.018 53 a.u., the transition dipoles for the upper polariton are reduced by two thirds from its gas-phase value, leading to only marginal oscillator strengths in Fig. 4.

Such collective enhancement (weakening) of the lower (upper) polariton transition dipole by many higher excited states would be difficult to capture with the construction of multi-state Jaynes–Cummings model Hamiltonians. As shown in Fig. S1, with strong coupling, tens of excited states need to be included in the model before the converged value of the transition dipole moment can be approached. However, it holds the key to our understanding of the absorption spectra of benzaldehyde in this work as well as other molecules displaying non-symmetric Rabi splitting, such as merocyanine in Fig. 3(a) of Ref. 27, benzene in Fig. 6 of Ref. 91, and formaldehyde in Fig. 3(a) of Ref. 93 and Fig. S2 of the supplementary material.

V. CONCLUSIONS

In summary, some progress has been made in this work on the formulation, implementation, and understanding of QED-TDDFT models, including:

• •The two-state Jaynes–Cummings model could be considered as an appropriate approximation when the coupling strength is weak enough that the higher excited states can be ignored.
• •Through linear-response and equation-of-motion formulations, simple QED-TDDFT working equations are obtained for the Pauli–Fierz Hamiltonian. The Gaussian-basis implementation of the TDDFT-PF and associated approximate models paves the way for their routine applications.
• •In the strong and ultra-strong coupling regime, the polaritons might get perturbed notably by higher excited states with significant transition dipole moments. For our test molecules, these excited states reduce the electron contribution to the lower polariton but enhance its transition dipole moment and oscillator strength, whereas they affect the upper polariton in exactly the opposite manner. While the QED-TDDFT/TDA method accounts for these effects naturally, it would be cumbersome (if feasible at all with the slow decay) to identify all these states from gas-phase calculations and then include them in the model Hamiltonian.
• •At the strong coupling limit, the dipole self-energy and counter-rotation terms can also cause notable changes to the energies of polariton states.

  On the other hand, within the TDDFT framework, several technical components are yet to be developed:

• •In this work, the photochromes are assumed to be separated in the vacuum. To capture the effect of other molecular species in the cavity (such as PMMA or solvents), implicit solvent models or combined quantum mechanical molecular mechanical models should be adopted.
• •Analytical energy derivatives are needed to allow for (a) the optimization of the photochromic geometry for different polariton states and (b) the modeling of photochemical reactions and absorption/emission spectra.
• •All molecules are assumed to adopt the same orientation within the optical cavity. Our models need to be extended to cases where molecules adopt random orientations.

Work along these lines is expected to be rather straightforward and will be reported in subsequent publications.

SUPPLEMENTARY MATERIAL

See the supplementary material for (a) details on the computation of absorption spectra, (b) conversion of TDDFT-PF and TDDFT-Rabi equations into the compact Hermitian form, (c) geometry of the three test molecules, and (d) the numerical results from gas-phase TDDFT as well as QED-TDDFT calculations on three molecules.

APPENDIX A: LINEAR-RESPONSE DERIVATION

In this section, we present a matrix derivation of the QED-TDDFT equations that closely follow Rubio and co-workers’ approach based on the linear-response formula.^{82–84,86,89,94–96}

1. Density response kernel

For a Kohn–Sham (KS)-DFT electronic ground state, its Fock matrix (i.e., effective one-electron Hamiltonian) is diagonal in the representation of Kohn–Sham orbitals,

$${\mathbf{F}}_0=\left[\begin{array}{cc}\hfill {\mathbf{F}}_{\text{oo}}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathbf{F}}_{\text{vv}}\hfill \end{array}\right],$$ (A1)

with F_ij = ɛ_iδ_ij and F_ab = ɛ_aδ_ab. The density matrix takes the format

$${\mathbf{P}}_0=\left[\begin{array}{cc}\hfill {\mathbf{I}}_{\text{oo}}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \end{array}\right]$$ (A2)

with a single occupancy for the lowest-energy spin orbitals.

Within the matrix formulation of TDDFT, the Fock matrix is subjected to a frequency-dependent perturbation,

$$\mathbf{F}(t)={\mathbf{F}}_0+\delta \mathbf{F}(t),$$ (A3)

$$\delta \mathbf{F}(t)=\left[\begin{array}{cc}\hfill \mathbf{0}\hfill & \hfill \delta {\mathbf{F}}_{\text{ov}}^{(\mathrm{\Omega })}{e}^{i\mathrm{\Omega }t}\hfill \\ \hfill \delta {\mathbf{F}}_{\text{vo}}^{(\mathrm{\Omega })}{e}^{-i\mathrm{\Omega }t}\hfill & \hfill \mathbf{0}\hfill \end{array}\right]+\left[\begin{array}{cc}\hfill \mathbf{0}\hfill & \hfill \delta {\mathbf{F}}_{\text{ov}}^{(-\mathrm{\Omega })}{e}^{-i\mathrm{\Omega }t}\hfill \\ \hfill \delta {\mathbf{F}}_{\text{vo}}^{(-\mathrm{\Omega })}{e}^{i\mathrm{\Omega }t}\hfill & \hfill \mathbf{0}\hfill \end{array}\right],$$ (A4)

where $\delta {\mathbf{F}}_{\text{ov}}^{(\mathrm{\Omega })}=\delta {\mathbf{F}}_{\text{vo}}^{(\mathrm{\Omega }),†}$ and $\delta {\mathbf{F}}_{\text{ov}}^{(-\mathrm{\Omega })}=\delta {\mathbf{F}}_{\text{vo}}^{(-\mathrm{\Omega }),†}$ to maintain a Hermitian matrix. Such a perturbation causes a response in the density matrix,

$$\mathbf{P}(t)={\mathbf{P}}_0+\delta \mathbf{P}(t),$$ (A5)

$$\delta \mathbf{P}(t)=\left[\begin{array}{cc}\hfill \mathbf{0}\hfill & \hfill \delta {\mathbf{P}}_{\text{ov}}^{(\mathrm{\Omega })}{e}^{i\mathrm{\Omega }t}\hfill \\ \hfill \delta {\mathbf{P}}_{\text{vo}}^{(\mathrm{\Omega })}{e}^{-i\mathrm{\Omega }t}\hfill & \hfill \mathbf{0}\hfill \end{array}\right]+\left[\begin{array}{cc}\hfill \mathbf{0}\hfill & \hfill \delta {\mathbf{P}}_{\text{ov}}^{(-\mathrm{\Omega })}{e}^{-i\mathrm{\Omega }t}\hfill \\ \hfill \delta {\mathbf{P}}_{\text{vo}}^{(-\mathrm{\Omega })}{e}^{i\mathrm{\Omega }t}\hfill & \hfill \mathbf{0}\hfill \end{array}\right],$$ (A6)

where $\delta {\mathbf{P}}_{\text{ov}}^{(\mathrm{\Omega })}=\delta {\mathbf{P}}_{\text{vo}}^{(\mathrm{\Omega }),†}$ and $\delta {\mathbf{P}}_{\text{ov}}^{(-\mathrm{\Omega })}=\delta {\mathbf{P}}_{\text{vo}}^{(-\mathrm{\Omega }),†}$.

The density response is governed by the time-dependent Kohn–Sham (TDKS) equation,^{101,103,105,108}

$$i\hslash \frac{\partial \mathbf{P}(t)}{\partial t}=[\mathbf{F}(t),\mathbf{P}(t)]=[\delta \mathbf{F}(t),{\mathbf{P}}_0]+[{\mathbf{F}}_0,\delta \mathbf{P}(t)],$$ (A7)

which is

$$\begin{array}{ll}\hfill i\hslash \frac{\partial \mathbf{P}(t)}{\partial t}& =\left[\begin{array}{cc}\hfill \mathbf{0}\hfill & \hfill -\delta {\mathbf{F}}_{\text{ov}}\hfill \\ \hfill \delta {\mathbf{F}}_{\text{vo}}\hfill & \hfill \mathbf{0}\hfill \end{array}\right]\hfill \\ \hfill & +\left[\begin{array}{cc}\hfill \mathbf{0}\hfill & \hfill {\mathbf{F}}_{\text{oo}}\delta {\mathbf{P}}_{\text{ov}}-\delta {\mathbf{P}}_{\text{ov}}{\mathbf{F}}_{\text{vv}}\hfill \\ \hfill {\mathbf{F}}_{\text{vv}}\delta {\mathbf{P}}_{\text{vo}}-\delta {\mathbf{P}}_{\text{vo}}{\mathbf{F}}_{\text{oo}}\hfill & \hfill \mathbf{0}\hfill \end{array}\right].\hfill \end{array}$$ (A8)

Below, we shall focus on the vo-block of this equation, which requires

$$i\hslash \frac{\partial {\mathbf{P}}_{\text{vo}}(t)}{\partial t}=\delta {\mathbf{F}}_{\text{vo}}+{\mathbf{F}}_{\text{vv}}\delta {\mathbf{P}}_{\text{vo}}-\delta {\mathbf{P}}_{\text{vo}}{\mathbf{F}}_{\text{oo}},$$ (A9)

noting that the ov-block equation is the complex conjugate.

Collecting the e^−iΩt and e^iΩt terms separately from both sides of Eq. (A9), one gets

$$(\hslash \mathrm{\Omega })\delta {\mathbf{P}}_{\text{vo}}^{(\mathrm{\Omega })}=\delta {\mathbf{F}}_{\text{vo}}^{(\mathrm{\Omega })}+{\mathbf{F}}_{\text{vv}}\delta {\mathbf{P}}_{\text{vo}}^{(\mathrm{\Omega })}-\delta {\mathbf{P}}_{\text{vo}}^{(\mathrm{\Omega })}{\mathbf{F}}_{\text{oo}},$$ (A10)

$$(-\hslash \mathrm{\Omega })\delta {\mathbf{P}}_{\text{vo}}^{(-\mathrm{\Omega })}=\delta {\mathbf{F}}_{\text{vo}}^{(-\mathrm{\Omega })}+{\mathbf{F}}_{\text{vv}}\delta {\mathbf{P}}_{\text{vo}}^{(-\mathrm{\Omega })}-\delta {\mathbf{P}}_{\text{vo}}^{(-\mathrm{\Omega })}{\mathbf{F}}_{\text{oo}},$$ (A11)

which can be written explicitly as

$$(\hslash \mathrm{\Omega }-{\epsilon }_a+{\epsilon }_i)\delta P_{ai}^{(\mathrm{\Omega })}=\delta F_{ai}^{(\mathrm{\Omega })},$$ (A12)

$$(-\hslash \mathrm{\Omega }-{\epsilon }_a+{\epsilon }_i)\delta P_{ai}^{(-\mathrm{\Omega })}=\delta F_{ai}^{(-\mathrm{\Omega })}.$$ (A13)

This shows how the density matrix would respond to a frequency-dependent change in the Fock matrix.

2. Electron equations within QED-TDDFT

For a molecule in an optical cavity, its Fock matrix is influenced by changes in both the electronic density matrix in Eq. (A6) as well as the electron–photon coupling,

$$\delta F_{ai}^{(\mathrm{\Omega })}=\delta F_{ai,\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{c}}^{(\mathrm{\Omega })}+\delta F_{ai,\text{elec–photon}}^{(\mathrm{\Omega })},$$ (A14)

$$\delta F_{ai}^{(-\mathrm{\Omega })}=\delta F_{ai,\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{c}}^{(-\mathrm{\Omega })}+\delta F_{ai,\text{elec–photon}}^{(-\mathrm{\Omega })}.$$ (A15)

For $F_{ai}^{(\mathrm{\Omega })}$, it is only perturbed by $P_{bj}^{(\mathrm{\Omega })}$ and $P_{jb}^{(-\mathrm{\Omega })}$, which carry the same e^−iΩt factor in Eq. (A6),

$$\begin{array}{ll}\hfill \delta F_{ai,\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{c}}^{(\mathrm{\Omega })}& =\sum _{bj}\left(\frac{\partial F_{ai}}{\partial P_{bj}}\delta P_{bj}^{(\mathrm{\Omega })}+\frac{\partial F_{ai}}{\partial P_{jb}}\delta P_{jb}^{(-\mathrm{\Omega })}\right)\hfill \\ \hfill & =\sum _{bj}\left[\left[A_{ai,bj}-({\epsilon }_a-{\epsilon }_i){\delta }_{ab}{\delta }_{ij}\right]\delta P_{bj}^{(\mathrm{\Omega })}+B_{ai,bj}\delta P_{jb}^{(-\mathrm{\Omega })}\right].\hfill \end{array}$$ (A16)

Similarly, for $F_{ai,\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{c}}^{(-\mathrm{\Omega })}$, one gets

$$\begin{array}{ll}\hfill \delta F_{ai,\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{c}}^{(-\mathrm{\Omega })}& =\sum _{bj}\left(\frac{\partial F_{ai}}{\partial P_{bj}}\delta P_{bj}^{(-\mathrm{\Omega })}+\frac{\partial F_{ai}}{\partial P_{jb}}\delta P_{jb}^{(\mathrm{\Omega })}\right)\hfill \\ \hfill & =\sum _{bj}\left[\left[A_{ai,bj}-({\epsilon }_a-{\epsilon }_i){\delta }_{ab}{\delta }_{ij}\right]\delta P_{bj}^{(-\mathrm{\Omega })}+B_{ai,bj}\delta P_{jb}^{(\mathrm{\Omega })}\right].\hfill \end{array}$$ (A17)

For the electron–photon interaction energy in Eq. (7),

$$V_{\text{elec–photon}}=\sum _{\alpha =1}^M\frac{1}{2}{\omega }_{\alpha }^2{\left(q_{\alpha }-\frac{1}{{\omega }_{\alpha }}{\mathit{\lambda }}_{\alpha }\cdot \mathit{\mu }\right)}^2.$$ (A18)

Its corresponding Fock matrix contribution is

$$\begin{array}{ll}\hfill F_{ai,\text{elec–photon}}& =\frac{\partial V_{\text{elec–photon}}}{\partial P_{ai}}\hfill \\ \hfill & =\sum _{\alpha =1}^M{\omega }_{\alpha }{\lambda }_{ai}^{\alpha }\left(q_{\alpha }-\frac{1}{{\omega }_{\alpha }}{\mathit{\lambda }}_{\alpha }\cdot \mathit{\mu }\right),\hfill \end{array}$$ (A19)

which uses the dipole derivative

$$\frac{\partial \mathit{\mu }}{\partial P_{ai}}=\frac{\partial \left({\mathit{\mu }}_{\text{nuc}}-{\mathit{\mu }}_{\text{mo}}\cdot \mathbf{P}\right)}{\partial P_{ai}}=-{\mathit{\mu }}_{ai}.$$ (A20)

Clearly, the Fock matrix contribution in Eq. (A19) is perturbed by the density matrix and the photon coordinate,

$$\begin{array}{ll}\hfill \delta F_{ai,\text{elec–photon}}^{(\mathrm{\Omega })}& =\delta F_{ai,\text{elec–photon}}^{(-\mathrm{\Omega })}\hfill \\ \hfill & =\sum _{bj}\left(\sum _{\alpha =1}^M{\lambda }_{ai}^{\alpha }{\lambda }_{bj}^{\alpha }\right)\left(\delta P_{bj}^{(\mathrm{\Omega })}+\delta P_{jb}^{(-\mathrm{\Omega })}\right)+\sum _{\alpha =1}^M{\omega }_{\alpha }{\lambda }_{ai}^{\alpha }\delta q_{\alpha }\hfill \\ \hfill & =\sum _{bj}{\mathrm{\Delta }}_{ai,bj}\left(\delta P_{bj}^{(\mathrm{\Omega })}+\delta P_{jb}^{(-\mathrm{\Omega })}\right)\hfill \\ \hfill & +\sum _{\alpha =1}^M\sqrt{\frac{\hslash {\omega }_{\alpha }}{2}}{\lambda }_{ai}^{\alpha }\left(M_{\alpha }+N_{\alpha }\right),\hfill \end{array}$$ (A21)

which uses the expression of Δ_ai,bj in Eq. (9) and replaces $\delta {\widehat{q}}_{\alpha }$ with dimensionless quantities (instead of the original amplitudes introduced in Ref. 91),

$$\delta q_{\alpha }=\sqrt{\frac{\hslash }{2{\omega }_{\alpha }}}\left(M_{\alpha }+N_{\alpha }\right).$$ (A22)

Substituting Eqs. (A16), (A17), and (A21) into the right-hand side of Eqs. (A12) and (A13), one obtains

$$\begin{array}{ll}\hfill (\hslash \mathrm{\Omega })\delta P_{ai}^{(\mathrm{\Omega })}& =\sum _{bj}\left(A_{ai,bj}+{\mathrm{\Delta }}_{ai,bj}\right)\delta P_{bj}^{(\mathrm{\Omega })}\hfill \\ \hfill & +\sum _{bj}\left(B_{ai,bj}+{\mathrm{\Delta }}_{ai,bj}\right)\delta P_{jb}^{(-\mathrm{\Omega })}\hfill \\ \hfill & +\sum _{\alpha =1}^M\sqrt{\frac{\hslash {\omega }_{\alpha }}{2}}{\lambda }_{ai}^{\alpha }\left(M_{\alpha }+N_{\alpha }\right),\hfill \end{array}$$ (A23)

$$\begin{array}{ll}\hfill (-\hslash \mathrm{\Omega })\delta P_{ai}^{(-\mathrm{\Omega })}& =\sum _{bj}\left(A_{ai,bj}+{\mathrm{\Delta }}_{ai,bj}\right)\delta P_{bj}^{(-\mathrm{\Omega })}\hfill \\ \hfill & +\sum _{bj}\left(B_{ai,bj}+{\mathrm{\Delta }}_{ai,bj}\right)\delta P_{jb}^{(\mathrm{\Omega })}\hfill \\ \hfill & +\sum _{\alpha =1}^M\sqrt{\frac{\hslash {\omega }_{\alpha }}{2}}{\lambda }_{ai}^{\alpha }\left(M_{\alpha }+N_{\alpha }\right).\hfill \end{array}$$ (A24)

Assume that $\delta P_{ai}^{(\mathrm{\Omega })}=\delta P_{ia}^{(\mathrm{\Omega })}$ and $\delta P_{ai}^{(-\mathrm{\Omega })}=\delta P_{ia}^{(-\mathrm{\Omega })}$ are all real and write them as X_ai and Y_ai, respectively; we obtain the electronic portion of the QED-TDDFT equation in Eq. (8).

3. Photon equations within QED-TDDFT

The photon equation of state is⁹¹

$$\begin{array}{ll}\hfill \left(\frac{{\partial }^2}{\partial t^2}+{\omega }_{\alpha }^2\right)q_{\alpha }(t)& =-\frac{1}{{\omega }_{\alpha }}{j}_{\alpha }^{\text{eff}}(t)\hfill \\ \hfill & =-\frac{1}{{\omega }_{\alpha }}\left(j_{\alpha }(t)-{\omega }_{\alpha }^2{\mathit{\lambda }}_{\alpha }\cdot \mathit{\mu }\right).\hfill \end{array}$$ (A25)

For q_α(t) and $j_{\alpha }^{\text{eff}}(t)$ oscillating with frequency Ω, they satisfy

$$\left({\mathrm{\Omega }}^2-{\omega }_{\alpha }^2\right)\delta q_{\alpha }=\frac{1}{{\omega }_{\alpha }}\delta j_{\alpha }^{\text{eff}}.$$ (A26)

Therefore, the photon response is

$$\begin{array}{ccc}\hfill \delta q_{\alpha }& =\hfill & \frac{1}{{\omega }_{\alpha }}\frac{1}{{\mathrm{\Omega }}^2-{\omega }_{\alpha }^2}\delta j_{\alpha }^{\text{eff}}\hfill \\ \hfill & =\hfill & \frac{1}{2{\omega }_{\alpha }^2}\left(\frac{1}{\mathrm{\Omega }-{\omega }_{\alpha }}-\frac{1}{\mathrm{\Omega }+{\omega }_{\alpha }}\right)\delta j_{\alpha }^{\text{eff}}.\hfill \end{array}$$ (A27)

A key to the QED-TDDFT method is the splitting of the right-hand side,⁹¹ which underlies Eq. (A22),

$$\left(\hslash \mathrm{\Omega }-\hslash {\omega }_{\alpha }\right)M_{\alpha }=\sqrt{\frac{\hslash }{2{\omega }_{\alpha }^3}}\delta j_{\alpha }^{\text{eff}},$$ (A28)

$$-\left(\hslash \mathrm{\Omega }+\hslash {\omega }_{\alpha }\right)N_{\alpha }=\sqrt{\frac{\hslash }{2{\omega }_{\alpha }^3}}\delta j_{\alpha }^{\text{eff}},$$ (A29)

where $\delta j_{\alpha }^{\text{eff}}$ can be easily derived from Eq. (A25),

$$\delta j_{\alpha }^{\text{eff},(\mathrm{\Omega })}={\omega }_{\alpha }^2\sum _{bj}{\lambda }_{bj}^{\alpha }\left(\delta P_{bj}^{(\mathrm{\Omega })}+\delta P_{jb}^{(-\mathrm{\Omega })}\right).$$ (A30)

Therefore,

$$(\hslash \mathrm{\Omega })M_{\alpha }=\sum _{bj}\sqrt{\frac{\hslash {\omega }_{\alpha }}{2}}{\lambda }_{bj}^{\alpha }\left(\delta P_{bj}^{(\mathrm{\Omega })}+\delta P_{jb}^{(-\mathrm{\Omega })}\right)+(\hslash {\omega }_{\alpha })M_{\alpha },$$ (A31)

$$-(\hslash \mathrm{\Omega })N_{\alpha }=\sum _{bj}\sqrt{\frac{\hslash {\omega }_{\alpha }}{2}}{\lambda }_{bj}^{\alpha }\left(\delta P_{bj}^{(\mathrm{\Omega })}+\delta P_{jb}^{(-\mathrm{\Omega })}\right)+(\hslash {\omega }_{\alpha })N_{\alpha },$$ (A32)

which are the photon portions of Eq. (8).

APPENDIX B: EQUATION-OF-MOTION DERIVATION

Below, we shall use an alternative approach, which is based on the equation-of-motion by transforming into a Heisenberg picture, to derive the same QED-TDDFT equation in Eq. (8).^109–111 Within this derivation, the split of q_α in Eq. (A22) will come naturally.

1. Unitary transformation of the electronic wavefunction

The electronic wavefunction evolves with a unitary transformation,

$$\left|\mathrm{\Phi }(t)\right.⟩=e^{-{\widehat{\mathrm{\Lambda }}}_{\text{e}}(t)}\left|{\mathrm{\Phi }}_0\right.⟩,$$ (B1)

$${\widehat{\mathrm{\Lambda }}}_{\text{e}}(t)=\sum _{ai}\left(-{\mathrm{\Theta }}_{ai}^{*}(t){\widehat{a}}_i^{†}{\widehat{a}}_a+{\mathrm{\Theta }}_{ai}(t){\widehat{a}}_a^{†}{\widehat{a}}_i\right).$$ (B2)

Using the following commutators:¹¹⁰

$$\left[{\widehat{a}}_a^{†}{\widehat{a}}_i,{\widehat{a}}_j^{†}{\widehat{a}}_b\right]={\delta }_{ij}{\widehat{a}}_a^{†}{\widehat{a}}_b-{\delta }_{ab}{\widehat{a}}_j^{†}{\widehat{a}}_i,$$ (B3)

$$\left[{\widehat{a}}_a^{†}{\widehat{a}}_i,{\widehat{a}}_b^{†}{\widehat{a}}_j\right]=\left[{\widehat{a}}_i^{†}{\widehat{a}}_a,{\widehat{a}}_j^{†}{\widehat{a}}_b\right]=0,$$ (B4)

one can find

$$\left[{\widehat{\mathrm{\Lambda }}}_{\text{e}},{\widehat{a}}_j^{†}{\widehat{a}}_b\right]=\sum _a{\mathrm{\Theta }}_{aj}(t){\widehat{a}}_a^{†}{\widehat{a}}_b-\sum _i{\mathrm{\Theta }}_{bi}(t){\widehat{a}}_j^{†}{\widehat{a}}_i,$$ (B5)

$$\left[{\widehat{\mathrm{\Lambda }}}_{\text{e}},{\widehat{a}}_b^{†}{\widehat{a}}_j\right]=\sum _a{\mathrm{\Theta }}_{aj}^{*}(t){\widehat{a}}_b^{†}{\widehat{a}}_a-\sum _i{\mathrm{\Theta }}_{bi}^{*}(t){\widehat{a}}_i^{†}{\widehat{a}}_j.$$ (B6)

Using the leading terms of the following Baker–Campbell–Hausdorff (BCH) expansion:

$$\begin{array}{ll}\hfill & e^{{\widehat{\mathrm{\Lambda }}}_{\text{e}}}\left({\widehat{a}}_j^{†}{\widehat{a}}_b+{\widehat{a}}_b^{†}{\widehat{a}}_j\right)e^{-{\widehat{\mathrm{\Lambda }}}_{\text{e}}}\hfill \\ \hfill & ={\widehat{a}}_j^{†}{\widehat{a}}_b+{\widehat{a}}_b^{†}{\widehat{a}}_j+\sum _a\left({\mathrm{\Theta }}_{aj}(t){\widehat{a}}_a^{†}{\widehat{a}}_b+{\mathrm{\Theta }}_{aj}^{*}(t){\widehat{a}}_b^{†}{\widehat{a}}_a\right)\hfill \\ \hfill & -\sum _i\left({\mathrm{\Theta }}_{bi}(t){\widehat{a}}_j^{†}{\widehat{a}}_i+{\mathrm{\Theta }}_{bi}^{*}(t){\widehat{a}}_i^{†}{\widehat{a}}_j\right)+\mathcal{O}({\mathrm{\Theta }}^2),\hfill \end{array}$$ (B7)

one finds

$$\begin{array}{ll}\hfill ⟨\mathrm{\Phi }(t)|\left({\widehat{a}}_j^{†}{\widehat{a}}_b+{\widehat{a}}_b^{†}{\widehat{a}}_j\right)|\mathrm{\Phi }(t)⟩& =⟨{\mathrm{\Phi }}_0|e^{{\widehat{\mathrm{\Lambda }}}_{\text{e}}}\left({\widehat{a}}_j^{†}{\widehat{a}}_b+{\widehat{a}}_b^{†}{\widehat{a}}_j\right)e^{-{\widehat{\mathrm{\Lambda }}}_{\text{e}}}|{\mathrm{\Phi }}_0⟩\hfill \\ \hfill & =-{\mathrm{\Theta }}_{bj}(t)-{\mathrm{\Theta }}_{bj}^{*}(t).\hfill \end{array}$$ (B8)

2. Unitary transformation of the photon wavefunction

Similarly, the photon wavefunction is also subjected to a unitary transformation [Eq. (26) in Ref. 97],

$$\left|\chi (t)\right.⟩=e^{-{\widehat{\mathrm{\Lambda }}}_{\text{ph}}(t)}\left|{\chi }_0\right.⟩,$$ (B9)

$${\widehat{\mathrm{\Lambda }}}_{\text{ph}}(t)=\sum _{\alpha }\left(-C_{\alpha }^{*}(t){\widehat{b}}_{\alpha }+C_{\alpha }(t){\widehat{b}}_{\alpha }^{†}\right).$$ (B10)

Using the commutators for bosons,

$$\left[{\widehat{b}}_{\alpha },{\widehat{b}}_{\beta }^{†}\right]={\delta }_{\alpha \beta },\left[{\widehat{b}}_{\alpha },{\widehat{b}}_{\beta }\right]=\left[{\widehat{b}}_{\alpha }^{†},{\widehat{b}}_{\beta }^{†}\right]=0,$$ (B11)

one gets

$$\left[{\widehat{\mathrm{\Lambda }}}_{\text{ph}},{\widehat{b}}_{\alpha }\right]=-C_{\alpha }(t),\left[{\widehat{\mathrm{\Lambda }}}_{\text{ph}},{\widehat{b}}_{\alpha }^{†}\right]=-C_{\alpha }^{*}(t).$$ (B12)

Accordingly, the following BCH expansions vanish after the first-order:

$$e^{{\widehat{\mathrm{\Lambda }}}_{\text{ph}}}{\widehat{b}}_{\alpha }{e}^{-{\widehat{\mathrm{\Lambda }}}_{\text{ph}}}={\widehat{b}}_{\alpha }-C_{\alpha }(t),$$ (B13)

$$e^{{\widehat{\mathrm{\Lambda }}}_{\text{ph}}}{\widehat{b}}_{\alpha }^{†}{e}^{-{\widehat{\mathrm{\Lambda }}}_{\text{ph}}}={\widehat{b}}_{\alpha }^{†}-C_{\alpha }^{*}(t).$$ (B14)

From this, one can compute

$$⟨\chi (t)|\left({\widehat{b}}_{\alpha }+{\widehat{b}}_{\alpha }^{†}\right)|\chi (t)⟩=-C_{\alpha }(t)-C_{\alpha }^{*}(t),$$ (B15)

$$\begin{array}{ll}\hfill ⟨\chi (t)|{\widehat{b}}_{\alpha }^{†}{\widehat{b}}_{\alpha }|\chi (t)⟩& =⟨{\chi }_0|\left(e^{{\widehat{\mathrm{\Lambda }}}_{\text{ph}}}{\widehat{b}}_{\alpha }^{†}{e}^{-{\widehat{\mathrm{\Lambda }}}_{\text{ph}}}\right)\left(e^{{\widehat{\mathrm{\Lambda }}}_{\text{ph}}}{\widehat{b}}_{\alpha }{e}^{-{\widehat{\mathrm{\Lambda }}}_{\text{ph}}}\right)|{\chi }_0⟩\hfill \\ \hfill & =C_{\alpha }(t)C_{\alpha }^{*}(t).\hfill \end{array}$$ (B16)

3. Pauli–Fierz energy components

The dipole moment operator can be written as

$$\widehat{\mathit{\mu }}={\mathit{\mu }}_0-\sum _{bj}{\mathit{\mu }}_{bj}\left({\widehat{a}}_j^{†}{\widehat{a}}_b+{\widehat{a}}_b^{†}{\widehat{a}}_j\right),$$ (B17)

$${\mathit{\lambda }}_{\alpha }\cdot \widehat{\mathit{\mu }}={\mathit{\lambda }}_{\alpha }\cdot {\mathit{\mu }}_0-\sum _{bj}{\lambda }_{bj}^{\alpha }\left({\widehat{a}}_j^{†}{\widehat{a}}_b+{\widehat{a}}_b^{†}{\widehat{a}}_j\right).$$ (B18)

The formulas suggest that the expectation value in the Pauli–Fierz Hamiltonian in Eq. (7) is

$$\begin{array}{ll}\hfill {\mathit{\lambda }}_{\alpha }\cdot 〈\widehat{\mathit{\mu }}〉& ={\mathit{\mu }}_0+〈\mathrm{\Delta }\widehat{\mathit{\mu }}〉={\mathit{\lambda }}_{\alpha }\cdot {\mathit{\mu }}_0-\sum _{bj}{\lambda }_{bj}^{\alpha }({\mathrm{\Theta }}_{bj}+{\mathrm{\Theta }}_{bj}^{*}),\hfill \end{array}$$ (B19)

where the ground-state dipole moment shifts the minimum of the quantum harmonic oscillator of the photon, ${\widehat{q}}_{\alpha }⟶{\widehat{q}}_{\alpha }-\frac{1}{{\omega }_{\alpha }}{\mathit{\lambda }}_{\alpha }\cdot {\mathit{\mu }}_0$. Then, the Pauli–Fierz Hamiltonian can be written as

$$\begin{array}{ccc}\hfill {\widehat{H}}_{\text{PF}}& =\hfill & {\widehat{H}}_{\text{elec}}(t)+\frac{1}{2}\sum _{\alpha =1}^M{\left({\mathit{\lambda }}_{\alpha }\cdot ⟨\mathrm{\Delta }\widehat{\mathit{\mu }}⟩\right)}^2-\sum _{\alpha =1}^M{\omega }_{\alpha }{\widehat{q}}_{\alpha }\left({\mathit{\lambda }}_{\alpha }\cdot ⟨\mathrm{\Delta }\widehat{\mathit{\mu }}⟩\right)\hfill \\ \hfill & \hfill & +\sum _{\alpha =1}^M\left[\frac{1}{2}{\widehat{p}}_{\alpha }^2+\frac{1}{2}{\omega }_{\alpha }^2{\widehat{q}}_{\alpha }^2\right]+\sum _{\alpha =1}^M\frac{j_{\alpha }(t)}{{\omega }_{\alpha }}{\widehat{q}}_{\alpha }.\hfill \end{array}$$ (B20)

With this Hamiltonian, the energy of the time-evolving wavefunction is

$$E_{\text{PF}}(\mathbf{\Theta },\mathbf{C})=⟨\chi (t)|⟨\mathrm{\Phi }(t)|{\widehat{H}}_{\text{PF}}|\chi (t)⟩|\chi (t)⟩.$$ (B21)

Its electronic component is^109–111

$$\begin{array}{ll}⟨\chi (t)|⟨\mathrm{\Phi }(t)|{\widehat{H}}_{\text{elec}}|\mathrm{\Phi }(t)⟩|\chi (t)⟩\hfill & =⟨\mathrm{\Phi }(t)|{\widehat{H}}_{\text{elec}}|\mathrm{\Phi }(t)⟩\hfill \\ \hfill & =E_0+\frac{1}{2}\sum _{ai,bj}\left({\mathrm{\Theta }}_{ai}^{*}{A}_{ai,bj}{\mathrm{\Theta }}_{bj}+{\mathrm{\Theta }}_{ai}{A}_{ai,bj}{\mathrm{\Theta }}_{bj}^{*}\right.\hfill \\ \hfill & +\left.{\mathrm{\Theta }}_{ai}{B}_{ai,bj}{\mathrm{\Theta }}_{bj}+{\mathrm{\Theta }}_{ai}^{*}{B}_{ai,bj}{\mathrm{\Theta }}_{bj}^{*}\right),\hfill \end{array}$$ (B22)

while the DSE contribution is

$$\begin{array}{ll}\hfill & ⟨\chi (t)|⟨\mathrm{\Phi }(t)|\frac{1}{2}\sum _{\alpha =1}^M{\left({\mathit{\lambda }}_{\alpha }\cdot ⟨\mathrm{\Delta }\widehat{\mathit{\mu }}⟩\right)}^2|\mathrm{\Phi }(t)⟩|\chi (t)⟩\hfill \\ \hfill & =\frac{1}{2}\sum _{ai,bj}{\mathrm{\Delta }}_{ai,bj}\left({\mathrm{\Theta }}_{ai}(t)+{\mathrm{\Theta }}_{ai}^{*}(t)\right)\left({\mathrm{\Theta }}_{bj}(t)+{\mathrm{\Theta }}_{bj}^{*}(t)\right),\hfill \end{array}$$ (B23)

which uses the expressions in Eqs. (B18) and (B8).

The electron–photon coupling energy is

$$\begin{array}{ll}\hfill & -⟨\chi (t)\left|⟨\mathrm{\Phi }(t)\left|\sum _{\alpha =1}^M,{\omega }_{\alpha },{\widehat{q}}_{\alpha },\left({\mathit{\lambda }}_{\alpha }\cdot ⟨\mathrm{\Delta }\widehat{\mathit{\mu }}⟩\right)\right|\mathrm{\Phi }(t)⟩\right|\chi (t)⟩\hfill \\ \hfill & =-\sum _{\alpha =1}^M{\omega }_{\alpha }⟨\chi (t)|{\widehat{q}}_{\alpha }|\chi (t)⟩⟨\mathrm{\Phi }(t)|\left({\mathit{\lambda }}_{\alpha }\cdot \mathrm{\Delta }\widehat{\mathit{\mu }}\right)|\mathrm{\Phi }(t)⟩\hfill \\ \hfill & =\sum _{\alpha ,bj}\sqrt{\frac{\hslash {\omega }_{\alpha }}{2}}\left[C_{\alpha }(t)+C_{\alpha }^{*}(t)\right]{\lambda }_{bj}^{\alpha }\left({\mathrm{\Theta }}_{bj}(t)+{\mathrm{\Theta }}_{bj}^{*}(t)\right),\hfill \end{array}$$ (B24)

which uses the definition of photon coordinate in Eq. (4) and the expression in Eq. (B15).

Finally, from Eq. (B16), the photon energy can be found to be

$$\begin{array}{ll}\hfill & ⟨\chi (t)\left|⟨\mathrm{\Phi }(t)\left|\sum _{\alpha =1}^M,\left[\frac{1}{2}{\widehat{p}}_{\alpha }^2+\frac{1}{2}{\omega }_{\alpha }^2{\widehat{q}}_{\alpha }^2\right]\right|\mathrm{\Phi }(t)⟩\right|\chi (t)⟩\hfill \\ \hfill & =\sum _{\alpha =1}^M⟨\chi (t)\left|\left[\frac{1}{2}{\widehat{p}}_{\alpha }^2+\frac{1}{2}{\omega }_{\alpha }^2{\widehat{q}}_{\alpha }^2\right]\right|\chi (t)⟩\hfill \\ \hfill & =\sum _{\alpha =1}^M\hslash {\omega }_{\alpha }⟨\chi (t)\left|\left[{\widehat{b}}_{\alpha }^{†}{\widehat{b}}_{\alpha }+\frac{1}{2}\right]\right|\chi (t)⟩\hfill \\ \hfill & =\sum _{\alpha =1}^M\hslash {\omega }_{\alpha }\left[C_{\alpha }(t)C_{\alpha }^{*}(t)+\frac{1}{2}\right].\hfill \end{array}$$ (B25)

Putting these together, we will get the following derivatives:

$$\begin{array}{ccc}\hfill \frac{\partial E_{\text{PF}}}{\partial {\mathrm{\Theta }}_{ai}}& =\hfill & \sum _{bj}\left[{\left(A+\mathrm{\Delta }\right)}_{ai,bj}{\mathrm{\Theta }}_{bj}^{*}(t)+{\left(B+\mathrm{\Delta }\right)}_{ai,bj}{\mathrm{\Theta }}_{bj}(t)\right]\hfill \\ \hfill & \hfill & +\hslash g_{ai}^{\alpha }\left[C_{\alpha }(t)+C_{\alpha }^{*}(t)\right],\hfill \end{array}$$ (B26)

$$\begin{array}{ccc}\hfill \frac{\partial E_{\text{PF}}}{\partial C_{\alpha }}& =\hfill & \sum _{bj}\hslash g_{bj}^{\alpha }\left({\mathrm{\Theta }}_{bj}(t)+{\mathrm{\Theta }}_{bj}^{*}(t)\right)+\hslash {\omega }_{\alpha }{C}_{\alpha }^{*}(t).\hfill \end{array}$$ (B27)

4. Equations-of-motion

Let us expand the Lagrangian to first-order,

$$\begin{array}{ccc}\hfill \mathcal{L}& =\hfill & ⟨\chi (t)\left|⟨\mathrm{\Phi }(t)\left|i,\hslash ,\frac{\partial }{\partial t},-,{\widehat{H}}_{\text{PF}}\right|\mathrm{\Phi }(t)⟩\right|\chi (t)⟩\hfill \\ \hfill & =\hfill & i\sum _{ai}{\mathrm{\Theta }}_{ai}^{*}(t)\frac{\partial }{\partial t}{\mathrm{\Theta }}_{ai}(t)+i\hslash \sum _{\alpha }{C}_{\alpha }^{*}(t)\frac{\partial }{\partial t}{C}_{\alpha }(t)\hfill \\ \hfill & \hfill & -E_{\text{PF}}(\mathbf{\Theta }(t),\mathbf{C}(t)).\hfill \end{array}$$ (B28)

The equation-of-motion for the orbital rotations is

$$-\frac{\partial }{\partial t}\left(\frac{\partial \mathcal{L}}{\partial {\dot{\mathrm{\Theta }}}_{ai}}\right)=-\frac{\partial \mathcal{L}}{\partial {\mathrm{\Theta }}_{ai}},$$ (B29)

namely,

$$-i\hslash \frac{\partial }{\partial t}{\mathrm{\Theta }}_{ai}^{*}=\frac{\partial E_{\text{PF}}}{\partial {\mathrm{\Theta }}_{ai}}.$$ (B30)

Let us parameterize the orbital rotations as

$${\mathrm{\Theta }}_{ai}(t)=X_{ai}{e}^{-i\mathrm{\Omega }t}+Y_{ai}{e}^{i\mathrm{\Omega }t},$$ (B31)

$${\mathrm{\Theta }}_{ai}^{*}(t)=X_{ai}{e}^{i\mathrm{\Omega }t}+Y_{ai}{e}^{-i\mathrm{\Omega }t}.$$ (B32)

and the photon phase change as

$$C_{\alpha }(t)=M_{\alpha }{e}^{-i\mathrm{\Omega }t}+N_{\alpha }{e}^{i\mathrm{\Omega }t},$$ (B33)

$$C_{\alpha }^{*}(t)=M_{\alpha }{e}^{i\mathrm{\Omega }t}+N_{\alpha }{e}^{-i\mathrm{\Omega }t}.$$ (B34)

Plugging in orbital rotation derivatives in Eq. (B26) and separating the e^iΩt and e^−iΩt terms in Eq. (B30), one gets the first two equations in Eq. (8),

$$\begin{array}{ll}\hfill \mathrm{\Omega }{X}_{ai}& =\sum _{bj}\left[{\left(A+\mathrm{\Delta }\right)}_{ai,bj}{X}_{bj}+{\left(B+\mathrm{\Delta }\right)}_{ai,bj}{Y}_{bj}\right]+\sum _{\alpha }\hslash g_{ai}^{\alpha }\left(M_{\alpha }+N_{\alpha }\right),\hfill \end{array}$$ (B35)

$$\begin{array}{ll}\hfill -\mathrm{\Omega }{Y}_{ai}& =\sum _{bj}\left[{\left(B+\mathrm{\Delta }\right)}_{ai,bj}{X}_{bj}+{\left(A+\mathrm{\Delta }\right)}_{ai,bj}{Y}_{bj}\right]+\sum _{\alpha }\hslash g_{ai}^{\alpha }\left(M_{\alpha }+N_{\alpha }\right).\hfill \end{array}$$ (B36)

The equation-of-motion for the photon phase is similar,

$$-i\hslash \frac{\partial }{\partial t}{C}_{\alpha }^{*}=\frac{\partial E_{\text{PF}}}{\partial C_{\alpha }},$$ (B37)

which, upon the insertion of the derivatives in Eq. (B27), leads to the last two equations in Eq. (8),

$$\mathrm{\Omega }{M}_{\alpha }=\sum _{bj}\hslash g_{bj}^{\alpha }{\left(X+Y\right)}_{bj}+\hslash {\omega }_{\alpha }{M}_{\alpha },$$ (B38)

$$-\mathrm{\Omega }{N}_{\alpha }=\sum _{bj}\hslash g_{bj}^{\alpha }{\left(X+Y\right)}_{bj}+\hslash {\omega }_{\alpha }{N}_{\alpha }.$$ (B39)

APPENDIX C: TWO-STATE AND THREE-STATE JC MODELS

Let us consider a two-level system made of |e₁⟩|0_α⟩ and |g⟩|1_α⟩, both of which have a resonance energy of ℏω. The two-state JC equation is

$$\left[\begin{array}{cc}\hfill \hslash \omega \hfill & \hfill s\hslash g_1\hfill \\ \hfill s\hslash g_1\hfill & \hfill \hslash \omega \hfill \end{array}\right]\left[\begin{array}{c}\hfill X_1\hfill \\ \hfill M\hfill \end{array}\right]=\hslash \mathrm{\Omega }\left[\begin{array}{c}\hfill X_1\hfill \\ \hfill M\hfill \end{array}\right],$$ (C1)

where a scaling factor s is added to track the perturbation order. Its solutions are known to be the lower and upper polaritons,

$$|1_{-}〉=\frac{1}{\sqrt{2}}|e_1〉|0_{\alpha }〉-\frac{1}{\sqrt{2}}|g〉|1_{\alpha }〉,$$ (C2)

$$|1_{+}〉=\frac{1}{\sqrt{2}}|e_1〉|0_{\alpha }〉+\frac{1}{\sqrt{2}}|g〉|1_{\alpha }〉,$$ (C3)

with the energies being

$$\hslash {\mathrm{\Omega }}_{1-}=\hslash \omega -s\hslash g_1,$$ (C4)

$$\hslash {\mathrm{\Omega }}_{1+}=\hslash \omega +s\hslash g_1,$$ (C5)

respectively.

Now, let us introduce a third state, |e₂⟩|0_α⟩, which has an energy of ℏω₂ and is well separated from the two polariton states. The corresponding three-state JC equation is

$$\left[\begin{array}{ccc}\hfill \hslash {\omega }_2\hfill & \hfill 0\hfill & \hfill s\hslash g_2\hfill \\ \hfill 0\hfill & \hfill \hslash \omega \hfill & \hfill s\hslash g_1\hfill \\ \hfill s\hslash g_2\hfill & \hfill s\hslash g_1\hfill & \hfill \hslash \omega \hfill \end{array}\right]\left[\begin{array}{c}\hfill X_2\hfill \\ \hfill X_1\hfill \\ \hfill M\hfill \end{array}\right]=\hslash {\mathrm{\Omega }}^{\prime }\left[\begin{array}{c}\hfill X_2\hfill \\ \hfill X_1\hfill \\ \hfill M\hfill \end{array}\right].$$ (C6)

Upon switching to the basis of $\left[|e_2〉|0_{\alpha }〉,|1_{+}〉,|1_{-}〉\right]$, the three-state JC equation becomes

$$\left[\begin{array}{ccc}\hfill \hslash {\omega }_2\hfill & \hfill \frac{s\hslash g_2}{\sqrt{2}}\hfill & \hfill -\frac{s\hslash g_2}{\sqrt{2}}\hfill \\ \hfill \frac{s\hslash g_2}{\sqrt{2}}\hfill & \hfill \hslash \omega +s\hslash g_1\hfill & \hfill 0\hfill \\ \hfill -\frac{s\hslash g_2}{\sqrt{2}}\hfill & \hfill 0\hfill & \hfill \hslash \omega -s\hslash g_1\hfill \end{array}\right]\left[\begin{array}{c}\hfill X_2\hfill \\ \hfill P_{1+}\hfill \\ \hfill P_{1-}\hfill \end{array}\right]=\hslash {\mathrm{\Omega }}^{\prime }\left[\begin{array}{c}\hfill X_2\hfill \\ \hfill P_{1+}\hfill \\ \hfill P_{1-}\hfill \end{array}\right].$$ (C7)

We can get the second-order perturbation to the energy of upper and lower polaritons as

$$\hslash {\mathrm{\Omega }}_{1-}^{\prime }=\hslash \omega -s\hslash g_1-\frac{\frac{1}{2}{s}^2{\hslash }^2{g}_2^2}{\hslash {\omega }_2-(\hslash \omega -s\hslash g_1)}+\cdots ,$$ (C8)

$$\hslash {\mathrm{\Omega }}_{1+}^{\prime }=\hslash \omega +s\hslash g_1-\frac{\frac{1}{2}{s}^2{\hslash }^2{g}_2^2}{\hslash {\omega }_2-(\hslash \omega +s\hslash g_1)}+\cdots .$$ (C9)

To the second-order of s, we, thus, have

$$\hslash {\mathrm{\Omega }}_{1-}^{\prime }=\hslash \omega -s\hslash g_1-s^2\frac{{\hslash }^2{g}_2^2}{2(\hslash {\omega }_2-\hslash \omega )}+\mathcal{O}(s^3),$$ (C10)

$$\hslash {\mathrm{\Omega }}_{1+}^{\prime }=\hslash \omega +s\hslash g_1-s^2\frac{{\hslash }^2{g}_2^2}{2(\hslash {\omega }_2-\hslash \omega )}+\mathcal{O}(s^3).$$ (C11)

Within the perturbation theory, the lower polariton wavefunction becomes

$$\begin{array}{ll}\hfill {|1_{-}〉}^{\prime }& ={|1_{-}〉}^{(0)}+{|1_{-}〉}^{(1)}+{|1_{-}〉}^{(2)}+\cdots \hfill \\ \hfill & =|1_{-}〉+\frac{-s\hslash g_2/\sqrt{2}}{(\hslash \omega -s\hslash g_1)-\hslash {\omega }_2}|e_2〉|0_{\alpha }〉\hfill \\ \hfill & +\frac{-\frac{1}{2}{s}^2{\hslash }^2{g}_2^2}{(-2s\hslash g_1)\left[(\hslash \omega -s\hslash g_1)-\hslash {\omega }_2\right]}|1_{+}〉+\cdots .\hfill \end{array}$$ (C12)

Sustituting the expressions in Eqs. (C2) and (C3) and truncating at the first-order of s, one gets

$$\begin{array}{ccc}\hfill {|1_{-}〉}^{\prime }& =\hfill & -\frac{1}{\sqrt{2}}\left(1+\frac{s{g}_2^2}{4g_1({\omega }_2-\omega )}\right)|g〉|1_{\alpha }〉\hfill \\ \hfill & \hfill & +\frac{1}{\sqrt{2}}\left(1-\frac{s{g}_2^2}{4g_1({\omega }_2-\omega )}\right)|e_1〉|0_{\alpha }〉\hfill \\ \hfill & \hfill & +\frac{s{g}_2}{\sqrt{2}({\omega }_2-\omega )}|e_2〉|0_{\alpha }〉+\mathcal{O}(s^2).\hfill \end{array}$$ (C13)

Similarly, the perturbed upper polariton wavefunction is

$$\begin{array}{ccc}\hfill {|1_{+}〉}^{\prime }& =\hfill & \frac{1}{\sqrt{2}}\left(1-\frac{s{g}_2^2}{4g_1({\omega }_2-\omega )}\right)|g〉|1_{\alpha }〉\hfill \\ \hfill & \hfill & +\frac{1}{\sqrt{2}}\left(1+\frac{s{g}_2^2}{4g_1({\omega }_2-\omega )}\right)|e_1〉|0_{\alpha }〉\hfill \\ \hfill & \hfill & -\frac{s{g}_2}{\sqrt{2}({\omega }_2-\omega )}|e_2〉|0_{\alpha }〉+\mathcal{O}(s^2).\hfill \end{array}$$ (C14)

The corresponding transition dipole moments are

$$\begin{array}{ccc}\hfill {\mathit{\mu }}_{-}^{\prime }& =\hfill & 〈g|〈0_{\alpha }|\mathit{\mu }{|1_{+}〉}^{\prime }=\frac{1}{\sqrt{2}}\left(1-\frac{s{g}_2^2}{4g_1({\omega }_2-\omega )}\right){\mathit{\mu }}_1\hfill \\ \hfill & \hfill & +\frac{s{g}_2}{\sqrt{2}({\omega }_2-\omega )}{\mathit{\mu }}_2+\mathcal{O}(s^2),\hfill \end{array}$$ (C15)

$$\begin{array}{ccc}\hfill {\mathit{\mu }}_{+}^{\prime }& =\hfill & 〈g|〈0_{\alpha }|\mathit{\mu }{|1_{+}〉}^{\prime }=\frac{1}{\sqrt{2}}\left(1+\frac{s{g}_2^2}{4g_1({\omega }_2-\omega )}\right){\mathit{\mu }}_1\hfill \\ \hfill & \hfill & -\frac{s{g}_2}{\sqrt{2}({\omega }_2-\omega )}{\mathit{\mu }}_2+\mathcal{O}(s^2).\hfill \end{array}$$ (C16)

If larger coupling occurs with the second-excited state of the gas-phase molecule (g₂ ≫ g₁), the upper polariton |1₊⟩ (at small s values) gradually loses photon contributions as the s values increase and the coupling between other states becomes more dominant. In the limit that M approaches zero, its corresponding eigenvector in Eq. (C6) becomes ${(X_2,X_1,0)}^{\text{T}}$. The third equation of Eq. (C6) requires that X₂g₂ + X₁g₁ = 0 or X₂/X₁ = −g₁/g₂. For this state without any photon character, the normalized eigenvector is, thus,

$$\underset{g_2\gg g_1,s\gg 0}{\lim }{|1_{+}〉}^{\prime }=\frac{g_2}{g_1^2+g_2^2}|e_1〉|0_{\alpha }〉-\frac{g_1}{g_1^2+g_2^2}|e_2〉|0_{\alpha }〉,$$ (C17)

with the energy being

$$\underset{g_2\gg g_1,s\gg 0}{\lim }{\mathrm{\Omega }}_{1_{+}}^{\prime }=\omega +\frac{g_1^2({\omega }_2-\omega )}{g_1^2+g_2^2}.$$ (C18)

DATA AVAILABILITY

The data that support the findings of this study are available from the corresponding author upon reasonable request. The code implementation will be made available through PySCF and Q-Chem.