Synergistic Organization of Neural Inputs from Spinal Motor Neurons to Extrinsic and Intrinsic Hand Muscles

Abstract

Our current understanding of synergistic muscle control is based on the analysis of muscle activities. Modules (synergies) in muscle coordination are extracted from electromyographic (EMG) signal envelopes. Each envelope indirectly reflects the neural drive received by a muscle; therefore, it carries information on the overall activity of the innervating motor neurons. However, it is not known whether the output of spinal motor neurons, whose number is orders of magnitude greater than the muscles they innervate, is organized in a low-dimensional fashion when performing complex tasks. Here, we hypothesized that motor neuron activities exhibit a synergistic organization in complex tasks and therefore that the common input to motor neurons results in a large dimensionality reduction in motor neuron outputs. To test this hypothesis, we factorized the output spike trains of motor neurons innervating 14 intrinsic and extrinsic hand muscles and analyzed the dimensionality of control when healthy individuals exerted isometric forces using seven grip types. We identified four motor neuron synergies, accounting for >70% of the variance of the activity of 54.1 ± 12.9 motor neurons, and we identified four functionally similar muscle synergies. However, motor neuron synergies better discriminated individual finger forces than muscle synergies and were more consistent with the expected role of muscles actuating each finger. Moreover, in a few cases, motor neurons innervating the same muscle were active in separate synergies. Our findings suggest a highly divergent net neural inputs to spinal motor neurons from spinal and supraspinal structures, contributing to the dimensionality reduction captured by muscle synergies.

SIGNIFICANCE STATEMENT We addressed whether the output of spinal motor neurons innervating multiple hand muscles could be accounted for by a modular organization, i.e., synergies, previously described to account for the coordination of multiple muscles. We found that motor neuron synergies presented similar dimensionality (implying a >10-fold reduction in dimensionality) and structure as muscle synergies. Nonetheless, the synergistic behavior of subsets of motor neurons within a muscle was also observed. These results advance our understanding of how neuromuscular control arises from mapping descending inputs to muscle activation signals. We provide, for the first time, insights into the organization of neural inputs to spinal motor neurons which, to date, has been inferred through analysis of muscle synergies.

Introduction

It has been suggested that neuromuscular control might be mediated by modular organization of descending neural inputs. This modular control, embedded within the spinal cord, underlies elementary functional muscle coordination patterns, whose combination allows for the generation of a large number of movements (for review, see Bizzi and Cheung, 2013; d'Avella et al., 2015; Flash and Bizzi, 2016). The muscle coordination prescribed by spinal modules is associated with invariant muscle activation patterns identified by electromyographic (EMG) recordings, i.e., muscle synergies (Bizzi et al., 2008). Muscle synergies have been identified in several species (Bizzi et al., 2008), e.g., by microstimulation of the spinal cord in frogs (Saltiel et al., 2001) and in non-human primates (Takei et al., 2017). In humans, muscle synergies have been identified in a variety of multijoint tasks, such as during early locomotion in newborn infants (Dominici et al., 2011), standing (Torres-Oviedo and Ting, 2007), walking (Ivanenko et al., 2004; Chvatal and Ting, 2013), reaching (d'Avella et al., 2006), and during hand gestures and manipulation (Weiss and Flanders, 2004; Ajiboye and Weir, 2009).

Muscle synergies have been traditionally quantified in humans by dimensionality-reduction techniques applied to EMG amplitudes (envelopes) from multiple muscles (Tresch et al., 2006). The EMG amplitude indirectly reflects the overall activity of the motor neurons innervating the muscle. Therefore, by averaging the activity of all innervating motor neurons, the EMG envelopes recorded from multiple muscles constrain the dimensionality of control of a muscle to a maximum of one. However, the number of spinal motor neurons is orders of magnitude greater than the number of muscles. Therefore, correlation in EMG amplitudes across muscles might not necessarily capture the correlation of activity among motor neurons innervating those muscles (Del Vecchio et al., 2019). It is also possible that subsets of motor neurons within the same motor pool may not share the same neural inputs. However, the dimensionality of control of populations of motor neurons innervating multiple muscles in complex tasks is currently unknown.

Neural activity of motor neuron pools innervating one or more muscles can be observed using invasive and non-invasive recording techniques (Winges et al., 2008; Muceli et al., 2015; Farina et al., 2016; Negro et al., 2016b). Previous studies that have analyzed motor neuron spiking activity from individual muscles have shown that motor neurons in a motor pool receive a relatively large amount of common synaptic input (Negro and Farina, 2011; Negro et al., 2016a). The input shared across pools of motor neurons innervating different muscles has been rarely assessed and only for pairs of muscles in simple tasks (Laine et al., 2015; De Luca and Erim, 2002). Common input across two pools of motor neurons has been observed (Laine et al., 2015; De Luca and Erim, 2002; Del Vecchio et al., 2019) but not across tasks and not in relation to the dimensionality of control across several motor neuron pools. These previous observations led us to hypothesize that motor neuron activities should show a synergistic organization in multijoint tasks. Consequently, we expected that the common input to motor neurons, for which there is preliminary evidence in single tasks and muscles, should result in a large dimensionality reduction in motor neuron outputs. If true, the dimensionality of motor neuron control across multiple task conditions would be equal or lower than the number of pools of motor neurons. Here, we tested this hypothesis by quantifying the synergistic organization of motor neuron output by factorization. Specifically, we decoded the activity of motor neurons innervating several hand muscles while human participants exerted isometric forces with different grip types. We then identified the components explaining the variance of the motor neuron outputs, which we will refer to as motor neuron synergies. To gain further insight into the functional role of motor neuron synergies, we compared them with synergies extracted from EMG amplitudes, i.e., muscle synergies. Moreover, we compared the dimensionality of motor neuron output to that of muscle control, identified from EMG amplitudes.

Materials and Methods

Subjects

Seven men (age: 27.0 ± 2.2 years; weight: 79.0 ± 8.3 kg; height: 180.1 ± 5.0 cm) participated in the experiments after signing an informed consent form in accordance with the Declaration of Helsinki and approved by the Imperial College London Research Ethics Committee (approval 18IC4685).

Experimental protocol

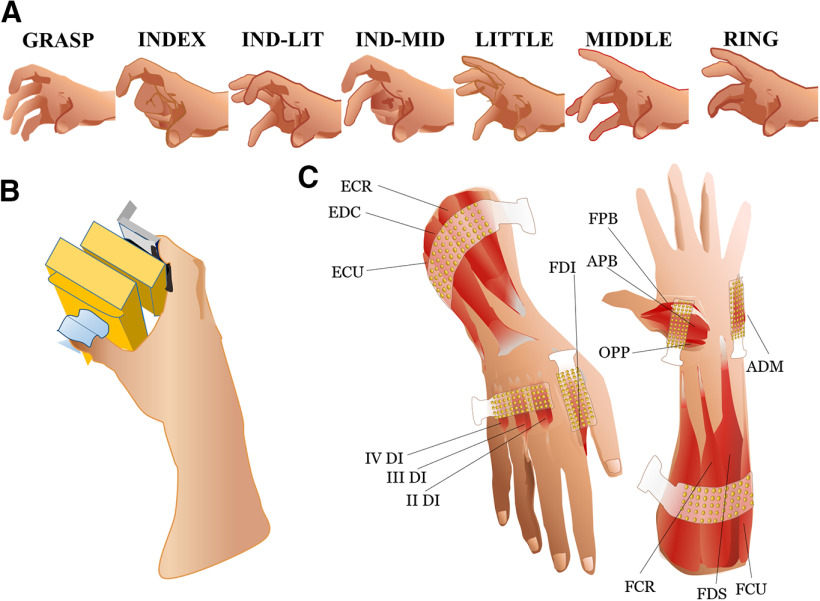
Subjects sat with the wrist kept in a neutral position, the forearm semi-pronated, and the elbow flexed (∼90°). They were asked to exert isometric fingertip forces to perform seven grip types (Fig. 1A) by making contact with (1) all digits (GRASP), or the thumb in opposition to (2) the index and middle fingers (IND-MID); (3) the index and little fingers (IND-LIT), and (4–7) each finger in isolation (INDEX, MIDDLE, RING, and LITTLE). The maximum voluntary contraction (MVC) force was measured for each grip and used as reference to determine the submaximal target force in subsequent trials. Following the MVCs, the subjects were instructed to match sinusoidal force traces. For each grip type (trial), the task consisted of a 30-s sinusoidal contraction at 15 ± 5% MVC at 1-Hz frequency, which was preceded and followed by a 5-s ramp contraction to reach the target force (15% MVC) and return to rest. A rest of 2 min was given between trials.

Figure 1.

Experimental setup and grip types. A, Subjects exerted sinusoidal isometric forces using seven grip types: all digits (GRASP), thumb in opposition to the index and middle fingers (IND-MID), index and little fingers (IND-LIT), and thumb in opposition to each finger in isolation (INDEX, MIDDLE, RING, and LITTLE, respectively). B, Hand posture grasping the sensorized grip device used for the experiment. C, Electrode placement for HD-sEMG recordings using six 13 × 5-electrode grids (total of 384 channels). Two larger grids (8-mm IED) were placed over the extensor and flexor extrinsic muscles of the hand. The grid on the dorsal side of the forearm was positioned to detect EMG signals from the ECU, the EDC, and the ECR muscles. The grid on the volar side of the forearm was positioned to detect EMG signals from the FCU, the flexor FDS and the FCR muscles. The four smaller grids (4-mm IED) were placed over the FDI, the other three dorsal interossei (II–IV DI), the ADM muscles, and the three thenar muscles: OPP, FPB, and APB.

Experimental setup

The subjects exerted isometric forces for each grip type while the forearm rested on a 3D-printed mold to prevent changes in arm posture as well as in elbow and wrist joint angles. A 3D-printed sensorized device with two plastic handles was used to record grip force. A coaxial force/torque sensor (ATI Industrial Automation) was mounted on each handle (Fig. 1B) to record, respectively, the force exerted by the thumb and the force exerted by the combination of the finger(s) in opposition with the thumb, depending on the grip type. Force signals were digitized by a 12-bit A/D converter (ADC) board (sampling frequency: 2048 Hz; PCI-6225, National Instruments).

We recorded EMG signals from 14 muscles controlling the wrist and digits using high-density surface EMG electrode grids (HD-sEMG; Fig. 1C). Two 64-channel grids (with electrodes arranged in a 13 × 5 configuration and one electrode missing at the corner) with 8-mm interelectrode distance (IED) were placed over the extrinsic extensor muscles of the hand, i.e., extensor carpi ulnaris (ECU), extensor digitorum communis (EDC) and extensor carpi radialis (ECR), and over the extrinsic flexor muscles, i.e., flexor carpi ulnaris (FCU), flexor digitorum superficialis (FDS), and flexor carpi radialis (FCR). Four additional 64-channel grids (with the same electrode configuration but IED of 4 mm) were placed over the first dorsal interosseus (FDI), three other dorsal interossei (II–IV DI), the abductor digiti minimi (ADM) and the three muscles of the thenar eminence: opponens pollicis (OPP), abductor pollicis brevis (APB), and flexor pollicis brevis (FPB). Since four of these six grids covered more than one muscle, we used a muscle assignment procedure to identify the correspondence between identified motor neurons and muscles (see below, Motor neuron synergy anatomic maps).

EMG signals from the six electrode grids were recorded in monopolar derivation by a 400-channels amplifier (Quattrocento, OT Bioelettronica). Signals were amplified with a gain of 150, bandpass filtered between 10 and 900 Hz, sampled at 2048 Hz, and A/D converted to 16 bits. A reference electrode was placed at the wrist. EMG and force data were recorded with the same computer and synchronized offline by means of a trigger signal sent from the force ADC board to the EMG amplifier. A custom-made application developed in MATLAB (The MathWorks) was used to inspect the signals, display the target force on a monitor in front of the subjects, and provide them with visual feedback of the force exerted during the task.

Processing

The primary goal of the present study was to quantify the spatial and temporal organization of the output of motor neurons innervating extrinsic and intrinsic hand muscles. We pursued this objective by first decomposing EMG signals recorded through HD-sEMG grids (Fig. 1C) into motor neuron discharges. This procedure was followed by the application of non-negative matrix factorization (NMF; see below, Synergy extraction by NMF) to the series of motor neuron discharges. Application of NMF to motor neuron discharge patterns across grip types allowed to compute motor neuron synergies (Fig. 2A). The same NMF procedure was also applied to interference EMG signals to extract muscle synergies (Fig. 2A). To assess a correspondence between motor neuron synergies and muscle synergies, we need to answer the question whether motor neurons innervating the same muscle might have alternative synergistic behaviors, i.e., if multiple groups of motor neurons innervating the same muscle are alternatively activated in different motor neuron synergies.

Figure 2.

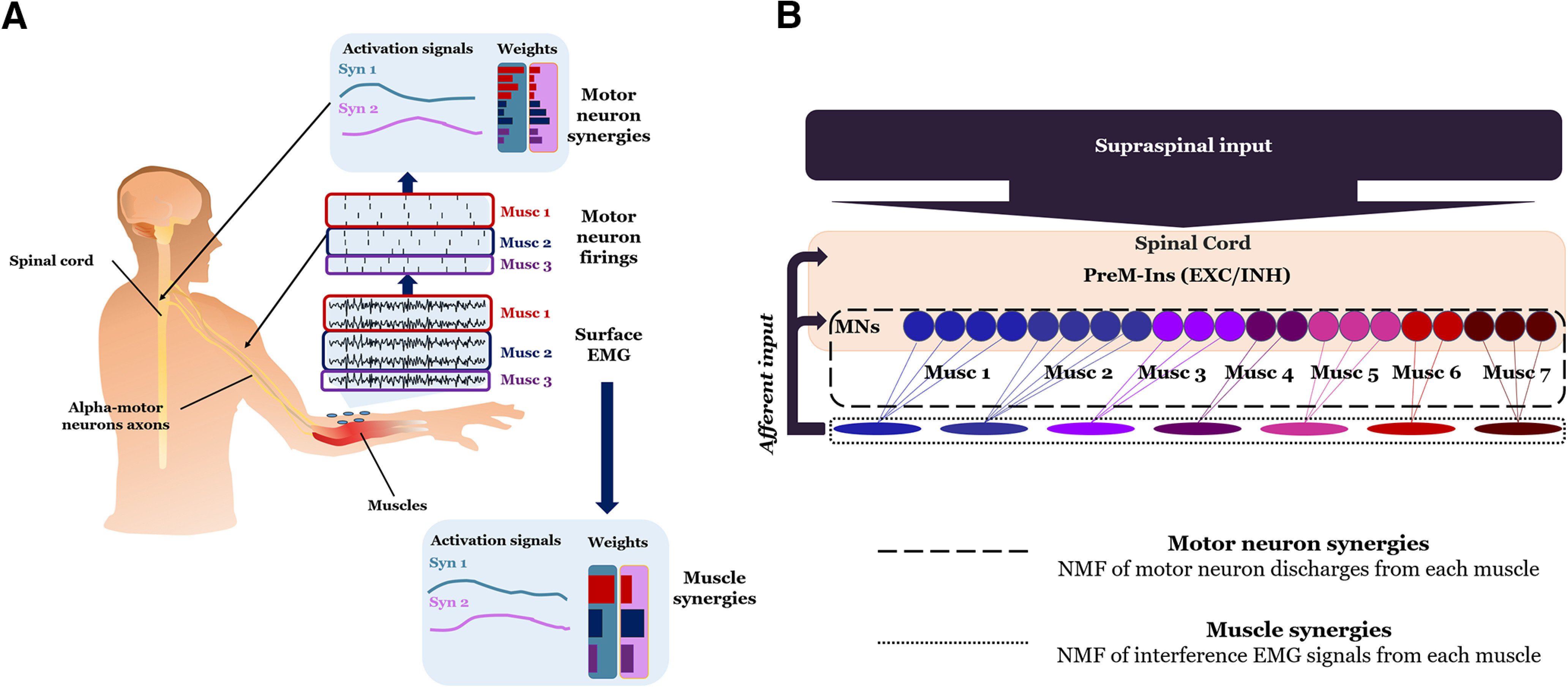
Experimental approaches for estimating motor neuron and muscle synergies. A, Extraction of motor neuron discharges from HD-sEMG used for computing motor neuron synergies. Muscle synergies were computed using the interference EMG signals (in figure represented for three muscles, respectively, red, blue, and violet). Motor neuron synergy weights represent the contribution of motor neurons into each synergy. Muscle synergy weights represent the contribution of individual muscles. B, The diagram shows how individual excitatory (EXC) and inhibitory (INH) PreM-INs synapse onto multiple motor neurons (MNs) innervating different muscles. Motor neuron pools are denoted by different colors. The computation of motor neuron synergies estimates how the discharges of concurrently active motor neurons can be grouped based on the spatial and temporal spiking patterns (dashed line box). In contrast, muscle synergies are computed based on the spatial and temporal coordination of interference EMG activity patterns (dotted line box).

The difference in the information provided by NMF applied to extract motor neuron synergies relative to muscle synergies is shown in Figure 2B. The synergistic organization of motor neuron activity (motor neuron synergies) is hypothesized to depend on the extent to which direct and indirect corticospinal inputs might spatially and temporally constrain their output to multiple muscles. For the case of indirect corticospinal inputs, i.e., inputs mediated by premotor interneurons (PreM-INs), each motor neuron can receive inputs from several PreM-INs. The final output of this spatiotemporal spinal constraint can be directly observed with motor neuron synergies. In contrast, extraction of muscle synergies considers the spatial and temporal organization of interference EMG from individual muscles. The rationale and advantages of extracting motor neuron synergies relative to muscle synergies are described below (see below, EMG signal decomposition).

For each grip type and both types of myoelectric features factorized by NMF (motor neuron discharges and interference EMG), we selected the central 10-s portion of the sinusoidal force production for further analysis and excluded the first and the last 10-s portion of the trial because of the transition from the ramp to the sinusoidal force production, and from the latter to zero force. EMG data from each grip type was bandpass filtered so that there was no difference in offset among different recordings and the transitory part for the filtering was removed to avoid signal discontinuities. Then, these recordings were concatenated to provide a 70-s long signal (10 s for each grip type; Fig. 3A) consisting of 384 EMG channels. EMG signals were digitally filtered between 20 and 500 Hz with a fourth-order Butterworth filter to remove baseline drifts and high frequency noise. Preprocessed EMG data underwent a series of nonlinear and linear operations that differed for the computation of motor neuron synergies or muscle synergies (Fig. 3). For the computation of muscle synergies, we extracted 14 bipolar channels from monopolar HD-sEMG channels, one for each muscle (explained in detail below, Synergy extraction by NMF), to reduce cross talk. Then, we applied rectification (converting negative to positive values) of interference EMG signals (Fig. 3B).

Figure 3.

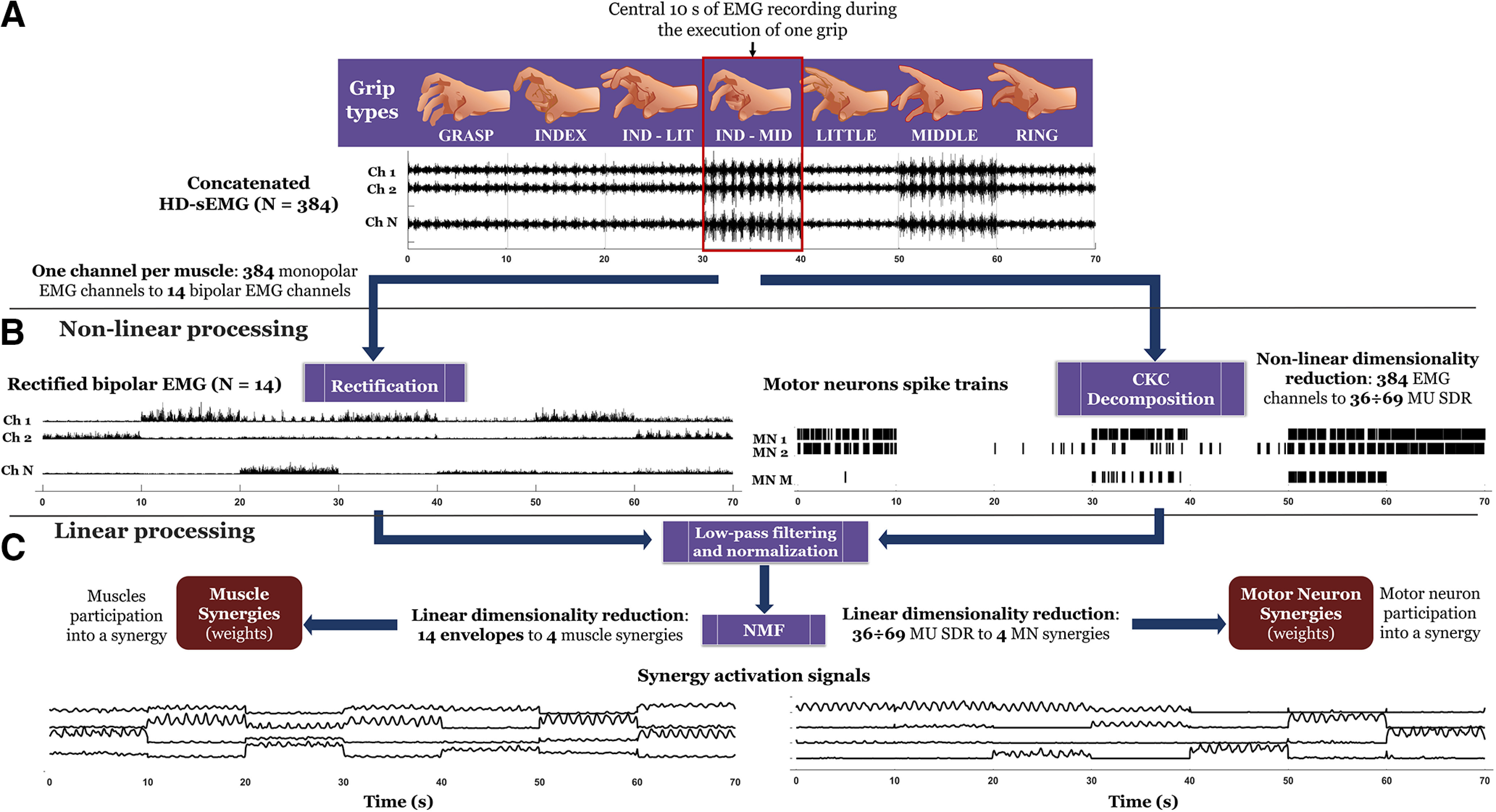
EMG signal processing, decomposition and dimensionality reduction. For each grip type (top), the central 10 s of EMG recordings was concatenated to obtain 70-s long EMG signals (10 s per grip type). These concatenated monopolar signals were either differentiated (selection of one bipolar channel per muscle; see Fig. 4A) and rectified or decomposed with the CKC algorithm into motor neuron spike trains. Both rectification and CKC are nonlinear operations. Additionally, CKC reduces the dimensionality of the original signals. The results of these two nonlinear operations were low-pass filtered to generate smooth myoelectric signals with a bandwidth of 2.5 Hz. The two smoothed signals were factorized using NMF to extract muscle synergies (where one channel is related to a muscle) and motor neuron synergies, respectively. NMF is a linear dimensionality reduction operation.

EMG signal decomposition

To enable computation of motor neuron synergies, we applied convolution kernel compensation (CKC) motor unit decomposition (Fig. 3B; see below, Synergy extraction by NMF) to obtain the correspondent neural command received by each motor unit from the respective innervating motor neuron. The HD-sEMG signals were decomposed separately for each grid into the constituent motor unit activities by the CKC algorithm (Holobar and Zazula, 2007) to obtain the firing output of the respective motor neurons. To assess the accuracy of motor unit identification from HD-sEMG, we adopted the pulse-to-noise ratio (PNR; Holobar et al., 2014) as a signal-based metrics. The motor unit innervation pulse trains (Holobar and Zazula, 2007) extracted by the algorithm were manually inspected by experts. This inspection led to rejecting all the motor units with PNR lower than 25 dB, corresponding to a confidence interval of 0–70%, discarding the false-positive peaks over the physiological firing rate (35–40 Hz), and including false-negative undetected peaks (Del Vecchio et al., 2020). To identify the same motor neuron across different grip types, motor neurons were tracked across all grip types by decomposing the concatenated EMG signals from all tasks for each subject. By doing so, the decomposition algorithm identified the activity of the same motor unit (thus, the same motor neuron) when it fired in one or more grip types. To evaluate the capacity of the decomposition algorithm to identify the same motor units across different grip types despite the variability in the level of muscle contraction, an analysis based on spike-triggered averaging (STA) was conducted. For each subject, we performed a STA for each motor unit and for each grip type to estimate the motor unit action potential waveforms. We then computed the 2D cross-correlation between these estimated action potential waveforms (Martinez-Valdes et al., 2017) both for the same motor unit (across different grip types) and for different motor units (for each grip type separately). The aim of this analysis was to prove the stability of the estimated action potential waveforms across different tasks and the fact that motor unit action potentials assigned to the same motor unit were more similar than action potentials assigned to different motor units. Similar analyses have been proposed in previous work for validating the tracking of motor units by EMG decomposition across a variety of conditions (see Del Vecchio et al., 2019).

A binary sequence was created to represent each spike train, with 1 indicating the occurrence of a spike and 0 otherwise, having the length of the original EMG signals. The binary sequence of spikes for each detected motor unit was smoothed by a fourth-order Butterworth low-pass filter with cutoff frequency of 2.5 Hz and then normalized between 0 and 1. This frequency bandwidth corresponds to the one obtained using a 400-ms Hanning window, as done in previous work (De Luca et al., 1982; Negro et al., 2009). The smoothed discharge rates (SDRs) provide an estimation of the instantaneous firing rate (De Luca et al., 1982) for each motor unit. We used sinusoidal contractions to focus on the modulation of motor neuron discharge rates rather than the average baseline value. We note that the baseline of the sinusoidal SDR signals would be determined by the average discharge rates, whereas motor neuron discharge rate oscillations around the average value would be determined by the modulation in discharge rates.

A motor neuron was considered active for a given grip type when discharging at least 20 firings in the 10-s interval analyzed. The percentage of motor neurons active in two tasks was quantified for each task pair.

Synergy extraction by NMF

To test the hypothesis of a low-dimensional representation of motor neuron activity, we factorized motor neuron SDRs and interference EMG envelopes using NMF (Fig. 3C). We will use the term motor neuron synergies to indicate the time-invariant weights extracted by factorization of motor neuron SDRs and muscle synergies to indicate the weights identified with the same factorization applied to 14 interference EMG envelopes (one per muscle). To select the bipolar EMG channels for each muscle to compute muscle synergies (Bizzi et al., 2008; Cheung et al., 2009), we divided the electrode grids placed over the extrinsic muscles, the DI, and the thenar eminence (Fig. 4A) in bands of four, five, and four columns, consisting of five channels each. This subdivision was made by assuming the main three muscles under each grid were roughly equally represented in terms of channels. This assumption was based on the standardized placement of the electrode grids according to anatomic landmarks, as previously described (Tanzarella et al., 2020). This muscle assignment was used exclusively to extract bipolar EMG signals for a comparison with muscle synergy weights and for the anatomic map representation (see below, Motor neuron synergy anatomic maps). We note that this muscle assignment procedure was not required by nor impacts the NMF analysis because motor neurons from all the muscles were factorized as a unique pool (i.e., without grouping). By adopting this division in bands, the central pair of electrodes of each band was chosen to compute the bipolar derivation, so that for both the small (4-mm IED) and large grids (8-mm IED) the equivalent bipolar IED was 16 mm. The bipolar EMG signals were then rectified and smoothed with the same filter applied to the motor neuron SDR.

Figure 4.

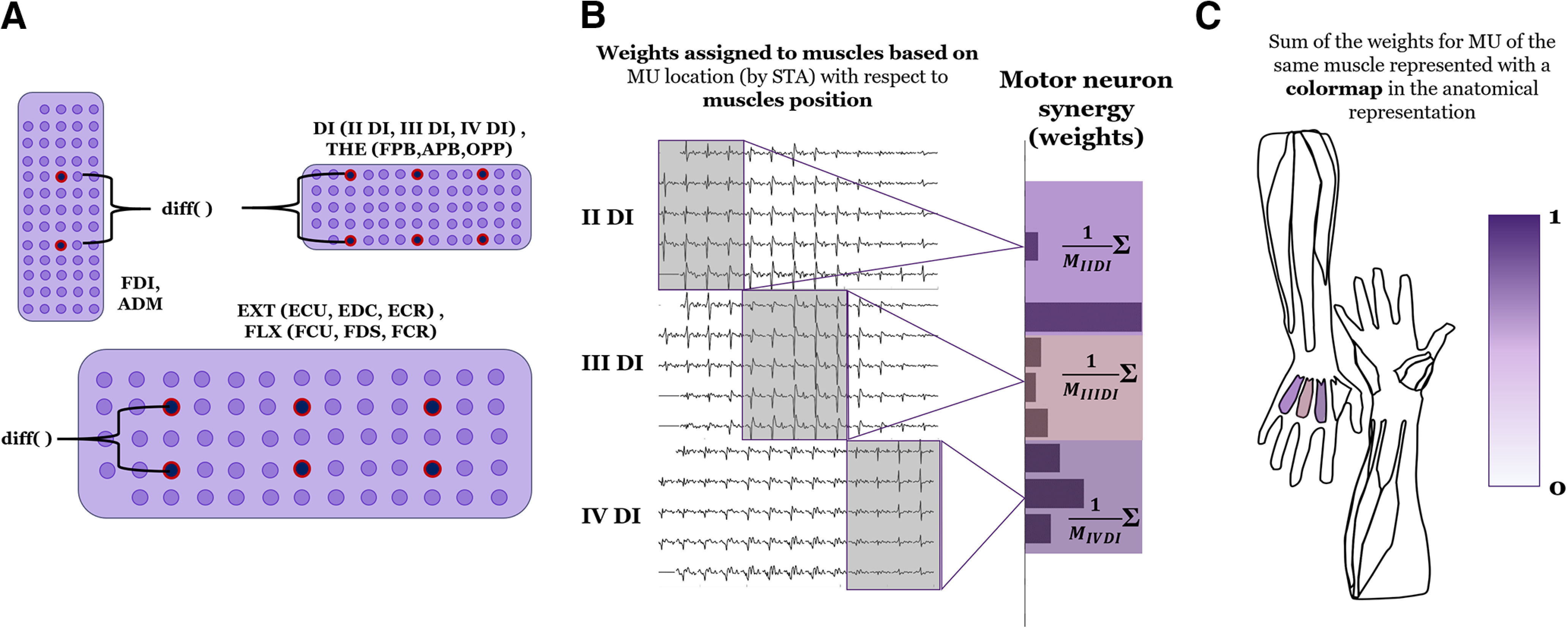
Methods to obtain bipolar EMG channels and anatomic representation of hand motor neuron synergies and muscle synergies. A, Extraction of one 16 mm-IED bipolar channel for each of the 14 investigated muscle compartments for all six electrode grids used to compute muscle synergies. B, Each motor neuron is identified by STA (left) and associated with one of the muscles under the same grid (for FDI and ADM, there was only one muscle per grid). Here, we show the example of the interossei grid. For each synergy, the motor neuron weights associated with a certain muscle were averaged and this average corresponded to a muscle activity. C, Muscle activity is represented with a color scale and normalized from 0 to 1, indicating muscle activation in an anatomic representation.

Let X be the original matrix, where the M rows represent the SDRs of motor neurons (alternatively N rows represent the 14 EMG envelopes), and the L columns represent the time samples of the original motor neuron or EMG signal. The NMF factorization represents X as follows (Lee and Seung, 2001):

$$X\approx WH,$$

where W is the matrix of the synergies, with dimension M × S (N × S for EMG envelopes), and H is the matrix of the activation signals, with dimension S × L, with S being the number of extracted synergies. While the time-invariant W represents, for each column, how a motor neuron (muscle) contributes to a synergy, H contains the time-varying activation of each synergy during isometric force production for each grip type.

NMF is an iterative process that minimizes the Euclidean distance between the original signals X and the reconstruction obtained by the multiplication of the matrices W and H. In this study, the NMF iterations were repeated 10 times (Cheung et al., 2009) for each number of extracted synergy, i.e., from 1 to 10 synergies, with different initial random values for the matrices W and H.

We note that the extraction of motor units from the EMG signal may remove variance from the data that could be potentially informative about synergistic motor neuron control. To address this issue, we repeated the same analysis of extraction of muscle synergies both from the EMG signal derived only from the decomposed motor units and from the residual EMG signal, i.e., the original EMG signal minus the EMG obtained when adding only the decomposed motor unit action potential trains. We aimed to test whether the synergistic information could be preserved in both these signals. This analysis aimed at proving that the identified motor unit activities from the EMG decomposition were representative of the information contained in the full EMG signal.

Number of synergies across grip types

We examined the extent to which a given set of synergies extracted from the motor neuron and EMG datasets were sensitive to grip type. Because of the vast range of possible simultaneous activations of available degrees of freedom, synergies extracted from a small set of grips could predict more complex grips (Ajiboye and Weir, 2009; Muceli et al., 2010). Thus, if the number of synergies does not scale with the number of grip types, fewer synergies than grip types should be able to account for all grip types. In particular, the seven grip types we considered involved the thumb in opposition with different combinations of fingers. Therefore, we examined whether the number of extracted synergies changed when considering grips involving the thumb and only one finger versus combinations of fingers.

The reconstruction of the original dataset by W and H, either representing the seven grips or only the four single-finger grips, was quantified with the coefficient of determination (R²), as done in Muceli et al. (2010). The greatest R² among the 10 repetitions with different initial random weights was retained for each number of synergies (Muceli et al., 2010).

The selection of the number of synergies was performed by identifying the number for which the R² curve showed a change in slope (Cheung et al., 2005; d'Avella et al., 2011). This was quantified by computing the mean squared error (MSE) of a line fitting the part of the R² curve from each number of synergies between 1 and 9, to the maximum number evaluated, i.e., 10. The minimum MSE threshold chosen to determine the number of synergies was 5e-4, as done in d'Avella et al. (2011).

To assess the functional role of each synergy in relation to the actuation of individual fingers coupled to the thumb, synergies extracted from each subject were re-ordered by associating four of the total extracted synergies (according to the R²-curve-change-in-slope criterion) to individual finger control. This procedure consisted of considering the variance of the 10-s segment for each grip type of each synergy and assigning progressively each synergy to the finger with the highest variance accounted for by the relative thumb-single finger grip.

Motor neuron synergy anatomic maps

We associated motor neuron spike trains to a given muscle according to the amplitude distribution of the corresponding single motor unit action potentials estimated by STA (Farina et al., 2002). The association of motor neurons to muscles was done using the same partitioning used for HD-sEMG (Fig. 4A) but applied to the root mean square values of the single motor unit action potentials across the grid (Fig. 4B).

Weights of each synergy are usually represented with a bar graph, where each bar represents the synergistic contribution of a muscle or, introduced here, a motor neuron. To enable an easier functional interpretation of muscle or motor neuron synergies, we introduce a way to represent them with an anatomic map (Fig. 4C). This could be done either when a single source of myoelectric activity is recorded for each muscle or when more motor neuron SDR are associated to the same muscle. In the latter case, for each synergy, the weights associated with the same muscle have been normalized and then averaged to produce a value which was represented with a color scale, normalized from 0 to 1, in the anatomic map.

Force and synergy activation signals

In order to evaluate the extent to which the activation signals extracted by NMF accounted for the isometric force exerted with each grip, we computed, for each subject, the cross-correlation between each 10-s epoch of each synergy activation signal (i.e., during the execution of a given grip) and the respective 10-s epoch of the exerted force. For this cross-correlation, we used only the forces exerted by the fingers in opposition with the thumb for each grip type. This allowed also to test how much a synergy associated to a finger, as defined above, in Synergy extraction by NMF, correlated with the force exerted during the grip types involving that finger.

Synergistic behavior of motor neurons within each muscle

We assessed the existence of a consistent synergistic behavior of motor neurons within each muscle. To do so, for each subject, we analyzed whether motor neurons innervating the same muscle were activated in different synergies. For this purpose, we identified motor neurons of the same muscle with a large difference in weight across different synergies.

Subsequently, we assessed whether in two or more synergies, for the same muscle, groups of motor neurons were alternatively synergistically recruited with respect to most of the motor neurons for the same muscles. We identified these motor neurons as the ones that were activated less than one half of the mean across all the motor neuron weights for the synergy when the relative muscle was maximally activated, and at the same time, were activated more than one half of the mean across all the motor neuron weights for at least another synergy.

Testing the effect of number of motor neurons per muscle on synergy identification

As the number of motor neurons included in each muscle might affect the structure of the identified synergies and, therefore, the comparison between motor neuron synergies with muscle synergies, we extracted synergies from subsets of motor neurons, each subset consisting of the same number of motor neurons per muscle. Subsets with one to four motor neurons per muscle were considered, and five permutations for each subset were tested. When the number of motor neurons in a given muscle was lower or equal than the one required for the subset, all the motor neurons of that muscle were taken into account. Muscle synergies were extracted as explained above, Synergy extraction by NMF, and the number of chosen synergies was determined with the above-described change-in-slope criterion. Cross-correlation peaks between activation signals and force were computed as done for the data obtained from the analysis of all motor neurons.

Results

EMG decomposition

The total number of motor neurons identified for each subject was 66, 55, 35, 62, 52, 40, and 69, for a total of 379 motor neurons (Table 1). The level of accuracy (PNR) for the identified discharge times across subjects was 30.7 ± 4.6 dB, corresponding to an average range of accuracy between 90% and 100% (Holobar et al., 2014). From Table 1, only three MUs could be identified for FPB across all subjects. Moreover, the global activity of FPB could be observed only in two subjects. This can be because of the position of this muscle, the closest to the palm, from which it can be difficult to identify motor units. For this reason, the results for this muscle should be considered cautiously.

Number of identified motor neurons associated with each muscle across the total 379 identified motor neurons

Number of identified motor neurons for each muscle
Muscles	s1	s2	s3	s4	s5	s6	s7	Mean	Std
FDI	12	11	6	13	8	6	13	9.9	3.1
II DI	6	6	3	7	5	1	8	5.1	2.4
III DI	6	5	2	1	1	6	3	3.4	2.2
IV DI	2	3	4	2	0	0	2	1.9	1.5
ADM	10	6	1	6	9	5	11	6.9	3.4
FPB	0	0	0	2	0	0	1	0.4	0.8
APB	4	2	0	0	4	3	4	2.4	1.8
OPP	2	2	1	8	5	5	4	3.9	2.4
ECU	4	5	2	2	3	4	6	3.7	1.5
EDC	2	5	6	8	5	2	0	4.0	2.8
ECR	2	1	2	0	1	2	3	1.6	1.0
FCU	4	3	4	6	3	2	2	3.4	1.4
FDP	4	4	0	4	7	2	9	4.3	3.0
FCR	8	2	4	3	1	2	3	3.3	2.3

Values for each subject and also mean and SD across subjects are reported.

Each row in Figure 5A shows discharges of a distinct motor neuron obtained from one subject across all the grip types. A total of 69 motor neurons across 13 muscles were identified for this subject. In this example, most motor neurons exhibited phasic discharges for almost all the grip types, while some motor neurons for ADM, APB and for extrinsic muscles exhibited tonic discharges for some grip types. Figure 5B shows motor neuron discharges obtained from the IND-MID grip type shown in Figure 5A but enlarged to show both spike trains and MVC-normalized grip force measured from thumb opposed to the index and middle fingers. Figure 5 and Table 1 show that, for some grip types and muscles, it was not possible to identify active motor neurons. For example, in Figure 5, motor neuron activity was not extracted for the EDC muscle whereas in Table 1 motor neurons of the FPB were identified only for two subjects, as mentioned above.

Figure 5.

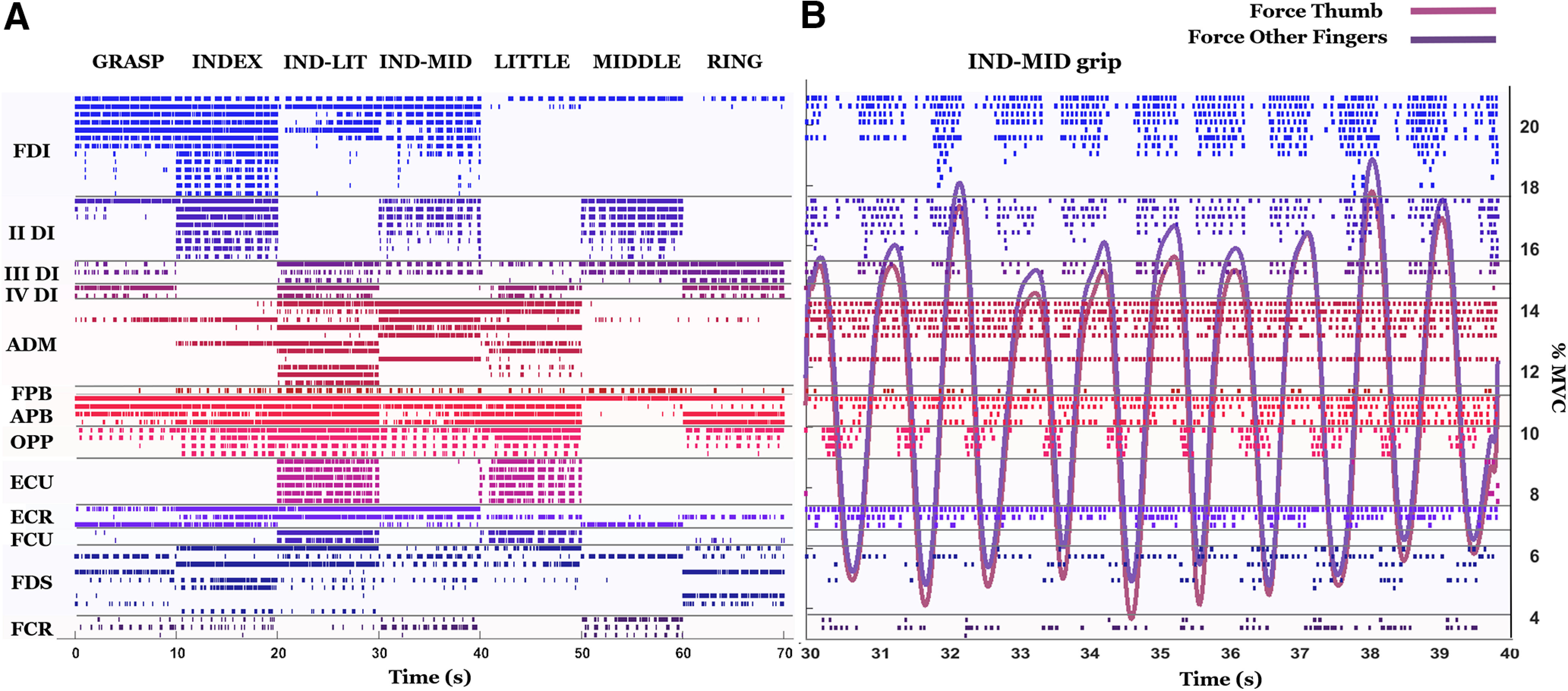
Motor neuron spike trains and grip force. A, Motor neuron discharges identified for one subject (69 motor neurons across all muscles) are shown in each row and color-coded for each muscle. B, Motor neuron discharges extracted during force production using the IND-MID grip type are enlarged and plotted with normalized grip force exerted by the thumb and two fingers (index and middle fingers).

To demonstrate that the sparse activation of motor units across grip types represented in Figure 5 was not because of an erroneous identification of the decomposition algorithm, we computed the STA for each motor unit and for each grip type (see Materials and Methods, EMG signal decomposition). Across all subjects, some units were identified in all grip types and the normalized 2D cross-correlation of the STAs within each motor unit across all grip types was 0.91 ± 0.11, while some were identified only in some grip types and the cross-correlation within motor units for these grip types was 0.86 ± 0.04. These correlations were higher than the cross-correlation values between different units (0.64 ± 0.18 across all subjects and grip types). This confirms that the action potential waveform of motor units active in several tasks did not substantially change among tasks. It would be highly unlikely that the action potential waveforms of other units would change substantially since they are part of the same muscle. We conclude that the decomposition algorithm tracked the units across tasks correctly without splitting units and that the sparsity in recruitment is an actual physiological phenomenon.

Sparse recruitment across grip types

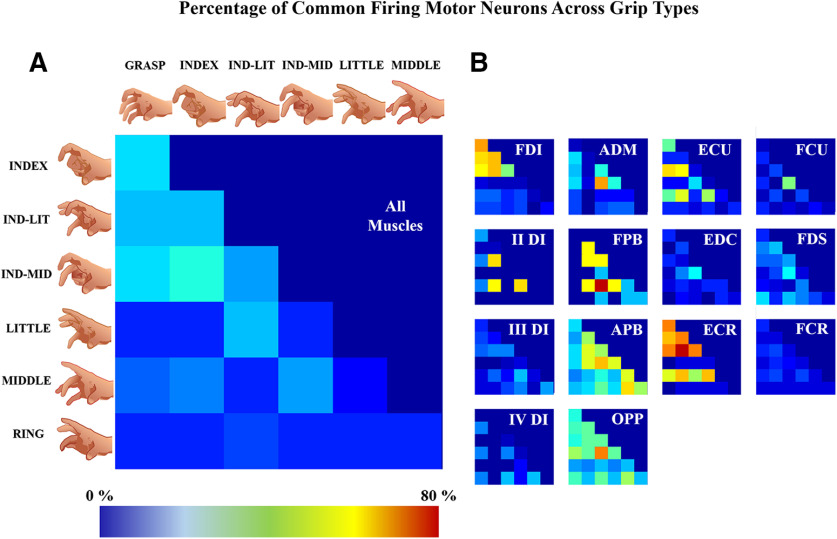
As seen in Figure 5, among the identified motor neurons, some were active only for some grip types (a motor neuron was defined not active when it discharged <20 spikes in the 10-s-long grip observation, see Materials and Methods, Synergy extraction by NMF). Figure 6A shows the percentage of motor neurons that were active in two grip types. The grips involving the index finger (GRASP, INDEX, IND-MID, and IND-LIT) contained the highest number of motor neurons firing in a pair of grip types (the maximum was 33% between INDEX and IND-MID grips, the minimum was 22% between IND-MID and IND-LIT grips). Moreover, for IND-LIT/LITTLE, IND-MID/MIDDLE and INDEX/MIDDLE grip pairs, a similar percentage of motor neurons firing in two grip types was found (25%, 22%, and 21%, respectively). Percentages of motor neurons firing in a pair of grip types among other grip type pairs were below 20%.

Figure 6.

Percentage of motor neurons firing in two grip types. These results were obtained by computing for each pair of grips the percentage of motor neurons firing in two grip types (Fig. 2B). In A, the percentage is represented for motor neurons from all muscles, while in B, it is represented for each muscle. The color scale is represented between 0% and 80%, the maximum value found for these results.

Figure 6B shows data obtained using the same analysis but applied to motor neurons innervating each muscle. For FDI, the grips involving the index finger had the highest proportion of motor neurons active in more than one grip type (the maximum was 58% between GRASP and INDEX, the minimum was 40% between IND-MID and IND-LIT). There was a correspondence between the main activated muscles and the finger activated in grip pairs, e.g., motor neurons innervating the II DI activated with the index and middle finger actuation, ADM exhibited little activity, and different thenar and extrinsic muscles were involved to different extents according to the finger(s) involved in the grip. These results are similar to the motor neuron synergy anatomic maps discussed below (Figs. 8, 9).

Figure 8.

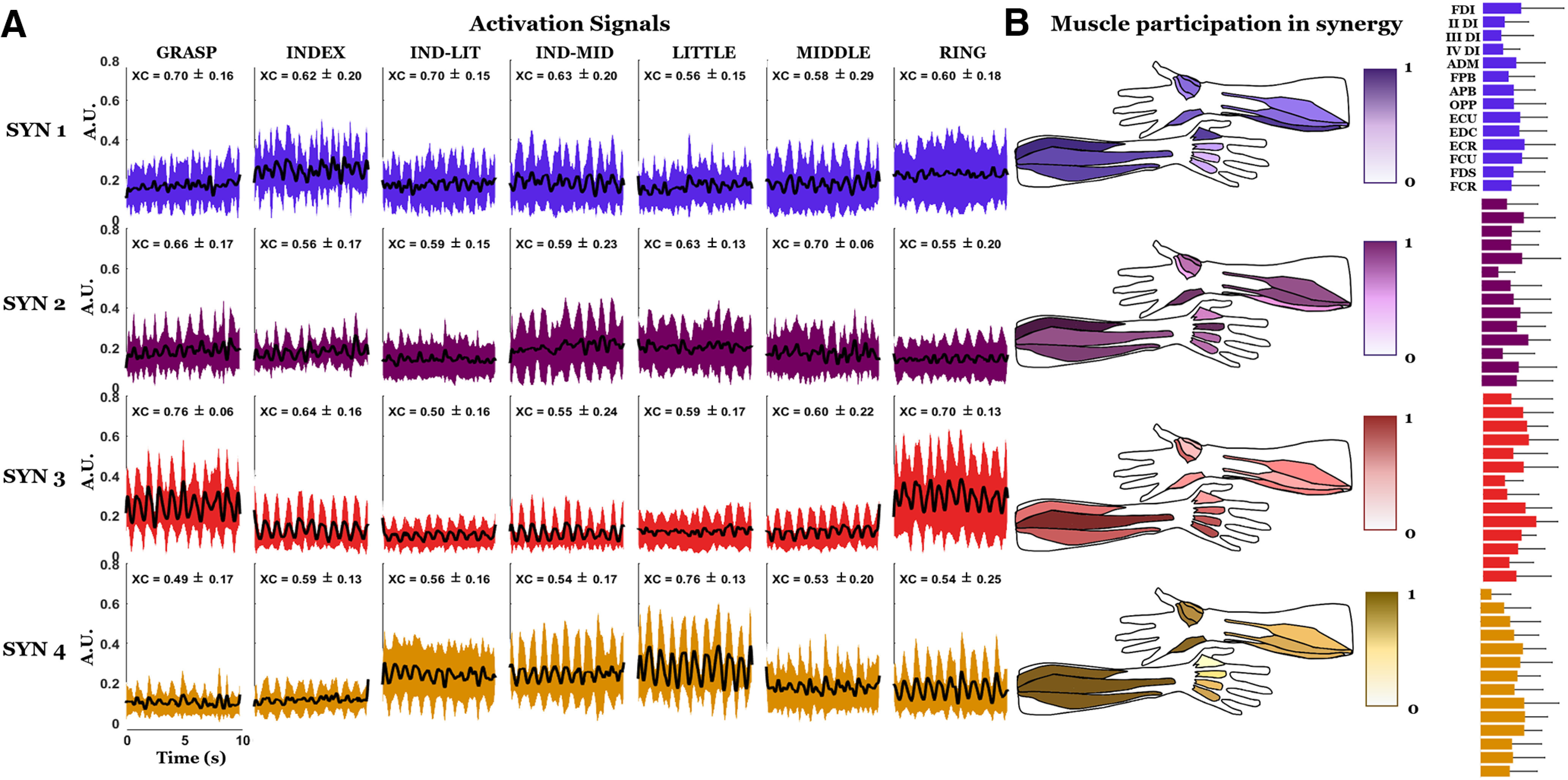
Activation signals and anatomic maps of muscle synergy weights. A, First four synergies averaged across all subjects. Mean and SD of the peak of the cross-correlation function (XC) between each segment of the activation signals and the respective segment of the exerted force are shown above each segment. B, Values for the anatomic maps are represented with a color scale between 0 and 1 and denote the estimated contribution of each muscle to each synergy. For each subject, the four synergies were ranked and assigned to a given finger (for details, see Materials and Methods, Synergy extraction by NMF). On the right of each anatomic map, the bar graph representation of the mean and the SD of the synergy weights is also provided.

Figure 9.

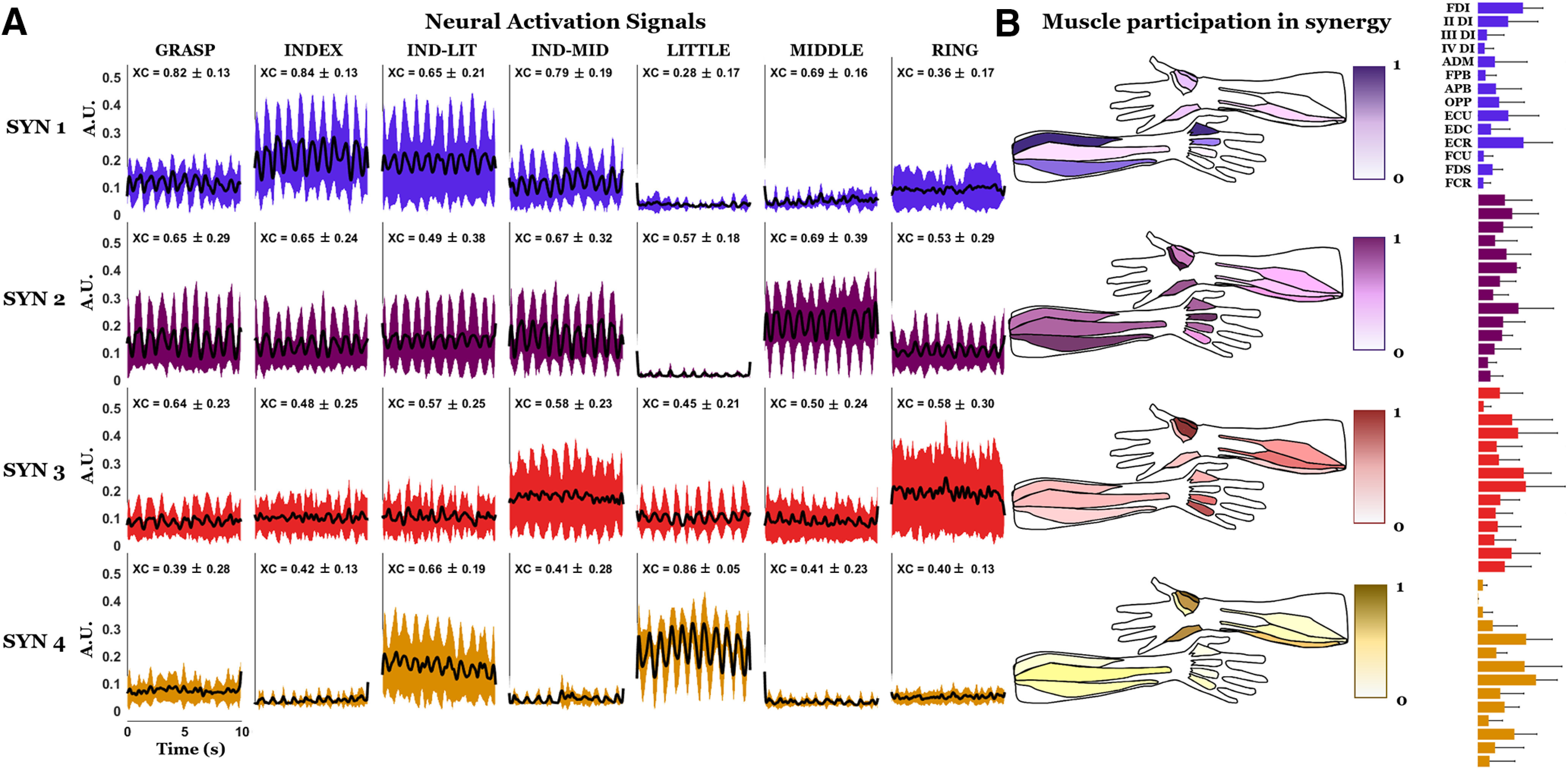
Activation signals and anatomic maps of the motor neuron synergy weights. A, First four motor neuron synergies and their cross-correlation peak (XC) with grip force. B, Anatomical maps. On the right of each anatomic map, the bar graph representation of the mean and the SD of the synergy weights is also provided. Data are shown in the same format as Figure 8.

Thus, the sparse recruitment of motor neurons shown in Figure 5 can be related to the muscle coordination by the CNS to fulfil different tasks shown in Figure 6, by analyzing coordination of individual motor neurons. We further elaborate this observation in Discussion.

Dimensionality

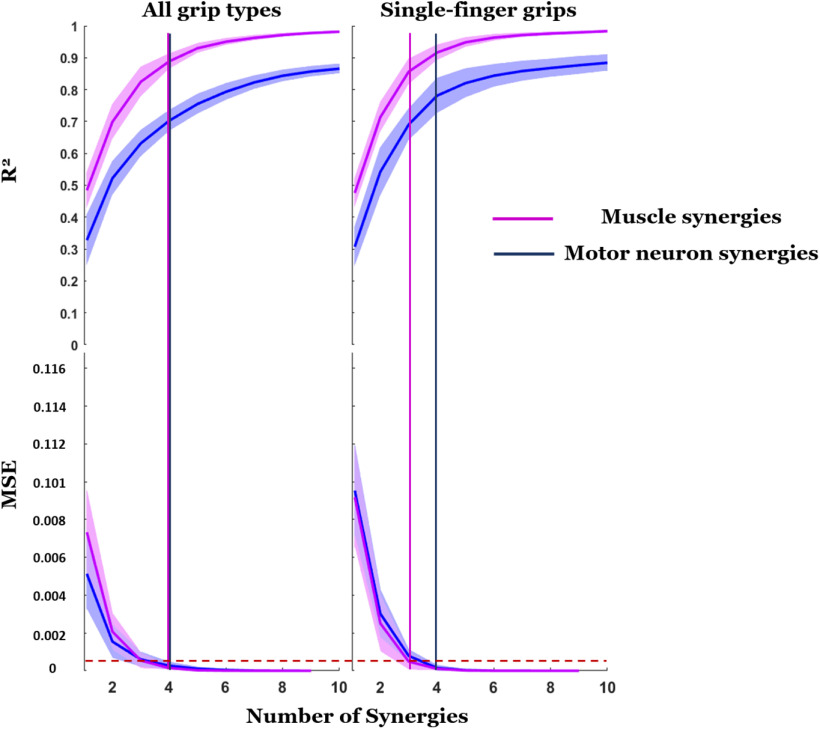
Figure 7 shows the extent to which each type of synergy could reconstruct the original datasets quantified by the R² as a function of the number of synergies. Mean and SD (thick line and shaded area, respectively) of R² averaged across subjects is shown as a function of number of synergies used to reconstruct the original data (1–10). For each type of synergy, the first column represents the average R² curves from synergies extracted from all grip types combined. The second column represents the averaged R² curves from synergies extracted from the four thumb-single finger grips. In all cases, we found a systematic difference in R² for motor neuron and EMG synergies, with R² values associated with reconstructing EMG envelopes being always higher than those associated with reconstructing motor neuron SDRs. The vertical line in Figure 7 determines the number of synergies selected which is the minimum value of synergies required to bring the MSE below the 5e-4 threshold (dashed red line; d'Avella et al., 2011). According to this criterion, the number of motor neuron synergies was 4, for both selections of concatenated grip recordings, for a mean and SD of R² across all subjects, respectively, of 0.70 ± 0.03 (seven grips) and 0.78 ± 0.05 (four grips). For muscle synergies, the identified value was four for synergies extracted from all grips (R² = 0.89 ± 0.02) and three for synergies extracted only from single-finger grips (R² = 0.86 ± 0.04).

Figure 7.

Reconstruction of original EMG data: comparison among motor neuron synergies and muscle synergies. The R² quantifies the ability of each type of synergy (motor neuron or muscle) to reconstruct the original data (motor neuron SDR or EMG envelopes, respectively) as a function of the number of synergies used for the reconstruction. The top panel shows mean and SD (thick line and shaded area, respectively) of the R² averaged across subjects. The bottom panel shows the corresponding MSE of linear fits. The drop of MSE below the threshold of 5e-4 (horizontal dashed red line; d'Avella et al., 2011) is used to determine the minimum number of synergies to reconstruct the original signals (vertical lines).

Muscle synergies

Figure 8 shows activation signals associated with muscle synergies across the seven grip types for all subjects. We show four synergies because this was the number of synergies identified according to the MSE criterion (Fig. 7, first column). Each row of the plot in Figure 8A represents the average activation signal across subjects (row of the H matrix) for the synergy associated with a finger (Materials and Methods, Synergy extraction by NMF). To further address the functional role of each synergy, we represent the anatomic maps of the synergy weights next to each respective activation signal and also the mean and the SD of the weights as bar graphs (Fig. 8B). This figure provides the spatiotemporal information about muscle coordination, among the 14 extrinsic and intrinsic hand muscles examined in this study. While the spatial aspect of this coordination is described by synergy weights, the correspondent temporal aspect is described by the activation signals. Moreover, the correlation between activation signals and the force is indicative of how groups of muscles are coordinated to generate the target force. The participation of each muscle in each synergy is intuitively represented anatomically for a quicker functional interpretation. A high variability among the weights can be observed from the SD of the bar graphs.

By examining the muscle synergies extracted from the EMG signal reconstructed from the decomposed motor units and the residual EMG signal, we found three to four dimensions for both reconstructed signals and the residual. When we found three synergies (36% of the cases across subjects and the two types of signals), often the synergy associated with the ring was missing. For the reconstructed signals, the mean cross-correlation between activation signals and force was comparable with that obtained for the original EMG signal. This analysis confirmed that, for each synergy, the mean value of cross-correlation was highest for the single-finger grip involving the finger associated to that synergy. In contrast, for the residual we found very weak mean cross-correlation values (<0.2) for all grips and synergies. Therefore, only the decomposable portion of the EMG signal contained information related to finger force modulation.

Motor neuron synergies

Figure 9 shows the time course of mean activation signals for the first four motor neuron synergies extracted from each grip type and averaged across all subjects. The activation of the first, second, third, and fourth synergy occurs in grips involving a single finger coupled to the thumb, i.e., index, middle, ring, and little finger, respectively.

For each grip type and synergy, the mean and SD across subjects of the peak of the cross-correlation function between each 10-s activation signal and the relative segment of exerted force is reported in Figure 9A (XC). The highest mean value of the cross-correlation peak for the first synergy, associated with the index finger, is obtained for the grip actuating thumb and index finger, and the same observations can be made for synergies associated with thumb-middle and thumb-little finger (synergies 2 and 4, respectively). For the synergy associated with the ring finger (synergy 3), the highest value is for the GRASP grip, followed by the RING and the IND-LIT grips, which exhibited on average a cross-correlation peak of 0.58. When eliminating the outliers outside four times the SD, the delay between the activations signals and the force was 190 ± 55 ms, in accordance with the study of Del Vecchio et al. (2018).

A greater functional discrimination for motor neuron synergies compared with muscle synergies can be observed in the anatomic representation of the weights. Specifically, the activation of the intrinsic muscle responsible for the activation of each finger observed in the case of motor neuron synergies (Fig. 9), is much less discriminable in the case of muscle synergies (Fig. 8). For example, FDI and II DI are more active than other intrinsic muscles for the motor neuron synergy associated with the index finger, while for the respective muscle synergies more intrinsic muscles seem equally involved. The same could be observed for the ADM in the motor neuron synergy associated with the little finger, and for the different dorsal interossei in the synergies, respectively, associated with the middle and ring fingers. For all these cases, the muscles have a more uniform activation in the muscle synergies compared with motor neurons in the motor neuron synergies, with a consequent less discriminate functional role. For each motor neuron synergy, the mean values of the cross-correlation peak with the grip force exhibited greater differences across grip types involving the thumb and one of the fingers associated with a given synergy than across cross-correlation peaks computed using muscle synergies (Fig. 8). The only exception to this pattern, observable for motor neuron synergies as well as for muscle synergies, is the RING grip, which nevertheless exhibited the highest cross-correlation peak value for the GRASP grip. The mean values of the cross-correlation peak with the force for the INDEX grip in the motor neuron synergy associated with the index finger were higher than for the respective muscle synergies. The same was true for the LITTLE grip in the motor neuron synergy associated with the little finger and for the MIDDLE grip in the motor neuron synergy associated with the middle finger. For motor neuron synergies the mean value of the cross-correlation with the force in the index synergy was higher for the INDEX grip, while in muscle synergies this value was higher for the GRASP grip and the IND-LIT grip.

In Figure 9B, the anatomic maps are obtained using the W columns (Materials and Methods), after the reordering based on the finger association (Materials and Methods, Synergy extraction by NMF). By inspection of the anatomic maps, it is evident that in the synergy assigned to the index finger, the FDI is the most activated muscle, along with the II DI and the extensors of the wrist (mainly ECR). In the synergy assigned to the middle finger, the II DI and FPB are the most activated muscles, whereas in the synergy assigned to the ring finger the III and the IV DI are the most activated muscles, together with OPP and APB. ADM, along with OPP, APB, and FCU are characterized by the largest weights in the synergy assigned to the little finger. The different contribution of the muscles of the thenar eminence in the four weight maps is consistent with their anatomic function: the thumb must flex to oppose the index and the middle fingers (synergies 1 and 2), while it must abduct and oppose to approach the tip of the ring and little fingers (synergies 3 and 4).

The findings represented in the anatomic maps of the motor neuron synergies are in agreement with the motor neuron firing in two grip types (Fig. 6). In fact, quantifying the contribution of each muscle by summing the contribution of the relative motor neurons in each synergy, is similar to counting the activated motor neurons for pairs of grips, where for each grip a different combination of fingers is activated. For example, in the map associated to the first synergy and index finger (Fig. 9), FDI and II DI are the most activated muscles. Similarly, in Figure 9, FDI motor neurons are mainly active for all the grips involving the index finger. The same observation applies to ADM, for which the innervating motor neurons are commonly activated for grips where the little finger is involved, confirming the anatomic maps. ECU and ECR, which present motor neuron firing across grips involving index and middle fingers, are mainly activated in the anatomic maps of the motor neuron synergies involving those fingers (Fig. 9). Finally, the differential activation of the muscles of the thenar during the grips with different fingers is confirmed by results in Figure 6 (APB during ring activation and OPP during ring and little activation).

Association of synergies to digits

To provide a more accurate comparison of the extent to which each type of synergy could be associated with a given finger, we compared the number of synergies that correlated the most with grip force in (1) single-finger grips involving the finger associated with a given synergy; (2) combined-finger grips (GRASP, IND-LIT, IND-MID) involving the finger associated with a given synergy; and (3) grips involving fingers other than those associated with a given synergy. Across all subjects (n = 7) and the first four synergies for each subject (i.e., 28 synergies), analyses (1), (2), and (3) applied to motor neuron synergies revealed 17, 4, and 7 synergies, respectively. The same analyses applied to muscle synergies revealed 12, 7, and 9 synergies, respectively. This means that a motor neuron synergy associated with a finger was more frequently correlated, in most cases, with force during single-finger grip, e.g., index-synergy during INDEX grip, than for muscle synergies. Moreover, a motor neuron synergy associated with a finger was mostly correlated with force in a single-finger grip in fewer cases relative to another finger. Thus, among the synergies observed for the seven subjects, motor neuron synergies provided more frequently a higher discrimination of the activity of a single finger in a given grip type than muscle synergies.

Synergistic behavior of motor neurons within muscles

Lastly, we assessed an alternative synergistic organization of motor neurons within a muscle (Materials and Methods). Figure 10 shows the motor neuron synergy weights for all subjects together with the alternative synergistic organization (black and red bars, respectively). Note that these motor neurons can be mostly active in more than one synergy, thus in the figure they can be highlighted for all these synergies. Conversely, these motor neurons are mostly inactive in the synergy where the considered muscle is mainly activated. For instance, motor neurons #10 and #12 for FDI of Subject 1 in Figure 10 are active less than one half of the mean activation of the synergy where FDI is most active (synergy 1), but they are active more than one half of the mean for another synergy (synergy 4). This alternative organization indicates the existence of different spinal neural pathways from interneuron modules to groups of motor neurons of the same muscles, thus suggesting that the CNS controls groups of motor neurons rather than groups of muscles. Indeed, if different motor units of the same muscle do not act in concert, the muscle is not necessarily activated as a whole (see Discussion). The number of these alternative organizations of activated motor neurons was between 10% and 15% of the total (with a minimum of 6.4% and a maximum of 16.7% depending on the subject). This result suggests that most motor neurons of the same pool mainly belonged to a single synergy. These results also suggest that a minority of motor neurons in the same muscle may be controlled with a different synergistic behavior.

Figure 10.

Motor neuron synergy normalized weights (from 0 to 1, where 1 is the highest weight in the synergy) of all subjects. In red, the motor neurons recruited synergistically in a different way with respect with the majority of motor neurons of their muscle, are highlighted in all the synergies where they are more active (see Materials and Methods, Synergistic behavior of motor neurons within each muscle). For each subject, synergies are ordered by finger association (index, little, middle, ring).

Synergies were extracted for different numbers of motor neurons per muscle by creating subsets consisting of permutations of motor neurons (see Materials and Methods). For all sizes of the motor neuron subsets (in the range one to four motor neurons per muscle), we identified either 3 or four synergies for each permutation across all subjects. In the case of three synergies (38% of all cases), the excluded synergy was the one associated with the ring finger, except for subject #3 where the synergy associated with the index finger was missing. This change in dimensionality was not clearly related to the dimensionality of the subsets, but rather because of the different randomizations of the selected motor neurons. The mean and the SD of the cross-correlation between force and activation signals is reported across all subjects and all the subset permutations (thus also all the subset numerosities) for each synergy and each grip type in Table 2. The strongest mean cross-correlation for each synergy corresponded to the single-finger grip when the finger associated to that synergy was involved. This was true for all sizes of the motor neuron subsets (1–4), except for the ring finger with subset sizes more than two motor neurons per muscles. Overall, these results confirm that the above-described observations on motor neuron synergies extracted from all the motor neurons and grip types were not influenced by the different numbers of motor neurons identified per muscle.

Table 2.

Mean and SD of the cross-correlation peak between activation signals and force for synergies extracted from subsets of motor neurons (MN) ranging from 1 to 4 MNs per muscle (five permutations in each case)

		GRASP	INDEX	IND-LIT	IND-MID	LITTLE	MIDDLE	RING
Syn “index”	1 MN/musc	0.71 ± 0.17	0.75 ± 0.12	0.63 ± 0.22	0.63 ± 0.22	0.53 ± 0.18	0.63 ± 0.17	0.48 ± 0.18
	2 MN/musc	0.79 ± 0.13	0.75 ± 0.16	0.64 ± 0.23	0.74 ± 0.21	0.55 ± 0.19	0.71 ± 0.16	0.51 ± 0.19
	3 MN/musc	0.77 ± 0.18	0.78 ± 0.14	0.63 ± 0.22	0.76 ± 0.19	0.55 ± 0.19	0.74 ± 0.12	0.50 ± 0.24
	4 MN/musc	0.81 ± 0.16	0.81 ± 0.12	0.60 ± 0.20	0.82 ± 0.14	0.56 ± 0.16	0.77 ± 0.12	0.55 ± 0.22
Syn “middle”	1 MN/musc	0.62 ± 0.20	0.60 ± 0.22	0.56 ± 0.16	0.70 ± 0.20	0.46 ± 0.15	0.76 ± 0.14	0.53 ± 0.20
	2 MN/musc	0.74 ± 0.17	0.69 ± 0.20	0.65 ± 0.20	0.76 ± 0.13	0.58 ± 0.16	0.75 ± 0.17	0.61 ± 0.21
	3 MN/musc	0.62 ± 0.25	0.68 ± 0.20	0.59 ± 0.18	0.68 ± 0.22	0.56 ± 0.17	0.72 ± 0.19	0.53 ± 0.18
	4 MN/musc	0.59 ± 0.25	0.60 ± 0.25	0.61 ± 0.22	0.66 ± 0.24	0.57 ± 0.17	0.71 ± 0.20	0.48 ± 0.18
Syn “ring”	1 MN/musc	0.55 ± 0.27	0.53 ± 0.19	0.57 ± 0.20	0.57 ± 0.21	0.48 ± 0.19	0.55 ± 0.16	0.63 ± 0.23
	2 MN/musc	0.58 ± 0.23	0.54 ± 0.14	0.56 ± 0.22	0.62 ± 0.18	0.52 ± 0.20	0.60 ± 0.16	0.66 ± 0.19
	3 MN/musc	0.68 ± 0.19	0.58 ± 0.17	0.61 ± 0.20	0.67 ± 0.19	0.52 ± 0.17	0.54 ± 0.21	0.67 ± 0.20
	4 MN/musc	0.63 ± 0.18	0.54 ± 0.20	0.61 ± 0.21	0.67 ± 0.16	0.54 ± 0.18	0.57 ± 0.23	0.65 ± 0.22
Syn “little”	1 MN/musc	0.46 ± 0.17	0.49 ± 0.15	0.58 ± 0.22	0.53 ± 0.19	0.68 ± 0.22	0.49 ± 0.21	0.46 ± 0.17
	2 MN/musc	0.52 ± 0.18	0.50 ± 0.16	0.71 ± 0.16	0.61 ± 0.11	0.77 ± 0.15	0.53 ± 0.13	0.53 ± 0.18
	3 MN/musc	0.58 ± 0.17	0.55 ± 0.21	0.80 ± 0.11	0.66 ± 0.13	0.80 ± 0.13	0.49 ± 0.14	0.51 ± 0.17
	4 MN/musc	0.54 ± 0.15	0.55 ± 0.19	0.77 ± 0.13	0.62 ± 0.17	0.82 ± 0.11	0.49 ± 0.15	0.52 ± 0.18

Values are provided for each grip type, each synergy, and each size of the MN subset per muscle. Results are for all subjects.

Discussion

Our study was designed to test the hypothesis that pools of motor neurons of different hand muscles are synergistically organized and, therefore, that their activity should be accounted for by a substantially smaller dimensionality than the number of motor neurons we recorded from. Our findings support this hypothesis and further indicate a similar synergistic structure for whole muscles and motor neuron pools. However, some deviations in this correspondence were also observed.

The modular behavior among motor neurons can be observed through the sparse activation in motor neuron discharge patterns across different grips (Fig. 5A). This sparsity reflects excitatory and inhibitory spinal interneuron output to motor neurons that differs across grip types, as represented schematically in Figure 2B. We quantified the coactivation of the same motor neuron across different grip types (Fig. 6) and used this data to define motor neuron synergy anatomic maps (Fig. 9). We note that, for motor neuron synergistic behavior to occur, recruitment of one motor neuron for some but not all grip types would reflect a modular organization presumably arising from the output of spinal interneuronal circuitry.

We identified the number of motor neuron and muscle synergies necessary to account for the signals obtained from all grips or only the four grips that involved one finger in opposition to the thumb. We found a comparable number of synergies when analyzing muscle or motor neuron activities (Fig. 7). Surface EMG signals are inevitable corrupted by cross talk, especially in the hand and forearm where muscles are small and closely spaced (Muceli et al., 2014). On the contrary, signals extracted from SDR are cross-talk free and therefore more independent from each other compared with the surface EMG counterpart.

A low dimensionality in motor neuron output, even across different task conditions, implies that the dimensionality reduction is implemented at the motor neuron level by spinal interneuron modules and other supraspinal and/or afferent inputs. This is a new and more detailed perspective in examining muscle synergistic control that is rooted on previous evidence of predominant common synaptic input to a motor neuron pool. Thus, for the first time this study integrates findings about modularity in muscle coordination (muscle synergy paradigm) with reports of common synaptic input to motor neurons (Negro et al., 2009; Del Vecchio et al., 2019; Tanzarella et al., 2020). In fact, motor neurons may receive input from different interneurons whose activity is modulated in common, possibly because such interneurons receive a common input or because of other complex network dynamics. Our approach allows us to interpret the activation signals of each synergy as the common input to the corresponding group of motor neurons for each task condition. These groups include innervation to multiple muscles such that the dimensionality of control is significantly lower than the number of motor neuron pools. Finally, we have found a similar low dimensionality (three to four identified synergies) for different subsets of motor neurons used for this analysis, suggesting that the number of motor neurons per muscle included in the analysis did not affect the structure of the extracted synergies.

By focusing on the functional role of the identified synergies, we observed that motor neuron synergies were usually characterized by a greater average correlation with force than muscle synergies. Moreover, there was a better correspondence of the activated muscles to the expected biomechanical function when the anatomic representation of the synergy weights was derived from motor neuron than from muscle synergies. It was therefore possible to functionally explain the synergistic organization of motor neuron pools innervating multiple muscles. This functional role is preserved regardless of the number of motor neurons per muscle included in the analysis (Table 2).

Finally, we investigated whether motor neurons innervating the same muscle belonged to different synergies by analyzing the motor neuron synergy weights. Most motor neurons innervating the same muscle were activated within the same synergy, whereas only a small percentage (between 6.4% and 16.7%, depending on the subject) of motor neurons of the same pool were active in different synergies (Fig. 10). Thus, motor neurons appear to be controlled in clusters and exhibit the same behavior within a cluster (Madarshahian et al., 2021). This is in agreement with a low dimensionality in the synaptic input that the motor neurons receive. However, we note that there were a few exceptions to this rule, which indicate some variability in the synergistic organization. These exceptions are particularly important when considering the correspondence between muscles, as anatomic units, and motor neuron pools, as neural units. Although a general correspondence between muscles and motor neuron pools was observed, which corresponded to a similar synergistic organization of muscles and motor neurons, this was not exact in all conditions. This result leads to the speculation, which needs to be assessed in future work with additional data, that the CNS may not control synergies across muscles but across motor neurons, with only a partial overlap between the two. At a single muscle level, this conclusion is in agreement with the motor unit modes identified in a single pool of motor neurons by Madarshahian et al. (2021).

This study also contributes to our knowledge on hand motor control. As reviewed by Santello et al. (2013), motor primitives have been usually analyzed in terms of biomechanics (kinematic and kinetic synergies) and neuromechanics (muscle synergies and neural synergies). We infer for the first time those neural synergies during hand grip execution, by relating them directly with muscle synergies and by also computing a correlation with the exerted force measures. In fact, although we can observe only the final output of spinal motor neurons, their synergistic organization must be strictly related to the common input they receive, thus establishing a synergistic behavior at the neural level, not only muscular. Studies about motor primitives in hand control (Santello et al., 1998; Weiss and Flanders, 2004; Ajiboye and Weir, 2009) showed that fingers are often synergistically combined together during natural grips. Our experimental protocol also included some grip types (MIDDLE, RING, LITTLE) that involve activation of one finger at a time (along with the thumb) that we do not often use in activities of daily living. However, they were introduced to equally represent and isolate each finger, as also done in other studies (Madarshahian et al., 2021). The selection of the grip types investigated in this study may have contributed to the result that each motor neuron synergy mainly contributed to the force exerted by an individual finger. However, we speculate that the phenomenon of low-dimensional, synergistic control of motor neurons innervating multiple hand muscles might extend to a broader range of hand-object interaction tasks, and possibly to other sets of upper and lower limb muscles engaged in tasks that share requirements similar to our task conditions.

From a more general perspective, our study provides a new perspective on the hierarchical nature of synergistic motor control. By observing the synergistic organization of motor neurons, we are capturing the net effect of all inputs to motor neurons, which would include ascending signals (Fetz et al., 2002). However, for a comprehensive identification of neural synergies of the hand, we would have to directly observe the whole chain determining the neural drive to muscles, from descending pathways to the spinal and motor neuron level. Our investigation cannot discern the mechanisms underlying the excitation and the inhibition of the interneuron at the spinal level, as directly observed in non-human primates by Takei and Seki during grip (Takei and Seki, 2010, 2013a,b). Takei et al. (2017) showed that muscle fields of PreM-INs are distributed as clusters, spatiotemporally correlated with muscle synergies, suggesting that the fundamental coordination of multiple muscles is prescribed by spinal premotor circuits. To expand these results beyond the well-studied role of spinal modules for muscle synergies (Ting and McKay, 2007; Tresch and Jarc, 2009; Bizzi and Cheung, 2013), it is necessary to assess the concurrent motor neuron behavior. Also, the function of motor cortex in this synergistic control should be clarified. It was indeed shown that a synergistic structure of motor control may be coded in the primary motor cortex (Schieber and Santello, 2004; Ejaz et al., 2015; Leo et al., 2016; Fricke et al., 2020). Invasive cortical stimulation of monkeys further confirmed this phenomenon (Overduin et al., 2015), which nevertheless needs to be associated with how descending commands are organized at the spinal level.

Future studies should combine cortical activity recording, invasive recordings of PreM-INs (in primates), motor neuron discharge patterns and biomechanical measurements in a large repertoire of tasks, to address the interaction among central and peripheral mechanisms responsible for the coordination of activity across multiple muscles. To provide a robust framework for interpreting these studies, a computational model of the neural command integration at the spinal level by PreM-INs is necessary. This model should describe the relation among (1) motor neuron synergies (defined in this paper); (2) behavior and tuning of motor neuron subsets within individual muscles; and (3) how afferent and cortical inputs are integrated by PreM-INs to produce the net input to motor neurons.