Sensory Coding of Limb Kinematics in Motor Cortex across a Key Developmental Transition

Abstract

Primary motor cortex (M1) undergoes protracted development in mammals, functioning initially as a sensory structure. Throughout the first postnatal week in rats, M1 is strongly activated by self-generated forelimb movements—especially by the twitches that occur during active sleep. Here, we quantify the kinematic features of forelimb movements to reveal receptive-field properties of individual units within the forelimb region of M1. At postnatal day 8 (P8), nearly all units were strongly modulated by movement amplitude, especially during active sleep. By P12, only a minority of units continued to exhibit amplitude tuning, regardless of behavioral state. At both ages, movement direction also modulated M1 activity, though to a lesser extent. Finally, at P12, M1 population-level activity became more sparse and decorrelated, along with a substantial alteration in the statistical distribution of M1 responses to limb movements. These findings reveal a transition toward a more complex and informationally rich representation of movement long before M1 develops its motor functionality.

SIGNIFICANCE STATEMENT Primary motor cortex (M1) plays a fundamental role in the generation of voluntary movements and motor learning in adults. In early development, however, M1 functions as a prototypical sensory structure. Here, we demonstrate in infant rats that M1 codes for the kinematics of self-generated limb movements long before M1 develops its capacity to drive movements themselves. Moreover, we identify a key transition during the second postnatal week in which M1 activity becomes more informationally complex. Together, these findings further delineate the complex developmental path by which M1 develops its sensory functions in support of its later-emerging motor capacities.

Introduction

Despite its name, primary motor cortex (M1) also processes and integrates sensory input (Asanuma, 1981; Hatsopoulos and Suminski, 2011; Omrani et al., 2016). The sensory-processing capabilities of M1 are especially evident in early development before it plays a clear role in the production of movement: in kittens and rat pups, M1 functions as a prototypical sensory structure (Bruce and Tatton, 1980; Chakrabarty and Martin, 2000, 2005), with substantial increases in M1 activity occurring after self-generated movements have occurred (An et al., 2014; Tiriac et al., 2014; Dooley and Blumberg, 2018). Motor outflow from M1 emerges gradually: electrical stimulation of M1 begins to reliably produce movement at postnatal day 25 (P25) to P35 (Young et al., 2012; Singleton et al., 2021; but see An et al., 2014). At earlier ages, self-generated movements appear to rely on brainstem structures, including the red nucleus (Del Rio-Bermudez et al., 2015). Given the somatotopic alignment between the early sensory map of M1 and its later motor map, it seems clear that the former provides a structural foundation for the latter (Chakrabarty and Martin, 2005; Dooley and Blumberg, 2018). This structural foundation may subsequently serve as a “ground truth” reference by which emerging motor outflow is directed to its correct efferent target.

In early development, self-generated movements and the sensory feedback that arises from those movements (i.e., reafference) are modulated by behavioral state. During wake (W) movements are typically continuous and sustained, involve many muscles within and across limbs, and occur against a background of high muscle tone; in contrast, the myoclonic twitches of active sleep (AS) are characteristically brief, entail discrete activation of individual limb muscles, and occur against a background of muscle atonia. Moreover, twitch-related reafference triggers high-fidelity proprioceptive input to sensorimotor structures across the neuraxis, including M1 (for review, see Blumberg et al., 2020). By comparison, before P11, reafference arising from wake movements is inhibited early in the processing stream (Tiriac and Blumberg, 2016; Dooley and Blumberg, 2018), perhaps to prevent a saturated reafferent signal from muddying developing sensory representations. Given these unique features of twitching and the fact that cortical development is an activity-dependent process (Katz and Shatz, 1996; Blankenship and Feller, 2010; Ackman et al., 2012), we have proposed that twitches help to establish and refine M1's somatotopically precise sensory map (Dooley and Blumberg, 2018).

In adult monkeys, motor activity in M1 is correlated with movement amplitude (Ashe and Georgopoulos, 1994). In P5 rats, we recently found that neural activity in primary somatosensory cortex (S1) is similarly correlated with the amplitude of whisker movements (Dooley et al., 2020). Because M1 initially functions as a sensory structure, we predicted that it also codes for movement amplitude. To test this prediction, we tracked the trajectory of limb movements with machine vision tools (Mathis et al., 2018; Nath et al., 2019) while simultaneously recording extracellular activity in the forelimb region of M1. As predicted, we demonstrate that M1 activity at P8 is robustly tuned to the amplitude of forelimb movements during active sleep, but not wake. Moreover, nearly all M1 units exhibit similar amplitude-tuning curves, leading to a repetitive—and thus, redundant—coding of movement amplitude. In contrast, at P12, only a minority of M1 units exhibit amplitude tuning, regardless of sleep–wake state. M1 units also exhibit sensitivity to movement direction at both ages, though to a lesser extent. Measures of “background” activity (occurring in the absence of movements), sparsity, and entropy increase dramatically by P12, indicating a key transition from discontinuous to continuous activity and increasing the informational content of M1 activity. Indeed, redundant “all-or-nothing” reafferent responses across units are common at P8 and rare at P12, further increasing the informational content of M1 activity. Altogether, these results highlight multiple transitional features in M1's developmental cascade from an exclusively sensory structure to one that will ultimately integrate sensorimotor information to organize motor outflow and support motor learning (Kawai et al., 2015; Heindorf et al., 2018).

Materials and Methods

All experiments were conducted in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals (NIH Publication No. 80–23) and were approved by the Institutional Animal Care and Use Committee of the University of Iowa.

Subjects.

Sprague Dawley Norway rats (Rattus norvegicus) were used at P8–P9 (hereafter referred to as P8; n = 8; body weight, 18.8 ± 0.4 g) and P12–P13 (hereafter referred to as P12; n = 8; body weight, 30.6 ± 0.7 g). Equal numbers of males and females were used, and all subjects were selected from separate litters. Animals were housed in standard laboratory cages (48 × 20 × 26 cm) on a 12 h light/dark cycle, with food and water available ad libitum. The day of birth was considered P0, and litters were culled to eight pups by P3.

Surgery.

As described previously (Blumberg et al., 2015; Dooley and Blumberg, 2018), a pup with a visible milk band was removed from the litter and anesthetized with isoflurane gas (3–5%; Phoenix Pharmaceuticals). A custom-made bipolar hook electrode (diameter, 0.002 inch; epoxy coated; California Fine Wire) was inserted into the nuchal muscle for state determination. Carprofen (5 mg/kg, s.c.; Putney) was administered as an anti-inflammatory analgesic. After removing the skin above the skull, an analgesic was applied topically (bupivacaine; Pfizer). The skull was dried with bleach. Vetbond (3M) was applied to the skin around the skull, and a head plate (Neurotar) was secured to the skull using cyanoacrylate adhesive.

A trephine drill bit (1.8 mm; Fine Science Tools) was used to drill a hole into the skull above the left forelimb representation of M1 (1.0 mm anterior to bregma, 2.2–2.5 mm lateral from the sagittal suture). Two smaller holes were drilled distally to the recording site for insertion of a thermocouple and reference/ground electrode. A small amount of peanut oil was applied over the recording site to prevent drying of the cortical tissue. Surgical procedures lasted ∼15 min.

The pup was then secured to a custom-made head-restraint apparatus inside a Faraday cage, with the torso of the animal supported on a narrow platform. Brain temperature was monitored using a fine-wire thermocouple (Omega Engineering) distal to the M1 recording site. The pup was allowed to recover from anesthesia and acclimate for at least 1 h. The 1 h recording period did not begin until brain temperature was 36–37°C and the pup was cycling regularly between sleep and wake.

Electrophysiological recordings.

The nuchal EMG electrode was connected to a Lab Rat LR-10 Acquisition System (Tucker-Davis Technologies). The EMG signal was sampled at ∼1.5 kHz and high-pass filtered at 300 Hz. A 16-channel silicon depth electrode (Model A4x4-3 mm-100–125-177-A16; NeuroNexus) was coated in fluorescent Dil (Vybrant Dil Cell-Labeling Solution, Thermo Fisher Scientific) before insertion. The electrode was inserted 600–1000 µm (i.e., layers V–VI) into the forelimb region of M1, angled 6° medially (Dooley and Blumberg, 2018). A chlorinated Ag/Ag-Cl wire (diameter, 0.25 mm; Medwire) was inserted distal to the M1 recording site, serving as both a reference and a ground. The neural signal was sampled at ∼25 kHz, with a high-pass filter (0.1 Hz) and a harmonic notch filter (60, 120, and 180 Hz) applied.

Electrode placement in the forelimb region of M1 was confirmed by manually stimulating the forelimb and observing exafferent neural activity. [Because forelimb stimulation also triggers activity in primary somatosensory cortex, histology was performed to further confirm electrode placement in M1 (see below).] Neural activity from M1 was recorded for 1 h using SynapseLite (Tucker-Davis Technologies) while the animal cycled between sleep and wake states.

Video data collection.

To digitally reconstruct forelimb movements in three dimensions, video of the forelimb was recorded from front and side camera angles using two Blackfly-S cameras (TELEDYNE FLIR). Video was collected in SpinView (TELEDYNE FLIR) at 100 frames/s, with a 3000 μs exposure time and 720 × 540 pixel resolution. The two cameras were hardwired to acquire frames synchronously and were initiated using a common software trigger.

The synchronization of video and electrophysiological data was ensured by using an external time-locking stimulus. A red LED controlled by SynapseLite (Tucker-Davis Technologies) was set to pulse every 3 s for a duration of 20 ms. The LED was positioned to be in view of both cameras. Each video was analyzed frame by frame with custom MATLAB scripts to ensure an equal number of frames between LED pulses. Although infrequent, when the number of frames between pulses was less than expected, the video was adjusted by duplicating and inserting one adjacent frame at that time point so as to preserve timing across the recording. Thus, all videos were ensured to be time locked to the electrophysiological data within 10 ms.

Histology.

At the end of the recording period, the pup was killed with ketamine/xylazine (10:1; >0.08 mg/kg) and perfused with 0.1 m PBS, followed by 4% paraformaldehyde. The brain was extracted and postfixed in 4% paraformaldehyde for at least 24 h and was transferred to a 30% sucrose solution 24–48 h before sectioning.

To confirm the location of the electrode within the forelimb region of M1, the left cortical hemisphere was dissected from the subcortical tissue and flattened between two glass slides (separated using two pennies) for 5–10 min. Small weights (10 g) applied light pressure to the top glass slide. The flattened cortex was sectioned tangentially to the pial surface. A freezing microtome (Leica Microsystems) was used to section the cortex (80 µm sections). Free-floating sections were imaged at 2.5× using a fluorescent microscope and digital camera (Leica Microsystems) to mark the location of the DiI.

Electrode placement in the forelimb region of M1 was confirmed by staining cortical sections for cytochrome oxidase, which reliably delineates the divisions of primary sensory cortex at this age (Seelke et al., 2012). The M1 forelimb representation is immediately medial to (and partially overlaps) the primary sensory forelimb representation (Fig. 1B,C). Cytochrome C (0.3 mg/ml; Sigma-Aldrich), catalase (0.2 mg/ml; Sigma-Aldrich), and 3,3′-diaminobenzidine tetrahydrochloride (0.5 mg/ml; Spectrum) were dissolved in a 1:1 dilution of 0.1 m phosphate buffer and distilled water. Sections were developed in 24-well plates on a shaker (35–40°C, 100 rpm) for 3–6 h, rinsed in PBS, and mounted on a glass slide. The stained sections were imaged at 2.5× or 5× magnification and composited with the fluorescent image to confirm the electrode tract within the forelimb region of M1.

Figure 1.

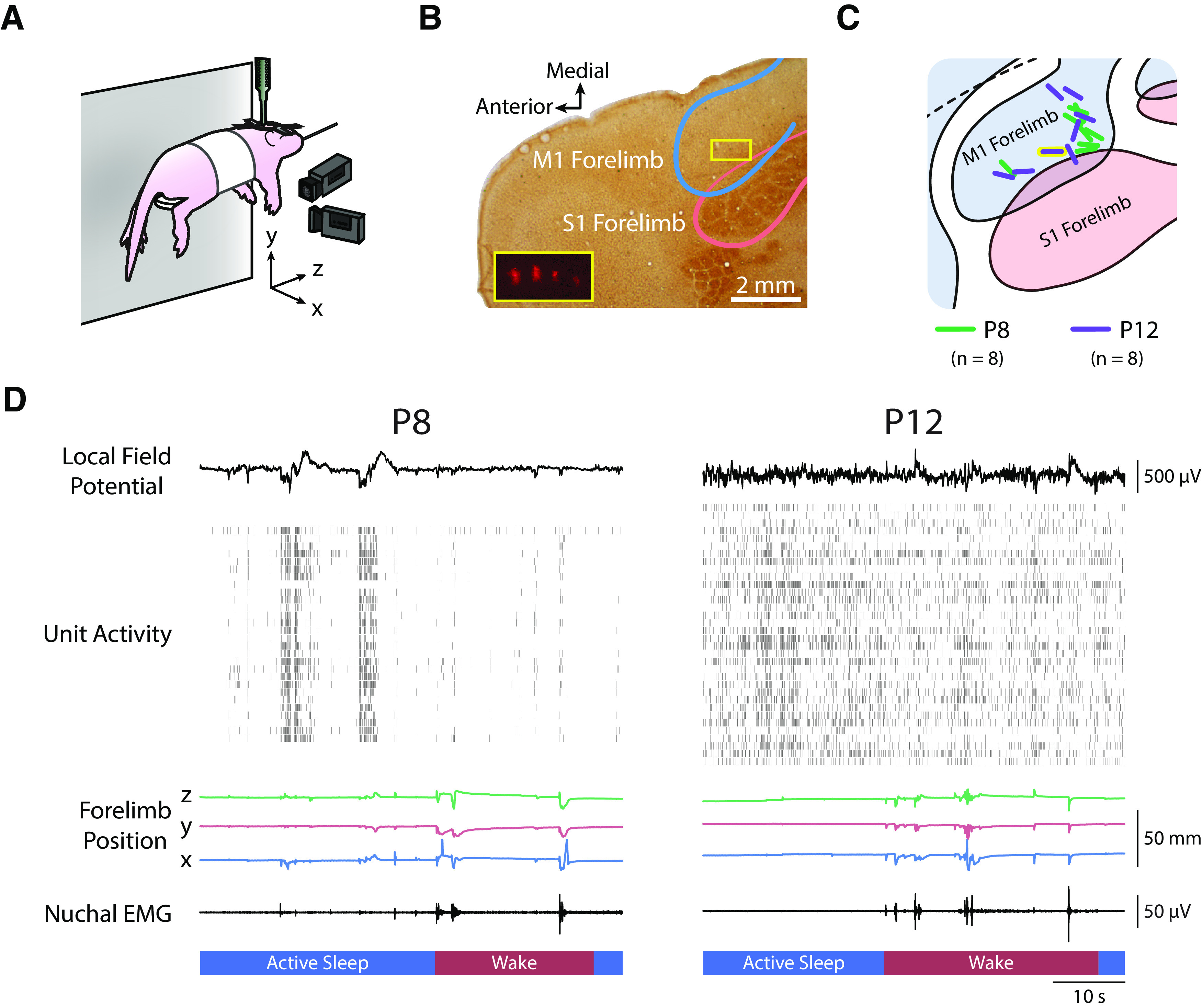
Experimental setup, histology, and representative data. A, P8 and P12 rats were head-fixed with their torso supported and their limbs free to dangle. Two cameras were placed perpendicularly: one front-view camera captured the x-dimension (medial–lateral) of right forelimb movements, and one side-view camera captured the y-dimension (dorsal–ventral) and z-dimension (anterior–posterior). A 4 × 4 silicon depth electrode was lowered into the forelimb region of contralateral M1 to record extracellular activity. B, Photomicrograph of electrode placement in M1. Cortical tissue was flattened before sectioning, followed by staining with cytochrome oxidase to reveal the primary somatosensory cortical representations. The M1 and S1 forelimb boundaries are depicted as blue and pink lines, respectively. The yellow box in the M1 forelimb region delineates the location of the four-shank electrode for this pup. Inset, Magnified view of the four-shank electrode revealed using fluorescence. C, Electrode placements for the eight subjects at P8 and P12 represented as green and purple lines, respectively. The location of the electrode in B is shown with a yellow border. D, Representative data from a P8 (left) and P12 (right) rat. From top to bottom: the local field potential (LFP) in M1; single-unit and multiunit activity in M1, with each row denoting a different single unit or multiunit and each vertical tick denoting an action potential; traces of right forelimb position in the x-, y-, and z-dimensions; nuchal EMG activity; and active sleep (blue bars) and wake (red bars).

Behavioral state and forelimb movements.

As described previously (Tiriac et al., 2014; Dooley and Blumberg, 2018), nuchal EMG and behavior were used to assess behavioral state (the experimenter was blind to the neurophysiological record while scoring behavior). The wake state was defined by the presence of high-amplitude movements of the limbs against a background of high nuchal muscle tone. Active sleep was defined by the presence of discrete myoclonic twitches of the face, limbs, and tail against a background of nuchal muscle atonia.

Forelimb movements were quantified using DeepLabCut (DLC), a markerless tracking solution that uses a convolutional neural network to track features (e.g., limbs) of animals in a laboratory setting (Mathis et al., 2018; Nath et al., 2019). At least 200 manually labeled frames (tracking the wrist of the right forelimb) were used to initially train the network. After the initial training, newly analyzed frames with marker estimates that were deemed inaccurate were relabeled and used to retrain the neural network until satisfactory tracking was achieved. Separate neural networks were trained for the front-facing and side-facing camera angles. The networks reached training root mean square error (RMSE) values of 0.18 and 0.19 mm, and test RMSE values of 0.28 and 0.42 mm, respectively.

Forelimb twitches and wake movements were identified using custom MATLAB scripts. Although infrequent (0.5 ± 0.1% of frames), individual frames in which the wrist position was associated with a low confidence value (<0.80; identified by DLC) were removed and linearly interpolated from the position data of adjacent frames. Forelimb position data were derived to obtain forelimb velocity, and forelimb twitches and wake movements were detected by peak detection of forelimb velocities reaching 2× the SD of quiet periods for twitches, and 3× the SD of the quiet period for wake movements. All movements were required to be preceded by a 250 ms period of quiescence in the forelimb. Every forelimb twitch and wake movement was visually confirmed by the experimenter to identify and discard false positives.

For the analysis of movement amplitude, the forelimb position was summed across the x-, y-, and z-dimensions using the Pythagorean theorem. The peak amplitude was measured as the difference between the point of maximum displacement (using a shared time point for each dimension) and the median baseline position from −0.5 to 0 s before the initiation of a twitch or wake movement. Because twitch amplitude follows an exponential distribution (see Fig. 3A), movements were sorted into logarithmic bins of 0–1, 1–2, 2–4, 4–8, and 8–16 mm.

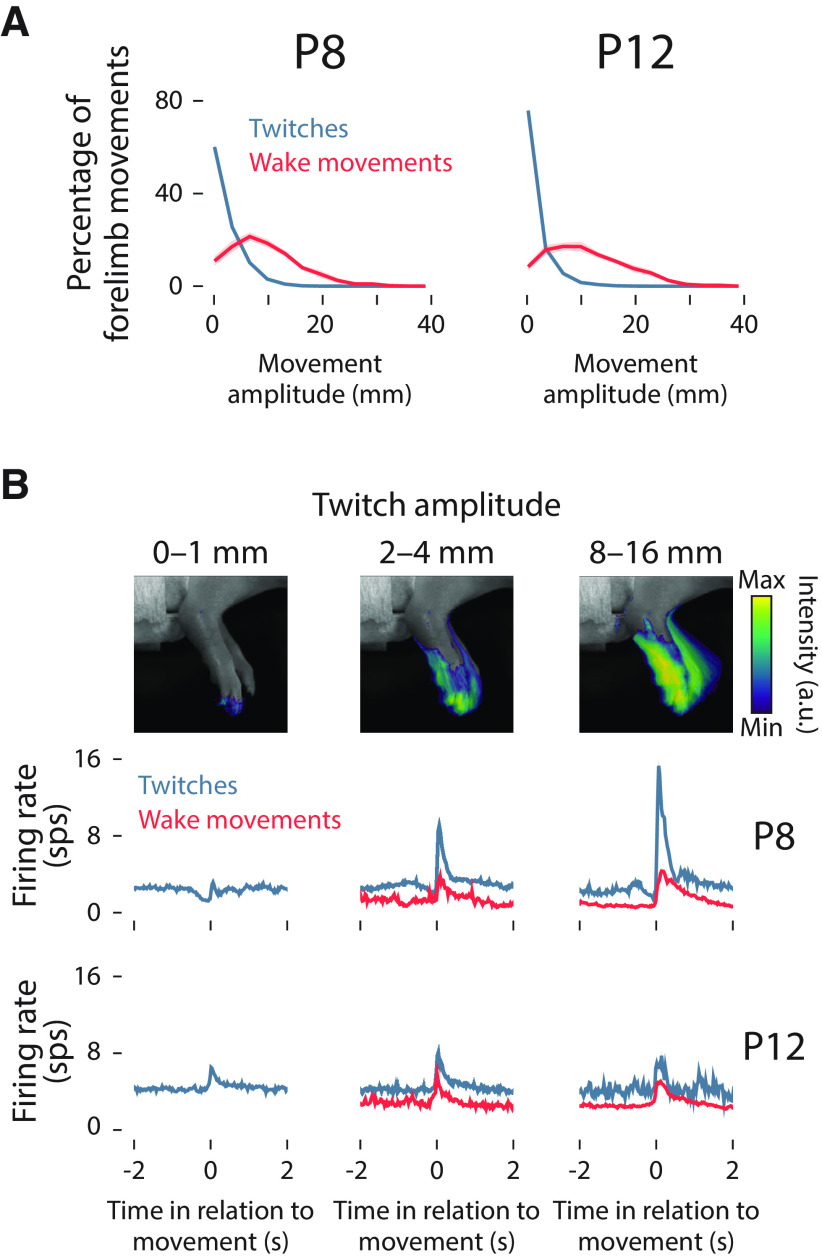
Figure 3.

Relationship between movement amplitude and M1 activity. A, Mean (±SEM) of the percentage of forelimb twitches (blue) and wake movements (red) as a function of amplitude at P8 (left) and P12 (right). B, The average change in pixel intensity within the region of interest across small-amplitude (top-left), medium-amplitude (top-center), and large-amplitude (top-right) twitches is shown as a heatmap. Smaller twitches primarily reflect displacement of the digits, and larger twitches typically reflect displacement of the digits, wrist, and elbow. Below, peristimulus time histograms of the mean firing rate of M1 units in relation to the onset of twitches (blue), and wake movements (red) are shown for P8 (middle row) and P12 rats (bottom row) according to twitch amplitude.

For the analysis of movement direction, the forelimb position was transformed into polar coordinates along the rostral–caudal and medial–lateral axes (see Fig. 5A). Movements were sorted into anterior–posterior or medial–lateral bins. Because wake movements occur during sustained bouts of continuous activity and regularly involve multidirectional trajectories, they could not be analyzed for direction tuning in M1.

Figure 5.

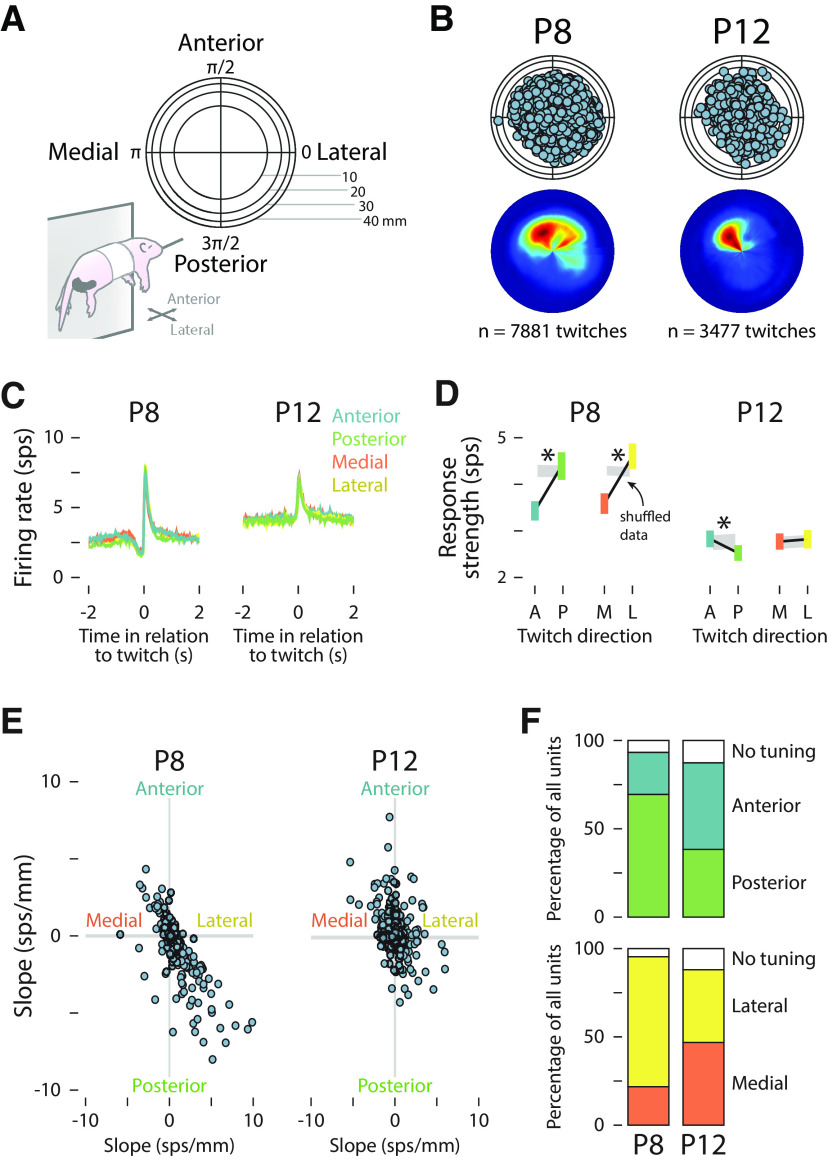
Effect of movement direction on M1 unit activity. A, Two-dimensional representation of twitch direction in polar space. The x-dimension (medial–lateral) and the z-dimension (anterior–posterior) are shown. B, Top, Scatterplot showing the position of the right forelimb at peak twitch displacement for all twitches at P8 (left) and P12 (right). Bottom, Heatmap showing the most common position of the right forelimb at peak twitch displacement for all twitches at P8 and P12. C, Peristimulus time histograms of the mean (±SEM) firing rate of M1 units in relation to the onset time of anterior (blue), posterior (green), medial (orange), and lateral (yellow) forelimb twitches at P8 (left) and P12 (right). D, Mean (±SEM) response strength (Δfiring rate in relation to baseline) for anterior (blue) and posterior (green) twitches, and for medial (orange) and lateral (yellow) twitches at P8 (left) and P12 (right). The gray-shaded regions indicate 99% confidence intervals based on shuffled data. Asterisks indicate a significant difference between movement directions (p < 0.05). E, The slope (magnitude of the relationship between response strength and movement direction) for individual units is represented along the medial–lateral (x) and anterior–posterior (y) axes. The gray-shaded horizontal and vertical lines indicate 99% confidence intervals based on shuffled data. F, Top row, Stacked plots show the percentage of units tuned to anterior (blue) or posterior (green) twitches at P8 and P12. Bottom row, Stacked plots show the percentage of units tuned to medial (orange) or lateral (yellow) twitches at P8 and P12. The white regions indicate untuned units.

Spike sorting.

SynapseLite files were converted to binary files using custom MATLAB scripts and sorted with Kilosort (Pachitariu et al., 2016). Briefly, the 16 channels of neural data were whitened (covariance-standardized) and bandpass filtered (300–5000 Hz) before spike detection. Next, template matching was implemented to sort the event waveforms into clusters. The first-pass spike detection threshold was set to 6 SDs below the mean and the second-pass threshold was set to 5 SDs below the mean. The minimum allowable firing rate was set to 0.01 spikes/s (sps), and the bin size for template detection was set to 656,000 sample points for P8 animals and 262,400 sample points for P12 animals (∼27 s and 11 s, respectively). All other Kilosort parameters were left at their default values.

Clusters were visualized and sorted in Phy2 (Rossant and Harris, 2013). Putative single units (hereafter referred to as “single units”) were defined as having (1) spike waveforms that reliably fit within a well isolated waveform template, (2) a distribution along seven principal components that was absent of clear outliers, and (3) an autocorrelogram with a decreased firing rate at time lag 0 (indicative of the refractory period of a single unit). Clusters meeting the first two criteria but not the third were considered multiunits. Any cluster with a waveform template indicative of electrical noise, a significantly low firing rate (<0.01 sps), or amplitude drift across the recording period was discarded.

In total, 37 single units and 180 multiunits were isolated at P8, and 106 single units and 144 multiunits were isolated at P12. In preliminary analyses, multiunits showed parsimonious results with single units and thus were combined in all analyses (217 and 250 combined units at P8 and P12, respectively). Both single units and unique multiunit clusters are hereafter referred to as “individual units.”

Spindle bursts.

As described previously (Dooley et al., 2020), the neural signal was bandpass filtered at 5–40 Hz with a stopband attenuation of −60 dB and a 1 Hz transition gap. A Hilbert transformation was applied to the filtered waveform, and spindle burst onset was defined as the first point at which the waveform amplitude exceeded the median plus 2 SDs. Spindle bursts were defined as having a minimum duration of 150 ms.

Data shuffling.

Two shuffling procedures were used to approximate the null hypotheses in (1) kinematic analyses and (2) population-activity analyses. First, for all kinematic analyses (see Figs. 3, 4, 5, 7C,D), twitches and wake movements were randomly selected in proportion to the number of movements used in the main analysis. One hundred analyses were performed using randomly selected forelimb movements, and the 99% confidence interval was computed to approximate the distribution of the null hypothesis. For example, see Figure 4A, in which twitches were randomly selected (i.e., amplitude was ignored, but direction was controlled for) and analyzed 100 times, and the 99% confidence interval was taken to obtain the shuffled data.

Figure 4.

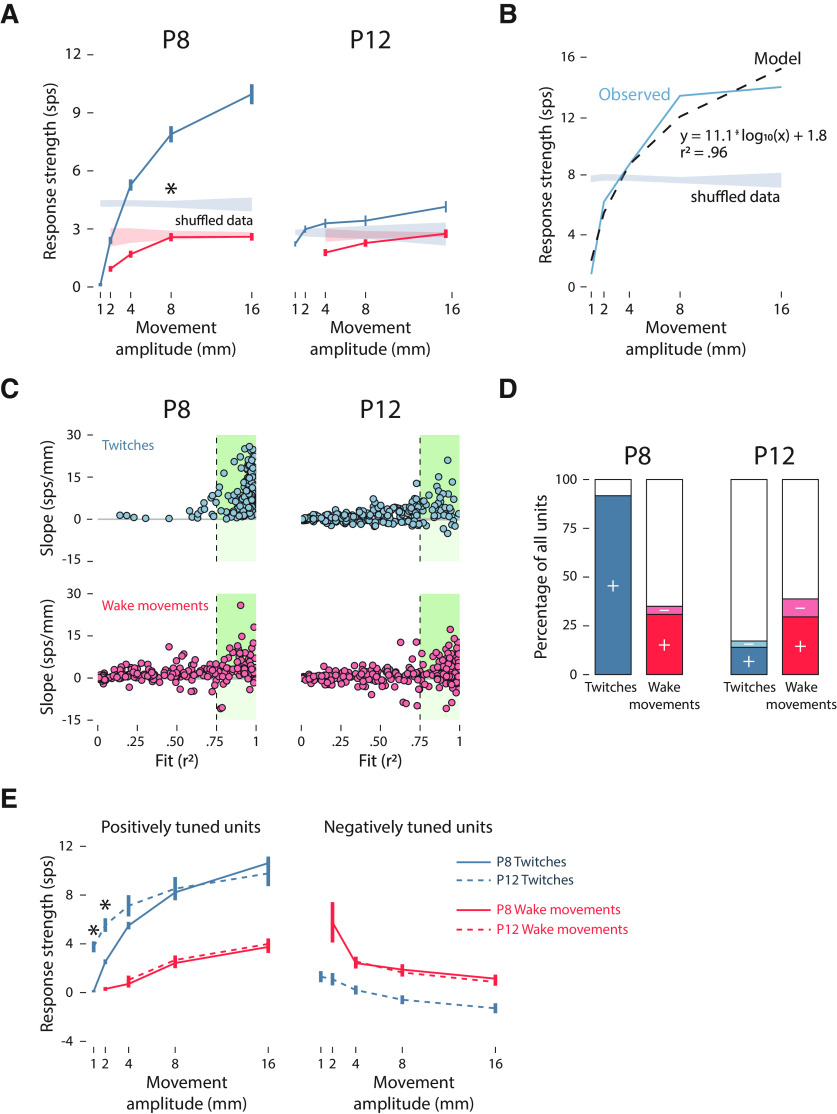
Individual-unit analysis of amplitude tuning in M1. A, Mean (±SEM) response strength (Δfiring rate in relation to baseline) for twitches (blue) and wake movements (red) for all M1 units at P8 (left) and P12 (right). The right edge of each amplitude bin is labeled on the x-axis. Color-coded shaded regions indicate 99% confidence intervals based on shuffled data. Asterisk indicates significant difference between twitches and wake movements at P8 (p < 0.05). B, Representative example of the relationship of an individual M1 unit between response strength and movement amplitude at P8, and its fit to a logarithmic model. The observed data (blue solid line) and model data (black dashed line) are shown alongside the 99% confidence interval based on shuffled data (blue shaded region). The slope of the model (11.1 sps/mm) indicates the magnitude of the relationship between response strength and movement amplitude, and the r² value (0.96) represents the goodness of fit to the logarithmic function. C, Applying the method in B to all M1 units, the slope and r² value for each unit is shown for twitches (blue) and wake movements (red) at P8 and P12. The gray-shaded horizontal lines represent the 99% confidence intervals based on shuffled data, and the dashed vertical lines represent an r² threshold of 0.75. The shaded green regions to the right of the 0.75 threshold show units that are positively (slope > 0) and negatively (slope < 0) correlated with movement amplitude. D, Based on the r² threshold of 0.75 used in C, stacked plots show the percentage of units at P8 and P12 that are positively tuned to movement amplitude for twitches (dark blue) and wake movements (dark red), negatively tuned for twitches (light blue) and wake movements (light red), or not tuned (white). E, As in A, the mean (±SEM) response strength is shown as a function of movement amplitude. Solid and dashed blue lines denote P8 and P12 twitches, respectively; solid and dashed red lines denote P8 and P12 wake movements, respectively. Positively and negatively tuned units were identified using an r² threshold of 0.75. Asterisks indicate significant difference between P8 and P12 (p < 0.05).

Figure 7.

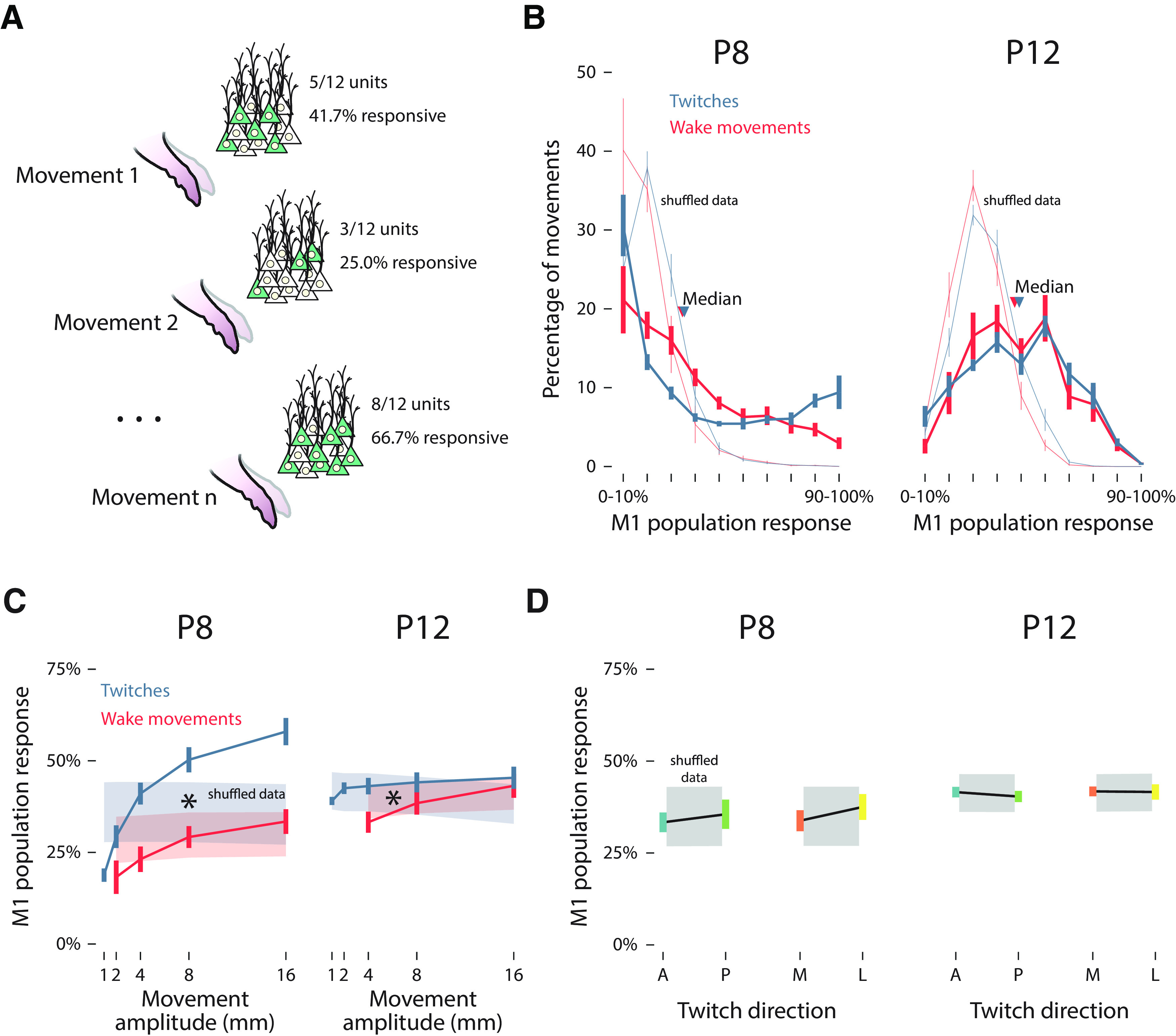
Population responses in M1. A, Illustration of the relationship between forelimb movements (1 through n) and the percentage of M1 units responding to a given movement (i.e., population response). B, Mean (±SEM) percentage of twitches (blue) and wake movements (red) that yielded population responses of 0–10% to 90–100% at P8 (left) and P12 (right). Median values for twitches (blue arrows) and wake movements (red arrows) are also shown. Light blue and red lines indicate shuffled data for twitches and wake movements, respectively. C, Mean (±SEM) population response for M1 units as a function of the amplitude of twitches (blue) and wake movements (red) at P8 (left) and P12 (right). Color-coded shaded regions represent 99% confidence intervals based on shuffled data. Asterisks indicate significant main effect of twitches versus wake movements (p < 0.05). D, Mean (±SEM) population response of M1 units for anterior (blue), posterior (green), medial (orange), and lateral (yellow) twitches at P8 (left) and P12 (right). Gray-shaded regions indicate 99% confidence intervals based on shuffled data.

Second, for all population–activity analyses (i.e., see Figs. 6, 7B), the interspike intervals of each spike train were resampled and used to create shuffled spike trains. This procedure conserves the overall firing rate and temporal dynamics of each unit (Perkel et al., 1967; Rivlin-Etzion et al., 2006). Analyses using the resampled spike trains were repeated 100 times, and the 99% confidence interval computed to obtain the shuffled data.

Figure 6.

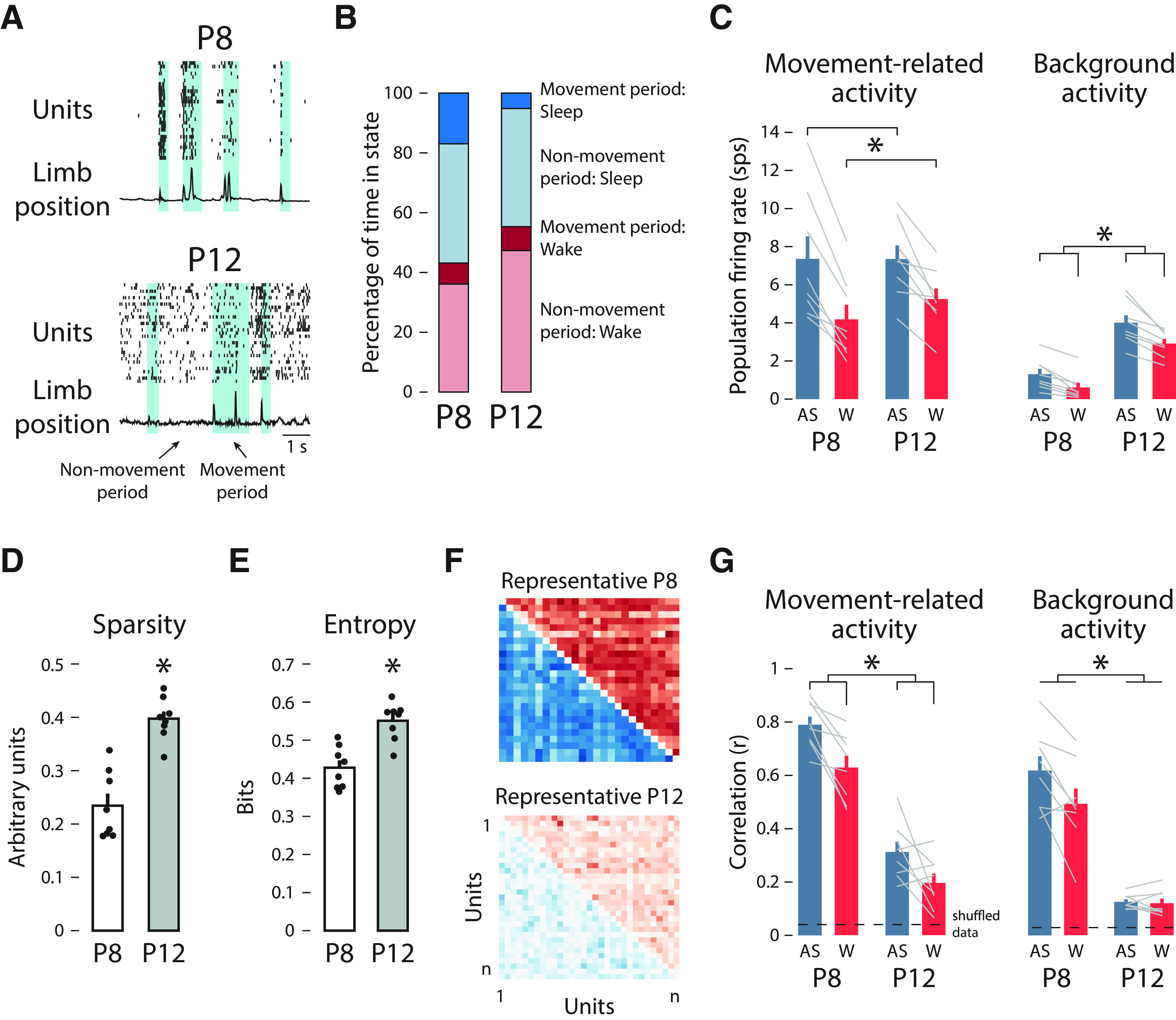
Population spiking activity decorrelates between P8 and P12. A, Population spiking activity and limb position from a representative P8 (top) and P12 (bottom) rat are shown. A spike raster (each row represents one unit) and limb position trace (normalized) is shown for each pup. Shaded regions represent movement periods, and the unshaded regions represent nonmovement periods. B, The percentage of time spent in movement or nonmovement periods (movement period (sleep), blue; nonmovement period (sleep), light blue; movement period (wake), red; nonmovement period (wake), light red) is shown for P8 (left) and P12 (right) animals. C, Mean (±SEM) movement-related activity (left-hand plot) and background activity (right-hand plot) firing rate for active sleep (blue) and wake (red) for P8 (left) and P12 (right). Firing rates for each rat are shown as gray lines. Asterisks denote a significant main effect of behavioral state (left-hand plot; p < 0.05) and significant main effects of behavioral state and age (right-hand plot; p < 0.05). D, Mean (±SEM) values of sparsity for P8 (white) and P12 (gray) rats. Black dots show the values for individual pups. The asterisk indicates a significant difference between P8 and P12 (p < 0.05). E, Mean (±SEM) values of entropy for P8 (white) and P12 (gray) rats. Black dots show the values for individual pups. The asterisk indicates a significant difference between P8 and P12 (p < 0.05). F, Representative correlation matrices for each unit–unit pair (x- and y-axes) for a P8 (top) and a P12 (bottom) rat during movement periods. Blue squares indicate correlations during active sleep, and red squares indicate correlations during wake. Darker colors denote higher r² values. G, Mean (±SEM) correlation coefficient (r) during active sleep (blue) and wake (red) for P8 (left) and P12 (right) animals for movement-related activity (left-hand plot) and background activity (right-hand plot). Correlation coefficients for each rat are shown as gray lines. Dashed horizontal lines indicate 99% confidence interval based on shuffled data. Asterisks represent significant main effects of behavioral state and age (left-hand plot; p < 0.05) and a significant main effect of age (right-hand plot; p < 0.05).

Population analyses.

The onset of movement periods was defined as the onset of twitches and wake movements described above. The offset of each movement period was defined as the time point 250 ms after the displacement of the forelimb returned below the threshold for detection (described above) for the first time. Therefore, each movement period was followed by 250 ms to account for reafference arising from each movement. The onset of nonmovement periods was defined as the offset of movement periods, and therefore were preceded by 250 ms of quiescence in the limb. The offset of the nonmovement periods was defined as the initiation of the next movement. All nonmovement periods <250 ms and all periods that overlapped were discarded from analysis (<2% of the duration of any recording).

Sparsity was defined according to Rolls and Tovee (1995) as follows:

$$S={\left(\frac{{{\displaystyle \sum }}_{i=1}^n{r}_i}{n}\right)}^2/\frac{{{\displaystyle \sum }}_{i=1}^n{r}_i^2}{n},$$

where n represents the number of forelimb movements of a given pup and $r_i$ represents the firing rate of a given unit from 0 to 250 ms after the ith forelimb movement. Entropy (of a discrete random variable) was defined according to the study by Shannon (1948), as follows:

$$H={\displaystyle \sum }_{x=1}^{n}p\left(x\right)\text{*}{\log }_2\left(\frac{1}{p(x)}\right),$$

where n represents the number of possible states for a unit (based on its firing rate) and $p(x)$ represents the probability distribution of a given unit in that state. Firing rate data were discretized according to procedures outlined in the study by Timme and Lapish (2018). Briefly, the firing rate of a unit was calculated in 250 ms time windows, and each window was assigned to one of three possible states based on a uniform-width binning of the firing rate distribution.

For correlation analyses, movement and nonmovement periods were broken down into 250 ms time windows and a Pearson correlation coefficient of the firing rate was computed across time windows for every possible unit–unit pair. All Pearson coefficients for an animal were averaged together before comparison between P8 and P12.

“Population response” was defined as the percentage of all units of a given pup that were “responsive” to a given forelimb movement. A unit was considered responsive if its firing rate significantly increased (i.e., above the 95% confidence interval of baseline firing rate) after a forelimb movement; otherwise, a unit was considered unresponsive.

Statistical analysis.

All data were tested for normality using the Shapiro–Wilk test, for equal variance using Levene's test (for between-subjects variables), and for sphericity using Mauchly's test (for within-subjects variables with greater than two groups) before analysis. In analyses in which the variance between groups was not equal, a pooled error term was not used when generating simple main effects and post hoc tests. In analyses in which sphericity was violated, a Huynh–Feldt correction was applied to the degrees of freedom. Probabilities and r² values were arc-sin transformed before analysis. The mean and SEM are used throughout as measures of central tendency and dispersion, respectively.

All analyses were performed as independent t tests, or two- or three-way mixed-design ANOVAs. Simple main effects were only tested if the interaction term was significant. In all two- and three-way ANOVAs, an adjusted partial η² was used as an estimate of effect size that corrects for positive bias because of sampling variability (Mordkoff, 2019). For all t tests and one-way ANOVAs, an adjusted η² estimate of effect size was reported.

Data availability.

Raw data (action potential time stamps, behavioral event time stamps, and forelimb position time series) will be made available on request. Select custom MATLAB scripts used here can be found on Github (https://github.com/rglanz/Glanz_et_al._2021). Additional scripts and data used will be made available on request.

Results

To characterize the relationship between movement kinematics and M1 activity, we tracked forelimb movements in three dimensions for 1 h using two high-speed (100 frames/s) cameras oriented perpendicularly to each other (Fig. 1A). The trajectory of forelimb movements was quantified using DLC, a machine-vision tool for behavioral analysis (Mathis et al., 2018; Nath et al., 2019). At the same time, we performed extracellular recordings in the contralateral forelimb region of M1 (Fig. 1B,C). Because preliminary analyses indicated similar results for single units and multiunits, all units were analyzed together. Figure 1D depicts representative behavioral and electrophysiological data collected at each age; most striking is the transition from discontinuous to continuous unit activity from P8 to P12 (Movies 1, 2).

Relationship between forelimb twitching (left) and unit activity in the contralateral forelimb region of M1 (top right) in a P8 rat. Limb movement was tracked using DeepLabCut and visualized in MATLAB (bottom right). Each row in the M1 record represents 1 of 26 simultaneously recorded units; each unit is associated with a distinct audible tone. Note the discontinuous pattern of M1 activity at this age.

Movie 2.

Same as for Movie 1 except for 31 M1 units in a P12 rat. Note the continuous pattern of M1 activity at this age.

M1 activity is strongly modulated by behavioral state

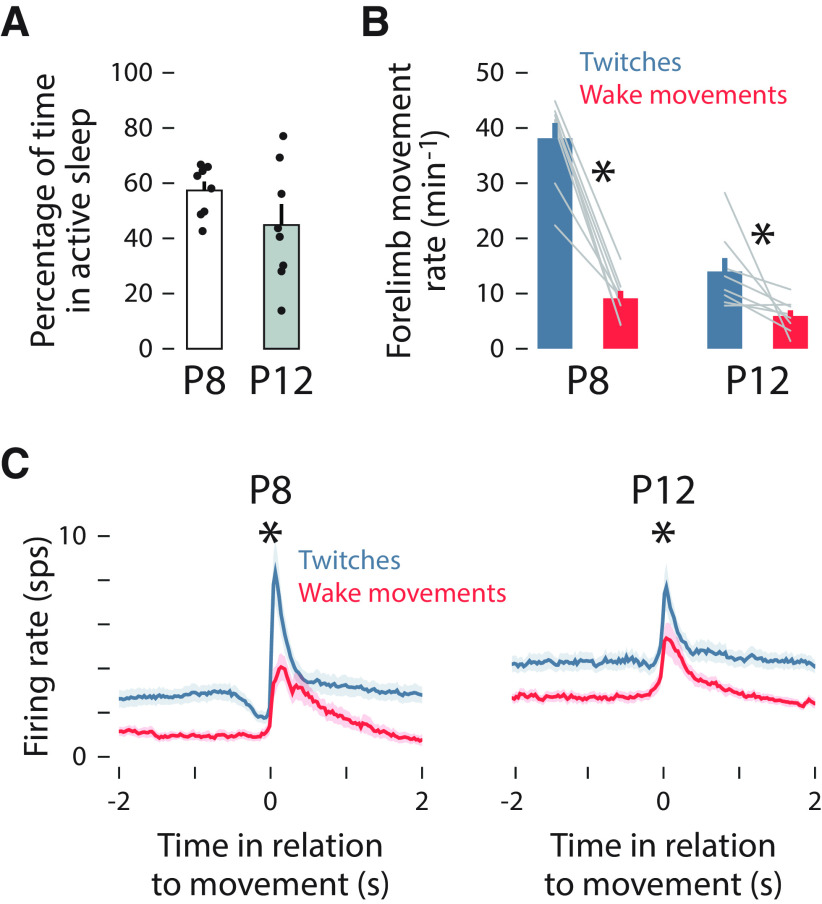
Over the 60 min recording periods, P8 and P12 rats spent 57.4 ± 3.2% and 44.8 ± 7.6% of the time in active sleep, respectively (t₍₁₄₎ = 1.51, p = 0.153, adjusted ${\widehat{\eta }}^2$ = 0.140; Fig. 2A). Twitches occurred significantly more frequently than wake movements at both ages (P8: F_(1,7) = 92.08, p < 0.001, adjusted ${\widehat{\eta }}^2$ = 0.859; P12: F_(1,7) = 7.11, p = 0.018, adjusted ${\widehat{\eta }}^2$ = 0.289; Fig. 2B). The relative abundance of active sleep and twitches, especially at P8, provides ample opportunity for reafference from twitching limbs to drive M1 activity.

Figure 2.

Twitch and wake movements trigger reafferent responses in M1. A, Mean (±SEM) percentage of time spent in active sleep at P8 (white) and P12 (gray). Black dots show values for individual pups. B, Mean (±SEM) rate of forelimb movements for twitches during active sleep (blue) and movements during wake (red) at P8 (left) and P12 (right). Gray lines show values for individual pups. Asterisks denote significant difference between twitches and wake movements (p < 0.05). C, Peristimulus time histograms of mean firing rate of M1 units in relation to twitches (blue) and wake movements (red) at P8 (left) and P12 (right). Asterisks denote significant difference between responses to twitches and wake movements (p < 0.05).

Consistent with previous reports (Tiriac and Blumberg, 2016; Dooley and Blumberg, 2018), we found here at P8 that twitches drove relatively more M1 activity than did wake movements (Fig. 2C). This state dependence in reafferent activity was significant across age (F_(1,14) = 30.16, p < 0.001, adjusted ${\widehat{\eta }}_p^2$ = 0.660). Compared with previous studies that relied on EMG recordings in a single limb muscle to detect movement (Tiriac et al., 2014; Tiriac and Blumberg, 2016; Dooley and Blumberg, 2018), the video-based method used here substantially increased the number of twitches and wake movements that could be detected across the entire limb. As a consequence, at P8 we now reliably detected more M1 activation in response to wake movements than previously reported (Tiriac and Blumberg, 2016; Dooley and Blumberg, 2018); nonetheless, reafferent responses to twitches were still larger than they were to wake movements.

M1 units are tuned to movement amplitude at P8

As mentioned above, we recently reported in P5 rats that whisker movement amplitude reliably predicts activity in S1 barrel cortex (Dooley et al., 2020). Accordingly, we hypothesized here that M1 similarly codes for limb movement amplitude during the sensory stage of its development. To test this hypothesis, the amplitude of forelimb twitches and wake movements was aggregated across three dimensions and compared with reafferent responses in M1. To avoid potential bias, equal numbers of anterior/posterior and medial/lateral movements were selected at random for these analyses. Finally, movement velocity and acceleration were highly correlated with movement amplitude and thus were not analyzed further (Pearson's r, 0.71–0.98; data not shown).

We found that the amplitude of forelimb twitches was exponentially distributed at P8 and P12, with small twitches being more frequent than large twitches (Fig. 3A). In contrast, the amplitude of wake movements followed a positively skewed normal distribution. To account for the exponential distribution of twitches, forelimb movements were sorted into logarithmically scaled amplitude bins from 2⁰ to 2⁴ mm (i.e., 1–16 mm). Whereas small forelimb movements resulted primarily in the displacement of the distal forelimb (i.e., wrist and digits; Fig. 3B, top), large forelimb movements resulted in greater displacement of the proximal forelimb (i.e., forearm and elbow). At P8, twitches of increasing amplitude triggered increasing unit activation in M1 (Fig. 3B, bottom). This amplitude tuning was not observed for wake movements at P8, or for twitches or wake movements at P12.

The relationship between movement amplitude and response strength—defined as the difference the mean firing rate 0–250 ms after a movement and the mean baseline firing rate determined at −3 to −2 s before a movement—is quantified in Figure 4A. At P8, response strength significantly increased with respect to increasing twitch amplitude, but not wake movement amplitude (F_(1,216) = 250.27, p < 0.001, adjusted ${\widehat{\eta }}^2$ = 0.535). This was not the case at P12 (F_(1,249) = 0.42, p = 0.520, adjusted ${\widehat{\eta }}^2$ < 0.001).

Although wake movements at P8, and all movements at P12, did not show a significant relationship with amplitude when averaged across units, it is still possible that some individual units were tuned to movement amplitude. To characterize the relationship between movement amplitude and response strength on a unit-by-unit basis, the response strength of each unit was fit to a logarithmic model with respect to movement amplitude (Fig. 4B). A logarithmic model was chosen based on the relationship between twitch amplitude and response strength observed at P8. Both the slope and the goodness of fit (r²) of the model were used to assess the relationship of each unit with movement amplitude. In Figure 4C, the r² value and slope of the model for each M1 unit are shown. A minimum r² value of 0.75 was chosen to consider an individual unit to be tuned to movement amplitude. At P8, the vast majority of M1 units showed positive tuning to amplitude, with r² values >0.75 and slopes that exceeded the 99% confidence interval of shuffled data. In contrast, for wake movements at P8 and all movements at P12, only a fraction of M1 units met these criteria, and some units even displayed negative relationships with amplitude (i.e., negative tuning).

As shown in the stacked plots in Figure 4D, nearly all M1 units at P8 exhibited a positive tuning to twitch amplitude (positive, 91.7%; negative, 0%), indicating highly redundant responses across units. In contrast, at P8, far fewer units exhibited amplitude tuning to wake movements (positive, 30.9%; negative, 4.2%). At P12, relatively few units exhibited tuning to twitch amplitude (positive, 14.0%; negative, 3.2%) or wake movement amplitude (positive, 29.6%; negative, 9.2%), indicating a reduction in response redundancy across units. Finally, to confirm that these findings were not driven by an arbitrary selection of an r² threshold of 0.75, we repeated these tests using thresholds of 0.50 and 0.90 and found the same pattern of results (data not shown).

When positively and negatively tuned units are considered separately, only twitches showed an age-related change in tuning strength: small twitches (0–2 mm) at P12 were better able than small twitches at P8 to drive M1 activity (F_{(1.31,291.02)} = 10.01, p = 0.001, adjusted ${\widehat{\eta }}^2$ = 0.039; Fig. 4E). In contrast, amplitude tuning for wake movements did not change with age for either positively or negatively tuned units. Such a finding indicates that M1 is better able to detect small twitches, but not wake movements, at P12.

In summary, these findings extend previous reports (Tiriac and Blumberg, 2016; Dooley and Blumberg, 2018) by showing that forelimb twitches in early development differentially trigger M1 activity across a range of movement amplitudes. This is the first demonstration of amplitude coding in infant M1 and is consistent with similar findings in S1 barrel cortex (Dooley et al., 2020).

M1 units are sensitive to movement direction

We next analyzed M1 activity as a function of twitch direction. (Because wake movements occur in prolonged bouts with multiple changes in direction, they could not be included in this analysis.) Twitch direction was analyzed separately along the following two dimensions: anterior–posterior and medial–lateral (Fig. 5A). Because the pup's limbs dangled freely in our testing environment, forelimb twitches nearly always traveled in a pendular motion (i.e., with dorsal, not ventral, displacement). Thus, the dorsal–ventral dimension did not provide unique information about twitch direction and was therefore not analyzed. Again, to avoid potential bias, we ensured that twitches in each direction had identical amplitude distributions.

Forelimb twitches occurred in all directions relative to the resting position of the limb (Fig. 5B), but were most likely to travel anteriorly at P8 and anteriorly and medially at P12. In any direction, twitches produced similar responses in M1 units at both P8 and P12 (Fig. 5C). However, as shown in Figure 5D, the average response strength at P8 was significantly lower for anterior compared with posterior twitches (F_(1,216) = 51.05, p < 0.001, adjusted ${\widehat{\eta }}^2$ = 0.187) and medial compared with lateral twitches (F_(1,216) = 53.75, p < 0.001, adjusted ${\widehat{\eta }}^2$ = 0.195). At P12, there was a small but statistically significant difference in response strength between anterior and posterior twitches (F_(1,249) = 9.80, p = 0.002, adjusted ${\widehat{\eta }}^2$ = 0.034), but not between medial and lateral twitches (F_(1,249) = 0.28, p = 0.599, adjusted ${\widehat{\eta }}^2$ < 0.001).

Again, the trends in direction-related response strength, averaged across all units, may have obscured the direction tuning of individual units. Accordingly, the direction tuning of individual units was assessed by measuring the difference in response strength between anterior/posterior and medial/lateral twitches. At P8, individual units tended to be responsive to twitches that traveled posteriorly and laterally (Fig. 5E). By P12, receptive fields were more uniformly distributed across all four direction combinations. Indeed, at P8, the majority of units were tuned to posterior rather than anterior movements (69.6% and 24.0%, respectively) and to lateral rather than medial movements (73.3% and 22.1%, respectively; Fig. 5F). At P12, however, direction tuning was more evenly distributed (range, 38.4–49.2%). Thus, as with amplitude tuning, there was an age-related reduction among M1 units in the redundancy of direction tuning.

Sparse background activity emerges at P12

Thus far, we have focused on the correlation between movement kinematics and the firing rate of individual units. However, the activity across units (i.e., population spiking activity) also undergoes a marked developmental shift: population activity shifts from discontinuous at P8 to continuous at P12 (Fig. 6A). To characterize this change in population activity, we draw a distinction between movement-related activity—M1 activity occurring during and immediately after (i.e., within 250 ms) limb movements—and background activity—M1 activity occurring during periods in which limb movements are absent.

To characterize the change in population spiking activity between P8 and P12, we first characterized four periods during each recording session: (1) movement periods during active sleep (i.e., periods of twitches); (2) nonmovement periods during active sleep; (3) movement periods during active wake (i.e., periods of wake movements); and (4) nonmovement periods during wake (Fig. 6B). Pups at both ages spent a greater percentage of time in nonmovement periods (P8: AS = 39.9%, W = 36.1%; P12: AS = 39.5%, W = 47.4%) than in movement periods (P8: AS = 17.0%, W = 7.0%; P12: AS = 5.2%, W = 8.0%). As shown in Figure 6C, movement-related population activity was significantly higher during active sleep than wake (F_(1,14) = 53.97, p < 0.001, adjusted ${\widehat{\eta }}_p^2$ = 0.779), and this state difference did not change between P8 and P12 (F_(1,14) = 0.22, p = 0.644, adjusted ${\widehat{\eta }}_p^2$ < 0.001). Conversely, background population activity was not only higher during active sleep compared with wake (F_(1,14) = 47.31, p < 0.001, adjusted ${\widehat{\eta }}_p^2$ = 0.756), but exhibited a threefold to fourfold increase between P8 and P12 (F_(1,14) = 39.21, p < 0.001, adjusted ${\widehat{\eta }}_p^2$ = 0.718). Thus, the increase in the population spiking activity of M1 between P8 and P12 occurred almost entirely during nonmovement periods.

Next, we asked whether the patterning of M1 population activity changed between P8 and P12. We first measured the change in sparsity (the degree to which action potentials are uniformly distributed across time) and entropy (the informational capacity available given the patterning of activity) from P8 to P12. Importantly, sparsity and entropy interact to efficiently encode sensory features in cortical networks (Barranca et al., 2014). Indeed, across M1 units, both sparsity and entropy increased significantly between P8 and P12 (sparsity: t_(10.89) = 5.97, p < 0.001, adjusted ${\widehat{\eta }}^2$ = 0.744; entropy: t₍₁₄₎ = 4.71, p < 0.001, adjusted ${\widehat{\eta }}^2$ = 0.585; Fig. 6D,E).

To assess whether the increase in uniform background activity affected population dynamics in M1, we computed unit-by-unit correlations of activity during each of the four periods outlined above. Figure 6F shows correlation matrices for representative pups at P8 and P12 during active sleep (blue) and wake (red) movement periods. Movement-related activity, but not background activity, was significantly more correlated during active sleep than wake (F_(1,14) = 28.02, p < 0.001, adjusted ${\widehat{\eta }}_p^2$ = 0.643; Fig. 6G). Moreover, movement-related activity was significantly less correlated at P12 than at P8 (F_(1,14) = 91.97, p < 0.001, adjusted ${\widehat{\eta }}_p^2$ = 0.859), as was background activity (F_(1,14) = 53.41, p < 0.001, adjusted ${\widehat{\eta }}_p^2$ = 0.777). This decorrelation of population activity further indicates a transition toward sparse—and therefore less redundant—M1 activity at P12. Although population activity was significantly less correlated at P12, the observed correlations were still stronger than expected (i.e., compared with shuffled data). In other words, population spiking activity at P12 continued to exhibit an organized temporal structure.

Next, we sought to characterize the population-level activity of M1 units in response to forelimb movements. For each given movement, an M1 unit was considered responsive if its firing rate increased significantly (i.e., exceeded the 95% confidence interval) relative to its baseline firing rate. If this threshold was not reached, the M1 unit was considered “unresponsive” to that particular movement. For each limb movement, then, the percentage of responsive M1 units—the population response—was calculated (Fig. 7A). Figure 7B plots the mean percentage of forelimb movements across pups (y-axis) that triggered a given population response (x-axis).

At P8, a plurality (20–30%) of forelimb movements during sleep and wake triggered only a small percentage of M1 units (Fig. 7B, left). Also, twitches, but not wake movements, regularly triggered activity (∼10% of responses) in nearly all M1 units. As a consequence, population responses at P8 followed a near-exponential distribution, with “all-or-nothing” responses occurring frequently—especially in response to forelimb twitches.

At P12, the distributions of the population responses to twitches and wake movements changed substantially (Fig. 7B, right). Overall, forelimb movements at this age tended to trigger activity in approximately half of the M1 units, resulting in an approximately normal distribution. Indeed, all eight of the P12 rats—but only two of the eight P8 rats—exhibited normal distributions of their population responses (data not shown). Population responses were significantly larger for twitches than wake movements, but this effect was smaller than that of age (P8 vs P12: F_(3.51,49.15) = 26.93, p < 0.001, adjusted ${\widehat{\eta }}_p^2$ = 0.607; AS vs W: F_(1,14) = 4.63, p = 0.049, adjusted ${\widehat{\eta }}_p^2$ = 0.194). Furthermore, the distributions of population responses shifted as “all-or-nothing” responses (i.e., <10% or >90% of units responding) decreased from 26.9% at P8 to just 1.4% at P12. In other words, M1 population responses became substantially less redundant by P12.

We next determined whether movement kinematics predict M1 population responses. As shown in Figure 7C, the population response increased significantly as a function of movement amplitude at both ages, but the state-dependence of this relationship was stronger at P8 (F_(1,7) = 22.06, p < 0.001, adjusted ${\widehat{\eta }}^2$ = 0.571) than at P12 (F_(1,7) = 9.37, p = 0.008, adjusted ${\widehat{\eta }}^2$ = 0.357). Overall, larger movements drove more activity within and across M1 units, especially during active sleep at P8.

In contrast with movement amplitude, twitch direction was not significantly related to population response at either age (anterior vs posterior: F_(1,14) = 2.26, p = 0.155, adjusted ${\widehat{\eta }}_p^2$ = 0.078; medial vs lateral: F_(1,14) = 2.70, p = 0.123, adjusted ${\widehat{\eta }}_p^2$ = 0.101; Fig. 7D). This finding mirrors the small (though significant) differences in direction tuning observed in individual M1 units at P8.

In summary, we found that M1 background activity increased sharply between P8 and P12, and that all population activity became sparser and more decorrelated across these ages. Also, population responses became less sensitive to movement amplitude at P12, and at the same time displayed a substantially different statistical distribution (i.e., normal vs exponential) in response to self-generated movements.

Kinematic tuning is not mediated by spindle bursts

Spindle bursts are brief thalamocortical oscillations (10–20 Hz; Fig. 8A,B) that are thought to contribute to early cortical development (Hanganu et al., 2006; Tolner et al., 2012; Yang et al., 2013; Dooley et al., 2020). Because spindle bursts are readily detectable at P8 but not P12 (Shen and Colonnese, 2016), they could potentially mediate the effect of twitch amplitude on M1 activity at that earlier age. Indeed, spindle bursts were more likely to occur during active sleep than during wake (t₍₇₎ = 2.94, p = 0.022, adjusted ${\widehat{\eta }}^2$ = 0.489; Fig. 8C). However, whereas twitches and wake movements occurred at a rate of 28.3 ± 4.6 and 11.7 ± 1.2 min⁻¹, respectively, spindle bursts occurred at a rate of 4.0 ± 0.7 min⁻¹ during active sleep and 2.5 ± 0.4 min⁻¹ during wake. Consequently, only a small percentage of forelimb movements (10.0 ± 1.4%) occurred within ±0.5 s of a spindle burst.

Figure 8.

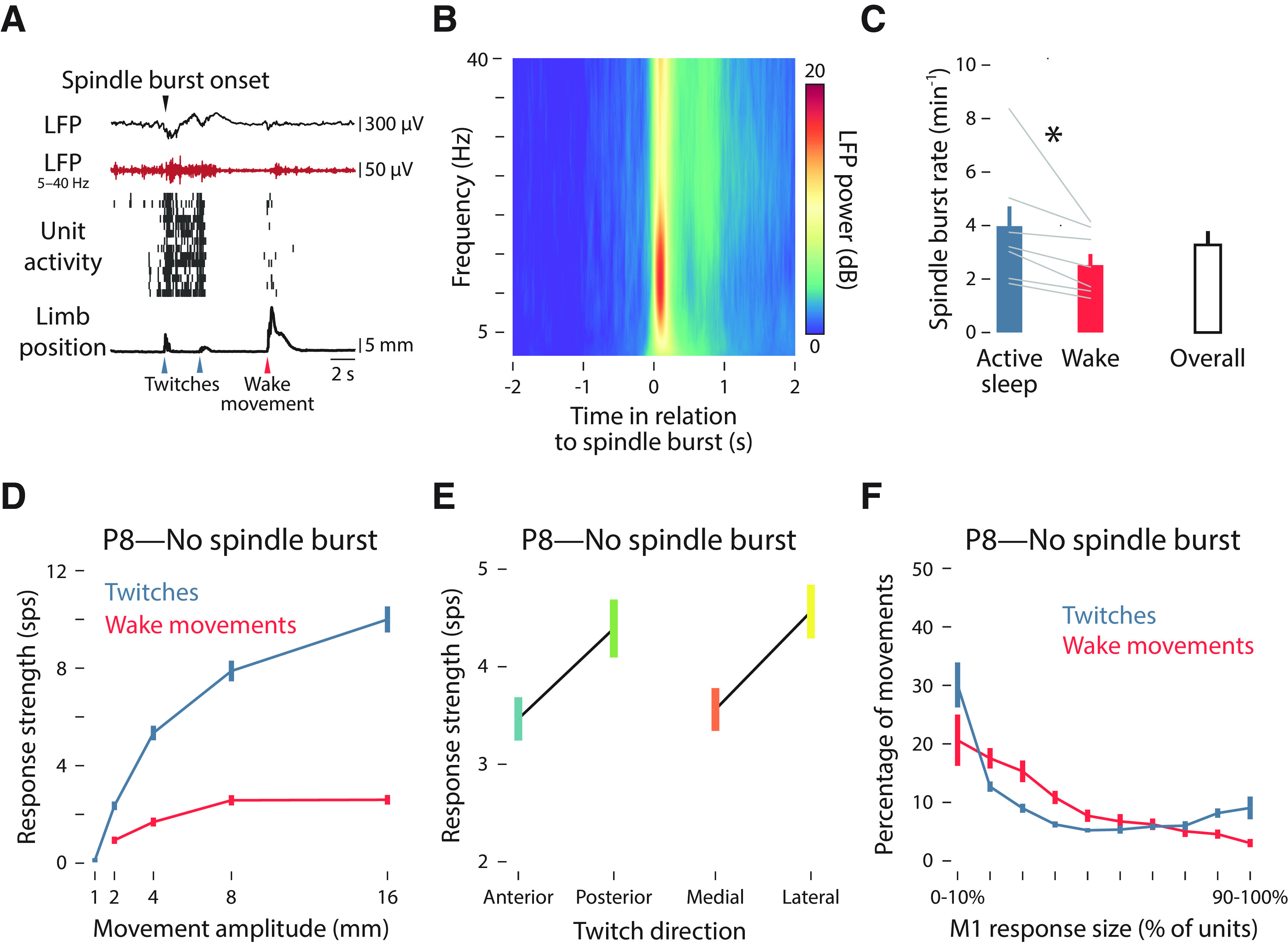
Kinematic tuning is not mediated by spindle bursts. A, Representative data from a P8 rat. From top to bottom: a trace of the local field potential (LFP) in M1, including the onset of a spindle burst denoted with a black arrow; a filtered (5–40 Hz) LFP trace (red); unit activity in M1, with each row denoting a different unit and each vertical tick denoting an action potential; a trace of forelimb displacement (black), with twitches and wake movements denoted by blue and red arrows, respectively. B, Time–frequency spectrogram of LFP activity in M1, averaged across all P8 rats. The analysis was triggered on the onset of detected spindle bursts. C, The rate of spindle bursts during active sleep (blue bar) and wake (red bar), as well as the overall rate (white bar) is shown for P8 rats. Gray lines show the values for individual pups. Asterisk denotes significance difference between sleep and wake (p < 0.05). D, Same as in Figure 4A, but triggered only on movements that did not occur within ±0.5 s of a spindle burst. E, Same as in Figure 5D, but triggered only on twitches that did not occur within ±0.5 s of a spindle burst. F, Same as in Figure 7B, but triggered only on movements that did not occur within ±0.5 s of a spindle burst.

We determined the response strength within individual M1 units triggered on forelimb movements that did not occur within ±0.5 s of a spindle burst as a function of movement amplitude (Fig. 8D) and movement direction (Fig. 8E); response strength was largely unchanged compared with the earlier analyses for movement amplitude (Fig. 4A) and movement direction (Fig. 5D). M1 activity across units (population response) was similarly unaffected when triggered only on forelimb movements that did not occur within ±0.5 s of a spindle burst (Fig. 8F). Altogether, these findings indicate that the kinematic properties of M1 units observed at P8, and the shift in kinematic properties at P12, are not mediated by spindle bursts.

Discussion

We have demonstrated here in sleeping P8 rats that the processing of reafference in M1 is sensitive to the kinematic features of twitches—especially twitch amplitude. This is the first such demonstration of rate coding of movement amplitude in M1. Recently, in P5 rats, we similarly found that larger whisker twitches more strongly drive neural activity in S1 barrel cortex (Dooley et al., 2020). Although spontaneous activity also occurs in the developing retina (Hanganu et al., 2006; Ackman et al., 2012) and cochlea (Tritsch et al., 2007), it is not known whether this activity produces rate-coded responses in visual and auditory cortex, respectively.

It is not clear whether M1 amplitude coding indicates tuning to the position of the forelimb in space per se, or simply tuning to the muscles that produce forelimb movements. For example, it is possible that larger forelimb movements tend to be produced by larger forelimb muscles (e.g., those at the shoulder), consequently triggering stronger reafferent activation of M1. If this were the case, one might expect that individual units would respond selectively to twitches of either large or small muscles (and thus either large or small movements). On the contrary, we found at P8 that individual units were responsive across a range of movement amplitudes. This observation suggests that each unit is not tuned to a specific muscle, but rather to movement amplitude across the entire limb.

Interestingly, once reafferent activity is conveyed to M1, it is modulated in a state-dependent manner that, again, resembles the state-dependent modulation found in S1 barrel cortex (Dooley et al., 2020). In fact, although equally sized forelimb twitches and wake movements are presumably similar in terms of their patterns of forelimb muscle activation, twitches nonetheless produce substantially greater M1 activation (Fig. 2C). This state-dependent amplitude tuning was particularly clear at the level of individual units: of the 217 units recorded from at P8, 91% were tuned to twitch amplitude and 62% were tuned exclusively to twitch amplitude (data not shown).

At P8, nearly all M1 units were sensitive to twitch direction (Fig. 5). Assuming that twitches in different directions are caused by recruitment of different combinations of muscles, this finding suggests that M1 neurons at P8 are sensitive to the combination of forelimb muscles producing each twitch. However, EMG recordings of each forelimb muscle would be necessary to accurately assess the contributions of each muscle to M1 activity at this age. Notably, twitches with uncommon characteristics (e.g., large twitches, posterior/lateral twitches) produced the most unit activity, suggesting that neural activity in M1 is biased toward the detection of these twitches at P8. Thus, it may be that self-generated movements with relatively rare kinematic properties are amplified so as to ensure their continued representation in the forelimb region of M1. This issue could be explored further by monitoring the development of M1 tuning parameters in response to experimental manipulation of twitch amplitude or direction.

We also found that the informational content provided to M1 by twitch reafference increased from P8 to P12. At P8, amplitude and direction tuning were uniformly distributed across M1 units: 91% of units were tuned to twitch amplitude (Fig. 4D) and 70–73% of units were tuned to a single twitch direction (Fig. 5F). Thus, when considering all units together, the kinematic information about twitches was represented redundantly within M1. Redundancy decreased by P12: the number of amplitude-tuned units decreased to just 17% of all units, and at most 49% of units were tuned to a single direction. This decrease in redundancy, along with the increased responses of M1 units to small twitches at P12 (Fig. 4E), indicates an increase in informational content provided by twitches at P12. Therefore, whereas the system at P8 seems to prioritize the detection of self-generated movements, the system at P12 seems to prioritize the most efficient and informative representation of those movements.

Finally, spindle bursts, a predominant thalamocortical oscillation in neonatal rats (Hanganu et al., 2006; Tolner et al., 2012; Yang et al., 2013; Dooley et al., 2020), were too infrequent at P8 to mediate the observed effects of movement amplitude and direction on M1 activity (Fig. 8C). Only 10% of forelimb movements coincided with spindle bursts, and exclusion of those movements from analysis did not alter the M1 response profiles (Fig. 8D–F). Although one proposed role for spindle bursts is to strengthen developing thalamocortical circuitry (Tolner et al., 2012; Yang et al., 2013; Murata and Colonnese, 2016), it is unclear how spindle bursts, compared with spiking activity alone, are contributing to this process at P8. However, because the rate of spindle bursts peaks during the first postnatal week and decreases thereafter (Hanganu et al., 2006; Yang et al., 2009; Shen and Colonnese, 2016), P8 may be beyond the age for properly identifying the functional contributions of spindle bursts to M1 development.

Population activity in developing M1

At P8, population-level activity in M1 is discontinuous, occurring primarily in discrete, correlated bursts of unit activity separated by periods of silence (Fig. 6A). Neural activity in S1 (Golshani et al., 2009; van der Bourg et al., 2017) and primary visual cortex (V1; Rochefort et al., 2009; Riyahi et al., 2021) is similarly discontinuous at this age. It has been hypothesized that discontinuous activity helps to maximize the detection of spontaneous peripheral activity (Colonnese and Phillips, 2018), thereby aiding in the activity-dependent development of sensory networks (Katz and Shatz, 1996; Blankenship and Feller, 2010; Ackman et al., 2012).

At P12, however, correlated activity disappears as background activity, sparsity (a measure of the uniform distribution of action potentials), and entropy (a measure of informational capacity) increase. Such sparsification of cortical activity in M1 also occurs at approximately P12 in S1 (Golshani et al., 2009; van der Bourg et al., 2017) and V1 (Rochefort et al., 2009; Riyahi et al., 2021). Sparsification of cortical activity is timed contemporaneously with the sudden emergence of local cortical inhibition (Ben-Ari et al., 2007; Colonnese, 2014; Dooley and Blumberg, 2018). Moreover, recent modeling studies suggest that developmental changes to the balance of inhibitory and excitatory processes in cortex contribute to the sparsification of cortical activity at P12 (Rahmati et al., 2017; Romagnoni et al., 2020). Finally, given that inhibitory interneurons strongly modulate cortical sensory processing in adulthood (Wood et al., 2017; Azim and Seki, 2019), the development of inhibition in M1 may explain the developmental reduction in redundant tuning properties observed here at P12.

It is possible that the onset of sparsification in M1 depends on the prior development of the forelimb representation of M1 via sensory experience (i.e., reafference). Consequently, perturbing early sensory experience may disrupt the onset of sparsification in M1. Indeed, in neonatal mice, dark rearing (an example of sensory deprivation) delays sparsification in V1 by 2–3 d (Rochefort et al., 2009); in contrast, whisker plucking in neonatal mice does not delay sparsification in S1 barrel cortex (Golshani et al., 2009). Given such conflicting results, more work is needed to clarify the conditions under which cortical sparsification is affected by early sensory experience.

Surprisingly, the distribution of the M1 population response to forelimb movements shifted from an approximately exponential to an approximately normal distribution over just 4 d (Fig. 7B). This shift in response distributions meant that M1 at P12 was less likely to exhibit an all-or-none response to a forelimb movement and more likely to exhibit a response comprising approximately half of the M1 units. This absence of redundant population responses at P12 implies that forelimb movements provide more informational content to M1 at this age. This new phase in M1 development in which reafferent input is more reliably detected and more informationally dense may serve to improve the effectiveness of M1's sensory map as a reference for its later-developing motor map.

Conclusion

The increase in variability in kinematic coding and robust changes to population-level activity shown here foreshadows M1 functioning in adulthood: adult M1 neurons are exquisitely versatile and heterogeneous, with each neuron able to simultaneously represent multiple kinematic (as well as temporal) features of movement in both Cartesian and body-centered reference frames (Wu and Hatsopoulos, 2006; Churchland and Shenoy, 2007; Hatsopoulos et al., 2007). The complexity of M1 activity in adulthood is partially supported by sparse coding—in which complex sensory input is reflected in precise, energetically efficient responses (Olshausen and Field, 2004). The transition to more complex sensory coding at P12, then, signifies an important transition toward the development of complex network properties, such as sparse coding, that will eventually enable M1 to produce complex movements and participate in motor learning (Kawai et al., 2015; Heindorf et al., 2018).