Current approaches to flexible loop modeling

Abstract

Loops are key components of protein structures, involved in many biological functions. Due to their conformational variability, the structural investigation of loops is a difficult topic, requiring a combination of experimental and computational methods. This paper provides a brief overview of current computational approaches to flexible loop modeling, and presents the main ingredients of the most standard protocols. Despite great progress in recent years, accurately modeling the conformational variability of long flexible loops remains a challenging problem. Future advances in this field will likely come from a tight coupling of experimental and computational techniques, which would enable a better understanding of the relationships between loop sequence, structural flexibility, and functional roles. In fine, accurate loop modeling will open the road to loop design problems of interest for applications in biomedicine and biotechnology.

Loops are protein fragments with an irregular structure connecting two secondary structure elements (typically α-helices and β-strands) and are main actors in many biological functions. They are often located at the surface of globular proteins, and their conformational versatility plays key roles in processes such as molecular recognition, allosteric regulation or signaling. On average, loops correspond to about one third of a protein sequence, and up to one half of the residues of enzyme active sites are located in loops (Bartlett et al., 2002).

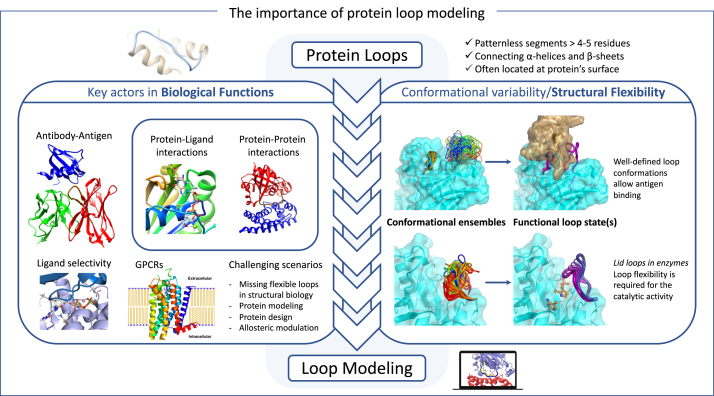
Protein loops can have very different dynamic behaviors. In some cases, loops adopt a relatively stable conformation in the folded state of the protein, being part of the overall protein scaffold. Based on this static perspective, some efforts have been made for the classification of loop structures (Oliva et al., 1997). However, conformational changes in loop regions are frequently observed to drive enzyme function or regulation (Malabanan et al., 2010). For example, flexible loops (P-loop and T-loop) modulate protein kinases activity. Loops are also essential in many protein-ligand/cofactor interactions. For instance, extracellular loops of G-Protein-Coupled Receptors (GPCRs) are crucial for ligand recognition and binding (Hilger et al., 2018). Note that GPCRs and protein kinases are by far the major drug targets for pharmaceutical industry. Together with their variable motion amplitude, loop conformational transitions can take place in a broad range of timescales. A comprehensive list of cases demonstrating the functional importance of protein loops can be found in a recent review (Papaleo et al., 2016). Fig. 1 is an illustrative summary of loop functions and of the interplay between their structural properties and functional roles.

Fig. 1.

Illustration of important functional roles of protein loops. Their location at the protein surface together with their conformational versatility make them key actors in intermolecular interactions. Their flexibility constitutes a challenge for their structural investigation, which requires a combination of experimental and computational methods.

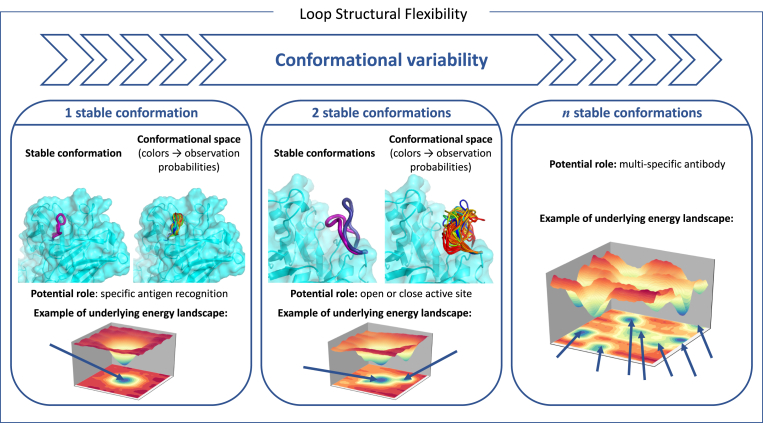
To better understand the dynamic nature of loops, a suitable representation of their conformational space is based on the concept of energy landscape (Wales, 2003). Although one loop can exist in multiple conformations, they are not equally likely to be adopted. More precisely, the probability of each possible state depends on its associated free energy. The energy landscape provides an overall view by displaying the energy at each point of the conformational space. The topology of this landscape gives insight into the main conformational and dynamic properties of the loop: the basins constitute meta-stable conformations, while saddle regions are associated with transition states. A visual representation can then be obtained by projecting this landscape along two meaningful coordinates, but other representations based on stationary points of the landscape can also be utilized. This is illustrated in Fig. 2.

Fig. 2.

Loops exhibit different levels of conformational variability. In some cases, they fluctuate around a main conformational state. For example, some CDR loops in antibodies adopt a single conformation suited to the recognition of a specific antigen. In other cases, a loop can adopt two main conformational states. For instance, this may correspond to a loop opening and closing the access to the active site of an enzyme. In general, the energy landscape of a loop is more complex, involving several basins corresponding to different meta-stable states. These multiple states can also be functionally important, for example in the case of multi-specific antibodies.

The structural investigation and characterization of flexible loops is challenging. X-ray crystallography, which is the most widely used experimental method to determine high-resolution protein structures, only provides static snapshots in particular experimental conditions (e.g. presence/absence of a ligand). Furthermore, flexible regions are often missing in X-ray structures, or even in electron microscopy maps, because of lacking electron density. According to Djinovic-Carugo and Carugo (2015), 69% of the structures deposited in the Protein Data Bank (PDB) have missing fragments, and this percentage increases up to 80% for structures solved with a resolution above 2.0 ​Å. In more than 90% of the cases, these missing fragments are located in loops or unstructured terminal regions. Other experimental techniques, such as X-ray solution scattering (Petoukhov et al., 2002) or nuclear magnetic resonance (NMR) (Boehr et al., 2006), can provide very relevant but limited structural and kinetic information regarding these flexible regions. Therefore, since an accurate atomistic representation of the diverse conformations adopted by the loop from experimental measurements is extremely difficult, computational methods are an essential complement to study flexible protein loops.

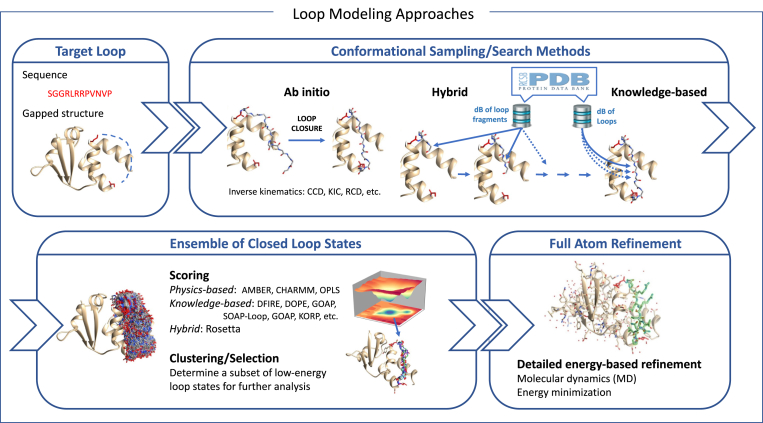
From a practical point of view, loop modeling techniques usually implement a multi-stage protocol, which varies depending on the underlying modeling approach. Fig. 3 aims to provide a general scheme in which most of the existing loop modeling techniques can fit. In brief, modeling can be divided into three major stages: (1) conformational sampling or search, (2) scoring and clustering, and (3) a final post-processing or refinement stage.

Fig. 3.

Schematic workflow of a prototype loop modeling protocol. It involves several stages. Given a three-dimensional model of a protein and the loop sequence (required if the loop is missing in the input structure), the first stage generates possible states of the loop. This can be based on ab initio sampling, searches in structural repositories, or a combination of both approaches. When the number of sampled states is large, scoring and clustering methods are useful to select a reduced number of the most likely loop models. These models can be subsequently refined at the all-atom level, considering the flexibility of the surrounding parts of the protein, and possibly including a model of the solvent.

The core of loop modeling is the exploration of the vast conformational space to be performed at the sampling/search step. Note that the volume of the conformational space grows exponentially with loop length. Very different approaches to protein loop modeling have been proposed over the years depending on the sampling/search protocol (Shehu and Kavraki, 2012; Papaleo et al., 2016; Kundert and Kortemme, 2019). Overall, they can be divided into three main classes: knowledge-based, ab initio and hybrid approaches. Knowledge-based approaches, also called template-based or homology-based, exploit structural repositories to retrieve observed loop conformations for a given set of sequence and geometric descriptors about the anchoring points (Choi and Deane, 2010; Messih et al., 2015; Shirvanizadeh et al., 2018; Karami et al., 2018). These methods are in general computationally fast since they do not rely on expensive simulations, but they are limited by the availability of suitable loop conformations from known protein structures, and only provide a small set of solutions. Especially for long loops, there is not enough structural data currently to cover the whole conformational space.

On the other end of the spectrum, ab initio approaches can perform a wider sampling of the conformational space, for example by exhaustively varying the torsional angles of the loop (Jacobson et al., 2004; López-Blanco et al., 2016). Their computational cost is highly variable, mainly depending on the underlying sampling method, but overall they are more demanding than knowledge-based approaches. To a lesser extent, they are also limited when dealing with long loops, as sampling coverage decreases with loop length.

Numerous loop modeling methods combine ideas from knowledge-based and ab initio approaches. Hybridization is performed at different levels: some methods apply a consensus between results obtained from different types of approaches (Deane and Blundell, 2001), while other methods apply a more intricate combination of strategies to explore the conformational space. In particular, many hybrid approaches use small fragments from structural databases within an ab initio sampling technique (Stein and Kortemme, 2013; Tang et al., 2014; Park et al., 2014; Marks et al., 2017; Barozet et al., 2019). The interest of one type of approach over the others may depend on the specific application and on the nature of the loop. For instance, knowledge-based approaches can be a suitable choice to predict the most probable conformations of more structurally conserved L1, L2, L3, H1, and H2 antibody CDR loops, whereas the more exhaustive sampling performed by ab initio and hybrid approaches will be more adequate to the highly variable H3 loop.

One of the main ingredients of ab initio and hybrid sampling approaches are loop-closure methods. They are required to ensure that N-terminal and C-terminal ends of the loop keep bonded to the anchoring points in the protein, while correct bond geometry is preserved. They are usually based on the concept of inverse kinematics, very common in robotics. Two classes of loop-closure methods have been proposed: those based on numerical optimization techniques (Canutescu and Dunbrack, 2003; Chys and Chacón, 2013), and those based on analytical solutions (Coutsias et al., 2004; Cortés et al., 2004). Numerical methods are conceptually simpler and directly applicable to long loops, but analytical methods are successfully used within iterative algorithms for the same purpose.

Scoring methods are another key ingredient, required to evaluate the quality of the sampled loop states. Scoring methods can also be classified into knowledge-based (López-Blanco and Chacón, 2019; Dong et al., 2013), physics-based (generally based on molecular mechanics approaches, not quantum physics models) and hybrid methods (Park et al., 2014; Alford et al., 2017). As before, knowledge-based scoring functions, typically linked to a coarse-grain representation of the loop, are the most computationally efficient alternative. However, their implicit simplifications prevent a faithful representation of the rugged energy surface of the all-atom conformational space. Conversely, the computational cost of detailed physics-based energy functions prevents a thorough exploration of the space. Hybrid approaches try to balance the best of these two worlds. A common practice is to use less accurate scoring functions in an initial search, and an atomistic detailed potential to refine only the high-scoring loop states. A suitable combination of sampling protocols and scoring functions is the major burden for loop modeling, and the key for future progress in the field.

In addition to the aforementioned loop modeling methods, Monte Carlo (MC) and molecular dynamics (MD) simulations can be used to investigate thermodynamic and kinetic properties of loops. Note however that in this context, MC-derived approaches are mainly employed as a sampling engine within more sophisticated loop prediction techniques, e.g. (Stein and Kortemme, 2013; Tang et al., 2014). Enhanced MD methods (Bernardi et al., 2015) are suitable tools to study loop dynamics (Papaleo et al., 2016). For example, MD simulations coupled with a higher-level representation such as Markov state models are a relevant approach to investigate the role of loop conformational changes in enzyme catalysis (Liao et al., 2018). Nevertheless, due to their very high computational cost, MD simulations are often only applied in a post-processing stage to refine solutions provided by much faster loop sampling methods (Lee et al., 2016).

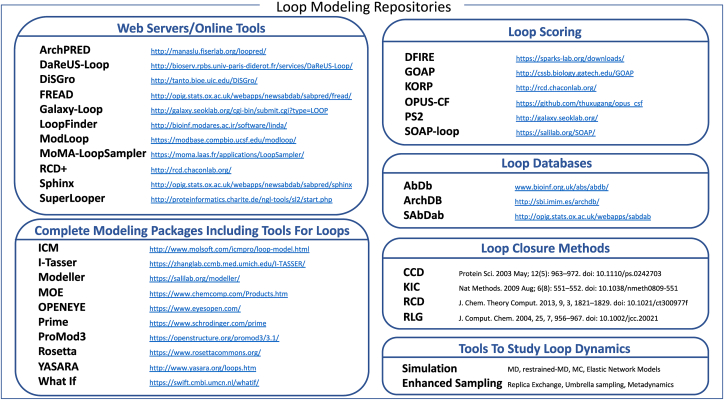
Fig. 4 provides a (non-exhaustive) list of loop modeling protocols, related techniques for sampling and scoring, and structural repositories. Note also that other methods (in addition to MD) have been proposed to model loop conformational transitions rather that loop conformations, but they are not covered by this review.

Fig. 4.

Non-exhaustive list of available tools for protein loop modeling, classified in different categories.

Despite huge progress over the last two decades, flexible loop modeling remains an open problem (Marks et al., 2018; Barozet et al., 2021). State-of-the-art methods are able to predict stable conformations of relatively short loops (up to 12 residues). However, accurately sampling, scoring and representing the great diversity of loop conformations and transitions between them is still a computational challenge, in particular for long loops. Nowadays, Machine/Deep-Learning (ML/DL) approaches are showing huge potential in many areas, including structural bioinformatics (Gao et al., 2020; Gkeka et al., 2020; Pakhrin et al., 2021). In the context of loop modeling, ML/DL-based approaches have already provided good results as scoring methods (Ruffolo et al., 2020). To the best of our knowledge, the ability of ML/DL methods to generate meaningful conformational ensemble models of flexible loops remains to be demonstrated, but it is undoubtedly a promising research direction.

The main limitation for the development of more accurate and general loop modeling methods is the lack of experimental data. As mentioned before, loop flexibility is a challenge for biophysical methods: X-ray crystallography provides only static and possibly biased snapshots, NMR methods have difficulties dealing with large proteins, other methods (such as small-angle X-ray scattering or Förster resonance energy transfer) only provide coarse-grained constraints to build models. Therefore, new integrated approaches, tightly coupling several experimental and computational methods, are necessary for advances in this field.

Future improvements in loop modeling will help us to better understand the relationships between loop sequence, structural flexibility and biological function. Meanwhile, current approaches, with their limitations, are ready to use in challenging problems such as loop design in enzymes and antibodies (Kundert and Kortemme, 2019). Encouraging results in these fields bring us closer to the ultimate goal of designing loops able to recognize partner molecules with high specificity and affinity, or to enhance the catalytic activity of enzymes thanks to optimized dynamic properties.

Authorship contribution statement

All the authors contributed equally to this work.

CRediT authorship contribution statement

Amélie Barozet: Writing – original draft, Writing – review & editing, Visualization. Pablo Chacón: Writing – original draft, Writing – review & editing, Visualization. Juan Cortés: Writing – original draft, Writing – review & editing, Visualization.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.