Using a Response Time–Based Expected A Posteriori Estimator to Control for Differential Speededness in Computerized Adaptive Test

Abstract

This study investigates using response times (RTs) with item responses in a computerized adaptive test (CAT) setting to enhance item selection and ability estimation and control for differential speededness. Using van der Linden’s hierarchical framework, an extended procedure for joint estimation of ability and speed parameters for use in CAT is developed following van der Linden; this is called the joint expected a posteriori estimator (J-EAP). It is shown that the J-EAP estimate of ability and speededness outperforms the standard maximum likelihood estimator (MLE) of ability and speededness in terms of correlation, root mean square error, and bias. It is further shown that under the maximum information per time unit item selection method (MICT)—a method which uses estimates for ability and speededness directly—using the J-EAP further reduces average examinee time spent and variability in test times between examinees above the resulting gains of this selection algorithm with the MLE while maintaining estimation efficiency. Simulated test results are further corroborated with test parameters derived from a real data example.

Computerized adaptive testing (CAT) systems are particularly suited for situations where an accurate and efficient estimation of an examinee’s true score is important, such as in large-scale, high-stakes admissions exams. Computer-based tests, such as CATs, also allow for easy collection of response times. With this abundance of essentially free data, methods and applications for using response time data have become en vogue. Some of the applications include cheating detection (van der Linden, 2009a), compromised item detection (Choe, Zhang, & Chang, 2018), shortening the time needed to take a test (Fan et al., 2012), and item selection (van der Linden, 2008). It only seems natural to design CATs to take advantage of response time information, especially since it is well-known that response accuracy and response time are related.

To use response times to their greatest potential, a model connecting observed response times and a latent trait describing the speededness of the test-takers is needed. Several categories of response time models exist. For instance, there are those that model response times only (Douglas et al., 1999; Maris, 1993; Rouder et al., 2003; Scheiblechner, 1979; Tatsuoka & Tatsuoka, 1980; van der Linden, 2006), those that model response times and response accuracy separately (Gorin, 2005; Jansen, 1997a, 1997b; Rasch, 1960; van der Linden, 1999), those that incorporate either response times or response accuracy into models for the other (Maris & van der Maas, 2012; Roskam, 1997; Thissen, 1983; van Rijn & Ali, 2018; Verhelst et al., 1997; T. Wang & Hanson, 2005), and those that follow a hierarchical approach (Fox et al., 2007; Klein Entink et al., 2009; Molenaar et al., 2015; van der Linden, 2007; C. Wang et al., 2013). As shown, there has been an extensive amount of research interest in this topic. For a more comprehensive review of response time modeling in testing, see either Schnipke and Scrams (2002), Lee and Chen (2011), or De Boeck and Jeon (2019).

One model that has seen a considerable amount of attention is van der Linden’s (2007) hierarchical framework. His approach, he argues, is appropriate for high-stakes testing situations where the test-taker can be reasonably assumed to have constant speed during the test. While this may not hold in testing situations with time limits, if the time limit is of a reasonable length then this assumption can be reasonably held. Another key assumption is that of the local independence between responses and response times. While not considered in the current study, one can investigate whether this assumption holds and take into account the dependence in the model accordingly (Bolsinova, De Boeck, & Tijmstra, 2017; Bolsinova & Maris, 2016; van der Linden & Glas, 2010). In a subsequent study, this hierarchical model was demonstrated in a fixed-length CAT context (van der Linden, 2008).

The main goal of a fixed-length CAT is to maximize the information of a test so that the accuracy of ability estimation is maximized given a fixed number of items. Traditionally, this is done by simply choosing items at every step of the test so that the chosen item maximizes Fisher information given the current estimate of ability $\hat{\theta }$ (Lord, 1980). That is, the next item $i$ to be administered is the one that makes

$$I_i\left(\hat{\theta }\right)=\frac{{\left[\frac{\partial }{\partial \hat{\theta }}P\left(\hat{\theta }\right)\right]}^2}{P_i\left(\hat{\theta }\right)(1-P_i\left(\hat{\theta }\right))}$$ (1)

as large as possible. This item selection approach is known as the maximum information criterion (MIC).

When response times are involved, another possible goal of item selection could be to minimize the total time taken to complete a test—that is, given a fixed number of items, to minimize length in terms of real time. This is an important consideration from a couple perspectives. First, organizations are always in need of improving efficiency where possible. Less time spent on assessment means more time spent on other activities. For instance, within schools, the less time that is spent on testing, the more time that can be spent on instruction. Second, to the extent that a test is speeded, different test-takers may experience that speededness differently, affecting their scores, which may undermine the validity of the test (Bridgeman & Cline, 2004; Lu & Sireci, 2007). This often results from the imposition of time limits, which, for practical reasons, are often used in real-life testing administrations. These effects can be minimized if overall test times are lessened such that examinees do not reach the time limit. This can be assured by minimizing both the average overall test time and the variability in overall test times.

Undoubtedly, more difficult items tend to take more time to complete (Goldhammer et al., 2015; van der Linden & van Krimpen-Stoop, 2003). As a result, minimizing test time by itself would mean that most items would be too easy for the majority of examinees. In turn, this means that the tests would be inappropriate for finding the locations of many examinees on the high end of the ability scale (van der Linden, 1999). Thus, when minimizing test time, it should be done in conjunction with maximizing ability estimation accuracy, creating a dual objective for the item selection algorithm. One method that does this in a simple way is the maximum information per time unit (MICT) method (Fan et al., 2012). In this method, the next item is chosen to maximize the function

$$\mathrm{MIC}{\mathrm{T}}_i=\frac{I_i\left(\hat{\theta }\right)}{\mathrm{E}(T_i|\hat{\tau })},$$ (2)

where $\hat{\theta }$ and $\hat{\tau }$ are the current estimates of ability and speededness. Since the response time is lognormally distributed, it is easy to show that

$$\mathrm{E}(T_i|\hat{\tau })=\exp ({\beta }_i-\hat{\tau }+\frac{1}{2{\alpha }_i^2}).$$

This method works great for minimizing total test time while maintaining a high fidelity in the ability latent trait estimate, and has been shown to work better than other competing item selection methods for this purpose (Veldkamp, 2016). Examination of Equation 2 shows that estimates for both ability, $\hat{\theta }$, and speededness, $\hat{\tau }$, are used in the item selection scheme for MICT. In their method, they used the maximum likelihood estimates for both of these.

Previously, van der Linden (2008) created a response time-based empirical Bayes procedure to estimate ability based on the hierarchical model. In his approach, he did not jointly estimate speededness. He argued that by having more accurate estimation of ability, even though items were selected using maximum information of ability without taking response times into account, item selection was improved. By similar reasoning, it can be argued that if one utilizes a method for selecting items that uses estimates for both ability and speededness, such as MICT, then similar gains can be gleaned by using joint Bayesian estimates of the two latent traits.

As such, a method for incorporating response times in a joint expected a posteriori (J-EAP) estimator will be pursued. Noting that the MICT was previously studied using the MLE for latent trait estimation (Fan et al., 2012), the authors wish to see if they can improve upon previous findings by using the J-EAP. Thus, the main goal of this article is to investigate whether the J-EAP has an advantage over the MLE when trying to balance ability estimation accuracy and time spent on the test using the MICT as the item selection method.

The rest of this article is as follows. First, van der Linden’s (2007) hierarchical framework is used, and an EAP estimation method is developed for the joint estimation of the person parameters for ability and speededness (J-EAP). It is also shown that the J-EAP is an extension of van der Linden’s (2008) empirical Bayes ability estimator. Next, a simulation study comparing the performance of the new EAP estimation method using response times (J-EAP) with the standard MLE method is done for a variety of relationships between ability and speededness to determine when the J-EAP and the MLE perform best. In addition, comparisons for two item selection methods—namely, the maximum information criterion (MIC) and the maximum information per time unit criterion (MICT; Fan et al., 2012)—are made on performance of the two estimators. A second simulation study is also performed which compares the performance of the two estimation methods for the two different item selection methods when using a real item bank, showing that the conclusions made from the first simulation can hold in an operational setting. Finally, the article is concluded with a short discussion.

Model

A hierarchical modeling framework was proposed by van der Linden (2007) to model speed and accuracy on test items. One level consists of an item response theory (IRT) model and a response time (RT) model, while a second level accounts for interdependencies between the item and person parameters within the two models.

First-Level Models

Let the items be indexed by $i=1,\dots ,I$ and the persons be indexed by $j=1,\dots ,J$. For each examinee $j$, there is a vector of responses ${\mathbf{X}}_j=(X_{1j},\dots ,X_{\mathrm{Ij}})$ and a vector of response times ${\mathbf{T}}_j=(T_{1j},\dots ,T_{\mathrm{Ij}})$. The responses are assumed to follow a three parameter logistic model (3PLM). That is, given the $j$ th person’s ability parameter ${\theta }_j$, the probability of answering the $i$ th item correctly is modeled as

$$P_i\left({\theta }_j\right)=c_i+(1-c_i)\frac{1}{1+e^{-a_i({\theta }_j-b_i)}},$$ (3)

where $a_i$, $b_i$, and $c_i$ are the discrimination, difficulty, and guessing parameters of item $i$, respectively. Then, the likelihood of examinee $j$’s responses is given as

$$l_j\left({\mathbf{X}}_j\right)=\underset{i=1}{\overset{I}{\Pi }}{P}_i({\theta }_j{)}^{x_{\mathrm{ij}}}{(1-P_i\left({\theta }_j\right))}^{1-x_{\mathrm{ij}}}.$$ (4)

The response times $T_{\mathrm{ij}}$ for the $j$ th person on the $i$ th item are assumed to follow the lognormal model proposed by van der Linden (2006), and so the log of the response times $\ln T_{\mathrm{ij}}$ are normally distributed. This is expressed as follows:

$$\ln T_{\mathrm{ij}}~f(\ln t_{\mathrm{ij}}|{\tau }_j,{\alpha }_i,{\beta }_i)=N({\beta }_i-{\tau }_j,{\alpha }_i^{-2}),$$ (5)

where ${\tau }_j$ is the speed parameter for examinee $j$, and ${\alpha }_i$ and ${\beta }_i$ are the time-intensity and discriminating power parameters of item $i$, respectively.

Let ${\mathbf{\xi }}_{\mathit{j}}=({\theta }_j,{\tau }_j)$ denote the vector of person parameters for person $j$, and let ${\mathbf{\Psi }}_{\mathit{i}}=(a_i,b_i,c_i,{\alpha }_i,{\beta }_i)$ denote the vector of item parameters for item $i$. Here, it is noted that an important assumption, beyond the usual IRT assumptions, is that $X_{\mathrm{ij}}$ is conditionally independent from $T_{\mathrm{ij}}$ given $(\theta ,\tau )$. Due to this conditional independence, the joint sampling distribution of ${\mathbf{X}}_j$ and ${\mathbf{T}}_j$, $j=1,\dots ,J$, follows directly from Equations 4 and 5:

$$f({\mathbf{x}}_j,\ln {\mathbf{t}}_j|{\mathbf{\xi }}_j,\mathbf{\Psi })=\underset{i=1}{\overset{I}{\Pi }}l(x_{\mathrm{ij}}|{\theta }_j,a_i,b_i,c_i)f(\ln t_{\mathrm{ij}}|{\tau }_j,{\alpha }_i,{\beta }_i).$$ (6)

Second-Level Models

At the second level, there is one model that describes the joint distribution of the person parameters. It is assumed that the values of ${\mathbf{\xi }}_j$ come from a multivariate normal distribution

$${\mathbf{\xi }}_j~N_2({\mathbf{\mu }}_p,{\mathbf{\Sigma }}_p)=f({\mathbf{\xi }}_j|{\mathbf{\mu }}_p,{\mathbf{\Sigma }}_p),$$ (7)

with a mean vector

$${\mathbf{\mu }}_p=({\mu }_{\theta },{\mu }_{\tau })$$

and a covariance matrix

$${\mathbf{\Sigma }}_p=\left(\begin{array}{cc}{\sigma }_{\theta }^2\hfill & {\sigma }_{\theta \tau }\hfill \\ \multicolumn{1}{c}{{\sigma }_{\theta \tau }}& {\sigma }_{\tau }^2\hfill \end{array}\right)$$

Finally, combining Equations 6 and 7, it is found that the joint density for responses, response times, and person parameters for the $j$ th examinee is given as

$$f({\mathbf{x}}_j,\ln {\mathbf{t}}_j,{\mathbf{\xi }}_j|\mathbf{\Psi })=f({\mathbf{x}}_j,\ln {\mathbf{t}}_j|{\mathbf{\xi }}_j,\mathbf{\Psi })f({\mathbf{\xi }}_j|{\mathbf{\mu }}_p,{\mathbf{\Sigma }}_p).$$ (8)

For ease of notation, where the meaning is clear, the person index $j$ is dropped throughout the rest of the present article.

Joint Expected a Posteriori (J-EAP) Estimation of Person Parameters

To find the joint EAP estimate of $\theta$ and $\tau$, it is necessary to find the expected value of the posterior distribution of $\mathbf{\xi }$; that is, to find $\mathrm{E}(\mathbf{\xi }|\mathbf{x},\ln \mathbf{t},\mathbf{\Psi })$, where $\mathbf{x}$ and $\ln \mathbf{t}$ are the data. For ease of presentation, the person index $j$ and the vector of item parameters $\mathbf{\Psi }$ will be suppressed. This is just equivalent to separately finding the mean of $\theta$ and $\tau$ under the joint posterior distribution. Thus,

$$\begin{array}{cc}\multicolumn{1}{c}{\mathrm{E}(\theta |\mathbf{x},\ln \mathbf{t})}& =\int \theta f(\theta |\mathbf{x},\ln \mathbf{t})d\theta =\int \int \theta f(\theta ,\tau |\mathbf{x},\ln \mathbf{t})d\tau d\theta \hfill \\ \multicolumn{1}{c}{}& =\frac{\int \int \theta f(\mathbf{x},\ln \mathbf{t}|\theta ,\tau )f(\theta ,\tau )d\tau d\theta }{\int \int f(\mathbf{x},\ln \mathbf{t}|\theta ,\tau )f(\theta ,\tau )d\tau d\theta }=\frac{\int \int \theta f(\mathbf{x}|\theta )f(\ln \mathbf{t}|\tau )f(\theta ,\tau )d\tau d\theta }{\int \int f(\mathbf{x}|\theta )f(\ln \mathbf{t}|\tau )f(\theta ,\tau )d\tau d\theta }\hfill \end{array}$$

and

$$\begin{array}{cc}\multicolumn{1}{c}{\mathrm{E}(\tau |\mathbf{x},\ln \mathbf{t})}& =\int \tau f(\tau |\mathbf{x},\ln \mathbf{t})d\tau =\int \int \tau f(\theta ,\tau |\mathbf{x},\ln \mathbf{t})d\theta d\tau \hfill \\ \multicolumn{1}{c}{}& =\frac{\int \int \tau f(\mathbf{x},\ln \mathbf{t}|\theta ,\tau )f(\theta ,\tau )d\theta d\tau }{\int \int f(\mathbf{x},\ln \mathbf{t}|\theta ,\tau )f(\theta ,\tau )d\theta d\tau }=\frac{\int \int \tau f(\mathbf{x}|\theta )f(\ln \mathbf{t}|\tau )f(\theta ,\tau )d\theta d\tau }{\int \int f(\mathbf{x}|\theta )f(\ln \mathbf{t}|\tau )f(\theta ,\tau )d\theta d\tau }.\hfill \end{array}$$

Because of the non-conjugate nature of the likelihoods and the prior, this requires computing numerical integrals. Unfortunately, for this problem that means computing the integral over a two-dimensional space, which is much more difficult than computing a one-dimensional integral. However, it can be shown that a routine developed by van der Linden (2008) for estimating person ability, which he called an empirical Bayesian approach, is equivalent to the ability estimation side of this joint EAP. This allows the ability parameter $\theta$ to be estimated via J-EAP with only a one-dimensional integral.

$$\begin{array}{c}\mathrm{E}(\theta |\mathbf{x},\ln \mathbf{t})=\frac{\int \theta f(\mathbf{x}|\theta )f(\theta |\ln \mathbf{t})d\theta }{\int f(\mathbf{x}|\theta )f(\theta |\ln \mathbf{t})d\theta }.\hfill \end{array}$$

The great savings in computation comes from the fact that under the hierarchical model $\theta |\ln \mathbf{t}$ is normally distributed with mean

$${\mu }_{\theta |\ln \mathbf{t}}={\mu }_{\theta }+\frac{{\sigma }_{\theta \tau }}{{\sigma }_{\tau }^2}[\frac{{\sigma }_{\tau }^{-2}{\mu }_{\tau }+\sum _i{\alpha }_i^2({\beta }_i-\ln t_i)}{{\sigma }_{\tau }^{-2}+\sum _i{\alpha }_i^2}-{\mu }_{\tau }]$$

and variance

$${\sigma }_{\theta |\ln \mathbf{t}}^2={\sigma }_{\theta }^2-\frac{{\sigma }_{\theta \tau }^2\sum _i{\alpha }_i^2}{1+{\sigma }_{\tau }^2\sum _i{\alpha }_i^2}$$

as shown by van der Linden (2008). An equivalent savings in computing the person speededness parameter $\tau$ using this approach can also be gained.

$$\begin{array}{cc}\multicolumn{1}{c}{\mathrm{E}(\tau |\mathbf{x},\ln \mathbf{t})}& =\frac{\int \int \tau f(\mathbf{x}|\theta )f(\tau |\ln \mathbf{t})f(\theta |\tau )d\theta d\tau }{\int f(\mathbf{x}|\theta )f(\theta |\ln \mathbf{t})d\theta }=\frac{\int \mathrm{E}(\tau |\theta ,\ln \mathbf{t})f(\mathbf{x}|\theta )f(\theta |\ln \mathbf{t})d\theta }{\int f(\mathbf{x}|\theta )f(\theta |\ln \mathbf{t})d\theta }.\hfill \end{array}$$

The resulting value is the J-EAP. Further explication of these results can be found in the Appendix.

Note that for use in a CAT, reasonable estimates for ${\sigma }_{\theta }^2$, ${\sigma }_{\tau }^2$, and ${\sigma }_{\theta \tau }$ are needed. Also, ${\mu }_{\theta }$ and ${\mu }_{\tau }$ are needed. When estimating an item bank, these values are largely arbitrary, and need to be set for identification purposes. For instance, let ${\mu }_{\theta }={\mu }_{\tau }=0$, and ${\sigma }_{\theta }^2=1$. The other values, ${\sigma }_{\tau }^2$ and ${\sigma }_{\theta \tau }$, would be estimated. With a known, operational item bank, these values for a given population of test-takers are not arbitrary. They would need to be known (from past experience) ahead of time for use within a single examinee’s test.

Simulation 1: Simulated Item Bank and Examinee Populations

Method

Simulation studies are carried out to compare the J-EAP estimator with the standard MLE estimator. To determine when using response times in CAT improves ability estimation over a standard setting, several factors are manipulated. First, the person parameters are simulated as

$$\left(\begin{array}{c}\theta \hfill \\ \multicolumn{1}{c}{\tau }\end{array}\right)~N_2(\left(\begin{array}{c}0\hfill \\ \multicolumn{1}{c}{0}\end{array}\right),\left(\begin{array}{cc}1\hfill & {\rho }_{\theta \tau }\hfill \\ \multicolumn{1}{c}{{\rho }_{\theta \tau }}& 1\hfill \end{array}\right)),$$

where ${\rho }_{\theta \tau }$ is either 0, .25, .50, or .75. For these four conditions, ability and speededness are estimated using the J-EAP and the MLE. Furthermore, each CAT uses either the MIC method or the MICT method for item selection. For each of these conditions, tests have fixed lengths of either 10, 15, or 30 items. Thus, there are a total of $4\times 2\times 2\times 3=48$ conditions.

A 1,000-item bank is simulated with the item parameters $a$, $b$, $c$, $\alpha$, and $\beta$ as defined earlier. Parameters are generated as follows:

$$(a^{*},b,\beta )~N_3(\left(\begin{array}{c}0.3\hfill \\ \multicolumn{1}{c}{0.0}\\ \multicolumn{1}{c}{0.0}\end{array}\right),\left(\begin{array}{ccc}0.10\hfill & 0.15\hfill & 0.00\hfill \\ \multicolumn{1}{c}{0.15}& 1.00\hfill & 0.50\hfill \\ \multicolumn{1}{c}{0.00}& 0.50\hfill & 1.00\hfill \end{array}\right))$$

where $a^{*}=\log a$; $c~\mathrm{beta}(2,10)$; and $\alpha ~\mathrm{unif}(1,4)$.

These distributions were chosen to simulate items that are commonly found in standardized testing, are similar to what is found in our real item bank, and are similar to those used in previous studies (Choe, Kern, & Chang, 2018; Fan et al., 2012a); they were used both in the data generation process and in the simulated CAT. Because it is known that there is typically a relationship between item difficulty and discrimination parameters (Chang et al., 2001), the covariance matrix has a non-zero relationship between $a^{*}$ and $b$. Furthermore, in the same covariance matrix, the covariance between the item difficulty and time-intensity parameters is chosen because it is believed there is a moderate association between these parameters (Cheng et al., 2017; van der Linden, 2009bb).

Finally, for every factor combination, 2000 examinees are simulated with true ability parameters $\theta$ at evenly spaced increments of 0.10 from −3 to 3, for a total of 61 values of $\theta$. This is done to better assess the performance for typically undersampled points along the distribution. The true speededness parameters $\tau$ are generated from the conditional distribution of $\tau |\theta$. Here, that is given as

$$\tau |\theta ~N({\mu }_{\tau }+{\rho }_{\theta \tau }\frac{{\sigma }_{\tau }}{{\sigma }_{\theta }}(\theta -{\mu }_{\theta }),{\sigma }_{\tau }^2(1-{\rho }_{\theta \tau }^2)).$$

The values for the population parameters of ${\mu }_{\theta }$, ${\mu }_{\tau }$, ${\sigma }_{\theta }$, and ${\sigma }_{\tau }$ were chosen to standardize the latent variables. They are as follows: ${\mu }_{\theta }={\mu }_{\tau }=0$ and ${\sigma }_{\theta }={\sigma }_{\tau }=1$.

Ability (and speededness) estimation is assessed using bias, root mean square error (RMSE), and correlation. Due to the oversampling at the extremes of the ability distribution, these statistics must be weighted to account for this. This weighting can be accomplished using the density of the ability parameter $f({\theta }_j)$ for all $J=2000\times 61=122000$ simulated examinees. Thus, the weighted outcome statistics are calculated as follows:

Weighted bias:

$$\mathrm{Bias}(\mathbf{\theta },\hat{\mathbf{\theta }})=\frac{\sum _{j=1}^{J}f\left({\theta }_j\right)({\hat{\theta }}_j-{\theta }_j)}{\sum _{i=1}^{J}f\left({\theta }_j\right)}.$$

Weighted RMSE:

$$\mathrm{RMSE}(\mathbf{\theta },\hat{\mathbf{\theta }})=\sqrt{\frac{\sum _{j=1}^{J}f\left({\theta }_j\right){({\hat{\theta }}_j-{\theta }_j)}^2}{\sum _{i=1}^{J}f\left({\theta }_j\right)}}.$$

Weighted correlation:

$$\mathrm{Cor}(\mathbf{\theta },\hat{\mathbf{\theta }})=\frac{\mathrm{Cov}(\mathbf{\theta },\hat{\mathbf{\theta }})}{\left[\mathrm{Var}{(\mathbf{\theta },\mathbf{\theta })}^{1/2}\right]\left[\mathrm{Var}{(\mathbf{\theta },\hat{\mathbf{\theta }})}^{1/2}\right]},$$

where

$$\mathrm{Var}(\mathbf{\theta },\hat{\mathbf{\theta }})=\frac{\sum _{j=1}^{J}f\left({\theta }_j\right){({\hat{\theta }}_j-\frac{1}{J}\sum _{j=1}^J{\hat{\theta }}_j)}^2}{\sum _{j=1}^{J}f\left({\theta }_j\right)}$$

and

$$\mathrm{Cov}(\mathbf{\theta },\hat{\mathbf{\theta }})=\frac{\sum _{j=1}^{J}f\left({\theta }_j\right)({\hat{\theta }}_j-\frac{1}{J}\sum _{j=1}^J{\hat{\theta }}_j)({\theta }_j-\frac{1}{J}\sum _{j=1}^J{\theta }_j)}{\sum _{j=1}^{J}f\left({\theta }_j\right)}.$$

Each test design is also assessed on its average item time, average test time, and SD of test time, which are all weighted as above. Ability estimation is further assessed using bias and RMSE conditioned on the ability level; because these are conditional, these are not weighted. Finally, weighted absolute bias is computed by computing the conditional absolute bias at each value of $\theta$ and then computing the weighted mean as above.

Results

Results of the simulation are summarized in Tables 1 and 2. Bias and absolute bias is very small for all conditions, although, as expected, it does decrease as the test length increases. As ${\rho }_{\theta \tau }$ increases, there seems to be a very small effect on bias for J-EAP. Overall, (absolute) bias tends to be smaller for MLE than J-EAP. Interestingly, for J-EAP, bias is larger for MICT than MIC. On the other hand, RMSE($\hat{\theta }$) is smaller for J-EAP than MLE in all cases, whereas RMSE($\hat{\tau }$) is larger for J-EAP than MLE. As with bias, RMSE decreases as test length increases. Furthermore, as ${\rho }_{\theta \tau }$ increases, RMSE($\hat{\theta }$) decreases for J-EAP, whereas there is no effect on RMSE($\hat{\theta }$) for MLE or on RMSE($\hat{\tau }$) in any case. We also find that RMSE of $\hat{\theta }$ is smaller for MIC than it is for MICT, but that the item selection method seems to have no effect on RMSE of $\hat{\tau }$. Correlation for trait estimation, $\mathrm{Corr}(\theta ,\hat{\theta })$ follows a similar pattern to RMSE($\hat{\theta }$) in terms of estimation precision. Across cases, $\mathrm{Corr}(\theta ,\hat{\theta })$ is larger for J-EAP than MLE. Also, as test length increases, the $\mathrm{Corr}(\theta ,\hat{\theta })$ increases. As ${\rho }_{\theta \tau }$ increases, the $\mathrm{Corr}(\theta ,\hat{\theta })$ increases. Furthermore, $\mathrm{Corr}(\theta ,\hat{\theta })$ is larger for MIC than it is for MICT, though the difference is very slight. Finally, correlation for speededness estimation is nearly perfect for all cases.

Table 1.

Results for Simulation 1 (MIC).

										M	M	SD
Estimation method	${\rho }_{\theta \tau }$	Test length	RMSE ($\hat{\theta }$)	RMSE ($\hat{\tau }$)	Bias ($\hat{\theta }$)	Bias ($\hat{\tau }$)	Abs-Bias ($\hat{\theta }$)	Cor ($\theta$,$\hat{\theta }$)	Cor ($\tau$,$\hat{\tau }$)	Item time	Test time	Test time
MLE	0.00	10	0.54	0.12	0.04	–0.00	0.04	0.88	0.99	2.71	27.13	47.34
MLE	0.00	15	0.38	0.10	0.01	0.00	0.02	0.94	0.99	2.46	36.83	60.97
MLE	0.00	30	0.24	0.07	–0.00	0.00	0.01	0.97	0.99	2.26	67.75	104.32
MLE	0.25	10	0.54	0.12	0.04	0.00	0.04	0.88	0.99	2.51	25.10	41.78
MLE	0.25	15	0.38	0.10	0.01	0.00	0.02	0.94	0.99	2.25	33.71	51.88
MLE	0.25	30	0.24	0.07	–0.00	0.00	0.01	0.97	0.99	2.05	61.40	85.00
MLE	0.50	10	0.54	0.12	0.04	0.00	0.04	0.88	0.99	2.33	23.29	36.08
MLE	0.50	15	0.38	0.10	0.01	0.00	0.02	0.94	0.99	2.06	30.97	42.68
MLE	0.50	30	0.24	0.07	–0.00	0.00	0.01	0.97	0.99	1.86	55.88	66.63
MLE	0.75	10	0.54	0.12	0.04	0.00	0.04	0.88	0.99	2.16	21.60	30.06
MLE	0.75	15	0.38	0.10	0.01	0.00	0.02	0.94	0.99	1.90	28.54	34.34
MLE	0.75	30	0.24	0.07	–0.00	0.00	0.01	0.97	0.99	1.70	51.04	49.57
J-EAP	0.00	10	0.34	0.13	–0.00	–0.00	0.08	0.94	0.98	1.78	17.76	28.40
J-EAP	0.00	15	0.28	0.12	–0.00	–0.00	0.06	0.96	0.98	1.83	27.39	42.29
J-EAP	0.00	30	0.21	0.12	–0.00	–0.00	0.03	0.98	0.99	1.95	58.50	88.35
J-EAP	0.25	10	0.34	0.13	–0.00	0.00	0.08	0.94	0.98	1.62	16.16	22.92
J-EAP	0.25	15	0.28	0.12	–0.00	0.00	0.06	0.96	0.99	1.65	24.73	33.41
J-EAP	0.25	30	0.21	0.12	–0.00	0.00	0.03	0.98	0.99	1.75	52.58	68.93
J-EAP	0.50	10	0.33	0.13	–0.00	0.00	0.08	0.94	0.99	1.49	14.88	18.45
J-EAP	0.50	15	0.28	0.12	–0.00	0.00	0.06	0.96	0.99	1.50	22.56	26.02
J-EAP	0.50	30	0.21	0.12	–0.00	0.00	0.03	0.98	0.99	1.59	47.60	52.13
J-EAP	0.75	10	0.31	0.13	–0.00	0.00	0.07	0.95	0.99	1.39	13.85	14.26
J-EAP	0.75	15	0.26	0.12	–0.00	0.00	0.05	0.96	0.99	1.39	20.79	19.15
J-EAP	0.75	30	0.20	0.12	–0.00	0.00	0.03	0.98	0.99	1.45	43.44	36.71

Note. MIC = maximum information criterion; RMSE = root mean square error; MLE = maximum likelihood estimator; J-EAP = joint expected a posteriori.

Table 2.

Results for Simulation 1 (MICT).

										M	M	SD
Estimation method	${\rho }_{\theta \tau }$	Test length	RMSE ($\hat{\theta }$)	RMSE ($\hat{\tau }$)	Bias ($\hat{\theta }$)	Bias ($\hat{\tau }$)	Abs-Bias ($\hat{\theta }$)	Cor ($\theta$,$\hat{\theta }$)	Cor ($\tau$,$\hat{\tau }$)	Item time	Test time	Test time
MLE	0.00	10	0.55	0.12	0.00	0.00	0.03	0.88	0.99	0.76	7.57	14.11
MLE	0.00	15	0.41	0.09	–0.01	0.00	0.02	0.93	0.99	0.64	9.62	16.59
MLE	0.00	30	0.28	0.07	–0.00	0.00	0.01	0.96	0.99	0.56	16.79	25.59
MLE	0.25	10	0.54	0.12	0.00	0.00	0.03	0.88	0.99	0.72	7.18	13.27
MLE	0.25	15	0.41	0.10	–0.01	0.00	0.02	0.93	0.99	0.60	9.06	15.04
MLE	0.25	30	0.28	0.07	–0.00	0.00	0.01	0.96	0.99	0.52	15.68	22.55
MLE	0.50	10	0.55	0.12	0.00	0.00	0.03	0.88	0.99	0.68	6.84	12.08
MLE	0.50	15	0.41	0.09	–0.01	0.00	0.02	0.93	0.99	0.57	8.56	13.27
MLE	0.50	30	0.28	0.07	–0.00	0.00	0.01	0.96	0.99	0.49	14.73	19.01
MLE	0.75	10	0.55	0.12	0.00	0.00	0.03	0.88	0.99	0.65	6.53	10.91
MLE	0.75	15	0.41	0.09	–0.01	0.00	0.02	0.93	0.99	0.54	8.12	11.61
MLE	0.75	30	0.28	0.07	–0.00	0.00	0.01	0.96	0.99	0.46	13.94	15.42
J-EAP	0.00	10	0.40	0.13	–0.00	0.00	0.12	0.91	0.98	0.57	5.72	11.92
J-EAP	0.00	15	0.33	0.12	–0.00	0.00	0.08	0.94	0.99	0.52	7.79	14.09
J-EAP	0.00	30	0.25	0.12	–0.00	0.00	0.04	0.97	0.99	0.50	15.04	23.03
J-EAP	0.25	10	0.40	0.13	–0.00	0.00	0.12	0.91	0.98	0.55	5.49	10.96
J-EAP	0.25	15	0.33	0.12	–0.00	–0.00	0.08	0.94	0.99	0.49	7.37	12.62
J-EAP	0.25	30	0.25	0.12	–0.00	–0.00	0.04	0.97	0.99	0.47	14.06	19.80
J-EAP	0.50	10	0.39	0.13	–0.00	0.00	0.11	0.92	0.99	0.53	5.31	10.34
J-EAP	0.50	15	0.32	0.12	–0.00	0.00	0.08	0.94	0.99	0.47	7.05	11.56
J-EAP	0.50	30	0.24	0.12	–0.00	0.00	0.04	0.97	0.99	0.44	13.29	17.15
J-EAP	0.75	10	0.36	0.13	–0.00	0.00	0.10	0.93	0.99	0.52	5.17	9.29
J-EAP	0.75	15	0.31	0.12	–0.00	0.00	0.07	0.95	0.99	0.45	6.80	10.12
J-EAP	0.75	30	0.24	0.12	–0.00	0.00	0.04	0.97	0.99	0.42	12.68	14.08

Note. RMSE = root mean square error; MLE = maximum likelihood estimator; J-EAP = joint expected a posteriori; MICT = maximum information per time unit criterion.

In terms of the average and standard deviation of test time and average item time, it is clear that J-EAP is smaller on all measures than MLE in all cases. To further break it down, it is found that for increasing test length, mean and SD of test time is increasing in all cases. On the other hand, mean item time is decreasing in all cases except when estimating with J-EAP and items are selected using MIC. This means that for J-EAP with MIC, the CAT algorithm is tending to choose quicker items earlier on in the test. The exact mechanism for why this is occurring is unclear, but it may be partially a result of the simulated relationship between item difficulty and item time intensity. As ${\rho }_{\theta \tau }$ increases, decreasing values are found for all measures. Finally, it is found that the MICT method has smaller mean and SD of test times and mean item times than MIC does.

To further compare performance across conditions, bias and RMSE conditioned on the level of $\theta$ are examined. Figures 1 and 2 show the conditional bias and absolute bias for all conditions. For all conditions, there is a higher bias toward the extremes of the scale than in the middle of scale. This is expected due to the item pool design having very few items at the extremes compared with the middle. For MLE, there is a negative bias for values of $\theta$ less than ${\mu }_{\theta }=0$, and a positive bias for values of $\theta$ greater than ${\mu }_{\theta }=0$; this is reversed for J-EAP. This is a result of shrinkage, a common observation of Bayesian estimators where they tend to pull estimates inward toward the prior. As the length of the test increases, bias is lessened across the scale of $\theta$ for J-EAP, but actually increases slightly at the low end of the scale for MLE while remaining roughly the same elsewhere. After further investigation, it was determined that this is an artifact of the method used to handle non-finite estimates of the MLE (i.e., cases where an examinee either answers all items correctly or all items incorrectly); in this case, the algorithm sets the estimate to be $\hat{\theta }=-4$ or $4$. The J-EAP has greater bias than the MLE across most of $\theta$ for all levels of ${\rho }_{\theta \tau }$. However, as ${\rho }_{\theta \tau }$ increases, bias in the J-EAP decreases, while it has no effect on the bias in MLE. This is expected, because the strength of the relationship between $\theta$ and $\tau$ should have no effect on estimation accuracy unless it is used in estimation. Furthermore, it is found that bias is smaller when using MIC than MICT, especially for J-EAP, which makes sense because the dual objective encoded in MICT will inherently sacrifice estimation accuracy to further decrease response times.

Figure 1.

Plot of conditional bias of estimates by true ability for Simulation 1.

Figure 2.

Plot of conditional absolute bias of estimates by true ability for Simulation 1.

Figure 3 shows conditional RMSE for all conditions. For any given level of $\theta$, RMSE decreases as the test length increases. Also, at the extremes of the $\theta$-scale, RMSE is highest, decreasing as $\theta$ moves toward the middle of the scale. As with bias, this is due to the item pool design having fewer items at the extremes than the middle. As ${\rho }_{\theta \tau }$ increases, RMSE decreases across the $\theta$-scale for J-EAP, while having no effect on RMSE for MLE. Finally, for all levels of $\theta$ on J-EAP, MIC has smaller RMSE than MICT, except in some cases at the extremes of the $\theta$-scale for MLE. As discussed above, this is really just an artifact of the approach taken to resolve non-finite MLE estimates.

Figure 3.

Plot of conditional RMSE of estimates by true ability for Simulation 1.

Note. RMSE = root mean square error.

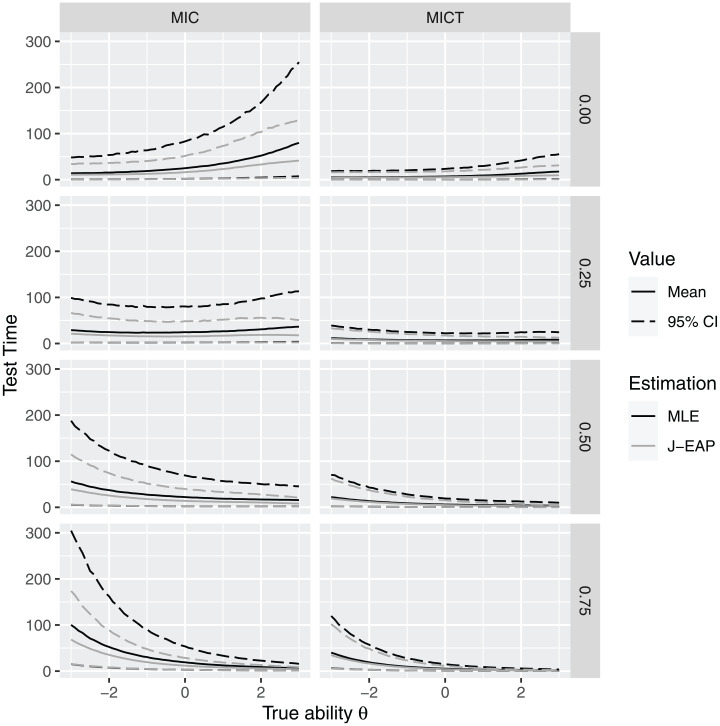
Finally, an investigation of the test times by condition across the scale of $\theta$ was done. To simplify the presentation, Figure 4 only shows the conditional test times by condition for tests of length 10; other test lengths showed the same overall patterns just with longer test times. General findings are that across the $\theta$ scale (a) average test times are smaller for MICT than MIC, and (b) average test times are smaller for J-EAP than MLE. Moreover, the variability of test times is lessened in these cases as well. These findings hold regardless of the value of ${\rho }_{\theta \tau }$. While the test time distributions themselves are also contingent upon ${\rho }_{\theta \tau }$—for small ${\rho }_{\theta \tau }$, high ability examinees take longer than low ability examinees, with the opposite being true for large ${\rho }_{\theta \tau }$—test time variability is more constant across the ability scale for J-EAP and MICT than MLE and MIC, respectively.

Figure 4.

Plot of test times by true ability for Simulation 1.

Simulation 2: Real Item Bank and Examinee Population

Method

Simulation studies with a real item bank are carried out to determine when using the J-EAP estimator is an improvement over the MLE in a closer to operational setting. Several factors are manipulated. First, estimation method is either the J-EAP or the MLE. Second, the item selection method is either the MIC or the MICT. Since both latent variables $\theta$ and $\tau$ are used in item selection for MICT, it would be interesting to see how having joint Bayesian estimates of both $\theta$ and $\tau$ affects the test. Third, the tests have fixed lengths of either 10, 15, or 30. Thus, there are a total of $2\times 2\times 3=12$ conditions.

To help simulate the operational setting, the item bank parameters and latent trait distribution are estimated from a set of responses on a real high-stakes, large-scale standardized CAT. The calibration data set consists of raw responses and RTs from about 2,000 examinees with an item pool containing about 500 multiple-choice items that were pre-calibrated according to 3PLM. The resulting item parameters and latent trait distribution parameters were then used in the current simulation. The lognormal model item parameters $\alpha$ and $\beta$ were estimated using a modified version of van der Linden’s (2007) Markov chain Monte Carlo (MCMC) routine that fixed the 3PLM item parameters to the pre-calibrated values, and the distribution of $\tau$ was set to have a mean of 0. All parameters converged using three independent chains with 10,000 MCMC draws with a burn-in size of 5,000 each with Gelman and Rubin’s (1992)$\hat{R}<1.1$ for all parameters. Estimates used in the simulation were taken to be the means of the posterior distributions. The resulting item parameters were used both in the response generation process and in the simulated CAT. Examinees are simulated as in Simulation 1, except the values for the population parameters as follows: ${\mu }_{\theta }=0.5$, ${\mu }_{\tau }=0$, ${\sigma }_{\theta }=1$, ${\sigma }_{\tau }=0.16$, and ${\rho }_{\theta \tau }=0.76$. For comparison purposes, it is important to note that this item bank consists generally of easier ($\overline{b}=-0.18$), less discriminative ($a^{*}=-0.23$) and more time-intensive ($\overline{\beta }=0.37$) than the item bank in Simulation 1.

Bias, RMSE, and correlation are used to assess ability and speededness estimation. As discussed previously, the oversampling at the extremes of the ability distribution must be taken into account in these statistics, so they are weighted as in Simulation 1. Furthermore, ability estimation is assessed with a combination of (unweighted) bias, absolute bias, and RMSE conditioned on the ability level. Finally, mean overall test and item time across individuals and the standard deviation of test times across individuals is assessed, along with conditional test time.

Results

Results of the simulation are summarized in Table 3. Most general patterns that were found in Simulation 1 also hold in the current simulation as well. First, overall estimation accuracy is evaluated. Bias for $\hat{\theta }$ and $\hat{\tau }$ is very small for all conditions. It is also found that absolute bias of $\hat{\theta }$ is fairly small, and decreasing with test length increases. Overall, absolute bias tends to be smaller for MLE than J-EAP. For J-EAP, absolute bias is larger for MICT than MIC; for MLE, absolute bias is approximately the same for the two selection methods. Furthermore, RMSE (for both latent traits) is found to be smaller for the J-EAP than MLE in every case. Unlike bias, RMSE is larger for MICT than MIC for both estimation methods. Furthermore, for all cases, RMSE decreases as test length increases. Finally, correlation follows a similar pattern to RMSE. Across cases, correlation is smaller for MICT than MIC (though the differences are small), and larger for J-EAP than MLE. Interestingly, the increase in correlation for the J-EAP over MLE is fairly large, especially for speededness. For instance, for a small test length of 10 with items selected via MICT, the correlation of the true value and the estimate of speededness is 0.63 for MLE and 0.79 for the J-EAP. This is possibly due to the fact that the variability in time-intensity parameters is larger than the variability in the person speed parameters, allowing for better measurement across the $\tau$ scale. Finally, as test length increases, the correlation increases.

Table 3.

Results for Simulation 2.

										M	M	SD
Selection method	Estimation method	Test length	RMSE ($\hat{\theta }$)	RMSE ($\hat{\tau }$)	Bias ($\hat{\theta }$)	Bias ($\hat{\tau }$)	Abs-Bias ($\hat{\theta }$)	Cor ($\theta$,$\hat{\theta }$)	Cor ($\tau$,$\hat{\tau }$)	Item time	Test time	Test time
MIC	MLE	10	0.74	0.19	–0.00	–0.00	0.05	0.82	0.61	1.96	19.64	6.54
MIC	MLE	15	0.58	0.15	–0.00	–0.00	0.04	0.87	0.69	1.90	28.49	7.82
MIC	MLE	30	0.40	0.11	–0.00	–0.00	0.02	0.93	0.81	1.89	56.67	11.47
MIC	J-EAP	10	0.48	0.09	0.00	0.00	0.17	0.87	0.80	1.79	17.95	4.93
MIC	J-EAP	15	0.42	0.08	–0.00	0.00	0.13	0.91	0.83	1.81	27.11	6.50
MIC	J-EAP	30	0.32	0.07	–0.00	0.00	0.07	0.94	0.88	1.84	55.25	10.15
MICT	MLE	10	0.79	0.18	–0.01	–0.00	0.05	0.80	0.62	1.23	12.30	4.16
MICT	MLE	15	0.62	0.16	–0.02	0.00	0.04	0.86	0.68	1.20	18.00	5.07
MICT	MLE	30	0.42	0.11	–0.01	–0.00	0.03	0.92	0.80	1.21	36.19	7.31
MICT	J-EAP	10	0.52	0.09	–0.00	0.00	0.20	0.85	0.78	1.17	11.65	3.61
MICT	J-EAP	15	0.45	0.09	0.00	0.00	0.15	0.89	0.81	1.15	17.21	4.41
MICT	J-EAP	30	0.34	0.07	–0.00	0.00	0.09	0.94	0.87	1.19	35.72	6.58

Note. MIC = maximum information criterion; MICT = maximum information per time unit criterion; RMSE = root mean square error; MLE = maximum likelihood estimator; J-EAP = joint expected a posteriori.

In terms of the average and standard deviation of test time and average item time, J-EAP is found to be smaller on all measures than MLE in all cases, though the effect is smaller than in Simulation 1. To further break it down, for increasing test length, mean and SD of test time is increasing in all cases, as expected. However, looking at mean item time, there is no indication of an effect due to test length. However, the MICT method has smaller mean and SD of test times and mean item times than MIC does. These effects are a bit muted compared with what was found in Simulation 1. More investigation is needed, but this is most likely due to the differing item distributions.

To further compare how the the J-EAP performs against the MLE, bias and RMSE conditioned on the level of $\theta$ are examined. Figures 5 to 7 show the conditional bias, absolute bias, and RMSE for all conditions. For MLE, there is a negative bias for values of $\theta$ on the left-side of the scale, and a positive bias for values of $\theta$ on the right-side of the scale; this is reversed for the J-EAP. As the length of the test increases, absolute bias is generally lessened across the scale of $\theta$. The J-EAP has greater (absolute) bias than the MLE for most across ability scale. The difference in conditional bias between the MIC and MICT for each estimation method is very small, with larger increases for J-EAP than MLE. For any given level of $\theta$, RMSE decreases as the test length increases. Also, RMSE is found to be smaller for J-EAP than for MLE. As in Simulation 1, RMSE is lessened toward the ends of the scales, but as previously discussed, this is just an artifact of resolving the non-finite estimate problem in MLE estimation. Although the effect is small, RMSE is larger across the $\theta$-scale for MICT than for MIC. Finally, as with bias, RMSE is smallest close to the center of the distribution of $\theta$, increasing as $\theta$ is progressively farther from the center.

Figure 5.

Plot of conditional bias of estimates by true ability for Simulation 2.

Figure 7.

Plot of conditional RMSE of estimates by true ability for Simulation 2.

Figure 6.

Plot of conditional absolute bias of estimates by true ability for Simulation 2.

Figure 8.

Plot of test times by true ability for Simulation 2.

Finally, the distribution test times by condition across the scale of $\theta$ is examined. Figure 4 shows the conditional test times by condition. Generally, average test times are smaller for MICT than MIC, and average test times are smaller for J-EAP than MLE. These are especially true at the high end of the ability scale. It is also found that the variability of test times is lessened across the scale. Importantly, these findings hold regardless of the test length.

Discussion

CATs have one basic goal in mind: to accurately measure an examinee’s true score as efficiently as possible. Efficiency can be defined in multiple ways, including decreasing the number of items administered. It is also possible to decrease the amount of real time needed to finish a test. This study proposes a method that can improve on both tasks in a simple fashion, with minimal extra cost. Of course, this is all predicated on the assumption that ability and speededness of an individual are related in the context of a high-stakes exam. If they are, then that relationship can be exploited. While the increase in performance is largely dependent on knowing this relationship, in an actual operational test, a good estimate should emerge as the number of examinees increases; this should happen as part of the precalibration process (Kang et al., 2020).

From the results, it is found that using response time information improves estimation of $\theta$ when using J-EAP, which is not the case for MLE. Moreover, as the relationship between $\theta$ and $\tau$ becomes stronger, the gains in efficiency increase; this is especially true for short tests. However, as is commonly found in Bayesian estimation approaches, decreasing overall RMSE coincides with increasing bias. If the increase in bias is small, however, this may be worthy price to pay, especially if the correlation between true and estimated parameters increases as well. When the MICT item selection method is introduced, an even stronger argument is found for using the J-EAP for estimation: If we have the dual-objective of maximizing information in the test while minimizing time taken on the test, using J-EAP with MICT combines the strengths of both approaches over the standard approach (i.e., MLE with MIC) with minimal extra cost.

From a fairness perspective, as defined by differences in test-taking time, the J-EAP decreases variability in test-taking times, thus creating a test that may be perceived as more fair, and may also potentially allay feelings of anxiety by the test-taker in situations when someone finishes before themselves. Moreover, average test (and item) times decreased using the J-EAP. These effects are present even when using MICT to choose items. Not only is this important from an examinee’s point of view, but it should also be important from the test user’s point of view. First, the test user will have an easier time setting a reasonable time limit within which most test-takers will complete the test. Second, there should be less of an effect on the test scores due to examinees coming up against the test’s time limit; if a reasonable time limit is set, then the examinee should not come dangerously close to the time limit and alter their test-taking behavior. Whenever this happens, the test score will reflect not only ability, but also their changing speededness toward the end of the test, reducing the effectiveness of the test scores as a measure of ability. Importantly, this is not the same as including a latent speed variable into the model for the data. Insofar as there is a relationship between ability and speed for a given person, then accounting for that relationship can only increase construct validity. The use of this model does rely on the assumption of constant speededness, which can be reasonably assumed if the time limit is properly set as discussed above (van der Linden, 2007). All of the foregoing effects are also present in the real data simulation.

One potential reason for why J-EAP does such a good job at minimizing test times is that the shrinkage of the Bayesian estimator means that high-ability examinees are administered slightly easier items than expected. Due to the positive relationship between the item difficulty and time-intensity parameters, this means that high-ability examinees are getting quicker items than might otherwise be expected. While this argument is reasonable for high-ability examinees, this does not explain the observation that the test times are also slower for low-ability examinees. Why this is occurring should be explored further.

Other future directions for this work are to consider the effects that practical constraints, as imposed by content and item exposure constraints, will have on the effectiveness of the J-EAP–MICT CAT scheme. For instance, it is possible that with these constraints, the item pool becomes more limited and results in suboptimal item selection at the extremes of the ability scale. Another potential direction is to consider how the latent trait and item distributions, in conjunction with the J-EAP, affect the estimation accuracy and response times. Thus far, limited evidence from the real data simulation, as well from preliminary investigation, suggests that they do affect estimation accuracy and test times, but it would be worthwhile to understand their effects more fully.

Appendix

As mentioned in the main body of this article, the ability estimate part of the J-EAP is equivalent to van der Linden’s (2008) empirical Bayes estimator. By using definitions of integrals, and an application of Bayes’ theorem, this is fairly easy to show.

$$\begin{array}{cc}\multicolumn{1}{c}{\mathrm{E}(\theta |\mathbf{x},\ln \mathbf{t})}& =\frac{\int \int \theta f(\mathbf{x}|\theta )f(\ln \mathbf{t}|\tau )f(\theta ,\tau )d\tau d\theta }{\int \int f(\mathbf{x}|\theta )f(\ln \mathbf{t}|\tau )f(\theta ,\tau )d\tau d\theta }=\frac{\int \int \theta f(\mathbf{x}|\theta )f(\ln \mathbf{t}|\tau )f(\theta |\tau )f(\tau )d\tau d\theta }{\int \int f(\mathbf{x}|\theta )f(\ln \mathbf{t}|\tau )f(\theta |\tau )f(\tau )d\tau d\theta }\hfill \\ \multicolumn{1}{c}{}& =\frac{f(\ln \mathbf{t})}{f(\ln \mathbf{t})}\times \frac{\int \int \theta f(\mathbf{x}|\theta )f(\ln \mathbf{t}|\tau )f(\theta |\tau )f(\tau )d\tau d\theta }{\int \int f(\mathbf{x}|\theta )f(\ln \mathbf{t}|\tau )f(\theta |\tau )f(\tau )d\tau d\theta }\hfill \\ \multicolumn{1}{c}{}& =\frac{\int \int \theta f(\mathbf{x}|\theta )\frac{f(\ln \mathbf{t}|\tau )f(\tau )}{f(\ln \mathbf{t})}f(\theta |\tau )d\tau d\theta }{\int \int f(\mathbf{x}|\theta )\frac{f(\ln \mathbf{t}|\tau )f(\tau )}{f(\ln \mathbf{t})}f(\theta |\tau )d\tau d\theta }\hfill \\ \multicolumn{1}{c}{}& =\frac{\int \int \theta f(\mathbf{x}|\theta )f(\tau |\ln \mathbf{t})f(\theta |\tau )d\tau d\theta }{\int \int f(\mathbf{x}|\theta )f(\tau |\ln \mathbf{t})f(\theta |\tau )d\tau d\theta }\hfill \\ \multicolumn{1}{c}{}& =\frac{\int \theta f(\mathbf{x}|\theta )[\int f(\tau |\ln \mathbf{t})f(\theta |\tau )d\tau ]d\theta }{\int f(\mathbf{x}|\theta )[\int f(\tau |\ln \mathbf{t})f(\theta |\tau )d\tau ]d\theta }\hfill \\ \multicolumn{1}{c}{}& =\frac{\int \theta f(\mathbf{x}|\theta )f(\theta |\ln \mathbf{t})d\theta }{\int f(\mathbf{x}|\theta )f(\theta |\ln \mathbf{t})d\theta }.\hfill \end{array}$$

The main crux of this proof is that the integral $\int f(\tau |\ln \mathbf{t})f(\theta |\tau )d\tau$ can be separately calculated within the overall integral. From elementary mathematical probability, the conditional probability density function of $\theta |\ln \mathbf{t}$ is simply the normal distribution; this, as explained by van der Linden (2008), is a result of the fact that $\theta |\tau$ and $\tau |\ln \mathbf{t}$ are both normally distributed as well. This is important, because as mentioned in the main text, the majority of the gain in speed comes from the result that $\theta |\ln \mathbf{t}~N({\mu }_{\theta |\ln \mathbf{t}},{\sigma }_{\theta |\ln \mathbf{t}}^2)$, which is a simple closed-form solution. To complete this, using the law of total expectation, the resulting conditional mean is

$$\begin{array}{cc}\multicolumn{1}{c}{{\mu }_{\theta |\ln \mathbf{t}}}& ={\mathrm{E}}_{\theta }(\theta |\ln \mathbf{t})={\mathrm{E}}_{\tau }({\mathrm{E}}_{\theta }(\theta |\tau ,\ln \mathbf{t})|\ln \mathbf{t})={\mathrm{E}}_{\tau }({\mathrm{E}}_{\theta }(\theta |\tau )|\ln \mathbf{t})\hfill \\ \multicolumn{1}{c}{}& ={\mathrm{E}}_{\tau }({\mu }_{\theta }+\frac{{\sigma }_{\theta \tau }}{{\sigma }_{\tau }^2}(\tau -{\mu }_{\tau })|\ln \mathbf{t})={\mu }_{\theta }+\frac{{\sigma }_{\theta \tau }}{{\sigma }_{\tau }^2}(E_{\tau }(\tau |\ln \mathbf{t})-{\mu }_{\tau })\hfill \\ \multicolumn{1}{c}{}& ={\mu }_{\theta }+\frac{{\sigma }_{\theta \tau }}{{\sigma }_{\tau }^2}[\frac{{\sigma }_{\tau }^{-2}{\mu }_{\tau }+\sum _i{\alpha }_i^2({\beta }_i-\ln t_i)}{{\sigma }_{\tau }^{-2}+\sum _i{\alpha }_i^2}-{\mu }_{\tau }].\hfill \end{array}$$

Similarly, using the law of total variance, we can find the resulting conditional variance as

$$\begin{array}{cc}\multicolumn{1}{c}{{\sigma }_{\theta |\ln \mathbf{t}}^2}& =\mathrm{Va}{\mathrm{r}}_{\theta }(\theta |\ln \mathbf{t})\hfill \\ \multicolumn{1}{c}{}& ={\mathrm{E}}_{\tau }(\mathrm{Va}{\mathrm{r}}_{\theta }(\theta |\tau ,\ln \mathbf{t})|\ln \mathbf{t})+\mathrm{Va}{\mathrm{r}}_{\tau }({\mathrm{E}}_{\theta }(\theta |\tau ,\ln \mathbf{t})|\ln \mathbf{t})\hfill \\ \multicolumn{1}{c}{}& ={\mathrm{E}}_{\tau }(\mathrm{Va}{\mathrm{r}}_{\theta }(\theta |\tau )|\ln \mathbf{t})+\mathrm{Va}{\mathrm{r}}_{\tau }({\mathrm{E}}_{\theta }(\theta |\tau )|\ln \mathbf{t})\hfill \\ \multicolumn{1}{c}{}& ={\mathrm{E}}_{\tau }({\sigma }_{\theta }^2-\frac{{\sigma }_{\theta \tau }^2}{{\sigma }_{\tau }^2}|\ln \mathbf{t})+\mathrm{Va}{\mathrm{r}}_{\tau }({\mu }_{\theta }+\frac{{\sigma }_{\theta \tau }}{{\sigma }_{\tau }^2}(\tau -{\mu }_{\tau })|\ln \mathbf{t})\hfill \\ \multicolumn{1}{c}{}& ={\sigma }_{\theta }^2-\frac{{\sigma }_{\theta \tau }^2}{{\sigma }_{\tau }^2}+{\left(\frac{{\sigma }_{\theta \tau }}{{\sigma }_{\tau }^2}\right)}^2\mathrm{Va}{\mathrm{r}}_{\tau }(\tau |\ln \mathbf{t})={\sigma }_{\theta }^2-\frac{{\sigma }_{\theta \tau }^2}{{\sigma }_{\tau }^2}+{\left(\frac{{\sigma }_{\theta \tau }}{{\sigma }_{\tau }^2}\right)}^2\frac{1}{{\sigma }_{\tau }^{-2}+\sum _i{\alpha }_i^2}\hfill \\ \multicolumn{1}{c}{}& ={\sigma }_{\theta }^2-\frac{{\sigma }_{\theta \tau }^2}{{\sigma }_{\tau }^2}+\frac{{\sigma }_{\theta \tau }^2}{{\sigma }_{\tau }^2}\frac{1}{1+{\sigma }_{\tau }^2\sum _i{\alpha }_i^2}={\sigma }_{\theta }^2-\frac{{\sigma }_{\theta \tau }^2}{{\sigma }_{\tau }^2}(1-\frac{1}{1+{\sigma }_{\tau }^2\sum _i{\alpha }_i^2})\hfill \\ \multicolumn{1}{c}{}& ={\sigma }_{\theta }^2-\frac{{\sigma }_{\theta \tau }^2}{{\sigma }_{\tau }^2}\left(\frac{{\sigma }_{\tau }^2\sum _i{\alpha }_i^2}{1+{\sigma }_{\tau }^2\sum _i{\alpha }_i^2}\right)={\sigma }_{\theta }^2-\frac{{\sigma }_{\theta \tau }^2\sum _i{\alpha }_i^2}{1+{\sigma }_{\tau }^2\sum _i{\alpha }_i^2}.\hfill \end{array}$$

A similar gain in computational speed for the speededness estimate part of the J-EAP can be obtained like the above result. To get the result, we first must recognize the following:

$$\begin{array}{cc}\multicolumn{1}{c}{f(\tau |\theta ,\ln \mathbf{t})}& =\frac{f(\tau ,\theta ,\ln \mathbf{t})}{f(\theta ,\tau )}=\frac{f(\theta |\ln \mathbf{t},\tau )f(\tau ,\ln \mathbf{t})}{f(\theta ,\ln \mathbf{t})}=\frac{f(\theta |\ln \mathbf{t},\tau )f(\tau |\ln \mathbf{t})f(\ln \mathbf{t})}{f(\theta |\ln \mathbf{t})f(\ln \mathbf{t})}\hfill \\ \multicolumn{1}{c}{}& =\frac{f(\theta |\ln \mathbf{t},\tau )f(\tau |\ln \mathbf{t})}{f(\theta |\ln \mathbf{t})}=\frac{f(\theta |\tau )f(\tau |\ln \mathbf{t})}{f(\theta |\ln \mathbf{t})}\hfill \end{array}$$

$$\Rightarrow f(\tau |\theta ,\ln \mathbf{t})f(\theta |\ln \mathbf{t})=f(\theta |\tau )f(\tau |\ln \mathbf{t}).$$

Next, the conditional expectation of $\tau |\theta ,\ln \mathbf{t}$ is found to be

$${\mathrm{E}}_{\tau }(\tau |\theta ,\ln \mathbf{t})=\int \tau f(\tau |\theta ,\ln \mathbf{t})d\tau =\frac{1}{f(\theta |\ln \mathbf{t})}\int \tau f(\theta |\tau )f(\tau |\ln \mathbf{t})d\tau$$

$$\Rightarrow {\mathrm{E}}_{\tau }(\tau |\theta ,\ln \mathbf{t})f(\theta |\ln \mathbf{t})=\int \tau f(\theta |\tau )f(\tau |\ln \mathbf{t})d\tau$$

The final result can be obtained by using definitions of integrals, like with the ability estimator portion, and an application of Bayes’ theorem.

$$\begin{array}{cc}\multicolumn{1}{c}{\mathrm{E}(\tau |\mathbf{x},\ln \mathbf{t})}& =\frac{\int \int \tau f(\mathbf{x}|\theta )f(\ln \mathbf{t}|\tau )f(\theta ,\tau )d\theta d\tau }{\int \int f(\mathbf{x}|\theta )f(\ln \mathbf{t}|\tau )f(\theta ,\tau )d\theta d\tau }=\frac{\int \int \tau f(\mathbf{x}|\theta )f(\ln \mathbf{t}|\tau )f(\theta |\tau )f(\tau )d\tau d\theta }{\int \int f(\mathbf{x}|\theta )f(\ln \mathbf{t}|\tau )f(\theta |\tau )f(\tau )d\tau d\theta }\hfill \\ \multicolumn{1}{c}{}& =\frac{f(\ln \mathbf{t})}{f(\ln \mathbf{t})}\times \frac{\int \int \tau f(\mathbf{x}|\theta )f(\ln \mathbf{t}|\tau )f(\theta |\tau )f(\tau )d\tau d\theta }{\int \int f(\mathbf{x}|\theta )f(\ln \mathbf{t}|\tau )f(\theta |\tau )f(\tau )d\tau d\theta }\hfill \\ \multicolumn{1}{c}{}& =\frac{\int \int \tau f(\mathbf{x}|\theta )\frac{f(\ln \mathbf{t}|\tau )f(\tau )}{f(\ln \mathbf{t})}f(\theta |\tau )d\tau d\theta }{\int \int f(\mathbf{x}|\theta )\frac{f(\ln \mathbf{t}|\tau )f(\tau )}{f(\ln \mathbf{t})}f(\theta |\tau )d\tau d\theta }\hfill \\ \multicolumn{1}{c}{}& =\frac{\int \int \tau f(\mathbf{x}|\theta )f(\tau |\ln \mathbf{t})f(\theta |\tau )d\tau d\theta }{\int \int f(\mathbf{x}|\theta )f(\tau |\ln \mathbf{t})f(\theta |\tau )d\tau d\theta }\hfill \\ \multicolumn{1}{c}{}& =\frac{\int f(\mathbf{x}|\theta )[\int \tau f(\tau |\ln \mathbf{t})f(\theta |\tau )d\tau ]d\theta }{\int f(\mathbf{x}|\theta )[\int f(\tau |\ln \mathbf{t})f(\theta |\tau )d\tau ]d\theta }\hfill \\ \multicolumn{1}{c}{}& =\frac{\int {\mathrm{E}}_{\tau }(\tau |\theta ,\ln \mathbf{t})f(\mathbf{x}|\theta )f(\theta |\ln \mathbf{t})d\theta }{\int f(\mathbf{x}|\theta )f(\theta |\ln \mathbf{t})d\theta }.\hfill \end{array}$$

As noted above, $\theta |\ln \mathbf{t}~N({\mu }_{\theta |\ln \mathbf{t}},{\sigma }_{\theta |\ln \mathbf{t}}^2)$, which is a simple closed-form solution with ${\mu }_{\theta |\ln \mathbf{t}}$ and ${\sigma }_{\theta |\ln \mathbf{t}}^2$ computed as before. Finally, the value of ${\mathrm{E}}_{\tau }(\tau |\theta ,\ln \mathbf{t})$ is simply

$${\mathrm{E}}_{\tau }(\tau |\theta ,\ln \mathbf{t})=\frac{{\sigma }_{\tau |\ln \mathbf{t}}^2[{\left(\frac{{\sigma }_{\theta \tau }}{{\sigma }_{\tau }^2}\right)}^2{\mu }_{\tau }+\frac{{\sigma }_{\theta \tau }}{{\sigma }_{\tau }^2}(\theta -{\mu }_{\theta })]+{\sigma }_{\theta |\tau }^2{\mu }_{\tau |\ln \mathbf{t}}}{{\sigma }_{\tau |\ln \mathbf{t}}^2{\left(\frac{{\sigma }_{\theta \tau }}{{\sigma }_{\tau }^2}\right)}^2+{\sigma }_{\theta |\tau }^2}.$$