High Dynamic Range Nanowire Resonators

Abstract

Dynamic range quantifies the linear operation regime available in nanomechanical resonators. Nonlinearities dominate the response of flexural beams in the limit of very high aspect ratio and very small diameter, which leads to expectation of low dynamic range for nanowire resonators in general. However, the highest achievable dynamic range for nanowire resonators with practical dimensions remains to be determined. We report dynamic range measurements on singly clamped silicon nanowire resonators reaching remarkably high values of up to 90 dB obtained with a simple harmonic actuation scheme. We explain these measurements by a comprehensive theoretical examination of dynamic range in singly clamped flexural beams including the effect of tapering, a usual feature of semiconductor nanowires. Our analysis reveals the nanowire characteristics required for broad linear operation, and given the relationship between dynamic range and mass sensing performance, it also enables analytical determination of mass detection limits, reaching atomic-scale resolution for feasible nanowires.

Nanowire resonators are currently established as one of the most prolific families of nanostructured devices for the realization of nanoelectromechanical systems (NEMS). Their unique physical properties, ranging from optomechanical interactions,^1,2 resonance degeneration breakage,³⁻⁵ or mode coupling mechanisms,^6,7 have enabled a number of high-performance applications as transducers,⁸⁻¹⁰ sensors,^3,11−14 or microscopy probes.¹⁵⁻¹⁷ In nanomechanical resonators, nanowires function as flexural beams whose operational regime is determined by the onset of nonlinearity. Standard functionalities require linear schemes based for instance on resonance frequency tracking, which ensures high sensitivity, stable operation, and calibrated measurements. Beyond the nonlinear onset, such schemes cannot be readily used. However, the singular phenomena that emerge in the nonlinear regime enable alternative methods that provide unique functionalities which are otherwise impossible to implement.¹⁸ In consequence, the practical development of applications based on nanowire resonators requires accurate knowledge about the boundaries between the linear and nonlinear operational regimes. The extent of linear regime available for a particular device is determined by its dynamic range (DR), given by the ratio of the highest linearly driven amplitude to the lowest detectable signal level.

Nanowire resonators, particularly in their single clamp (SC) configuration, have been largely overlooked in terms of DR evaluation. The earliest reports were focused on the double clamp (DC) configuration in the limit of very low diameter and very high aspect ratio.¹⁹ In such a scenario, nonlinearities appear at low amplitudes and dominate the resonant response, resulting in low values of DR. Although various aspects regarding the onset of nonlinearity in SC beam resonators have been studied,²⁰⁻²⁶ a comprehensive analysis that determines the physical characteristics of nanowire resonators that result in a broad DR is not available. In this work we examine the DR of SC Si nanowire resonators grown by vapor–liquid–solid (VLS) synthesis with a wide range of dimensions. We measure values up to 90 dB with simple harmonic piezoelectric actuation driving and without using any nonlinear compensation scheme. In order to analyze these results, we develop an analytical theoretical approach to determine the DR of SC flexural beam resonators as a function of their dimensions and geometry, including the effect of cross-section tapering, a common feature in the growth of semiconductor nanowires.^27,28 The DR predicted by our theoretical analysis for nanowire resonators, which is significantly larger for the SC configuration than for the DC case, is in very good agreement with our experimental characterization, and it allows expectation of values in the 70–100 dB range for nanowires with dimensions both feasible and relevant for nanomechanical technology. Finally, we discuss the implications of our results in the context of nanomechanical mass sensing, where DR directly determines the fundamental mass detection limit. Our analytical approach leads to an expression for this limit as a function of the resonator characteristics, which allows predicting an excellent sensing performance for nanowires with ordinary features.

In order to derive an expression for the DR of SC nanowire resonators, we consider that only the fundamental flexural mode is active and that the resonator is driven by an external harmonic force of amplitude F₀ at frequency ω. Then, the displacement at the free end, x, can be described by the following equation of motion:^24,29,30

1

where the dot denotes the time derivative and a damping term associated with a finite quality factor Q is included. Consistent with the morphology of most frequently reported nanowire resonators,¹² we consider a nanowire of length L and hexagonal cross-section with linear tapering described by the coefficient α_T = 1 – D_tip/D₀, where D_tip and D₀ are the diameter values at the tip and base, respectively. The effective mass m, effective spring constant k, and natural frequency ω₀ are related by ω₀² = k/m. These parameters, together with the geometrical β_G and inertial β_I nonlinear coefficients, are determined by the nanowire geometry (cross-section area at the base S₀, second moment of area at the base I₀, and tapering coefficient α_T), material properties (density ρ and Young’s modulus E), and flexural mode shape as given by Euler–Bernoulli theory³¹ (see Supporting Information).

Introducing a global nonlinear coefficient as α_NL = β_G/k – 2β_I/(3m) leads to a compact expression for the frequency response of the nanowire. In the case of large aspect ratio (L ≫ D₀), α_NL is positive for the fundamental mode,^25,26 and the frequency response can be written as

2

where a represents the beam oscillation amplitude and we define a₀ = QF₀/k and a_M = 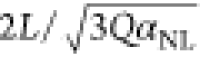. Thus, a₀ represents the beam oscillation amplitude at the natural frequency in the linear regime and a_M is a characteristic magnitude of the nonlinear onset. If α_NL = 0, eq 2 reduces to the Lorentzian response of a linear resonator, and the resonance frequency is ω_R ≈ ω₀ for Q ≫ 1; if α_NL > 0, the resonance frequency is given by ω_R² ≈ ω₀²[1 + a₀²/(Qa_M²)]. The parameter a_M provides a measure of the ultimate limit of the linear regime (Figure 1a): when the driving force is large enough to raise the amplitude at the natural frequency to a(ω₀) = a_M, then the resonance frequency becomes multivalued so that 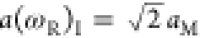(resonance peak amplitude) and a(ω_R)_II = a_M (bifurcation point). Thus, the driving force for which a(ω₀) = a_M represents the threshold for a multivalued resonance frequency, above which standard resonance frequency tracking schemes used in the linear regime become absolutely impracticable.

Figure 1.

Dynamic range of nanowire resonators. (a) Schematic representation of frequency response curves for varying driving strength, indicating the thermomechanical response curve (brown), the 1 dB compression curve (black), the critical amplitude curve (purple), and the multivalued resonance frequency threshold curve (green). (b) Schematic representation of the corresponding amplitude vs driving strength curves at ω = ω₀ for the linear (red) and nonlinear (blue) responses, indicating the 1 dB compression reference points and the resulting spread of the dynamic range (note that if Q ≫1, for a given driving strength the amplitude at ω = ω₀ for the purely linear case matches the amplitude at ω = ω_R for the nonlinear response).

A practical reference to define the onset of nonlinearity is the 1 dB compression point,³² referred to as the point where the oscillation amplitude at the natural frequency a_1dB(ω₀) is 1 dB lower than the amplitude that would result from a purely linear response for the same driving force (Figure 1b). The 1 dB compression point can be related to the critical amplitude a_C, defined as the amplitude at the bifurcation point in the frequency response curve corresponding to a driving force for which the curve begins to be multivalued (Figure 1a). This relation results in a_1dB(ω₀) ≃ 0.664a_C, although the relation of a_C with the amplitude at resonance a_1dB(ω_R) ≃ 0.745a_C has been typically considered in previous works^19,33,34 (see Supporting Information). A more straightforward approach to determine a_1dB(ω₀) can be followed by using eq 2 for writing the 1 dB compression condition as a₀/a_1dB(ω₀) = 10^1/20, which leads to

3

The lower limit for determining the DR is given by the noise floor of the amplitude signal. Here we model the intrinsic DR of a beam, so we consider thermomechanical noise as the dominant noise source. Thus, the corresponding spectral density at resonance is

4

where k_B is the Boltzmann’s constant and T is the temperature.

We define the dynamic ratio r_D as the ratio of the amplitude at the onset of nonlinearity (1 dB compression point) to the lowest measurable amplitude (thermomechanical spectral density integrated for the measurement bandwidth Δf):

5

We preserve the term dynamic range (DR) for the ratio r_D expressed in dB so that DR = 20 log₁₀ r_D. The exact calculation of the DR from eq 5 involves the computation of m, ω₀, and α_NL as a function of the beam geometry, material properties, and mode shape, which requires numerical methods. Note that this calculation requires considering the mode shape of a tapered nanowire, as computed in a previous work.²⁸ However, an excellent analytical approximation can be obtained by separating the contribution of tapering in a function h(α_T). Then, introducing the corresponding expressions of S₀ and I₀ for a hexagonal cross-section, the DR of nanowire resonators can be calculated from

6

The function h(α_T) can be approximated by h(α_T) = ∑_ic_iα_Tⁱ, and the coefficients c_i can be obtained by fitting h(α_T) to numerical calculations of r_D from eq 5 (see Supporting Information). For α_T < 0.9, h(α_T) can be simplified to h(α_T) ≃ 1 – 0.677α_T so that for nanowires with uniform section, h(0) ≃ 1.

Equation 6 points out some important differences between SC and DC beams, particularly regarding the dependence on the aspect ratio L/D₀. This expression is notably analogous to the ones previously derived for the DC configuration.¹⁹ However, the SC case shows a weaker dependence on the aspect ratio, r_D ∝ D₀(L/D₀)^−3/2, as compared to the DC configuration, where r_D ∝ D₀(L/D₀)^−5/2 so that DR does not degrade for increasing aspect ratio as fast as for the DC case. The quantitative relation between the DR of SC and DC nanowires with equal characteristics is approximated by r_D(SC)/r_D(DC) ≃ 0.233L/D₀. Therefore, for approximately L/D₀ > 50, the DR of SC nanowires is more than 20 dB larger than that of equivalent DC nanowires. Similar results are obtained for beams with circular and rectangular cross-section (see Supporting Information). The physical origin of this disparity lies in the different mechanisms that dominate nonlinearities for each clamping configuration. In DC beams, a relatively small beam deflection necessarily implies that the beam stretches so that bending-induced tension dominates. In SC beams, bending produces negligible stretching, and nonlinearity is provided by bending-induced curvature. This is a lower magnitude effect so that SC beams reach the nonlinear onset at higher amplitudes than equivalent DC beams.

In order to characterize the DR of nanowire resonators, we have performed experimental measurements on Si nanowires vertically grown on flat Si substrates by the VLS mechanism (see Supporting Information), resulting in SC beam resonators where the clamp is defined by the epitaxial union of the nanowire base to the substrate.³⁵Figure 2a shows a representative scanning electron microscopy (SEM) image of the Si nanowires under test. The nanowires have lengths in the range of 10–50 μm, base diameters of 125–425 nm, and tapering coefficients of 0.1–0.9. The resulting aspect ratio L/D₀ is in the range 30–180. A precise measurement of nanowire dimensions is obtained from high resolution SEM images.¹⁰ The cross-section at the base is hexagonal with an approximately regular geometry, but the sidewall facets evolve along the nanowire length so that near the tip the cross-section becomes polyhedral (Figure 2b). The gold catalyst nanoparticle used for the VLS synthesis generates a gold–silicon oxide core–shell nanostructure that remains at the tip of the nanowire.³⁶ The nanowires are grown on plain Si(111) substrates without any kind of prefabricated structure.

Figure 2.

Experimental system and measurement setup. (a) Scanning electron microscopy image of a representative sample of the Si nanowires used in this work (scale bar 5 μm). (b) Details of the cross-section geometry along a nanowire length, which evolves from hexagonal at the base (lower image section) and most nanowire length (>50%) to polyhedral near the tip (upper image section; scale bar 300 nm in both sections). (c) Schematic depiction of the measurement setup, based on backscattered light modulation transduction. A diode laser (λ = 633 nm) is focused by a 0.42 NA objective on the Si nanowires placed in a high-vacuum chamber (∼10^–5 mbar). The incident laser beam is linearly polarized along the longitudinal axis of the nanowires, and its optical power ranges from 72 to 216 μW. The backscattered beam is collected by an amplified photodetector whose output signal is processed either by a digital acquisition (DAQ) board or by a lock-in amplifier (LIA).

The frequency response of the nanowires is measured in high vacuum by the optical transduction setup depicted in Figure 2c (see Supporting Information). The nanowires are driven by a piezoelectric actuator placed under the substrate, and their vibrations are measured by collecting the backscattered light resulting from the incidence of a focused laser beam.¹⁰ We use a laser beam incidence perpendicular to the nanowires in order to match the most commonly extended configuration in applications of nanowire resonators.¹² The transduction mechanism relies on vibration-induced light scattering modulation (see Supporting Information). Such mechanism provides a wide linear transduction range that ensures undistorted oscillation amplitude measurements, whereas interferometric approaches can be more limited regarding this issue.²⁵ For every single nanowire tested in this work we have verified that the thermomechanical amplitude at the natural frequency is above the transduction detection limit and that the amplitude at the 1 dB compression point is within the transduction linear range (see Supporting Information).

The results of the characterization of the DR of the Si nanowires under analysis are shown in Figure 3. In Figure 3a we present an example of a set of resonance curves acquired with varying driving strength, revealing the nanowire response from the thermomechanical spectrum to slightly above the onset of nonlinearity. This example corresponds to the upper resonance peak of the fundamental mode doublet,³ acquired by upward frequency sweeps on a Si nanowire with a length of 10.8 μm, a base diameter of 183 nm, and a tapering coefficient of 0.3. Thermomechanical calibration has been used to convert the measured signal into length units.³⁷ These measurements allow determination of the natural frequency and quality factor of the nanowires, which for this example result in 1.906 MHz and 4867, respectively. Figure 3b shows a plot of the fundamental natural frequency of the 20 nanowires presented in this study. The natural frequencies are in the range of 0.2–3.5 MHz and the quality factors in the range of 3000–30000. The experimental frequency data are fitted to the equation derived for a tapered hexagonal cross-section in which the tapering effect is contained in a polynomic function k₀(α_T).²⁸ The fitting results in a value of Young’s modulus E = 164 ± 6 GPa, in good agreement with the bulk value for Si(111) of 187 GPa as expected for Si nanowires in this range of diameters assuming the bulk Si density ρ = 2329 kg/m³.³⁸ The small discrepancy is attributed to the varying geometry of the nanowire cross-section along its length, to the presence of sidewall sawtooth faceting, and to the core–shell nanostructure at the tip, which may affect the effective mass and spring constant.

Figure 3.

Dynamic range measurements and experiment–theory comparison. (a) Representative example of the measured frequency response curves for varying driving strength for a nanowire with f₀ = 1905.7 kHz (dotted line) and Q = 4867. The lower section shows the full set of curves from the thermomechanical response to the nonlinear regime. The upper section shows a subset of curves around the nonlinear onset (Δf = 14.82 Hz). (b) Measurements and fitting of the natural frequencies of all nanowires tested in this work, from which a Young’s modulus E = 164 ± 6 GPa is obtained. (c) Example of a measurement of the amplitude at the natural frequency for varying driving strength and fitting to the theoretical expression derived in the main text (Δf = 1.098 Hz). (d) Experimental results and theoretical calculation of the dynamic range for all nanowires under test.

Precise measurements of DR are performed as exemplified in Figure 3c. We determine the amplitude at the 1 dB compression point by a series of measurements of the amplitude at the natural frequency for varying actuator driving voltage V_p. We fit such measurements to the theoretical expression that can be derived by making ω = ω₀ in eq 2:

7

where we assume that the amplitude in the linear regime is proportional to V_p so that a₀ = κV_p. From such fitting we extract κ and a_M, and the latter is used to calculate a_1dB(ω₀) by using eq 3. The thermomechanical response amplitude a_TH(ω₀) is measured by setting V_p = 0, and then the experimental DR is obtained from r_D = a_1dB(ω₀)/a_TH(ω₀). Figure 3d presents all the measured values (dots) of DR vs the factor that combines all the experimentally measured parameters that determine the DR according to eq 6. We also directly plot (line) the theoretical behavior expected from eq 6 by using the value of E determined from the fitting of the resonance frequencies and considering the experimental conditions (Δf = 1.098 Hz, T = 325 K). Table 1 summarizes all experimental and theoretical values for the DR and other relevant parameters for the whole set of nanowires analyzed in this work. The very good agreement between measurements and theory supports our analytical approach and the compliance of nanowire dynamics with Euler–Bernoulli theory in their full dynamic range.

Table 1. Set of Si Nanowire Resonators Tested in This Work.

no.	L (μm)	D0 (nm)	L/D0	aT	m (fg)	Q	fexp (kHz)	ftheo (kHz)	DRexp (dB)	DRtheo (dB)	δm (zg)
1	43.2	241	179	0.89	46	15116	294	278	53	54	6.61
2	44.2	256	173	0.88	56	20947	280	278	55	53	4.91
3	43.7	276	158	0.81	100	15717	267	278	56	58	10.27
4	25.9	199	130	0.72	50	19110	550	508	60	57	2.79
5	17.6	212	83	0.34	145	27860	925	869	60	64	5.17
6	25.7	237	108	0.69	81	12411	589	596	63	65	4.46
7	25.1	219	115	0.73	55	11790	582	607	65	63	2.75
8	27.0	294	92	0.52	255	23921	621	576	66	65	5.44
9	27.1	326	83	0.46	378	25566	646	608	67	67	6.63
10	17.5	190	92	0.38	105	16724	903	804	67	65	2.65
11	18.1	309	58	0.28	369	26806	1181	1162	69	72	4.75
12	19.3	347	56	0.27	502	25265	1135	1141	72	74	5.11
13	10.3	145	71	0.46	29	7557	1912	1866	72	73	0.90
14	10.3	192	53	0.29	79	9567	2222	2240	77	78	1.17
15	11.6	338	34	0.17	357	20909	2909	2915	81	83	1.60
16	19.5	422	46	0.24	802	20365	1270	1329	82	81	3.28
17	10.8	183	59	0.31	71	4867	1906	1956	83	82	1.10
18	10.7	194	55	0.24	94	3789	2139	2039	84	86	1.61
19	10.5	203	52	0.29	91	4701	2134	2260	86	85	0.95
20	11.0	326	34	0.18	308	9097	3127	3116	90	90	1.02

The highest DR measured for the set of nanowires under test in this work is 90 dB. This value is comparable to the highest DR values reported for other nanomechanical resonators based on either nonlinearity compensated DC beams,³⁹⁻⁴¹ SC rectangular beams with lower aspect ratio,⁴² or harmonically driven atomically thin membranes,^33,34 which have been recently reported to naturally provide large DR values. Moreover, the theoretical analysis presented here allows us to estimate that even higher DR values can be achieved with nanowire resonators with feasible dimensions. Figure 4 displays a calculation of the DR of Si nanowires as a function of their aspect ratio and diameter. For this calculation we consider Q = 10000, Δf = 1.098 Hz, E = 164 GPa, T = 325 K, and ρ = 2329 kg/m³. The graphs in Figure 4a and Figure 4b allow us to compare the cases of a SC nanowire with α_T = 0.9 (highly tapered) and α_T = 0 (uniform), respectively. From the approximation used for h(α_T), it can be estimated that a nanowire with uniform cross-section provides around 8.2 dB of DR above a tapered nanowire with α_T = 0.9 and the same dimensions and quality factor. Figure 4b shows that values of DR above 70 dB and up to the 100 dB level can be reached in uniform Si nanowires when combining an aspect ratio below 100 and a diameter above 100 nm. This range of dimensions is consistent with values typically found in reports of Si nanowire resonator applications,¹² which point out the feasibility and relevance of nanowire resonators with dimensions resulting in high dynamic range.

Figure 4.

Theoretical calculations of dynamic range and fundamental mass detection limit for singly clamped Si nanowire resonators. (a) Dynamic range for tapered nanowires (a_T = 0.9). (b) Dynamic range for uniform nanowires (a_T = 0). (c) Fundamental mass detection limit for tapered nanowires (a_T = 0.9). (d) Fundamental mass detection limit for uniform nanowires (a_T = 0).

SC beam resonators have been extensively used as excellent platforms for ultrasensitive mass detection,⁴³⁻⁴⁵ and Si nanowires in particular provide various unique functional features.^1,3,28,46 The fundamental mass detection limit δm in frequency tracking measurement with a phase lock loop readout at constant mean square amplitude is determined by DR as δm = m/(Qr_D),⁴⁷ which assumes (1) driving at the onset of nonlinearity, (2) frequency stability limited by thermomechanical fluctuations, and (3) added mass placed at the point of maximum displacement. Although mass sensing with beam resonators is feasible in the nonlinear regime⁴⁸ and frequency stability may not be limited by thermomechanical fluctuations but other noise sources,⁴² it is useful to refer to δm as an ultimate limit that allows to compare different devices.^26,34 Our derivation of the DR for nanowire resonators leads to

8

where j(α_T) contains the tapering effect, and it can be approximated by j(α_T) ≃ 1 – 1.171α_T + 0.200α_T² (see Supporting Information). Table 1 presents the values of δm obtained for the nanowire resonators under test, which lay in the range of a few zeptograms. Figure 4c and Figure 4d present the calculations of δm for SC Si nanowires with the same parameters as in Figure 4a and Figure 4b, respectively. Tapered nanowires approach 1 yg for aspect ratio below 100 and diameter below 100 nm. Remarkably, δm is in general much lower for tapered nanowires than for uniform cross-sections. By evaluating j(α_T), we find δm(α_T = 0.9)/δm(α_T = 0) ≃ 0.11, which implies that δm for tapered nanowires is around 1 order of magnitude lower than that of uniform cross-section nanowires with the same length and diameter at the base. Although tapering results in lower DR, the effective mass contribution, significantly reduced with tapering, dominates in δm. Regarding the Q factor, in spite of improving resonance frequency tracking, a high Q has the effect of reducing DR and it has no contribution to δm. A high Q reduces DR because it implies a higher thermomechanical amplitude and the appearance of nonlinear effects at lower amplitudes. In δm, the effect of better frequency tracking provided by a high Q is canceled by the consequently lower DR.

In summary, we have shown that nanowire resonators with common physical characteristics can provide a broad DR: the presented measurements reach up to 90 dB, and the theoretical analysis allows expectation of values up to the 100 dB level, which compares to the highest reported for any other sort of nanomechanical resonator. The presented analysis provides a foundation for the suitability of nanowire resonators as building blocks for NEMS with high performance linear operation and specifically for mass sensing applications.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.1c02056.

• Detailed theoretical description of the equations of motion of SC and DC flexural beam resonators and their nonlinear frequency response, onset of nonlinearity, and derivation of the expressions for dynamic range and fundamental mass detection limit for hexagonal, cylindrical, and rectangular beams, including the effect of tapering in SC beams; details of the Si nanowire growth and characterization; details of the transduction mechanism involved in the DR measurements regarding the experimental setup, the transduction sensitivity, and its linear range (PDF)

The authors declare no competing financial interest.