Comparative biomechanics of the Pan and Macaca mandibles during mastication: finite element modelling of loading, deformation and strain regimes

Abstract

The mechanical behaviour of the mandibles of Pan and Macaca during mastication was compared using finite element modelling. Muscle forces were calculated using species-specific measures of physiological cross-sectional area and scaled using electromyographic estimates of muscle recruitment in Macaca. Loading regimes were compared using moments acting on the mandible and strain regimes were qualitatively compared using maps of principal, shear and axial strains. The enlarged and more vertically oriented temporalis and superficial masseter muscles of Pan result in larger sagittal and transverse bending moments on both working and balancing sides, and larger anteroposterior twisting moments on the working side. The mandible of Pan experiences higher principal strain magnitudes in the ramus and mandibular prominence, higher transverse shear strains in the top of the symphyseal region and working-side corpus, and a predominance of sagittal bending-related strains in the balancing-side mandible. This study lays the foundation for a broader comparative study of Hominidae mandibular mechanics in extant and fossil hominids using finite element modelling. Pan's larger and more vertical masseter and temporalis may make it a more suitable model for hominid mandibular biomechanics than Macaca.

1. Introduction

Mandibular morphology, including size and shape of the symphysis, corpus and ramus, varies considerably across hominids and has been used to diagnose species [1–8], test phylogenetic hypotheses [9–23] and make inferences about the material properties of diet and feeding behaviours of extinct species [24–28]. Reconstructions of diet and feeding behaviour of fossil hominids often focus on the mandible because of its key role in feeding and because mandibles are one of the most commonly recovered skeletal elements in the fossil record. However, attempts to relate variation in mandibular morphology to dietary variation in fossil hominids have been remarkably unsuccessful [27,29–32] because we lack a clear understanding of the mechanical consequences of this variation. Current models of hominid (great ape, human and extinct ancestors) mandible function rely heavily on extrapolation from in vivo studies of feeding in a non-hominid primate, Macaca [24,33–37]. The validity of this extrapolation rests in part on the similarity of masticatory dynamics across Anthropoidea (monkeys, apes and humans) [38,39]; however, differences in the interspecific shape of the masticatory apparatus, including the orientation [40] and relative size [41] of anthropoid jaw elevator muscles, have been well documented. Thus, the primary goal of this study is to evaluate this assumption by describing similarities and differences between the loading, deformation and strain regimes of the mandibles of Pan and Macaca during mastication [42,43].

Most work relating diet and feeding behaviour to mandibular morphology in primates has used beam models, the limitations of which are widely acknowledged [42,44–47], but our understanding of jaw function can be broadened using an engineering approach—finite element analysis (FEA)—which combines experimental levels of control with three-dimensional (3D) anatomical detail [42,43,48–64]. Here, we present a finite element model (FEM) of the mandible of a Pan troglodytes female and compare its loading, deformation and strain regimes with those of an FEM of a mandible of a Macaca mulatta female [42,43]. Mechanical similarities between models will support and extend previous biomechanical studies of fossil hominin mandibles based on macaques. Differences will point to ways in which hominid mandibular mechanics might differ from those of other catarrhines, and suggest new testable hypotheses and research questions. Our null hypothesis is that loading, deformation and strain regimes in the FE model of Pan are the same as those of Macaca, the predictions of which are as follows.

1.1. Predictions of mandible function

We first asked whether loading and deformation regimes in our chimp FEM match those predicted for the power stroke of mastication in macaques and humans [24,33,34,36,37,42,65–70]. Because our FEMs are loaded with muscle forces proportional to those reported for Macaca, we expect the following deformation and strain regimes, reported by Panagiotopoulou et al. [42]. The balancing-side mandible is hypothesized to be subjected to negative sagittal bending, negative sagittal shear, negative axial (anteroposterior (AP)) twisting (eversion of the mandibular base) and lateral transverse bending (wishboning). Negative sagittal bending moments and their associated negative sagittal shear forces are predicted to dominate. Sagittal shear forces are hypothesized to be greatest in the ramus, between the masticatory muscle and joint, and AP twisting moments are hypothesized to be relatively low and to peak in the anterior corpus, below the premolars. The balancing-side mandible is also expected to be subjected to lateral transverse bending moments that are greatest anteriorly and decrease posteriorly. A human- or macaque-like deformation pattern would be ‘helically upward and towards the working-side’ [69 p.131], with sagittal deformation and negative twisting of the balancing-side mandible producing eversion of the basal border [42,68].

The working-side mandible below the bite point is hypothesized to be subjected to negative sagittal bending moments, producing positive sagittal bending deformation; positive transverse bending moments, producing lateral transverse bending; and negative AP torsion, inverting the basal border below the bite point. Torques are hypothesized to vary along with the corpus: in the posterior corpus, transverse, vertical and AP torques decrease to zero at or immediately behind M₃ before reversing in the ramus. Sagittal shear forces are expected to be positive anterior to the bite points, strongly negative between bite points and ramus, then positive in the ramus [42].

The symphyseal region is hypothesized to be subject to positive frontal bending with the centre of flexure at the bite point, to experience negative frontal shear forces and deformation, lateral transverse bending and negative twisting about the mediolateral axis (ML twisting).

2. Material and methods

2.1. Specimen selection

We selected a specimen for analysis based on a geometric morphometric (GM) analysis of mandible shape. CT scans of 10 adult female chimpanzee mandibles (including members of three subspecies) were taken from specimens housed in museum collections (table 1). 3D surface files were generated from each CT scan, then 504 landmarks and semilandmarks were digitized on these 3D surfaces. These data were converted to shape coordinates by generalized Procrustes analysis (GPA), and principal components analysis (PCA) was used to determine patterns of shape variation. The P. troglodytes mandible AMNH 89351 was closest to the mean form and was selected for modelling.

Table 1.

Specimens included in geometric morphometric analysis.

specimen number	institution
AMNH 89351a	American Museum of Natural History
AMNH 89354	American Museum of Natural History
USNM 174699	Smithsonian
USNM 174701	Smithsonian
USNM 220062	Smithsonian
USNM 220063	Smithsonian
USNM 220064	Smithsonian
USNM 477333	Smithsonian
USNM 481803	Smithsonian
USNM 599173	Smithsonian

^aSpecimen closest to mean form, and selected for modelling.

2.2. FEM construction

CT scans were imported as TIFF stacks to Mimics v. 20 (Materialise NV, Leuven, Belgium), where cortical bone and teeth and trabecular bone were segmented to create separate surface files. Surface meshes were imported into 3D editing software (Geomagic Studio v. 12; Geomagic, Research Triangle Park) to correct minor errors in geometry (holes and intersections), ensuring meshability of the embedded volumes, and to define the global coordinate system (figure 1) before volume meshing in 3-Matic v. 12 (Mimics). Meshed volumes were imported to FEA software Strand7 (Strand7 Pty Ltd, Sydney) to apply boundary conditions and perform linear static FEA. The completed model was composed of 2,587,382 4-noded tetrahedral brick elements.

Figure 1.

Mandible morphology terminology, following Keiter [71], Lenhossek [72], Panagiotopoulou et al. [42], Rasche [73], Weidenreich [74] and White et al. [75]. See Panagiotopoulou et al. [43] for a discussion of the origins of terminology. AP, axial; ML, mediolateral; SI, superoinferior.

2.3. Material properties

The material properties of cortical bone were derived from the mean of great ape craniofacial cortical bone [76,77], are isotropic and homogeneous and are similar to those used in modelling of the macaque [78]. Trabecular bone was modelled as a volume of bulk tissue, which is less stiff than the macaque [79]. Deep elements of the teeth were assigned cortical bone properties, while dental enamel properties were assigned to surface elements by selecting all surface elements on the teeth protruding from the alveolus to create enamel ‘caps’ [80] (table 2).

Table 2.

Material properties applied to models.

	Pan		Macacaa
material	modulus (MPa)	Poisson's ratio	modulus (MPa)	Poisson's ratio
cortical boneb	17 300	0.28	11 000–30 000	0.34
trabecular bonec	640	0.28	1,000	0.3
dental enameld	80 000	0.3	24 000	0.3

^aFrom Panagiotopoulpou et al. [42].

^bFrom Schwartz-Dabney & Dechow [76,77].

^cFrom Ashman et al. [79].

^dFrom Habelitz et al. [80].

2.4. Muscle modelling

Forces exerted by the anterior and posterior temporalis, superficial and deep masseters and medial pterygoids were applied to the FEMs. A maximum possible force-generating capacity for each muscle was calculated using estimates of physiological cross-sectional area (PCSA) made by author A.B.T. using the averages of seven specimens of P. troglodytes (table 3; electronic supplementary material).

Table 3.

PCSA, estimated maximum muscle force capacity, EMG-based force scaling and force applied to FEM of Pan, compared with data for Macaca.

muscle	side	PCSA (cm2)		maximum force capacitya (N) = PCSA * 30 N/cm2		ratio of Pan/Macaca capacity	proportion of maximum force capacityb	force applied to macaque FEM (N)	force applied to chimp FEM (N)
		Macaca	Pan	Macaca	Pan femalec		Macaca	Macaca	Pan female
anterior temporalisd	working (L)	3.91	16.97	117.3	398.6	3.4	0.28	32.94	111.93
	balancing (R)	3.91	16.97	117.3	398.6	3.4	0.39	45.46	154.48
posterior temporalis	working	2.20	9.55	66.0	224.3	3.4	0.25	16.22	55.10
	balancing	2.20	9.55	66.0	224.3	3.4	0.57	37.79	128.40
total temporalis	working	6.11	26.52	183.3	622.8	3.4	0.27	49.16	167.04
	balancing	6.11	26.52	183.3	622.8	3.4	0.45	83.25	282.85
superficial masseter	working	4.14	25.19	124.2	591.6	4.8	0.51	63.42	302.10
	balancing	4.14	25.19	124.2	591.6	4.8	0.26	32.40	154.34
deep masseter	working	1.65	3.95	49.5	92.7	1.9	0.10	4.94	9.25
	balancing	1.65	3.95	49.5	92.7	1.9	0.51	25.20	47.18
medial pterygoid	working	6.83	17.27	204.9	405.5	2.0	0.21	43.72	86.53
	balancing	6.83	17.27	204.9	405.5	2.0	0.08	15.90	31.46

^aAs per Sinclair & Alexander [81].

^bEMG-scaled force estimates are based on Macaca muscle activity during chewing on nuts.

^cMuscle force scaled to model mandible length of 113.5 mm.

^dTemporalis PCSA of Pan was divided into anterior and posterior temporalis based on proportions (64/36%) in Macaca [42].

The goal of this study was a controlled comparison of mandible mechanics in Pan with those of Macaca during simulated mastication, so electromyographic (EMG) data [41] recorded from Macaca were used to estimate the proportions of Pan's maximum jaw-muscle force capacity applied to the model. Table 3 gives the Pan and Macaca PCSAs, the corresponding maximal muscle force capacities and the proportions of those forces applied to the models based on the macaque EMG data (table 3). In this way, we ensured that differences in loading regime (external force vector locations and moments) and internal deformation and strain regimes reflect differences in the shape and size of the Pan and Macaca models. The superoinferior (SI), AP and ML components of the muscle forces acting on the model are given in table 4, along with the resulting temporomandibular joint and bite point reaction forces.

Table 4.

Components of force (N) in Pan model.

		SI	AP	ML
anterior temporalis	working (L)	111.8	3.7	−2.4
	balancing (R)	154.2	6.9	5.9
posterior temporalis	working	48.8	−25.6	−0.1
	balancing	112.6	−61.7	3.6
superficial masseter	working	264.9	124.0	75.7
	balancing	138.7	58.0	−34.9
deep masseter	working	7.4	0.2	5.5
	balancing	39.3	1.6	−26.1
medial pterygoid	working	76.2	17.1	−37.3
	balancing	27.3	5.2	14.7
condyle	working	−119.1	−34.4	3.8
	balancing	−340.6	12.6	0.0
left M1		−490.9	−109.6	−9.2

The model was loaded using BoneLoad v. 9 [82], a program that simulates the physiological wrapping of muscles around rigid bony surfaces and extrapolates muscle forces to vectors based on origin and insertion areas [83]. Muscle insertion areas on the mandible were determined using our dissection records and the images and descriptions in [40]. Muscle attachment areas were modelled as plates on the surfaces of the cranium and mandible. The cranial plates were used to determine focal coordinates of each muscle by calculating the centroids of muscle origin areas. The mandibular plates were used to apply global pressure face loads oriented along the vectors from origins to insertions (electronic supplementary material, figure S1). Unit vectors for muscle forces acting on our models are given in table 5 [42].

Table 5.

Unit vectors of muscle forces in models of Macaca and Pan.

muscle	side	Macaca			Pan			difference (Pan−Macaca)
		SI	AP	ML	SI	AP	ML	SI	AP	ML
anterior temporalis	working (L)	0.96	−0.28	0.09	1.00	0.03	−0.02	0.04	0.31	−0.11
	balancing (R)	0.97	−0.22	0.03	1.00	0.04	0.04	0.03	0.26	0.01
posterior temporalis	working	0.65	−0.74	0.18	0.89	−0.46	0.00	0.24	−0.28	−0.18
	balancing	0.66	−0.75	−0.07	0.88	−0.48	0.03	0.22	−0.27	0.10
deep masseter	working	0.72	−0.14	0.68	0.80	0.03	0.59	0.08	0.17	−0.09
	balancing	0.75	−0.04	−0.66	0.83	0.03	−0.55	0.08	0.07	0.11
superficial masseter	working	0.79	0.49	0.36	0.88	0.41	0.25	0.09	−0.08	−0.11
	balancing	0.85	0.31	−0.43	0.90	0.38	−0.23	0.05	0.07	0.20
medial pterygoid	working	0.9	0.19	−0.38	0.88	0.20	−0.43	−0.02	0.01	−0.05
	balancing	0.89	0.17	0.43	0.87	0.16	0.47	−0.02	−0.01	0.04

2.5. Constraints

Boundary conditions were applied to the model to minimally constrain movement at the mandibular condyles and bite point, to prevent rigid body motion and to simulate joint and bite reaction forces [50,57,84]. The working-side (left) condyle was fixed against all translations and rotations; the balancing (right)-side was constrained against displacement in the SI and AP directions; the occlusal surface of the M₁ was constrained against displacements. Reaction forces generated at bite point and joints are given in table 4.

2.6. Terminology and metrics

Morphological terminology is from various sources [71–75] as synthesized by Panagiotopoulou et al. [42] (figure 1), and biomechanical terminology follows Ross et al. [85] and Panagiotopoulou et al. [42] (figure 2). Combinations of external forces acting on the mandible are referred to as loading regimes, quantified here as shear forces and twisting moments (or torques) due to muscle, joint and bite forces applied to the mandible. Deformation regimes are the patterns of deformation associated with loading regimes and are described using bending, shear and twisting (figure 2a–e). Strain regimes describe patterns of internal strain (deformation) in the mandible. Here, we report axial strains, principal strains, shear strains and, for comparison with work of others, von Mises strains (see electronic supplementary material).

Figure 2.

Definitions of terms used to describe loading, deformation and strain regimes following Ross et al. [85] and Panagiotopoulou et al. [42].

3. Results and discussion

The overall deformation regime of the Pan FEM is negative twisting deformation of both working- and balancing-side corpora, the deformation regime also seen in models of the mandible during mastication in Homo [68,86,87] and Macaca [42]. This suggests that, to the extent that catarrhines share similar recruitment patterns and morphology of the jaw elevator muscles, their mandibles will show similar deformation regimes during mastication. However, differences in relative magnitudes and orientations of the temporalis and superficial masseters mean that similarities in the overall deformation regime are accompanied by differences in loading and strain regimes, especially in the anterior corpus at its intersection with the symphyseal region. Differences between the loading regimes of the Pan and Macaca FEMs are due to differences in the relative magnitudes of the jaw-muscle PCSAs and the orientations of the jaw-muscle vectors. These differences in loading regime, plus differences in mandible shape (e.g. cross-sectional geometry), result in differences in the deformation and strain regimes [88].

3.1. Comparison of muscle forces

Our P. troglodytes mandible is 1.5 times longer than the female Macaca mandible (113.5 mm versus 76 mm), so isometric scaling predicts Pan's maximum jaw-muscle force to be 2.25 times those of Macaca. In fact, compared with the muscles of Macaca, the deep masseters and medial pterygoids of Pan can only generate up to twice the force, whereas the temporalis muscles can generate up to 3.4 times and the superficial masseters up to 4.8 times the force [41] (table 3). It is likely that muscle forces adjusted for fibre-type proportions and their specific tensions would increase the magnitude of these differences [89]. Differences in loading regimes between Macaca and Pan are also due to differences in the orientations and locations of the muscle force vectors, which are driven by differences in the mandible and cranial shape. The components of the muscle force unit vectors in Macaca and Pan are presented in table 5, with the difference (Macaca − Pan) in the right columns. Force vectors of the deep masseter and medial pterygoid are similarly oriented in Macaca and Pan, but, as reported by Gaspard [40, pp. 137–139], Pan's anterior and posterior temporalis are more vertically oriented in sagittal planes and Pan's superficial masseter is less transversely oriented. Thus, differences in relative magnitudes of moments acting on the Pan and Macaca mandibles are primarily due to differences in moments generated by the temporalis and superficial masseter muscles.

3.2. Comparison of moments and strain regimes: balancing side

Positive allometry of superficial masseter and temporalis muscle forces in Pan is apparent in comparisons of sagittal shear forces. On the balancing side, in Macaca these peak at 100 N at the ramus [42] (figure 3 whereas in Pan they are over 300 N (figure 4), significantly more than the 225 N predicted by isometric scaling. On the working side in Macaca sagittal shear peaks at –80 N [42] (figure 5), whereas in Pan it is –300 N (figure 5; 180 N predicted by isometry). Higher shearing forces in Pan are associated with wider fields of elevated sagittal shear strains (bilaterally) than seen in Macaca (figures 4 and 6). Shear strain magnitudes are especially high in the mandibular prominences.

Figure 3.

Moments (in Nm) acting about axes through coronal sections through the working-side mandibles of Macaca and Pan. Macaca moments are scaled isometrically to the mandible length of the Pan model. (Assuming moments scale as length³, an increase in mandible length of 1.5× predicts moments will increase 3.375×.) Y-axes scaled to the same range (±12.5 Nm). Moments about ML axes are sagittal bending moments; moments about AP axes are twisting moments; moments about SI axes are transverse bending moments. Inc, incisor; Can, canine; Diast, diastema.

Figure 4.

The comparison of Pan and Macaca deformation (a,b,c) and strain (d,e) regimes in the balancing-side (right) corpus and ramus during simulated chewing on the left M₁. The strain scale is the same in both models, i.e. −500 to +500 me, and applies to principal, axial and shear strains. (a) Pan model deformation, in posterior, right lateral and anterior views. The left side is the working (biting) side and the right side is the balancing side; biting teeth are constrained against all displacements; the undeformed model is a black mesh, the deformed model is solid; the deformation scale factor is 10%, such that the maximum displayed displacement is 10% of the size of the model. Curved black arrows indicate negative AP twisting of the balancing-side mandible; straight black arrows indicate lateral transverse bending. F_j.bal., vertical component of the balancing-side joint reaction force; F_m.bal., vertical component of the balancing-side muscle force; F_bite, vertical component of the bite force. (b,c) Maximum principal strain in lateral and superior views for (b) Pan and (c) Macaca. (d,e) Minimum principal strain in lateral and basal views for (d) Pan and (e) Macaca. (f,g) Anteroposterior strains in superior, basal, lateral and medial views for (f) Pan and (g) Macaca. (h) Transverse shear strain in medial view for Pan and Macaca. (i) Sagittal shear forces and strains in lateral view for Pan and Macaca. (j) Frontal shear strain in medial view for Pan and Macaca.

Figure 5.

The comparison of Pan and Macaca deformation and strain regimes in the working-side (left) corpus and ramus during simulation of chewing on the left M₁. The strain scale is the same in both models, i.e. −500 to +500 me, and applies to principal, axial and shear strains. (a) Pan model deformation, in posterior, left lateral and anterior views. The left side is the working (biting) side, and the right side is the balancing side; biting teeth are constrained against all displacements; the deformed model is solid; the undeformed model is a mesh; the deformation scale factor is 10%. Curved black arrows indicate negative AP twisting of the working-side mandible; the straight black arrow indicates medial transverse bending. F_j.bal., vertical component of the balancing-side joint reaction force; F_m.bal., vertical component of the balancing-side muscle force; F_m.work., vertical component of the working-side muscle force; F_bite, vertical component of the bite force. (b,c) Maximum principal strain (ε₁) in lateral and superior views for (b) Pan and (c) Macaca. (d,e) Minimum principal strain (ε₂) in lateral and basal views for (d) Pan and (e) Macaca. (f,g) Anteroposterior strains in superior, basal, lateral and medial views for (f) Pan and (g) Macaca. (h) Sagittal shear forces and strains in lateral view for Pan and Macaca. (i) Transverse shear strains in superior and basal views for Pan and Macaca. Black curved arrows represent axial torsion about the anteroposterior axis and black straight arrows represent transverse bending.

Figure 6.

Comparison of Pan and Macaca strain and deformation regimes in the symphyseal region during simulation of chewing on the left M₁. The strain scale is the same in both models, i.e. −500 to +500 me, and applies to principal, axial and shear strains. (a) Deformation of the anterior corpora and symphyseal region in posterior view for Pan and Macaca. Curved black arrows represent anteroposterior torsion and black straight arrows represent transverse bending. (b) Mediolateral strains in posterior and anterior views for Pan and Macaca. (c) Comparison of moments acting about a mid-symphyseal plane for Pan and Macaca. (d) Transverse shear strains in posterior view for Pan and Macaca. (e) Frontal shear strains in posterior and oblique views for Pan and Macaca. (f) Deformation of Pan and Macaca in superior view.

Moments acting on coronal sections through balancing- and working-side mandibles in Pan and Macaca are compared in figure 2. The moments acting on the Pan mandible are almost all larger than expected on the basis of isometry; differences in moments with high magnitudes or relatively large differences are of particular interest.

The largest moments acting on the mandibles of Pan and Macaca are sagittal bending moments (about the ML axis), which in both taxa peak at a section through the balancing-side ramus. In Pan, these moments are a relatively modest 1.6 times larger than in Macaca. However, in Pan (figure 4a–d), high-magnitude maximum principal (ε₁) strains are more widespread across the lateral surface of the balancing-side corpus than in Macaca. The mandibular prominence in this Pan individual is less prominent than it is in this Macaca individual, suggesting that the mandibular prominence in Macaca reduces tensile strain magnitudes in the buccal corpus below the molars. If true, this supports the idea that the morphology of this region is important for the transmission and resistance of muscle forces acting on the mandible [74,90].

Pan also exhibits interesting differences from Macaca in strain distributions in the lingual surface of the balancing-side ramus (figures 4h,i and 6d). Like other hominids [72,74,90], Pan has a prominent endocoronoid crest extending superiorly from torus triangularis towards the tip of the coronoid process, a ridge that is less pronounced, or is absent, in macaques (figure 1). By contrast, Macaca has a robust endocondylar ridge extending all the way from torus triangularis to the condylar neck, whereas in Pan (and other hominids, including Homo) the endocondylar ridge is less prominent, especially behind the level of the mandibular notch. In Pan, transverse shear strain magnitudes are high in the endocoronoid crest, torus triangularis and the endocondylar ridge (to the level of the mandibular notch). By contrast, transverse shear strains in Macaca are low in the coronoid process, but high in the endocondylar ridge (figure 4h). In Pan, frontal shear strains are especially high in the endocoronoid crest, torus triangularis, recessus mandibulae and crista pharyngea (at the back of the alveolar prominence). A similar concentration in Macaca is restricted to recessus mandibulae (figure 4i). This suggests that prominent endocoronoid crests in hominids (compared with Macaca) may be functionally related to strains generated by their relatively enlarged temporalis muscles [72,74,90].

In Pan, AP strains in the lateral surface of the balancing-side mandible are a mix of tensile strains superiorly and compressive strains inferiorly, reflecting dominance of sagittal bending strains (figure 4e). By contrast, in Macaca the lateral surface of the balancing-side mandible is dominated by AP compressive strain, indicating a dominance of lateral transverse bending over sagittal bending (figure 4f). This difference in strain regime is the opposite of that predicted by the large lateral transverse bending moments (SI torques) acting on the balancing-side anterior corpus of Pan (see above) (figure 4). The likely source of this effect is differences in the cross-sectional properties of the corpus: the mandible of Pan is stronger under transverse bending and weaker under sagittal bending than that of Macaca [24]. Comparisons of cross-sectional geometry between Macaca and Pan would be informative in this context [88,91].

The most important differences in moments between the two models are in coronal sections through the mandibles around the bite point (P₃–M₁). This area is the junction of the anterior corpus and the symphyseal region, which in the Pan model is level with P₃ and in the Macaca model is level with P₄ (figure 3). On the balancing side, the SI torques in Pan are four to five times larger than expected under isometry and peak at a coronal section through the P₃ instead of the P₄. The difference in magnitude of the wishboning torque at the balancing P₃ is due to high levels of EMG activity in the enlarged working-side superficial masseter in Pan. Although this muscle is more vertical in Pan than in Macaca (table 5), its large size and robust recruitment (table 3) means that its lateral force component is nearly 76 N and its anterior component is 124 N (table 5). Multiplied by their lever arms about the balancing-side P₃, their summed torques about a vertical axis through that tooth are ca –11 Nm. Counteracting positive torques from the balancing-side superficial masseter and the bite force ameliorate these effects, but because Pan's large superficial masseter is active during the power stroke, lateral bending torques acting on the balancing-side corpus are much larger than predicted by isometry. Thus, activity in the balancing-side deep masseter is not the only external force capable of producing lateral transverse bending in the hominid mandible.

3.3. Comparison of working-side loading and strain regimes

On the working side, the largest differences in the loading regime are under the bite point. Sagittal bending moments peak in the plane of the M₁ bite point; at greater than –8 Nm, they are the largest moments acting on either corpus and are 3.5 times larger in Pan than in the scaled Macaca (figure 5). The primary source of these high bending moments is large vertical components of working- and balancing-side joint reaction forces (−119 N, −341 N), which are in turn driven primarily by the large vertical components of superficial masseter and temporalis muscle forces (table 4). As a result, AP and principal strains below the bite point are significantly higher over a wider area in Pan than in Macaca (figure 5a–f).

The working-side corpus of Pan also experiences high-magnitude (5 Nm) AP twisting moments at the level of the P₄–M₁, five times larger than predicted by isometry (figure 3). Again, these differences are primarily attributable to torques generated by the greatly enlarged superficial masseter, augmented by torques from an enlarged posterior temporalis. AP torques acting on a section through the working-side corpus immediately posterior to the bite point (M₁) in Pan and Macaca are compared in table 6. The ratios of Pan/Macaca moments are given in the right column: isometric increases in moments would yield ratios of 3.4. As in the macaque, and as predicted in the literature [40], bite forces acting on the left anterior toothrow in Pan generate negative AP torques, everting the toothrow. However, the magnitude of this torque is minimal compared with that generated by balancing-side muscles and joint reaction force. As expected from the comparisons of muscle forces and unit vectors reported above, the torques of the balancing-side deep masseter and medial pterygoid in Pan are close to those predicted by isometry. By contrast, negative AP torques due to the (mostly vertical) components of balancing-side superficial masseter are nine times larger in Pan than in Macaca, and those of the posterior temporalis are 8.3 times larger in Pan. These differences in negative torques are accompanied by counteracting differences in positive AP torques at the balancing-side condyle (5.4 times larger in Pan), so that the AP torque acting on the working-side corpus behind the bite point is only 5.8 times larger in Pan than it is in Macaca (table 6). Nevertheless, even this value reflects substantial positive allometry of AP torques acting on the corpus under the bite point. As a result, high-magnitude positive transverse shear strains are widespread in the superior aspect of the corpus and planum alveolare in Pan, but not in Macaca (figure 5g).

Table 6.

Twisting moments (Nm) acting about an AP axis anterior to a coronal section through the working side (left) M₁.

	Macaca			Pan			Pan/Macaca
muscle, bite and joint moment	Fx*dz	Fz*dx	torque sum	Fx*dz	Fz*dx	torque sum	ratio
right anterior temporalis	−1.59	0.03	−1.62	−8.85	0.21	−9.06	5.6
right posterior temporalis	−0.91	−0.07	−0.84	−6.78	0.16	−6.94	8.3
right superficial masseter	−0.9	−0.02	−0.88	−8.03	−0.18	−7.85	8.9
right deep masseter	−0.69	−0.3	−0.39	−2.32	−0.75	−1.57	4.0
right medial pterygoid	−0.41	0.01	−0.42	−1.5	0.08	−1.58	3.8
right condyle	3.62	0	3.62	19.53	0	19.53	5.4
bite force left P3–M1	−0.55	0.21	−0.76	−0.41	−0.34	−0.07	0.1
summed torques	−1.43	−0.14	−1.29	−8.36	−0.82	−7.54	5.8

Data are for coronal section no. 9 (electronic supplementary material, figure S2). Bite point for Pan is M₁; for Macaca is P₃–M_1.

Abbreviations: Fx = forces in SI direction (vertical, positive is up); Fz = forces acting in ML direction (mediolateral, positive is to animal left); dX = vertical distance between section centroid and muscle attachment or reaction force centroid; dZ = mediolateral distance between section centroid and muscle attachment or reaction force centroid.

Moments acting on the mandible behind the section of interest (working-side M₁) are 0, and are excluded. Fz is 0 at the balancing-side condyle because the condyle is unconstrained in ML.

Isometry of moments for a mandible 1.5× the size of Macaca is 3.375×.

In Macaca, the transverse shear strains in the top of the mandible are negative under the premolars, positive under the molars and negative in the ramus. Shear strains in the basal surface mirror this pattern, but with the opposite sign (figure 5g). This strain pattern is consistent with a shift in the postcanine deformation regime from positive, to negative, to positive AP torsion. By contrast, Pan undergoes only a single reversal of transverse shear strain along the superior aspect of the mandible, shifting from positive in the corpus to negative in the ramus, reflecting a shift from negative to positive AP torsion (figure 5g). This is in part due to the fact that in Pan AP axis moments exceed SI axis moments along the entire working-side corpus, whereas in Macaca SI axis moments exceed AP axis moments anterior to the bite point. However, these differences in AP torsion are also due to the more medial location of the bite point in Pan (M₁) than in Macaca (P₃–M₁). The M₁ of Pan is directly over the corpus whereas that of Macaca is lateral to the long axis of the corpus, highlighting the impact of toothrow position relative to the basal corpus [74].

3.4. Comparison of loading and strain regimes in the symphyseal region

The loading and strain regimes in the symphyseal region are of particular interest because the morphology of this region has featured prominently in discussions of primate mandibular mechanics and of hominid mandibular evolution [24–36]. There are important differences between Macaca and Pan in relative magnitudes of moments acting to the right of the mid-sagittal symphyseal region. In Macaca, the SI (transverse bending) moments are the highest, followed by the ML and AP twisting moments (SI, 1.0 Nm; ML, –0.7 Nm; AP –0.4 Nm). In Pan, the more vertical temporalis, the relatively large superficial masseter and the less transverse deep masseter means that the largest torques acting on the symphyseal region are ML moments (–4.4 Nm versus 2.7 Nm predicted by isometry), followed by SI (–3.3 Nm versus 3.4 Nm under isometry) and then AP twisting moments (–3.0 Nm versus 1.4 Nm under isometry) (figure 6c). The greater predominance of ML and AP moments in Pan means that, compared with Macaca, the balancing-side corpus and incisor toothrow deform further upwards and towards the left than in Macaca (figure 6f), and Pan displays a broader field of high-magnitude transverse shear strains across planum alveolare, extending onto the working side (figure 6d).

As in Macaca, wishboning in Pan should result in ML compression on the labial aspect (and tension on the lingual aspect) of the symphysis. Both models do show ML tension on the lingual extremes of the transverse tori and low levels of ML compression on the labial surface. However, the magnitudes of these transverse axial strains and the associated principal strains are low, and the highest magnitude areas are small (figure 6b). ML compression of planum alveolare and ML tension of the inferior transverse torus are better explained by positive frontal bending resulting from large negative AP torques on the balancing side (figure 6).

Differences in relative proportions of moments acting on the symphysis are most prominently reflected in the distribution of transverse shear strain. In Macaca, high positive transverse shear strains extend from the anterior balancing-side corpus and across planum alveolare, but stop abruptly at the mid-sagittal line. In Pan, however, high positive transverse shear strains extend across the entire planum alveolare and superior aspect of the working-side corpus to the bite point, reflecting a shift from transverse bending to the right of the midline to AP torsion to the left of midline.

3.5. Comparison with two-dimensional FEMs

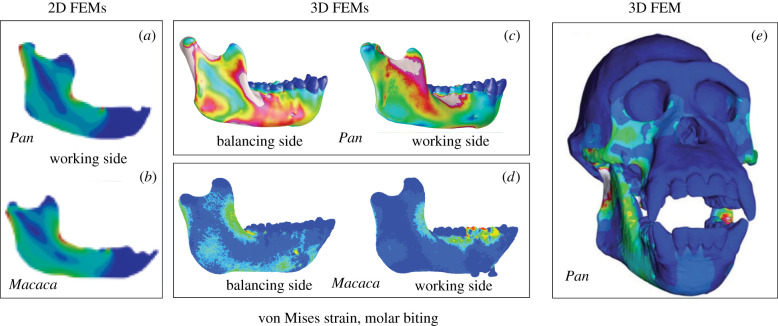
Recent two-dimensional (2D) FEM studies of mandibular biomechanics in extant primates and fossil hominids are at odds with our results [92,93]. However, serious methodological issues in those studies limit their utility for relating variation in mandibular shape and strain regimes to diet. The first issue is the omission of balancing-side muscle and joint reaction forces, which are significant even in animals with unfused mandibular symphyses [94]. In both Macaca and Pan, the largest torques acting about the working-side mandible are due to balancing-side muscle and joint reaction forces and the associated forces that are transmitted across the symphysis anterior to the bite point (table 6). If balancing-side forces and moments are not transmitted across the symphysis, models will experience no von Mises strain anterior to the bite point (figure 7a,b). In contrast with Marcé-Nogué et al.'s [92,93] results, our FEMs of Macaca and Pan during chewing, which include balancing-side forces, experience significant von Mises strains anterior to the bite point on the working side (figure 7c,d). Models that ignore balancing-side forces do not accurately model the loading regime and are unlikely to yield correct results.

Figure 7.

The comparison of von Mises strain regimes in two-dimensional (2D) hemi-mandible FEMs and 3D full mandible FEMs. (a,b) von Mises strain colour maps from Marcé-Nogué et al. [92]. (c) von Mises strain colour maps of Pan from this study. (d) von Mises strain colour maps of Macaca from the study by Panagiotopoulou et al. [42]. (e) von Mises strain colour map from Wroe et al. [95]. Note lack of strain anterior to the bite point in the 2D models, while all 3D models show some strain in this region.

It is possible to calculate the moments generated by balancing-side forces and apply them to the working-side model anteriorly in the symphyseal region. However, this is unlikely to significantly improve the accuracy of a 2D model of the working side, for two reasons. First, in most mammals, the strain environment in the mandible is the sum of both working- and balancing-side strains. Models that focus only on the working side ignore the fact that balancing-side strain magnitudes can be larger than those on the working side [42]. Indeed, the balancing sides of our models reveal large discrepancies from the strain regime in Marcé-Nogués et al.'s models [92]: the balancing-side mandible experiences von Mises strains from the ramus all the way to the symphyseal region, strains that are ignored by only modelling the working-side mandible. The second limitation of 2D models is that they do not accurately model the effects of lateral transverse shear, transverse bending and AP torsion, the magnitudes of which can be quite large (figures 4–6). The cross-sectional geometrical properties that resist these loading regimes are dependent on bone distribution in the transverse dimension, the dimension that is ignored in their analyses. In sum, the inaccuracies introduced by 2D modelling of working-side mandibles far outweigh any apparent methodological advantages, rendering their conclusions about relationships between diet and mandibular morphology in primates of doubtful accuracy and utility.

4. Conclusion

The FEM experiment reported here reveals that the mandibles of Macaca and Pan share similar loading, deformation and strain regimes during mastication. Moreover, the overall deformation regimes of our mandible models resemble those reported for humans [86]. A similar conclusion has been reached for the catarrhine cranium [85]. Fundamental similarities in the mechanics of the catarrhine feeding system—size and shape of cranium, mandible and jaw elevator muscles—suggest that comparisons among extant catarrhines can provide valuable insight into feeding system design in fossil hominids [24,27,38,96]. Our modelling also reveals that the enlarged and vertically oriented temporalis and superficial masseter muscles in Pan [40,41] result in important differences in loading regimes, especially in the anterior corpus. On the balancing side, the corpus of Pan is subjected to sagittal bending moments that are only marginally higher than those expected under isometry, but lateral transverse bending (wishboning) moments that are several times larger, even rising to five times larger in the anterior corpus. Importantly, however, the strain regime of the balancing-side mandible of Pan is more strongly influenced by sagittal bending whereas that of Macaca is more reflective of lateral transverse bending, a difference in strain regime that is probably attributable to differences in cross-sectional geometry of the corpus [88,91,97]. On the working side in Pan, the anterior corpus is subjected to much larger sagittal bending and AP torsional moments, with associated differences from the strain regime in Macaca. These results suggest that more detailed mechanical analyses of the lateral symphyseal/anterior corpus region may yield important insight into form–function relationships of the hominid mandible.

This FEM experiment reveals the importance of changes in muscle size and orientation on mandibular loading and strain regimes. The cranium of our Macaca specimen is narrower than the mandible, and the muscle vectors are more transversely oriented in transverse planes, whereas the cranium of our Pan specimen is nearly as wide as the mandible, and the muscle vectors are more vertically oriented. The ramus of Pan is broader anteroposteriorly, reflecting the enlarged superficial masseter, and the anterior temporalis force vector is more vertical, reflecting the enlargement of the anterior temporalis. Differences in strain between models are predicted by the differences in moments and highlight regional anatomical variation between taxa. All of these factors alter the loading regime acting on the mandible. Given that fossil hominins also differ in the spatial relationship of the mandible and cranium, changes in loading regime consequent on shifts in diet and feeding behaviour should be incorporated into hypotheses about the functional evolution of the hominin mandible.

Data accessibility

FE models are available upon request. Data are provided in the electronic supplementary material

Authors' contributions

A.L.S. and O.P. built the FE models; A.L.S., O.P., C.F.R. and Z.A. designed the experiments; A.L.S., O.P., A.B.T. and C.R. performed experiments; A.L.S., C.F.R., O.P., C.R. and A.B.T. analysed the data; A.L.S., C.R., O.P., A.B.T., J.D., C.V.W., W.H.K., Z.A. and C.F.R. wrote the paper.

Competing interests

We declare we have no competing interests.

Funding

We thank the National Science Foundation (grant nos. NSF BCS-1515240, BCS-0962677 and BCS-0833394) and National Institutes of Health (NIH R24 HD050837).