The influence of jaw-muscle fibre-type phenotypes on estimating maximum muscle and bite forces in primates

Abstract

Numerous anthropological studies have been aimed at estimating jaw-adductor muscle forces, which, in turn, are used to estimate bite force. While primate jaw adductors show considerable intra- and intermuscular heterogeneity in fibre types, studies generally model jaw-muscle forces by treating the jaw adductors as either homogeneously slow or homogeneously fast muscles. Here, we provide a novel extension of such studies by integrating fibre architecture, fibre types and fibre-specific tensions to estimate maximum muscle forces in the masseter and temporalis of five anthropoid primates: Sapajus apella (N = 3), Cercocebus atys (N = 4), Macaca fascicularis (N = 3), Gorilla gorilla (N = 1) and Pan troglodytes (N = 2). We calculated maximum muscle forces by proportionally adjusting muscle physiological cross-sectional areas by their fibre types and associated specific tensions. Our results show that the jaw adductors of our sample ubiquitously express MHC α-cardiac, which has low specific tension, and hybrid fibres. We find that treating the jaw adductors as either homogeneously slow or fast muscles potentially overestimates average maximum muscle forces by as much as approximately 44%. Including fibre types and their specific tensions is thus likely to improve jaw-muscle and bite force estimates in primates.

1. Introduction

Considerable effort in anthropology has been directed at modelling feeding mechanics in extant primates with the goal of gaining insights into feeding-system adaptations in extant and extinct taxa. Research linking feeding-system design and function has relied heavily on biomechanical models based fundamentally on engineering principles. For example, from decades of in vivo experimental studies of how the mandible is strained during chewing, incision and isometric biting (e.g. [1–3]), a large body of literature has emerged applying beam theory to hypothesize how the mandibular corpus should be expected to model, remodel and adapt to withstand various loads during feeding, and to infer feeding behaviour and diet from mandibular morphology [4–9]. Additionally, the primate masticatory complex is often treated as a lever system (e.g. [10–12]), which, in conjunction with estimates of jaw-muscle force, have been used to model and estimate bite force capabilities (e.g. [13–18]). More recently, finite-element analysis (FEA) has become widely employed in biological anthropology to characterize the stress and strain patterns of the craniofacial complex under a variety of loading conditions (e.g. [19–22]) and to test hypotheses of craniofacial function and feeding adaptations (e.g. [23–26]).

All of these approaches are based on mechanical engineering principles and involve the application of a variety of input parameters. For instance, in FEA models of stress and strain patterns associated with feeding, bone tissue and bone material properties must be assigned, as well as applied muscle force vectors and muscle forces [24,25,27–29]. Similarly, bite force calculations require the input of muscle forces, often estimated from the anatomical (ACSA) or physiological cross-sectional area (PCSA) (e.g. [15,30–34]; for a review of methods for estimating PCSA see [35]). The validity of these models is in part dependent on the accuracy of the input parameters.

A focus of many studies of craniofacial structure and function has been modelling bite forces. This is because bite force is an important performance variable related to feeding (e.g. [36,37]) as well as non-feeding behaviours such as aggressive biting [38]. Bite force capacity is one of a number of factors that influence an animal's feeding strategies (e.g. seed predation, frugivory, folivory) and dietary range (e.g. accessing items across a range of material and geometric properties), and plays a crucial role in an animal's ability to efficiently ingest and break down food [39–41].

Bite force is modulated by a number of factors, including leverage (i.e. moment arms of the chewing muscles and bite points) and the force-generating capacity of the chewing muscles. Two important properties that influence muscle force are a muscle's PCSA and the physiological properties of muscle fibre types (fibre phenotype). Over the past 25 years, there has been a sizeable increase in static architectural estimates of ACSAs and PCSAs of the chewing muscles of strepsirrhine [30,33,42–46] and anthropoid [30–32,34,47–53] primates. This work has facilitated combining architectural estimates of jaw-adductor muscle force with muscle leverage to estimate bite force in extant [15,33,54,55] and, though a more formidable task, extinct human and non-human primates (e.g. [16,46,54,56]).

To convert muscle force estimates to bite force requires estimating the maximum isometric muscle force of the jaw adductors, i.e. the masseter, temporalis and medial pterygoid muscles. This is achieved by multiplying muscle ACSAs or PCSAs by a specific tension, i.e. force/area [57]. To date, however, studies estimating muscle force in primates, and converting muscle force to bite force, have assigned a specific tension value to muscle force estimates derived using whole muscles, and even muscle groups (e.g. [58–60]). This is despite considerable intra- and intermuscular heterogeneity of muscle fibre types and their contractile properties, including specific tensions (see table 1 and references therein; see Close [77] for an early review).

Table 1.

Range of specific tension values reported in the literature. Both the muscles and muscle level sampled are reported.^a

mammal(s)	muscle(s)	muscle level sampled	specific tension reported (N cm−2)	author
cat	gastrocnemius, soleus	whole muscle	22.5	Spector et al. [59]
cat	gastrocnemius, soleus	single fibre	10.3–43.8	Lucas et al. [61]
cat	flexor digitorum longus	single motor unit	5.9–34.3	Dum et al. [62]
cat	tibialis anterior	single motor unit	16.8–27.5	Bodine et al. [63]
cat, dog	diaphragm, longissimus dorsi, masseter, semimembranosus, soleus, temporalis, tibialis anterior	single fibre	10.2–38	Toniolo et al.b [64]
chimpanzee	gastrocnemius, vastus lateralis	single fibre	9.6–15	O'Neill et al. [65]
cow	diaphragm, longissimus dorsi, masseter	single fibre	5–11.3	Toniolo et al. [66]
dog	longissimus dorsi, semimembranosus, extraocular, laryngeal, temporalis	single fibre	10–13	Toniolo et al.b [67]
human	vastus lateralis	single fibre	6.2–22.2	Gilliver et al. [68]
human	soleus, vastus lateralis	single fibre	8–21	Larsson & Moss [69]
human	latissimus dorsi	single fibre	11.6–16.4	Paoli et al. [70]
human	vastus lateralis	single fibre	4.37–6.47	Bottinelli et al. [71]
mouse	gastrocnemius, soleus, tibialis anterior, vastus lateralis	single fibre	22.4–37.7	Andruchov et al. [72]
mouse, rat, rabbit, sheep, cow	extensor digitorum longus, soleus	single fibre	6–24.8	Seow & Ford [73]
mouse, rabbit, rat, human	extensor digitorum longus, gastrocnemius	single fibre	4–7.5	Pellegrino et al. [74]
rabbit	extraocular	single fibre	14–46	Lynch et al.b [75]
rat	extensor digitorum longus, soleus, plantaris	single fibre	21.1–43.9	Bottinelli et al. [76]

^aThe ranges reported for each study reflect variation across muscles, fibre types within a muscle and/or experiments under different conditions.

^bThese values were not reported directly in the text. They were determined to the nearest approximation from graphic data presented by the author.

Here, we present a novel extension of these studies by combining jaw-adductor muscle force estimates from PCSAs with muscle fibre types quantified from the same muscles. We assign specific tension values (P_o) based on the percentage cross-sectional area (%CSA) of fibres expressing a particular fibre type by taking advantage of recent empirically derived P_o values for the major myosin heavy chain (MHC) proteins that contribute to the fibre types found in mammalian jaw muscles. We compare our fibre-type adjusted muscle force estimates with those obtained assuming either homogeneously slow or homogeneously fast fibre phenotypes. We show that jaw-muscle force estimates based on the presumption of homogeneous fibre types assigned a single specific tension potentially overestimate average maximum muscle forces by as much as 44% and 36% for the masseter and temporalis muscles, respectively. These data add to the longstanding work of anthroengineering by providing a method for potentially fine-tuning jaw-muscle and bite force estimates in primates.

1.1. Estimating muscle force

Muscle function is largely dependent on two intrinsic properties of muscle: muscle fibre architecture [78] and the composition and distribution of fibre types within a muscle [76,79,80]. Muscle fibre architecture represents the internal organization of a muscle and the orientation of fibres relative to the muscle's force-generating capacity [78]. PCSA is proportional to a muscle's maximum force-generating capacity [57], while the expression and distribution of the various MHC isoforms within a muscle influence the contractile properties of muscle fibres, including speed of shortening, isometric tension and tension cost [81]. Combining a muscle's PCSA with its specific tension allows for an estimate of a muscle's maximum tetanic tension.

Numerous studies have combined architectural estimates of muscle force with specific tension values to estimate maximum tetanic tension for limb (e.g. [57,82,83]) and jaw musculature (e.g. [16,51]). A wide range of specific tension values, from as low as 4 N cm⁻² [74] to as high as 46 N cm⁻² [75] (table 1), have been reported for skeletal muscles and attributed to fibre type. Studies have generally assigned a single specific tension value to whole muscles, or to muscle groups. However, there is ample evidence from single-fibre studies that tension values are lower in slow (type 1) as compared with fast (type 2) fibres, in many cases significantly so (e.g. [62–67,70,71,74–76]).

Fibre-specific tensions have the potential to significantly influence muscle and, by extension, bite force estimates. One reason is that mammalian chewing muscles express a greater variety of MHC isoforms than limb muscles [84]; these isoforms add considerably to the range of contractile properties expressed in the chewing muscles. Another reason is that mammalian chewing muscles show a large degree of heterogeneity in fibre-type distribution, both within and between muscles (e.g. [85,86]). Lastly, mammalian chewing muscles express large quantities of hybrid fibres, i.e. fibres that express more than one MHC isoform along their length (see reviews by [87,88]). Notably, anthropoid primate chewing muscles display an abundance of hybrid fibres [89,90]. Fibres expressing multiple MHC isoforms are reported to have contractile properties intermediate between ‘nearest neighbour’ pure MHC isoforms [91] (figure 1). For the chewing muscles, in particular, these factors collectively suggest that applying a single specific tension value to whole muscles is likely to over- or underestimate maximum muscle tension and, thus, bite forces.

Figure 1.

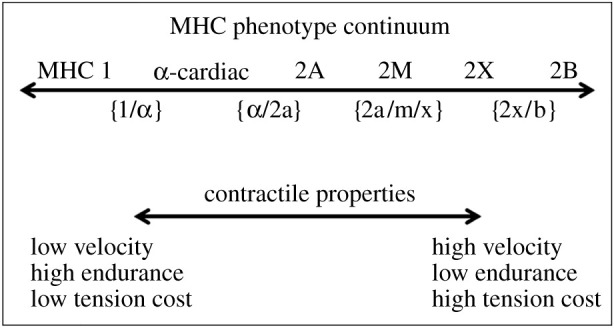
Fibre phenotype continuum illustrating the six main myosin heavy chain isoforms observed in mammalian jaw muscles, each operating at different capacities along the continuum. Hybrid fibres are denoted with brackets below the arrow but may occur in any combination. Maximum unloaded shortening velocity and tension cost increases from left to right while fatigue resistance decreases left to right.

1.2. Jaw-muscle fibre phenotypes

A muscle's fibre phenotype is the quantitative expression of MHC isoforms within that muscle. The contractile properties of these isoforms can be expressed along a continuum, from slower contracting, fatigue resistant (type 1: MHC-1, MHC α-cardiac) to fast contracting, fatigable (type 2: MHC-2A, MHC-M, MHC-2X; figure 1). MHC-1 and MHC-2 (MHC-2A and MHC-2X) isoforms, common to the limb muscles, are expressed in mammalian jaw-closing muscles, including those of primates [86,92–94]. Additional major MHC isoforms are expressed in the chewing muscles, but not the limb muscles. These include MHC α-cardiac [95] and MHC-M (fast-type 2 or masticatory myosin) [85]. MHC α-cardiac has been reported in a variety of mammals (e.g. [96,97]), including human [87,98] and more recently non-human [90,99] primates. This fibre type has a higher contraction velocity than MHC-1 but it is similar to MHC-1 in having high endurance and a low energy cost of activation [100,101]. Animals that execute tens of thousands of chews a day at low force amplitudes, such as marsupial grazers [96], have chewing muscles that homogeneously express MHC α-cardiac. This fibre phenotype is believed to confer a benefit to animals that chew with exceptionally high frequency but do not ruminate, because the higher rate of cross-bridge cycling compared with MHC-1 fibres [101] facilitates the rapid and efficient breakdown of food into fine particles for fermentation. MHC-M is a phylogenetically ancient myosin specific to the masticatory muscles [102] and has been functionally linked to rapid, powerful muscle and bite forces for prey capture [85].

Most single-fibre studies that have measured isometric tension in mammalian skeletal muscles have reported on MHC-1 and MHC-2 fibres in limb muscles (e.g. [64–67,103]). By contrast, isometric tension measured from single fibres that express MHC α-cardiac and MHC-M are far more limited, having been reported for the jaw muscles of cow [65] and dog and cat [64,67]. MHC α-cardiac tension in cow masseter has been reported at approximately 5 N cm⁻² [66], lower than specific tension estimates for MHC-1 fibres. Fibres expressing MHC-M developed significantly higher isometric tension (38 N cm⁻²) when compared with MHC-1, MHC α-cardiac and MHC-2 fibres [64]. Isometric tension reported for hybrid fibres indicates that their contractile forces are intermediate relative to the combination of pure myosin isoforms expressed within that fibre [66,71]. Their intermediate tension is consistent with their other physiological characteristics, such as their contractile velocity and fatigue resistance [65,80,91,104–106].

2. Material and methods

2.1. Sample

We estimated PCSAs and determined the four major MHC isoforms present in the superficial masseter and temporalis muscles of five anthropoid primates: Sapajus apella (N = 3), Cercocebus atys (N = 4), Macaca fascicularis (N = 3), Gorilla gorilla (N = 1) and Pan troglodytes (N = 2). All tissues were from captive individuals with no evidence of craniodental or temporomandibular joint pathology or muscle atrophy. All had been fresh frozen for varying amounts of time, then thawed and fixed in 10% buffered formalin and stored in 10% buffered formalin until use. Specimens were obtained from regional primate centres or zoological institutions and no animals were sacrificed for the purposes of this study (see electronic supplementary material).

2.2. Measurements

2.2.1. Physiological cross-sectional area

The fibre architecture methods used in this study have been described in detail elsewhere (e.g. [30,50,51,53,55,107]). Briefly, the masseter and temporalis muscles were dissected en masse from the cranium. The deep and superficial portions of the masseter were separated and the superficial masseter and temporalis weighed to the nearest 0.01 or 0.1 g, depending on muscle size. The superficial masseter muscles were sectioned from superficial to deep along their lengths into multiple segments while the temporalis muscles were sectioned into anterior, middle and posterior segments (figure 2), using stress lines visible on the epimysium as guides (e.g. [108]). For each muscle segment, fibre length (Lf) from adjacent fibres was measured from multiple sampling sites from the superficial and intermediate compartments of the masseter (but excluding the deep masseter) and from the superficial and deep temporalis. Only intact fibres running from tendon attachment to tendon attachment were included (i.e. no cut fibres were measured). Pinnation angle (θ) was estimated for each fibre following Anapol & Barry [107]. We included only specimens whose jaws were fixed in comparable postures (i.e. at occlusion). Thus, for the purposes of this study (following Taylor & Vinyard [50]), we did not normalize fibre length by a standard sarcomere length.¹

Figure 2.

Photograph of a female M. fascicularis head depicting the temporalis and masseter muscles exposed in situ. Black lines depict the sectioning of the temporalis into anterior (A), middle (M) and posterior (P) regions. Red lines depict sections of the masseter along the length of the muscle into muscle segments. Modified from Terhune et al. [53].

Using our estimates of muscle mass, Lf and pinnation angle, we calculated PCSA using the following equation [110]:

$$\mathrm{PCSA}\hspace{0.17em}({\mathrm{cm}}^2)=\frac{\mathrm{muscle}\hspace{0.17em}\hspace{0.17em}\mathrm{mass}\hspace{0.17em}(\mathrm{g})\times \cos \theta }{\mathrm{Lf}\hspace{0.17em}(\mathrm{cm})\times \hspace{0.17em}1.0564\hspace{0.17em}(\mathrm{g}\hspace{0.17em}{\mathrm{cm}}^{-3})},$$

where 1.0564 g cm⁻³ is an estimate of the specific density of skeletal muscle [111].

2.2.2. Immunohistochemistry

We excised small blocks of muscle tissue from the anterior superficial masseter (ASM), superficial anterior temporalis (SAT) and deep anterior temporalis (DAT). The muscle blocks (approx. 8–10 mm long × approx. 8–10 mm wide × approx. 4 mm deep) were cut perpendicular to the muscle's long axis and immersed in 70% ethanol solution for 48–72 h before paraffin embedding to aid in the reconstitution of the fibres. Immunohistochemistry (IHC) sample preparation and staining were subsequently carried out in the Immunohistology Laboratory, Department of Pathology, Duke University School of Medicine, Durham, NC, USA. Tissue preservation and formalin fixation can reduce the availability of reactive sites, potentially resulting in variable and diminished staining intensity [112,113]. We thus used an IHC protocol specifically developed and tested by the Department of Pathology to improve the staining of formalin-fixed tissue [55,99,114].

Briefly, each paraffin-embedded muscle block was sectioned at 5 µm using a cryostat. Serial sections were mounted on glass microscope slides to undergo final IHC procedures. Each section was pre-treated with 1% bovine serum albumin (BSA; Sigma) and then dissolved in Tris-buffered saline, 0.1% with Tween 20 (TBST) for 20 min. Four serial sections per muscle region were stained against MHC-1 (reacting with skeletal-slow myosin; 1 : 400 dilution; NOQ7.5.4D; Sigma), MHC α-cardiac (reacting with α-cardiac-slow myosin; 1 : 400 dilution; MYH6; Sigma), MHC-2 (reacting with skeletal-fast myosin; 1 : 400 dilution; MY-32, no. 4276; Sigma; we did not differentiate among the various MHC-2 isoforms) and MHC-M (reacting with masticatory myosin; 1 : 200 dilution; 2F4; Developmental Studies Hybridoma Bank, University of Iowa) antibodies.

Photographs were taken of the resulting stained histological sections using a Nikon DS-Fi3 high-definition camera attached to a Nikon 50i microscope and NIS Elements software v. 4.5 (Nikon Instruments Inc., Melville, NY). Photographs were saved as digital images at 4× magnification and stitched together in Microsoft PowerPoint to create a complete image of each stained muscle section. Regions of interest (ROIs) were selected for counting and scoring staining intensities and for measuring cross-sectional areas (CSAs) of selected cells, ensuring that the ROIs were representative of the range of variation in staining across the muscle section.

Each ROI was photographed at 10× and imported into ImageJ v. 1.52 [115]. Using the ‘Multi-point’ tool in ImageJ, a minimum of 300 fibres was counted per muscle region for each specimen and scored for staining intensity as strong, intermediate, weak or unstained [86,90,99]. Serial sections for the same muscle region enabled us to determine if a cell stained against only one of the four antibodies (pure fibre) or two or more antibodies (hybrid fibre). Based on the antibodies used in this study, three different hybrid types were possible: (i) slow hybrids, expressing more than one slow myosin (MHC-1 and MHC α-cardiac) [116,117]; (ii) fast hybrids, expressing more than one fast myosin (MHC-2 and MHC-M) [118]; and (iii) intermediate hybrids, expressing combinations of both slow and fast myosins.

CSAs (µm²) of a subset of approximately 50 cells [114] per muscle region were measured using the ‘Polygon’ and ‘Freehand selection’ tools in ImageJ. Selected cells were representative of the staining patterns for each of the four antibodies for each muscle region. We used these cell CSAs to calculate the %CSA representing each fibre type expressed in our sampled muscle section.

2.2.3. Muscle force estimation

To estimate maximum muscle force (MF %CSA), we used a modified version of the conventional formula where a muscle PCSA is multiplied by a muscle-specific tension [57]. Here, we multiplied the %CSA of each fibre type within a muscle by the muscle's PCSA (cm²), yielding a fibre-type specific estimate of PCSA (cm²). For example, the superficial masseter PCSA of C. atys ABT8 was estimated as 6.73 cm² (electronic supplementary material, table S1). Of that 6.73 cm², 57% %CSA was represented by the MHC-1 + MHC α-cardiac + MHC-2 hybrid fibre type (slow + 2), 20% %CSA was represented by MHC α-cardiac + MHC-2 + MHC-M hybrid fibre type (fast + α-cardiac) and 23% %CSA was represented by the MHC-1 + MHC α-cardiac hybrid fibre type (pure–slow hybrid). Each of these fibre-type specific CSAs was then multiplied by empirically derived specific tension estimates for each fibre type (as reported in table 2) and these were summed across the muscle to estimate MF %CSA (see electronic supplementary material, S1 methods and table S1). Based on the intermediate contractile properties of hybrid fibres, we averaged the known isometric tensions of all myosin isoforms expressed within a hybrid fibre to determine specific tension for that hybrid fibre type [99]:

$$\begin{array}{rl}& \mathrm{MF}\hspace{0.17em}\text{\%}\mathrm{CSA}=\hspace{0.17em}[(\text{\%}\mathrm{CSA}\hspace{0.17em}\mathrm{MHC}-1\times \mathrm{PCSA})\times 22.5\hspace{0.17em}\mathrm{N}\hspace{0.17em}{\mathrm{cm}}^{-2}]\\ & +[(\text{\%}\mathrm{CSA}\hspace{0.17em}\mathrm{MHCa}-\mathrm{cardiac}\times \mathrm{PCSA})\times 5\hspace{0.17em}\mathrm{N}\hspace{0.17em}{\mathrm{cm}}^{-2}]\\ & +[(\text{\%}\mathrm{CSA}\hspace{0.17em}\mathrm{MHC}-2\times \mathrm{PCSA})\times 26.3\hspace{0.17em}\mathrm{N}\hspace{0.17em}{\mathrm{cm}}^{-2}]\\ & +\hspace{0.17em}[(\text{\%}\mathrm{CSA}\hspace{0.17em}\mathrm{MHC}-\mathrm{M}\hspace{0.17em}\times \hspace{0.17em}\mathrm{PCSA})\times 38\hspace{0.17em}\mathrm{N}\hspace{0.17em}{\mathrm{cm}}^{-2}]\\ & +[(\text{\%}\mathrm{CSA}\hspace{0.17em}\mathrm{hybrid}\times \mathrm{PCSA})\times \mathrm{hybrid}\hspace{0.17em}\mathrm{isometric}\hspace{0.17em}\mathrm{tension}\hspace{0.17em}\mathrm{N}\hspace{0.17em}{\mathrm{cm}}^{-2}].\end{array}$$

Table 2.

Isometric tension values (P_o) used in this study.

	MHC-1	MHC α-cardiac	MHC-2	MHC-M
isometric tension (N cm−2)a	22.5	5	26.3	38

^aAll isometric tension values reported here are from single-fibre studies. P_o for MHC-1 (N = 8 fibres) and MCH-2 are from carnivore trunk and limb muscle [64]. The current study did not differentiate among the MHC-2 isoforms; thus, we used an average P_o of MHC-2A and MHC-2X (N = 32 fibres). MHC α-cardiac values are from cow (Bos taurus) masseter (N = 25 fibres) [66]. P_o for MHC-M (N = 23 fibres) is from carnivore masseter and temporalis muscles [64].

Studies that employ estimates of the contractile properties of muscle (e.g. P_o, V_o) generally report and use the mean values (for example, see O'Neill et al. [65], and electronic supplementary material therein). We follow this approach here. While variation in tension estimates (table 1) could impact the reported means that we used in our muscle force estimates, we believe this is no different from employing mean values of fibre length and pinnation angle that are used to estimate muscle PCSAs.

To determine the impact of proportionally adjusting muscle force estimates by their fibre types and associated specific tensions, we compared our MF %CSAs with muscle forces estimated using specific tension values for a homogeneously slow (PCSA × 22.5 N cm⁻²) and homogeneously fast muscle (PCSA × 26.3 N cm⁻²). We used the specific tension value for MHC-2 (table 2) to be consistent with most studies that have applied specific tension estimates from limb muscles. Employing these two specific tension estimates thus allows us to bracket the range of muscle force estimates typically used to estimate jaw-muscle (and bite) forces.

3. Results

Hybrid fibres were ubiquitous throughout the sampled species. Very few fibres expressed pure–slow or pure–fast phenotypes (figure 3), the single exception being the SAT in one S. apella (S. apella 31) that expressed 24% %CSA pure α-cardiac. The two most common hybrid combinations observed were: MHC-1 + MHC α-cardiac + MHC-2 and MHC α-cardiac + MHC-2 + MHC-M (table 3). Following Taylor & Holmes [99], we refer to these hybrid fibre phenotypes as the slow + 2 and fast + α-cardiac, respectively. The distinction between the slow + 2 and fast + α-cardiac hybrids is based on the nearly invariant counterstaining between MHC-1 and MHC-M. Other fibre types observed included MHC α-cardiac + MHC-2, pure–slow hybrid (MHC-1 + MHC α-cardiac), pure–fast hybrid (MHC-2 + MHC-M), MHC α-cardiac + MHC-M and pure MHC-2; a small percentage of fibres (less than or equal to 5%) co-stained for all four antibodies (table 3). Representative figures of the MHC expression patterns for each species are shown in figure 4.

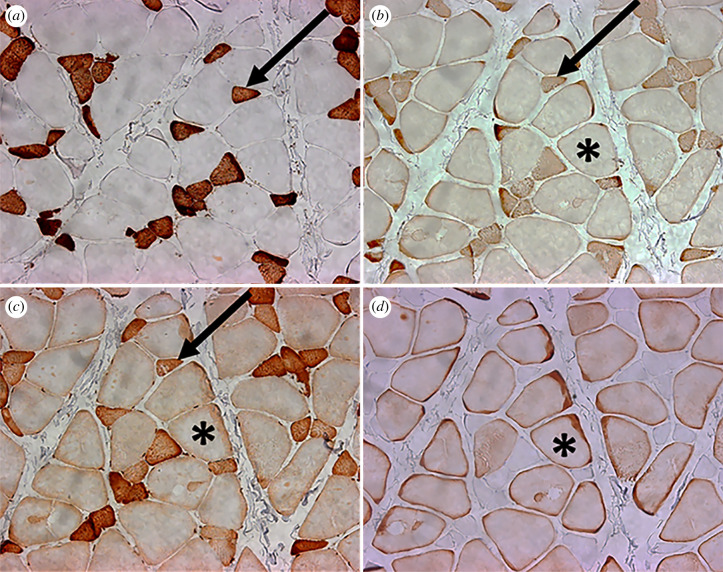
Figure 3.

20× images of the same muscle fascicle in the anterior superficial masseter of M. fascicularis. (a) NOQ7.5.4D (MHC-1); (b) MYH6 (MHC α-cardiac); (c) MY32 (MHC-2); (d) (MHC-M). Note the abundance of hybrid fibres. Arrows point to the same cell co-staining with intermediate or dark intensity for MHC-1, MHC α-cardiac and MHC-2 (the slow + 2 hybrid). Asterisks indicate the same cell co-staining with light or intermediate intensity for MHC α-cardiac, MHC-2 and MHC-M (the fast + α-cardiac hybrid). Note the counter-staining between (a) cells that express MHC-1 and (d) those that express MHC-M.

Table 3.

%CSA of each fibre type observed in each specimen. slow + 2 and fast + α-cardiac were the most common hybrid fibre types observed. slow + 2 = MHC-1 + MHC α-cardiac + MHC-2; fast + α-cardiac = MHC α-cardiac + MHC-2 + MHC-M; slow-hybrid = MHC-1 + MHC α-cardiac; fast-hybrid = MHC-2 + MHC-M; all = MHC-1 + MHC α-cardiac + MHC-2 + MHC-M.

species	slow + 2 (%)	fast + α-cardiac (%)	MHC α-cardiac + MHC-2 (%)	pure–slow hybrid (%)	pure–fast hybrid (%)	MHC α-cardiac + MHC-M (%)	pure MHC α-cardiac (%)	pure MHC-2 (%)	all (%)
superficial masseter
S. apella 30	23	77	—	—	—	—	—	—	—
S. apella 31	23	62	16	—	—	—	—	—	—
S. apella 32	16	84	—	—	—	—	—	—	—
C. atys (ABT4)	98	1	—	—	—	—	—	1	—
C. atys (ABT5)	92	—	—	—	—	—	—	8	—
C. atys (ABT6)	32	67	—	—	—	—	—	—	—
C. atys (ABT8)	57	20	—	23	—	—	—	—	—
M. fascicularis (ABTWLH3)	63	3	34	—	—	—	—	—	—
M. fascicularis (CJV222)	39	61	—	—	—	—	—	—	—
M. fascicularis (CJV221)	16	84	—	—	—	—	—	—	—
G. gorilla (NCZ488)	94	6	—	—	—	—	—	—	—
P. troglodytes (CJV190)	19	76	—	—	—	—	—	—	5
P. troglodytes (CJV189)	23	75	2	—	—	—	—	—	—
anterior temporalis
S. apella 30	18	82	—	—	—	—	—	—	—
S. apella 31	27	—	—	5	—	44	24	—	—
S. apella 32	31	66	1	1	—	—	—	—	—
C. atys (ABT 4)	56	—	—	—	44	—	—	—	—
C. atys (ABT 5)	87	—	—	—	13	—	—	—	—
C. atys (ABT 6)	61	39	—	—	—	—	—	—	—
C. atys (ABT 8)	56	44	—	—	—	—	—	—	—
M. fascicularis (ABTWLH3)	47	—	—	53	—	—	—	—	—
M. fascicularis (CJV222)	32	68	—	—	—	—	—	—	1
M. fascicularis (CJV221)	51	45	—	—	—	—	—	—	3
G. gorilla (NCZ 488)	73	27	—	—	—	—	—	—	—
P. troglodytes (CJV190)	16	81	—	—	—	—	3	—	—
P. troglodytes (CJV189)	20	60	20	—	—	—	—	—	—

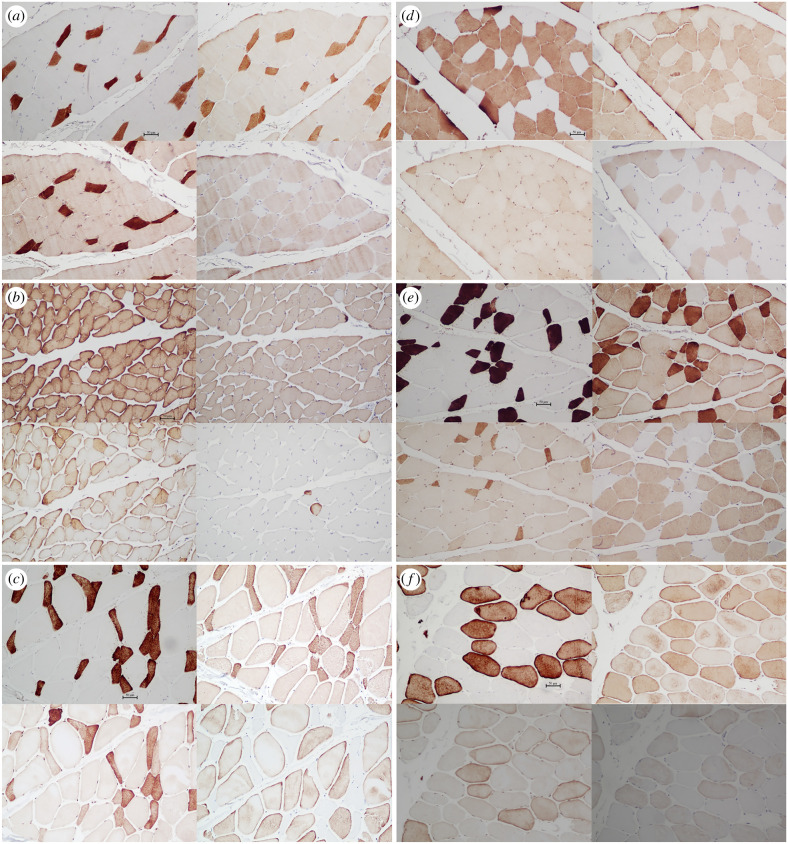
Figure 4.

Representative serial sections for left column: (a) S. apella SAT; (b) C. atys ASM; (c) M. fascicularis DAT; right column: (d) G. gorilla ASM; (e) G. gorilla SAT; and (f) P. troglodytes ASM, stained for NOQ7.5.4D (MHC-1; upper left square), MYH6 (MHC α-cardiac; upper right square), MY-32 (MHC-2; lower left square) and 2F4 (MHC-M; lower right square). Note the ubiquitous expression of fibres co-expressing two or more MHC isoforms, the abundance of α-cardiac fibres and the consistent counterstaining between NOQ7.5.4 and 2F4. For G. gorilla, note the intermuscular differences in distribution and staining intensities between the ASM (d) and SAT (e; see also Taylor & Holmes [99]). All figures were taken at 10×. Scale bar, 50 µm.

Table 4 compares our estimated maximum muscle forces (MF %CSA) with muscle forces estimated assuming a homogeneously slow (MF slow = 100% MHC-1) and a homogeneously fast (MF fast = 100% MHC-2) fibre type. The percentage difference between our estimates and homogeneously slow or fast muscles ranged from 4.4% to 44.1% for the masseter and from 7.3% to 36.1% for the temporalis. Whether treated as a homogeneously slow or homogeneously fast muscle, maximum muscle forces were always greater than those estimated for our MF %CSA (the difference between MF slow and MF %CSA was negligible for S. apella).

Table 4.

Average maximum muscle force estimates (N cm⁻²) for the superficial masseter and temporalis muscles assuming a homogeneously slow fibre expression (MF slow), incorporating %CSA of all fibre types expressed (MF %CSA), and assuming a homogeneously fast fibre expression (MF fast).^a–c.

species	superficial masseter					temporalis
	MF slow	MF %CSA	MF fast	%Dif MF %CSA versus MF slow	%Dif MF %CSA versus MF fast	MF slow	MF %CSA	MF fast	%Dif MF %CSA versus MF slow	%Dif MF %CSA versus MF fast
S. apella	220.9	211.5	258.2	4.4	22.1	391.6	356.2	457.8	9.9	28.5
s.d.	(39.7)	(30.8)	(46.4)			(146.0)	(166.9)	(170.6)
C. atys	149.0	126.9	174.2	17.4	37.3	359.9	335.5	420.7	7.3	25.4
s.d.	(31.6)	(36.9)	(36.9)			(106.7)	(95.3)	(124.7)
M. fascicularis	90.98	83.12	106.34	9.5	27.9	271.9	238.0	317.8	14.2	33.5
s.d.	(28.6)	(34.4)	(33.4)			(64.0)	(87.4)	(74.8)
G. gorilla	777.7	630.7	909.1	23.3	44.1	1272.4	1092.8	1487.3	16.4	36.1
s.d.	—	—	—			—	—	—
P. troglodytes	813.3	792.2	950.6	2.7	20.0	1132.8	1065.6	1324.1	6.3	24.3
s.d.	—	—	—			—	—	—

^aMF slow: muscle force estimates based on 100% MHC-1 with P_o = 22.5 N cm⁻²; MF fast: muscle force estimates based on 100% MHC-2 with P_o = 26.3 N cm⁻²; %Dif: % difference; s.d., standard deviation.

^bValues are averaged by muscle for each species.

^c% difference calculated by subtracting MF slow or MF fast from MF %CSA, taking the absolute value (ABS) of that difference, dividing by MF %CSA and multiplying by 100, e.g. ABS [(MF %CSA − MF slow)/(MF %CSA)] * 100.

4. Discussion and conclusion

Anthropological studies that have estimated maximum muscle and bite forces in extant human and non-human primates have generally applied either a slow-type (e.g. 22.5 N cm⁻²) [51] or fast-type (e.g. [16,119,120]) specific tension value uniformly across the chewing muscles; faster tension values have also been applied to studies that have modelled bite forces in extinct primates and non-primate mammals (e.g. [21,54,121]). Importantly, tension values applied to the jaw adductors derive exclusively from work on non-primate mammalian limb muscles (e.g. [57,59,83]).

We show that average maximum jaw-muscle force estimates that account for fibre-type proportions and their fibre-specific tensions (MF %CSA) are smaller by as much as 30% than those assigned a single specific tension across the entire muscle (table 4). As might be expected, these differences in jaw-muscle force estimates translate into differences in bite force (see electronic supplementary material). At first glance, it may seem counterintuitive that our fibre-type specific tension estimates of muscle force are lower than those obtained when assigning specific tensions that are either homogeneously slow or fast. This pattern is explained by the fact that MHC α-cardiac is abundantly expressed across both the superficial masseter and temporalis in all our sample species, consistent with previous studies of non-primate mammals (e.g. [122]), as well as human [98] and non-human primates [90,99]. The reported P_o of approximately 5 N cm⁻² for MHC α-cardiac [66] is lower than the P_o reported for MHC-1 (e.g. [64–67] and references therein). Incorporating the high proportion of fibres expressing MHC α-cardiac in our samples, with its lower P_o, thus lowers the maximum muscle force estimates compared with those obtained when using even a slow-type specific tension.

We used mean P_o values estimated from single fibres in our muscle force estimates, following previous muscle performance studies (e.g. [65]). As with all estimates of muscle kinetic and contractile properties, as well as input parameters of muscle PCSA (e.g. [47]), the mean values used in this study exhibit a range (e.g. [64,66]). We were unable to bracket the range of specific tension for each of the four MHC isoforms used in the current study as these were not explicitly reported by Toniolo et al. [64,66]. These authors do report significant differences in mean P_o between MHC-1 and MHC-M, and between MHC 2A and MHC-M [64]. The P_o for MHC α-cardiac is roughly 25% of that of MHC-1 [64,66], suggesting this value likely differs significantly from MHC-1, MHC-2A, MHC-2X and MHC-M. We are thus reasonably confident that the variation around the mean P_o values within each MHC isoform is substantially lower than the variation between MHC isoforms. When P_o is estimated from single fibres from the same muscle using the same experimental protocol, as is the case in the work reported by Toniolo et al. [64,67], the mean can be expected to represent the best estimate. Future work to explore variation in contractile properties and how it effects muscle force estimates could be better addressed by resampling techniques where the ranges of specific tension could be explicitly incorporated in the model.

Fibre-type adjusted jaw-muscle PCSAs (like PCSAs unadjusted for fibre type) represent static estimates of the relative force contribution of each chewing muscle to total jaw-adductor muscle force. Our focus in this study is to further refine static muscle force estimates by incorporating an additional and important parameter—the P_o of the various fibre types that make up a given muscle and their proportions—and to evaluate the impact of accounting for various fibre types on these muscle force estimates. These parameters do not account for the fact that the jaw adductors fire both synchronously and asynchronously during chewing [123,124]. However, when combined with estimates of jaw-muscle mechanical advantage, they can be used to estimate maximum isometric bite force anywhere along the tooth row using static models (e.g. [10–12]) and have been fruitfully applied to biomechanical and evolutionary questions of feeding behaviour and diet in a wide range of extant primates (e.g. [16,17,33]) and non-primate mammals (e.g. [36]) and in palaeobiological contexts (e.g. [125]).

Similar to other studies of mammalian jaw-muscle fibre types (e.g. [86,88,90,98,99]), hybrid fibres were ubiquitous in our primate sample and fibres that expressed MHC α-cardiac generally co-expressed MHC-1 (e.g. [122]) as well as MHC-2 (figure 3; see also [90,99]). As such, hybrid fibres were proportionally averaged across all the MHC isoforms expressed. It is also important to point out that, to date, mammalian single-fibre specific tension values reported for MHC-1 and MHC-2 are known only from limb and trunk muscles; to our knowledge, these have not been reported from the chewing muscles of any mammal. We employed a P_o for MHC-1 of 22.5 N cm⁻² [64], which is higher than those reported for humans (e.g. [65] and references therein) and at least some other mammals (e.g. [64,66,67,74]). Had we employed a specific tension for MHC-1 closer to those reported for humans (many report P_o approx. 10–18 N cm⁻²; [65] and references therein), our MF %CSAs would have been lower still.

The variation reported across specific tension estimates is likely to be due to a number of factors. While there is no clear correlation between specific tension and body mass [65,73,74], some of these differences can be attributed to variation across muscles and species (table 1). Different methods used to measure maximum isometric muscle force (P_o) are also likely to account for some of this variation. For example, experimental measurements of maximum isometric muscle force (P_o) are temperature dependent [126] as well as dependent on tissue preparation, e.g. whether estimated from skinned single muscle fibres (e.g. [127]) versus from stimulated intact whole muscle (e.g. [59]). Measuring isometric tension from single fibres of primate chewing muscles has proven challenging (P. Reiser 2019, personal communication). Given this, valuable next steps would include measuring isometric tension of single fibres expressing MHC-1 and MHC-2 from a variety of mammalian chewing muscles to determine if their contractile properties are similar to those expressed in limb muscles. Likewise, estimating P_o from mammalian chewing muscles that express MHC α-cardiac and hybrid combinations would further contribute to refining estimates of maximum muscle forces.

Our results for a select subset of anthropoid primates suggest that fibre types have the potential to strongly impact muscle (and bite) force estimates. Accounting for the intra- and intermuscular heterogeneity of primate jaw-muscle fibre phenotypes is thus likely to improve muscle and bite forces estimates in extant taxa. While fibre types cannot be directly estimated in palaeontological specimens, skeletal estimates of bite force have been modelled in extinct hominins by applying correction factors based in part on architectural estimates of jaw-muscle PCSAs derived from extant primates (e.g. Eng et al. [16]). Adjusting these PCSAs by fibre type in extant taxa may thus improve bite force estimates in palaeobiological contexts, particularly if the bite force estimates in extant taxa can be validated by in vivo bite force studies.

Data accessibility

Additional data are provided in the electronic supplementary material [128].

Authors' contributions

M.H. and A.B.T contributed equally to conceptualization, methodology, data collection and formal analysis, original draft preparation, writing and editing, and visualization.

Competing interests

We declare we have no competing interests.

Funding

This work was funded by grants from the National Science Foundation (grant nos. NSF BCS 1719743, 0962677, 0833394, 0635649, 0552285 and 0452160), a Duke Arts and Sciences Council Research Grant and the Duke University School of Medicine Core Voucher Program.