Mechanism of the Arene‐Limited Nondirected C−H Activation of Arenes with Palladium

Abstract

Recently palladium catalysts have been discovered that enable the directing‐group‐free C−H activation of arenes without requiring an excess of the arene substrate, thereby enabling methods for the late‐stage modification of complex organic molecules. The key to success has been the use of two complementary ligands, an N‐acyl amino acid and an N‐heterocycle. Detailed experimental and computational mechanistic studies on the dual‐ligand‐enabled C−H activation of arenes have led us to identify the catalytically active species and a transition state model that explains the exceptional activity and selectivity of these catalysts. These findings are expected to be highly useful for further method development using this powerful class of catalysts.

A mechanistic study of the dual‐ligand‐enabled directing‐group‐free C−H activation of arenes with palladium catalysts and the arene as limiting reagent is described. A detailed experimental and computational investigation supports a 1:1:1 complex of palladium and the two complementary ligands as the active species that enables a partially rate‐limiting concerted C−H activation as part of a Pd⁰/Pd^II cycle.

Introduction

The prevalence of aromatic cores in natural products and bioactive molecules leads to a continued interest in the development of methods to access such compounds efficiently. In this context the use of C−H activation has been identified as an enabling technology, often complementing the selectivity patterns obtained in classic aromatic substitution reactions and allowing for the formation of otherwise challenging bond types.^[1]

Many methods in this field rely on directing effects^[2] to address the two critical challenges associated with C−H activation: the low reactivity of C−H bonds and the control of regioselectivity.^[3] With unbiased substrates, catalyst design has to be used to achieve the desired reactivity. Such nondirected (non‐chelate‐assisted) methods offer an inherently orthogonal selectivity pattern and potentially broader applicability due to their independence from directing groups.^[4] However, nondirected methods have faced a long‐standing challenge: in order to achieve reactivity, the arene substrate had to be used in excess, often as (co)solvent. Intensive studies over the last two decades have led to the development of methods overcoming this limitation. As a result of these studies, a variety of synthetic methods mostly based on Ir‐ and Rh‐catalysis has been reported, which have proven particularly useful for late‐stage C−heteroatom bond formation.[⁵, ⁶]

In contrast, Pd‐catalysis has remained underdeveloped and until recently no general methods were available that allowed for the arene‐limited nondirected formation of aryl–palladium species.

In 2017, Yu described the use of pyridones, which form 2:1 complexes with palladium, as ligands for the nondirected C−H olefination (Fujiwara–Moritani reaction)^[7] of arenes (Scheme 1).^[8] In parallel, Fernández‐Ibáñez described S,O‐ligands for a nondirected olefination.^[9] While most substrates were used in excess, this study also included selected arene‐limited examples. Later, the use of these ligands was extended to a nondirected olefination of aniline derivatives. In a third contemporary study, our group developed a dual‐ligand‐based catalyst system for the nondirected C−H olefination of arenes.^[10] Subsequent studies by Ritter, Yu, and us have enabled arene‐limited nondirected late‐stage C−H cyanation reactions.^[11] We have furthermore developed an arene‐limited nondirected C−H alkynylation and applied our catalyst design to devise sterically controlled heteroarene functionalizations.^[12]

Scheme 1.

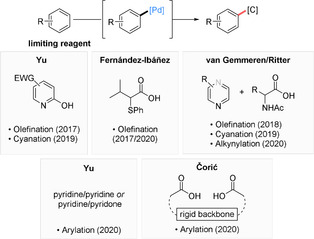
Overview of ligand systems used for the arene‐limited nondirected C−H activation/functionalization of arenes with palladium.

Recently, the nondirected C−H arylation of arenes was enabled by several catalyst systems. Yu described dual‐ligand‐based catalysts involving either the combined use of pyridones and pyridines or the use of two electronically distinct pyridines to achieve this target reaction.^[13] In a conceptually different approach Čorić described the use of spacial anion control to enable this type of reaction.^[14]

These studies indicate that the generation of aryl–palladium species through nondirected C(sp²)‐H activation bears tremendous potential. A detailed understanding of the catalytic systems and reaction mechanisms will be essential for future developments. Our dual‐ligand‐enabled catalyst systems rely on two complementary ligands acting in concert: an N‐acyl amino acid and an N‐heterocycle. Interestingly, while catalysts based on either of these ligand classes have been studied extensively,[¹⁵, ¹⁶, ¹⁷, ¹⁸, ¹⁹] very little is known about their combined use.[⁹, ¹¹]

Herein we describe experimental and theoretical studies on the mechanism of the dual‐ligand‐enabled nondirected olefination of arenes. The results lead to a mechanistic model that explains the role of each ligand in this process as well as the observed trends in reactivity and selectivity. In light of the rapid development this research field has experienced over the past years, we expect that our studies will prove highly valuable to guide future method development.

Results and Discussion

Initial studies. We began by focusing on the key C−H activation step. Based on detailed mechanistic studies on Pd‐catalysis using N‐acetyl amino acids as single ligands and the regioselectivities observed in our synthetic methods, we began with the working hypothesis that the C−H activation step proceeds via a concerted C−H activation with base assistance, likely in the BIES/eCMD regime.[¹⁹, ²⁰, ²¹, ²²] This notion was further supported by a computational study, in which Zhang and co‐workers find that for Pd^II/pyridine‐catalyzed Fujiwara–Moritani reactions the C−H activation likewise proceeds through a base‐assisted concerted mechanism and precedes the reaction of the catalyst with the olefin reaction partner.^[23] Note that for our mechanistic studies we replaced the malonate‐derived ligand 2 used in our seminal report by commercially available 6‐methyl methylnicotinate (ligand 3), which delivers nearly identical results. We first performed parallel (k _H/k _D=1.8±0.3) and competition (k _H/k _D=1.9–2.0) KIE experiments, which confirmed that the C−H activation is, as expected, rate‐determining (for details see the SI).

We proceeded to assess the kinetic orders of both reaction partners. Initial rates were determined for different starting concentrations of the respective components and the obtained data analyzed using a non‐linear least squares fit. As shown in Figure 1, the best fits are obtained for an order in arene of 0.9 and an order in olefin of 0.2.^[24]

Figure 1.

Determination of kinetic orders in both reactants.

The order in arene that approaches unity corroborates the finding from KIE measurements that the C−H activation step is rate‐determining. The small fractional order in olefin is remarkable, since an order of zero is expected for a component entering the catalytic cycle after the rate‐limiting step.^[23] We interpreted the observed orders to indicate that the C−H activation event is in principle reversible. While most of the material, once C−H activated, proceeds to product formation, a small fraction undergoes reversion to the starting material. Thus, while the C−H activation remains the key step for the observed reactivity, the balance between olefination and retro‐C−H activation can be influenced by changes in the olefin concentration.

To support this finding, we probed the reversibility of the C−H activation step. For this purpose the deuterated benzoate substrate 1 b‐d₅ was subjected to the catalyst system without adding the olefin reaction partner (note that a change of model substrate was required, since a background H/D exchange is known to occur for more electron‐rich substrates).[¹¹, ²⁵] We observed substantial H/D exchange, proving the reversibility of the C−H activation. We subjected the same substrate to the reaction conditions in the presence of the olefin and found that the H/D exchange in the remaining substrate was strongly reduced. This shows that when the product‐forming pathway is accessible the retro‐C−H activation is mostly suppressed.

At this stage, we could establish that the C−H activation step is in principle reversible but nevertheless rate‐determining (and since the reversion of C−H activation only occurs to a small degree also selectivity‐determining) under the reaction conditions.

Stoichiometry variation experiments. We proceeded to gather further knowledge about the nature of the catalytically active species. Given that under the optimized reaction conditions an excess of both ligands is employed, we began with stoichiometry variation experiments in order to determine the composition of the active species.

We studied the performance of catalysts generated upon combining different ratios of Pd(OAc)₂, Ac‐Gly‐OH, and ligand 3 in our model reaction (Table 1). We were pleased to find that the reaction with substrate 1 b does not proceed until Pd(OAc)₂ and both ligands are present (entries 1–4, Table 1, with 1 a a more complex behavior was observed, see the SI for details). Notably, an improved reaction outcome was observed with the previously optimized ratio of palladium and ligands (entry 5).

Table 1.

Stoichiometry variation experiments.

Entry	Ratio Pd/Ac‐Gly‐OH/Pyr	Yield [%]	o/m/p
1	1:0:0	4	–
2	1:1:0	3	–
3	1:0:1	2	–
4	1:1:1	37	18:70:12
5	1:3:2	49	18:71:11

These results confirm that the formation of the catalytically active species requires both ligands and palladium to be present. The identical distribution of regioisomers observed in entries 4 and 5 implies that under the optimized conditions the same active species is formed as with a 1:1:1‐ratio.

We next studied the initial rates of reactions conducted with varied catalyst compositions (Figure 2). The initial rate with varied loading of the pyridine‐derived ligand (Figure 2 A) increased sharply up to a plateau in the range between 0.1 and 0.2 equivalents. Similarly, for Ac‐Gly‐OH a maximum in catalytic activity is reached at 0.1 equivalents (Figure 2 B). The addition of further ligand leads to decreased activities for both ligands.

Figure 2.

Dependence of the initial rate on ligand quantities.

These results show that a catalyst with a 1:1:1‐stoichiometry between palladium and both ligands (ratios given as Pd(OAc)₂/Ac‐Gly‐OH/ligand 3) gives superior results due to an increased catalytic activity, not merely due to an increased catalyst lifetime. The detrimental effect of adding larger quantities of either ligand can be interpreted as the result of a shift in catalyst speciation away from the active 1:1:1 complex and towards species containing a second equivalent of either ligand. Under the optimized reaction conditions, where a 1:3:2 ratio between the components is employed, a 1:1:2‐species (presumably with the pyridine ligand, see below) may serve as resting state, thereby increasing the stability of the catalytic system.[¹⁸, ²⁴, ²⁵, ²⁶, ²⁷, ²⁸]

At this stage, we could establish that the C−H activation occurs through a catalyst with a 1:1:1 stoichiometry between palladium and the two ligands. We could further show that additional ligand leads to catalytically inactive species, which might serve as resting states.

Nuclearity of the active species. While the data obtained so far established the stoichiometry of the catalyst, its nuclearity remained to be investigated. It is well documented that Pd^II‐catalysts for C−H activation can adopt a variety of forms, such as monomers, dimers, trimers, and oligomers. The question of nuclearity becomes particularly relevant when N‐acetyl amino acids are used as ligands, since they can interact with palladium through a number of known binding modes, the most common of which are the bidentate di‐anionic (κ²‐(N,O)⁻²), the bidentate mono‐anionic (κ²‐(N,O)⁻¹), and the bridging mono‐anionic (μ‐(O,O)⁻¹) coordination.^[29]

The potential role of dinuclear Pd‐species in Pd‐pyridine, as well as Pd‐N‐acetyl amino acid systems, has been investigated intensively with both experimental and computational methods.[³⁰, ³¹] Depending on the system studied, dinuclear or higher‐order complexes have been found both as on‐cycle and as off‐cycle species.^[31]

Kinetic measurements have been established as a highly useful tool to determine the nuclearity of active catalysts.^[31] We thus measured the influence of catalyst loading on the initial rate of the reaction using two different approaches. First, we varied the loading of all catalyst components keeping the ratio between them constant (Figure 3 A). The results were analyzed using a non‐linear least squares fit and the order in catalyst was determined to be 0.5. Such a half order in catalyst can have different causes. One common scenario is the occurrence of equilibria between mononuclear active species that are in equilibrium with inactive dimeric species(for a derivation of the kinetic orders expected for the different scenarios and experiments discussed here, see the SI).^[31] Here, the half order is caused by the fact that with increasing catalyst concentration the equilibrium shifts towards the inactive species thereby reducing the positive impact of an increasing catalyst amount. For the same reason, in case of catalytically active di‐ or oligonuclear species, kinetic orders above unity would be observed. An alternative mechanistic scenario involves equilibria between mononuclear complexes with one (active) and two (inactive) equivalents of a ligand. Such a case has, for example, been observed by Stahl and co‐workers,^[26] as well as Sanford and co‐workers.^[24] The half order in this case originates from the fact that when the catalyst concentration is increased one not only increases the concentration of palladium, but the concentration of the free ligand is concomitantly increased, which in turn shifts the equilibrium towards the inactive state (see the SI for derivation of the expected kinetic orders). Importantly, the results in Figure 3 A already establish that the active species is mononuclear, the different models only differing in the assignment of the inactive state.

Figure 3.

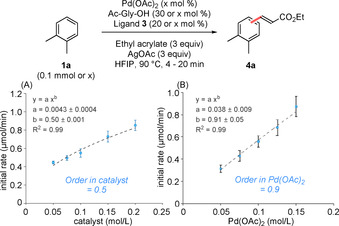
Determination of the kinetic order in [catalyst] (A) and [Pd(OAc)₂] with fixed ligand quantities (B).

To gain insights regarding the resting state, we determined the kinetic order of Pd(OAc)₂ by varying only this component and providing a constant excess of both ligands (Figure 3 B). For equilibria between mono‐ and oligonuclear species, a half order in catalyst would again be expected in this experimental design, since for these types of equilibria the square root dependence stems from the concentration of the metal rather than its relative concentration to the ligands. In contrast, for mononuclear complexes with varying metal‐to‐ligand ratios, the experimental setup in Figure 3 B is expected to yield a kinetic order close to unity, since now the concentration of the central metal would increase without a concomitant detrimental shift towards the resting state. The data shown in Figure 3 B thus allow us to exclude di‐ or oligonuclear species as the resting states of our catalytic system, but are fully compatible with a resting state involving a 2:1 ratio between the ligand and palladium. We could thus establish the nuclearity of both the active state and the resting state of our catalyst through kinetic measurements, which we interpret to indicate that under our reaction conditions a catalytically active mononuclear species with a 1:1:1 stoichiometry is in equilibrium with a resting state having a 1:1:2 stoichiometry (Scheme 2).

Scheme 2.

Proposed active species and resting state.

Notably, when we studied our catalyst system through mass spectrometry, mononuclear species corresponding to the active state and the resting state could be observed, while no indication of oligonuclear species was obtained (see the Supporting Information for details). While the observation of a complex in the gas phase alone does not necessarily coincide with relevance for catalysis,^[32] these data agree well with the conclusions from our kinetic studies.

NMR studies. Diffusion‐ordered NMR spectroscopy (DOSY) has emerged as a powerful tool to determine the molecular weight of complexes in solution since the diffusion constant (D) is proportional to the MW (log MW∝log D).[²⁴, ³³] After preliminary studies to determine a suitable model system and set of internal standards (see SI for a detailed discussion),^[34] we used ¹⁹F‐DOSY with 3,5‐difluoropyridine as a ¹⁹F‐labeled ligand to analyze the catalyst species in solution. Notably, the suitability of ¹⁹F‐DOSY to determine monomer/dimer equilibria and molecular weights of complexes in solution has been established in the literature.^[35] The ¹⁹F‐NMR of a 1:1:2 Pd(OAc)₂/Ac‐Gly‐OH/3,5‐difluoropyridine mixture in HFIP gave a complex but well‐resolved spectrum, showing the presence of several pyridine‐containing complexes. The MW calculated for these species lie within a range marked in red in Figure 4. The observed range of MW agrees well with the presence of mononuclear Pd‐species, but is incompatible with oligonuclear complexes.

Figure 4.

¹⁹F‐DOSY NMR. Log‐log plot of molecular weight (MW) as a function of mobility (D). Blue circles=standards. The range of log D values for the palladium complexes is shown as red area.

The presence of signals for heavier mononuclear species can tentatively be ascribed to species such as a 1:2:2 complex between palladium and the ligands, which both Ritter et al.^[11c] and ourselves (see the Supporting Information) could observe by mass spectrometry. Qualitatively, these NMR experiments show that the speciation behavior of our catalyst system is more complex than can be derived from kinetic data alone, likely involving several inactive species in equilibrium with the active catalyst (for a more detailed discussion on the interpretation of the ¹⁹F‐DOSY experiments, see the Supporting Information).

In agreement with our findings from kinetic measurements and mass spectrometry, the above ¹⁹F‐DOSY results thus indicate that mononuclear complexes are predominantly formed from the three catalyst components in HFIP. The NMR results thus corroborate the identification of these mononuclear complexes as the relevant resting states and catalytically active species.

Experimental data on the mechanism of C−H activation. Based on the above experimental results, the following statements can be derived regarding the mechanism of dual‐ligand‐enabled C−H activation:

1. The C−H activation step, although in principle reversible, is rate‐limiting and selectivity‐determining under the reaction conditions.

2. Palladium and both ligands are part of the catalytically active species.

3. The active species is mononuclear and has a stoichiometry of 1:1:1 between palladium and the ligands.

4. The active species is in equilibrium with a mononuclear resting state that has a 1:1:2 stoichiometry between palladium, Ac‐Gly‐OH, and the pyridine‐derived ligand. Further mononuclear inactive species are likely involved in this equilibrium.

Experimental methods cannot deliver detailed information about the subsequent steps of the catalytic cycle, since these steps occur after the rate‐limiting step. In analogy to literature reports we expected the reaction to continue with a ligand exchange, bringing the olefin into the coordination sphere of the Ar–Pd species.[¹⁶, ¹⁹, ²³, ³⁶] Given that we observe a small broken order in the olefin, these steps must, as observed in previous studies, proceed through activation barriers that are lower but in the same order of magnitude than that of the C−H activation step and do not contribute significantly to the rate or selectivity of the overall process.[¹⁹, ³⁶]

DFT studies. In order to obtain further insights into the reactivity and selectivity determining transition state, we proceeded to study the C−H activation step computationally.

We started the theoretical investigation by determining the free energy of intermediates and transition states using benzene (1 c) as substrate. Computational studies were performed using the TURBOMOLE program.^[37] Structures were optimized with the hybrid functional PBE0‐D3 and electronic energies calculated with the hybrid meta GGA functional PW6B95(‐D3).^[38] It should be noted that after identifying a reasonable reaction pathway in vacuum calculations, we initially encountered difficulties in our attempts to include a solvation model. Simple solvation models led to a relative destabilization of species in which potential hydrogen bond acceptors are exposed. We ultimately found that a combination of explicit solvation for very strong hydrogen bond acceptors and an implicit solvation with COSMO‐RS, which is known to better reflect the solvation of hydrogen bond acceptors than simpler models, led to satisfactory results (see the SI for details). This agrees well with our NMR‐studies in which a strong interaction between catalytically relevant species and the solvent was demonstrated. Solvation free energies at T=363 K were obtained with COSMO‐RS using the COSMOtherm program package.^[39]

An energy profile for the dual‐ligand‐enabled C−H activation of benzene is shown in Figure 5.

Figure 5.

Reaction coordinate for the C−H activation step [free energy profile, ΔG ₃₆₃(sol) in kcal mol⁻¹ computed with PW6B95‐D3//PBE‐D3/def2‐TZVP+COSMO‐RS(HFIP)].

The resting state of the catalyst system 5, a complex with a stoichiometry of 1:1:2 (Pd/Ac‐Gly‐OH/pyridine), is significantly more stable than the active state 6 in which one pyridine is dissociated. The free energy of dissociation is +14.6 kcal mol⁻¹. The association of benzene 1 c to form the pre‐reactive complex 8 is slightly endergonic (+2.2 kcal mol⁻¹). From here, the formation of the CMD‐transition state 9 requires an additional free energy of activation of +4.8 kcal mol⁻¹. The total energy barrier for the C−H activation of benzene thus amounts to ΔG ^≠ ₃₆₃(5→9)=21.6 kcal mol⁻¹. This comparably low activation barrier implies that the C−H activation should in principle also be possible at temperatures substantially below the optimized 90 °C. We thus studied the outcome of our reaction at reduced temperatures (See the SI for details). At 40 °C turnover of the catalyst was observed, proving that at this temperature all steps of the catalytic cycle can take place. The increased optimal reaction temperature can likely be attributed to the need to outcompete catalyst decomposition pathways in order to obtain high yields.

The formation of the aryl–palladium intermediate 7 is endergonic with respect to the catalyst resting state by 8 kcal mol⁻¹, which agrees well with the observation that the C−H activation step is generally reversible.

Since our kinetic data implied that the C−H activation step is rate‐ and selectivity‐determining, the relative activation barriers of this step for different positions of substituted arenes should correlate with the experimentally observed regioselectivities and reactivities of these arenes. We thus studied a series of arenes with varied steric and electronic properties (Figure 6).

Figure 6.

Computed barriers of activation in kcal mol⁻¹ for representative arenes and experimentally observed regioselectivities.

The computed barriers reflect the experimentally observed relative reactivities well. Anisole (1 d) is predicted to be the most reactive substrate, followed by benzene (1 c) and tert‐butylbenzene (1 e), the electron‐poor methyl benzoate (1 f) being the least reactive. Indeed, we experimentally observe a large degree of overreaction with anisole, leading to low isolated yields. No reliable ratios of regioisomers can be reported, since the primary products undergo overreaction to a different degree, which substantially alters the observed ratios. We thus focused on tert‐butylbenzene (1 e) and methyl benzoate (1 f) as substrates. In both of cases the relative barriers of activation correlate well with the observed regioselectivities. For 1 e the barriers of activation for the meta and para positions are 21.0 kcal mol⁻¹ and 21.1 kcal mol⁻¹, respectively, the barrier of activation for the ortho position is substantially higher (23.8 kcal mol⁻¹), which agrees well with the experimentally observed ratio of m/p=58:42 (no ortho product being formed). Analogously, the barrier of activation for the meta position of methyl benzoate (23.4 kcal mol⁻¹) is computed to be substantially lower than those for the ortho and para positions (24.4 kcal mol⁻¹ and 25.7 kcal mol⁻¹), which fits with the experimental ratio of o/m/p=13:70:17. Qualitatively, the computations confirm the experimental observation that this catalyst system favors the electron‐rich positions of a given substrate. This can also be rationalized considering the bond orders in the transition states, which are consistent with a highly synchronous yet somewhat electrophilic concerted C−H activation mechanism (BIES/eCMD, for further discussion, see the SI).[²¹, ²²]

We continued our studies by probing various possible pathways for the carbopalladation step (Figure 7).

Figure 7.

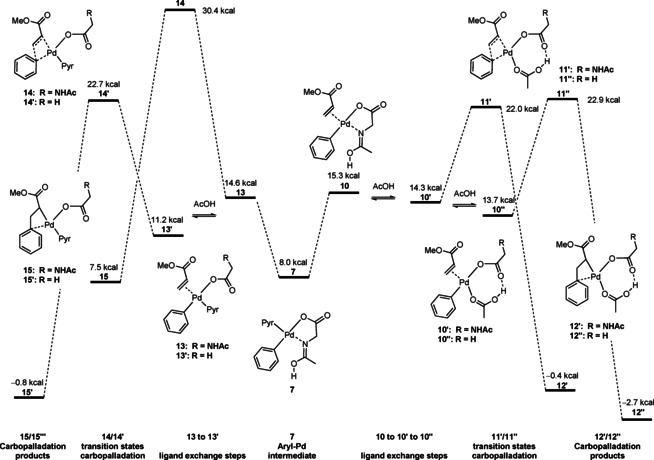
Reaction coordinate for the carbopalladation step [free energy profile, ΔG ₃₆₃(sol) in kcal mol⁻¹ computed with PW6B95‐D3//PBE‐D3/def2‐TZVP+COSMO‐RS(HFIP)].

In order for the reaction to proceed to product formation, a ligand exchange bringing the acrylate into the coordination sphere of palladium is required, leading to intermediate 10. We found that the transition state for a carbopalladation from intermediate 10 was substantially above the transition state of C−H activation, which would be incompatible with the C−H activation as rate‐determining step. However, further ligand exchange processes in which Ac‐Gly‐OH becomes monodentate (10′) or is replaced by two acetate ligands (10′′) can enable substantially lower barriers for the subsequent carbopalladation (11′/11′′ with 22.0 kcal mol⁻¹ and 22.9 kcal mol⁻¹, respectively), which are very close to the activation barrier of the C−H activation. These findings are analogous to a report by Zhang and co‐workers^[23] and agree well with the broken‐orders kinetic in arene and olefin. This step gives carbopalladation products 12′ and/or 12′′ in an overall exergonic process. For intermediate 12′′ the subsequent steps (β‐hydride elimination/reductive elimination) were found to be highly exergonic and proceed through very low activation barriers by Zhang et al., leading to the conclusion that the formation of 12′ and/or 12′′ occurs irreversibly.^[23] An alternative pathway for the carbopalladation in which the pyridine remains on palladium was likewise studied. Starting from 7 intermediates 13 and 13′ can be generated through ligand exchange processes. While the transition state for the carbopalladation 14 starting from 13 is too high for a productive pathway (30.4 kcal mol⁻¹), the analogous transition state 14′ starting form 13′ (22.7 kcal mol⁻¹) is energetically very close to the transition sates 11/11′ discussed above. We thus conclude that several pathways are likely to coexist for the carbopalladation/β‐hydride elimination sequence.

Proposed catalytic cycle. Based on experimental and computational data presented above, as well as analogies to related literature reports, we propose the catalytic cycle shown in Scheme 3.

Scheme 3.

Proposed catalytic cycle.

The C−H activation of the arene by active species 6 is preceded by an equilibrium with the resting state 5 and likely further catalytically inactive species. The arene coordinates to palladium forming pre‐reactive complex 8. The regio‐determining C−H activation proceeds through a concerted 6‐membered transition state to form the Ar–Pd intermediate 7. Subsequent ligand exchange processes bring the olefin and acetate into the coordination sphere of palladium giving intermediate 10′/10′′.[¹⁶, ¹⁹, ²³] A subsequent carbopalladation through a second comparably high transition state gives intermediate 12′ in the first overall exergonic step. It has already been established for the analogous 12′′ that a subsequent sequence of β‐hydride elimination giving 15 and product liberation can take place through a pathway involving very low barriers, such that the formation of 12′/12′′ is irreversible.^[23] Alternatively, the carbopalladation/β‐H‐elimination sequence towards 15 can also proceed via the intermediates 13′ and 14′ in a second energetically comparable pathway. Finally, the Pd^II−hydride species undergoes reductive elimination followed by a re‐oxidation to Pd^II by the silver salt as terminal oxidant.^[23]

The involvement of the silver salt (only) after the product forming step of the catalytic cycle was probed experimentally: In a stoichiometric reaction without silver salt the HFIP‐benzoate 1 b could be functionalized in 39 % yield.^[40] The regioselectivity was found to be very similar to the one observed under catalytic conditions (o/m/p=20:59:21), indicating that the mechanism of the C−H activation step remained unaffected by the absence of silver.

Conclusion

We have conducted a combined experimental and computational investigation of the arene‐limited nondirected C−H olefination of arenes by dual‐ligand‐enabled palladium catalysis.

Our investigations have revealed that both ligands play an essential role at various stages of the catalytic cycle. The electron‐poor nature of the pyridine leads to a relatively weak N−Pd bond that favors formation of the active state 6 from the resting state 5.[¹⁸, ²³, ²⁴] At the same time the formation of the resting state likely protects the catalyst against decomposition.

The amide carbonyl group of Ac‐Gly‐OH facilitates the C−H activation step by acting as internal base.[¹⁵, ¹⁹, ⁴¹] The bidentate nature of this ligand additionally brings the pyridine into the cis position relative to the substrate. As a result the C−H activation step proceeds through a transition state that closely resembles those encountered in directed C−H activation processes. By recreating the particularly suitable electronic and geometric situation on the catalyst as in directed pathways, but without requiring a directing group on the substrate, the cooperative action of both ligands enables highly efficient nondirected C−H functionalizations of arenes.^[21]

Dual ligand catalysis has only recently been recognized as a design principle for the nondirected C−H activation of arenes, leading to catalysts with unprecedented activities and selectivities. The tremendous potential of such catalysts in late‐stage modification is reflected by a rapidly increasing number of applications of dual ligand catalysis. We expect that the insights into the underlying mechanism presented herein will provide the theoretical foundation for the rational development of novel catalysts and synthetic methods.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

P. Wedi, M. Farizyan, K. Bergander, C. Mück-Lichtenfeld, M. van Gemmeren, Angew. Chem. Int. Ed. 2021, 60, 15641.