Are Methylaluminoxane Activators Sheets?

Abstract

Density functional theory calculations on neutral sheet models for methylaluminoxane (MAO) indicate that these structures, containing 5‐coordinate and 4‐coordinate Al, are likely precursors to ion‐pairs seen during the hydrolysis of trimethylaluminum (Me₃Al) in the presence of donors such as octamethyltrisiloxane (OMTS). Ionization by both methide ([Me]⁻) and [Me₂Al]⁺ abstraction, involving this donor, were studied by polarizable continuum model calculations in fluorobenzene (PhF) and o‐difluorobenzene (DFB) media. These studies suggest that low MW, 5‐coordinate sheets ionize by [Me₂Al]⁺ abstraction, while [Me]⁻ abstraction from Me₃Al‐OMTS is the likely process for higher MW 4‐coordinate sheets. Further, comparison of anion stabilities per mole of aluminoxane repeat unit (MeAlO)_n, suggest that anions such as [(MeAlO)₇(Me₃Al)₄Me]⁻=[7,4]⁻ are especially stable compared to higher homologues, even though their neutral precursors are unstable.

Hydrolysis of trimethylaluminum (Me₃Al): Viewed through the lenses of electrospray ionization mass spectrometry and density functional theory, methylaluminoxane activators adopt sheet structures while the larger sheets form chelated anions on reaction with neutral donors. Calculated ion‐pair stabilities in polar media agree well with experimental spectra collected during formation of activators.

1. Introduction

Methylaluminoxane is a widely used activator in olefin polymerization.^[1] Despite its beneficial properties as an activator, combining several roles in one material, it is a complex mixture of oligomers of indeterminate structure.^[2] Moreover, a large excess over the catalyst precursor is needed in slurry or solution polymerization using group 4 metallocene catalysts.^[3]

Various theories have been proposed to account for the latter finding,^[4] initially based on the early work of Barron and co‐workers, who showed that strained cages of t‐butylaluminoxane could be used, ideally in the presence of Me₃Al, to activate metallocene catalysts.^[5] The strained cages are expected to be only a trace component of MAO and hence the need for a large excess, the remainder being relatively unreactive, larger cages^[6] or other structures such as nanotubes.^[7]

We have used electrospray ionization mass spectrometry (ESI‐MS) to characterize the ion‐pairs that form from commercial MAO and various donors in polar media.^[8] This work has revealed that the activators present in MAO are higher in MW (700 to >2000 g mol⁻¹) than predicted based on the theory of strained cages. Other studies concur that bulk MAO has an average MW in this range,^[9] and thus the otherwise attractive theory originally proposed for the large excess of MAO seems invalid.

Related studies have revealed that the ion‐pairs [Me₂Al(D)₂]⁺ [(MeAlO)_n(Me₃Al)_mMe]⁻ (D=neutral, Lewis base) which form from MAO and various donors^[8a] undergo facile substitution of structural Me₃Al^[10] by other alkylaluminums‐i. e. Me₂AlCl,^[11] Me₂AlOMe^[12] and R₃Al (R=Et, n‐C₈H₁₇, i‐Bu).^[13] The more recent study with R₃Al indicated the amount of easily exchangeable Me₃Al is much larger than one would predict based on large cage or tube structures for MAO.[⁶, ⁷] Also, both neutrals and anions are susceptible to exchange of bound Me₃Al, as the resulting negative ion spectra do not depend on the order of addition of R₃Al vs. OMTS.

While monitoring the hydrolysis of Me₃Al by ESI‐MS in fluoroarene solvent, low MW anions were detected shortly after mixing, upon quenching with OMTS and the mixture evolved into one consistently predominantly of one anion [(MeAlO)₁₆(Me₃Al)₆Me]⁻, hereinafter [16,6]⁻.^[14] The low MW anions detected were similar in composition to neutral sheets (MeAlO)_n(Me₃Al)_m (hereinafter n,m) located by theory,^[6a] while the final composition of the anion mixture resembled commercial material.^[8] The neutral sheets were lower in electronic and Gibbs free energy than cages in the size range n=4‐13.^[6a]

This work led us to the proposal that the reactive precursors in MAO are sheets,^[15] possibly stable forms of MAO based on earlier theoretical work.[^6c, ¹⁶] Also, a chelated anion was located for [16,6]⁻ and it too has a sheet structure^[14] and was much more stable than a previous cage model.^[8c] We discuss here new sheet models for the neutral MAO activators (MeAlO)_n(Me₃Al)_m that are more stable than isomeric cages over the entire size range consistent with the monitoring experiments (n=4‐18, m=3–7).

In prior work we determined anionization potentials (AP, neutral‐[Me₂Al]⁺) and ionization potentials (IP, neutral+[Me]⁻)^[17] of large cage models for MAO.^[8b] The anion intensities in aged MAO did not correlate with these calculations, possibly because the cage models were not relevant anion precursors. These discrepancies prompted an examination of other motifs for the reactive components of MAO.

This paper reports AP and IP calculations as well as the results of solvent calculations^[18] on ion‐pairs formed from the neutral sheets and OMTS. The latter studies were motivated by recent work reported by Ehm and co‐workers who examined 2,2’‐bipyridine (bipy) vs. pyridine donors and our old cage model for (MeAlO)₁₆(Me₃Al)₆.^[19]

2. Results and Discussion

2.1. Structure and stability of neutral sheets

Shown in Figure 1 are the free energies in terms of ΔG/n and ΔG‐c/n for sheets with n=4‐18 using the M06‐2X^[20]/TZVP^[21] method as implemented in Gaussian 16.^[22] The condensed phase ΔG‐c/n values were reported in ref. [15], while the gas phase ΔG/n values for larger sheets are reported here for the first time (all values are included as Supporting Information). Some of the lower MW sheets were reported in previous work.^[6a] The condensed phase estimate of Gibbs energy (G‐c), is given by G‐c=H‐$2/3$ TS,^[23] while both ΔG values are for the reaction

$${\displaystyle 0.5\times (n+m)\mathrm{Me}{}_6\mathrm{Al}{}_2+n\mathrm{H}{}_2\mathrm{O}\to \left(\mathrm{MeAlO}\right){}_n\left(\mathrm{Me}{}_3\mathrm{Al}\right){}_m+2n\mathrm{CH}{}_4}$$

Figure 1.

ΔG/n in gas (solid lines) and condensed phase (dashed lines) for neutral sheets n,m. Open circles correspond to sheets with 5‐coordinate Al, filled to 4‐coordinate Al. The x‐axis is located at ΔG/n for the previous cage model.^[6a]

at T=298 K and p=1 atm.

For lower MW sheets (n=4–9), structures with O₄AlMe groups featuring 5‐coordinate Al, and strained, four‐membered Al₂O₂ rings are stable. By the time n=10, sheets with O₃AlMe groups with 4‐coordinate Al, and six‐membered Al₃O₃ rings are more stable for m=5, while 5‐coordinate Al sheets are only most stable until n=12 for m=7. At intermediate sizes both types of structures have comparable energies. In the case of neutral 9,6, 5‐ and 4‐coordinate Al sheets differ in ΔG by 6.0 kJ mol⁻¹. One would predict facile conversion from 5‐coordinate to 4‐coordinate Al structures, through isomerization (Figure 2).

Figure 2.

Top. Isomerization of 5‐ to 4‐coordinate Al 9,6 sheets. H‐atoms omitted for clarity with Al atoms in pink, O atoms in red and C atoms in grey. The Al atoms involved in isomerization are color coded in the reactant and product. Bottom. [Me₂Al]⁺ abstraction from each neutral (red rectangle) leads to [9,5]⁻ anions with 4‐coordinate Al via ring opening and rearrangement.

One common characteristic of these sheet structures is that their edges have strained AlMe₂ groups bonded to 3‐ and even 4‐coordinate O atoms. The latter, unusual bonding motif for oxygen^[24] is common in all of these sheets and has been previously observed in high oxygen content Al compounds, along with 5‐coordinate Al and even fused Al₂O₂ rings.^[25]

It should be noted that only in one case, neutral 9,5, use of ΔG/n vs. ΔG‐c/n leads to different predictions as to the most stable structure; 5‐coordinate with ΔG/n=−400.00 and ΔG‐c/n=−400.96 kJ mol⁻¹ vs. 4‐coordinate with ΔG/n=−399.54 and ΔG‐c/n=−401.63 kJ mol⁻¹. In comparing ΔG/n and ΔG‐c/n, the free energy changes in condensed phase are over‐estimated, particularly for the lower MW 5‐coordinate sheets (Figure 1).

These ΔG values depend on the entropy changes for these hydrolysis reactions. It is well known that entropy is very difficult to calculate with experimental accuracy, even using the M06‐2X functional which is well suited to modeling dispersive interactions such as Al−Me−Al bridging.^[26]

For example, in the case of Me₃Al the accepted value for the entropy of dimerization is −180.3 J mol⁻¹ K⁻¹ in gaseous Me₆Al₂.^[27] Using the M06‐2X functional the calculated value is −238.1 J mol⁻¹ K⁻¹ in gas phase, while calculated entropies of gaseous Me₃Al and Al₂Me₆ are 383.5 and 529.0 J mol⁻¹ K⁻¹, respectively. The latter value is very close to the experimental value of 524.8,^[27] so most of the discrepancy in ΔS arises from over‐estimation of entropy for monomeric Me₃Al, where we have not corrected the entropy for either symmetry or hindered rotation.^[26]

We will use the ΔG formalism going forward, especially as continuum calculations in fluorinated solvents track more closely with gas phase results.

Before discussing ionization, we should emphasize that what we define as ion‐pair stability depends on the metric used for comparing the energies of the corresponding neutrals. Shown in Figure 3 are two charts showing the intensity of neutrals, based on two different metrics for comparing their free energies‐ΔG/n (Figure 3a) vs. ΔG/(n+m) (Figure 3b). Both of these metrics are strictly a measure of thermodynamic stability only in the case of isomers. ΔG/n is correlated with Al−O bonding in these sheets and allows one to compare sheets differing in m but with the same n which are related through binding of Me₃Al. Another metric, ΔG/(n+m), the free energy change associated with the amount of Al incorporated into these sheets, results in a different ordering of structures (Figure 3b). This is because this metric also reflects Al−C bonding above that found in a classical MAO with the repeat unit (MeAlO)_n. Sheet 16,6 is the lowest energy structure based on ΔG/n while 18,6 (Figure 3b) is lowest in energy based on ΔG/(n+m). We will use the ΔG/n formalism going forward to better represent all neutrals in the ionization processes.

Figure 3.

Relative intensity of neutral precursors n,m in gas phase based on a) ΔΔG/n or b) ΔΔG/(n+m) and the Boltzmann distribution. In the case of ΔΔG/(n+m) the energy differences are scaled by a factor of $1/2$ . Four coordinate sheets in red, 5‐coordinate sheets in blue. Most stable structures shown for each.

In 16,6, the most stable sheet based on ΔG/n (Figure 3a), there are 12 Me₂Al groups arranged along the edges of this molecule. It is anticipated that all of these should be easily exchanged with R₃Al and this value is identical to the statistically most probable number of exchangeable Me groups when using a large excess of Et₃Al.^[13] If interior AlMe groups also involved in binding to 4‐coordinate O are included, the number of potentially exchangeable groups exceeds the maximum number observed.

2.2. Experimental Ion Intensities

Shown in Figure 4a) are the intensities for major anions detected in DFB upon completion of the growth reaction.[¹⁴, ¹⁵] The spectrum is dominated by [16,6]⁻ (yellow) with lesser amounts of [18,6]⁻ (yellow), [16,5]⁻ (green), [15,6]⁻ (yellow), and [14,5]⁻ (green). The logarithmic intensity plot (Figure 4b) reveals anions with compositions [22,8]⁻ to [24,8]⁻ (maroon), [18,7]⁻ to [23,7]⁻ (red), [14,6]⁻ to [19,6]⁻ (yellow) [11,5]⁻ to [16,5]⁻ (green) and [6,4]⁻ to [11,4]⁻ (blue).

Figure 4.

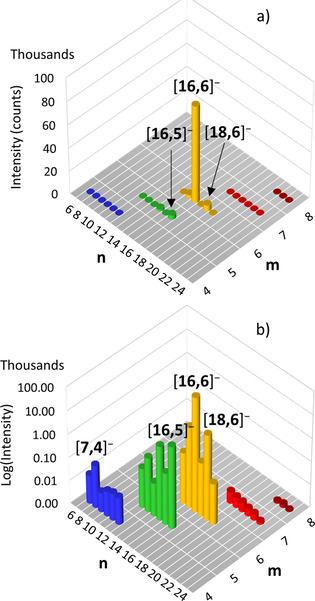
a) Experimental anion [n,m]⁻ intensities obtained from the ESI MS of Me₃Al and water in DFB ([Me₃Al]=1.2[H₂O]=0.064 M).^[14] b) Logarithmic intensity plot of the same data.

To a first approximation, anions with the same n but different m will be in equilibrium with each other through binding of Me₃Al. The electrospray ionization process will produce ions which differ from those present in solution if binding of Me₃Al is freely reversible‐even with equilibrium constants on the order of 10⁻⁴ M governing individual dissociation equilibria.[⁸, ²⁸]

For ions other than [16,6]⁻ (which is the dominant anion in commercial h‐MAO and where Me₃Al fragmentation has been studied in detail^[8]) it is therefore somewhat difficult to relate the experimental intensities to the theoretical ones, as we are not sure for any given anion sequence [n,m]⁻ with variable m which is the dominant solution ion. For example, we see the anions [14,m]⁻ with m=5‐6 in Figure 4 and it could be that [14,6]⁻ instead of [14,5]⁻ is the principal ion in solution.

2.3. Ionization and anionization potentials

To study ion formation we determined the ionization (IP) and anionization (AP) potentials. The former involves [Me]⁻ donation to a Lewis acidic neutral and is expressed relative to $1/2$ Me₆Al₂ while latter involves [Me₂Al]⁺ abstraction, and is expressed relative to Me₆Al₂.^[17] In each case all possibilities were examined for each neutral precursor with a composition that spans the n,m range of the experimental results. The AP and IP values corresponding to the most favourable site for each process, along with the structures of the anions formed are included as Supporting Information.

In earlier work, we identified various kinds of reactive sites present in cage models for MAO,[^6a, ^12a] and examined their reactivity using the same calculations of AP and IP.^[8b] In cages, the reactive sites for [Me]⁻ abstraction from a methyl donor (IP) are characterized by Lewis acidity involving terminal μ³−O−AlMe₂ groups, either isolated (type E, Scheme 1) or involved in bridging to adjacent AlMe groups (types A and B). In contrast, terminal μ³−O−Al₂Me₅ moieties (type D) or those featuring weaker μ⁴−O−Al₂Me₅ (type C) interactions, are susceptible to [Me₂Al]⁺ abstraction (AP). These same sites, with the exception of sites D, are also found in the new sheet models.

Scheme 1.

Reactive sites present in MAO. Three‐ and 4‐coordinate O atoms are highlighted with light and dark red, respectively.

In addition, due to the prevalence of 4‐coordinate O in these sheets, additional sites are reactive towards both processes. In particular, exterior AlMe₂ moieties bonded to one 4‐coordinate O atom (site F) are reactive towards [Me]⁻ abstraction and [Me₂Al]⁺ abstraction. Sites G which feature AlMe₂ coordinated to two, 4‐ coordinate O atoms are much less common but are reactive towards [Me₂Al]⁺ abstraction. Finally, unlike cages, sheets feature internal AlMe groups which are coordinated to one and two, 4‐coordinate O atoms and these sites (H and I, respectively) are reactive towards [Me]⁻ abstraction.

An important finding is that sheets with 5‐coodinate Al, reacting by either ionization mechanism, form sheet anions with 4‐coordinate Al via ring opening. This process is illustrated in Figure 2 for the isomeric 9,6 sheets and [Me₂Al]⁺ abstraction forming isomeric [9,5]⁻ anions. These reactions are accompanied by rearrangement and relief of ring strain in the smaller sheets; this mechanism is not operative for the larger cages studied earlier. Similarly, the larger 4‐coordinate sheets are reactive along their edges involving strained, but tetrahedral AlMe₂ or AlMe groups (vide infra). Together the reactivity of these sheets towards ionization via either process (i. e. the release of ring strain) is reminiscent of the latent Lewis acidity invoked by Barron and co‐workers in their studies of strained t‐butyl‐aluminoxane cages.^[5]

2.4. Ion pair stabilities

Through use of polarizable continuum models for solvation^[18] in PhF or DFB, we determined the free energies of ionization and anionization involving OMTS as donor. These can be compared to the gas‐phase results for the same process.

We define ion‐pair stability by referencing the free energies of ion‐pair formation to the most stable neutral, undergoing ionization by the most favorable process. Neutral 16,6 is the most stable based on ΔG/n while the lowest energy process for ionization is via [Me]⁻ abstraction from Me₃Al‐OMTS. The results are summarized in Table 1, along with the relative stability of the corresponding neutrals, based on ΔΔG/n. It is possible to compare [Me₂Al]⁺ and [Me]⁻ abstraction separately but the relative anion intensities do not differ. Further, by putting all intensities referenced to a common species and process, the relative ease of ionization by either process becomes clearer.

Table 1.

ΔΔG (kJ mol⁻¹) for Ion‐Pair Formation in Gas Phase, PhF and DFB.

Neutral			ΔΔG/n a			+[Me]− b			−[Me2Al]+[c]			Neutral			ΔΔG/n a			+[Me]− b			−[Me2Al]+[c]
n	m	Typed	gpe	PhF	DFB	gp e	PhF	DFB	gp e	PhF	DFB	n	m	Typed	gp e	PhF	DFB	gp e	PhF	DFB	gp e	PhF	DFB
4	3	5‐C	12.0	13.2	12.9	99.1	64.3	64.9	148.6	99.7	100.7	10	5	4‐C	3.2	3.5	3.1	44.7	22.2	22.7	60.2	38.3	39.8
5	3	5‐C	14.2	14.5	15.8	54.1	27.3	34.4	153.9	113.9	110.8	10	6	5‐C	5.4	5.5	5.8	62.8	58.7	66.8	54.0	41.7	27.9
5	4	5‐C	8.0	8.3	9.3	64.3	45.2	42.6	66.4	44.5	43.4	10	6	4‐C	7.5	7.9	7.5	80.2	75.7	68.5	72.9	59.3	60.8
6	4	5‐C	7.1	7.9	8.7	59.8	47.9	47.5	87.6	64.5	60.6	11	5	4‐C	4.8	4.9	5.3	57.0	51.0	55.1	71.8	61.6	62.5
6	4	4‐C	10.5	10.8	11.5	50.6	38.9	41.4	87.7	64.5	60.6	11	6	4‐C	4.5	4.7	4.8	75.2	79.4	71.8	73.4	52.4	48.2
6	5	5‐C	5.6	7.0	6.8	78.3	62.7	63.1	67.9	46.9	39.5	11	6	5‐C	5.7	5.6	5.8	57.4	69.8	52.2	112.1	126.9	107.0
6	5	4‐C	9.9	11.1	10.2	82.0	71.0	64.3	73.9	53.2	49.5	12	5	4‐C	4.1	2.9	3.4	40.0	37.9	33.0	57.9	45.1	73.9
7	4	5‐C	9.7	9.4	10.4	75.3	60.2	65.8	103.1	89.0	81.1	12	6	4‐C	4.5	4.5	4.6	75.3	63.3	51.4	83.3	80.5	59.1
7	5	5‐C	6.7	6.8	7.6	31.1	22.5	23.1	29.8	19.9	19.0	13	5	4‐C	5.4	6.4	5.5	53.1	35.3	35.7	105.2	90.7	88.3
8	4	5‐C	8.5	8.1	8.4	68.0	45.4	49.8	96.0	77.0	75.1	13	6	4‐C	2.2	1.3	1.1	33.9	31.4	28.1	41.0	24.2	14.3
8	4	4‐C	10.0	9.8	11.2	68.6	51.8	53.1	192.7	157.8	167.6	13	7	5‐C	5.0	6.7	6.5	f	f	f	85.7	91.9	90.1
8	5	4‐C	8.6	7.4	8.9	86.3	79.0	77.9	64.1	50.1	32.6	14	6	4‐C	2.3	3.4	2.6	35.6	34.8	29.9	61.2	49.4	57.9
8	5	5‐C	9.2	9.9	10.2	46.6	32.4	32.6	91.3	77.0	72.0	14	7	4‐C	2.8	2.5	2.3	f	f	f	47.6	32.2	15.7
8	6	5‐C	6.3	7.3	7.1	46.9	44.4	42.6	48.9	43.8	35.4	15	6	4‐C	1.5	1.6	1.6	34.4	39.3	46.1	41.5	36.5	36.9
9	4	5‐C	8.7	8.1	8.4	47.1	35.9	42.9	141.1	115.4	117.8	15	7	4‐C	2.3	2.9	3.0	f	f	f	64.1	52.0	45.5
9	4	4‐C	10.4	9.6	11.1	108.4	76.0	86.3	196.9	167.8	166.7	16	6	4‐C	0.0	0.0	0.0	0.0	0.0	0.0	13.1	6.5	26.4
9	5	4‐C	6.7	6.6	7.0	79.9	68.8	70.1	91.6	75.5	73.6	16	7	4‐C	1.6	2.9	1.8	38.1	45.1	30.4	42.6	38.2	28.6
9	5	5‐C	6.3	6.6	6.4	90.4	75.4	79.0	134.0	116.2	113.3	17	6	4‐C	1.6	1.6	1.6	8.3	18.7	18.6	32.3	26.5	20.0
9	6	4‐C	7.2	7.3	7.5	41.8	46.0	41.2	39.5	40.0	32.4	17	7	4‐C	0.4	0.3	0.2	8.8	7.3	4.0	20.7	13.8	9.3
9	6	5‐C	7.9	8.7	8.6	56.6	56.8	51.4	51.8	46.1	38.9	18	6	4‐C	1.3	0.8	0.6	15.5	10.2	8.6	31.1	16.8	25.2
10	4	5‐C	7.5	7.0	7.7	55.0	44.7	52.4	129.6	110.3	118.2	18	7	4‐C	1.2	0.9	1.2	17.7	32.7	17.8	26.4	24.9	14.6

[a] ΔΔG/n for the reaction (n+m)/2 Al₂Me₆+n H₂O→(MeAlO)_n(Me₃Al)_m+2n CH₄. [b]. ΔΔG for the reaction Me₃Al‐OMTS+n,m→[Me₂Al(OMTS)]⁺[n,m]⁻ [c] ΔΔG for the reaction n,m+OMTS→[Me₂Al(OMTS)]⁺ [n,m‐1]⁻. [d] 5‐C=5‐coordinate Al, 4‐C=4‐coordinate Al sheet [e] Gas phase result. [f] The ions [13,7]⁻ to [15,7]⁻ were not detected by ESI‐MS.

We first compare the different mechanisms for ionization. Shown in Figure 5 are the anion [n,m]⁻ intensities predicted for [Me]⁻ abstraction from Me₃Al‐OMTS by the corresponding neutral sheet in gas phase vs. PhF. There are subtle differences between gas, and solution phases, but the two solvents appear nearly equivalent in agreement with experiment. As one would expect, ionization is favored in the most polar medium (Table 1).

Figure 5.

Relative anion [n,m]⁻ intensity for ion‐pairs formed by [Me]⁻ abstraction from Me₃Al‐OMTS in a) gas phase and b) PhF. Red bars are for 4‐coordinate sheet, blue bars for 5‐coordinate sheet precursors. Data from Table 1 and the Boltzmann distribution (ΔΔG values have been scaled by $1/2$ ). Most intense anion [16,6]⁻ shown in a).

The most intense anion predicted by theory is [16,6]⁻ in excellent agreement with experiment (Figure 4). In the gas phase, theory predicts that anions [17,m]⁻ should be more intense than [18,m]⁻ (m=6,7) while the opposite effect is observed experimentally. In PhF and DFB (not shown) the theoretical [n,6]⁻ (n=16‐18) anion intensities are in good agreement with those observed experimentally, though [17,7]⁻ is still predicted to be the most intense anion after [16,6]⁻. It should be noted that use of the Boltzmann distribution to depict the results is a very demanding test of theory vs. experiment!

In contrast, if ionization occurs via [Me₂Al]⁺ abstraction from MAO by OMTS, the results in Figure 6 suggest that [16,5]⁻ should be prominent in PhF while [17,6]⁻ should dominate in DFB with [18,6]⁻, and [13,5]⁻ having comparable but lower stability. In an absolute sense, this process is also less favourable than [Me]⁻ abstraction from Me₃Al‐OMTS for the larger sheets (compare vertical scales in Figure 5 vs. 6).

Figure 6.

Relative anion [n,m]⁻ intensity for ion‐pairs formed by [Me₂Al]⁺ abstraction by OMTS in a) PhF and b) DFB with most stable anion shown. Energy scaling as for Figure 5.

These theoretical results are at odds with experiment; to the extent that these sheet structures do seem better models for the experimental results we see than cages,[⁸, ¹³, ¹⁴, ¹⁵] one should accept that [Me]⁻ abstraction from Me₃Al‐OMTS would be the preferred process for larger sheets.

Of the lowest MW anions, [7,4]⁻ and [8,4]⁻ or [9,4]⁻ are usually prominent in solution during initial growth while following completion, [7,4]⁻ is the most intense anion detected.[¹⁴, ¹⁵] Of the two mechanisms for ionization, only [Me₂Al]⁺ abstraction predicts the latter result (Figure 6, blue columns).

Theory predicts that [Me]⁻ abstraction from Me₃Al‐OMTS also involves the neutral 7,5 sheet but the resulting anion would have the composition [7,5]⁻. We do not detect this anion in these experiments, though we can't exclude that it might easily lose Me₃Al during the electrospray ionization process.

It seems that the appearance of the experimental spectra[¹⁴, ¹⁵] cannot be explained by a common ionization mechanism for all species detected. In essence, low MW anions likely form via [Me₂Al]⁺ abstraction from 5‐coordinate sheet precursors, while high MW anions form by [Me]⁻ abstraction from Me₃Al‐OMTS by 4‐coordinate sheets.

2.5. Methide vs. Me₂Al⁺ Abstraction

In earlier work we have mentioned the difficulty in distinguishing between these two ionization processes when it comes to the interaction of MAO with neutral, chelating donors.^[8a] As shown in Scheme 2 using OMTS as an example, and sites F and D, related through binding of free Me₃Al, one cannot easily distinguish between these processes experimentally. This is because the ion‐pair that is formed by either process features an identical m/z ratio, while ESI‐MS is not probing the structure of the neutral precursor nor even the anions formed.

Scheme 2.

Methide vs. [Me₂Al]⁺ abstraction and OMTS.

Moreover, as indicated in other work, when MAO is chemically depleted of free Me₃Al it is still capable of activating catalysts by alkylation and ionization due to the presence of structural Me₃Al.[^10a, ¹⁹] Also, the reaction of donors, even of similar base strength, such as bipy vs. pyridine, can result in different chemo‐selectivity towards Me₃Al vs. Me₂Al⁺ abstraction,^[8a] even using MAO depleted in free Me₃Al.[^10a, ¹⁹] Thus, a donor like OMTS might react with e. g. site D to remove Me₃Al prior to ion‐pair formation instead of undergoing direct [Me₂Al]⁺ abstraction.

Thus, for sheet 16,6 we cannot assert that [Me]⁻ abstraction from Me₃Al‐OMTS, which is favored on a free energy basis, is necessarily the process involved in ionization. For example, 16,6 might be in equilibrium with a higher energy isomer of 16,7 through binding of Me₃Al and it is that isomer that reacts with OMTS through [Me₂Al]⁺ abstraction.

To address this issue computationally we located this isomer (i‐16,7) and examined its energy in gas phase vs. fluorinated solvent with respect to the competing ionization processes. Unlike any other stable sheet that we have located, i‐16,7 has a site D (Scheme 2) that we know is reactive towards [Me₂Al]⁺ abstraction in cages.[^6a, ^8b] Shown in Figure 7 are the free energy differences for the different pathways in fluorinated media.

Figure 7.

Free energies of formation of [Me₂Al(OMTS)][16,6] in fluorinated solvent from 16,6, OMTS and Me₃Al. Blue symbols and lines are for ionization in DFB while red symbols and lines are for ionization in PhF. Transition structures (≠) have not been located.

Formation of i‐16,7 from 16,6 and Me₆Al₂ (0.5 equiv.) is endergonic in gas phase (ΔG=25.6 kJ mol⁻¹) or solution, and by a significantly larger amount in both fluorinated solvents (ΔG=40.1 and 42.5 kJ mol⁻¹). One can estimate that the equilibrium ratio of 16,6:i‐16,7 at 298 K in PhF with [Me₆Al₂]=0.032 M (conditions corresponding to the monitoring reactions) would be≥58.4×10⁶:1–i. e. less than ppm amounts of i‐16,7 relative to 16,6.

κ¹‐Binding of Me₃Al by OMTS is also unfavorable due to the large negative entropy change for this process. The ratio of Me₃Al‐OMTS:OMTS present at equilibrium would be about 1 part per thousand, even under the most unfavorable conditions in PhF (ΔG=12.5 kJ mol⁻¹). Thus, [Me]⁻ abstraction from Me₃Al‐OMTS by 16,6 would enjoy a concentration advantage of at least 58,000 : 1, a not insignificant amount in free energy terms (ca. 28 kJ mol⁻¹ at 298 K).

Ion‐pair formation is unfavorable in the gas phase (ΔG=190.0 kJ mol⁻¹), reversible in PhF (ΔG=1.8 kJ mol⁻¹), and exergonic in the most polar solvent DFB (ΔG=−27.8 kJ mol⁻¹). In gas phase it can be asserted (though it is really not relevant) that the higher energy pathway involving i‐16,7 and [Me₂Al]⁺ abstraction by OMTS is important whereas, absent information of the actual barriers to ionization, [Me]⁻ abstraction from Me₃Al‐OMTS is a much lower energy pathway in solution. As shown in the figure, ionization via methide abstraction from Me₃Al‐OMTS would have to involve a barrier in excess of 50 kJ mol⁻¹ for [Me₂Al]⁺ abstraction to be competitive.

We did attempt to locate both barriers and intermediates involved in this complex process, involving structural rearrangements in both the cation and anion. For example, methide abstraction by 16,6 involving a least motion pathway generates initially an unchelated anion as a local minimum. Future work will address this issue in detail. We do note that discrete activators featuring [R₂Al]⁺ stabilized by donors have been used to activate catalysts, and most recently effectively combine both alkylation and ionization.^[29]

2.6. Anion stabilities per repeat unit

In the earlier work we noted that the anion formed from 16,6 by [Me]⁻ abstraction (or from i‐16,7 and [Me₂Al]⁺ abstraction) features a chelated structure.^[14] It should be mentioned that the anions formed by this process from the sheets 14,6–18,6 also feature chelation and in fact the site of highest reactivity is very similar in these precursors.

This feature is illustrated in Scheme 3 which compares the structures of the neutrals vs. anions formed; note the high degree of structural similarity. For sheets 16,6 to 18,6 the site of reactivity (F) is basically identical, while the site switches to another site F’ that is similar for 14,6 and 15,6. In comparing these structures, it can be seen that one needs a flanking MeAlO₃ group in order for ionization to occur at an adjacent site of type F. As soon as that group is replaced by an Me₂AlO₂ moiety, (as in 14,6 or 15,6) the favored site for ionization switches to the other site F’.

Scheme 3.

Ionization of large 4‐coordinate sheets by [Me]⁻ abstraction from Me₃Al‐OMTS. The n,6 sheets differ in structure at positions indicated by the dashed lines with the site of ionization labelled.

While this effect may be largely inductive in origin it should be recalled that even in tetrahedral Al, one expects some delocalization of electron density due to O p to Al σ* conjugation.^[30] In essence the interior MeAlO₃ moieties in these sheets should be effective in stabilizing a negative charge through both inductive and resonance effects.

Given the structural similarities present, the anions formed from these sheets can be compared in the same manner as the neutrals by defining a stability per aluminoxane repeat unit n. In the case of an anion this involves correction for the amount of Me₃Al incorporated (m‐1), and also the anionic moiety in the form of Me₄Al⁻. This is not valid for small vs. larger structures but is instructive for comparing the sheets of similar size. We note that this correction is also applicable to neutrals and leads to free energy differences identical to that given by ΔG/n. The values are provided in Table 2 while a graphical representation appears in Figure 8 for the most stable anions with composition [n,m]⁻ in PhF.

Table 2.

ΔΔG/n (kJ mol⁻¹) for Neutrals and Ion‐Pairs in Gas Phase, PhF and DFB.

Neutral			ΔΔG/n a			+[Me]− b			−[Me2Al]+ c			Neutral			ΔΔG/n a			+[Me]− b			−[Me2Al]+ c
n	m	Typed	gpe	PhF	DFB	gp e	PhF	DFB	gp e	PhF	DFB	n	m	Typed	gp e	PhF	DFB	gp e	PhF	DFB	gp e	PhF	DFB
4	3	5‐C	12.0	13.2	12.9	6.5	8.6	8.7	15.8	14.3	16.3	10	5	4‐C	3.2	3.5	3.1	8.6	3.7	2.6	8.9	4.1	3.7
5	3	5‐C	14.2	14.5	15.8	0.0	1.0	2.0	17.5	15.8	16.1	10	6	5‐C	5.4	5.5	5.8	10.4	7.4	7.0	10.2	6.2	5.8
5	4	5‐C	8.0	8.3	9.3	2.1	4.6	3.6	0.0	1.9	2.7	10	6	4‐C	7.5	7.9	7.5	12.2	9.1	7.2	8.3	4.4	2.6
6	4	5‐C	7.1	7.9	8.7	4.2	5.5	4.7	6.7	6.2	6.0	11	5	4‐C	4.8	4.9	5.3	10.7	6.7	5.8	10.9	6.5	6.0
6	4	4‐C	10.5	10.8	11.5	2.6	4.0	3.7	6.7	6.2	6.0	11	6	4‐C	4.5	4.7	4.8	12.3	9.3	7.3	11.0	5.7	4.7
6	5	5‐C	5.6	7.0	6.8	7.2	8.0	7.3	3.4	3.2	2.5	11	6	5‐C	5.7	5.6	5.8	10.7	8.4	5.5	14.6	12.5	10.0
6	5	4‐C	9.9	11.1	10.2	7.8	9.3	7.6	4.4	4.3	4.2	12	5	4‐C	4.1	2.9	3.4	10.0	5.7	3.9	10.4	4.8	4.4
7	4	5‐C	9.7	9.4	10.4	8.5	7.5	7.5	10.7	9.9	8.9	12	6	4‐C	4.5	4.5	4.6	12.9	7.8	5.5	12.5	8.2	5.7
7	5	5‐C	6.7	6.8	7.6	2.2	2.2	1.4	0.2	0.0	0.0	13	5	4‐C	5.4	6.4	5.5	11.7	5.6	4.3	14.7	8.9	7.9
8	4	4‐C	10.0	9.8	11.2	9.0	6.5	5.7	22.9	18.2	19.3	13	6	4‐C	2.2	1.3	1.1	10.2	5.3	3.7	9.8	3.8	2.2
8	4	5‐C	8.5	8.1	8.4	8.9	5.7	5.2	10.9	8.1	7.7	13	7	5‐C	5.0	6.7	6.5	f	f	f	13.2	9.0	8.0
8	5	4‐C	8.6	7.4	8.9	11.2	9.9	8.8	6.9	4.7	2.4	14	6	4‐C	2.3	3.4	2.6	10.9	5.7	3.9	11.9	5.9	5.5
8	5	5‐C	9.2	9.9	10.2	6.2	4.1	3.1	10.3	8.1	7.3	14	7	4‐C	2.8	2.5	2.3	f	f	f	10.9	4.6	2.5
8	6	5‐C	6.3	7.3	7.1	6.2	5.6	4.3	5.0	3.9	2.8	15	6	4‐C	1.5	1.6	1.6	11.4	6.1	5.1	11.1	5.1	4.2
9	4	4‐C	10.4	9.6	11.1	14.5	9.3	9.3	23.0	18.1	17.6	15	7	4‐C	2.3	2.9	3.0	f	f	f	12.6	6.2	4.7
9	4	5‐C	8.7	8.1	8.4	7.7	4.8	4.5	16.8	12.3	12.2	16	6	4‐C	0.0	0.0	0.0	9.7	3.8	2.3	9.8	3.4	3.6
9	5	4‐C	6.7	6.6	7.0	11.4	8.5	7.5	11.3	7.8	7.3	16	7	4‐C	1.6	2.9	1.8	12.1	6.6	4.2	11.6	5.4	3.7
9	5	5‐C	6.3	6.6	6.4	12.5	9.2	8.5	16.0	12.4	11.7	17	6	4‐C	1.6	1.6	1.6	10.8	5.1	3.6	11.5	4.8	3.3
9	6	4‐C	7.2	7.3	7.5	7.1	6.0	4.3	5.5	3.9	2.7	17	7	4‐C	0.4	0.3	0.2	10.8	4.4	2.7	10.8	4.1	2.7
9	6	5‐C	7.9	8.7	8.6	8.7	7.2	5.4	6.9	4.6	3.4	18	6	4‐C	1.3	0.8	0.6	11.6	4.8	3.1	11.8	4.4	3.7
10	4	5‐C	7.5	7.0	7.7	9.6	6.0	5.5	15.9	11.3	11.6	18	7	4‐C	1.2	0.9	1.2	11.8	6.0	3.6	11.6	4.9	3.1

[a] ΔΔG/n for the reaction (n+m)/2 Al₂Me₆+n H₂O→(MeAlO)_n(Me₃Al)_m+2n CH₄. [b]. ΔΔG/n for the reaction Me₃Al‐OMTS+n,m→[Me₂Al(OMTS)]⁺[n,m]⁻ [c] ΔΔG/n for the reaction n,m+OMTS→[Me₂Al(OMTS)]⁺ [n,m‐1]⁻ [d] 5‐C=5‐coordinate Al, 4‐C=4‐coordinate Al sheet, [e] Gas phase result. [f] The ions [13,7]⁻ to [15,7]⁻ were not detected by ESI‐M.

Figure 8.

Relative anion [n,m]⁻ intensities in PhF based on ΔΔG/n and the Boltzmann distribution. Columns are colour coded according to the neutral sheet undergoing ionization (blue=5‐coordinate, red=4‐coordinate).

In the case of anions [14,m]⁻ to [18,m]⁻ (m=5–7) it is obvious that these anions have similar stabilities, confirming that the corresponding neutrals possess similar reactivity towards ionization. Thus, at least for these larger structures, one gains more confidence that the ESI‐MS results are more directly related to solution concentration of the neutrals, and thus their stability vs. reactivity towards ionization.^[14]

On the other hand, [7,4]⁻ is the most stable anion per mole of repeat unit in either fluorinated solvent, and anions in this size range, usually derived from 5‐coordinate sheets, have comparable stability depending on the mechanism for ionization vs. the precursor involved (Table 2). Thus, their high intensity seen during monitoring reactions at the start[¹⁴, ¹⁵] is certainly related to the higher stability of the anions vs. the corresponding neutrals. Finally, anions intermediate in size (n=10–13, m=4 or 5) have marginally lower average stabilities than higher MW anions, and certainly lower than those derived from 5‐coordinate sheets. Thus, their intensity as intermediates in the growth process ought to be lower than their corresponding solution concentrations.

3. Conclusions

Anionization and ionization potentials were determined for new sheet models for the reactive components of MAO, as well as the free energies of ion‐pair formation in gas phase, PhF and DFB involving either [Me]⁻ or [Me₂Al]⁺ abstraction and Me₃Al‐OMTS or OMTS as a donor. These results show much better agreement between theory and experimental ESI‐MS spectra of hydrolytic MAO and this donor, indicating the activators have sheet rather than cage structures. Of the m=6 anions, [16,6]⁻ is predicted to be the most stable per mole of repeat unit (MeAlO)n and this is also true of its likely precursor, neutral 16,6, which forms this chelated anion through [Me]⁻ abstraction from Me₃Al‐OMTS. In addition, some of the trends seen in ESI‐MS experiments monitoring the hydrolysis of Me₃Al in either solvent can be explained with reference to the relative stability of the anions detected vs. the energies of the corresponding neutral precursors. It seems that lower MW anions formed at the start of this process such as [7,4]⁻ are derived from 5‐coordinate sheets via the process of [Me₂Al]⁺ abstraction whereas the final product anions form from 4‐coordinate sheet precursors. Future work will focus on comparing the stability and reactivity of isomeric cages and sheets or other morphologies, and to try to delineate how they are formed from lower MW, linear, cyclic or branched aluminoxane precursors.

Experimental Section

Calculations were carried out by Gaussian 16 software,^[22] using the M06‐2X metahybrid GGA functional of the Minnesota series^[20] combined with the def‐TZVP basis set by Ahlrichs et al.^[21] Harmonic vibrational frequencies were calculated to confirm the structures as a true minimum in the potential energy surface. Gas phase Gibbs free energies were calculated at T=298 K and p=1 atm. The condensed phase energy corrections to Gibbs free energy (ΔG‐c), were estimated by multiplication of the TΔS term of Gibbs free energy by 2/3, as recommended and used in the previous literature.[^6a, ²³]

The neutral sheet structures of the MAOs, partially adopted from our previous report,^[15] but extended to include comparison of 4‐C and 5‐C structures of the same composition, were located by systematically following the TMA hydrolysis reactions, as described previously,[^17b, ³¹] but focusing on condensed phase corrected Gibbs free energy rather than electronic energy in the choice of the followed reaction pathway. Anions were derived from the corresponding neutral sheet structures by both [Me₂Al]⁺ cleavage and [Me]⁻ abstraction from each potentially reactive edge site. Anionization potentials (AP) were calculated as relative energies for the reaction MAO→[Me₂Al]⁺ [MAO]^– and ionization potentials (IP) as MAO+Me⁻→[MAO−Me]^–, using MAO=$1/2$ Me₆Al₂ as a reference.^[17]

Solvent Calculations

Solvent calculations were calculated by the SMD variation of the polarizable continuum model.^[18] For o‐F₂C₆H₄, which is not included in the pre‐defined solvents in Gaussian 16, the following parameters were used in definition of the solvent: ϵ=13.4 Debye, Index of refraction $n_{20}^D$ =2.082, Abraham's H‐bond acidity α=$\sum {\alpha }_2^H$ =0.00, Abraham's H‐bond basicity β=$\sum {\beta }_2^H$ =0.09, γ=relative (dimensionless) surface tension=37.85, ϕ=fraction of non‐hydrogenic atoms which are aromatic carbons=0.75, Ψ=fraction of non‐hydrogenic atoms which are halogen=0.25.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

S. Collins, G. Hasan, A. Joshi, J. S. McIndoe, M. Linnolahti, ChemPhysChem 2021, 22, 1326.