Causal organic indirect and direct effects: closer to the original approach to mediation analysis, with a product method for binary mediators

Abstract

Mediation analysis, which started in the mid–1980s, is used extensively by applied researchers. Indirect and direct effects are the part of a treatment effect that is mediated by a covariate and the part that is not. Subsequent work on natural indirect and direct effects provides a formal causal interpretation, based on cross-worlds counterfactuals: outcomes under treatment with the mediator set to its value without treatment. Organic indirect and direct effects avoid cross-worlds counterfactuals, using so-called organic interventions on the mediator while keeping the initial treatment fixed at treatment. Organic indirect and direct effects apply also to settings where the mediator cannot be set. In linear models where the outcome model does not have treatment-mediator interaction, both organic and natural indirect and direct effects lead to the same estimators as in the original formulation of mediation analysis. Here, we generalize organic interventions on the mediator to include interventions combined with the initial treatment fixed at no treatment. We show that the product method holds in linear models for organic indirect and direct effects relative to no treatment even if there is treatment-mediator interaction. Moreover, we find a product method for binary mediators. Furthermore, we argue that the organic indirect effect relative to no treatment is very relevant for drug development. We illustrate the benefits of our approach by estimating the organic indirect effect of curative HIV treatments mediated by two HIV persistence measures, using data on interruption of antiretroviral therapy without curative HIV treatments combined with an estimated or hypothesized effect of the curative HIV treatments on these mediators.

Introduction: indirect and direct effects

Indirect and direct effects decompose the effect of a treatment A on an outcome Y into (1) a part that is mediated through covariate M: the indirect effect, and (2) a part that is not: the direct effect. For example, treatment A could be a blood pressure lowering medication, and the outcome Y whether a person had a heart attack. The mediation questions are: how much of the effect of treatment A on heart attacks Y is mediated by its effect on blood pressure M (A → M → Y), and how much (if any) by other pathways? Another example: new HIV–curative therapies are being developed to reduce HIV reservoirs while patients are on antiretroviral therapy (ART). Researchers assess the clinical effects of such therapies by ART withdrawal in the study participants, to identify off-ART viral control. The mediation question is: What is the effect of an HIV–curative therapy A on off-ART viral control Y, mediated by the effect of A on the HIV reservoir M, as measured by on–ART single–copy plasma HIV RNA?

Mediation analysis¹ is especially important in the health sciences, like epidemiology and psychology. Knowing the assumptions under which these analyses are valid or causal is paramount. Several approaches to causal mediation analysis have been proposed.^2-12 Important causal contributions are interpretation, extension of mediation analysis to various outcome types, and the inclusion of pre-treatment common causes of mediator M and outcome Y, even for randomized treatment. Nguyen et al. (2020)¹³ provide an overview of causal mediation analysis.

One disadvantage of most current causal interpretations of mediation analysis^2-7 is the reliance on quantities such as: the outcome under treatment but with the mediator set to its value without treatment. These so-called cross-worlds counterfactuals rely on two simultaneous but different situations or worlds, treatment and no treatment, which never occur concurrently. The identifying assumptions are also cross-worlds, have been disputed,^10;11;14 and lead some researchers to entirely forego causal mediation analysis. Randomized effects^8;15;16 avoid cross-worlds quantities, but still require setting the mediator after a random draw. Separable effects^10;11;14 separate a treatment’s effect on the mediator from its direct effect on the outcome, but still need all Y^(a,m): the outcomes under treatment a with the mediator set to m. Geneletti (2007)⁹ considers stochastic interventions on the mediator, but without conditioning on common causes C of mediator and outcome, unless effects conditional on C or manipulating C are of interest.

Organic indirect and direct effects¹⁷ provide causal mediation analyses that do not require setting the mediator, or cross-worlds quantities and assumptions. This article generalizes these organic indirect and direct effects. This generalization brings organic indirect and direct effects closer to the original approach to mediation analysis by Baron and Kenny.¹ It also leads to a product method for binary mediators. Furthermore, we show that by combining organic interventions on the mediator with a = 0, indirect effects can be estimated in data-scarce settings.

This article has four purposes: to bring organic indirect and direct effects to the attention of epidemiologists and clinical trialists, to bring causal mediation analysis closer to the original mediation approach, to introduce a product method for binary mediators, and to illustrate causal mediation analysis for selecting promising treatments for randomized trials.

Setting and notation

We start with randomized treatment A. Denote the pre-treatment common causes of mediator M and outcome Y by C. As is usual, see, e.g., VanderWeele (2015)⁵ page 464, assume there are no post-treatment common causes of M and Y. This can be relaxed.¹⁸ Throughout, superscript ⁽⁰⁾ indicates without treatment and superscript ⁽¹⁾ indicates under treatment. Figure 1 illustrates the mediation set-up. Notice the absence of an arrow from C into A since treatment is randomized.

Figure 1:

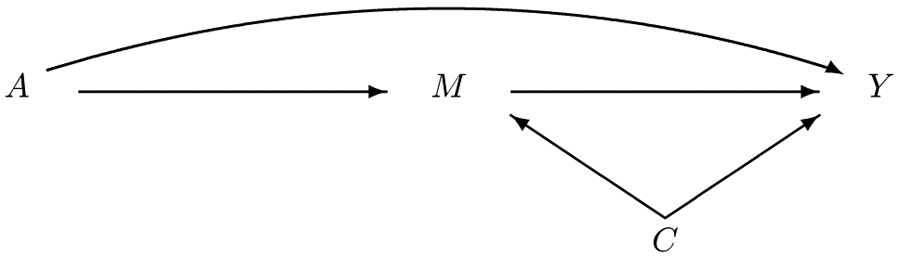
Causal diagram summarizing the data. This causal diagram indicates which variables might affect one another. Formal assumptions can be found in the text.

Definition of causal indirect and direct effects

Natural indirect and direct effects

Historically,^2-7 causal indirect and direct effects have been defined using the following counterfactuals: the outcomes under treatment had the mediator been set to the mediator level without treatment: Y^(1,M(0)). There are two issues with these counterfactual outcomes Y^(1,M(0)). First, how to set the mediator is usually left unspecified, so the outcomes Y^(1,m) under treatment with the mediator set to m are undefined in many practical situations. When the mediator is another medication,^3;14 setting the mediator is interpretable. When the mediator is a patient characteristic or covariate, as in many applications including our HIV application, setting the mediator is harder to interpret. An illustrative example: “There are many competing ways to assign (hypothetically) a body mass index of 25 kg/m² to an individual, and each of them may have a different causal effect on the outcome”.¹⁹ Moreover, even if we could set the mediator, under treatment M⁽⁰⁾ is not observed. Thus, it remains unclear how under treatment the mediator could be set to M⁽⁰⁾.

Based on outcomes Y^(1,M(0)), most current causal approaches to mediation analysis focus on the natural indirect effect,

$$E\left(Y^{(1)}-Y^{(1,M^{(0)})}\right),$$

mediated through M: it compares M⁽¹⁾ with M⁽⁰⁾; and the natural direct effect,

$$E\left(Y^{(1,M^{(0)})}-Y^{(0)}\right),$$

not mediated: M is always M⁽⁰⁾.

To estimate natural indirect and direct effects, since treatment A is randomized, estimating E(Y⁽¹⁾) and E(Y⁽⁰⁾) is standard. We focus on E(Y^(1,M(0)). Under strong conditions, with C all pre-treatment common causes of mediator M and outcome Y, the Mediation Formula³ holds:

$$E\left(Y^{(1,M^{(0)})}\right)={\int }_{(m,c)}E[Y\mid M=m,C=c,A=1]f_{M\mid C=c,A=0}(m)f_C(c)dmdc.$$ (1)

Equation (1) was proven under cross-worlds assumptions (see Introduction). In addition, most causal mediation approaches^2-12 need many counterfactual outcomes: not only Y^(1,M(0)), also all Y^(a,m): the outcomes under treatment a with the mediator set to m.

Under linear models and outcome models without exposure-mediator interaction, the resulting estimators for the indirect and direct effect are the same as in the original mediation approach, ¹ and thus add a causal interpretation. Natural and randomized indirect and direct effects include all outcome types, with causal interpretations.

Organic indirect and direct effects: an intervention-based approach avoiding cross-worlds counterfactuals and assumptions

We generalize the approach and main results from Lok (2016).¹⁷ I is an intervention on the mediator that does not affect C (pre-treatment common causes of mediator M and outcome Y). M^(a,I=1) and Y^(a,I=1) denote the mediator and the outcome under treatment A = a combined with intervention I on the mediator. For observables without intervention on the mediator (I = 0), we omit superscript ^(I=0).

Definition:I is an organic intervention relative to a = 0 and C if

$$M^{(0,I=1)}\sim M^{(1)}\mid C=c$$ (2)

and

$$Y^{(0,I=1)}\mid M^{(0,I=1)}=m,C=c\sim Y^{(0)}\mid M^{(0)}=m,C=c,$$ (3)

where ~ indicates having the same conditional distribution; that is, Equation (3) states that the distribution of Y^(0,I=1) given M^(0,I=1) = m, C = c is the same as the distribution of Y⁽⁰⁾ given M⁽⁰⁾ = m, C = c. I is an organic intervention relative to a = 1 and C if Equations (2) and (3) hold with the roles of a = 0 and a = 1 reversed.

Equation (2) states that I changes the distribution of the mediator to that under treatment, given C. Equation (3) states that I “has no direct effect on the outcome”: without treatment, whether mediator = m came about due to I or without I does not affect a person’s prognosis. Or, how the mediator came about is irrelevant. Equation (3) can be relaxed to

$$E[Y^{(0,I=1)}\mid M^{(0,I=1)}=m,C=c]=E[Y^{(0)}\mid M^{(0)}=m,C=c]:$$

whether mediator = m came about due to I or without I does not affect a person’s mean prognosis. A similar relaxation holds for effects relative to a = 1.¹⁷

For example,¹⁷ A = 1 could be a blood pressure lowering medication, M a person’s blood pressure, and Y the subsequent occurrence of a heart attack. The mediation questions are: what is the effect of A = 1 mediated by its effect on blood pressure, and does A = 1 also have a direct effect on heart attacks? It could be that A = 1 lowers blood pressure by 10, on average for each C, without changing the shape of the blood pressure distribution. I should then be an intervention, in the untreated, that also lowers blood pressure by 10, on average for each C, without changing the shape of the blood pressure distribution. Then, M^(0,I=1) ~ M⁽¹⁾ ∣ C. I could be salt reduction in a dosage dependent on C. Since the effect of salt on heart attacks is believed to be through its effect on blood pressure,^20;21 one can posit that Equation (3) holds for salt reduction intervention I. Salt reduction I keeps the effect of A = 1 through blood pressure M, but does not have the direct effect of A = 1.

For Equation (3) to hold for any intervention I, one will often need the pre-treatment common causes of mediator M and outcome Y in C:¹⁷ without C, the statement “the mediator under no treatment equals m” likely implies a different prognosis under intervention I (M^(0,I=1) = m) versus without intervention I (M⁽⁰⁾ = m), because M⁽⁰⁾ and M^(0,I=1) are related differently to C, so convey different information about C, which may well predict the outcome Y.

Definitions:

$$E(Y^{(0,I=1)})-E(Y^{(0)})$$

is the organic indirect effect of treatment A, relative to a = 0 and C, based on I. The treatment is 0 for both Y⁽⁰⁾ and Y^(0,I=1), so this effect is mediated.

$$E(Y^{(1)})-E(Y^{(0,I=1)})$$

is the organic direct effect of treatment A, relative to a = 0 and C, based on I. The mediator has the same distribution for Y⁽¹⁾ and Y^(0,I=1), so this effect is not mediated.

Organic indirect and direct effects relative to a = 1 and C are defined similarly, with the roles of a = 0 and a = 1 reversed.

Combining organic interventions I with no treatment provides the effect of an intervention I that affects the mediator M the same way as A = 1, but has no direct effect on the outcome Y. Below, we show that such effect can be highly relevant for drug development.

The Mediation Formula holds for organic interventions¹⁷ (eAppendix A):

Theorem: Organic indirect and direct effects: the Mediation Formula. Under randomized treatment, for an intervention I that is organic relative to a and C:

$$E(Y^{(a,I=1)})={\int }_{(m,c)}E[Y\mid M=m,C=c,A=a]f_{M\mid C=c,A=1-a}(m)f_C(c)dmdc.$$ (4)

The Mediation Formula implies that for given C, organic indirect and direct effects do not depend on the intervention I, as long as I is organic. The resulting expression is in terms of observable quantities only. All ingredients can be estimated using standard methods (eAppendix F); the empirical distribution function of C estimates f_C, so we estimate E (Y^(a,I=1)) by the average of the integrand over the C_i.

Furthermore, if C has all pre-treatment common causes of mediator M and outcome Y, as defined in eAppendix D, organic indirect and direct effects are unique: which set of all pre-treatment common causes C is chosen does not affect organic indirect and direct effects¹⁷ (eAppendix D). Thus, we can define:

Definitions: Whenever C includes all common causes of mediator M and outcome Y^(a), we call the organic indirect and direct effect relative to a and C the organic indirect and direct effect relative to a.

Organic indirect and direct effects relative to a = 1 generalize natural indirect and direct effects: in settings where an intervention I exists that sets the mediator under a = 1 to the value it would have taken under a = 0, that is, M^(1,I=1) = M⁽⁰⁾ exists, the usual cross-worlds assumptions, see e.g., pages 463–464 in VanderWeele 2015,⁵ imply that this I is organic relative to a = 1.¹⁷ This approach also provides a proof of the Mediation Formula for natural indirect and direct effects under conditions that are somewhat weaker than usual (eAppendix E).

In linear models without treatment–mediator interaction in the outcome model, the product method¹ holds for all these causal estimands: natural, randomized, and organic effects.^3-8;10;17 When the outcome model has treatment–mediator interaction, the product method holds for organic indirect effects relative to A = 0 (eAppendix B), and for natural and randomized indirect effects after reversing the roles of a = 0 and a = 1, leading to pure indirect effects.²

A product method for binary mediators

For binary mediators, the organic indirect effect relative to a = 0, and the pure indirect effect, equal

$$\begin{gathered} {\int }_c(E[Y\mid M=1,C=c,A=0]-E[Y\mid M=0,C=c,A=0]) \\ (P(M=1\mid C=c,A=1)-P(M=1\mid C=c,A=0))f_C(c)dc \end{gathered}$$ (5)

(eAppendix F): a product method for binary mediators.

If there are no common causes C, or mediation conditional on C is of interest as in Chapters 2-7 of VanderWeele (2015),⁵ (5) is a true product. Otherwise, indirect effects are indirect effects conditional on C (a true product), averaged over C. While averaging over C may result in a complicated integral, for estimation one can use the empirical average over all observed C_i. The product method holds for binary mediators regardless of outcome type; for binary outcomes, it holds on the risk difference scale.

Intuitively, the indirect effect relative to a = 0 is the product of the treatment effect on the mediator times the effect of this mediator change on the outcome under A = 0, averaged over C. If A increases the probability of M = 1, the indirect effect relative to a = 0 is the increased probability of M = 1 times the effect that changing M = 0 into M = 1 has on the outcome under A = 0, averaged over C. This is similar to the original product method.

A similar product method holds for organic indirect effects relative to a = 1 and natural indirect effects; in the conditional expectation of Y, A = 1 replaces A = 0 (eAppendix F). Equation (5) implies that there is a maximum indirect effect that can be mediated through a binary mediator.

Selecting new treatments with promising indirect effects for clinical trials

From the Mediation Formula (4), the organic indirect effect relative to a = 0 equals

$$\begin{gathered} {\int }_{(m,c)}E[Y\mid M=m,C=c,A=0](f_{M\mid C=c,A=1}(m)-f_{M\mid C=c,A=0}(m))f_C(c)dmdc \\ \text{or}{\int }_{(m,c)}E[Y\mid M=m,C=c,A=0]f_{M\mid C=c,A=1}(m)f_C(c)dmdc-E(Y^{(0)}). \end{gathered}$$ (6)

Thus, the organic indirect effect relative to a = 0 can be estimated with (1) the distribution of the mediator M under treatment, A = 1, and without treatment, A = 0, and (2) the expected outcome Y given the mediator M and pre-treatment common causes C without treatment, A = 0; expected outcomes only under A = 0.

The same holds for natural and randomized indirect effects after reversing the roles of a = 0 and a = 1, that is, for pure indirect effects. This observation allows estimating indirect effects relative to a = 0 of potential new treatments aiming to affect a mediator M,²² without observing treated outcomes (see below). eAppendix F provides estimators of (6) under various model specifications.

Similarly, but with less practical relevance, organic indirect effects relative to a = 1 and natural indirect effects could be estimated without observing untreated outcomes.

Selecting HIV–curative treatments with promising indirect effects for clinical trials

ART, the standard of care for HIV, has rendered HIV a chronic disease. Substantial research now focuses on HIV eradication, or functional cure aimed at long-term ART–free HIV remission.²³ Trials interrupt ART in HIV–infected study participants, to investigate the effect of curative treatments and on–ART biomarkers on the time to viral rebound after stopping ART. Viral rebound is the time the HIV viral load in the participants’ blood rises above a pre-specified level.²⁴

ART interruption trials have to be carried out with extreme care, since interruption of ART carries substantial risks.^24-27 Because there are many potential treatments in pre–clinical stages, it is advantageous to carry out ART interruption trials for the most promising therapies.²⁸

Many new curative HIV therapies A are designed to affect on–ART HIV persistence, let us tentatively call its measurement M, which has an effect on the time to viral rebound, Y (Figure 2). For such therapies, Equation (6) leads to an estimate of their organic indirect effect relative to a = 0 mediated by M, with M single–copy plasma HIV RNA or cell–associated HIV RNA. Pre-ART HIV viral load measures the magnitude of viral replication before ART initiation, which is predictive of virologic outcomes after stopping ART, Y,²⁹ and of on–ART HIV persistence measures, M.^30;31 Without information on pre-ART viral load, nadir CD4 count is our surrogate C: a potential pre-treatment common cause of mediator and outcome.²⁴

Figure 2:

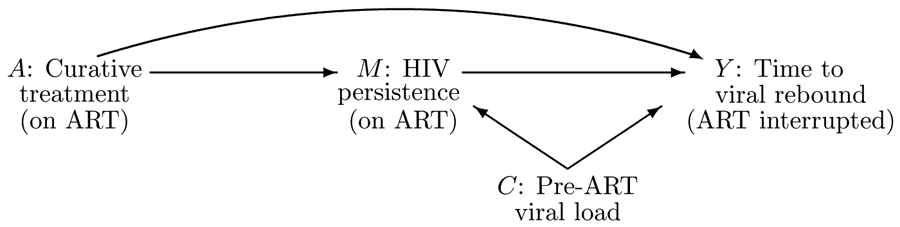
Causal diagram summarizing the HIV cure setting. This causal diagram indicates which variables might affect one another. Formal assumptions can be found in the text.

We use data from completed AIDS Clinical Trials Group trials:²⁴ one hundred twenty-four HIV–infected study participants without curative treatments and with ART interruptions, (Y_i, M_i C_i), i = 1,…, n (assumed independent and identically distributed). Combining these existing data, all with A_i = 0, with hypothesized effects of potential new curative HIV treatments A on biomarkers M, we estimate the indirect effect relative to a = 0 of new treatments A: the effect of organic interventions with the same effect on the mediator as such new treatments A = 1, and no effect on Y through other pathways.

We categorize the outcome viral rebound to suppressed (Y = 1)/not suppressed (Y = 0) through week 4 of ART interruption. Let $\overline{M}=1$ if the HIV persistence measure is below the assay limit, and $\overline{M}=0$ if it is above. First, we estimate the indirect effect of a treatment A that increases by three–fold the odds that the HIV persistence measure is below the assay limit, given C. The indirect effect mediated by the binary on–ART HIV persistence measure $\overline{M}$ equals (Equation (6)):

$$\begin{gathered} {\int }_{c}P(Y=1\mid \overline{M}=1,C=c,A=0)P({\overline{M}}^{(1)}=1\mid C=c)f_C(c)dc \\ +{\int }_{c}P(Y=1\mid \overline{M}=0,C=c,A=0)P({\overline{M}}^{(1)}=0\mid C=c)f_C(c)dc-P(Y^{(0)}=1). \end{gathered}$$

$P({\overline{M}}^{(1)}=m\mid C=c)$ and $P(Y=1\mid \overline{M},C,A=0)$ can be estimated from the data,²⁴ $(Y_i,{\overline{M}}_i,C_i)$, i = 1,…, n, all with A_i = 0, under the hypothesized effect of treatment on the mediator. We fit a logistic regression model

$$\log \text{it}P({\overline{M}}_i=1\mid C_i=c,A_i=0)=\log \text{it}{p}_{0,\eta }(c)={\eta }_0+{\eta }_{1}c.$$ (7)

If treatment increases this odds three–fold,

$${\widehat{P}}_{\widehat{\eta }}({\overline{M}}^{(1)}=1\mid C=c)=p_{1,\widehat{\eta }}(c)=3p_{0,\widehat{\eta }}(c)∕(1+(3-1)p_{0,\widehat{\eta }}(c))$$

(eAppendix H). We also fit a logistic regression model

$$\log \text{it}P(Y_i=1\mid {\overline{M}}_i=m,C_i=c,A_i=0)=\log \text{it}{p}_{\alpha }(m,c)={\alpha }_0+{\alpha }_{1}m+{\alpha }_{2}c.$$ (8)

The indirect effect is estimated by

$$\frac{1}{n}\sum _{i=1}^n\sum _{m=0}^1{p}_{\widehat{\alpha }}(Y=1\mid \overline{M}=m,C=c_i,A=0)P_{\widehat{\eta }}({\overline{M}}^{(1)}=m\mid C=c_i)-\frac{1}{n}\sum _{i=1}^n{y}_i,$$

that is,

$$\frac{1}{n}\sum _{i=1}^n\left(p_{\widehat{\alpha }}(1,c_i)\frac{3p_{0,\widehat{\eta }}(c_i)}{1+(3-1)p_{0,\widehat{\eta }}(c_i)}+p_{\widehat{\alpha }}(0,c_i)\frac{1-p_{0,\widehat{\eta }}(c_i)}{1+(3-1)p_{0,\widehat{\eta }}(c_i)}-y_i\right).$$

Table 1 summarizes the results.

Table 1:

Organic indirect effects of curative HIV treatments that increase the odds of HIV reservoir measures below the assay limit. The estimated probability of virologic suppression without treatment was 63/124 or 51% (week 4) and 17/122 or 14% (week 8).

Binary mediator	OR of below assay limita	Weekb,c	Indirect effectd	95% CIe	RRf	95% CIe
SCA HIV RNAg	2	4	2%	(−0.48%,5.1%)	1.0	(0.99,1.1)
SCA HIV RNAg	3	4	3%	(−0.70%,7.5%)	1.1	(0.99,1.1)
SCA HIV RNAg	∞i	4	6%	(−1.3%,14%)	1.1	(0.98,1.3)
CA HIV RNAh	2	4	4%	(0.86%,6.4%)	1.1	(1.0,1.1)
CA HIV RNAh	3	4	6%	(1.3%,9.9%)	1.1	(1.0,1.2)
CA HIV RNAh	10	4	10%	(2.3%,18%)	1.2	(1.0,1.4)
CA HIV RNAh	∞i	4	13%	(3.0%,23%)	1.2	(1.1,1.5)
SCA HIV RNAg	2	8	2%	(0.39%,4.1%)	1.1	(1.0,1.2)
SCA HIV RNAg	3	8	3%	(0.55%,6.0%)	1.2	(1.0,1.4)
SCA HIV RNAg	∞i	8	6%	(0.94%,11%)	1.3	(1.1,1.7)
CA HIV RNAh	2	8	4%	(1.7%,6.3%)	1.3	(1.1,1.4)
CA HIV RNAh	3	8	6%	(2.8%,10%)	1.5	(1.2,1.7)
CA HIV RNAh	10	8	12%	(5.1%,19%)	1.9	(1.4,2.4)
CA HIV RNAh	∞i	8	16%	(6.9%,26%)	2.1	(1.6,2.9)

^aOdds Ratio (OR) the mediator is below the assay limit, given the common cause C, relative to no curative treatment a = 0.

^bFor the week-4 analysis, analyzing viral rebound in the first 4 weeks after ART treatment interruption, C is NNRTI-based (versus not).

^cFor the week-8 analysis, analyzing viral rebound in the first 8 weeks after ART treatment interruption, C is the nadir CD4 count (categorized as ≤ 500 versus > 500). Not available in 2 patients, who were excluded from the week-8 analysis.

^dDifference in probability of virologic suppression that is mediated by binary mediator, expressed as a percentage.

^e95% Confidence Interval, calculated by bootstrap with 5000 replicates using Efron’s percentile method (Van der Vaart (1998)³⁹ page 327). This leads to consistent coverage because of the bootstrap Z-estimator master theorem, Theorem 10.16 from Kosorok (2008).⁴⁰

^fIndirect effect effect on the Risk Ratio (RR) scale.

^gSingle-copy plasma HIV RNA, on–ART. Analysis restricted to the 94 patients with SCA HIV RNA measured.

^hCell-associated HIV RNA, on–ART. All 124 patients had CA HIV RNA measured.

ⁱTreatment A which causes all mediator values below the assay limit.

Next, consider the original HIV persistence measure M, usually measured on the log₁₀ scale. Mathematical models predicted that a ten-fold reduction of the HIV reservoir increases the time to viral rebound by only a few weeks to a month.³² This has not been confirmed in clinical studies, which have seen smaller reservoir reductions.³² We estimate the organic indirect effect relative to a = 0 of a new curative treatment A that leads to a ten–fold reduction of the HIV reservoir. On the log₁₀ scale, such A shifts the mediator distribution M by one–log₁₀ given C:

$$M^{(1)}\sim M^{(0)}-1{\log }_{10}\mid C.$$ (9)

Treatment A shifts the distribution of the mediator rather than the actual values: we do not assume rank preservation.^33;34 The distribution of M⁽¹⁾ is estimated by subtracting one–log₁₀ from the mediator under no treatment M⁽⁰⁾.

The organic indirect effect relative to a = 0 of a treatment A that shifts the distribution of the mediator by one–log₁₀ given C equals (Equation (6))

$$\begin{gathered} {\int }_{(m,c)}P(Y=1\mid M=m,C=c,A=0)f_{M\mid C=c,A=1}(m)f_C(c)dmdc-P(Y^{(0)}=1) \\ ={\int }_{(m,c)}P(Y=1\mid M=m,C=c,A=0)f_{M\mid C=c,A=0}(m+1lo{g}_{10})f_C(c)dmdc-P(Y^{(0)}=1) \\ ={\int }_{(m,c)}P(Y=1\mid M=\tilde{m}(m),C=c,A=0)f_{M\mid C=c,A=0}(m)f_C(c)dmdc-P(Y^{(0)}=1), \end{gathered}$$ (10)

with a change-of-variables argument (eAppendix F), where $\tilde{m}(m)=m-1lo{g}_{10}$ if m − 1 log₁₀ is above the assay limit, and $\tilde{m}(m)$ is “below the assay limit” otherwise. We fit the logistic regression model

$$\begin{gathered} \mathrm{logit}P(Y_i=1\mid M_i=m,C_i=c,A_i=0)=\mathrm{logit}{p}_{\beta }(m,c) \\ =\{\begin{array}{cc}{\beta }_0+{\beta }_{1}m+{\beta }_{2}c\hfill & \text{if}m\text{above the assay limit}\hfill \\ {\beta }_3+{\beta }_{2}c\hfill & \text{if}m\text{below the assay limit}.\hfill \end{array}\phantom{\}} \end{gathered}$$ (11)

The organic indirect effect (10) is estimated by

$$\frac{1}{n}\sum _{i=1}^n\left(p_{\widehat{\beta }}(\tilde{m}(m_i),c_i)-y_i\right).$$

eAppendix J fits outcome and mediator models. Table 2 summarizes the results.

Table 2:

Organic indirect effects of curative HIV treatments that shift the distribution of the HIV reservoir measures downwards. The estimated probability of virologic suppression without treatment was 63/124 or 51% (week 4) and 17/122 or 14% (week 8).

Mediator	Shift (log10 scale)a	Weekb,c	Indirect effectd	95% CIe	RRf	95% CIe
SCA HIV RNAg	0.5 log10	4	3%	(−2.5%,7.0%)	1.0	(0.96,1.1)
SCA HIV RNAg	1 log10	4	6%	(−1.3%,13%)	1.1	(0.98,1.2)
SCA HIV RNAg	∞i	4	6%	(−1.4%,14%)	1.1	(0.97,1.3)
CA HIV RNAh	0.5 log10	4	7%	(1.7%,13%)	1.1	(1.0,1.3)
CA HIV RNAh	1 log10	4	10%	(2.7%,17%)	1.2	(1.1,1.4)
CA HIV RNAh	∞i	4	13%	(3.0%,23%)	1.2	(1.1,1.5)
SCA HIV RNAg	0.5 log10	8	3%	(0.61%,6.3%)	1.2	(1.0,1.4)
SCA HIV RNAg	1 log10	8	5%	(0.92%,10%)	1.3	(1.1,1.6)
SCA HIV RNAg	∞i	8	6%	(0.95%,11%)	1.3	(1.1,1.7)
CA HIV RNAh	0.5 log10	8	9%	(3.5%,15%)	1.7	(1.3,2.2)
CA HIV RNAh	1 log10	8	12%	(4.9%,19%)	1.9	(1.4,2.5)
CA HIV RNAh	∞i	8	16%	(6.8%,26%)	2.1	(1.6,2.9)

^aDownwards shift of the mediator distribution, given the common cause C, on the log₁₀ scale, relative to no curative treatment a = 0.

^bFor the week-4 analysis, analyzing viral rebound in the first 4 weeks after ART treatment interruption, C is NNRTI-based (versus not).

^cFor the week-8 analysis, analyzing viral rebound in the first 8 weeks after ART treatment interruption, C is the nadir CD4 count (categorized as ≤ 500 versus > 500). Not available in 2 patients, who were excluded from the week-8 analysis.

^dDifference in probability of virologic suppression that is mediated, expressed as a percentage.

^e95% Confidence Interval, calculated by bootstrap with 5000 replicates using Efron’s percentile method (Van der Vaart (1998)³⁹ page 327). This leads to consistent coverage because of the bootstrap Z-estimator master theorem, Theorem 10.16 from Kosorok (2008).⁴⁰

^fIndirect effect effect on the Risk Ratio (RR) scale.

^gSingle-copy plasma HIV RNA, on–ART. Analysis restricted to the 94 patients with SCA HIV RNA measured.

^hCell-associated HIV RNA, on–ART. All 124 patients had CA HIV RNA measured.

ⁱTreatment A which causes all mediator values below the assay limit.

From Table 2, a one–log₁₀ decrease in cell–associated HIV RNA may lead to a more promising indirect effect on viral control than a one–log₁₀ decrease in single–copy plasma HIV RNA, and cell–associated HIV RNA may thus be a better target for curative HIV treatments. This may however be influenced by measurement error, present for both mediators, and/or due to a larger fraction of single–copy plasma HIV RNA measurements below the assay limit without curative treatment (60/94 (64%) versus 52/124 (42%)).

If we have measurements of the on–ART biomarker M⁽¹⁾ and C for HIV–infected individuals under a curative treatment, say $(m_j^{(1)},c_j^{(1)}{)}_{j=1}^J$ in a population similar to our study population, but not necessarily ART interruption data for the new treatment, the organic indirect effect is estimated by

$$\frac{1}{J}\sum _{j=1}^J{p}_{\widehat{\beta }}(m_j^{(1)},c_j^{(1)})-\frac{1}{n}\sum _{i=1}^n{y}_i,$$ (12)

with p_β and $\widehat{\beta }$ as before, estimated in patients with A_i = 0. eAppendix G describes settings with on-treatment measurements of C and M in a different population.

Discussion

For organic indirect and direct effects, one does not need to envision setting the mediator; one needs to envision affecting the distribution of the mediator, which potential new treatments often aim to do. Our initial approach¹⁷ generalized natural^2-7 and randomized^8;15;16 indirect and direct effects by combining organic interventions with treatment, a = 1. When combining organic interventions on the mediator with a = 0, the no treatment scenario, organic indirect effects relative to a = 0 and pure indirect effects^2;13 only depend on the model for E[Y∣M, A, C] restricted to a = 0, where interactions between treatment and mediator are irrelevant. We show that a product method even holds for binary mediators.

Intervention–based reasoning helps determine whether combining interventions on the mediator with a = 0 or with a = 1 is most practically relevant. For the desired effect of a treatment through the mediator, as in our HIV cure example or the effect of AZT on HIV transmission¹⁷ (eAppendix C), combining interventions on the mediator with a = 0 is interesting. If interest lies in preventing a treatment’s side effects M, combining interventions on the mediator with a = 1 is interesting. VanderWeele (2015)⁵ pages 193–196 describes related work on three-way decompositions.

Under the respective conditions usually made and if there are no post–treatment common causes of mediator and outcome, natural direct and indirect effects, their randomized counterparts,^8;15;16 and their organic counterparts relative to a = 1 all lead to the same numerical results in settings where these effects are all well defined: the respective interventions are organic under those conditions¹⁷ (eAppendix E). This also proves that randomized indirect and direct effects do not depend on the choice of all common causes C of mediator and outcome (eAppendix D). Organic indirect and direct effects relative to a = 0 can differ from those relative to a = 1, and similarly lead to the same numerical results as for natural and randomized indirect and direct effects when reversing also there the roles of a = 1 and a = 0.

Organic indirect effects relative to a = 0 can be estimated without outcome data under treatment. Our application illustrates how this is useful for selecting potential new treatments with promising indirect effects for further evaluation in clinical trials. There are often many candidate treatments A targeting a process which can be measured by a biomarker M. Data on clinical outcomes and mediators under no treatment may be available from observational studies, or from placebo arms of completed studies. Our proposed method is particularly useful in data-scarce settings, such as the current evaluation of COVID-19 treatments. Combining the hypothesized treatment effect on biomarker M (potentially informed by early-phase studies or pre–clinical animal studies) with outcomes under no or ineffective treatment, one could estimate the potential indirect effect mediated by M relative to a = 0 using Equation (6), as in our HIV application. Randomized trials could be reserved for treatments with the most promising indirect effects.

It may sound counterintuitive that we do not need outcomes under treatment, and the treatment effect on the mediator suffices to estimate organic indirect effects relative to a = 0 and pure indirect effects. However, this only provides indirect effects, not total effects or the proportion mediated. For organic indirect effects relative to a = 0, one can think of the mediator being affected and then the outcome taking its course as under A = 0; for that, outcome data under treatment are not needed. If outcome data under treatment are available, for outcomes under A = 1 to affect predictions from a full model E[Y∣C, A, M] restricted to a = 0 (and thus indirect effects), E[Y∣C, A, M] has to include parameters that are common for A = 0 and A = 1. In fact, the same reasoning holds for pure indirect effects. In contrast, depending again on the outcome model specification, for the natural indirect effect, outcome data without treatment might not affect the estimated indirect effect.

A key lesson from the HIV example is the importance of collecting pre-treatment common causes C of mediator and outcome. Even in randomized trials, data on pre-treatment common causes C is needed to estimate indirect and direct effects. The indirect effect is expected to not be large if C, not M, is the main predictor of Y. A sensitivity analysis for missing C exists for linear structural equation models.⁶

In our HIV example, the probability of virologic suppression was assumed not to depend on how far below the assay limit a mediator value lies. If new treatments also lower the mediator further below the assay limit, the indirect effect relative to a = 0 of new treatments could be larger than we estimated. An interesting topic for future research is estimating the impact of an intervention that shifts the mediator, incorporating that mediators further below the assay limit could lead to longer times to viral rebound.

As usual in mediation analysis, when the mediator M is just a marker for some underlying disease process, it cannot be expected that the distribution of the outcome given M^(0,I=1) = m and C is similar to the distribution of the outcome given M⁽⁰⁾ = m and C, unless the intervention I affects the marker because it affects the underlying disease process. A famous counterexample is the effect of yellow fingers on lung cancer. Yellow fingers would constitute an irrelevant mediator, unless used as a measure of smoking intensity. The meaning of mediation analysis is distorted when the interpretation of the potential mediator is different under treatment than without treatment. For example, in HIV studies^35;36 IL-2 increased CD4 counts, and in prior ART treatment trials, CD4 count increases predicted better clinical outcomes. However, IL-2 did not improve clinical outcomes in randomized trials. Stated in terms of interventions, when the CD4 count mediator came about due to IL-2, it had a different prognostic effect on the outcome than when it came about without IL-2: IL-2 is not an organic intervention. This is further illustrated by the fact that CD4 counts resulting from IL-2 can be much higher than typically seen in any HIV–infected patient, resulting in Equation (3) conditioning on null events. Mechanism of action and subject matter knowledge are important considerations for causal mediation analysis.

If treatment results in mediator values rarely seen without treatment, the organic indirect effect relative to a = 0 is unidentified: some conditioning events in the Mediation Formula are null events, events that never happen, so the Mediation Formula is ambiguous. Any effects identified by the Mediation Formula, including natural, randomized,^8;15;16 and separable^10;11;14 effects, suffer from this phenomenon. Extrapolation using parametric models can render results very model-dependent.³⁷

Since the Mediation Formula holds for organic indirect and direct effects, many results for natural indirect and direct effects generalize to organic indirect and direct effects. For example, organic indirect and direct effects can be estimated when there is measurement error.³⁸ If there is measurement error in the mediator, as in our HIV example, the indirect effect is typically underestimated.³⁸ Measurement error in the mediator combined with mediator assay lower limits is an interesting topic for future research.

The proposed organic indirect and direct effects can also be estimated from observational data, if all confounders have been measured¹⁷ (eAppendix I). We have published preliminary results on incorporating post-treatment common causes of mediator and outcome¹⁵ into our framework.¹⁸

Table 3:

Odds Ratio Estimates of virologic suppression (Y = 1) given the mediator and pre-treatment common causes

week	predictor	ORa	95% Wald CIb
4	On-ART SCA HIV RNAc belowe	2.1	(0.86,5.0)
	NNRTI-based ARTe	2.3	(1.0,5.5)
4	On-ART SCA HIV RNAc belowe	2.3	(0.58,9.4)
	Continuous on–ART SCA HIV RNAc	1.2	(0.20,7.4)
	NNRTI-based ARTe	2.4	(1.0,5.6)
4	On-ART CA HIV RNAd belowe	2.7	(1.2,6.0)
	NNRTI-based ARTe	3.9	(1.8,8.6)
4	On-ART CA HIV RNAd belowe	0.67	(0.048,9.3)
	Continuous on–ART CA HIV RNAd	0.58	(0.22,1.5)
	NNRTI-based ARTe	4.0	(1.8,8.7)
8	On-ART SCA HIV RNAc belowe	4.6	(0.95,22)
	Nadir CD4 ≤ 500e	4.6	(0.95,22)
8	On-ART SCA HIV RNAc belowe	4.1	(0.30,57)
	Continuous on–ART SCA HIV RNAc	0.83	(0.015,45)
	Nadir CD4 ≤ 500e	4.5	(0.93,22)
8	On-ART CA HIV RNAd belowe	9.0	(2.5,32)
	Nadir CD4 ≤ 500e	6.0	(1.5,24)
8	On-ART CA HIV RNAd belowe	0.36	(<0.001,2.1 · 102)
	Continuous on–ART CA HIV RNAd	0.27	(0.019,3.8)
	Nadir CD4 ≤ 500e	5.9	(1.5,24)

^aOdds Ratio.

^b95% Wald Confidence Interval.

^cSingle-copy plasma HIV RNA, on ART. Analysis restricted to the 94 patients with SCA HIV RNA measured.

^dCell-associated HIV RNA, on ART. All 124 patients had CA HIV RNA measured.

^e:yes versus no.

Table 4:

Odds Ratio Estimates of the mediator below the assay limit given the pre-treatment common cause

Mediator	Common cause	ORa	95% Wald CIb
On-ART SCA HIV RNAc belowe	NNRTI-based ARTe	1.9	(0.81,4.5)
on–ART CA HIV RNAd belowe	NNRTI-based ARTe	0.65	(0.32,1.3)
On-ART SCA HIV RNAc belowe	Nadir CD4 ≤ 500e	1.0	(0.43,2.5)
On-ART CA HIV RNAd belowe	Nadir CD4 ≤ 500e	0.30	(0.14,0.64)

^aOdds Ratio.

^b95% Wald Confidence Interval.

^cSingle-copy plasma HIV RNA, on ART. Analysis restricted to the 94 patients with SCA HIV RNA measured. Without treatment, the probability of on–ART SCA HIV RNA below the assay limit was 60/94, or 64%.

^dCell-associated HIV RNA, on ART. All 124 patients had CA HIV RNA measured. Without treatment, the probability of on–ART CA HIV RNA below the assay limit was 52/124, or 42%.

^e:yes versus no.