Deep Convolutional Neural Networks for Displacement Estimation in ARFI Imaging

Abstract

Ultrasound elasticity imaging in soft tissue with acoustic radiation force requires the estimation of displacements, typically on the order of several microns, from serially-acquired raw data A-lines. In this work, we implement a fully convolutional neural network (CNN) for ultrasound displacement estimation. We present a novel method for generating ultrasound training data, in which synthetic 3-D displacement volumes with a combination of randomly-seeded ellipsoids are created and used to displace scatterers, from which simulated ultrasonic imaging is performed using Field II. Network performance was tested on these virtual displacement volumes as well as an experimental ARFI phantom dataset and a human in vivo prostate ARFI dataset. In simulated data, the proposed neural network performed comparably to Loupas’s algorithm, a conventional phase-based displacement estimation algorithm; the RMS error was 0.62 μm for the CNN and 0.73 μm for Loupas. Similarly, in phantom data, the contrast-to-noise ratio of a stiff inclusion was 2.27 for the CNN-estimated image and 2.21 for the Loupas-estimated image. Applying the trained network to in vivo data enabled the visualization of prostate cancer and prostate anatomy. The proposed training method provided 26,000 training cases, which allowed for robust network training. The CNN had a computation time that was comparable to Loupas’s algorithm; further refinements to the network architecture may provide an improvement in the computation time. We conclude that deep neural network-based displacement estimation from ultrasonic data is feasible, providing comparable performance with respect to both accuracy and speed compared to current standard time delay estimation approaches.

I. Introduction

Ultrasound elastography techniques assess the stiffness of soft tissue by monitoring the tissue response to an applied deformation [1]. One such technique, acoustic radiation force impulse (ARFI) imaging, generates displacement magnitudes of several microns in tissue using a focused ultrasound pulse [2]. Immediately following the impulsive excitation, the relative tissue displacements within the region of excitation are tracked with ultrasound, with stiffer tissues associated with lower displacement magnitudes. The use of ARFI imaging to detect and assess disease states has been demonstrated in several clinical applications, including cancer detection [3], [4], [5], cardiac ablation imaging [6], and carotid plaque characterization [7].

To form an ARFI image, ultrasound data are obtained before and after the radiation force excitation. These data can be in the form of radiofrequency (RF) signals, or demodulated to in-phase and quadrature (I/Q) signals. A displacement estimation algorithm then computes the tissue displacement magnitudes between the two time steps [8]. For RF data, normalized cross-correlation methods or iterative phase zero estimation algorithms can be used to compute the displacements [9]. For I/Q data, commonly used displacement estimation algorithms include those described by Kasai et al. [10] and Loupas et al. [11]. These autocorrelation techniques compute phase differences between ultrasound data at the two time steps of interest to estimate the displacements. A 2-D ARFI displacement image is reconstructed by laterally translating the ARFI excitation across the field of view and performing displacement estimation on each A-line.

Recently, deep learning methods have been investigated for a variety of ultrasound imaging applications, including beamforming [12], [13], speckle reduction [14], [15], [16], and sparse image recovery [17]. Within the field of ultrasound elastography, recent studies have explored a deep learning approach for strain imaging applications. In strain imaging, the transducer is used to physically compress the surface of the tissue by several millimeters [1], [18]. The strain profile along the axis of the transducer is then computed and can be used to reconstruct the elastic modulus of the tissue. Kibria and Rivaz developed a strain imaging algorithm using FlowNet 2.0, a neural network that was originally designed for optical flow motion estimation, to obtain a coarse estimate of the time delay that was further refined with global ultrasound elastography (GLUE) strain imaging [19]. Tehrani and Rivaz used a modified version of pyramid warping and cost volume network (PWC-Net), which estimates the optical flow at different levels with increasingly fine resolution and requires fewer parameters compared to FlowNet 2.0 [20]. Peng et al. also retrained existing models—FlowNet-CSS, PWC-Net, and LiteFlowNet—for strain imaging in phantom and in vivo breast tissue data after envelope detection [21]. Wu et al. used a two-stage deep neural network to first estimate motion after soft tissue compression and then compute the strain field [22]. Gao et al. developed an implicit strain reconstruction framework using a deep neural network with a learning using privileged information (LUPI) paradigm [23]. Additionally, recent studies from Haukom et al. [24], Delaunay et al. [25], and Tehrani et al. [26] have explored the use of unsupervised or semi-supervised learning for strain estimation, in which the neural network is directly trained or fine-tuned on unlabeled clinical ultrasound data.

To investigate whether a machine learning approach could be used to map raw I/Q ultrasound ARFI data to the underlying tissue displacements, this study used a deep convolutional neural network (CNN) as an alternative to traditional displacement estimation algorithms used in ARFI imaging. The challenges associated with displacement estimation in ARFI imaging are distinct from those associated with strain imaging [8]. Primarily, the displacements encountered in ARFI imaging are several orders of magnitude smaller—typically at most several microns—nearing the theoretical fundamental limit on time delay estimation imposed by the Cramér-Rao lower bound [27]. In recent work, we demonstrated the feasibility of training a CNN for estimating small displacements from raw I/Q ultrasound data [28]. To our knowledge, this was the first application of a deep learning approach for the estimation of ARFI displacements.

In this study, we describe our novel approach to generating displacement training data that does not require finite-element simulations, which are often specific to a particular ARFI excitation configuration and are computationally intensive. Our proposed approach enables the creation of a sufficiently large training dataset to train the neural network to estimate ARFI displacements without overfitting the training data. We conduct a learning curve analysis to assess the necessary dataset size to avoid overfitting by the CNN, which uses the same architecture as the neural network examined in the previous feasibility study [28]. The performance of the trained network is evaluated in simulated data, as well as experimentally acquired data in a tissue-mimicking phantom and in vivo in human prostate tissue, and compared with the conventional phase-shift displacement estimator described by Loupas et al. [11].

II. Methods

A. Generating the Training Dataset

The data used to train a deep neural network are ultimately critical to the performance of the network, since these data are used to learn the weights that map the input data to the final output. Because the true underlying displacements must be known to generate the ground-truth labels used to train a network for displacement estimation, the training dataset in this case was limited to simulation data. Without using a complex experimental setup incorporating optical tracking of targets embedded within a translucent phantom [29], the true displacements following an ARFI excitation are not typically known in experimental ARFI acquisitions. This limitation is primarily due to displacement underestimation in the focal zone resulting from lateral and elevation shearing underneath the point spread function (PSF) of the ultrasound tracking beam [30], [31].

One approach to generating the training dataset involves performing finite-element simulations of ARFI excitation dynamics in heterogeneous materials of varying stiffness, and to model ultrasonic tracking of the resulting displacements [31], [32]. This method would be similar to the approach used in recent studies that explored the application of deep learning to strain imaging [21], [20], [22], [23]. However, finite-element simulations can often be computationally costly, particularly for large volumes or materials containing complex, heterogeneous structures. Long simulation runtimes may preclude the generation of a large training dataset to robustly train the neural network, or make it difficult to recreate the dataset if simulation parameters need to be modified. Furthermore, a neural network trained with data specific to a particular simulated ARFI excitation configuration, where the focal gain is consistently located in the same region for each case, may not necessarily generalize to the wide variety of displacement patterns that may be encountered with different push configurations.

Instead, we developed a novel training approach for this study in which the training dataset was created by generating synthetic 3-D axial displacement volumes, as shown in Figure 1. Different ellipsoids with randomly-assigned sizes, spatial orientations, locations, and amplitudes were summed to create a complex displacement field within the volume. Both positive and negative ellipsoid amplitudes, from −15 μm to 15 μm, were included to train the network to detect potential displacements in either axial direction. This range of displacements is consistent with the magnitudes of displacement typically encountered in ARFI imaging [33], including in our prostate ARFI imaging study [5]. For each volume, 150 ellipsoids in total were summed to create a complex displacement field, with the resultant displacement amplitudes of several microns, as typically encountered in ARFI imaging applications. To prevent sharp discontinuities in displacement that would be inconsistent with a realistic ARFI tissue response, an isotropic 3-D Gaussian spatial smoothing filter with a standard deviation of 0.15 mm in each dimension was applied after the summation. The standard deviation of the smoothing filter was below the smallest desired structural resolution of the prostate imaging application.

Fig. 1.

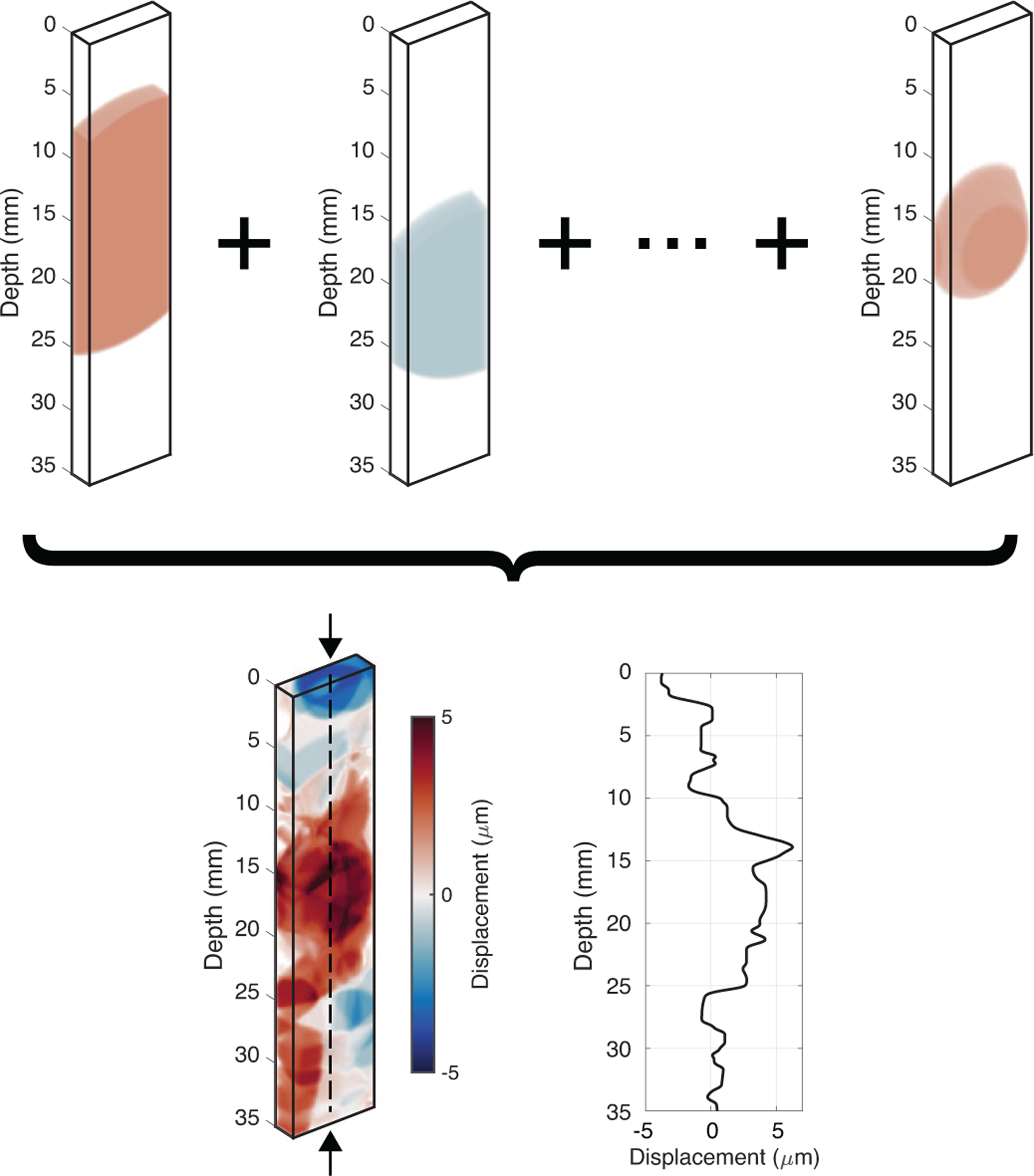
Example of a synthetic 3-D displacement field generated by summing ellipsoids of random size, orientation, location, and amplitude. These displacement fields were used to displace scatterers and simulate ultrasonic tracking in Field II to produce in-phase and quadrature (I/Q) data. The arrows pointing to the dashed axial line in the center of the summed volume indicate the ground-truth displacement values, which are also plotted. In total, 30,000 displacement volumes were generated to train, validate, and test the neural network.

These displacement volumes were used to introduce scatterer motion in Field II simulations [34], [35]. Field II was used to simulate imaging of randomly-placed scatterers in a 3-D volume with a linear Siemens 12L4 transducer (Siemens Healthcare, Mountain View, CA), which we are using in an ongoing prostate ARFI imaging study [5]. The 5-MHz tracking transmit beam was focused at a depth of 60 mm in an F/2 focal configuration, with dynamic receive focusing; these tracking parameters were matched to our experimental parameters. A scatterer density of 160,000 scatterers/cm³ was used in the simulation.

For each scatterer realization, two simulations were performed: one with the scatterers in their original locations within the field, and one after the scatterers were displaced axially by a given magnitude based on the displacement volume generated by the ellipsoids. To make the simulated results more closely resemble the data from our experimental setup, the resulting raw simulated radiofrequency data were demodulated to produce in-phase and quadrature (I/Q) data, and then downsampled to a sampling frequency of 5 MHz. After downsampling, the data were then re-upsampled to a sampling frequency of 25 MHz using spline interpolation; this step is typically performed prior to conventional displacement estimation in experimentally acquired data [8]. The simulation of ultrasonic imaging with Field II models speckle and its associated biases in ultrasonic displacement data [31], but does not model electronic noise that is present in experimental data. Thus, electronic noise was added to the data in order to train the network to be able to estimate displacements from noisy data. For each simulated dataset, a random amount of additive Gaussian noise (standard deviation ranging from 0 μm to 1 μm) was added to the input data before the training data were input to the network.

To successfully train a supervised neural network, the network must be supplied with the ground-truth labels as well. During the training process, the weights of the neural network are adjusted to minimize the loss between the network output and the ground truth. In this case, the ground-truth displacement values were produced by taking the center axial line of each virtual displacement volume (i.e., the axial line located at the central azimuthal and elevational positions). This ground-truth axial line is shown in Figure 1 as the dashed vertical line running through the center of the summed displacement volume.

Figure 1 also plots the ground-truth displacements for this displacement volume. The displacements are slightly negative at shallow depths, increase to positive values near the middle of the volume, and decrease back to approximately zero at the deepest part of the volume. Note that the displacement magnitudes that were simulated are similar to the magnitudes that would typically be expected for in vivo ARFI imaging applications (several microns). Furthermore, the applied 3-D Gaussian spatial smoothing filter generates subtle gradients in the displacement pattern and prevents sudden discontinuities in the data.

In total, 30,000 unique displacement volumes were randomly generated using the process described above, and each volume was used to displace scatterers in Field II to produce simulated I/Q data lines. For each displacement volume, the two simulated I/Q data A-lines (before and after the displacements were applied) were used as the input to the neural network, and the ground-truth displacements through depth were used as the output that the neural network would attempt to reconstruct.

The generated data were divided into three datasets: 26,000 cases were used as the training dataset and 2,000 cases each were used as validation and test datasets to assess the performance of the network.

B. Neural Network Design and Training

Figure 2 shows a diagram of the architecture of the deep convolutional neural network that was used in this study, with the labeled dimensions in the figure corresponding to the dimensions of the training dataset. The input to the neural network was a 1200×2×2 data array, where 1200 was the number of depth samples in each training data array, and the remaining two dimensions corresponded to the time step (before and after the scatterers’ applied ARFI displacements) and I/Q data channel, respectively. The final output of the neural network was a one-dimensional vector with the same height as the input data (1200 samples in the training data case), and corresponded to the network’s estimated displacement values through depth.

Fig. 2.

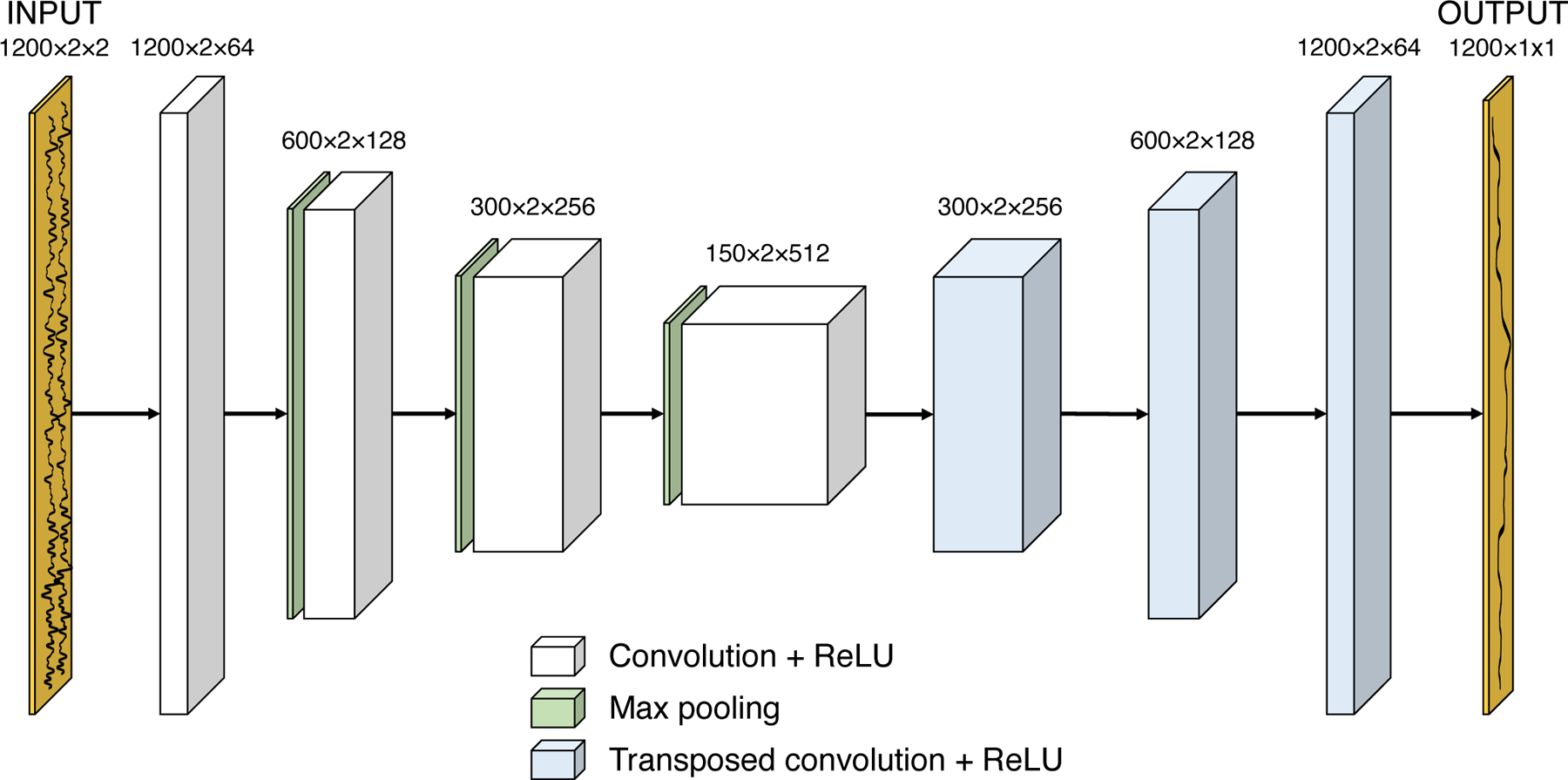
Diagram of the neural network architecture. The input size is 1200 × 2 × 2, where 1200 is the number of depth samples and the last two dimensions specify the time step (before and after the ARFI excitation) and I/Q data channel. A series of convolutional and max pooling layers are used, followed by a series of transposed convolutional layers to build the image size back up to 1200 samples. A final convolutional layer collapses the last two dimensions to produce a 1-D displacement output vector.

Notably, the neural network’s fully convolutional architecture did not contain any fully connected layers, which connect all of the nodes in a given layer to all of the nodes in the subsequent layer. The exclusion of fully connected layers from the architecture not only simplified the model by reducing the number of parameters that had to be learned during the training process, but it also suggested that the trained network would be robust to different input sizes. As a result, the input to the trained network was not limited to data containing 1200 depth samples, potentially allowing the network to generalize to different imaging conditions.

A fully convolutional architecture was selected for this displacement estimation task, since the displacement information should be locally encoded in the I/Q data. In other words, data from spatially-distant regions do not need to be combined for local displacement estimation, so a fully-connected layer should not be needed.

Within the deep convolutional neural network, the input I/Q data are fed into a series of convolutional layers with rectified linear unit (ReLU) nonlinearity, with the number of features (third array dimension) increasing with each convolutional layer due to the increasing complexity of features being represented at each layer. After four sets of convolutional layers (3×3 filter size) with 2×1 max pooling, a series of transposed convolutional layers are used to build the image back up to the original number of depth samples (e.g., 1200 samples for the training data). For the convolutional layers, a filter size of 3×3 was selected; before each convolution, the data were zero-padded using the “SAME” parameter in TensorFlow to preserve the same data size after the operation. Finally, a single additional convolutional layer is used to collapse the last two dimensions to produce a 1-D output vector of the network’s estimated displacements. Batch normalization was applied to the inputs of each network layer to reduce internal covariate shift [36].

The L1 loss, calculated as the mean absolute error, was used to train the network and evaluate its performance. During the training process, the displacements that were output by the network were subtracted element-wise from the ground-truth displacement labels, and the mean absolute difference across the data was computed. A minibatch size of 75 was used for training, meaning that 75 sets of training data were processed at a time and used in conjunction to update the parameters of the neural network at each iteration. ADAM (adaptive moment estimation), which is a stochastic gradient descent optimization algorithm commonly used in deep learning applications, was used to train this network with an initial learning rate of 0.001 [37].

Before training, the parameters of the neural network were initialized using the approach described by He et al. [38]. This initialization, in which the variance of the nodes in a layer of the network is set to 2.0/n where n is the number of units in the previous layer, was derived specifically for ReLU activation functions, which were used in this architecture. Using this initialization method can prevent an undesirable exploding variance value as the number of inputs to the neural network grows.

The open-source TensorFlow machine learning interface (version 1.9.0) was used to develop the model in this study [39]. Network training was performed on an NVIDIA Tesla V100 GPU. To evaluate the performance of the neural network, the I/Q data were also processed using the algorithm described by Loupas et al., which is a conventional phase-shift approach based on a 2-D autocorrelation algorithm that is commonly used for ARFI displacement estimation applications [8], [11]. A 1.5-wavelength axial kernel was used with Loupas’s algorithm for this analysis. A comparison of the computation time between the proposed network and Loupas’s algorithm was performed on a 2.3-GHz Intel Core i7 CPU.

C. Experimental Data Collection

Phantom and in vivo prostate data were obtained using a modified Siemens 12L4 linear side-fire transducer on a modified Siemens ACUSON SC2000 scanner. For an extended pushing depth of field for the ARFI excitation, three focal depths (30 mm, 22.5 mm, and 15 mm) were rapidly and successively transmitted deep-to-shallow for each radiation force excitation [40]. The track transmit beam was focused at 60 mm in an F/2 configuration with dynamic receive focusing, using the same tracking sequence as the Field II simulation described above.

To build up a 2-D ARFI displacement image, eighty-two push beams were laterally translated across the transducer aperture, with each push beam spaced 0.62 mm apart. The ARFI track beams were obtained with 4:1 parallel receive and 0.16-mm track beam spacing [41]. ARFI data were acquired in a custom CIRS elastic phantom (Norfolk, VA) containing a stiff spherical inclusion with a diameter of 10 mm. The Young’s modulus of the spherical inclusion was 16.3 kPa, while the Young’s modulus of the background material was 10 kPa.

In an institutional review board-approved study, ARFI and B-mode prostate data were acquired in subjects with biopsy-confirmed prostate cancer after obtaining written informed consent, immediately before they underwent a radical prostatectomy procedure [5]. The same ARFI pushing and tracking sequence used to acquire the phantom dataset was also used to obtain the in vivo data. For each subject, a 3-D prostate ARFI data volume was populated by rotating the side-fire transducer in approximately 1 degree increments in elevation using a mechanical rotation stage with an optical encoder to track the trajectory of the transducer [5]. Immediately following the ARFI data acquisition, the transducer was rotated in the reverse direction to acquire high-quality B-mode data, using a 7-MHz transmit frequency and 126 transmits spanning the field of view at each elevation angle. Scan conversion and visualization of the ARFI and B-mode prostate volumes were performed in 3D Slicer, an open-source software package designed for image analysis and display [42].

III. Results

To assess the size of the training dataset needed to train a neural network for a displacement estimation task, a learning curve was constructed, shown in Figure 3. This plot was generated by varying the size of the training dataset used to learn the parameters of the network. In other words, instead of using all 26,000 displacement volumes in the training dataset, only a subset of those volumes were selected to train the network. After training, the mean absolute error between the network’s outputs and the ground-truth displacements was computed using both the subset of the training data and the validation dataset. The error bars in Figure 3 indicate the standard deviation of the mean absolute error over ten training repetitions. The convergence of the two curves towards the right side of the figure demonstrates that a large training dataset of this size (26,000 cases for this study) was needed for robust training of the network and to prevent excessive overfitting of the training data. During training, L2 loss (mean squared error) and log-cosh loss were compared with L1 loss (data not shown); in each case, the neural network converged to the same baseline loss value, indicating that the training loss function did not impact the performance of the final trained network.

Fig. 3.

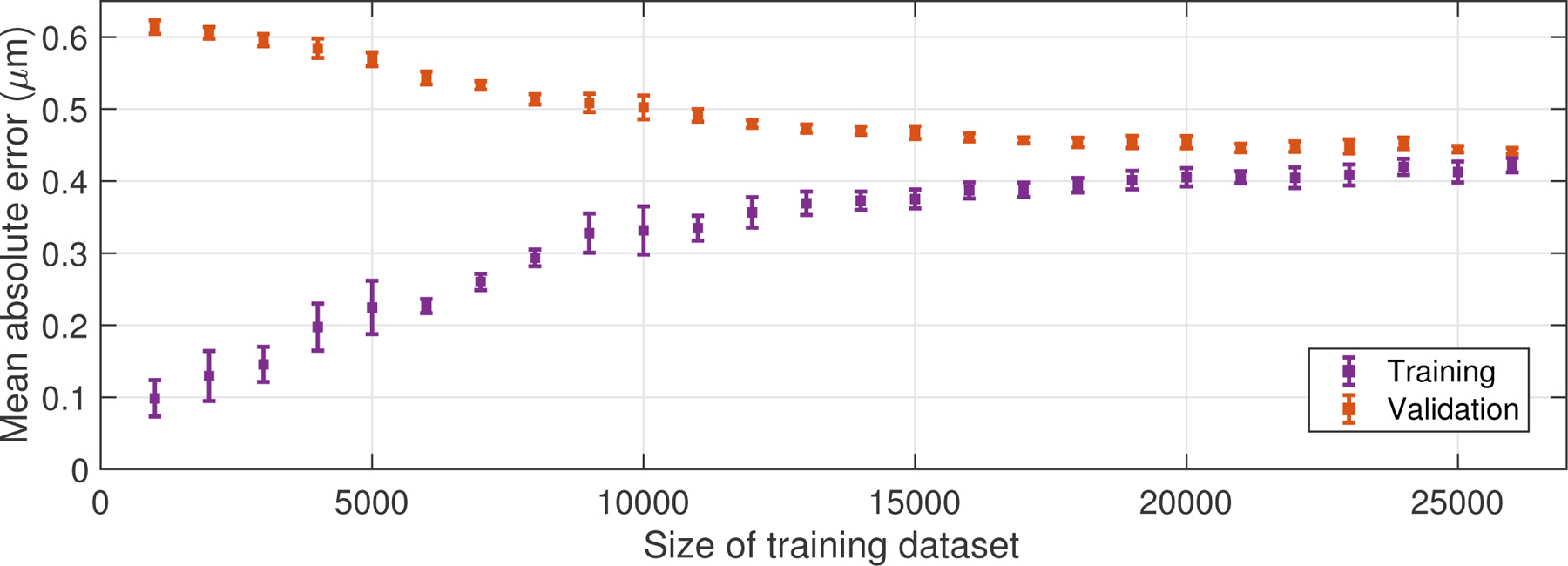
Learning curve, generated by varying the size of the training dataset and computing the mean absolute error between the output displacements and the ground-truth displacement labels, across both the training and validation datasets after training on the subset of data. Error bars indicate the standard deviation computed across ten training repetitions. The convergence of the two curves indicates the large number of training cases used in this study (26,000) was required to robustly train the network and prevent overfitting of the training data.

Figure 4 shows the results of the trained neural network in one of the simulated datasets (i.e., tracked data from a randomly generated 3-D displacement volume in the test dataset). In this figure, the ground-truth displacement labels extracted from the central line of the displacement volume are shown in black, while the CNN-estimated displacements and Loupas-estimated displacements are shown in orange and green, respectively. The root-mean-square (RMS) error between the neural network and the true displacements was 0.62 μm, while the RMS error between Loupas’s algorithm and the true displacements was 0.73 μm. Across the entire test dataset (2000 test cases), the mean RMS error between the neural network and the true displacements was 0.66 μm (standard deviation [SD] = 0.06 μm), and the mean RMS error between Loupas’s algorithm and the true displacements was 0.75 μm (SD = 0.05 μm).

Fig. 4.

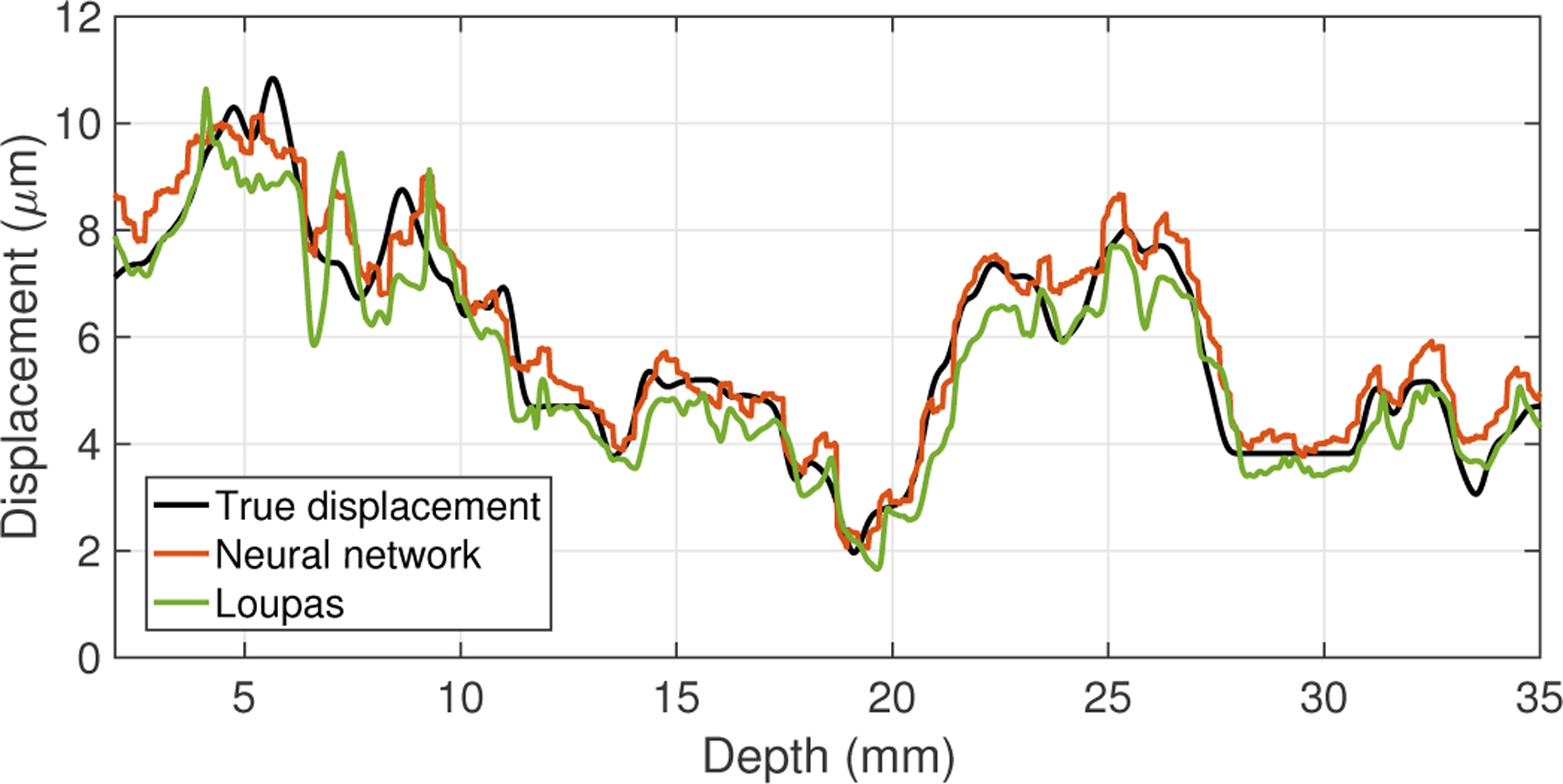
Displacement estimation results for a simulated dataset generated from a synthetic 3-D displacement field, including the ground-truth displacements (black) and the outputs from the neural network (orange) and Loupas’s algorithm (green). The RMS error between the neural network output and the true displacements was 0.62 μm, and the RMS error between Loupas’s algorithm output and the true displacements was 0.73 μm.

To investigate the performance of the trained network versus scatterer displacement, the displacements in the simulated training data were divided into two groups: smaller displacements less than 5 μm and larger displacements greater than 5 μm. For the smaller displacements group, the RMS error between the neural network and the true displacements was 0.61 ± 0.04 μm. For the larger displacements group, the RMS error was 0.70 ± 0.04 μm.

Figure 5 shows the results of the trained neural network in data that were experimentally acquired in an elastic stiffness phantom. While the phantom contained a stiff spherical inclusion, the data shown in this figure were taken from a region of the phantom that had homogeneous stiffness; the variation in amplitude across depth is due to focal gain from the ARFI push excitation. For these data, there was no ground-truth displacement label available, since the true displacement magnitudes within the phantom are unknown. Therefore, only the results of the neural network (orange) and Loupas’s algorithm (green) are shown in this figure. For the data shown in this plot, the RMS difference between the displacements output by the neural network and those estimated using Loupas was 0.24 μm.

Fig. 5.

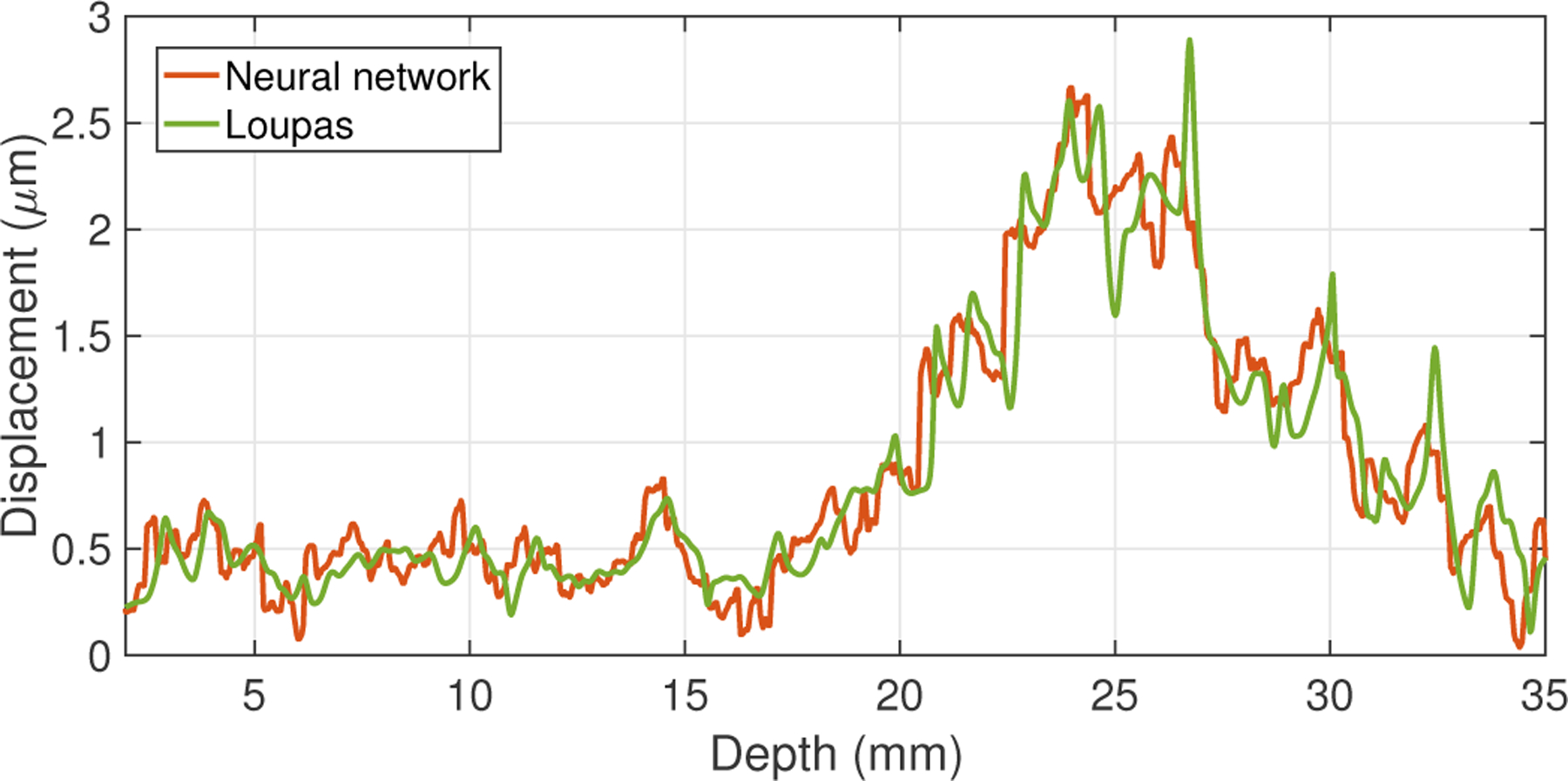
Displacement estimation results from the neural network (orange) and Loupas’s algorithm (green) for experimental data acquired in a phantom. The RMS difference between the outputs from the neural network and Loupas’s algorithm was 0.24 μm.

Figure 6 shows images from the same experimental phantom dataset, where the stiff spherical inclusion is visualized as a circular region of low displacement. The left and middle sub-figures show the output of the neural network and Loupas’s algorithm, respectively; both are shown on the same colorbar scale. Across the entire image, the RMS difference between the two was 0.40 μm. The contrast-to-noise ratio (CNR) of the inclusion was 2.27 for the CNN-estimated image and 2.21 for Loupas-estimated image.

Fig. 6.

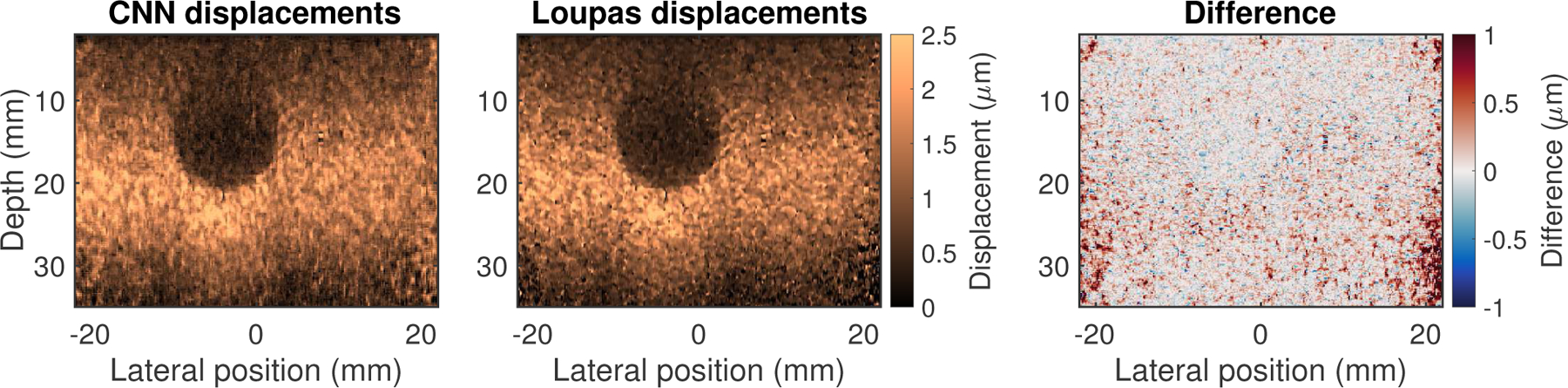
Displacement estimation results for experimental data acquired in a phantom with a stiff 16.3 kPa spherical inclusion in a 10 kPa background. The RMS difference between the CNN- and Loupas-estimated displacements was 0.40 μm. The right sub-figure shows the difference image obtained by subtracting the Loupas-estimated image from the CNN-estimated image. The contrast-to-noise ratio (CNR) of the inclusion was 2.27 for the CNN-estimated image and 2.21 for Loupas-estimated image.

The right sub-figure of Figure 6 shows the difference image obtained by subtracting the Loupas estimates from the neural network estimates. In this difference image color scheme, red pixels indicate that the CNN estimate was greater than the Loupas estimate, while blue pixels indicate the opposite, and gray regions correspond to pixels where the estimates were similar. Note that this difference image indicates increased discrepancies between the CNN- and Loupas-estimated displacements towards the edges of the field of view; in these regions, the CNN tended to slightly overestimate the displacements relative to Loupas’s algorithm.

Figure 7 shows the output of the neural network for the full-size phantom dataset (top row), as well as for an input dataset where the I/Q data has been truncated in depth. This analysis was performed to assess the robustness of the network to inputs with different numbers of depth samples, even though the entire training dataset was generated with 1200 depth samples. Considering the truncated region of the image, the RMS difference between the two ARFI images shown was negligible (<5.07 × 10⁻⁷ μm), likely a result of small rounding errors.

Fig. 7.

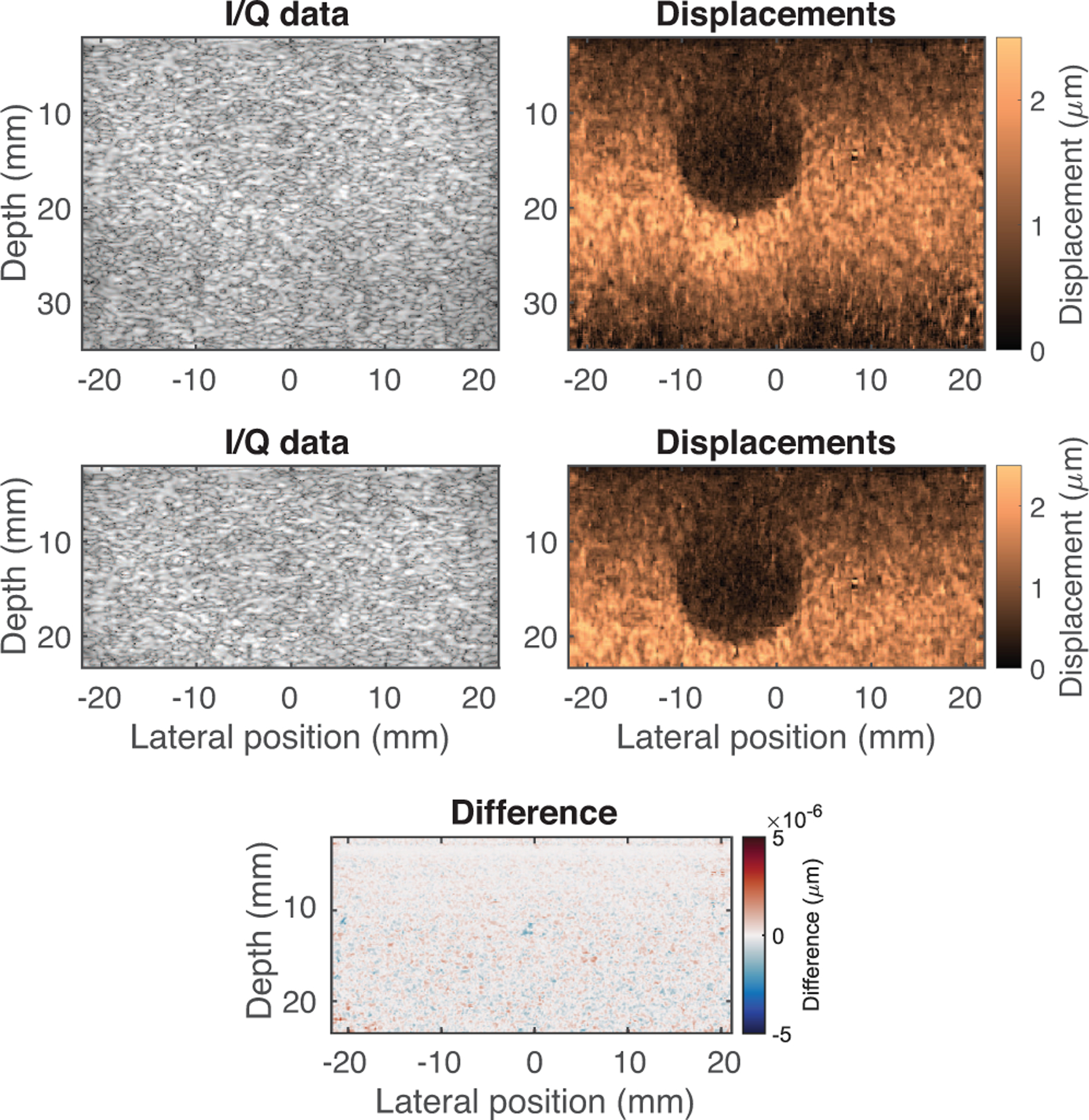
Results of the neural network for full-size phantom dataset (top row) and truncated phantom dataset (bottom row). For the truncated region, the RMS difference between the two displacement outputs was negligible (<5.07 × 10⁻⁷ μm), demonstrating that the data length does not impact performance, supporting the translation of this approach to a variety of datasets.

Figure 8 shows the results of the comparison of the processing time on a 2.3-GHz Intel Core i7 CPU between the CNN and Loupas’s algorithm. The computation time for a single A-line was longer for the CNN (2.40 ms) than Loupas (0.34 ms); however, for an increased number of input A-lines, the CNN was faster (40.11 ms versus 49.25 ms for 200 lines).

Fig. 8.

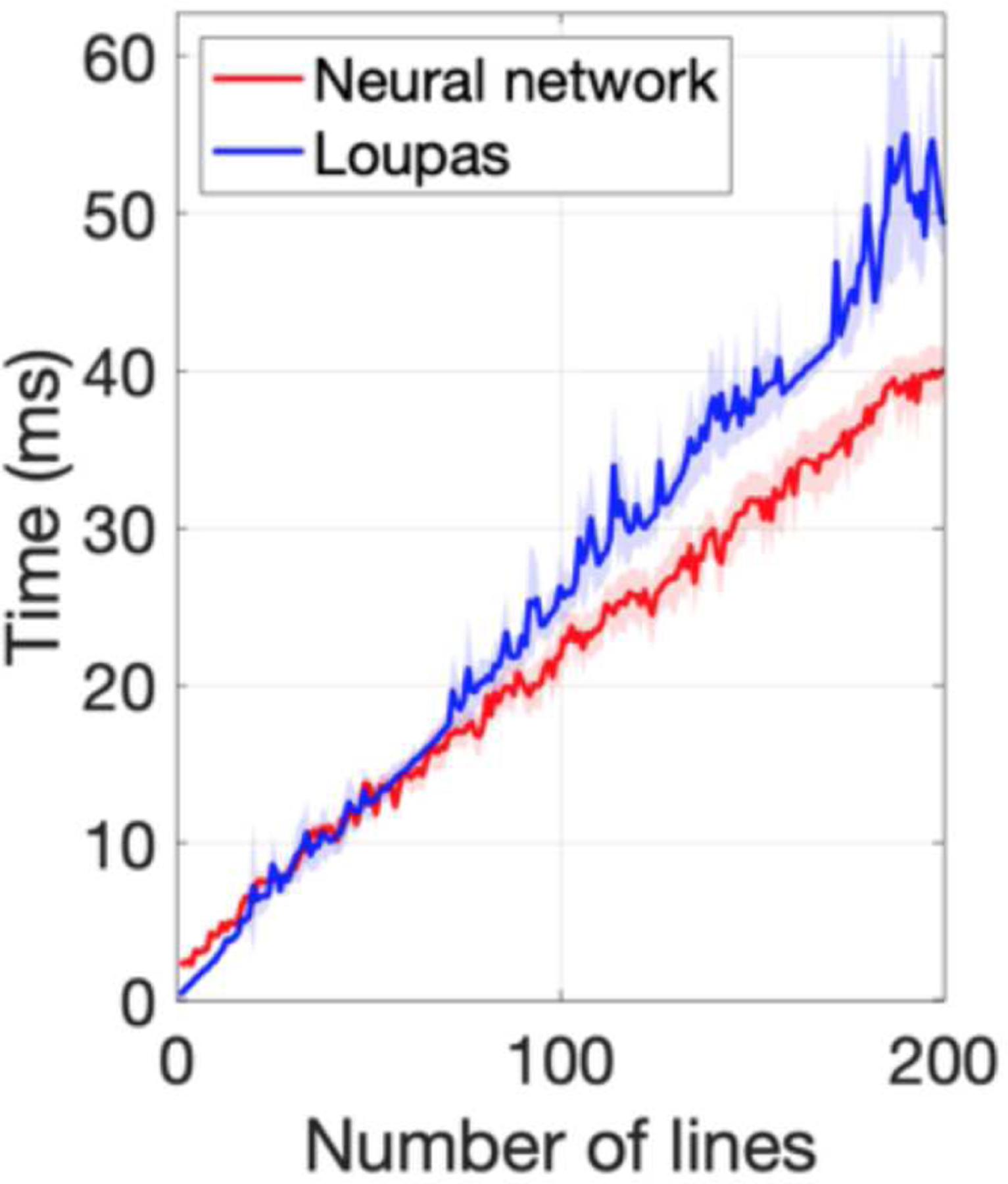
Comparison of processing time between the neural network and Loupas’s algorithm, performed on a 2.3-GHz Intel Core i7 CPU. For a single A-line, the computation time was longer for the neural network (2.40 ms) than Loupas’s algorithm (0.34 ms); however, as the number of lines was increased, the CNN was faster (40.11 ms vs. 49.25 ms for 200 lines).

Figure 9 shows results of applying the trained convolutional neural network displacement estimator to an in vivo human prostate dataset. The image shows scan-converted axial (sub-figures A, B, and C) and coronal (sub-figures D, E, and F) views from the CNN- and Loupas-estimated 3-D ARFI prostate volumes. In each image, the green arrow points to a clinically significant Gleason Grade Group 2 (Gleason Score 3+4) prostate lesion, which appears stiffer than the surrounding noncancerous tissue. In the axial images (sub-figures A and B), the yellow and cyan outlines respectively indicate the cancerous and non-cancerous segmentations used to compute the lesion CNR. The CNR of the lesion was 1.42 for the CNN-estimated image and 1.34 for the Loupas-estimated image. Across the entire prostate volume, the RMS difference between the CNN-estimated displacements and the Loupas-estimated displacements was 0.44 μm.

Fig. 9.

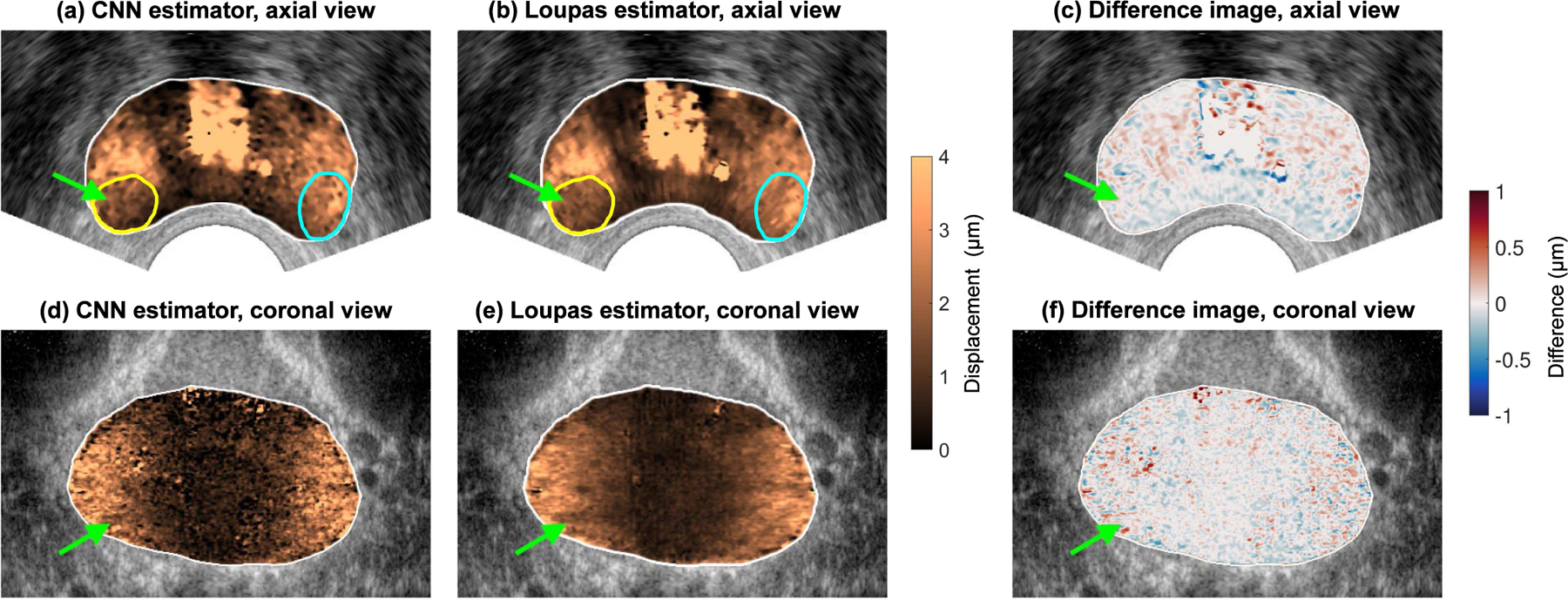
In vivo prostate ARFI images. Sub-figures (A) and (B) show an axial view of the prostate, and sub-figure (C) shows the difference image between the CNN and Loupas estimates. Sub-figures (D) and (E) show a coronal view of the prostate, and sub-figure (F) shows the difference image between the CNN and Loupas estimates. In each image, the green arrow indicates a clinically significant Gleason Grade Group 2 (Gleason Score 3+4) prostate lesion. In the axial images, the yellow and cyan outlines respectively indicate the cancerous and non-cancerous segmentations used to compute contrast-to-noise ratio.

IV. Discussion

In assessing the size of the training dataset that is needed to adequately train a neural network, the learning curves (Fig. 3) provide some insight into when the network is overfitting the training data and when it is actually learning to generalize its algorithm. For example, when the training dataset is relatively small (less than 5000), the training loss (purple points) is very low but the validation loss (orange points) is high. This discrepancy indicates that the network is not actually generalizing to the data, but rather overfitting or “memorizing” the few (5000) training examples that it is presented with, and failing to correctly process the validation examples that it has not seen before the time of testing, resulting in a high mean absolute error.

On the other hand, as the size of the training dataset increases, the training and validation losses become more similar (Fig. 3, right side of plot). The training loss increased, compared to the small training dataset case, since the network is no longer memorizing the training dataset and therefore does not perform as well. However, the validation loss has decreased, corresponding to more accurate displacement estimation for cases that the CNN was not trained on. Ultimately, this is desirable since the trained network will be applied to new data.

Fig. 3 indicates that the entirety of the relatively large training dataset (26,000 training cases) was needed to properly train the neural network and allow it to generalize to the validation dataset (2,000 cases). The method for easily generating training data that was introduced here allowed for the creation of that large training dataset, without having to run computationally-expensive finite element simulations. More importantly, this method enables the generation of a diverse set of training data, since the displacement volumes are randomly seeded; this allows the trained network to be adaptable to a variety of displacement estimation tasks and reduces the potential network bias that would result from a non-random training dataset. In other words, while the displacement volumes in the training dataset may not necessarily resemble a realistic ARFI displacement distribution, this approach allows for the trained network to potentially be used with applications beyond ARFI, including perfusion imaging and super-resolution techniques.

In the learning curve, the training and validation losses appeared to both converge to an asymptote of about 0.42 μm as the size of the training dataset was increased. This asymptote is known as the irreducible error, or the error that is inherent in the observation of the data that cannot be reduced by refining the model architecture. In other words, this irreducible error is the error that fundamentally limits the accuracy of displacement estimation from ultrasound I/Q data.

This can be likened to the Cramér-Rao lower bound that places a theoretical limit on the variance of time-delay estimates in ultrasound imaging, due to factors such as decorrelation noise, thermal noise, and finite sample volumes [27]. Applying the formula for the estimated jitter magnitude given in [27] and assuming a signal-to-noise ratio of 40 dB and a signal correlation of 0.98 (estimated from the training dataset), the expected jitter level for axial time delay estimation would be 0.205 ns, or 0.16 μm when converted to round-trip distance using the speed of sound. This predicted theoretical jitter magnitude is on the same order of magnitude as the irreducible error of the CNN that was observed in this study.

Fig. 4 demonstrated that the neural network could accurately reconstruct the displacement profile for data generated using the synthetic displacement volumes, with comparable performance to Loupas’s algorithm. The finding that larger displacements had a slightly larger estimation bias is consistent with results from previous studies [8]. Here, deviations from the ground-truth displacements are likely due to an averaging effect of the imaging point spread function (”shearing”) [31]. Shearing occurs when an inhomogeneous scatterer displacement field within the ultrasound track beam causes the different displacements to be averaged together, often leading to underestimation of the true displacement. One opportunity for future work to investigate this effect could be to re-train the network using realistic finite-element simulations of ARFI excitations; by generating a training dataset with consistent patterns of radiation force, the neural network may learn to detect and compensate for shearing in the tracked data. This would, however, require running finite-element ARFI simulations and would bias the CNN to only this specific application.

Figs. 5 and 6 demonstrated that the CNN, which was trained exclusively on simulated data, was able to generalize and estimate displacements for experimental data, with comparable results compared to Loupas’s algorithm. The stiff spherical inclusion was clearly visible in the CNN-estimated phantom image. The difference image in Fig. 6 showed some discrepancies towards the edge of the field of view, where the CNN estimates were slightly higher than the Loupas estimates. The likely reason for this is that as the edge of the array was approached, the imaging sub-aperture became smaller due to a lack of elements, resulting in a large lateral PSF in the received data that was distorted compared to the focal configuration used to train the network. This resulted in biases in the outputted displacements in these regions compared to Loupas’s algorithm, which does not involve training on a dataset. Future work will explore whether simulating the aperture size in the generated training data can mitigate these biases.

As previously described, the neural network was designed with a fully convolutional architecture for a more streamlined network with fewer parameters to train and a goal of robustness to input data size. This was validated in Fig. 7, where truncating the I/Q data in depth and re-processing it with the same trained network resulted in an identical output within numerical accuracy. This is a useful feature of the network since the input data shape can easily change in different situations depending on the specific transducer, transmit frequency, interpolation settings, and other parameters. Additionally, the convolutional nature of the displacement estimator readily enables an entire ensemble of tracked ARFI data to be processed simultaneously, regardless of the ensemble length.

One limitation of this study is that the training dataset was generated with a single track configuration (specifically matched to the one used in an ongoing clinical study), and tested only on data acquired with the same sequence. A next step will be to evaluate the robustness of the trained network to changes in a variety of track configuration parameters, including fundamental versus harmonic imaging, track transmit frequency, sampling frequency, and focal configuration (deep focused, plane wave, or diverging wave). Additionally, while a 3×3 convolutional filter size was selected to potentially accommodate a longer track ensemble with multiple time steps, the training and test data used in this study had only two time steps; further analysis is needed to fully explore the advantages of this filter size.

This work used raw ARFI ultrasound data in the in-phase and quadrature (I/Q) format, corresponding to the format of the data outputted by the ultrasound scanner in our clinical prostate imaging study. Recent work by Jin et al. has examined the impact of ultrasonic data format on the performance of deep neural networks for various ultrasound signal processing tasks [43]. They found that for displacement estimation, the baseline performance was similar for I/Q data, radiofrequency (RF) data, and the phase angle of the IQ signal, though RF data were more robust to changes in the frequency of the tracking beam.

The objective of this study was to demonstrate the feasibility of using a deep neural network for ARFI displacement estimation. Figure 8 demonstrated that the model’s computation time, as currently implemented on a CPU, is comparable to the computation time for Loupas’s algorithm. While the neural network requires upfront model training, it may be advantageous for displacement estimation of a larger number of input A-lines. Future work will explore further streamlining and optimization of the neural network, to determine whether deep learning could provide further improvements in computation time and/or estimation accuracy compared to conventional phase-shift algorithms used for displacement estimation.

V. Conlusions

In this study, a fully convolutional neural network was trained to extract micron-level ARFI displacements from ultrasound data with comparable timing to Loupas’s algorithm. In addition, a novel method for generating training data by creating synthetic 3-D displacement volumes used to displace tracked scatterers was described, which facilitated rapid generation of a large number of datasets (30,000). In simulated data, the network accurately reconstructed the ground-truth displacements. The trained network had comparable, but slightly lower, RMS error than Loupas’s algorithm when compared to the ground truth displacements. The CNN generalized to experimentally-acquired phantom data, enabling the visualization of a stiff spherical inclusion contained within an elastic phantom. Application of the network to a truncated ultrasound dataset demonstrated that the CNN is robust to the input data size. Using the neural network in human in vivo prostate data, prostate anatomy and prostate cancer were well-visualized. We conclude that while Loupas’s algorithm may be currently preferable since it does not require model training, deep neural network-based displacement estimation from I/Q ultrasonic data is feasible, providing comparable performance with respect to both accuracy and speed, with potential for further improvements.

Biographies

Derek Y. Chan (S’17) received the B.S.E. and M.S. degrees in biomedical engineering from Duke University, Durham, NC, USA, in 2017 and 2019, respectively. He is currently pursuing the Ph.D. degree in biomedical engineering at Duke University.

He was an Ultrasonics Student Representative to the IEEE Ultrasonics, Ferroelectrics, and Frequency Control Society in 2019 and 2020. His current research interests include prostate elasticity imaging and machine learning in medical ultrasound.

D. Cody Morris (S’16) received two B.S. degrees in biomedical engineering and computer science from the University of Miami, Miami, FL, USA in 2015 and an M.S. degree in biomedical engineering from Duke University, Durham, NC, USA in 2018. He is currently pursuing the Ph.D. degree in biomedical engineering at Duke University.

His current research interests include prostate elasticity imaging and multiparametric ultrasound for prostate cancer detection.

Thomas J. Polascik received the M.D. degree from the University of Chicago Pritzker School of Medicine, Chicago, IL, USA in 1991. He completed his residency training in general surgery and urology, and a fellowship in urologic oncology, at Johns Hopkins Hospital, Baltimore, MD, USA.

He is currently a Professor of Surgery at Duke University Medical Center and the Director of Surgical Technology at the Duke Prostate and Urological Cancer Center. His clinical and research interests focus on prostate and kidney cancer.

Mark L. Palmeri (S’99–M’07) received the B.S. degree in biomedical and electrical engineering and the Ph.D. degree in biomedical engineering from Duke University, Durham, NC, USA, in 2000 and 2005, respectively, and the M.D. degree from the Duke University School of Medicine, Durham, NC, USA, in 2007. He was a James B. Duke graduate fellow.

He is currently a Professor of the Practice in Biomedical Engineering and an Assistant Research Professor of Anesthesiology at Duke University. His research interests include acoustic radiation force shear wave elasticity imaging, ultrasonic imaging, finite element analysis of soft tissue response to acoustic radiation force excitation, medical image processing, deep learning, and medical instrumentation design.

Kathryn R. Nightingale (S’88–M’89–SM’12) received the B.S. degree in electrical engineering and the Ph.D. degree in biomedical engineering from Duke University, Durham, NC, USA, in 1989 and 1997, respectively.

She is currently a member of the NIH’s National Advisory Council for Biomedical Imaging and Bioengineering. She is an Associate Editor for Ultrasonic Imaging and a fellow of the American Institute of Medical and Biological Engineering and the National Academy of Inventors. Her research interests include elasticity imaging, acoustic radiation force based imaging methods, shearwave imaging, finite element modeling of soft tissues, and harmonic/nonlinear imaging methods.