Jones matrix holography with metasurfaces

A new mathematical framework uncovers overlooked possibilities for polarization-dependent metasurfaces.

Abstract

We propose a new class of computer-generated holograms whose far-fields have designer-specified polarization response. We dub these Jones matrix holograms. We provide a simple procedure for their implementation using form-birefringent metasurfaces. Jones matrix holography generalizes a wide body of past work with a consistent mathematical framework, particularly in the field of metasurfaces, and suggests previously unrealized devices, examples of which are demonstrated here. In particular, we demonstrate holograms whose far-fields implement parallel polarization analysis and custom waveplate-like behavior.

INTRODUCTION

In a 1965 paper (1), Adolf Lohmann, a pioneer of the computer-generated hologram (CGH), remarked that while “holography” translates as “total recording” from Greek, “a hologram is not really a total recording, since only one amplitude and one phase are recorded, which would be adequate if light were a scalar wave.” As this suggests, light’s polarization is often omitted in the study of holography and diffractive optics. However, a variety of holographic materials and technologies do permit the control of polarization in a spatially varying fashion. Over the past five or so decades, these have taken on various forms and names, among them polarization holograms (2, 3), polarization gratings (4, 5), stress-engineered optical elements (6), a variety of liquid crystal devices (7), and, more recently, metasurfaces (8, 9). These metasurfaces, subwavelength-spaced arrays of phase-shifting elements that may be strongly form-birefringent, are the specific focus and implementation medium of this work. However, the generalized viewpoint we discuss here has broader applicability.

In the paraxial regime—often an unstated assumption in holography and Fourier optics—a propagator, commonly the Fourier transform ℱ, links the “near-field,” an electric field with a phase and/or amplitude distribution created by the hologram (though not to be confused with the optical near-field owing to evanescent waves), with the “far-field,” a desired phase and/or amplitude (though more commonly, amplitude-only) distribution some distance many wavelengths away. In this work, for clarity’s sake, “hologram” refers to the physical field-modifying object rather than a holographic image in the far-field, which might also be more colloquially referred to as a hologram. Often, a hologram is described by its spatially varying, aperture transmission (or reflection) function t(x, y), a single complex-valued scalar function given by an amplitude and a phase. For normally incident, plane wave–like light, t(x, y) can be used as a stand-in for the field itself (an assumption that, if necessary, is easily relaxed with the convolution theorem). This picture can be generalized to handle polarization by describing the hologram instead by a 2 × 2 Jones matrix transfer function J(x, y) (matrix-valued quantities are denoted by bold lettering here), permitting the analysis of polarization-sensitive holographic media like those above. J(x, y), which describes the polarization response at each point (x, y), contains four complex numbers, in contrast to the single complex number t(x, y).

In a common approach, the response of a metasurface (or other polarization-sensitive holographic element) is considered separately upon illumination with one of two orthogonal “basis” polarization states, which can be elliptical in general. An incident plane wave in one of the basis states, after passing through the metasurface, is designed to create a scalar field that is everywhere uniform in polarization, with a designer-specified overall phase profile. This approach permits the realization of optical elements—gratings, lenses, and, in general, holograms—whose far-field function can switch on the basis of incident polarization [as in (8, 9), to name only a few examples from what is now a vast literature]. However, this switchability is global in nature: One entire far-field response is ascribed to each polarization state in the chosen basis, and the polarization-dependent response cannot vary over the far-field. For all other polarizations, the response is a weighted superposition of the two. In other words, what is inherently a polarization-dependent problem is, in this scheme, reduced to two scalar ones (imparting two scalar phase profiles); accordingly, we dub this the “scalar” approach.

In another now-common approach, the metasurface is designed to produce a distribution of polarization ellipses, described by the Jones vector function ∣j(x, y)⟩, so that the far-field is given by ∣a(k_x, k_y)⟩ = ℱ{∣j(x, y)⟩}, where ℱ now denotes the Fourier transform operator distributed over both elements of the Jones vector (Jones vectors are denoted throughout by kets in the bra-ket notation). In this way, the polarization state of the far-field can be made to vary in a desired fashion (10–16). However, this vectorial approach assumes that the incident light has a particular polarization state. If this changes, so too does the carefully choreographed far-field polarization distribution.

JONES MATRIX HOLOGRAPHY

Concept

Neither the scalar nor vector approaches recognize the most general polarization control enabled by the ability to spatially manipulate light’s polarization (e.g., with a metasurface). In this work, we rely instead on a top-level design of the metasurface, specified without regard for any particular incident polarization state. In particular, the metasurface is described by a spatially varying Jones matrix J(x, y) and a far-field A(k_x, k_y) = ℱ{J(x, y)} where the Fourier transform now distributes over all four elements (four complex-valued functions) of the Jones matrix as

$$\mathit{A}(k_x,k_y)=\left[\begin{array}{cc}\mathcal{F}\{J_{11}(x,y)\}& \mathcal{F}\{J_{12}(x,y)\}\\ \mathcal{F}\{J_{21}(x,y)\}& \mathcal{F}\{J_{22}(x,y)\}\end{array}\right]$$ (1)

If we assume plane wave incidence, A(k_x, k_y)—itself a Jones matrix—gives the polarization-dependent behavior of each plane wave (k_x, k_y) component of the far-field (Fig. 1A). In other words, in this approach, rather than trying to control the far-field’s intensity for some incident polarization or its polarization state, we seek to control its polarization transfer function. For instance, if A(k_x, k_y) corresponds to an x polarizer, light will be directed into the plane wave component with direction (k_x, k_y) in a way that depends on the incident polarization state in accordance with a polarizer—bright if it is∣x〉, dark if it is∣y〉.

Fig. 1. Jones matrix holography.

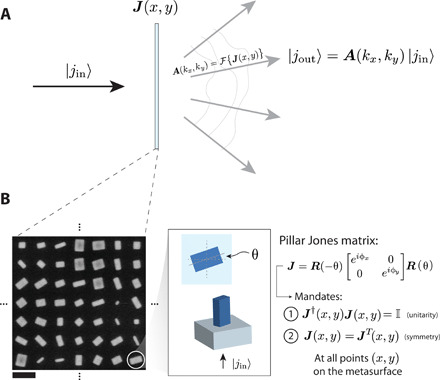
(A) A Jones matrix hologram implements a polarization-dependent mask (J(x, y)) with a far-field, plane wave spectrum polarization response (A(k_x, k_y)) whose behavior can be controlled. The far-field response to an incident polarization state with Jones vector ∣j〉_in can be found by matrix multiplication. (B) These can be implemented with metasurfaces composed of dielectric pillars, whose Jones matrices, as discussed in the text, are subject to certain mathematical constraints. An example SEM (scanning electron micrograph) of a small section of a sample from this work is shown. Scale bar, 500 nm.

This matrix approach encompasses the aforementioned vector and scalar ones as subcases: ∣j(x, y)〉 = J(x, y)∣η〉 is a distribution of polarization states for a chosen incident polarization∣η〉, and ⟨j(x, y)∣κ⟩ is a scalar field for a chosen analysis polarization state∣κ〉. This approach thus provides a simple language in which to frame light’s interaction with polarization-sensitive metasurfaces and classify past works.

Now, if a far-field with a polarization-dependent response described by some A(k_x, k_y) is desired, a Jones matrix hologram implementing it is given by inverse Fourier transform as

$$\mathit{J}(x,y)={\mathcal{F}}^{-1}\{\mathit{A}(k_x,k_y)\}$$ (2)

The J so-obtained (and, for that matter, any Jones matrix) can be decomposed as

$$\mathit{J}=\mathit{HU}$$ (3)

where H is a Hermitian (lossy, polarizer-like) Jones matrix with H^† = H and U is a unitary (lossless, waveplate-like) Jones matrix with ${\mathit{U}}^{†}\mathit{U}=\mathbb{I}$ ($\mathbb{I}$ being the 2 × 2 identity matrix and † being the Hermitian conjugate). This is known as the matrix polar decomposition, derived from the more common singular value decomposition, and is the matrix analog of the scalar polar decomposition of a complex number into amplitude and phase with U playing the role of a phasor and H playing the role of an amplitude (17). In general, the near-field J(x, y) corresponding to a desired far-field A(k_x, k_y) by Eq. 2 will be neither strictly Hermitian nor unitary.

Metasurface implementation

To extend beyond mathematics into the regime of application, however, the Jones matrix function J(x, y) so-obtained must be physically realizable as an optic. In this work, this is accomplished with metasurfaces composed of dielectric pillars. In a now-common implementation, these pillars are everywhere uniform in height (for ease of fabrication), with cross sections having two perpendicular mirror symmetry axes (e.g., rectangles or ellipses). These metasurfaces exhibit form birefringence, implementing a local Jones matrix of the form

$$\mathit{J}(x,y)=\mathit{R}(-\mathrm{\theta })\left[\begin{array}{cc}{e}^{i{\mathrm{\varphi }}_{x\prime }}& 0\\ 0& e^{i{\mathrm{\varphi }}_{y\prime }}\end{array}\right]\mathit{R}(\mathrm{\theta })$$ (4)

where ϕ_x^′ and ϕ_y^′ are phases imparted on light polarized along the symmetry axes of the pillar, controlled by varying the elements’ transverse dimensions, and θ is its angular orientation (8) (Fig. 1B). Equation 4 has just three scalar degrees of freedom, while an arbitrary Jones matrix (with its four complex entries) has eight. A pillar-based dielectric metasurface, then, cannot implement any desired Jones matrix at a given point (x, y). Equation 4 instead describes a Jones matrix subject to two key restrictions, those being (i) unitarity, such that ${\mathit{J}}^{†}\mathit{J}=\mathbb{I}$, and (ii) symmetry, such that J^T = J, where T denotes a matrix transpose. The former is a matrix generalization of the statement for scalar light that certain holographic media are phase-only. The latter is a way of stating that the eigen-polarizations of Eq. 4 must be linear (no chirality).

These two restrictions imposed by this particular metasurface platform themselves impose restrictions on the far-field polarization function A(k_x, k_y) achievable with such a metasurface. Any desired far-field function A_des(k_x, k_y) we ask of the metasurface must first be compatible with these. The first restriction (matrix symmetry) is easily accounted for: J(x, y) will only be symmetric if the far-field behavior specified by A(k_x, k_y) is everywhere a symmetric Jones matrix, too, since the matrix Fourier transform linking the two, being essentially an (infinitesimal, exponential-weighted) summation, preserves matrix symmetry. A metasurface whose local Jones matrix is of the form of Eq. 4, then, may only implement polarization behavior in the far-field described by symmetric Jones matrices; some practical consequences of this rule are elaborated below.

However, in general, even if we limit ourselves to a desired far-field behavior A(k_x, k_y) that is symmetric everywhere, the hologram J(x, y) obtained by Eq. 2 will contain both Hermitian and unitary behavior in general, incompatible with the second restriction imposed by Eq. 4. This issue is less easily addressed. However, progress can be made by recognizing the problem’s simpler, scalar analog: the phase problem.

Jones matrix phase retrieval

The phase problem describes the inverse problem of finding a scalar function that is strictly phase-only, which may, nonetheless, have a Fourier transform (far-field) whose amplitude can be arbitrarily specified (while its phase is allowed to freely vary). This problem is well known in holography, where the Fourier transform is over space, but also appears in time domain problems, for instance, in determining modal phases from autocorrelation in lasers (18).

The phase problem is inherently one of variational calculus, of finding a function ϕ(x, y) such that the functional ℱ{e^{iϕ(x, y)}} is optimum with respect to some merit criterion and given constraints. Rather than resorting to a brute-force gradient optimization (which would be numerically impractical over the scale of a large CGH, where the phase at each grid location becomes a free parameter), a number of “gradient-free” numerical techniques have emerged that are in wide use in diffractive optics to implement arbitrary far-fields with phase-only platforms [see, e.g., (19, 20)]. By far, the best-known among these is iterative phase retrieval (21), most commonly implemented with the well-known Gerchberg-Saxton (GS) algorithm (22). The GS algorithm repeatedly switches between the near- and far-fields by Fourier transform, keeping the near-field phase and neglecting amplitude variations while retaining the far-field phase and replacing its amplitude with the desired CGH pattern. It can be shown that the GS algorithm implements gradient descent on the phase function ϕ(x, y), optimizing deviation from a desired far-field intensity pattern in the least-squares sense, without ever computing a Jacobian (21).

Unitarity is the matrix analog of “phase-only.” Here, we generalize the scalar GS algorithm to operate on matrix quantities using the matrix polar decomposition (for which highly efficient numerical schemes exist) in place of the scalar one. The modified algorithm is shown in Fig. 2. An initial near-field Jones matrix distribution J(x, y) is chosen and Fourier-transformed, yielding A′(k_x, k_y). Its polar decomposition is found everywhere, and its Hermitian (lossy) part is discarded. From the remaining unitary part, an overall phase ϕ is extracted. This is the overall phase of the matrix and can be taken from any element of the Jones matrix (such as the upper left element) so long as this choice is consistently applied. The designer-specified, desired far-field polarization behavior, described by A_des(k_x, k_y), is multiplied by this overall phase distribution ϕ(k_x, k_y). The resultant quantity is inverse Fourier-transformed to yield J′(x, y). After a matrix polar decomposition, the unitary part can be extracted, becoming the new near-field Jones matrix hologram. This cycle continues iteratively until the far-field converges to a distribution of Jones matrices that is, ideally, everywhere proportional to A_des(k_x, k_y) up to an overall phase profile ϕ(k_x, k_y), a free parameter that evolves upon iteration (Fig. 2).

Fig. 2. Jones matrix phase retrieval.

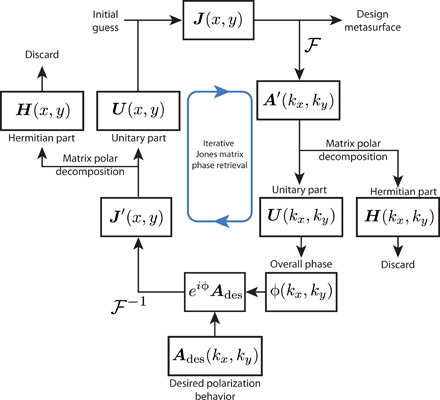
The Gerchberg-Saxton (GS) algorithm can be generalized to allow a unitary Jones matrix mask to implement a far-field whose polarization dependence A_{(kx, ky)} may be arbitrary. Much like the scalar GS algorithm, this matrix generalization uses a division into phase-like (unitary) and amplitude-like (Hermitian) components using the matrix polar decomposition.

The Fourier transform and the matrix polar decomposition both preserve matrix symmetry. That is, if the desired far-field behavior A_des(k_x, k_y) = A^T(k_x, k_y) ∀ (k_x, k_y) [and the initial guess for J(x, y) is as well], no asymmetric matrices are introduced into the iterative scheme of Fig. 2. The resultant J(x, y) will, by definition, be of the form of Eq. 4 so that ϕ_x^′, ϕ_y^′, and θ can be extracted at each point, and a metasurface may be designed and fabricated in a dielectric platform of choice. The metasurfaces of this work are made of TiO₂ pillars for operation at λ = 532 nm using a process documented elsewhere (23); what is described here could apply at any wavelength given a suitable material platform.

In short, the matrix GS algorithm of Fig. 2 permits Jones matrix holograms whose far-fields exhibit designer-specified polarization behavior (so long as they obey the above symmetry constraint) to be straightforwardly realized with conventional, pillar-based dielectric metasurfaces. It is a higher-dimensional generalization of previous GS-like algorithms used for polarization-dependent metasurface design, enabled by the matrix polar decomposition that does not require the incident polarization state to be known a priori.

RESULTS

The preceding discussion has been purely hypothetical. What desired polarization functionality A_des(k_x, k_y) should a metasurface be designed to implement as an experimental proof of concept? By the polar decomposition (Eq. 3), any Jones matrix can be decomposed into a Hermitian (polarizer-like, amplitude-modulating) and a unitary (waveplate-like, phase-modulating) component. This provides a natural categorization of possible experimental test cases. In what follows, we demonstrate Jones matrix holograms whose far-fields implement both polarizer- and waveplate-like behaviors, beginning with the former. The examples that follow are specifically enabled by the Jones matrix approach of this work (see Discussion and Conclusion and section S2 of the Supplementary Materials).

Polarization-analyzing holograms

An ideal polarizer passes its preferred polarization state ∣λ〉 (elliptical in general) without attenuation while extinguishing ∣λ^⊥〉 with 〈λ∣ λ^⊥〉 = 0. If this extinction is imperfect, the device is known as a diattenuator (17). Diattenuators are described by Hermitian Jones matrices.

We seek here to demonstrate Jones matrix holograms whose far-fields implement designer polarizer-like behavior. A conventional polarizer transmits light at its output whose polarization state matches that being analyzed. In other words, a conventional polarizer is of the form

$$\mathit{A}\propto \mid \mathrm{\lambda }\rangle \langle \mathrm{\lambda }\mid$$ (5)

It can be shown that the Jones matrix of Eq. 5 is only symmetric if ∣λ〉 is a linear polarization state. The presence of any chirality in the pass polarization ∣λ〉 destroys the symmetry of the polarizer’s Jones matrix and, consequently, its ability to be implemented in the far-field of a conventional pillar-based metasurface Jones matrix hologram (a rule elaborated above). However, it can also be shown that a Jones matrix A ∝∣λ^*〉〈λ∣, where * denotes complex conjugation, will always be symmetric, irrespective of whether ∣λ〉 is linear, circular, or elliptical. Such a Jones matrix matches a polarizer’s output intensity transfer characteristic but differs in that the polarization of exiting light is always of flipped-handedness relative to that being analyzed. We refer to this as a polarization analyzer, to distinguish from a true polarizer.

In this section, then, we demonstrate devices whose far-fields can be described by the target Jones matrix function

$${\mathit{A}}_{\text{des}}(k_x,k_y)=a(k_x,k_y)\mid {\mathrm{\lambda }}^{*}(k_x,k_y)\rangle \langle \mathrm{\lambda }(k_x,k_y)\mid$$ (6)

Equation 6 describes a far-field where each point receives light as though a virtual polarizer were placed there—the overall amplitude of light directed there a and the incident polarization ∣λ〉 analyzed for can be controlled and may vary arbitrarily from point to point.

Figure 3 makes this capability tangible with a simple example. Using the methods above (i.e., matrix phase retrieval, see Supplementary Materials S1), a dielectric metasurface can be designed and fabricated based on a given design. In this case, the metasurface implements a Jones matrix mask J(x, y) whose far-field contains holographic images of different polarization ellipses (eight linear states of varying orientation and both circular polarization states). The region containing each image acts as a polarization analyzer for its respective, depicted polarization state. For example, the holographic image of ∣x〉 (horizontal arrow) is brightest when the incident polarization ∣j〉_in = ∣x〉 and dark when ∣j〉_in = ∣y〉, as though the pixels contained within the drawing act as an analyzer of ∣x〉 polarized light. The schematic of the far-field shown in Fig. 3A shows all polarization ellipses equally bright for clarity’s sake; this would be the case in reality only if the incident light were perfectly unpolarized, with equal projection onto all polarization states.

Fig. 3. Illustrative example of a polarization-analyzing hologram.

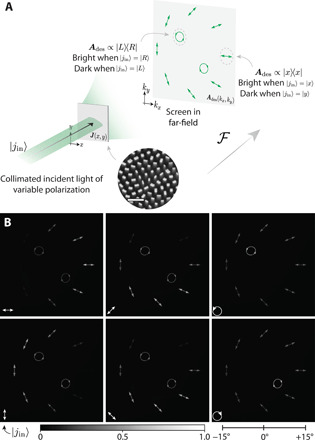
(A) When illuminated with collimated laser light, a suitably designed metasurface hologram implements a far-field in which light is directed on the basis of its incident polarization state. In this particular example, the hologram is designed to produce a pattern of illustrations of different polarization states. Each drawing acts as an “analyzer” for its depicted polarization state. For instance, the drawing of x-polarized light (horizontal line) is bright when ∣j〉_in = ∣x〉 and dark when ∣j〉_in = ∣y〉; this part of the far-field implements the Jones matrix A_des = ∣x〉〈x∣. SEM scale bar, 1 μm. (B) The far-field measured on a digital image sensor reflects this desired behavior for six incident polarization states (∣j〉_in is denoted in white at the lower left of each image). The right scale bar shows the cone angle subtended by the far-field, while a color bar denotes the image intensity.

As shown in Fig. 3A, the fabricated metasurface is illuminated with collimated laser light (λ = 532 nm in this case) of variable polarization. The angular spectrum (far-field) that results is imaged onto a digital image sensor using a relay setup described in the Supplementary Materials (section S1D), filtering out the undiffracted zero order along the way. Images are acquired for many input polarization states (without saturation), permitting a full polarimetric characterization of the grating’s response.

Figure 3B depicts the far-field produced by the metasurface hologram for six incident polarization states, each of which is denoted in the bottom left corner of its image by a white label. As can be seen, each incident polarization state prompts the strongest response in the region of the hologram corresponding to itself. For example, ∣j〉_in = ∣45° 〉 prompts the hologram to direct most power to the drawing of diagonal, linearly polarized light, while the image of antidiagonal polarization is dark with a gradient in between, while drawings of ∣x〉, ∣y〉, ∣R〉, and ∣L〉 are all about half as bright. When each circular polarization is incident, all linear polarizations are about equally bright (and half as bright as the image of the incident circular state). The intensity of each polarization depiction is proportional to the projection of the incident polarization state onto the depicted state in accordance with Malus’ law. In a way, then, the hologram of Fig. 3 is a “visual full-Stokes polarimeter” from which an incident polarization state can be simply read out by inspection (this behavior would generalize to partial polarization states as well).

In Fig. 4, three additional examples showcasing this design freedom are shown. Figure 4A depicts the response of a polarization-analyzing hologram that is, in some sense, a continuous version of Fig. 3. Light is directed into an annular ring with A(k_x, k_y) acting as a linear polarizer that “turns” with azimuthal angle. The brightest and darkest parts of the ring rotate with incident linear polarization, always remaining 180° apart with Malus’ law governing the intensity in between; for incident circular polarization, the ring appears equally bright everywhere, with half the power of the maxima observed under linearly polarized illumination.

Fig. 4. Parallel polarization analysis by a metasurface Jones matrix hologram.

Four examples of Jones matrix holograms (A, B, and C, each described in Results) are shown in which incident light is directed to the far-field in accordance with its projection onto arbitrarily selected analyzer polarizations across the far-field. Each column corresponds to an incident polarization (depicted at the top). Scale bars at the right side of each row show the angular bandwidth of the hologram, with each division corresponding to 15^∘ centered about 0^∘. These holograms are measured with a polarimetric relay imaging system described in the Supplementary Materials (section S1D). Larger-form versions of the images—and animations of their response with changing polarization—are also provided in the Supplementary Materials (movies S1 to S3). The color map of this figure is identical to that of Fig. 3.

Figure 4B, on the other hand, is a more sophisticated version of the hologram of Fig. 3, depicting a polar projection of the northern and southern hemispheres of the Poincaré sphere. Each drawing of a polarization ellipse again acts as an analyzer for its own state. Unlike the example in Fig. 3, Fig. 4B shows that this approach extends to arbitrary, in-general elliptical polarization states and, moreover, permits features (in particular, the grid lines) that are not sensitive to polarization at all (that is, ${\mathit{A}}_{\text{des}}\propto \mathbb{I}$ there) to be mixed with those that are. Supplementary movies S1 to S3 show animations of the response of this hologram to variable linear polarization states, light from a polarizer/rotating quarter-waveplate combination, and partially polarized light, respectively (described in their captions and section S3C).

Last, the example of Fig. 4C reprises the holographic images from (9) showing that this Jones matrix control can be extended to CGHs with rich features. Here, different parts of the image act as polarization analyzers for linear polarization states. The azimuth of these linear polarization states changes smoothly in the vertical direction from ∣y〉 at the bottom, to ∣45^∘〉, ∣x〉 in the middle, to ∣135^∘〉, and finally ∣y〉 again at the top. Consequently, the image is uniformly bright (subject to the underlying holographic image) under circularly polarized illumination.

In each example in Fig. 4 (and Fig. 3), a scale bar denotes the extent of the image in angle space with each division denoting 15^∘ of cone angle (a length scale is not appropriate, as the hologram expands and contracts depending on the screen’s placement). The maximum angular bandwidth over which holographic control can be exerted is dictated by the interelement separation of the metasurface’s phase shifters (see Supplementary Materials S1). The intensity color map defined in Fig. 3 applies throughout this work. The images in Figs. 3 and 4 are difficult to decipher clearly in this small format (especially Fig. 4B); larger-form images are provided in the Supplementary Materials and in the Supplemental Movies. An infinity of other similar examples are possible subject to energy conservation through a modified form of Parseval’s identity (section S1).

Waveplate-like holograms

The examples of the previous section involve a redirection of light depending on its polarization state. A given location in the far-field of these polarization-analyzing holograms receives or does not receive incident light depending on its polarization state, akin to the behavior of a polarizer.

This differs fundamentally from waveplate-like behavior in which output polarization state, rather than intensity, varies with changing input polarization. Waveplates—phase retarders—in contrast, are represented by unitary operators that represent a dephasing of the components of the incident polarization projected onto an orthogonal basis of polarization states (with a possible overall phase shift).

In this section, we demonstrate a Jones matrix hologram whose far-field implements operators of the form

$${\mathit{A}}_{\text{des}}(k_x,k_y)=e^{i\frac{\mathrm{\Delta }}{2}}\mid \mathrm{\lambda }\rangle \langle \mathrm{\lambda }\mid +e^{-i\frac{\mathrm{\Delta }}{2}}\mid {\mathrm{\lambda }}^{\perp }\rangle \langle {\mathrm{\lambda }}^{\perp }\mid$$ (7)

where Δ is a retardance angle, while ∣λ〉 and ∣λ^⊥〉 are the eigen-polarizations of the waveplate representing its “fast axis.” Equation 7 projects incoming light into the eigen-basis and retards the two components by the angle Δ before reconstructing the output. The retardance Δ and orthogonal eigen-polarization basis defined by ∣λ〉 can vary across the far-field (along with an overall, polarization-independent amplitude). Equation 7 will always represent a symmetric Jones matrix and can be implemented in the far-field of a dielectric metasurface, if the eigen-polarizations ∣λ〉 and ∣λ^⊥〉 represent strictly linear polarization states, as is the case with a conventional birefringent waveplate (as opposed to a crystal possessing, e.g., optical activity).

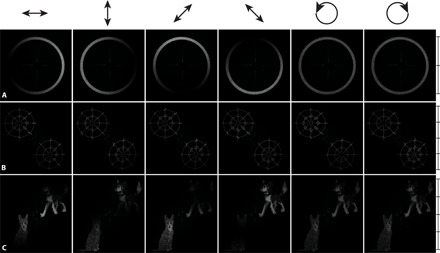
This capability is demonstrated in Fig. 5. A metasurface is designed to diffract light into a disk in the far-field of uniform intensity. As sketched in Fig. 5A, each point in the disk is designed to implement a different waveplate operation (cf. Eq. 7) whose retardance Δ varies from 0 to π along the radial direction and whose fast-axis direction ∣λ〉 corresponds to the azimuthal coordinate. For example, the outer edge of the disk is an isoline of all retarders with Δ = π, i.e., the set of all half-wave (λ/2) plates with all possible orientations. The circle halfway between the origin and the edge, denoted by a red dotted line in Fig. 5A, is similarly the set of all quarter-wave (λ/4) plates with Δ = π/2. All other linearly birefringent waveplates are present, too. The blue dot in Fig. 5A, for example, denotes a 3λ/8 plate whose fast axis is oriented at 90^∘. In other words, the disk, through a proper parameterization of Eq. 7, contains all linearly birefringent waveplates, at all possible angular orientations, within its extents.

Fig. 5. Hologram with a far-field exhibiting waveplate-like behavior.

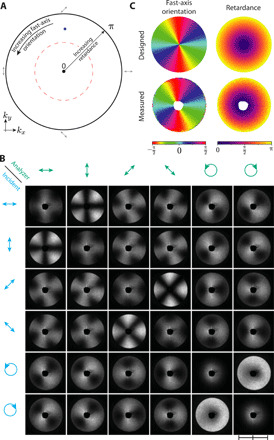
(A) A metasurface is designed whose far-field diffracts light into a circular disk. Each point in this disk is designed to implement a Jones matrix A_des that acts as a birefringent waveplate. The retardance Δ of this virtual waveplate increases from 0 to π along the radial coordinate, while its fast-axis orientation matches the azimuthal coordinate (as denoted by arrows outside the circle). Within this disk, all possible linearly birefringent waveplates can be found. For example, the perimeter of the disk represents all possible half-waveplate operations, while the red dotted circle in the center represents the set of all possible quarter-waveplates. A blue dot denotes a 3λ/8 plate oriented at 90^∘ as a specific example. (B) The metasurface is illuminated with light of variable input polarization (rows) and its far-field viewed through several polarization analyzers (columns), producing a diverse array of patterns. An angular scale bar denotes the cone angle subtended by the far-field with 15^∘ divisions. The center of each image is black because the zero order has been filtered away. The color map is identical to that of Fig. 3. (C) Illuminating the metasurface with different input polarization states and imaging its far-field through different polarization analyzers permit reconstruction of the retardance and fast-axis orientation at each point. These closely match design.

In contrast to the polarization-analyzing holograms of the previous section, the far-field produced by this waveplate-like hologram does not appear to vary (in an intensity sense) when ∣j〉_in changes. However, the changes are revealed when the disk is viewed through a polarization analyzer, which is also allowed to vary. Figure 5B shows the patterns produced for six different incident polarization states (again, the cardinal polarization states, ∣x〉, ∣y〉, ∣45^∘〉, ∣135^∘〉, ∣R〉, and ∣L〉) viewed through six polarization analyzers (a turning linear polarizer paired with a λ/4 plate, for the circular columns). The diverse array of patterns in Fig. 5B make intuitive sense when the incident polarization is “propagated through” the desired behavior of the far-field as described in Fig. 5A. For instance, consider the far-field image produced when ∣45^∘〉 is incident on the metasurface viewed through an ∣R〉 analyzer (second column from right). When diagonally polarized light passes through a quarter-waveplate oriented at 0^∘, one circular polarization state is produced; if the quarter-waveplate is oriented at 45^∘, the opposite handedness results. This explains the successive maxima and minima of the images along the quarter-waveplate circle at half the disk’s radius, 90^∘ apart. Theoretical versions of these images, derived from the design, are also given in the Supplementary Materials for comparison (section S3).

Each image in Fig. 5B could be similarly intuited. There is, however, a simpler and more direct way of verifying that the far-field behaves in accordance with design. By illuminating the metasurface with a number of different polarization states and viewing these through a number of different polarization analyzers, the 4 × 4 Mueller matrix describing each point in the far-field can be derived. This Mueller matrix maps the Stokes vector of the polarization state incident on the metasurface to the measured polarization state (Stokes vector) at each location in the far-field. The Lu-Chipman decomposition (24) can be applied to each Mueller matrix so that the measured retardance and the fast-axis orientation exhibited by each point in the far-field can be compared to design. This is shown in Fig. 5C. As designed, the retardance exhibited by the “waveplates” within the far-field disk increases from 0 to π at its edge. The orientation rotates smoothly from 0 to π/2 and back again twice around the circle (due to the twofold angle degeneracy of polarization states; an azimuthal orientation of 3π/2 is the same as π/2). In the images acquired of the disk, the center is missing due to undiffracted zero-order light being filtered out in the experimental setup by a physical block. Further details on this measurement and analysis are provided in the Supplementary Materials (section S1D).

DISCUSSION AND CONCLUSION

Dielectric metasurfaces exhibiting form birefringence and, for that matter, a number of other technologies enabling spatially varying control of optical polarization already constitute an active area of research with an established literature and are not in themselves a novel contribution of this work. Here, we have instead focused on a way of viewing these optical elements. A description at the level of the Jones calculus permits the polarization operations enacted by individual elements to be mapped to the polarization transfer function of the far-field.

The idea of merging Fourier optics and the Jones calculus in this way does have some precedent [such as (25), and in the analysis of polarization aberrations of optical systems (17)]. However, to our knowledge, it has not been widely applied as a tool for the design of polarization-sensitive diffractive elements [with one notable exception, in which some of us (26) used similar methods based on a brute-force optimization to design polarization-sensitive diffraction gratings rather than holograms]. The methods of this work provide a unified mathematical framework that generalizes past work in this area and suggests new possibilities.

For instance, past works have extensively discussed “polarization switchable” metasurfaces, that is, metasurfaces that exhibit separate responses or act as an independent optical element depending on the polarization state of illuminating light. In this way, metasurfaces have been shown to enable, e.g., lenses that focus in separate locations for x and y polarized light (8), holograms with independent far-fields for incident circular polarization of opposite handedness (9), and gratings directing light to either the +1 or −1 order depending on which of two orthogonal polarizations is incident. In these works, the polarization basis to which the metasurface is sensitive is fixed across the far-field. The response to a general incident polarization is governed by its projection onto these two chosen basis states.

This work (and, in particular, the polarization-analyzing holograms of section S3 of the Supplementary Materials) shows that this “switchability” need not be limited to just two polarization states. Rather than ascribing two global responses to one orthogonal polarization basis, the polarization basis can itself change over the extent of the far-field, as in the holograms of Figs. 3 and 4. The “polarization-analyzing” behavior exhibited there, as described through the Jones matrix formalism, is a generalization of the “polarization switchability” of previous works, one which would not have been possible with previous design strategies. Rather than being limited to just two discrete polarization states, the far-field can “switch” on the basis of N in general. This is described in more detail in the Supplementary Materials (section S2). This is achieved without interlacing multiple separately designed metasurfaces together (often dubbed “spatial multiplexing”), a now-common strategy (14–16, 27).

Moreover, the ability to enact customizable unitary waveplate-like transformations in the far-field is a possibility overlooked by these previous works. Several previous works enable control of the polarization state of the far-field, e.g., on a set of diffraction orders (11) or over whole holographic images (10, 12), but only for a given incident polarization state. This work instead suggests that far-field polarization transformation, rather than just polarization state, may be controlled.

In this work, we have introduced Jones matrix holography, in which a polarization-sensitive mask generates a far-field with customizable polarization response. A treatment based on the Jones calculus enables the design and analysis of these holograms without specification of the incident polarization state. Consequently, this generalizes a wide body of past work in polarization-sensitive diffractive optics and metasurfaces. Moreover, the formalism provides a clear link between recent research in this area and extensive work in (scalar) holography of decades past. We have additionally shown how the traditional GS phase retrieval algorithm may be extended to matrix quantities.

Several possible future directions could broaden this work. For example, the requirement that strictly unitary and symmetric Jones matrix behavior be realized by the far-field could be relaxed with more advanced nanophotonic structures. Metasurfaces composed of, for instance, two cascaded layers of dielectric pillars would strongly break mirror symmetry along the z direction, allowing for chiral behavior and thus eliminating the restriction of Jones matrix symmetry. Moreover, lossy structures incorporating, e.g., metals, can implement Hermitian behavior that, when paired with other structures, would afford the designer more freedom to create fully general J(x, y) with mixed Hermitian and unitary responses, perhaps without the use of iterative phase retrieval.

This work may find application in a variety of areas. A Jones matrix hologram could add custom polarization dependence to an optical system’s point spread function, either to address systematic polarization aberrations (17) in precision imaging systems or to enable wholly new functionality. Elements based on spatially varying liquid crystals are already used in astrophysical measurements for, e.g., exoplanet detection (28); the present work and the expanded control it offers may suggest new possibilities there. Active photonic platforms provide a second promising application area. Light distribution in the holograms of this work is governed by linearity and Malus’ law. Gain-associated nonlinearities in, e.g., a laser cavity could potentially surmount this. This could enable polarization-controlled beamsteering if a far-field pattern such as the annular ring of Fig. 4A is used. Last, this work bears qualitative similarity to research surrounding structured light and optical orbital angular momentum (e.g., the images of Fig. 5B), an area where it may find additional interest.

MATERIALS AND METHODS

Hologram design

A desired far-field Jones matrix distribution A_des(k_x, k_y) (everywhere symmetric with A^T = A) is passed through the matrix-valued phase retrieval algorithm described above and in the Supplementary Materials. This gives a Jones matrix profile J(x, y) defined on a lattice, which can be implemented with a single-layer dielectric metasurface since it is everywhere symmetric and unitary. J(x, y) can be converted to the form of Eq. 4, allowing the parameters ϕ_x, ϕ_y, and θ to be extracted at each point. Referring to a library of structures of varying sizes simulated at the design wavelength, a structure is chosen at each point that best implements ϕ_x and ϕ_y, allowing for a complete design of the metasurface. This process is described in detail in section S1 of the Supplementary Materials (A to C).

Device fabrication

The metasurface holograms of this work consist of TiO₂ pillars on a fused silica substrate. TiO₂ exhibits high refractive index contrast with air (n ∼ 2.3) and low loss across the visible spectrum, enabling flexible shape-birefringent phase control at this work’s design wavelength (λ = 532 nm). The TiO₂ pillars are fabricated and patterned by a combination of electron beam lithography, atomic layer deposition, and reactive ion etching. Process parameters and details are identical to the description provided in (23). We emphasize that while TiO₂ here serves as a convenient implementation medium for demonstration purposes, its use is not fundamental to the work’s conclusions. Jones matrix holograms could be realized at other wavelengths by metasurfaces composed of a suitable high-index, low-loss dielectric [such as, e.g., amorphous silicon for near-IR wavelengths (8) or hafnium dioxide for the near- and middle-ultraviolet (29)] or by a nonmetasurface device exhibiting polarization control (some of which are mentioned in Introduction).

Experimental characterization

Each hologram is illuminated by laser light at λ = 532 nm whose polarization state can be varied. The hologram’s far-field is imaged onto a CMOS sensor using an afocal relay setup, allowing undiffracted zero order to be blocked. As the input polarization is varied, the far-field intensity response of the hologram is recorded on the sensor. The input polarization states are known, having been premeasured with a commercial polarimeter. This permits determination of the polarization state to which each part of the hologram’s far-field is sensitive (Stokes polarimetry). For the waveplate-like hologram, light also passes through a variable polarization analyzer (composed of a quarter-waveplate and polarizer) before the sensor, allowing for measurement of the far-field’s polarization transfer characteristic (Mueller polarimetry). This is described in detail in section S1 of the Supplementary Materials (D and E).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/33/eabg7488/DC1