Abstract
As suggested by many guidelines, a high ventilation rate is required to dilute the indoor virus particles and reduce the airborne transmission risk, i.e., dilution ventilation (DV). However, high ventilation rates may result in high energy costs. Ventilative cooling (VC), which requires high ventilation rates like DV, is an option to reduce the cooling energy consumption. By combining DV and VC, this paper investigated the operation of the mechanical ventilation system in high-rise buildings during the COVID-19 pandemic, aiming to minimizing the cooling related energy consumption and reducing COVID-19 transmission. First, a modified Wells-Riley model was proposed to calculate DV rates. The ventilation rate required to achieve VC was also introduced. Then, a new ventilation control strategy was proposed for achieving DV and VC. Finally, a case study was conducted on a real high-rise building, where the required DV rate and the impact of the settings of the mechanical ventilation on the energy savings were evaluated. The results indicate that the required ventilation rates vary from 36 m3/s to 3306 m3/s depending on the protective measures. When the occupants follow the protective measures, the proper settings of the mechanical ventilation system can reduce energy consumption by around 40%.
Keywords: COVID-19, infection probability, ventilative cooling, energy savings, mechanical ventilation
Nomenclature
air change rate, ACH
- B
initial infection rate
concentration of CO2 at step n, PPM
specific heat of air, kJ/(kg•K)
- COP
coefficient of performance
number of new infection cases
- d
social distance, m
- and
correlation coefficients for cooling tower fans
mask index
fraction of people with immunity
- and
fraction of infectors and susceptible individuals who wear masks
CO2 generation rate per person, L/s
number of initial infectors
- N
number of occupants/components
- P
electric power, kW
social distance index
probability of infection
pulmonary ventilation rate of susceptible individuals, m3/h
volume flow rate, m3/s
- q
quantum generation rate, /h
cooling load, kW
- R
ratio of actual rotation speed to nominal rotation speed
basic reproductive number
number of susceptible individuals
- SFP
specific fan power, kW/m3/s
- T
temperature, ºC
exposure time, h
- V
space volume, m3
- Z
status of chillers operation
Greek symbols
density, kg/m3
difference
correlation coefficients for i th chiller COP
correlation coefficients for condenser inlet water temperature
correlation coefficients for water flow rate in i th pump
- and
exhalation filtration efficiency and inhalation filtration efficiency
Subscripts
- ch
chiller system
- ci
condenser inlet water
- CL
building cooling load
- CT
cooling tower
- DV
dilution ventilation
- F
fans
- ia
indoor air
- IAQ
indoor air quality
- max
maximum value
- min
minimum value
- nom
nominal
- oa
outdoor air
- P
pumps
- VC
ventilative cooling
- w
water
- wb
wet-bulb
1. Introduction
COVID-19 is a disease caused by a new coronavirus called SARS-CoV-2. From the first report of this new virus on December 31, 2019 to March 2021, more than 115 million cases of COVID-19 have been confirmed, including 2 million confirmed deaths worldwide (World Health Organization, 2021). At present, this disease still significantly impacts every aspect of human life. For example, because of the potential high risk of infection, the COVID-19 pandemic has forced the shutdown of many high-rise buildings in cities, which have a high occupancy density. As suggested by the WHO, maintaining social distancing, wearing masks, limiting the time in a crowded space are the necessary protective measures to be followed in a public area (World Health Organization, 2021). The reasons for implementing these protective measures are the transmission routes of SARS-CoV-2, which mainly transmits through direct contact and inhaling airborne respiratory droplets (airborne transmissions) (REHVA, 2020).
One of the important measures for mitigating the risks of COVID-19 airborne transmission is building ventilation. Many countries have published HVAC operating guidelines for reducing COVID-19 transmission risks. Guo et al. (Guo et al., 2021) reviewed and compared different HVAC operation guidelines during the COVID-19 pandemic. The typical guidelines are summarized in Table 1 (Canadian Committee on Indoor Air Quality, 2020; National Health Commission of the People's Republic of China, 2020; REHVA, 2020; Schoen, 2020; WHO, 2020). In summary, all the guidelines recommended increasing the outdoor air flow rate and operating the ventilation beyond building occupancy time. Ventilation is an important mechanism for the removal of the airborne virus. The airborne virus can persist longer when the air change rate (ACH) is low (Yang & Marr, 2011). Also, ventilation during the unoccupied time can help to remove the virus particles from surfaces (REHVA, 2020). A dilution ventilation (DV) system refers to the ventilation system that aims to dilute the contaminants concentration, which can reduce the contaminants concentration below a threshold limit value (Talty, 1998). For mitigating the risks of COVID-19 airborne transmission, DV systems are required. Li et al., (2021) conducted measurements using tracer gas techniques to identify the routes of COVID-19 airborne transmission and investigate the relationship between the infection risk and ventilation rate. It was concluded that poor ventilation is one of the major factors for the COVID-19 outbreaks. Wang et al., (2021) proposed an occupant-density-detection ventilation system, aiming to reduce the infection risks of airborne disease and energy consumption of fans which will increase the ventilation rate when the number of occupants exceeds the threshold. It was reported that the new ventilation system can reduce the infection risk to 2% whereas the infection risk under a traditional ventilation system aiming to fulfill the indoor air quality (IAQ) reaches 8%.
Table 1.
Typical building ventilation system guidelines in different countries to reduce the risk of COVID-19 transmission.
| Region & institution | Typical building ventilation system guidelines |
|---|---|
| Canada Canadian Committee on Indoor Air Quality (Aug. 2020 version) (Canadian Committee on Indoor Air Quality, 2020) |
|
| USA ASHRAE/CDC (May. 2020 version) (Schoen, 2020) |
|
| European REHVA (Nov. 2020 version) (REHVA, 2020) |
|
| China National Health Commission of the People's Republic of China (Jul. 2020 version) (National Health Commission of the People's Republic of China, 2020) |
For all-air air conditioning system:
|
| WHO (Mar. 2021 version) (WHO, 2020) |
For non-residential spaces:
|
However, in practice, the ventilation system is determined by the IAQ requirement, e.g., the ASHRAE standard 62.1 (ASHRAE, 2010). Although the ventilation system can be operated at the maximum fresh air flow rate all the time, it cannot ensure that its maximum fresh air flow rate is enough to reduce the probability of COVID-19 infection. For example, the previous WHO guideline (Atkinson et al., 2009) recommended that the minimum ventilation rate in the mechanical isolation rooms should be higher than 12 ACH to reduce the probability of infection, which is much higher than the ventilation rate for maintaining IAQ.
Some studies have evaluated the effects of ventilation rates on the reduction of COVID-19 infection risk with the Wells-Riley (WR) model (Dai & Zhao, 2020; Katal, Albettar, & Wang, 2021; Li et al., 2020; S. L. Miller et al., 2020; REHVA, 2020; Sun & Zhai, 2020); an equation widely used to associate ventilation rates and infection risk. For example, Dai and Zhao (2020) evaluated the infection risks with different ventilation rates in confined spaces, such as buses, classrooms, aircraft cabins, and offices. It was found that the required ventilation rate for ensuring an infection probability of less than 1% varies from 0.6 to 18 ACH, when there is one infector, and all occupants wear masks. This large range of ACH is caused by different scenarios. In the classroom, students may only stay at the classroom for two hours, and the quantum generation rate can be at a very low level, e.g., 14 h-1. Thus, the required ventilation rate is as low as 0.6 ACH. However, the required ventilation rate reaches 18 ACH for an office room, if the employees have eight hours exposure time and a relatively high quantum generation rate of 48 h-1. It was pointed out that the designed ventilation rate (required minimum fresh air rate for IAQ) in office buildings cannot ensure a low level of infection risks. Sun and Zhai (2020) modified the WR model by considering the social distance, and then evaluated the minimum ventilation rate requirement for the typical confined spaces, e.g. classrooms, restaurants, offices, etc. As with the Dai and Zhao study, the results indicated that the designed ventilation rates (required minimum fresh air rate for IAQ) for the typical confined spaces cannot ensure a low infection probability under a designed number of occupants.
Furthermore, the higher ventilation rates required by the guidelines result in higher cooling related and ventilation energy consumption. Other than for hospital or industrial designs, non-residential buildings usually need to balance the ventilation control strategy between the prevention of COVID-19 and an economical solution (REHVA, 2020). Agarwal et al., (2021) compared different techniques for improving air quality. It is concluded that the main disadvantage of ventilation is energy-consuming compared with using face masks, lockdown, social distancing. Many studies aim to limit the ventilation rate and reduce ventilation energy consumption. Ren et al., (2021) evaluated the physical barriers to mitigate the risk of airborne transmission of COVID-19 under a standardized ventilation rate (i.e., minimum ventilation rate for IAQ). Kong et al., (2021) examined the four different ventilation forms (the combination of top supply and exhaust, side supply and exhaust). The results show that when the ventilation rate is 10 ACH, the diffusers should be located on the sidewall for healthcare workers, which have the minimum cumulative exposure level. Wang et al., (2021) proposed an occupant-detection ventilation control strategy, aiming to reduce the infection risks of airborne disease and energy consumption of fans. Compared with the traditional ventilation control strategy that uses a fixed fresh air supply rate, this new ventilation control strategy can achieve 12% energy savings. However, actually, higher ventilation rates may be helpful for ventilative cooling (VC) during the summer and shoulder seasons, especially for cold climates (Qi, Cheng, Katal, Wang, & Athienitis, 2019; Sha, Moujahed, & Qi, 2021; Sha & Qi, 2020a).
VC refers to introducing fresh outdoor air to remove excessive indoor heat and reduce cooling energy consumption (IEA-EBC, 2018). VC is an attractive technology to decrease the cooling energy consumption and improve building resilience (Attia et al., 2021; C. Zhang et al., 2021), which mitigates the hazard caused by the extreme events, e.g., heat wave (W. Miller et al., 2021). However, for achieving mechanical VC, there are requirements on the energy efficiency of fans and the ventilation rate. Kolokotroni and Aronis (1999) reported that the use of mechanical VC could lead to increased energy consumption because the reduction of cooling energy consumption did not offset the increase of fan energy consumption. The previous studies have shown that a proper mechanical ventilation system can achieve large cooling-related energy savings for VC when there is a sufficient fresh air flow rate (Bakhtiari, Akander, Cehlin, & Hayati, 2020; Sha & Qi, 2020b; Z. Wang, Yi, & Gao, 2009; Y. Zhang, Wang, & Hu, 2018). Zhang et al., (2018) proposed an optimal control strategy and investigate the required ventilation rate for mechanical VC through a theoretical model. The results show that using mechanical VC, the sum of cooling and ventilation energy consumption can reduce by about 47%. The required ventilation rates vary according to the outdoor conditions, and the highest required ventilation rates reach 16 ACH, which is much higher than the 0.5 ACH required by the design standard. Wang et al., (2009) investigated the mechanical VC based on a medium-rise building using EnergyPlus simulation. It was found that with the ventilation rate of 10 ACH, the sum of cooling and ventilation energy consumption reduces 10 MWh for the three months of the cooling seasons. Sha and Qi (2020b) proposed a control strategy for VC and investigated its energy savings under different settings. The results indicated that a proper mechanical ventilation setting can result in 43% energy savings in the measured period. In this proper setting, the fan flow rate should be six times higher than the fan flow rate designed for IAQ. Bakhtiari et al. (2020) found that a fan flow rate three times higher than the designed fan flow rate could achieve up to 40% cooling related energy savings due to VC. Due to the high building cooling load caused by the high internal heat gain and the use of a large glazing façade, high-rise buildings can greatly benefit from VC to reduce cooling energy consumption (Sha & Qi, 2020a). Therefore, the proper mechanical ventilation setting for VC combined with the concept of DV should be studied to achieve low COVID-19 infection probability and reduce cooling related energy consumption, and electricity demand (energy consumption) for fans in high-rise buildings.
To fill in the research gaps presented above, this study aims to determine the DV rate to reduce COVID-19 infection risk in real high-rise buildings, and to obtain a proper design and control strategy of mechanical ventilation for achieving VC and low COVID-19 infection probability. First, a modified WR model is proposed to determine the DV (Section 2.1). Then the energy models of cooling systems are introduced (Section 2.2). A new control strategy for the mechanical ventilation system is developed, which combines DV and VC (Section 2.3). Finally, a case study is conducted in a real 16-storey high-rise building in Montreal to illustrate the COVID-19 infection risk of the ventilation system and energy performance of the proposed new control strategy under different mechanical ventilation setting conditions. The DV rates required under the different protective measure conditions, e.g., wearing masks, maintaining social distancing, and limiting the time in buildings, are presented (Section 3.1). Then, energy simulations are conducted to obtain a proper design and control of mechanical ventilation (Section 3.2).
Compared with former studies, this study has two distinguishes. First, this study proposes a new ventilation control strategy that prevents COVID-19 airborne transmission and achieves ventilative cooling based on the real-time demand. Previous studies investigated the ventilation rate to prevent the airborne transmission of COVID-19 (Dai & Zhao, 2020; Hou, Katal, Wang, Katal1, & Wang, 2021; Sun & Zhai, 2020), which only utilized the WR models to determine the ventilation rates that reduce the airborne transmission risk of COVID-19 to a target value. The most recent studies focused on the demand control ventilation for preventing airborne transmission, i.e., demand control for dilution ventilation, which aim to reduce the energy consumption of fans (J. Wang et al., 2021). However, few previous studies focus on dilution ventilation and ventilative cooling in mechanical ventilation control simultaneously. Second, this study proposes a method to obtain an optimal ventilation rate that prevents COVID-19 airborne transmission and reaches the maximum cooling-related energy savings.
2. Methodology
2.1. Ventilation rates required to reduce the risk of COVID-19 transmission
In this section, a modified WR model was developed to present the relationship between ventilation rates and the infection risk of COVID-19. Different from the previous WR models to evaluate infection risks (Riley, C.E., Murphy, G. and Riley, 1978; Sze To & Chao, 2010), the modified WR model aims to calculate a safe DV rate that reduces the infection risk of COVID-19 to an acceptable range. The safe DV rate obtained can guide ventilation fan selection based on fan flow rates (i.e., maximum fresh airflow rates) and be used for ventilation control. The following provides details on the development of the modified WR model.
The WR model is one of the most common models to describe the relationship between the infection probability and ventilation rates (Riley, C.E., Murphy, G. and Riley, 1978; Sze To & Chao, 2010), which is shown as:
| (1) |
where is the probability of infection; is the number of new infection cases; is the number of susceptible individuals; is the number of initial infectors; is the pulmonary ventilation rate of susceptible individuals, which can be 0.5 m3/h when people are sedentary (Health Canada, 2014); is the exposure time, h; is the room ventilation rate, m3/h; is the quantum generation rate, /h. The quantum generation rate, , is a key parameter in the WR model. A quantum is defined as the number of infectious airborne particles required to infect a person. The quantum generation rate cannot be measured directly but needs to be obtained by a back-calculation from epidemiological studies (Dai & Zhao, 2020). It should be noted that there is no uniform value of for COVID-19 worldwide. However, several previous studies have estimated the value of through different methods, which are summarized in Table 2 .
Table 2.
Estimation of the quantum generation rate for COVID-19.
| Reference | Methods | Quantum generation rate (/h) |
|---|---|---|
| Sun and Zhai (2020) (Sun & Zhai, 2020) | Estimated from real cases. The impacts of social distancing and ventilation air distribution on the estimation of quantum generation rate were considered. | 857 |
| Dai and Zhao (2020) (Dai & Zhao, 2020) | Correlated from the association between quantum generation rate and basic reproductive number with known infectious diseases (e.g., SARS and MERS). | 14 ∼ 48 |
| Buonanno et al. (2020) (Buonanno, Stabile, & Morawska, 2020) | Estimated from a mass balance equation. This equation assumes that the quantum generation rate of an infected person is the same as the quantum generation rate in sputum. | light exercise: 142 |
| Miller et al. (S. L. Miller et al., 2020) | Estimated from a real super spreader event by using a Monte Carlo simulation*. The influence of quanta loss due to viral decay and deposition onto surfaces was considered. | mean value in singing: 970 (680 ∼ 1190) |
Monte Carlo simulation is a statistical technique. The details can be found in reference (S. L. Miller et al., 2020).
It can be found that the value of different studies varies significantly depending on the estimation methods. Although these studies did not clarify the version of COVID-19, they provide an approximate range for the value. In this study, three different quantum generation rates were selected to discuss, which are 28, 142, and 857 h-1. The highest one, 857 h, was selected for the calculation in Section 3.2, and for the design and operation of the mechanical ventilation system. These three rates represent three different conditions of the infectors: sedentary state, light exercise (e.g., speaking), and heavy exercise or super spreading events. As shown in the Table 2, the quantum generation rate for the sedentary state is within 14 ∼ 48 h-1. Hou et al. indicated that the quantum generation rate can be 28 h-1 in a classroom (Hou et al., 2021). The value of 142 h-1 applied for the light exercise conditions, which has been used in several studies (Buonanno et al., 2020; Mokhtari & Jahangir, 2021). The value of 857 h-1 is high enough to show the infection risks in a super spreader event of COVID-19, i.e., it is within 680-1190 /h (S. L. Miller et al., 2020). Furthermore, this value is estimated by considering the impacts of social distancing on the transmission of COVID-19 (Sun & Zhai, 2020).
To further investigate the relationship between the infection probability and ventilation rates under different protective measures (i.e., wearing masks and maintaining social distancing) and the prevalence of the disease (i.e., how many infectors are in buildings), different parameters can be incorporated to modify the WR model. This study proposes a new modified Wells-Riley model. Three coefficients were considered, i.e., social distancing, wearing a mask, and initial infection rates. The previous studies had validated the effects of these coefficients respectively (Davies et al., 2013; Sun & Zhai, 2020); thus the following Eq. (2) is accurate for estimating the infection risk.
| (2) |
where the is the social distance index, see Eq. (3); is the mask index, see Eq. (4); is the initial infection rate; is the total number of occupants.
The social distance index, , is expressed as a correlation function of distance, which shows the relationship between the statistical probability of droplets that carry virus and their transmission distances (Sun & Zhai, 2020). The correlation equation shown below is with an R square 0.92 (Sun & Zhai, 2020).
| (3) |
where is social distance, m.
According to reference (Feng, Marchal, Sperry, & Yi, 2020), 1.8-m social distancing is the minimum requirement but it is better to keep a longer social distance of 3.1 m. The social distance indices can be 0.32 for a 1.8-m social distance or 0.23 for a 3.1-m social distance.
Mask index, , presents the mask effects on reducing COVID-19 transmission, which can be regarded as increasing the ventilation rate to reduce the virus quantum. The mask can reduce the virus quantum generation of infectors and reduce the amount of quantum inhaled by the susceptible individuals. Therefore, the mask index, , can be calculated by (Dai & Zhao, 2020):
| (4) |
where and are the exhalation filtration efficiency and inhalation filtration efficiency for infectors and susceptible individuals; and are the fraction of infectors and susceptible individuals who wear masks. It is reported that the filtration efficiency of ordinary medical surgical masks is about 50% (Davies et al., 2013). Considering that it is mandatory to wear the mask in public buildings, and are assumed to be 1. Therefore, the mask index is assumed to be 0.25.
B is the initial infection rate in the population, which indicates the transmission source. Combined with the number of occupants, the initial infector number can be estimated (i.e., ) (Sun & Zhai, 2020). Considering that high-rise buildings can accommodate thousands of people, it is not reasonable to assume the initial infector number to be a fixed value at all times. Currently, due to the differences in COVID-19 testing and tracing across countries, the infection rate, B, can be different for different countries. The previous studies used different methods, such as Monte Carlo simulation, to estimate the B value (Bohk-Ewald, 2020; Phipps, Grafton, & Kompas, 2020). It can be found that the B value varies between 1% and 10% for different countries. For Canada, it can be assumed as 1% (Phipps et al., 2020).
After rearranging the modified WR model (Eq. (2)), a ventilation rate that reduces the probability of COVID-19 infection to a target value can be obtained, called (Eq. (5a)). This ventilation rate can also be presented as air change rate (ACH) as shown in Eq. (5b)
| (5a) |
| (5b) |
where is the space volume, m3.
The probability of COVID-19 infection, , must be controlled to a low level. A lower indicates a lower number of new infection cases. However, when the target is extremely low, the required DV rates can be too high to be achieved in buildings. The target can be set as 1% or 2% (Dai & Zhao, 2020; Sun & Zhai, 2020). In this study, the target is determined by the basic reproductive number, (Rudnick & Milton, 2003; Sze To & Chao, 2010). The basic reproductive number, , is the number of secondary infections that arises when a single infection case (one infector) is introduced into a population where everyone is susceptible. Based on the definition and Eq. (2), can be calculated by:
| (6) |
should be lower than 1, which means that COVID-19 cannot spread in the population (Rudnick & Milton, 2003). A higher value indicates a more rapid reproduction rate of the infection in the form of an epidemic. Since the initial infection rate in the population can be assumed as 1% in the case study (see Section 2.4) (Phipps et al., 2020), the target is around 1%.
The global vaccine actions make efforts on preventing COVID-19 infection. It was reported that two-doses of the BNT162b2 vaccine can provide 95% protection against COVID-19 (Polack et al., 2020). Furthermore, it was reported that 50% of people in Canada are fully vaccinated against COVID-19, and over 70% of people had received one dose of vaccines (BBC news, 2021). Therefore, the vaccination impacts should be evaluated. Considering the vaccine protection performance is different for different vaccine types, the fraction of people with immunity, , is used to show the vaccination impacts. The fraction of people with immunity is integrated into Eq. (6) of basic reproductive number.
| (7) |
2.2. Energy models of cooling systems
This section briefly introduces the models used to calculate the energy consumption of the integrated chiller and mechanical ventilative systems. With these energy models, the ventilation rates required for VC can also be obtained. Details of the energy models have been presented in our previous study (Sha & Qi, 2020b).
The components of the chiller cooling and mechanical ventilation system includes the chiller, water pump, cooling tower, and fans. The power of the chiller can be simulated by the following equations.
| (8) |
| (9) |
| (10) |
where is the cooling load on the i th chiller, kW; is the condenser inlet water temperature, °C; is the outdoor wet-bulb temperature, °C; and are the correlation coefficients. It can be found that the power of the chiller is related to the outdoor wet-bulb temperature and the cooling load on the chillers.
The power of water pumps, cooling towers, and fans can all be simulated using the same model. For convenience, only is presented:
| (11) |
Where is the number of fans; is the ratio of rotation speed to nominal rotation speed of the th fan; and are the airflow rate and nominal airflow rate of the th fan, m3/s; is the nominal power of the th fan, kW. The total power of the supply fans is related to the fresh air flow rate, and the total power of the exhaust fan can also be related to the fresh air flow rate when the ratio of exhaust airflow rate to fresh airflow rate is known.
For the pumps and cooling towers, the th pump's water flow rates,, or the fan speed of the th cooling tower,, can be determined by two correlation equations.
| (12) |
| (13) |
where and are the correlation coefficients. It can be found that the power of the water pumps is related to the cooling load on the chillers, and the power of the cooling towers is related to the outdoor wet-bulb temperature and the cooling load on the chillers.
The outdoor wet-bulb temperature can be measured directly. The cooling load on the chillers can be calculated by the thermal model below.
| (14) |
| (15) |
where is the building cooling load; is the cooling load on all chillers; is the fresh air thermal load; is specific heat of air, kJ/(kg۰K); is air density, kg/m3; and are the outdoor and indoor air temperatures, °C; and are the outdoor and indoor humidity ratios, kg/kgdry; is the vaporization water latent heat, kJ/kgdry. When the enthalpy of outdoor air is lower than the indoor setpoint, is negative, i.e., VC.
To simplify the calculation, heat loss or gains in the distribution systems are neglected. Based on Eqs. (8) ∼ (15), the total power of the chiller cooling and mechanical ventilation system can be obtained when the values of the building cooling load, , outdoor wet-bulb temperature, , indoor-outdoor temperature difference, , and fresh airflow rate, , are known. Then, the cooling and ventilation energy consumption can be calculated based on the total power and time.
Considering that the fresh airflow rate can be adjustable, an optimal ventilation rate, , can be calculated based on Eq. (16). can minimize the energy consumption of whole cooling systems (chiller cooling system and VC system). Eq. (16) is subject to Eqs. (17a) ∼ (17d).
| (16) |
| (17a) |
| (17b) |
| (17c) |
| (17d) |
where , , and are the temperature and humidity ratio setpoints to ensure the thermal comfort; and are the total nominal fresh airflow rate and the fresh airflow rate to maintain IAQ, m3/s; and are the maximal and minimal cooling capacity of the chiller, kW; Z presents the chiller working state (Z = 1: chiller works; Z = 0: chiller stops). Eqs. (17a) and (17b) mean VC can only be applied when the outdoor air temperature and humidity ratio are within the constraints. Eq. (17c) presents the adjustable range of the ventilation rates. Eq. (17d) can constrain the ventilation rates by limiting the interaction between VC and the chiller system. VC cannot reduce the cooling load on the chiller to an impossible range, e.g., negative cooling load on the chillers. Eq. (16) can be solved by exhaustive search techniques.
2.3. New ventilative cooling control strategy to reduce the risk of COVID-19 transmission
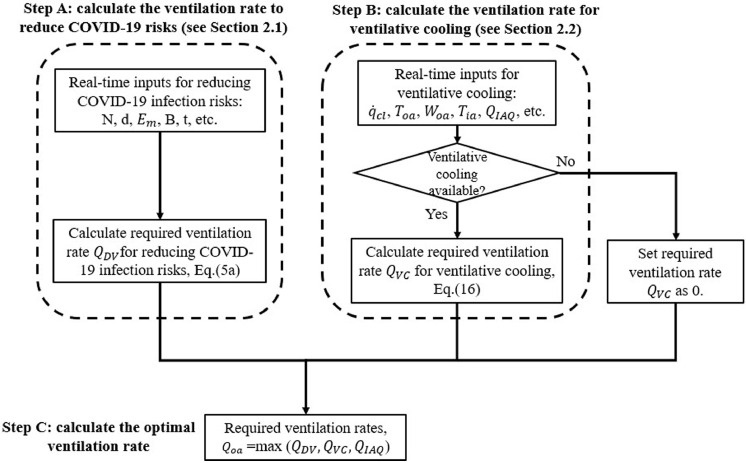
A new ventilative cooling control strategy was developed to reduce COVID-19 transmission. This strategy, named Dilution Ventilation and Ventilative Cooling (DVVC), shown in Fig. 1 , is used to calculate the ventilation rate that reduces COVID-19 transmission and achieves VC. This new control strategy is developed based on the previous study for only achieving VC (Sha & Qi, 2020b). Three steps are required in the control strategy. Step A calculates the ventilation rate for COVID-19, . Step B calculates the ventilation rate for VC, . Step C uses the highest ventilation rate in the calculation as the optimal ventilation rate. is calculated by Eq. (5a), which has been illustrated in Section 2.1. is calculated by Eq. (16), which has been illustrated in Section 2.2. The related inputs for , , and the criteria of availability of VC vary depending on a specific case. In this study, the related inputs will be introduced in the case study in Section 2.4. For Step C, there are two scenarios: 1) When VC is available, the higher value between and will be selected as the optimal ventilation rate; 2) when the outdoor conditions are not suitable for VC (i.e., the ventilation rate for VC does not exist), the higher value between and will be selected as the optimal ventilation rate. For both two scenarios, if the VC is not enough to remove all the excessive heat, the chiller cooling system will cool and dehumidify the air.
Fig. 1.
Ventilative cooling control strategy to reduce COVID-19 transmission (DVVC).
2.4. Case study
In this study, a 16-storey high-rise institutional building in Montreal (Canada) was selected for the case study. This section first introduces the selected building and its HVAC system. The information about the building and HVAC system will be used to calculate the required DV rates and build the energy models. Then, different settings of the mechanical ventilation systems are introduced. The results of DV rates are presented in Section 3.1. After validating the energy models (Section 3.2.1), the effects of the settings of the mechanical ventilation system on cooling and ventilation energy consumption are presented in Section 3.2.2.
2.4.1. Building and HVAC system
There are thousands of rooms in the case study building; mainly classrooms, offices, and laboratories. The centralized HVAC system provides around 155000 m3 volume of fresh air, which covers around 32000 m2 floor area. This building is usually occupied from 5:00 a.m. to midnight and can accommodate a maximum of around 3,489 occupants (estimated according to the default occupant density in ASHRAE 62.1 (ASHRAE, 2010)). During the summertime, the indoor air temperature is maintained at 23°C, and the chiller cooling system will start to work and cool the building when the outdoor temperature is above 15 ºC, which indicates that the VC availability is within 15∼23°C. During the COVID-19 pandemic in 2020, all the occupants inside the building needed to wear masks and maintain a social distance of at least 1.8 meters.
A centralized HVAC system is located on the top floor. All these components can be simulated by the energy model shown in Section 2.3. The detailed information about the chiller system is introduced here. The chiller system consists of three chillers, nine water pumps, and two cooling towers. The three chillers work for different conditions: the centrifugal chiller is used for the large building cooling load (higher than 260 kW, nominal cooling capacity of 1969 kW with 347 kW nominal power), the scroll chiller for the small building cooling load (lower than 260 kW with 62.3 kW nominal power), and the screw chiller for backup. The centrifugal chiller has one chilled water pump and one cooling water pump. The scroll chiller has one chilled water pump and two cooling water pumps. The chiller system only operates when the outdoor temperature is higher than 15 ºC. The mechanical ventilation system contains four supply air fans and four exhaust air fans, with a fan flow rate of around 35.7 m3/s (i.e., 0.8 ACH). The heat recovery is not considered in this study, because the heat recovery techniques cannot be used when the ventilative cooling is available. The fresh airflow rates of the four supply air fans depend on the indoor air quality (IAQ) monitored by CO2 sensors on each floor (Johnson Controls, 2016). The exhaust airflow rates are controlled by the Building Automation System (BAS) to keep the building in positive pressure. All the components of the centralized HVAC system are monitored by the BAS.
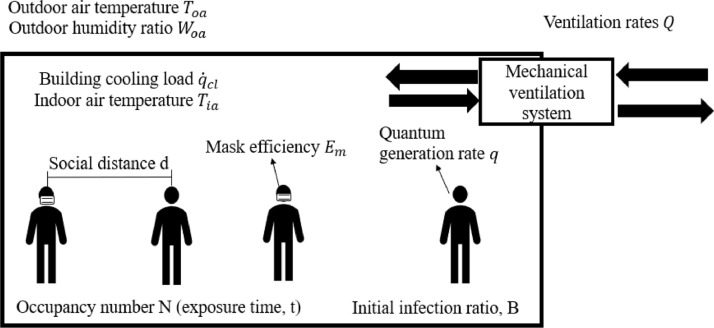
Based on the building information, Fig.2 . presents the schematic diagram for the parameters used in the calculation of DV rates and VC ventilation rates. The parameters used in the calculation of DV rates are listed in Table 3 . Three parameters are considered: mask index (indicate with/without mask), social distancing, and exposure time. The mask index has two values depending on whether the occupants all wear masks or not (Dai & Zhao, 2020). The social distance index has three values. When there is no COVID-19 pandemic, occupants do not need to follow social distancing (i.e., occupants may have a close contact, assuming the social distance is 0 m in the worst situation). During the COVID-19 pandemic, the recommended social distance is 1.8 m and 3.1 m in the building (Feng et al., 2020). However, it was reported that the SARS-CoV virus particles can diffuse in indoor environments up to 10 m from the sources, which means that the social distance longer than 3.1 m should be considered when the other protective measures are limited (Setti et al., 2020). Furthermore, when the social distance changes, the maximum number of occupants should change due to the limitation of the area of the building. In this study, the maximum number of occupants is recalculated according to the building room types and ASHRAE standard 62.1. The exposure time depends on the time the occupants stay in the building. The reference suggests an office building can have 4-hour exposure time (Sun & Zhai, 2020), but the standard hours of work for an employee in a day can extend to 8 hours in Canada (Government of Canada, 2020). Although it is rare to stay continuously in a space for 8 hours in real scenarios, the 8-hours exposure is often considered as the worst scenario. For example, the study in the REHVA COVID-19 guidance used 8 hours as the exposure time to investigate the required ventilation rate (REHVA, 2020). Therefore, the 8-hours exposure and 4-hours exposure are selected in this study. The criteria of VC availability are: the outdoor temperature should be between 15 and 23 ºC (15 ºC is the temperature that the building starts to need cooling and 23 ºC is the indoor setting temperature in summer) and the outdoor humidity ratio should be less than 11.6 g/kgdry (for maintaining thermal comfort) (Yuan, Vallianos, Athienitis, & Rao, 2018).
Fig. 2.
Schematic diagram of the parameters for calculating the required ACH to reduce infection risks of COVID-19 and achieve ventilative cooling.
Table 3.
Summary of the parameters for calculating DV rates.
| Parameters | Values |
|---|---|
| Mask index, | 1 without a surgical mask or 0.25 with a surgical mask |
| Social distance, d | 0 m or 1.8 m or 3.1 m |
| Design number of occupants, N | 3489 (close contact) or 2971 for d=1.8 m or 1326 for d=3.1m |
| Social distance index, | 1 (close contact) or 0.32 for d=1.8 m or 0.23 for d=3.1 m |
| Exposure time, t | 4 h or 8 h |
| Quantum generation rate, q | 28 or 142 or 857 |
| Pulmonary ventilation rate, p | 0.5 m3/h |
| Initial infection rate, B | 1% |
Six months of BAS data (June to August in 2019 and 2020) were used to conduct energy simulations. The August 2019 data were used to correlate the energy models (i.e., calculating correlation coefficients in Eqs. (8) ∼ (13)). Since the June to August 2020 data reflect the real energy consumption during the COVID-19 pandemic, they were used to validate the correlated energy models. However, during the COVID-19 pandemic in 2020, many services in the building were stopped, and the number of occupants was significantly reduced. Therefore, after validation, the June to August data in 2019 were used to conduct energy simulations to investigate the impacts of the mechanical ventilation system on energy consumption, because the building was in normal operation in 2019. The mechanical ventilation system should be designed and controlled for the normal building operation rather than for the COVID-19 shutdown. The detailed information about the correlated energy models and the accuracy of sensors in the BAS can be found in our previous study (Sha & Qi, 2020b) and in Appendix.
The BAS system provides measured fresh air flow rate (i.e., the ventilation rate to maintain IAQ,), indoor CO2 concentration, outdoor temperature, outdoor relative humidity, electricity consumption data, etc. The measured data used for energy simulations are summarized in Table 4 , including the hourly dry-bulb temperature, humidity ratio, total cooling load, and total cooling related energy consumption. It should be noted that the BAS system does not record the number of occupants directly. In this study, the number of occupants is estimated by CO2 concentrations. Several studies have shown that the following equation can accurately determine the indoor number of occupants (Mumma, 2004; Ng, Qu, Zheng, Li, & Hang, 2011; S. Wang, Burnett, & Chong, 2003).
| (18) |
where the superscript n represents current step; is the CO2 generation rate per person, which is 0.00825L/s for a sedentary adult (Ng et al., 2011); is the i th space volume, m3; is the CO2 concentration in the space at time n, ppm; is the outdoor CO2 concentration at time n, which can be assumed to be constant at 400 ppm (Ng et al., 2011); is the time step, s. There is at least one CO2 sensor and one fresh airflow rate sensor on each floor. The fresh airflow rates and CO2 concentrations at a six-minute time step are used to estimate the occupancy of each floor separately. Since the estimated the number of occupants may fluctuate a lot, the upper and lower limits (the number of occupants cannot exceed the design number and cannot be lower than zero) are added to limit the fluctuation of the results (Mumma, 2004). The calculated the hourly number of occupants for the hourly simulation energy consumption is summarized in Table 4.
Table 4.
Summary of the measured data used for energy simulations.
| Year | Dry-bulb temperature (℃) | Humidity ratio(g/kgdry) | Hourly number of occupants | Total cooling load/related energy consumption(MWh) | |
|---|---|---|---|---|---|
| 2019 | Min | 8.3 | 2.7 | 10 | 1442/378 |
| Mean | 21.5 | 8.6 | 143 | ||
| Max | 32.3 | 16.4 | 715 | ||
| 2020 | Min | 6.5 | 3.5 | 3 | 1325/276 |
| Mean | 22.1 | 9.5 | 89 | ||
| Max | 33.7 | 17.6 | 322 | ||
2.4.2. Case design
To evaluate the energy performance of mechanical ventilation for ventilative cooling and reducing COVID-19 infection risks, nine cases (one baseline case (Baseline) and eight cases with different mechanical ventilation system settings) are proposed and listed in Table 5 . Three different factors are considered as shown in Table 5: specific fan power, fan flow rates, and ventilation control strategy.
Table 5.
Energy simulation cases.
| Cases | Ventilation control strategy | Specific fan power (kW/m3/s) | Fan flow rates (m3/s; ACH) |
|---|---|---|---|
| Baseline |
Same as ASHRAE guidelines | 3.76 | 35.7; 0.8 |
| DVVC | DVVC | 3.76 | 35.7; 0.8 |
| DVVC+LSFP | DVVC | 0.86 | 35.7; 0.8 |
| DVVC+LSFP+F2 | DVVC | 0.86 | 72.2; 1.7 |
| DVVC+LSFP+F3 | DVVC | 0.86 | 112.6; 2.6 |
| DVVC+LSFP+F6 | DVVC | 0.86 | 225.2; 5.2 |
| DVVC+LSFP+F8 | DVVC | 0.86 | 298.0; 6.7 |
| DVVCG+LSFP+F6 | Combine DVVC and ASHRAE guidelines | 0.86 | 225.2; 5.2 |
| VCO | Ventilative cooling only | 3.76 | 35.7; 0.8 |
Note: DVVC: the new ventilation control proposed in Section 2.3; DVVCG: combination of the new ventilation control and ASHRAE guidelines; VCO: ventilation control strategy considering ventilative cooling only; LSFP: low specific fan power (i.e., specific fan power equals 0.86 kW/m3/s; F2 ∼ F8: the increased fan flow rates, which are two (F2), three (F3), six (F6), and eight (F8) times of the existing maximum fan flow rate (35.7 m3/s, 0.8 ACH).
Specific fan power (SFP) is a crucial parameter for describing the energy efficiency of the fan system to transport air. SFP is defined as the ratio of the nominal electric power of both supply and exhaust fans to fresh air flow rate. The previous study indicates that the SFP not only influences the fan energy consumption directly, but also influences VC energy performance. The lower the SFP, the better VC energy performance (i.e., VC can save more energy) (Sha & Qi, 2020b). Therefore, two different SFPs are considered here: 0.86 kW/(m3/s) and 3.76 kW/(m3/s). The possible range of SFP is not affected by the weather conditions in different countries, and it is only related to the pressure head and efficiency of fans, which depends on the ductwork and the manufacture of fans. If the engineer designs proper ductwork and selects the high-efficiency fans in the market, the SFP can be as low as what is required by the standards. Considering it is impractical to set the SFP as zero, the upper limit of SFP in the standards was selected, which is the possible SFP that can be achieved in practice. To our best knowledge, the Chinese energy efficiency standard has the lowest SFP limit for the fresh air system, which is 0.86 kW/m3/s (Ministry of Construction China, 2015). The SFP in the Baseline (real applications in the case study) is 3.76 kW/(m3/s). A lower SFP, i.e., 0.86 kW/(m3/s), is selected from the Chinese energy efficiency standard for fresh air systems (Ministry of Construction China, 2015), which is LSFP in Table 5.
Considering that higher fan flow rates could reduce infection risks of COVID-19 and may improve VC potential energy savings (Sha & Qi, 2020b), four higher fan flow rates (named F2, F3, F6, and F8, which are two, three, six, and eight times higher than the existing fan flow rate) are considered (see calculation in Section 3.1).
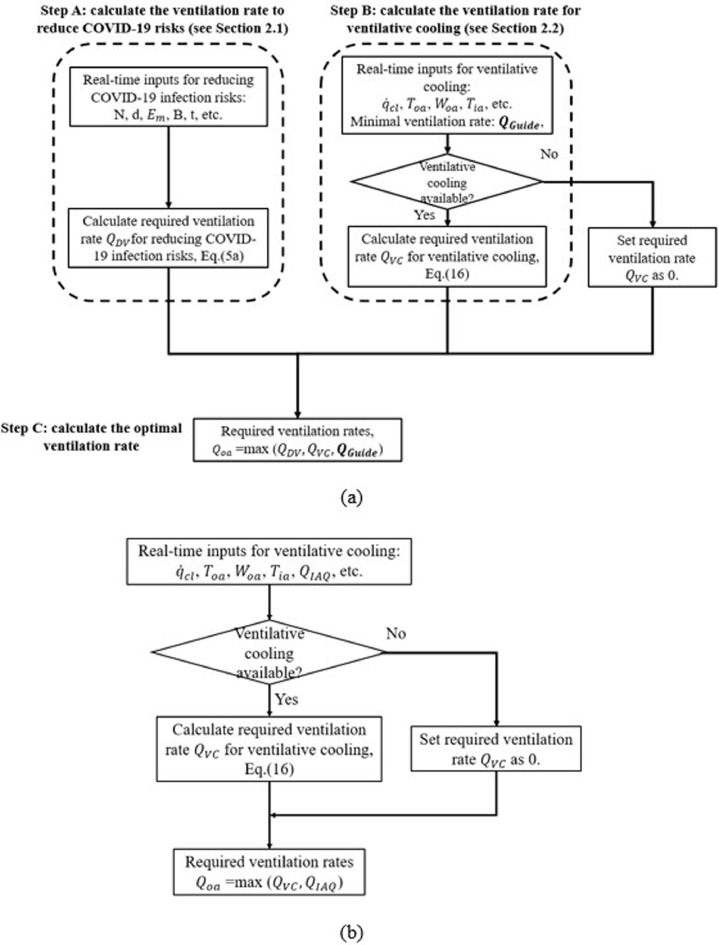
Four types of ventilation control strategies were considered: the control method which is the same as in the ASHRAE guidelines (Schoen, 2020), the new ventilation control (named DVVC), the combination of the new ventilation control and the ASHRAE guidelines (named DVVCG), and control for VC only (named VCO). As suggested by the guidelines (increase outdoor air ventilation; keep ventilation systems running longer hours) (Schoen, 2020), the maximum fresh air flow rates (i.e., equal to the fan flow rate) are provided all the time. The new ventilation control, DVVC, refers to the ventilation control for reducing COVID-19 infection risks and achieving VC, which has been presented in Fig.1. The new ventilation control strategy considering the ASHRAE guidelines, DVVCG, combines the new ventilation control method and the guidelines. To clarify the difference between DVVC and DVVCG, this control strategy is presented in Fig.3 (a). In Fig. 3 (a) Step B, a fixed ventilation rate, named as , is set, indicating that the actual ventilation rate cannot be lower than . Since the ASHRAE guideline asks for the maximum fresh air flow rate to fulfill the IAQ requirement, this control strategy will keep the minimum ventilation rate of 35.7 m3/s (0.8 ACH). This control strategy is safer than the ASHRAE guidelines and is applied to a case with the fan flow rate higher than the Baseline because the ventilation rates of this control strategy can always achieve lower COVID-19 infection risks than the guidelines. The control strategy with VC only (VCO) means that DV is not considered, therefore this control strategy cannot ensure a low level of COVID-19 infection risks. To clarify the difference between DVVC and DVVCG, this control strategy is presented in Fig.3 (b). This control strategy is the same as Step B and Step C in Fig.1. For the DVVC and DVVCG control strategies, assuming under an 857 h-1 quantum generation rate (the worst condition), the protective measures consider wearing masks, maintaining social distancing of more than 1.8 meters, no vaccination, and staying eight hours in the building.
Fig. 3.
Ventilation control strategies for energy simulations: (a) DVVCG;(b) VCO.
Eight cases are designed to study the effects of the three factors (specific fan power, fan flow rates, and ventilation control strategy) on cooling and ventilation energy consumption. The effects of the new ventilation control on energy consumption can be seen by comparing the Baseline and DVVC cases. Case DVVC+LSFP presents the effects of the fan system with low SFP on energy consumption. Cases DVVC+LSFP+F2 ∼ F6 demonstrate the impacts of the fan flow rate on energy consumption. Case DVVCG+LSFP+F6 illustrates an ideal case, which has the safest ventilation control strategy (DVVCG), the energy efficient fans (low SFP), and the optimal fan flow rates. Case VCO is used to highlight the difference between the control strategy with and without considering DV.
3. Results and discussion
3.1. Mechanical ventilation rates to reduce the risk of COVID-19 transmission
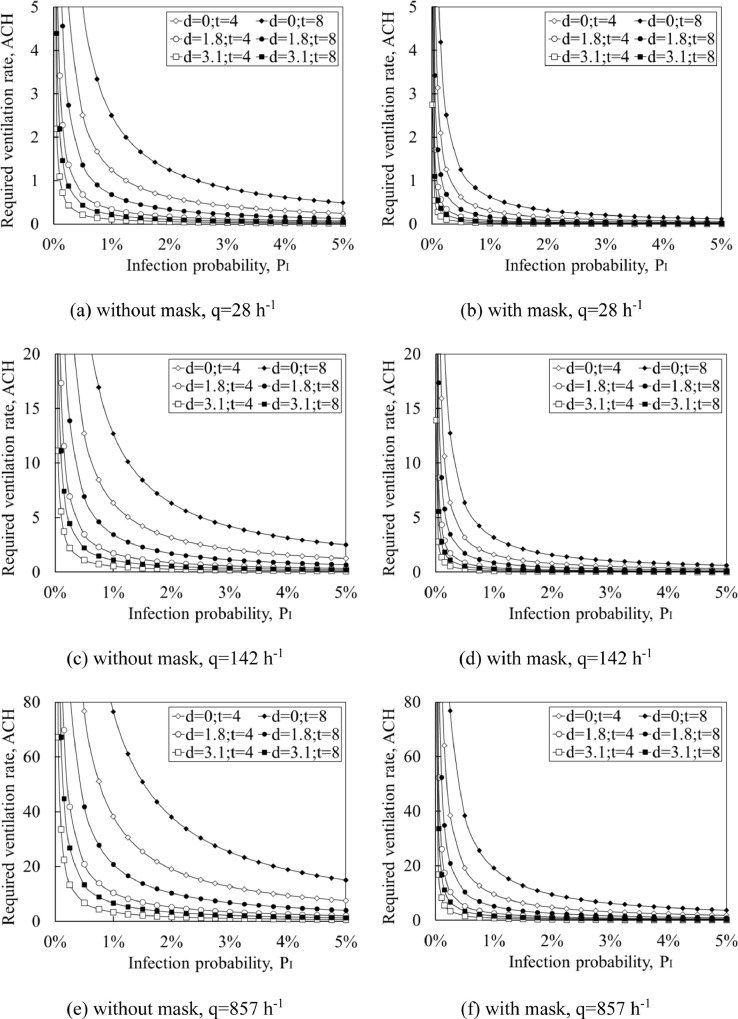
The required ventilation rate is calculated using the data shown in Table 3. The relationship between the infection probability and required ventilation rates is presented in Fig. 4 . It can be seen that the required ventilation rate is significantly affected by five factors: infection probability (), quantum generation rate (q), social distance (d), with/without masks, and exposure time (t). When the infection probability reduces to a certain range, the required ventilation rate could increase sharply. For example, in Fig. 4f, with a 1.8 m social distance and 8 h exposure time (d=1.8; t=8), the required ventilation rate increases from 2.6 ACH (112.6 m3/s) to 5.2 ACH (225.2 m3/s) when the infection probability reduces from 2% to 1%. However, when the infection probability reduces from 1% to 0.1%, the required ventilation rate needs to increase from 5.2 ACH (225.2 m3/s) to 52.4 ACH (2262.1 m3/s). These results are caused by the relationship between the infection risk and ventilation rate, which is nonlinear (See Eq. (5b)). Therefore, instead of using a very low fixed target infection risk from former studies, it is better to use the basic reproductive number and initial infection rate to determine the target infection risk, as shown in Eq. (6).
Fig. 4.
Relationship between the infection probability and required ventilation rates under different exposure times and social distances for (a) without mask, q=28 h-1, (b) with mask, q=28 h-1, (c) without mask, q=142 h-1, (d) with mask, q=28 h-1, (e) without mask, q=857 h-1, (f) with mask, q=857 h-1
From Eq. (5b), it can be found that the required ventilation rate is linearly related to the quantum generation rate. When the quantum generation rate increases to 857 h-1 from 28 h-1, the required ventilation rate increases around 30 times. For example, according to Fig. 4b and Fig. 4f, the required ventilation rate increases from 0.17 ACH (7.4 m3/s) to 5.2 (225.2 m3/s) for the 1% infection risk, when the generation rate increases from 28 h-1 to 857 h-1 (Fig. 4f). A ventilation rate 5.2 ACH is possible even considering the thermal comfort. For example, healthcare facilities can have 12 ACH (Atkinson et al., 2009). However, if the infection risk needs to be maintained lower than 1% under a ventilation rate of 5.2 ACH, 1.8 m social distance must be respected. Thus, the number of occupants could be limited.
The social distance has two effects on the required ventilation rate: (1) Greater social distance can decrease the amount of quantum directly inhaled by the susceptible individuals; (2) The social distance can limit the maximum number of occupants inside the building and indirectly change the number of initial infectors. Based on the standard occupancy density in ASHRAE 62.1, the case study building can accommodate around 3500 people. When 1.8 m social distance is regulated in the building, in some types of spaces (e.g., classroom or conference room), the occupancy density should be less than the standard occupancy density. The whole building can only accommodate around 3000 occupants. Therefore, when the social distance increases, the required ACH reduces significantly. Fig.4. shows that if the occupants maintain a 3.1 m social distance instead of 1.8 m, the required ACH can be reduced to around one-third. For example, in Fig. 34, with 8 hours of exposure time and masks, the required ACH for maintaining a 1% infection risk decreases from 5.2 ACH (225.2 m3/s) to 1.7 ACH (72.2 m3/s) when the social distance is decreased from 3.1 m to 1.8 m. Wearing masks and exposure time have a linear relationship with the required ventilation rate, as shown in Eq. (5a). Therefore, the required ACH when the occupants all wear masks is only a quarter of the ACH when occupants do not wear masks. For example, with a 1.8 m social distance and 8 hours of exposure time, the required ventilation rate for maintaining a 1% infection risk, decreases from 20.9 ACH (900.8 m3/s) without masks (Fig. 4e) to 5.2 ACH (225.2 m3/s) with masks (Fig. 4f).
In summary, the existing fan flow rate (35.7 m3/s; 0.8 ACH) designed for IAQ in the case study can almost fulfill the requirement when the quantum generation rate is low and the protective measures are strict. For example, in Fig. 4a and 4b, the infection probability can be higher than 1% only when the occupants have close contact. However, the fan flow rate needs to be increased when the quantum generation rate is high and the protective measures are limited. For example, in Fig. 4c and 4d, the infection probability can not be maintained at 1% except the occupants follow the protective measures strictly (i.e., social distancing, wearing masks, and reducing exposure time). The required DV rate can be extremely high in the worst situation: high quantum generation rate (857 /h), long exposure time (8 hours), no other protective measures (no social distancing and no masks). If the infection probability needs to be maintained at 1% in the worst situation, the required DV rate should be as high as 77 ACH (3305.7 m3/s) as shown in Fig. 4 (e), which is impractical for mechanical ventilation systems.
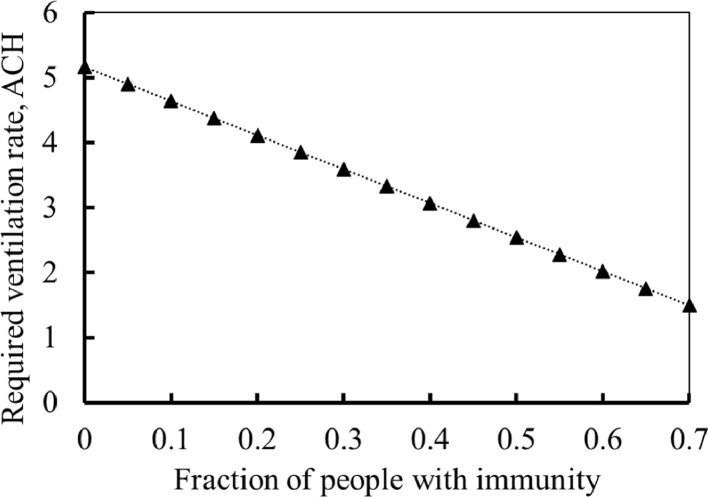
Fig. 5 presents the impacts of the fraction of people with immunity on the required DV rate. Considering the actual conditions in the case study, the other parameters were selected as follows: 1. wearing masks; 2. maintaining a social distance of more than 1.8 m; 3. eight hours exposure time; 4. quantum generation rate of 857 /h; 5. initial infection rate of 1%. Fig. 5 shows that the increase of (i.e., receiving vaccines) will decrease the required ventilation rate. For example, when increases to 70% from 0, the required ventilation rate decreases from 5.2 to 1.5 ACH. Eq. (7) indicates that higher means fewer susceptible population. Thus, even though the required ventilation rate reduces, the secondary transmission is still under control (i.e., the basic reproductive number is still less than 1).
Fig. 5.
Relationship between the fraction of people with immunity and required ventilation rates.
The previous reference point out that, for the disease control, the engineering measures (i.e., increasing ventilation rate) are at a higher level than the application of administrative measures (social distancing) and personal protective equipment (wearing masks) (REHVA, 2020). Also, a high quantum generation rate of COVID-19 (i.e., the super spreading events) has been confirmed in the real situation (S. L. Miller et al., 2020; Sun & Zhai, 2020). Therefore, increasing fan flow rate is necessary. Moreover, increasing the fan flow rate can contribute to a high energy savings due to the VC (see Section 3.2.2.).
This study investigated the impacts of different fan flow rates on cooling and ventilation energy consumption in the following sections. Assuming the quantum generation rate is in the worst case (857 h-1, see Fig. 4e and 4f), without considering the vaccination, the required fan flow rates can be around two (with mask; d=3.1; t=8), three (with mask; d=1.8; t=4), six (with masks; d=1.8; t=8), and eight times (no mask; d=3.1; t=8) higher than the existing fan flow rate. Considering the actual protective measures in the case study, i.e., wearing masks and maintaining a social distance of more than 1.8 m for eight hours, a fan flow rate six times higher than the existing fan flow rate (225.2 m3/s; 5.2 ACH) is recommended, which can maintain a lower than 1% infection risk at the design occupancy number. It should be noted that this fan flow rate is optimal for this case study building under the specific conditions: quantum generation rate (857 /h), exposure time (8h), protective measures (all occupants wear masks and have 1.8m social distance). However, if one of these conditions changes, the optimal ventilation rate will change too.
3.2. Energy performance
3.2.1. Model validation
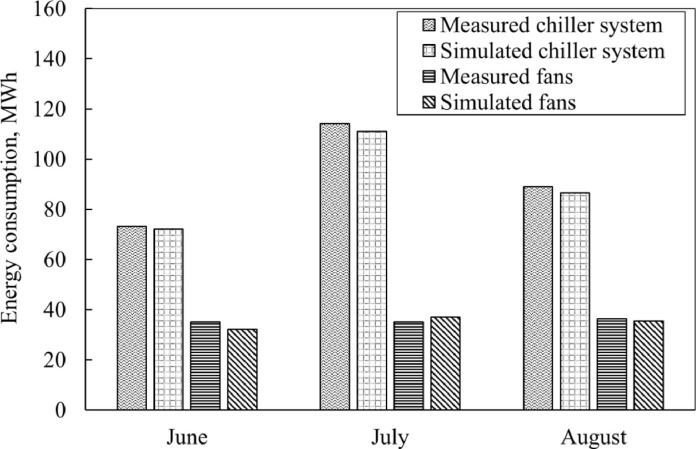
Before conducting the energy simulation of the different cases, the prediction accuracy of the energy models had to be validated. Fig. 6 compares the measured and calculated energy consumption of the chiller and ventilation systems during the COVID-19 pandemic from June to August 2020. It can be seen that the monthly difference between the measured and calculated results is very close; less than 10%. Rahman et al.(Rahman, Rasul, & Khan, 2010) suggested that the acceptable relative difference between simulated and measured energy use of the HVAC system can be up to 15 ∼ 25% monthly. The hourly CV(RMSE) and NMBE are also used here to evaluate the simulation accuracy. According to the requirements in ASHRAE guideline-14, the hourly CV(RMSE) and NMBE between the measurement and simulation should be within 30% and ±10% respectively (ASHRAE, 2014). For this model, the CV(RMSE) and NMBE of the chiller system are 7% and 2%, and the CV(RMSE) and NMBE of the ventilation system are 15% and 2%. These values are much lower than the requirements. Therefore, the accuracy of the energy models is acceptable for the energy consumption estimation of the cooling and ventilation systems during the COVID-19 pandemic.
Fig. 6.
Monthly measured ventilation and cooling energy usage vs. calculated ventilation and cooling energy usage during the COVID-19 pandemic in 2020.
3.2.2. Energy simulations
This section shows the energy simulations for the different cases listed in Table 5. Considering that the mechanical ventilation system should be designed and controlled for normal building operation rather than shutdown conditions, the June to August data in 2019 are used to conduct the energy simulations.
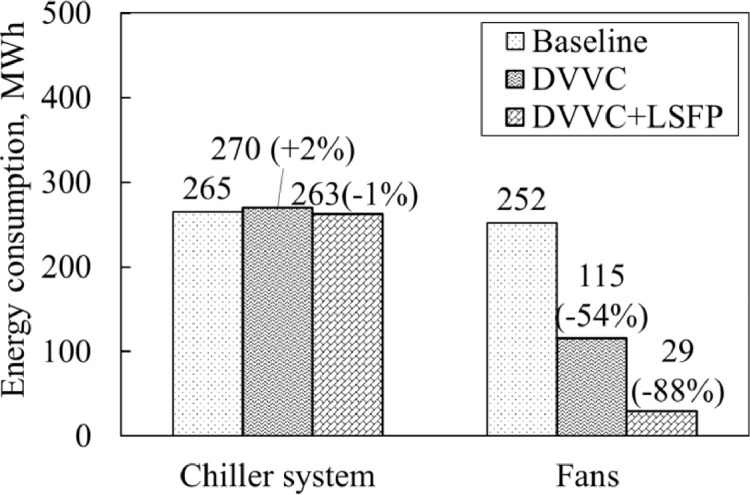
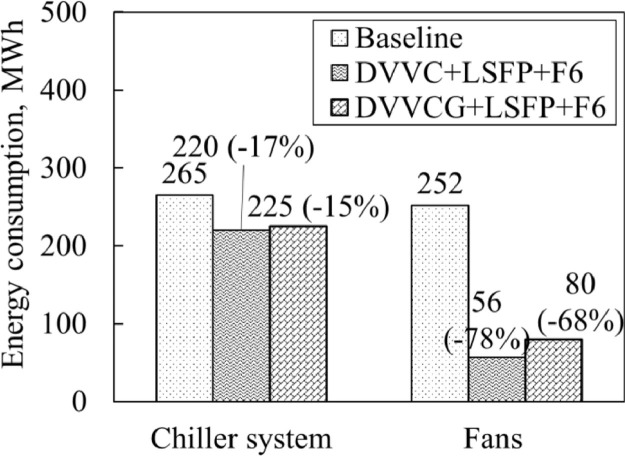
Fig. 7 compares the cooling and fan energy consumption between the Baseline, DVVC, and DVVC+LSFP cases in June, July and August of 2019, which explains the impacts of the new ventilation control and low specific fan power on energy consumption. Compared with Baseline, DVVC cannot reduce the chiller cooling energy consumption but reduces the fan energy consumption significantly. The reduction of fan energy consumption is due to the reduced ventilation rate. As shown in Table 4, the mean hourly number of occupants was only 143 in 2019. Based on the calculated DV rate (Eq. (5a)), the required DV rate is lower than the existing fan flow rate, which is only 10.8 m3/s. Therefore, the new ventilation control (DVVC) reduces the ventilation rates and contributes to large energy savings (up to 54%) for the ventilation system. The change in chiller cooling energy consumption can also be explained by the ventilation rate: a large amount of outdoor air can be introduced into the building to remove the cooling load in Baseline, and thus the chiller cooling energy consumption of Baseline (265 MWh) can be slightly lower than the chiller cooling energy consumption of DVVC (270 MWh). Therefore, this result shows that the ventilation control strategy in the ASHRAE guidelines may lead to higher fan energy consumption, because more fresh air than is required is introduced into building.
Fig. 7.
Impact of new ventilation control (DVVC) and low specific fan power (LSFP) on energy consumption.
Furthermore, in Fig. 7, it can be seen that DVVC+LSFP can reduce fan energy consumption by ∼90% vs. ∼54% for DVVC while slightly reducing the chiller cooling energy consumption (+2% vs. -1%). This is because the low SFP fans can reduce fan energy consumption directly. The reduction of the chiller cooling energy consumption is due to more cooling load taken by VC (the chiller takes less cooling load). However, the reduced energy consumption of the chiller system is exceedingly small (around 1%), because the fan flow rates are so small and limit VC capacity.
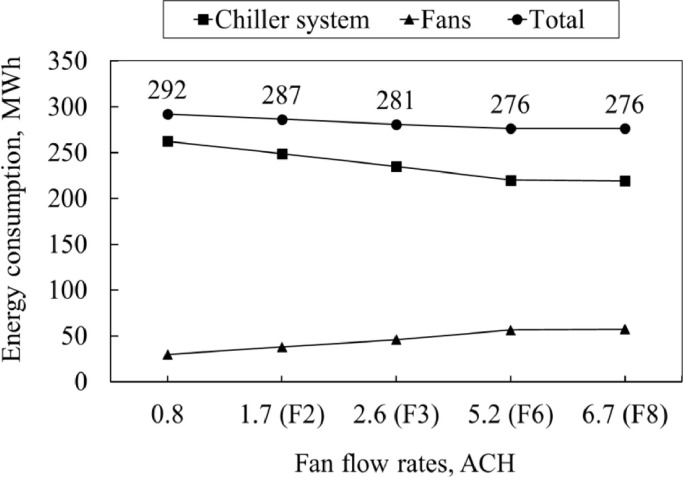
Fig. 8 compares the chiller cooling, ventilation and total energy consumption for the cases at the existing fan flow rate (35.7 m3/s, 0.8 ACH in DVVC+LSFP) to eight times the existing fan flow rate (298.0 m3/s, 6.7 ACH in DVVC+LSFP+F8) in June, July and August of 2019. It can be seen that increasing the fan flow rate can further reduce the total energy consumption. For example, the total energy consumption reduces from 292 MWh (263 of chiller +29 of fans) for DVVC+LSFP to 276 MWh (220 of chiller +56 of fans) for DVVC+LSFP+F6. However, the total electricity consumption is not linear in Fig.8. The actual ventilation rate that fulfills the requirements of ventilative cooling and dilution ventilation may be not the maximum fan flow rate, because the building cooling load and the number of occupants vary with time. For example, when the fan flow rate increases from 225.2 m3/s (5.2 ACH) to 298.0 m3/s (6.7 ACH), there are no additional energy savings, because the fan flow rate of 225.2 m3/s (5.2 ACH) already provides enough cooling capacity to reduce cooling related energy consumption. Therefore, a six-time higher fan flow rate (225.2 m3/s, 5.2 ACH) is the optimal fan flow rate for the case study because: (1) the mechanical ventilation system with a six-time higher fan flow rate has the greatest energy savings; (2) as mentioned in Section 3.1, the mechanical ventilation system with a six-time higher fan flow rate can maintain the infection risks lower than 1% under the design number of occupants.
Fig. 8.
Impact of fan flow rates on energy consumption from existing fan flow rates (35.7 m3/s, 0.8 ACH in DVVC+LSFP) to an eight-time higher fan flow rate (298.0 m3/s, 6.7 ACH in DVVC+LSFP+F8).
Fig. 9 compares the cooling energy consumption and electricity consumption of fans between the Baseline and the ideal case DVVCG+LSFP+F6 in the three months. The DVVC+LSFP+F6 case is also presented here, which highlights the influences of DVVCG on total energy consumption. Compared with DVVC+LSFP+F6, DVVCG+LSFP+F6 has higher chiller cooling and ventilation energy consumption. This is because the minimum ventilation rate in DVVCG is set as 35.7 m3/s (0.8 ACH), but the required DV rates can be lower than 35.7 m3/s (0.8 ACH), as shown in Fig. 7. The ventilation rates in DVVCG are higher than in DVVC, resulting in higher ventilation energy consumption. The higher ventilation rates in DVVCG may also introduce more hot outdoor air into the building, leading to higher chiller system energy consumption. However, although the total energy consumption of DVVCG+LSFP+F6 is higher than for DVVC+LSFP+F6, the total energy savings (chiller cooling + fans) of DVVCG+LSFP+F6 can still be up to 40% compared with Baseline. This result indicates that if SFP, fan flow rate, and ventilation control strategy are selected and set properly (i.e., select low SFP fans, operate with optimal fan flow rate and use ventilation control strategy by considering VC and DV), the ventilation system can make the building safe and energy-efficient.
Fig. 9.
Comparison of energy consumption between Baseline and DVVCG+LSFP+F6.
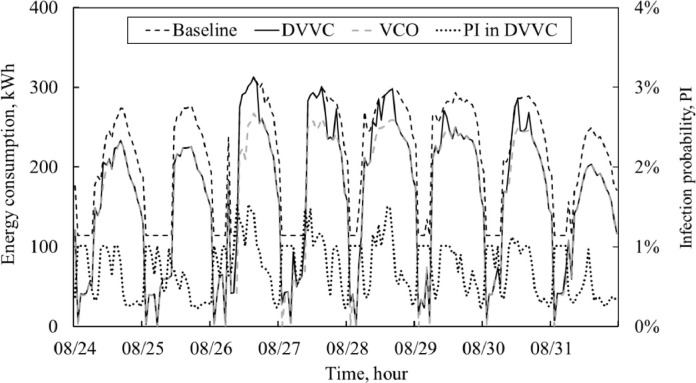
To highlight the influences of DV on total energy consumption (i.e., to compare the DVVC and VCO cases), detailed hourly ventilation rates and hourly total energy consumption for a specific week in 2019 (Aug.24 to Aug.31) are presented in Fig. 10, Fig. 11 , respectively. Fig. 10 presents the calculated ventilation rates of DVVC, VCO, and measurement () and the number of occupants. It can be seen that the ventilation rates of DVVC, VCO, and the measurement are close when the number of occupants is less than 400. However, when the number of occupants is more than 400, the ventilation rates of DVVC are obviously higher than VCO and measurement. This is because the ventilation rates of VC and measurement (around 26.0 m3/s, 0.6 ACH) can ensure around 400 occupants inside the building with an infection probability lower than 1% (calculated by Eq. (5a)). Furthermore, the existing fan flow rate (35.7m3/s, 0.8 ACH) can ensure around 470 occupants inside the building with a low infection risk. Therefore, when there are more than 470 occupants, the ventilation rate of DVVC will increase to the maximum fan flow rate.
Fig. 10.
Ventilation rates of cases DVVC, VCO and measurement and the number of occupants in a specific week (Aug.24-Aug.31.2019).
Fig. 11.
Hourly total energy consumption of Baseline, DVVC, and VCO cases and the infection probability of DVVC in a week (Aug. 24-Aug.31, 2019).
Fig. 11. presents the hourly total energy consumption of the Baseline, DVVC, and VCO cases. The COVID-19 infection risk in the DVVC case is also presented in Fig.11 to show the limitation of the existing fan flow rate on reducing infection risk. The variation of the DVVC energy consumption matches the variation of the ventilation rate shown in Fig. 10. Since VCO always provides the ventilation rate that can minimize energy consumption (see Eq. (16)), the DVVC energy consumption will always be equal to or more than VCO. It can be summarized that when the number of occupants is between 400 and 470, DVVC consumes more energy than VCO. When the number of occupants is more than 470, DVVC consumes the same amount of energy as Baseline. For example, when the ventilation rate of DVVC increases to the maximum fan flow rate in 08/26-08/28, the hourly DVVC energy consumption is the same as Baseline. Furthermore, the COVID-19 infection risk in DVVC shows that the existing fan flow rate (35.7 m3/s, 0.8 ACH) is not high enough to reduce the infection risk of COVID-19 to lower than 1% at all times. For example, the infection risk of COVID-19 in DVVC can achieve 1.5% at the peak occupancy rate in 08/26, but the ventilation rate is at maximum and cannot further reduce the infection risk. Therefore, the fan flow rate must be increased.
In this study, we calculate the required ventilation rates for controlling the COVDI-19 infection risk under different scenarios. Table 6 compares the required ventilation rates of previous studies, and the corresponding key input parameters for obtaining the required ventilation rates. From Table 6, it was found that the required ventilation rate is strongly affected by the input parameters. For example, the required ventilation rate under a full occupancy is around six times higher than the ventilation rate under a quarter occupancy ratio in the study of Sun and Zhai (2020). The difference between required ventilation rates even reaches 87.4 ACH in the study of Dai and Zhao (2020). The results of this study are consistent with the findings in the references. Section 3.1 shows that under different protective measures, the required ventilation can vary from 0.8 (masks; 3.1 m social distance; 4-hours exposure) to 76.6 ACH (no masks; no social distancing; 8-hours exposure) when the target infection probability is less than 1% under an 857 h-1 quantum generation rate.
Table 6.
Required ventilation rates in previous studies.
| References | Required ventilation rates | Key input parameters |
|---|---|---|
| (Dai & Zhao, 2020) | 0.6∼88 ACH | 0.6 ACH for a 348 m2 classroom, =1, =14 /h, =2, =1%, =0.25. 88 ACH for a 150 m2 office, =1, =48 /h, =8, =1%, =1 (No masks). |
| (Sun & Zhai, 2020) | 78 ∼438 m3/h• person (No room volume presented) |
78 m3/h• person for a 20 m2 office, =1, =857 /h, =4, =2%, full occupancy. 438 m3/h• person for a 20 m2 office,=1, =857 /h, =4, =2%, quarter occupancy. |
| (Hou et al., 2021) | 3 ∼ 8 ACH | virus quantum loss rate: 0.92. 3 ACH for a 165 m2 classroom, =1, =28 /h, =8, =1, =0.35. 8 ACH for a 236 m2 classroom,=1, =28 /h, =8, =1, =0.35. |
Different from former studies that only investigated the required ventilation rate to reduce the infection risk of COVID-19, this study further examined the cooling and ventilation energy consumption under the different fan flow rates. An optimal fan flow rate (5.2 ACH; 225 m3/s) is obtained. Considering the protective measures implemented in the building (wearing masks and 1.8 m social distance), this fan flow rate not only fulfills the infection control requirement (R0=1) under a high virus quantum generation rate (857 /h), but also minimizes the cooling related energy consumption due to ventilative cooling.
The energy simulations show three findings for the mechanical ventilation system settings. First, under the normal building operating conditions, the ventilation control in the ASHRAE guidelines may introduce redundant fresh air and lead to high ventilation energy consumption. This ventilation control strategy can be replaced by the new ventilation control strategy proposed in this study. Figs. 10 and 11 show that the maximum fresh air rate is only required when the number of occupants exceeds 470. As shown in Table 4, the hourly number of occupants is lower than 470 during the daily operation. Therefore, when applying the new ventilation control (case DVVC), the ventilation energy savings can reach 54%, as seen in Fig 7. It should be noted that the ventilation rate in the DVVC case already reduces the infection risk to 1% most of the time. As shown in Fig. 4 (b), if the infection probability is expected to be reduced from 1% to <1%, the required ventilation rate needs to increase significantly. Therefore, it is important to consider whether the ventilation control strategy in the ASHRAE guidelines is needed to control the spread of COVID-19.
Second, it is recommended that the mechanical ventilation system have a high fan flow rate with a low SFP. On the one hand, the high fan flow rate, e.g., six times higher than the existing fan flow rate, can protect more occupants at peak times if protective measures are limited. On the other hand, the high fan flow rate with a low SFP can contribute to VC energy savings (see Fig. 8). For the case study building, 0.86 kW/(m3/s) SFP fans with six-times higher fan flow rate can be an optimal fan flow rate to reduce cooling energy consumption. A higher fan flow rate cannot further reduce cooling energy consumption. Therefore, the six-time higher fan flow rate (225.2 m3/s, 5.2 ACH) is selected as the optimal fan flow rate. With the low SFP and optimal fan flow rate, the ideal case (DVVCG+LSFP+F6), which is safer than the Baseline, still saves around 40% of the total energy consumption. The methods to lower SFP and increase the fan flow rate have been discussed in our previous study about mechanical ventilative cooling in high-rise buildings (Sha & Qi, 2020b).
Thirdly, both DV and VC require high ventilation rates, but the ventilation rate required by DV (i.e., Step A in Fig. 1.) in the new ventilation control can increase the total energy consumption. As explained in Fig. 11, the total energy consumption in DVVC will always be equal to or higher than in the VCO case, because the VCO case always provides the ventilation rates minimizing the energy consumption (see Eq. (16)). In the energy simulation for the case study, a threshold of 400 occupants has been identified. When there are more than 400 occupants, the total energy consumption of DVVC is higher than VCO, because the ventilation rate increases to achieve DV. Assuming the parameters used in Eq. (5a) change to accommodate the higher DV rates, the total energy consumption in DVVC will be higher. For example, if social distancing cannot be maintained in the building, a higher DV rate will be required to maintain low infection risks of COVID-19. In an extreme case, the total energy consumption of DVVC will be the same as Baseline if the required DV rate is high all the time.
It should be noted that this study focuses on the ventilation and cooling energy consumption. When dilution ventilation requires a high ventilation rate during the winter when the outdoor temperature is very low, heating is needed for maintaining thermal comfort (Katal et al., 2021), which is out of the scope of this paper and will be investigated in future. Furthermore, the DV rate in this study is calculated based on a modified steady-state WR model. More factors, such as the initial virus quantum concentration, can be included by the transient WR model, which affects the required ventilation rate for infection control and thus influence the cooling and ventilation energy simulation. However, it is easy to further modify the WR model and adjust the control for DV. The impacts of WR model on the ventilation control will be investigated thoroughly in the future.
Also, this study does not consider the heat recovery techniques, because ventilative cooling is available for a long time due to the climate conditions in the case study (see Table 4, averaged outdoor air temperature is 21 ºC). However, for the area with limited time for ventilative cooling, heat recovery may be critical to energy saving, which should be simulated.
4. Conclusion
In this paper, first a modified WR model is proposed for evaluating the required DV rate in real buildings. The energy models to estimate the cooling and ventilation energy consumption and required VC rates are also introduced. Then, a new ventilation control strategy is proposed, which considers the ventilation rates for DV and VC. A 16-storey institutional high-rise building in Montreal is selected for the case study to illustrate the energy performance of the proposed new ventilation control strategy. This study reached the following major conclusions:
-
1
With the design number of occupants, operating a ventilation system to provide maximum outdoor airflow rates all the time may be insufficient in preventing the transmission of COVID-19, because the ventilation system is designed to maintain IAQ. When designing a ventilation system, it is suggested to consider not only the IAQ but also the requirement for diluting airborne pathogen using the WR model. In the case study building, the fan flow rate of the existing ventilation system is 0.8 ACH (35.7 m3/s), but the required DV rates can reach 77 ACH (3305.7 m3/s) when considering different quantum generation rate and protective measures. Under a high quantum generation rate (857 h-1) and the actual protective measures, i.e., wearing masks and maintaining a social distance of greater than 1.8 m, the required DV rate is 225.2 m3/s (5.2 ACH), which is around six times higher than the existing fan flow rates.
-
2
When the building is operating under normal conditions, the number of occupants is much lower than the design value, and thus the ventilation control in the ASHRAE guidelines during the COVID-19 pandemic leads to high energy consumption. When the protective measures are implemented, the required ventilation rates for reducing infection risk may be much lower than the maximum outdoor airflow rates when the number of occupants is small. Therefore, the new ventilation control strategy based on the building's real-time occupant number can save energy. For example, the new ventilation control proposed in the case study reduces ventilation energy consumption by 54% compared with providing a maximum outdoor airflow rate all the time.
-
3
It is recommended to use low SFP fans with a high fan flow rate, which can contribute to more cooling and ventilation energy savings due to VC. Also, there is an optimal fan flow rate (225.2m3/s in the case study) for VC. With a low SFP (0.86 kW/m3/s) fan and the optimal fan flow rate, an ideal setting for the ventilation system (i.e., DVVCG control strategy) can be determined, which contributes to around 40% energy savings compared with the existing ventilation system.
-
4
With the proper protective measures and low occupancy, the ventilation requirements of DV and VC are consistent. However, without proper protective measures and a low occupancy. ventilation requirements of DV can exceed those of VC and lead to more cooling-related energy consumption. For the case study building, when there are fewer than 400 occupants (with masks and maintaining a social distance of 1.8 m), the VC ventilation rate can usually fulfill the DV requirement at the same time. However, when there are more than 400 occupants, the required DV ventilation rate will be higher than that of VC.
Declaration of Competing Interest
We wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.
We confirm that the manuscript has been read and approved by all named authors and that there are no other persons who satisfied the criteria for authorship but are not listed. We further confirm that the order of authors listed in the manuscript has been approved by all of us.
We confirm that we have given due consideration to the protection of intellectual property associated with this work and that there are no impediments to publication, including the timing of publication, with respect to intellectual property. In so doing we confirm that we have followed the regulations of our institutions concerning intellectual property.
We understand that the Corresponding Author is the sole contact for the Editorial process (including Editorial Manager and direct communications with the office). He is responsible for communicating with the other authors about progress, submissions of revisions and final approval of proofs. We confirm that we have provided a current, correct email address which is accessible by the Corresponding Author and which has been configured to accept email from dahai.qi@usherbrooke.ca
Acknowledgements
We appreciate the support from Mr. Sylvain Corbeil and Mr. Michaël Ménard in the Building Service Department of the Université de Sherbrooke (UdeS). This work was supported by the Start-up Fund of the UdeS and Discovery Grants of Natural Sciences and Engineering Research Council of Canada (NSERC) (Grant number: RGPIN-2019-05824).
Appendix
The details of the energy model correlation coefficients in Section 2.2 are presented in Table A1 .
Table A1.
Correlation coefficients of the models in section 2.2 for the case study.
| Items | Control scheme and model coefficients | Correlation R2 |
|---|---|---|
| Chillers | COP of centrifugal chiller, in Eq. (8): |
0.53 |
| COP of scroll chiller, in Eq. (8): |
0.73 | |
| Chilled water pump | For centrifugal chiller system, water flow rate is constant, 47.55 L/s. | / |
| For scroll chiller system, water flow rate is constant, 5.77 L/s | / | |
| Cooling water pump | Water flow rate for centrifugal chiller, in Eq. (12): |
0.99 |
| Water flow rate for the primary cooling water pump of scroll chiller, in Eq. (12): |
0.99 |
|
| Water flow rate for the secondary cooling water pump of scroll chiller system, Eq. (12): |
0.94 | |
| Cooling towers | Power of cooling towers for centrifugal chiller, in Eq. (13): Condenser inlet water temperature can be calculated by Eq. (9): |
0.98 for Eq. (13) 0.82 for Eq. (9) |
| Power of cooling towers for scroll chiller, in Eq. (13): Condenser inlet water temperature, in Eq. (9): |
0.79 for Eq. (13) 0.87 for Eq. (9) |
|
| Ratio of exhaust airflow rate to fresh airflow rate | 0.66 | / |
References
- Agarwal N., Meena C.S., Raj B.P., Saini L., Kumar A., Gopalakrishnan N.…Aggarwal V. Indoor air quality improvement in COVID-19 pandemic: Review. Sustainable Cities and Society. 2021;70 doi: 10.1016/j.scs.2021.102942. April. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ASHRAE . Ashrae Standard; 2010. ASHRAE STANDARD 62.1 ventilation for acceptable indoor air quality. 2010. [Google Scholar]
- ASHRAE ASHRAE guideline 14-2014 Measurement of energy, demand, and water savings. ASHRAE. 2014;2014 [Google Scholar]
- Atkinson, J., Chartier, Y., Lúcia Pessoa-Silva, C., Jensen, P., Li, Y., & Seto, W.-H. (2009). Natural ventilation for infection control in health-care settings. Geneva: WHO; (Vol. 1). [PubMed]
- Attia S., Levinson R., Ndongo E., Holzer P., Berk Kazanci O., Homaei S.…Heiselberg P. Resilient cooling of buildings to protect against heat waves and power outages: Key concepts and definition. Energy and Buildings. 2021;239 doi: 10.1016/j.enbuild.2021.110869. [DOI] [Google Scholar]
- Bakhtiari H., Akander J., Cehlin M., Hayati A. On the performance of night ventilation in a historic office building in nordic climate. Energies. 2020;(6):13. doi: 10.3390/en13164159. [DOI] [Google Scholar]
- BBC news. (2021). Canada's vaccination rate overtakes US. Retrieved from https://www.bbc.com/news/world-us-canada-57869947.
- Bohk-Ewald C. A demographic scaling model for estimating the total number of COVID-19 infections. MedRxiv. 2020;45(Supplement):S–102. doi: 10.1093/ije/dyaa198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buonanno G., Stabile L., Morawska L. Estimation of airborne viral emission: Quanta emission rate of SARS-CoV-2 for infection risk assessment. Environment International. 2020:141. doi: 10.1016/j.envint.2020.105794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Canadian Committee on Indoor Air Quality. (2020). Addressing COVID-19 in buildings. Retrieved from https://iaqresource.ca/wp-content/uploads/2020/09/CCIAQB-Module15-Eng.pdf.
- Dai H., Zhao B. Association of the infection probability of COVID-19 with ventilation rates in confined spaces. Building Simulation. 2020;13:1321–1327. doi: 10.1007/s12273-020-0703-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davies A., Thompson K.A., Giri K., Kafatos G., Walker J., Bennett A. Testing the efficacy of homemade masks: would they protect in an influenza pandemic? Disaster Medicine and Public Health Preparedness. 2013;7(4):413–418. doi: 10.1017/dmp.2013.43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng Y., Marchal T., Sperry T., Yi H. Influence of wind and relative humidity on the social distancing effectiveness to prevent COVID-19 airborne transmission: A numerical study. Journal of Aerosol Science. 2020;147 doi: 10.1016/j.jaerosci.2020.105585. May. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Government of Canada. (2020). Hours of work. Retrieved March 7, 2021, from https://www.canada.ca/en/employment-social-development/programs/employment-standards/work-hours.html.
- Guo M., Xu P., Xiao T., He R., Dai M., Miller S.L. Review and comparison of HVAC operation guidelines in different countries during the COVID-19 pandemic. Building and Environment. 2021;187(4800) doi: 10.1016/j.buildenv.2020.107368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Health Canada. (2014). General exposure factor inputs for dietary, occupational, and residential exposure assessments, 52. https://doi.org/H113-13/2014-1E-PDF.
- Hou, D., Katal, A., Wang, L. (Leon), Katal1, A., & Wang, L. (Leon). (2021). Bayesian Calibration of Using CO2 Sensors to Assess Ventilation Conditions and Associated COVID-19 Airborne Aerosol Transmission Risk in Schools. MedRxiv, 2021.01.29.21250791. Retrieved from http://medrxiv.org/content/early/2021/02/03/2021.01.29.21250791.abstract.
- IEA-EBC. (2018). Annex 62 ventilative cooling design guide. Retrieved from http://www.iea-ebc.org/Data/publications/EBC_Annex_62_Design_Guide.pdf.
- Johnson Controls. (2016). CD-Px0-00-0 series duct mount CO2 transmitters. Retrieved from https://cgproducts.johnsoncontrols.com/met_pdf/216525.pdf.
- Katal, A., Albettar, M., & Wang, L. (Leon). (2021). City Reduced Probability of Infection (CityRPI) for indoor airborne transmission of SARS-CoV-2 and urban building energy impacts. MedRxiv, 2021.01.19.21250046. Retrieved from http://medrxiv.org/content/early/2021/01/20/2021.01.19.21250046.abstract.
- Kolokotroni M., Aronis A. Cooling-energy reduction in air-conditioned offices by using night ventilation. Applied Energy. 1999;63(4):241–253. doi: 10.1016/S0306-2619(99)00031-8. [DOI] [Google Scholar]
- Kong X., Guo C., Lin Z., Duan S., He J., Ren Y., Ren J. Experimental study on the control effect of different ventilation systems on fine particles in a simulated hospital ward. Sustainable Cities and Society. 2021;73 doi: 10.1016/j.scs.2021.103102. April. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y., Qian H., Hang J., Chen X., Cheng P., Ling H.…Kang M. Probable airborne transmission of SARS-CoV-2 in a poorly ventilated restaurant. Building and Environment. 2021;196 doi: 10.1016/j.buildenv.2021.107788. February. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, Y., Qian, H., Hang, J., Chen, X., Hong, L., Liang, P., … Kang, M. (2020). Evidence for probable aerosol transmission of SARS-CoV-2 in a poorly ventilated restaurant. MedRxiv, 1–19. https://doi.org/10.1101/2020.04.16.20067728.
- Miller S.L., Nazaroff W.W., Jimenez J.L., Boerstra A., Buonanno G., Dancer S.J.…Noakes C. Transmission of SARS-CoV-2 by inhalation of respiratory aerosol in the Skagit Valley Chorale superspreading event. MedRxiv. 2020 doi: 10.1101/2020.06.15.20132027. June2020.06.15.20132027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller W., Machard A., Bozonnet E., Yoon N., Qi D., Zhang C.…Levinson R. Conceptualising a resilient cooling system: A socio-technical approach. City and Environment Interactions. 2021;11 doi: 10.1016/j.cacint.2021.100065. November 2020. [DOI] [Google Scholar]
- Ministry of Construction China . 2015. GB 50189-2015 Design standard for energy efficiency of public buildings. [Google Scholar]
- Mokhtari R., Jahangir M.H. The effect of occupant distribution on energy consumption and COVID-19 infection in buildings : A case study of university building. Building and Environment. 2021;190 doi: 10.1016/j.buildenv.2020.107561. December 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mumma S.A. Transient occupancy ventilation by monitoring CO2. ASHRAE IAQ Applications. 2004;5(1):21–23. [Google Scholar]
- China National Health Commission of the People's Republic of. Hygienic specifications for operation and management of air-conditioning ventilation systems in office buildings and public places during COVID-19 epidemic (in Chinese) Beijing. Retrieved from. 2020 http://www.nhc.gov.cn/fzs/s7852d/202007/992a8d0b6c754e0db3df7458d604962e.shtml [Google Scholar]
- Ng M.O., Qu M., Zheng P., Li Z., Hang Y. CO2-based demand controlled ventilation under new ASHRAE Standard 62.1-2010: A case study for a gymnasium of an elementary school at West Lafayette, Indiana. Energy and Buildings. 2011;43(11):3216–3225. doi: 10.1016/j.enbuild.2011.08.021. [DOI] [Google Scholar]
- Phipps, S. J., Grafton, R. Q., & Kompas, T. (2020). Estimating the true (population) infection rate for COVID-19: a backcasting approach with Monte Carlo methods. MedRxiv, 2020.05.12.20098889. https://doi.org/10.1101/2020.05.12.20098889.
- Polack F.P., Thomas S.J., Kitchin N., Absalon J., Gurtman A., Lockhart S.…Gruber W.C. Safety and Efficacy of the BNT162b2 mRNA Covid-19 Vaccine. New England Journal of Medicine. 2020;383(27):2603–2615. doi: 10.1056/nejmoa2034577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qi, D., Cheng, J., Katal, A., Wang, L. (Leon), & Athienitis, A. (2019). Multizone modelling of a hybrid ventilated high-rise building based on full-scale measurements for predictive control. Indoor and Built Environment, 0(0), 1–12. https://doi.org/10.1177/1420326X19856405.
- Rahman M.M., Rasul M.G., Khan M.M.K. Energy conservation measures in an institutional building in sub-tropical climate in Australia. Applied Energy. 2010;87(10):2994–3004. doi: 10.1016/j.apenergy.2010.04.005. [DOI] [Google Scholar]
- REHVA. (2020). REHVA COVID-19 guidance document version 4.0. Retrieved from https://www.rehva.eu/fileadmin/user_upload/REHVA_COVID-19_guidance_document_V4_09122020.pdf.
- Ren, C., Xi, C., Feng, Z., Nasiri, F., Cao, S., & Haghighat, F. (2021). Mitigating COVID-19 infection disease transmission in indoor environment using physical barriers. Sustainable Cities and Society, 74(April), 103175. https://doi.org/10.1016/j.scs.2021.103175. [DOI] [PMC free article] [PubMed]
- Riley C.E., Murphy G., Riley R.L. Airborne spread of measles in a suburban elementary school. American Journal of Epidemiology. 1978;107(5):421–432. doi: 10.1093/oxfordjournals.aje.a112560. [DOI] [PubMed] [Google Scholar]
- Rudnick S.N., Milton D.K. Risk of indoor airborne infection transmission estimated from carbon dioxide concentration. Indoor Air. 2003;13(3):237–245. doi: 10.1034/j.1600-0668.2003.00189.x. [DOI] [PubMed] [Google Scholar]
- Schoen L.J. Guidance for building operations during the COVID-19 pandemic. ASHRAE Journal. 2020:72–74. doi: 10.1056/NEJMc2004973. May. [DOI] [Google Scholar]
- Setti L., Passarini F., De Gennaro G., Barbieri P., Perrone M.G., Borelli M.…Miani A. Airborne transmission route of Covid-19: Why 2 meters/6 feet of inter-personal distance could not be enough. International Journal of Environmental Research and Public Health. 2020;(8):17. doi: 10.3390/ijerph17082932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sha H., Moujahed M., Qi D. Machine learning-based cooling load prediction and optimal control for mechanical ventilative cooling in high-rise buildings. Energy & Buildings. 2021;242 doi: 10.1016/j.enbuild.2021.110980. [DOI] [Google Scholar]
- Sha, H., & Qi, D. (2020a). A review of high-rise ventilation for energy efficiency and safety. Sustainable Cities and Society, 54(August 2019), 101971. https://doi.org/10.1016/j.scs.2019.101971.
- Sha H., Qi D. Investigation of mechanical ventilation for cooling in high-rise buildings. Energy and Buildings. 2020;228 doi: 10.1016/j.enbuild.2020.110440. [DOI] [Google Scholar]
- Sun C., Zhai Z. Sustainable Cities and Society. 2020. The efficacy of social distance and ventilation effectiveness in preventing COVID-19 transmission; p. 62. July. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sze To G.N., Chao C.Y.H. Review and comparison between the Wells-Riley and dose-response approaches to risk assessment of infectious respiratory diseases. Indoor Air. 2010;20(1):2–16. doi: 10.1111/j.1600-0668.2009.00621.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talty, J. T. (1998). Industrial hygiene engineering (Second Edition).
- Wang J., Huang J., Feng Z., Cao S.J., Haghighat F. Occupant-density-detection based energy efficient ventilation system: Prevention of infection transmission. Energy and Buildings. 2021;240 doi: 10.1016/j.enbuild.2021.110883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, S., Burnett, J., & Chong, H. (2003). Experimental validation of CO2-based occupancy detection for demand-controlled ventilation. Indoor and Built Environment, 8(6), 377–391. https://doi.org/10.1159/000057493.
- Wang, Z., Yi, L., & Gao, F. (2009). Night ventilation control strategies in office buildings. Solar Energy, 83(10), 1902–1913. https://doi.org/10.1016/j.solener.2009.07.003.
- WHO. (2020). Roadmap to improve and ensure good indoor ventilation in the context of COVID-19. Retrieved from https://www.who.int/publications/i/item/9789240021280.
- World Health Organization. (2021). Coronavirus disease (COVID- 19) pandemic. Retrieved March 5, 2021, from https://www.worldometers.info/coronavirus/.
- Yang W., Marr L.C. Dynamics of airborne influenza A viruses indoors and dependence on humidity. PLoS ONE. 2011;(6):6. doi: 10.1371/journal.pone.0021481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan S., Vallianos C., Athienitis A., Rao J. A study of hybrid ventilation in an institutional building for predictive control. Building and Environment. 2018;128:1–11. doi: 10.1016/j.buildenv.2017.11.008. Retrieved from. [DOI] [Google Scholar]
- Zhang C., Kazanci O.B., Levinson R., Heiselberg P., Olesen B.W., Chiesa G.…Zhang G. Vol. 111312. 2021. Resilient cooling strategies - a critical review and qualitative assessment. (Energy and Buildings). [DOI] [Google Scholar]
- Zhang Y., Wang X., Hu E. Optimization of night mechanical ventilation strategy in summer for cooling energy saving based on inverse problem method. Journal of Power and Energy. 2018;232(8):1093–1102. doi: 10.1177/0957650918766691. [DOI] [Google Scholar]