Continuous Post-Market Sequential Safety Surveillance with Minimum Events to Signal

Abstract

The CDC Vaccine Safety Datalink project has pioneered the use of near real-time post-market vaccine safety surveillance for the rapid detection of adverse events. Doing weekly analyses, continuous sequential methods are used, allowing investigators to evaluate the data near-continuously while still maintaining the correct overall alpha level. With continuous sequential monitoring, the null hypothesis may be rejected after only one or two adverse events are observed. In this paper, we explore continuous sequential monitoring when we do not allow the null to be rejected until a minimum number of observed events have occurred. We also evaluate continuous sequential analysis with a delayed start until a certain sample size has been attained. Tables with exact critical values, statistical power and the average times to signal are provided. We show that, with the first option, it is possible to both increase the power and reduce the expected time to signal, while keeping the alpha level the same. The second option is only useful if the start of the surveillance is delayed for logistical reasons, when there is a group of data available at the first analysis, followed by continuous or near-continuous monitoring thereafter.

1. Introduction

Post-market drug and vaccine safety surveillance is important in order to detect rare but serious adverse events not found during pre-licensure clinical trials. Safety problems may go undetected either because an adverse reaction is too rare to occur in sufficient numbers among the limited sample size of a phase three clinical trial, or because the adverse reaction only occur in a certain sub population that was excluded from the trial, such as frail individuals.

In order to detect a safety problem as soon as possible, the CDC Vaccine Safety Datalink project pioneered the use of near real-time safety surveillance using automated weekly data feeds from electronic health records[1, 2, 3]. In such surveillance, the goal is to detect serious adverse reactions as early as possible without too many false signals. It is then necessary to use sequential statistical analysis, which adjusts for the multiple testing inherent in the many looks at the data. Using the maximized sequential probability ratio test (MaxSPRT)[4], all new childhood vaccines and some adult vaccines are now monitored in this fashion [1, 5, 6, 7, 8, 9, 10, 11, 12, 13]. There is also interest in using sequential statistical methods for post-market drug safety surveillance [14, 15, 16, 17, 18, 19], and the methods presented in this paper may also be used in either settings.

In contrast to group sequential analyses, continuous sequential methods can signal after a single adverse event, if that event occurs sufficiently early. In some settings, such as a phase 2 clinical trial, that may be appropriate, but in post-market safety surveillance it is not. In post-market vaccine surveillance, an ad-hoc rule that require at least two or three events to signal has sometimes been used, but that leads to a conservative type 1 error (alpha level). In this paper we provide exact critical values for continues sequential analysis when a signal is required to have a certain minimum number of adverse events. We also evaluate power and expected time to signal for various alternative hypotheses. It is shown that it is possible to simultaneously improve both of these by requiring at least 3 or 4 events to signal. Note that it is still necessary to start surveillance as soon as the first few individuals are exposed, since they all could have the adverse event.

For logistical reasons, there is sometimes a delay in the start of post-marketing safety surveillance, so that the first analysis is not conducted until a group of people have already been exposed to the drug or vaccine. This is not a problem when using group sequential methods, as the first group is then simply defined to correspond to the start of surveillance. For continuous sequential surveillance, a delayed start needs to be taken into account when calculating the critical values. In this paper, we present exact critical values when there is a delayed start in the sequential analysis. We also calculate the power and time to signal for different relative risks.

In addition to ensuring that the sequential analysis maintains the correct overall alpha level, it is important to consider the statistical power to reject the null hypothesis; the average time until a signal occurs when the null hypothesis is rejected; and the final sample size when the null hypothesis is not rejected. For any fixed alpha, there is a trade-off between these three metrics, and the trade-off depends on the true relative risks. In clinical trials, where sequential analyses are commonly used, statistical power and the final sample size are usually the most important design criteria. The latter is important because patient recruitment is costly. The time to signal is usually the least important, as a slight delay in finding an adverse event only affects the relatively small number of patients participating in the clinical trial, but not the population-at-large. In post-market safety surveillance, the trade-off is very different. Statistical power is still very important, but once the surveillance system is up and running, it is easy and cheap to prolong the length of the study by a few extra months or years to achieve a final sample size that provides the desired power. Instead, the second most critical metric is the time to signal when the null is rejected. Since the product is already in use by the population-at-large, most of which are not part of the surveillance system, a lot of people may be spared the adverse event if a safety problem can be detected a few weeks or months earlier. This means that for post-market vaccine and drug safety surveillance, the final sample size when the null is not rejected is the least important of the three metrics.

All calculations in this paper are exact, and none are based on simulations or asymptotic statistical theory. The numerical calculation of the exact critical values is a somewhat cumbersome process. So that users do not have to do these calculations themselves, we present tables with exact critical values for a wide range of parameters. For other parameters, we have developed the open source R package ‘Sequential’, freely available at ‘cran.r-project.org/web/packages/Sequential’.

2. Continuous Sequential Analysis for Poisson Data

Sequential analysis was first developed by Wald [20, 21], who introduced the sequential probability ratio test (SPRT) for continuous surveillance. The likelihood based SPRT proposed by Wald is very general in that it can be used for many different probability distributions. The SPRT is very sensitive to the definition of the alternative hypothesis of a particular excess risk. For post-market safety surveillance, a maximized sequential probability ratio test with a composite alternative hypothesis has often been used instead. This is both a ‘generalized sequential probability ratio test’ [22] and ‘sequential generalized likelihood ratio test’[23, 24]. In our setting, it is defined as follows, using the Poisson distribution to model the number of adverse events seen [4].

Let C_t be the random variable representing the number of adverse events in a pre-defined risk window from 1 to W days after an incident drug dispensing that was initiated during the time period [0, t]. Let c_t be the corresponding observed number of adverse events. Note that time is defined in terms of the time of the drug dispensing rather than the time of the adverse event, and that hence, we actually do not know the value of c_t until time t + W.

Under the null hypothesis (H₀), C_t follows a Poisson distribution with mean μ_t, where μ_t is a known function reflecting the population at risk. In our setting, μ_t reflects the number of people who initiated their drug use during the time interval [0, t] and a baseline risk for those individuals, adjusting for age, gender and any other covariates of interest. Under the alternative hypothesis (H_A), the mean is instead RRμ_t, where RR is the increased relative risk due to the drug/vaccine. Note that C₀ = c₀ = μ₀ = 0.

For the Poisson model, the MaxSPRT likelihood ratio based test statistic is

$$L{R}_t=\underset{H_A}{\text{max}}\frac{P\left(C_t=c_t|H_A\right)}{P\left(C_t=c_t|H_0\right)}=\underset{RR>1}{\text{max}}\frac{e^{-RR{\mu }_t}{\left(RR{\mu }_t\right)}^{c_t}/c_t!}{e^{-{\mu }_t}{\mu }_t^{c_t}/c_t!}=\underset{RR>1}{\text{max}}{e}^{(1-RR){\mu }_t}{(RR)}^{c_t}$$

The maximum likelihood estimate of RR is c_t/μ_t, so

$$L{R}_t=e^{{\mu }_t-c_t}{\left(c_t/{\mu }_t\right)}^{c_t}$$

Equivalently, when defined using the log likelihood ratio

$$LL{R}_t=ln\left({LR}_t\right)=\underset{RR>1}{\text{max}}\left((1-RR){\mu }_t+c_{t}ln(RR)\right)=\left({\mu }_t-c_t\right)+c_{t}ln\left(c_t/{\mu }_t\right)$$

This test statistic is sequentially monitored for all values of t > 0, until either LLR_t ≥ CV, in which case the null hypothesis is rejected, or until μ_t = T, in which case the alternative hypothesis is rejected. T is a predefined upper limit on the length of surveillance, defined in terms of the sample size, expressed as the expected number of adverse events under the null hypothesis. It is roughly equivalent to a certain number of exposed individuals, but adjusted for covariates. Exact critical values (CV) are available for the MaxSPRT[4], obtained through iterative numerical calculations.

3. Minimum Number of Events Required to Signal

Continuous sequential probability ratio tests may signal at the time of the first event, if that event appears sufficiently early. One could add a requirement that there need to be a minimum of M events before one can reject the null hypothesis. This still requires continuous monitoring of the data from the very start, as M events could appear arbitrarily early. Hence, there is no logistical advantage of imposing this minimum number. The potential advantage is instead that it may reduce the time to signal and/or increase the statistical power of the study. Below, in Section 3.2, it is shown that both of these can be achieved simultaneously.

3.1. Exact Critical Values

In Table 1 we present the critical values for the maximized SPRT when requiring a minimum number of events M to signal. When M = 1, we get the standard maximized SPRT, whose previously calculated critical values[4] are included for comparison purposes.

Table 1:

Exact critical values for the Poisson based maximized SPRT, when a minimum of M events is required before the null hypothesis can be rejected. T is the upper limit on the sample size (length of surveillance), expressed in terms of the expected number of events under the null. The type 1 error is α = 0.05. When T is small and M is large, no critical value will result in α ≤ 0.05, which is denoted by ‘..’

	Minimum Number of Events Required to Reject the Null
T	M=1	2	3	4	6	8	10
1	2.853937	2.366638	1.774218	..	..	..	..
1.5	2.964971	2.576390	2.150707	1.683209	..	..	..
2	3.046977	2.689354	2.349679	2.000158	..	..	..
2.5	3.110419	2.777483	2.474873	2.187328	..	..	..
3	3.162106	2.849327	2.565320	2.317139	1.766485	..	..
4	3.245004	2.937410	2.699182	2.498892	2.089473	1.564636	..
5	3.297183	3.012909	2.803955	2.623668	2.267595	1.936447	..
6	3.342729	3.082099	2.873904	2.699350	2.406810	2.093835	1.740551
8	3.413782	3.170062	2.985560	2.829259	2.572627	2.337771	2.086032
10	3.467952	3.238009	3.064248	2.921561	2.690586	2.484834	2.281441
12	3.511749	3.290551	3.125253	2.993106	2.781435	2.589388	2.415402
15	3.562591	3.353265	3.199953	3.075613	2.877939	2.711996	2.556634
20	3.628123	3.430141	3.288216	3.176370	2.997792	2.846858	2.717137
25	3.676320	3.487961	3.356677	3.249634	3.081051	2.947270	2.827711
30	3.715764	3.534150	3.406715	3.307135	3.147801	3.019639	2.911222
40	3.774663	3.605056	3.485960	3.391974	3.246619	3.130495	3.030735
50	3.819903	3.657142	3.544826	3.455521	3.317955	3.210428	3.117553
60	3.855755	3.698885	3.590567	3.505220	3.374194	3.271486	3.184196
80	3.910853	3.762474	3.659939	3.580900	3.458087	3.362888	3.284030
100	3.952321	3.810141	3.711993	3.636508	3.520081	3.430065	3.355794
120	3.985577	3.847748	3.753329	3.680584	3.568679	3.482966	3.411235
150	4.025338	3.892715	3.802412	3.732386	3.626150	3.544308	3.476655
200	4.074828	3.948930	3.862762	3.796835	3.696511	3.619825	3.556799
250	4.112234	3.990901	3.908065	3.844847	3.748757	3.675703	3.615513
300	4.142134	4.024153	3.944135	3.882710	3.790143	3.719452	3.661830
400	4.188031	4.075297	3.998950	3.940563	3.852658	3.785930	3.731524
500	4.222632	4.113692	4.040021	3.983778	3.899239	3.835265	3.783126
600	4.250310	4.144317	4.072638	4.018090	3.936175	3.874183	3.823908
800	4.292829	4.191167	4.122559	4.070466	3.992272	3.933364	3.885600
1000	4.324917	4.226412	4.160022	4.109665	4.034210	3.977453	3.931529

The exact critical values are based on numerical calculations using the R package ‘Sequential’. The critical values were calculated in the same manner as the exact critical values for the Poisson based MaxSPRT [4], with the modified requirement that the first possible time to signal is at M rather than 1 event. In brief, first note that the time when the critical value is reached and the null hypothesis is rejected can only happen at the time when an event occurs. For any specified critical value CV and maximum sample size T, it is then possible to calculate alpha, the probability of rejecting the null, using an iterative approach. Critical values are then obtained through an iterative mathematical interpolation process, until the desired precision is obtained. In 3 to 7 iterations, the procedure converges to a precision of 0.00000001. Note that these numerical calculations only have to be done once for each alpha, T and M. Hence, users do not need to do their own numerical calculations, as long as they use one of the parameter combinations presented in Table 1.

The critical values are lower for higher values of M. This is natural. Since we do not allow the null hypothesis to be rejected based on only a small number of adverse events, it allows us to be more inclined to reject the null later on when there are a larger number of events, while still maintaining the correct overall alpha level. In essence, we are trading the ability to reject the null with a very small number of events for the ability to more easily reject the null when there are a medium or large number of events. Note also that the critical values are higher for larger values of the maximum sample size T. This is also natural, as there is more multiple testing that needs to be adjusted for when T is large.

3.2. Statistical Power and Expected Time to Signal

In Table 2 we present statistical power and average time to signal for different values of M, the minimum number of events needed to signal. These are exact calculations, done for different relative risks and for different upper limits T on the length of surveillance. When T increases, power increases, since the maximum sample size increases. For fixed T, the power always increases with increasing M. This is natural, since power increases by default when there are fewer looks at the data, as there is less multiple testing to adjust for. The average time to signal may either increase or decrease with increasing values of M. For example, with T = 20 and a true RR = 2, the average time of signal is 6.96, 6.62, 6.57 and 6.96 for M = 1, 3, 6 and 10, respectively. For the same parameters, the statistical power is 0.921, 0.936, 0.948 and 0.957 respectively. Hence, when the true RR = 2 and when T = 20, both power and the average time to signal is better if we use M = 3 rather than M = 1. The same is true for M = 6 versus M = 3, but not for M = 10 versus M = 6.

Table 2:

Statistical power and average time to signal, when the null hypothesis is rejected, for the Poisson based maximized SPRT when a minimum of M events is required before the null hypothesis can be rejected. T is the upper limit on the sample size (length of surveillance), expressed in terms of the expected number of events under the null. The type 1 error is α = 0.05.

		Statistical Power					Average Time to Signal
T	M	RR=1.5	2	3	4	10	RR=1.5	2	3	4	10
1	1	0.107	0.185	0.379	0.573	0.987	0.30	0.35	0.39	0.39	0.22
1	3	0.129	0.234	0.466	0.665	0.993	0.59	0.58	0.55	0.51	0.30
2	1	0.130	0.255	0.561	0.799	1.000	0.63	0.75	0.79	0.73	0.24
2	3	0.157	0.315	0.645	0.857	1.000	0.92	0.94	0.89	0.78	0.31
5	1	0.190	0.447	0.876	0.987	1.000	1.82	2.09	1.78	1.22	0.26
5	3	0.224	0.507	0.905	0.991	1.000	2.10	2.17	1.73	1.17	0.31
5	6	0.255	0.559	0.928	0.994	1.000	2.71	2.58	2.05	1.54	0.60
10	1	0.280	0.685	0.989	1.000	1.000	4.02	4.13	2.45	1.35	0.27
10	3	0.321	0.733	0.993	1.000	1.000	4.25	4.07	2.31	1.30	0.32
10	6	0.358	0.770	0.995	1.000	1.000	4.71	4.25	2.50	1.61	0.60
10	10	0.391	0.803	0.996	1.000	1.000	5.67	5.03	3.40	2.50	1.00
20	1	0.450	0.921	1.000	1.000	1.000	8.68	6.96	2.67	1.41	0.28
20	3	0.492	0.936	1.000	1.000	1.000	8.65	6.62	2.53	1.37	0.33
20	6	0.531	0.948	1.000	1.000	1.000	8.92	6.57	2.69	1.65	0.60
20	10	0.562	0.957	1.000	1.000	1.000	9.47	6.96	3.50	2.51	1.00
50	1	0.803	1.000	1.000	1.000	1.000	20.45	8.94	2.82	1.48	0.30
50	3	0.829	1.000	1.000	1.000	1.000	19.82	8.45	2.71	1.45	0.33
50	6	0.847	1.000	1.000	1.000	1.000	19.41	8.24	2.86	1.71	0.60
50	10	0.863	1.000	1.000	1.000	1.000	19.35	8.46	3.59	2.52	1.00
100	1	0.978	1.000	1.000	1.000	1.000	29.93	9.30	2.92	1.53	0.31
100	3	0.982	1.000	1.000	1.000	1.000	28.52	8.87	2.82	1.51	0.34
100	6	0.985	1.000	1.000	1.000	1.000	27.58	8.71	2.97	1.75	0.60
100	10	0.987	1.000	1.000	1.000	1.000	27.04	8.93	3.65	2.53	1.00
200	1	1.000	1.000	1.000	1.000	1.000	33.00	9.62	3.01	1.58	0.32
200	3	1.000	1.000	1.000	1.000	1.000	31.47	9.25	2.93	1.56	0.35
200	6	1.000	1.000	1.000	1.000	1.000	30.47	9.11	3.07	1.78	0.60
200	10	1.000	1.000	1.000	1.000	1.000	29.88	9.33	3.71	2.54	1.00

The trade-off between statistical power and average time to signal is not easily deciphered from Table 2, and it is hence hard to judge which value of M is best. Since T, the upper limit on the length of surveillance, is the least important metric, let’s ignore that for the moment, and see what happens to the average time to signal if we keep both the alpha level and the power fixed. That will make it easier to find a good choice for M, which will depend on the true relative risk. Figure 1 shows the average time to signal as a function of statistical power, for different values of M. The lower curves are better, since the expected time to signal is shorter. Suppose we design the sequential analysis to have 95 percent power to detect a relative risk of 1.5. We can then look at the left side of Figure 1 to see the average time to signal for different true relative risks. We see that for a true relative risk of 1.5, time to signal is shortest for M = 10. On the other hand, for a true relative risk of 2, it is shortest for M = 6, for a true relative risk of 3, it is shortest for M = 3 and for a true relative risk of 4, it is shortest for M = 2. On the right side of Figure 1, we show the expected time to signal when the surveillance has been designed to attain a certain power for a relative risk of 2. The results are similar.

Figure 1:

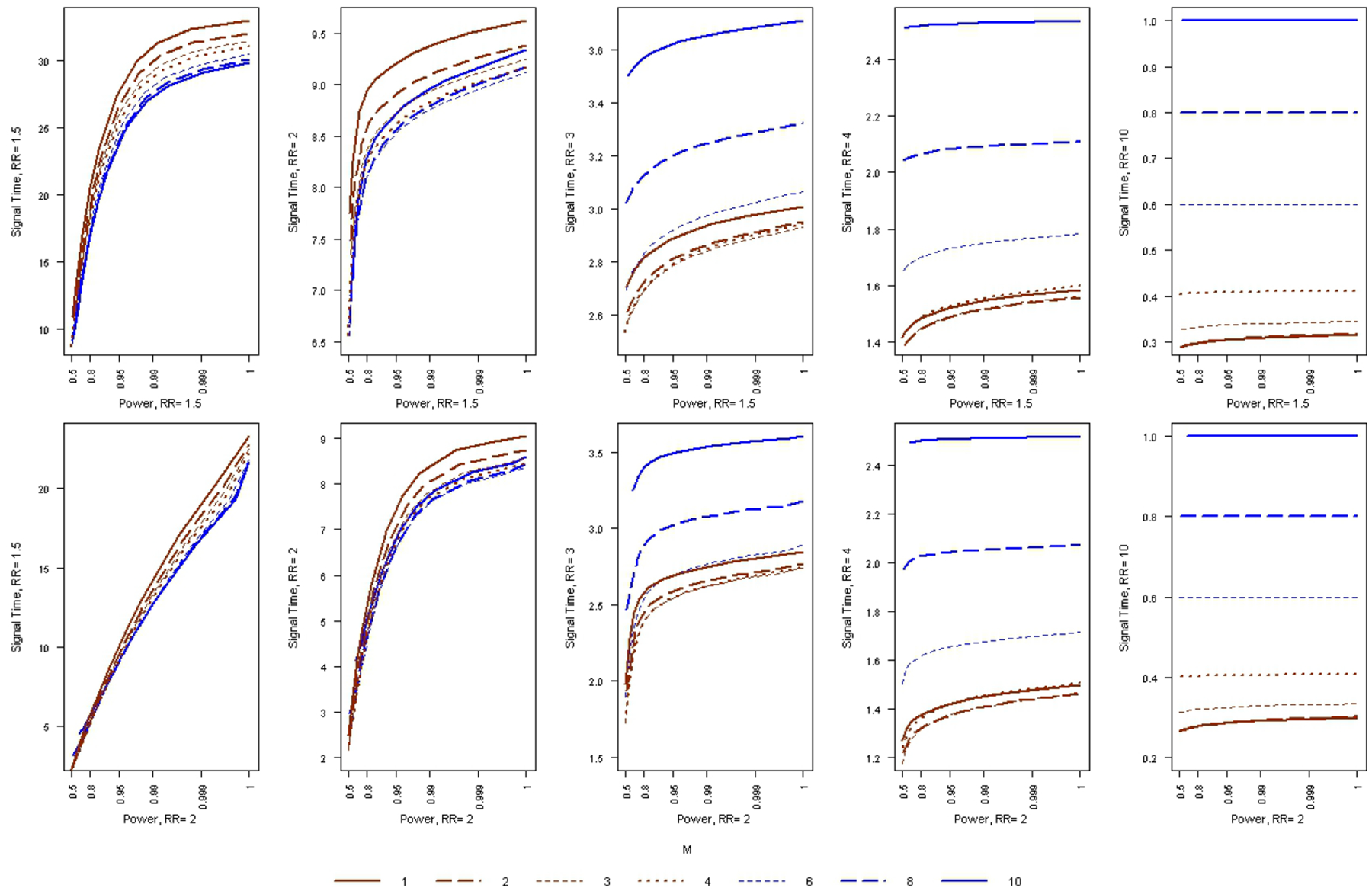
The average time to signal, as a function of statistical power, for the Poisson based MaxSPRT when a minimum of M events is required before the null hypothesis can be rejected. The type 1 error is α = 0.05.

When the true relative risk is higher, it is a more serious safety problem, and hence, it is more important to detect it earlier. So, while there is no single value of M that is best overall, anywhere in the 3 to 6 range may be a reasonable choice for M. The cost of this reduced time to signal when the null is rejected is a slight delay until the surveillance ends when the null is not rejected.

4. Delayed Start of Surveillance

For logistical or other reasons, it is not always possible to start post-marketing safety surveillance at the time that the first vaccine or drug is given. If the delay is short, one could ignore this and pretend that the sequential analyses started with the first exposed person. One could do this either by starting to calculate the test statistic at time D or by calculating it retroactively for all times before D. The former will be conservative, not maintaining the correct alpha level. The latter will maintain the correct alpha level, but, some signals will be unnecessarily delayed without a compensatory improvement in any of the other metrics. A better solution is to use critical values that take the delayed start of surveillance into account.

4.1. Exact Critical Values

In Table 3 we present exact critical values for the maximized SPRT when surveillance does not start until the expected number of events under the null hypothesis is D, without any requirement on having a minimum umber of events to signal. When D = 0, we get the standard maximized SPRT, whose critical values [4] are included for comparison purposes. Note that the critical values are lower for higher values of D. Since surveillance is not performed until the sample size have reached D expected counts under the null, one can afford to use a lower critical value for the remaining time while still maintaining the same overall alpha level. As before, the critical values are higher for larger values of T. When D > T, the surveillance would not start until after the end of surveillance, so those entries are blank in Table 3. When D = T, there is only one non-sequential analysis performed, so there are no critical values for a sequential test procedure. Hence, they are also left blank in the Table.

Table 3:

Exact critical values for the Poisson based maximized SPRT, when surveillance does not start until the sample size is large enough to generate D expected events under the null hypothesis. T > D is the upper limit on the sample size. The minimum number of events needed to reject is set to M = 1. The type 1 error is α = 0.05. For some values of T and D, the critical values are conservative with α < 0.05. These are denoted in italics.

	D
T	0	1	2	3	4	6	8	10
1.5	2.964971	1.683208	..	..	..	..	..	..
2	3.046977	2.000158	..	..	..	..	..	..
2.5	3.110419	2.187328	1.600544	..	..	..	..	..
3	3.162106	2.317139	1.766484	..	..	..	..	..
4	3.245004	2.498892	2.089473	1.842319	..	..	..	..
5	3.297183	2.545178	2.267595	1.936447	1.611553	..	..	..
6	3.342729	2.546307	2.406809	2.093835	1.921859	..	..	..
8	3.413782	2.694074	2.572627	2.337771	2.211199	1.829011	..	..
10	3.467952	2.799333	2.591675	2.484834	2.298373	2.087405	1.834622	..
12	3.511749	2.880721	2.683713	2.589388	2.415402	2.254018	1.965660	1.755455
15	3.562591	2.970411	2.794546	2.711996	2.556634	2.347591	2.203782	2.020681
20	3.628123	3.082511	2.918988	2.846635	2.717137	2.542045	2.425671	2.260811
25	3.676320	3.159490	3.011001	2.886783	2.827711	2.668487	2.527763	2.432668
30	3.715764	3.223171	3.080629	2.963485	2.911222	2.765594	2.634068	2.553373
40	3.774663	3.313966	3.186878	3.078748	3.030735	2.903286	2.789967	2.684730
50	3.819903	3.381606	3.261665	3.162197	3.117553	2.999580	2.897811	2.802863
60	3.855755	3.434748	3.320749	3.226113	3.162908	3.051470	2.978063	2.890933
80	3.910853	3.515052	3.407923	3.321868	3.247872	3.151820	3.090356	3.019184
100	3.952321	3.574091	3.472610	3.391377	3.321971	3.232345	3.155596	3.109251
120	3.985577	3.620223	3.523446	3.445695	3.379278	3.294843	3.222053	3.177847
150	4.025338	3.675035	3.583195	3.509028	3.446674	3.367227	3.298671	3.238461
200	4.074828	3.742843	3.655984	3.587079	3.528662	3.454679	3.391821	3.336012
250	4.112234	3.792978	3.710128	3.644349	3.588871	3.518954	3.459256	3.406929
300	4.142134	3.832686	3.752749	3.689355	3.636272	3.568952	3.512138	3.462111
400	4.188031	3.893093	3.785930	3.757574	3.707431	3.644405	3.591092	3.544518
500	4.222632	3.938105	3.835264	3.808087	3.760123	3.700032	3.649189	3.605012
600	4.250310	3.973710	3.874183	3.847892	3.801678	3.743656	3.694832	3.652326
800	4.292829	4.028089	3.933363	3.887512	3.864597	3.809685	3.763627	3.723608
1000	4.324917	4.047191	3.977453	3.931529	3.911308	3.858669	3.814122	3.776275

With a delayed start, there are some values of T and D for which there is no critical value that gives an alpha level of exactly 0.05. For those combinations, denoted with italics, Table 3 presents the critical value that gives the largest possible alpha less than 0.05. In Table 4, we present the exact alpha levels obtained for those scenarios, as well as the α > 0.05 obtained for a slightly smaller liberal critical value.

Table 4:

Critical values and exact alpha levels for those combinations of T, D and M for which there does not exist a critical value for α = 0.05. T is the upper limit on the sample size (length of surveillance), expressed in terms of the expected number of events under the null. D is the sample size at which the sequential analyses start, also expressed in terms of the expected number of events under the null. M is the minimum number of events required to signal. CV_cons and CV_lib are the conservative and liberal critical values, respectively, while α_cons and α_lib are their corresponding alpha levels.

T	D	M	CV cons	α cons	CV lib	α lib
5	1	1,4	2.545178	0.04587	2.545177	0.05323
10	2	1,4	2.591675	0.04998	2.591674	0.05478
10	4	1,4	2.298373	0.04924	2.298372	0.05379
10	8	1,4	1.834622	0.04373	1.834621	0.05001
15	10	1,4	2.020681	0.04755	2.020680	0.05124
20	3	1,4	2.846635	0.04712	2.846634	0.05001
60	4	1,4	3.162908	0.04922	3.162907	0.05094
60	6	1,4	3.051470	0.04953	3.051469	0.05101
80	8	1,4	3.090356	0.04906	3.090355	0.05023
800	3	1,4	3.887512	0.04992	3.887511	0.05091
1000	1	1,4	4.047191	0.04944	4.047190	0.05094
1000	8	1,4	3.814122	0.04944	3.814121	0.05002

The exact critical values are based on numerical calculations done in the same iterative way as for the original MaxSPRT and the version described in the previous section. The only difference is that there is an added initial step where the probabilities are calculated for different number of events at the defined start time D. Open source R functions[25] have been published as part of the R package ‘Sequential’ (cran.r-project.org/web/packages/Sequential/).

4.2. Statistical Power and Timeliness

For a fixed value on the upper limit on the sample size T, the statistical power of sequential analyses always increases if there are fewer looks at the data, with the maximum attained when there is only one non-sequential analysis after all the data has been collected. Hence, for fixed T, a delay in the start of surveillance always increases power, as can be seen in Table 5. For fixed T, the average time to signal almost always increases with a delayed start. The rare exception is when T is very large and the true RR is very small. For example, for T = 100 and RR = 1.5, the average time to signal is 29.9 without a delayed start, 27.2 with a delayed start of D = 3 and 27.0 with a delayed start of D = 6. With a longer delay of D = 10, the average time to signal increases to 27.4.

Table 5:

Statistical power and average time to signal for the Poisson based maximized SPRT, when the analyses does not start until the sample size is large enough to correspond to D expected events under the null hypothesis. T is the upper limit on the sample size (length of surveillance), expressed in terms of the expected number of events under the null. The minimum number of events required to signal is set to M = 1. The type 1 error is α = 0.05.

		Power					Average Time to Signal
RR=		1.5	2	3	4	10	1.5	2	3	4	10
T	D
5	0	0.190	0.447	0.876	0.987	1.000	1.82	2.09	1.78	1.22	0.26
5	3	0.275	0.595	0.943	0.996	1.000	3.81	3.65	3.30	3.08	3.00
10	0	0.280	0.685	0.989	1.000	1.000	4.02	4.13	2.45	1.35	0.27
10	3	0.377	0.789	0.996	1.000	1.000	5.33	4.84	3.53	3.10	3.00
10	6	0.408	0.819	0.997	1.000	1.000	6.94	6.59	6.07	6.00	6.00
20	0	0.450	0.921	1.000	1.000	1.000	8.68	6.96	2.67	1.41	0.28
20	3	0.543	0.952	1.000	1.000	1.000	9.44	7.06	3.78	3.17	3.00
20	6	0.583	0.963	1.000	1.000	1.000	10.42	8.20	6.15	6.01	6.00
20	10	0.609	0.969	1.000	1.000	1.000	12.33	10.83	10.01	10.00	10.00
50	0	0.803	1.000	1.000	1.000	1.000	20.45	8.94	2.82	1.48	0.30
50	3	0.860	1.000	1.000	1.000	1.000	19.39	8.50	3.85	3.18	3.00
50	6	0.871	1.000	1.000	1.000	1.000	19.65	9.43	6.16	6.01	6.00
50	10	0.885	1.000	1.000	1.000	1.000	20.64	11.82	10.02	10.00	10.00
100	0	0.978	1.000	1.000	1.000	1.000	29.93	9.30	2.92	1.53	0.31
100	3	0.987	1.000	1.000	1.000	1.000	27.16	8.95	3.90	3.18	3.00
100	6	0.988	1.000	1.000	1.000	1.000	26.98	9.97	6.24	6.01	6.00
100	10	0.990	1.000	1.000	1.000	1.000	27.40	12.09	10.02	10.00	10.00
200	0	1.000	1.000	1.000	1.000	1.000	33.00	9.62	3.01	1.58	0.32
200	3	1.000	1.000	1.000	1.000	1.000	30.01	9.35	3.94	3.18	3.00
200	6	1.000	1.000	1.000	1.000	1.000	29.78	10.31	6.26	6.01	6.00
200	10	1.000	1.000	1.000	1.000	1.000	30.16	12.48	10.04	10.00	10.00

For fixed T, we saw that there is a trade-off between power and the time to signal, but in post-market safety surveillance it is usually easy and inexpensive to increase power by increasing T. Hence, the critical evaluation is to compare the average time to signal when holding both power and the alpha level fixed. This is done in Figure 2. When the study is powered for a relative risk of 2, then the average time to signal is lower when there is less of a delay in the start of the surveillance, whether the true relative risk is small or large. When the study is powered for a relative risk of 1.5, we see the same thing, except when the true relative risk is small. Hence, in terms of performance, smaller D is always better.

Figure 2:

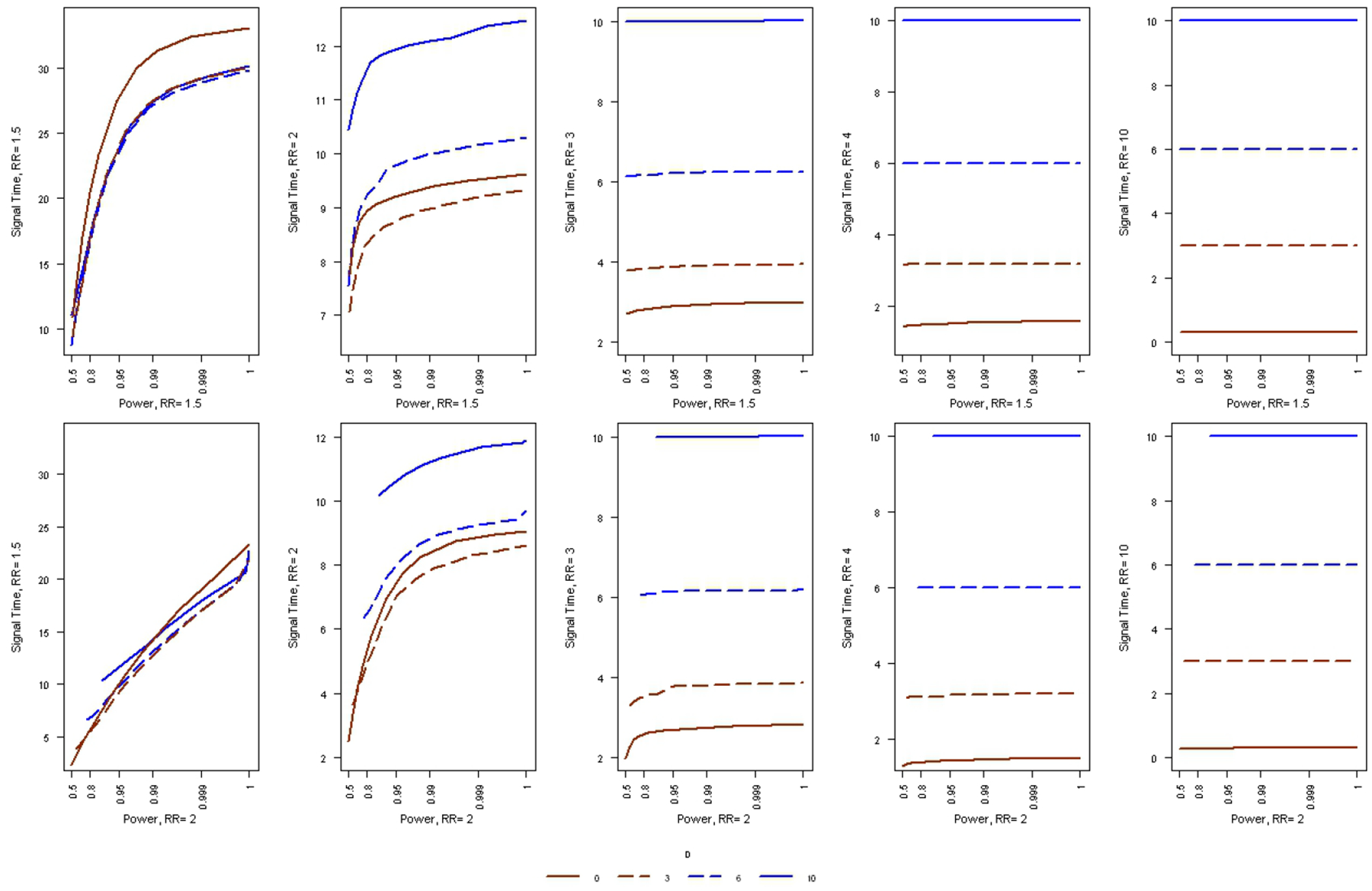
The average time to signal, as a function of statistical power, for the Poisson based maximized SPRT, when the analyses does not start until the sample size is large enough to correspond to D expected events under the null hypothesis. The type 1 error is α = 0.05.

5. Discussion

With the establishment of new near real-time post-market drug and safety surveillance systems [16, 26, 27, 28, 29], sequential statistical methods will become a standard feature of the phramacovigilance landscape. In this paper we have shown that it is possible to reduce the expected time to signal when the null is rejected, without loss of statistical power, by requiring a minimum number of adverse events before generating a statistical signal. This will allow users to optimize their post-market sequential analyses.

In this paper we calculated the critical values, power and timeliness for Poisson based continuous sequential analysis with either a minimum events to signal requirement or when there is delayed start for logistical reasons. The reported numbers are based on exact numerical calculations rather than approximate asymptotic calculations or computer simulations. From a mathematical and statistical perspective, these are straight forward extensions of prior work on exact continuous sequential analysis. The importance of the results are hence from practical public health perspective rather than for any theoretical statistical advancements.

A key question is which sequential study design to use. There is not always a simple answer to that question, as the performance of the various versions depends on the true relative risk, which is unknown. One important consideration is that the early detection of an adverse event problem is more important when the relative risk is high, since more patients are affected. As a rule of thumb, it is reasonable to require a minimum of about M = 3 to 6 adverse events before rejecting the null hypothesis, irrespectively of whether it is a rare or common adverse event. For those who want a specific recommendation, we suggest M = 4.

Critical values, statistical power and average time to signal has been presented for a wide variety of parameter values. This is done so that most user will not have to perform their own calculations. For those who want to use other parameter values, critical values, power and expected time to signal can be calculated using the ‘Sequential’ R package that we have developed.

It is possible to combine a delayed start with D > 0 together with a requirement that there are at least M > 1 events to signal. It does not always make a difference though. For M = 4, the critical values are the same as for M = 1, for all values of D ≥ 1. That is because with D = 1 or higher, one would never signal with less than three events anyhow. Since the critical values are the same, the statistical power and average time to signal are also the same. This means that when there is a non-trivial delayed start, there is not much benefit from also requiring a minimum number events to signal, but the ‘Sequential’ R package has a function for this dual scenario as well.

There is no reason to purposely delay the start of the surveillance until there is some minimum sample size D. In the few scenarios for which such a delay improve the performance, the improvement is not measurably better than the improvements obtained by using a minimum number of observed events. Only when it is logistically impossible to start the surveillance at the very beginning should such sequential analyses be conducted, and then it is important to do so in order to maximize power, to minimize the time to signal and to maintain the correct alpha level.

For self-controlled analyses, a binomial version of the MaxSPRT [4] is used rather than the Poisson version discussed in this paper. For concurrent matched controls, a flexible exact sequential method is used that allows for a different number of controls per exposed individuals [30]. By default, these types of continuous sequential methods will not reject the null hypothesis until there is a minimum number of events observed. To see this, consider the case with a 1:1 ratio of exposed to unexposed and and assume that the first four adverse events all are in the exposed category. Under the null hypothesis, the probability of this is (1/2)⁴ = 0.0625, which does not give a low enough p-value to reject the null hypothesis even in a non-sequential setting. Hence, the null will never be rejected after only four adverse events, even when there is no minimum requirement. One could set the minimum number of exposed events to something higher, and that may be advantageous. If there is a delayed start for logistical reasons, then it makes sense to take that into account when calculating the critical value, for these two types of models as well.

Since the Vaccine Safety Datalink [31] launched the first near real-time post-marketing vaccine safety surveillance system in 2004 [2], continuous sequential analysis has been used for a number of vaccines and potential adverse events [1, 5, 6, 7, 8, 9, 10, 12]. The critical value tables presented in this paper has already been used by the Vaccine Safety Datalink project. As new near real-time post-market safety surveillance systems are being developed, it is important to fine-tune and optimize the performance of near-real time safety surveillance systems [16, 17, 27, 32, 33, 34]. While the improved time to signal is modest compared to the original version of the Poisson based MaxSPRT, there is no reason not to use these better designs.