Electronic structures and topological properties in nickelates Ln_n+1Ni_nO_2n+2

Abstract

After the significant discovery of the hole-doped nickelate compound Nd_0.8Sr_0.2NiO₂, analyses of the electronic structure, orbital components, Fermi surfaces and band topology could be helpful to understand the mechanism of its superconductivity. Based on first-principle calculations, we find that Ni 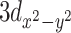states contribute the largest Fermi surface. The 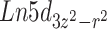states form an electron pocket at Γ, while 5d_xy states form a relatively bigger electron pocket at A. These Fermi surfaces and symmetry characteristics can be reproduced by our two-band model, which consists of two elementary band representations: B_1g@1a ⊕ A_1g@1b. We find that there is a band inversion near A, giving rise to a pair of Dirac points along M-A below the Fermi level upon including spin-orbit coupling. Furthermore, we perform density functional theory based Gutzwiller (DFT+Gutzwiller) calculations to treat the strong correlation effect of Ni 3d orbitals. In particular, the bandwidth of 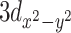has been renormalized largely. After the renormalization of the correlated bands, the Ni 3d_xy states and the Dirac points become very close to the Fermi level. Thus, a hole pocket at A could be introduced by hole doping, which may be related to the observed sign change of the Hall coefficient. By introducing an additional Ni 3d_xy orbital, the hole-pocket band and the band inversion can be captured in our modified model. Besides, the nontrivial band topology in the ferromagnetic two-layer compound La₃Ni₂O₆ is discussed and the band inversion is associated with Ni and La 5d_xy orbitals.

INTRODUCTION

After the discovery of high-T_c superconductivity in the cuprates [1,2], mixed-valent nicklates with similar crystals and electronic configurations as cuprates have attracted a lot of attention  [3]. In particular, the configuration of Ni⁺ in infinite-layer nickelates LnNiO₂ (Ln = La, Nd, Pr) is almost identical to that of Cu⁺⁺ in the parent compounds of cuprates. Although much effort has been devoted along this direction in the past two decades, the possible superconductivity in mixed-valent nicklates remains elusive. Until very recently, the superconductivity with T_c = 9 ∼ 15 K was discovered in hole doped Nd_0.8Sr_0.2NiO₂ for the first time [4]. For the parent compound NdNiO₂, previous studies have established several experimental facts that are distinct from the parent compound of cuprates. First, no long-range magnetic order is observed experimentally [5,6], while an antiferromagnetically ordered state is formed in the cuprates [7]. Second, NdNiO₂ exhibits a metallic behavior above 50 K [4], while the parent cuprates are Mott insulators [8]. Third, the superconductivity (so far) is only found in the hole doped Nd_0.8Sr_0.2NiO₂, while it is found in the electron-doped cuprate Sr_1−xLa_xCuO₂ in the same structure [9]. These experimental facts indicate that the ground state of the parent nickelates could have significant difference from the cuprates. Analyses of their electronic band structures, orbital components, Fermi surfaces and the band topology are needed. In addition, a minimal-band effective model is very helpful to further understand the mechanism of superconductivity.

In this work, we perform detailed first-principle calculations within the framework of density functional theory (DFT). The obtained band structure of the parent (undoped) compound NdNiO₂ is similar to that of LaNiO₂ reported previously [10] and PrNiO₂ (Nd-4f and Pr-4f orbitals are treated as core states). In this article, LaNiO₂ is taken as a representative and the band structures of NdNiO₂ and PrNiO₂ are presented in the online supplementary material. In the undoped case, there are three bands intersecting the Fermi level (E_F), mainly from Ni 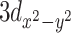, La 5d_xy and La 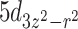orbitals. They form a large cylinderlike electron pocket (EP) surrounding the Γ-Z line, a spherelike EP at A and a comparatively smaller spherelike EP at Γ, respectively. These Fermi surfaces and symmetry characteristics can be reproduced by our two-band model, which consists of two elementary band representations (EBRs): B_1g@1a ⊕ A_1g@1b. The EBR of B_1g@1a refers to the 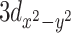orbital at Wyckoff site 1a[0,0,0], while the EBR of A_1g@1b refers to the A_1g orbital at Wyckoff site 1b[0,0,0.5], where no atoms sit.

We find that a band inversion near A happens between the Ni 3d_xy states and Ln 5d_xy states (the effect of Coulomb interaction U is discussed in the online supplementary material). With small U and spin-orbital coupling (SOC), this gives rise to a pair of Dirac points along M-A. After considering the renormalization of Ni 3d bands, the Dirac point becomes very close to the charge neutrality level and accessible by hole doping. As a result, a hole pocket (HP) could emerge at A, which may be responsible for the sign change of the Hall coefficient in the experiment  [4]. By introducing an additional Ni 3d_xy orbital, the hole-pocket band and the band inversion can be captured in the modified model. Besides, the nontrivial band topology in the ferromagnetic two-layer compound La₃Ni₂O₆ (n=2) is discussed and a band inversion happens between the Ni 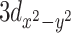and La 5d_xy orbitals.

CRYSTAL STRUCTURE AND METHODOLOGY

The parent compound LaNiO₂ can be obtained from the perovskites LaNiO₃ by removing the apical oxygens (i.e. b site), as shown in Fig. 1(a). Consequently, it has a tetragonal lattice, and has the same planes as the cuprate superconductors with Ni⁺ instead of Cu⁺⁺ ions. Similarly, the two-layer nickelate La₃Ni₂O₆ (see Fig. 1(b)) can be produced [11] from the two-layer perovskite La₃Ni₂O₇. We perform first-principle calculations using the VASP package [12,13] based on density functional theory with the projector augmented wave method [14,15]. The generalized gradient approximation (GGA) and the exchange-correlation functional of Perdew, Burke and Ernzerhof [16] are employed. The kinetic energy cutoff is set to 500 eV for the plane wave basis. A 10 × 10 × 10 k mesh for self-consistent Brillouin zone (BZ) sampling is adopted. The experimental lattice parameters of LaNiO₂ and La₃Ni₂O₆ are employed  [4,11].

Figure 1.

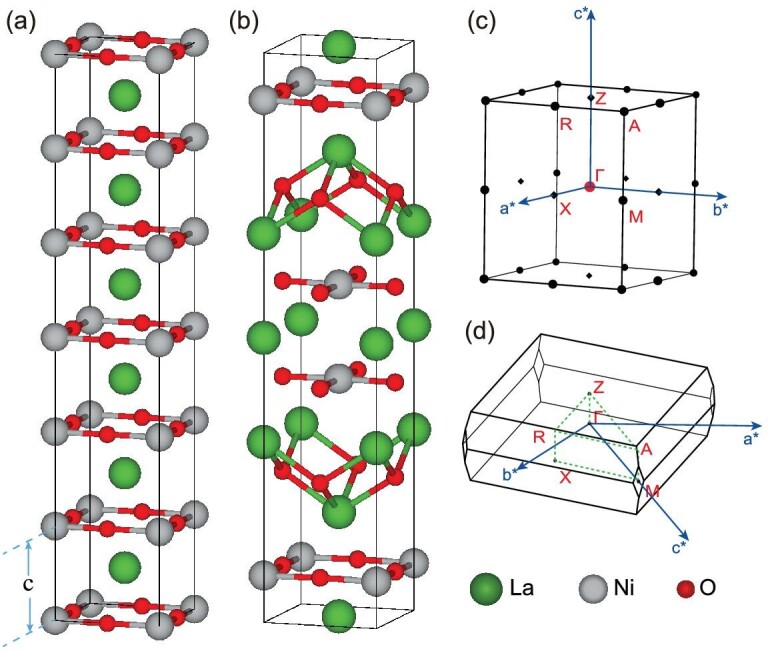
Crystal structures and Brillouin zones. The crystals of the two end members LaNiO₂ (n = ∞, P4/mmm) and La₃Ni₂O₆ (n = 2, I4/mmm) are presented in (a) and (b), respectively. The panel (a) contains six unit cells of LaNiO₂ (c is the lattice parameter in the 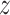direction). The primitive reciprocal lattice vectors and high-symmetry k points are indicated in the first Brillouin zones of (c) LaNiO₂ and (d) La₃Ni₂O₆. a^*, b^* and c^* refer to the primitive reciprocal lattice vectors.

RESULTS AND DISCUSSIONS

Band structure and density of states

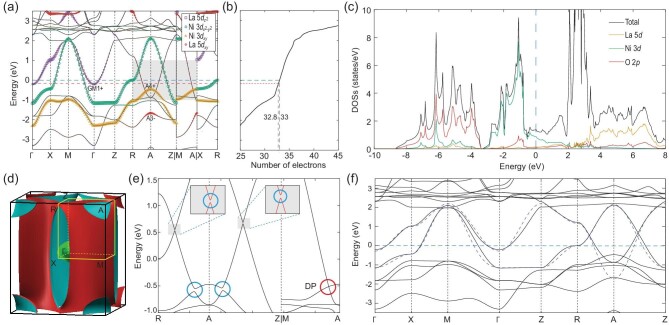
We first perform first-principle calculations on LaNiO₂ without SOC. The band structure is presented in Fig. 2(a) and the total density of states is given in Fig. 2(c). The blue dashed horizontal line corresponds to the charge neutrality level of the undoped case. The red dashed line in Fig. 2(b) is the theoretically estimated chemical potential for the 20% hole-doped superconductivity Nd_0.8Sr_0.2NiO₂. Moreover, the partial DOSs are also computed for O 2p, Ni 3d and La 5d orbitals, respectively. Since the main quantum numbers of different atom’s orbitals are distinct, we call them 2p, 3d and 5d orbitals (states) for short in the following discussion. From the plotted partial DOSs in Fig. 2(c), we note that 2p states are mainly located from −10 to −3.5 eV below E_F, while 3d states are around E_F, from −3.5 to 1.5 eV. The situation is much different from the situation in copper-based superconductors, where O 2p states are slightly below E_F and hybridize strongly with Cu 3d states  [10]. In addition, from the orbital projections in Fig. 2(a), we note that there are 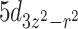states at Γ and 5d_xy states at A around E_F, suggesting that the 5d states are more extended, compared to the Ca 3d states in CaCuO₂  [17].

Figure 2.

(a) The band structure of LaNiO₂ without SOC. The weights of the La 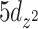, Ni 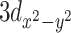, Ni 3d_xy and La 5d_xy states are indicated by the size of the purple squares, green circles, yellow triangles and red diamonds, respectively. The La 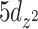band at Γ is labeled GM1+, while the Ni 3d_xy and La 5d_xy bands at A are labeled A4+ and A3−, respectively. The blue dashed line represents the Fermi level E_F and the red dashed line represents the estimated chemical potential in the hole-doped Nd_0.8Sr_0.2NiO₂. The total number of electrons as a function of the chemical potential is plotted in (b). The partial density of states (DOSs) is given in (c). The Fermi surfaces of LaNiO₂ are shown in (d). In the band structure with SOC (e), the crossings in the shadowed area of (a) are gapped except the Dirac point (DP) along M-A. The bands of our two-band model are shown as blue dashed lines in (f).

Evolution of Fermi surfaces

At the charge neutrality level, we find that there are three bands crossing E_F, which are mainly from 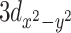, 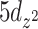and 5d_xy orbitals, respectively. The weights of these orbitals are depicted by the size of the different symbols in Fig. 2(a). Therefore, as shown in Fig. 2(d), three EPs are formed: (i) the 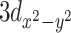orbital forms the largest electron pocket around the Γ and Z points, which has a strong two-dimensional (2D) feature; (ii) the second larger EP is nearly a sphere around A, formed by the 5d_xy orbital; (iii) the smallest EP is a sphere around Γ, formed by the 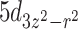orbital (which is also hybridized with the Ni 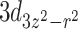orbital in the DFT calculations, yet we still call it 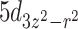for simplicity).

In the hole-doped superconductor Nd_0.8Sr_0.2NiO₂, the estimated chemical potential of the 20% Sr-doped level is denoted by a red dashed line, which corresponds to 32.8 electrons per unit cell (the charge neutrality level corresponds to 33 electrons). Needless to say that all the electron pockets become smaller with hole doping. In particular, the 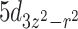-orbital-formed Γ-centered EP is about to be removed. On the other hand, the states from the 3d_xy orbital become closer to the chemical potential, especially in the vicinity of point A.

Band inversion and Dirac points

The band crossings along R-A, A-Z and M-A are protected by m₀₀₁, m₁₁₀ and C₄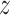, respectively. After considering SOC, the band crossings open small gaps (blue circles) along the mirror protected R-A and A-Z lines, but remain gapless along the C₄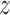-invariant line M-A, as shown in Fig. 2(e). The gapless Dirac points along M-A [highlighted in the red circle in Fig. 2(e)] are protected by C₄ 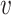symmetry. Namely, the two doubly degenerate bands belong to different 2D irreducible representations (IRs) of the C₄ 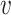double group. In our GGA+U calculations, we find that the band inversion is sensitive to the value of the Coulomb interaction U, as we show in the online supplementary material.

Analysis of EBRs and orbitals

By doing an analysis of EBRs in the theory of topological quantum chemistry [18], we can also obtain orbital information in real space. An EBR of ρ@q is labeled by the Wyckoff position q and the IR ρ of its site symmetry group. The IRs of the six low-energy bands at maximal high symmetry k points  [19,20] are computed without SOC. The results are listed in Table 1. In the crystal of LaNiO₂, the Ni atom sits at Wyckoff position 1a[0, 0, 0], while the La atom sits at Wyckoff position 1d[0.5, 0.5, 0.5]. Both Wyckoff positions have the site-symmetry group of 4/mmm. Note that five d orbitals only support the IRs of 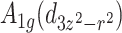, , 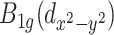B_2g (d_xy) and E_g (d_{xz, yz}) under the single group of 4/mmm.

Table 1.

The upper rows give the IRs for the lowest six bands in Fig. 2(a) at the maximal high-symmetry points in SG 123. The IRs are given in ascending energy order. The notation Zm(n) denotes the IR m at the Z point with degeneracy n. The lower rows give the elementary band representations, labeled as ρ@q. Here, ρ indicates the IR supported by the orbital(s), while q stands for the Wyckoff site, where the orbital(s) is (are) located. See https://www.cryst.ehu.es/cgi-bin/cryst/programs/bandrep.pl [21–23] for all eBRs and IRs.The gray IRs indicate that those energy bands are at least 1.0 eV above E_F.

	A	Γ	M	Z	R	X
DFT bands	A3 −(1)	GM1+(1)	M1+(1)	Z4+(1)	R4+(1)	X1+(1)
	A1+(1)	GM4+(1)	M4+(1)	Z5+(2)	R1+(1)	X4+(1)
	A5+(2)	GM5+(2)	M5+(2)		R2+(1)	X2+(1)
				Z1+(1)	R3+(1)	X3+(1)
	A4 +(1)	GM2+(1)		Z2+(1)	R1+(1)	X1+(1)
	A2+(1)	GM1+(1)	M5 −(2)	Z1+(1)	R2 −(1)	X4 −(1)
EBRs
A1g@1a	A1+	GM1+	M1+	Z1+	R1+	X1+
B1g@1a	A2+	GM2+	M2+	Z2+	R1+	X1+
B2g@1a	A4+	GM4+	M4+	Z4+	R2+	X2+
Eg@1a	A5+	GM5+	M5+	Z5+	R3+	X3+
					R4+	X4+
A1g@1d	A2 −	GM1+	M4+	Z3 −	R3+	X4 −
B2g@1d	A3 −	GM4+	M1+	Z2 −	R4+	X3 −
A1g@1b	A3 −	GM1+	M1+	Z3 −	R2 −	X1+

The results of the EBR analysis on atomic orbitals are as follows. First, by switching the IRs of A3− and A4+ at A, we find that the four occupied bands can be represented as the sum of three EBRs: A_1g@1a ⊕ B_2g@1a ⊕ E_g@1a. Among them, the 3d_xy-based EBR B_2g@1a has highest states at A, which may intersect with the chemical potential in the hole-doping case. Second, the band of the 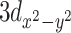-induced EBR B_1g@1a is clearly shown by the weights in Fig. 2(a). There is no doubt that the 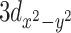orbital contributes the largest Fermi surface. Third, the IR GM1+ at Γ is from the 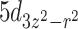-induced EBR A_1g@1d. Last, the inverted IR A3− is from the 5d_xy-induced EBR B_2g@1d. So far, all of the orbital compounds are consistent with our DFT calculations in Fig. 2(a).

We now aim to construct a minimal effective model to reproduce the bands and symmetry characteristics near E_F. Besides the 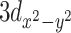-induced EBR of B_1g@1a, the two IRs of A3− and GM1+ can be generated in the EBR of A_1g@1b[0,0,0.5]. Therefore, we derive a two-band model, consisting of two EBRs: B_1g@1a ⊕ A_1g@1b, which reproduces the exact IRs of the bands near E_F from the DFT calculations. Even through there is no actual atomic orbital at Wyckoff position 1b (the apical oxygens are removed), it could be formed by the hybridization of the atomic orbitals on other sites. The two-band model will be constructed for the undoped case in the following section.

Two-band effective model

Under the basis of the B_1g orbital at the 1a Wyckoff position and the A_1g orbital at the 1b Wyckoff position, the tight binding model is constructed as follows. The diagonal terms in the Hamiltonian are

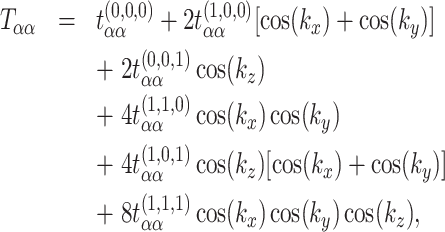(1)

where α = 1, 2 represent the B_1g orbital and the A_1g orbital, respectively. Here 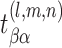stands for the hopping parameter from orbital β of the original cell to α of the (l, m, n) cell:

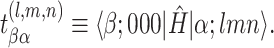(2)

In the off-diagonal term, the nearest and next-nearest hoppings between different orbitals are given as

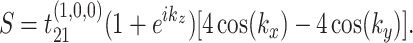(3)

Thus, our two-band model Hamiltonian is written as

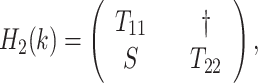(4)

where the dagger symbol means the Hermitian conjugate of the lower left part of the Hamiltonian matrix (same below). The fitting results are shown as blue dashed lines in Fig. 2(f) and the parameters can be found in Box 1. This two-band model can reproduce all the Fermi surfaces and symmetry characteristics obtained from the DFT calculations. It can be used for further study of superconductivity in the systems.

Box 1.

The hopping parameters for the two-band and three-band model Hamiltonians.

Parameters for the two-band model
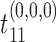
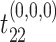
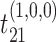
		0.1470		0.8318		0.0098
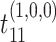
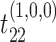
		−0.4125		0.0913
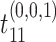
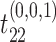
		−0.0538		0.0650
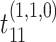
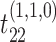
		0.0894		−0.0606
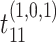
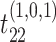
		0.0000		0.1988
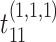
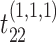
		0.0134		0.0281
Parameters for the three-band model
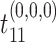
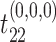
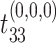
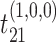
	0.0100		0.8280		−0.7960		0.0098
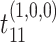
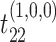
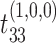
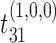
	0.0042		−0.0510		−0.1655		−0.0132
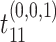
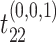
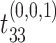
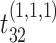
	0.0378		−0.0079		−0.0360		0.0001
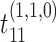
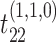
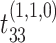
	0.0043		0.0105		−0.0497
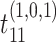
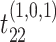
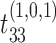
	−0.1338		0.0000		0.0105
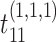
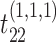
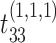
	0.0038		0.0018		−0.0113

DFT+Gutzwiller method

To treat the correlation effect of five Ni 3d orbitals, we employ the DFT+Gutzwiller method  [24,25]. The corresponding Gutzwiller trial wave function has been constructed as 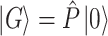with

(5)

where |0〉 is the noninteracting wave function and 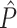is the Gutzwiller local projector with |i, Γ〉 the atomic eigenvectors on site i. The are the so-called Gutzwiller variational parameters that adjust the weights of different local atomic configurations. Ground states are obtained by minimizing the total energy E = 〈G|(H_tb + H_dc + H_int)|G〉 with some Gutzwiller constraints. The noninteracting Hamiltonian (H_tb) is extracted using the Wannier90 package  [26] from the DFT calculations without SOC, which contains two La 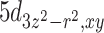orbitals and five Ni 3d orbitals. The double-counting term H_dc is given self-consistently. The on-site interacting term takes the Slater–Kanamori rotationally invariant atomic interaction  [27]

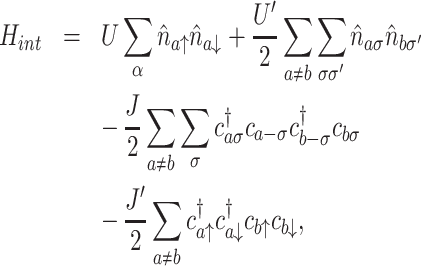(6)

where 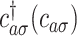creates (annihilates) an electron in the state of the orbital a and the spin σ, and .

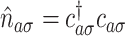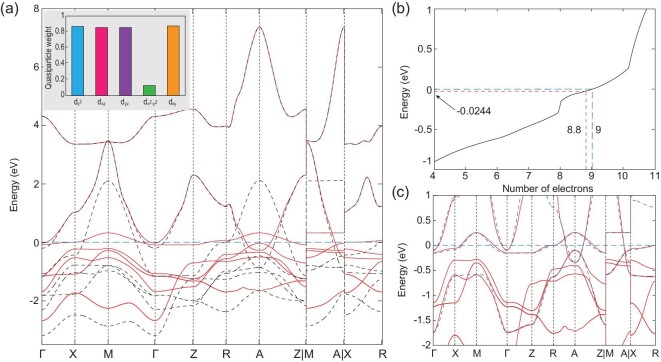
For simplicity, we adopt diagonal variational parameters, which mean that 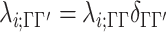here. Five Ni 3d orbitals are treated as correlated orbitals in the calculations (which correspond to 10 bands upon considering the spin degree of freedom). We take a Coulomb interaction U of 5 eV, Hund’s coupling J of 0.18U, where U^′ = U − 2J and J^′ = J. Besides, the occupancy of Ni 3d orbitals has been forced to be 8.462 obtained from the DFT calculations. The results show that the quasiparticle weight of the 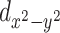orbital is very small, 0.12, while the weights of the other four orbitals are about 0.85. After considering the renormalization of the correlated 3d orbitals, the modified band structure is obtained and shown in Fig. 3(a). Two significant features are found after the Gutzwiller correction: (i) the bandwidth of 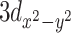has been largely renormalized, leading to a DOS peak around E_F, which may contribute to the large peak around zero energy in the resonant inelastic X-ray scattering spectrum (RIXS) [28]; (ii) the 3d_xy states near the A point become very close to E_F. As a result, a HP could be induced by hole doping, which may be related to the observed sign change of the Hall coefficient.

Figure 3.

(a) The band structure of the noninteracting tight-binding Hamiltonian H_tb, extracted by the Wannier90 package, is given by black dashed lines, while the DFT+Gutzwiller bands are plotted in red solid lines. The inset of (a) shows the quasiparticle weights of five 3d orbitals. In panel (b) we show the total number of electrons as a function of the chemical potential in the DFT+Gutzwiller band structure. In panel (c), the bands of the three-band model are given by blue dashed lines.

In addition, the band inversion between the 3d_xy states and 5d_xy states near the A point could be important in the hole-doped nickelate compound Nd_0.8Sr_0.2NiO₂, since they are very close to E_F. Therefore, we modify our model by simply adding an additional 3d_xy orbital to capture the potential band inversion in this hole-doped compound. The modified model is written as

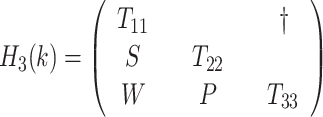(7)

with

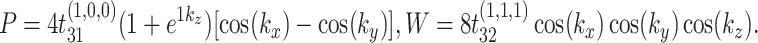The parameters are obtained by fitting with the renormalized bands, as shown in Box 1. The results of the modified model H₃(k) are shown as blue dashed lines in Fig. 3(c), which fit very well with the DFT+Gutzwiller bands, which can be compared with the angle-resolved photoemission spectroscopy (ARPES) experimental data. In any case, a four-band model constructed totally from the real atomic orbitals is presented in the online supplementary material.

Ferromagnetic state in La₃Ni₂O₆

To better understand the electronic structures of T^′-type La_n+1Ni_nO_2n+2 compounds (n ≥ 2), we calculate the other end member La₃Ni₂O₆ (i.e. n = 2 corresponds to the most reduced case) [29,30]. The ferromagnetic band structure of La₃Ni₂O₆ with SOC is shown in Fig. 4(a). The 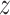-oriented magnetism [31] reduces the symmetry from type-II magnetic SG 139 to type-I magnetic SG 87. Near the M/A point, the four downward parabolic bands (i.e. 89–92 bands) are mainly from the 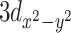states of Ni atoms in two planar Ni–O layers, while the two upward parabolic bands (i.e. 93–94 bands) are mainly from the 5d_xy states of the La atoms sandwiched by two Ni–O planes (Fig. 1(b)). Looking closely at the crossings between the 90th and 91st bands in Fig. 4(b), we find that there is a gap along X-M (R-A), while there are two crossing points along M-Γ (A-Z). These crossing points are parts of the tiny M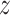-protected nodal rings at the k 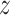= 0, 2π/c planes, which can be easily removed by very small perturbations (without changing the ordering of energy bands at high symmetry k points). According to symmetry indicators defined in magnetic systems [32], insulators in type-I MSG 87 are characterized by the indicators 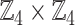[33,34], which can be explained by two mirror Chern numbers in the k 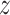= 0 plane. By using the C₄ eigenvalues [35], we find that the Chern numbers are 0 and 2 for the mirror eigenvalue +i and −i sectors, respectively, which indicate that nontrivial edge states can emerge on the M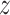-preserving surfaces.

Figure 4.

(a) The ferromagnetic band structure of the La₃Ni₂O₆ with SOC. The weights of La 5d_xy and Ni 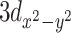states are indicated by the size of red diamonds and green circles, respectively. (b) The crossing points between 90th and 91st bands. Bands with different mirror eigenvalues are shown as blue (for +i) and red (for −i) lines.

CONCLUSION

Based on our first-principle calculations, we find that in the undoped case there are three EPs: the largest EP coming from the Ni 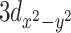orbital, a small EP at Γ from the La 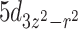orbital and a relatively larger EP at A from La 5d_xy. These Fermi surfaces and symmetry characteristics can be reproduced by our two-band model, which consists of two elementary band representations: B_1g@1a ⊕ A_1g@1b. This two-band model could be used for further study of superconductivity in these systems. In the obtained band structure, a band inversion occurred at A, which gives rise to a pair of Dirac points along M-A upon including SOC. The correlation effect of Ni 3d orbitals has been estimated in our DFT+Gutzwiller calculation, and the renormalized band structure obtained, which shows that Ni 3d_xy states become very close to E_F around A. A hole pocket is likely induced by hole doping, which may be related to the observed sign change of the Hall coefficient. The potential hole pocket and the band inversion can be captured in the modified model by simply including another Ni 3d_xy orbital. In addition, we show that the nontrivial band topology in the ferromagnetic two-layer compound La₃Ni₂O₆ is associated with Ni 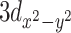and La 5d_xy orbitals.

Note added. While finalizing the present paper, similar works on nickelates were published  [36–40].

FUNDING

This work was supported by the National Natural Science Foundation of China (11974395, 11504117, 11774399, 11622435, U1832202, 11921004, 11925408 and 11674370), the Beijing Natural Science Foundation (Z180008), the Ministry of Science and Technology of China (2016YFA0300600, 2016YFA0401000, 2018YFA0305700 and 2016YFA0302400), the Strategic Priority Research Program of Chinese Academy of Sciences (XXH13506-202 and XDB33000000), the Beijing Municipal Science and Technology Commission (Z181100004218001, Z171100002017018) and the Center for Materials Genome. H.W. acknowledges support from the K. C. Wong Education Foundation (GJTD-2018-01). Z.W. acknowledges support from the CAS Pioneer Hundred Talents Program and the National Thousand-Young-Talents Program.

AUTHOR CONTRIBUTIONS

H.W., C.F. and Z.W. proposed and supervised the project. J.G. carried out the DFT calculations and built the effective models. J.G. and Z.W. did the symmetry analysis. S.P. performed the DFT+Gutzwiller calculations. All authors contributed to analyzing the results and writing the manuscript.

Conflict of interest statement. None declared.