Predicting special care during the COVID-19 pandemic: a machine learning approach

Abstract

More than ever, COVID-19 is putting pressure on health systems worldwide, especially in Brazil. In this study, we propose a method based on statistics and machine learning that uses blood lab exam data from patients to predict whether patients will require special care (hospitalization in regular or special-care units). We also predict the number of days the patients will stay under such care. The two-step procedure developed uses Bayesian Optimisation to select the best model among several candidates. This leads us to final models that achieve 0.94 area under ROC curve performance for the first target and 1.87 root mean squared error for the second target (which is a 77% improvement over the mean baseline)—making our model ready to be deployed as a decision system that could be available for everyone interested. The analytical approach can be used in other diseases and can help to plan hospital resources in other contexts.

Introduction

The COVID-19 pandemic is a considerable challenge for Brazil and many other countries around the world. The disease is putting tremendous pressure on health care services and there is no strong consensus on what measures are the most effective in terms of dealing with it. There are various independent reports that indicate a high occupancy rate in intensive care units with facilities to support patients who have severe respiratory tract failure and related conditions, thus creating a unique opportunity to solve this problem with scientific rigor helping to improve this difficult situation. The disease is spreading quickly, and social distancing measures are being phased out in several countries despite recommendations on the contrary issued by the World Health Organization (WHO) and the Centers for Disease Control and Prevention (CDC) [45].

As pointed out by [43], the massive amount of data acquired from several sources should be put into fair use for intensive training of machine learning algorithms to better understand the disease, the patients, and possible prognosis, enabling informed decision-making. Our main motivation is to unify subjects, such as Machine Learning, Optimization, Hospital Planning and applied AI to serve the purpose of using hospital resources responsibly and improve the quality of care provided to patients. We propose an analytical approach that leverages the most recent discoveries in each one of these areas and uses laboratory blood test data to estimate the probability of one given patient to require special-care treatment, also estimating the number of days the same patient will be under such care. Our aim is to create the basis of a decision system that can be used by anyone interested in replicating and estimating such outcomes, with the capability to expand the proposed method to deal with other diseases when needed.

We used data available in [14], which joins laboratory test data from the Sírio Libanês Hospital, Albert Einstein Israeli Hospital, and Fleury Laboratories (all located in the city of São Paulo, Brazil). These data comprise several different laboratory tests performed on patients (mostly blood tests). This preference for blood tests is not coincidental: most of them are well-standardized and usually inexpensive to perform, accessible in most situations, even for developing countries.

This article is organized as follows. In “Literature review” section , we examine some of the most relevant literature present in machine learning with a healthcare perspective. In “Method” section, we present our analytical approach used to create ML models to predict special care probability and extend the same techniques to predict how many days any given patient will spend under such care—focusing on the overall applicability and explainability of the models trained. The overall numerical results are then presented for both targets in “ Computational results” section, considering the candidate models and the final selected optimized ones. Finally, we present our conclusions, limitations and possible extensions that should follow for other diseases and situations where our approach could be useful.

Literature review

This literature review will focus on shedding light on recent efforts using ML and decision systems from a healthcare perspective. Some specific references concerning COVID-19 will be analyzed. Moreover, we will also focus on new, interesting and emerging applications for other diseases and situations to clarify research in the subject and compare this article with others in the same field.

Using statistical methods in healthcare for a large number of individuals comprising a great number of data points dates back to the 1950s. The Framingham Heart Study was established, showing correlations between doctors’ health measurements (including some laboratory test results) and heart diseases, diabetes, and obesity. See [35] for a historical perspective and [4] for a statistical point of view. This study is considered one of the finest and earliest examples of how statistics and decision systems could be implemented to help governments and policymakers make well-informed decisions that have a huge impact on a specific individual’s quality of life and overall survival rate.

After the 1950s, with the advent of faster computers that have high-level programming languages and frameworks, several studies arose under the ML and decision systems umbrella. From medicine to economics and social sciences, these studies helped people and governments to make more scientifically informed decisions with really huge and diverse data coming from different sources. From now on, we will focus on recent developments.

Recent examples of ML being used to detect and diagnose different types of diseases using test data appear in other contexts. In [19], classifiers can be observed that are applied to detect hematological disorders and are sometimes better than hematologists themselves. They are frontiers that algorithms, in general, are reaching leading to substantial implications.

In [1], the authors use laboratory data on patients also to detect blood diseases. In their approach, they select several candidate models within minimal pre-treatment of data to understand which algorithm behaves better. In the present study, we expand our reach by proposing a second optimization procedure on the selected algorithm type to improve the specificity-sensitivity characteristics of the final optimized model. Please see the scheme in Fig. 1 for more details.

Fig. 1.

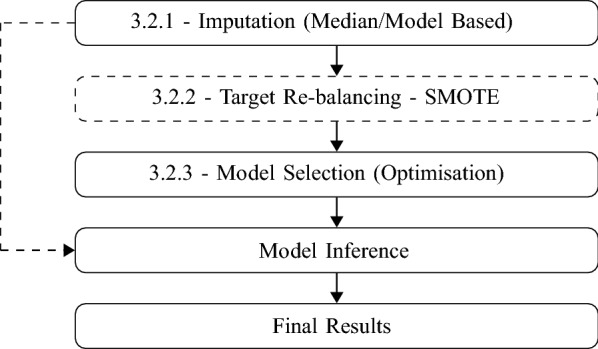
Steps in second part for our targets. Black continuous arrows are for training phase and dash one for prediction phase. Dashed step is not applied in number of days target

Blood test data are also being used to detect more complex types of diseases. There is a particular interest in several areas, in which [32] is an excellent example. They aim to detect more than 50 types of different cancers by analyzing different DNA signatures, showing a 99.3% specificity rate. This article can be seen as an improvement in the field of ”liquid biopsies,” reducing the need for patients to undergo complicated procedures to be given a diagnosis.

There are other diseases where ML algorithms-aided diagnosis could play a significant role. For example, [51] applies random forests for the final selected model to predict fatty liver disease and create an indicator to separate high-risk patients from low-risk ones, effectively allowing customization in treatments and improving overall outcomes. Considering other perspectives, there is also a substantial number of studies using algorithms that do not rely on laboratory data to predict outcomes (for example, deep learning to learn from medical images). A useful review on this topic is provided by [15], where heart disease applications, dengue fever, hepatitis, and diabetes are explored.

Analyzing the interface in decision systems, we can cite [3] as an application of ML-backed classifiers to understand the potential of bacterial infection in a given patient in a hospital setting. Special attention is given to prioritizing hospital resources and early detection of bacteremia, an infectious disease caused by microorganisms that propagate much like COVID-19. On the same topic, we can also cite [11], an article showing the creation of a decision system given to hospitals to predict the outcomes of Ebola in West African patients (Ebola is a highly contagious virus that demands special care of patients, resembling COVID-19).

There is also a wide range of books on these topics. In [25], various ML applications can be observed in different areas spanning disease diagnostics with laboratory data, image recognition methods, unsupervised learning and the Internet of Things.

Interest in these topics is becoming more substantial as time passes and technology advances. Conferences and meetings are being held in several places. One notable example is the Machine Learning for Healthcare [37] conference, which took place virtually in 2020 due to the COVID-19 pandemic.

Specifically linked to COVID-19, there are several reports on the use of ML to detect the disease using laboratory data. In [8], the authors trained classifiers that attained an 82%-86% accuracy while keeping high levels of specificity and sensitivity, therefore increasing the general applicability of the method selected. There is also an example in [12] of deep learning-based methods used to estimate the overall epidemiological parameters for the disease considering stacked Long Short-term Memory (LSTM) models and polynomial neural networks.

Some novel and fresh approaches are emerging from the need to diagnose patients using any data available. In [13], a novel feature generation approach can be observed in X-ray images combined with optimization techniques and high-performance computing used to create a classifier for patients with 96-98% accuracy. On an even more unusual front, text data is being used to diagnose patients in [27].

Considering that COVID-19 is itself a relatively novel subject, extensive reviews for articles relating it with ML algorithms are only beginning to emerge. One of the first examples is addressed in [29].

There are two main differences between this article and the ones cited earlier. The first one is the target itself: instead of predicting the presence/absence of COVID-19 in one give patient, we attempt to explore the probability of this patient requiring special care at hospital (and the number of days required under special care). The second main difference is the number of algorithms: instead of focusing on one or two algorithms, we firstly considered several, and then we select the best algorithm class overall to perform the Bayesian Optimisation. Table 1 summarizes the findings in this section and positions our study among them.

Table 1.

Review of machine learning for disease prediction

References	Algorithm	Key results
[4]	Logistic Regression, Random Forests	0.72 AUC
[11]	Model Ensembles	0.80 AUC
[51]	Random Forests	0.92 AUC
[3]	Random Forests	0.82 AUC
[1]	Several	0.69–0.97 AUC
[19]	Random Forests	59–$80\%$ Precision
[32]	Several	$99.3\%$ specificity
[8]	Random Forests, SVM and others	92–$95\%$ sensitivity
[12]	LSTM	62–$87\%$ accuracy
[13]	DNNs	96–$98\%$ accuracy
[27]	Naïve Bayes	$96.20\%$ accuracy
[25]	Several	–
[29]	Several	–
[15]	Several	–
This article	xgBoost + Bayesian Optimization	0.94 AUC

Method

This section addresses all the groundwork used in this study. Firstly, we present some medical basis, showing some results and references linking blood test results and their respective impacts on COVID-19 patients. We also offer the algorithmic reasoning behind all the techniques involved and why we selected them.

Medical basis

As COVID-19 is a virus, it is coherent to assume that it causes changes in patients’ blood tests. The article [31] brings a structured review on the parameters that show abnormalities in blood tests to a given patient when contracting COVID-19. Table 2 contains an excerpt of the main tests that show significant changes in laboratory test results for the patients analyzed in this study.

Table 2.

Main abnormalities found in COVID-19 patients, according to [31]

Lab exam	COVID-19 effects
Albumin	Decrease
Reactive C-Protein – PCR	Increase
Eritrocytes	Increase
Haemoglobin	Decrease
Leukocytes	Increase
Neutrofils	Increase
Lymphocytes	Decrease
TGP-ALT	Increase
TGO-AST	Increase
Lactate Desidrogenase-LDH	Increase
D Dimer	Increase
Bilirrubin	Increase
Creatinin	Increase
Troponin I	Increase
Procalcitonin-PCT	Increase
Protrombin	Increase

There are also consistent abnormalities described in [16], mainly dealing with white-blood cells, platelets, C-reactive protein, AST, ALT, GGT, and LDH parameters. This study concludes that some cutoffs for these tests could be applied as an alternative to RT-PCR tests when necessary and pave the way for automated tests using ML when more patient data becomes available.

In [53], the patients were separated using the overall gravity of the infection, which could be used as a proxy for special-care treatment. This study’s main results point out significant changes comparing the patients with established reference values and within different infection gravity groups. The most relevant values obtained were for the white-blood-cell count, LDH, C-reactive protein and others. Moreover, the article concludes by stating that the virus could be related to a state of hyper-coagulation in critically-ill patients, exposing a possible interaction between COVID-19 and laboratory blood test results. Knowing these facts, we propose an extension to use the same test data jointly with hospital outcomes to predict whether the same given patient will also need special care—effectively anticipating the use of valuable medical time and resources. We also model the number of days each patient will be in special care using the same data.

Machine learning procedure

Even without analyzing the available data, it is expected from the domain of science data that three things should be present: sparsity, as some laboratory tests are not performed for all patients, revealing many gaps (NAs) in the dataset. Moreover, one should expect unbalancing, as not all patients will require special care (only a small number of them will need it). The last thing expected is non-linearity and interaction. As every patient will have a different set of variables, the final combination and composition will express the outcome distinguished for each patient.

We will focus primarily on Sirio Libanês Hospital data, which includes patient outcomes and dates of admission and discharge, making it possible to analyze the number of days each patient stays in special care and associate it with laboratory test data. All data is taken for each patient, and a pre-processing step is carried out to relate the first test ever recorded for the patient, therefore we preserve the time dependency relevant to the problem. Later test should not constitute reliable data as they introduce temporal leaks.

To model the situation correctly, we propose (for both targets) a two-part procedure that addresses all issues cited above. The first part comprises an initial exploration of data to understand its particular shape and properties, focusing on age and blood white-cell components, as discussed earlier. After that, we explore the usage of off-the-shelf algorithms with little to no customization to better understand which candidate suits best - considering the baselines for each model (a coin for the classifier and the average training value for the target number of days in special care), as well the overall capacity to accept different hyperparameters to increase the fitness of the model. We also consider the training time and complexity trade-offs of all algorithms as a secondary but important factor.

Once the selected class of model is chosen, we follow the procedure outlined in Fig. 1, composed of data imputation, re-balancing, and estimation steps. The following subsections will deal with practicalities and possible choices showing the pros and cons for each one of the steps to pave the way to establish a precise method that can be used in other similar situations.

Imputation strategies

To process the data sparsity, we have three options with different assumptions, and each one implies model dynamics that are discussed in the next paragraphs. A sparsity treatment similar to ours can be found in [36], a seminal article in the field.

The first one retains the sparsity, i.e., not applying any technique to deal with the completion of variables. There are two disadvantages to this—the first one is that most models do not handle sparsity very well. Some of them even fail altogether during the training phase as they depend on a dense matrix for parameter estimation (a significant part of the ”classical statistical” models fall in this category). The second major issue is that models, in general, need some variance to ”learn” the most relevant variables in a dataset. When a dataset is substantially sparse, some variables lose their ”protagonism” and may become irrelevant even whether they are essential considering the application domain. The main advantage of using this approach is that data can be used as it is, without resorting to pre-processing and cleaning.

The second major option relies on model-based variable completion, such as the ones presented in [28, 50]. Most of these procedures consist of Singular Value Decomposition variants, commonly used in biological and medical applications. These model-assisted matrix completion algorithms introduce interaction terms that can be very useful whether the number of patients is high enough in the dataset. This technique’s main disadvantage is the care needed to find the optimal values for each of the hyperparameters in each of the algorithms, in turn consuming more time and computation resources. This is a barrier to implementing it for a huge dataset. However, there are some developments in running the algorithms more efficiently and parallelly distributed.

The third and more straightforward way is by inputting some known statistics of the sample as the default value for each variable. The most common values used for this are the mean and median (using the points with observations). Overall justification for this procedure relies on the fact that assuming that there are more healthy patients than unhealthy ones (or more patients that do not require special care), the mean and median for a sample describes a healthy population as the number of samples increase, helping models to identify abnormal values. The main disadvantage remains that some tests can be prescribed more for unhealthy (or healthy) patients, therefore, skewing the mean to be used as input, generating some sample bias.

In this study, we choose the second and third options interchangeably in different parts of the analysis—with a particular preference to use the third one, simplifying the calculations.

Data re-balancing

We should expect from the data that not all patients require special care. Moreover, it is likely that only a few of them will. In machine learning, this type of problem is known as unbalancing between classes. By having only a few samples of one specified occurrence, the model cannot generalize well, considering the few examples giving a low specificity/sensitivity model. Here accuracy is not essential because a model that responds to the predominant class will generally present a good value for accuracy. The Receiver Operating Characteristics (ROC) statistics can also be affected by this situation to a minor extent.

Some studies have attempted to understand the overall effect of unbalancing on classifiers of different types. For example, [40] tries to understand the widespread impact in several publicly available datasets and even proposes changes in calculating performance metrics that are more adequate to these situations. This is undoubtedly an improvement to the original problem, but we will use another alternative that is more automated and depends less on human interaction.

Manual techniques such as undersampling of the majority class or oversampling of the minority class through bootstrapping were usually considered in the past for some studies and practical applications, with mixed results and poor reproducibility when new data arrives for model updates. To avoid this, here we will use the Synthetic Minority Oversampling Technique as described by [39], a technique to combine the minority class oversampling and synthetic example generation with majority class undersampling, augmenting the area under the ROC curve statistics, making the model more sensitive to the minority class.

Model estimation and optimization

When selecting models for a specific application, several aspects should be considered. The most relevant is the overall ”capacity” of the algorithm—how a particular algorithm learns about different patterns existing in data without over-fitting to it. Most algorithms regulate this capacity by the change of hyperparameters controlling various aspects. Finding optimal hyperparameters is a matter of discussion in scientific debates as ML has gained traction as an everyday tool, as pointed out by [17], and is still a growing field for discoveries. Well-known libraries among data scientists for computational ML implement different strategies (see [42] for a good example). Most of them are based on grid searches of several parameters. Moreover, there are two major disadvantages doing this. The first and more obvious one is in the process itself, requiring a high number of evaluations in the cross-validation process, directly proportional to the number of folds. The second is less apparent and more critical which refers to the search space that needs to be crafted and selected (considering all relevant parameters for the problem).

While most techniques cannot deal well with the second disadvantage (crafting the search space), there is a possible improvement usually requiring fewer evaluations in our cross-validation procedure with its roots in optimization and statistics. Here we propose Bayesian Optimization as in [38] to select model hyperparameters achieving optimal performance within the selected grid. Our procedure will be very similar to the method described in [48]. The parameters we optimize will be discussed in the Results section for the selected algorithm.

Other algorithms and heuristics can be considered in this optimization problem. There are articles considering this in different contexts; good examples are [30, 33, 44], which consider some variations on heuristics from traditional particle swarms with different hyperparameter selections to more intricate heuristics such as gravitational search algorithm. There is a recent example of heuristics that was applied to a biological context in [22]. We consider applying heuristics in future revisions of our technique with new datasets. The authors opted for a Bayesian Optimization approach because our previous experience with the algorithm helped us to validate our results quickly.

Brief discussion about feature selection

A good statistical point-of-view in feature selection for biometrical applications can be seen in [24]. A ML approach can be seen in [9, 20]. We opted not to use feature selection methods in our analysis for two main reasons. The first one is increased algorithm complexity and running time. The second one is that we want for the algorithm to select the best variables based on the optimization process. In “Computational results” section, we detail the hyperparameters we used in our selected algorithm. We selected $L_1$ and $L_2$ regularization parameters to be optimized, and values for these parameters tend to shrink feature contribution, effectively working as a coupled feature selection mechanism inside our procedure, resembling the inner workings of LASSO [49].

Computational results

Here we present the computational results of our work, divided into three parts. First, in “Data” section, we analyze some data features of our problem, examining some variables already mentioned in other sections. In “Preliminary models” section , we use several algorithms with default parameters to select the best algorithm type to use together with Bayesian Optimization considering the hyperparameters to be tuned and their overall performance. In “Optimized models” section, we introduce the optimized models for both targets and discuss their results.

Data

Our dataset consists of laboratory test data collected from 9633 patients from the Sírio Libanês Hospital, who sought treatment in several different departments during the COVID-19 pandemic in Brazil. All patients from this list had a COVID-19 test (we included both positives and negatives), and 674 (7%) of them required special care treatment (hospitalization in common, semi-, or intensive care units). Among the ones requiring special treatment, the mean number of days needed for each patient was 1.52 days with a high variation, considering a standard deviation of 6.92 days.

There are 165 different types of laboratory test results (which in turn helps to understand the aforementioned sparsity). Considering demographics, the age and gender is available for each patient. Age will be analyzed further ahead in more detail.

We first show our exploratory analysis results in Table 3 considering some statistics for the dataset variables (for the ones with most coverage). We also show the two-sample Kolmogorov-Smirnov (KS) statistic value for each one considering special care target values as a class variable to understand the overall statistical difference between distributions that can arise between classes.

Table 3.

Variable metrics for the ones with most coverage within dataset (146 variables omitted)

	Mean	Std	Min	IQR	Max	Coverage (%)	KS statistic
Sex	0.46	0.50	0.0	1.0	1.0	100.0	0.00
Age (years)	42.48	13.99	15.0	17.0	87.0	99.0	0.00
MCH (pg)	29.16	2.26	18.0	2.0	38.0	18.0	0.17
Hematocrit (%)	39.61	5.48	15.0	6.0	62.0	18.0	0.00
CMCH (pg)	33.09	1.23	27.0	2.0	37.0	18.0	0.00
Erythrocytes (million/$m{m}^3$)	4.06	0.80	1.0	1.0	7.0	18.0	0.06
Leukocytes (/$m{m}^3$)	6258.91	3541.01	100.0	3015.0	55110.0	18.0	0.00
RDW (%)	13.22	2.51	11.0	2.0	38.0	18.0	0.02
Hemoglobin (g/dL)	12.97	1.99	5.0	2.0	21.0	18.0	0.00
Platelets	205748.36	78948.08	7000.0	95000.0	529000.0	18.0	0.00
Neutrophils (%)	61.71	14.57	1.0	19.0	97.0	18.0	0.00
Eosinophils ($m{m}^3$)	81.96	112.61	0.0	100.0	950.0	18.0	0.00
Monocites (%)	9.24	4.49	0.0	5.0	43.0	18.0	0.00
Eosinophils (%)	1.04	1.72	0.0	2.0	14.0	18.0	0.00
Lymphocytes (%)	25.75	12.38	0.0	16.0	84.0	18.0	0.00
Basofils (%)	0.07	0.30	0.0	0.0	4.5	18.0	0.19
Neutrophils ($m{m}^3$)	4132.13	3142.68	20.0	2550.0	53730.0	18.0	0.00
Lymphocytes (/$m{m}^3$)	1463.58	841.17	20.0	920.0	14350.0	18.0	0.00
Basofils ($m{m}^3$)	24.15	25.71	0.0	20.0	410.0	18.0	0.00
Monocites ($m{m}^3$)	575.24	420.51	10.0	310.0	9170.0	18.0	0.00
Platelet Volume	9.85	0.92	8.0	1.0	13.0	18.0	0.10
Creatinine (mg/dL)	0.51	0.86	0.0	1.0	11.0	16.0	0.00
Urea (mg/dL)	34.71	18.32	10.0	14.0	201.5	16.0	0.00
Potassium (mEq/L)	3.54	0.55	2.0	1.0	6.5	15.0	0.00
Sodium (mEq/L)	138.42	3.05	121.0	3.0	152.0	14.0	0.00
ALT (U/L)	37.26	38.03	6.0	25.0	521.0	13.0	0.00
AST (U/L)	35.76	45.41	9.0	16.0	1140.5	13.0	0.00
DHL (U/L)	488.87	345.04	201.5	166.0	8958.0	11.0	0.00

As pointed out in [5], age seems to be a critical factor overall considering COVID-19 and the sample of the population we are considering. As it is the only continuous demographic variable, we display the class histogram for age with adjusted kernels in Fig. 2. We see a very distinct separation between classes arising for each one of the groups. Moreover, this pattern by itself is not substantial in terms of making any assumptions or conclusions about our targets.

Fig. 2.

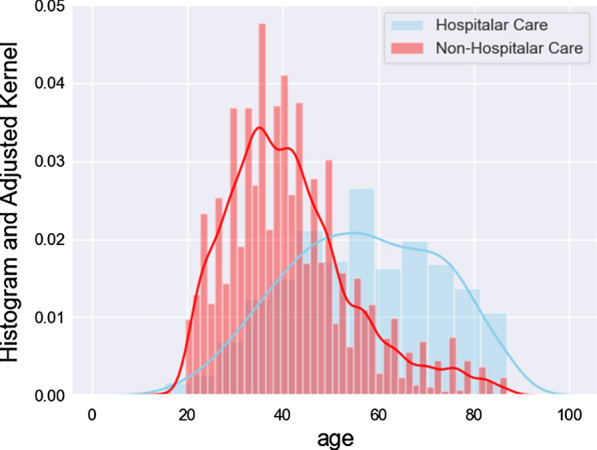
Histogram and adjusted kernels for age, divided using the special care target

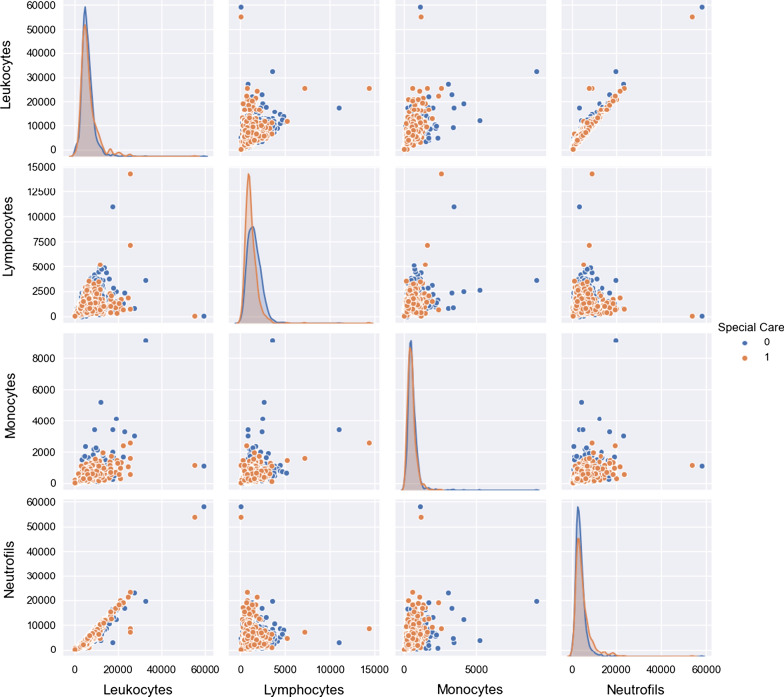
In Fig. 3, we see the histograms and adjusted kernels for selected white blood cell components count, which superficially represents immunological responses for each one of the patients in data and also mentioned as necessary by other authors investigating samples coming from similar conditions, as mentioned earlier. By close inspection, we see that separation for the variables considering the classes is not evident using only univariate reasoning, which again points to the necessity to use multivariate and non-linear algorithms.

Fig. 3.

Histogram and adjusted kernels for white-cell blood components, divided using the special care target

This brief analysis shows a perfect match for ML applications: We have sufficient patient data, with no identifiable univariate patterns relating to our target, thus opening up the possibilities of multivariate analysis and algorithms recognizing several different types of trends and interactions (the aforementioned non-linearity).

Preliminary models

To begin our modeling, we used several ML algorithms without tuning the parameters to select the best algorithm type to be optimized later. Our tests considered Naïve Bayes, Decision Trees, AdaBoost, Support Vector Machines (SVD), Linear Discriminant Analysis (LDA), Quadratic Discriminant Analysis (QDA), Logistic Regression (and regularized ones such as Ridge Regression and Least Absolute Shrinkage and Selection Operator (LASSO)), Orthogonal Matching Pursuit (OMP) and other algorithms based on ensembles of trees, such as Extra Trees [18], Random Forests [6], xgBoost [10], and LightGBM [26]. All results were obtained using Python 3.7 as our programming language. To obtain the following results, data were treated as-is, i.e., without any treatment or imputation strategies.

Model type selection for further optimization should consider three critical practical aspects, emphasizing the first two. The first one is predictive power—we want an algorithm that predicts well and does not overfit our data while capturing the multivariate effects that we expect. The second aspect involves the number of hyperparameters available to tune the model. The more parameters, the more opportunities we have to improve our algorithm predictive power while keeping the generalization capacity. The third reason is the training time—which, although less important, generates problems when the datasets are large enough and which can be considered even within our context because the algorithm requires several full training passes through our data when considering the optimization process. Table 4 presents results considering algorithms for the special care target and all relevant metrics. The baseline for this model is a coin with a ROC AUC value of 0.5. Table 5 presents results and relevant metrics for the number of days under special care target. The baseline here is the mean value of the training set.

Table 4.

Results from preliminary models on special care target (Top 10 of all models tested)

Model	Balanced accuracy	ROC AUC	F1 score	Time taken (s)
Bernoulli Naïve Bayes	0.90	0.90	0.92	0.14
QDA	0.88	0.88	0.91	0.22
Gausssian Naïve Bayes	0.85	0.85	0.95	0.15
xgBoost	0.85	0.85	0.96	1.31
LightGBM	0.82	0.82	0.96	0.47
AdaBoost	0.82	0.82	0.96	0.92
SVC	0.81	0.81	0.95	2.52
Random forest	0.81	0.81	0.96	1.14
Baging	0.80	0.80	0.96	0.78
Decision tree	0.80	0.80	0.96	0.23

Chosen algorithm for optimisation is highlighted

Table 5.

Results from models on number of days of special care needed (Top 10 of all models tested)

Model	R-squared	RMSE	Time taken (s)
xgBoost	0.70	2.15	1.28
Vanilla gradient boosting	0.68	2.22	1.98
Random forest	0.66	2.31	7.67
Bagging	0.64	2.38	0.92
LightGBM	0.60	2.49	0.36
Extra trees	0.60	2.50	9.65
Histogram gradient boosting	0.60	2.52	4.75
Huber regression	0.45	2.94	1.70
LinearSVR	0.44	2.96	3.14
Decision tree	0.43	2.99	0.22

Chosen algorithm for optimization is highlighted

The final selected algorithm is xgBoost for both targets. The primary rationale for this is the characteristics mentioned above: high predictive power, hyperparameter tuning, and overall training time. We could also select LightGBM interchangeably as the results were very close (and the algorithms are similar). Moreover, it was faster. Between the two algorithms, our previous experience with xgBoost motivated us to choose it. Algorithms such as the Naïve Bayes one stand out as they have almost no hyperparameters to tune and were unconsidered, even performing very well in the preliminary analysis.

Optimized models

Having selected the final algorithm type to use, we must define which hyperparameters to use in Bayesian Optimization and which strategy to deal with sparsity and unbalancing. Table 6 shows all parameters considered in the Bayesian Optimization and its respective intervals and descriptions. All optimization is performed using Ax [2], a platform created inside Facebook that streamlines all optimization processes and makes it possible to use integer hyperparameters, which are not available in other solvers.

Table 6.

Parameter grid and intervals used in Bayesian Optimisation procedure

	Interval	Description
Eta	[0.01, 1]	Learning rate (shrinkage applied in weights calculation)
Gamma	[0, 100]	Minimum loss reduction to split a node in tree
Max_depth	[1, 9]	Maximum depth of each tree in training process
Subsample	[0.5, 1]	Number of features used to train a tree
Lambda	[1, 100]	$L_2$ regularization term using in training
Alpha	[0, 100]	$L_1$ regularization term using in training
n_Estimators	[10, 200]	Total number of trees

For a classification model to be useful, we need to analyze Receiver Operating Characteristic (ROC) curves and Precision-Recall (P/R) curves, which can be a different format considering the variable distribution. Figure 4 summarizes the ROC curve and Fig. 5 summarizes the P/R curve. Using the median as imputer in our tests gave us the best results overall for the special care target.

Fig. 4.

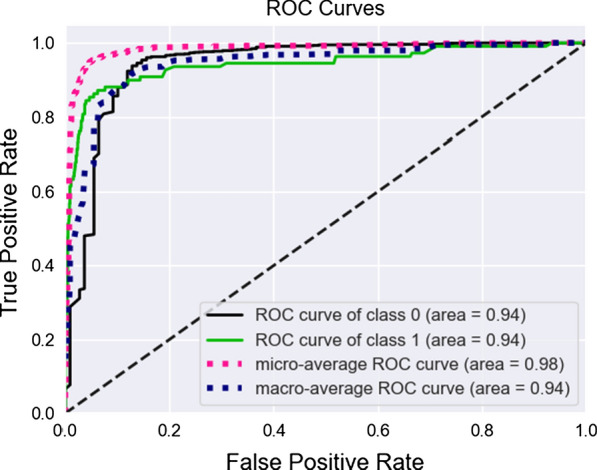
ROC Curve for special care target, both classes

Fig. 5.

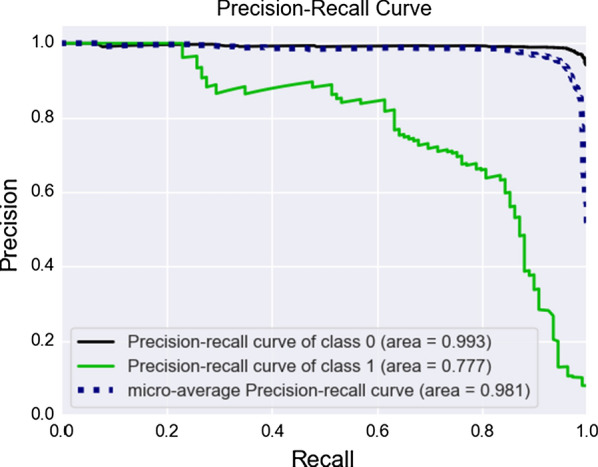
Precision-Recall Curves for special care target, both classes

It can be observed that our optimization improved the ROC statistic by selecting a new set of hyperparameters different from the defaults. By doing that, we guarantee that we have the best model while keeping model generalization capabilities.

From a hospital perspective, False Positives (the abscissa from our ROC plot) constitutes the most lost resources. They are patients that do not need any special care, but the model indicates the opposite, and we should keep them on a minimum level. We see by close inspection of the curves that this is satisfied, and the model is indeed useful for classifying patients using blood-test samples. At the best threshold value for cutoff, we obtained 0.94 for ROC AUC and 0.77 for P/R AUC.

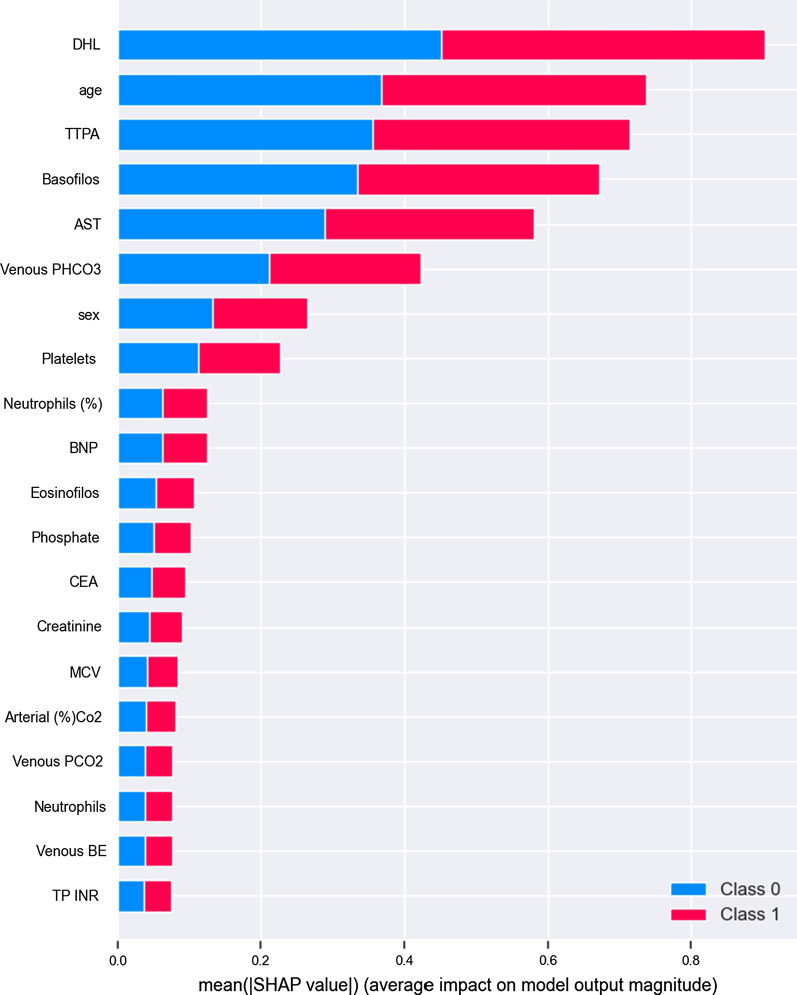
Moreover, as we used ensembles of trees to make predictions, one thing that arises naturally is a variable importance plot. To obtain this plot, we used Shap [34], which creates this plot using a game-theoretical approach to calculate the variable importance for row and data levels. In Fig. 6, it can be observed that some of the variables presented as important (mentioned in “Method” section) in [16, 53] are indeed some of the most relevant in our model, which are in line with the expectations (This plot should not be seen as indicating any direct causal relationships as our data is not experimental, but observational).

Fig. 6.

Variable importance plot for special care target, both classes

Results for the days under special care were similar in performance achievements. Table 7 summarizes the findings and compares them with the baseline for this model, the mean value of days spent in special care for the training set. Best results were obtained using no imputer at all (using model-based input gave us the worst results in comparison), defying some preconceptions we had from the start. This effect is explained in [23]: adding variables to boosted or bagged regressors can make the model worse. Using imputers, we forced the model to be non-sparse, giving protagonism to all variables at once, amplifying this condition. The condition for classifiers is the opposite: adding variables to boosted or bagged models always increases the performance (but the improvement could be marginal).

Table 7.

Results for days under special care target, baseline and percentual improvement over baseline

	Model	Baseline	Improvement (%)
RMSE	1.87	3.96	77.78
MAE	0.41	1.27	67.96
R-squared	0.78	0.00	–

Although our model is capable of making good predictions as guaranteed by statistical tests, in Fig. 7 we see a tendency to overshoot and undershoot the results caused by the very nature of the model (splits in trees have a very poor tendency in addressing extreme situations as the capacity to extrapolate wanes as we go to the ends of our interval). A more in-depth discussion on model improvement can be found in “Limitations and possible extensions” section.

Fig. 7.

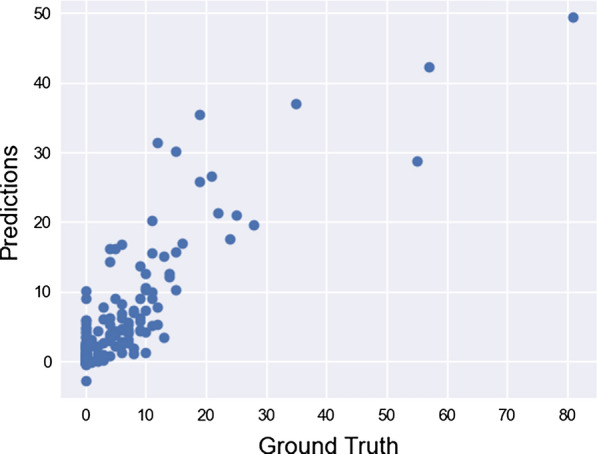
Scatterplot for days under special care target

Limitations and possible extensions

So far, with our classification model we have only dealt with 0/1 outcomes. But what happens if we want to order our patients according to their risk (risk being associated with a measure of probability ranging from 0 to 1)? The algorithm used to learn our special care from data is not well suited for this specific task. In [41], this effect is described as the algorithms having difficulties making predictions near the frontiers of the [0,1] interval because the variance of the base trees drives the result away from the edges in a way to minimize the overall cost function. To diagnose this problem, one can calculate the overall Brier score [7] for a given model or make a calibration plot. To solve this issue, we could apply Platt’s method [47], which essentially adjusts a Logistic Regression on a different fold during the model training phase or use an Isotonic Regression [52], again on a different fold during model training. However, more data for patients is required to perform that in a meaningful way.

To deal with negative predictions arising in the number of days under special care targets, we must first understand that the model used to make the predictions is not restricted in any form about the prediction interval itself. All of its predictions lie within the real line $\mathrm{I}\mathrm{R}$, but we know that our values are at least limited by 0. A recent way to deal with this is emerging in disciplines such as Finance and Banking, presented in [46] where ensembles of trees are trained to perform the Tobit regression. The overall maturity for the packages is increasing fast, posing as an exciting development as ensembles of trees have very high predictive power in general and several hyperparameters that can be optimized using Bayesian Optimization in the same process.

To deal with overshooting and undershooting for our number of days under special care targets, several possibilities are arising from traditional statistics worth exploring such as the Zero Inflated Negative Binomial (ZINB) models [21] in which the target distribution comprises a very high proportion of zeroes, such as our target. The result for this type of model usually consists of a probability attached to a counter, probability measuring the overall chance of a given patient needing special care, and the counter giving the number of days the same patient will spend under such care. The major drawback for this from the model is the predictive power (especially for the probability part), where standard packages use only linear terms (which introduce needs on data pre-processing, such as multicollinearity removal or variance inflation factors analysis) and no ensembles to make predictions. A viable but not tested alternative could be mixing two “worlds,” trying different sets of variables on the dataset guided by Bayesian Optimization, and then applying a ZINB model for each one, averaging the results. The counting model in this situation is discrete, also solving the issue with non-integer predictions.

Final remarks

The growing necessity to predict hospital resources’ needs guided the exploration of novel methods to create and plan policies accessible for everyone. More than ever, the COVID-19 pandemic is pushing health systems to the limit. Having this in mind, we developed an analytical approach based on mathematical models and algorithms adopting the most recent techniques available in the fields of statistics and machine learning using public data available online.

We obtained promising results in this study. The estimated 0.94 area under the ROC Curve combined with 0.77 P/R statistic proves that the analytical approach can indeed be used in a decision system for hospitals, governments, and health providers alike to guide their resource allocation with minimal requirements as we use test data that is available and affordable. The target for the number of days under special care certainly needs refinement but is adequate in our view. Other interesting results are also in line with other studies conducted by researchers all around the world.

Our biggest contribution was standardizing a method to create decision systems/ML models that can be applied to several different diseases, with low processing requirements, using cheap datasets that can be collected and analyzed easily. Our method also allows for suitable customization in the methods used and also for other infectious diseases.