Nonlinear dynamics and acoustic emissions of interacting cavitation bubbles in viscoelastic tissues

Highlights

• •The radial and translational motions of two interacting bubbles are studied.
• •Bubble dynamics is analyzed by bifurcation structures and acoustic emission spectra.
• •Small bubble is remarkably suppressed, while large bubble is slightly enlarged.
• •Bubble−bubble interaction reduces the nonlinear dynamics and acoustic emissions.
• •Viscoelasticity of the medium reduces the radial and translational bubble motions.

Abstract

The cavitation-mediated bioeffects are primarily associated with the dynamic behaviors of bubbles in viscoelastic tissues, which involves complex interactions of cavitation bubbles with surrounding bubbles and tissues. The radial and translational motions, as well as the resultant acoustic emissions of two interacting cavitation bubbles in viscoelastic tissues were numerically investigated. Due to the bubble–bubble interactions, a remarkable suppression effect on the small bubble, whereas a slight enhancement effect on the large one were observed within the acoustic exposure parameters and the initial radii of the bubbles examined in this paper. Moreover, as the initial distance between bubbles increases, the strong suppression effect is reduced gradually and it could effectively enhance the nonlinear dynamics of bubbles, exactly as the bifurcation diagrams exhibit a similar mode of successive period doubling to chaos. Correspondingly, the resultant acoustic emissions present a progressive evolution of harmonics, subharmonics, ultraharmonics and broadband components in the frequency spectra. In addition, with the elasticity and/or viscosity of the surrounding medium increasing, both the nonlinear dynamics and translational motions of bubbles were reduced prominently. This study provides a comprehensive insight into the nonlinear behaviors and acoustic emissions of two interacting cavitation bubbles in viscoelastic media, it may contribute to optimizing and monitoring the cavitation-mediated biomedical applications.

1. Introduction

Acoustic cavitation is a typical phenomenon in a medium subjected to ultrasound excitation, including the microbubble formation, oscillation, and violent collapse [1], [2], [3], [4], [5]. According to the nature of the bubble oscillation, cavitation can be categorized as stable cavitation, inertial cavitation, or a mixture of both [6], [7]. Stable cavitation is dominant at lower acoustic pressures, and it denotes the prolonged and periodic small-amplitude bubble oscillations. During stable cavitation, microstreaming can be generated in the surrounding medium, exerting shear stress on nearby objects [8], [9], and consequently leading to various bioeffects, such as sonoporation for site-specific drug/gene delivery [10], [11], [12], [13], opening of the blood–brain-barrier [14], [15] and neuromodulation [16], [17], etc. With the acoustic pressure increasing, inertial cavitation occurs and microbubbles undergo large-amplitude oscillations followed by violent collapse, which is more likely to produce serious cell/tissue damage, such as endothelial cell damage [18], vascular disruption [19] and tumor ablation [20], [21], etc. The bioeffects associated with cavitation are caused primarily by the dynamic behaviors of bubbles in viscoelastic tissues, hence the inappropriate cavitation type and intensity may result in inadequate treatment or potentially damaging bioeffects. To monitor the bubble dynamics, acoustic emissions generated by the cavitation bubbles could be recorded, and it enables continuous monitoring of cavitation activity over time, serving as a powerful approach to analyze the bubble dynamics and cavitation type [6], [7], [22], [23]. Specifically, stable cavitation is typically characterized by subharmonic and ultraharmonic acoustic emissions, while inertial cavitation is characterized by broadband emissions. Therefore, understanding the bubble dynamics in viscoelastic tissues and further monitoring the cavitation in a real-time manner with its acoustic emissions is crucial to achieve precise cavitation-mediated therapeutic applications.

During these biomedical applications, the cavitation bubble dynamics and resultant acoustic emissions would be extremely complex due to the influences of multiple factors, including the ultrasound parameters, the viscoelastic properties of the surrounding tissues, the bubble–boundary and/or bubble–bubble interactions, and so on [1], [2], [3], [4], [5]. Therefore, to achieve an accurate description of the dynamic behaviors of the cavitation bubbles in viscoelastic tissues, it is essential to develop a comprehensive model by coupling a cavitation model with a viscoelastic model that represents the surrounding tissues, and meanwhile taking the bubble–bubble interactions into account. Various viscoelastic models exist for describing the viscoelastic medium, and plenty of them have been coupled with the cavitation models (e.g., Keller-Miksis equation, Gilmore equation, etc.) to describe the cavitation bubble dynamics in soft tissues and to analyze the resultant acoustic emissions, but only focusing on a single bubble for simplicity [24], [25], [26], [27]. For the bubble–bubble interactions, many researches have been focused on the translational motions or radial pulsations of bubbles in Newtonian fluids [28], [29], [30], [31], [32], [33], [34], [35], [36], [37], [38], [39], [40]. It has demonstrated that the bubble–bubble interactions make them behave very differently from individual bubbles. Specifically, the expansion ratios of bubbles can be suppressed or enlarged, which largely depends on the ultrasound parameters, the ambient bubble radii, the distances between bubbles and the number of bubbles [35], [39], [40]. Recently, several studies have attempted to clarify the impacts of the viscoelasticity of the surrounding medium on the translational and/or radial motions of bubbles with considering bubble–bubble interactions [41], [42]. It was found that increasing elasticity, viscosity or both would significantly reduce the translational and radial motions of bubbles and consequently reduce the bubble–bubble interactions [42]. However, less attention has been paid to the characteristics of the nonlinear bubble dynamics and the resultant acoustic emissions while considering the impacts of the bubble–bubble interactions and the viscoelasticity of the surrounding medium simultaneously.

In this study, the nonlinear dynamics and accompanying acoustic emissions of two interacting cavitation bubbles in a viscoelastic medium were investigated numerically via a comprehensive model. The influences of the bubble–bubble interactions and the viscoelasticity of the surrounding medium on both radial and translational motions of bubbles were considered simultaneously. Then, the radial oscillations were analyzed through two bifurcation structures in tandem, and the frequency spectra of the acoustic emissions generated by the two interacting bubbles were analyzed to characterize the bubble dynamics. Furthermore, the effects of the acoustic pressures, initial bubble radii, initial distance between bubbles, and viscoelastic properties of the surrounding medium on the bubble dynamics and acoustic emissions were further examined.

2. Theory and methods

2.1. Modelling cavitation in viscoelastic media with bubble–bubble interactions

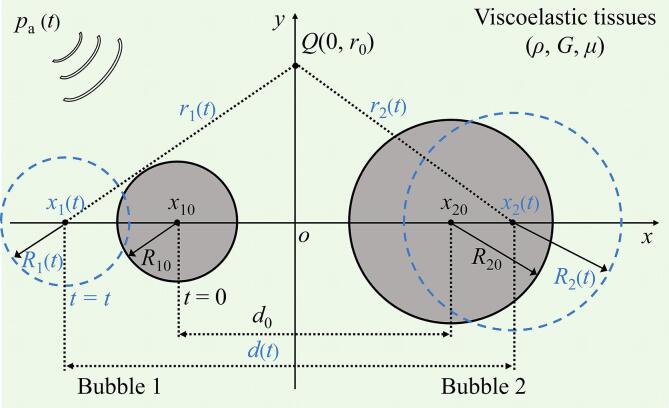
The schematic of the cavitation model describing the dynamic behaviors of two interacting bubbles in a viscoelastic medium was shown in Fig. 1. Under ultrasound excitation, two bubbles with initial radii (R₁₀ and R₂₀) and positions (bubble centers x₁₀ and x₂₀) could occur radial and translational motions (i.e., R₁(t), R₂(t) and x₁(t), x₂(t)) over time, respectively. It is assumed that both bubbles remain spherical during their oscillations, and the mass exchange (i.e., evaporation/condensation and gas diffusion) at the gas–liquid interfaces and chemical reactions inside the bubbles are neglected for simplicity as demonstrated in earlier works [28], [34], [35], [36], [39], [40], [41], [42].

Fig. 1.

Schematic of the cavitation bubble dynamics for a coupled two-bubble system in viscoelastic tissues.

The translational motions of bubbles were always neglected in previous studies [30], [31], [32], [34], [35], [36], [39], [40], nevertheless, the radial and translational motions of bubbles, as well as the viscoelastic drag experienced by bubbles while moving in the viscoelastic medium were comprehensively considered herein. The Keller-Miksis equations coupled with the bubble–bubble interactions were used as follows [28], [42]:

$$\begin{array}{c}\left(1-\frac{{\dot{R}}_i}{c}\right)R_i{\ddot{R}}_i+\left(\frac{3}{2}-\frac{{\dot{R}}_i}{2c}\right){\dot{R}}_i^2-\frac{1}{\rho }\left(1+\frac{{\dot{R}}_i}{c}\right)p_{s,i}-\frac{R_i}{\rho c}\frac{d{p}_{s,i}}{\mathit{dt}}\\ =\frac{{\dot{x}}_i^2}{4}-\frac{R_j^2{\ddot{R}}_j+2R_j{\dot{R}}_j^2}{d}-{\left(-1\right)}^i\frac{R_j^2\left({\dot{x}}_i{\dot{R}}_j+R_j{\ddot{x}}_j+5{\dot{R}}_j{\dot{x}}_j\right)}{2d^2}-\frac{R_j^3{\dot{x}}_j\left({\dot{x}}_i+2{\dot{x}}_j\right)}{2d^3}\end{array}$$ (1)

$$\frac{R_i{\ddot{x}}_i}{3}+{\dot{R}}_i{\dot{x}}_i-{\left(-1\right)}^i\frac{1}{d^2}\frac{d}{\mathit{dt}}\left(R_i{R}_j^2{\dot{R}}_j\right)-\frac{R_j^2\left(R_i{R}_j{\ddot{x}}_j+R_j{\dot{R}}_i{\dot{x}}_j+5R_i{\dot{R}}_j{\dot{x}}_j\right)}{d^3}=-\frac{D_{e,i}}{2\pi \rho R_i^2}$$ (2)

where R_i(t), R_j(t) and x_i(t), x_j(t) are the radii and center positions of the i^th and j^th bubble, respectively. The indexes i = 1, 2 and j = 3 − i denote the bubble number. The overdot denotes the time derivative. The d(t) = |x_i(t)-x_j(t)| denotes the distance between the centers of bubbles i and j at any time t, c is the speed of sound in the surrounding medium, ρ is the medium density, D_e,i is the viscoelastic drag acting on the i^th bubble during its translational motion in the viscoelastic medium, p_s,i (t) is the pressure at the wall of i^th bubble, which is determined by [24]:

$$p_{s,i}=p_{g,i}-\frac{2\sigma }{R_i}+{\left({\tau }_{\mathit{rr}}\right|}_{R_i}+p_a\left(t\right)-p_0$$ (3)

where p_g,i is the pressure inside the i^th bubble, which is assumed to obey the van der Waals equation [32], [35], [40]:

$$p_{g,i}=\left(p_0+\frac{2\sigma }{R_{i0}}\right){\left(\frac{R_{i0}^3-h_i^3}{R_i^3-h_i^3}\right)}^{\kappa }$$ (4)

where σ is the surface tension, ${{\tau }_{\mathrm{r}\mathrm{r}}|}_{{\mathrm{R}}_{\mathrm{i}}}$ is the stress in radial direction at r = R_i, which was introduced to be able to couple the cavitation model with the viscoelastic models. The p₀ is the atmospheric pressure, R_i0 is the initial radius of the i^th bubble, h_i is the van der Waals hard-core radius for i^th bubble, κ is the polytropic exponent of the gas within bubble. The acoustic pressure p_a =  − p_A sin(2πft), where p_A and f are the ultrasound amplitude and frequency, respectively. Note that the time delay while the pressure radiated by one bubble propagating to the other bubble was neglected in Eq (1), it is reasonable because the initial bubble−bubble distances are small (d₀ < 100 μm) in this study, in which case the time delays become insignificant [36], [43]. Sojahrood et al. have provided a nice review of the time delays in the interacting bubble simulations [43]. Moreover, taking the time delay into account would make the numerical simulations more complex and computationally intensive, especially for the time-varying bubble−bubble distance while the translational motions of bubbles were simultaneously considered in this study.

2.2. Viscoelastic model and viscoelastic drag for the surrounding medium

To describe the viscoelastic behaviors of the surrounding medium, the Kelvin-Voigt model was used due to its superiority for describing the creep behavior of soft tissues, which is expressed as [24]:

$${\tau }_{\mathit{rr}}=2G{\gamma }_{\mathit{rr}}+2\mu {\dot{\gamma }}_{\mathit{rr}}$$ (5)

where τ_rr is the stress in the r direction, γ_rr is the strain, ${\dot{\gamma }}_{\mathrm{r}\mathrm{r}}$ is the strain rate, G is the shear modulus, and μ is the viscosity. According to the continuity equation, one can obtain ${\dot{\gamma }}_{\mathrm{r}\mathrm{r}}=-2{\mathrm{R}}^2\dot{\mathrm{R}}/{\mathrm{r}}^3$ and ${\gamma }_{\mathrm{r}\mathrm{r}}=-(2/3{\mathrm{r}}^3)({\mathrm{R}}^3-{\mathrm{R}}_0^3)$, then substituting these conditions into Eq. (5), the stress at the i^th bubble interface (r = R_i) is:

$${\left({\tau }_{\mathit{rr}}\right|}_{R_i}=-\frac{4G}{3R_i^3}\left(R_i^3-R_{i0}^3\right)-\frac{4\mu {\dot{R}}_i}{R_i}$$ (6)

Regarding the translational motion of bubbles in a viscoelastic medium, the viscoelastic drag D_e,_i experienced by the i^th bubble in Eq. (2) is given by [28], [42]:

$$D_{e,i}=12\pi R_i{\int }_0^{t}E\left(t-t_1\right)U_i\left(t_1\right)d{t}_1$$ (7)

where U_i(t) is the translational velocity of the moving i^th bubble. For the Kelvin-Voigt viscoelastic model, the relaxation modulus function is E(t) = G + μδ(t), where δ(t) is the Dirac delta function. Substitution of this condition into Eq. (7) can obtain

$$\begin{array}{c}{D}_{e,i}\text{=}12\pi R_i{\int }_0^t\left[G+\mu \delta \left(t-t_1\right)\right]{\dot{x}}_i\left(t_1\right)d{t}_1\\ =12\pi R_{i}G\left[x_i\left(t\right)-x_{i0}\right]+12\pi R_i\mu {\dot{x}}_i\left(t\right)\left[2\epsilon \left(t\right)-1\right]\end{array}$$ (8)

where ε(t) is a Heaviside function. At t = 0, the viscoelastic drag is equal to zero. Hence, the drag forces for each bubble are defined as follows for t > 0:

$$D_{e,i}=12\pi R_i\left[G\left(x_i-x_{i0}\right)+\mu {\dot{x}}_i\right],i=\{1,2\}$$ (9)

where x_i0 is the initial center position of the i^th bubble.

2.3. Acoustic emissions from cavitation bubbles

When the time delay due to the finite propagation velocity of acoustic wave is neglected, the pressure of an acoustic wave radiated from a cavitation bubble p_rad is given by [44]:

$$p_{\mathit{rad}}\left(r,t\right)=\frac{\rho }{r}\left(\ddot{R}{R}^2+2{\dot{R}}^{2}R\right)$$ (10)

where r is the distance from the bubble center. Considering that the law of acoustic propagation is linear and it satisfies the superposition theorem, the pressure of acoustic waves radiated from a coupled two-bubble system p_rad1,2 shown in Fig. 1 can be expressed as [31], [32]:

$$p_{rad1,2}\left(r_1,r_2,t\right)=\frac{\rho }{r_1}\left({\ddot{R}}_1{R}_1^2+2{\dot{R}}_1^2{R}_1\right)+\frac{\rho }{r_2}\left({\ddot{R}}_2{R}_2^2+2{\dot{R}}_2^2{R}_2\right)$$ (11)

where r₁ and r₂ are the distances from the centers of the 1^st bubble and 2^nd bubble, respectively. Due to the two bubbles undergoing radial and translational oscillations simultaneously, a rectangular coordinate system was established with the midpoint between initial bubbles (t = 0) as the origin point to calculate the acoustic emissions from the coupled two-bubble system. As shown in Fig. 1, the receiving point of acoustic emissions was set to (0, r₀), thus r₁ and r₂ can be calculated as follows:

$$r_1=\sqrt{x_1^2+r_0^2},r_2=\sqrt{x_2^2+r_0^2}$$ (12)

To characterize the acoustic cavitation with its acoustic emissions, the temporal signal of acoustic emission x_a(m) in a sampling period (m = 0, 1, ···, M − 1; where M is the number of sampling points in a sampling period) was first processed by fast Fourier transform to obtain its frequency spectrum [7]:

$$X_a\left(k\right)=\sum _{m=0}^{M-1}{x}_a\left(m\right)e^{-j\frac{2\pi }{M}km}\left(k=0,1,...,M-1\right)$$ (13)

where k was the frequency point in the frequency spectrum. Moreover, the power spectrum of the signal was calculated by Y_a(k) = X_a(k)² to characterize the intensity of the signal at different frequencies.

2.4. Investigation methods for the nonlinear bubble dynamics

As a powerful and valuable tool to analyze the nonlinear characteristics of one system, the bifurcation analysis has been extensively used to investigate the nonlinear dynamics of the interacting bubbles [43], [45], [46], [47], [48], [49]. It has demonstrated that the qualitative and quantitative changes of the nonlinear dynamics could be investigated effectively over a wide range of control parameters [43], [45], [46], [47], [48], [49]. However, the conventional bifurcation analysis may be misleading and cannot reliably identify features that are responsible for the identification of super-harmonic and ultra-harmonic oscillations [43], [50], [51], [52], [53]. Thus, a more comprehensive bifurcation analysis method was used herein to investigate the nonlinear dynamics of the coupled two-bubble system for a wide range of control parameters as described previously [43], [50], [51], [52], [53]. Firstly, the conventional bifurcation analysis (i.e., Poincaré analysis) was employed by sampling the R(t) curves using a specific point in each driving period, which is expressed as [43], [50], [51], [52], [53]:

$$P\equiv (R(\mathrm{\Theta }))\{(R(t),\dot{R}(t)):\mathrm{\Theta }=\frac{n}{f}\}$$ (14)

where P denotes the points in the bifurcation diagram. Then, another bifurcation diagram by constructing points with the local maxima of the radial peaks Q was also used as follows [43], [50], [51], [52], [53]:

$$Q\equiv max\left(R(t)\right)\left\{\left(R(t),\dot{R}(t)\right):\dot{R}(t)=0,\ddot{R}(t)<0\right\}$$ (15)

The bifurcation diagrams of the normalized bubble oscillations (R_i/R_i0) were calculated using the two methods in tandem. In this work, the results were plotted for n = 50–100 to ensure a steady state solution has been reached.

2.5. Non-dimensional formulation and simulation conditions

The physical parameters used in the simulation were nondimensionalized according to the following schemes: Length (L) = R₀; Time (T) = (2πf)^-1; Mass (M) = p₀LT². The nondimensionalized parameters are indicated by asterisks and the simulation conditions unless specified otherwise are given in Table 1. The dimensionless system of implicit differential equations was numerically solved by using the ode 15i solver built in MATLAB (MathWorks Inc., R2018a) with a time step of 0.001/f, as well as a relative tolerance and an absolute tolerance of 10^-10 and 10^-11, respectively.

Table 1.

The non-dimensional formulation and simulation conditions.

Physical parameters	Non-dimensional formulation	Simulation conditions
f (MHz)	f* = fT	3.5
ρ (kg/m3)	ρ*=ρL3/M	1050
c (m/s)	c* = cT/L	1540
σ (N/m)	σ* = σT2/M	0.056
μ (mPa∙s)	μ* = μLT/M	15
G (kPa)	G* = GLT2/M	20
p0 (Pa)	p0* = p0LT2/M	1.01 × 105
pA (MPa)	pA* = pALT2/M	0.8–2.3
R10 (μm)	R10* = R10/L	2
R20 (μm)	x20* = x20/L	5
x10 (μm)	x10* = x10/L	–10
x20 (μm)	x20* = x20/L	10
r0 (mm)	r0* = r0/L	10
κ	/	1.4

3. Results and discussion

3.1. Bubble dynamics and acoustic emissions of two interacting bubbles

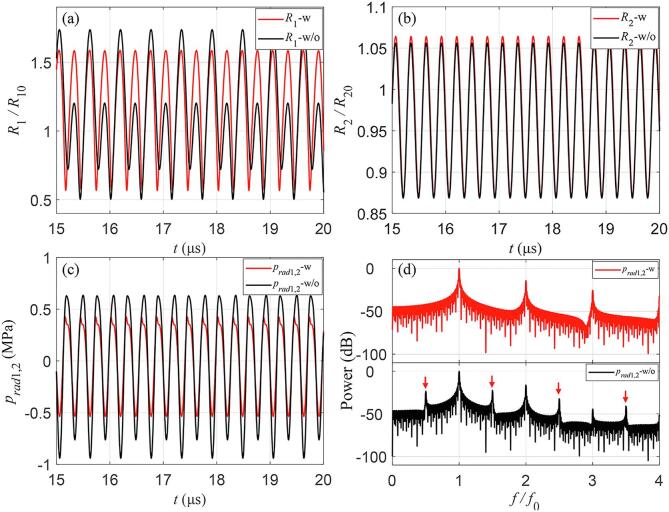
The bubble dynamics of a coupled two-bubble system in a viscoelastic medium with considering the bubble–bubble interactions were compared to the ones calculated using the isolated bubble model at the same conditions. As shown in Fig. 2(a) and (b), the radial oscillations of the small bubble in the two-bubble system (R₁-w) were obviously suppressed, whereas those of the large one (R₂-w) were slightly enlarged as compared to the cases of an isolated bubble model (R₁-w/o and R₂-w/o), respectively. Furthermore, it can be seen that the bubble–bubble interactions have a much stronger effect on the dynamics of the small bubble than that of the large one, which agree well with the previous results [32], [35]. The acoustic emissions generated by the bubbles were calculated as shown in Fig. 2(c), and the radiated acoustic pressure p_rad1,2 obtained from the coupled two-bubble model is slightly smaller than that from the two isolated bubbles. This can be ascribed to the stronger suppression effects on the oscillations of the small bubble due to the bubble–bubble interactions. Correspondingly, the frequency spectrum analysis exhibited that the acoustic emissions of the coupled two-bubble system only contain fundamental (f) and harmonic (2f, 3f…) components, while the subharmonic (f/2) and ultraharmonic (3f/2, 5f/2…) components appear in the emission spectrum of the two isolated bubbles (as displayed by the arrows). Both the amplitude and frequency component of the acoustic emissions further indicated that the bubble dynamics was ultimately suppressed due to the bubble–bubble interactions. The distinct difference in the bubble dynamics and acoustic emission spectrum highlights the necessity to consider the bubble–bubble interactions while investigating the practical cavitation phenomenon and its utilization in biomedical applications.

Fig. 2.

Bubble dynamics and acoustic emissions of two bubbles in a viscoelastic medium with (w) or without (w/o) considering bubble–bubble interactions under ultrasound stimulation (p_A = 1.15 MPa), including the relative radii of (a) a small bubble and (b) a large bubble, (c) acoustic emissions, and (d) corresponding power spectra.

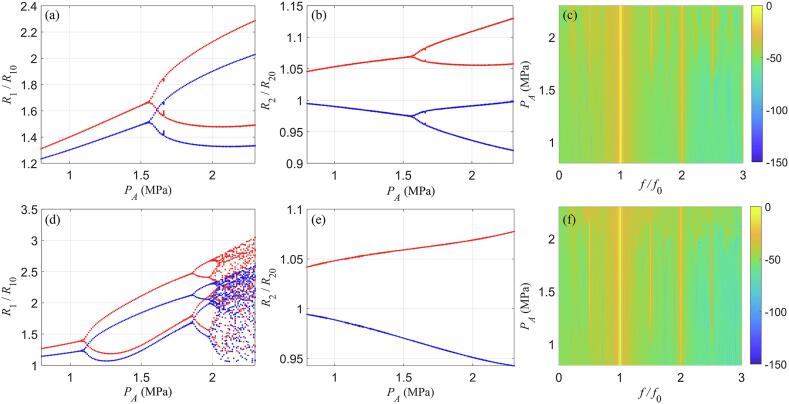
Furthermore, the bifurcation structure of the normalized oscillations (R_i/R_i0) and the corresponding acoustic emission spectra as a function of the acoustic pressure p_A were presented in Fig. 3. The blue and red points were constructed using the Poincaŕe analysis and the method of maxima, respectively. As shown in Fig. 3(a), the oscillations of the small bubble in the coupled two-bubble system are of period 1 (P1) with one maximum until p_A = 1.55 MPa; above this pressure, period doubling (PD) occurs in both methods. A similar behavior was presented for the large bubble, but note that the expansion ratio of the large bubble is much smaller than that of the small one as shown in Fig. 3(b), indicating that the oscillation of the small bubble is more drastic. Correspondingly, the acoustic emission spectra shown in Fig. 3(c) consist of peaks at the fundamental and harmonic frequencies as p_A < 1.55 MPa, and then distinct subharmonic and ultraharmonic components appear. Note that the maximum bubble expansion is more than twice of the initial radius (R_max/R₀ ≥ 2) at high acoustic pressures (p_A ≥ 1.82 MPa), where bubble often undergoes a short and violent collapse dominated by inertial forces, termed as inertial cavitation [24], [54], [55]. Thus, the R_max/R₀ = 2 is commonly chosen as the criterion to determine the threshold of inertial cavitation and possible bubble destruction because it may lead to fragmentation of a bubble into a number of smaller bubbles [24], [54], [55]. Below the inertial cavitation threshold, the non-destructive stable cavitation occurs and the accompanying subharmonic emissions are usually utilized for real-time monitoring therapeutic applications associated with stable cavitation [36], [50], [51]. Moreover, it also demonstrated that the initial stable cavitation can evolve into inertial cavitation with the acoustic pressure increasing.

Fig. 3.

Bifurcation structure of the R_i/R_i0 for a small bubble and a large bubble with (a and b) or without (d and e) considering bubble–bubble interactions in a viscoelastic medium versus acoustic pressure, as constructed by the conventional method (blue points) and the method of maxima (red points). (c) and (f) represent the mapping of the corresponding power spectra versus acoustic pressure. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

The bifurcation structure and corresponding acoustic emission spectra of the two bubbles without considering bubble–bubble interactions were presented in Fig. 3(d)–(f). It showed that the P1 oscillations of the small bubble undergo PD with 2 maxima at p_A = 1.08 MPa, which is much lower than the PD threshold shown in Fig. 3(a). Subsequently, the P2 oscillations undergo PD to P4 (p_A = 1.85 MPa) and finally become chaotic (p_A = 1.98 MPa). Compared to the Fig. 3(a), it further confirmed that the nonlinear dynamics of the small bubble was remarkably suppressed due to the bubble–bubble interactions. However, for the large bubble, only P1 oscillations occur as shown in Fig. 3(e), suggesting that the bubble–bubble interactions manifest an enhancement effect on its nonlinear dynamics as compared to Fig. 3(b). The corresponding acoustic emission spectra showed the successive appearance of subharmonics, ultraharmonics and broadband components as acoustic pressure increases (Fig. 3(f)). These qualitative changes in the bubble dynamics and the spectrum characteristics of the acoustic emissions indicated that the bubbles underwent different dynamic behaviors depending on the strength of the ultrasonic field. More importantly, any nonlinear change in the bubble dynamics could clearly be observed in the acoustic emission spectra. Specifically, with the evolution of the bubble dynamics (P1 oscillations) through a multiple cascade of PDs to chaos, the corresponding acoustic emission spectra would exhibit an appropriate appearance of the harmonics, subharmonics and ultraharmonics, as well as broadband components.

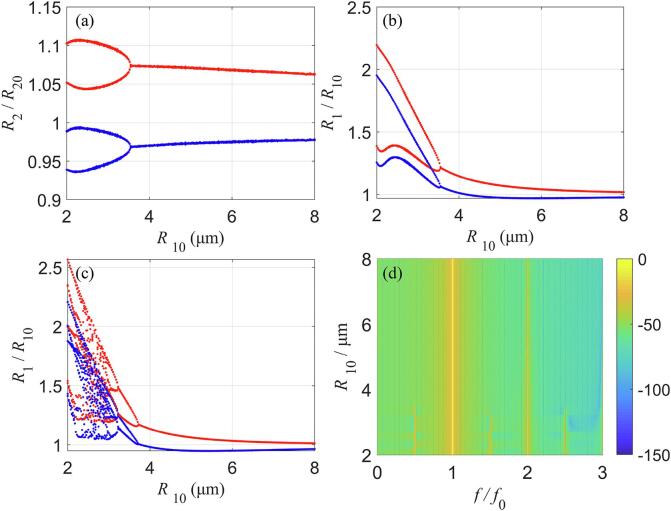
3.2. Effects of the initial radii of bubbles

Considering that the cavitation bubbles with different initial radii might undergo different effects (i.e., suppression or enlargement effect) due to the bubble–bubble interactions, the effects of the initial radii of the two interacting bubbles on the bubble dynamics and the resultant acoustic emissions were further investigated as presented in Fig. 4. The initial radius of one bubble is fixed (R₂₀ = 5 μm) and that of the other bubble (R₁₀) changes from 2 μm to 8 μm. With R₁₀ increasing, bifurcation structures of the two interacting bubbles shown in Figs. 4(a) and (b) both display P2 oscillations followed by P1 oscillations, whereas the bubble oscillation of R₁/R₁₀ becomes P1 oscillations from chaotic through a cascade of reverse PDs for the cases without considering bubble–bubble interactions (Fig. 4(c)). Compared to Fig. 4(c), it is evident that the nonlinearity of bubble dynamics for the bubble (R₁) is notably weakened because of the bubble–bubble interactions as its initial radius is smaller than R₂₀, and results in only harmonics and subharmonics in the corresponding acoustic emission spectra (Fig. 4(d)). It can be explained that the bubble–bubble interactions have a strong suppression effect on the dynamics of the small bubble, and consequently reduce the nonlinear dynamics of the two interacting bubbles.

Fig. 4.

The effects of the initial radii of two interacting bubbles on the bubble dynamics and the acoustic emission spectra at p_A = 1.9 MPa. Bifurcation structures of (a) a bubble (R₂) with a fixed initial radius (R₂₀ = 5 μm) and (b) a bubble (R₁) with varying initial radius (R₁₀) as a function of R₁₀, while (c) represents the bifurcation structures of R₁/R₁₀ without bubble–bubble interactions. (d) The power spectra of the acoustic emissions obtained from the two interacting bubbles.

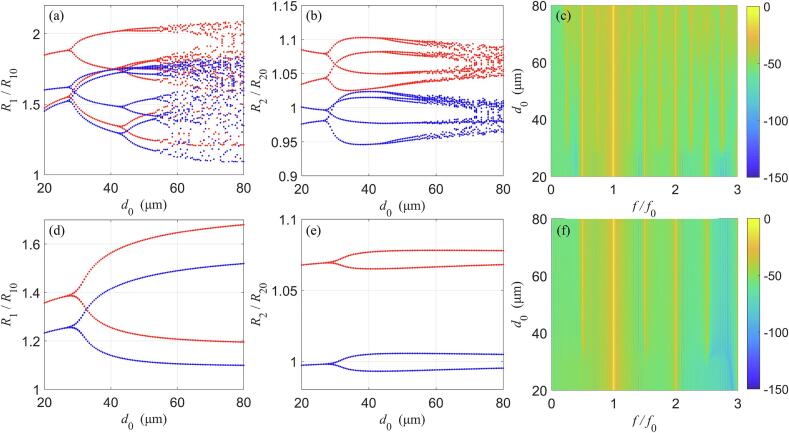
3.3. Effect of the initial distance between bubbles

As shown in Fig. 5, the initial distance between bubbles d₀ dramatically influences their dynamic behaviors and the resultant acoustic emissions. When the viscoelastic properties of the medium are relatively small (G = 50 kPa, μ = 7.5 mPa∙s), the small bubble (R₁) displays a sensitive response to the change in the initial distance between the two bubbles. The bubble oscillations show the period doubling route to chaos as the distance increasing as displayed in Fig. 5(a). Correspondingly, the dynamics of the large bubble (R₂) in Fig. 5(b) exhibit a similar evolution with the distance increasing. Moreover, the corresponding acoustic emission spectra exhibit a gradual increase in the subharmonics, ultraharmonics and broadband components with an increase in the initial distance between the two bubbles as shown in Fig. 5(c). This reveals that the bubble–bubble interactions strongly depend on their distance, and the closer the two bubbles get, the more intensive the bubble–bubble interactions (i.e., suppression effects) exerts on the dynamics of the small bubble. When the elasticity and viscosity of medium increase (G = 100 kPa, μ = 15 mPa∙s), similar variation trends can be observed as shown in Fig. 5(d)–(f). Nevertheless, it is worth noting that both bubbles only undergo P1 to P2 oscillations with the initial distance between bubbles increasing. Moreover, the evolution of bubble dynamics becomes less sensitive to the increasing of the initial distance and the distance threshold for the initiation of P2 oscillations (d₀ = 26 μm) is much larger as compared to Fig. 5(a) and (b), respectively. In addition, the corresponding acoustic emission spectra only contain the harmonics, subharmonics and ultraharmonics. This can be due to the increased damping in the bubble oscillations with the elasticity and viscosity of medium increasing [24], [25], [26], [27], [42].

Fig. 5.

The effects of the initial distance between bubbles on the bubble dynamics and the acoustic emissions in the media with different viscoelastic properties at p_A = 1.15 MPa. Bifurcation structure of (a) the small bubble, and (b) the large bubble, as well as (c) the acoustic emission spectra at G = 50 kPa, μ = 7.5 mPa∙s, while (d)–(f) represent the corresponding results at G = 100 kPa, μ = 15 mPa∙s.

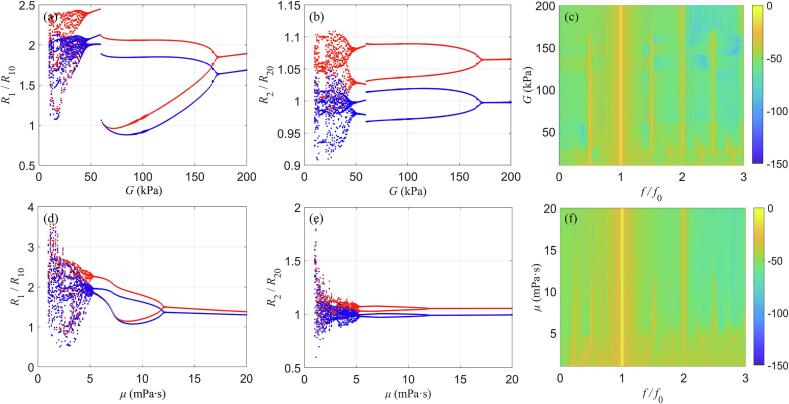
3.4. Effects of the viscoelasticity of the surrounding medium

The bifurcation structures and the corresponding acoustic emission spectra versus the viscoelastic properties of the surrounding medium were presented in Fig. 6. As the elasticity of the surrounding medium G increases, the oscillations of the small bubble (R₁) in the coupled two-bubble system evolve from chaotic oscillations to P2 oscillations, and further undergo a reverse PD to P1 oscillations as shown in Fig. 6(a). The changes in the oscillations of the large bubble are similar to those of the small bubble (Fig. 6(b)). Correspondingly, the acoustic emission spectra exhibit a progressive evolution from broadband components to subharmonics and ultraharmonics followed by harmonics as displayed in Fig. 6(c). It can be explained that the elasticity of surrounding medium dampens the nonlinear oscillations of bubbles [24], [25], [26], [27], [42]. With the viscosity increasing, the oscillations of the small and large bubbles both change from chaos to P2 oscillations followed by P1 oscillations as shown in Fig. 6(d) and (e), respectively. Accordingly, the acoustic emission spectra also exhibit an evolution of broadband components, subharmonic and ultraharmonic components, and harmonic components as shown in Fig. 6(f). It indicates that the viscosity of the medium would also reduce the oscillations of the bubbles and suppress the nonlinear bubble dynamics. Overall, the elasticity and viscosity of the surrounding media could significantly damp the nonlinear oscillations of bubbles, and it also emphasizes the importance and necessity of considering the influences of viscoelasticity while describing the acoustic cavitation in tissue fluid or blood that owns certain viscoelasticity.

Fig. 6.

The bifurcation structures of (a) the small bubble (R₁) and (b) the large bubble (R₂), as well as (c) the acoustic emission spectra versus the elasticity of the surrounding medium (μ = 5 mPa∙s) at p_A = 1 MPa, while (d)–(f) represent the corresponding results versus the viscosity of the surrounding medium (G = 20 kPa).

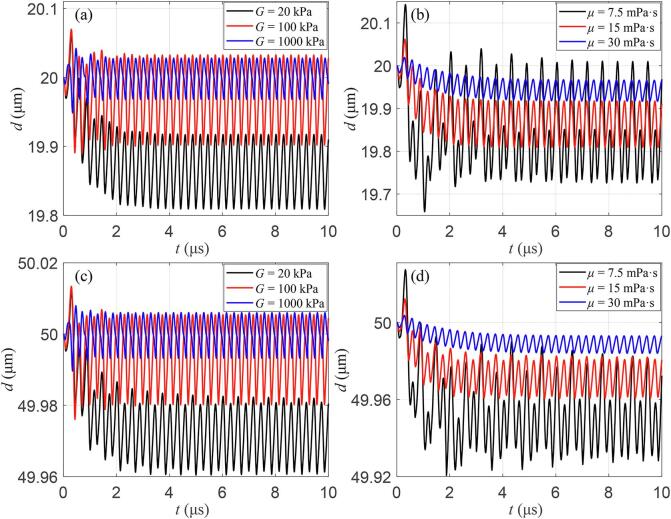
3.5. Translational motions of bubbles in a viscoelastic medium

The viscoelastic properties of the surrounding medium not only influence the radial oscillations significantly (Fig. 6), but also are expected to influence the translational motions of bubbles [42]. The translational motions of bubbles in the viscoelastic medium were examined as shown in Fig. 7. When the elasticity of the medium is small, bubbles are observed to be drawn to each other over time and a dynamical steady state can be achieved as shown in Fig. 7(a). With the elasticity increasing, the translational motions of the bubbles become smaller, and the bubbles would remain near their initial locations in space as the elasticity is high enough (e.g., 1.0 MPa). Similarly, it is obvious in Fig. 7(b) that the translational motion was significantly reduced as the viscosity increases. It exemplified that increasing the elasticity or viscosity (or both) of the surrounding medium tends to resist translational motions of bubbles, which is consistent with the previous study [42]. Moreover, when the initial distance between bubbles increases (d₀ = 50 μm), Fig. 7(c) and (d) presented that the translational motions of bubbles are distinctly reduced as compared with the cases of d₀ = 20 μm. These results implied that the translational motions of bubbles in a medium with small elasticity or/and viscosity (e.g., water) are relatively large and need to be considered, whereas the translational motions could reduce gradually and even could be ignored with the elasticity, viscosity as well as the initial distance between bubbles increasing, probably due to the reduced bubble–bubble interactions [42].

Fig. 7.

Representative translational motions of bubbles in the viscoelastic media at p_A = 1 MPa. Distances between bubbles over time at different (a) elasticities and (b) viscosities with an initial distance d₀ = 20 μm, while (c) and (d) represent those under the same conditions but d₀ = 50 μm.

4. Conclusions

A comprehensive model, allowing for the acoustic radiation coupling between bubbles, the viscoelastic drag exerted on bubbles, the viscoelasticity of surrounding medium, as well as the radial and translational motions of bubbles, was developed to investigate the nonlinear bubble dynamics and resultant acoustic emissions of two interacting cavitation bubbles in viscoelastic tissues. The bubble dynamics is noticeably affected by the nearby bubble due to the bubble–bubble interactions as expected. It exemplified that the small bubble is remarkably suppressed, whereas the large bubble is slightly enlarged, as compared to the cases without considering bubble–bubble interactions at various acoustic pressures and initial radii of bubbles. Moreover, as the initial distance between the interacting bubbles increases, the bubble–bubble interaction decreases gradually and it could effectively enhance the nonlinear oscillations of the bubbles, resulting in a similar mode of successive period doubling to chaos in the bifurcation diagrams and meanwhile accompanying with a successive appearance of harmonics, subharmonics, ultraharmonics and broadband components in the frequency spectra of the acoustic emissions. Besides, the viscoelasticity of the surrounding medium has a strong influence on the radial and translational motions of bubbles as well as the accompanying acoustic emissions. Increasing the elasticity and/or viscosity of the medium prominently reduce the radial and translational motions, leading to a decrease in the nonlinearity of bubble dynamics with an absence of subharmonic, ultraharmonic and broadband acoustic emissions. This study provides a comprehensive insight into the nonlinear behaviors and acoustic emissions of two interacting cavitation bubbles in viscoelastic media, and consequently it may be conducive to the optimization and real-time monitoring of the cavitation-mediated therapy.

CRediT authorship contribution statement

Dui Qin: Conceptualization, Methodology, Visualization, Writing - original draft, Writing - review & editing, Funding acquisition. Qingqin Zou: Methodology, Software, Validation, Writing - original draft, Writing - review & editing. Shuang Lei: Software, Validation. Wei Wang: Writing - review & editing. Zhangyong Li: Conceptualization, Project administration, Supervision, Resources.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.