Robust surface-to-mass coupling and turgor-dependent cell width determine bacterial dry-mass density

Significance

Intracellular biomass density is an important variable for cellular physiology. It defines the crowded state of the cytoplasm and thus influences macromolecular interactions and transport. To control density during growth, bacteria must expand their cell volumes in synchrony with biomass. The regulation of volume growth and biomass density remain fundamentally not understood—in bacteria or any other organism. Using advanced microscopy, we demonstrate that cells control dry-mass density indirectly through two independent processes. First, cells expand surface area, rather than volume, in proportion with biomass growth. Second, cell width is controlled independently, with an important influence of turgor pressure. Our findings overturn a long-standing paradigm of mass-density constancy in bacteria and reveal fundamental determinants of dry-mass density and shape.

Abstract

During growth, cells must expand their cell volumes in coordination with biomass to control the level of cytoplasmic macromolecular crowding. Dry-mass density, the average ratio of dry mass to volume, is roughly constant between different nutrient conditions in bacteria, but it remains unknown whether cells maintain dry-mass density constant at the single-cell level and during nonsteady conditions. Furthermore, the regulation of dry-mass density is fundamentally not understood in any organism. Using quantitative phase microscopy and an advanced image-analysis pipeline, we measured absolute single-cell mass and shape of the model organisms Escherichia coli and Caulobacter crescentus with improved precision and accuracy. We found that cells control dry-mass density indirectly by expanding their surface, rather than volume, in direct proportion to biomass growth—according to an empirical surface growth law. At the same time, cell width is controlled independently. Therefore, cellular dry-mass density varies systematically with cell shape, both during the cell cycle or after nutrient shifts, while the surface-to-mass ratio remains nearly constant on the generation time scale. Transient deviations from constancy during nutrient shifts can be reconciled with turgor-pressure variations and the resulting elastic changes in surface area. Finally, we find that plastic changes of cell width after nutrient shifts are likely driven by turgor variations, demonstrating an important regulatory role of mechanical forces for width regulation. In conclusion, turgor-dependent cell width and a slowly varying surface-to-mass coupling constant are the independent variables that determine dry-mass density.

During growth, cells must coordinate many seemingly independent processes. Well-studied examples include the coordination of DNA replication with cell division (1–3) and of metabolism with protein translation (4). A process that has received little attention thus far is the coordination of cell volume with biomass growth (5, 6).

On short timescales or in the absence of growth, cell volume can be modulated through variations of turgor pressure (5). However, on timescales comparable or longer than a generation time, volume growth requires the active expansion and addition of cell-surface material. Cell-surface expansion thus allows cells to control dry-mass density and therefore the level of cytoplasmic macromolecular crowding during growth. Crowding, in turn, impacts processes comprising macromolecular diffusion (7, 8), bacterial nucleoid organization (9), and protein–DNA interactions (10). Accordingly, it was suggested that biomass growth rate depends on dry-mass density and crowding (11–13). Yet, the connection of cell-volume growth, biomass growth, and to the crowded state of the cytoplasm remain largely unknown (5).

Previous experiments in Escherichia coli demonstrate that wet- and dry-mass density are approximately constant between different nutrient conditions and during the cell cycle (14–16). Bacteria are therefore often assumed to increase their volumes V in perfect proportionality to dry mass M (17, 18). However, this has not been precisely demonstrated at the single-cell level or during nonsteady growth conditions, such as nutrient shifts.

In microbial and plant cells, the cell envelope contains a cell wall, which in turn requires plastic remodeling for surface expansion. In many cell types, turgor pressure is required for surface expansion (19–21). More specifically, turgor is thought to drive the expansion of the cell wall by lowering the free-energy barrier of cell wall–modifying enzymes. However, on long timescales, other variables such as envelope-precursor production can be equally important. Different organisms have been demonstrated to undergo “stored growth” (21–23): While their envelope expansion is reduced during transient periods of reduced turgor, they experience a sudden burst of envelope growth once turgor is restored. In the gram-negative bacterium E. coli, surface expansion is only weakly responsive to variations of turgor (24). Here, the rate of surface expansion might be governed enzymatically by the abundance and/or activity of cell envelope–synthesizing enzymes, as suggested by Harris and Theriot (17). While the principles and implementation of such a process remain to be discovered, it could naturally link surface growth to biomass and therefore determine the surface-to-mass ratio S/M (17). We will come back to the determinants of S/M and the model proposed by Harris and Theriot further down.

If the cell controls the ratio of S/M, how does dry-mass density come about? Dry-mass density $\rho \hspace{0.17em}=\hspace{0.17em}M/V$ can be decomposed as a ratio of the surface-to-volume and the surface-to-mass ratios,

$$\rho =(S/V)/(S/M).$$ [1]

The surface-to-volume ratio of spherocylindrical cells, such as E. coli, decreases with both cell width and length. If dry-mass density was indeed independent of cell shape as previously hypothesized, the two ratios S/M and S/V would need to be tightly correlated. Indeed, Harris and Theriot hypothesized that the length-dependent decrease of S/V during the cell cycle is compensated by a reduction of S/M and that deterministic changes of S/V (specifically, of width) after nutrient changes of other perturbations of physiology constitute a response to hypothesized variations of S/M (17). However, S/V and S/M were never simultaneously measured in single cells. It is therefore possible that S/V and S/M are controlled independently, which would then lead to systematic variations of $\rho$.

Here, we developed quantitative phase microscopy to measure single-cell mass and shape of growing bacteria in absolute terms. We found that mass density of E. coli shows small variations between single cells and between different nutrient conditions despite large differences in average cell shapes, in agreement with previous reports (14–16). Therefore, steady-state population averages of $\langle S/V\rangle$ and $\langle S/M\rangle$ are strongly correlated. However, on the generation timescale, cells control S/V and S/M independently: While S/V changes deterministically with cell dimensions, S/M remains nearly constant, which leads to variations of dry-mass density on the generation timescale, contrary to previous assumptions (17, 18). S/M remains constant even during growth-rate changes. We thus propose an empirical surface-growth law that replaces the model by Harris and Theriot (17). The major cause of mass-density variations after nutrient shifts are variations of S/V and more specifically of cell width. To our surprise, we observed that nutrient shifts lead to rapid changes of turgor pressure, even if medium osmolality is maintained constant. Through independent osmotic ramp experiments, we found evidence that width changes are driven mechanically, through changes of turgor pressure. In summary, we demonstrate that dry-mass density is indirectly controlled through a robust surface-to-mass coupling and turgor-dependent width regulation, independently of dry-mass density.

Results

Quantitative Phase Microscopy and Computational Image Analysis Provide Absolute Measurements of Single-Cell Dry Mass and Cell Shape.

To study the determinants of single-cell volume and surface expansion during growth, we developed a method to infer absolute single-cell volume V and surface area S and to measure absolute dry mass M simultaneously and with unprecedented accuracy and precision during time-lapse microscopy (Fig. 1 and SI Appendix, Supplementary Note 1). Volume and surface area are inferred from two-dimensional cell contours obtained from phase-contrast or fluorescence images (Fig. 1A and SI Appendix, Fig. S1A). For dry-mass measurements we used spatial light interference microscopy (SLIM), a form of quantitative phase imaging (25) (SI Appendix, Fig. S2 and Supplementary Note 1). This is implemented on a commercial phase contrast microscope with a SLIM addon module (SI Appendix, Fig. S3). The integrated optical phase shift of a cell obtained through SLIM is proportional to its dry mass (Fig. 1B), with similar contributions per biomass from different molecules (proteins, RNA, DNA, small molecules, etc.). The conversion factor between integrated phase and dry mass is obtained from the known cellular dry-mass composition (SI Appendix, Supplementary Note 1). Optical artifacts like a halo around phase objects are inherent to phase contrast and SLIM microscopy and decrease the measured phase. These artifacts can be quantitatively explained based on microscope parameters. Since these artifacts are cell-shape dependent, we simulate images based on cell shape and microscope parameters to correct for the attenuation in our phase measurement (26, 27). This step proved essential for accurate measurements of both cell dimensions and dry mass (SI Appendix, Fig. S1B and Supplementary Note 1).

Fig. 1.

Measuring bacterial dry mass and volume using quantitative phase microscopy. (A) Snapshots of WT cell (MG1655) grown in MM + mannose in different imaging modalities (Top) used for different measurements (Bottom) with contour (blue) and centerline (yellow). The membrane dye FM4-64 stains predominantly the outer membrane (scale bar, 1 µm). (B, Left) Illustration of optical phase shift of light passing through a cell with refractive index $n_{\text{cell}}>n_0$. (Right) Volume and surface inference from calibrated two-dimensional cell contour. Dry mass M equals the optical phase shift, corrected for n₀, divided by the refraction increment γ. (C) Relative changes of single-cell dry mass and volume (mean ± SD) during hyperosmotic shock (Top) and medium osmolality (Bottom). Since cell volume is inferred from phase-contrast images, the volume is possibly underestimated due to potential shrinkage of the cytoplasm. (D) Dry-mass density and optical density (OD600) during exponential growth (blue shade), during early (red), and during late (yellow) stationary phase in Luria Bertani (LB) Miller medium (MG1655 at 30 °C). Growth phases were annotated according to OD600. Comparison to values inferred from wet-mass densities (diamonds) (29). (E) Dry-mass density increases with osmolality in MM + glucose (MG1655 at 37 °C), comparing SLIM and radiochemical-free water measurements (dashed line) (30) (gray rectangles = interquartile range; white circles = median; for numbers of cells see Table S2).

As a validation of our method, we found that dry mass remains constant after a hyperosmotic shock, demonstrating that mass measurements are independent of cell shape (Fig. 1C). Furthermore, mass density increases upon entering stationary phase and with increasing medium osmolality, both in quantitative agreement with independent measurements (28–30) (Fig. 1 D and E). We confirmed mass-density measurements also through immersive refractometry (31) (SI Appendix, Fig. S4). Finally, we also correctly measured the integrated refractive index of well-characterized polystyrene beads (SI Appendix, Fig. S5).

Variations in Dry-Mass Density During Steady-State Exponential Growth Are Small.

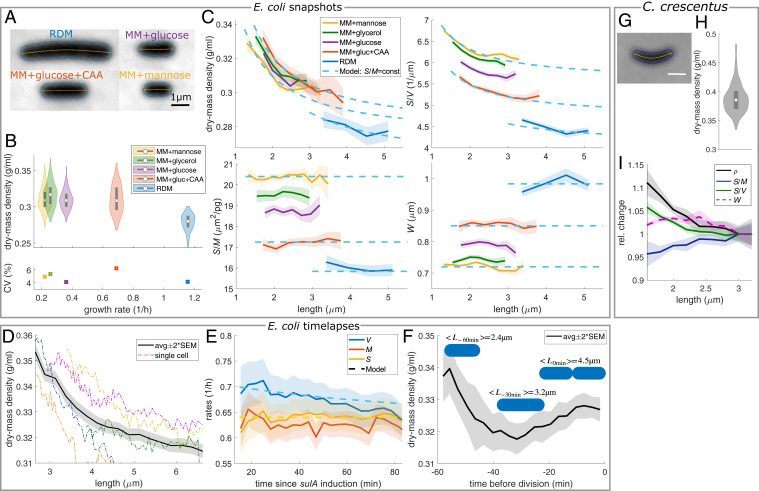
To investigate the capacity of E. coli to increase cell volume in response to biomass growth and thus control mass density during steady-state exponential growth, we measured single-cell distributions of M, V, and dry-mass density $\rho =M/V$ in two different E. coli strains (MG1655 and NCM3722) cultured in different growth media of equal osmolality (Fig. 2 A and B and SI Appendix, Fig. S6). Despite fivefold changes in average cell mass and volume and despite 1.7-fold changes in the average surface-to-volume ratio (SI Appendix, Fig. S6), the average density $\langle \rho \rangle$ of ∼300 mg/mL varies by less than 15% between conditions (Fig. 2B), in agreement with previous work (14–16). Therefore, population averages of $\langle S/V\rangle$ and $\langle S/M\rangle$ are correlated between different steady-state growth conditions.

Fig. 2.

Cells increase cell-surface area but not cell volume in proportion to dry mass. (A and B) Snapshots of nondividing WT cells (MG1655) in different media at 30° C. (A) Phase-contrast images. (B) Dry-mass density (white circles = median; gray rectangles = interquartile range) and CV. (C) Length dependencies of dry-mass density, surface-to-volume ratio, surface-to-mass ratio, and width. Dashed lines: model prediction for spherocylinder with constant $\langle S/M\rangle$ and $\langle W\rangle$. (D and E) Timelapse of filamenting cells (S290) in MM + glucose + CAA. (D) Length dependency of dry-mass density. (E) Relative rates of volume, mass, and surface area (${\lambda }_X=\text{d}\left(\log X\right)/\text{d}t;X=V,M,S$) and model (dashed line). (F) Dry-mass density during time lapse of dividing cells (MG1655) in MM + glucose + CAA. (G–I) Snapshots of nondividing C. crescentus cells (CB15) grown in PYE. (G) Phase-contrast image. (H) Dry-mass density distribution as in B. (I) Length dependency of normalized dry-mass density, surface-to-mass and surface-to-volume ratios, and width in nondividing cells (solid lines + shadings = average ± 2 × SEM).

While mass density shows no systematic dependency on growth rate, mass density is reduced for the richest growth medium in both strains. We confirmed these variations by refractive-index modulation (SI Appendix, Fig. S7).

Cell-Length–Dependent Variations of Mass Density Support Surface-to-Mass Coupling.

Remarkably, cell-to-cell variations of dry-mass density within different nutrient conditions are smaller than 3 to 6% (coefficient of variation [CV]) (Fig. 2B). Yet, part of the variations between nondividing cells (without visible constrictions) can be explained by a deterministic decrease of density as a function of cell length (Fig. 2 C, Upper Left), different from previous hypotheses (15, 17) but consistent with previous reports of mass-density dependency on single-cell volume (32).

To understand the seemingly complex dependency of mass density on length, we investigated the possibility that cells might expand surface area, rather than volume, in direct proportion to biomass. If cells grew in surface as they grow in mass, the surface-to-mass ratio should remain constant, while density should vary in proportion to the surface-to-volume ratio according to Eq. 1. Rod-shaped cells resemble spherocylinders of length L and width W. The surface-to-volume ratio thus decreases as a function of L according to

$$S/V=4/\left[W(1-W/3L)\right].$$ [2]

Indeed, the length-dependent behavior of both S/V and $\rho$ are well-described by a model spherocylinder of fixed width $\langle W\rangle$ and surface-to-mass ratio $\langle S/M\rangle$ (Fig. 2 C, Upper Left and Upper Right). On the contrary, S/M shows no systematic dependency on length (Fig. 2 C, Lower Left), in agreement with our hypothesis. Furthermore, W is also independent of length (Fig. 2 C, Lower Right) as previously shown (33). For our model, possible correlations between cell-to-cell variations of S/V and ${\left(S/M\right)}^{-1}$ can be ignored, as fluctuations in either quantity are small (SI Appendix, Supplementary Note 2). These observations suggest that cell volume is controlled indirectly during steady-state growth through the robust coupling of surface to mass.

To study differences between volume and mass growth directly, we inhibited cell division by expressing the protein SulA (34) and monitored growth in time-lapse microscopy (Movie S1). First, we confirmed that dry-mass density decreases with cell length (Fig. 2D and SI Appendix, Fig. S8 A–C), in agreement with single-cell snapshots (Fig. 2C) and immersive refractometry (SI Appendix, Fig. S9). Next, we observed that mass growth rate is roughly constant as a function of time (Fig. 2E), in agreement with ref (35). Surface, and mass grow nearly at the same constant rate. On the contrary, volume growth rate ${\lambda }_V=\text{d}\left(\text{log}V\right)/\text{d}t$ of short cells exceeds the constant mass growth rate ${\lambda }_M=\text{d}\left(\text{log}M\right)/\text{d}t$ by about 10%, and subsequently decreases with increasing length. This observation is a direct consequence of the length-dependent decrease of dry-mass density, as predicted by our model (SI Appendix, Supplementary Note 2). In dividing cells, $\rho$ increases toward the end of the cell cycle due to the increase of $\langle S/V\rangle$ during septum formation (Fig. 2F and SI Appendix, Fig. S8 E and F).

To study whether surface growth is conserved across evolutionarily distant bacteria, we also studied a different gram-negative bacterium, Caulobacter crescentus grown in peptone yeast extract (PYE) medium (Fig. 2 G–I). As in E. coli, mass density shows relatively small variations from cell to cell (CV = 7%) (Fig. 2H) but decreases systematically with cell length (Fig. 2I), contrary to previous assumptions (17). This decrease is mainly caused by a decrease of S/V of similar relative magnitude, similar to E. coli (Fig. 2C). Interestingly, S/M increases mildly with length, possibly because of the well-described secretion of capsule, which is likely not measured by our method. Capsule is secreted in a cell-cycle–dependent manner by stalked cells (36), which are longer than swarmer cells on average. If cells maintain the ratio of surface area to total dry mass (cellular mass plus capsule) constant, S/M is expected to increase with length, which is indeed observed (Fig. 2I).

In conclusion, surface area is coupled to dry mass, independently of length-dependent changes of the surface-to-volume ratio. In consequence and contrary to previous suggestions (15, 17), dry-mass density and volume growth rate vary systematically during the cell cycle.

Surface-to-Mass Coupling Is Robust with Respect to Drug-Induced Changes of Cell Dimensions.

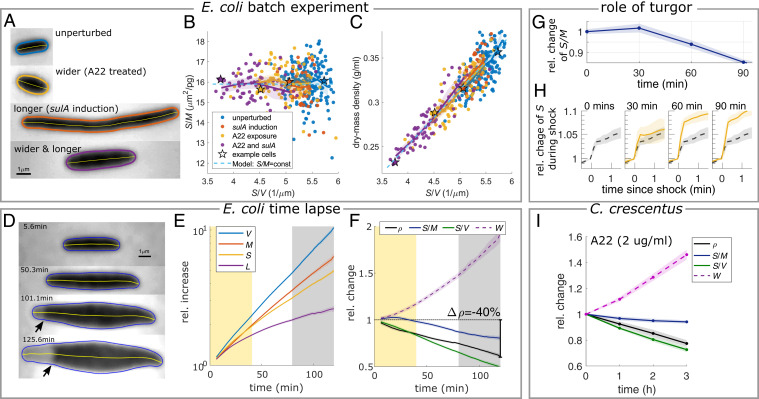
Next, we tested whether the observed surface-to-mass coupling was also robust with respect to nonphysiological perturbations of cell dimensions. To increase cell width and decrease S/V in E. coli, we transiently inhibited the peptidoglycan-inserting multienzyme Rod complex responsible for rod-like cell shape using the small molecule A22 (37, 38) and took snapshots after one mass-doubling time (∼70 min) (Fig. 3A). To decrease S/V further, we additionally inhibited division. S/M remains constant over an almost twofold range of single-cell S/V values (Fig. 3B), while mass density changes in proportion to S/V (Fig. 3C).

Fig. 3.

Perturbation of cell shape demonstrates robust surface-to-mass coupling despite variations of dry-mass density. (A–C) Snapshots (phase contrast) (A), surface-to-mass ratio (B), and dry-mass density (C) of cells (S290) grown for one mass-doubling time after inducing a shape change through the rod-shape–perturbing drug A22 and/or sulA expression in MM + glucose + CAA batch culture. The stars and colors in B and C correspond to specific cells in A. (D–F) Timelapse of filamenting cells (S290) in RDM as a function of time since A22 treatment. (D) Snapshots (phase contrast) demonstrate detachment of the cytoplasmic membrane (arrows) and drop of turgor. (E) Relative increase of volume, mass, surface, and length. (F) Relative change of mass density, S/M, S/V, and width. Shaded regions: S/M constant (yellow) and plasmolysis (gray). (G and H) Contribution of turgor to long-term changes of S/M for WT cells grown in RDM. (G) Relative change of S/M at different time points during A22 treatment and sulA induction (S290) from single-cell snapshots. (H) Relative change of surface area after hypo-osmotic shocks in fluidic channels (250 mOsm, through 10× dilution of growth medium) applied to cells extracted at the indicated time points in G (solid, yellow), in comparison to control cells (dashed, black). (I) Snapshots of C. crescentus (CB15) treated with A22 (2 μg/mL) for different durations in PYE. Relative change of mass density, S/M, S/V, and width (SI Appendix, Table S4 has conversion factors to absolute values; Solid lines + shadings = average ± 2 × SEM).

We also followed single-cell growth during time-lapse microscopy. Drug treatment leads to rapid cell widening and a concomitant drop of $\langle S/V\rangle$ (Fig. 3 D–F) (for a control, see SI Appendix, Fig. S10 A–C), with very little cell-to-cell variation (SI Appendix, Fig. S11A). Despite the severe perturbation, $\langle S/M\rangle$ decreases by less than 3% during one mass-doubling time of ∼40 min (Fig. 3F). Accordingly, dry-mass density drops (Fig. 3F).

At longer timescales, $\langle S/M\rangle$ slowly decreases, up to about 20% after 90 min (Fig. 3F), as also reflected by a gradual reduction of the surface growth rate (SI Appendix, Fig. S12). At the same time, the cytoplasmic membrane detaches from the cell envelope (Fig. 3D and Movie S2), which demonstrates a drop of turgor, possibly in response to cytoplasmic dilution. Remarkably, cells continue to grow their surface area for a long time after plasmolysis has occurred (Movie S2).

Sudden loss of turgor is known to cause the cell envelope (outer membrane and cell wall) to shrink by about 10% in width and length, respectively (24), which corresponds to a reduction of surface area by about 20%. We thus hypothesized that the gradual decrease of $\langle S/M\rangle$ is due to a gradual reduction of turgor, while enzymatic envelope expansion proceeds at an unperturbed rate. To test this hypothesis, we grew cells for different durations of A22 treatment and filamentation in liquid culture and took single-cell snapshots, like those in Fig. 3A. In agreement with the time-lapse movie, $\langle S/M\rangle$ remains constant for about one mass-doubling time and subsequently slowly decreases (Fig. 3G). We then exposed cells taken from the same culture to hypo-osmotic shocks in fluidic channels and measured the elastic stretch of cell-surface area (Fig. 3H). Cells treated for 60 or 90 min show a much stronger increase (8 to 10%) than untreated cells or cells treated for only 30 min (4 to 5%) (for changes of width and length, see SI Appendix, Fig. S13), confirming that turgor pressure has decreased. Furthermore, the difference in elastic response of about 5% after 60 min can quantitatively account for a reduction of $\langle S/M\rangle$ by the same relative magnitude (Fig. 3G). On longer timescales (>90 min), reduced surface growth rate might also contribute to a reduction of $\langle S/M\rangle$.

To test whether the observed constancy of S/M on the generation timescale is also observed in other bacteria, we took snapshots of C. crescentus, also treated with A22 (Fig. 3I). As expected, $\langle S/V\rangle$ decreases due to a strong increase of width, and mass density drops by a similar relative amount as $\langle S/V\rangle$. On the contrary, $\langle S/M\rangle$ decreases only mildly, possibly due to a decrease of turgor. Thus, C. crescentus behaves qualitatively similarly to E. coli.

Independence of envelope expansion on turgor pressure on short timescales, referred to as “stored growth,” was also reported previously (24). Our findings demonstrate that cells grow their envelopes in proportion to mass, irrespectively of dry-mass density, cell dimensions, turgor pressure, and perturbations of the MreB-based cell-wall insertion machinery, on the generation timescale. This behavior is conserved across evolutionarily distant gram-negative bacteria.

Elongation Rate Is a Function of Surface Growth and Cell Widening.

During A22 treatment of E. coli, cell elongation rate ${\lambda }_L=\text{d}(\log L)/\text{d}t$ is reduced (Fig. 3F), suggesting that not only volume but also length is indirectly controlled through surface and width. This dependency is further supported by correlations between rates of elongation, widening, and surface expansion in unperturbed single cells (SI Appendix, Fig. S14): With surface area $S\approx \pi WL$, the elongation rate is given by ${\lambda }_L\approx {\lambda }_S\hspace{0.17em}-\hspace{0.17em}{\lambda }_W$, where ${\lambda }_{S,W}=\text{d}\left(\log S,W\right)/\text{d}t$. We found that fluctuations in elongation rate ${\lambda }_L$ are proportional to fluctuations in surface rate ${\lambda }_S$ and inversely proportional to fluctuations of widening rate ${\lambda }_W$, while ${\lambda }_S$ and ${\lambda }_W$ are uncorrelated. These observations support the dependency of elongation rate on widening and surface growth, while rates of widening and surface growth are seemingly independent of each other.

During Nutrient Shifts, Cell Widening Leads to Changes of Dry-Mass Density, While S/M Remains Constant.

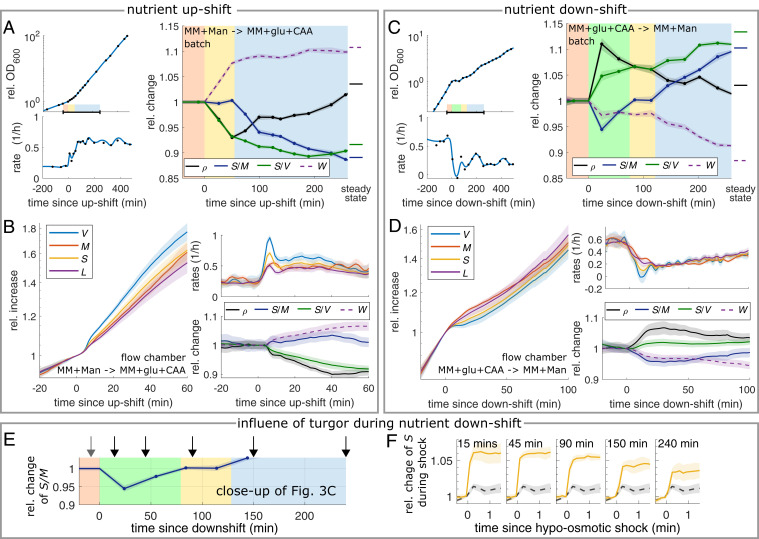
E. coli shows natural variations of the surface-to-volume ratio between different growth media (Fig. 2C), predominantly due to differences in cell width (SI Appendix, Fig. S6). We therefore studied a nutrient upshift from a minimal medium (MM) containing mannose as carbon source (MM + mannose) to the same medium containing glucose and casamino acids (CAA) (MM + glucose + CAA) in batch culture and took regular single-cell snapshots (Fig. 4A). Rapidly after the shift, mass growth rate increases and $\langle S/V\rangle$ decreases, the latter predominantly due to changes of cell width. Yet, $\langle S/M\rangle$ and the corresponding single-cell distribution remain constant during about 0.5 mass doublings (∼50 min) (Fig. 4A and SI Appendix, Fig. S15). According to Eq. 1, mass density drops in proportion to $\langle S/V\rangle$. Only afterward, $\langle S/M\rangle$ starts to decrease, reaching its new steady-state value after ∼3.3 mass doublings. Concomitantly, mass density is nearly restored.

Fig. 4.

Nutrient shifts confirm robust surface-to-mass coupling on the generation time scale, despite variations of growth rate, dry-mass density, and turgor. (A) Nutrient upshift from MM + mannose to MM + glucose + CAA in batch culture of WT cells (MG1655). (Left) Growth curve and relative rate. (Right) Relative changes of dry-mass density, surface-to-mass and -volume ratios, and width from single-cell snapshots. Shaded backgrounds: prior to shift (red), S/M constant (yellow), and S/M approaching new steady state (blue). (B) Single-cell timelapse of the same nutrient shift as in A applied to filamenting cells (S290) in flow chamber. Relative increase (Left) and single-cell rates (Top Right) of volume, mass, surface, and length. (Bottom Right) Same quantities as in A. (C and D) Nutrient downshift from MM + glucose + CAA to MM + mannose in batch culture (D) and flow chamber (E). Otherwise same conditions as in A and B. Shaded backgrounds: for red, yellow, and blue, see A; green: S/M is decreased due to turgor pressure drop. (E and F) Hypo-osmotic shocks (250 mOsm, through 10× dilution of growth medium) of WT cells measured at different time points after a nutrient downshift as in C. (E) Average of S/M already shown in C, with arrows indicating time points of sample preparation for osmotic shocks in flow chambers. (F) Relative change of surface area at different time points (solid, yellow) in comparison to control before nutrient shift (dashed, black) (SI Appendix, Table S4 has conversion factors to absolute values; solid lines + shadings = average ± 2 × SEM of n > 460 cells (up-shift) and n > 88 cells (down-shift) per time point).

We confirmed the short-time behavior in single-cell time lapses (Fig. 4B and SI Appendix, Fig. S11 and Movie S3). Apart from a spike in growth rates during the first 10 min discussed in the subsequent paragraph, cell volume increases about 15% faster than cell mass during about 50 min after the shift. This difference leads to a 10% reduction of mass density, similar to the batch experiment. Despite slight variations of $\langle S/M\rangle$, possibly due to cell filamentation or attachment to the microscopy chamber, $\langle S/M\rangle$ is equal to its preshift value after 50 min, in agreement with the batch experiment. We observed the same qualitative behavior in a different nutrient upshift, from MM + glucose to Rich Defined Medium (RDM) (SI Appendix, Fig. S16 and Movie S4).

The initial spike in rates of surface, length, and volume expansion corresponds to a rapid increase of length and width by about 1% each (SI Appendix, Fig. S17). This expansion is reminiscent of a hypo-osmotic shock with NaCl (39) (SI Appendix, Fig. S17 C and F). This finding suggests that cytoplasmic turgor pressure has increased. This is remarkable, given that we maintained medium osmolality constant between the two different growth media, and none of the exchanged media components are known to penetrate the cytoplasmic membrane freely. Thus, turgor pressure depends on the metabolic state of the cell. Accordingly, the initial surface expansion constitutes an elastic response, while the subsequent cell-diameter increase requires plastic cell-wall expansion. We will come back to the role of turgor in the section Plastic Changes of Cell Width during Osmotic Ramps and Nutrient Shifts Are Likely Driven by Variations of Turgor.

In conclusion, surface growth remains robustly coupled to mass growth despite variations of mass growth rate, cell dimensions, and dry-mass density for about 0.5 mass doublings, while S/V changes rapidly and nearly inversely proportional to width. However, on long timescales, the surface-to-mass ratio changes such that dry-mass density is nearly restored (Fig. 2).

Our findings demonstrates that S/V varies independently of $\rho$, S/M, and growth rate. This independence is further supported by the absence of single-cell correlations between rates of cell widening and mass density during unperturbed steady-state growth (SI Appendix, Fig. S18).

Nutrient Downshift Confirms Independence of S/V and S/M and Demonstrates a Nutrient-Dependent Change of Turgor.

We also investigated the dynamics of shape and mass during a corresponding nutrient downshift, both through time-lapse and batch-culture experiments (Fig. 4 C and D and SI Appendix, Fig. S15 and Movie S5). Similar to the upshift, we identified three phases. Within about 10 min, cells partially shrink in volume (SI Appendix, Fig. S11), suggesting that turgor is quickly reduced, while medium osmolality remains constant. We observed a similar volume reduction upon depletion of ATP and GTP using 2,4-dinitrophenol (DNP) (SI Appendix, Fig. S19 and Movie S6), in agreement with previous reports (40). Plasmolysis was recently also reported upon complete starvation (41). Therefore, turgor depends on the nutrient-dependent energy state of the cell.

About 100 min (0.5 doublings) after the nutrient shift, $\langle S/M\rangle$ reaches its preshift value (Fig. 4 C and D). We therefore reasoned that the transient decrease of $\langle S/M\rangle$ is mainly due to the reduction of turgor, while surface material and dry mass increase at equal rates. In support of this hypothesis, we observed that cells stretched more in response to a hypo-osmotic shocks after nutrient downshift (∼8%) than before (∼1%) (Fig. 4F). The difference in elastic stretch of about 7% is identical to the reduction of $\langle S/M\rangle$ observed 25 min after the shift. While we observed a partial initial recovery within about 45 min, the amount of stretch remains elevated for at least 240 min after the shift, suggesting that turgor is reduced for a long time after the shift.

Cell diameter and $\langle S/M\rangle$ reach their new steady-state values after about 3.5 and 6 h, respectively. These observations support the independence of S/V and S/M already observed in the upshift experiments.

In the following two sections, we address potential mechanisms underlying the robust surface-to-mass coupling and the nutrient-dependent changes of width, respectively.

Surface-to-Mass Coupling Supports an Empirical Surface-Growth Law.

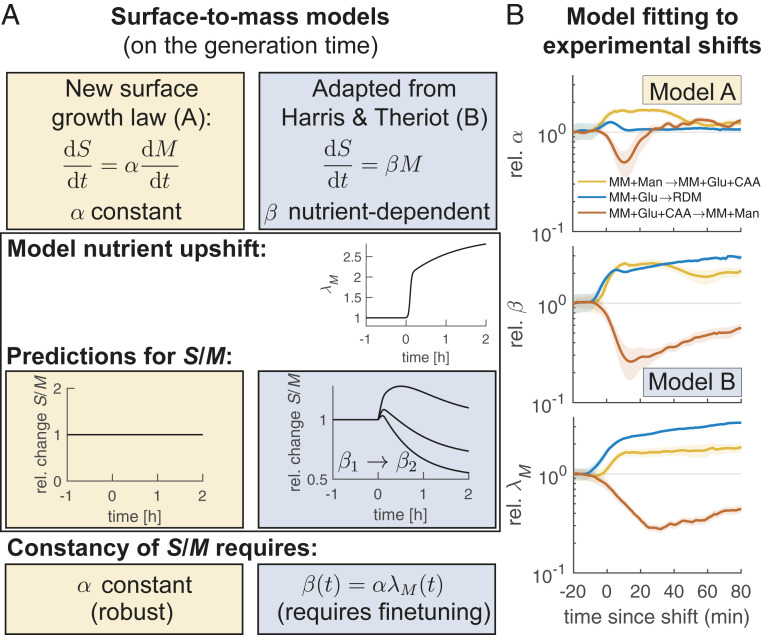
The robust coupling between surface and mass after sudden growth-rate changes gives support to a simple surface-growth law of the form

$$\text{d}S/\text{d}t=\alpha \hspace{0.17em}\text{d}M/\text{d}t,$$ [3]

where $\alpha =\text{d}S/\text{d}M$ is a coupling constant. During steady-state exponential growth α_ss = (S/M)_ss. The model predicts that $S/M$ remains constant during growth-rate shifts, as long as $\alpha$ remains constant (see Fig. 5A for a hypothetical upshift). Consistently with our observations of near-constant $S/M$ during three growth-rate shifts (Fig. 4 and SI Appendix, Fig. S16), the empirical value of $\langle \alpha \rangle =\langle \text{d}S/\text{d}M\rangle$ also remains roughly constant (Fig. 5B). Specifically, $\langle \alpha \rangle$ is found within ∼20% of its preshift value after 10 to 50 min, depending on the shift, and then remains constant for the whole observation window of 0.5 to 1 mass-doubling times.

Fig. 5.

Robust coupling of surface and mass growth rates during nutrient shifts supports an empirical surface-growth law. (A) Math box. (Top) Two alternative models of surface growth, the surface-growth law proposed here (model A), and a model adapted from Harris and Theriot (17) (model B). (Middle) During a model nutrient shift, S/M remains constant according to model A and changes in a $\beta$-dependent manner according to model B. (Bottom) S/M is robustly maintained according to model A but requires finetuning according to model B. (B) Time-dependent coupling constants $\alpha =\text{d}S/\text{d}M$ (Top) and $\beta =1/M(\text{d}S/\text{d}t)$ (Middle) obtained by fitting models A and B, respectively, to three experimental nutrient shifts (Fig. 4 B and D and SI Appendix, Fig. S16). (Bottom) Mass growth rate ${\lambda }_M$. Apart from transient changes, $\alpha$ varies little before and after the shift, while $\beta$ changes nearly proportionally to ${\lambda }_M$ (solid lines + shadings = average ± 2 × SEM).

Previously, Harris and Theriot suggested a different surface-growth model, of the form $\text{d}S/\text{d}t=\beta \text{'}V$ (17), and more recently Shi et al. suggested a time-delayed variant of the same model (42). Both works implicitly used cell volume to measure relative changes of the abundance of proteins that contribute to surface growth, but this approach only works if protein density is a constant. Since mass density is apparently not constant upon changes of $\langle S/V\rangle$ both in E. coli and C. crescentus, a mass-based model of surface growth appears generally as more appropriate. We then wondered whether the initial model of Harris and Theriot could be rescued by replacing volume by mass, according to $\text{d}S/\text{d}t=\beta M$ (Fig. 5A). Mathematically, the latter equation is equivalent to Eq. 3, with $\beta =\alpha {\lambda }_M$, where ${\lambda }_M$ is the mass growth rate. However, since $\alpha$ is roughly constant during three different growth-rate shifts, $\beta$ must change roughly in proportion to ${\lambda }_M$ (Fig. 5B). Therefore, Eq. 3 (Model A in Fig. 5) is apparently the more-appropriate model for the nutrient shifts considered in our work if compared to Model B (or if compared to volume-based models). It remains to be seen whether the growth law suggested here (Model A) also applies during more-complex shifts, such as outgrowth from stationary phase (17, 42).

On timescales longer than one mass doubling, $\alpha$ approaches a new steady-state value (SI Appendix, Fig. S20). During the upshift experiment (Fig. 4A) this happens monotonically within about one mass-doubling time, while the nutrient downshift (Fig. 4C) shows a transient overshoot.

The robust relationship between the increase of surface and mass on the generation timescale suggests that a fraction $s=\alpha {\rho }_S$ of any dry-mass increment dM is devoted to surface expansion, where ${\rho }_S$ is the area-mass density of one or multiple surface-limiting envelope components. It is generally thought that cell-envelope expansion in bacteria is limited by cell-wall synthesis (17, 43, 44). We found that the inhibition of the cell-wall–synthesizing Rod complex leaves cell-surface expansion nearly unperturbed (Fig. 3E), even though this perturbation is known to cause a strong reduction of the rate of peptidoglycan insertion (45, 46). Cell-wall synthesis is therefore likely not rate limiting for surface growth, in contrast to our recent reports on the gram-positive bacterium Bacillus subtilis (47), and a surface-limiting envelope component potentially responsible for the surface-growth law (Eq. 3) remains to be identified.

Plastic Changes of Cell Width during Osmotic Ramps and Nutrient Shifts Are Likely Driven by Variations of Turgor.

A major source of transient mass-density variations after nutrient shifts are rapid changes of cell width. Since nutrient shifts also display unexpected and fast variations of turgor pressure at same medium osmolality as explained in the section During Nutrient Shifts, Cell Widening Leads to Changes of Dry-Mass Density, While S/M Remains Constant, we wondered whether changes of width might be driven by changes of cytoplasmic turgor, as previously hypothesized (17, 48). We therefore continuously changed medium osmolality $c_{\text{ext}}\left(t\right)$ by removing or adding NaCl through diffusion (Fig. 6A and Movie S7). Using osmolality ramps rather than sudden osmotic shocks, we prevented rapid osmoadaptation. As hypothesized, removing or adding NaCl leads to an increase or decrease of cell width, respectively (Fig. 6B), while biomass growth rate is only mildly affected on the generation timescale (SI Appendix, Fig. S21). Interestingly, the time-dependent rate of cell widening $\text{d}W/\text{d}t$ is strongly correlated with the osmolality ramp rate $\text{d}{c}_{\text{ext}}/\text{d}t$ (Fig. 6C). We confirmed this behavior using an even-stronger ramp in Luria-Bertani (LB) Miller growth medium (SI Appendix, Fig. S21). According to a simple model of osmoadaptation (SI Appendix, Supplementary Note 3), turgor pressure is roughly proportional to the osmolality ramp rate, $P\simeq P_0+\zeta \frac{\text{d}{c}_{\text{ext}}}{\text{d}t}$. Here, $P_0$ is the adapted pressure, and $\zeta =RT/k$ is inversely proportional to the osmoadaptation rate $k$ (R is gas constant, and T is temperature). Accordingly, our observations are compatible with a turgor-dependent rate of cell-width changes of the form

$$\frac{\text{d}W}{\text{d}t}\propto P-P_0,$$ [4]

where $P$ and $P_0$ are the current and adapted turgor pressures, respectively. After long-term osmoadaptation, cell width is nearly constant between osmotic conditions (SI Appendix, Fig. S21B), compatible with previous reports (49).

Fig. 6.

Cell-diameter changes in response to osmolality ramps. (A) Three different diffusion-limited ramps of external osmolality c_ext (for implementation, see SI Appendix, Fig. S21) lead to sustained variations of turgor pressure, despite osmoadaptation. (B) Normalized cell width of filamenting cells (S290) grown in in RDM on agar pads increases or decreases in response to hypo- or hyperosmotic gradients, respectively. Colors correspond to ramps in A. Initial drop of width and partial recovery within 20 min during hyperosmotic ramp likely represent elastic response and partial osmoadaptation, while subsequent decrease represents plastic remodeling. (C) The rate of cell widening (solid lines) correlates with the predicted rate of osmolality change (dashed lines), which in turn is expected to be approximately proportional to turgor (SI Appendix, Supplementary Note 3) (SI Appendix, Table S4 has conversion factors to absolute values; solid lines + shadings = average ± 2 × SEM).

Since we observed rapid changes of turgor pressure followed by changes of cell width after nutrient shifts (Fig. 4 and SI Appendix, Figs. S11 and S17), our findings suggest that changes of width upon nutrient shifts might also be driven by variations of turgor. However, at long times, other processes likely also contribute to cell width.

Discussion

In conclusion, we found that the rates of surface expansion and biomass growth are robustly coupled on the generation timescale, independently of instantaneous changes of growth rate, cell dimensions, or turgor. Changes of S/M observed after more than one mass-doubling time of A22 treatment or immediately after nutrient shifts are likely caused by changes of turgor pressure, while plastic envelope growth continues in synchrony with mass growth. Our experiments in C. crescentus suggest that surface-to-mass coupling is conserved across evolutionarily distant gram-negative bacteria.

Contrary to previous assumptions (17), cell width is controlled independently of mass density or S/M on the generation timescale. We thus identified two independent variables that are predominantly responsible for cell volume and dry-mass density: cell width and the coupling constant $\alpha$, which relates surface expansion to biomass growth (Model A in Fig. 5). All other variables (surface area, volume, length, and mass density) depend on these two and on the processes of mass growth and cell division. Additional changes of volume and mass density are caused by changes of turgor pressure. Interestingly, turgor pressure affects cell dimensions not only through immediate elastic stretching of the cell envelope but also through a process of plastic changes of cell width.

On long timescales, we observe that $\langle S/M\rangle$ and $\langle S/V\rangle$ are correlated (SI Appendix, Fig. S6 F and G), which guarantees that mass density is almost constant across different nutrient environments (Fig. 2B). How these correlations come about and whether they are maintained under different long-term environmental perturbations remains to be investigated.

How is the surface-growth law (Eq. 3) implemented mechanistically? Previously, it has often been assumed that cell-wall insertion is rate limiting for surface growth (17, 43, 44). Cell-wall insertion is likely not the rate-limiting process for cell-envelope expansion in E. coli, since Rod-complex arrest does not inhibit surface expansion (Fig. 3) while causing a strong reduction of peptidoglycan insertion (45, 46). In future work, we will therefore test peptidoglycan and other envelope components for their potentially limiting role for envelope expansion in E. coli and other bacteria, similar to our recent work in B. subtilis (47).

Independently of the molecular mechanism, the robust coupling between surface growth and mass growth might be a general design feature for walled cells. Indeed, our recent work in B. subtilis (47) suggests that the surface-to-mass coupling is conserved in gram-positive bacteria, despite their fundamentally different envelope architectures. Recent cell-cycle–dependent variations of dry-mass density in fission yeast are also compatible with this picture (50). It will thus be interesting to study the relationship between surface and mass in other organisms and specifically in spherically shaped bacteria, which undergo more-dramatic variations of S/V during the cell cycle.

Methods

Strain Construction.

For a strain list, see SI Appendix, Table S1. To obtain strain S290 (MG1655/pDB192), the plasmid pDB192 (bla P_lac::sulA) [gift from Jun laboratory (University of California San Diego, La Jolla, CA) (51)] was transformed into MG1655 as described (52).

Sample Preparation.

E. coli cell cultures were grown to exponential phase in LB Miller, defined 3-(N-morpholino)propanesulfonic acid (MOPS) buffered MM with different carbon sources, or MOPS RDM at 30 °C, as detailed in SI Appendix, SI Methods and Table S3. Antibiotics were added as needed. Osmolality of MM and RDM was adjusted using NaCl to be 280 ± 10 mOsm. Osmolality of LB was measured to be 390 mOsm. Before microscopy, we kept cultures in exponential phase for >10 population doubling times. To inhibit division, sulA was induced with 1 mM isopropyl β-d-thiogalactoside (IPTG) during microscopy. C. crescentus cell cultures were grown from an individual colony in PYE (0.2% peptone, 0.1% yeast extract, and 0.007% calcium chloride dihydrate wt/vol) at 30°C to exponential phase. For microscopy, cells were either sandwiched between an agarose pad and the coverslip or immobilized in flow chambers using APTES ((3-Aminopropyl)triethoxysilane). While growth media and temperature are maintained constant throughout experiments presented in Fig. 2 and SI Appendix, Fig. S10, the change from liquid culture to growth on a solid support and the inhibition of division can be sources of perturbation, which are likely responsible for slight variations of average width and growth rates (SI Appendix, Figs. S8 and S10). For immersive refractometry, we changed the refractive index of the medium using bovine serum albumin (BSA) or dextran (see SI Appendix, SI Methods for details).

Microscopy and Image Analysis.

Microscopy was carried out on an inverted phase-contrast and epi-fluorescence microscope equipped with a custom-designed module for SLIM (25) (SI Appendix, Figs. S2 and S3). Microscopy and our image-analysis pipeline for cell dimensions and cell mass are described in detail in SI Appendix, SI Methods and Supplementary Note 1.

In brief, quantitative phase images are obtained from four independent phase-contrast images (25), each with an additional $\pi /2$ phase shift of the nonscattered light (SI Appendix, Fig. S2), which in turn is imposed by a spatial light modulator (SI Appendix, Fig. S3).

Cell dimensions are obtained from phase-contrast images using the MATLAB-based Morphometrics package (26). To be able to correct for differences between phase-contrast–based contours and physical cell contours, we conducted independent measurements of cells stained with the fluorescent outer-membrane stain FM4-64 (53). Those cells allowed us to measure physical cell contours based on FM4-64 and fluorescent-image simulations using BlurLab (26) (SI Appendix, Fig. S1A). Systematic differences between phase-contrast and physical cell contours then allow us to correct phase-contrast–based contours in all experiments. Surface area and volume are calculated from corrected cell contours assuming cylindrical symmetry around the cell axis.

We obtain cell mass from the integrated phase shift of individual cells (Fig. 1B). Due to the finite size of the phase ring in the microscope, the integrated phase is underestimated by about twofold (SI Appendix, Fig. S1B), with the precise attenuation depending on cell geometry. To correct for this attenuation, we computationally simulate phase-contrast images for every cell in every image based on refs. 27 and 54, assuming a homogeneous-phase object that has the same dimensions as the physical cell (SI Appendix, Fig. S1B). The simulation yields the attenuation factor, which is used to correct the experimentally measured integrated phase. All parameters of the simulation are measured. To get from integrated phase to mass, we choose a refraction increment $\gamma =0.175$ ml/g (Fig. 1B), which is based on the average molecular composition of E. coli and the individual refraction increments of its molecular components. The method is accurate (Fig. 1 D and E and SI Appendix, Figs. S4 and S5) and robust with respect to variations of the underlying assumptions. As a variant of this method, we also carried out experiments by alternating two media with different refractive indices (SI Appendix, Fig. S4). This allows us to infer dry mass and volume independently of each other and, notably, independently of accurate cell segmentation (SI Appendix, Supplementary Note 1, Section 11). See SI Appendix, Supplementary Note 1 for details about the method, accuracy, precision, and robustness.

We calculate relative rates ${\lambda }_X=\text{d}\left(logX\right)/\text{d}t$ with $X=S,W,L,M$ and coupling parameters $\hspace{1em}\alpha =\text{d}S/\text{d}M$ and $\beta ={\lambda }_M\alpha$ from dimensions and dry mass, as detailed in SI Appendix, SI Methods.

Theoretical Model of Mass Density in Elongating Cells.

To predict the behavior of dry-mass density as a function of length (Fig. 2C) and the rate of volume growth during cell elongation (Fig. 2E), we use a deterministic model of a spherocylinder of fixed width W, which maintains the ratio of S/M constant. For details, see SI Appendix, Supplementary Note 2.

Theoretical Model of Turgor Pressure.

During osmolality ramp experiments (Fig. 6), we placed a second agarose pad on top of the sample-holding agarose pad, which differ in their NaCl concentrations. We calculate the time-dependent change of osmolality based on a one-dimensional diffusion equation. To determine turgor pressure from the time-dependent osmolality curve, we then use a simple model of osmoadaptation, as detailed in SI Appendix, Supplementary Note 3.

Data Availability

Relevant information for all experiments and for plots of relative quantities are found in SI Appendix, Tables S1–S3. Single-cell data and and Matlab code are freely available at https://doi.org/10.5061/dryad.zgmsbccbz (55).